On the Existence of Neutrinos

Preprint

Article

On the Existence of Neutrinos

Altmetrics

Downloads

295

Views

107

Comments

Bryan Sanctuary^*

This version is not peer-reviewed

Submitted:

30 December 2023

Posted:

03 January 2024

Read the latest preprint version here

Alerts

Abstract

We change the symmetry of the Weak Force from SU(2) to the quaternion group $Q_8$, and discuss the solution of the Dirac equation under this group. We find that spin spacetime separates into two complementary spaces: a spin polarization spacetime of even parity states, and a spin coherence space, in the $S^3$ hypersphere, of odd parity coherent states. The former gives a 2D Dirac equation, that is a disc of polarization, and the latter gives a unit quaternion that spins the disc. Under the quaternion group, spin is a boson of spin 1 in free flight and a fermion of spin $\frac{1}{2}$ when measured. Immediately we find that a beta electron is a boson and this obviates the need for neutrinos.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

Introduction

The successes of the Standard Model are marred by problems with the Weak Force primarily with parity violation, and the role and properties of neutrinos, [1,2,3]. We suggest this questions the validity of the underlying symmetry, SU(2), from which the Weak Force properties follow, and we propose a change to the quaternion group,

Q_{8}

There are many consequences, [7], from this change, and here we show that one is that neutrinos are no longer needed to conserve energy and balance spin angular momentum in beta decay. The reason is that Q-spin is a boson in free-flight, and a fermion when measured. The quaternion group brings out the details of the wave-particle duality of spin.

To understand this change, it is first necessary to describe Q-spin. For that, one must imagine spin, not as a point particle, but as oriented in a plane, which is formed from two orthogonal spin axes, we use

e_{1}

and

e_{3}

. Technically, the symmetry change is simply accomplished by multiplying one of the gamma matrices by the imaginary number.

The geometric product of two components of the Pauli spin operator includes a bivector,

σ_{i} σ_{j} = δ_{i j} + ε_{i j k} i σ_{k}

. The first term is a totally symmetric contribution giving the polarization, and the second term is totally anti-symmetric giving the coherence. Spin is universally measured and accepted as a point particle of intrinsic angular momentum: a polarized property with two states of up and down from the vector operator,

σ

. There is no bivector in this definition, nor in the Dirac equation. Including the bivector leads to the formulation of quaternion spin, or Q-spin, [5,6], and a formal formulation of helicity. The details of much of the following description of Q-spin can be found in these papers.

One consequence of changing symmetry by adding the bivector, is the introduction of helicity as an element of reality of spin. Spin polarization and helicity are complementary properties of spin, analogous to position and momentum. Spin polarization is defined in a 2D spacetime with two spatial components, while helicity is defined in the complementary space of quaternions, which spins the axis of linear momentum either L or R. This changes the point particle description of spin, to a 2D spinning disc of angular momentum. The disc of angular momentum is a result of two orthogonal fermionic axis of spin on the same particle, each with magnetic moment of

μ

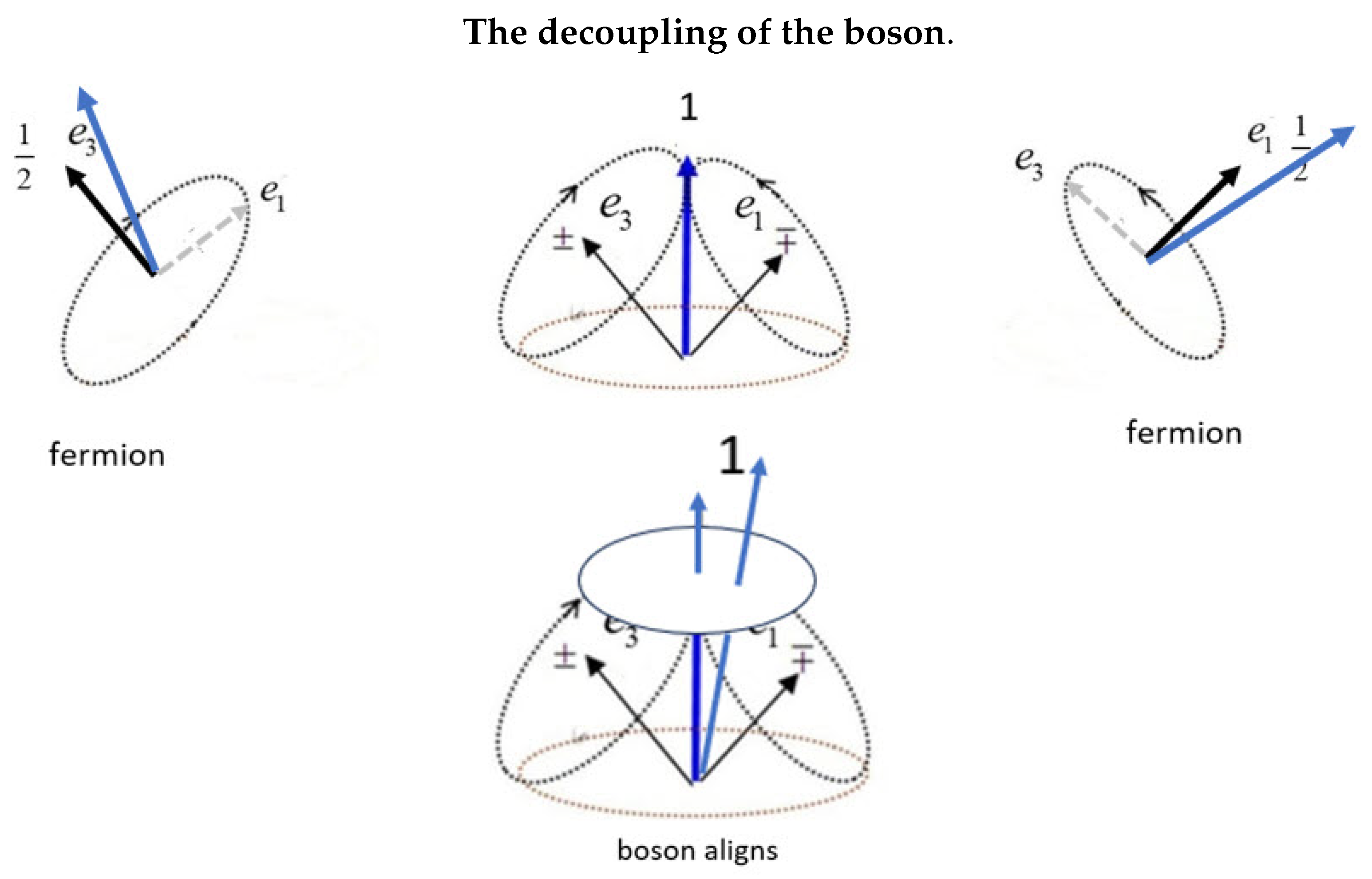
. In free-flight, the two axes are indistinguishable, and they couple to give a boson of spin 1, center upper figure of Figure 1. Upon encountering a polarizing filter, the boson decouples into a fermion.

The figure shows two ways the boson decouples. If the filter axis lies close to one of the fermionic axes, that axis will decouple and align. This is the least action principle. It is shown by the two figures on the left and right, depicting the transition from a boson to a fermion. However, if the filter lies close to the coupled boson, say within 22.5 degrees on either side of the boson, center lower of Figure 1, then the boson does not initially decouple, but persists as a spin 1 and precesses with Larmor frequency double that of the fermions, with magnetic moment of

2 μ

It is compelling that the structure of quaternion, or Q-spin, Figure 2 is geometrically identical to a photon in free-flight. That is, the photon’s two axes, which are orthogonal to the direction of linear momentum, are the magnetic and electric components. Q-spin carries two magnetic components that are also orthogonal to the direction of motion.

To justify these changes, note first that the usual point particle spin is a Pauli vector,

σ

, and its components are in Minkowski spacetime,

(I, σ_{X}, σ_{Y}, σ_{Z})

. These form the SU(2) group, and follows from the Dirac equation, [8] which is represented in the Dirac field by the gamma matrices,

(γ^{0}, γ^{1}, γ^{2}, γ^{3})

. However, this is a four dimensional field and contains two particles, one with spin

\frac{1}{2}

and, as Dirac interpreted it, the second spin

\frac{1}{2}

is the antimatter twin of the first. The main problem with this, is the energies from solving the Dirac equation are equal and opposite,

E = \pm \sqrt{m^{2} + p_{X}^{2} + p_{Y}^{2} + p_{Z}^{2}}

. The negative energy solutions caused Dirac problems which he resolved by creating a fermionic continuum of negative eneregy and filled it with electrons, leading to the sea of electron model and hole theory. This is, however, not easy to accept and is more of a rationalization than based upon sound theory. Q-spin offers an alternate explanation.

Under the quaternion group, the matter-antimatter interpretation is replaced by one particle with two axes, rather than two particles with one axis each. To see this, we create the symmetry change by multiplying one of the gamma matrices by the imaginary number. This changes the Dirac field to

(γ_{s}^{0}, γ_{s}^{1}, i γ_{s}^{2}, γ_{s}^{3})

. We include the subscript s because now the spin has structure and can be oriented in any direction, so the spacetime coordinates of Minkowski spacetime,

(β, X, Y, Z)

, are different from the body fixed coordinates of the spin spacetime, denoted by

(β_{s}, e_{1}, e_{2}, e_{3})

. We choose the direction of linear momentum to be

Y = e_{2}

so the plane formed from the two fermionic axes,

e_{1}

and

e_{3}

, is coplanar to the

X, Z

plane where the filter is oriented. We can express each axis by coordinates,

(σ_{s}^{1}, {\tilde{σ}}_{s}^{2})

and

(σ_{s}^{3}, {\tilde{σ}}_{s}^{2})

, and define the Hermitian gamma matrix by,

{\tilde{γ}}_{s}^{2} \equiv i γ_{s}^{2} = (\begin{matrix} 0 & i σ_{s}^{2} \\ - i σ_{s}^{2} & 0 \end{matrix}) = (\begin{matrix} 0 & {\tilde{σ}}_{s}^{2} \\ - {\tilde{σ}}_{s}^{2} & 0 \end{matrix})

(1)

The consequences of this change are depicted in the upper center figure in Figure 1, and shows the two spin axes coupled to give the spin 1 boson. We assert the coupling and forming of this resonance spin lowers the energy of the structure and stabilizes it. This coupling can only occur in the isotropy of free-flight when the 1 and 3 axes are indistinguishable and can be permuted without changing the spatial dependence of the Q-Dirac equation. Notice in Figure 1, center upper, that the two axes have opposite spin, and they are precessing with equal and opposite energy and in phase: they are mirror states. From the solution to the Q-spin Dirac equation the energy is given by

E = \pm \sqrt{m^{2} + p_{1}^{2} + p_{3}^{2}}

where the

p_{1}

and

p_{3}

are energies from the two axes and express internal energy of Q-spin in free flight. Since the two axes are precessing oppositely, they therefore balance each other. Q-spin resolves the negative energy problem that Dirac encountered.

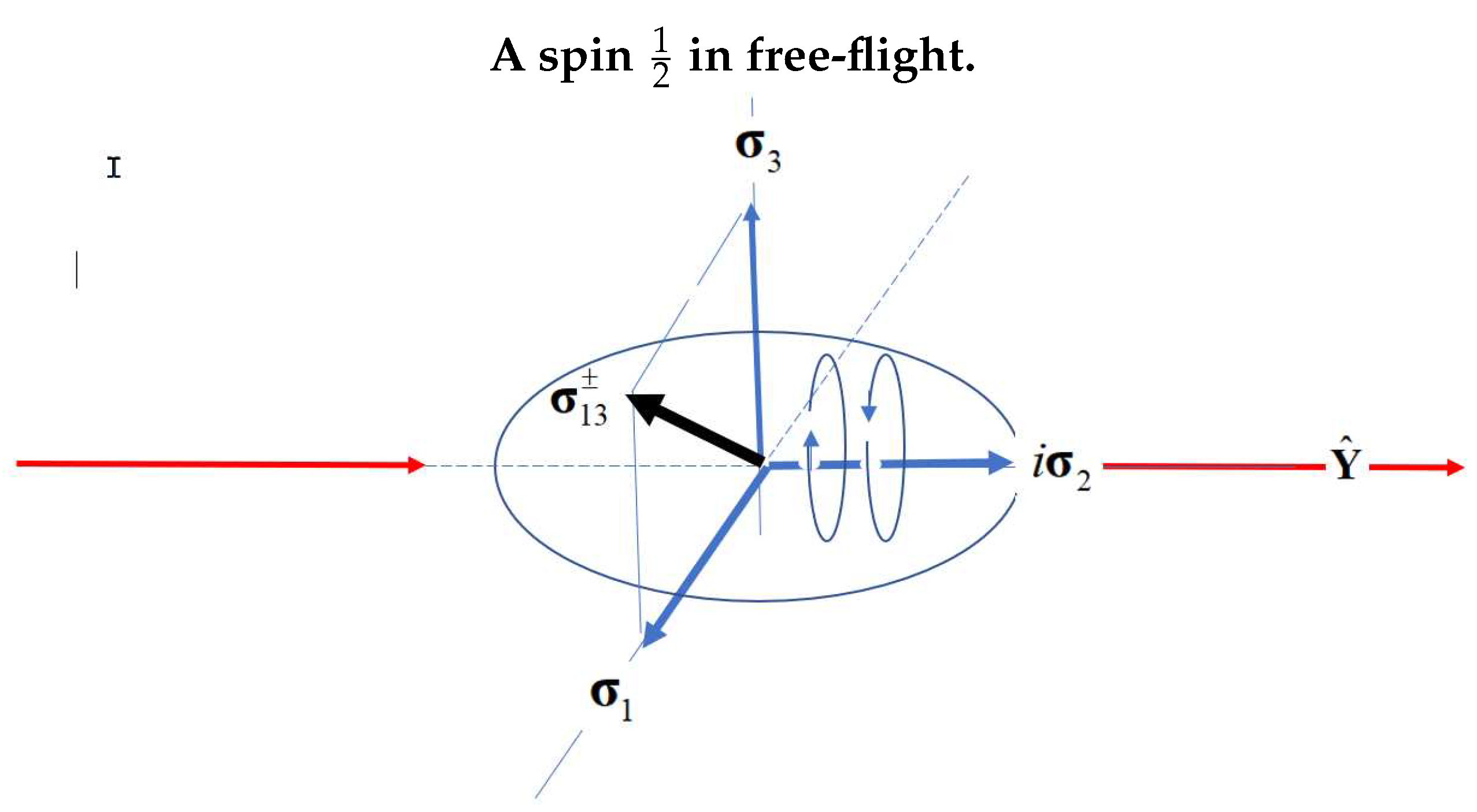
In free flight, in summary, Q-spin is one particle in the four dimensional Q-spin field of

(γ_{s}^{0}, γ_{s}^{1}, \pm {\tilde{γ}}_{s}^{2}, γ_{s}^{3})

which describes the coupling of two fermionic axes to give a boson, which is spun by the quaternion giving L or R helicity. Notice that in free flight, the axis, Y which is the direction of linear momentum, is spun by the quaternion and this averages the polarization axis to zero. In free flight, only helicity is present, and the polarization is zero. This is the wave nature of a spin.

The decoupling of the boson is governed by two properties: first the spin-spin coupling strength relative to the applied field strength; and second the orientation of the filter relative to the spin orientation.

Before the boson spin decouples, the spin-spin coupling is stronger than the filter strength. Eventually, however, the boson must decouple as it approaches closer to the filter, and it then breaks up into a fermion. We assert the fermionic axis closer to the filter will align: in the case shown in Figure 1, center lower, the

e_{1}

axis eventually aligns. It is important to know which axis aligns since they have opposite spin polarization.

Another change from the two state Dirac spin is when spin is in free-flight and when measured, it is always perpendicular to the axis of linear momentum. This is seen from Figure 1. In contrast, Dirac spin is parallel to the axis of linear momentum. Whereas for point particle spin, helicity and the direction of spin polarization are the same, Q-spin distinguish between them. In particle physics, helicity is the projection of spin along the axis of linear momentum, whereas for Q-spin this measure is always zero. Helicity spinning of the axis L and R, and spin precession to give spin up and down are independent properties.

The Dirac Equation under the Quaternion Group

Most of what is described above for Q-spin follows from the Dirac equation but with the change in symmetry using Equation (1). This gives a non-Hermitian Dirac equation,

(i γ_{s}^{0} \partial_{0} + i γ_{s}^{1} \partial_{1} \pm i {\tilde{γ}}_{s}^{2} \partial_{2} + i γ_{s}^{3} \partial_{3} - m) ψ^{\pm} = 0

(2)

and we suppress the subscript s on the derivatives. We call this the quaternion Dirac or Q-Dirac equation. The anti-commutation of the

γ_{s}^{μ}

matrices ensures that energy and mass are conserved and the Klein-Gordon equation is recovered, [9]. Note that the symmetry change also changes the signature of the Dirac field with diagonal elements in Minkowski spacetime of

η^{μ ν} = (1, - 1, - 1, - 1)

{\hat{η}}_{s}^{μ ν} = (1, - 1, + 1, - 1)

in spin spacetime.

The term

{\tilde{γ}}_{s}^{2}

is not a spatial component, but rather a time being the frequency. This dimension is the origin of quantum coherence that leads to the formulation of helicity. We find that helicity is the complementary property to spin polarization, and the two form a complementary pair with complementary spaces, a polarization spacetime and a coherence space.

In free-flight, as mentioned above, the spin is in an isotropic environment, rendering the two axes

(1, 3)

indistinguishable. Therefore, permutation with the parity operator,

P_{13}

does not change the

(1, 3)

spatial dependence in Equation (2), but the bivector,

i σ_{2} = σ_{3} σ_{1}

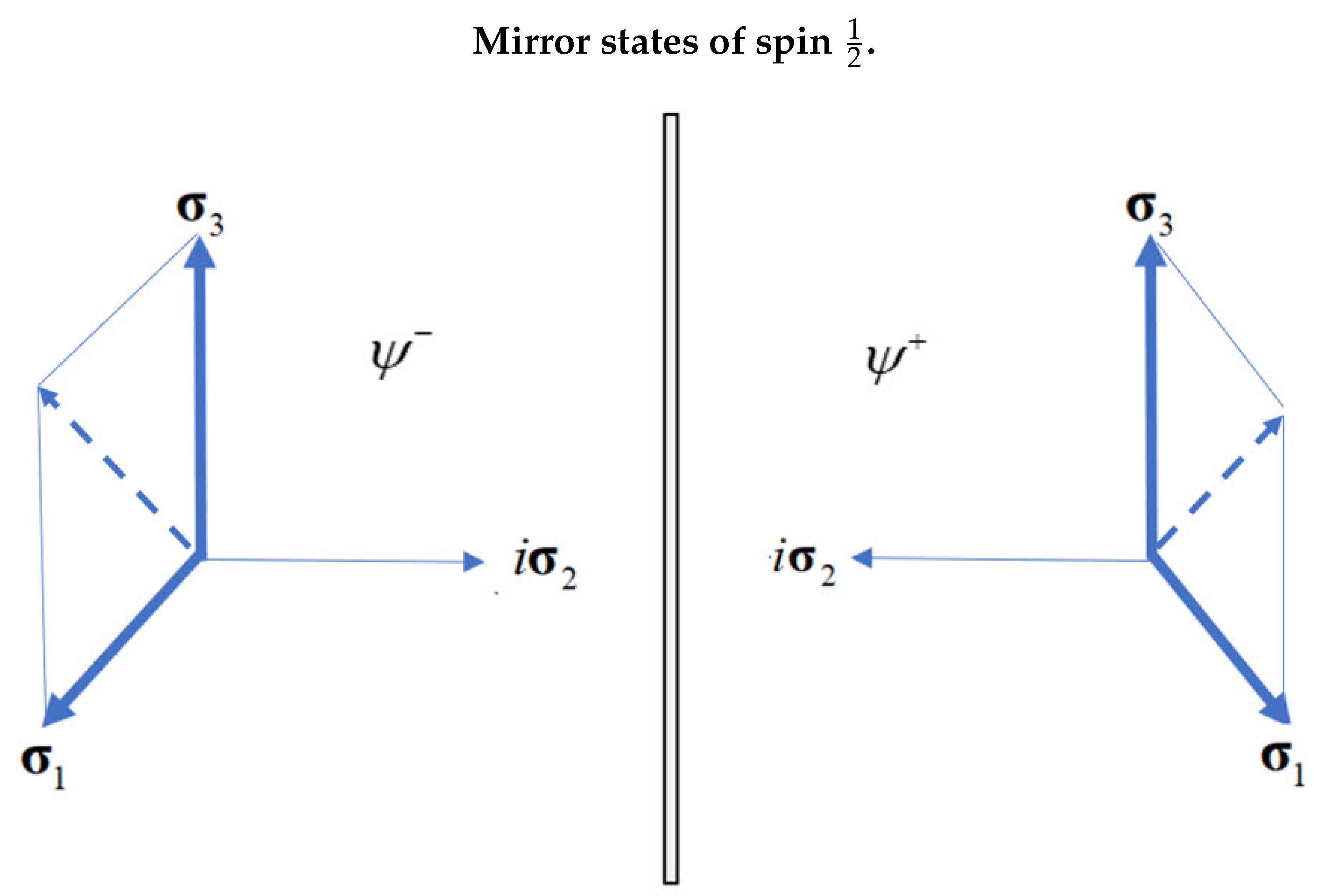
is anti-symmetric to 13 permutation. Therefore the above equation admits two solutions in left and right handed coordinate frames, which are mirror states, Figure 3,

P_{13} ψ^{\pm} = ψ^{\mp}

(3)

Figure 3 shows the mirror images of

ψ^{\pm}

with

ψ^{+}

in a right handed frame and

ψ^{-}

in a left handed frame. Note that summing the two states cancels the bivector and subtracting them cancels the (1,3) polarizations, leading to separate states that are odd and even with respect to parity,

\begin{matrix} P_{13} Ψ^{\pm} = \pm Ψ^{\pm} = \pm \frac{1}{\sqrt{2}} (ψ^{+} \pm ψ^{-}) \end{matrix}

(4)

This separates the Dirac equation into two distinct equations which describe complementary attributes of Q-spin: the first is a 2D Dirac equation in the (1,3) plane, and the second is the Weyl equation for a massless spinor,

\begin{matrix} (i γ_{s}^{' 0} \partial_{0} + i γ_{s}^{1} \partial_{1} + i γ_{s}^{3} \partial_{3} - m) Ψ^{+} & = 0 \end{matrix}

(5)

\begin{matrix} {\tilde{γ}}_{s}^{2} \partial_{2} Ψ^{-} & = 0 \end{matrix}

(6)

Concomitantly the quaternion spin spacetime separates into two distinct complementary spaces: polarization spacetime,

(0, 1, 3)

, for Equation (5); and coherent space (not spacetime)

(2)

, for Equation (6). The Hermitian part, Equation (5), is the same as the usual Dirac equation, but in two dimensions rather than three.

Without giving details, the solution to the Weyl equation is a unit quaternion. This is an element of reality but in the

S^{3}

hypersphere of quaternions which we are unable to observe. The only role of the quaternion is to spin the axis of linear momentum, thereby generating the helicity of L and R.

The 2D Dirac equation, Equation (5), gives an even parity spin which is the sum of its two mirror states as seen in Figure 3. This formulation shows the two spin

\frac{1}{2}

axes coupled to form a spin 1 boson from the resonance, and in phase, precession of the two fermionic axes in Figure 1. When encountering a polarizing field, space becomes anisotropic and the mirror states uncouple to give one axis in Figure 1 aligning with the field and the other averaging away.

In a polarizing field the boson undergoes a transition to a fermion, [6]. This is the particle nature of spin.

We conclude Q-spin epitomizes the wave-particle duality, being a boson in free flight and a fermion when measured. From the fact that Q-spin is a spinning disc, identifies it as an anyon [10] which can display both boson and fermion properties. This only works for a 2D system. Point particles or 3D structures do not act as anyons.

Beta Decay

Beta decay, [1], is fundamentally expressed as a neutron in a nucleus decaying into a proton by emitting a beta particle, a fermion electron, subscript F, and an anti-neutrino,

\begin{matrix} {}_{0}^{1}n \to_{1}^{1} p + e_{F}^{-} + {}_{0}^{0}{\bar{ν}} \\ \frac{1}{2} \to \frac{1}{2} + \frac{1}{2} + \frac{1}{2} \end{matrix}

(7)

The reason that Pauli, [11] with Fermi, [12] hypothesized neutrinos was because energy and angular momentum are not conserved by fermion electrons alone. The neutrino was therefore hypothesized to be a fermion, without mass nor charge with the fermion parallel to the axis of linear momentum. This immediately reveals that neutrinos have no mirror image and violate parity. They carry no magnetic moment. A neutrino without a spin appears to be identical to the helicity property of Q-spin.

Moreover, neutrinos have an exceedingly small collision cross section, so neutrinos are not significantly removed by reactions. That is, once produced, neutrinos are basically of no use, yet they are postulated to keep on being produced at enormous rates. All particles have a purpose. For neutrinos, once they have balanced energy and spin in beta decay, they have no further use and simply fill up the Universe ad infinitum.

Boson beta electrons, in contrast, have a spin of 1 and internal structure. The latter should account for the energy distribution, and therefore not violate the conservation of energy. The spin 1 boson balances the spin without a neutrino,

\begin{matrix} {}_{0}^{1}n \to_{1}^{1} p + e_{B}^{-} \\ \frac{1}{2} \to \frac{1}{2} + 1 \end{matrix}

(8)

If we had a neutrino without its fermion property, then all it can do is spin nothing. Moreover with almost no detection; strange parity properties; their uselessness after production; and now the boson obviating the need for a fermi anti-neutrino, we assert that neutrinos do not exist.

The largest detector is the water-filled Super-Kamiokande with 50,000 tons of water and 11,000 photomultiplier tubes one km undergroundm at a cost in 1996 of US

$ 600

million. Hardly any neutrino events were detected. None were direct detection of neutrinos, but were identified by their collision products based upon the usual Standard Model, with the Weak Force of SU(2) symmetry. We suggest that these are not the products of neutrino collisions. Nonetheless, over a flux of neutrinos of about

10^{57}

only 19 such events were detected that were attributed to neutrinos.

We assert this puts into doubt the existence of neutrinos. Rather we suggest that neutrinos are mistaken for the complementary property of spin, it’s helicity.

To determine if this description of Q-spin can replace neutrinos, the Standard Model needs to be investigated by using the quaternion group

SU (3) Q_{8} U (1)

(9)

Finally, following Noether’s Theorem [13], there can be no objection in changing the symmetry to the quaternion group. The test is whether the change leads to nonsense or to sense. We believe it leads to the latter and resolves many problems in the Foundations of Physics.

Note

Please see the pedagogical video, Yes, there are no neutrinos. https://youtu.be/Jdh6SEnhLaQ?si=pJdOCVIfeNBTJ7_n

References

Griffiths, David (2009). Introduction to Elementary Particles. pp. 59–60. ISBN 978-3-527-40601-2.
Bose, T., Boveia, A., Doglioni, C., Griso, S. P., Hirschauer, J., Lipeles, E., ... & Wang, L. T. (2021). Physics beyond the standard model.
Lee, T. D., & Yang, C. N. (1956). Question of parity conservation in weak interactions. Physical Review, 104(1), 254. [CrossRef]
Sanctuary, B. Extrinsic Quaternion Spin. Preprints.org 2023, 2023020055. [Google Scholar] [CrossRef]
Sanctuary, B. Spin with Hyper-helicity. Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
Sanctuary, B. Non-Local EPR Correlations using Quaternion Spin. Preprints 2023, 2023010570. [Google Scholar]
Sanctuary, B. Quaternion-Spin and Some Consequences. Preprints 2023, 2023121277. [Google Scholar] [CrossRef]
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624. [CrossRef]
Peskin, M. E., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Physical review letters, 49(14), 957. [CrossRef]
Pauli, W. (1930). Pauli letter collection: letter to Lise Meitner (No. CERN-ARCH-PLC, pp. Letter-2412).
Fermi, E. (1934). Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik, 88(3-4), 161-177. [CrossRef]
Noether, E. Invariante Variationsprobleme. Gott. Nachr. 1918, 1918, 235–257. [Google Scholar]

Figure 1. center upper, the two polarization axes form Q-spin of magnitude 1 from the coupling of two mirror states in free flight. Left and right fermions: When a filter axis is closer to one of the axes,

e_{1}

e_{3}

then that axis decouples into a fermion and the other precesses orthogonal to the aligned spin and averages away. Center figure, lower: when the filter is placed so it is within 22.5 degrees on either side of the boson vector, then the boson does not initially decouple, but precesses as a spin 1 with Larmor frequency which is double that of the fermions.

e_{1}

e_{3}

Figure 2. Two properties of Q-spin in free-flight: its polarization axes,

σ_{3}

and

σ_{1}

, are perpendicular to its axis of linear momentum

e_{2} = Y

. These two fermionic axes couple to give a boson of spin 1. The helicity is in the direction of propagation and averages out the polarizations. Q-spin is geometrically identical to a photon in free-flight.

Figure 2. Two properties of Q-spin in free-flight: its polarization axes,

σ_{3}

and

σ_{1}

, are perpendicular to its axis of linear momentum

e_{2} = Y

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the left and

ψ^{-}

on the right. Note that adding these states is independent of

e_{2}

and subtracting them is independent of

e_{1}

and

e_{3}

. Since we are blind to the imaginary axis, it is impossible to know which is the real object, or its reflection.

Figure 3. The mirror states of a Q-spin with

ψ^{+}

on the left and

ψ^{-}

on the right. Note that adding these states is independent of

e_{2}

and subtracting them is independent of

e_{1}

and

e_{3}

. Since we are blind to the imaginary axis, it is impossible to know which is the real object, or its reflection.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

On the Existence of Neutrinos

Abstract

Introduction

The Dirac Equation under the Quaternion Group

Beta Decay

Note

References

MDPI Initiatives

Important Links

Subscribe