Beta Decay with No Neutrinos and Parity Conservation

Preprint

Article

Beta Decay with No Neutrinos and Parity Conservation

Altmetrics

Downloads

309

Views

109

Comments

Bryan Sanctuary^*

This version is not peer-reviewed

Submitted:

05 March 2024

Posted:

06 March 2024

You are already at the latest version

Alerts

Abstract

We changed the symmetry of the Weak Force from SU(2) to the quaternion group $Q_8$, and found that spin spacetime separates into two complementary spaces: a spin polarization spacetime of even parity states, and a spin coherence space, in the $S^3$ hypersphere, of odd parity coherent states. Under the quaternion group, spin is a boson of spin 1 in free flight and a fermion of spin $\frac{1}{2}$ when measured. It immediately follows that neutrinos are not needed to balance spin and conserve energy in beta decay. Additionally, we find the boson electrons emitted in beta decay are odd to parity, leading to parity conservation even though the observed beta distribution is asymmetrical.

Keywords:

Subject: Physical Sciences - Quantum Science and Technology

Introduction

Changing the symmetry of the weak force from SU(2) to the quaternion group,

Q_{8}

, changes the two point-particle spins,

i . e

, Dirac’s matter-antimatter pair, to one particle with two orthogonal fermionic axes of spin on the same particle, [1,2,3,4]. That is, the four dimensional Dirac field, [5], changes from two, 2-state point particles, to one, 4-state structured particle. The structure that emerges is a spinning disc of spin 1 in free flight (isotropy) reminiscent of the “world sheet” description of Susskind, [6]. A two dimensional system, moreover, is an anyon [7], allowing for both fermionic and bosonic properties.

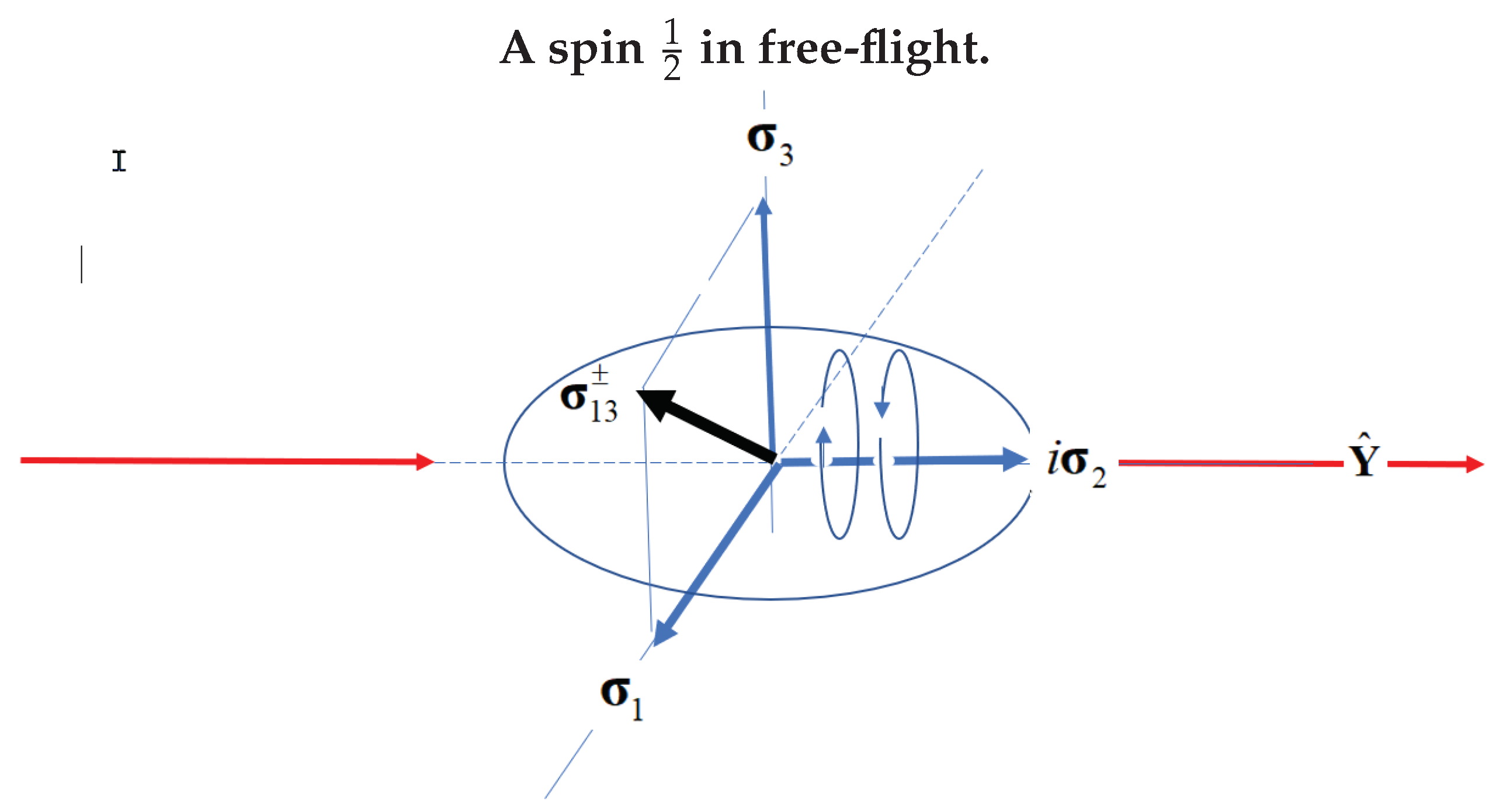
Figure 1 depicts Q-spin structure which is geometrically equivalent to a photon, with the two orthogonal spin axes, each perpendicular to the axis of linear momentum, which spins with helicity L or R. The two fermionic axes,

e_{3}, e_{1}

, couple to form composite bosons,

e_{13}^{\pm}

. There is, here, a subtle point. The boson only forms in free flight. In that case, the helicity spins the axis of linear momentum and averages out the spin, so the particle displays helicity only, and no net spin angular momentum, visualize the axis spinning in Figure 1. The wave function for the helicity is odd to parity, which the particle displays, albeit it is still a boson. Only when the particle is influenced by a polarizing field does the vector property of the boson spin emerge as the energy from the helicity is transferred to the spin polarization, that then itself decouples into a fermion of spin of

\frac{1}{2}

. Quaternion symmetry means the beta electron is odd to parity.

In this letter, we discuss beta decay without the need for neutrinos. Then we examine the famous experiment of Wu, [8] and show that parity is conserved under quaternion symmetry for beta decay. To understand these changes, we first summarize Q-spin and its origin.

We denote fermion electrons by

e_{F}^{-}

and boson electrons by

e_{B}^{-}

Q-Spin

The full details of this summary of Q-spin can be found in references [1,2,3,4].

The 4 dimensional gamma matrices, [5],

(γ^{0}, γ^{1}, γ^{2}, γ^{3})

represent the Dirac field. Dirac interpreted this as a matter-antimatter pair, with each spin defined by SU(2) symmetry of

(I, σ_{X}, σ_{Y}, σ_{Z})

in Minkowski spacetime,

(β, X, Y, Z)

. The matter-antimatter pair are mirror twins, being the reflection of each other. The major problem with this is the negative energies of the antimatter particle which Dirac resolved with his sea of electron model, [9].

Changing the symmetry to the quaternion group is easily accomplished by multiplying one of the gamma matrices by the imaginary number, [1], which changes the Dirac field to

(γ_{s}^{0}, γ_{s}^{1}, \pm {\tilde{γ}}_{s}^{2}, γ_{s}^{3})

. Since this endows structure on spin, and each can be oriented differently, we use the subscript s to denote spin spacetime with Body Fixed Frame of

(e_{1}, e_{2}, e_{3})

. Define

{\tilde{γ}}_{s}^{2} \equiv i γ_{s}^{2}

which renders it Hermitian, and the Dirac equation non-Hermitian.

The signature of the Dirac field has diagonal elements in Minkowski spacetime of

η^{μ ν} = (1, - 1, - 1, - 1)

which changes to

{\hat{η}}_{s}^{μ ν} = (1, - 1, + 1, - 1)

in spin spacetime using,

{\tilde{γ}}_{s}^{2}

, which is not a spatial component, but rather a time being a frequency. This dimension is the origin of quantum coherence that leads to the formulation of helicity, [2]. The remaining two spatial components are interpreted as two orthogonal axes of magnetization on the same particle, each carrying a magnetic moment of

μ

, and each described by a quaternion spin defined by [2],

Σ^{i} = σ^{j} + {\underset{̲}{\underset{̲}{h}}}_{g}^{j} (j = 1 or, 3)

(1)

Each axis carries a spin operator of,

σ

, and bivector,

i σ

. The origin of these two terms is from Geometric Algebra giving the geometric product between to Pauli spin components,

σ_{i} σ_{j} = δ_{i j} + ε_{i j k} i σ_{k}

. The first term is totally symmetric, and describes polarization. The second term is totally anti-symmetric, in terms of the bivector and the Levi-Civita tensor, which describes coherence, that is helicity. The helicity is defined by a bivector, [2],

{\underset{̲}{\underset{̲}{h}}}_{g} = \underset{̲}{\underset{̲}{\underset{̲}{ε}}} \cdot i σ

(2)

Quaternion spins have components of,

(I, σ_{s}^{1}, i σ_{s}^{2}, σ_{s}^{3})

which form a normal subgroup of

Q_{8}

Similar to usual spin, these two axes couple giving,

Σ_{31}^{\pm} = \pm \frac{1}{\sqrt{2}} (Σ^{3} \pm Σ^{1})

(3)

In the section “Q-spin” of reference [3] it is shown that the two axes couple to give a resultant that bisects the quadrants,

(e_{1}, e_{3})

of the spin’s BFF plane. Again there is a similarity with a photon. A head-on view the spinning axis displays the electric and magnetic components in the same configuration as the bosons in the BFF.

Σ_{31}^{\pm}

expresses a coherent composite boson in isotropy, but in an anisotropic field, the boson decouples into two fermions

Σ^{3}

and

Σ^{1}

The Dirac equation has no bivector, but changing to the quaternion group introduces one to give a non-Hermitian equation with ± states, [1],

(i γ_{s}^{0} \partial_{0} - i γ_{s}^{1} \partial_{1} \pm i {\tilde{γ}}_{s}^{2} \partial_{2} - i γ_{s}^{3} \partial_{3} - m) ψ^{\pm} = 0

(4)

which we call the Q-Dirac equation.

In free-flight, or isotropy, the 1 and 3 spatial components are indistinguishable, so permuting with a parity operator,

P_{13}

, leaves the spatial components unchanged, but the bivector,

i σ_{2} = σ_{3} σ_{1}

is odd to parity, leading to the ± sign in Equation (4), and shows the two states are reflective or mirror states with no parity,

P_{13} ψ^{\pm} = ψ^{\mp}

(5)

Figure 2 (upper middle), depicts the two spatial axes with one axis described by

ψ^{+}

and the other by

ψ^{-}

, its mirror state, which is precessing oppositely and in phase. One of the two states,

ψ^{\pm}

, is in a right handed frame and the other is in a left handed frame. These two fermionic components couple, thereby lowering the energy and stabilizing the structure to give a purely resonance and composite spin of 1. Forming the boson depends upon the spin-spin coupling strength between the two axes.

Although the states,

ψ^{\pm}

, have no parity, they can be added and subtracted to give combinations that are odd and even to parity,

P_{13} Ψ^{\pm} = \pm Ψ^{\pm} = \pm \frac{1}{\sqrt{2}} (ψ^{+} \pm ψ^{-})

(6)

Introducing these states of fixed parity separates the non-Hermitian Q-Dirac equation, Equation (4). Adding and subtracting the ± forms leads to two independent equations,

\begin{matrix} (i γ_{s}^{0} \partial_{0} + i γ_{s}^{1} \partial_{1} + i γ_{s}^{3} \partial_{3} - m) Ψ^{+} & = 0 \\ {\tilde{γ}}_{s}^{2} \partial_{2} Ψ^{-} & = 0 \end{matrix}

(7)

The first is a two dimensional Dirac equation and the second is the equation for a massless Weyl spinor, [1]. The former solves to give a 2D disc of spin angular momentum with even parity. It has two energies,

E = \pm \sqrt{m^{2} + p_{1}^{2} + p_{3}^{2}}

. Here

p_{1}

and

p_{3}

are the energies from the two axes, and express internal energy of the structured Q-spin. The mirror property of the axes is shown in Figure 2 (middle upper), and we associate the ± energies with the equal, opposite, and coherent precession of the two coupled axes. The energies of these balance each other. Quaternion spin resolves the negative energy issue Dirac faced by replacing his matter-antimatter pair with one particle with two mirror axes.

The solution to the Weyl equation is a unit quaternion, [1,5], with only one role which is to spin the axis of linear momentum either left or right. These are the two helicity states of the spin.

This development reveals the complementary properties of Q-spin. The 2D spin spacetime has components,

(β_{s}, e_{1}, e_{3})

, and a space (not spacetime) of unit quaternions in the

S^{3}

hypersphere. The 2D Dirac equation describes the disc, and this is spun by the unit quaternion, which is odd to parity, giving the L and R helicity states. As we said, the rapid spinning by the helicity averages out the 2D disc in free flight so only helicity is present. An electron boson,

e_{B}^{-}

, is odd to parity.

Spin polarization and helicity are complementary elements of reality, albeit the quaternion cannot be measured since it is beyond our dimension. All we see of the quaternion is the spinning of the axis of linear momentum in Minkowski spacetime. As the boson spin approaches a filter, it transforms and decouples to a fermion. In that cross over region, the boson properties are evident. Most strikingly, the violation of Bell’s Inequalities is explained by this transition, and resolves the EPR paradox, [3].

The free-flight boson,

e_{B}^{-}

, expresses the wave nature of spin.

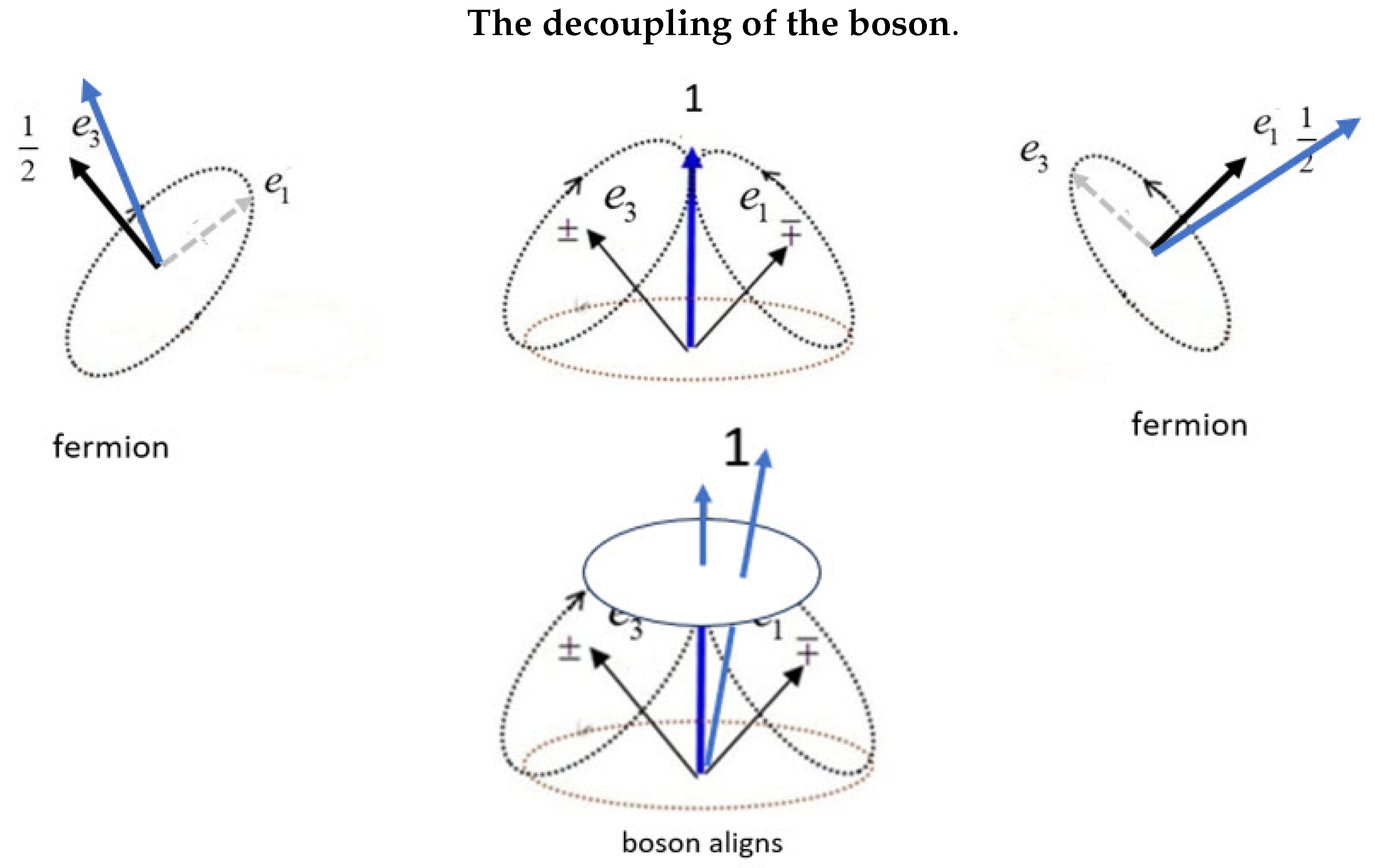
When a free-flight boson encounters a polarizing field, the two spin axes are no longer indistinguishable, so that when the field strength exceeds the spin-spin coupling, the boson decouples. Figure 2, (left and right figures), show two ways the boson decouples into one of its fermionic axes. If the field is closer to one axis than the other, then the least action principle asserts that axis will align and its twin averages out, and vise versa for the other axis. This is one mechanism for the decoupling.

However there is a second mechanism, whence the boson spin 1 aligns with the field intact, and precesses as a spin 1. This is shown in the same figure, (middle bottom). When the field is less than 22.5 degrees from the boson, it spins without decoupling, and since the magnetic moment is

2 μ

, its Larmor frequency is double that of the fermions.

The fermion form,

e_{F}^{-}

, expresses the particle nature of spin.

When in a polarizing field, the electron is

e_{F}^{-}

. In free-flight, the axis spins either L or R helicity of

e_{B}^{-}

. Which spin occurs depends upon the environment,

e_{F}^{-} (anisotropy) \leftrightarrow e_{B}^{-} (isotropy)

(8)

Q-spin epitomizes the wave-particle duality.

As currently used, the point particle Dirac spin is defined only by a Pauli spin vector, which is co-linear to the axis of linear momentum. In contrast, Q-spin’s axes are orthogonal to the linear momentum axis like a photon. Even more, neither a photon nor a boson electron have an

m = 0

component, [1]. Particle physics, [10], defines helicity as the projection of spin along the axis of linear momentum, giving the observed spin of up or down. Helicity in particle physics determines the spin state.

Q-spin is quite different. It has structure and is not a point. There are four states: in isotropy, the helicity spins the axis of linear momentum L or R; in anisotropy, the polarization displays two states of spin, up, ↑, and down, ↓. The state of the helicity is a unit quaternion, and is a distinct property from spin polarization. They are a complementary pair and elements of reality.

Beta Decay

Beta decay, [10], can be expressed as a neutron in a nucleus decaying into a proton by emitting a beta particle,

i . e .

a fermion electron, and an anti-neutrino,

{}_{0}^{1}n \to {}_{1}^{1}p + e_{F}^{-} + {}_{0}^{0}{\bar{ν}}

(9)

\frac{1}{2} \to \frac{1}{2} + \frac{1}{2} + \frac{1}{2}

(10)

The reason that Pauli, [11] with Fermi, [12] hypothesized neutrinos was because energy and angular momentum are not conserved by fermion electrons alone. The neutrino was therefore hypothesized to be a fermion, with neither mass nor charge, with the fermion axis colinear to the axis of linear momentum. This immediately reveals that neutrinos have no mirror image and violate parity. Neutrinos are only left handed while antineutrions are only right handed. They carry no magnetic moment.

Moreover, neutrinos have an exceedingly small collision cross section, so they are not significantly removed by reactions. That is, once produced, neutrinos are basically of no use, yet they are postulated to keep on being produced at enormous rates. All particles have a purpose. For neutrinos, once they have balanced energy and spin in beta decay, they have no further use and simply fill up the Universe ad infinitum. Neutrinos have a source but no known sinks.

We consider these properties peculiar.

Boson beta electrons,

e_{B}^{-}

, in contrast, have a spin of 1 and internal structure. The latter should account for the energy distribution, and therefore not violate the conservation of energy. The spin 1 boson balances the spin without a neutrino,

{}_{0}^{1}n \to {}_{1}^{1}p + e_{B}^{-}

(11)

\frac{1}{2} \to \frac{1}{2} + 1

(12)

If we had a neutrino without its fermion property, then all it can do is spin nothing. Moreover with almost no detection; strange parity properties; their uselessness after production; and now the boson obviating the

r a i s o n d^{'} \hat{e} t r e

for a fermion electron neutrino, we assert they do not exist. Since the boson electrons carry the exact properties that obviate neutrinos, we note that they appears to be identical to either L helicity, called antineutrinos, and R helicity, called neutrinos.

Considerable effort has been put into neutrino detection with, at best, equivocal results. The water-filled Super-Kamiokande detector, [13], one km underground, cost in 1996 US

$ 600

million. No neutrinos were directly detected, but were identified by their collision products based upon the usual Standard Model, with the Weak Force of SU(2) symmetry. We suggest that these are not the products of neutrino collisions. Nonetheless, using this method, over a flux of postulated neutrinos of about

10^{57}

only 19 such events were detected. A larger detector was built deep within the ice of the Antarctic, [14] with similar results to the Kamiokande.

We assert this puts into doubt the experimental existence of neutrinos.

Conservation of Parity under the Quaternion Group

The current situation with respect to the parity of the weak force follows. In the 1950’s, Yang and Lee, [15], suggested that the weak force may not obey parity which motivated experiments. The 1956 experiment, conducted by physicist Chien-Shiung Wu and her colleagues, [8], was a crucial contribution to the field of particle physics, [10], and remains so today. Parity conservation was a widely accepted principle that stated that the mirror image of a physical process should be indistinguishable from the original process in the real world.

Wu’s experiment focused on the beta decay of cobalt-60 nuclei. Under the usual SU(2) symmetry, beta decay transforms a neutron into a proton, emitting an electron (

e_{F}^{-}

), and an electron antineutrino, Equation (9). According to the law of parity conservation, this process should be isotropic in all directions. However, Wu’s team observed a clear asymmetry in the emitted electrons’ distribution. Wu stated, [8],

“If an asymmetry in the distribution between

θ

and

(180 - θ)

… is observed, it provides unequivocal proof that parity is not conserved in beta decay.”

Q-spin challenges this statement.

Under quaternion symmetry, Q-spin is a boson of odd parity,

e_{B}^{-}

. As discussed in the last section, this immediately shows that for beta decay, the antineutrino is not needed to balance spin, and the internal structure of Q-spin conserves the energy. Therefore, without neutrinos, we assert the beta decay process of cobalt is given by,

{}_{27}^{60}{Co} \to {}_{28}^{60}{Ni} + e_{B}^{- 1} + 2 γ

(13)

In the experiment, [8], the cobalt sample was placed in a solenoid that produced a polarizing field along the polar axis and which can be reversed. Wu measured the gamma rays, the distribution of which is the same as that for the beta particles. Equatorial counts were used to normalize the polarization. By reversing the current in the solenoids, the experiment detected an asymmetry in the number counts between the north and south. The mirror symmetry is not faithful and parity is violated.

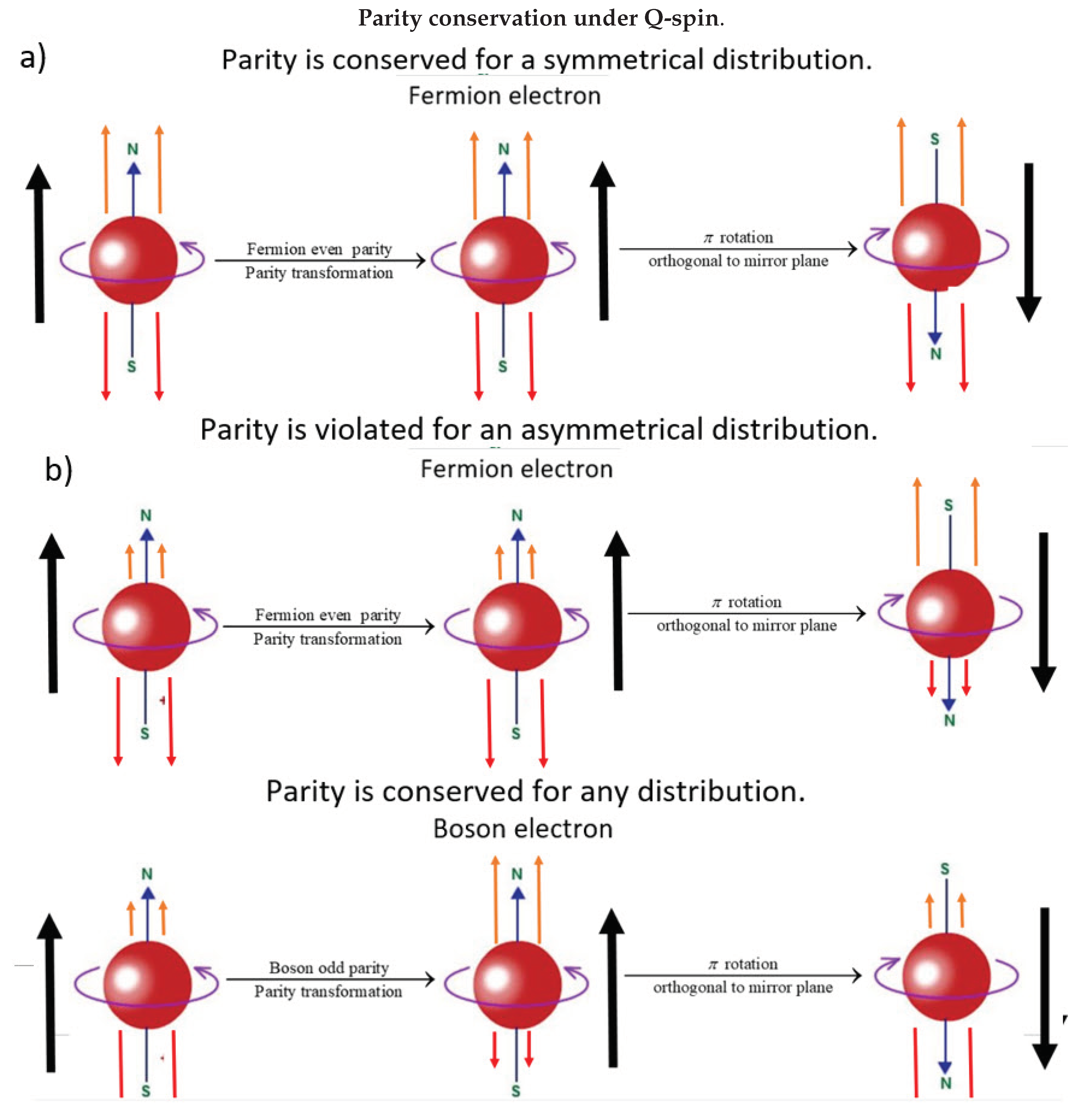
This is shown in Figure 3). The first column is the real world. The second column depicts the parity transformations, and the last column is after the

π

rotation, needed so the first and third columns are mirror images.

If parity is conserved the expected distribution must be symmetrical, which is shown in the first row,

(a) Since the magnetic field; the cobalt atoms; and the fermion electrons; are all axial vectors, they are symmetrical under parity. As stated above, Wu expected this result if parity is conserved.

The real world image in the second row,

(b) This is what Wu actually observed, an asymmetrical distribution of beta events. Performing the same transformations as in (a), it is clear that the mirror reflection is not faithful, showing parity is violated. For this reason it is concluded that parity is violated in Nature.

In contrast, if the beta particle is a boson electron with odd parity, then row

(c) of Figure 3 shows the real world data is faithfully reproduced for any distribution observed. Parity is not violated under the quaternion group.

Conclusion

A number of surprising results are a direct consequence of changing from SU(2) to

Q_{8}

: the replacing of Dirac’s matter-antimatter pair with one particle with two axes; the resolving of the negative energy issue of Dirac’s solution; the obviating of neutrinos in beta decay; and the conservation of parity. Additionally, we have found the observed violation of Bell’s inequalities, [16,17,18,19], is not evidence of non-locality but due to the transition from a boson to a fermion, [3]. Q-spin explains quantum weirdness, [20], shows entanglement cannot be non-local, and resolves the EPR paradox.

Finally, following Noether’s Theorem [21], there can be no objection to changing the symmetry to the quaternion group. The test is whether the change leads to nonsense or to sense. The concepts of non-locality; the infinite negative fermionic continuum (needed for the sea of electron model); and parity violation are difficult concepts to accept. That these properties are not present using Q-spin is auspicious, and suggests the Standard Model be investigated by using the quaternion group

Q_{8}

for the Weak Force rather than SU(2).

Note

Please see the pedagogical video, Yes, there are no neutrinos.

References

Sanctuary, B. Extrinsic Quaternion Spin. Preprints 2023, 2023020055. [Google Scholar] [CrossRef]
Sanctuary, B. Spin with Hyper-helicity. Preprints 2023, 2023010571. [Google Scholar] [CrossRef]
Sanctuary, B. Non-local EPR Correlations Using Quaternion Spin. Preprints 2023, 2023010570. [Google Scholar] [CrossRef]
Sanctuary, B. Quaternion-Spin and Some Consequences. Preprints 2023, 2023121277. [Google Scholar] [CrossRef]
Peskin, M. E., Schroeder, D. V. (1995). An Introduction To Quantum Field Theory (Frontiers in Physics), Boulder, CO.
Susskind, Leonard (1970). "Dual-symmetric theory of hadrons, I.". Nuovo Cimento A. 69 (1): 457–496. [CrossRef]
Wilczek, F. (1982). Quantum mechanics of fractional-spin particles. Physical review letters, 49(14), 957. [CrossRef]
Wu, C. S., Ambler, E., Hayward, R. W., Hoppes, D. D., & Hudson, R. P. (1957). Experimental test of parity conservation in beta decay. Physical review, 105(4), 1413. [CrossRef]
Dirac, P. A. M. (1928). The quantum theory of the electron. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 117(778), 610-624.
Griffiths, David (2009). Introduction to Elementary Particles. pp. 59–60. ISBN 978-3-527-40601-2.
Pauli, W. (1930). Pauli letter collection: letter to Lise Meitner (No. CERN-ARCH-PLC, pp. Letter-2412).
Fermi, E. (1934). Versuch einer Theorie der β-Strahlen. I. Zeitschrift für Physik, 88(3-4), 161-177. [CrossRef]
Fukuda, S., Fukuda, Y., Hayakawa, T., Ichihara, E., Ishitsuka, M., Itow, Y., … & Ichikawa, Y. (2003). The super-kamiokande detector. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 501(2-3), 418-462. [CrossRef]
Abbasi, R., Ackermann, M., Adams, J., Ahlers, M., Ahrens, J., Andeen, K., … & Madsen, J. (2009). The IceCube data acquisition system: Signal capture, digitization, and timestamping. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, 601(3), 294-316. [CrossRef]
Lee, T. D., & Yang, C. N. (1956). Question of parity conservation in weak interactions. Physical Review, 104(1), 254. [CrossRef]
Bell, John S. “On the Einstein Podolsky Rosen paradox.” Physics Physique Fizika 1.3 (1964): 195. [CrossRef]
Clauser, J. F., Horne, M. A., Shimony, A., & Holt, R. A. (1969). Proposed experiment to test local hidden-variable theories. Physical review letters, 23(15), 880. [CrossRef]
Aspect, Alain, Jean Dalibard, and Gérard Roger. “Experimental test of Bell’s inequalities using time-varying analyzers.” Physical review letters 49.25 (1982): 1804.
Aspect, Alain (15 October 1976). “Proposed experiment to test the non separability of quantum mechanics”. Physical Review D. 14 (8): 1944–1951.
Weihs, G., Jennewein, T., Simon, C., Weinfurter, H., Zeilinger, A. (1998). Violation of Bell’s inequality under strict Einstein locality conditions. Physical Review Letters, 81(23), 5039. [CrossRef]
Mullin, W. J. (2017). Quantum weirdness, Oxford University Press.
Emmy Noether. Invariante Variationsprobleme. Gott. Nachr., pages 235–257, 1918.

Figure 1. Two properties of Q-spin in free-flight: its polarization axes,

σ_{3}

and

σ_{1}

, are perpendicular to its axis of linear momentum

e_{2} = Y

. These two fermionic axes couple to give a composite boson of spin 1. The helicity is in the direction of propagation and averages out the polarizations. Q-spin is geometrically identical to a photon in free-flight.

Figure 1. Two properties of Q-spin in free-flight: its polarization axes,

σ_{3}

and

σ_{1}

, are perpendicular to its axis of linear momentum

e_{2} = Y

Figure 2. center upper, the two polarization axes form Q-spin of magnitude 1 from the coupling of two mirror states in free flight. Left and right fermions: When a filter axis is closer to one of the axes,

e_{1}

e_{3}

then that axis decouples into a fermion and the other precesses orthogonal to the aligned spin and averages away. Center figure, lower: when the filter is placed so it is within 22.5 degrees on either side of the boson vector, then the boson does not initially decouple, but precesses as a spin 1 with Larmor frequency which is double that of the fermions.

e_{1}

e_{3}

Figure 3. The cobalt nuclei are the large spheres. The thick arrows are the magnetic fields. The small arrows are beta particles. The first column is the real world and the last is the mirror world. a) For a symmetrical distribution of beta fermion electrons parity is conserved. b) For a asymmetrical distribution of beta fermion electrons parity is not conserved. c) Using boson electrons, parity is conserved for any distribution.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Beta Decay with No Neutrinos and Parity Conservation

Abstract

Introduction

Q-Spin

Beta Decay

Conservation of Parity under the Quaternion Group

Conclusion

Note

References

MDPI Initiatives

Important Links

Subscribe