Relativity Cosmology

Jeongin Choi

doi:10.20944/preprints202312.2215.v1

Submitted:

20 December 2023

Posted:

29 December 2023

Read the latest preprint version here

Abstract

This paper presents the perspective that universe is relative. The universe, which changes according to the observer’s proper time, is dynamic. Generally, the universe expands, but if the observer accelerates enough, contraction is also possible. The Hubble parameter merely represents that change. If the Hubble parameter is dependent on the proper time, the measurement can only be uncertain. Identifying the factors that influence the proper time could potentially lead to a more accurate measurement of the universe’s age, and it could also offer insights into the state of the early universe and the causes of the accelerated expansion observed in the current epoch.

Keywords:

Cosmology

;

Cosmological parameters

;

Hubble tension

Subject:

Physical Sciences - Space Science

Introduction

The inconsistency in the measurement of the Hubble parameter has been raised as a significant issue in contemporary cosmology. Solutions have been sought by refining existing theories or sophisticating measurement techniques, but the problem has not been resolved. The increasing Hubble tension over time suggests the need for a new perspective and approach to the universe. This paper briefly introduces a cosmology considering the observer’s proper time. Through a simple thought experiment, it redefines the cosmic spacetime and deduces the Hubble parameter. It explores the cosmological reasons for the variation in proper time and speculates on the potential causes of the accelerated expansion of the universe.

Theory

The spaceship is orbiting a planet at a constant velocity close to the speed of light. At that moment, a stellar A, located one light-year away, bursts into a supernova. One year later, the flash from the explosion engulfs the planet.

Δ t^{'} = \frac{Δ t}{γ}

(1)

Where

Δ t^{'}

represents the time interval for a moving observer,

Δ t

for a stationary observer, and

γ

signifies the Lorentz factor [1]. From the point of a supernova explosion, inhabitants of a planet die approximately a year later. However, for a traveler aboard a spaceship, this duration is less than a year. Considering the constant speed of light, the travel time for the burst of light must decrease. This implies a contraction of space. The distance between the traveler and stellar A contracts by

1 / γ

compared to a stationary observer. The travel time of light is shortened by

1 / γ

. As a result, the traveler dies relatively quickly.

Consider that, before the arrival of the flash from the explosion, the traveler changes his mind and decides to land on a planet. What would happen at the moment the spaceship decelerates? The distance from stellar A expands, causing an increase in the time it takes for the flash to travel. As a result, the traveler can survive a bit longer. The size of space changes according to the proper time, and this concept is directly applied to the universe.

R (t) = c τ

(2)

Where

R (t)

is the size of the universe and

τ

is the traveler’s proper time. The size of the universe, denoted as

R (t)

, is defined as the distance that light has traversed in a vacuum over the proper time

τ

since the beginning of time. The value of

R (t)

reaches its maximum when at rest in the cosmic rest frame, especially, the total travel time of light at this point is defined as the age of the universe, denoted as T.

Consider a situation where an observer at rest in the cosmic rest frame is observing a spaceship accelerating. In this case, the proper time of the traveler on board the spaceship varies from

τ_{a}

to

τ_{b}

.

\frac{R (t + Δ τ)}{R (t)} = \frac{c τ_{b}}{c τ_{a}}

(3)

Where

R (t + Δ τ)

and

R (t)

represent the size of the universe defined in the traveler’s timeframe when the traveler’s proper time is respectively

τ_{b}

,

τ_{b}

. Since the time of the stationary observer flows the same as the universe’s time, it can be designated as T. From the perspective of a stationary observer, if time h passes, the same amount of time, h, also elapses in the universe’s time.

\frac{R (t + Δ τ)}{R (t)} = \frac{γ (t)}{γ (t + Δ τ)} (1 + \frac{h}{T})

(4)

Considering

τ = T / γ

, The equation is then restructured, ensuring that

Δ τ

converges to 0.

lim_{Δ τ \to 0} \frac{R (t + Δ τ) - R (t)}{R (t)} = \frac{h}{T} \frac{γ (t)}{γ (t + Δ τ)} + \frac{γ (t) - γ (t + Δ τ)}{γ (t + Δ τ)}

(5)

By Lorentz invariance [2],

Δ τ

is defined as follows. [3]

\begin{matrix} Δ τ & = \int_{P} \frac{1}{c} \sqrt{η_{μ ν} d x^{μ} d x^{ν}} \end{matrix}

(6)

\begin{matrix} = \int_{P} \sqrt{d t^{2} - \frac{d x^{2}}{c^{2}} - \frac{d y^{2}}{c^{2}} - \frac{d z^{2}}{c^{2}}} \end{matrix}

(7)

\begin{matrix} = \int \sqrt{1 - \frac{1}{c^{2}} [{(\frac{d x}{d t})}^{2} + {(\frac{d y}{d t})}^{2} + {(\frac{d z}{d t})}^{2}] d t} \end{matrix}

(8)

\begin{matrix} = \int \frac{d t}{γ (t)} \end{matrix}

(9)

Since

d τ = d h / γ (t)

, substitute it and rearrange.

\frac{R^{'} (t)}{R (t)} = \frac{γ (t)}{T} - \frac{γ^{'} (t)}{γ (t)}

(10)

By defining

H (t) = \frac{R^{'} (t)}{R (t)}

and generalizing it, the following equation is derived.

H (t) = \frac{1}{τ} - \frac{γ^{'}}{γ}

(11)

If

γ^{'} = 0, γ = 1

, then

H (t) = 1 / T

, which matches the Hubble parameter

H_{0}

as defined in the Hubble-Lemaître law [4]. The expansion rate of the universe varies depending on the traveler’s motion. If the traveler accelerates sufficiently, the universe could even contract. (However,

- 1 < H (t) < γ + \frac{1}{τ} - 1

)

In Figure 1, if the value of

θ

is constant, the universe expands at the speed of light at any proper time coordinate. However, the universe is chaotic state where interactions between matter do not cease. The expansion of the universe is not constant and is bound to fluctuate.

H (t) = \frac{1}{τ} - \frac{γ^{'}}{γ}

(12)

Multiplying the equation derived above by

c τ

yields the expansion speed of the universe,

V (t)

.

V (t) = c - c τ \frac{γ^{'}}{γ}

(13)

If

γ^{'} < 0

, the expansion speed of the universe surpasses the speed of light. This is indicative of the typical universe.

Applying Theory

The CMB (Cosmic Microwave Background Radiation), a powerful evidence of the Big Bang theory, is a microwave background radiation that pervades the entire universe. The CMB originated from an extremely high energy state in the early universe, but is observed in a greatly reduced energy state due to redshift. In other words, it can be simply defined as light that has traveled the universe for a proper time

τ

since the beginning. Therefore, by applying the Hubble-Lemaitre law, it can be expressed in the following relationship.

τ = \frac{1}{H_{c m b}}

(14)

If calculated with

H_{c m b} = 67 k m / s / M p c

, it concludes that approximately 14.587 billion years have passed in terms of the proper time. This greatly exceeds the widely accepted age of the universe, 13.8 billion years. And by Equation (12), the following holds true.

H_{c m b} - H (t) = \frac{γ^{'}}{γ}

(15)

By substituting the above results into Equation (13) and rearranging, expansion speed of universe

V (t)

, can be simply derived.

V (t) = c \frac{H (t)}{H_{c m b}}

(16)

If calculated with

H (t) = 73 k m / s / M p c

, the expansion speed of universe,

V (t) \approx 1.0895 c

, which exceeds speed of light by about

9 %

. This aligns with the principle that objects beyond the Hubble length

c / H (t)

exceed the speed of light. The last-scattering surface(LSS) is the location from which the cosmic microwave background radiation originates. [5] It delineates the edge of the observable Universe. In other words, the limiting point of the information observable is defined as the cosmological horizon, and in Figure 1, this distance aligns with the size of the universe. Therefore, the distance to the last-scattering surface can be defined as

c τ

, and the expansion limit size is

c T

.

c T = c τ + c γ Δ t_{l s s}

(17)

Where

γ Δ t_{l s s}

is the completion time of the last-scattering calculated in current time value. By summarizing, the following equation can be derived.

γ = \frac{1}{1 - H_{c m b} Δ t_{l s s}}

(18)

If calculated with

Δ t_{l s s} = 380000

years, the current time delay

γ \approx 1.000026

is derived. Interestingly, this is similar to the Lorentz factor

\frac{1}{\sqrt{1 - α^{2}}}

calculated with the speed of the ground state electron orbiting the hydrogen atom. (

α

= fine structure constant). Physical constants may vary depending on

γ

. In conclusion, the age of the universe T is as follows.

T = \frac{1}{H_{c m b} (1 - H_{c m b} Δ t_{l s s})} \approx 14.5873 G y r

(19)

Hypothesis

While there are various factors that influence proper time, such as observation methods or observation environments (artificial acceleration), among these, astronomical reasons are presumed to be the main cause.

Δ t^{'} = Δ t \sqrt{1 - \frac{2 G M}{r c^{2}}}

(20)

The Sun loses approximately 5.5 million tonnes of mass per second due to solar wind and nuclear fusion [6]. This mass loss from the Sun not only reduces the gravitational time delay effect, derived from the Schwarzschild metric [7], but also expands its orbit, thereby decreasing its orbital velocity [8]. The Milky Way harbors over a hundred billion stars, and its mass is estimated to be over 200 billion times that of the Sun [9]. While the gravitational time-delay effect diminishes with increasing distance, the sheer mass of the Milky Way makes it impossible to ignore its impact. During the main-sequence phase, stellar mass loss is relatively uniform. However, as a stellar object undergoes evolution, significant changes occur. The rate of fusion increases, causing it to become brighter, and stellar mass loss intensifies [10]. In its final stage, this stellar object either forms a planetary nebula or undergoes massive mass loss through a supernova explosion. These factors can contribute to short-term fluctuations in the measurement of the Hubble parameter.

According to research findings, it has been reported that the Milky Way and the Sagittarius dwarf galaxy collided three times over the span of approximately the past 6 billion years. [11]. These collisions disrupted the internal balance of the Milky Way, causing changes in the density of gas and dust and triggering the explosive birth of stars. A hypothesis has been proposed that even our solar system was formed as a result of these events. Interestingly, this period is similar to the time when the accelerated expansion of the universe began. While it remains merely a hypothesis, it is conjectured that if the time-delay effect of the material that once constituted the primitive solar system diminished due to the impact of those collisions, it could potentially explain the accelerated expansion of the universe.

Conclusion

This paper is based on three assumptions. 1) The universe is relative to the observer’s proper time. 2) The size of the universe is defined as the distance that light has traversed in a vacuum over the proper time

τ

since the beginning of time. It is represented as

R (t) = c τ

. 3) The concept of the cosmic rest frame is introduced. In the cosmic rest frame, the universe expands uniformly at the speed of light when it is in a state of maximum size. The age of the universe, T is defined as the total travel time for light in this state. If the premise is correct, the rate of expansion of the universe can be expressed by the following equation.

H_{c m b} - H (t) = \frac{γ^{'}}{γ}

(21)

The Hubble tension problem is speculated to arise from the omission of changes in proper time. The discrepancies and variability in data are natural occurrences when considering the capricious nature of celestial bodies in the universe. In the absence of special circumstances, the observed cosmic space within the solar system is expected to continue expanding, but the rate of expansion will decrease over time. The accelerated expansion is conjectured to be caused by the explosive emergence of stars resulting from the collision between the Milky Way and the Sagittarius dwarf galaxy, the birth of the solar system, and the subsequent reduction in the time-delay effect of primitive solar system materials. This is a transient event on a cosmological scale, and over an extended period of time, the expansion speed of the universe will eventually converge to the speed of light, and the expansion rate will converge to zero.

References

Lorentz, H.A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light. In Collected Papers: Volume V; Springer, 1937; pp. 172–197.
Poincaré, H. La dynamique de l’électron; A. Dumas, 1913.
Foster, J.; Nightingale, J.D.; Foster, J. A short course in General Relativity; Springer, 1995.
Lemaître, G. Un Univers homogène de masse constante et de rayon croissant rendant compte de la vitesse radiale des nébuleuses extra-galactiques. Annales de la Société Scientifique de Bruxelles, A47, p. 49-59 1927, 47, 49–59.
Chown, M. The Oxford Companion to Cosmology by Andrew Liddle and Jon Loveday, and Cosmology by Steven Weinberg| The Oxford Companion to Cosmology, Andrew Liddle and Jon Loveday, Oxford University Press,£ 35, 9780198608585| Cosmology, Steven Weinberg, Oxford University Press,£ 45, 9780198526827, 2008.
Akpootu, D.O.; Salifu, S.I.; Nnaemeka, O.C.; Adesina, S. Comparative Study on Mass loss by the Sun and Energy Available for Utilization between two Tropical Stations in Nigeria. International Journal of Adv in Sci Res and Eng (ijasre) 2020, 6, 82–91.
Schwarzschild, K. Über das gravitationsfeld eines massenpunktes nach der einsteinschen theorie. Sitzungsberichte der königlich preussischen Akademie der Wissenschaften 1916, pp. 189–196.
Noerdlinger, P.D. Solar mass loss, the astronomical unit, and the scale of the solar system. arXiv preprint arXiv:0801.3807 2008. [CrossRef]
Jiao, Y.; Hammer, F.; Wang, H.; Wang, J.; Amram, P.; Chemin, L.; Yang, Y. Detection of the Keplerian decline in the Milky Way rotation curve. Astronomy; Astrophysics 2023, 678, A208. [CrossRef]
Shukure, N.T.; Tessema, S.B.; Mengistu, E. Mass-loss varying luminosity and its implication to the solar evolution. Proceedings of the International Astronomical Union 2019, 15, 403–404. [CrossRef]
Ruiz-Lara, T.; Gallart, C.; Bernard, E.J.; Cassisi, S. The recurrent impact of the Sagittarius dwarf on the Milky Way star formation history, 2020, [arXiv:astro-ph.GA/2003.12577]. [CrossRef]

Figure 1. The size of the universe varies according to the proper time of the traveler. The slope of the graph is the reciprocal of

γ

, and

θ

varies in the range of

0 < θ < π / 4

. The universe is at its maximum size when

γ

= 1

Figure 1. The size of the universe varies according to the proper time of the traveler. The slope of the graph is the reciprocal of

γ

, and

θ

varies in the range of

0 < θ < π / 4

. The universe is at its maximum size when

γ

= 1

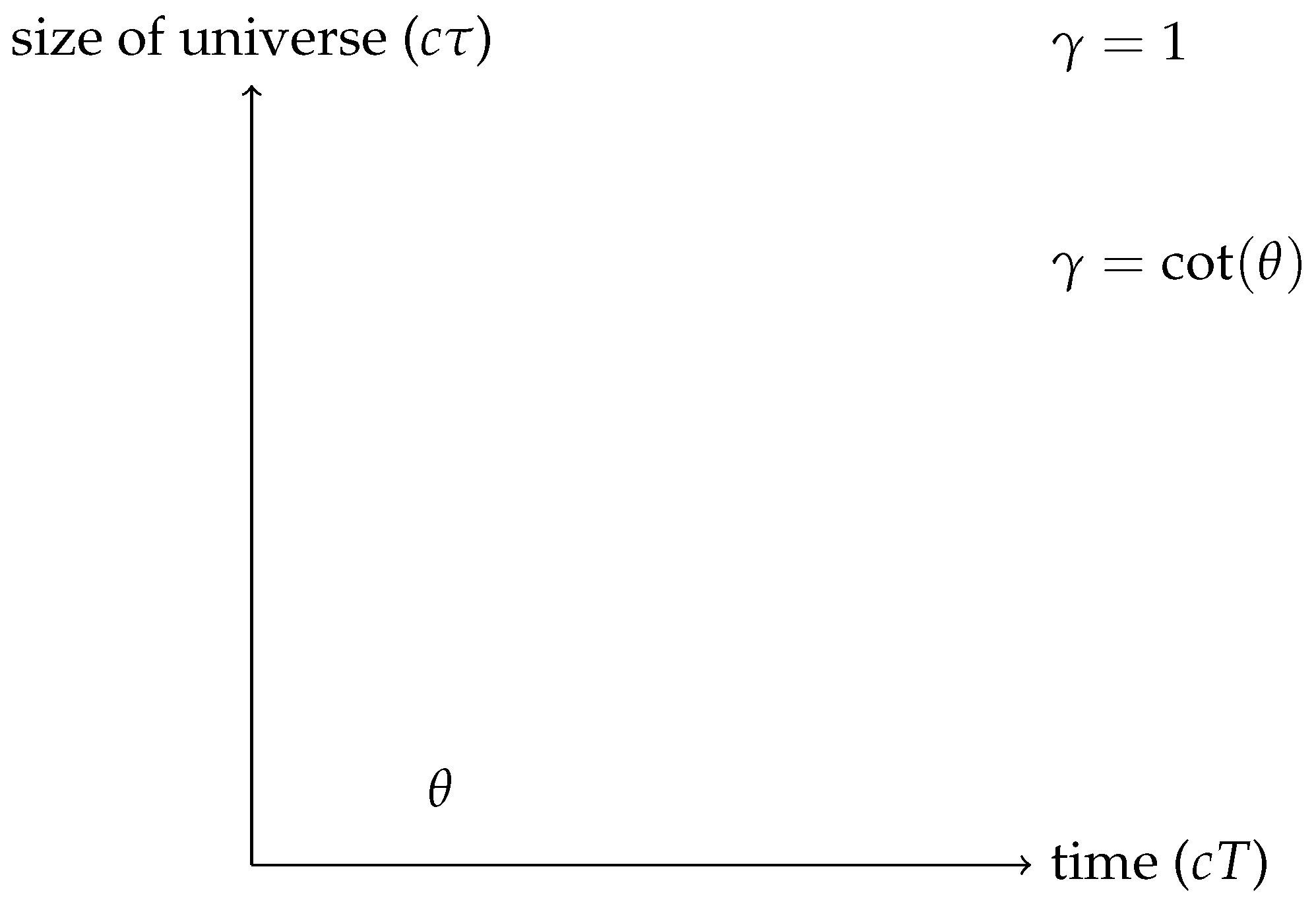
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Relativity Cosmology

Abstract

Keywords:

Subject:

Introduction

Theory

Applying Theory

Hypothesis

Conclusion

References

MDPI Initiatives

Important Links

Subscribe