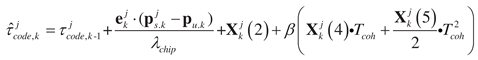Performance Enhancement and Evaluation of a Vector Tracking Receiver using Adaptive Tracking Loops

The traditional receiver employs scalar tracking loops, resulting in degraded navigation performance in weak signal and high dynamic scenarios. An innovative design of a vector tracking receiver based on nonlinear Kalman filter (KF) tracking loops is proposed in this paper, which combines the strengths of both vector tracking and KF tracking loops. Firstly, a comprehensive description of the vector tracking receiver model is presented, and unscented Kalman filter (UKF) is applied to nonlinear tracking loop. Secondly, to enhance the stability and robustness of the KF tracking loop, we introduce square root filtering and an adaptive mechanism. The tracking loop based on square root UKF (SRUKF) can dynamically adjust its filtering parameters based on signal noise and feedback Doppler error. Finally, the proposed method is implemented on a software-defined receiver (SDR), and the field vehicle experiment demonstrates the superiority of this method over other receivers in complex dynamic environments.

Keywords:

Subject: Engineering - Aerospace Engineering

1. Introduction

Global satellite navigation system (GNSS) has become one of the most widely used navigation systems because of its advantages of high precision, all-weather, continuous positioning, extensive coverage, convenience and flexibility [1,2]. As the demand for navigation performance rises, GNSS will inevitably be affected by the specific application scenario and the movement characteristics of the carrier, such as low signal carrier-to-noise ratio (

{C / N}_{0}

) environments (e.g., signal blocking and interference) and high dynamic motion [3,4,5,6].

GNSS receivers acquire position, velocity, and time (PVT) information by tracking satellite broadcast signals in real time, demodulating navigation messages, and acquiring pseudo-range, Doppler frequency, and other observation information. Therefore, the tracking loop accuracy of the receiver directly determines the PVT accuracy. Consequently, the accuracy of the receiver's tracking loop is a direct determinant of the precision in PVT estimation. Traditional GNSS receivers usually adopt scalar tracking loops (STL) to track each satellite independently using individual pre-assigned channel, and the signal processing among each channel is independent of each other. This tracking mode is simple to implement, without interference and pollution between channels [7]. However, it ignores the inherent correlation of GNSS tracking loops to the receiver’s PVT information, so information cannot be shared between each channel. In contrast, vector tracking loops (VTL) interlink the tracking loops and navigation solutions of diverse channels, facilitating the exchange of information between them, which has been widely concerned in recent years [8,9,10,11]. Compared with the STL, the VTL exploits and makes full use of the redundant information of different satellite signals and the intrinsic coupling between signal tracking and navigation solution, and its advantages mainly include: 1) with the aid of navigation information, VTL mitigates the dynamic stress on the tracking loop, enhancing the dynamic performance of the receiver; 2) VTL excels in balance the correlation of information between receiver signal channels, showcasing superior performance in scenarios involving weak signal tracking and rapid retracking; 3) it also exhibits superior anti-interference performance.

In general, STL tracks satellite signals by using conventional tracking loops (CTL) based on classical control theory, encompassing phase locking loops (PLL), frequency locking loops (FLL), and delay locking loops (DLL). The characteristics of CTL are determined by noise bandwidth and loop order. Notably, the selection of noise bandwidth involves a delicate trade-off between achieving low noise and maintaining high dynamic performance. Within the VTL, the dynamic stress of the loop filter is significantly alleviated through the incorporation of feedback information, which allows the tracking loop to concentrate exclusively on thermal noise, crystal frequency error, and dynamic residual [12,13]. Consequently, there is an opportunity to diminish the loop bandwidth, simultaneously improving tracking accuracy. It is important to note, however, that the loop bandwidth remains constrained by crystal frequency errors and feedback errors. In complex environments, signals may be affected by high dynamics, shadows, strong attenuation, multipath effects, or ionospheric scintillation, in which scenarios the performance of fixed-bandwidth tracking loop will deteriorate or even become ineffective. Therefore, the adaptive loop tracking (ALT) technology has garnered substantial research attention due to its ability to dynamically adjust the loop bandwidth in response to the varying noise levels encountered in different scenarios [14,15,16]. The contribution of the [17] derives the Doppler aiding error due to the uncertainty of the navigation error in the GPS/INS ultra-tight integration, and designs a PLL loop filter whose noise bandwidth can be adaptively adjustable according to the performance of the integrated navigation and the

{C / N}_{0}

of the GPS signal. In the [18], the adaptive scalar tracking techniques used by the fast adaptive bandwidth (FAB), the fuzzy logic (FL), and the loop-bandwidth control algorithm (LBCA) are delineated. A meticulous analysis of the tracking performance and time complexity of each method is conducted. These techniques dynamically adjust the loop bandwidth based on predefined discriminant criteria, thereby optimizing tracking performance for different scenarios. However, the adaptability of these adjustments is contingent upon specific discriminant criteria and thresholds.

Kalman filter (KF) based on optimal estimation theory stands out as an alternative method for dynamically adjusting loop noise bandwidth, gaining substantial attention in recent years owing to its superior performance in comparison to CTL [19,20]. The KF-based tracking loops replace conventional loop filters by estimating the loop parameters (e.g., carrier phase, Doppler frequency, and code phase) as state variables. Recherche process noise covariance Q and measurement noise covariance R enable KF to optimally adjust its gain coefficient in time-varying scenarios to achieve minimum mean square error (MMSE) criterion. Therefore, the real-time estimation and adjustment of Q and R play a crucial role in determining the filtering accuracy for time-varying scenarios. Numerous studies have delved into methods for adjusting KF parameters. Tang et al. [21,22] analyzes the relationship between the equivalent bandwidth of KF-based tracking loop and noise covariance, subsequently deducing the criteria for parameter setting. In [23], variational Bayesian (VB) theory is employed to dynamically estimate the measurement noise matrix, which improves the tracking accuracy in high dynamic scenes. Moreover, the process noise matrix can be adaptively tuned based on the characteristics of the crystal oscillator and receiver dynamics in STL [24]. However, there is a scarcity of research regarding the implementation of KF-based tracking loops in the VTL.

According to the different measurement information used, the signal tracking based on KF usually has two forms: one structure uses the output of traditional discriminator as measurement information and is implemented by linear KF; the other structure is measured by coherent integration results and implemented by nonlinear KF. Unfortunately, the loop discriminator introduces nonlinear noise in highly dynamic applications, deviating from the Gaussian white noise (GWN) property, thereby constraining the estimation accuracy. Therefore, in order to improve the tracking accuracy and dynamic range, the entire discriminator and tracking loop filter are replaced by a nonlinear tracking filter. In this case, the measurement is the outcome of the correlation between the input signal and the local signal, showcasing a nonlinear relationship with the estimated vector. Therefore, the application of a nonlinear filtering method is essential to achieve improved accuracy. Tang et al. [25] provides a comprehensive analysis of the practical implementation architecture for tracking loops based on extended Kalman filters (EKF). Zeng et al. [26] compared the EKF-based tracking loop of GPS receiver with the CTL, demonstrating that the EKF-based tracking loop excels in both high dynamic and tracking accuracy. Nevertheless, the EKF algorithm is a sub-optimal filtering algorithm based on nonlinear functionalization and adopts approximation or neglect method for higher order terms to solve nonlinear problems [27]. In the case of strong nonlinearity, it may result in a significant estimation error and even lead to filter divergence. Moreover, in practical applications, the computational complexity of obtaining the derivative of the Jacobian matrix for nonlinear functions is substantial.

To address the challenges inherent in the EKF, alternative methods such as the particle filter (PF) and unscented Kalman filter (UKF) have been proposed for nonlinear filtering problems [28,29]. PF, a recursive Bayesian filtering (BF) method, employs random samples to represent the posterior probability distribution of system state variables, overcoming certain limitations of EKF. However, PF requires a substantial number of particles to achieve high-precision estimation, resulting in a significant computational burden, particularly in scenarios with a high update rate for the tracking loop, which makes it difficult to operate in real time. The UKF is a method for approximating nonlinear distributions using a deterministic sampling strategy, which relies on the Unscented Transform (UT) and maintains the framework of a linear KF. In contrast to PF, the UKF replaces random sampling with deterministic sampling, while maintaining comparable computational complexity to the EKF. However, the performance is better than EKF, making it a widely adopted choice for nonlinear filtering [30,31].

Inspired by the above research, a vector tracking receiver has been developed that leverages an adaptive square root UKF (ASRUKF) tracking loops to enhance the precision and robustness of GNSS receivers in complex dynamic environments. The primary contributions of this research are as follows:

1): A vector receiver model based on a nonlinear tracking loop is designed, with comprehensive details provided on its implementation. The discriminator and traditional filter in the tracking loop are substituted with the UKF, and the Doppler feedback calculated by the navigation solution is incorporated into the loop filter. It accomplishes not only the loop tracking assistance by Doppler frequency but also establishes indirect connections between each channel, fostering mutual assistance.
2): To enhance the stability and robustness of the tracking loop, the square root filter is introduced into UKF. Additionally, the measurement noise covariance and process noise covariance of UKF are adjusted adaptively according to the signal ${C / N}_{0}$ and feedback information error, respectively. This adaptive adjustment enables real-time modification of the loop noise bandwidth, consequently enhancing the performance of the tracking loop.
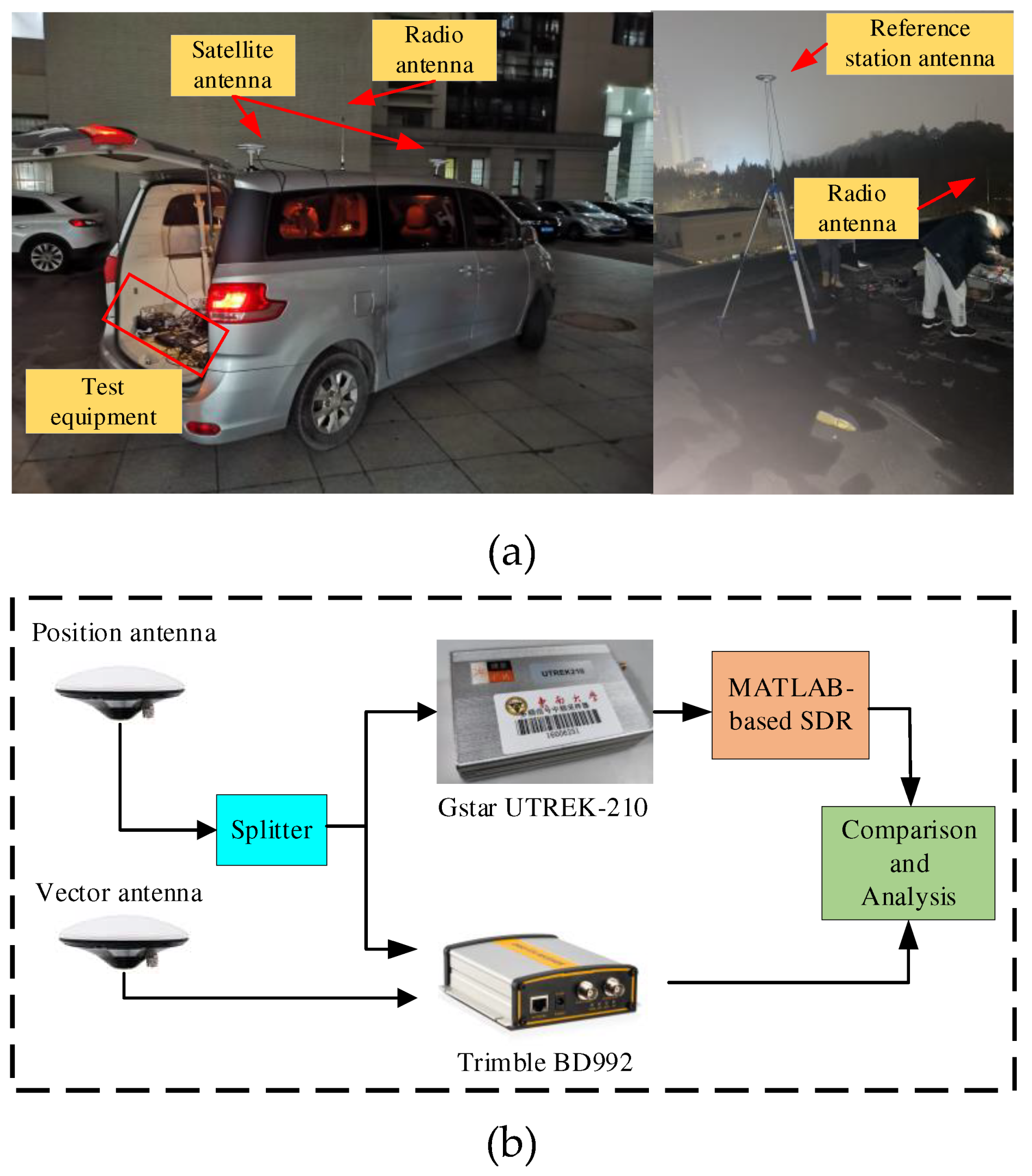
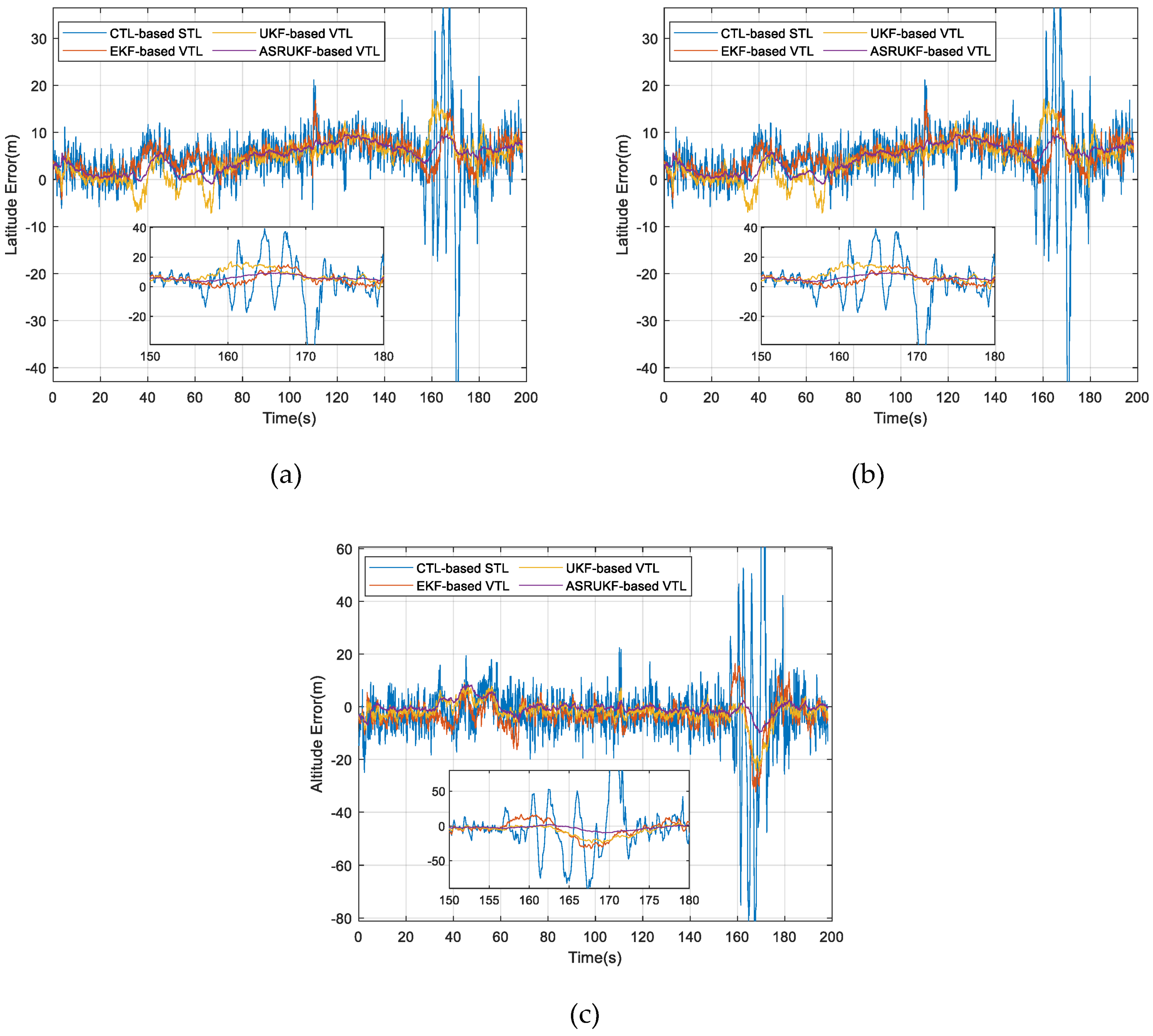
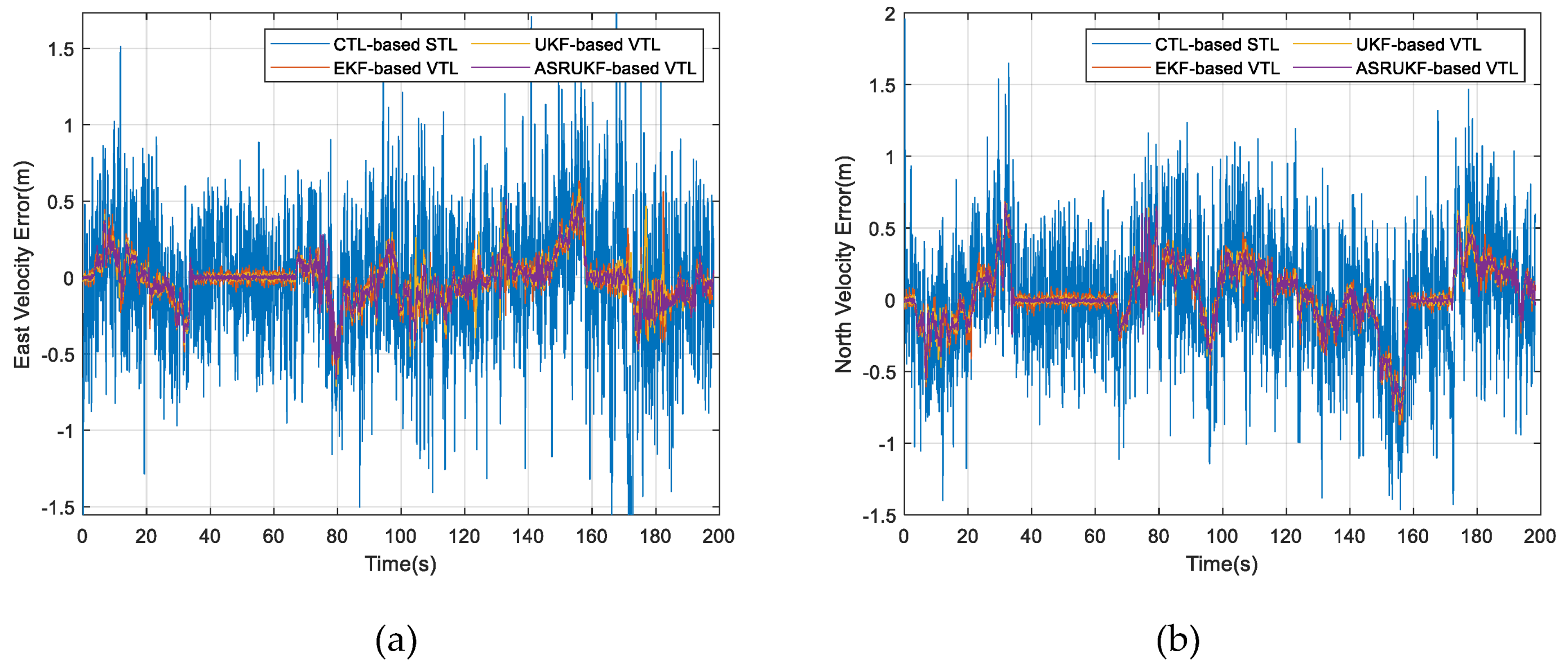
3): The effectiveness of the proposed method was verified through field vehicle experiments conducted on urban roads. Software-defined receiver (SDR) with different structures were developed to facilitate performance comparison and analysis. The results affirm that the KF-based VTL offers a substantial improvement over the CTL-based VTL, while demonstrating that the tracking accuracy of the UKF-based VTL surpasses that of the EKF-based VTL. Moreover, the ASRUKF-based VTL exhibits further performance improvement in complex dynamic environments.

The structure of this paper is organized as follows. In Section 2, the overall model of the vector tracking receiver is divided into three parts to describe in detail. Section 3 describes the design method of tracking loop based on adaptive square root UKF. In Section 4, the proposed VTL architecture is evaluated in a practical scenario and its performance is compared and analyzed within the SDR framework. Eventually, the conclusions and prospects are summarized in Section 5.

2. System Model of Vector Tracking

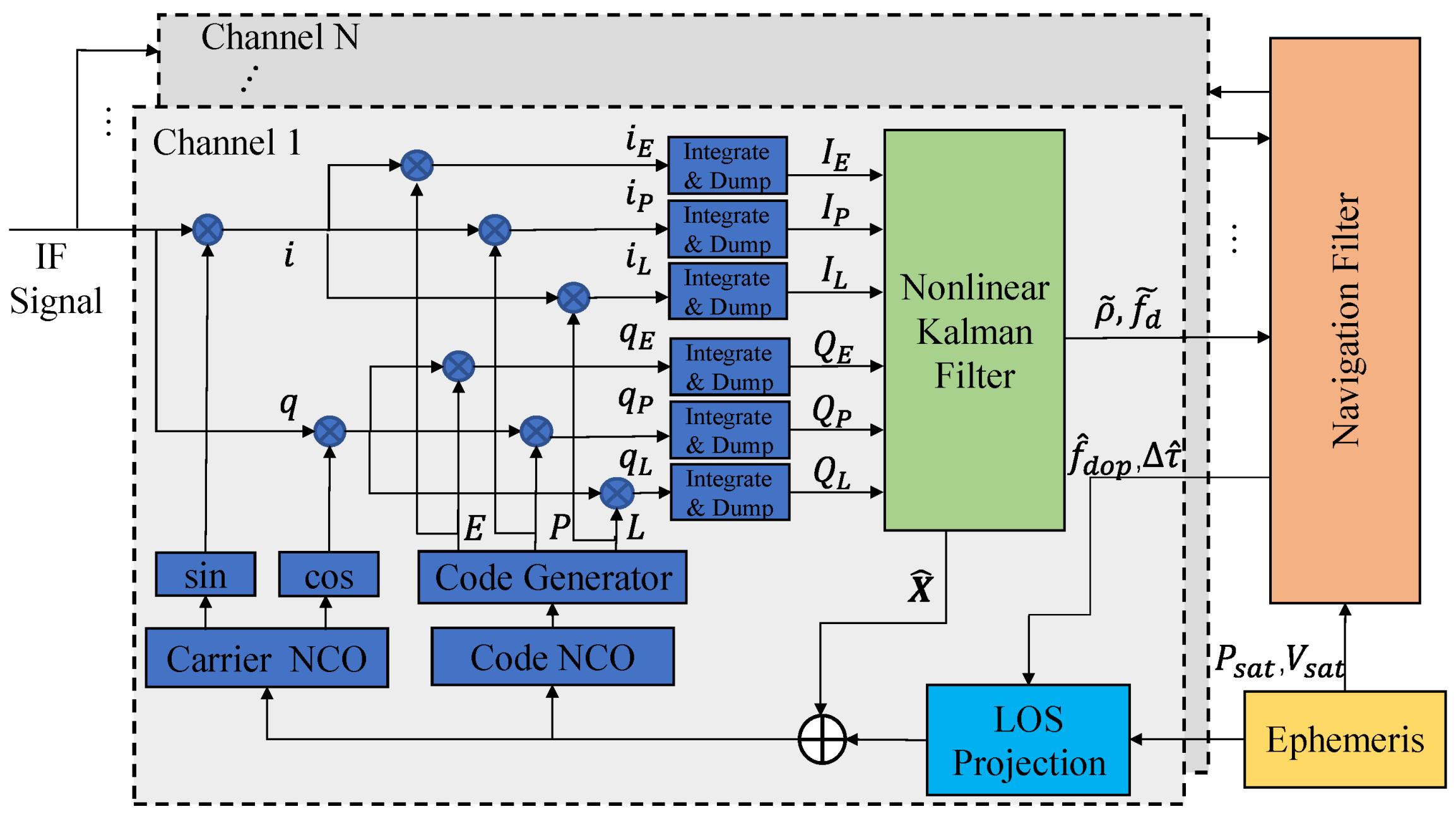
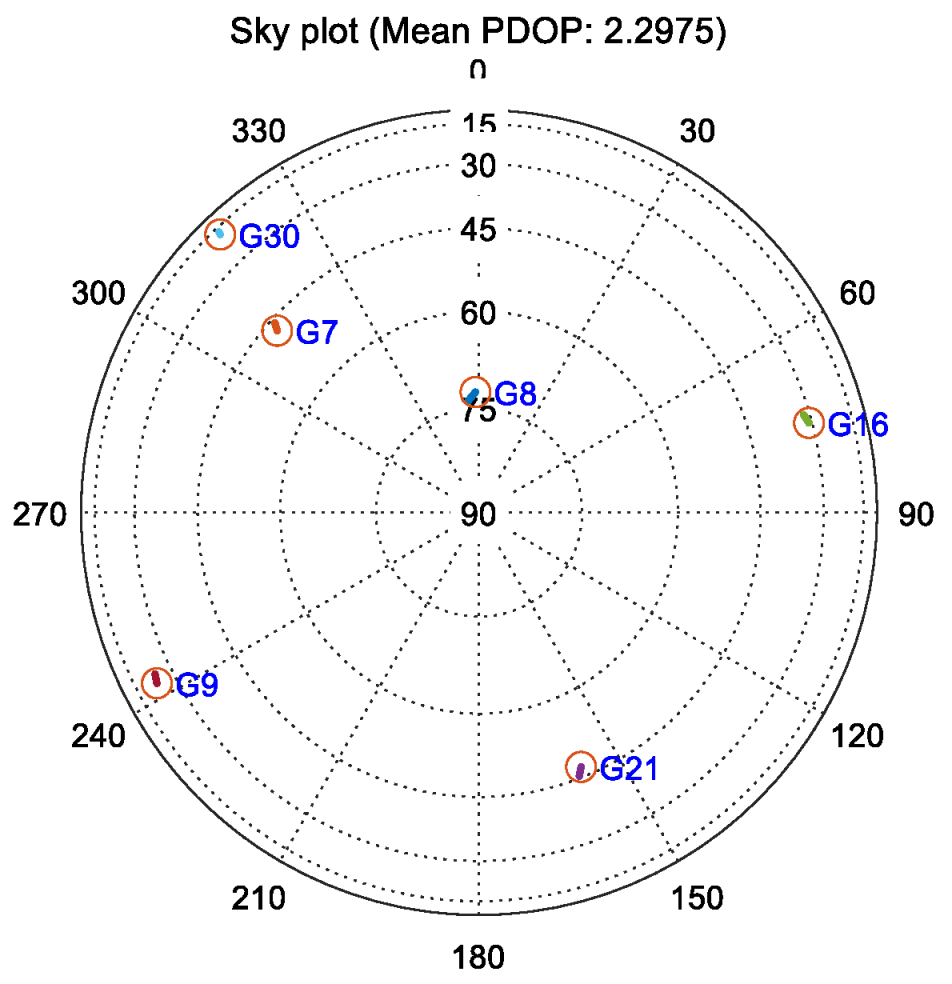
Generally, VTL receiver primarily comprises three components: nonlinear KF-based tracking loop; navigation solution module, and vector feedback calculation. The structure block diagram is illustrated in Figure 1.

The GNSS intermediate frequency (IF) signal is correlated with the local signal to obtain the I/Q components, which are then processed by the loop filter to generate pseudo-range and Doppler frequency information as the measurement of the navigation solution. After the navigation filter estimates the receiver’s PVT information, the satellite line-of-sight (LOS) vector for each channel is calculated by incorporating the satellite ephemeris information. Then, the feedback code phase and Doppler frequency are calculated and combined with the loop filtering results to adjust the local numerically controlled oscillator (NCO), thereby establishing a closed-loop system. The EKF is typically employed in the navigation solution module, resulting in the development of a cascaded vector tracking structure with the nonlinear KF-based tracking loop. This proposed structure not only lowers the update rate of the navigation filter but also reduces computational complexity and enhances ease of implementation.

2.1. Nonlinear KF-based Tracking Loop

Given that the discriminator is substituted with a loop filter, the I/Q information is utilized directly as the measurement for KF. The state vector to be estimated comprises the following components: signal amplitude

A

, code phase error

Δ τ

, carrier phase error

Δ θ

, carrier frequency error

Δ f

, and carrier frequency rate error

Δ α

. The system model can be formulated as follows:

[\begin{matrix} \dot{A} \\ Δ \dot{τ} \\ Δ \dot{θ} \\ Δ \dot{f} \\ Δ \dot{α} \end{matrix}] = [\begin{matrix} 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & β & 0 \\ 0 & 0 & 0 & 2 π & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 \end{matrix}] \cdot [\begin{matrix} A \\ Δ τ \\ Δ θ \\ Δ f \\ Δ α \end{matrix}] + [\begin{matrix} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & β & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} w_{A} \\ w_{τ} \\ w_{θ} \\ w_{f} \\ w_{α} \end{matrix}]

(1)

where the coefficient

β

is utilized to convert the cycles into chips, enabling unit conversion (e.g., for GPS L1:

β = 1 / 1540

). The value

w_{A}, w_{τ}, w_{θ}, w_{f}, w_{α}

represent the process noises of the signal amplitude, code phase error, clock bias, clock drift and frequency rate error, respectively.

The I/Q correlation values serve as the measurement of the filter, expressed in terms of:

Z = {[\begin{matrix} I_{P} & I_{E} & I_{L} & Q_{P} & Q_{E} & Q_{L} \end{matrix}]}^{T}

(2)

The variables

I_{P}

I_{E}

, and

I_{L}

represent the ‘prompt’, ‘early’, and ‘late’ correlation results of the In-phase correlator, respectively. Similarly,

Q_{P}

Q_{E}

, and

Q_{L}

represent the corresponding correlation results of the Quadrature-phase correlator.

The expression for the output of loop correlation value I/Q has been formulated:

\begin{array}{l} I = \frac{A}{2} \cdot D \cdot R (Δ τ + ξ d) \cdot \sin c (π T_{c o h} Δ f) \cdot \cos (\bar{Δ φ}) + η_{I} \\ Q = \frac{A}{2} \cdot D \cdot R (Δ τ + ξ d) \cdot \sin c (π T_{c o h} Δ f) \cdot \sin (\bar{Δ φ}) + η_{Q} \end{array}

(3)

where

D

is the navigation message,

R (\cdot)

is the autocorrelation function,

T_{c o h}

is the coherence integration time, represents the duration over which the received signals are integrated to estimate the coherence function.

d

is the correlator interval. For the early, prompt, and late branches,

ξ

are -1, 0, and +1 respectively. Additionally,

η_{I}

and

η_{Q}

represent zero-mean GWN that is independent of the I/Q branches. The average carrier phase error

\bar{Δ φ}

in the coherent integration time

T_{c o h}

is computed according to the following formula:

\bar{Δ φ} = Δ θ + Δ f \frac{T_{c o h}}{2} + Δ α \frac{T_{c o h}^{2}}{6}

(4)

Note that the Equation (3) signifies a nonlinear relationship between the measurement and the state vector of the tracking loop.

2.2. Nonlinear KF-based Tracking Loop

The VTL employs the EKF instead of the least square (LS) method to fuse pseudo-range and Doppler frequency for calculating the optimal PVT solution. This decision is based on its superior filtering performance and simplified fault detection and isolation capabilities.

The state vector representing the navigation solution is outlined as follows:

X_{n a v} = {[\begin{matrix} δ P_{1 \times 3} & δ V_{1 \times 3} & δ t_{b} & δ t_{d} \end{matrix}]}^{T}

(5)

where

δ P = [\begin{matrix} δ x & δ y & δ z \end{matrix}]

is the errors vector of position in ECEF coordinate system;

δ V = [\begin{matrix} δ v_{x} & δ v_{y} & δ v_{z} \end{matrix}]

is the corresponding velocity errors vector.

δ t_{b}

and

δ t_{d}

refer to the errors associated with clock bias and drift of receiver.

The system adopts the constant velocity model, thus enabling the expression of the discrete state transition matrix of the system as follows:

F_{n a v} = [\begin{matrix} \begin{matrix} I_{3} & T_{n a v} I_{3} \\ 0_{3} & I_{3} \end{matrix} & 0_{6 \times 2} \\ 0_{2 \times 6} & \begin{matrix} 1 & T_{n a v} \\ 0 & 1 \end{matrix} \end{matrix}]

(6)

where

T_{n a v}

represents the navigation filter update time,

I_{3}

is a three-dimensional identity matrix.

The measurement of the navigation filter consists of the difference between the calculated and estimated pseudo-range, along with the Doppler frequency for each channel:

Z_{n a v} = {[{\tilde{ρ}}^{(1)} - {\hat{ρ}}^{(1)}, \dots, {\tilde{ρ}}^{(m)} - {\hat{ρ}}^{(m)}, {\tilde{f}}_{d o p}^{(1)} - {\hat{f}}_{d o p}^{(1)}, \dots, {\tilde{f}}_{d o p}^{(m)} - {\hat{f}}_{d o p}^{(m)}]}^{T}

(7)

The variables

{\tilde{ρ}}^{(m)}

and

{\tilde{f}}_{d o p}^{(m)}

represent the measured pseudo range and Doppler frequency of channel m respectively, while

{\hat{ρ}}^{(m)}

and

{\hat{f}}_{d o p}^{(m)}

denote the estimated pseudo-range and Doppler frequency correspondingly.

The matrix representing the transfer of measurements is presented below [32]:

H_{n a v} = [\begin{matrix} e_{x}^{1} & e_{y}^{1} & e_{z}^{1} & 0 & 0 & 0 & 1 & 0 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ e_{x}^{m} & e_{y}^{m} & e_{z}^{m} & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e_{x}^{1} & e_{y}^{1} & e_{z}^{1} & 0 & 1 \\ ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ & ⋮ \\ 0 & 0 & 0 & e_{x}^{m} & e_{y}^{m} & e_{z}^{m} & 0 & 1 \end{matrix}]

(8)

where, is the LOS vector from the receiver to the m-th satellite, calculation as follows:

e^{m} = \frac{p_{s}^{m} - p_{u}}{‖ p_{s}^{m} - p_{u} ‖}

(9)

where,

p_{u}

and

p_{s}^{m}

represent the position vectors of the receiver and the m-th satellite respectively.

2.3. Nonlinear KF-based Tracking Loop

When the PVT information is estimated by the navigation filter, the carrier and code NCO feedback correction information of each channel can be calculated by combining the satellite ephemeris.

The Doppler frequency estimation of the tracking channel j at time k can be computed as follows:

{\hat{f}}_{d o p, k}^{j} = [t_{d, k} + e_{k}^{j} \cdot (v_{s, k}^{j} - v_{u, k})] \cdot \frac{f_{c a r r i e r}}{c}

(10)

where

v_{u, t}

and

v_{s, t}^{j}

are the receiver velocity and the velocity of the channel j satellite, respectively, while

t_{d, t}

denotes the clock drift at time k. Additionally,

f_{c a r r i e r}

corresponds to the carrier frequency (e.g., for GPS L1

f_{c a r r i e r} = 1575.42 M H z

), and

c

signifies the velocity of light (e.g.,

c = 29979245 m / s

Combined with the results of the loop filter, the final carrier frequency is:

{\hat{f}}_{c a r r i e r, k}^{j} = f_{I F} + {\hat{f}}_{d o p, k}^{j} + X_{k}^{j} (4) + X_{k}^{j} (5) \cdot T_{c o h}

(11)

where,

f_{I F}

is the IF signal of the RF front-end output, and

X_{k}^{j} (n)

is the n-th element of the state vector

X_{k}^{j}

of tracking loop at time k.

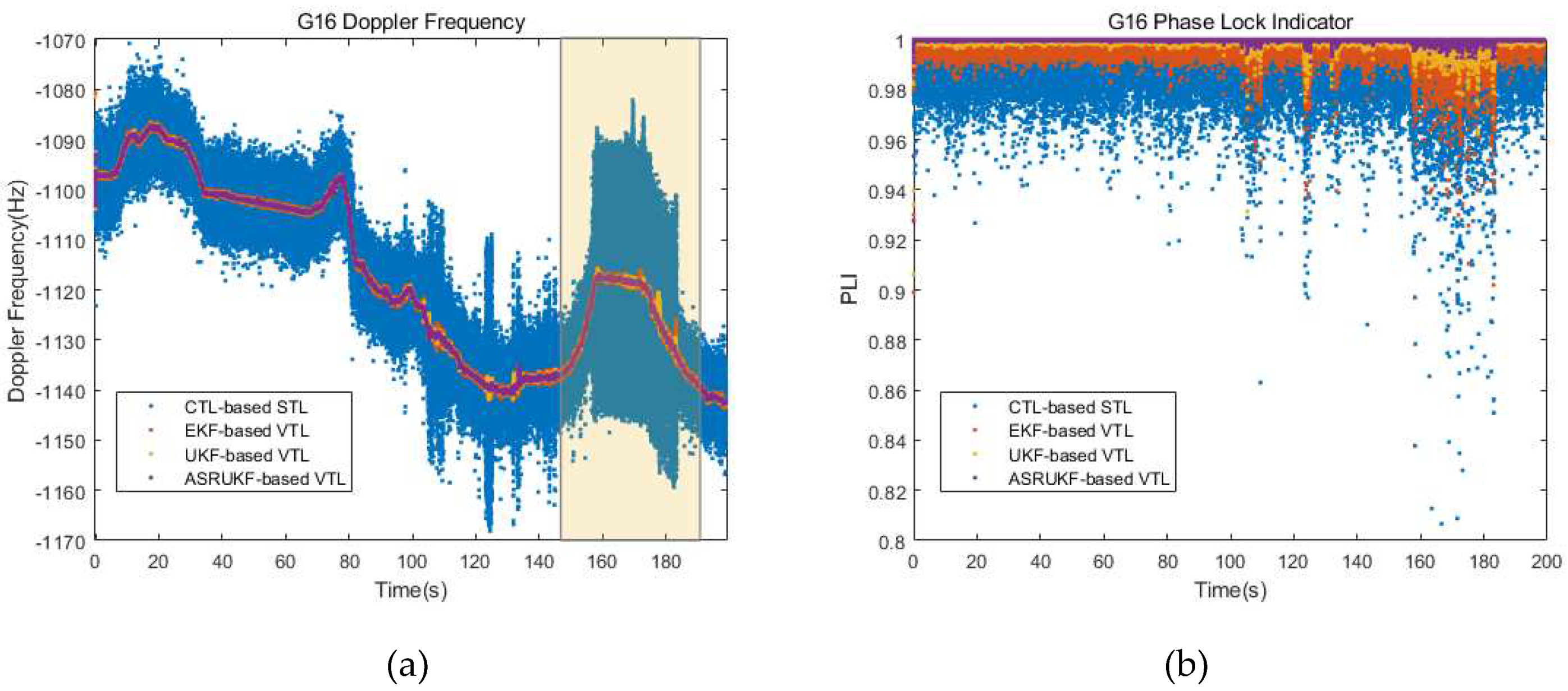
As evident from the Equation (11), the incorporation of Doppler frequency significantly alleviates the dynamic stress of the loop. This not only enhances the dynamic performance of the receiver, but also allows the loop filter to further decrease the noise bandwidth, consequently improving tracking accuracy and sensitivity.

Accordingly, the estimation of code frequency can be calculated directly using a carrier Doppler assisted form:

{\hat{f}}_{c o d e, k}^{j} = f_{c o d e} \cdot (1 + {\hat{f}}_{d o p, k}^{j} \cdot \frac{1}{f_{c a r r i e r}})

(12)

The code phase is computed according to the following procedure:

(13)

where

λ_{c h i p}

is the length of the pseudo-code chip (e.g., for GPS L1

C / A

signal:

λ_{c h i p} = 1023

Furthermore, following the completion of the NCO update, the state vector is reset to zero, thereby initiating the subsequent cycle’s state estimation process.

3. Proposed Adaptive SRUKF-based Loop Tracking

The tracking loop filter can be represented by a nonlinear state space model:

{\begin{matrix} X_{k} = f (X_{k - 1}) + W_{k - 1} \\ Z_{k} = h (X_{k}) + V_{k} \end{matrix}

(14)

where,

X_{k}

denotes the state vector and

Z_{k}

is the measurement vector, while

f (\cdot)

and

h (\cdot)

are nonlinear functions of the system and measurement model, respectively. The vectors

W_{k - 1}

and

V_{k}

correspond to process noise and measurement noise with zero-mean and covariance

Q_{k}

and

R_{k}

, respectively.

3.1. Square Root Unscented Kalman Filter

The UKF utilizes sigma points to approximate the functional probability density distribution, thereby facilitating nonlinear filtering. However, the necessity of calculating sigma points at each update, which involves taking the square root of the state covariance matrix, can lead to issues such as computational burden and numerical instability. By integrating the concept of square root filtering within the UKF framework, it is possible to reduce computational complexity and enhance efficiency. This is achieved through direct recursion updating in the form of the square root of the covariance matrix. Moreover, this approach guarantees the non-negativity of the covariance matrix, effectively prevents filter divergence, and fosters the convergence speed and numerical stability of the filter.

The Square Root Unscented Kalman Filter (SRUKF) utilizes QR decomposition and Cholesky factor update techniques to replace the covariance matrix with its square root, thereby enhancing the efficiency of the filtering iteration. The specific procedural steps are delineated in Table 1.

3.2. Adaptive SRUKF-based Loop Tracking for Vector Tracking

In the VTL, different from STL, the tracking loop can eliminate most of the dynamic stress with the assistance of Doppler frequency. However, this also introduces additional frequency errors due to navigation inaccuracies. Beyond addressing loop thermal noise and receiver crystal error, the tracking loop also tracks the Doppler auxiliary error induced by navigation error, which constitutes the majority of the tracking error. Given the uncertainty of navigation solution error, the signal dynamics generated by the navigation solution cannot be optimally tracked using SRUKF-based loop filter with constant parameters.

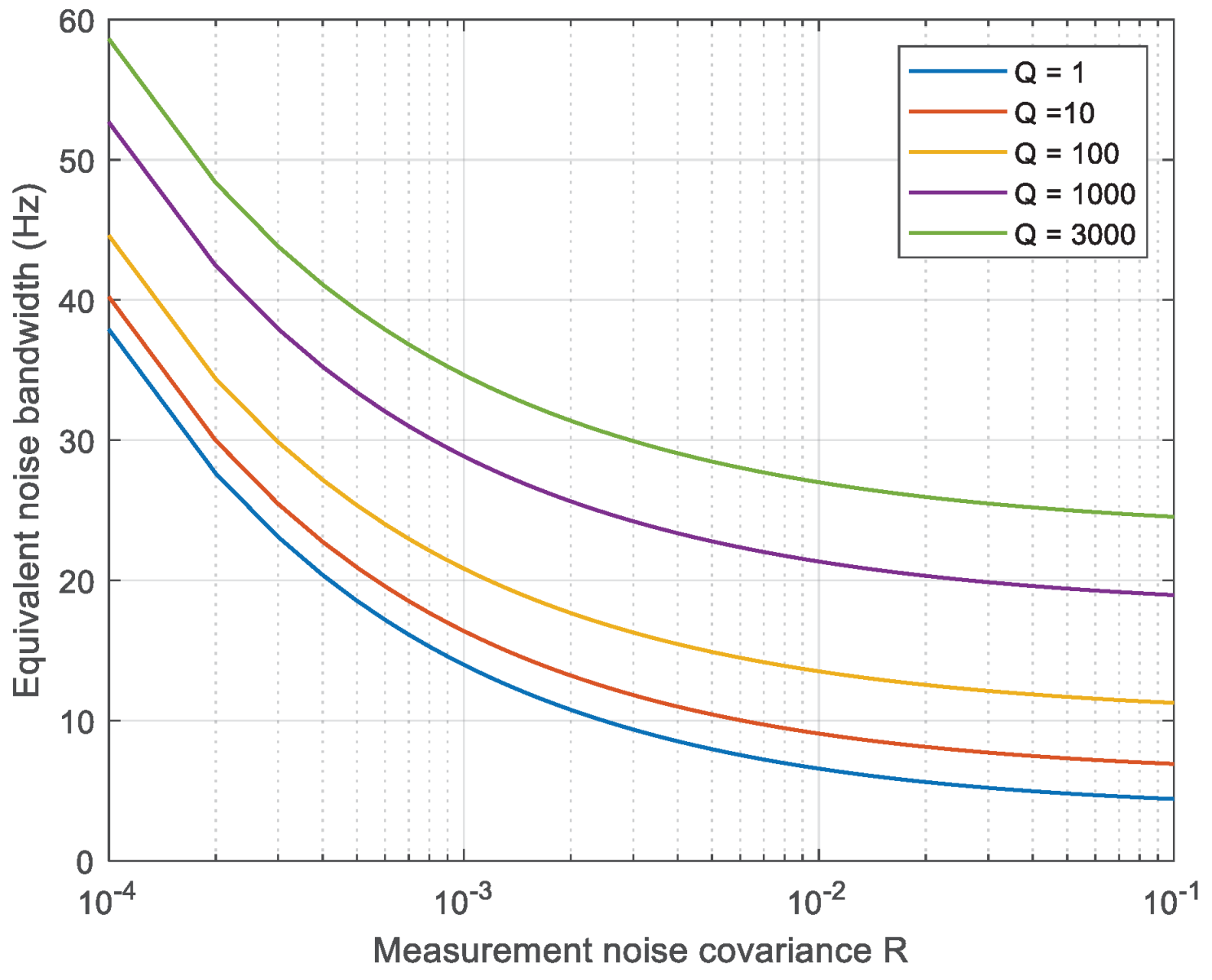
The steady-state equivalent bandwidth of the KF-based tracking loop is determined by the ratio of the process noise covariance to the measurement noise covariance (Q/R), and its specific value can be derived from the filter parameters [21]. The Figure 2 illustrates the equivalent noise bandwidth of the KF-based tracking loop in steady-state, considering various process noise covariances Q, with respect to the measurement noise covariance R. When the signal is weak (i.e., low

{C / N}_{0}

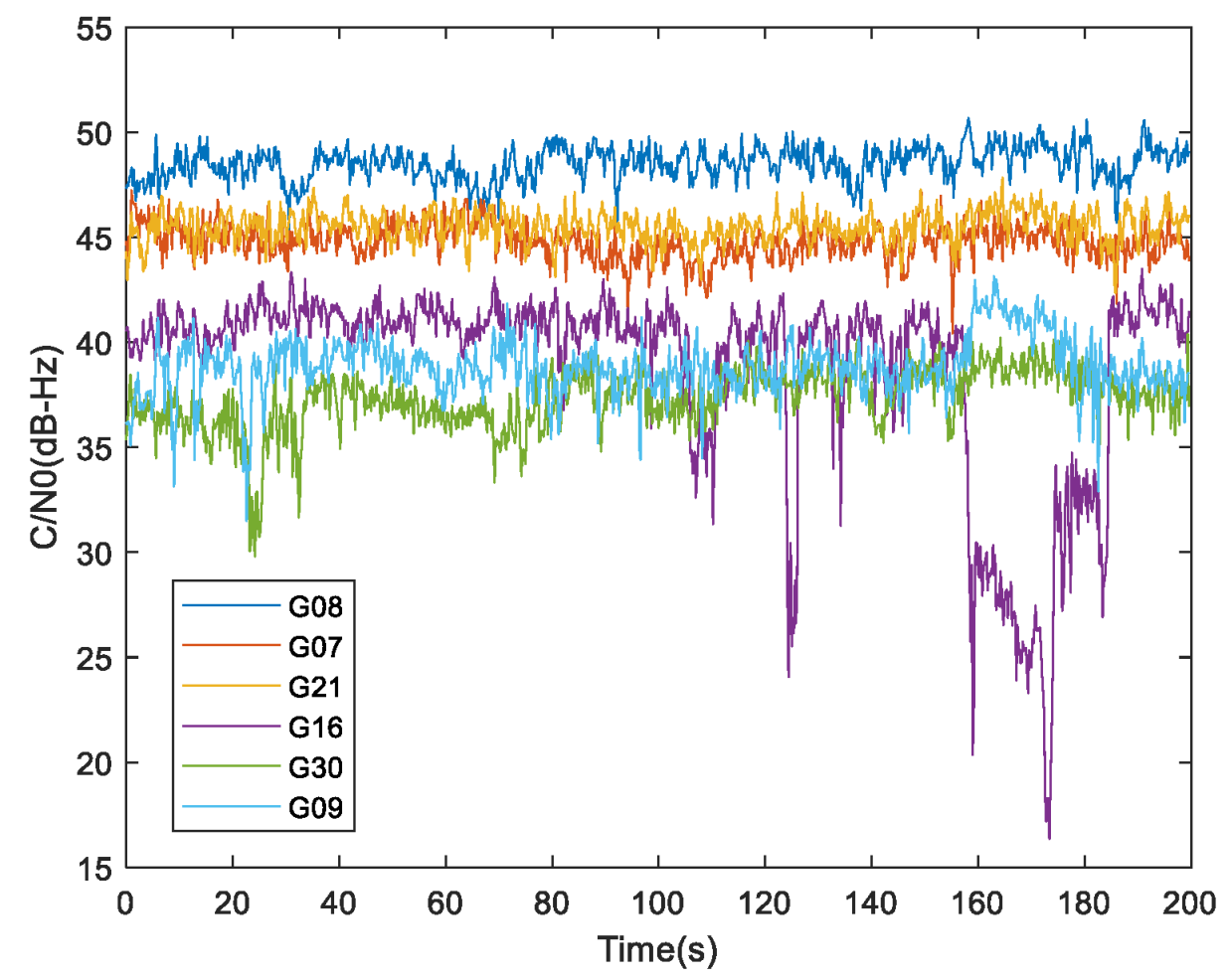
), the loop bandwidth is reduced in order to enhance noise filtering. However, excessively reducing the loop bandwidth may lead to inadequate tracking of dynamic signals during rapid fluctuations. Consequently, adaptive mechanisms are frequently employed to dynamically adjust parameters in real time based on external information, thereby achieving optimal state estimation.

The measurement noise covariance of prompt component in previous studies can be calculated by considering the

{C / N}_{0}

r_{η_{I_{p}}}^{2} = r_{η_{Q_{p}}}^{2} = \frac{S P}{2 \cdot 10^{({C / N}_{0}) / 10} \cdot T_{c o h}}

(15)

where,

η_{I}

and

η_{Q}

can be referred to the description in the Equation (3). The signal power is denoted as

S P = A^{2} / 2

, while the

{C / N}_{0}

is expressed in units of dBHz. The narrowband broadband power ratio method (NWPR) is employed in this paper for calculating the

{C / N}_{0}

due to its superior estimation performance when dealing with weak signals.

In addition, the noise covariance of the early and late branches is calculated as follows:

(16)

Thus, corresponding to Equation (2), the measurement noise covariance matrix

R_{k}

of the loop filter is represented as a diagonal matrix in the following form:

R_{k} = d i a g [\begin{matrix} r_{η_{I_{P}}}^{2} & r_{η_{I_{E}}}^{2} & r_{η_{I_{L}}}^{2} & r_{η_{Q_{P}}}^{2} & r_{η_{Q_{E}}}^{2} & r_{η_{Q_{L}}}^{2} \end{matrix}]

(17)

However, the determination of dynamic stress in the tracking loop solely based on is insufficient. Therefore, this research also considers adaptive adjustment of process noise covariance

Q_{k}

, which can be modified based on estimated Doppler frequency error resulting from the uncertainty of the navigation solution. Essentially, the imprecision associated with navigation error manifests the dynamics of the tracking loop, which resulting in an inherent uncertainty in the state equation.

Primarily, in accordance with Equation (10), the uncertainty of the estimated Doppler frequency is determined through the examination of the state covariance during the navigation solution process.

σ_{a i d, k}^{2} = [P_{d, k} + e_{k}^{j} \cdot P_{v, k} \cdot {(e_{k}^{j})}^{T}] \cdot {(\frac{f_{c a r r i e r}}{c})}^{2}

(18)

where

P_{d, k}

and

P_{v, k}

represent the noise covariance matrices associated with the clock drift and velocity components, respectively.

Subsequently, the process noise covariance matrix

Q_{k}

of the loop filter is adjusted adaptively based on the Doppler frequency error covariance and thereby effectively regulate the loop noise bandwidth:

{\hat{Q}}_{k} = Q_{0} + Δ Q_{k}

(19)

where,

Q_{0}

signifies the initial value of state noise covariance, with the setting criteria available in reference 22. Additionally,

Δ Q_{k}

represents the additional process noise covariance resulting from the uncertainty associated with navigation errors.

Δ Q_{k} = α \sqrt{σ_{a i d, k}^{2}} \cdot I_{Q}

(20)

where,

α

represents the scale factor governing the conversion from Doppler frequency error to process noise covariance, while

I_{Q}

is the identity matrix of the same dimension as

Q_{k}

. It is worth noting that

α

determines the sensitivity of the

Δ Q_{k}

matrix concerning Doppler frequency error. Therefore,

α

can adjust itself according to

{C / N}_{0}

α = \frac{α_{0}}{{C / N}_{0}}

(21)

It becomes evident that inverse proportionality between the sensitivity of matrix

Δ Q_{k}

to Doppler frequency error and

{C / N}_{0}

. The sensitivity of the Doppler error can be appropriately reduced when the

{C / N}_{0}

is high, while a decrease in

{C / N}_{0}

results in heightened sensitivity.

4. Experimental Evaluation and Results

4.1. Experimental Setup

The efficacy of the proposed method underwent evaluation through the establishment of a vehicle verification platform, depicted in Figure 3. The Trimble BD992 receiver are employed to deliver accurate position and velocity references. Operating in fixed RTK mode, the receiver demonstrated outstanding horizontal positioning accuracy of 0.8 cm and vertical positioning accuracy of 1.5 cm. The Gstar UTREK-210 IF signal collector is employed for the collection of the satellite’s IF signal, with the IF

f_{I F} = 4.5 M H z

and sampling rate

f_{s} = 19.1999 M H z

. The two devices are interconnected through a power splitter, enabling them to share the same satellite antenna installed on the vehicle’s rooftop.

The MATLAB-based GPS L1 SDR was used to evaluate the receiver performance of various methods. This research encompasses the evaluation of four distinct SDR architectures, which include:

Scheme 1: Scalar tracking receivers based on conventional tracking loops (CTL-based STL);

Scheme 2: Vector tracking receiver based on EKF loop filter (EKF-based VTL);

Scheme 3: Vector tracking receiver based on SRUKF loop filter (UKF-based VTL);

Scheme 4: Vector tracking receiver based on ASRUKF loop filter (ASRUKF-based VTL).

The parameter configurations specific to the aforementioned methods are presented in Table 2.

d

Coherence integration time T_{c o h}

Navigation filter update time T_{n a v}

4.2. Tracking Performance Analysis

The vehicle experiment was conducted on the city road in Nanjing, China. The experimental environment encompasses various elements such as open sky, high buildings and trees, and other natural settings. The driving maneuvers encompassed acceleration, deceleration, and turning maneuvers. The data collection is scheduled to commence at UTC 11:28:46, December 18, 2021, with a designated analysis period of 200 seconds. There are six satellites were acquired successfully in the course of the experiment. The satellite sky-plot is displayed in Figure 4, with an average Position Dilution of Precision (PDOP) value of 2.2975.

The

{C / N}_{0}

of all satellites throughout the entire experiment is illustrated in Figure 4. It is apparent that the

{C / N}_{0}

remains relatively stable during vehicle operation; however, certain satellite signals exhibit a more significant decline when encountering severe interference or occlusion. This significantly impacts the continuity of the tracking loop, potentially leading to inaccuracies in positioning results.

A closer look at Figure 5 reveals that, owing to the low elevation angle of satellite G16, the signal experiences severe blockage is in motion around 150 seconds, leading to a sharp decline in the

{C / N}_{0}

and significantly impacting the tracking loop. Illustrated in Figure 6a, the Doppler frequency estimation of the conventional STL is notably affected within the corresponding signal interruption interval. However, the VTL can combine all the channel information and utilizes the navigation information calculated by the navigation solution module to estimate the carrier frequency. This enables continuous tracking even under short periods of signal interruption.

In addition, phase lock indicator (PLI) serves as a metric to evaluate the tracking performance of each method, and the closer the PLI value is to 1, the higher the tracking accuracy [33]. It can be clearly seen from Figure 6b that the independence of each channel in traditional scalar tracking has a significant impact on the tracking performance of the single loop when influenced by external factors. In contrast, the VTL facilitates mutual assistance between channels, thereby enhancing tracking accuracy even when a single channel is disturbed.

4.3. PVT Results Evaluation

In addition, we utilize the navigation results generated by the high-precision Trimble RTK receiver as a benchmark to evaluate the position and velocity accuracy of the proposed method. The PVT results are crucial in determining the performance of the receiver, and their precision also impacts the accuracy of feedback Doppler frequency information, which indirectly influences loop tracking performance.

The position errors of different methods are illustrated in Figure 7, revealing that the VTL based on KF loop significantly improve the positioning accuracy compared to the STL receiver using the CTL. Especially when the signal is occluded (150s-180s data segment), all methods are affected. However, the VTL method, by combining feedback information calculated by all channels, effectively shares information between channels, leading to improved positioning accuracy in interference environments. Among these methods, the VTL method based on ASRUKF demonstrates the highest level of accuracy, followed by the VTL method based on UKF, while the VTL method based on EKF exhibits comparatively lower performance. This demonstrates the superior efficacy of UKF over EKF in nonlinear approximation. Furthermore, by incorporating a parameter adaptation method, ASRUKF dynamically adjusts the UKF bandwidth in real time based on the dynamics of the vehicle, so as to obtain more stable navigation and positioning results.

The root mean square error (RMSE) and standard deviation (STD) of position in three directions are summarized in Table 3. The table clearly demonstrates a significant enhancement in the accuracy of EKF-based VTL compared to CTL-based STL. Moreover, the advantages of UKF-based VTL and ASRUKF-based VTL have been convincingly demonstrated.

Furthermore, Figure 8 and Table 4 present the results of velocity error and their corresponding statistics, respectively, showing the same conclusion as the positions. The observation from Figure 8 reveals that, during the vehicle driving process, ASRUKF-based VTL adaptively adjusts the measurement noise covariance matrix R and process noise covariance Q respectively according to the signal

{C / N}_{0}

and feedback Doppler error. This adaptive adjustment optimizes the noise bandwidth, facilitating more effective tracking of dynamic signals. The experimental results prove that the proposed method achieves PVT outcomes with enhanced precision, thus improving the robustness and accuracy of the receiver in complex environments.

5. Conclusion

The paper introduces a vector tracking receive based on a nonlinear Kalman Filter (KF) tracking loop to enhance the receiver’s performance in complex environments. Firstly, the structure of the VTL is described in detail. Secondly, to address the strong nonlinearity arising from the loop filter using I/Q information as the measurement, the UKF is employed instead of the EKF to avoid the truncation errors associated with the first-order approximation. Additionally, square root filtering and adaptive criteria are introduced. ASRUKF dynamically adjusts the noise bandwidth based on the signal

{C / N}_{0}

and feedback error, thereby improving the stability and robustness of the tracking loop. Finally, a field vehicle experiment is designed, and the results of SDR based on different structures are compared, demonstrating the superiority of the proposed method in complex dynamic environments.

In addition, the successful implementation of the proposed method provides a way to introduce other sensors to assist the receiver loop tracking and improve GNSS receiver dynamic range and robustness, such as GNSS/INS ultra-tight integration.

Author Contributions

Conceptualization, N.G. and Z.Y.; methodology, N.G.; software, N.G.; validation, N.G.; formal analysis, N.G.; investigation, N.G.; resources, X.C.; data curation, N.G.; writing—original draft preparation, N.G.; writing—review and editing, N.G. and Z.J.; visualization, N.G.; supervision, X.C.; project administration, X.C.; funding acquisition, X.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by National Natural Science Foundation of China, grant number No. 61873064.

Data Availability Statement

The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.

Acknowledgments

The authors would like to thank Yulu Zhong and Junwei Wang for their assistance in the completion of experiments.

Conflicts of Interest

The authors declare no conflicts of interest.

References

Locubiche-Serra, S.; Seco-Granados, G.; López-Salcedo, J. A. Performance assessment of a low-complexity autoregressive Kalman filter for GNSS carrier tracking using real scintillation time series. GPS Solut. 2022, 26, 1–14. [Google Scholar] [CrossRef]
Jiang, C.; Chen, S.; Chen, Y.; Liu, D.; Bo, Y. GNSS vector tracking method using graph optimization. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 68, 1313–1317. [Google Scholar] [CrossRef]
Yan, Z.; Ruotsalainen, L.; Chen, X.; Tang, X. An INS-assisted vector tracking receiver with multipath error estimation for dense urban canyons[J]. GPS Solut. 2023, 27, 88. [Google Scholar] [CrossRef]
Peng, Z.; Gao, Y.; Gao, C.; Shang, R.; Gan, L. Improving Smartphone GNSS Positioning Accuracy Using Inequality Constraints. Remote Sens. 2023, 15, 2062. [Google Scholar] [CrossRef]
Ding, Y.; Chauchat, P.; Pages, G.; Asseman, P. Learning-enhanced adaptive robust GNSS navigation in challenging environments. IEEE Robot. Autom. Lett. 2022; 7, 9905–9912. [Google Scholar]
Shen, C.; Zhao, X.; Wu, X.; Cao, H.; Wang, C.; Tang, J.; Liu, J. Multi-aperture Visual Velocity Measurement Method based on Biomimetic Compound-eye for UAVs. IEEE Internet Things J. 2023. [Google Scholar]
Jiang, C.; Chen, Y.; Xu, B.; Jia, J.; Sun, H.; Chen, C.; Zhiyong Duan; Yuming Bo Hyyppä, J. Vector tracking based on factor graph optimization for GNSS NLOS bias estimation and correction. IEEE Internet Things J. 2022, 9, 16209–16221. [Google Scholar] [CrossRef]
Lashley, M.; Bevly, D, M. ; Hung, J, Y. Performance analysis of vector tracking algorithms for weak GPS signals in high dynamics. IEEE J. Sel. Top. Signal Process. 2009, 3, 661–673. [Google Scholar] [CrossRef]
Yan, Z.; Chen, X.; Tang, X.; Zhu, X. Design and Performance Evaluation of the Improved INS-Assisted Vector Tracking for the Multipath in Urban Canyons. IEEE Trans. Instrum. Meas. 2022, 71, 1–16. [Google Scholar] [CrossRef]
Zhao, S.; Akos, D. An open source GPS/GNSS vector tracking loop-implementation, filter tuning, and results. In Proceedings of the 2011 International Technical Meeting of The Institute of Navigation (ITM), San Diego, California, USA, 24-26, Jan 2011; pp. 1293–1305. [Google Scholar]
Xu, B.; Hsu, L, T. Open-source MATLAB code for GPS vector tracking on a software-defined receiver. GPS Solut. 2019, 23, 1–9. [Google Scholar] [CrossRef]
GEBRE-EGZIABHER, D. E. M. O. Z.; Razavi, A.; Enge, P. K.; Gautier, J.; Pullen, S.; Pervan, B. S.; Akos, D. M. Sensitivity and Performance Analysis of Doppler-Aided GPS Carrier-Tracking Loops. Navigation, 2005, 52, 49–60. [Google Scholar] [CrossRef]
Zhang, T.; Zhang, H.; Lin, T.; Yan, K.; Niu, X. Modeling and verifying the impact of time delay on INS-aided GNSS PLLs. GPS Solut. 2016, 20, 725–736. [Google Scholar] [CrossRef]
Cheng, Y.; Chang, Q. A carrier tracking loop using adaptive strong tracking Kalman filter in GNSS receivers. IEEE Commun. Lett. 2020, 24, 2903–2907. [Google Scholar] [CrossRef]
Yang, H.; Zhou, B.; Wang, L.; Wei, Q.; Ji, F.; Zhang, R. Performance and evaluation of GNSS receiver vector tracking loop based on adaptive cascade filter. Remote Sens. 2021, 13, 1477. [Google Scholar] [CrossRef]
Wu, M.; Zhao, L.; Ding, J.; Gao, Y.; Li, Y.; Kang, Y. A BDS-3 B1C/B2a dual-frequency joint tracking architecture based on adaptive Kalman filter and extended integration time. GPS Solut. 2020, 24, 1–16. [Google Scholar] [CrossRef]
Sun. D.; Petovello, M, G.; Cannon, M, E. Use of a reduced IMU to aid a GPS receiver with adaptive tracking loops for land vehicle navigation. GPS Solut. 2010, 14, 319–329. [Google Scholar] [CrossRef]
Cortés, I.; van der Merwe, J. R.; Lohan, E. S.; Nurmi, J.; Felber, W. Performance evaluation of adaptive tracking techniques with direct-state Kalman filter. Sensors, 2022, 22, 420. [Google Scholar] [CrossRef] [PubMed]
Jin T, Wang C, Lu X, et al. Analysis of a federal Kalman filter-based tracking loop for GPS signals. GPS Solut. 2019, 23, 1–13. [Google Scholar]
Klokov, A.; Kanouj, M.; Mironchev, A. A novel carrier tracking approach for GPS signals based on Gauss–Hermite Kalman filter. Electronics, 2022, 11, 2215. [Google Scholar] [CrossRef]
Tang, X.; Wang, C.; Lu, X.; Ling, K. V.; Cong, L. The explicit tuning investigation and validation of a full Kalman filter-based tracking loop in GNSS receivers. IEEE Access, 2019, 7: 111487-111498.
Tang, X.; Falco, G.; Falletti, E.; Lo Presti, L. Theoretical analysis and tuning criteria of the Kalman filter-based tracking loop. GPS Solut. 2015, 19, 489–503. [Google Scholar] [CrossRef]
Miao, Z. Y.; Lv, Y. L.; Xu, D. J.; Shen, F.; Pang, S. W. Analysis of a variational Bayesian adaptive cubature Kalman filter tracking loop for high dynamic conditions. GPS Solut. 2017, 21, 111–122. [Google Scholar] [CrossRef]
Cortés, I.; Conde, N.; Van Der Merwe, J. R.; Lohan, E. S.; Nurmi, J.; Felber, W. Low-complexity adaptive direct-state Kalman filter for robust GNSS carrier tracking. In 2022 International Conference on Localization and GNSS (ICL-GNSS). Tampere, Finland, 7-9 Jun 2022; pp. 1–7.
Tang, X.; Falco, G.; Falletti, E.; Presti, L. L. Practical implementation and performance assessment of an Extended Kalman Filter-based signal tracking loop. In 2013 International Conference on Localization and GNSS (ICL-GNSS). Turin, Italy,25-27 Jun 2013; pp. 139–144.
Zeng, C.; Li, W. Application of extended Kalman filter for tracking high dynamic GPS signal. In 2016 IEEE International Conference on Signal and Image Processing (ICSIP). Beijing, China, 13-15 Aug 2016; pp. 503–507.
Tu, Z.; Lou, Y.; Guo, W.; Song, W.; Wang, Y. Design and Validation of a Cascading Vector Tracking Loop in High Dynamic Environments. Remote Sens. 2021, 13, 2000. [Google Scholar] [CrossRef]
Liu, J.; Chen, X.; Wang, J. Strong Tracking UKF-Based Hybrid Algorithm and Its Application to Initial Alignment of Rotating SINS With Large Misalignment Angles. IEEE Trans. Ind. Electron. 2022, 70, 8334–8343. [Google Scholar] [CrossRef]
Zhong, Y.; Chen, X.; Zhou, Y.; Wang, J. Adaptive Particle Filtering with Variational Bayesian and Its Application for INS/GPS Integrated Navigation. IEEE Sens. J. 2023. [Google Scholar] [CrossRef]
Gao, Z.; Mu, D.; Gao, S.; Zhong, Y.; Gu, C. Adaptive unscented Kalman filter based on maximum posterior and random weighting. Aerosp. Sci. Technol. 2017, 71, 12–24. [Google Scholar] [CrossRef]
Jwo, D. J.; Yang, C. F.; Chuang, C. H.; Lee, T. Y. Performance enhancement for ultra-tight GPS/INS integration using a fuzzy adaptive strong tracking unscented Kalman filter. Nonlinear Dyn. 2013, 73, 377–395. [Google Scholar] [CrossRef]
Zhang, T.; Shi, J.; Lin, T.; Feng, X.; Niu, X. GNSS position-aided delay-locked loops for accurate urban navigation. GPS Solut. 2023, 27, 1–15. [Google Scholar] [CrossRef]
Chen, S.; Gao, Y. Improvement of carrier phase tracking in high dynamics conditions using an adaptive joint vector tracking architecture. GPS Solut. 2019, 23, 15. [Google Scholar] [CrossRef]

Figure 1. Structure block diagram of proposed VTL.

Figure 2. Equivalent noise bandwidth of the KF-based tracking loop in steady-state.

Figure 3. (a) Experiment equipment and (b) performance evaluation method.

Figure 4. Sky-Plot of the acquired satellites and the mean PDOP value.

Figure 5. of all satellites during the test.

Figure 6. (a) Doppler frequency estimation and (b) PLIs of G16 of both schemes.

Figure 7. (a)Latitude errors, (b)longitude errors and (c) altitude errors of both schemes.

Figure 8. The velocity error in the (a) east and (b) north direction for both schemes.

Table 1. Procedures of the SRUKF.

Algorithm. SRUKF algorithm for tracking loop

Table 2. Parameter configurations of comparison scheme.

Special parameter	Value
Correlator interval $d$	0.5 chip
DLL noise bandwidth	1 Hz
PLL noise bandwidth	10 Hz
$Coherence integration time T_{c o h}$	1 ms
$Navigation filter update time T_{n a v}$	100 ms

Table 3. Positioning errors of the different schemes.

Method	Latitude Error (m)		Longitude Error (m)		Altitude Error (m)
Method	RMSE	STD	RMSE	STD	RMSE	STD
CTL-based STL	8.54	7.12	8.72	8.72	17.16	17.02
EKF-based VTL	5.94	3.08	4.07	4.06	6.57	5.75
UKF-based VTL	5.84	4.07	3.46	3.46	4.81	4.36
ASRUKF-based VTL	5.48	2.79	2.34	2.25	2.69	2.65

Table 4. Velocity errors of the different schemes.

Method	East Velocity Error (m/s)		North Velocity Error (m/s)
Method	RMSE	STD	RMSE	STD
CTL-based STL	0.48	0.48	0.45	0.45
EKF-based VTL	0.16	0.15	0.22	0.22
UKF-based VTL	0.14	0.15	0.22	0.21
ASRUKF-based VTL	0.13	0.14	0.20	0.20

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Performance Enhancement and Evaluation of a Vector Tracking Receiver using Adaptive Tracking Loops

Abstract

1. Introduction

2. System Model of Vector Tracking

2.1. Nonlinear KF-based Tracking Loop

2.2. Nonlinear KF-based Tracking Loop

2.3. Nonlinear KF-based Tracking Loop

3. Proposed Adaptive SRUKF-based Loop Tracking

3.1. Square Root Unscented Kalman Filter

3.2. Adaptive SRUKF-based Loop Tracking for Vector Tracking

4. Experimental Evaluation and Results

4.1. Experimental Setup

4.2. Tracking Performance Analysis

4.3. PVT Results Evaluation

5. Conclusion

Author Contributions

Funding

Data Availability Statement

Acknowledgments

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe