1. Introduction
Superconductivity is a basic fundamental phenomenon in solid-state physics. Although being discovered more than a century ago, it still generates a plethora of research activities. Recently, its importance flourished again in the context of topological superconductivity[
1,
2,
3], which is an essential field of research for the realization of quantum computing. Certainly, the intricate interplay of standard spintronics and quantum information concepts can give rise to unforeseen breakthroughs in basic research and in future technologies for storing, computing and transmitting information. This calls for the development of theoretical frameworks based on a realistic description of the electronic structure of superconducting materials interfaced with magnetic systems in order to understand and predict various related phenomena.
Interesting topics emerged in superconducting spintronics [
4,
5,
6,
7], where the interplay of Cooper pairs and other electronic degrees of freedom (such as spin, charge and orbital) give rise to fascinating phenomena, ranging from supercurrents, triplet superconductivity, and torques. Simultaneously, the potential design of topological superconductivity and the creation of Majorana states[
8,
9,
10] is driving a lot of research in the context of topological qubits [
11].
The microscopic theory to describe conventional superconductivity goes back to the work of John Bardeen, Leon Cooper, and Robert Schrieffer (BCS) [
12]. In this context, the Bogoliubov–de Gennes (BdG) method [
13,
14,
15,
16] is an elegant mean-field approximation that relies upon Bogoliubov–Valatin transformations that take the Hamiltonian from a particle space into a particle-hole one—a framework that has been frequently used, see for example Refs. [
17,
18,
19,
20,
21,
22,
23,
24,
25,
26,
27]. Nowadays, several methods based on a realistic description of the electronic structure of materials are capable of treating fundamental aspects related to superconductivity. For instance, powerful theoretical frameworks have been proposed and utilized within density functional theory (DFT) combined with the BdG formalism [
28,
29,
30,
31,
32,
33], or by proposing an extension of DFT to account for superconductivity [
34,
35,
36,
37]. Tight-binding schemes are very appealing since they allow a versatile description of superconductivity-related physics with a potential control of various levels of approximations, which could enable the treatment of problems not attainable with conventional DFT.
Among the superconducting materials, Nb stands out and is often utilized as a key component to investigate superconductivity-related physics [
38,
39]. The surface of Nb(110) became recently the standard substrate [
40], where Yu-Shiba-Rusinov in-gap states [
8,
9,
10] and the topological Majorana states [
8,
9,
10] are explored in adatoms [
29,
41,
42,
43], at the edges of magnetic wires [
24,
26,
27,
44], or films [
45,
46,
47,
48].
The goal of this article is to introduce our recently developed method that allows the treatment of superconductivity on the basis of a tight-binding approach as implemented in TITAN [
49,
50,
51,
52]. The framework enables a realistic description of the electronic structure, with parameters obtained from DFT [
53]. Examples of applications of TITAN ranges from dynamical magnetic responses [
54], dynamical transport and torques [
50,
52], magnetic damping [
51], as well as ultrafast magnetization dynamics triggered by laser pulses [
55,
56]. In the context of superconductivity, the method was already introduced in Ref. [
57], with a focus on magnetic exchange interactions at superconducting-magnetic interfaces. Here, we pay attention to Nb in bulk and thin films with the aim of highlighting fundamental aspects in the simulations procedure. Aspects related to the choice of the electron-phonon coupling to open the appropriate band gap are discussed together with the impact of temperature and self-consistency on the underlying physics. Dimensionality affects superconductivity, as we unveil, which can be utilized to tune the superconducting gap for different applications in modern investigations of superconductivity-related problems.
The article is organized as follows. We first introduce the method in
Section 2, which is based on multi-orbital tight-binding theory. Then we present in
Section 3 the results of our simulations in Nb bulk, (001) and (110) monolayers, which are followed by Nb(110) thin films of different thicknesses. Finally, we present our concluding remarks in
Section 4.
2. Tight-Binding and the Bogoliubov–de Gennes Method
To simulate the superconducting properties of Nb across dimensions, we introduce here the tight-binding methodology together with the BdG method that we utilized, as implemented in our code TITAN [
49,
51,
52,
55,
56,
57]. The hopping parameters were obtained from first-principles calculations [
53]. More details on superconducting related aspects are elaborated in Ref. [
57].
The fundamental tight-binding Hamiltonian reads:
where
and
consist of the creation and annihilation operators associated to electrons having a wave vector
and spin
in the orbitals
and spin
in the orbitals
, respectively.
and
are specific atoms in the bulk unit cell, or layers in the film geometry.
is a reciprocal vector, while
N is the number of wave vectors in the three-dimensional (for bulk) or two-dimensional (for films) Brillouin zone. To enable the formation of Cooper pairs, which ultimately gives rise to superconductivity, we introduce
in the second term of the previous equation, as induced by the electron-phonon coupling.
In the mean-field approximation, Equation (
1) simplifies to
with
is known as the superconducting gap parameter, which corresponds to the energy required to scatter Cooper pairs [
58].
The term
corresponds to the regular Hamiltonian where superconductivity is not accounted for:
with
being the spin-independent tight-binding term, the second term is responsible for the intra-atomic exchange interaction (originating from a Hubbard-like contribution [
50,
52]), which can lead to magnetism, and the third term corresponds to the spin-orbit interaction.
The BdG methodology consists in utilizing the Bogoliubov–Valatin transformation [
16] to rewrite Equation (
2) in the electron-hole representation instead of the electron one, which leads to the BdG Hamiltonian:
with
being the Fermi energy while the associated eigenvalue problem to solve reads:
The transformation is canonical and enabled by rewriting
with
where the prime indicates that the sums run only over the states with positive energy[
16,
59]. This restriction in the sum is done to counteract the doubling of the degrees of freedom originated from the change of basis.
The eigenvector of Equation (
6) is
Our numerical procedure to evaluate the various properties of a given material is based on the self-consistency of the charge density, which is also pursued once the electron-phonon coupling is included. In practice, we start the simulations considering the normal metallic phase then we incorporate the Cooper pairing and repeat the computational runs until convergence.
3. Results
In this section we explore the results of simulations done for various Nb structures. Our choice on Nb is motivated by its relatively large superconducting gap, which facilitates the exploration of in-gap states. Simulating low temperatures phenomena requires finer computational meshes, thus for the first investigations we choose high temperatures and large values for the superconducting coupling . We start with bulk Nb, where we recover a superconducting gap opening in the electronic structure around the Fermi energy. Then we explore the case of thin films down to the single monolayer along the [001] or [110] directions. We monitor how the superconducting gap is affected by the self-consistency of the electronic structure calculations.
3.1. Bulk superconducting Nb
Nb has a superconducting critical temperature of
[
60], which leads to a significant superconducting gap
. A rough approximation relates
with the size of the gap—at T=0 K—through [
58]
Large values of
are desirable when investigating states that appear inside the gap. In our simulation procedure, we start with bulk Nb at high temperatures. In TITAN, the thermal effects enter through the parameter
, which broadens the Fermi-Dirac function; in this case, we will use
(
). For a reference, this is higher than room temperature, which is at
, but nevertheless, considerably lower than the melting point of Nb
. Nb has a body-centered cubic crystal structure. We make use of the Slater-Koster (SK) parameters from Ref. [
53], the spin-orbit coupling strength comes from Ref. [
61]. In
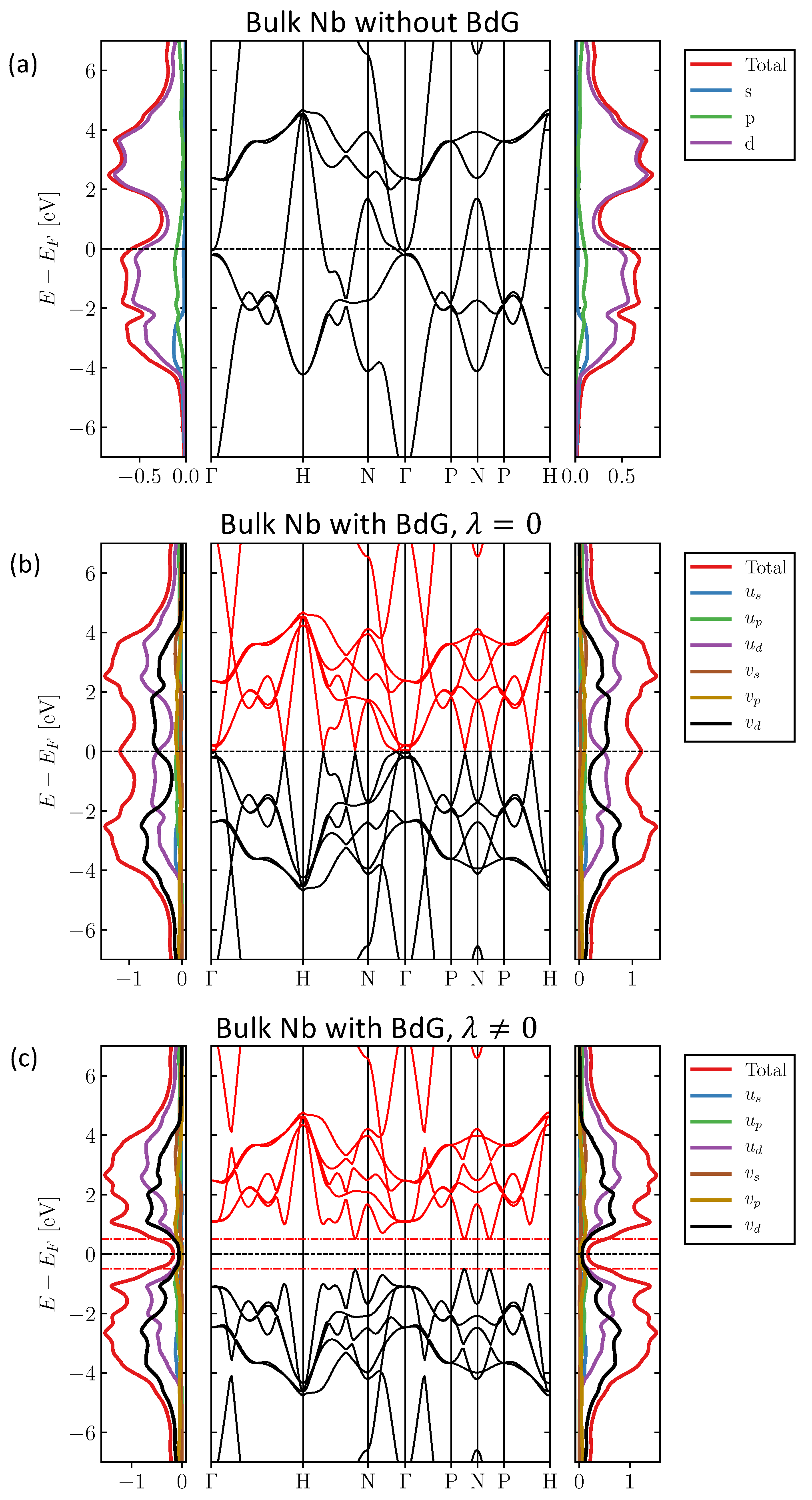
Figure 1(a), we show the density of states of both spin channels (left and right panels), and in the middle the band structure of bulk Nb. The charge occupancy per orbital is
The density of states (DOS) and the band structure agree with the results displayed in Ref. [
53].
Repeating the calculations by solving the BdG equations but setting
on all orbitals, we naturally recover the metallic band-structure shown in
Figure 1(b), where both the electron and hole parts are illustrated. Both parts are symmetric with respect to the Fermi level. This holds true for the DOS as well. We expect that by allowing for finite coupling
, degeneracies occurring at crossing points will be lifted.
In
Section 3.2, we describe a rather optimized search method to tune this parameter. From our explorations, we found that: (i) large values of
do not always mean large gaps and (ii) the size of the gap is not a linear function of
. From tabulated values of the electron-phonon
coupling constant we can evaluate the coupling parameter
utilizing the following relation [
62]
where
is the density of states at the Fermi energy. For example, for bulk Nb with the data from Refs. [
63] we obtain
. In Ref. [
62], the electron-phonon coupling constant is calculated for slabs of Nb(100) and Nb(110) of 3, 6, 9, 12, and 15 layers. For the Nb(110), the results for the system of 9 layers—the slab size closer to the one we will study later—lead to coupling parameters of
at the surfaces and
in the middle layer. When plotting the curve associated to
vs.
, we obtain a quadratic function, in agreement with Ref. [
64], where the self-consistent Korringa–Kohn–Rostoker method is used. There, the authors found that in order to obtain
the coupling parameter must be
for bulk Nb.
As a first example of our investigations, we set
. The occupancies are
, which experience a minor change of the order of
with respect to the case where
is set to zero. The self-consistent value of the superconducting gap parameter is
, which is obviously gigantic. The resulting band structure and LDOS plots are illustrated in
Figure 1(c). The red dotted lines delimit the range
. As a sanity check, it is reassuring that the gap in the band structure matches the self-consistent output value of
. The density of states does not show a perfect gap, but decays at the gap region. This effect is due to the thermal broadening induced artificially, which is in this case set to 43
.
In
Section 3.2 and
Section 3.4, we will systematically explore the impact of temperature and coupling strengths, searching for an optimal
that yields the experimental value of
.
3.2. Superconducting Gap Tuning: Single bcc (001) Nb Monolayer
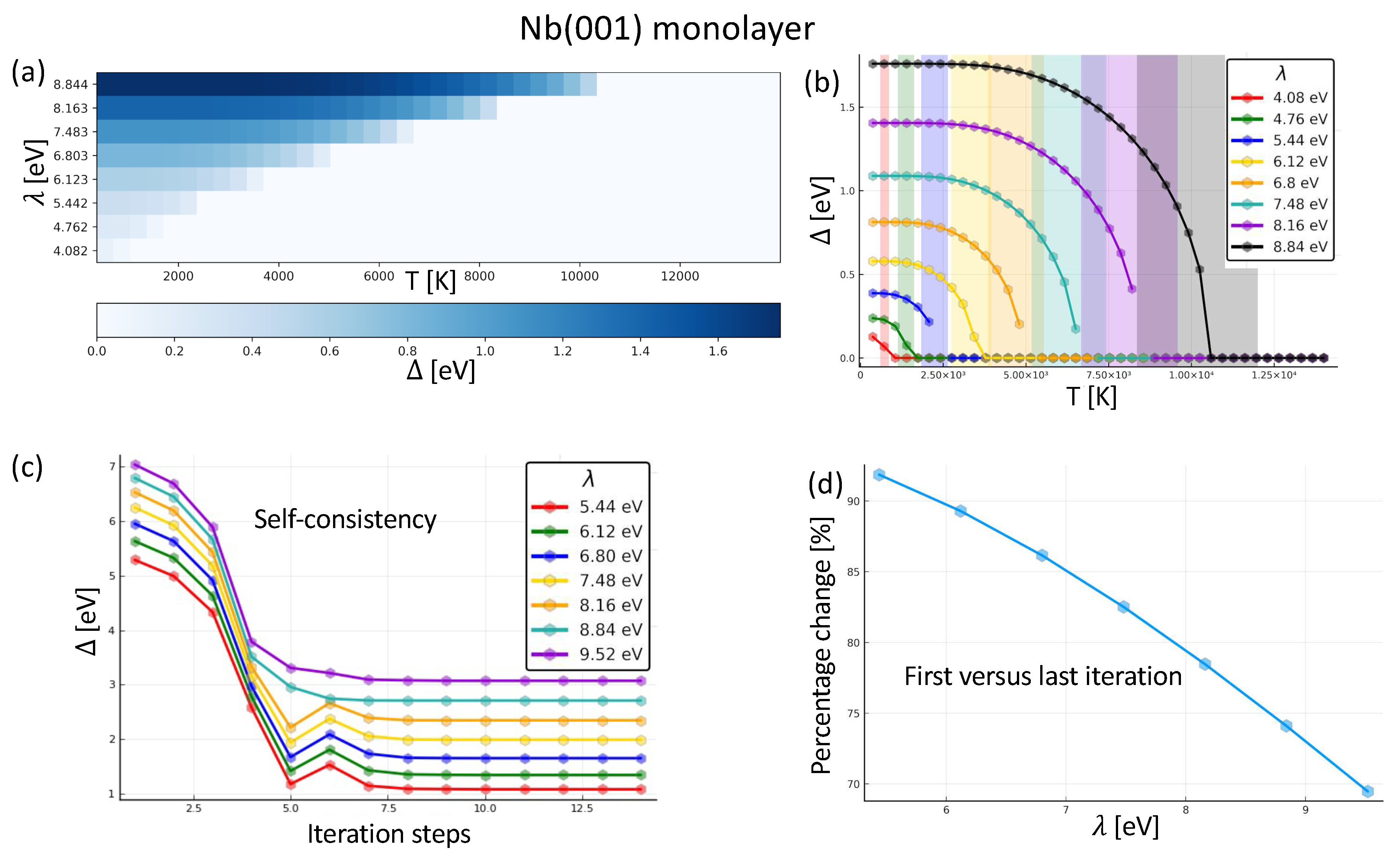
Explorations to find the appropriate coupling that results in the desired gap parameter involve systematic repeated simulations with different parameters. In this section, we show the typical curves for as a function of the temperature (via the broadening parameter) and the Cooper pair coupling parameter. To exemplify, we use a 2D system, namely a (001) monolayer of bcc Nb. As in our previous examples, we set the same for all orbitals, with eight values between 4 and 9 . We consider forty different temperature points between 300 and 14000 . Simulations at lower temperatures are computationally highly expensive since they require an increased number of k-points to be able to capture the narrow peaky structures in the Brillouin zone with lower broadening. All the simulations in this section use the same number of k-points, .
Figure 2(a) displays a heatmap with the results of the gap parameter for the different temperatures and couplings. We can see that the gap parameter drops to zero after reaching the corresponding critical temperature for every line. Directing our attention for fixed temperatures (i.e. the “columns” in the figure), it is clear that there is also a critical
below which
is zero. Throughout the heatmap,
ranges from 0.0 to
. We can analyze the same data from a different perspective, as shown in
Figure 2(b). There we see that the
vs.
T curve has indeed the shape predicted by the BCS theory. For sufficiently low temperatures,
approaches a plateau. Around the critical temperature
, the self-consistency procedure may become unstable and difficult to achieve a precise value, which lead some curves to miss points in that range. We can proceed to an extrapolation to evaluate the missing points on the basis of the asymptotic behavior of
around the critical temperature [
58]
We used the precedent equation to go from the data in
Figure 2(b) to the one in
Figure 2(a). The BCS theory predicts that, at zero Kelvin, the relation between
and
is the one in Equation (
10). Experimentally the reported values range from
to
, we signaled this range with the colored bands in
Figure 2(b). This plot establishes the aforementioned statement regarding the non-linearity of
with respect to
.
For a wide range of simulations, it is desirable and recommendable to place the superconducting system well below , at a point in the plateau of the vs. T curve. The superconducting state is frailer at the vicinity of the critical temperature, and internal changes in the material can perturb the properties of interest.
3.3. Renormalization after Self-Consistency: Single bcc (001) Nb Monolayer
A common problem in simulating superconductors interfaced with normal conductors is the artificially increased size of the gap in order to facilitate the exploration of emerging in-gap states and it is rather common to proceed to single-iteration simulations, which assumes the electronic structure is not significantly altered in comparison to the case, where instead one proceeds to self-consistency. The importance of self-consistency was highlighted in Ref. [
65]. In this subsection, we address this aspect of simulation of superconducting materials by comparing the size of the gap obtained after one iteration (starting from the converged electronic structure of the metallic phase) with respect to the one obtained after full self-consistency. In
Figure 2(c), we single out the value of the superconducting gap parameter through several simulations with different coupling parameters at a temperature of
. Our algorithm, based on the Powell method [
66] can halt the simulations when no improvement is detected in the last five steps. All shown cases converged without a problem.
In
Figure 2(d) we portray the percentage change of the gap parameter (
) between the first- and last-iteration calculated
for different
. We note that the change is bigger for smaller values of
.
So far, we have been discussing the numerics of the simulations assuming both large superconducting gaps and large electronic temperatures. In
Section 3.4, we drop
T to realistic values associated to a superconducting Nb layer. Additionally, we explore the impact on the orbital-dependent gaps
.
3.4. Superconducting Nb (110) Monolayer
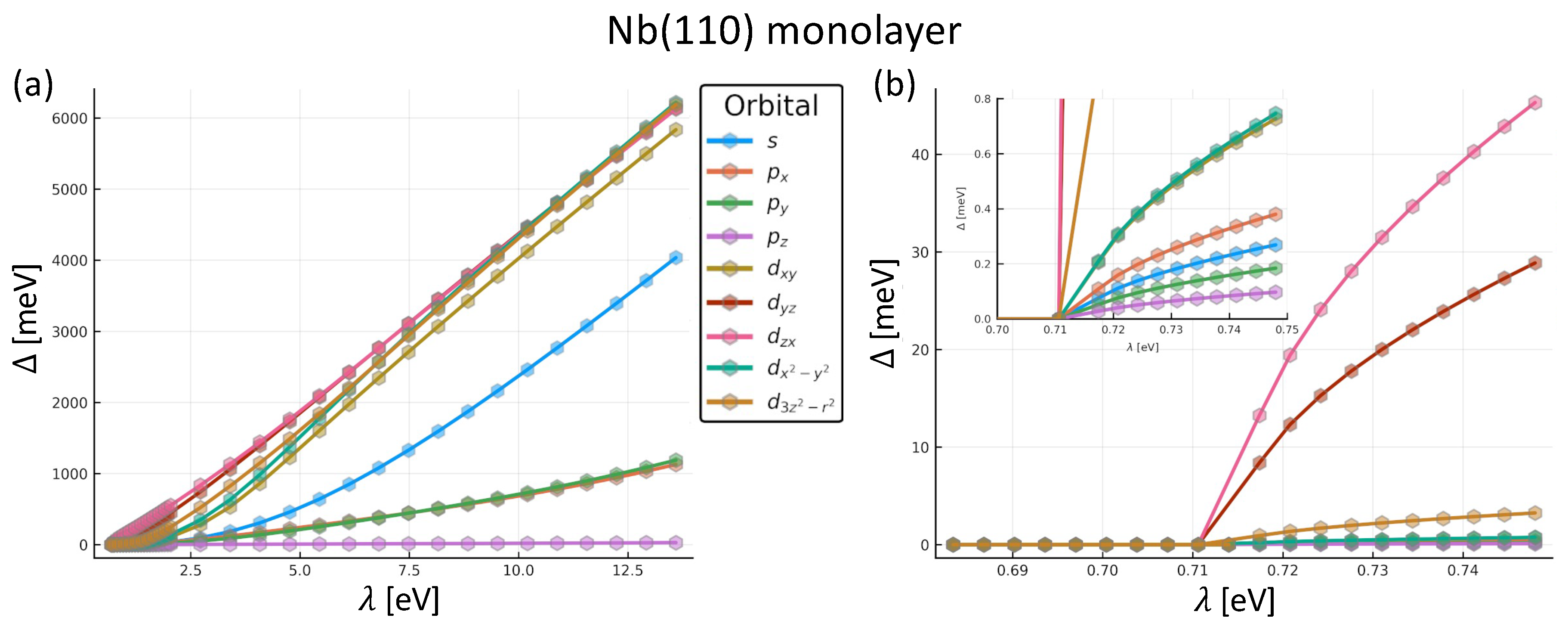
In this subsection we consider the cryogenic regime, which calls for computationally heavier simulations. As we hinted in previous subsections, sinking the temperature forces us to increase the number of k-points for each simulation to be able to capture the narrow states. Since these calculations will be more intensive, we will leave aside the testing structures we were using previously—bulk Nb and Nb (100) monolayers—and move to our main interest, which is Nb (110) films, heavily explored in various recent experiments.
We assume a thermal broadening of
(equivalent to a temperature of approximately
), shallow enough to be in the plateau of the
vs.
T curve for all the
we used. We consider a non-uniform grid with 57 points for
, ranging from
to
, with a higher resolution for lower energies. In
Figure 3(a), we display the results of the orbital-dependent
for the entire range. Obviously, some orbitals are more responsive to the coupling
. This is affected by the strength of the latter coupling. We notice an increment in
as we enlarge the coupling strength.
induces gaps of the order of
eV or larger, high enough to be considered unrealistic.
In
Figure 3(b), we focus only on the low energy range
, where the growth of
is more controlled. In the inset, we also restrict the values on the
y-axis from 0 to
to resolve better the smaller gap parameter for some of the orbitals. We observe that the
component is still quite small; this is a consequence of the shape of this orbital and the geometry of the monolayer. The orientation of the
orbital is out of the plane, and this means its in-plane component is zero, and it is hard for superconducting electrons in this orbital to interact with others.
The gap is opened around the Fermi surface when the u and v states mix due to the off-diagonal components of the Hamiltonian; this means that the gap must come from the bands that cross . Hence, the gap of the system comes from the minimum value of among orbitals whose bands traverse the Fermi level. Once we profile these bands, we can execute any searching algorithm—e.g., binary search, or nested intervals methods—until we find an appropriate . As a rule of thumb, each significant figure in requires two on ; In other words, having up to three significant digits typically requires knowing to six. Refining can be very expensive. In our case, induces .
In the next subsection, we explore the case of thin films of Nb (110) at and analyse the evolution of the superconducting gap parameter across the material.
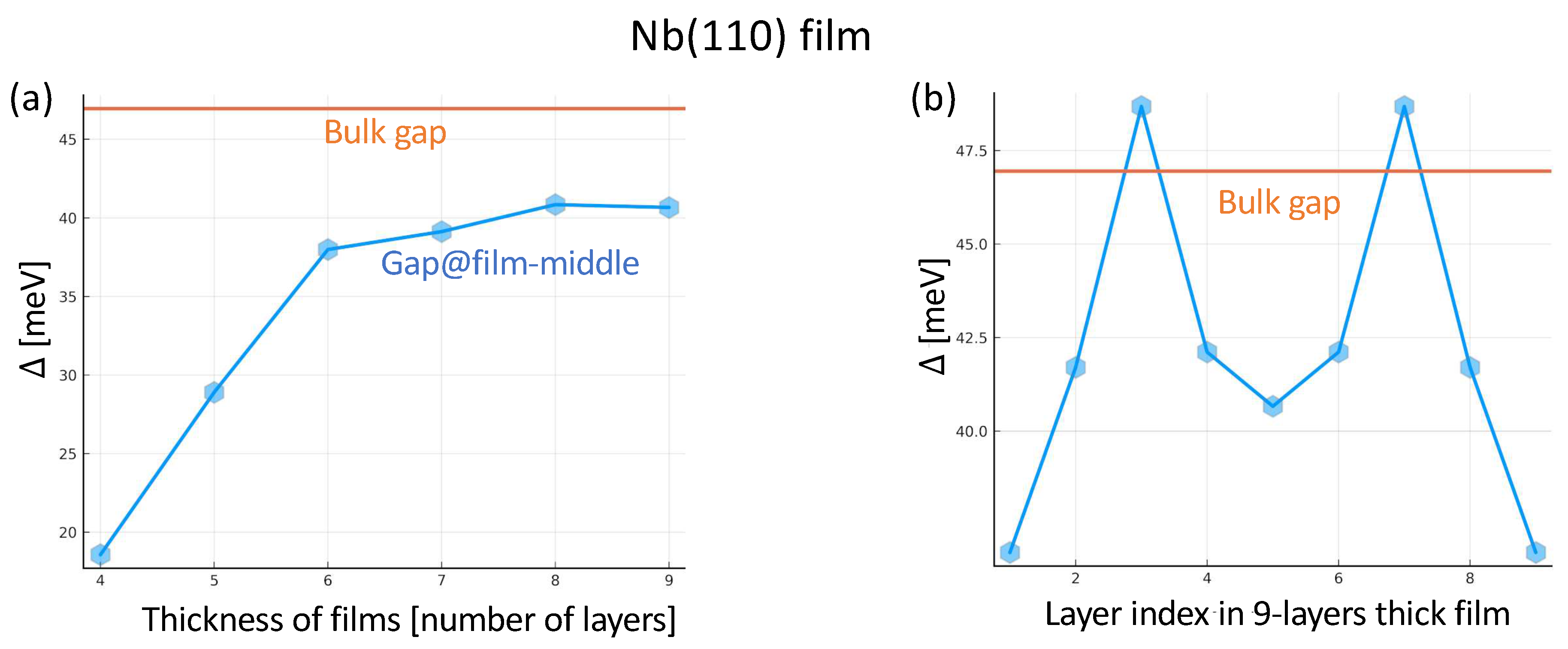
3.5. Superconducting Slab
It is difficult to predict if the coupling strength that works well for one given system still opens a reasonable gap for a different one. We started with the value found in the previous section, , which opened a gap for a single monolayer. It turns out, however, that as soon as the Nb film thickness is larger than 5 layers, a large coupling is required to open a gap. In the remained study, we assume at a temperature of .
In
Figure 4(a), we show the magnitude of the gap in the central layer of the films as a function of the slab thickness. The orange line corresponds to the gap parameter of the bulk Nb for
at the same temperature. One notices that the thicker the film gets, the closer the gap is to the one obtained for the bulk, a behavior comparable to what has been reported in Ref. [
67].
The superconducting gap is not homogeneous across the Nb films. An example is shown in
Figure 4(b) for a film with a thickness of 9 layers. The gap in the middle of the film is larger than at the surface and it seems to oscillate as a function of position, as we would expect for wave-like particles in a confined system. A lower gap at the surface is expected since the electrons there have fewer opportunities to couple in Cooper-pairs due to their lack of neighbors from one side. We must also consider surface effects; for example, we have around 1.5 electrons less than the inner parts. Electrons move from the surfaces to the middle layers. Interestingly some of the layers in the film can have a larger gap than the bulk one. This indicates that the dimensionality of a material, can be utilized to control the superconducting gap due to confinement effects.
4. Conclusions
After briefly introducing the tight-binding method that we developed to tackle superconductivity within the Bogoliubov-de Gennes formalism, we presented the results of our simulations on a material that is currently heavily utilized to explore the physics of superconductivity. We addressed the case of bulk and thin films of Nb along different directions. A major issue in this field from the computational point of view is to choose the right Cooper pair coupling that opens the desired superconducting gap since the calculations are extremely expensive to resolve gaps of a few or even smaller. We analysed how the superconducting order parameter correlates with both the Cooper pair coupling and temperature, and explored the impact of self-consistency on the emerging orbital-dependent superconducting gap. In the thin film geometry, we unveiled the possibility of engineering the magnitude of the gap via confinement effects. Indeed, the superconducting gap is found to be layer-dependent, either smaller or larger than the values found in the bulk phase.
Author Contributions
Conceptualization, S.L.; methodology, U.A.A.R. and F.S.M.G.; software, U.A.A.R and F.S.M.G; validation, U.A.A.R.; formal analysis, U.A.A.R.; investigation, U.A.A.R.; resources, S.L.; writing—original draft preparation, U.A.A.R, F.S.M.G. and S.L.; writing—review and editing, S.L.; visualization, U.A.A.R.; supervision, F.S.M.G. and S.L.; project administration, S.L.; funding acquisition, S.L. All authors have read and agreed to the published version of the manuscript.
Funding
The authors acknowledge funding provided by the Priority Programmes SPP 2137 “Skyrmionics” (Projects LO 1659/8-1) of the Deutsche Forschungsgemeinschaft (DFG). We acknowledge the computing time provided through JARA on the supercomputers JURECA
[68]. Simulations were also performed with computing resources granted by RWTH Aachen University under project jara0189 and p0020362
Data Availability Statement
All data needed to evaluate the conclusions of the paper are present in the paper. Additional data related to this paper may be requested from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lahtinen, V.; Pachos, J.K. A Short Introduction to Topological Quantum Computation. SciPost Phys. 2017, 3, 021. [Google Scholar] [CrossRef]
- Mishra, A.; Simon, P.; Hyart, T.; Trif, M. Yu-Shiba-Rusinov Qubit. PRX Quantum 2021, 2, 040347. [Google Scholar] [CrossRef]
- Pavešić, L.; Žitko, R. Qubit based on spin-singlet Yu-Shiba-Rusinov states. Phys. Rev. B 2022, 105, 075129. [Google Scholar] [CrossRef]
- Linder, J.; Robinson, J.W.A. Superconducting spintronics. Nature Physics 2015, 11, 307–315. [Google Scholar] [CrossRef]
- Eschrig, M. Spin-polarized supercurrents for spintronics: a review of current progress. Reports on Progress in Physics 2015, 78, 104501. [Google Scholar] [CrossRef] [PubMed]
- Buzdin, A.I. Proximity effects in superconductor-ferromagnet heterostructures. Rev. Mod. Phys. 2005, 77, 935–976. [Google Scholar] [CrossRef]
- Bergeret, F.S.; Silaev, M.; Virtanen, P.; Heikkilä, T.T. Colloquium: Nonequilibrium effects in superconductors with a spin-splitting field. Rev. Mod. Phys. 2018, 90, 041001. [Google Scholar] [CrossRef]
- Beenakker, C. Search for Majorana Fermions in Superconductors. Annual Review of Condensed Matter Physics 2013, 4, 113–136. [Google Scholar] [CrossRef]
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Physics-Uspekhi 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Tanaka, Y.; Yokoyama, T.; Nagaosa, N. Manipulation of the Majorana Fermion, Andreev Reflection, and Josephson Current on Topological Insulators. Phys. Rev. Lett. 2009, 103, 107002. [Google Scholar] [CrossRef]
- Aguado, R.; Kouwenhoven, L.P. Majorana qubits for topological quantum computing. Physics Today 2020, 73, 44–50. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Microscopic Theory of Superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Bogoliubov, N. A New Method in the Theory of Superconductivity. I. Journal of Experimental and Theoretical Physics 1958, 7, 41–46. [Google Scholar] [CrossRef]
- De Gennes, P.; Pincus, P. Superconductivity Of Metals And Alloys; Advanced Books Classics, Avalon Publishing, 1999.
- Alaberdin, E.R.; Vichorev, A.A.; Savchenko, A.M.; Sadovnikov, B.I. On Bogoliubov’s method in superconductivity. Theoretical and Mathematical Physics 1996, 107, 523–532. [Google Scholar] [CrossRef]
- Zhu, J. Bogoliubov-de Gennes Method and Its Applications; Lecture Notes in Physics, Springer International Publishing, 2016.
- Han, Q. A method of studying the Bogoliubov–de Gennes equations for the superconducting vortex lattice state. Journal of Physics: Condensed Matter 2009, 22, 035702. [Google Scholar] [CrossRef] [PubMed]
- Saunderson, T.G.; Gyorgypál, Z.; Annett, J.F.; Csire, G.; Újfalussy, B.; Gradhand, M. Real-space multiple scattering theory for superconductors with impurities. Phys. Rev. B 2020, 102, 245106. [Google Scholar] [CrossRef]
- Pellegrino, F.M.D.; Falci, G.; Paladino, E. Effect of dilute impurities on short graphene Josephson junctions. Communications Physics 2022, 5. [Google Scholar] [CrossRef]
- Stosiek, M.; Baretzky, C.; Balashov, T.; Evers, F.; Wulfhekel, W. Friedel oscillations and superconducting gap enhancement by impurity scattering. Phys. Rev. B 2022, 105, L140504. [Google Scholar] [CrossRef]
- Sato, M.; Ando, Y. Topological superconductors: a review. Reports on Progress in Physics 2017, 80, 076501. [Google Scholar] [CrossRef]
- Feldman, B.E.; Randeria, M.T.; Li, J.; Jeon, S.; Xie, Y.; Wang, Z.; Drozdov, I.K.; Bernevig, B.A.; Yazdani, A. High-resolution studies of the Majorana atomic chain platform. Nature Physics 2016, 13, 286–291. [Google Scholar] [CrossRef]
- Schneider, L.; Brinker, S.; Steinbrecher, M.; Hermenau, J.; Posske, T.; dos Santos Dias, M.; Lounis, S.; Wiesendanger, R.; Wiebe, J. Controlling in-gap end states by linking nonmagnetic atoms and artificially-constructed spin chains on superconductors. Nature Communications 2020, 11. [Google Scholar] [CrossRef]
- Schneider, L.; Beck, P.; Posske, T.; Crawford, D.; Mascot, E.; Rachel, S.; Wiesendanger, R.; Wiebe, J. Topological Shiba bands in artificial spin chains on superconductors. Nature Physics 2021, 17, 943–948. [Google Scholar] [CrossRef]
- Schneider, L.; Beck, P.; Neuhaus-Steinmetz, J.; Rózsa, L.; Posske, T.; Wiebe, J.; Wiesendanger, R. Precursors of Majorana modes and their length-dependent energy oscillations probed at both ends of atomic Shiba chains. Nature Nanotechnology 2022, 17, 384–389. [Google Scholar] [CrossRef] [PubMed]
- Brinker, S.; Küster, F.; Parkin, S.S.P.; Sessi, P.; Lounis, S. Anomalous excitations of atomically crafted quantum magnets. Science Advances 2022, 8, eabi7291. [Google Scholar] [CrossRef] [PubMed]
- Küster, F.; Brinker, S.; Hess, R.; Loss, D.; Parkin, S.S.P.; Klinovaja, J.; Lounis, S.; Sessi, P. Non-Majorana modes in diluted spin chains proximitized to a superconductor. Proceedings of the National Academy of Sciences 2022, 119. [Google Scholar] [CrossRef]
- Rüßmann, P.; Blügel, S. Density functional Bogoliubov-de Gennes analysis of superconducting Nb and Nb(110) surfaces. Phys. Rev. B 2022, 105, 125143. [Google Scholar] [CrossRef]
- Beck, P.; Schneider, L.; Rózsa, L.; Palotás, K.; Lászlóffy, A.; Szunyogh, L.; Wiebe, J.; Wiesendanger, R. Spin-orbit coupling induced splitting of Yu-Shiba-Rusinov states in antiferromagnetic dimers. Nature Communications 2021, 12. [Google Scholar] [CrossRef]
- Mier, C.; Choi, D.J.; Lorente, N. Calculations of in-gap states of ferromagnetic spin chains on s-wave wide-band superconductors. Phys. Rev. B 2021, 104, 245415. [Google Scholar] [CrossRef]
- Lászlóffy, A.; Nyári, B.; Csire, G.; Szunyogh, L.; Újfalussy, B. Topological superconductivity from first principles. II. Effects from manipulation of spin spirals: Topological fragmentation, braiding, and quasi-Majorana bound states. Phys. Rev. B 2023, 108, 134513. [Google Scholar] [CrossRef]
- Nyári, B.; Lászlóffy, A.; Csire, G.; Szunyogh, L.; Újfalussy, B. Topological superconductivity from first principles. I. Shiba band structure and topological edge states of artificial spin chains. Phys. Rev. B 2023, 108, 134512. [Google Scholar] [CrossRef]
- Rüßmann, P.; Bahari, M.; Blügel, S.; Trauzettel, B. Interorbital Cooper pairing at finite energies in Rashba surface states. Phys. Rev. Res. 2023, 5, 043181. [Google Scholar] [CrossRef]
- Oliveira, L.N.; Gross, E.K.U.; Kohn, W. Density-Functional Theory for Superconductors. Phys. Rev. Lett. 1988, 60, 2430–2433. [Google Scholar] [CrossRef] [PubMed]
- Lüders, M.; Marques, M.A.L.; Lathiotakis, N.N.; Floris, A.; Profeta, G.; Fast, L.; Continenza, A.; Massidda, S.; Gross, E.K.U. Ab initio theory of superconductivity. I. Density functional formalism and approximate functionals. Phys. Rev. B 2005, 72, 024545. [Google Scholar] [CrossRef]
- Marques, M.A.L.; Lüders, M.; Lathiotakis, N.N.; Profeta, G.; Floris, A.; Fast, L.; Continenza, A.; Gross, E.K.U.; Massidda, S. Ab initio theory of superconductivity. II. Application to elemental metals. Phys. Rev. B 2005, 72, 024546. [Google Scholar] [CrossRef]
- Essenberger, F.; Sanna, A.; Buczek, P.; Ernst, A.; Sandratskii, L.; Gross, E.K.U. Ab initio theory of iron-based superconductors. Phys. Rev. B 2016, 94, 014503. [Google Scholar] [CrossRef]
- Khaydukov, Y.N.; Vasenko, A.S.; Kravtsov, E.A.; Progliado, V.V.; Zhaketov, V.D.; Csik, A.; Nikitenko, Y.V.; Petrenko, A.V.; Keller, T.; Golubov, A.A.; Kupriyanov, M.Y.; Ustinov, V.V.; Aksenov, V.L.; Keimer, B. Magnetic and superconducting phase diagram of Nb/Gd/Nb trilayers. Phys. Rev. B 2018, 97, 144511. [Google Scholar] [CrossRef]
- Pal, B.; Chakraborty, A.; Sivakumar, P.K.; Davydova, M.; Gopi, A.K.; Pandeya, A.K.; Krieger, J.A.; Zhang, Y.; Date, M.; Ju, S.; Yuan, N.; Schröter, N.B.M.; Fu, L.; Parkin, S.S.P. Josephson diode effect from Cooper pair momentum in a topological semimetal. Nature Physics 2022, 18, 1228–1233. [Google Scholar] [CrossRef] [PubMed]
- Odobesko, A.B.; Haldar, S.; Wilfert, S.; Hagen, J.; Jung, J.; Schmidt, N.; Sessi, P.; Vogt, M.; Heinze, S.; Bode, M. Preparation and electronic properties of clean superconducting Nb (110) surfaces. Phys. Rev. B 2019, 99, 115437. [Google Scholar] [CrossRef]
- Küster, F.; Brinker, S.; Lounis, S.; Parkin, S.S.P.; Sessi, P. Long range and highly tunable interaction between local spins coupled to a superconducting condensate. Nature Communications 2021, 12. [Google Scholar] [CrossRef]
- Küster, F.; Montero, A.M.; Guimarães, F.S.M.; Brinker, S.; Lounis, S.; Parkin, S.S.P.; Sessi, P. Correlating Josephson supercurrents and Shiba states in quantum spins unconventionally coupled to superconductors. Nature Communications 2021, 12. [Google Scholar] [CrossRef]
- Odobesko, A.; Di Sante, D.; Kowalski, A.; Wilfert, S.; Friedrich, F.; Thomale, R.; Sangiovanni, G.; Bode, M. Observation of tunable single-atom Yu-Shiba-Rusinov states. Phys. Rev. B 2020, 102, 174504. [Google Scholar] [CrossRef]
- Friedrich, F.; Boshuis, R.; Bode, M.; Odobesko, A. Coupling of Yu-Shiba-Rusinov states in one-dimensional chains of Fe atoms on Nb(110). Phys. Rev. B 2021, 103, 235437. [Google Scholar] [CrossRef]
- Soldini, M.O.; Küster, F.; Wagner, G.; Das, S.; Aldarawsheh, A.; Thomale, R.; Lounis, S.; Parkin, S.S.P.; Sessi, P.; Neupert, T. Two-dimensional Shiba lattices as a possible platform for crystalline topological superconductivity. Nature Physics 2023. [Google Scholar] [CrossRef]
- Goedecke, J.J.; Schneider, L.; Ma, Y.; That, K.T.; Wang, D.; Wiebe, J.; Wiesendanger, R. Correlation of Magnetism and Disordered Shiba Bands in Fe Monolayer Islands on Nb(110). ACS Nano 2022, 16, 14066–14074. [Google Scholar] [CrossRef] [PubMed]
- Beck, P.; Schneider, L.; Bachmann, L.; Wiebe, J.; Wiesendanger, R. Structural and superconducting properties of ultrathin Ir films on Nb(110). Phys. Rev. Mater. 2022, 6, 024801. [Google Scholar] [CrossRef]
- Lo Conte, R.; Bazarnik, M.; Palotás, K.; Rózsa, L.; Szunyogh, L.; Kubetzka, A.; von Bergmann, K.; Wiesendanger, R. Coexistence of antiferromagnetism and superconductivity in Mn/Nb(110). Phys. Rev. B 2022, 105, L100406. [Google Scholar] [CrossRef]
- Souza Mendes Guimarães, F.; Suckert, J.R.; Hamamera, H.; Brinker, S.; Aceves Rodríguez, U.A.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. TITAN. Zenodo 2023. [Google Scholar] [CrossRef]
- Guimarães, F.S.M.; dos Santos Dias, M.; Bouaziz, J.; Costa, A.T.; Muniz, R.B.; Lounis, S. Dynamical amplification of magnetoresistances and Hall currents up to the THz regime. Scientific Reports 2017, 7, 3686. [Google Scholar] [CrossRef] [PubMed]
- Guimarães, F.S.M.; Suckert, J.R.; Chico, J.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. Comparative study of methodologies to compute the intrinsic Gilbert damping: interrelations, validity and physical consequences. Journal of Physics: Condensed Matter 2019, 31, 255802. [Google Scholar] [CrossRef]
- Guimarães, F.S.M.; Bouaziz, J.; dos Santos Dias, M.; Lounis, S. Spin-orbit torques and their associated effective fields from gigahertz to terahertz. Communications Physics 2020, 3, 19. [Google Scholar] [CrossRef]
- Papaconstantopoulos, D. Handbook of the Band Structure of Elemental Solids: From Z = 1 To Z = 112, second ed.; Springer US, 2015.
- Guimarães, F.S.M.; Lounis, S.; Costa, A.T.; Muniz, R.B. Dynamical current-induced ferromagnetic and antiferromagnetic resonances. Phys. Rev. B 2015, 92, 220410. [Google Scholar] [CrossRef]
- Hamamera, H.; Guimarães, F.S.M.; dos Santos Dias, M.; Lounis, S. Polarisation-dependent single-pulse ultrafast optical switching of an elementary ferromagnet. Communications Physics 2022, 5, 16. [Google Scholar] [CrossRef]
- Hamamera, H.; Guimarães, F.S.M.; dos Santos Dias, M.; Lounis, S. Ultrafast light-induced magnetization in non-magnetic films: from orbital and spin Hall phenomena to the inverse Faraday effect. arXiv 2023, arXiv:2312.07888. [Google Scholar] [CrossRef]
- Aceves Rodríguez, U.A.; Mendes Guimarães, F.S.; Brinker, S.; Lounis, S. Magnetic exchange interactions at the proximity of a superconductor. arXiv 2023, arXiv:2306.02906. [Google Scholar] [CrossRef]
- Tinkham, M. Introduction to Superconductivity; Dover Books on Physics Series, Dover Publications, 2004.
- De Gennes, P.; Pincus, P. Superconductivity Of Metals And Alloys; Advanced Books Classics, Avalon Publishing, 1999.
- Ikushima, A.; Mizusaki, T. Superconductivity in niobium and niobium-tantalum alloys. Journal of Physics and Chemistry of Solids 1969, 30, 873–879. [Google Scholar] [CrossRef]
- Veedu, S.; Popovic, Z.; Satpathy, S. Theoretical model for Rashba spin-orbit interaction in d electrons. Physical Review B 2014, 90. [Google Scholar] [CrossRef]
- Csire, G.; Schönecker, S.; Újfalussy, B. First-principles approach to thin superconducting slabs and heterostructures. Phys. Rev. B 2016, 94, 140502. [Google Scholar] [CrossRef]
- Klein, B.M.; Papaconstantopoulos, D.A. Electron-Phonon Interaction and Superconductivity in Transition Metals and Transition-Metal Carbides. Phys. Rev. Lett. 1974, 32, 1193–1195. [Google Scholar] [CrossRef]
- Saunderson, T.G.; Annett, J.F.; Újfalussy, B.; Csire, G.; Gradhand, M. Gap anisotropy in multiband superconductors based on multiple scattering theory. Phys. Rev. B 2020, 101, 064510. [Google Scholar] [CrossRef]
- Li, J.; Neupert, T.; Wang, Z.; MacDonald, A.H.; Yazdani, A.; Bernevig, B.A. Two-dimensional chiral topological superconductivity in Shiba lattices. Nature Communications 2016, 7, 12297. [Google Scholar] [CrossRef]
- Powell, M. An efficient method for finding the minimum of a function of several variables without calculating derivatives. The Computer Journal 1964, 7, 155–162. [Google Scholar] [CrossRef]
- Kodama, J.; Itoh, M.; Hirai, H. Superconducting transition temperature versus thickness of Nb film on various substrates. Journal of Applied Physics 1983, 54, 4050–4054. [Google Scholar] [CrossRef]
- Krause, D.; Thörnig, P. JURECA: Modular supercomputer at Jülich Supercomputing Centre. Journal of large-scale research facilities JLSRF 2018, 4. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).