Submitted:
08 December 2023
Posted:
11 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Basic equations
3. Simulation results
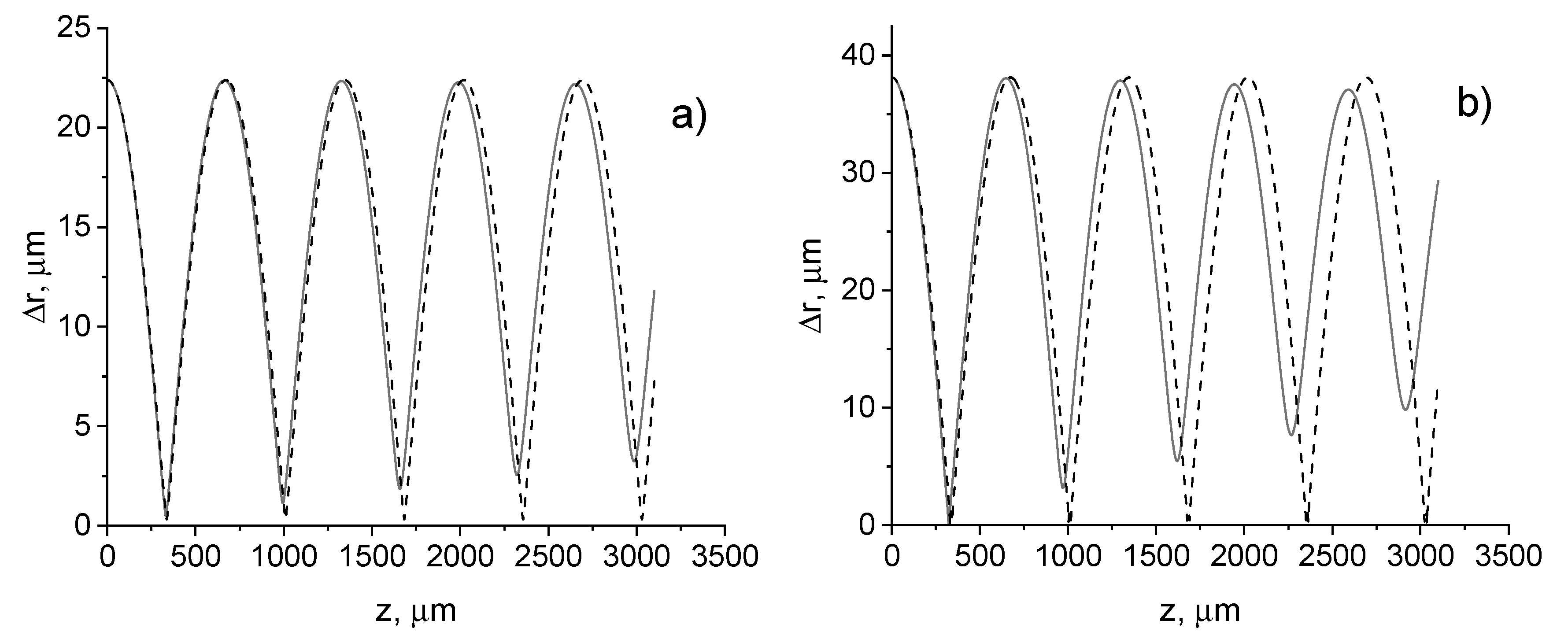
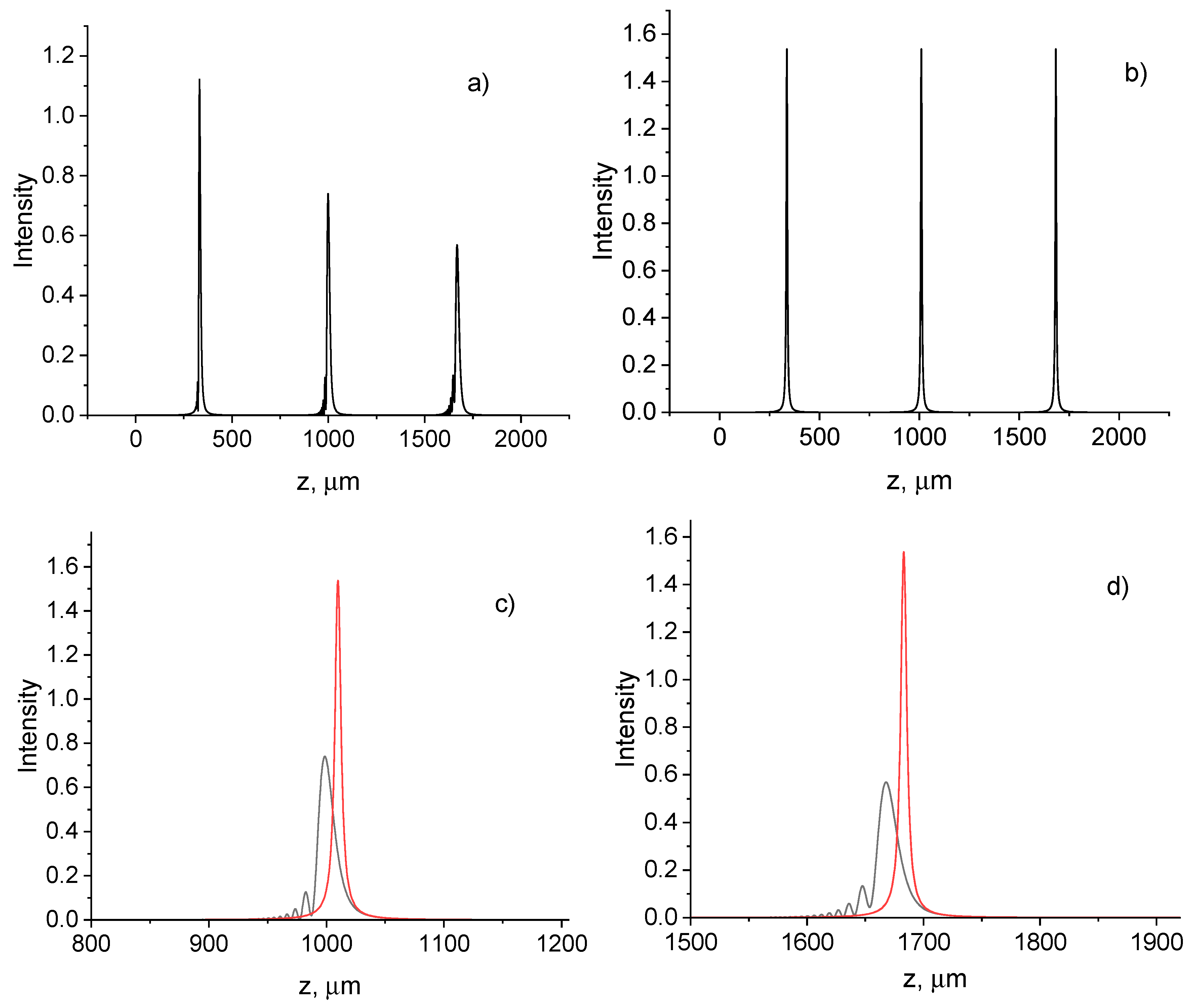
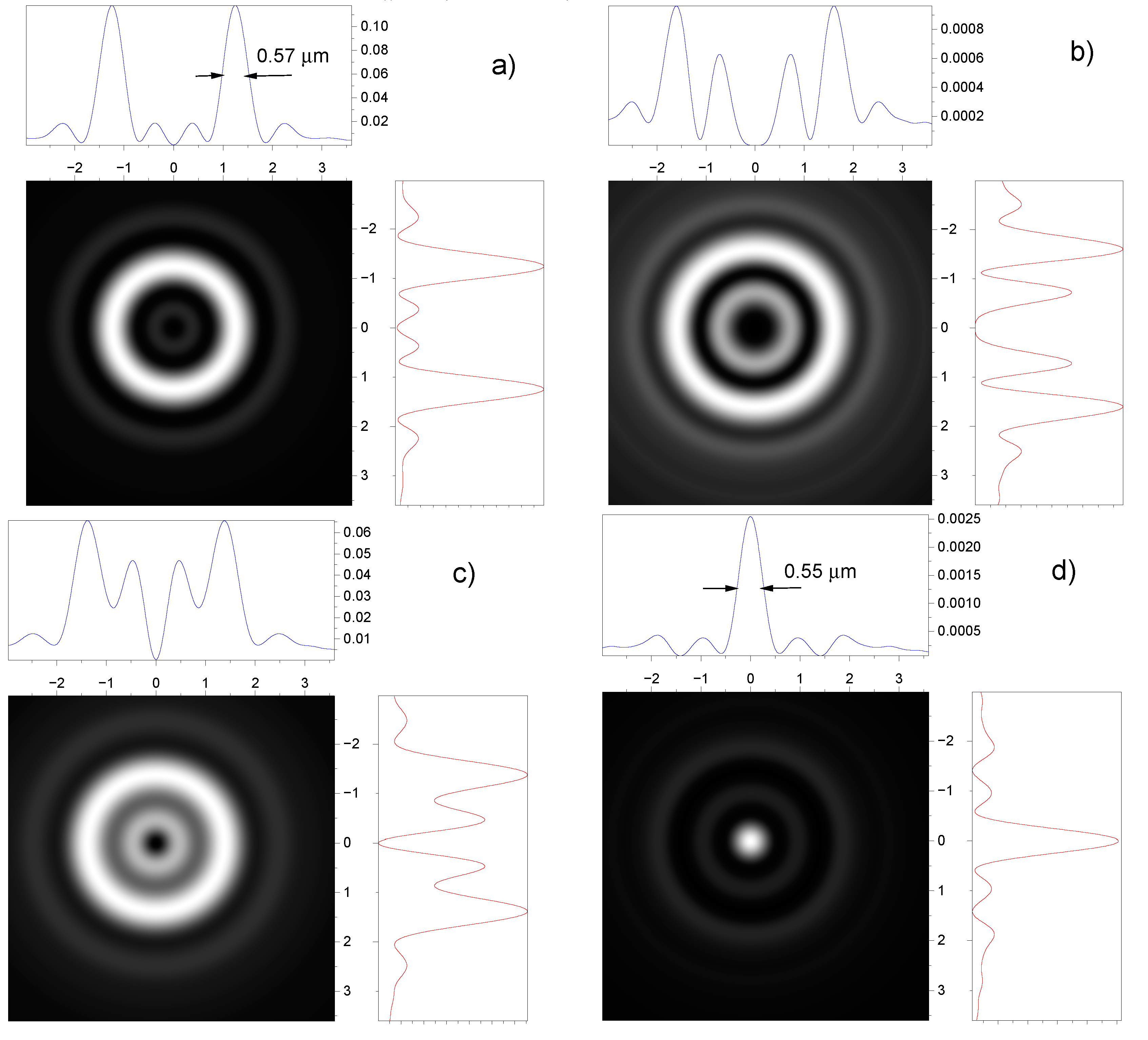
3.1. Effect of nonparaxiality on the beam width and axial intensity distribution
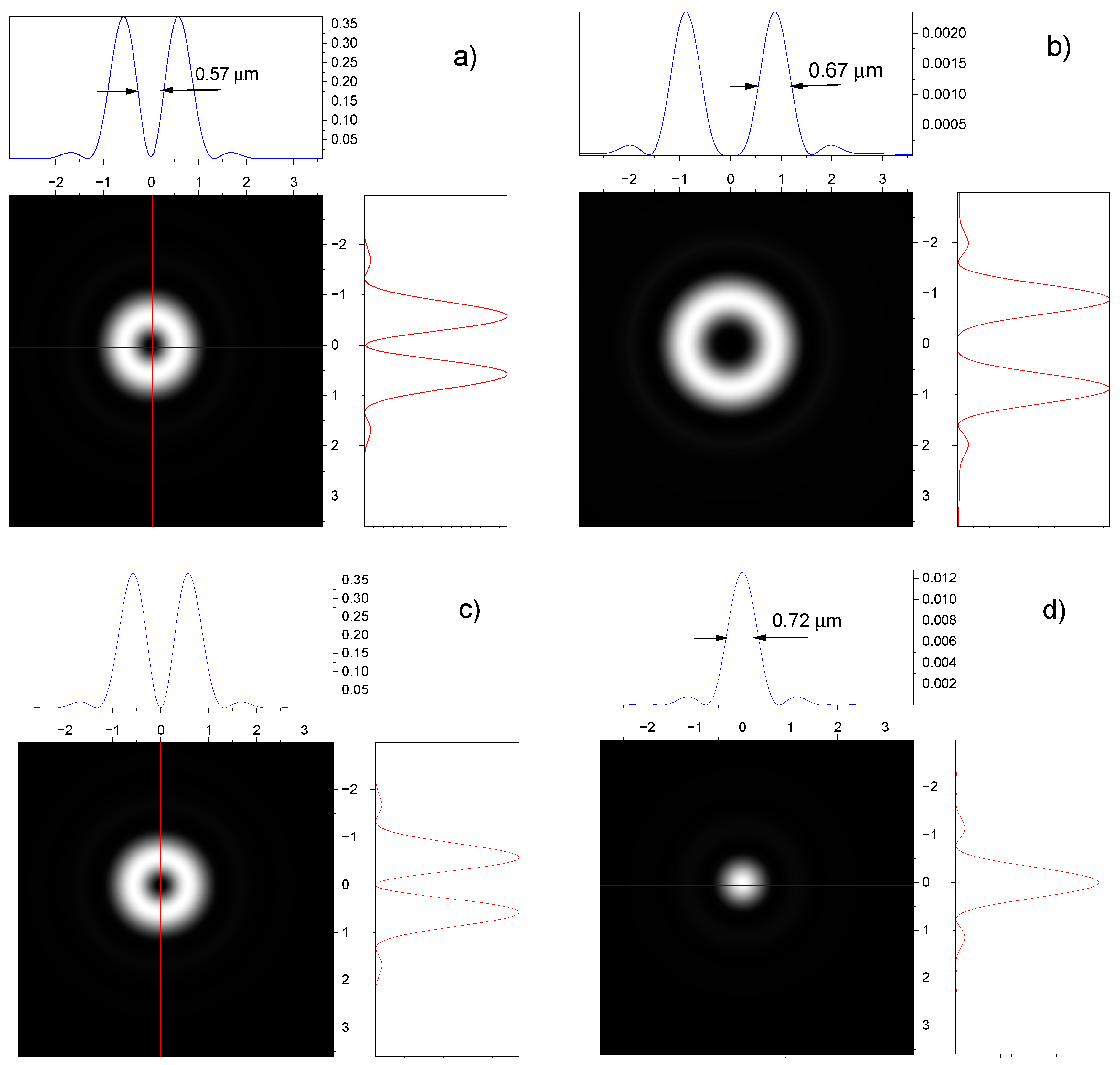
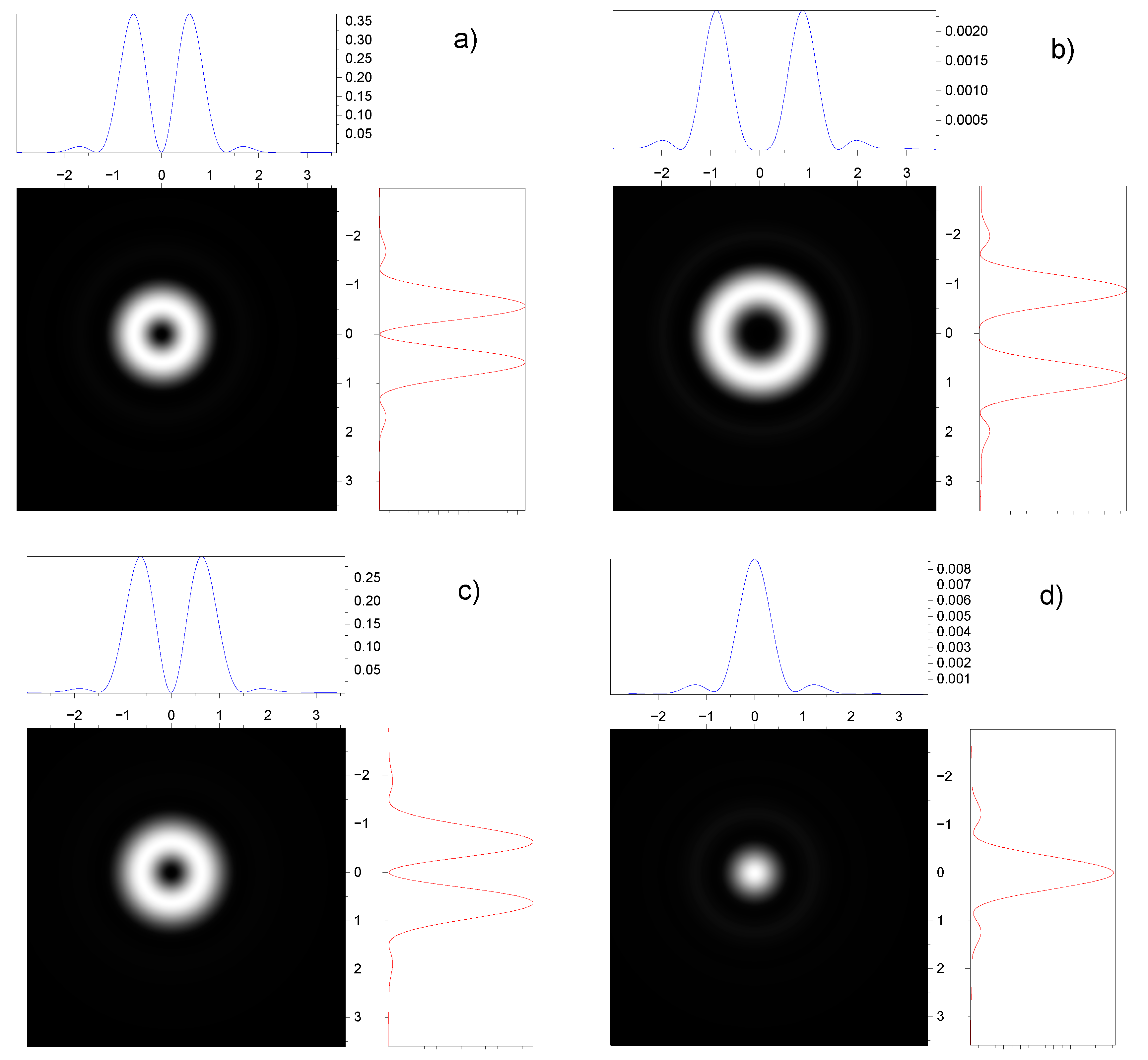
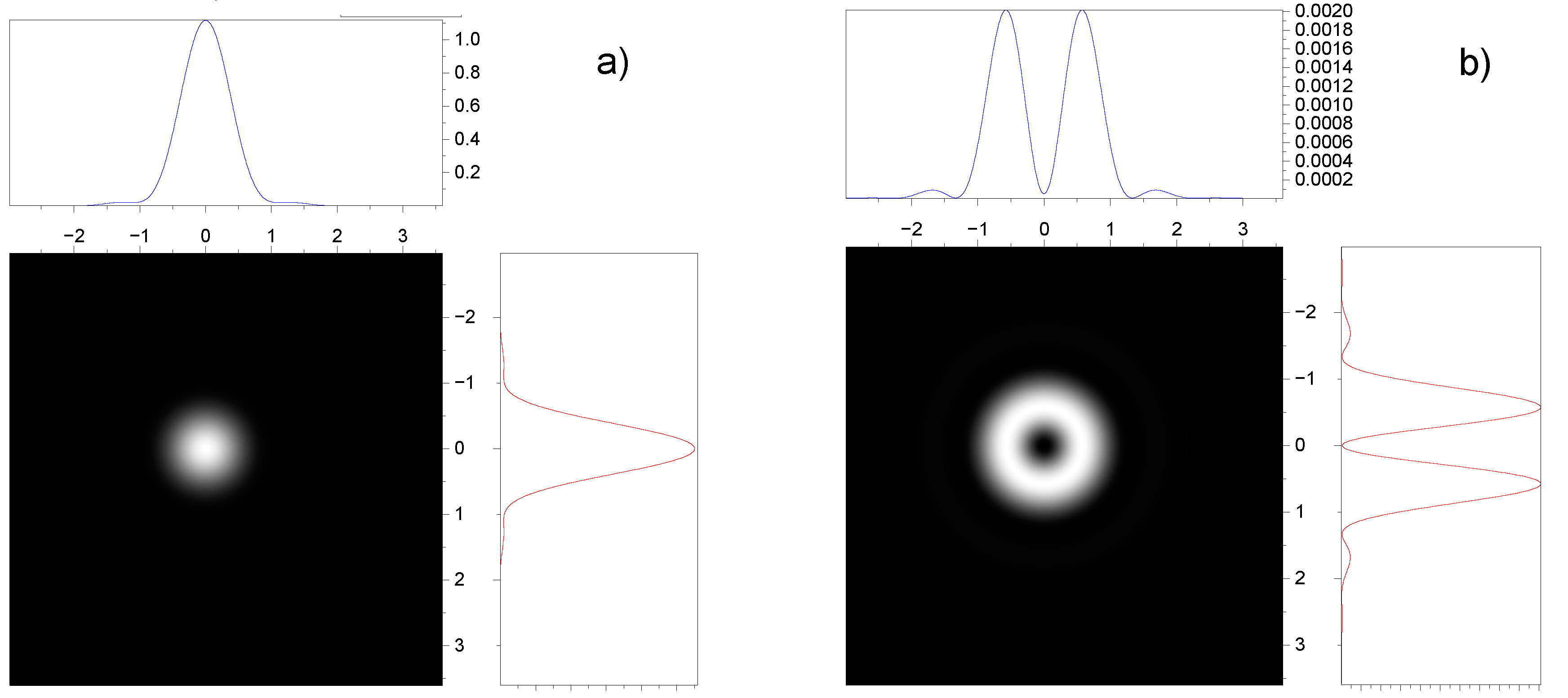
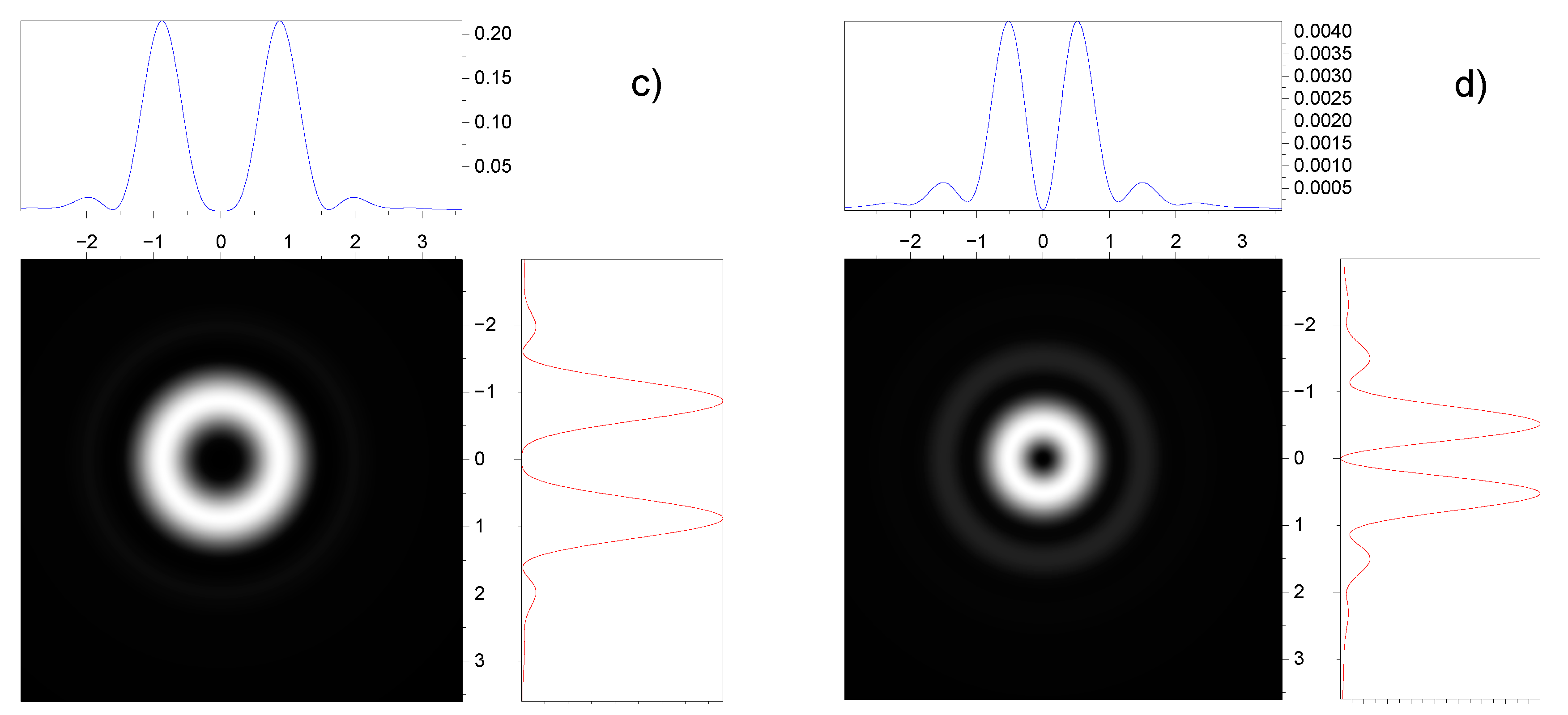
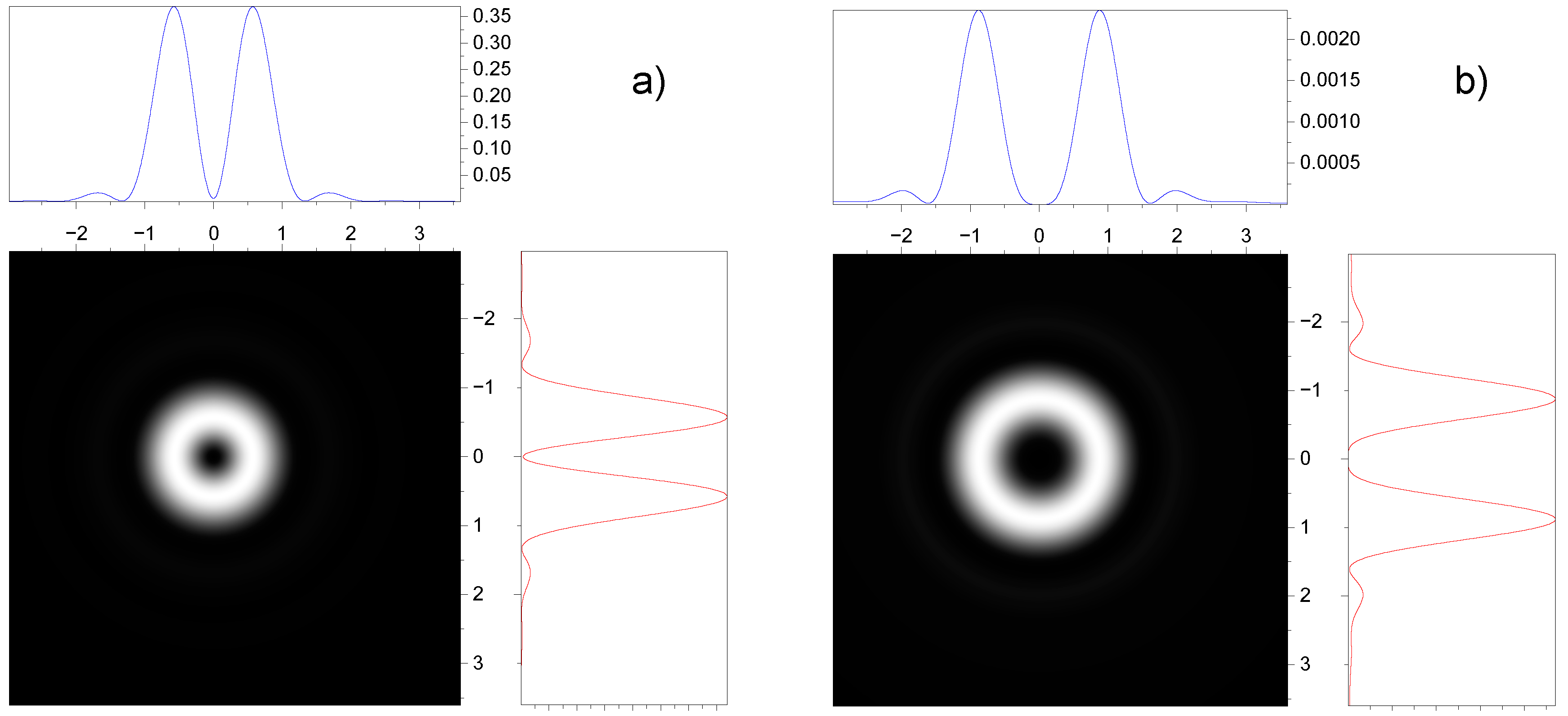
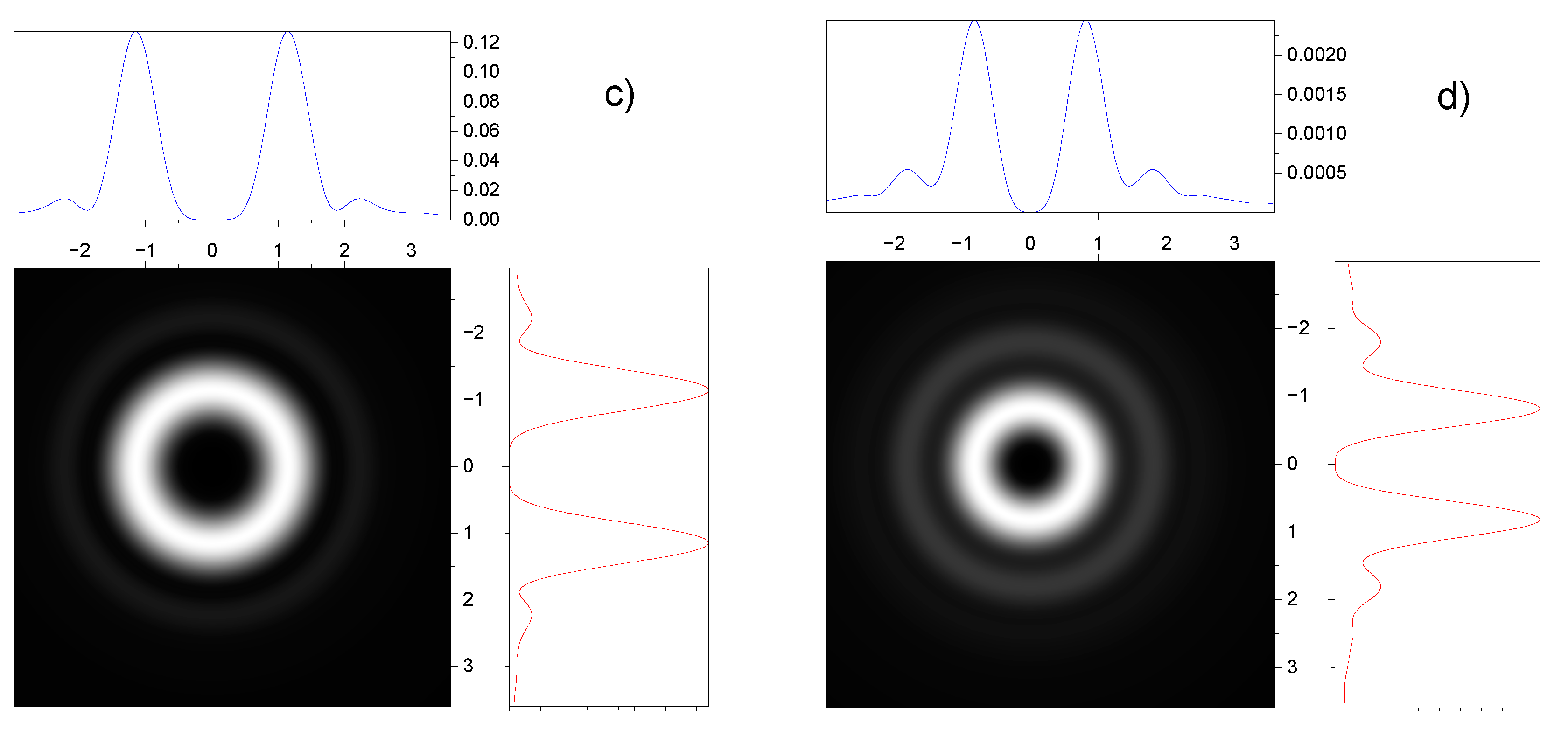
3.2. Effect of spin-orbit interaction on the intensity distribution
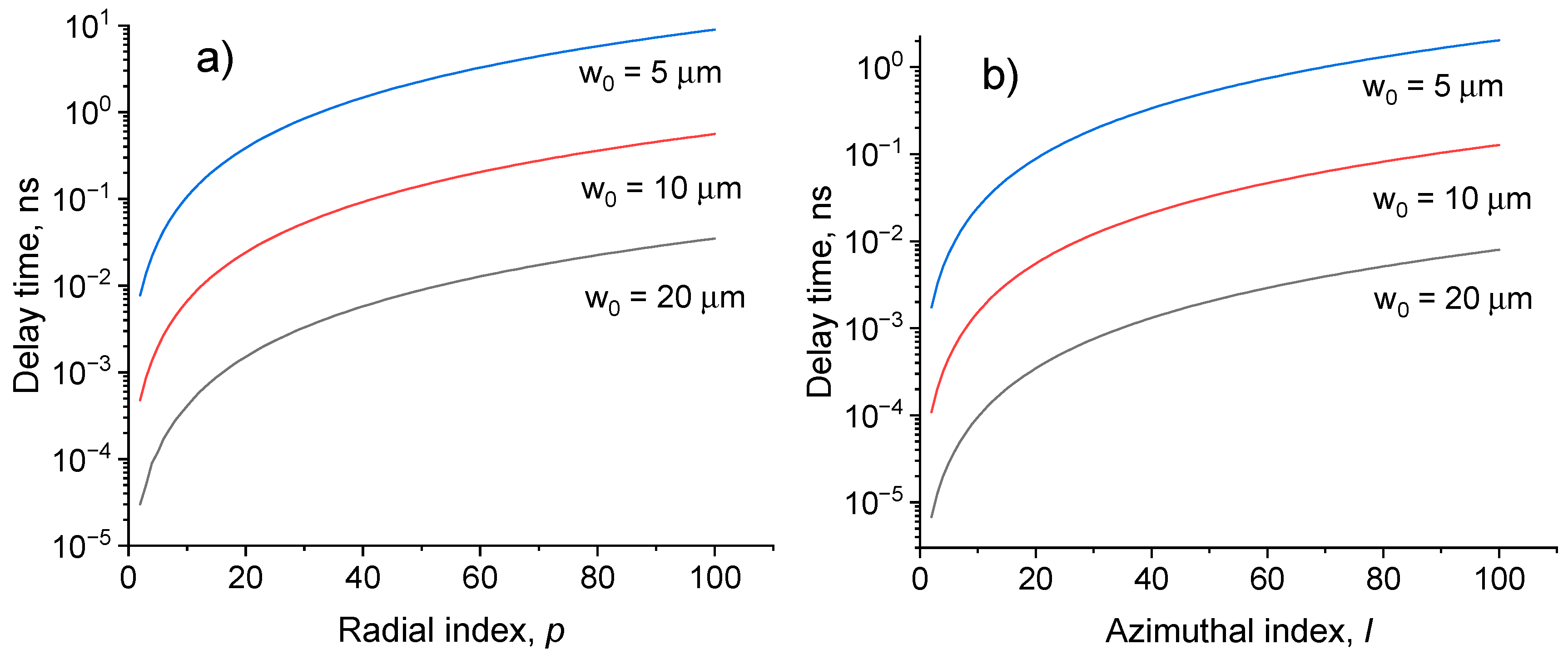
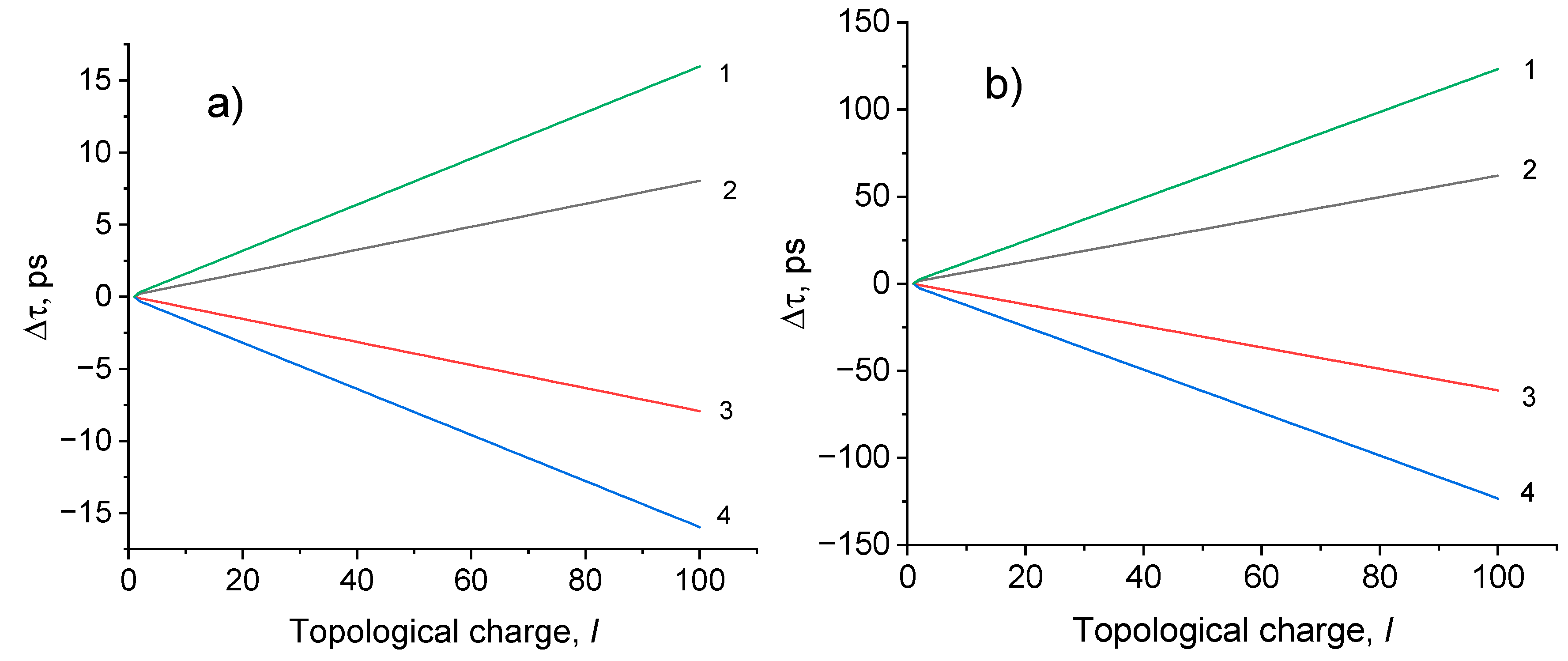
3.3. Effect of spin-orbit interaction on the speed of vortex beams in optical fiber
Spin-induced asymmetry
4. Conclusion
Funding
Data Availability Statement
Conflicts of Interest
References
- Fedotov, V.A.; Mladyonov, P.I.; Prosvirnin, S.I.; Rogacheva, A.V.; Chen, Y.; and Zheludev, N.I. Asymmetric Propagation of Electromagnetic Waves through a Planar Chiral Structure. Phys. Rev. Lett. 2006, 97, 167401. [Google Scholar] [CrossRef]
- Xu, Y.; Shi, Q.; Zhu, Z.; and Shi, J. Mutual conversion and asymmetric transmission of linearly polarized light in bilayered chiral metamaterial. Opt. Expr. 2014, 22, 25679–25688. [Google Scholar] [CrossRef] [PubMed]
- Plum, R.; Lin, X.X.; Fedotov, V.; Chen, Y.; Tsai, D.P.; Zheludev, N.I. Metamaterials: Optical Activity without Chirality. Phys. Rev. Lett. 2009, 102, 113902. [Google Scholar] [CrossRef]
- Goos, F.; Hanchen, H. Ein neuer und fundamentaler versuch zur total reflexion. Ann. Phys. (Leipzig) 1947, 1, 333–345. [Google Scholar] [CrossRef]
- Imbert, C. Calculation and experimental proof of the transverse shift induced by total internal reflection of a circularly polarized light beam. Phys. Rev. D 1972, 5, 787–796. [Google Scholar] [CrossRef]
- Petrov, N.I. Reflection and transmission of strongly focused light beams at a dielectric interface. J. Mod. Opt. 2005, 52, 1545–1556. [Google Scholar] [CrossRef]
- Petrov, N.I. Frustrated-total-internal-reflection-based thin-film color separator. Opt. Lett. 2007, 32, 2744–2746. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting the bandwidth of a frustrated total internal reflection filter with nanoparticle inclusions. OSA Cont. 2020, 3, 2591–2601. [Google Scholar] [CrossRef]
- Gorodetsky, Y.; Niv, A.; Kleiner, V.; and Hasman, E. Observation of the Spin-Based Plasmonic Effect in Nanoscale Structures. Phys. Rev. Lett. 2008, 101, 043903. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Gorodetski, Y.; Kleiner, V.; and Hasman, E. Coriolis effect in optics: unified geometric phase and spin-Hall effect. Phys. Rev. Lett. 2008, 101, 030404. [Google Scholar] [CrossRef]
- Petrov, N.I.; Danilov, V.A.; Popov, V.V.; and Usievich, B.A. Large positive and negative Goos-Hänchen shifts near the surface plasmon resonance in subwavelength grating. Opt. Express 2020, 28, 7552–7564. [Google Scholar] [CrossRef]
- Petrov, N.I.; Sokolov, Y.M.; Stoiakin, V.V.; Danilov, V.A.; Popov, V.V.; Usievich, B.A. Observation of Giant Angular Goos-Hanchen Shifts Enhanced by Surface Plasmon Resonance in Subwavelength Grating. Photonics 2023, 10, 180. [Google Scholar] [CrossRef]
- Gorodetski, Y.; Shitrit, N.; Bretner, I.; Kleiner, V.; and Hasman, E. Observation of optical spin symmetry breaking in nanoapertures. Nano Letters 2009, 9, 3016–3019. [Google Scholar] [CrossRef]
- Vuong, L.T.; Adam, A.J.L.; Brok, J.M.; Planken, P.C.M.; and Urbach, H.P. Electromagnetic spin-orbit interactions via scattering of subwavelength apertures. Phys. Rev. Lett. 2010, 104, 083903. [Google Scholar] [CrossRef]
- Rytov, S.M. On transition from wave to geometrical optics. Dokl. Akad. Nauk USSR 1938, 18, 263–266. [Google Scholar]
- Vladimirsky, V.V. On rotation of polarization plane in twisted ray of light. Dokl. Akad. Nauk USSR 1941, 31, 222–225. [Google Scholar]
- Tomita, A.; Chiao, R.Y. Observation of Berry's Topological Phase by Use of an Optical Fiber. Phys. Rev. Lett. 1986, 57, 937–940. [Google Scholar] [CrossRef]
- Berry, M.V. Quantal phase factors accompanying adiabatic changes. Proc. R. Soc. Lond. A 1984, 392, 45–57. [Google Scholar]
- Zel’dovich, B.Ya. , and Kundikova, N.D. Intrafibre rotation of the plane of polarization. Quant. Electron. 1995, 25, 172–174. [Google Scholar] [CrossRef]
- Zel’dovich, B. Y.; Liberman, V. S. Rotation of the plane of a meridional beam in a graded-index waveguide due to the circular nature of the polarization. Sov. J. Quant. Electron. 1990, 20, 427–428. [Google Scholar] [CrossRef]
- Zel’dovich, B. Y.; Kitaevskaya, I.V.; Kundikova, I.D. Inhomogeneity of the optical Magnus effect. Quant. Electron. 1996, 26, 87–88. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of light in a graded-index isotropic medium. J. Mod. Opt. 1996, 43, 2239–2249. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of polarization in an inhomogeneous isotropic medium. JETP 1997, 85, 1085–1093. [Google Scholar] [CrossRef]
- Petrov, N.I. Evolution of Berry's phase in a graded-index medium. Phys. Lett. A 1997, 234, 239–250. [Google Scholar] [CrossRef]
- Petrov, N.I. The influence of polarization on the trajectory and the width of a radiation beam in an inhomogeneous medium. Las. Phys. 2000, 10, 619–621. [Google Scholar]
- Bliokh, K.Y.; Niv, A.; Kleiner, V.; Hasman, E. Geometrodynamics of spinning light. Nat. Photon. 2008, 2, 748–753. [Google Scholar] [CrossRef]
- Liberman, V.S.; Zel’dovich, B.Y. Spin-orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 1992, 46, 5199–5207. [Google Scholar] [CrossRef] [PubMed]
- Onoda, M.; Murakami, S.; Nagaosa, N. Hall Effect of Light. Phys. Rev. Lett. 2004, 93, 083901. [Google Scholar] [CrossRef]
- Kavokin, A.; Malpuech, G.; Glazov, M. Optical Spin Hall Effect. Phys. Rev. Lett. 2005, 95, 136601. [Google Scholar] [CrossRef]
- Snyder, A. W.; Love, J. D. Optical waveguide theory; Chapman and Hall: London, N.Y., 1983. [Google Scholar]
- Bliokh, K.Y.; Desyatnikov, A.S. Spin and orbital Hall effects for diffracting optical beams in gradient-index media. Phys. Rev. A 2009, 79, 011807. [Google Scholar] [CrossRef]
- Bliokh, K. Y. Geometrodynamics of polarized light: Berry phase and spin Hall effect in a gradient-index medium. J. Opt. A: Pure Appl. Opt. 2009, 11, 094009. [Google Scholar] [CrossRef]
- Dugin, A.; Zel’dovich, B.; Kundikova, N.; Liberman, V. Effect of circular polarization on the propagation of light through an optical fiber. J. Exp. Theor. Phys. Lett. 1991, 53, 197–199. [Google Scholar]
- Liberman, V.S.; Zel’dovich, B.Y. Spin-orbit interaction of a photon in an inhomogeneous medium. Phys. Rev. A 1992, 46, 5199–5207. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Ostrovskaya, E.A.; Alonso, M.A.; Rodriguez-Herrera, O.G.; Lara, D.; and Dainty, C. Spin-to-orbital angular momentum conversion in focusing, scattering, and imaging systems. Optics Express 2011, 19, 26132–26149. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-orbit and tensor interactions of light in inhomogeneous isotropic media. Phys. Rev. A 2013, 88, 023815. [Google Scholar] [CrossRef]
- Petrov, N.I. Spin-dependent transverse force on a vortex light beam in an inhomogeneous medium. JETP Letters 2016, 103, 443–448. [Google Scholar] [CrossRef]
- Zhao, R.; Deng, F.; Yu, W.; Huang, J.; and Deng, D. Propagation properties of Airy–Gaussian vortex beams through the gradient-index medium. J. Opt. Soc. Am. A 2016, 33, 1025–1031. [Google Scholar] [CrossRef]
- Petrov, N.I. Vector Laguerre–Gauss beams with polarization-orbital angular momentum entanglement in a graded-index medium. J. Opt. Soc. Am. A 2016, 33, 1363–1369. [Google Scholar] [CrossRef]
- Yin, X.; Hao, P.; Zhang, Y.; Zhao, Z.; Wu, J.; and Li, J. Propagation of noninteger cylindrical vector vortex beams in a gradient-index fiber. Opt. Lett. 2023, 48, 2484–2487. [Google Scholar] [CrossRef]
- Pei, S.; Xu, S.; Cui, F.; Pan, Q.; and Cao, Z. Propagation of a Bessel–Gaussian beam in a gradient-index medium. Appl. Opt. 2019, 58, 920–926. [Google Scholar] [CrossRef]
- Chakravarthy, T.P.; Viswanatham, N.K. Direct and reciprocal spin-orbit interaction effects in a graded-index medium. OSA Continuum 2019, 2, 1576–1589. [Google Scholar] [CrossRef]
- Sodha, M. S.; Ghatak, A. K. Inhomogeneous Optical Waveguides; Plenum Press: New York, NY, USA, 1977. [Google Scholar]
- Loffler, W.; van Exter, M. P.; Hooft, G. W.; Eliel, E. R.; Hermans, K.; Broer, D. J.; Woerdman, J. P. Polarization-dependent Goos–Hänchen shift at a graded dielectric interface. Opt. Commun. 2010, 283, 3367–3370. [Google Scholar] [CrossRef]
- Petrov, N.I. Beam shift in a graded-index optical fiber. J. Opt. 2013, 15, 014011. [Google Scholar] [CrossRef]
- Fock, V.A.; Leontovich, M.A. Solution of the Problem of Propagation of Electromagnetic Waves along the Earth’s Surface by Method of Parabolic Equations. Journal of Physics—USSR 1946, 10, 13–23. [Google Scholar]
- Petrov, N.I. Vector and tensor polarizations of light beams. Las. Phys. 2008, 18, 522–525. [Google Scholar] [CrossRef]
- Petrov, N.I. Splitting of levels in a cylindrical dielectric waveguide. Opt. Lett. 2013, 38, 2020–2022. [Google Scholar] [CrossRef]
- Eide, H.A.; and Stamnes, J.J. Exact and approximate solutions for focusing of two-dimensional waves. J. Opt. Soc. Am. A 1998, 15, 1285–1319. [Google Scholar]
- Petrov, N.I. Nonparaxial focusing of wave beams in a graded-index medium. Rus. J. Quant. Electron. 1999, 29, 249–255. [Google Scholar] [CrossRef]
- Petrov, N.I. Focusing of beams into subwavelength area in an inhomogeneous medium. Opt. Exp. 2001, 9, 658–673. [Google Scholar] [CrossRef]
- Yuan, Y.; Du, S.; Dong, Y.; Wang, F.; Zhao, C.; and Cai, Y. Nonparaxial propagation properties of a vector partially coherent dark hollow beam. JOSA A 2013, 30, 1358–1372. [Google Scholar] [CrossRef]
- Petrov, N.I. Macroscopic quantum effects for classical light. Phys. Rev. A 2014, 90, 043814. [Google Scholar] [CrossRef]
- Petrov, N.I. Nonparaxial Propagation of Bessel Correlated Vortex Beams in Free Space. Micromachines 2023, 14, 38. [Google Scholar] [CrossRef]
- Petrov, N.I. Nonparaxial Focusing of Partially Coherent Gaussian Schell-Model and Bessel-Correlated Beams in Free Space. Photonics 2023, 10, 857. [Google Scholar] [CrossRef]
- Bliokh, K.Yu.; Frolov, D.Yu. Spin-orbit interaction of photons and fine splitting of levels in ring dielectric resonator. Optics Commun. 2005, 250, 321–327. [Google Scholar] [CrossRef]
- Petrov, N.I. Depolarization of Light in Optical Fibers: Effects of Diffraction and Spin-Orbit Interaction. Fibers 2021, 9, 34. [Google Scholar] [CrossRef]
- Matsuhara, M. Analysis of electromagnetic-wave modes in lens-like media. JOSA 1973, 63, 135–138. [Google Scholar] [CrossRef]
- Thyagarajan, R.; and Chatak, A.K. Perturbation theory for studying the effect of the ∇ε term in lens-like media. Optics Commun. 1974, 11, 417–421. [Google Scholar] [CrossRef]
- Bouchard, F.; Harris, J.; Mand, H.; Boyd, R.W.; and Karimi, E. Observation of subluminal twisted light in vacuum. Optica 2016, 3, 351–354. [Google Scholar] [CrossRef]
- Petrov, N.I. Speed of structured light pulses in free space. Sci. Rep. 2019, 9, 18332. [Google Scholar] [CrossRef]
- Guo, Y.; Pu, M.; Zhang, F.; Xu, M.; Li, X.; Ma, X.; and Luo, X. Classical and generalized geometric phase in electromagnetic metasurfaces. Photonics Insights 2022, 1, R03. [Google Scholar] [CrossRef]
- Dong, M.; Bai, Y.; Yao, J.; Zhao, Q.; and Yang, Y. Propagation properties of partially coherent modified Bessel-Gauss beams through the gradient-index medium. Appl. Opt. 2020, 59, 8023–8028. [Google Scholar] [CrossRef]
- Wang, J.; Yang, M.; Guo, Z.; Feng, Z.; Li, J. Change in phase singularities of a partially coherent Gaussian vortex beam propagating in a GRIN fiber. Opt. Expr. 2020, 28, 4661–4673. [Google Scholar] [CrossRef]
- Wadood, S.A.; Liang, K.; Agrawal, G.P.; Visser, T.D.; Stroud, C.R.; Vamivakas, A.N. Propagation of Gaussian Schell-model beams in modulated graded-index media. Opt. Expr. 2021, 29, 21240–21251. [Google Scholar] [CrossRef]
- Dong, M.; Bai, Y.; Yao, J.; Zhao, Q.; and Yang, Y. Propagation properties of partially coherent modified Bessel–Gauss beams through the gradient-index medium. Appl. Opt. 2020, 59, 8023–8028. [Google Scholar] [CrossRef]
- Petrov, N.I. Sharp focusing of partially coherent Bessel-correlated beams by a graded-index lens. Opt. Lett. 2023, 48, 6048–6051. [Google Scholar] [CrossRef]
- Petrov, N.I. Remote focusing of a light beam. Las. Phys. Lett. 2016, 13, 015101. [Google Scholar] [CrossRef]
- Eismann, J.S.; Nicholls, L.H.; Roth, D.J.; et al. Transverse spinning of unpolarized light. Nat. Photonics 2021, 15, 156–161. [Google Scholar] [CrossRef]
- Ketara, M.L.; Kobayashi, H.; Brasselet, E. Sensitive vectorial optomechanical footprint of light in soft condensed matter. Nat. Photon. 2021, 15, 121–124. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Longitudinal fields and transverse rotations. Nat. Photonics 2021, 15, 1–3. [Google Scholar] [CrossRef]
- Qin, Z.; Zhang, L.; Zhang, R.; Zhang, P.; Qi, R.; Zhang, Q.; Ren, L.; and Jiang, L. Effect of the incident polarization on in-plane and out-of-plane spin splitting near the critical angle. Opt. Exp. 2023, 31, 853–863. [Google Scholar] [CrossRef]
- Lee, Y.U.; and Wu, J.W. Visualization of the optical spin Hall effect in out-of-plane refraction. Opt. Lett. 2023, 48, 5988–5991. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




