Submitted:
16 August 2023
Posted:
17 August 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
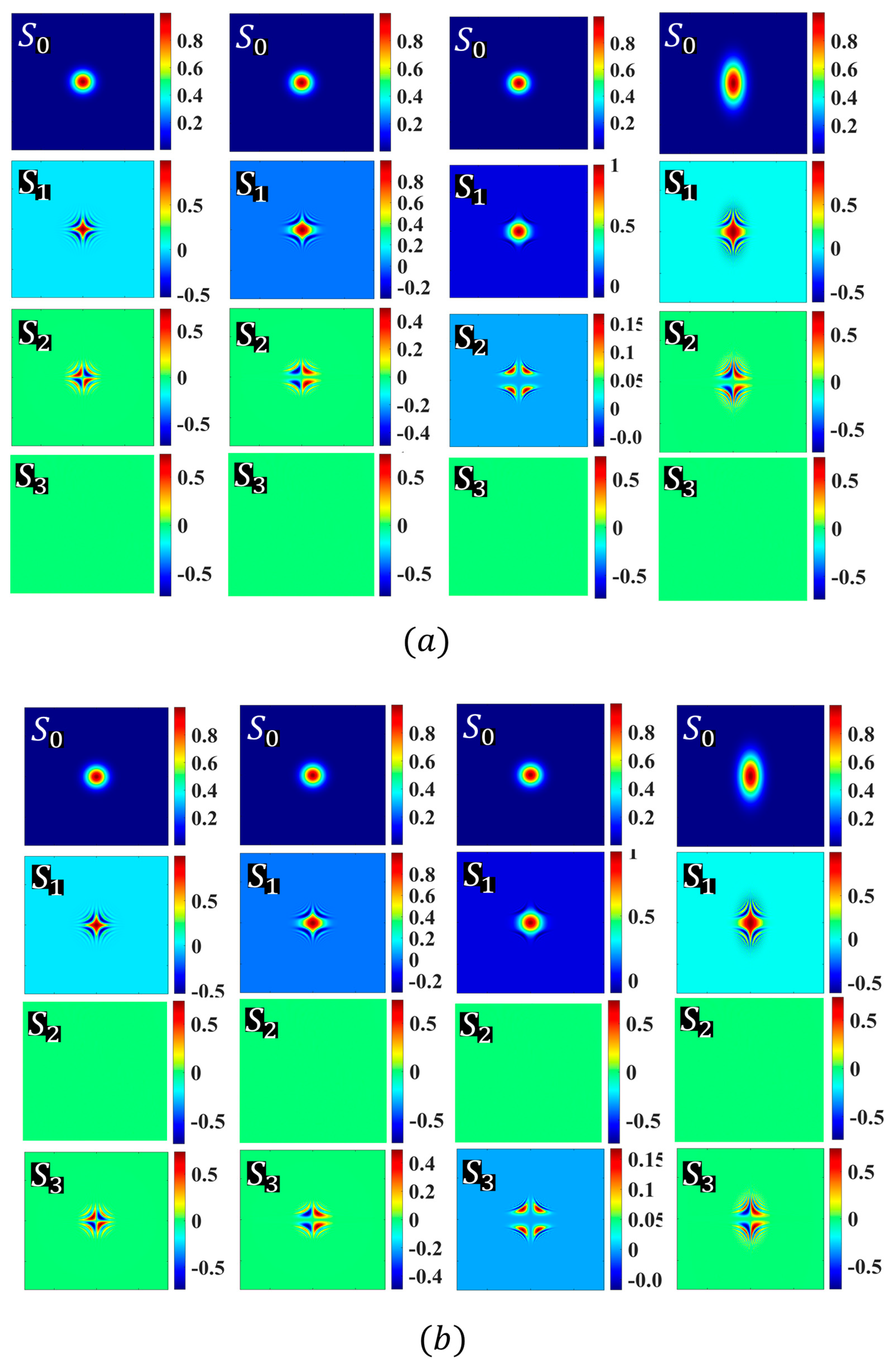
2. Evolution of polarization state in a high-order twisted vector optical field
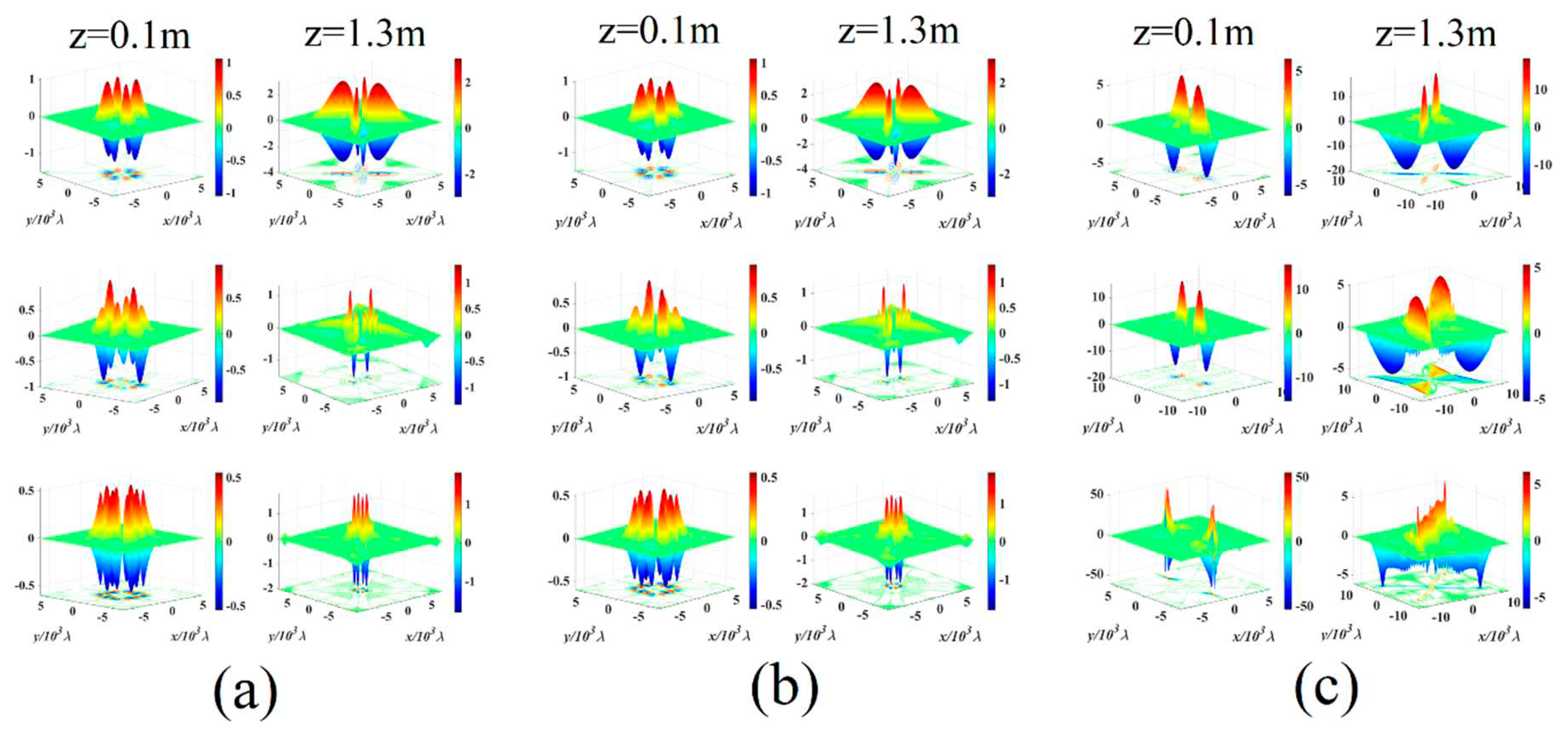
3. Effect of a high-order twisting phase on the optical angular momentum
4. Discussion
5. Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ndagano, B.; Nape, I.; Cox, M.A.; Rosales-Guzman, C.; Forbes, A. Creation and detection of vector vortex modes for classical and quantum communication. J. Light. Technol. 2018, 36, 292–301. [Google Scholar] [CrossRef]
- O’Holleran, K.; Flossmann, F.; Dennis, M.R.; Padgett, M.J. Methodology for imaging the 3D structure of singularities in scalar and vector optical fields. J. Opt. Pure Appl. Opt. 2009, 11, 094020. [Google Scholar] [CrossRef]
- Yao, G.; Li, Y.; Chen, R.-P. Collapse dynamics of vortex beams in a Kerr medium with refractive index modulation and PT-symmetric lattices. Photonics 2022, 9, 249. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Wu, F.; Chen, R.-P. Polarization state evolution of a twisted vector optical field in a strongly nonlocal nonlinear medium. J. Opt. Soc. Am. A 2023, 40, 620. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Lin, X.; Liao, M.; Zhao, G.; Fang, Y. Polarization manipulation of bright-dark vector bisolitons. Chin. Phys. B 2021, 30, 034208. [Google Scholar] [CrossRef]
- Buryy, O.; Andrushchak, A.; Chernovol, N. The optimal geometries of phase matching in uniaxial non-linear optical crystals determined by extreme surfaces method. In Proceedings of the 2020 IEEE 15th International Conference on Advanced Trends in Radioelectronics, Telecommunications and Computer Engineering (TCSET); IEEE: Lviv-Slavske, Ukraine, 2020; pp. 436–441. [Google Scholar]
- Hu, X.-B.; Zhao, B.; Chen, R.-P.; Rosales-Guzmán, C. Experimental generation of arbitrary abruptly autofusing circular Airy Gaussian vortex vector beams. Sci. Rep. 2022, 12, 18274. [Google Scholar] [CrossRef]
- Toussaint, K.C.; Park, S.; Jureller, J.E.; Scherer, N.F. Generation of optical vector beams with a diffractive optical element interferometer. Opt. Lett. 2005, 30, 2846. [Google Scholar] [CrossRef]
- De Oliveira, A.G.; Rubiano Da Silva, N.; Medeiros De Araújo, R.; Souto Ribeiro, P.H.; Walborn, S.P. Quantum optical description of phase conjugation of vector vortex beams in stimulated parametric down-conversion. Phys. Rev. Appl. 2020, 14, 024048. [Google Scholar] [CrossRef]
- Beversluis, M.R.; Novotny, L.; Stranick, S.J. Programmable vector point-spread function engineering. Opt. Express 2006, 14, 2650. [Google Scholar] [CrossRef]
- Bomzon, Z.; Kleiner, V.; Hasman, E. Formation of radially and azimuthally polarized light using space-variant subwavelength metal stripe gratings. Appl. Phys. Lett. 2001, 79, 1587–1589. [Google Scholar] [CrossRef]
- Niv, A.; Biener, G.; Kleiner, V.; Hasman, E. Propagation-invariant vectorial Bessel beams obtained by use of quantized Pancharatnam–Berry phase optical elements. Opt. Lett. 2004, 29, 238. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Hao, J.; Zhang, B.-F.; Xu, J.; Ding, J.; Wang, H.-T. Generation of vector beam with space-variant distribution of both polarization and phase. Opt. Lett. 2011, 36, 3179. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chew, K.-H.; Liu, C.; Wang, Z.; Chen, R.-P. Controllable linear-circular polarization conversion of radial variant vector beams in a strongly nonlocal nonlinear medium. J. Opt. 2019, 21, 065402. [Google Scholar] [CrossRef]
- Yue, Z.; Lu, P.; Xu, J.; Li, Z.; Teng, S. Vector beams encoded by diverse orthogonal polarization states and their generation based on metasurfaces. New J. Phys. 2023, 25, 013018. [Google Scholar] [CrossRef]
- Li, M.; Yue, X.; Xu, T. Asymptotic behaviors of mixed-type vector double-pole solutions for the discrete coupled nonlinear Schrödinger system. Eur. Phys. J. Plus 2021, 136, 62. [Google Scholar] [CrossRef]
- Spall, J.; Guo, X.; Barrett, T.D.; Lvovsky, A.I. Fully reconfigurable coherent optical vector–matrix multiplication. Opt. Lett. 2020, 45, 5752. [Google Scholar] [CrossRef]
- Long, Z.; Hu, H.; Ma, X.; Tai, Y.; Li, X. Encoding and decoding communications based on perfect vector optical vortex arrays. J. Phys. Appl. Phys. 2022, 55, 435105. [Google Scholar] [CrossRef]
- Simon, R.; Mukunda, N. Twisted Gaussian Schell-model beams. J. Opt. Soc. Am. A 1993, 10, 95. [Google Scholar] [CrossRef]
- Friberg, A.T.; Tervonen, E.; Turunen, J. Focusing of twisted Gaussian Schell-model beams. Opt. Commun. 1994, 106, 127–132. [Google Scholar] [CrossRef]
- Wan, L.; Zhao, D. Generalized partially coherent beams with nonseparable phases. Opt. Lett. 2019, 44, 4714. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Q. Controllable conversion between Hermite Gaussian and Laguerre Gaussian modes due to cross phase. Opt. Express 2019, 27, 10684. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Ren, Y.; Liu, T.; Liu, Z.; Qiu, S.; Li, Z.; Ding, Y.; Wu, H. Generating a new type of polygonal perfect optical vortex. Opt. Express 2021, 29, 14126. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q.; Chew, K.-H.; Huang, Y.; Liu, C.; Hu, X.; Li, Y.; Chen, R.-P. Effect of twisting phases on the polarization dynamics of a vector optical field. Photonics 2022, 9, 722. [Google Scholar] [CrossRef]
- Desyatnikov, A.S.; Buccoliero, D.; Dennis, M.R.; Kivshar, Y.S. Suppression of collapse for spiraling elliptic solitons. Phys. Rev. Lett. 2010, 104, 053902. [Google Scholar] [CrossRef]
- Liang, G.; Guo, Q. Spiraling elliptic solitons in nonlocal nonlinear media without anisotropy. Phys. Rev. A 2013, 88, 043825. [Google Scholar] [CrossRef]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef]
- Courtial, J.; Dholakia, K.; Allen, L.; Padgett, M.J. Gaussian beams with very high orbital angular momentum. Opt. Commun. 1997, 144, 210–213. [Google Scholar] [CrossRef]
- Wu, S.-D.; Chew, K.-H.; Chen, R.-P. Effect of twisting phases on linear–circular polarization and spin–orbital angular momentum conversions in tightly focused vector and scalar beams. Photonics 2023, 10, 151. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




