Prerpints.org logo
Preprint
Article

How Simply One Can Considerably Improve Performance of the Gas Stripper at the GSI UNILAC (Proposal)

This version is not peer-reviewed.

Submitted:

06 March 2024

Posted:

07 March 2024

You are already at the latest version

A peer-reviewed article of this preprint also exists.

Abstract
Here we propose a simple way in which one can considerably improve performance of the gas stripper setup at the GSI UNILAC. To do so, it will be enough to replace inside the main GSI stripper chamber the present nozzle and the short windowless storage gas cell (for pulsed gas-jet operation mode) by a simple conical diverging nozzle combined with a gas catcher tube placed on the axis of gas-jet at some distance downstream the nozzle exit. As a result, the background pressure in the main and differentially pumped adjacent vacuum chambers of the gas stripper at the GSI UNILAC will dramatically reduce, and it will make possible to achieve the required optimal thickness of gas targets. The pulsed gas stripper operation is simply realized by implementing a commercially available fast gas valve connected to the nozzle entrance. Moreover, the ion beam pulses repetition rate can be increased and it will allow for the considerably higher average intensity of the ion beams extracted from the GSI UNILAC. Performance of the proposed GSI UNILAC gas stripper modification we explored by means of detailed computer experiments, which give a realistic description of supersonic gas jets flowing out the nozzle into vacuum. Results of these computer experiments have presented and discussed.
Keywords: 
GSI UNILAC
;  
gas jet stripper
;  
supersonic nozzle
;  
gas catcher tube
;  
gas dynamic simulations
Subject: 
Physical Sciences  -   Nuclear and High Energy Physics

1. Introduction

An ion charge stripping system is one of the key components of high-intensity heavy-ion beam accelerator facilities, such as the FRIB (MSU, USA) [1], the RIBF (RIKEN, Japan) [2], and the future Facility for Antiproton and Ion Research (FAIR, Germany) [3].
In this article, we propose a simple method to considerably improve the performance of the gas stripper setup at the GSI Universal Linear Accelerator (UNILAC) in Germany. A detailed description of the design and operation of the GSI gas stripper reader can be found elsewhere, for example, in [4,5,6,7,8,9,10,11,12,13,14], as well as links between them. Therefore, in this article, we provide only a short description.
The schematic layout of the UNILAC with the gas stripper section is shown in Figure 1 in Ref. [4]. The following ion sources are used at the GSI centre for the production of high-intensity heavy-ion beams:
The Penning Ion Source (PIG) for ion beams of intermediate charge state (with ion pulse lengths up to 6 ms and a maximum repetition rate of 50 Hz);
The Multi Cusp Ion Source (MUCIS) for gaseous elements (with ion pulse lengths up to 3 ms and a maximum repetition rate of 17 Hz);
The Metal Vapor Vacuum Arc (MEVVA) source for metallic ions (with ion pulse lengths up to 3 ms and a maximum repetition rate of 17 Hz);
The Electron Cyclotron Resonance (ECR) source for highly charged ions (with ion pulse lengths up to 6 ms and a maximum repetition rate of 50 Hz).
The ion beam, having a +4 charge state after its acceleration up to the energy of 1.4 MeV/u, enters into the gas stripper where ions cross a gas target. As a result of a number of charge exchange ion collisions with atoms of the gas target, the charge states of the ions are increased. Then, the beam of highly charged ions undergoes a charge selection, passing fast switchable dipole magnets, and the part with the desired charge state is injected into a subsequent accelerating Alvarez-type section. Then, the selected ion beam accelerates up to the final energy of 11.4 MeV/u.
The following two gas stripper variants are used at the GSI UNILAC:
  • The first variant consists of an operation with the continuous nitrogen gas jet flowing out of the conical supersonic nozzle into the main stripper chamber (the 3D schematic of this setup can be seen in Figure 2 in Ref. [12]). The nozzle throat diameter is 0.85 mm, the length of the supersonic diverging part is 13.85 mm, and the exit nozzle diameter is 5 mm. The gas from the main stripper chamber is evacuated using a Roots vacuum pump with a capacity of 8000 m3/h (or 2222 l/s). Four subsidiary vacuum chambers serve as a differential pumping system (two chambers in front of the stripper and two chambers behind it). Each of these subsidiary chambers is pumped using a separate turbomolecular vacuum pump of 1200 l/s. The ion beam crosses the supersonic jet at a right angle to its axis.
  • In the second gas stripper variant, the supersonic nozzle is replaced by a pulsed gas valve, which exits the aperture directly connected to the T-fitting aligned with the ion beam axis (see Figure 2 in Ref. [11]). This short T-fitting has a length of 44 mm in the ion beam direction and a 21 mm aperture. The 3D schematic of this pulsed gas stripper setup is shown in Figure 1 in Ref. [11] and in Figure 2 in Ref. [14].
The characteristics of the ion beams that pass through the gas stripper section of the GSI UNILAC are presented in Figure 3, Figure 4 and Figure 5 in Ref. [14]: Figure 3 shows the charge state distributions of uranium ions stripped in a nitrogen continuous jet and via helium and hydrogen in pulsed operation mode; Figure 4 demonstrates the charge state distributions for stripped uranium ions for different hydrogen target thicknesses; and Figure 5 shows the equilibrated charge state distributions for 238U, 209Bi, 50Ti, and 40Ar ions that pass through the nitrogen and hydrogen gas targets.
It is common knowledge that the main limiting factor in the use of any internal gas target in accelerator technology and accelerator experiments is a deterioration of the background vacuum in the course of the operation of a gas target system. This is why the gas stripper at the GSI UNILAC can be used with the nitrogen continuous supersonic jet only when the gas stagnation pressure in the nozzle is not higher than 4 bar.
The gas stripper at the GSI UNILAC operates with hydrogen in pulsed mode with a low ion beam pulse repetition rate (gas pulses are synchronized with ion pulses) of about 3 Hz. Another disadvantage of the pulse stripper design at the GSI is that the gas flows out of both ends of the short T-fitting in the form of a pulsed supersonic jet in the direction of the ion beam (see Figure 1 in Ref. [11]). This can lead to additional vacuum deterioration in adjacent differential pumping chambers.
To considerably reduce background pressures in the vacuum chambers of the gas stripper at the GSI UNILAC and thus significantly improve its performance, we propose the straightforward installation of a supersonic conical diverging nozzle combined with a gas catcher tube with a conical entrance part. The distance between the nozzle exit and the gas catcher entrance is determined by the ion beam diameter. As a result, the main part of the gas flowing out of the nozzle into the main gas stripper vacuum chamber is evacuated through the gas catcher tube.
The gas catcher tube and the supersonic nozzle are located vertically on the axis of the main stripper chamber. The output end of the gas catcher tube is fixed to the center of the top flange, which is similar to the existing one (see Figure 2 in Ref. [11]). The supersonic nozzle exit is located below the horizontal ion beam axis. To pump gas out of the gas catcher tube, the output is connected through a flexible bellow with a relatively small additional Roots pump with a pumping capacity of 251 m3/h.
In other words, for the upgrade of the current gas stripper at the GSI UNILAC, we suggest using a classic design concept of internal gas jet targets, where the supersonic nozzle and gas catcher are key components. Internal gas jet targets have been used for more than 30 years and are nowadays widely applied in various accelerator experiments.
Descriptions of various internal gas jet target readers can be found, e.g., in reviews [15,16] and original works [17,18,19,20,21,22,23]. It is worth noting here that in order for the GSI UNILAC gas stripper upgraded in the described manner to work in the pulse mode with light gases (helium and hydrogen), a commercially available fast pulsed valve is connected to the entrance of the supersonic nozzle. For example, the pulsed valve presented in [24] and successfully used in our works [22] and [23] is effective. Moreover, switching the mode of the continuous gas–jet operation is achieved by keeping the valve open.
We explored the performance of the proposed GSI UNILAC gas stripper modification by means of detailed computer experiments with the use of the VARJET code. This code, described in detail in [25], is based on the solution of a full system of time-dependent Navier–Stokes equations. The code provides a realistic description of supersonic and subsonic gas jets flowing out of the nozzle and into the vacuum. Many times during the last 20 years, the accuracy of the VARJET code has been confirmed via direct comparison of our simulations with measurements for different applications (e.g., in our works [22,23,25], and recent review [26]). The results of similar computer experiments for the gas stripper are presented and discussed in the following sections.

2. Results of continuous nitrogen jet simulations

In order to demonstrate the advantage of the gas stripper equipped with a gas catcher tube over the current GSI UNILAC stripper (variant #1) with the supersonic nozzle, we conducted the following five computer simulations of the continuous nitrogen gas jet:
  • GSI nozzle (the nozzle throat diameter is 0.85 mm, the length of the supersonic diverging part is 13.85 mm, and the nozzle exit diameter is 5 mm) at 4-bar stagnation pressure.
  • GSI nozzle + gas catcher at 4-bar stagnation pressure.
  • New nozzle + gas catcher (the nozzle throat diameter is 1.0 mm, the length of the supersonic diverging part is 40 mm, and the nozzle exit diameter is 8 mm) at 4-bar stagnation pressure. We recommend this long and narrow new nozzle for use with a gas catcher tube in the upgraded gas stripper at the GSI.
  • GSI nozzle + gas catcher at 10-bar stagnation pressure.
  • New nozzle + gas catcher at 10-bar stagnation pressure.
Figure 1 and Figure 2 illustrate the results of the gas dynamic simulations of the nitrogen density flow field for the first and second calculation variants, respectively.
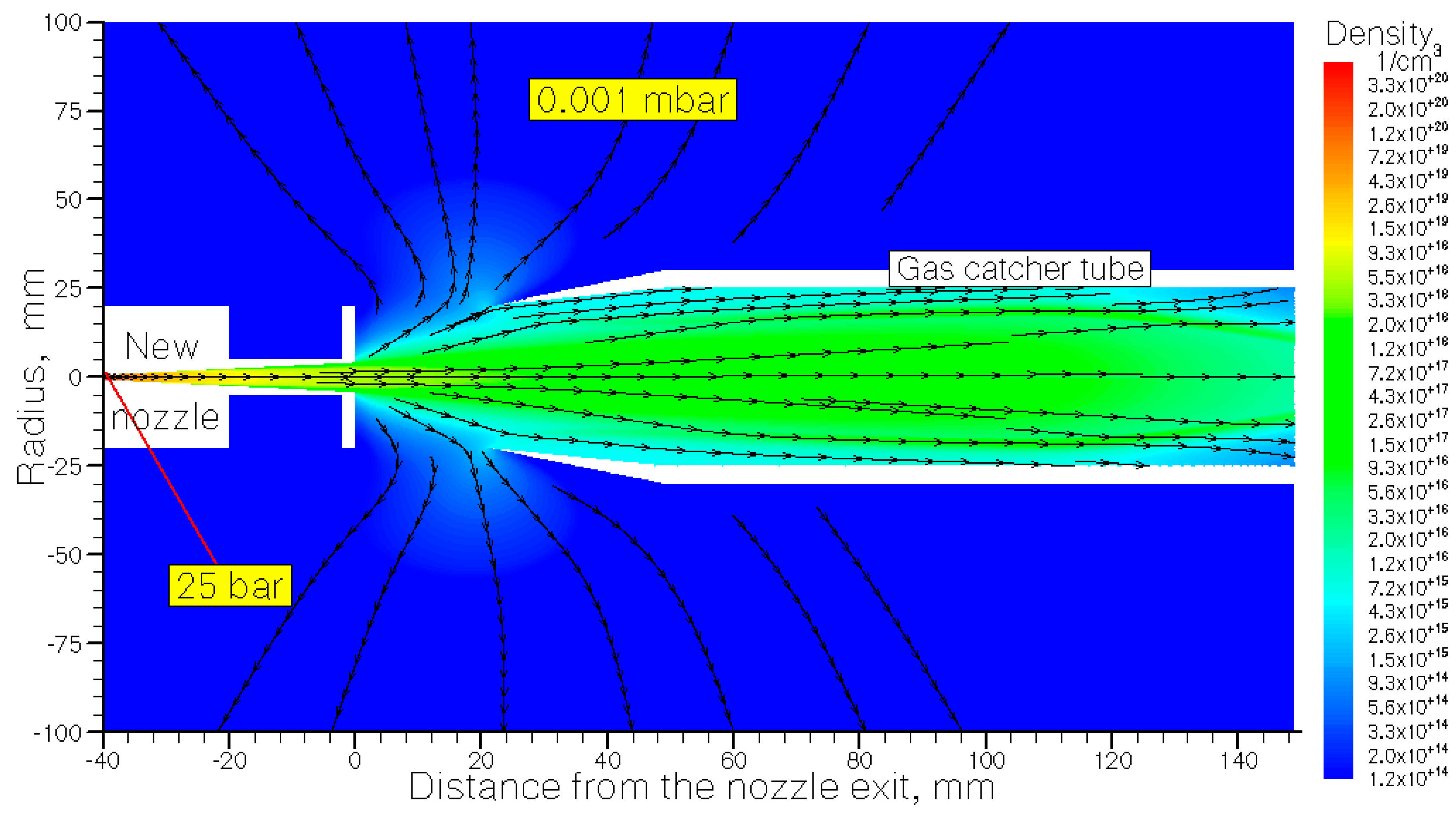
The gas catcher tube (shown in Figure 2), installed on the gas–jet axis at a 21 mm distance downstream from the nozzle exit, has a conical entrance part measuring 28 mm in length with entrance and exit inner diameters of 40 mm and 50 mm, respectively. The thickness of the catcher tube wall is not critical. The 21 mm gap between the nozzle and the gas catcher tube is equal to the aperture of the T-fitting shown in Figure 2 in Ref. [11].
The result of the gas dynamic simulation of the nitrogen density flow field for the third calculation variant is shown in Figure 3. Notice that a disk of 40 mm outer diameter is fixed to the nozzle exit. The thickness of this disk and its outer diameter are not critical.
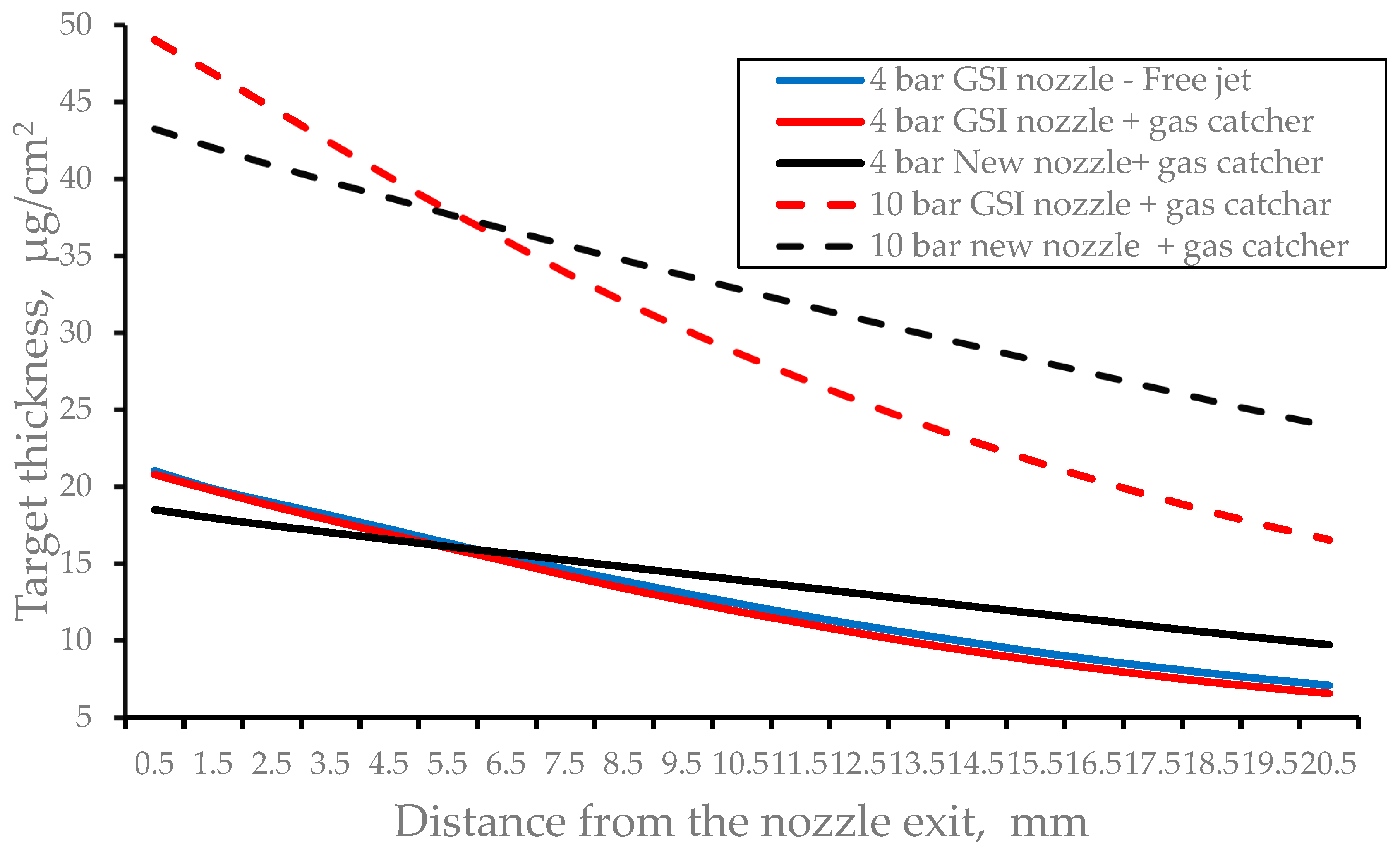
Figure 4 shows the results of the calculations of the nitrogen target thickness as a function of distance from the nozzle exit for the five above-mentioned calculation variants. The main gas flow characteristics calculated for these five variants of the gas stripper operation are listed in Table 1.
Note that a smaller slope of target thickness curves for the new nozzle (see Figure 4) means better thickness homogeneity of the gas targets. The better gas target homogeneity allows for obtaining narrower charge state distributions of ions stripped in this target.
The difference in the total gas flow rates for variants #2 and #3, as well as for #4 and #5, can be explained by the difference in throat diameters of the current “GSI nozzle” (0.85 mm) and the “New nozzle” (1.0 mm).

3. Results of the pulsed gas jet stripper operation mode

In order to determine how the geometry of a supersonic nozzle affects the performance of the gas stripper in the pulse operation mode, we performed gas dynamic calculations of conical diverging nozzles of different outlet diameters and lengths at a fixed nozzle throat diameter of 1.0 mm. The calculations were made for jets of nitrogen, helium, and hydrogen.

3.1. Helium pulsed jet target

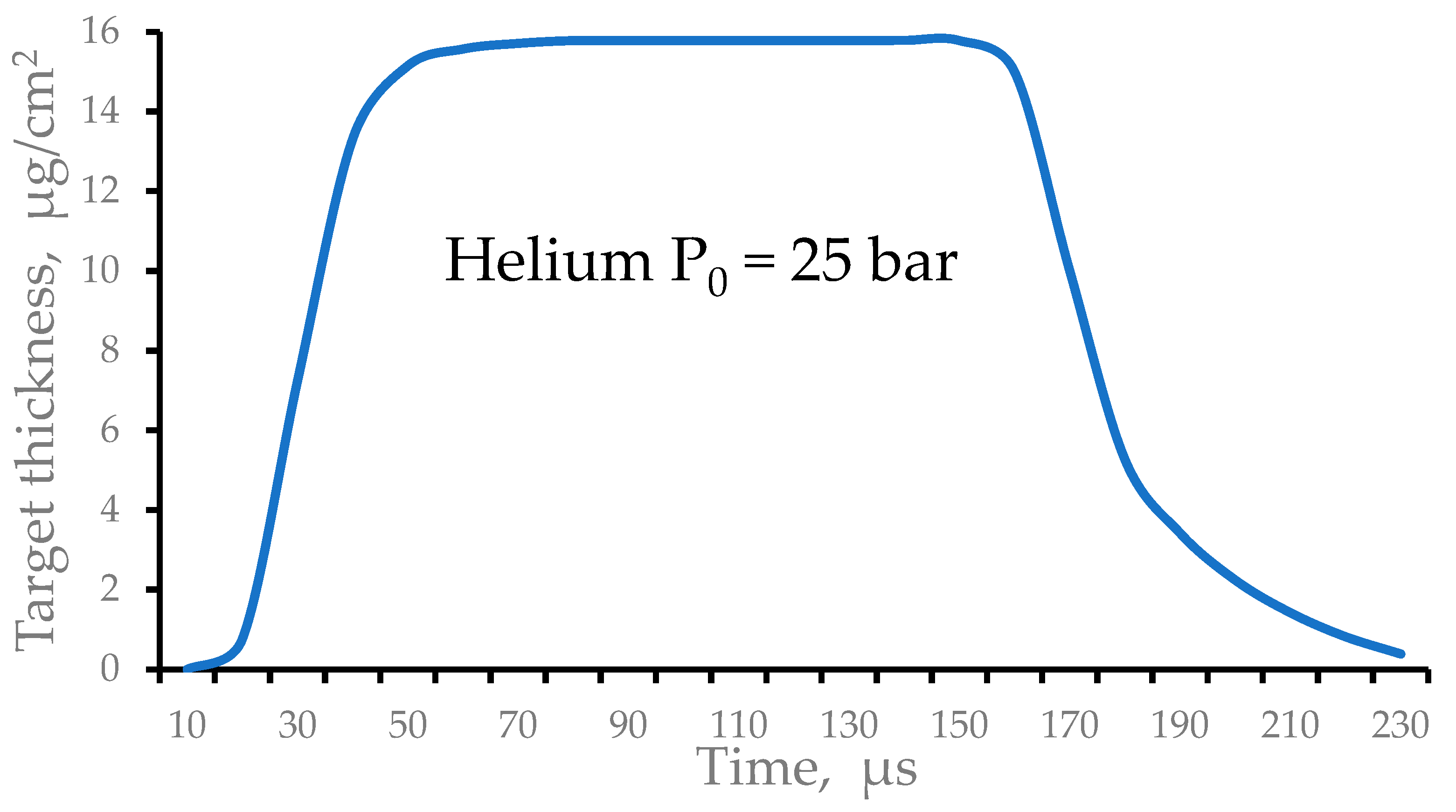
Figure 5 shows the result of the calculation of the time profile of the averaged helium target thickness. The gas valve opens at zero time and closes after 150 µs. The gas pulse has a long flat top in which the duration is sufficient for an effective stripping of the pulsed ion beam of 100 µs duration.
It should be noted that this study supposes that the pulsed valve fully opens instantly (without any delay). In reality, this is not true due to a finite velocity movement of the valve poppet upon opening. However, this does not affect the proper synchronization of the gas and ion beam pulses.
The result of the gas dynamic simulation of the helium density flow field at 100 µs after the valve-opening motion is illustrated in Figure 6.
The quasi-equilibrium background gas pressure Pbg in the main stripper chamber is determined as the following:
Pbg = G ∙f ∙τ / S,
where G is the instant mass gas flow rate into the main stripper chamber at ~100 µs after the valve-opening motion in [mbar l/s], f is the ion pulse repetition rate in [Hz], τ is the gas pulse duration in [s], and S is the pumping speed of the main stripper chamber in [l/s].
Next, we consider the case of the maximum possible ion beam repetition rate of f = 50 Hz, τ = 200 µs, and S =2222 l/s (the current Roots pump at the GSI UNILAC).
The gas catcher efficiency values of the helium pulsed jet evacuation and the averaged helium target thickness values for nozzles of different lengths and outlet diameters are listed in Table 2 and Table 3, respectively.
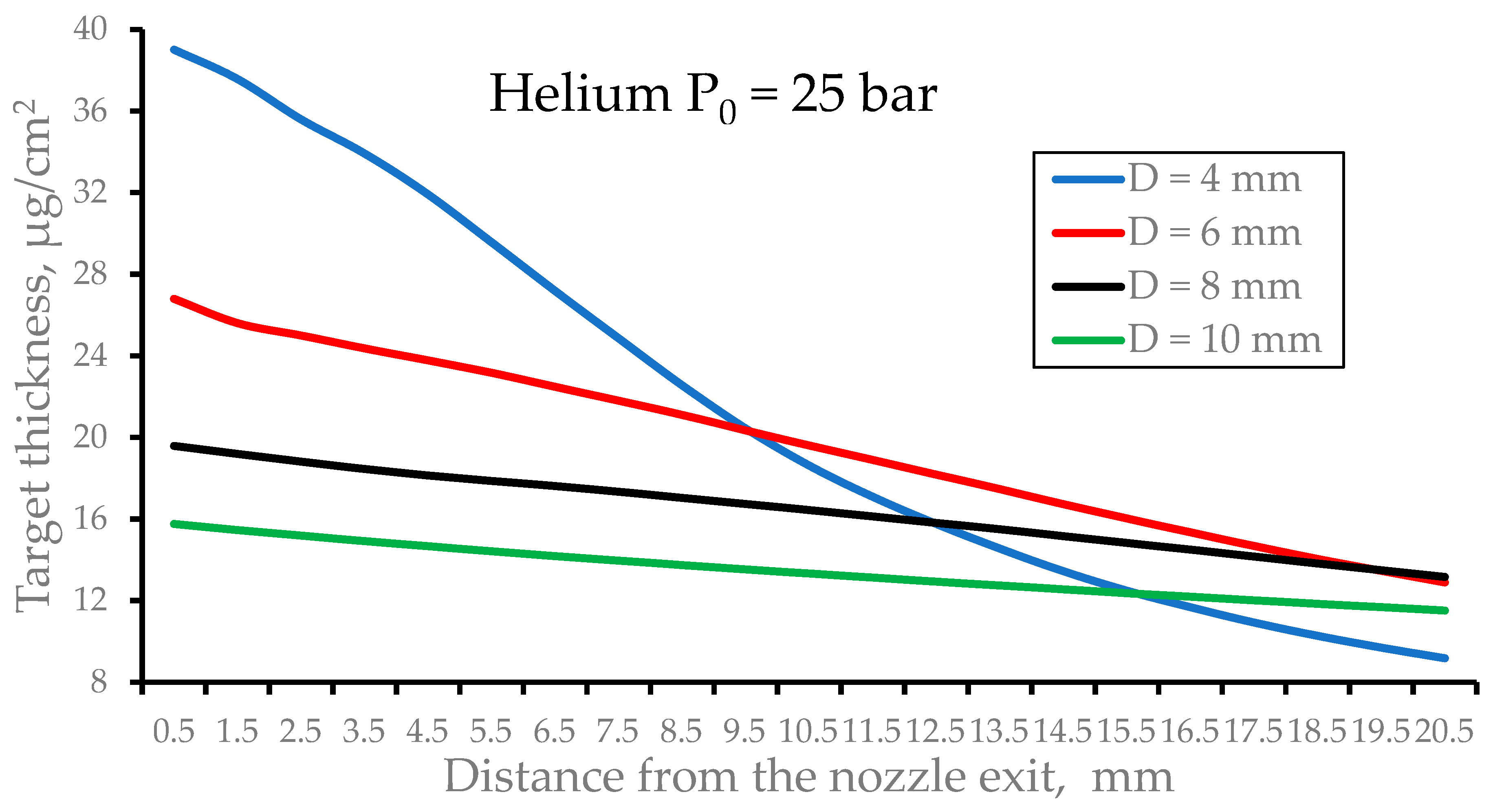
Figure 7 shows the results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length of L = 40 mm.
Figure 8 shows the results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different lengths (L) at the fixed nozzle outlet diameter of D = 8 mm.

3.2. Hydrogen pulsed jet target

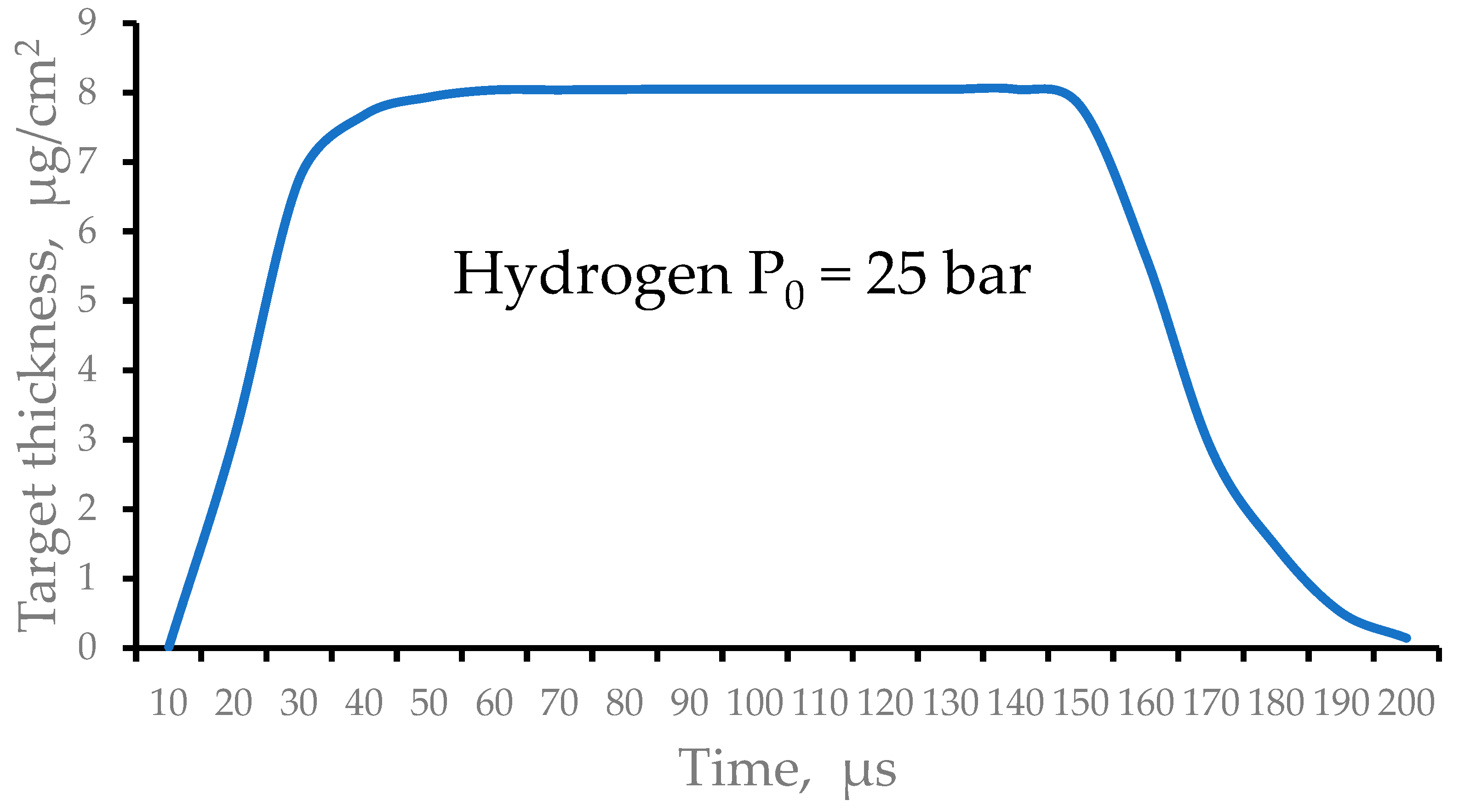
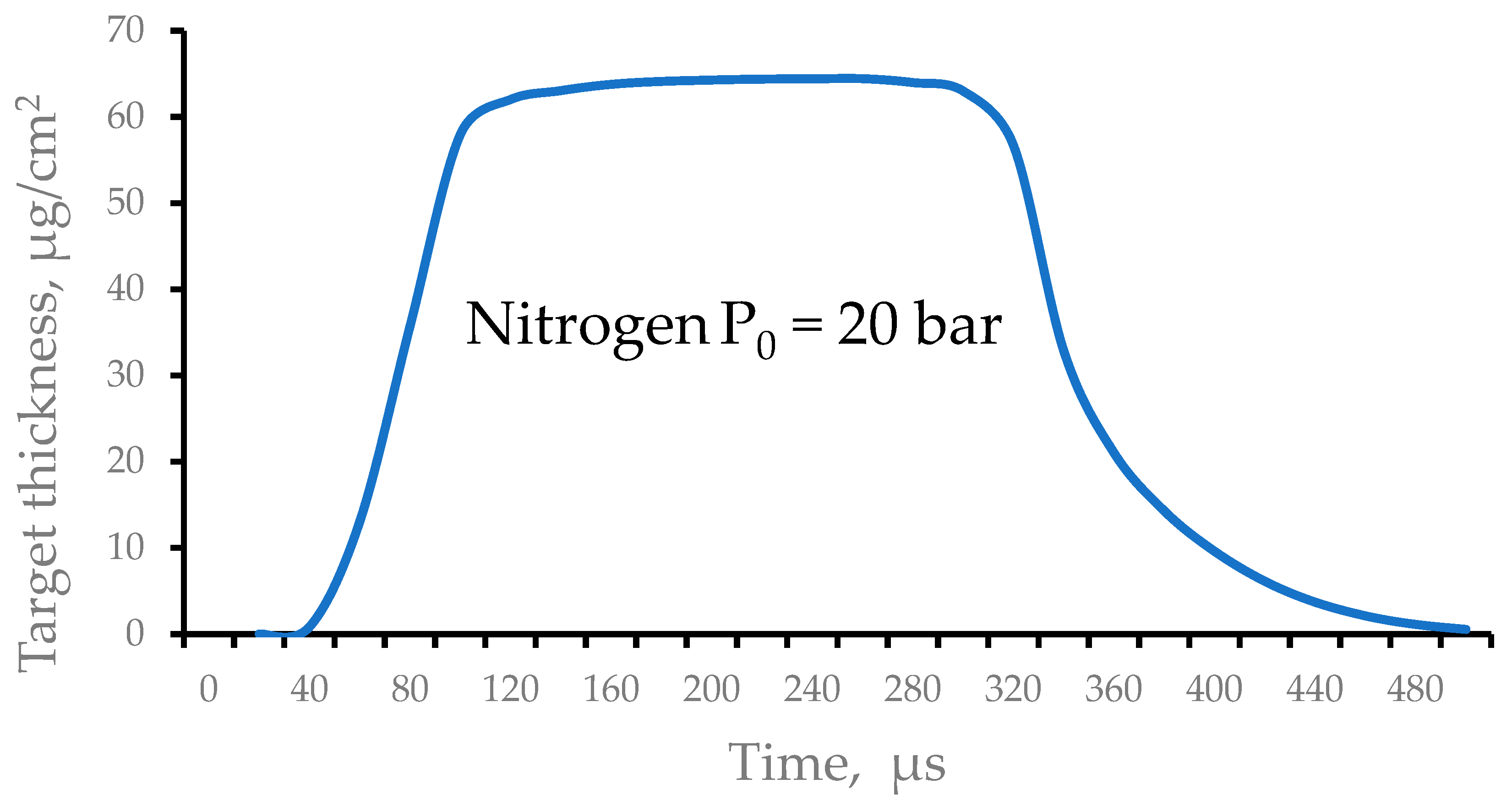
Figure 9 shows the result of the calculation of the time profile of the averaged hydrogen target thickness. The gas valve opens at zero time and closes after 140 µs.
The result of the gas dynamic simulation for the hydrogen density flow field at 100 µs after the valve-opening motion is illustrated in Figure 10.
The gas catcher efficiency for hydrogen pulsed jet evacuation and the averaged hydrogen target thickness for nozzles of different lengths and outlet diameters are listed in Table 4 and Table 5, respectively.
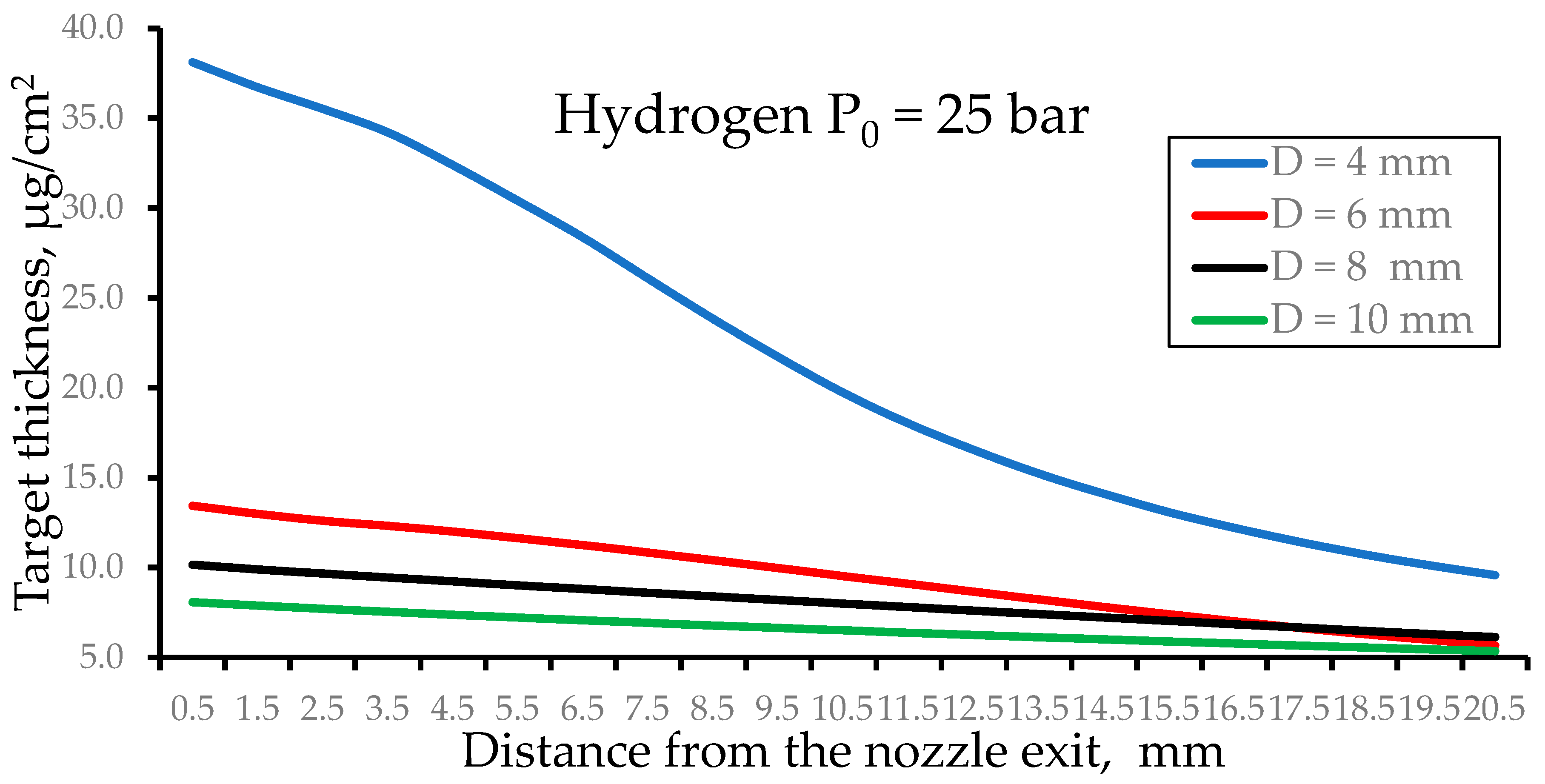
Figure 11 shows the results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length of L = 40 mm.
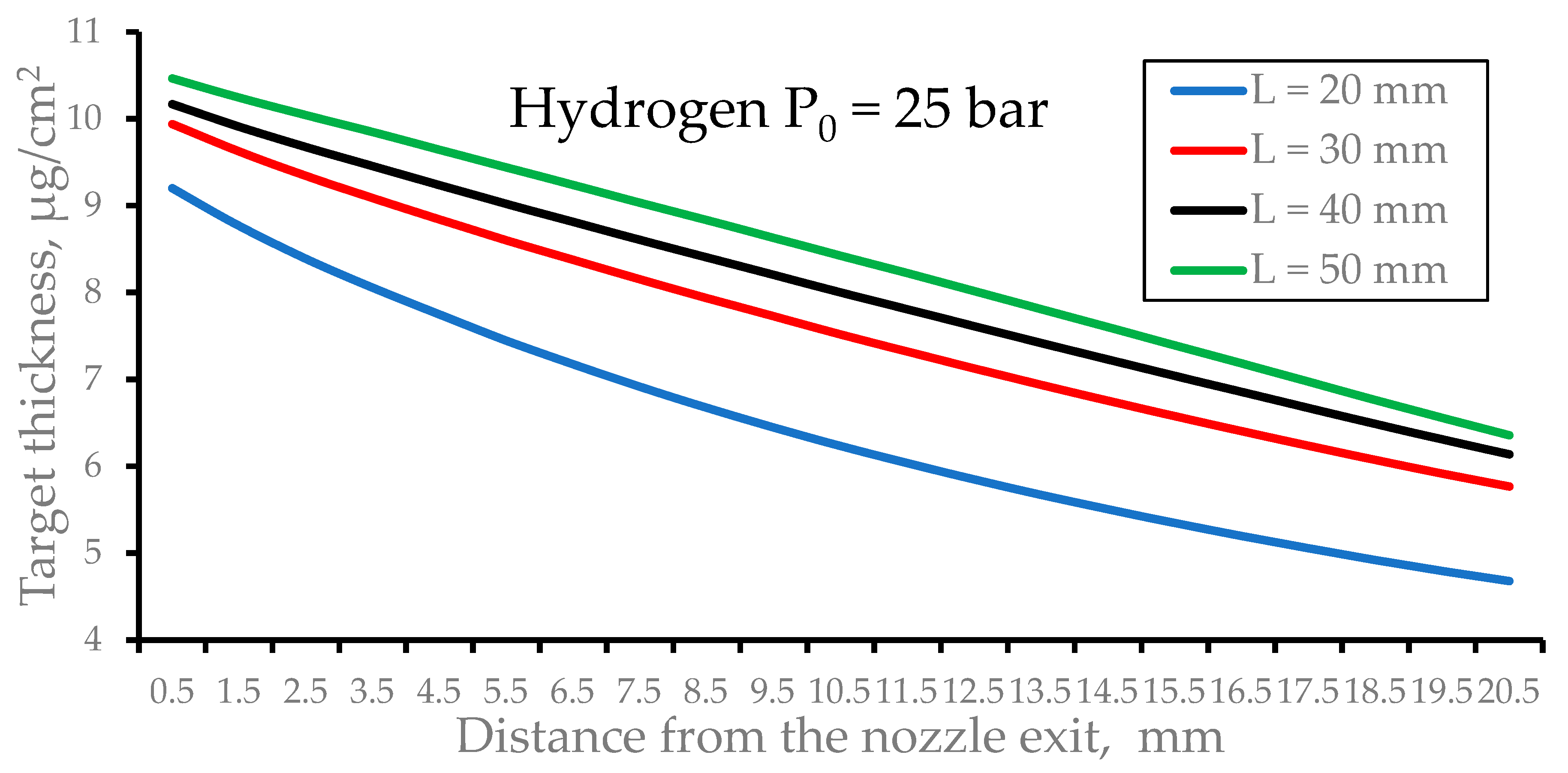
Figure 12 shows the results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different lengths (L) at the fixed nozzle outlet diameter of D = 8 mm.

3.3. Effect of the gap value between the nozzle exit and the gas catcher tube entrance

To show how the gas target thickness depends on the gap between the nozzle exit and the gas catcher tube entrance, we made a gas dynamic simulation for the gap value of 30 mm.
The result of the calculation of the pulsed hydrogen jet at P0 = 25 bar (with a nozzle length of L = 40 mm and an exit diameter of D = 8 mm) is shown in Figure 13. The result of the calculation of the gap of 21 mm (red solid line) is shown here for comparison.
In Figure 13, notice that both curves (the red solid and blue dashed lines) coincide. This is because the disturbance in the supersonic jet caused by its interaction with the gas catcher cannot propagate upstream.
Similarly, the gas target thickness does not depend on the diameter of the gas catcher entrance. To confirm this, we made additional calculations of the gas catcher tube entrance diameters of D = 30 mm and D = 50 mm. However, the gas catcher efficiency for the case of D = 30 mm is 87.6 %, which is 5.8 % less compared with the catcher with D = 40 mm (see Table 4). This also means that the gas load into the main stripper chamber for the case of D = 30 mm is a factor of 2 higher compared with that for the catcher tube with an entrance diameter of 40 mm.

3.4. How the gas target thickness depends on the stagnation pressure P0

To demonstrate how the gas target thickness depends on the stagnation pressure, P0, we conducted corresponding gas dynamic simulations for pulsed nitrogen, helium, and hydrogen supersonic jets.
Figure 14 shows the result of the calculation of the time profile of the averaged nitrogen target thickness. The gas valve opens at zero time and closes after 300 µs.
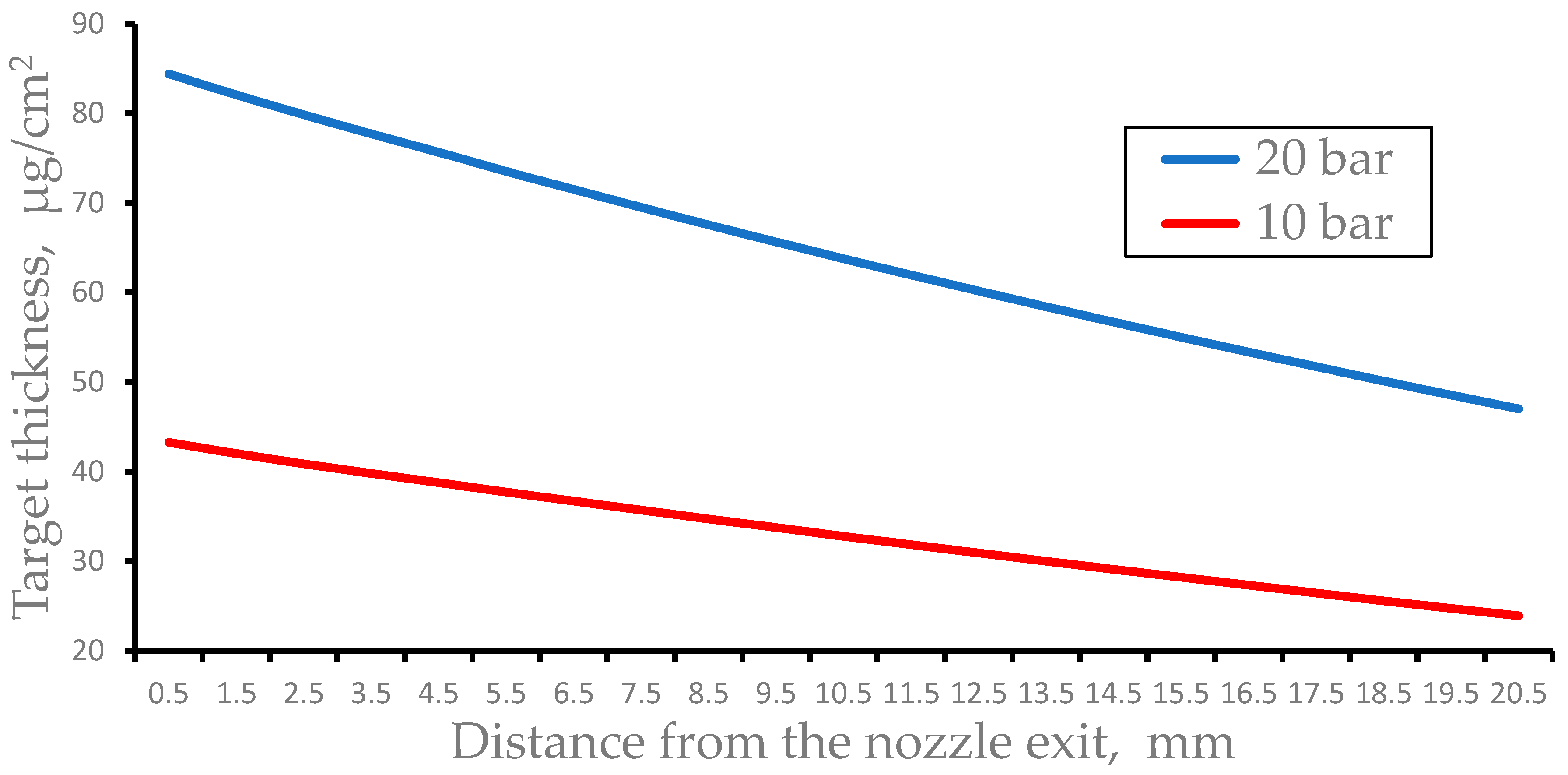
Figure 15 shows the results of the calculations of the pulsed nitrogen target thickness as a function of distance from the nozzle exit for different stagnation pressures. The gas catcher efficiencies for 10 bar and 20 bar are equal to 90.3 % and 89.8 %, respectively.
Figure 16 and Figure 17 show the results of the calculations of the pulsed helium and hydrogen target thickness values as a function of distance from the nozzle exit for different stagnation pressures. The gas catcher tube efficiencies for stagnation pressures of 50 bar and 75 bar are almost the same as the above-described case of 25-bar stagnation pressure.

4. Discussion and outlook

In our opinion, the authors and developers of the GSI gas stripper made two significant conceptual errors.
The first error occurred at the very beginning of the gas stripper development process when it was decided that nearly all gas flowing out of the supersonic nozzle should be removed from the main stripper chamber by using the Roots vacuum pump with a pumping capacity of 8000 m3/h. However, long before this, various internal gas jet target setups were constructed, in which supersonic gas flow, after its crossing with the ion beam, was removed from the target vacuum chamber using gas catchers of different designs. These setups are well known and described, for example, in reviews [15,16] and original articles [18,21]. Notice that the work [21] published in 1997 describes the internal gas target, which is still in operation at the ESR GSI.
The second error in the design of the gas stripper at the GSI UNILAC occurred about 10 years ago during the transition to the operation of a gas stripper in pulsed mode. At that time, it was decided to abandon the use of a supersonic nozzle and instead use the pulsed valve connected directly to the short T-fitting aligned with the ion beam axis. A short description of this pulsed gas stripper version is presented in Section 1.
Despite the significant advantage of using the gas stripper in pulse mode, this particular design solution, which is currently in use at the GSI UNILAC, suffers from the same disadvantage associated with vacuum limitation. An additional serious drawback of this design is that the gas flows out of the T-fitting in the direction of the apertures of adjacent differential pumping chambers (see Figure 1 and Figure 2 in Ref. [11]) in the form of pulsed supersonic jets. Therefore, it is our opinion that it would be better to simply continue the use of the gas stripper with a supersonic nozzle, providing it with a fast pulsed valve. In this case, the opening time duration of the valve required for effective operation with ion pulses of 100 µs could be reduced.
In this article, we propose a simple method to considerably improve the performance of the gas stripper setup at the GSI UNILAC. Our method consists of the use of classic and well-known design concepts of internal gas jet targets. In the case of the gas stripper at the GSI UNILAC, the gas jet catcher tube is installed at some distance downstream from the supersonic nozzle exit. This distance (or the gap between the nozzle exit and the gas catcher tube entrance) is mainly determined by the size of the ion beam crossing the gas jet at a right angle.
We explored the performance of the proposed GSI UNILAC gas stripper modification by means of detailed computer experiments, which provided a realistic description of supersonic gas jets flowing out of the nozzle into the vacuum.
We recommend using a simple conical supersonic diverging nozzle with a throat diameter, length, and exit diameter of 1 mm, 40 mm, and 8 mm, respectively.
For the entrance diameter of the conical part of the gas catcher tube, we recommend a value of 40 mm.
The evacuation of the gas from the gas catcher tube can be achieved by using an additional relatively small Roots pump of 251 m3/h.
The calculated gas catcher efficiencies in the pulse operation mode are about 98% for helium and 93% for hydrogen. These efficiency values represent a dramatic decrease in the background pressure in the main stripper vacuum chamber and, as a result, increase the repetition rates of the ion beams to values that are higher than the current standard.
It is our hope that those responsible for the operation of the gas stripper at the GSI UNILAC will consider our article’s recommendations in the course of the next and probably final upgrade of the gas stripper setup. The process of implementing our upgrade recommendations is expected to be both inexpensive and streamlined.

Funding

This research received no external funding.

Data Availability Statement

The data presented in this study are available upon request from the author.

Conflicts of Interest

The author declares no conflicts of interest.

References

  1. T. Kanemura, J. Gao, M. LaVere, R. Madendorp, F. Marti, Y. Momozaki, PROGRESS OF LIQUID LITHIUM STRIPPER FOR FRIB, North American Particle Acc. Conf. NAPAC2019, Lansing, MI, USA (2019) 636-638. [CrossRef]
  2. H. Imao, H. Okuno, H. Kuboki, S. Yokouchi, N. Fukunishi, O. Kamigaito, H. Hasebe, T. Watanabe, Y. Watanabe, M. Kase, Y. Yano, CHARGE STRIPPING OF URANIUM-238 ION BEAM WITH HELIUM GAS STRIPPER, Proceedings of IPAC2012, New Orleans, Louisiana, USA (2012) 3930-3932.
  3. FAIR Baseline Technical Report, Vol. 2, GSI Darmstadt, Germany (2006), p. 335.
  4. J. Glatz, J. Klabunde, U. Scheeler, D. Wilms, Operational aspects of the high current upgrade UNILAC Proceedings of Linear Accelerator Conference, Monterey, U.S.A (2000) 232–234.
  5. W. Barth, P. Forck, The new gas stripper and charge state separator of the GSI high current injector, Proceedings of Linear Accelerator Conference, Monterey, U.S.A (2000) 235–237.
  6. P. Gerhard, M. Maier, ON THE UNILAC PULSED GAS STRIPPER AT GSI, 31st Int. Linear Accel. Conf. LINAC2022, Liverpool, UK, (2022) 258-261. [CrossRef]
  7. W. Barth, M. Miski-Oglu, U. Scheeler, H. Vormann, M. Vossberg, S. Yaramyshev, UNILAC HEAVY ION BEAM OPERATION AT FAIR INTENSITIES, 31st Int. Linear Accel. Conf. LINAC2022, Liverpool, UK (2022) 102-105. https://doi.org/10.18429/JACoW-LINAC2022-MOPOPA16. [CrossRef]
  8. W. Barth, A. Adonin, Ch. E. Düllmann, M. Heilmann, R. Hollinger, E. Jäger, O. Kester, J. Khuyagbaatar, J. Krier, E. Plechov, P. Scharrer, W. Vinzenz, H. Vormann, A. Yakushev, and S. Yaramyshev, High brilliance uranium beams for the GSI FAIR, PHYS. REV. ACCEL. BEAMS 20, 050101 (2017) 1-4. [CrossRef]
  9. W. Barth, R. Hollinger, A. Adonin, M. Miski-Oglu, U. Scheeler and H. Vormann, LINAC developments for heavy ion operation at GSI and FAIR, Journal of Instrumentation, 15 (2020) T12012. [CrossRef]
  10. Scharrer, E. Jäger, W. Barth, M. Bevcic, C. E. Düllmann, L. Groening, K.-P. Horn, J. Khuyagbaatar, J. Krier, and A. Yakushev, Electron stripping of Bi ions using a modified 1.4 MeV/u gas stripper with pulsed gas injection, J. Radioanal. Nucl. Chem. 305 (2015) 837-842.
  11. P. Scharrer1, W. Barth, M. Bevcic, Ch. E. Düllmann, L. Groening, K. P. Horn, E. Jäger, J. Khuyagbaatar, J. Krier, A. Yakushev, Stripping of high intensity heavy-ion beams in a pulsed gas stripper device at1.4MeV/u, Proceedings of IPAC2015, Richmond, VA, USA (2015) 3773-3775.
  12. Winfried Barth, Aleksey Adonin, Christoph E. Düllmann, Manuel Heilmann, Ralph Hollinger, Egon Jäger, Jadambaa Khuyagbaatar, Joerg Krier, Paul Scharrer, Hartmut Vormann and Alexander Yakushev, U28+-intensity record applying a H2-gas stripper cell, Phys. Rev. ST Accel. Beams 18 040101 (2015) 1-9.
  13. P. Scharrer1, W. Barth, M. Bevcic, Ch. E. Düllmann, P. Gerhard, L. Groening, K. P. Horn, E. Jäger, J. Khuyagbaatar, J. Krier, H. Vormann, A. Yakushev, Applications of the pulsed gas stripper technique at the GSI UNILAC, Nucl. Instrum. Methods Phys. Res. A 863 (2017) 20-25. [CrossRef]
  14. P. Gerhard, W. Barth, M. Bevcic, Ch. E. Düllmann, L. Groening, K. P. Horn, E. Jäger, J. Khuyagbaatar, J. Krier, M. Maier, P. Scharrer, A. Yakushev, DEVELOPMENT OF PULSED GAS STRIPPERS FOR INTENSE BEAMS OF HEAVY AND INTERMEDIATE MASS IONS, 29th Linear Accelerator Conf. LINAC2018, Beijing, China (2018) 982-987. [CrossRef]
  15. M. Macri, Gas Jet Internal Target, CERN Acceleration School – Antiprotons for Colliding Beam Facilities, Geneva, Switzerland, 1983, Report CERN 84-15 (1984), ed. P. Bryant and S. Newman, p. 469.
  16. C. Ekström, Internal targets - a review, Nucl. Instrum. Methods Phys. Res. A 362 (1995) 1-16. [CrossRef]
  17. <i>17. </i>J.E. Doskov, F. J.E. Doskov, F. Sperisen, Development of internal jet targets for high-luminosity experiments, Nucl. Instr. and Meth. A 362 (1995) 20-25.
  18. Antonios Kontos, Daniel Schürmann, Charles Akers, Manoel Couder, Joachim Görres, Daniel Robertson, Ed Stech, Rashi Talwar, Michael Wiescher, HIPPO: A supersonic helium jet gas target for nuclear astrophysics, Nucl. Instrum. Methods Phys. Res. A 664 (2012) 272–281. [CrossRef]
  19. Zach Meisela, Ke Shi, Aleksandar Jemcov, Manoel Couder, Exploratory investigation of the HIPPO gas-jet target fluid dynamic properties, Nucl. Instrum. Methods Phys. Res. A 828 (2016) 8–14. [CrossRef]
  20. <b><i>20. </i></b>K. Schmidt, K.A. K. Schmidt, K.A. Chipps, S. Ahn, D.W. Bardayan, J. Browne, U. Greife, Z. Meisel, F. Montes, P.D. O’Malley, W-J. Ong, S.D. Pain, H. Schatz, K. Smith, M.S. Smith, P.J. Thompson, Status of the JENSA gas-jet target for experiments with rare isotope beams, Nucl. Instrum. Methods Phys. Res. A 911 (2018) 1–9. [CrossRef]
  21. H. Reich, W. Bourgeois, B. Franzke, A. Kritzer, V. Varentsov, The ESR internal target, Nuclear Physics A 626 (1997) 417-425.
  22. <b><i>22. </i></b>V.L. Varentsov, N. V.L. Varentsov, N. Kuroda, Y. Nagata, H. A. Torii, M. Shibata, and Y. Yamazaki, ASACUSA Gas-Jet Target: Present Status And Future Development, AIP Conference Proceedings 793 (2005) 328-340. [CrossRef]
  23. D. Tiedemann, K.E. Stiebing, D.F.A. Winters, W. Quint, V. Varentsov, A. Warczak, A. Malarz, Th. Stöhlker, A pulsed supersonic gas jet target for precision spectroscopy at the HITRAP facility at GSI, Nucl. Instrum. Methods Phys. Res. A 764 (2014) 387–393. [CrossRef]
  24. Parker Hannifin Corp. Available online: https://ph.parker.com/us/en/divisions/precision-fluidics-division-page/product/pulse-valves-miniature-high-speed-high-vacuum-dispense-valve/009-1669-900.
  25. V.L. Varentsov, A.A. Ignatiev, Numerical investigations of internal supersonic jet targets formation for storage rings, Nucl. Instrum. Methods Phys. Res. A 413 (1998) 447-456. [CrossRef]
  26. Victor Varentsov, Review of Gas Dynamic RF-Only Funnel Technique for Low-Energy and High-Quality Ion Beam Extraction into a Vacuum, Micromachines 2023, 14(9):1771. [CrossRef]
Preprints 100678 g001
Figure 1. The result of the gas dynamic simulation of the nitrogen density flow field for the proposed GSI nozzle. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The calculated background pressure in the main stripper chamber is Pbg = 0.17 mbar.
Figure 1. The result of the gas dynamic simulation of the nitrogen density flow field for the proposed GSI nozzle. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The calculated background pressure in the main stripper chamber is Pbg = 0.17 mbar.
Preprints 100678 g001
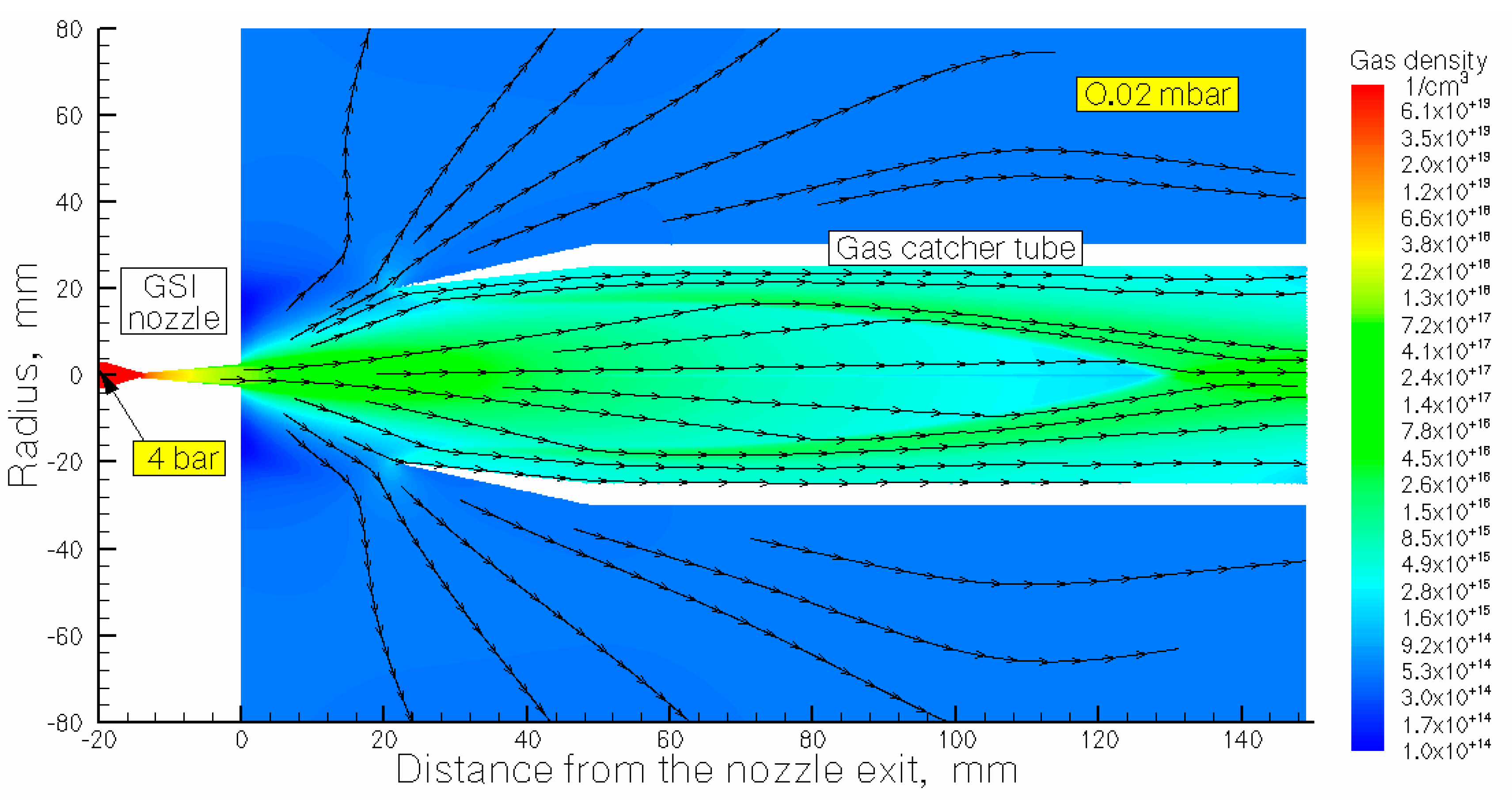
Preprints 100678 g002
Figure 2. The result of the gas dynamic simulation of the nitrogen density flow field for the calculation of variant #2: GSI nozzle + gas capture. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The background pressure in the main stripper chamber is Pbg = 0.02 mbar. The black arrow lines show the gas flow directions.
Figure 2. The result of the gas dynamic simulation of the nitrogen density flow field for the calculation of variant #2: GSI nozzle + gas capture. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The background pressure in the main stripper chamber is Pbg = 0.02 mbar. The black arrow lines show the gas flow directions.
Preprints 100678 g002
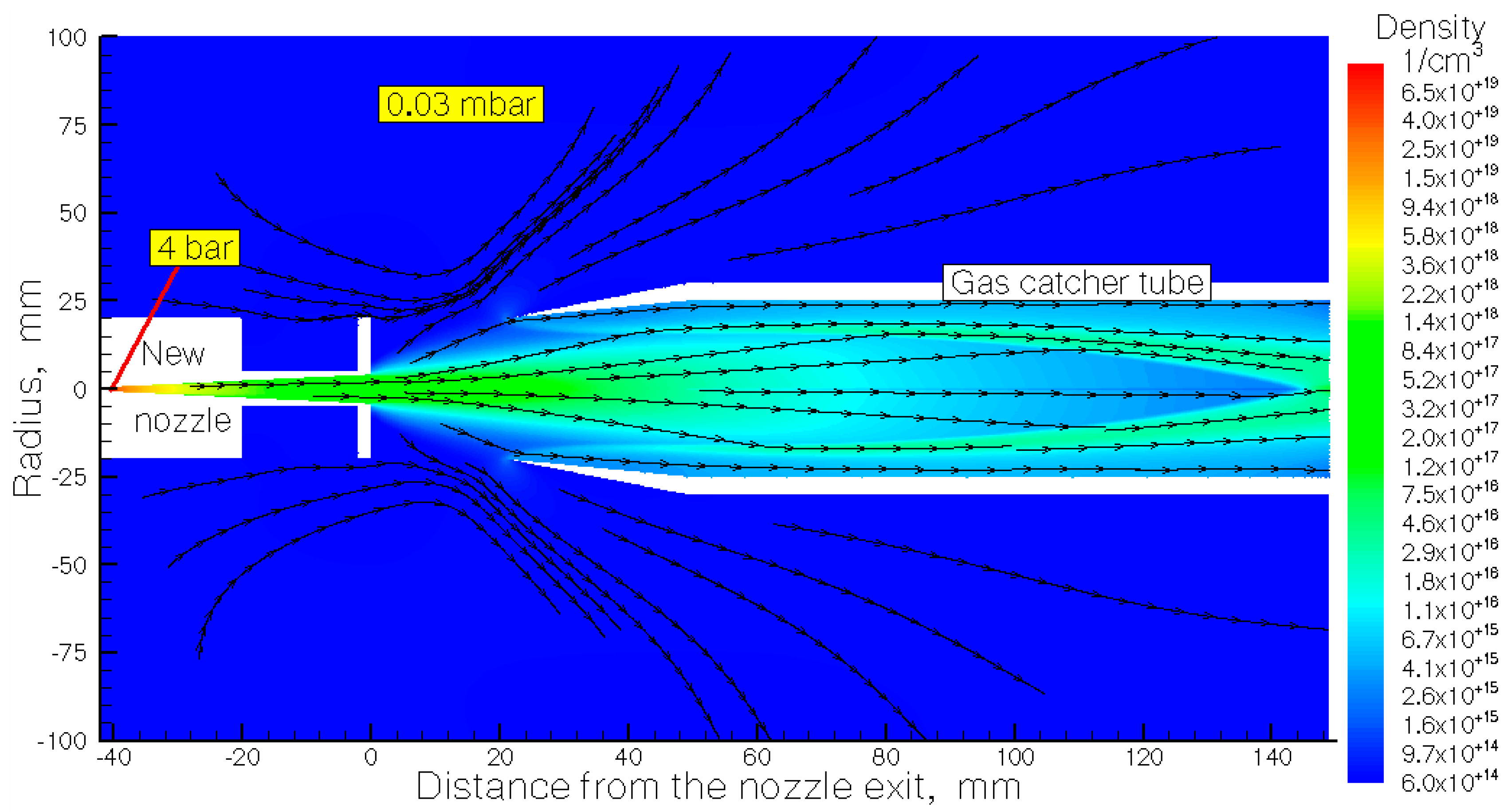
Preprints 100678 g003
Figure 3. The result of the gas dynamic simulation of the nitrogen density flow field for the calculation of variant #3: new nozzle + gas capture tube. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The background pressure in the main stripper chamber is Pbg = 0.03 mbar. The black arrow lines show the gas flow directions.
Figure 3. The result of the gas dynamic simulation of the nitrogen density flow field for the calculation of variant #3: new nozzle + gas capture tube. The stagnation pressure and temperature are P0 = 4 bar and T0 = 296 K, respectively. The background pressure in the main stripper chamber is Pbg = 0.03 mbar. The black arrow lines show the gas flow directions.
Preprints 100678 g003
Preprints 100678 g004
Figure 4. The results of the calculations of the nitrogen target thickness as a function of distance from the nozzle for different variants of the gas stripper operation with a continuous nitrogen gas jet. The nozzle temperature is T0 = 296 K for all calculation variants.
Figure 4. The results of the calculations of the nitrogen target thickness as a function of distance from the nozzle for different variants of the gas stripper operation with a continuous nitrogen gas jet. The nozzle temperature is T0 = 296 K for all calculation variants.
Preprints 100678 g004
Preprints 100678 g005
Figure 5. The result of the calculation of the time profile of the averaged helium target thickness. The gas valve opens at zero time and closes after 150 µs.
Figure 5. The result of the calculation of the time profile of the averaged helium target thickness. The gas valve opens at zero time and closes after 150 µs.
Preprints 100678 g005
Preprints 100678 g006
Figure 6. The result of the gas dynamic simulation of the helium density flow field at 100 µs after the valve-opening motion. The length of the supersonic nozzle is 40 mm; its outlet diameter is 8 mm. The stagnation pressure and temperature are P0 = 25 mbar and T0 = 296 K, respectively. The quasi-equilibrium background gas pressure in the main stripper chamber is Pbg = 0.001 mbar. The black arrow lines show the gas flow directions.
Figure 6. The result of the gas dynamic simulation of the helium density flow field at 100 µs after the valve-opening motion. The length of the supersonic nozzle is 40 mm; its outlet diameter is 8 mm. The stagnation pressure and temperature are P0 = 25 mbar and T0 = 296 K, respectively. The quasi-equilibrium background gas pressure in the main stripper chamber is Pbg = 0.001 mbar. The black arrow lines show the gas flow directions.
Preprints 100678 g006
Preprints 100678 g007
Figure 7. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length L = 40 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Figure 7. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length L = 40 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Preprints 100678 g007
Preprints 100678 g008
Figure 8. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different nozzle lengths (L) at the fixed nozzle outlet diameter of D = 8 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Figure 8. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for nozzles of different nozzle lengths (L) at the fixed nozzle outlet diameter of D = 8 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Preprints 100678 g008
Preprints 100678 g009
Figure 9. The result of the calculation of the time profile of the averaged hydrogen target thickness. The gas valve opens at zero time and closes at time 140 µs.
Figure 9. The result of the calculation of the time profile of the averaged hydrogen target thickness. The gas valve opens at zero time and closes at time 140 µs.
Preprints 100678 g009
Preprints 100678 g010
Figure 10. The result of the gas dynamic simulation for hydrogen density flow field at 100 µs after the valve-opening motion. The length of the supersonic nozzle is 40 mm; its outlet diameter is 8 mm. The stagnation pressure and temperature are P0 = 25 mbar and T0 = 296 K, respectively. The quasi-equilibrium background pressure Pbg in the main stripper chamber is 0.004 mbar. Black arrowed lines show the gas flow directions.
Figure 10. The result of the gas dynamic simulation for hydrogen density flow field at 100 µs after the valve-opening motion. The length of the supersonic nozzle is 40 mm; its outlet diameter is 8 mm. The stagnation pressure and temperature are P0 = 25 mbar and T0 = 296 K, respectively. The quasi-equilibrium background pressure Pbg in the main stripper chamber is 0.004 mbar. Black arrowed lines show the gas flow directions.
Preprints 100678 g010
Preprints 100678 g011
Figure 11. The results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length of L = 40 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Figure 11. The results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different outlet diameters (D) at the fixed nozzle length of L = 40 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Preprints 100678 g011
Preprints 100678 g012
Figure 12. The results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different nozzle lengths (L) at the fixed nozzle outlet diameter of D = 8 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Figure 12. The results of the calculations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for nozzles of different nozzle lengths (L) at the fixed nozzle outlet diameter of D = 8 mm. The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Preprints 100678 g012
Preprints 100678 g013
Figure 13. The result of the calculation of the pulsed hydrogen target thickness for the gap between the nozzle exit and the gas catcher tube entrance of 30 mm. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm; the stagnation pressure is P0 = 25 bar; and the nozzle temperature is T0 = 296 K. The red solid line shows the result of the calculation of the gap of 21 mm for comparison. The time after the pulsed valve-opening motion is 100 µs.
Figure 13. The result of the calculation of the pulsed hydrogen target thickness for the gap between the nozzle exit and the gas catcher tube entrance of 30 mm. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm; the stagnation pressure is P0 = 25 bar; and the nozzle temperature is T0 = 296 K. The red solid line shows the result of the calculation of the gap of 21 mm for comparison. The time after the pulsed valve-opening motion is 100 µs.
Preprints 100678 g013
Preprints 100678 g014
Figure 14. The result of the calculation of the time profile of the averaged nitrogen target thickness. The gas valve opens at zero time and closes after 300 µs.
Figure 14. The result of the calculation of the time profile of the averaged nitrogen target thickness. The gas valve opens at zero time and closes after 300 µs.
Preprints 100678 g014
Preprints 100678 g015
Figure 15. The results of the calculations of the pulsed nitrogen target thickness as a function of distance from the nozzle exit for stagnation pressures of 10 bar and 20 bar. The time after the pulsed valve-opening motion is 200 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Figure 15. The results of the calculations of the pulsed nitrogen target thickness as a function of distance from the nozzle exit for stagnation pressures of 10 bar and 20 bar. The time after the pulsed valve-opening motion is 200 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Preprints 100678 g015
Preprints 100678 g016
Figure 16. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for stagnation pressures of 25 bar, 50 bar, and 75 bar. The time after the pulsed valve-opening motion is 100 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Figure 16. The results of the calculations of the pulsed helium target thickness as a function of distance from the nozzle exit for stagnation pressures of 25 bar, 50 bar, and 75 bar. The time after the pulsed valve-opening motion is 100 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Preprints 100678 g016
Preprints 100678 g017
Figure 17. The results of the gas dynamic simulations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for stagnation pressures of 25 bar, 50 bar, and 75 bar. The time after the pulsed valve-opening motion is 100 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Figure 17. The results of the gas dynamic simulations of the pulsed hydrogen target thickness as a function of distance from the nozzle exit for stagnation pressures of 25 bar, 50 bar, and 75 bar. The time after the pulsed valve-opening motion is 100 µs. The nozzle length is L = 40 mm; the exit diameter is D = 8 mm.
Preprints 100678 g017
Table 1. The main calculated characteristics of the five variants of the GSI UNILAC gas stripper operation with a continuous nitrogen gas jet. ”Total gas flow rate” is a nitrogen gas flow rate through the nozzle. “Background pressure” is a pressure value in the main stripper chamber. “Gas catcher efficiency” is a fraction of the total gas flow rate pumped through the gas catcher tube. “Averaged target thickness” is a nitrogen target thickness averaged over the gap between the nozzle and catcher tube entrance.
Table 1. The main calculated characteristics of the five variants of the GSI UNILAC gas stripper operation with a continuous nitrogen gas jet. ”Total gas flow rate” is a nitrogen gas flow rate through the nozzle. “Background pressure” is a pressure value in the main stripper chamber. “Gas catcher efficiency” is a fraction of the total gas flow rate pumped through the gas catcher tube. “Averaged target thickness” is a nitrogen target thickness averaged over the gap between the nozzle and catcher tube entrance.
Calculation variant Total gas flow rate [mbar l/s] Background pressure [mbar] Gas catcher efficiency [%] Averaged target thickness [µg/cm2]
#1 377.7 0.17 - 12.98
#2 377.7 0.021 87.8 12.54
#3 522.2 0.03 87.3 13.97
#4 944.3 0.06 85.5 30.25
#5 1305.5 0.057 90.3 33.06
Table 2. Helium gas catcher efficiency in [%] for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Table 2. Helium gas catcher efficiency in [%] for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
L(mm) 20 30 40 50
D (mm)
4 94.7 93.9 92.7 91.4
6 97.5 96.8 96.4 95.8
8 97.8 97.6 97.9 97.0
10 97.6 97.6 97.9 97.2
Table 3. Helium target thickness in [µg/cm2] averaged over the gap between the nozzle exit and the catcher tube entrance for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
Table 3. Helium target thickness in [µg/cm2] averaged over the gap between the nozzle exit and the catcher tube entrance for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the valve-opening motion is 100 µs.
L(mm) 20 30 40 50
D (mm
4 21.61 21.94 21.25 21.76
6 17.70 18.57 19.61 20.04
8 13.68 15.09 16.37 11,19
10 9.90 12.04 13.44 13.86
Table 4. Hydrogen gas catcher efficiency in [%] for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Table 4. Hydrogen gas catcher efficiency in [%] for different nozzle lengths (L) and outlet diameters (D). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
L(mm) 20 30 40 50
D (mm)
4 85.5 85.7 94.9 83.5
6 91.9 90.7 89.1 89.2
8 95.8 94.2 93.4 92.5
10 96.5 96.6 95.2 94.3
Table 5. Hydrogen target thickness in [µg/cm2], averaged over the gap between the nozzle exit and the catcher tube entrance, for different nozzle lengths (L) and outlet diameters (R). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
Table 5. Hydrogen target thickness in [µg/cm2], averaged over the gap between the nozzle exit and the catcher tube entrance, for different nozzle lengths (L) and outlet diameters (R). The stagnation pressure is P0 = 25 bar and the nozzle temperature is T0 = 296 K for all calculation variants. The time after the pulsed valve-opening motion is 100 µs.
L(mm) 20 30 40 50
D (mm)
4 10.20 10.18 21.81 10.03
6 8.69 9.33 9.52 9.68
8 6.48 7.63 8.05 8.41
10 5.62 6.06 6.59 7.03
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Downloads

269

Views

1459

Comments

0

Subscription

Notify me about updates to this article or when a peer-reviewed version is published.

Email

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2025 MDPI (Basel, Switzerland) unless otherwise stated