Submitted:
04 December 2023
Posted:
05 December 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
- Comprehensive Time and Frequency Analysis: The study conducted a comprehensive time and frequency domain analysis under six different load conditions. This analysis has highlighted patterns and variations in fault severity, providing valuable insights into IM behaviour.
- Optimal Continuous Wavelet Transform (CWT) Approach: The selection of an optimal CWT approach using WSE contributes to improved signal processing for time-frequency feature extraction, denoising, and pattern recognition.
- Revealing Load-Dependent Fault Subclasses: This represents an innovative extension of traditional fault classification methods. It effectively accommodates load variations and dataset customization, making it adaptable to different IM datasets. The research has identified and classified load-dependent fault subclasses, including mild, moderate, and severe, which enhances the understanding of fault severity in different load scenarios.
- Proposing a Customized Load Assessment Framework (CLAF): The research introduces a novel CLAF, which represents a pioneering approach in the field of fault classification for Induction Motors (IMs). CLAF extends traditional fault classification methodologies by considering load variations and dataset customization.
2. Background and Related Work
2.1. Feature Extraction Domains
2.1.1. Time Domain Analysis
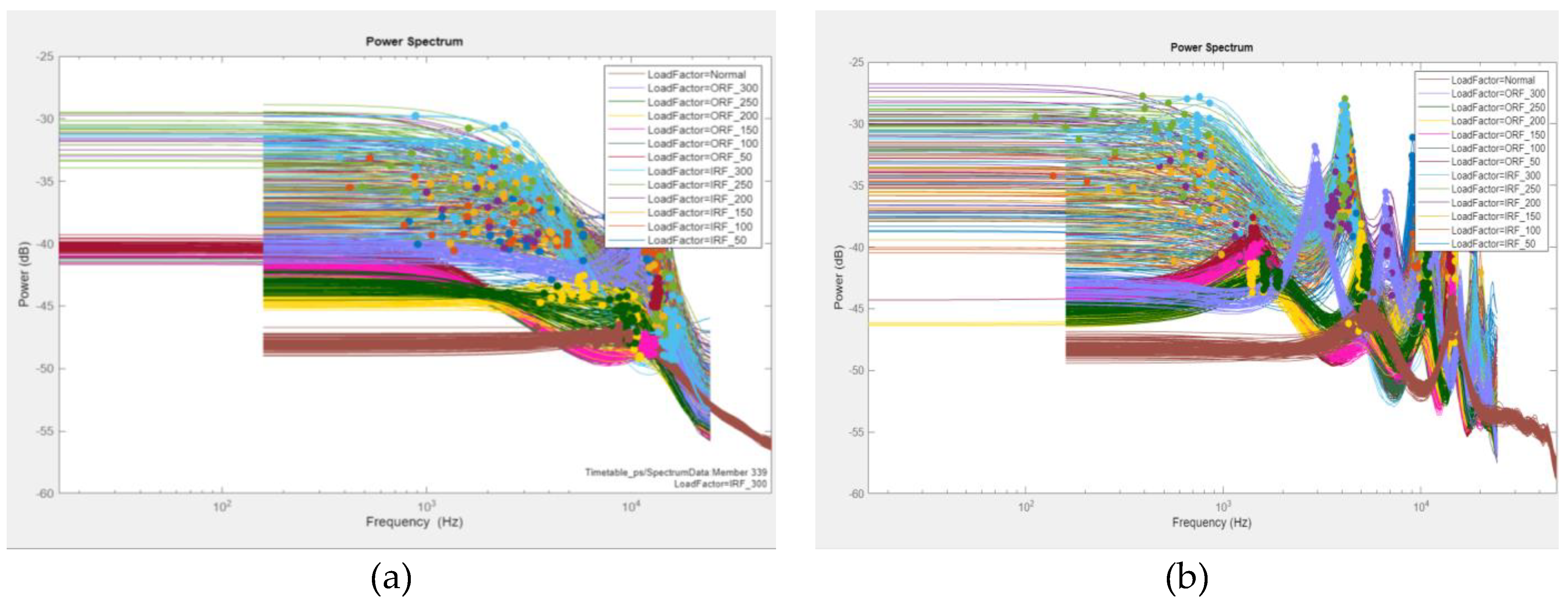
2.1.2. Frequency Domain Analysis
| Parameter | Formula | Description | |
|---|---|---|---|
| Harmonic Features | THD | Frequency domain, measuring the distortion caused by harmonics in the signal. | |
| SNR | Compares the level of a desired signal to the level of background noise. | ||
| SINAD | A measure of signal quality compares the level of desired signal to the level of background noise and harmonics. | ||
| Spectral Features | Peak amplitude | Represents the highest point (or peak) of the signal's waveform when viewed in the frequency domain. | |
| Peak frequency | Corresponds to the frequency component that is most prominent or dominant in the signal. | ||
| Band power | Quantifies the total energy within a specific frequency range, providing insights into the distribution of signal energy across the spectrum. | ||
2.1.3. Time-Frequency Domain Analysis
2.2. Continuous Wavelet Transform (CWT)
2.3. Wavelet Singular Entropy (WSE)
2.4. One-way Analysis of Variance (ANOVA) Features Selection.
2.5. State-Of-The-Art and Research Gaps
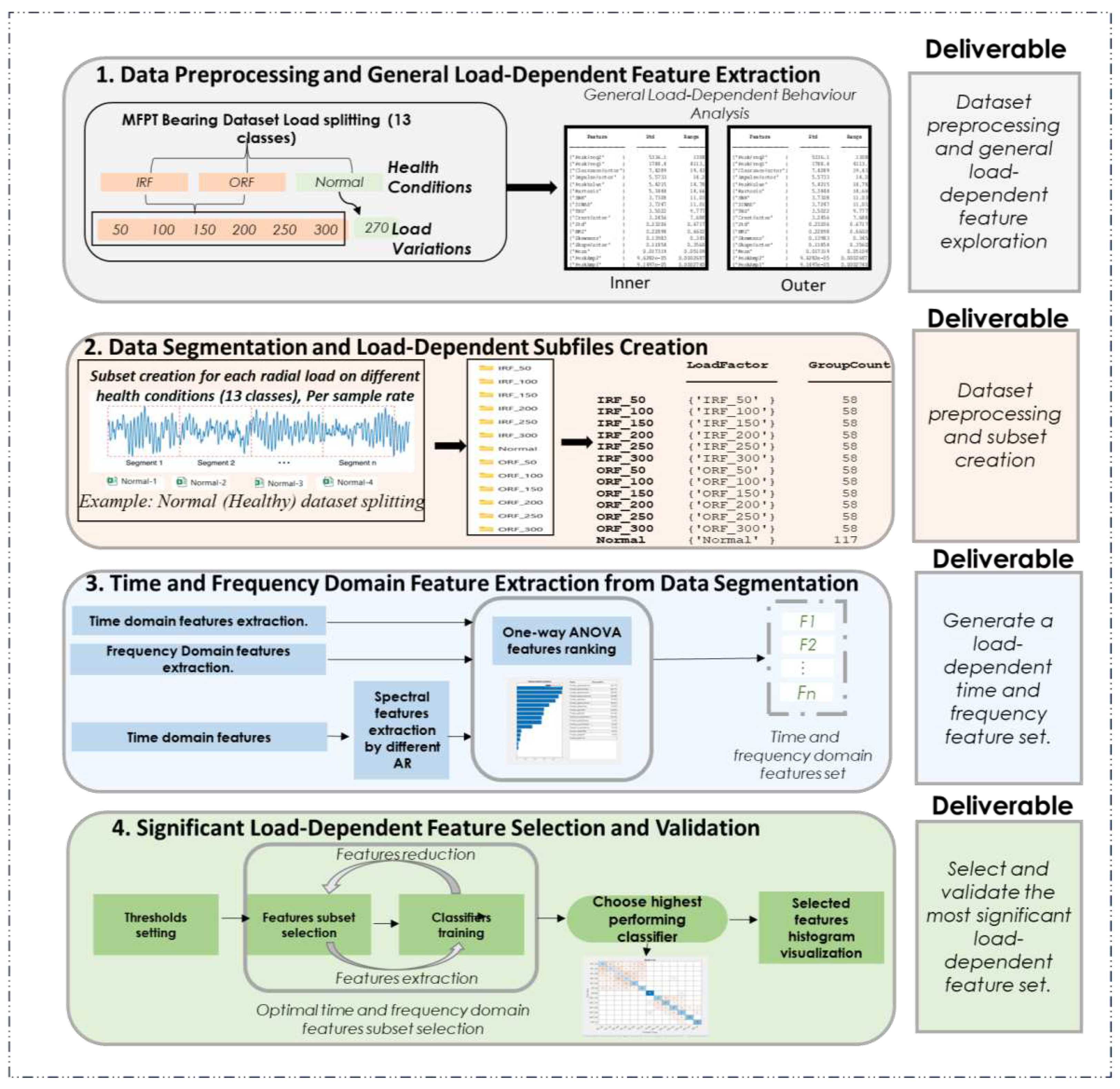
3. Methodology
- 5.
- Data Segmentation and Load-Dependent Subfiles Creation: time and frequency domain features are extracted from the segmented data, focusing on assessing feature variations during faults and their sensitivity to load changes.
- 6.
- Time and Frequency Domain Feature Extraction from Data Segmentation: generate a load-dependent time and frequency feature set, where an initial load-dependent feature set is created for use in the following step.
- 7.
- Significant Load-Dependent Feature Selection and Validation: select and validate the most significant load-dependent features using an iterative one-way ANOVA approach. Then, validate this feature set by assessing the accuracy of different classifiers.
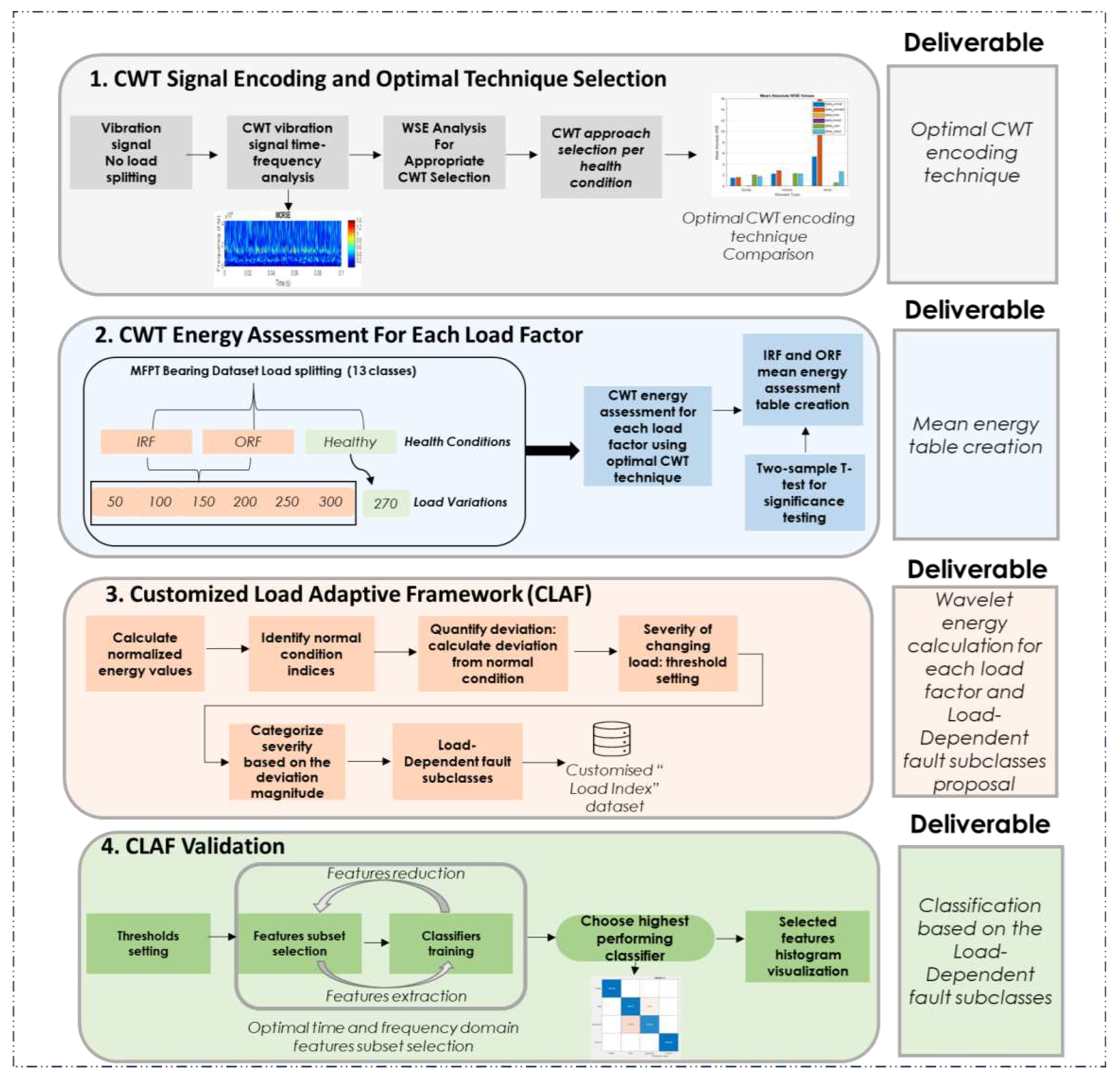
3.2. Phase 2: Customised Load Adaptive Framework (CLAF) for IM Fault Classification
- 8.
- CWT Energy Assessment For Each Load Factor: this step involves preprocessing, health condition classification, and categorization into thirteen classes corresponding to specific load levels. The research calculates wavelet singular entropy and mean energy, providing insights into fault severity and energy distribution.
- 9.
- Customized Load Adaptive Framework (CLAF): the research proposes a Load-Dependent Fault Subclasses tailored to assess radial load impact under different conditions, incorporating insights gained from the analysis for a customised evaluation.
- 10.
- CLAF Validation: train different classifiers on proposed Load-Dependent subclasses to examine the classification accuracy of the proposed classes.
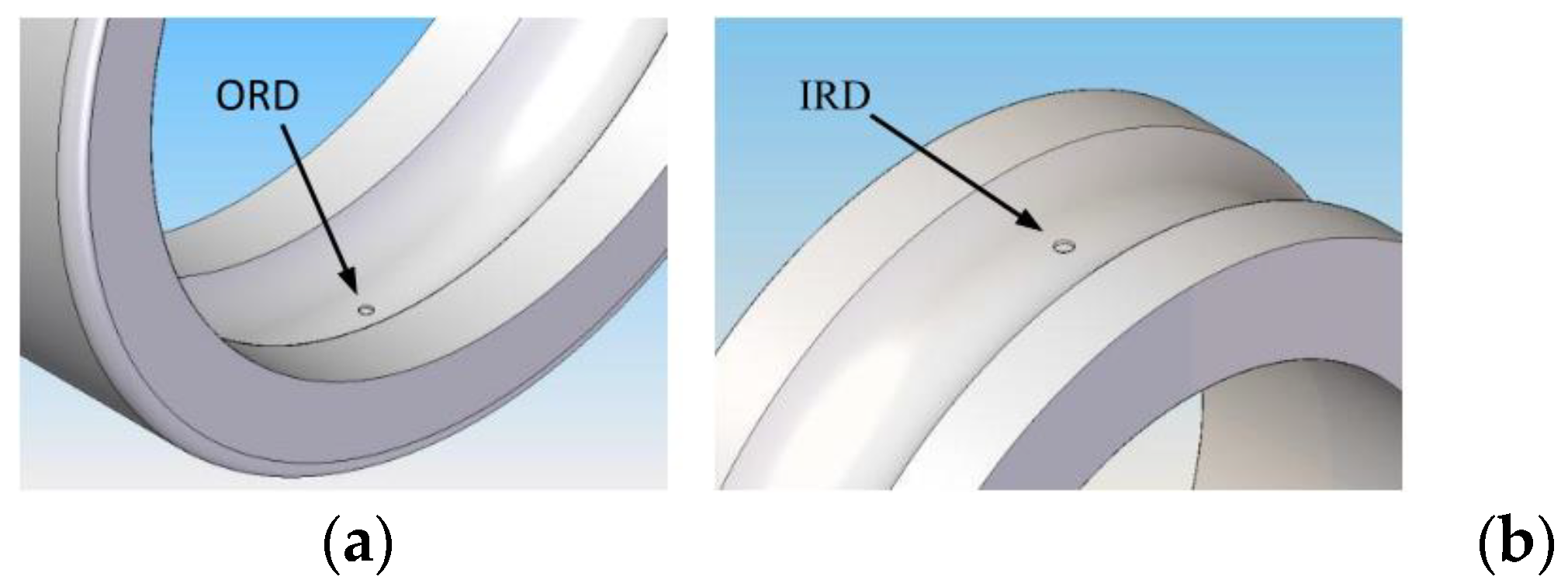
3.3. Dataset
4. Results and Discussion
4.1. Phase 1: Radial Load Features Assessment Framework
4.1.1. Step1: Data Preprocessing and General Load-Dependent Feature Extraction
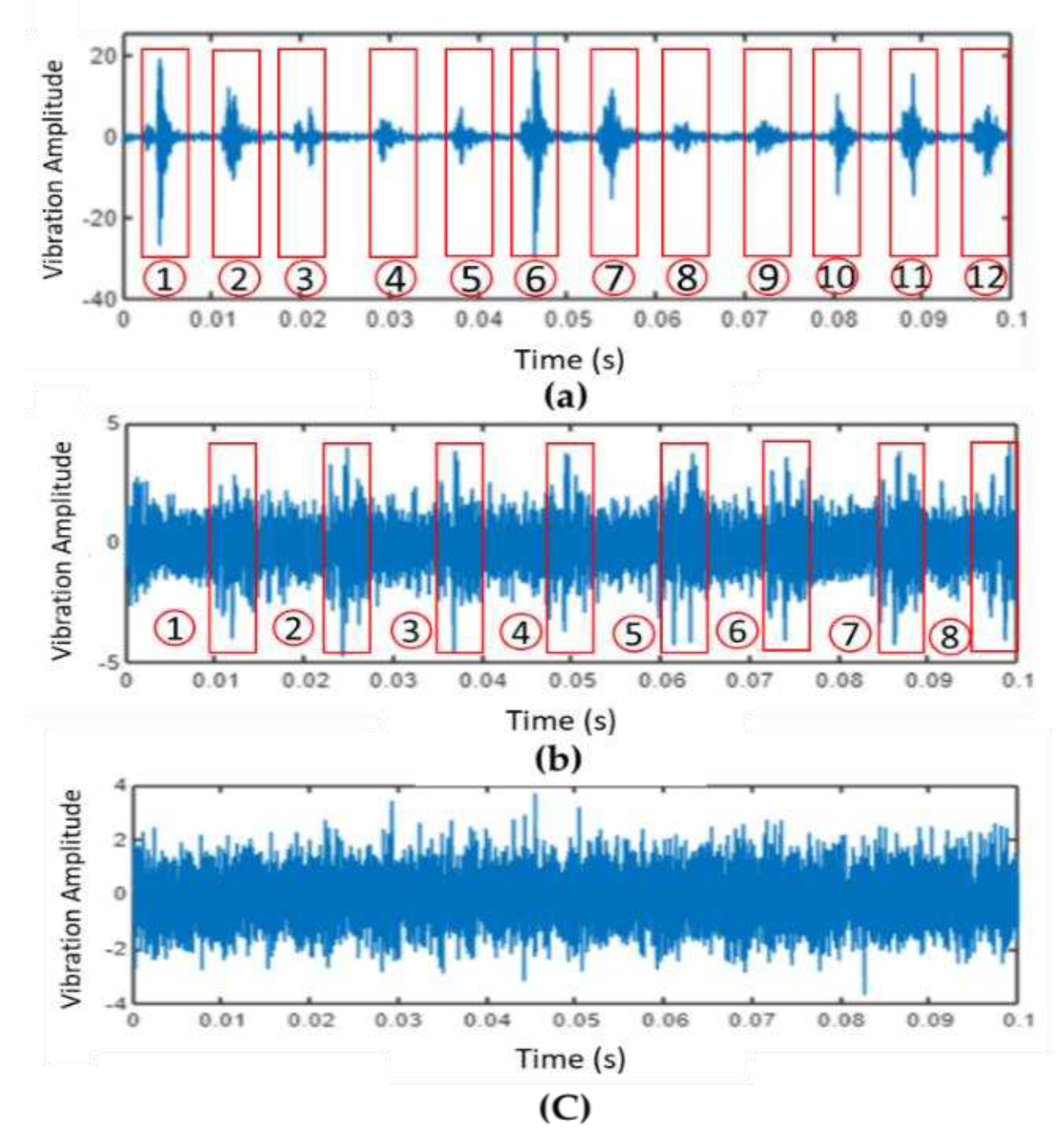
General Load-Dependent Behaviour Analysis
4.1.2. Step2: Data Segmentation and Load-Dependent Subfiles Creation
4.1.3. Step3: Time and Frequency Domain Feature Extraction from Data Segmentation
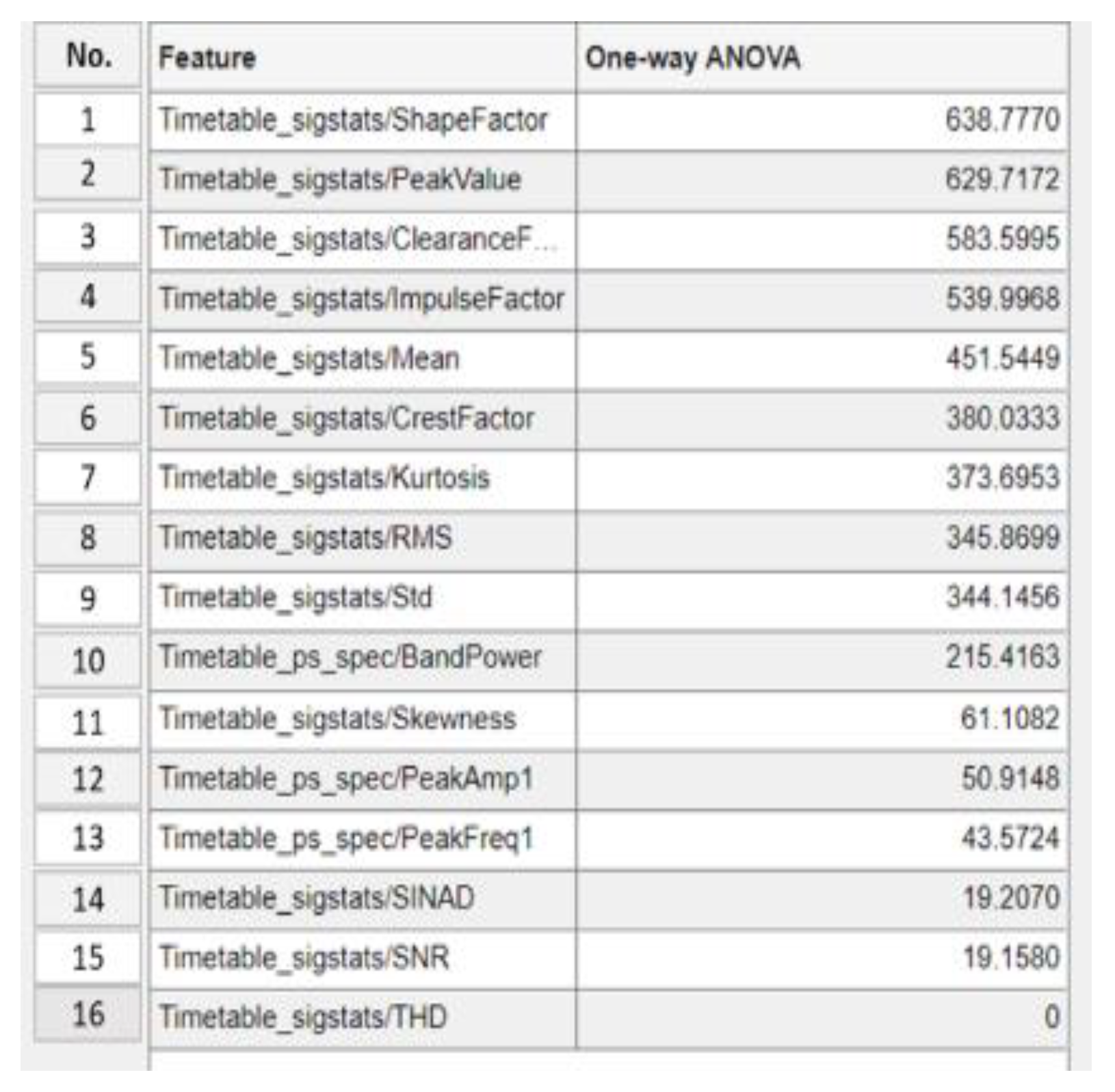
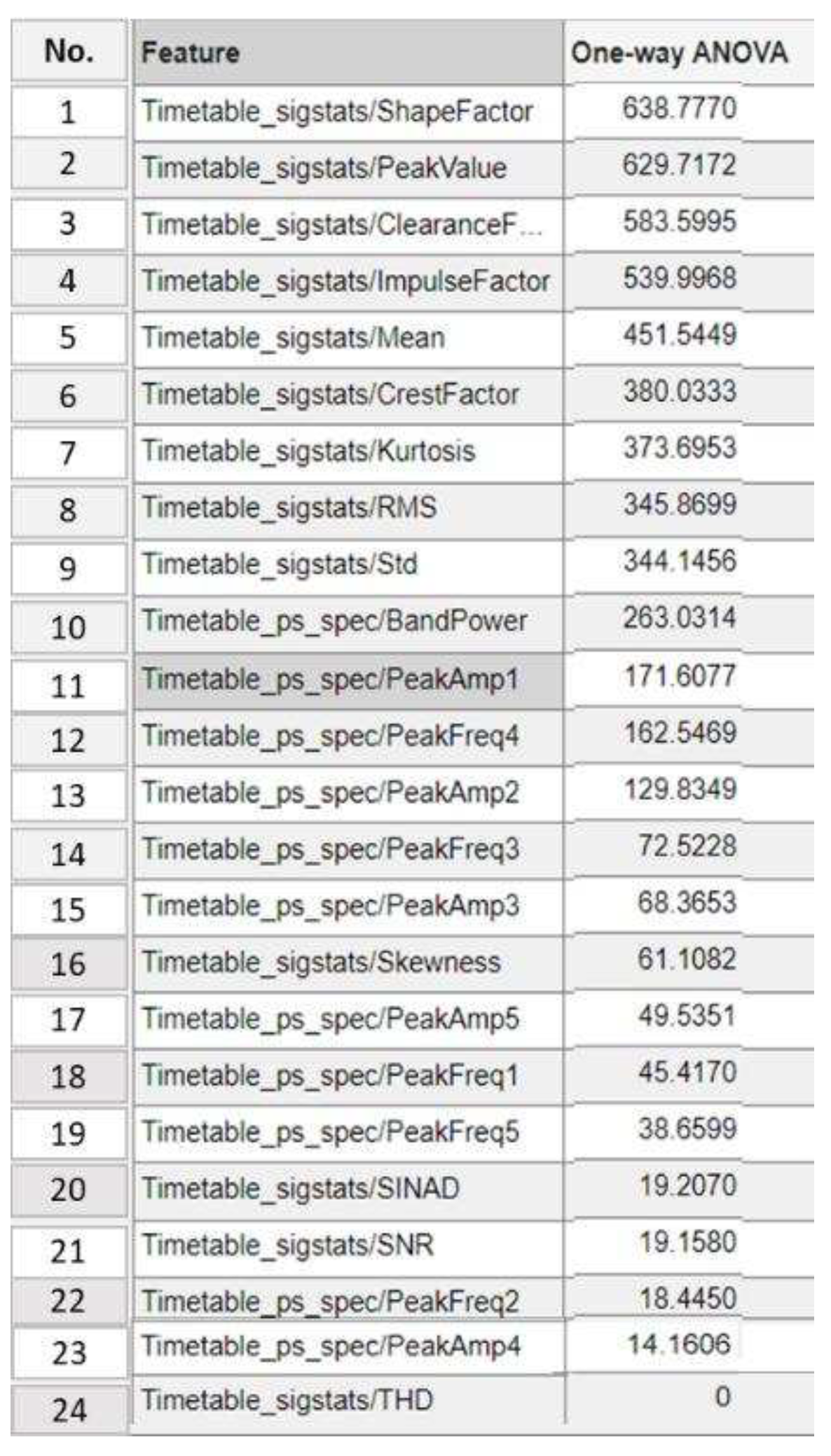
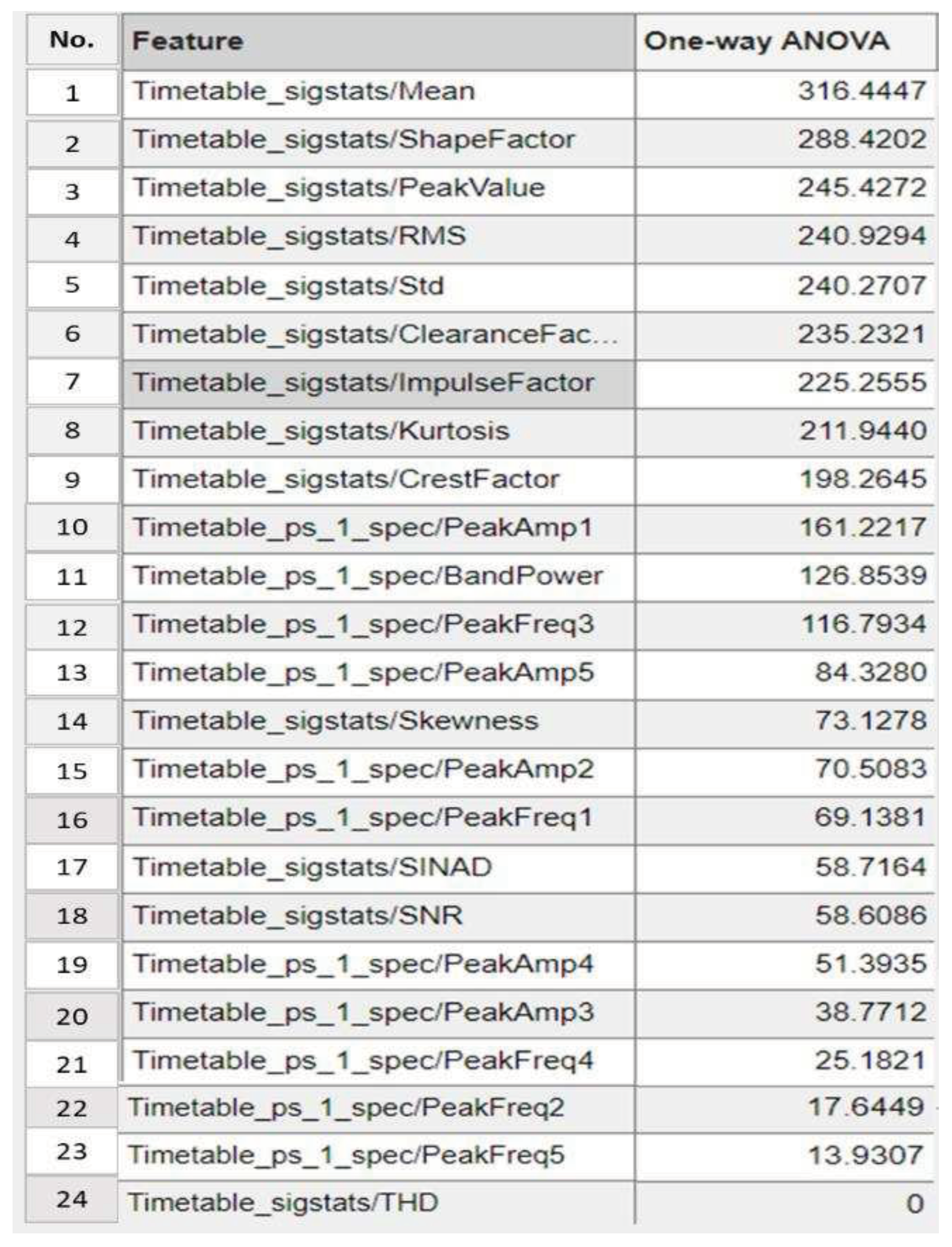
4.1.4. Step 4: Significant Load-Dependent Feature Selection and Validation
Summary of Selected Features
4.2. Phase 2: Customised Load Adaptive Framework (CLAF) for IM Fault Classification
4.2.1. Step1: CWT Signal Encoding and Optimal Technique Selection
CWT Vibration Signal Time-Frequency Analysis
Wavelet Singular Entropy Analysis For Appropriate CWT Selection
4.2.2. Step 2: CWT Energy Assessment For Each Load Factor
- Extract the vibration signal for load factor i:
- Perform the CWT on the vibration signal: , see Equation 12. The scale used in this study is 5.
- Calculate the wavelet energy for each scale j: , in Equation 13.
| Inner Race Fault Type | Outer Race Fault Type | |||
|---|---|---|---|---|
| Load Factor (lbs) | MeanEnergy | Mean Energy Increase % | MeanEnergy | Mean Energy Increase % |
| 50 | 25.549 | 347.70% | 7.699 | 35.16% |
| 100 | 27.547 | 383.65% | 5.431 | 4.76% |
| 150 | 24.915 | 337.68% | 5.573 | 2.08% |
| 200 | 33.742 | 491.88% | 7.604 | 33.35% |
| 250 | 36.147 | 533.49% | 7.178 | 25.90% |
| 270 | 5.7012 | 0% (baseline) | 5.701 | 0% (baseline) |
| 300 | 32.199 | 464.25% | 18.612 | 226.88% |
Two-Sample T-test for Significance Testing
4.2.3. Step 3: Customised Load Adaptive Framework
| LoadFactor (lb) | Mean Energy | NormalizedEnergy | Deviation | Load-Dependent Subclasses | ||||
|---|---|---|---|---|---|---|---|---|
| Fault Type | Inner | Outter | Inner | Outter | Inner | Outter | Inner | Outter |
| 50 | 25.549 | 7.6992 | 0.14035 | 0.05758 | 0.1403 | 0.05758 | {'Mild' } | {'Mild' } |
| 100 | 27.547 | 5.4309 | 0.15053 | 0.023062 | 0.15053 | 0.023062 | {'Mild' } | {'Mild' } |
| 150 | 24.915 | 5.5728 | 0.14063 | 0.031372 | 0.14063 | 0.031372 | {'Mild' } | {'Mild' } |
| 200 | 33.742 | 7.6036 | 0.28444 | 0.092816 | 0.28444 | 0.092816 | {'Moderate'} | {'Mild' } |
| 250 | 36.147 | 7.1779 | 0.29911 | 0.061822 | 0.29911 | 0.061822 | {'Moderate'} | {'Mild' } |
| 270 | 5.7012 | 5.7012 | 0.00930 | 0.027659 | 0 | 0 | {'Normal' } | {'Normal'} |
| 300 | 32.199 | 18.612 | 0.23412 | 0.89814 | 0.23412 | 0.89814 | {'Moderate'} | {'Severe'} |
4.2.4. Step 4: CLAF Validation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgements
Conflicts of Interest
References
- Alshorman, O.; Irfan, M.; Saad, N.; Zhen, D.; Haider, N.; Glowacz, A.; Alshorman, A. A Review of Artificial Intelligence Methods for Condition Monitoring and Fault Diagnosis of Rolling Element Bearings for Induction Motor. Shock Vib. 2020, 2020. [Google Scholar] [CrossRef]
- Cinar, E. A Sensor Fusion Method Using Deep Transfer Learning for Fault Detection in Equipment Condition Monitoring. 16th Int. Conf. Innov. Intell. Syst. Appl. INISTA 2022 2022, 1–6. [Google Scholar] [CrossRef]
- Nemani, V.; Bray, A.; Thelen, A.; Hu, C.; Daining, S. Health Index Construction with Feature Fusion Optimization for Predictive Maintenance of Physical Systems. Struct. Multidiscip. Optim. 2022, 65, 1–23. [Google Scholar] [CrossRef]
- Ye, L.; Ma, X.; Wen, C. Rotating Machinery Fault Diagnosis Method by Combining Time-Frequency Domain Features and Cnn Knowledge Transfer. Sensors 2021, 21. [Google Scholar] [CrossRef] [PubMed]
- Resendiz-Ochoa, E.; Osornio-Rios, R.A.; Benitez-Rangel, J.P.; Romero-Troncoso, R.D.J.; Morales-Hernandez, L.A. Induction Motor Failure Analysis: An Automatic Methodology Based on Infrared Imaging. IEEE Access 2018, 6, 76993–77003. [Google Scholar] [CrossRef]
- Silik, A.; Noori, M.; Altabey, W.A.; Ghiasi, R.; Wu, Z. Comparative Analysis of Wavelet Transform for Time-Frequency Analysis and Transient Localization in Structural Health Monitoring. SDHM Struct. Durab. Heal. Monit. 2021, 15, 1–22. [Google Scholar] [CrossRef]
- Iunusova, E.; Gonzalez, M.K.; Szipka, K.; Archenti, A. Early Fault Diagnosis in Rolling Element Bearings: Comparative Analysis of a Knowledge-Based and a Data-Driven Approach. J. Intell. Manuf. 2023. [Google Scholar] [CrossRef]
- Li, J.; Ying, Y.; Ren, Y.; Xu, S.; Bi, D.; Chen, X.; Xu, Y. Research on Rolling Bearing Fault Diagnosis Based on Multi-Dimensional Feature Extraction and Evidence Fusion Theory. R. Soc. Open Sci. 2019, 6. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.; Li, Y.; Liu, S. A Review of Fault Diagnosis Methods for Rotating Machinery. IEEE Int. Conf. Control Autom. ICCA 2020, 2020, 1618–1623. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, B.; Lin, Y. Machine Learning Based Bearing Fault Diagnosis Using the Case Western Reserve University Data: A Review. IEEE Access 2021, 9, 155598–155608. [Google Scholar] [CrossRef]
- Ahmed, H.; Nandi, A.K. Compressive Sampling and Feature Ranking Framework for Bearing Fault Classification With Vibration Signals. IEEE Access 2018, 6, 44731–44746. [Google Scholar] [CrossRef]
- Toma, R.N.; Gao, Y.; Piltan, F.; Im, K.; Shon, D.; Yoon, T.H.; Yoo, D.S.; Kim, J.M. Classification Framework of the Bearing Faults of an Induction Motor Using Wavelet Scattering Transform-Based Features. Sensors 2022, 22. [Google Scholar] [CrossRef]
- Nayana, B.R.; Geethanjali, P. Improved Identification of Various Conditions of Induction Motor Bearing Faults. IEEE Trans. Instrum. Meas. 2020, 69, 1908–1919. [Google Scholar] [CrossRef]
- Toma, R.N.; Prosvirin, A.E.; Kim, J.M. Bearing Fault Diagnosis of Induction Motors Using a Genetic Algorithm and Machine Learning Classifiers. Sensors (Switzerland) 2020, 20. [Google Scholar] [CrossRef]
- Martinez-Herrera, A.L.; Ferrucho-Alvarez, E.R.; Ledesma-Carrillo, L.M.; Mata-Chavez, R.I.; Lopez-Ramirez, M.; Cabal-Yepez, E. Multiple Fault Detection in Induction Motors through Homogeneity and Kurtosis Computation. Energies 2022, 15. [Google Scholar] [CrossRef]
- Yuan, L.; Lian, D.; Kang, X.; Chen, Y.; Zhai, K. Rolling Bearing Fault Diagnosis Based on Convolutional Neural Network and Support Vector Machine. IEEE Access 2020, 8, 137395–137406. [Google Scholar] [CrossRef]
- Hejazi, S.; Packianather, M.; Liu, Y. Novel Preprocessing of Multimodal Condition Monitoring Data for Classifying Induction Motor Faults Using Deep Learning Methods. In Proceedings of the 2022 IEEE 2nd International Symposium on Sustainable Energy, Signal Processing and Cyber Security (iSSSC), December 15 2022; IEEE; pp. 1–6. [Google Scholar]
- Zhang, H.; Borghesani, P.; Randall, R.B.; Peng, Z. A Benchmark of Measurement Approaches to Track the Natural Evolution of Spall Severity in Rolling Element Bearings. Mech. Syst. Signal Process. 2022, 166, 108466. [Google Scholar] [CrossRef]
- Han, T.; Zhang, L.; Yin, Z.; Tan, A.C.C. Rolling Bearing Fault Diagnosis with Combined Convolutional Neural Networks and Support Vector Machine. Meas. J. Int. Meas. Confed. 2021, 177, 109022. [Google Scholar] [CrossRef]
- Narayan, Y. Hb VsEMG Signal Classification with Time Domain and Frequency Domain Features Using LDA and ANN Classifier Materials Today: Proceedings Hb VsEMG Signal Classification with Time Domain and Frequency Domain Features Using LDA and ANN Classifier. Mater. Today Proc. 2021. [Google Scholar] [CrossRef]
- Jain, P.H.; Bhosle, S.P. Study of Effects of Radial Load on Vibration of Bearing Using Time-Domain Statistical Parameters. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1070, 012130. [Google Scholar] [CrossRef]
- Jain, P.H.; Bhosle, S.P. Analysis of Vibration Signals Caused by Ball Bearing Defects Using Time-Domain Statistical Indicators. Int. J. Adv. Technol. Eng. Explor. 2022, 9, 700–715. [Google Scholar] [CrossRef]
- Liu, M.K.; Weng, P.Y. Fault Diagnosis of Ball Bearing Elements: A Generic Procedure Based on Time-Frequency Analysis. Meas. Sci. Rev. 2019, 19, 185–194. [Google Scholar] [CrossRef]
- Pinedo-Sánchez, L.A.; Mercado-Ravell, D.A.; Carballo-Monsivais, C.A. Vibration Analysis in Bearings for Failure Prevention Using CNN. J. Brazilian Soc. Mech. Sci. Eng. 2020, 42, 1–16. [Google Scholar] [CrossRef]
- Granados-Lieberman, D.; Huerta-Rosales, J.R.; Gonzalez-Cordoba, J.L.; Amezquita-Sanchez, J.P.; Valtierra-Rodriguez, M.; Camarena-Martinez, D. Time-Frequency Analysis and Neural Networks for Detecting Short-Circuited Turns in Transformers in Both Transient and Steady-State Regimes Using Vibration Signals. Appl. Sci. 2023, 13, 12218. [Google Scholar] [CrossRef]
- Tian, B.; Fan, X.; Xu, Z.; Wang, Z.; Du, H. Finite Element Simulation on Transformer Vibration Characteristics under Typical Mechanical Faults. Proc. 9th Int. Conf. Power Electron. Syst. Appl. PESA 2022 2022, 1–4. [Google Scholar] [CrossRef]
- Kumar, V.; Mukherjee, S.; Verma, A.K.; Sarangi, S. An AI-Based Nonparametric Filter Approach for Gearbox Fault Diagnosis. IEEE Trans. Instrum. Meas. 2022, 71, 1–11. [Google Scholar] [CrossRef]
- MathWorks Analyze and Select Features for Pump Diagnostics. Available online: https://www.mathworks.com/help/predmaint/ug/analyze-and-select-features-for-pump-diagnostics.html (accessed on 27 November 2023).
- Hu, L.; Zhang, Z. EEG Signal Processing and Feature Extraction; Hu, L., Zhang, Z., Eds.; Springer Singapore: Singapore, 2019; ISBN 978-981-13-9112-5. [Google Scholar]
- Metwally, M.; Hassan, M.M.; Hassaan, G. Diagnosis of Rotating Machines Faults Using Artificial Intelligence Based on Preprocessing for Input Data. 2020.
- Djemili, I.; Medoued, A.; Soufi, Y. A Wind Turbine Bearing Fault Detection Method Based on Improved CEEMDAN and AR-MEDA. J. Vib. Eng. Technol. 2023. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, S.; Qiu, L.; Zhang, Y.; Wang, Y.; Wang, Z.; Yang, G. A Remaining Useful Life Prediction Method Based on PSR-Former. Sci. Rep. 2022, 12. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Fu, L.; Lin, S.; Bo, Z. Fault Detection and Classification in EHV Transmission Line Based on Wavelet Singular Entropy. IEEE Trans. Power Deliv. 2010, 25, 2156–2163. [Google Scholar] [CrossRef]
- Kaji, M.; Parvizian, J.; van de Venn, H.W. Constructing a Reliable Health Indicator for Bearings Using Convolutional Autoencoder and Continuous Wavelet Transform. Appl. Sci. 2020, 10, 8948. [Google Scholar] [CrossRef]
- Wang, S.; Wang, D.; Kong, D.; Wang, J.; Li, W.; Zhou, S. Few-Shot Rolling Bearing Fault Diagnosis with Metric-Based Meta Learning. Sensors (Switzerland) 2020, 20, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Amanollah, H.; Asghari, A.; Mashayekhi, M. Damage Detection of Structures Based on Wavelet Analysis Using Improved AlexNet. Structures 2023, 56, 105019. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, H.; Zhou, Y.; Xu, C.; Liao, Y. Recognising Drivers’ Mental Fatigue Based on EEG Multi-Dimensional Feature Selection and Fusion. Biomed. Signal Process. Control 2023, 79, 104237. [Google Scholar] [CrossRef]
- Suresh, S.; Naidu, V.P.S. Mahalanobis-ANOVA Criterion for Optimum Feature Subset Selection in Multi-Class Planetary Gear Fault Diagnosis. JVC/Journal Vib. Control 2022, 28, 3257–3268. [Google Scholar] [CrossRef]
- Alharbi, A.H.; Towfek, S.K.; Abdelhamid, A.A.; Ibrahim, A.; Eid, M.M.; Khafaga, D.S.; Khodadadi, N.; Abualigah, L.; Saber, M. Diagnosis of Monkeypox Disease Using Transfer Learning and Binary Advanced Dipper Throated Optimization Algorithm. Biomimetics 2023, 8, 1–21. [Google Scholar] [CrossRef] [PubMed]
- Sayyad, S.; Kumar, S.; Bongale, A.; Kamat, P.; Patil, S.; Kotecha, K. Data-Driven Remaining Useful Life Estimation for Milling Process: Sensors, Algorithms, Datasets, and Future Directions. IEEE Access 2021, 9, 110255–110286. [Google Scholar] [CrossRef]
- Toma, R.N.; Toma, F.H.; Kim, J. Comparative Analysis of Continuous Wavelet Transforms on Vibration Signal in Bearing Fault Diagnosis of Induction Motor. In Proceedings of the 2021 International Conference on Electronics, Communications and Information Technology (ICECIT), September 14 2021; IEEE; pp. 1–4. [Google Scholar]
- Toma, R.N.; Kim, J. Comparative Analysis of Continuous Wavelet Transforms on Vibration Signal in Bearing Fault Diagnosis of Induction Motor. 2021, 14–16. [CrossRef]
- Guo, T.; Zhang, T.; Lim, E.; Lopez-Benitez, M.; Ma, F.; Yu, L. A Review of Wavelet Analysis and Its Applications: Challenges and Opportunities. IEEE Access 2022, 10, 58869–58903. [Google Scholar] [CrossRef]
- Ozaltin, O.; Yeniay, O. A Novel Proposed CNN–SVM Architecture for ECG Scalograms Classification. Soft Comput. 2023, 27, 4639–4658. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Cao, M.; Deng, T.; Zhang, S. Wavelet Packet Singular Entropy-Based Method for Damage Identification in Curved Continuous Girder Bridges under Seismic Excitations. Sensors (Switzerland) 2019, 19. [Google Scholar] [CrossRef]
- Jayamaha, D.K.J.S.; Lidula, N.W.A.; Rajapakse, A.D. Wavelet-Multi Resolution Analysis Based ANN Architecture for Fault Detection and Localization in DC Microgrids. IEEE Access 2019, 7, 145371–145384. [Google Scholar] [CrossRef]
- Bechhoefer, E. A Quick Introduction to Bearing Envelope Analysis. J. Chem. Inf. Model. 2016, 53, 1–10. [Google Scholar]
- Bechhoefer, E. Condition Based Maintenance Fault Database for Testing of Diagnostic and Prognostics Algorithms. Available online: https://www.mfpt.org/fault-data-sets/ (accessed on 30 October 2023).




| Parameter | Formula | Description |
|---|---|---|
| Peak or Max | The highest amplitude value is observed within a given signal or dataset. | |
| Root Mean Square (RMS) | Gives a measure of the magnitude of the signal. | |
| Skewness | Measures the asymmetry of the distribution about the mean. | |
| Standard deviation (std) | The square root of the variance represents the average deviation from the mean. | |
| Kurtosis | Indicates the "tailedness" of the distribution. A high kurtosis might indicate the presence of outliers or impulses in the signal. | |
| Crest Factor | The ratio of the peak amplitude to its RMS value indicates the relative sharpness of peaks. | |
| Peak to Peak | Difference between the maximum and minimum values of the signal. | |
| Impulse Factor | Highlights the impulsive behaviours indicative of machinery faults. |
| Inner Fault Dataset | Code | Load (lbs) | Sampling rate (Hz) |
Duration (sec) |
|---|---|---|---|---|
| baseline_2 | data_normal | 270 | 97656 | 6 |
| InnerRaceFault_vload_2 | IRF_50 | 50 | 48828 | 3 |
| InnerRaceFault_vload_3 | IRF_100 | 100 | 48828 | 3 |
| InnerRaceFault_vload_4 | IRF_150 | 150 | 48828 | 3 |
| InnerRaceFault_vload_5 | IRF_200 | 200 | 48828 | 3 |
| InnerRaceFault_vload_6 | IRF_250 | 250 | 48828 | 3 |
| InnerRaceFault_vload_7 | IRF_300 | 300 | 48828 | 3 |
| Outer Fault Dataset | Code | Load (lbs) | Sampling rate (Hz) | Duration (sec) |
|---|---|---|---|---|
| baseline_2 | data_normal | 270 | 97656 | 6 |
| OuterRaceFault_vload_2 | ORF_50 | 50 | 48828 | 3 |
| OuterRaceFault_vload_3 | ORF_100 | 100 | 48828 | 3 |
| OuterRaceFault_vload_4 | ORF_150 | 150 | 48828 | 3 |
| OuterRaceFault_vload_5 | ORF_200 | 200 | 48828 | 3 |
| OuterRaceFault_vload_6 | ORF_250 | 250 | 48828 | 3 |
| OuterRaceFault_vload_7 | ORF_300 | 300 | 48828 | 3 |
| LoadFactor (lbs) |
Clearance Factor |
Crest Factor |
Impulse Factor |
Kurtosis | Mean | Peak Value |
RMS | Shape Factor |
Skewness | Std | SINAD* | SNR* | THD* |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 40.04 | 15.462 | 28.69 | 27.97 | -0.22 | 27.50 | 1.78 | 1.86 | 0.62 | 1.76 | -21.32 | -21.307 | -5.36 |
| 100 | 37.30 | 14.488 | 26.96 | 30.53 | -0.22 | 26.59 | 1.84 | 1.86 | 0.87 | 1.82 | -21.05 | -21.027 | -0.53 |
| 150 | 33.30 | 13.249 | 24.31 | 33.13 | -0.22 | 23.06 | 1.74 | 1.84 | 1.28 | 1.72 | -19.05 | -19.046 | -10.06 |
| 200 | 38.15 | 13.537 | 26.92 | 37.28 | -0.21 | 27.38 | 2.02 | 1.99 | 1.15 | 2.01 | -18.22 | -18.208 | -6.31 |
| 250 | 37.52 | 13.022 | 26.18 | 37.49 | -0.20 | 27.14 | 2.08 | 2.01 | 0.72 | 2.08 | -17.70 | -17.684 | -5.46 |
| 300 | 35.24 | 12.998 | 25.17 | 35.30 | -0.19 | 25.58 | 1.97 | 1.94 | 0.68 | 1.96 | -17.35 | -17.341 | -8.41 |
| 270** | 7.75 | 5.230 | 6.56 | 3.02 | -0.14 | 4.65 | 0.89 | 1.25 | 0.00 | 0.88 | -23.60 | -23.598 | -11.39 |
| LoadFactor (lbs) |
Clearance Factor |
Crest Factor |
Impulse Factor |
Kurtosis | Mean | Peak Value |
RMS | Shape Factor |
Skewness | Std | SINAD* | SNR* | THD* |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 50 | 10.26 | 6.39 | 8.48 | 5.09 | -0.19 | 6.35 | 0.99 | 1.33 | 0.04 | 0.98 | -14.41 | -14.40 | -11.97 |
| 100 | 9.15 | 5.84 | 7.62 | 4.40 | -0.18 | 4.93 | 0.84 | 1.31 | -0.01 | 0.82 | -13.15 | -13.12 | -9.06 |
| 150 | 9.54 | 6.10 | 7.94 | 4.04 | -0.18 | 5.21 | 0.85 | 1.30 | -0.04 | 0.83 | -12.59 | -12.56 | -9.934 |
| 200 | 21.81 | 12.46 | 17.67 | 11.90 | -0.17 | 12.28 | 0.99 | 1.42 | 0.31 | 0.97 | -17.54 | -17.52 | -5.54 |
| 250 | 15.03 | 9.07 | 12.30 | 6.59 | -0.16 | 8.66 | 0.96 | 1.36 | 0.12 | 0.94 | -16.09 | -16.06 | -4.92 |
| 300 | 27.18 | 12.92 | 20.80 | 17.69 | -0.16 | 19.43 | 1.50 | 1.61 | 0.27 | 1.50 | -15.10 | -15.10 | -14.69 |
| 270** | 7.75 | 5.23 | 6.56 | 3.02 | -0.14 | 4.65 | 0.89 | 1.25 | 0.01 | 0.88 | -23.60 | -23.60 | -11.39 |
| LoadFactor | PeakAmp1 | PeakAmp2 | PeakFreq1 | PeakFreq2 | BandPower | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Inner | Outer | Inner | Outer | Inner | Outer | Inner | Outer | Inner | Outer | |
| 50 | 0.00034 | 0.000109 | 0.00031 | 0.000093 | 4363.937 | 1413.267 | 13991.090 | 14179.042 | 1.474 | 0.454 |
| 100 | 0.00046 | 0.000075 | 0.00012 | 0.000028 | 4256.059 | 1379.739 | 13968.668 | 14258.280 | 1.476 | 0.322 |
| 150 | 0.00046 | 0.000080 | 0.00005 | 0.000036 | 4191.394 | 1377.111 | 14127.206 | 14462.995 | 1.330 | 0.327 |
| 200 | 0.00031 | 0.000063 | 0.00011 | 0.000058 | 4025.383 | 4947.698 | 10622.786 | 1391.188 | 1.663 | 0.461 |
| 250 | 0.00061 | 0.000058 | 0.00009 | 0.000049 | 4124.988 | 1621.552 | 10365.553 | 5212.034 | 1.807 | 0.430 |
| 300 | 0.00077 | 0.000302 | 0.00058 | 0.000296 | 4081.332 | 2915.517 | 748.668 | 11675.566 | 1.618 | 1.101 |
| Healthy 270 | 0.00003 | 0.000028 | 0.00003 | 0.000028 | 5490.855 | 5490.855 | 14478.764 | 14478.764 | 0.279 | 0.302 |
| Dataset Segmentation | CSV files | Code | Load Factor | Subfiles Count |
|---|---|---|---|---|
Example on baseline(Normal) with Matlab code. The segment is based on ratio, i.e., each segment in inner and outer fault contains 2500 samples, and each sample in normal condition contains 5000 data points.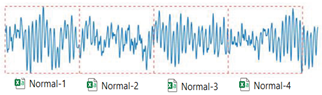 
|
 |
IRF_50 | {'IRF_50' } | 58 |
| IRF_100 | {'IRF_100'} | 58 | ||
| IRF_150 | {'IRF_150'} | 58 | ||
| IRF_200 | {'IRF_200'} | 58 | ||
| IRF_250 | {'IRF_250'} | 58 | ||
| IRF_300 | {'IRF_300'} | 58 | ||
| ORF_50 | {'ORF_50' } | 58 | ||
| ORF_100 | {'ORF_100' } | 58 | ||
| ORF_150 | {'ORF_150'} | 58 | ||
| ORF_200 | {'ORF_200'} | 58 | ||
| ORF_250 | {'ORF_250'} | 58 | ||
| ORF_300 | {'ORF_300'} | 58 | ||
| Normal | {'Normal' } | 117 |
| No. of features used in classifier training | Top 13 >20 |
Top 8 >345 |
Top 7 >373 |
Top 2 >629 |
|---|---|---|---|---|
| Classifier name | Boosted Trees | Narrow Neural Network | Bilayered Neural Network | Fine Gaussian SVM |
| Accuracy score on the testing dataset | 74.1% | 72.8% | 73.5% | 59.9% |
| Number of selected features from ANOVA ranking | Top 19 >20 |
Top 14 >72 |
Top 13 >129 |
Top 11 >171 |
Top 8 >345 |
|---|---|---|---|---|---|
| Classifier | Bagged trees | Cubic SVM | Quadratic SVM | Quadratic Discriminant | Quadratic SVM |
| Accuracy score on the testing dataset | 86.4% | 86.4% | 83.3% | 84.6% | 76.5% |
| Features Color Code | |||
 | |||
| Features (ANOVA Rank) | Features Histogram | Features (ANOVA Rank) | Features Histogram |
| 1. Shape Factor | 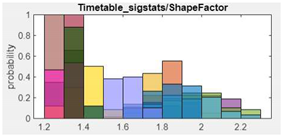 |
2. Peak Value | 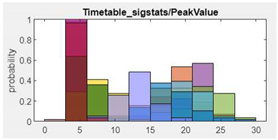 |
| 3. ClearanceFactor | 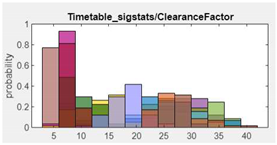 |
4. Impulse Factor |  |
| 5.Mean | 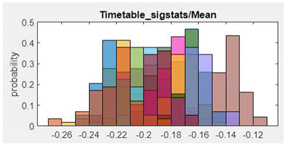 |
6.CrestFactor | 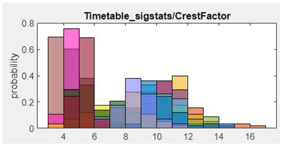 |
| 7. Kurtosis | 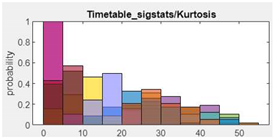 |
8.RMS | 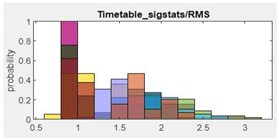 |
| 9.Standard deviation | 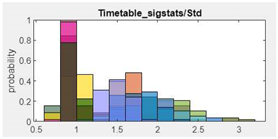 |
10.Band Power | 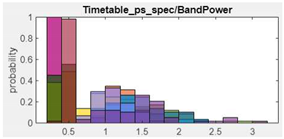 |
| 11.Peak Amplitude1 | 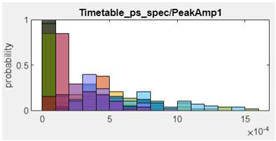 |
12.Peak Frequency4 |  |
| 13.Peak Amplitude 2 | 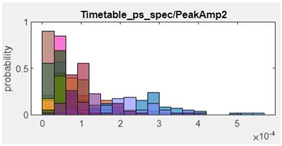 |
14.PeakFrequency3 | 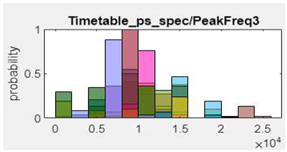 |
| Health State | Inner | Outter | Healthy |
|---|---|---|---|
| Dataset | InnerRaceFault_vload_1 | 'OuterRaceFault_3.mat' | 'baseline_1.mat' |
| 2D time-frequency diagrams | |||
| Bump | 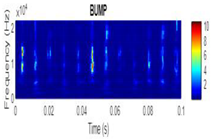 |
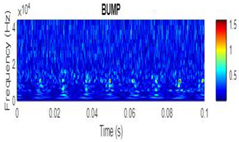 |
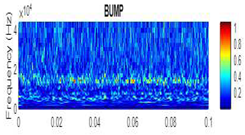 |
| Morse | 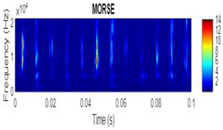 |
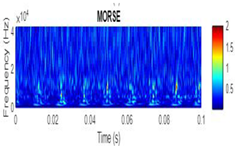 |
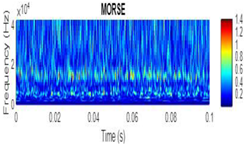 |
| Amor | 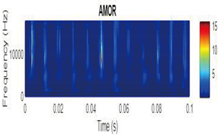 |
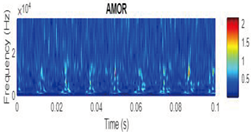 |
 |
| Health State Training set | Code | Morse | Bump | Amor | |
|---|---|---|---|---|---|
| Healthy | baseline_1 | data_normal | 2.236 | 1.483 | 5.381 |
| baseline_2 | data_normal2 | 2.836 | 1.600 | 15.830 | |
| WSE Avg. for 0.1 sec | 2.536 | 1.541 | 10.603 | ||
| Inner | InnerRaceFault_vload_1 | datat_inner | 0.011 | 0.017 | 0.009 |
| InnerRaceFault_vload_2 | datat_inner2 | 0.023 | 0.040 | 0.019 | |
| WSE Avg. for 0.1 sec | 0.017 | 0.028 | 0.014 | ||
| Outer | OuterRaceFault_3 | data_outer | 2.311 | 2.028 | 0.611 |
| OuterRaceFault_1 | data_outer_2 | 2.225 | 1.743 | 2.653 | |
| WSE Avg. for 0.1 sec | 2.268 | 1.886 | 1.632 | ||
| Classifier | ANOVA ranking | TTime 1 | Validation dataset | Testing Dataset | ||||
|---|---|---|---|---|---|---|---|---|
| (sec) | VA2 | HA3 | MA4 | MoA5 | SA 6 | Overall Accuracy | ||
| RUSBoostedTrees | Top 20 >26 |
11.539 | 92.6% | 100% | 92.4% | 91.2% | 100% | 93.8% |
| Fine Tree | Top 17 >58.6 |
4.393 | 92.6% | 100% | 95.7% | 82.4% | 100% | 93.8% |
| Wide neural network | Top 10 >161 |
18.155 | 91.2% | 100% | 97.8% | 88.2% | 100% | 96.3% |
| Cubic SVM | Top7 (a) >215 |
8.1055 | 93.1% | 100% | 96.7% | 82.4% | 100% | 94.4% |
| Medium Gaussian SVM | Top 7 (b) | 5.8059 | 91.6% | 100% | 96.7% | 82.4% | 100% | 94.4% |
| Fine Gaussian SVM | Top 5 >240 |
12.711 | 92.9% | 100% | 97.8% | 82.4% | 100% | 95.1% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.Top of Form |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





