Prerpints.org logo
Preprint
Review

The Scale Invariant Vacuum Paradigm: Main Results and Current Progress Review (Part II)

Altmetrics

Downloads

77

Views

27

Comments

0

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

27 November 2023

Posted:

30 November 2023

You are already at the latest version

Alerts
Abstract
We present a summary of the main results within the Scale Invariant Vacuum (SIV) paradigm based on the Weyl Integrable Geometry (WIG) as an extension to the standard Einstein General Relativity (EGR). After a brief review of the mathematical framework, where we also highlight the connection between the weak-field SIV equations and the notion of un-proper time parametrization within the reparametrization paradigm, we continue with the main results related to early Universe; that is, applications to inflation, Big Bang Nucleosynthesis, and the growth of the density fluctuations within the SIV. In the late time Universe the applications of the SIV paradigm are related to scale-invariant dynamics of galaxies, MOND, dark matter, and the dwarf spheroidals where one can find MOND to be a peculiar case of the SIV theory. Finally, within the recent time epoch, we highlight that some of the change in the length-of-the-day (LOD), about 0.92 cm/yr, can be accounted for by SIV effects in the Earth-Moon system.
Keywords: 
Subject: Physical Sciences  -   Astronomy and Astrophysics

1. Motivation

The paper is a summary of the main results, as of midyear 2023, within the Scale Invariant Vacuum (SIV) paradigm as related to the Weyl Integrable Geometry (WIG) as an extension to the standard Einstein General Relativity (EGR). Our main goal is to present a condensed overview of the key results of the theory so far, along with the latest progress in applying the SIV paradigm to variety of physics phenomenon, and in doing so to help the intellectually curious reader gain some understanding as to where the paradigm has been tested and what is the success level of the inquiry. As such, the paper follows closely our previous 2022 paper Gueorguiev and Maeder [8] that was based on the talk presented at the conference Alternative Gravities and Fundamental Cosmology, at the University of Szczecin, Poland in September 2021. Our initial presentation and its conference contribution were covering, back then, only four main results: comparing the scale factor a ( t ) within Λ CDM and SIV [9], the growth of the density fluctuations within the SIV [4], the application to scale-invariant dynamics of galaxies [5], and inflation of the early-universe within the SIV theory [2]. Back then, our article layout was aiming for focusing on each of these four main results via highlighting its most relevant figure or equation. As a result each topic was covered via one to two pages text preceded by short and concise description of the mathematical framework.
Here, we add a few new sections, one on the possible differentiators of SIV from Λ CDM based on our earlier paper [10], with a specific emphasis on the distance moduli as function of the redshift, along with three new topic sections related to the recent developments in the application of SIV paradigm since our previous summary paper in 2022 [8]. The sections are on MOND as a peculiar case of the SIV theory [5], local dynamical effects within SIV as pertained to the lunar recession [7], and our latest study of the Big-Bang Nucleosynthesis (BBNS) within the SIV Paradigm [3].
After a general introduction on the problem of scale invariance and physical reality, along with the similarities and differences of Einstein General Relativity and Weyl Integrable Geometry, we briefly review, once again for completeness and consistency, the mathematical framework as pertained to Weyl Integrable Geometry, Dirac Co-Calculus, and reparametrization invariance. As before, instead of re-deriving the weak-field SIV results for the equations of motion, we use the idea of reparametrization invariance [1] to illustrate the corresponding equations of motion. The relevant discussion on reparametrization invariance is in Section 2.2 on the Consequences of Going beyond Einstein’s General Relativity. This section precedes the brief review of the necessary results about the Scale Invariant Cosmology idea needed in the Section on Comparisons and Applications, where we highlight the main results related to the early and late Universe in the order seen in the table of contents and also discussed at the beginning of this section. We end the paper, in a standard way, with a section containing the Conclusions and Outlook for future research directions.

1.1. Scale Invariance and Physical Reality

The presence of a scale is related to the existence of physical connection and causality. The corresponding relationships are formulated as physical laws dressed in mathematical expressions. Numerical factors, in the formulas of the physics laws, change upon change of scale but maintain their mathematical form and thus exhibiting form-invariance. As a result, using consistent units is paramount in physics and leads to powerful dimensional estimates of the order of magnitude of physical quantities based on a simple dimensional analysis. The underlined scale is closely related to the presence of a material content, which reflects the energy scale involved.
However, in the absence of matter, a scale is not easy to define. Therefore, an empty universe would be expected to be scale invariant! Absence of scale is confirmed by the scale invariance of the Maxwell equations in vacuum when there is no charges and no currents, which are the sources of the electromagnetic fields. The field equations of general relativity are scale invariant for empty space with zero cosmological constant. What amount of matter is sufficient to kill scale invariance is still an open question. Such a question is particularly relevant to cosmology and the evolution of the Universe.

1.2. Einstein General Relativity and Weyl Integrable Geometry

Einstein’s General Relativity (EGR) is based on the premise of a torsion-free covariant connection that is metric-compatible and guarantees the preservation of the length of vectors along geodesics ( δ v → = 0 ) . The theory has been successfully tested at various scales, starting from local Earth laboratories, the Solar system, on galactic scales via light-bending effects, and even on an extragalactic level via the observation of gravitational waves. The EGR is also the foundation for modern cosmology and astrophysics. However, at galactic and cosmic scales, some new and mysterious phenomena have appeared. The explanations for these phenomena are often attributed to unknown matter particles or fields that are yet to be detected in our laboratories given the suggestive names – dark matter and dark energy.
Since no new particles or fields have been detected in the Earth labs for more than twenty years, it seems reasonable to revisit some old ideas that have been proposed as modifications of EGR. In 1918, Weyl proposed and extension by adding local gauge (scale) invariance [11]. Other approaches were more radical by adding extra dimensions, such as Kaluza–Klein unification theory. One comes back to the usual 4D spacetime as projective relativity theory via Jordan conformal equivalence, but with at least one additional scalar field. Such theories are also known as Jordan–Brans–Dicke scalar-tensor gravitation theories [12,13,14]. In most such theories, there is a major drawback – a varying Newton constant G. Some theories go even further to consider spatially varying–G gravity [15]. No such variations have been observed yet; so, we prefer to view Newton’s gravitational constant G as constant despite the experimental issues on its measurements [16].
In the light of the above discussion one may naturally ask: could the mysterious “dark” phenomena be artifacts of non-zero δ v → , but often negligible and with almost zero value ( δ v → ≈ 0 ) , which could accumulate over cosmic distances and fool us that the observed phenomena may be due to dark matter and/or dark energy? An extension of EGR, with the desired properties, was proposed by Weyl as soon as the General Relativity (GR) was proposed by Einstein. Weyl proposed an extension to GR by adding local gauge (scale) invariance that does have the consequence that lengths may not be preserved upon parallel transport. However, it was quickly argued that such a model will result in a path dependent phenomenon and, thus, contradicting observations. A remedy was later found to this objection [11] by introducing Weyl Integrable Geometry (WIG), where the lengths of vectors are conserved only along closed paths ( ∮ δ v → = 0 ). This idea leads to the scale invariant cosmology by Dirac [17], Canuto et al. [18]. Such formulation of the Weyl’s original idea defeats the Einstein objection! Furthermore, given that all we observe about the distant Universe are waves that reach us, the condition for Weyl Integrable Geometry is basically saying that the information that arrives to us via different paths is interfering constructively to build a consistent picture of the source object.
One way to build a WIG model is to consider conformal transformation of the metric field g μ ν ′ = λ 2 g μ ν and to apply it to various observational phenomena. As we will see in the discussion below, the demand for homogeneous and isotropic space restricts the field λ to depend only on the cosmic time and not on the space coordinates. The weak field limit of such a WIG model results in an extra acceleration in the equation of motion that is proportional to the velocity of the particle.
This behavior is somewhat similar to the Jordan–Brans–Dicke scalar-tensor gravitation; however, the conformal factor λ does not seem to be a typical scalar field as in the Jordan–Brans–Dicke theory [12,13].
The Scale Invariant Vacuum (SIV) idea provides a way of finding out the specific functional form of λ ( t ) as applicable to FLRW cosmology and its WIG extension.
We also find it important to point out that extra acceleration in the equations of motion, which is proportional to the velocity of a particle, could also be justified by requiring re-parametrization symmetry. Re-parametrization invariance is often overlooked as being part of the general covariance that guarantees the physics to be independent of the observer’s coordinate system. However, re-parametrization symmetry is much more, it is about the physics being independent of the choice of parametrization of a process under study. Not implementing re-parametrization invariance in a model could lead to un-proper time parametrization [1] that seems to induce “fictitious forces” in the equations of motion similar to the forces derived in the weak field SIV regime. It is a puzzling observation that may help us understand nature better given its relation to some of the key properties of physical systems [19].

2. Mathematical Framework

The framework for the Scale Invariant Vacuum paradigm is based on the Weyl Integrable Geometry and the Dirac co-calculus as mathematical tools for description of nature [11,17]. For a more modern treatment of the scale invariant gravity idea see [20], that is based on the Cartan’s formalism and along the more traditional scalar field approach, which due to its abstractness seems to have stayed disconnected from observational tests, apart of a few papers on the model parameters for conformal cosmology [21,22] where dark matter and energy seem to be replaced by the concept of rigid matter, which is still observationally questionable as its dark counterparts. Here, our approach is more traditional, physically motivated and with as little general abstraction as possible. For more mathematical details we refer the reader to the companion paper on the “Action Principle for Scale Invariance and Applications (Part I)” [23].

2.1. Weyl Integrable Geometry and Dirac Co-Calculus

The original Weyl geometry uses a metric tensor field g μ ν , along with a “connexion” vector field κ μ , and a scalar field λ . Here we use the french spelling of the word connection to avoid misinterpretation and confusion with the usual meaning and use of a connection vector field. In the Weyl Integrable Geometry, the “connexion” vector field κ μ is not an independent field, but it is derivable from the scalar field λ .
κ μ = − ∂ μ ln ( λ )
This form of the “connexion” vector field κ μ guarantees its irrelevance, in the covariant derivatives, upon integration over closed paths. That is, ∮ κ μ d x μ = 0 . In other words, κ μ d x μ represents a closed 1-form; furthermore, it is an exact form, as (1) implies κ μ d x μ = − d ln λ . Thus, the scalar function λ plays a key role in the Weyl Integrable Geometry. Its physical meaning is related to the freedom of choice of a local scale gauge. Thus, λ relates to the changes in the equations of a physical system upon change in scale via local re-scaling l ′ → λ ( x ) l . Such change could be induced via a local conformal transformation of the coordinates, in which case it is part of the general diffeomorphism symmetry, or it could be only a metric conformal transformation without any associated coordinate transformation.

2.1.1. Gauge Change and (co-) covariant Derivatives

The covariant derivatives utilize the rules of the Dirac co-calculus [17] where tensors also have co-tensor powers based on the way they transform upon change of scale. For the metric tensor g μ ν this power is Π ( g μ ν ) = 2 . This follows from the way the length of a line segment d s is defined via the usual expression d s 2 = g μ ν d x μ d x ν .
l ′ → λ ( x ) l ⇔ d s ′ = λ d s ⇒ g μ ν ′ = λ 2 g μ ν .
Thus, g μ ν is having co-tensor power of Π ( g μ ν ) = − 2 in order to make the Kronecker δ a scale invariant object ( g μ ν g ν ρ = δ μ ρ ). That is, a co-tensor is of power n when, upon local scale change, it satisfies:
l ′ → λ ( x ) l : Y μ ν ′ → λ n Y μ ν

2.1.2. Dirac Co-Calculus

In the Dirac co-calculus, this results in the appearance of the “connexion” vector field κ μ in the covariant derivatives of scalars, vectors, and tensors (see Table 1):
where the usual Christoffel symbol Γ μ α ν is replaced by
  ∗ Γ μ α ν = Γ μ α ν + g μ α k ν − g μ ν κ α − g α ν κ μ .
The corresponding equation of the geodesics within the WIG was first introduced in 1973 by Dirac [17] and in the weak-field limit was re-derived in 1979 by Maeder and Bouvier [24] ( u μ = d x μ / d s is the four-velocity):
u ∗ ν μ = 0 ⇒ d u μ d s +   ∗ Γ ν ρ μ u ν u ρ + κ ν u ν u μ = 0 .
This geodesic equation has also been derived from reparametrization-invariant action in 1978 by Bouvier and Maeder [25]:
δ A = ∫ P 0 P 1 δ d s ˜ = ∫ δ β d s = ∫ δ β d s d τ d τ = 0 .

2.2. Consequences of going beyond the EGR

Before we go into the specific examples, such as FLRW cosmology and weak-field limit, there are some remarks to be made. By using (3) in (4), one can see that the usual EGR equations of motion receive extra terms proportional to the four-velocity and its normalization:
d u μ d s + Γ ν ρ μ u ν u ρ = ( κ · u ) u μ − ( u · u ) κ μ
In the weak-field approximation within the SIV, one assumes an isotropic and homogeneous space for the explicit derivation of the new terms beyond the usual Newtonian equations [25]. As seen from (5), the result is a velocity dependent extra term κ 0 v → with κ 0 = − λ ˙ / λ , while the special components are set to zero ( κ i = 0 , i = 1 , 2 , 3 ) due to the assumption of isotropic and homogeneous space. At this point, it is important to stress that the usual normalization for the four-velocity, u · u = ± 1 with sign related to the signature of the metric tensor g μ ν , is a special choice of parametrization—the proper-time parametrization τ . We denote a general parametrization in (5) with s, while τ is reserved for the proper time, and t is the coordinate time parametrization.
Similar extra term ( κ 0 v → ) was recently obtained [1] as a consequence of reparametrization invariant mathematical modeling but without the need for a weak-field approximation. That is, insisting on reparametrization symmetry for the equations of motion demands such term to be present in order to account for the change of parametrization within a chosen coordinate system. Within the proper time-parametrization one usually has κ 0 = 0 . However, if one assumes that the equations used for the process under study are parametrized via the proper time-parametrization but relies on the observer coordinate time, without including the appropriate κ -term then one has incorrect modeling with un-proper time parametrization instead because coordinate time is often quite different from the proper time of a process. Therefore, not accounting for reparametrization symmetry leads to missing terms in the mathematical formulas utilized in the modeling of a system. Thus, the need for a κ -term is an effect due to reparametrization symmetry and is manifested as velocity dependent fictitious acceleration when accounted for properly [1]. In this respect, the term κ 0 v → is necessary for the restoration of the broken symmetry - the re-parametrization invariance of a process under study. To demonstrate this, one can apply an arbitrary time re-parametrization λ = d t / d s ; then, the first term on the LHS of (5) becomes:
λ d d t λ d r → d t = λ 2 d 2 r → d t 2 + λ λ ˙ d r → d t .
By moving the term linear in the velocity to the RHS (5), dividing by λ 2 , and by using κ ( t ) = − λ ˙ / λ , one obtains a κ 0 v → -like term on the RHS. If one was to do such manipulation in the absence of κ 0 v → on the LHS of (5), then the term will be generated, while if κ ˜ was present in the equations, then it will be transformed κ ˜ → κ + κ ˜ .
Furthermore, unlike in SIV, where one can justify λ ( t ) = t 0 / t , for re-parametrization symmetry the time dependence of λ ( t ) could be arbitrary. Finally, as discussed in [1], the extra term κ 0 v → is not expected to be present when the time parametrization of the process is the proper time of the system. Thus, a term of the form κ v → can be viewed as necessary for restoration of the re-parametrization symmetry and an indication of un-proper time parametrization of a process under consideration when omitted.
In the case of the FLRW cosmology, with the assumption of homogeneity and isotropy of space, one considers − c 2 d τ 2 = − c 2 d t 2 + a ( t ) 2 d Σ 2 , where c is the speed of light (to be set to 1), Σ is a three-dimensional space of uniform curvature, and a ( t ) is the scale factor for the three-dimensional space. Here, τ is the proper time parametrization, presumably of the cosmological evolution, while t is the coordinate time of an observer who is studying the cosmic evolution. Upon transitioning to WIG, one would have λ ( x ) multiplicative conformal factor and, in the case of λ ( t ) (time dependence only), one may argue that this factor could be absorbed into a ( t ) along with a suitable redefinition of the coordinate time t into d t ˜ = λ ( t ) d t . However, this does not guarantee proper-time parametrization in general. It is therefore likely to have un-proper time parametrization for the FLRW cosmology equations with missing velocity dependent terms, unless one makes sure that the re-parametrization symmetry is restored.

2.3. Scale Invariant Cosmology

The scale invariant cosmology equations were first introduced in 1973 by Dirac [17] and then re-derived in 1977 by Canuto et al. [18]. The equations are based on the corresponding expressions of the Ricci tensor and the relevant extension of the Einstein equations.

2.3.1. The Einstein Equation for Weyl’s Geometry

The conformal transformation ( g μ ν ′ = λ 2 g μ ν ) of the metric tensor g μ ν within the more general Weyl’s framework into Einstein’s framework, where the metric tensor is g μ ν ′ , induces a simple relation between the Ricci tensor and scalar within Weyl’s Integrable Geometry and the Einstein GR framework. Our convention is using the symbol prime (′) on mathematical objects to denote Einstein GR framework objects:
R μ ν = R μ ν ′ − κ μ ; ν − κ ν ; μ − 2 κ μ κ ν + 2 g μ ν κ α κ α − g μ ν κ ; α α , R = R ′ + 6 κ α κ α − 6 κ ; α α .
By using these expressions, we can extent the standard EGR equation into:
R μ ν − 1 2 g μ ν R = − 8 π G T μ ν − Λ g μ ν , R μ ν ′ − 1 2 g μ ν R ′ − κ μ ; ν − κ ν ; μ − 2 κ μ κ ν + 2 g μ ν κ ; α α − g μ ν κ α κ α =
− 8 π G T μ ν − Λ g μ ν .
Here Λ is in WIG and is expected that Λ = λ 2 Λ E , with Λ E beeing the Einstein cosmological constant in EGR. This relationship guarantees the explicit scale invariance of the equations. This makes explicit the appearance of Λ E as invariant scalar (in-scalar), since then: Λ g μ ν = λ 2 Λ E g μ ν = Λ E g μ ν ′ . That is, the co-scaler power of Λ in WIG is Π ( Λ ) = − 2 .
The above equations are a generalization of the original Einstein equation. Thus, they have an even larger class of local gauge symmetries that need to be fixed by a gauge choice. In Dirac’s work, the gauge choice was based on the large numbers hypothesis. Here, we discuss a different gauge choice.
The corresponding scale-invariant FLRW cosmology equations were first introduced in 1977 by Canuto et al. [18]:
8 π G ϱ 3 = k a 2 + a ˙ 2 a 2 + 2 λ ˙ a ˙ λ a + λ ˙ 2 λ 2 − Λ E λ 2 3 ,
− 8 π G p = k a 2 + 2 a ¨ a + 2 λ ¨ λ + a ˙ 2 a 2 + 4 a ˙ λ ˙ a λ − λ 2 ˙ λ 2 − Λ E λ 2 .
These equations reproduce the standard FLRW equations in the limit λ = c o n s t = 1 . The scaling of Λ was recently exploited to revisit the cosmological constant problem within quantum cosmology [26]; resulting in the conclusion that our Universe is unusually large, given that the expected mean size of all universes, where EGR holds, is expected to be of a Planck scale. In that study, λ = c o n s t was a key assumption as the various universes were expected to obey the EGR equations. What would be the expected mean size of a universe, if the condition λ = c o n s t is relaxed, remains an open question for an ensemble of WIG-universes.

2.3.2. The Scale Invariant Vacuum Gauge at T = 0 and R ′ = 0

The idea of the Scale Invariant Vacuum was introduced first in 2017 by Maeder [9]. For an empty universe model, the de Sitter metric is conformal to the Minkowski metric, thus, R μ ν ′ is vanishing Maeder [9]. Therefore, for conformally flat metric, that is, Ricci flat ( R μ ν ′ = 0 ) Einstein vacuum ( T μ ν = 0 ), the following vacuum equation can be obtained using (8):
κ μ ; ν + κ ν ; μ + 2 κ μ κ ν − 2 g μ ν κ ; α α + g μ ν κ α κ α = Λ g μ ν
For homogeneous and isotropic space ( ∂ i λ = 0 ), only κ 0 = − λ ˙ / λ and its time derivative κ ˙ 0 = − κ 0 2 can be non-zero. As a corollary of (11), one can derive the following set of equations [9]:
3 λ ˙ 2 λ 2 = Λ , and 2 λ ¨ λ − λ ˙ 2 λ 2 = Λ ,
or λ ¨ λ = 2 λ ˙ 2 λ 2 , and λ ¨ λ − λ ˙ 2 λ 2 = Λ 3 .
These equations can be derived by using the time and space components of the equations, or by looking at the relevant trace invariant along with the relationship κ ˙ 0 = − κ 0 2 . Any one pair among these equations is sufficient to prove the validity of the other pair of equations.
Theorem 1. 
Using the SIV Equations (12) or (13) with Λ = λ 2 Λ E one has:
Λ E = 3 λ 2 ˙ λ 4 , with d Λ E d t = 0 .
Corollary 1. 
The solution of the SIV gauge equations is then:
λ = t 0 / t ,
with t 0 = 3 / ( c 2 Λ E ) where c is the speed of light usually set to 1.
The choice of such gauge for λ can be used to replace the Dirac’s large numbers hypothesis invoked by Canuto et al. [18]. This is what we refer to as a Scale Invariant Vacuum (SIV) gauge for λ .
Even more, now we can have an alternative viewpoint on (8) and (11). Since (8) is scale invariant then one does not have to consider zero case for T μ ν and R μ ν in general, but if the scale factor λ satisfies (11), then all the κ terms and the Λ term in (8) will cancel out leaving us with the standard Einstein GR equation with zero cosmological constant. Thus, a proper choice of λ gauge satisfying (11) results in the standard Einstein equation with no cosmological constant! This is easily seen in the case of homogeneous and isotropic universe or when requiring only reparametrization invariance, then both cases are resulting in (12) and (13) along with (14). If one takes the reparametrization symmetry viewpoint then the presence of a non-zero cosmological constant is indication of un-proper time parametrization that can be cured upon suitable new time gauge deduced by the appropriate choice of λ.
Upon the use of the SIV gauge, first in 2017 by Maeder [9], one observes that the cosmological constant disappears from Equations (9) and (10):
8 π G ϱ 3 = k a 2 + a ˙ 2 a 2 + 2 a ˙ λ ˙ a λ ,
− 8 π G p = k a 2 + 2 a ¨ a + a 2 ˙ a 2 + 4 a ˙ λ ˙ a λ .
The solutions of these equations have been discussed in details in Maeder [9], together with various cosmological properties concerning the Hubble-Lemaître and deceleration parameters, the cosmological distances and different cosmological tests. The redshift drifts appear as one of the most promising cosmological tests [10]. Here, we limit the discussion to a few points pertinent to the subject of the paper. Analytical solutions for the flat SIV models with k = 0 have been found for the matter [27] and radiation [28] dominated models. In the former case, we have a simple expression:
a ( t ) = t 3 − Ω m 1 − Ω m 2 / 3 .
It is expressed in the SIV-timescale t where at present t 0 = 1 and a ( t 0 ) = 1 . Such solutions are illustrated in Figure 1. They are lying relatively close to the Λ CDM ones, the differences being larger for lower Ω m .
This is a general property: the effects of scale invariance are always larger for the lower matter densities, being the largest ones for the empty space. As usual, here Ω m = ϱ / ϱ c with ϱ c = 3 H 0 2 / ( 8 π G ) . Remarkably, Eqs. (16) and (17) allow flatness for different values of Ω m . It follows from (18) that the initial time at a ( t in ) = 0 is related to the value of Ω m :
t in = Ω m 1 / 3 .
The Hubble parameter and κ 0 ( t ) = − λ ˙ / λ are then, in the timescale t (which goes from t in at the Big-Bang to t 0 = 1 at present):
H ( t ) = a ˙ a = 2 t 2 t 3 − Ω m , and κ 0 ( t ) = − λ ˙ λ = 1 t .
From Eqs. (18) and (20), we see that there is no meaningful scale invariant solution for an expanding Universe ( H > 0 ) with Ω m equal or larger than 1. Thus, the model solutions are quite consistent with the causality relations discussed by Maeder and Gueorguiev [2].
The usual timescale τ in years or seconds is τ 0 = 13.8 Gyr at present [29] and τ in = 0 at the Big-Bang. One can change from the SIV-time t to the usual time scale τ by using the relationship ansatz [7]:
τ − τ in τ 0 − τ in = t − t in t 0 − t in ,
which is expressing that the age fraction with respect to the present age is the same in both timescales. This ansatz gives:
τ = τ 0 t − Ω m 1 / 3 1 − Ω m 1 / 3 and t = Ω m 1 / 3 + τ τ 0 ( 1 − Ω m 1 / 3 ) ,
The relevant derivatives are constants depending on t in = Ω m 1 / 3 and τ 0 only:
d τ d t = τ 0 1 − Ω m 1 / 3 , and d t d τ = 1 − Ω m 1 / 3 τ 0 .
For larger Ω m , timescale t is squeezed over a smaller fraction of the interval 0 to 1, (which reduces the range of λ over the ages). Using the above expressions one can write the Hubble parameter in the usual time scale τ via its expression in the t-scale:
H ( τ ) = a ˙ a = H ( t ) d t d τ = H ( t ) 1 − Ω m 1 / 3 τ 0 .
This finally gives for the Hubble constant:
H 0 = 2 1 − Ω m 1 − Ω m 1 / 3 τ 0 .
The last factor could be recognized as κ 0 ( τ 0 ) . To see this one can utilize the equations (22) and (23) to switch from the SIV-time t to the conventional time τ scale [7] in order to obtain:
κ 0 ( τ ) = − λ ˙ λ = κ 0 ( t ) d t d τ = 1 − t in t τ 0 = 1 − t in τ 0 1 t in + ( 1 − t in ) ( τ / τ 0 ) = ψ ( τ ) τ 0 ,
⇒ κ 0 ( τ 0 ) = 1 − Ω m 1 / 3 τ 0 and ψ ( τ ) = 1 − t in t in + ( 1 − t in ) ( τ / τ 0 ) .

3. Comparisons and Applications

The predictions and outcomes of the SIV paradigm were confronted with observations in a series of papers by the current authors. Highlighting the main results and outcomes is the subject of the current section.

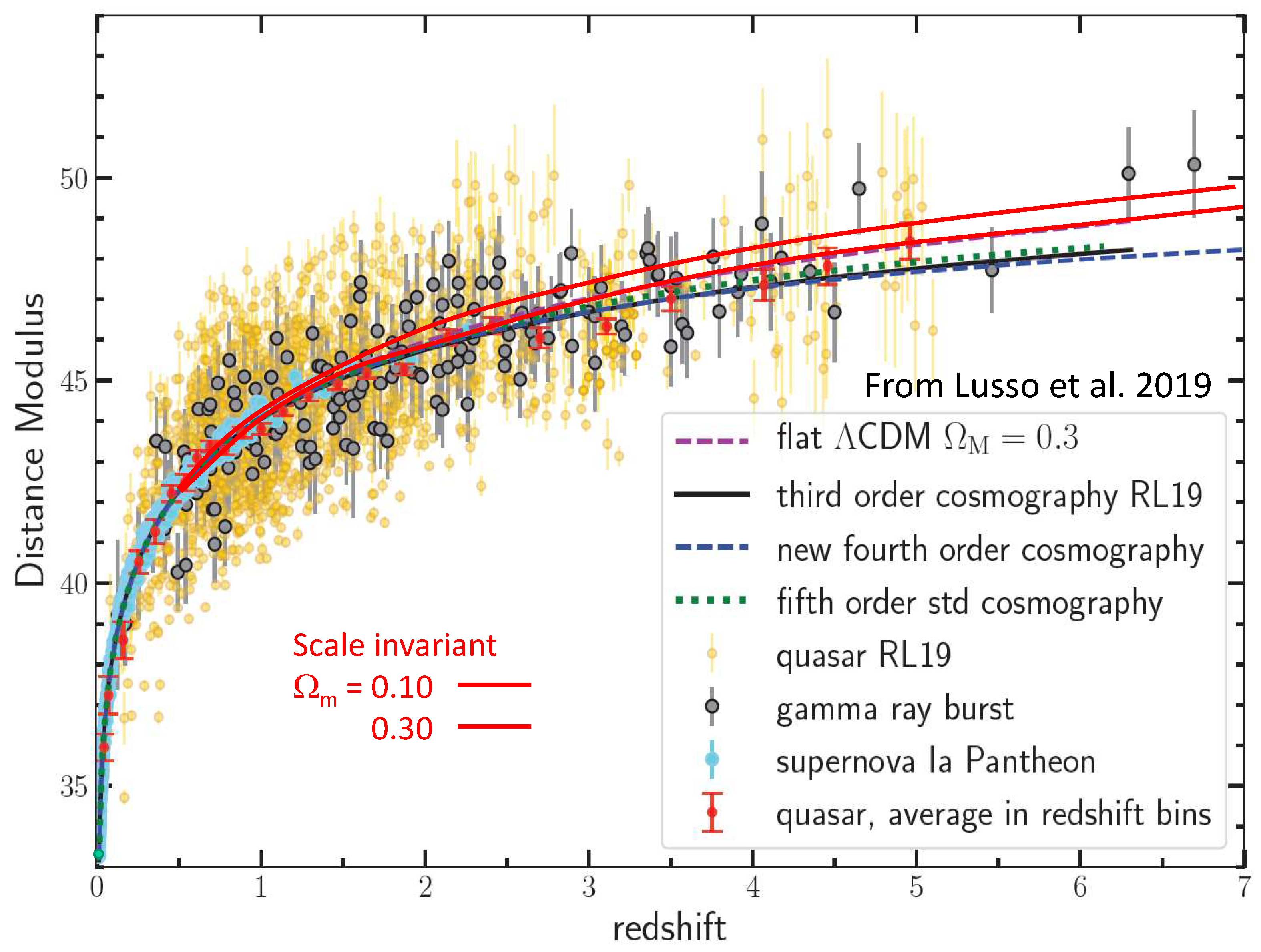
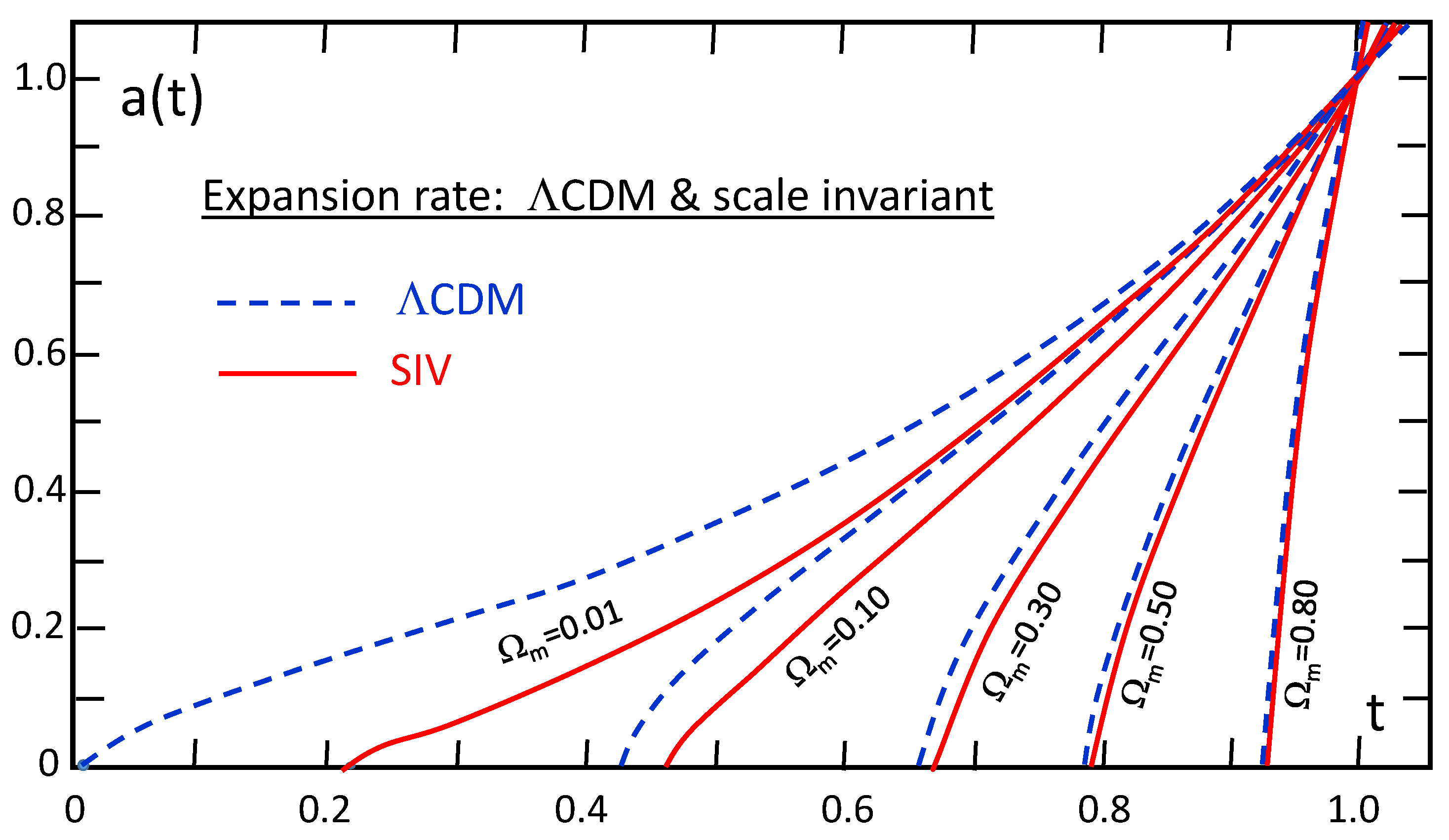
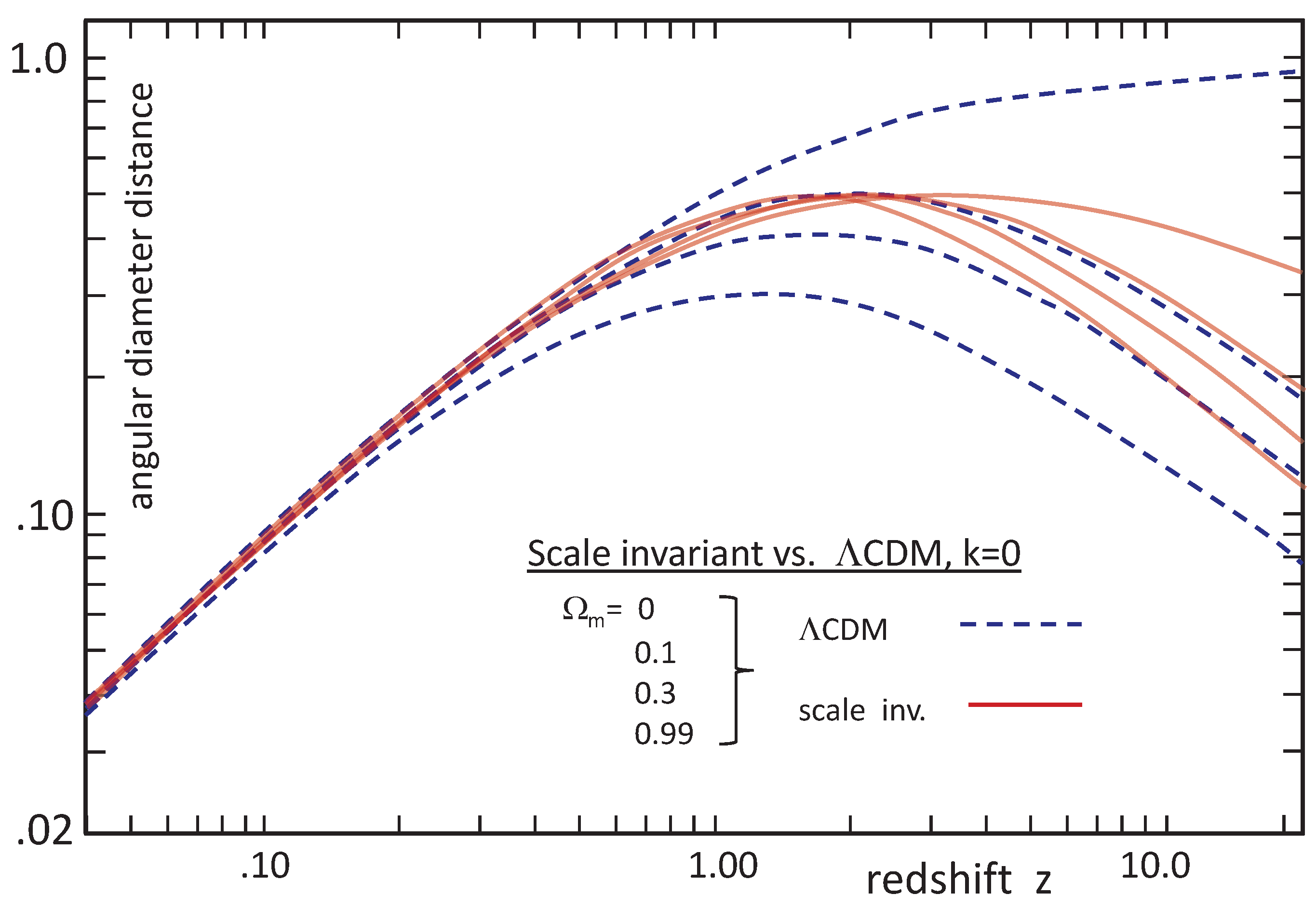
3.1. Comparing the Scale Factor a ( t ) within Λ CDM and SIV [9]

The SIV implications for cosmology were first discussed by Maeder [9] and later reviewed by Maeder and Gueorguiev [10]. For this study one is using the SIV equations (16) and (17), along with the gauge fixing (14), which implies λ = t 0 / t (15) with t 0 indicating the current age of the Universe since the Big-Bang ( a = 0 at t in ). The most important point in comparing Λ CDM and SIV cosmology models is the existence of SIV cosmology with slightly different parameters but almost the same curve for the standard scale parameter a ( t ) when the time scale is set so that t 0 = 1 at the present epoch [9,10].
As seen in Figure 1, the differences between the Λ CDM and SIV models decline for increasing matter densities [9]. Furthermore, the SIV solutions are lying relatively close to the Λ CDM ones, the differences being larger for lower Ω m . This is a general property: the effects of scale invariance are always larger for the lower matter densities, being the largest when approaching the empty space.

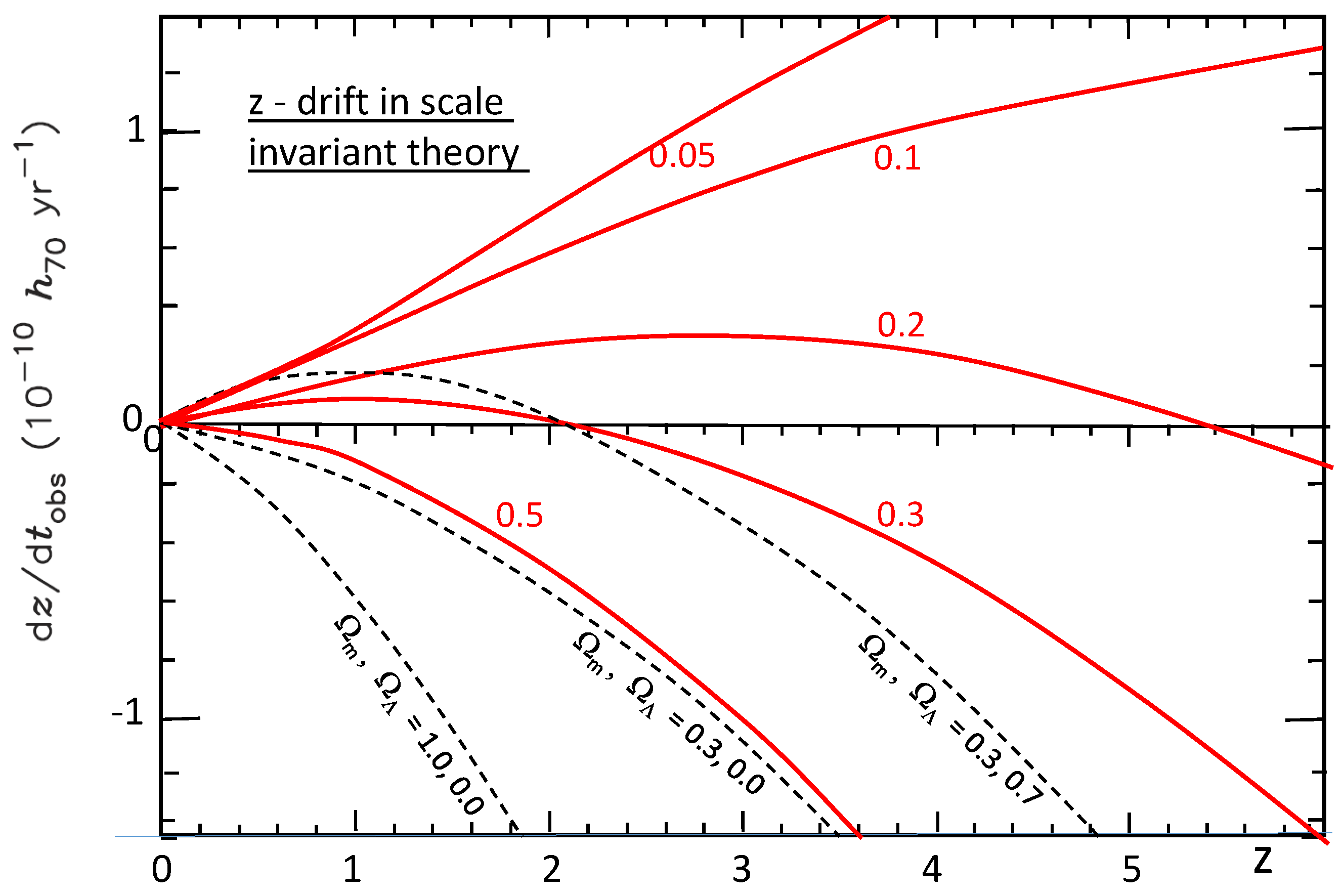
3.2. Possible differentiators of SIV from Λ CDM [10]

The major property of SIV cosmology is that it naturally predicts an acceleration of the expansion. This is the consequence of the additional term in Eqs. (16) and (17) which predicts an acceleration of the motion in the direction of the velocity. If the Universe were to contract, it would also receive an additional acceleration favoring a contraction.
Several observational tests of the SIV cosmology are performed and discussed in details in [10]. For example, based on Figure 3 in [10] one can see that the relation between the Hubble constant H 0 and the age of the Universe in the SIV Cosmology is suggesting a range of values for Ω m between 0.15 and 0.25 depending on the choice for H 0 using either the distance ladder or Planck collaboration measurements.
Most cosmological tests such as the magnitude-redshift, the angular diameter vs. redshift, the number count vs. redshifts, etc, depend on the expressions of the distances based on the angular diameters d A . The plot of d A vs. z in Figure 2 shows that the different curves are not well separated at lower z. At z = 1 , for Ω m = 0 , 0.1 , 0.3 , 0.99 , one respectively has log d A = − 0.383 , − 0.367 , − 0.349 , − 0.342 . Up to a redshift z = 2 , the relations between d A and z for scale invariant models are very close to each other whatever Ω m , with a deviation from the mean smaller than ± 0.05 dex. For Λ CDM models, higher density models always have lower d A with an increasing separation between the curves with increasing z. For the SIV models, this is the same, however with a very small differentiation, up to only z ≈ 2 . Above 2, the SIV models behave differently: higher density models have larger d A values. The above properties are evidently also shared by the magnitude-redshift, the angular diameter vs. redshift, as well as by number counts plots. A clear discrimination between the SIV and Λ CDM models with an access to Ω m requires high precision measurements at redshifts higher than 2.
Figure 3 shows the (m-M) vs. z plot based on SNIa, quasar, and GRB data by Lusso et al. [30] compared to different theoretical curves. The two red lines show the SIV models for Ω m = 0.10 and 0.30. This last model lies very close to the Λ CDM model with Ω m = 0.30 , illustrating the above mentioned difficulty to discriminate between the Λ CDM and SIV models. We note that the SIV models with Ω m = 0.10 better fits the high z points, which could perhaps support a lower value. However, internal effects in the evolution galaxies may also intervene in the comparison of distant and local galaxies, in addition to the cosmological effects and this imposes great care in the conclusions.
Preprints 91563 g003
Figure 3. The Hubble diagram for SNIa, quasars (binned), and GRBs from the samples collected by Lusso et al. [30]. The various models considered by Lusso et al. are indicated. The two red lines show the flat scale invariant models with k = 0 and Ω m = 0.10 and 0.30. Note that the Λ CDM and SIV models with Ω m = 0.30 are easily confused. The other lower curves are attempts of adjustments by series developments. Drawing originally published in [10].
Figure 3. The Hubble diagram for SNIa, quasars (binned), and GRBs from the samples collected by Lusso et al. [30]. The various models considered by Lusso et al. are indicated. The two red lines show the flat scale invariant models with k = 0 and Ω m = 0.10 and 0.30. Note that the Λ CDM and SIV models with Ω m = 0.30 are easily confused. The other lower curves are attempts of adjustments by series developments. Drawing originally published in [10].
Preprints 91563 g003
Figure 4 below, shows the curves of the redshift drifts as a function of z predicted in the SIV cosmology for different values of Ω m . (A z-drift is the change z for a given galaxy over time, a time interval longer than 20 yr appears necessary). The SIV-drifts are compared to a few standard models of different Ω Λ -values by Liske et al. [31]. We notice the relative proximity of the standard and scale invariant curves in the case of Ω m = 0.30 , which could make the separation of models difficult for such a density parameter. However, the expected value of Ω m in the SIV cosmology is likely significantly smaller than in the Λ CDM models; this makes the differences of the z-drifts between the two kinds of cosmological models possibly observable by very accurate observations in the future. The physical reason of these differences between the two models at high z is due to the flatter initial expansion curve in the SIV models. In this respect, we recall that the empty SIV model expand with t 2 , while the empty Λ CDM model is in fact de Sitter model which expands exponentially.
The above comparisons, see also [10], show a general agreement between SIV predictions and observations, alike for the Λ CDM models. The redshift drifts appear to have a particularly great differentiation power between SIV and Λ CDM models.

3.3. Application to Scale-Invariant Dynamics of Galaxies [5]

The next important application of the scale-invariance at cosmic scales is the derivation of a universal expression for the Radial Acceleration Relation (RAR) of g obs and g bar . That is, the relation between the observed gravitational acceleration g obs = v 2 / r and the acceleration from the baryonic matter due to the standard Newtonian gravity g N [5] ( g = g obs , g N = g bar ):
g = g N + k 2 2 + 1 2 4 g N k 2 + k 4 ,
For g N ≫ k 2 : g → g N but for g N → 0 ⇒ g → k 2 is a constant.
As seen in Figure 5, MOND deviates significantly for the data on the Dwarf Spheroidals. This is well-known problem in MOND due to the need of two different interpolating functions, one in galaxies and one at cosmic scales. The SIV universal expression (28) resolves this issue naturally, with one universal parameter k 2 related to the gravity at large distances [5].
The expression (28) follows from the Weak Field Approximation of the SIV upon utilization of the Dirac co-calculus in the derivation of the geodesic equation within the relevant WIG (4) (see Maeder and Gueorguiev [5] for more details, as well as the original derivation in Maeder and Bouvier [24]):
g i i = − 1 , g 00 = 1 + 2 Φ / c 2 ⇒ Γ 00 i = 1 2 ∂ g 00 ∂ x i = 1 c 2 ∂ Φ ∂ x i , d 2 r → d t 2 = − G t M r 2 r → r + κ 0 ( t ) d r → d t .
where i ∈ 1 , 2 , 3 , while the potential Φ = G t M / r is scale invariant and G t is the Newton’s constant of gravity in SIV t-time units system ( t 0 = 1 ) . When written in the usual units with present time τ 0 , based on (27) the modified Newton’s equation (29) is then [6,7]:
d 2 r → d τ 2 = − G M ( τ 0 ) r 2 r → r + ψ 0 τ 0 d r → d τ .
By considering the scale-invariant ratio of the correction term κ 0 υ to the usual Newtonian term in (29), one has:
x = κ 0 υ r 2 G M = H 0 ξ υ r 2 G M = H 0 ξ ( r g obs ) 1 / 2 g bar ∼ g obs − g bar g bar ,
Upon utilizing an explicit scale invariance, by considering ratios, for canceling the proportionality factor, we obtain:
g obs − g bar g bar 2 ÷ g obs − g bar g bar 1 = g obs , 2 g obs , 1 1 / 2 g bar , 1 g bar , 2 ,
by setting g = g obs , 2 , g N = g bar , 2 , and with k = k ( 1 ) containing all the system-1 terms, one finally obtains (28):
g g N − 1 = k ( 1 ) g 1 / 2 g N ⇒ g = g N + k 2 2 ± 1 2 4 g N k 2 + k 4 .
As it was noticed already, g N ≫ k 2 : g → g N but for g N → 0 ⇒ g → k 2 for the `+’ branch, while the `−’ branch gives g → 0 .

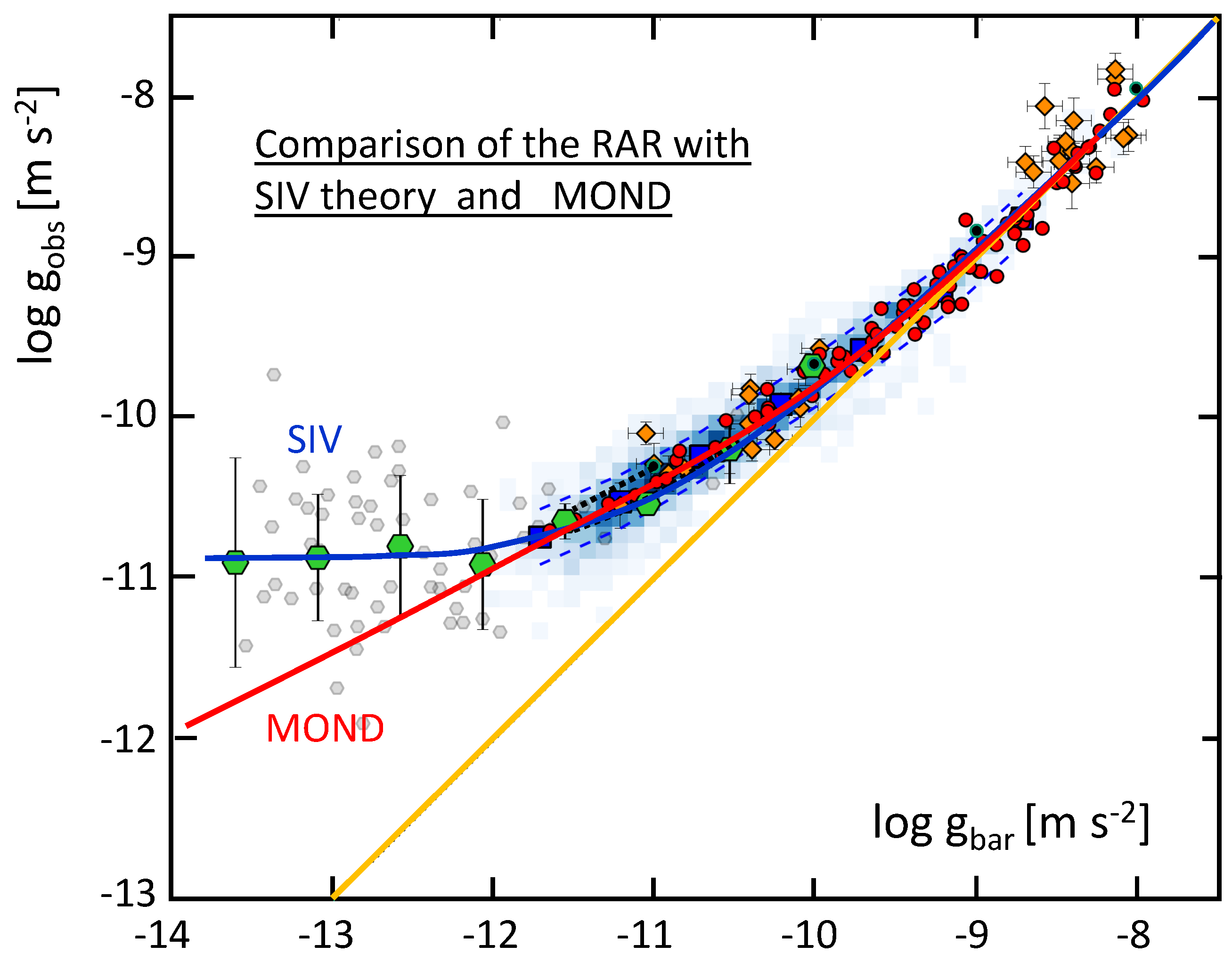
3.4. MOND as a peculiar case of the SIV theory [6]

The weak field limit of SIV tends to MOND, when the scale factor is taken as constant, an approximation valid ( < 1 % ) over the last 400 Myr. A better understanding of the MOND a 0 -parameter in g obs = a 0 g N could be obtained within the SIV where it corresponds to the equilibrium point of the Newtonian and SIV dynamical acceleration [6]; as such, the parameter a 0 is not a universal constant, it depends on the density and age of the Universe.
In order to see the correspondence one looks at x ξ = H 0 υ r 2 G M (31) in terms of densities: first consider the mass M spherically distributed in a radius r with a mean density ϱ = 3 M / ( 4 π r 3 ) , then use ϱ c = 3 H 0 2 8 π G ⇒ H 0 = 8 π G ρ c / 3 , along with the instantaneous radial accelerator relation υ 2 r = G M r 2 ⇒ υ = G M / r , to arrive at the expression x ξ = 2 ρ c / ρ . Since Newtonian gravity for a density ρ is g N = ( 4 / 3 ) π G ϱ r this translates into x ξ = 2 g c / g N . Then one can write (30) as
g = g N + x g N → x g N = 2 ξ g c g N 1 / 2 g N = 1 ξ 2 g c g N .
Therefore, one has the correspondence a 0 ⟺ 2 g c / ξ 2 , where ξ = H 0 / κ 0 . Thus, by using the SIV-time scale t, where κ 0 ( t ) = 1 / t due to (15), along with (20), one has ξ = 2 / ( 1 − Ω m ) which finally gives:
a 0 ⟺ ( 1 − Ω m ) 2 2 g c .
One may express the limiting value g c in term of the critical density over the radius r H 0 of the Hubble sphere. Thus, r H 0 is defined via n c = r H 0 H 0 where n depends on the cosmological model. For the EdS model n = 2 , while for SIV or Λ CDM models with Ω m = 0.2 − 0.3 , the initial braking and recent acceleration almost compensate each other, so that n ≃ 1 . By using the expression for H 0 (25) one finally obtains:
a 0 = ( 1 − Ω m ) 2 2 4 π 3 G ϱ c r H 0 = ( 1 − Ω m ) 2 4 n c H 0 = n c ( 1 − Ω m ) ( 1 − Ω m 1 / 3 ) 2 τ 0 .
Thus, the deep-MOND limit is found [6] to be an approximation of the SIV theory for low enough densities and for systems with timescales smaller than a few Myr where λ can be viewed as if it is a constant.
The product c H 0 is equal to 6.80 · 10 − 8 cm s−2. For Ω m =0, 0.10, 0.20, 0.30 and 0.50, one has a 0 ≈ (1.70, 1.36, 1.09, 0.83, 0.43) · 10 − 8 cm s−2 respectively. These values obtained from the SIV theory are remarkably close to the value a 0 about 1.2 · 10 − 8 cm s−2 derived from observations by Milgrom [32].
Thus, as it comes out for the more general SIV theory, there are several remarks to be made on the a 0 -parameter and its meaning:
  • The equation of the deep-MOND limit is reproduced by the SIV theory both analytically and numerically if λ and M can be considered as constant. This may apply to systems with a typical dynamical timescale up to a few hundred million years.
  • Parameter a 0 is not a universal constant. It depends on the Hubble-Lemaître H 0 parameter (or the age of the Universe) and on Ω m in the model Universe, cf. Eq. (35). The value of a 0 applies to the present epoch.
  • Parameter a 0 is defined by the condition that x > 1 , i.e. when the dynamical gravity κ 0 υ = ( ψ 0 υ ) / τ 0 in the equation of motion (30) becomes larger than the Newtonian gravity. This situation occurs in regions at the edge of gravitational systems.

3.5. Local dynamical effects within SIV: the lunar recession [7]

We have already pointed out that scale invariance is expected in empty Universe models, while the presence of matter tends to suppress it. Scale invariance is certainly absent in cosmological models with densities equal to or above the critical value ϱ c = 3 H 0 2 / ( 8 π G ) [2]. Clearly, the presence of matter tends to kill scale invariance as shown by [33]. For models with densities below ϱ c , the possibility of limited effects remains open. If present, scale invariance would be a global cosmological property. Some traces could be observable locally. For the Earth-Moon two-body system, the predicted additional lunar recession would be increased by 0.92 cm/yr, while the tidal interaction would also be slightly increased [7].
The Earth-Moon distance is the most systematically measured distance in the Solar System, thanks to the Lunar Laser Ranging (LLR) experiment active since 1970. The observed lunar recession from LLR amounts to 3.83 ( ± 0.009 ) cm/yr; implying a tidal change of the length-of-the-day (LOD) by 2.395 ms/cy [34,35]. The value of the lunar recession has not much changed since the first determination more than three decades ago [36], which illustrates the quality of the measurements. However, the observed change of the LOD since the Babylonian Antiquity is only 1.78 ms/cy [37], a result supported by paleontological data Deines and Williams [38], and implying a lunar recession of 2.85 cm/yr. The best and longest studies on the change of the LOD in History have been performed by Stephenson et al. [37], who analyzed the lunar and solar eclipses from 720 BC up to 1600 AD and found an average shift of the LOD by 1.78 (± 0.03) ms/cy. The reality of the difference between the above observed mean value of the LOD (1.78 ms/cy) and the value due to the tidal interaction (2.395 ms/cy) has been further emphasized by Stephenson et al. [39].
The significant difference of (3.83-2.85) cm/yr = 0.98 cm/yr, already pointed out by several authors over the last two decades [40,41], corresponds well to the predictions of the scale-invariant theory, which is also supported by several other astrophysical tests [7].
By using the correct treatment of the Earth-Moon tidal interaction within the SIV theory one derives an additional terms in the equation describing the lunar recession in current time units [7]:
d R d τ = k E d T E d τ − k E ψ 0 T E τ 0 + ψ 0 R τ 0 .
In a cosmological model with Ω m = 0.30 , the ratio ψ 0 = ( t 0 − t in ) t 0 = 0.331 (27). We use the following numerical values of the relevant astronomical quantities:
M E = 5.973 · 10 27 g , R E = 6.371 · 10 8 cm , M M = 7.342 · 10 25 g , R = 3.844 · 10 10 cm , I E = 0.331 · M E R E 2 = 8.0184 · 10 44 g · cm 2 .
The value 0.331 is obtained from precession data [42]. The coefficient k E is estimated to be 1.60 · 10 5 cm · s−1 [7,43].
Let us evaluate numerically the various contributions. With the LOD of 1.78 ms/cy from the antique data by [37], the first term contributes to a lunar recession of 2.85 cm/yr. The second term in (36) gives for the case of Ω m = 0.3 ,
0.33 · k E T E τ 0 = 0.33 · 1.60 · 10 5 c m · s − 1 86400 s 13.8 · 10 9 y r = 0.33 cm yr .
The direct SIV expansion effect κ 0 R = ψ 0 R / τ 0 is
0.33 · R τ 0 = 0.33 · 3.844 · 10 10 c m 13.8 · 10 9 y r = 0.92 cm yr .
This term corresponds to a third of the general Hubble-Lemaitre expansion. Summing the various contributions, we get the historical data value [37]:
d R d τ = ( 2.85 − 0.33 + 0.92 ) cm / yr = 3.44 cm / yr .
Thus, we see that the scale invariant analysis is giving a relatively good agreement with the lunar recession of 3.83 cm/yr obtained from LLR observations. The difference amounts only to 10 % of the observed lunar recession.
The difference in the lunar recession is well accounted for within the dynamics of the SIV theory (40). A minima, the above results shows that the problem of scale invariance is worth of some attention within the solar system as well.

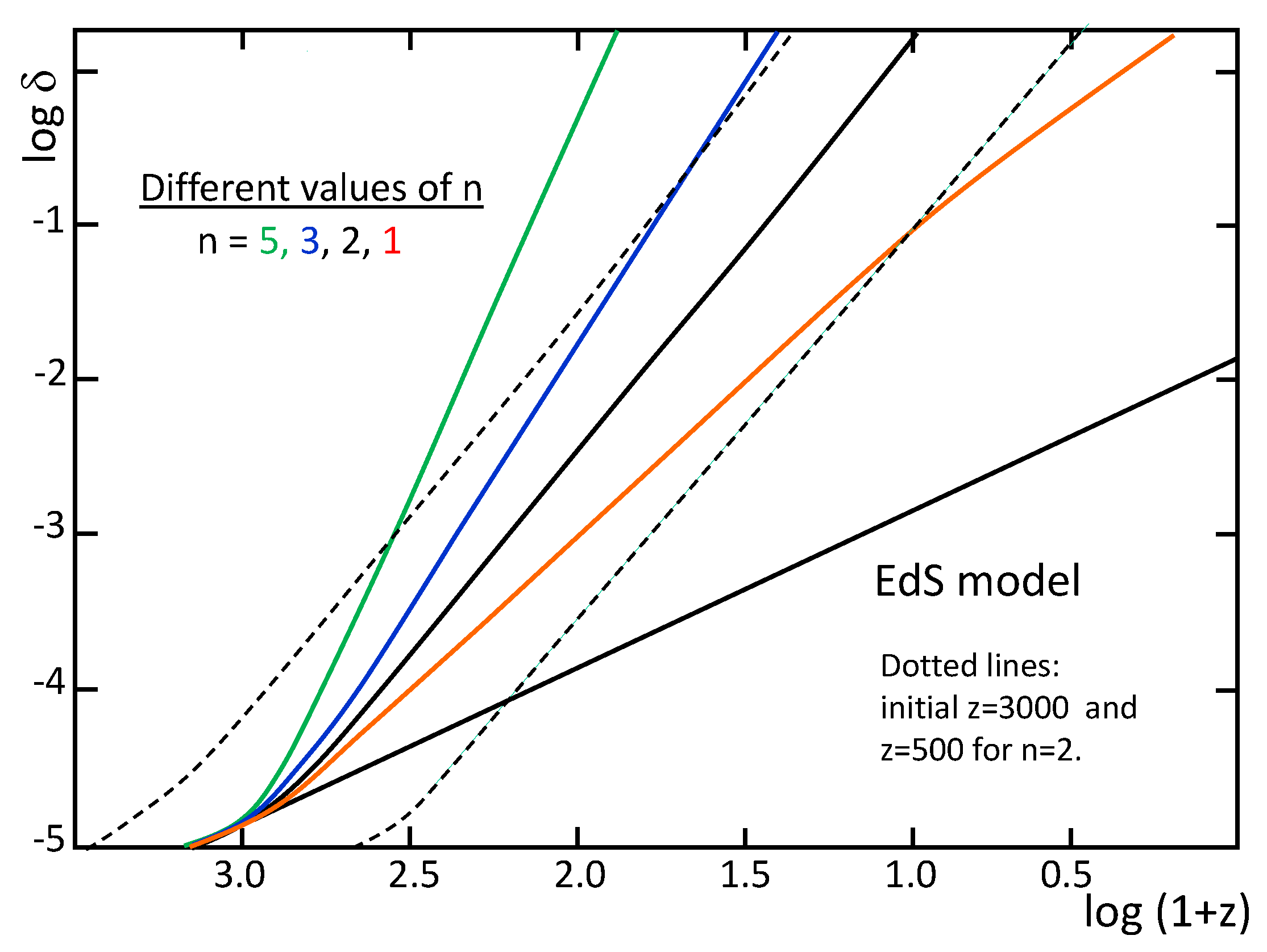
3.6. Growth of the Density Fluctuations within the SIV [4]

Another interesting result was the possibility of a fast growth of the density fluctuations within the SIV [4]. This study modifies appropriately the relevant equations such as the continuity equation, Poisson equation, and Euler equation within the SIV framework. Here, we outline the main equations and the relevant results. By using the notation κ = κ 0 = − λ ˙ / λ = 1 / t , the corresponding Continuity, Poisson, and Euler equations are:
∂ ρ ∂ t + ∇ → · ( ρ v → ) = κ ρ + r → · ∇ → ρ , ∇ → 2 Φ = ▵ Φ = 4 π G ϱ , d v → d t = ∂ v → ∂ t + v → · ∇ → v → = − ∇ → Φ − 1 ρ ∇ → p + κ v → .
For a density perturbation ϱ ( x → , t ) = ϱ b ( t ) ( 1 + δ ( x → , t ) ) the above equations result in:
δ ˙ + ∇ → · x → ˙ = κ x → · ∇ → δ = n κ ( t ) δ , ∇ → 2 Ψ = 4 π G a 2 ϱ b δ ,
x → ¨ + 2 H x → ˙ + ( x → ˙ · ∇ → ) x → ˙ = − ∇ → Ψ a 2 + κ ( t ) x → ˙ .
⇒ δ ¨ + ( 2 H − ( 1 + n ) κ ) δ ˙ = 4 π G ϱ b δ + 2 n κ ( H − κ ) δ .
The final result (43) recovers the standard equation in the limit of κ → 0 . The simplifying assumption x → · ∇ → δ ( x ) = n δ ( x ) in (41) introduces the parameter n that measures the perturbation type (shape). For example, a spherically symmetric perturbation would have n = 2 . As seen in Figure 6, perturbations for various values of n are resulting in faster growth of the density fluctuations within the SIV than in the Einstein–de Sitter model, even at relatively law matter densities. Furthermore, the overall slope is independent of the choice of recombination epoch z rec . The behavior for different Ω m is also interesting (see Figure 7), for example, the smaller Ω m is - the steeper the growth of the density fluctuations is. It is always much steeper then the Einstein-de Sitter model. For further details see the discussion by Maeder and Gueorguiev [4].
Over the recent years highly redshifted galaxies have been found, in particular with the observational data from JWST, which is suggesting very early times of galaxy formation [44]. We point out, as shown by Figure 6 , that very early galaxy formation is a process currently expected in the context of the SIV theory.

3.7. Big-Bang Nucleosynthesis within the SIV Paradigm [3]

The SIV paradigm has been recently applied to the Big-Bang Nucleosynthesis using the known analytic expressions for the expansion factor a ( t ) and the plasma temperature T as functions of the SIV time τ since the Big-Bang when a ( τ = 0 ) = 0 [3]. The results have been compared to the standard BBNS as calculated via the PRIMAT code [45]. Potential SIV-guided deviations from the local statistical equilibrium were also explored in [3]. Overall, it was found that smaller than usual baryon and non-zero dark matter content, by a factor of three to five times reduction, result in compatible to the standard light elements abundances (Table 2).
The SIV analytic expressions for a ( T ) and τ ( T ) were utilized to study the BBNS within the SIV paradigm [3,28]. The functional behavior is very similar to the standard model within PRIMAT except during the very early Universe where electron-positron annihilation and neutrino processes affect the a ( T ) function (see Table I and Figure 2 in [3]). The distortion due to these effects encoded in the function S ( T ) could be incorporated by considering the SIV paradigm as a background state of the Universe where these processes could take place. It has been demonstrated that incorporation of the S ( T ) within the SIV paradigm results in a compatible outcome with the standard BBNS see the last two columns of Table 2; furthermore, if one is to fit the observational data the result is λ ≈ 1 for the SIV parameter λ (see last column of Table 2 with λ = FRF ≈ 1 ). However, a pure SIV treatment (the middle three columns) results in Ω b ≈ 1 % and less total matter, either around Ω m ≈ 23 % when all the λ -scaling connections are utilized (see Table 2 column 6), or around Ω m ≈ 6 % without any λ -scaling factors (see column 5). The need to have λ close to 1 is not an indicator of dark matter content but indicates the goodness of the standard PRIMAT results that allows only for λ close to 1 as an augmentation, as such this leads to a light but important improvement in D/H as seen when comparing columns three with eight and nine.
The SIV paradigm suggests specific modifications to the reaction rates, as well as the functional temperature dependences of these rates, that need to be implemented to have consistence between the Einstein GR frame and the WIG (SIV) frame. In particular, the non-in-scalar factor T β in the reverse reactions rates may be affected the most due to the SIV effects. As shown in [3], the specific dependences studied, within the assumptions made within the SIV model, resulted in three times less baryon matter, usually around Ω b ≈ 1.6 % and less total matter - around Ω m ≈ 6 % . The lower baryon matter content leads to also a lower photon to baryon ratio η 10 ≈ 2 within the SIV, which is three tines less that the standard value of η 10 = 6.09 . As shown in [3], the overall results indicated insensitivity to the specific λ -scaling dependence of the mŤ-factor in the reverse reaction expressions within T β terms. Thus, one may have to explore further the SIV-guided λ -scaling relations as done for the last column in Table 2, however, this would require the utilization of the numerical methods used by PRIMAT and as such will take us away from the SIV-analytic expressions explored that provided a simple model for understanding the BBNS within the SIV paradigm. Furthermore, it will take us further away from the accepted local statistical equilibrium and may require the application of the reparametrization paradigm that seems to result in SIV like equations but does not impose a specific form for λ [1]. Thus, at this point the SIV theory is still a viable alternative model for cosmology.

3.8. SIV and the Inflation of the Early Universe [2]

Another important result within the SIV paradigm is the presence of inflationary stage at the very early Universe t ≈ t in ≪ t 0 = 1 with a natural exit from inflation in a later time t exit with value related to the parameters of the inflationary potential [2]. The main steps towards these results are outlined below.
If we go back to the general scale-invariant cosmology Equation (9), we can identify a vacuum energy density expression that relates the Einstein cosmological constant with the energy density as expressed in terms of κ = − λ ˙ / λ by using the SIV result (14). The corresponding vacuum energy density ρ , with C = 3 / ( 4 π G ) , is then:
ρ = Λ 8 π G = λ 2 ρ ′ = λ 2 Λ E 8 π G = 3 8 π G λ ˙ 2 λ 2 = C 2 ψ ˙ 2 .
This provides a natural connection to inflation within the SIV via ψ ˙ = − λ ˙ / λ or ψ ∝ ln ( t ) . The equations for the energy density, pressure, and Weinberg’s condition for inflation within the standard model for inflation by Guth [46], Linde [47,48], Weinberg [49] are:
ρ p = 1 2 φ ˙ 2 ± V ( φ ) , ∣ H ˙ infl ∣ ≪ H infl 2 .
If we make the identification between the standard model for inflation above with the fields present within the SIV (using C = 3 / ( 4 π G ) ):
ψ ˙ = − λ ˙ / λ , φ ↔ C ψ , V ↔ C U ( ψ ) , U ( ψ ) = g e μ ψ .
Here, U ( ψ ) is the inflation potential with strength g and field “coupling” μ . One can evaluate the Weinberg’s condition for inflation (45) within the SIV framework [2], and the result is:
∣ H ˙ infl ∣ H infl 2 = 3 ( μ + 1 ) g ( μ + 2 ) t − μ − 2 ≪ 1 f o r μ < − 2 , a n d t ≪ t 0 = 1 .
When the Weinberg’s condition for inflation (45) is not satisfied anymore, one can see that there is a graceful exit from inflation at the later time:
t exit ≈ n g 3 ( n + 1 ) n with n = − μ − 2 > 0 .
The derivation of the equation (47) starts with the use of the scale invariant energy conservation equation within SIV [2,9]:
d ( ϱ a 3 ) d a + 3 p a 2 + ( ϱ + 3 p ) a 3 λ d λ d a = 0 ,
which has the following equivalent form:
ϱ ˙ + 3 a ˙ a ( ϱ + p ) + λ ˙ λ ( ϱ + 3 p ) = 0 .
By substituting the expressions for ρ and p from (45) along with the SIV identification (46) within the SIV expression (50), one obtains modified form of the Klein–Gordon equation, which could be non-linear when using non-linear potential U ( ψ ) as in (46):
ψ ¨ + U ′ + 3 H infl ψ ˙ − 2 ( ψ ˙ 2 − U ) = 0 .
The above Equation (51) can be used to evaluate the time derivative of the Hubble parameter. The process is utilizing (14); that is, λ = t 0 / t , ψ ˙ = − λ ˙ / λ = 1 / t ⇒ ψ ¨ = − ψ ˙ 2 along with ψ = ln ( t ) + c o n s t and U ( ψ ) = g e μ ψ = g t μ when the normalization of the field ψ is chosen so that ψ ( t 0 ) = ln ( t 0 ) = 0 for t 0 = 1 at the current epoch. The final result is:
H infl = ψ ˙ − 2 U 3 ψ ˙ − U ′ 3 ψ ˙ = 1 t − ( 2 + μ ) g 3 t μ + 1 ,
H ˙ infl = − ψ ˙ 2 − 2 U 3 − U ′ − U ′ ′ 3 = − 1 t 2 − ( μ + 2 ) ( μ + 1 ) g 3 t μ .
For μ < − 2 the t μ terms above are dominant; thus, the critical ratio (45) for the occurrence of inflation near t ≈ t in is then:
∣ H ˙ infl ∣ H infl 2 = 3 ( μ + 1 ) g ( μ + 2 ) t − μ − 2 .
Based on (44), both ϱ and Λ (in the scale invariant space) behave like 1 / t 2 according to expression (15) based on the field equation of the vacuum. This implies that the energy density of the vacuum, and the cosmological constant Λ , in the scale invariant space become very large near the origin. For example, at the Planck time t Pl = 5.39 · 10 − 44 s, dominated by quantum effects, the cosmological constant would be a factor 4.355 · 10 17 5.39 · 10 − 44 2 = 6.4 · 10 121 larger than the value at the present cosmic age τ 0 = 13.7 Gyr = 4.323 · 10 17 s. Thus, as such this may solve the so-called cosmological problem by viewing the Planck-seed universes and the derivable universes as different stages of the same Universe rather than a disconnected universe [26]. In other words, the smallness of the Einstein cosmological constant Λ E is naturally related to the current age of the Universe, assuming that now λ = 1 by choice of units, because the solution (15) for (14) implies Λ E = 3 / τ 0 2 ≈ 1.6 × 10 − 35 s − 2 .

4. Conclusions and Outlook

The SIV hypothesis is a relatively new theory, and it is still under development. However, the results of the tests that have been conducted so far are promising. If the SIV hypothesis is correct, it could provide a new and important understanding of the universe.
From the results summarized in the previous section on various comparisons and potential further applications, we see that the SIV cosmology is a viable alternative to Λ CDM. In particular, within the SIV gauge (16) the cosmological constant disappears. There are diminishing differences in the values of the scale factor a ( t ) within Λ CDM and SIV at higher densities as emphasized in the discussion of (Figure 1) [9,10]. The SIV also shows consistency for H 0 and the age of the Universe, and the m-z diagram is well satisfied—see Maeder and Gueorguiev [10] for details.
Furthermore, the SIV provides the correct RAR for dwarf spheroidals (Figure 5) while MOND is failing, and dark matter cannot account for the phenomenon [5]. Therefore, it seems that within the SIV, dark matter is not needed to seed the growth of structure in the Universe, as there is a fast enough growth of the density fluctuations as seen in (Figure 6) and discussed in more detail by Maeder and Gueorguiev [4].
In our previous studies on the inflation within the SIV cosmology [2], we have identified a connection of the scale factor λ , and its rate of change, with the inflation field ψ → φ , ψ ˙ = − λ ˙ / λ (46). As seen from (47), inflation of the very-very early Universe, τ ≈ 0 ( t ≈ t in < < 1 ) , is natural, and SIV predicts a graceful exit from inflation (see (48))!
Our latest study on the primordial nucleosynthesis within the SIV [3] has shown that smaller than usual baryon and non-zero dark matter content, by a factor of three to five times reduction, result in compatible to the standard light elements abundances (Table 2).
Some of the obvious future research directions are related to the primordial nucleosynthesis, where preliminary results show a satisfactory comparison between SIV and observations [3,28]. Further investigations of potential SIV-guided deviations from the local statistical equilibrium should be studied since this may lead to mechanisms for understanding the matter-anti-matter asymmetry. The recent success of the R-MOND in the description of the CMB [50], after the initial hope and concerns [51], is very stimulating; it suggests that a generally covariant theory that has the correct Newtonian limit is likely to describe the CMB; Since SIV is generally covariant and has the correct limits, it demands testing the SIV cosmology as well against the MOND and Λ CDM successes in the description of the CMB, the Baryonic Acoustic Oscillations, etc.
Another important direction is the need to understand the physical meaning and interpretation of the conformal factor λ . As we pointed out in Section 1.2, a general conformal factor λ ( x ) seems to be linked to Jordan–Brans–Dicke scalar-tensor theory that leads to a varying Newton’s constant G, which has not been detected to date. Furthermore, a spacial dependence of λ ( x ) opens the door to local field excitations that should manifest as some type of fundamental scalar particles. The Higgs boson is such a particle, but a connection to Jordan–Brans–Dicke scalar-tensor theory seems a far fetched idea. On the other hand, the assumption of isotropy and homogeneity of space forces λ ( t ) to depend only on time, which is not in any sense similar to the usual fundamental fields we are familiar with.
In this respect, other less obvious research directions are related to the exploration of SIV within the solar system due to the high-accuracy data available, or exploring further and in more detail the possible connection of SIV with the re-parametrization invariance. For example, it is already known by Gueorguiev and Maeder [1] that un-proper time parametrization can lead to a SIV-like equation of motion (5) and the relevant weak-field version (29).

Author Contributions

Writing – original draft VG, Conceptualization - both authors; Formal analysis - both authors; Investigation - both authors; Methodology - both authors; Validation - both authors; Writing – review & editing - both authors; Both co-authors have been actively involved in the writing of the paper and its draft versions. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Data Availability Statement

No new data were created or analyzed in this study.

Acknowledgments

A.M. expresses his gratitude to his wife for her patience and support. V.G. is extremely grateful to his wife and daughters for their understanding and family support during the various stages of the research presented. This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Gueorguiev, V.G.; Maeder, A. Geometric Justification of the Fundamental Interaction Fields for the Classical Long-Range Forces. Symmetry 2021, 13, 379. [Google Scholar] [CrossRef]
  2. Maeder, A.; Gueorguiev, V.G. Scale invariance, horizons, and inflation. MNRAS 2021, 504, 4005. [Google Scholar] [CrossRef]
  3. Gueorguiev, V.G. and Maeder, A. “Big-Bang Nucleosynthesis within the Scale Invariant Vacuum Paradigm” under peer review (April 2023); arXiv e-Print: 2307.04269 [nucl-th].
  4. Maeder, A.; Gueorguiev, V.G. The growth of the density fluctuations in the scale-invariant vacuum theory. Phys. Dark Univ. 2019, 25, 100315. [Google Scholar] [CrossRef]
  5. Maeder, A.; Gueorguiev, V.G. Scale-invariant dynamics of galaxies, MOND, dark matter, and the dwarf spheroidals. MNRAS 2019, 492, 2698. [Google Scholar] [CrossRef]
  6. Andre Maeder, “MOND as a peculiar case of the SIV theory”. MNRAS 2023, 520, 1447. [CrossRef]
  7. Maeder, A., Gueorguiev, V. (2022). Local Dynamical Effects of Scale Invariance: the Lunar Recession. Conference Contribution to Cosmology on Small Scales (CSS2022); arXiv e-prints. [CrossRef]
  8. Gueorguiev, V. G., and Maeder, A. The Scale Invariant Vacuum Paradigm: Main Results and Current Progress. Universe 2022, 8, 213, e-Print: 2202.08412 [gr-qc]. [CrossRef]
  9. Maeder, A. An Alternative to the LambdaCDM Model: the case of scale invariance. Astrophys. J. 2017, 834, 194. [Google Scholar] [CrossRef]
  10. Maeder, A.; Gueorguiev, V.G. The Scale-Invariant Vacuum (SIV) Theory: A Possible Origin of Dark Matter and Dark Energy. Universe 2020, 6, 46. [Google Scholar] [CrossRef]
  11. Weyl, H. Raum, Zeit, Materie; Vorlesungen über Allgemeine Relativitätstheorie; Springer-Verlag: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
  12. Carl, H. Brans Jordan-Brans-Dicke Theory. Scholarpedia 2014, 9, 31358. [Google Scholar]
  13. Faraoni, V.; Gunzig, E.; Nardone, P. Conformal transformations in classical gravitational theories and in cosmology. Fundam. Cosm. Phys. 1999, 20, 121–175. [Google Scholar]
  14. Behnke, D., Blaschke, D. B., Pervushin, V. N., Proskurin, D. Description of supernova data in conformal cosmology without cosmological constant. Phys. Lett. B 2002, 530, 20–26. [CrossRef]
  15. Christodoulou, D. M., Kazanas, D. Varying-G gravity. MNRAS 2023, 519, 1277–1292.
  16. Xue, C.; Liu, J.P.; Li, Q.; Wu, J.F.; Yang, S.Q.; Liu, Q.; Shao, C., Tu, L., Hu, Z., Luo, J. Precision measurement of the Newtonian gravitational constant. Natl. Sci. Rev. 2020, 7, 1803.
  17. Dirac, P.A.M. Long Range Forces and Broken Symmetries. Proc. R. Soc. Lond. A 1973, 333, 403. [Google Scholar]
  18. Canuto, V.; Adams, P.J.; Hsieh, S.-H.; Tsiang, E. Scale-covariant theory of gravitation and astrophysical applications. Phys. Rev. D 1977, 16, 1643. [Google Scholar] [CrossRef]
  19. Gueorguiev, V. G. , Maeder, A. 2021. Reparametrization Invariance and Some of the Key Properties of Physical Systems. Symmetry 2021, 13, 522, e-Print:1903.02483. [Google Scholar] [CrossRef]
  20. Wheeler, J.T. Weyl geometry. Gen. Relativ. Gravit. 2018, 50, 80. [Google Scholar] [CrossRef]
  21. Zakharov, A. F., Pervushin, V. N. Conformal Cosmological Model Parameters with Distant SNe Ia Data:. “gold” and “silver”. Int. J. Mod. Phys. D 2010, 19, 1875–1887. [CrossRef]
  22. Pervushin, V. N., Arbuzov, A. B., Zakharov, A. F. Estimation of conformal cosmological model parameters with SDSS and SNLS supernova samples. Phys. Part. Nuc. Lett. 2017, 14, 368–370. [CrossRef]
  23. Maeder, A.; Gueorguiev, V.G. Action Principle for Scale Invariance and Applications (Part I). Symmetry 2023, 15(11), 1966. [Google Scholar] [CrossRef]
  24. Maeder, A.; Bouvier, P. Scale invariance, metrical connection and the motions of astronomical bodies. Astron. Astrophys. 1979, 73, 82–89. [Google Scholar]
  25. Bouvier, P.; Maeder, A. Consistency of Weyl’s Geometry as a Framework for Gravitation. Astrophys. Space Sci. 1978, 54, 497. [Google Scholar] [CrossRef]
  26. Gueorguiev, V.; Maeder, A. Revisiting the Cosmological Constant Problem within Quantum Cosmology. Universe 2020, 5, 108. [Google Scholar] [CrossRef]
  27. Jesus, J.F. Exact solution for flat scale-invariant cosmology, Rev. Mex. Astron. Astrophys. 55, 17 (2018). ArXiV: 1712.00697.
  28. Maeder, A. “Evolution of the early Universe in the scale invariant theory. arXiv 2019, arXiv:1902.10115. [Google Scholar]
  29. Frieman, J. A., Turner, M. S., & Huterer, D. ARA&A, 46, 385 (2008).
  30. Lusso, E. et al. Astron. Astrophys. 2019, 628, L4.
  31. Liske, J. et al. MNRAS 2008, 386, 1192.
  32. Milgrom, M. 2015, Phys. Rev. D. 91, 044009.
  33. Feynman, R. P. Mainly mechanics, radiation, and heat. Feynman lectures on physics, 1(1963).
  34. Williams, J.G., Boggs, D.H., Ratcliff, J.T.: Lunar Tidal Recession. 47th Lunar and Planetary Science Conference (2016a), 1096–1100.
  35. Williams, J.G., Boggs, D.H.: Secular tidal changes in lunar orbit and Earth rotation. Celestial Mechanics and Dynamical Astron 2016, 126, 89–129. [CrossRef]
  36. Christodoulidis, D. C., Smith, D. E., Williamson, R. G. et al.: Observed Tidal Braking in the Earth/moon/sun System. J. Geophys. Res. 93(B6) (1988), 6216–6236.
  37. Stephenson, F.R., Morrison, L.V., Hohenkerk, C.Y.: Measurement of the Earth’s rotation: 720 BC to AD 2015. Proc. R. Soc. A472 (2016), 404–430.
  38. Deines, S.D., Williams, C.A.: Earth’s rotational deceleration: determination of tidal friction independent of timescales. Astron.Journal. 151 (2016), 103–114.
  39. Stephenson, F.R., Morrison, L.V., Hohenkerk, C.Y.: Eclipses and the Earth’s Rotation General Assembly, Proceedings of the IAU IAU XXX (2020), 160–162.
  40. McCarthy, D.D., Babcock, A.: The length of day since 1656. Physics of the Earth and Planetary Interiors. 44 (1986), 281–292.
  41. Sidorenkov, N.S.: The effect of the El Nino Southern oscillation on the excitation of the Chandler motion of the Earth’s pole. Astron. Reports (in Russian) 41 (1997), 705–708.
  42. Williams, J.G.: Contribution to the Earth’s Obliquity Rate, Precession, and Nutation Astron. J. 108 (1994), 71.
  43. Maeder, A. M., Gueorguiev, V. G. On the relation of the lunar recession and the length-of-the-day. Astrophys Space Sci 366, 101 (2021).
  44. Bunker, A. J. and 61 colleagues (2023) JADES NIRSpec Spectroscopy of GN-z11: Lyman-α emission and possible enhanced nitrogen abundance in a z=10.60 luminous galaxy. arXiv e-prints. [CrossRef]
  45. Pitrou, C., Coc, A., Uzan, J.-P., Vangioni, E. “Precision big bang nucleosynthesis with improved Helium-4 predictions.” Physics Reports 754, 1–66 (2018). ArXiV: 1801.08023.
  46. Guth, A. Inflationary universe: A possible solution to the horizon and flatness problems. Phys. Rev. D 1981, 23, 347. [Google Scholar] [CrossRef]
  47. Linde, A. D. Lectures on Inflationary Cosmology in Particle Physics and Cosmology. In Proceedings of the Ninth Lake Louise Winter Institute, 20-26 February 1994. Lake Louise, Alberta, Canada. Lect. Notes Phys.1995,455, pp363-372.
  48. Linde, A. Particle Physics and Inflationary Universe. Contemp. Concepts Phys. 2005, 5, pp1–362. [Google Scholar]
  49. Weinberg, S. Cosmology; Oxford Univ. Press: Oxford, UK, 2008; p. 593. [Google Scholar]
  50. Skordis, C.; Złośnik, T. New Relativistic Theory for Modified Newtonian Dynamics. Phys. Rev. Lett. 2021, 2021 127, 1302. [Google Scholar] [CrossRef]
  51. Skordis, C.; Mota, D.F.; Ferreira, P.G.; Boehm, C. Large Scale Structure in Bekenstein’s Theory of Relativistic Modified Newtonian Dynamics. Phys. Rev. Lett. 2006, 96, 11301. [Google Scholar] [CrossRef]
Preprints 91563 g001
Figure 1. Expansion rates a ( t ) as a function of time t in the flat ( k = 0 ) Λ CDM and SIV models in the matter dominated era. The curves are labeled by the values of Ω m ; here Ω m = ϱ / ϱ c with ϱ c = 3 H 0 2 / ( 8 π G ) . Drawing originally published in [9].
Figure 1. Expansion rates a ( t ) as a function of time t in the flat ( k = 0 ) Λ CDM and SIV models in the matter dominated era. The curves are labeled by the values of Ω m ; here Ω m = ϱ / ϱ c with ϱ c = 3 H 0 2 / ( 8 π G ) . Drawing originally published in [9].
Preprints 91563 g001
Preprints 91563 g002
Figure 2. The angular diameter distance d A vs. redshift z for flat scale invariant models (continuous red lines) compared to flat Λ CDM models (broken blue lines). The curves are given for Ω m = 0 , 0.1 , 0.3 , 0.99 , from the upper to the lower curve in both cases (at z > 3 ). Original figure from Maeder [9].
Figure 2. The angular diameter distance d A vs. redshift z for flat scale invariant models (continuous red lines) compared to flat Λ CDM models (broken blue lines). The curves are given for Ω m = 0 , 0.1 , 0.3 , 0.99 , from the upper to the lower curve in both cases (at z > 3 ). Original figure from Maeder [9].
Preprints 91563 g002
Preprints 91563 g004
Figure 4. The drifts of redshifts d z / d t as a function of redshift in the scale invariant theory (red curves). The values of Ω m (usual definition) are indicated. The black broken lines give the results for some standard models of different couples ( Ω Λ , Ω m ) by Liske et al. [31]. Drawing originally published in [10].
Figure 4. The drifts of redshifts d z / d t as a function of redshift in the scale invariant theory (red curves). The values of Ω m (usual definition) are indicated. The black broken lines give the results for some standard models of different couples ( Ω Λ , Ω m ) by Liske et al. [31]. Drawing originally published in [10].
Preprints 91563 g004
Preprints 91563 g005
Figure 5. Radial Acceleration Relation (RAR) for the galaxies studied by Lelli et al. (2017). Dwarf Spheroidals as binned data (big green hexagons), along with MOND (red curve), and SIV (blue curve) model predictions. The orange curve shows the 1:1-line for g obs and g bar . Due to the smallness of g obs and g bar the application of the log function results in negative numbers; thus, the corresponding axes’ values are all negative. Drawing originally published in [5].
Figure 5. Radial Acceleration Relation (RAR) for the galaxies studied by Lelli et al. (2017). Dwarf Spheroidals as binned data (big green hexagons), along with MOND (red curve), and SIV (blue curve) model predictions. The orange curve shows the 1:1-line for g obs and g bar . Due to the smallness of g obs and g bar the application of the log function results in negative numbers; thus, the corresponding axes’ values are all negative. Drawing originally published in [5].
Preprints 91563 g005
Preprints 91563 g006
Figure 6. The growth of density fluctuations for different values of parameter n (the gradient of the density distribution in the nascent cluster), for an initial value δ = 10 − 5 at z = 1376 and Ω m = 0.10 . The initial slopes are those of the EdS models. The two light broken curves show models with initial ( z + 1 ) = 3000 and 500, with same Ω m = 0.10 and n = 2 . These dashed lines are to be compared to the black continuous line of the n = 2 model. All the three lines for n = 2 are very similar and nearly parallel. Due to to the smallness of δ the application of the log function results in negative numbers; thus, the corresponding vertical axes values are all negative. Drawing originally published in [4].
Figure 6. The growth of density fluctuations for different values of parameter n (the gradient of the density distribution in the nascent cluster), for an initial value δ = 10 − 5 at z = 1376 and Ω m = 0.10 . The initial slopes are those of the EdS models. The two light broken curves show models with initial ( z + 1 ) = 3000 and 500, with same Ω m = 0.10 and n = 2 . These dashed lines are to be compared to the black continuous line of the n = 2 model. All the three lines for n = 2 are very similar and nearly parallel. Due to to the smallness of δ the application of the log function results in negative numbers; thus, the corresponding vertical axes values are all negative. Drawing originally published in [4].
Preprints 91563 g006
Preprints 91563 g007
Figure 7. The black curve is the classical growth of the density fluctuations in the Einstein-de Sitter model. The other four curves illustrate the growth of δ for the density profile with n = 2 in the scale-invariant theory. There are four different values of the density parameter Ω m . An initial value δ = 10 − 5 at z = 1376 has been taken for all models, the initial derivative δ ˙ is taken equal to that of the EdS model. After a short evolution with a slope close to the initial one, all solutions indicate a much faster growth of the density fluctuations, reaching the non-linear regime between about z + 1 = 2.7 and z = 18 . Drawing originally published in [4].
Figure 7. The black curve is the classical growth of the density fluctuations in the Einstein-de Sitter model. The other four curves illustrate the growth of δ for the density profile with n = 2 in the scale-invariant theory. There are four different values of the density parameter Ω m . An initial value δ = 10 − 5 at z = 1376 has been taken for all models, the initial derivative δ ˙ is taken equal to that of the EdS model. After a short evolution with a slope close to the initial one, all solutions indicate a much faster growth of the density fluctuations, reaching the non-linear regime between about z + 1 = 2.7 and z = 18 . Drawing originally published in [4].
Preprints 91563 g007
Table 1. Derivatives for co-tensors of power n.
Table 1. Derivatives for co-tensors of power n.
Co-Tensor Type Mathematical Expression
co-scalar S ∗ μ = ∂ μ S − n κ μ S ,
co-vector A ν ∗ μ = ∂ μ A ν −   ∗ Γ ν μ α A α − n κ ν A μ ,
co-covector A ∗ μ ν = ∂ μ A ν +   ∗ Γ μ α ν A α − n k ν A μ .
Table 2. The observational uncertainties are 1.6% for Y P , 1.2% for D/H, 18% for T/H, and 19% for Li/H. FRF is the forwards rescale factor for all reactions, while mŤ and Q/Ť are the corresponding rescale factors in the revers reaction formula based on the local thermodynamical equilibrium. The SIV λ -dependences are used when these factors are different from 1; that is, in the sixth and ninth columns where FRF= λ , mŤ= λ − 1 / 2 , and Q/Ť= λ + 1 / 2 . The columns denoted by fit contain the results for perfect fit on Ω b and Ω m to 4He and D/H, while fit* is the best possible fit on Ω b and Ω m to the 4He and D/H observations for the model considered as indicated in the columns four and seven. The last three columns are usual PRIMAT runs with modified a ( T ) such that a ¯ / λ = a S I V / S 1 / 3 , where a ¯ is the PRIMAT’s a ( T ) for the decoupled neutrinos case. Column seven is actually a S I V / S 1 / 3 , but it is denoted by a ¯ / λ to remind us about the relationship a ′ = a λ ; the run is based on Ω b and Ω m from column five. The smaller values of η 10 are due to smaller h 2 Ω b , as seen by noticing that η 10 / Ω b is always ≈ 1.25 . Table originally presented in [3].
Table 2. The observational uncertainties are 1.6% for Y P , 1.2% for D/H, 18% for T/H, and 19% for Li/H. FRF is the forwards rescale factor for all reactions, while mŤ and Q/Ť are the corresponding rescale factors in the revers reaction formula based on the local thermodynamical equilibrium. The SIV λ -dependences are used when these factors are different from 1; that is, in the sixth and ninth columns where FRF= λ , mŤ= λ − 1 / 2 , and Q/Ť= λ + 1 / 2 . The columns denoted by fit contain the results for perfect fit on Ω b and Ω m to 4He and D/H, while fit* is the best possible fit on Ω b and Ω m to the 4He and D/H observations for the model considered as indicated in the columns four and seven. The last three columns are usual PRIMAT runs with modified a ( T ) such that a ¯ / λ = a S I V / S 1 / 3 , where a ¯ is the PRIMAT’s a ( T ) for the decoupled neutrinos case. Column seven is actually a S I V / S 1 / 3 , but it is denoted by a ¯ / λ to remind us about the relationship a ′ = a λ ; the run is based on Ω b and Ω m from column five. The smaller values of η 10 are due to smaller h 2 Ω b , as seen by noticing that η 10 / Ω b is always ≈ 1.25 . Table originally presented in [3].
Element Obs. PRMT a S I V fit fit* a ¯ / λ fit* fit
H 0.755 0.753 0.805 0.755 0.849 0.75 0.753 0.755
Y P = 4 Y He 0.245 0.247 0.195 0.245 0.151 0.25 0.247 0.245
D / H × 10 5 2.53 2.43 0.743 2.52 2.52 1.49 2.52 2.53
3 He / H × 10 5 1.1 1.04 0.745 1.05 0.825 0.884 1.05 1.04
7 Li / H × 10 10 1.58 5.56 11.9 5.24 6.97 9.65 5.31 5.42
N eff 3.01 3.01 3.01 3.01 3.01 3.01 3.01 3.01
η 10 6.09 6.14 6.14 1.99 0.77 1.99 5.57 5.56
FRF 1 1 1 1 1.63 1 1 1.02
mŤ 1 1 1 1 0.78 1 1 0.99
Q/Ť 1 1 1 1 1.28 1 1 1.01
Ω b [%] 4.9 4.9 4.9 1.6 0.6 1.6 4.4 4.4
Ω m [%] 31 31 31 5.9 23 5.9 86 95
χ ϵ 2 N/A 6.84 34.9 6.11 14.8 21.9 6.2 6.4
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated