1. Introduction
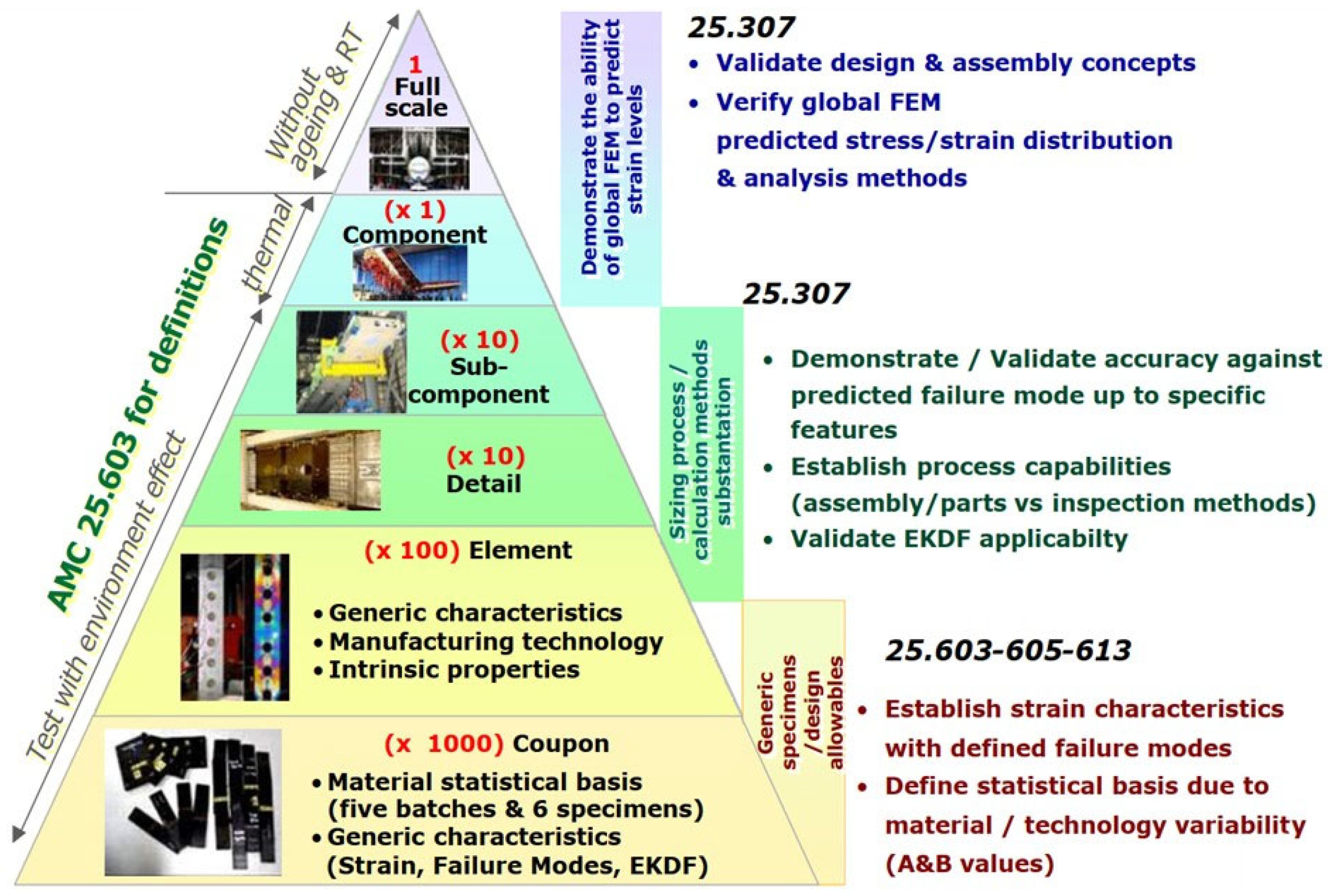
The certification of aeronautical structures is generally based on the pyramid of tests [
1] (
Figure 1), which is a representation of the design process and the structural validation for airworthiness certification [
2]. At the bottom of the pyramid, coupon tests give low-scale characterization of the material behavior, from design allowables to failure phenomenology [
3,
4]. Based on coupon characterizations, the next level of the pyramid focuses on structural detail issues such as the strength of bolted [
5], the unfolding of L-shaped specimens [
6] or the post-buckling behavior of stiffened structures [
7,
8]. Based on coupon and of elementary structural phenomena characterization, specimens of growing complexity and scale can be designed and validated, up to high scale testing. The design is performed to conservatively prove that the manufactured aircraft can withstand loads specified by regulation authorities. Numerical simulations can be extensively used to simulate the behavior of structures but structural performances demonstration need to be supported with test evidence. This numerical/experimental approach is also used for the analysis of particular problems such as the debonding of stiffeners [
7,
8] or the strength of Z-pinned junctions [
9,
10].
In recent decades, the aeronautical industry has been showing growing interest in composite materials for their competitive strength to mass ratio. However, each new material requires regeneration of the coupon level of the test pyramid with numerous tests to update allowables. Thus, the design/validation for new aircraft programs is generally costly and time consuming, and can also lead to structural oversizing because of some remaining unexploited potential of composite structures [
11].
Figure 1.
The pyramid of tests [
1] representing the numerous small mechanical tests providing a design basis for the fewer and larger tests [
12] (Courtesy of Airbus).
Figure 1.
The pyramid of tests [
1] representing the numerous small mechanical tests providing a design basis for the fewer and larger tests [
12] (Courtesy of Airbus).
This paper focuses on the testing of specimens at the intermediate scale of the test pyramid, situated between the coupon level and the sub-component level. The main interest of this scale lies in the study of elementary structures under uniaxial loadings (
Figure 2). This scale also studies the effects of local damages on the structural integrity, resulting from incidents such as stiffeners impacts or a notch on a fuselage caused by an uncontained engine failure. In-flight experiences stress the fuselage structures globally and locally generate multi-directional loading (combined and not uniform) on fuselage sections. Therefore, there is a need for multi-axial testing at this intermediate scale to assess the strength of elements under the wide range of possible loads. Whereas coupon tests mostly abstract from the way exterior loading is applied, larger tests must consider a specific test bench to load a specific sample. A test bench is designed to apply specific loads to a sample in a specific way, in order to address the sample behavior under such loading. A large spectrum of loads (tension, compression, bending, torsion, pressure, shear, etc.) can occur on a fuselage section: thus a few configurations are tested with specific test benches, then validated models and conservative approaches are used to address any relevant loading combination to be validated.
The intermediate-scale test benches are reviewed here to position the interest and originality of the tests considered in this paper. Basic test machines for coupons are introduced to contextualize the intermediate-scale practices, but full-scale tests at the component level are outside the scope of this literature review. Basically, the range of in-plane loadings is dealt with by using unidirectional coupon tests [
14,
15], with bi-axial tests on cruciform samples [
16,
17,
18] and with shear on deformable squares [
19,
20,
21]. Cruciform samples are cross-shaped specimens where the two main directions are loaded independently to enforce bi-axial loading states of tension-tension, compression-compression or tension-compression. Most cruciform tests study pure reference loads on a very small area of interest, which places them in the coupon level of the test pyramid, but structural issues similar to larger tests already appear: undesired failure at corner edges [
22], kinematic consistency regarding the two directions loaded simultaneously and the non-homogeneity of loading on the zone of interest (usually handled with [
23] for biaxial tests). Deformable square tests generally use small panels at the element level of the test pyramid, where approximate shear is applied to the full contour of the specimen. This is a first step towards structural testing with a specific bench, since, for each case, a somewhat different technical solution is implemented to enforce loading, which does not ensure the reproducibility of load shapes from one bench to another. Therefore, it becomes of interest to study the bench itself and the specific loads it produces.
Most tests at the intermediate scale enforce loading directly from actuators to the sample, so they will be referred to as "direct actuation benches". Uniaxial tension or compression on a large stiffened panel is often directly applied with a single powerful actuator [
24]. Some other benches are simply scaled up implementations of usual coupon principles, such as large deformable squares [
25,
26]. More complex loadings can also be applied directly to the sample, either by using many actuators along the specimen contour, or through a rigid structure that enforces specific kinetics on the sample [
27,
28].
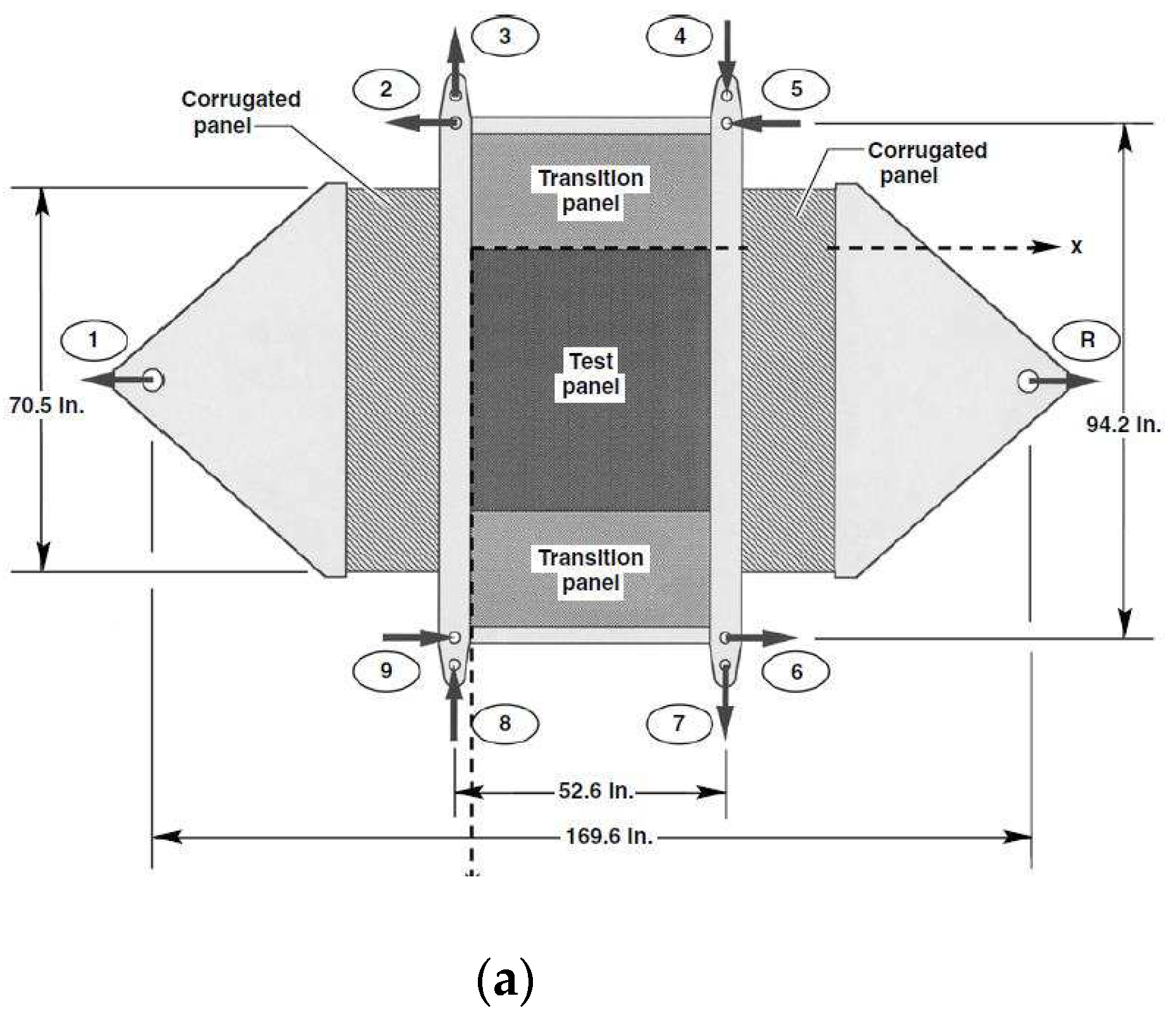
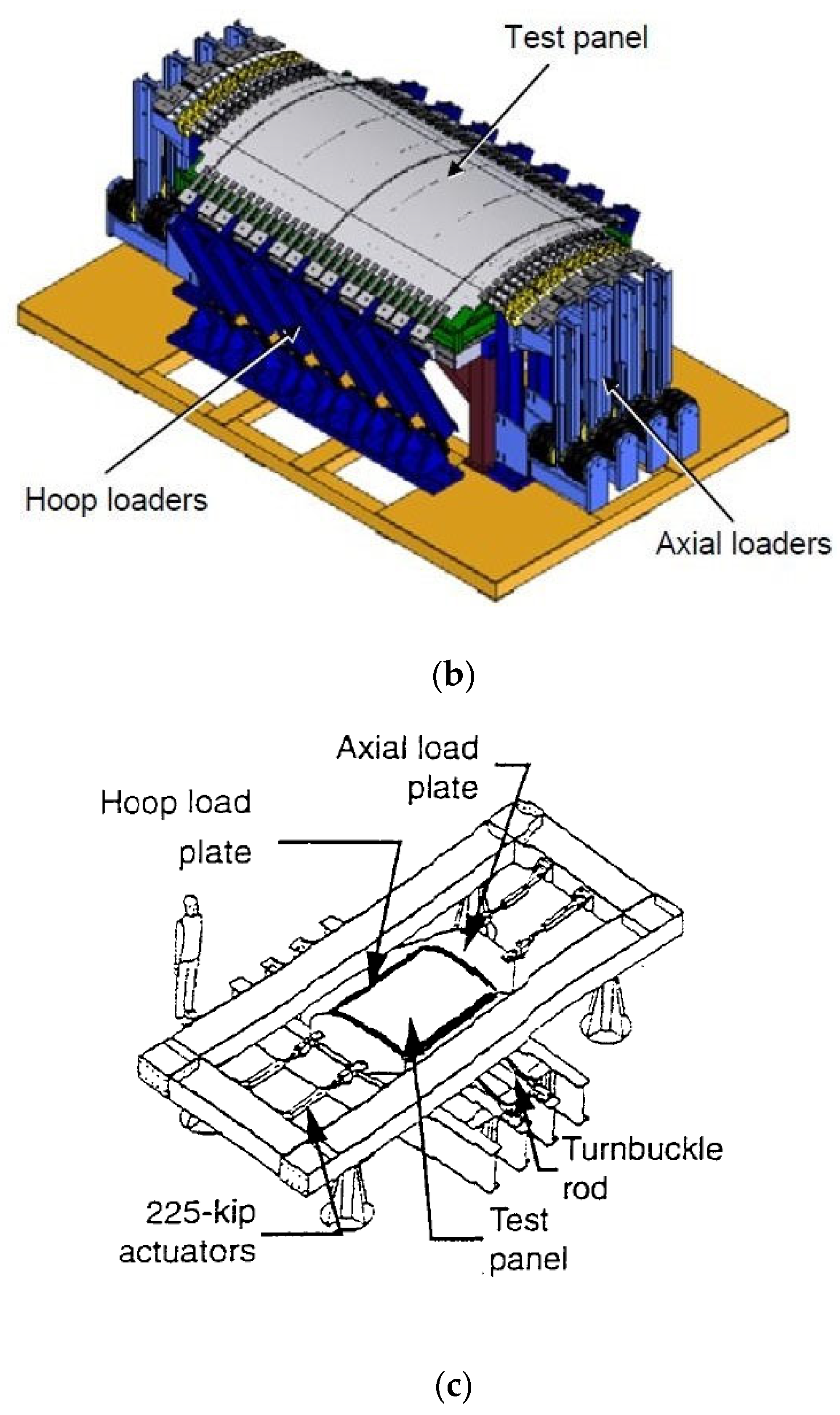
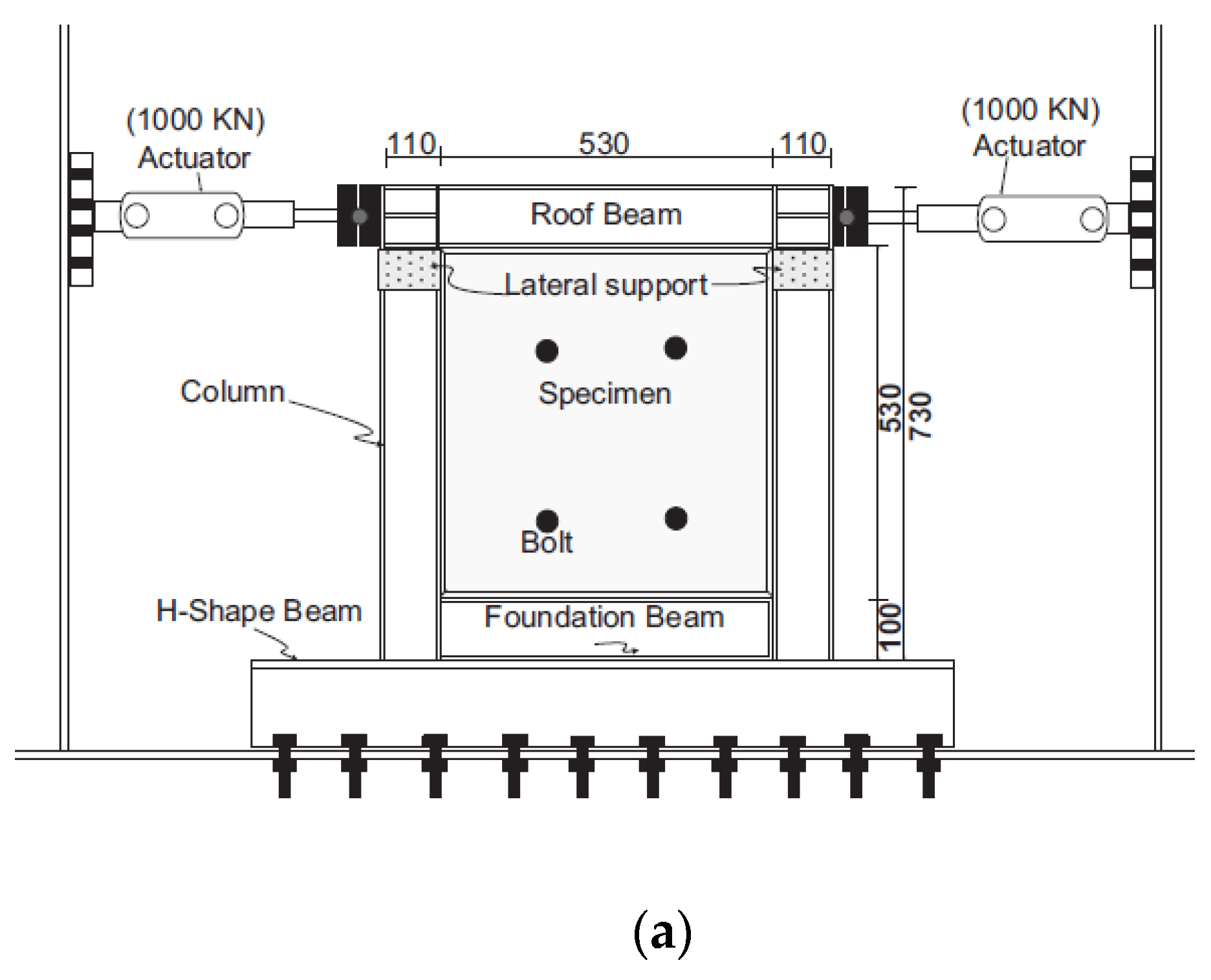
Figure 3 shows a few examples of such benches and points out load combination possibilities. The civil engineering field faces similar structural testing needs, so very similar test benches (generally bigger) are used to load wall structures (
Figure 4).
Tests at large scale on components or subcomponents are also directly loaded with global efforts and moments that are not properly representative of the in-flight experience of the global structure. However, local sections are loaded by the rest of the component, which generates local representative load shapes. Such major scale tests are rare and very costly but are necessary to validate the uppermost part of the test pyramid, notably to verify possible structural phenomena and effects of local damage (such as a large notch [
35,
36]) on a representative structure. The complexity and cost of such large tests can be substantial for development purposes so there is a need for intermediate scale testing with benches able to generate loadings representative of larger tests.
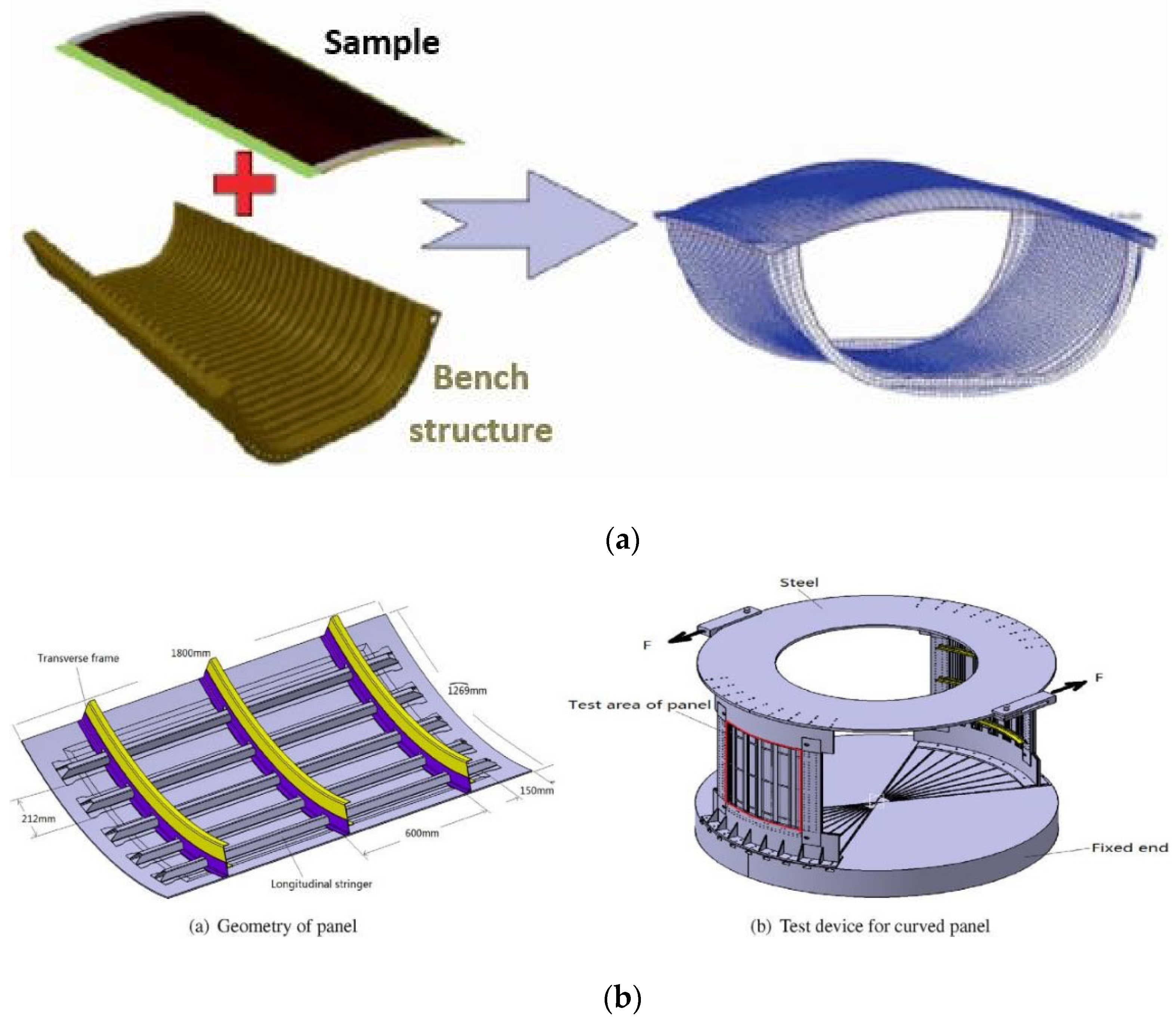
A second category of test benches exists, where the sample is fixed into a larger compliant structure, which role is to apply loading representative of sections of larger structures locally on the sample. This category will be referred to as "structurally embedding benches", in opposition to the "direct actuation benches" discussed above. The interest of this approach is to study representative intermediate scale structural issues without the cumbersome aspect of larger scale testing and its cost. Note that, in certain direct actuation benches, an intermediate structure is also often placed between the sample and the actuators, but with the fundamental difference that they are rigid and that the intention is to enforce simple kinetics instead of reproducing an interaction with a larger structure.
Figure 5 shows such benches with loading structures explicitly representing fuselage sections, with large panel specimens that can be positioned at the top of the intermediate-scale range of tests. Alternatively, bench loading structures can be built from compliant closed sections, typically rectangular boxes as initially published by Peters [
37] as early as 1946. Klein et al. [
38] later considered a rectangular box and bolted the sample to the lower face; When the box was globally loaded in bending or torsion, the specimen was subjected to tension/compression or shear. Castanié et al. [
39,
40] developed a test bench on the same principle, but with a more compliant structure to apply realistic loading on asymmetric sandwich structures used for helicopters. However, the area of interest of the sample was found to be limited, and this later motivated the development of the VERTEX test rig, basically a larger version of the previous machine, "to investigate composite structures at the scale of technological specimens and under complex loads" [
35,
36,
41]. Recently, Zucco et al. [
42] have developed a specific test bench to introduce combined loads of bending, shear and torsion on a thermoplastic wingbox specimen. A compliant intermediate structure of "aluminum dummy wingboxes" was designed to minimize boundary effects of load introduction on the useful composite wingbox. The same authors [
43] also developed a numerical model of the specimen and the loading structure, to assess stress concentrations and the effect of the loading structure on the prescribed loading of the useful specimen.
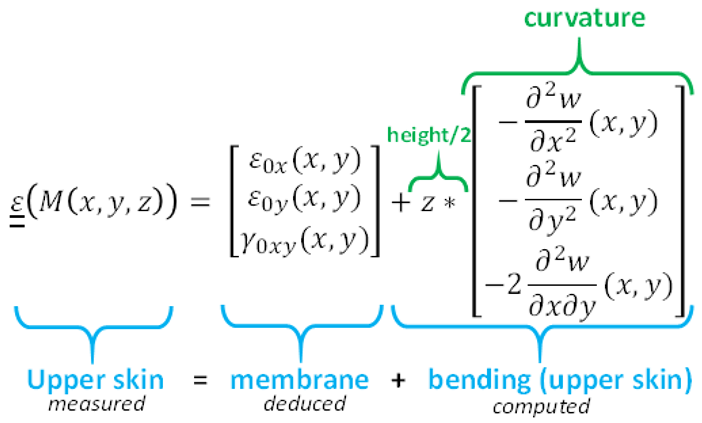
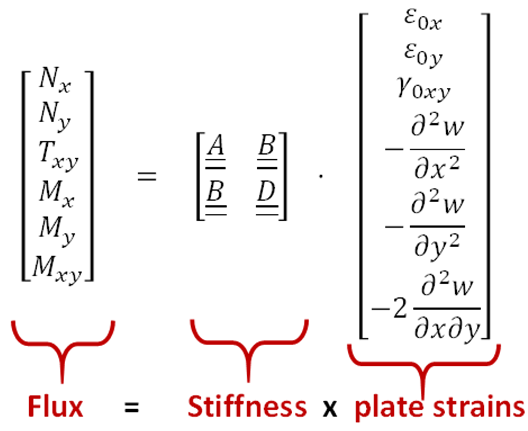
Mechanical experiments require instrumentation to monitor the test, especially the loading state of the sample. To numerically simulate the tests (for model identification, numerical investigation, virtual testing or validation), boundary conditions need to be applied to the model: the load shape (nature and spatial distribution of boundary conditions) can be assumed ideal (uniform/constant or basic kinetics) or realistic fields can be applied (generally displacement measured during the test, to simulate the same test). Forces and displacements of the actuators are the first data easily obtained from such tests. In the case of direct actuation benches, this provides very rich information for boundary conditions; possible intermediate parts between the actuators and the specimen can be considered rigid or modelled with a coarse description. In the case of structurally embedding benches, the transfer function of the bench (relation between actuator setpoints and the resulting loading on the sample) is complex. Previous studies on the VERTEX test bench [
47] showed non-uniform load shapes for reference loads of tension and shear. Moreover, structural phenomena came into play to complexify the reference loadings: longitudinal tension was followed by substantial transverse compression, and the Wagner effect deviated shear post-buckling towards combined shear and tension.
Hopgood et al. [
22] and Williamson et al. [
48] considered bi-axial testing on cross-shaped samples, to assess the failure envelope of open-hole specimens under combined in-plane loads. They systematically performed a "calibration" process on each sample, to know the relation between the actuator forces and the resulting nominal strain on the sample; the open hole on the sample was drilled after the calibration and then tested up to failure. The loading state of the sample during the tests was therefore assumed, given the measured forces of the actuators and the basic transfer function obtained by calibration. A similar process could be applied to more complex test benches but, for compliant loading structures, the dependency on the sample stiffness evolution must be considered: boundary conditions may be sensitive to the loss of stiffness of the sample (initial central defect of interest and damage propagation).
Carpiuc-Prisacari [
49] considered a hexapod test bench to directly apply tension-shear load on a double edge notch specimen. Various complexities of boundary conditions were tried (from constant/uniform to regular shapes and actual measured displacements without smoothing) to numerically simulate crack propagation in the tested specimen. It was found that the crack propagation (maximum stable crack length and direction) was sensitive to the load shape (uniform, linear, parabolic, raw measurement) and that more complex load shapes gave more representative propagation of the experiment. The authors emphasized "the importance of using the measured boundary conditions and the high sensitivity to the applied boundary conditions" [
49] as opposed to the configuration with ideal boundary conditions: "boundary conditions in the numerical simulations are assumed to be matching the ideal prescribed conditions, i.e. as if the experimental setup was perfect"[
49]. Therefore, specific load shape complexities need to be captured by the transfer function used for numerical simulations.
One solution is to use in situ local measurements: rosette strain gauges are massively used to measure strains locally. To compensate for the rosette’s spatial restriction to a single point, arrays of them can be placed in order to have many measuring points to appreciate spatial distributions of loads [
40]. Digital Image Correlation allows extremely rich data (fields of displacements and strains) to be simply obtained over the total area of the sample. The loading state of the sample can therefore be measured comprehensively instead of being assumed from distant actuator forces or assessed from poor local data of rosettes. Actual fields of displacements measured on the sample during the test can therefore be imposed as boundary conditions of numerical simulations [
35,
36,
41,
50]. However, this method is limited to the simulation of experiments already tested, and complexity arises with damage of the sample, as they may interact with the boundary conditions.
Given the interest in structurally embedding benches because of the load shape they produce, the interest in the bench transfer function (sample loading resulting from the bench load setpoint), and the importance of load shapes in the tests, it is important develop a transfer function representative of the specific load shapes of the bench. A calibration process or test measurements offer in-situ solutions to deal with this problem. However, they do not provide suitable predictions for tests on new specimens or new complex load paths. The numerical modelling of the test bench and the specimen with Finite Elements was therefore the solution adopted here to assess the transfer function, predictively and relatively to the load shape specificities. To the best of the authors' knowledge, the literature hardly ever covers the modelling of mechanical test benches [
42], especially for compliant test benches with consideration of load shapes.
The modelling of the test rig was a first step towards representative virtual testing of crack propagation and towards the study of envelope loadings as introduced by Serra et al. [
35], which requires quantitative estimations of loading states.
The first part of this paper presents the working principle of the VERTEX test rig (loading and measurements), to assess some modelling complexities and actually model the VERTEX bench with Finite Elements in the following part. Results from this model are compared with both experiments and simulations with ideal boundary conditions, to evaluate the model’s ability to make predictions and to evaluate the load shape specificities of the VERTEX bench. Finally, test cases are shown to illustrate the capabilities of the model regarding virtual testing.
4. Results and Validation
The VERTEX model behavior was identified on previous ALU and TSs tests, as discussed in section 3.2.2. Then, the VERTEX model was evaluated on TP tests to validate its representativeness.
The critical buckling loads were not compared because the experimental buckling event on such a slender structure cannot be properly simulated, because manufacturing defects and clamping pre-loading were not modelled.
First, this section focuses on the model’s capacity to predict the machine useful stiffness, without consideration of the loading shapes. It should not be forgotten that the ideal boundary conditions model does not give any information on the machine stiffness; therefore, only the VERTEX model is considered for this matter (
Figure 27). The machine stiffness was found to be very sensitive to most bolted joints' stiffnesses, as illustrated in
Figure 24 and
Figure 25.
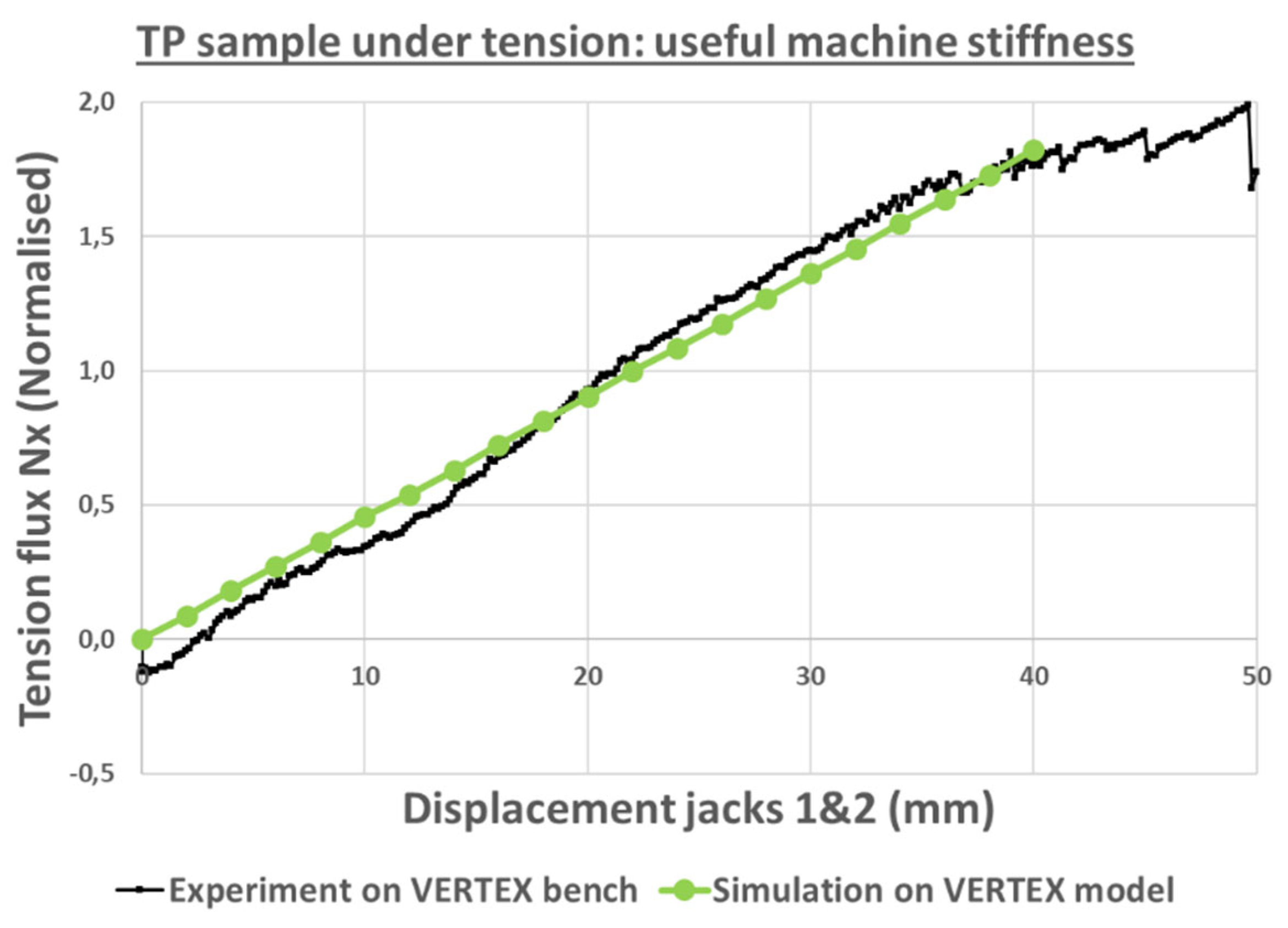
Figure 27 shows a great loss of machine useful stiffness in the experiments for displacements of jacks 1-2 above 40 mm. This was due to a major crack propagation in the sample that directly reduced the structural stiffness of the sample itself. The model developed was purely elastic so it could not represent this structural softening of the sample and therefore was not evaluated on such far stages of the test.
Finally, this section disregards the model’s prediction capacity of amplitudes to focus on the representativeness of loading shapes. The loading shapes predicted by simulation with the VERTEX model are compared to VERTEX experiments and simulations of the reference model of ideal boundary conditions. The simpler model with ideal boundary conditions (as introduced above) was also developed to offer a basis for comparison with the bench model. In this way, the load shape specificities of the VERTEX bench could be appreciated by comparison with ideal loadings. Moreover, this provided the tools for later studies dealing with the damage severity of various load shapes. In order to directly compare the results from the two models, exactly the same sample modelling file was used in both cases. In the case of the VERTEX bench model, the sample was loaded through each bolt-hole (peripheral slave nodes), interacting with the rest of the bench with coupling-connectors. For the ideal boundaries model, the same couplings were used on each bolt-hole, but they were loaded according to imposed ideal displacement (
Figure 14), applied to each central master node.
Figure 28 and
Figure 29 show the in-plane displacement fields and the out-of-plane position field to compare three configurations: the experiment on the VERTEX test rig, the simulation of the VERTEX model and the simulation with ideal boundary conditions. Tension and shear test cases on the TP sample were considered to evaluate and validate the VERTEX model after identification on ALU and TSs tests. The three configurations were compared with the same global load amplitudes (
Nx≈0.60 (normalized) for all tension configurations and
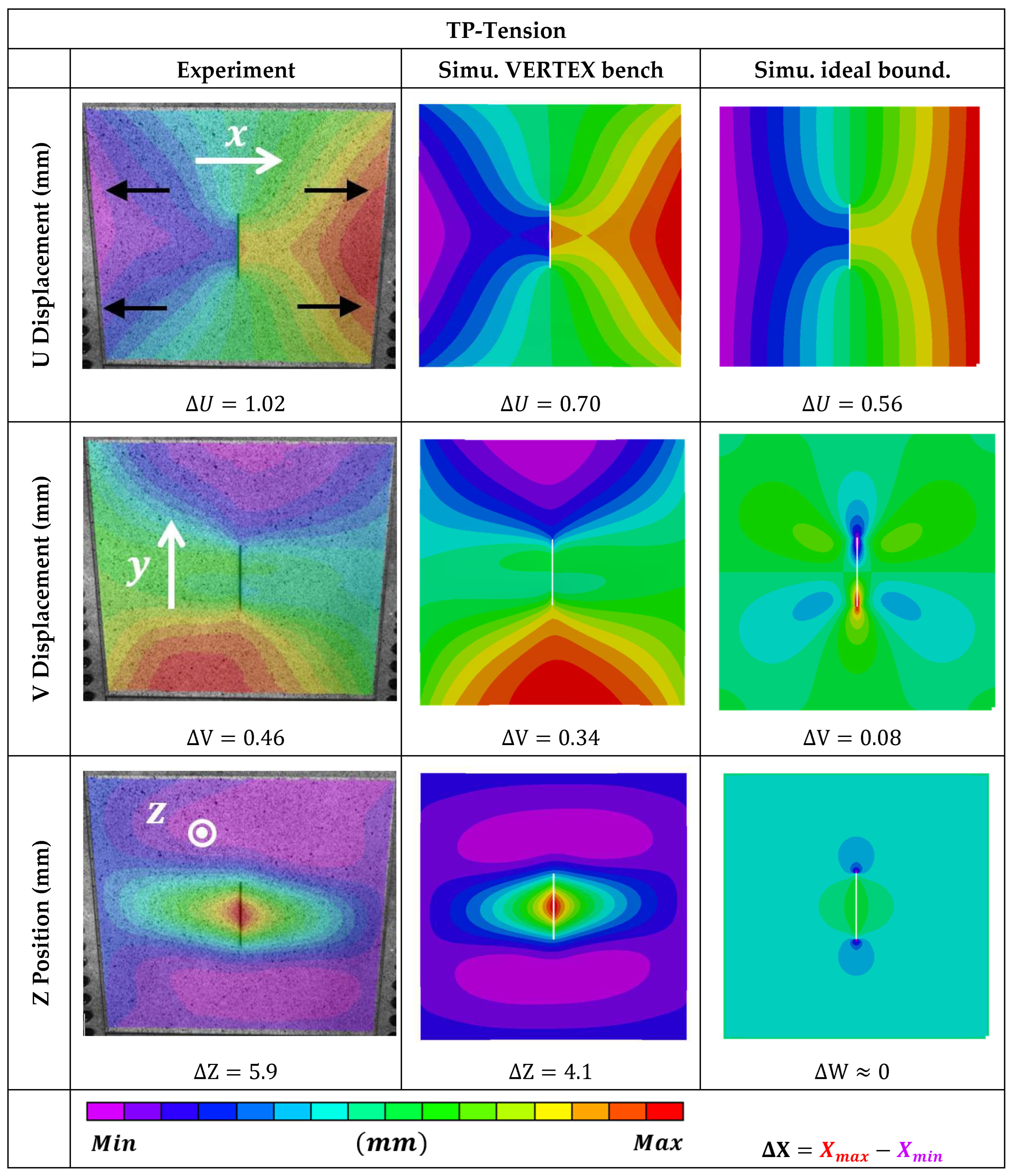
Txy≈-0.23 (normalized) for all shear configurations) so the focus is on the field shapes here and not on how well the machine stiffness is predicted. Note that in plane displacement amplitudes were an order of magnitude lower than the out-of-plane position/displacement because of the large post-buckling of such a slender sample. The reference position for the visualization of experimental displacement fields was chosen to be the sample after clamping (bolting of the sample's holes), and not the free sample before clamping, so as to neglect the parasitic rigid motion and the pre-loading induced by the clamping phase, which was variable and not modelled. The reference position of the sample was substantially curved (because of manufacturing defects and the buckling induced by clamping) so the Z out-of-plane position represents a meaningful bending state to compare configurations, whereas experimental W displacement was impaired and gave misleading shapes.
Figure 28 shows the load shapes induced by tension loading on the TP sample. The VERTEX model captured the useful U displacement field of the experiment really well, whereas the ideal tension showed straight isolines and linear evolutions on the four edges. Usually, longitudinal tension is expected to produce transverse tension through the Poisson effect when the edges are supported. However, the tension experiments with the VERTEX test rig showed transverse compression (
Figure 28 -V displacement) that generated buckling on the sample (
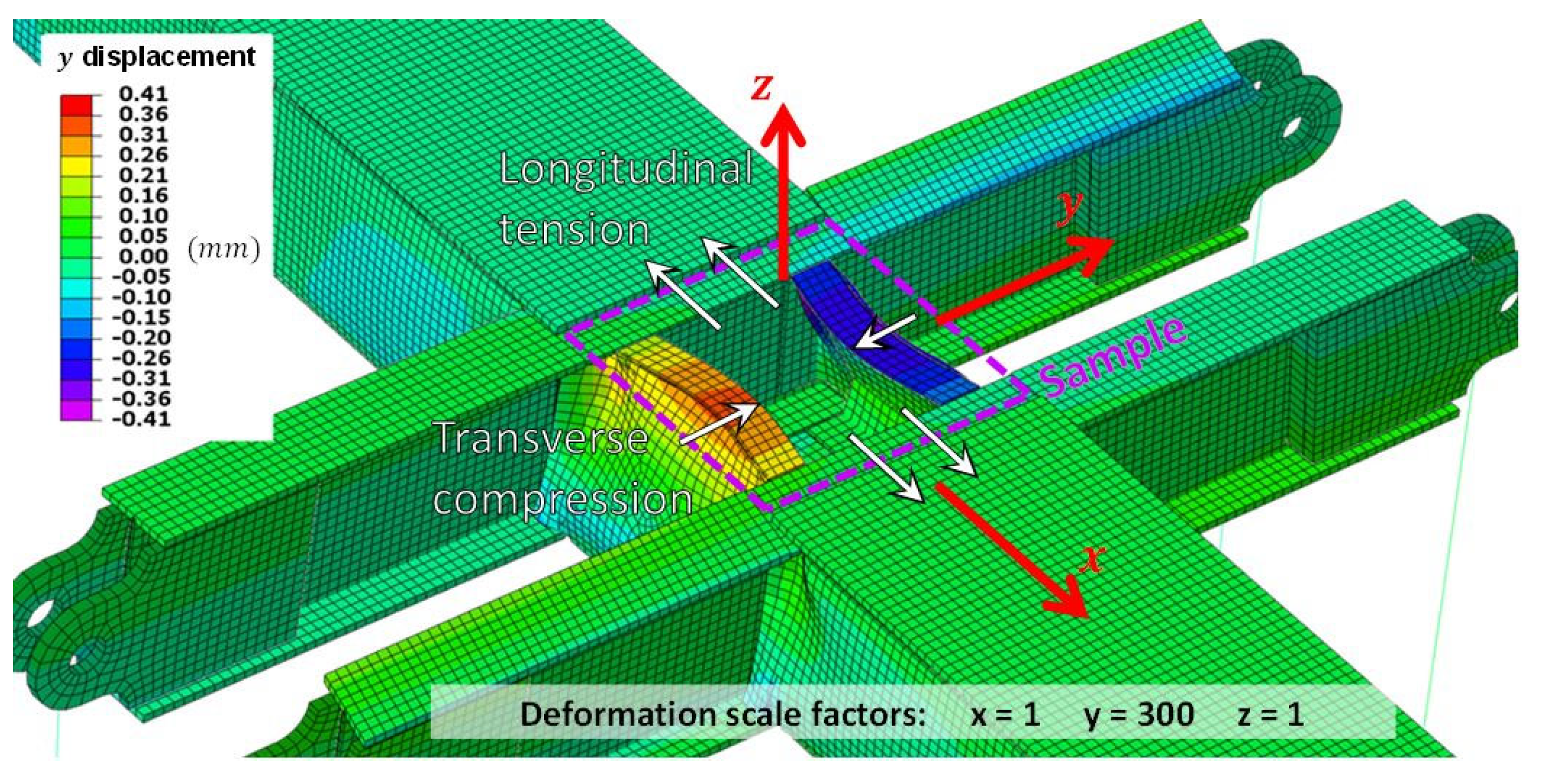
Figure 28 - Z position): the "tension" load case with VERTEX was actually a longitudinal tension with secondary transverse compression. The VERTEX model was able to capture that aspect and allowed the phenomenon to be understood through numerical investigation:
Figure 30 illustrates and explains that, in the VERTEX test bench, for the tension configuration, the flanks bent towards the center of the central box, which directly induced transverse compression on the sample. The ideal boundary model could not capture this effect and thus failed to represent both the substantial transverse compression and the buckling of the sample. Note that, experimentally, the buckle was not properly aligned with the longitudinal direction and, accordingly, the V displacement field was not properly symmetrical: this was considered to be a backlash take-up issue resulting from the previously tested shear load [
47]. The VERTEX model did not represent backlash history but also showed a very slight misalignment in the opposite direction, attributed to the slight un-symmetry of the bench in the
(Oxz) plane: see diagonally opposed jacks 3-4 in
Figure 8.
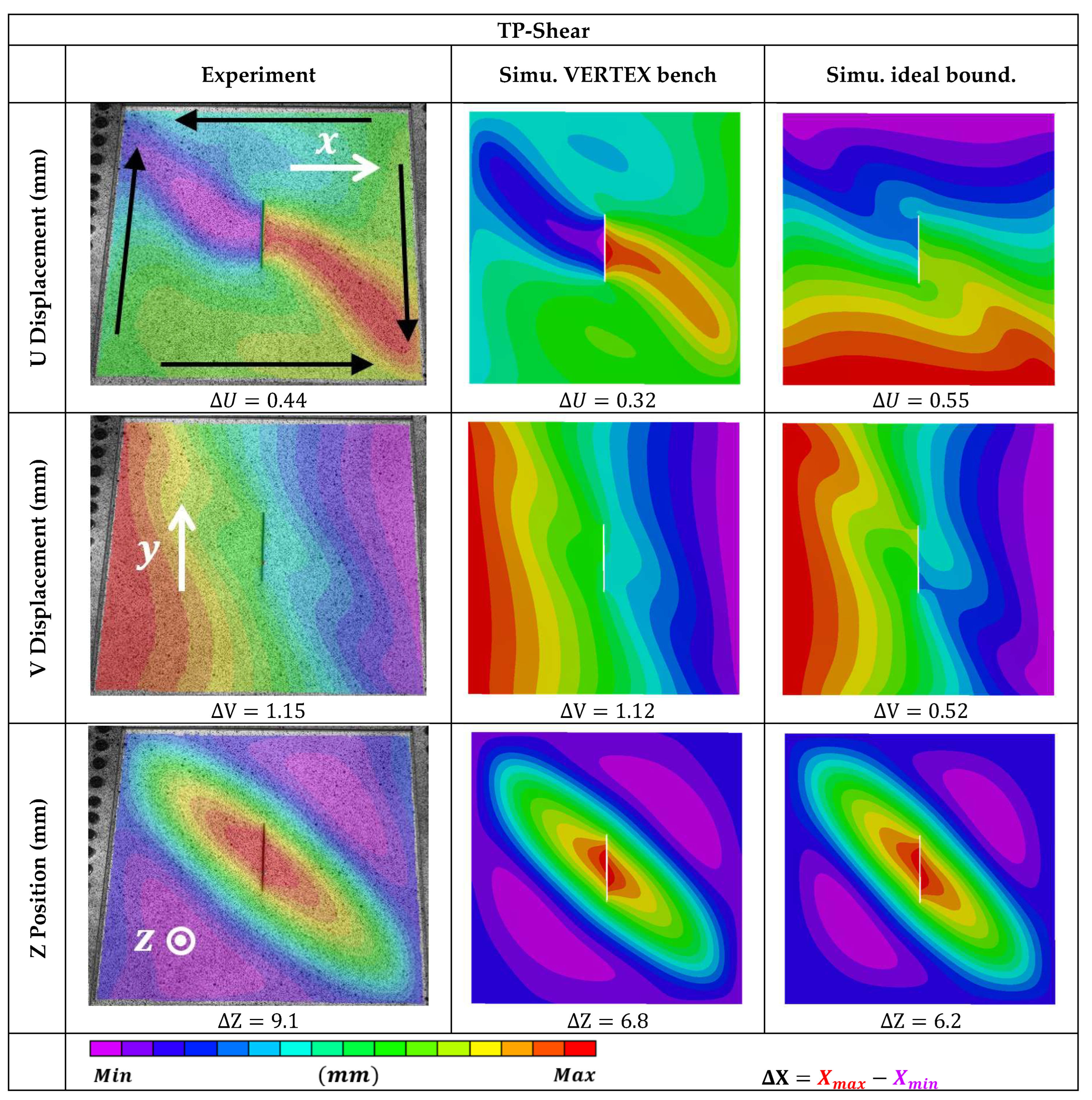
Figure 29 shows the load shapes induced by shear loads on the TP sample. As for the tension discussed above, the VERTEX model managed to capture the specific complex load shapes whereas the ideal model captured the general idea but failed to represent relevant specificities. In particular, the VERTEX bench generated shear mostly through V displacements applied to the left and right edges, in contrast to the U displacements that were expected to be applied additionally on the bottom and top edges to generate complete ideal shear.
The samples were modelled perfectly flat with no manufacturing defect, so mode I buckling could occur upward or downward without a clear trend, whereas experimental buckling was upward for tension and shear on TP samples. Given that the buckling direction of the sample could significantly alter the in-plane displacements observed on the upper face, the shear simulations were run with an initial flick to initiate the upward buckling, thus allowing proper comparison of in-plane displacements separately from the buckling direction issue. Likewise, the substantial discrepancy between experimental and simulated out-of-plane amplitudes was attributed to the unmodeled initial curvature of the real samples, which were initially curved upward by approximately 2 mm in their center. Numerically simulated in-plane displacement amplitudes were also substantially lower than those found in experiments for the same useful force flux. This lack of experimental stiffness was also attributed to the samples' initial curvatures and to variable backlash take-up issues.
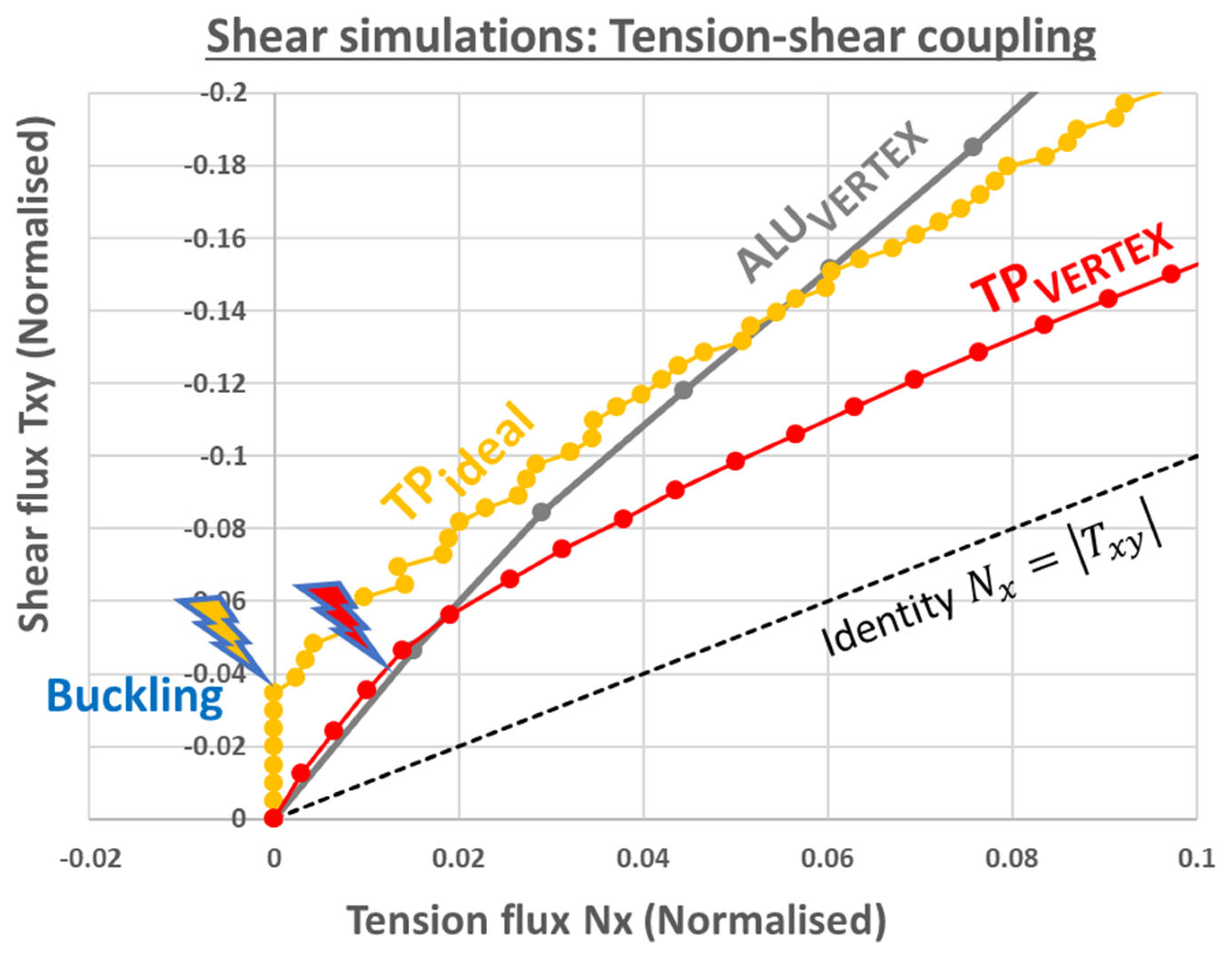
Finally,
Figure 31 compares the VERTEX model and the ideal boundary model, exploiting the non-modelling of sample defects to clearly observe shear buckling and subsequent tension-shear coupling in post-buckling. The ideal shear simulated shows a characteristic Wagner behavior: before buckling the imposed shear displacement gives pure shear flux, then, after buckling, the additional loading gives an additional combination of tension and shear fluxes. For the VERTEX shear simulated on the TP sample, the same Wagner effect was observed. However, there was an additional tension bias from the start. The ALU-shear has been added to
Figure 31 because it did not buckle, therefore it also gives an insight into the VERTEX's tension-shear coupling independently of the Wagner effect. Hence, the confrontation of the two models explains that, additionally to the Wagner effect, the VERTEX bench behavior enforces a tension coupled to shear when jacks 3-4 are pushed.
5. Case Studies
The transfer function of the VERTEX test rig was chosen to be implemented with Finite Element modelling, to extend the domain of application (geometry, material, defects). This section is a brief presentation of the model capabilities regarding its virtual testing capabilities, rather than a development of results of case studies.
The model of the VERTEX test rig is capable of investigating plasticization and failure on any part, since they are all meshed with Finite Elements. This is especially relevant for the flanks and the bottom face of the central BOX because these parts were designed to undergo plasticization and to be replaceable. The model is also capable of evaluating bolts load distribution.
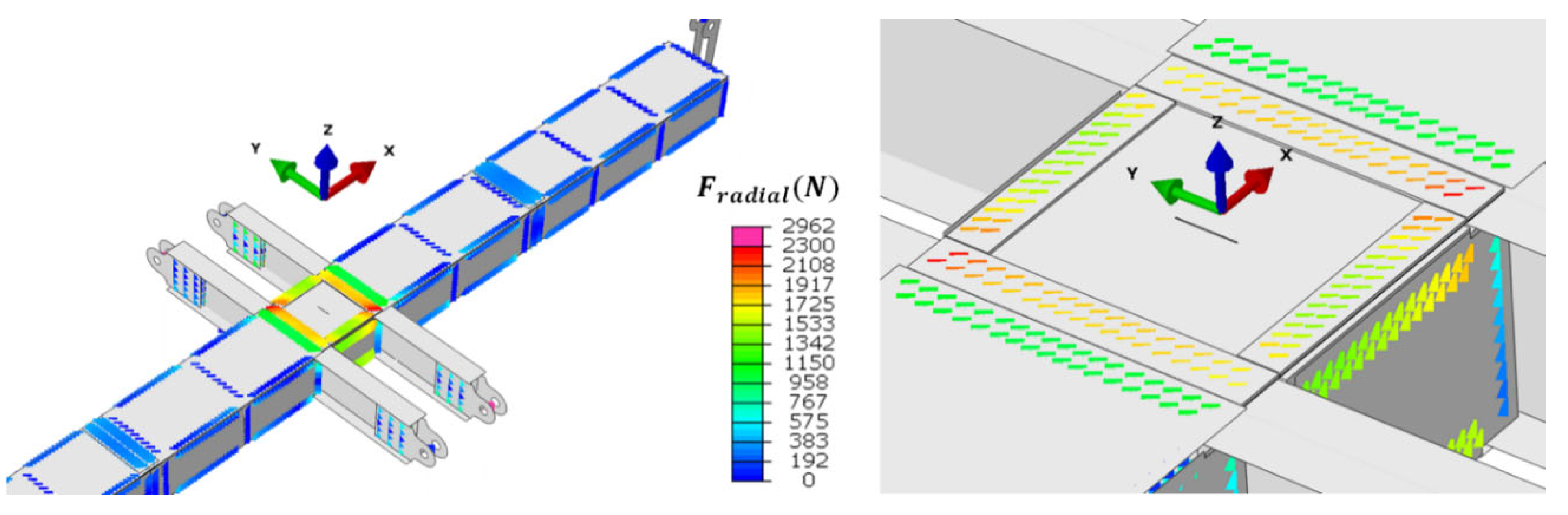
Figure 32 shows the radial force of each connector element, representing the radial local force going through the screws. Specifically,
Figure 32 shows radial forces on the sample bolts, and, notably, a load concentration on the corner bolts (see red points on the tab tips).
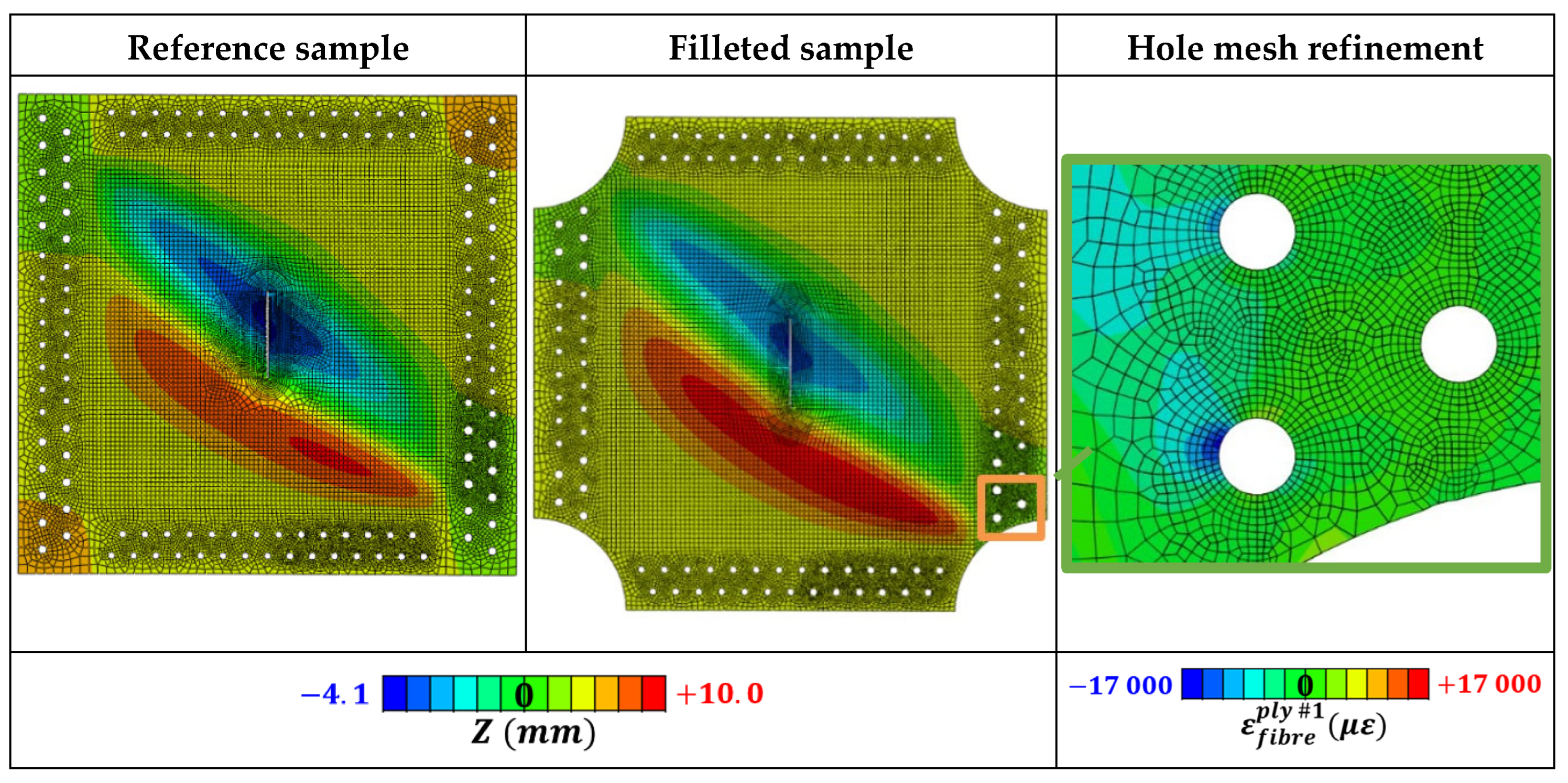
Figure 33 shows modelling of fillets on the sample corners, inspired from cruciform samples [
56] and experience from shear deformable square tests, which is an ongoing investigation to avoid corner failures in shear tests [
47]. The numerical investigation of this configuration had three main goals: i) to verify the negligible impact of the new geometry on load shapes on the useful part of the sample, ii) secondly to investigate bearing occurrences on the sample's remaining bolting holes, and iii) to optimize the geometry of the filleted corners to avoid corner failures. Meshing was refined on the tab region and especially on the contours of the relevant holes to obtain meaningful results regarding the sample's bearing failure. As mentioned earlier (
Figure 21), the coupling between a connector and a sample hole was anchoring on all peripheral nodes of the hole meshing. This feature was introduced precisely with a view to meaningful bearing evaluation on the holes of samples. Since the compression of the bolts tightening is not modelled, the bolt radial load is mostly transferred as bearing instead of friction, so the maximum radial loads of the bolts give conservative values for the composite bearing.
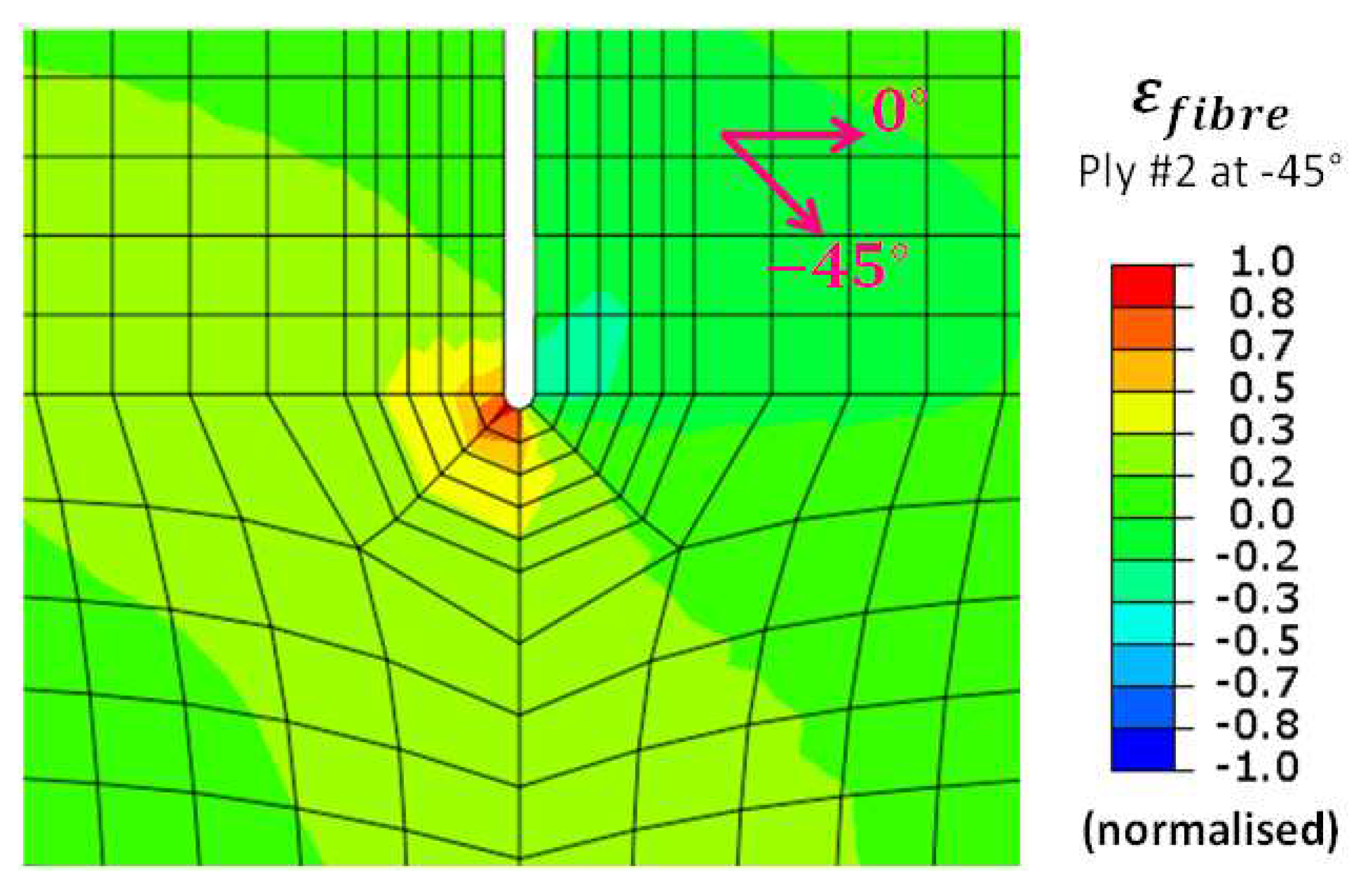
Figure 34 focuses on the strain along the fiber direction, for the most critical ply of the TSs sample under shear (ply #2 at -45°). Meshing refinement around the notch tips was too coarse for the failure mechanisms to be properly studied but still allowed the first failure occurrence of the specimen to be evaluated, for example with a criterion of maximum fiber strain.
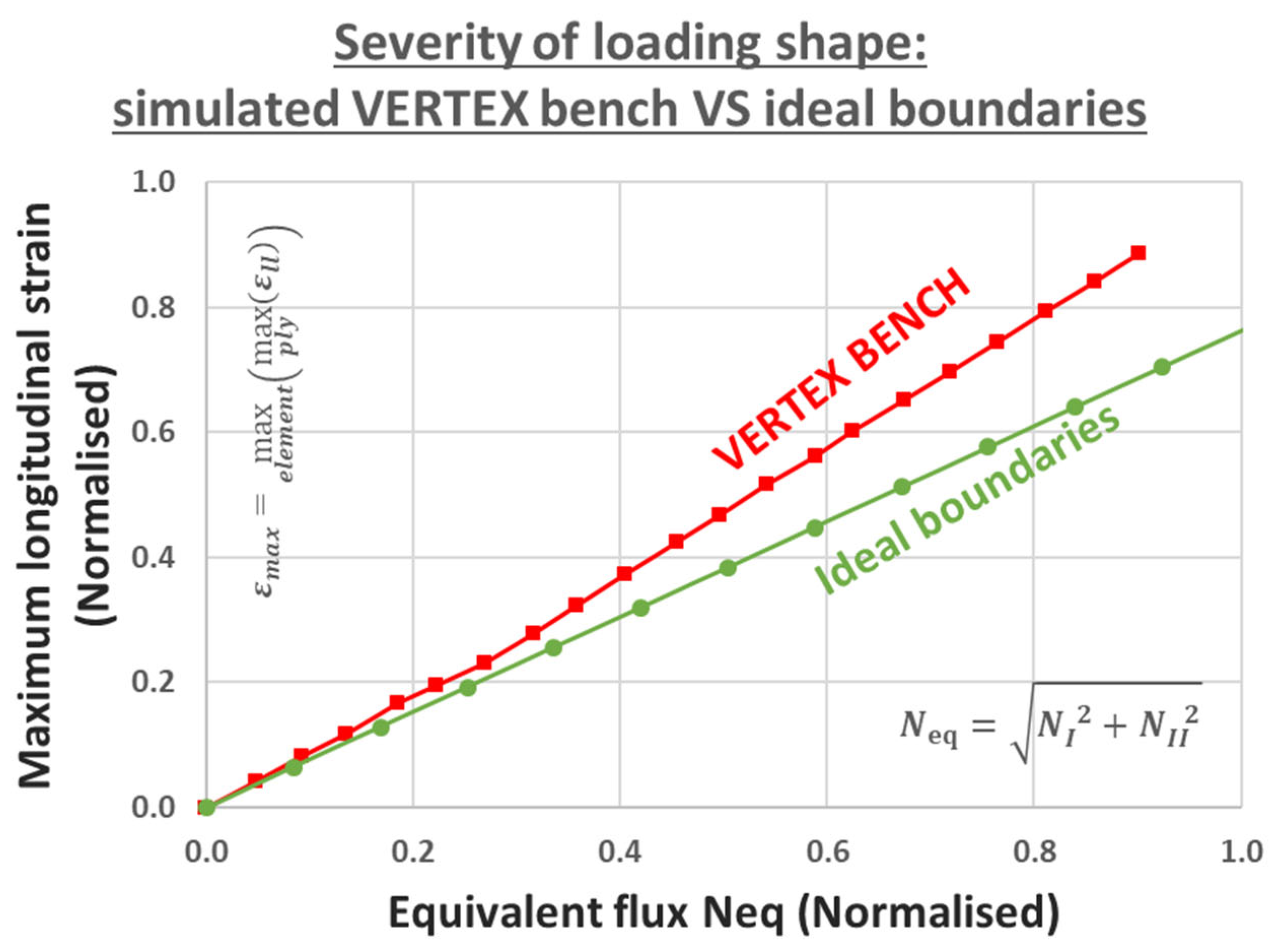
Figure 35 plots the maximum strain evolution for a tension loading, with the VERTEX model and with the ideal boundary condition model: for the same equivalent flux [
47] on the same sample, the VERTEX case generated higher strains than the ideal boundary conditions. This is a first step towards assessing the relative severities of load shapes but this issue needs a specific study because the severity interpreted depends on the failure criterion and the metric used to quantify the nature and intensity of loading [
47]. For the example of
Figure 35, the overall multi-directional loading intensity is quantified by the equivalent flux, which is the quadratic norm of force fluxes in the principal directions:
Neq=√(NI2+NII2).
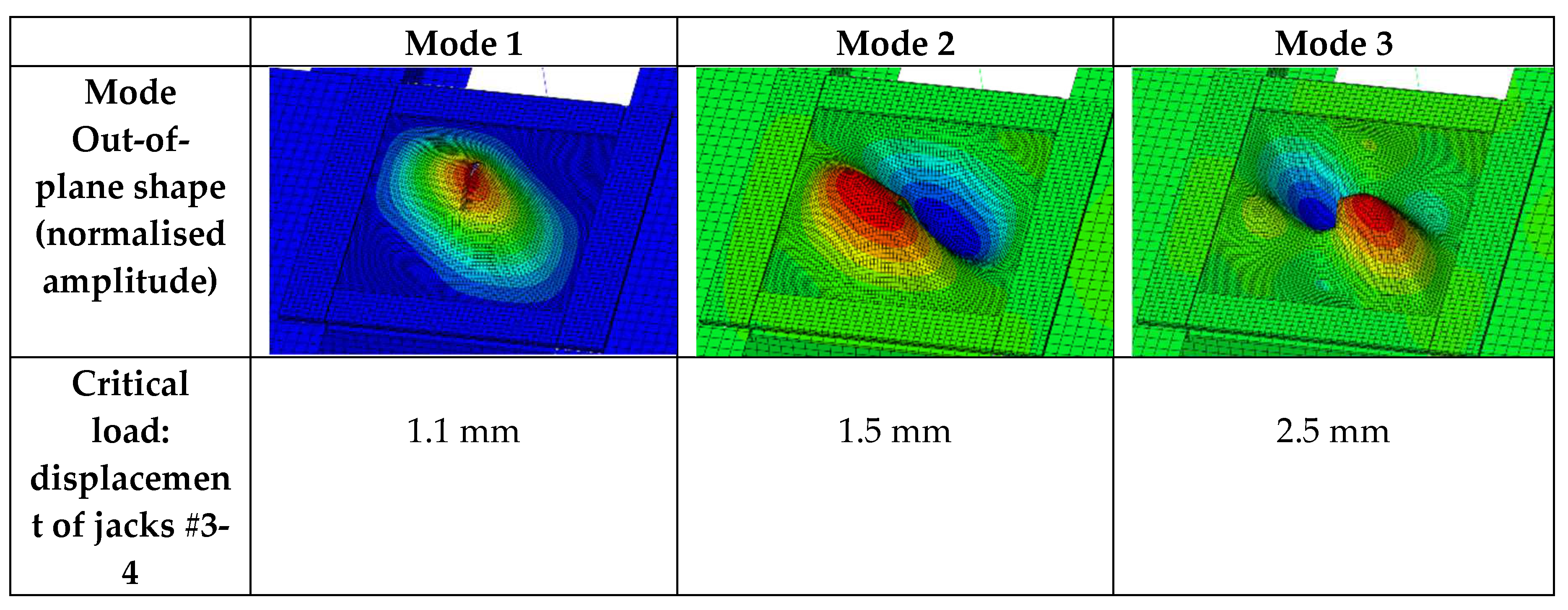
The VERTEX model can also be solved with a linear buckling approach to estimate the sample's buckling mode shapes and critical values (
Figure 36). Twenty-three shear buckling modes were found with critical loads below the failure load. The first two modes were found to have small and similar critical loads compared with failure loads of interest, which were higher by an order of magnitude.
6. Conclusion and Perspectives
In this paper the VERTEX test bench was numerically modelled with Finite Elements using an explicit scheme to implement a predictive transfer function, that is the knowledge of the sample loading (boundary conditions' shape and amplitude) from the displacement setpoints applied to the bench actuators. This relation is complex because the VERTEX bench is a compliant structure, in order to load the sample so that it is representative of large structure sections.
A special modelling effort was made concerning bolted joints, because their stiffnesses were found to have a major impact on the transfer function. Each bolted joint of the test bench structure was modelled with connector elements and coupling interactions, binding the modelled part together. A sensitivity analysis was performed to evaluate relevant parameters (axial/radial stiffness, SAMPLE/BOX/BEAM region) for the transfer function. Tension and shear loadings on two different samples (TSs and ALU) were considered to identify stiffness parameters on a large range of past tests.
Afterwards, the VERTEX model and a reference model (ideal boundary conditions) were compared with VERTEX experiments, on TP samples under tension and shear. The VERTEX model was found to produce good predictions of the load amplitudes and of the complex load shapes. However, the ideal boundary condition model did not manage to properly grasp load shape features and it did not give any notion of amplitude prediction. The complex modelling effort of the VERTEX test bench was therefore necessary to be able to represent the load shape of such a structurally embedding bench.
Ultimately, application cases were shown to demonstrate the scalability of the chosen modelling complexity. The model allowed structural phenomenology to be investigated and failure to be evaluated on any configuration, especially at the notch in the sample. The bench modelling is essential to better understand such structural element tests, which are still generic but more representative than coupon tests and cheaper than large scale structure tests.
Other applications of the VERTEX model are also possible and currently being studied, such as an exploration of the failure envelopes with non-proportional loadings in the tension-shear domain. Other ongoing research is studying the debonding of stiffened samples under loading after impact. These two applications are tackling important validation points of aircraft sizing. Thus, it is of interest to study them with intermediate-scale tests/simulations, representative of larger structural experiments. The bench modelling allows complex/costly tests to be better prepared, and a true test-simulation dialogue to take place.
Author Contributions
Conceptualization, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; methodology, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; software, Florent Grotto, Oscar Peta, Joël Serra; validation, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; formal analysis, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; investigation, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; resources, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; data curation, Florent Grotto, Oscar Peta, Joël Serra; writing—original draft preparation, Florent Grotto, Oscar Peta; writing—review and editing, Florent Grotto, Oscar Peta, Christophe Bouvet, Bruno Castanié, Joël Serra; visualization, Florent Grotto, Oscar Peta; supervision, Christophe Bouvet, Bruno Castanié, Joël Serra; project administration, Joël Serra; funding acquisition, Joël Serra. All authors have read and agreed to the published version of the manuscript.
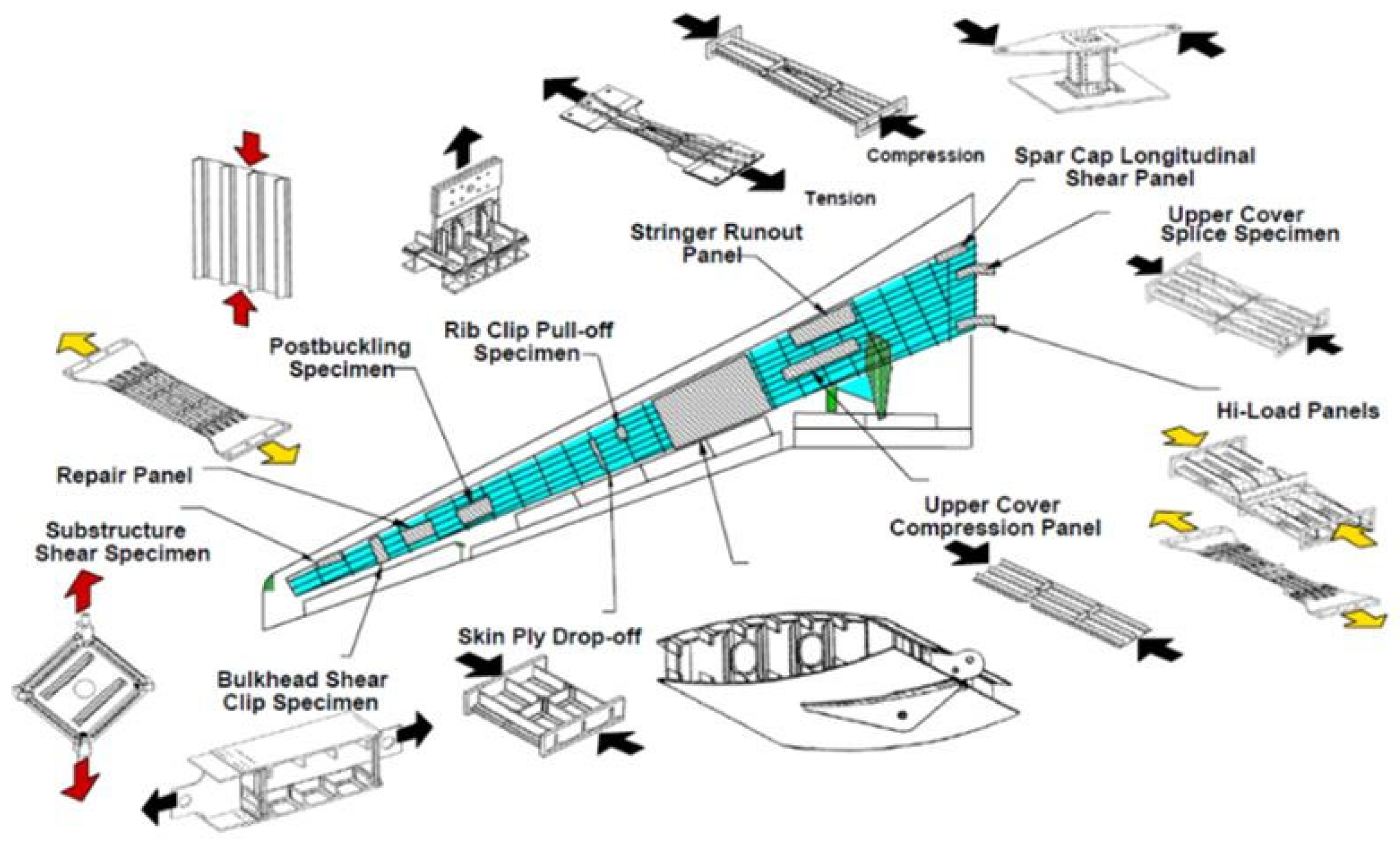
Figure 2.
Building block approach for an aircraft wing-extensive testing of structural elements under unidirectional loadings [
13].
Figure 2.
Building block approach for an aircraft wing-extensive testing of structural elements under unidirectional loadings [
13].
Figure 3.
Test benches from the aerospace field with direct actuation of the sample: a) shear deformable square test enriched with tension/compression combination capability [
29], b) internal pressure combined with tension and shear applied by numerous actuators on the large curved panel [
30], c) internal pressure and tension with few actuators on a curved panel [
31].
Figure 3.
Test benches from the aerospace field with direct actuation of the sample: a) shear deformable square test enriched with tension/compression combination capability [
29], b) internal pressure combined with tension and shear applied by numerous actuators on the large curved panel [
30], c) internal pressure and tension with few actuators on a curved panel [
31].
Figure 4.
Test benches from the civil engineering field with direct actuation of the sample: a) deformable square test on a wall specimen [
32], b) numerous actuators to directly load the sample in plane and out-of-plane [
33], c) few actuators to enforce load combinations on the sample through a rigid intermediate structure [
34].
Figure 4.
Test benches from the civil engineering field with direct actuation of the sample: a) deformable square test on a wall specimen [
32], b) numerous actuators to directly load the sample in plane and out-of-plane [
33], c) few actuators to enforce load combinations on the sample through a rigid intermediate structure [
34].
Figure 5.
Test benches that structurally embed the sample: a) Shear, tension and pressure introduced to the sample through a D-box assembly [
44] (from [
45] concept), b) Shear on large stiffened panel: deformable square principal, loaded by a rotating structure emulating a fuselage torsion [
46].
Figure 5.
Test benches that structurally embed the sample: a) Shear, tension and pressure introduced to the sample through a D-box assembly [
44] (from [
45] concept), b) Shear on large stiffened panel: deformable square principal, loaded by a rotating structure emulating a fuselage torsion [
46].
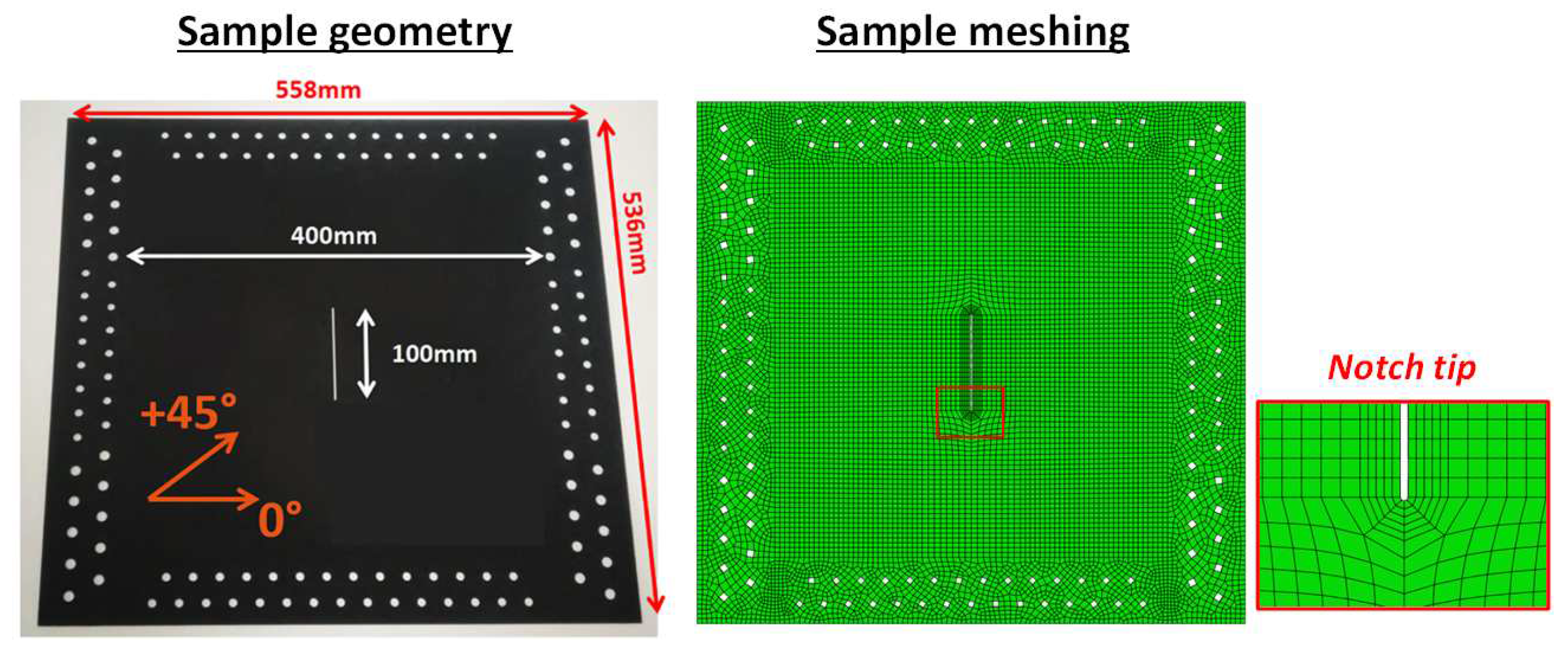
Figure 6.
(left) VERTEX specimen geometry, with a central notch - (right) sample bolted to the VERTEX test bench, viewed through one of the two optical cameras used for digital image stereo-correlation (5 Mpx, 2 fps).
Figure 6.
(left) VERTEX specimen geometry, with a central notch - (right) sample bolted to the VERTEX test bench, viewed through one of the two optical cameras used for digital image stereo-correlation (5 Mpx, 2 fps).
Figure 7.
The VERTEX test rig.
Figure 7.
The VERTEX test rig.
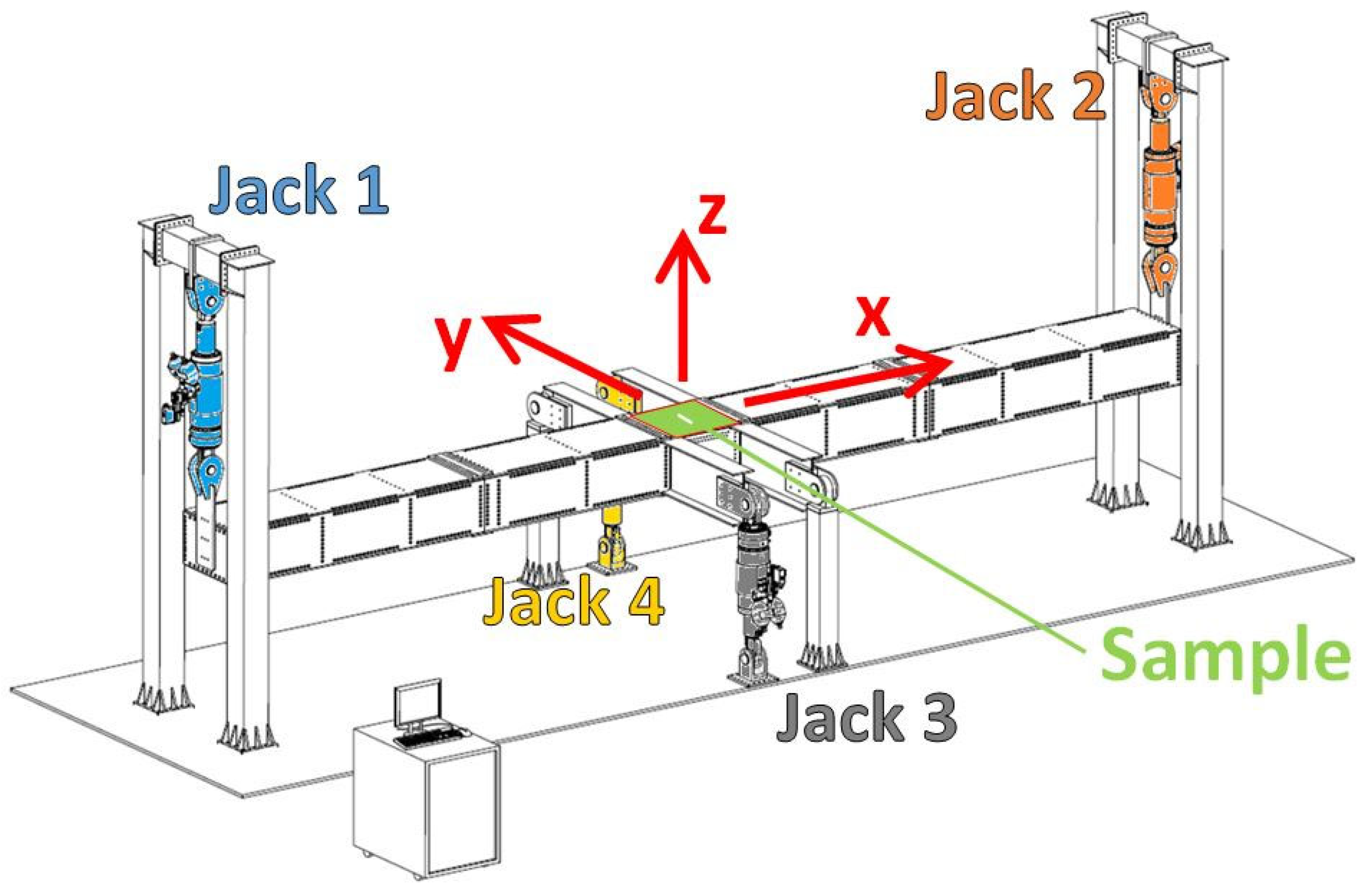
Figure 8.
Scheme of the VERTEX test rig and its four jacks to load the sample placed in the middle.
Figure 8.
Scheme of the VERTEX test rig and its four jacks to load the sample placed in the middle.
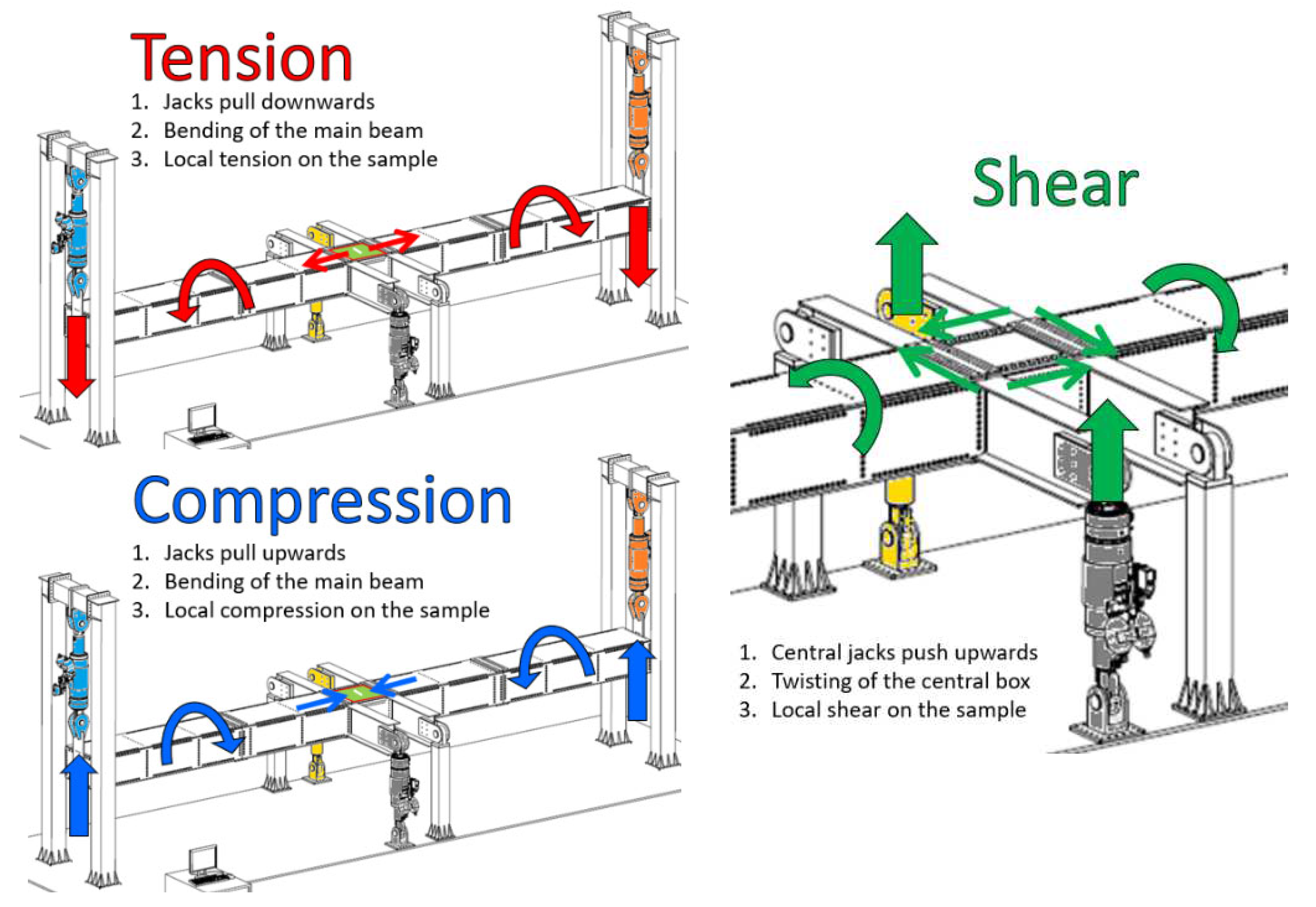
Figure 9.
Actuation of the four jacks of the VERTEX test rig to deform the bench and locally apply tension/compression and shear to the sample.
Figure 9.
Actuation of the four jacks of the VERTEX test rig to deform the bench and locally apply tension/compression and shear to the sample.
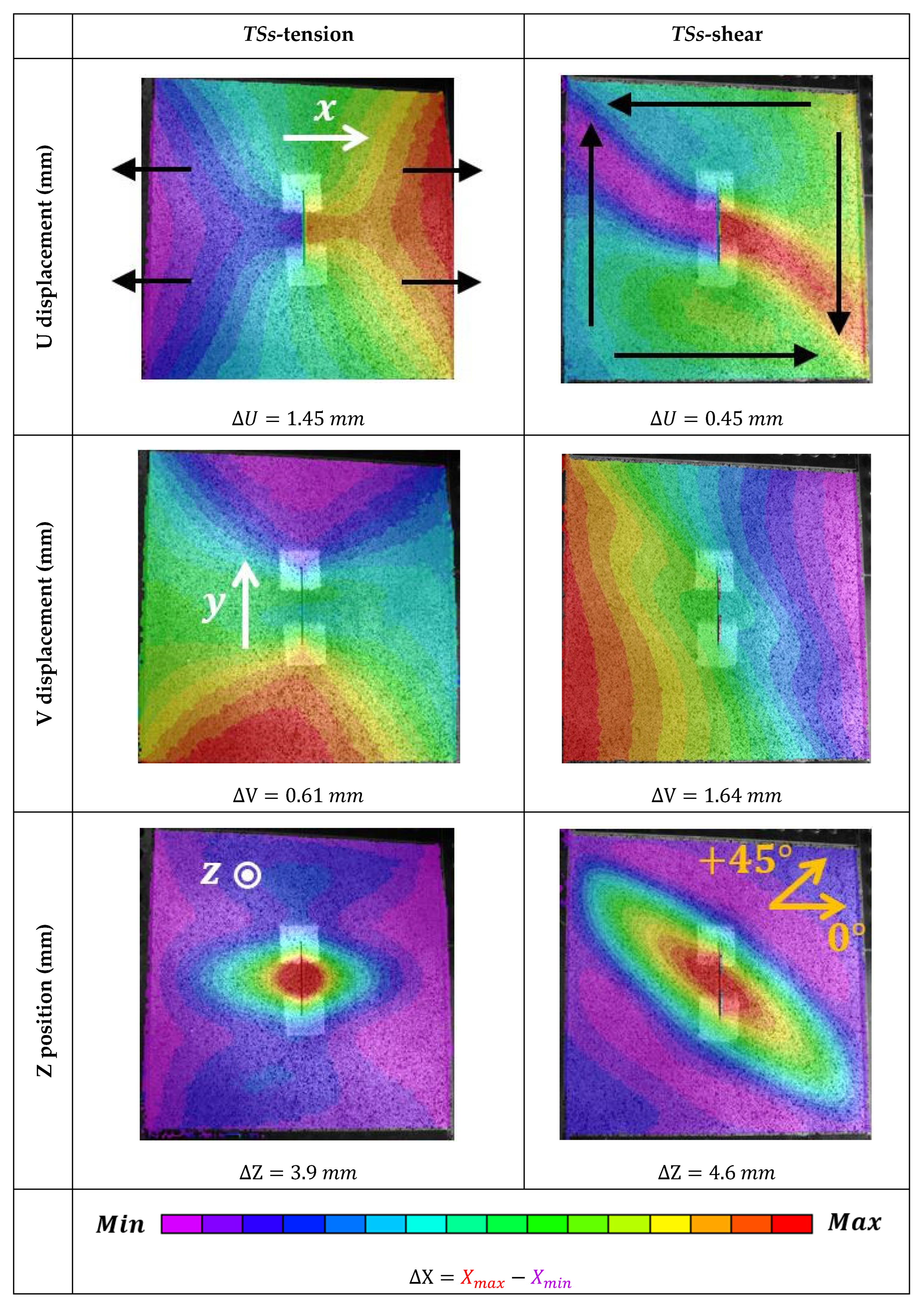
Figure 10.
Shapes of loading illustrated through in-plane displacements and out-of-plane shape, for tension and shear tests on TSs samples, using stereo-correlation on the 400 mm × 400 mm useful zone.
Figure 10.
Shapes of loading illustrated through in-plane displacements and out-of-plane shape, for tension and shear tests on TSs samples, using stereo-correlation on the 400 mm × 400 mm useful zone.
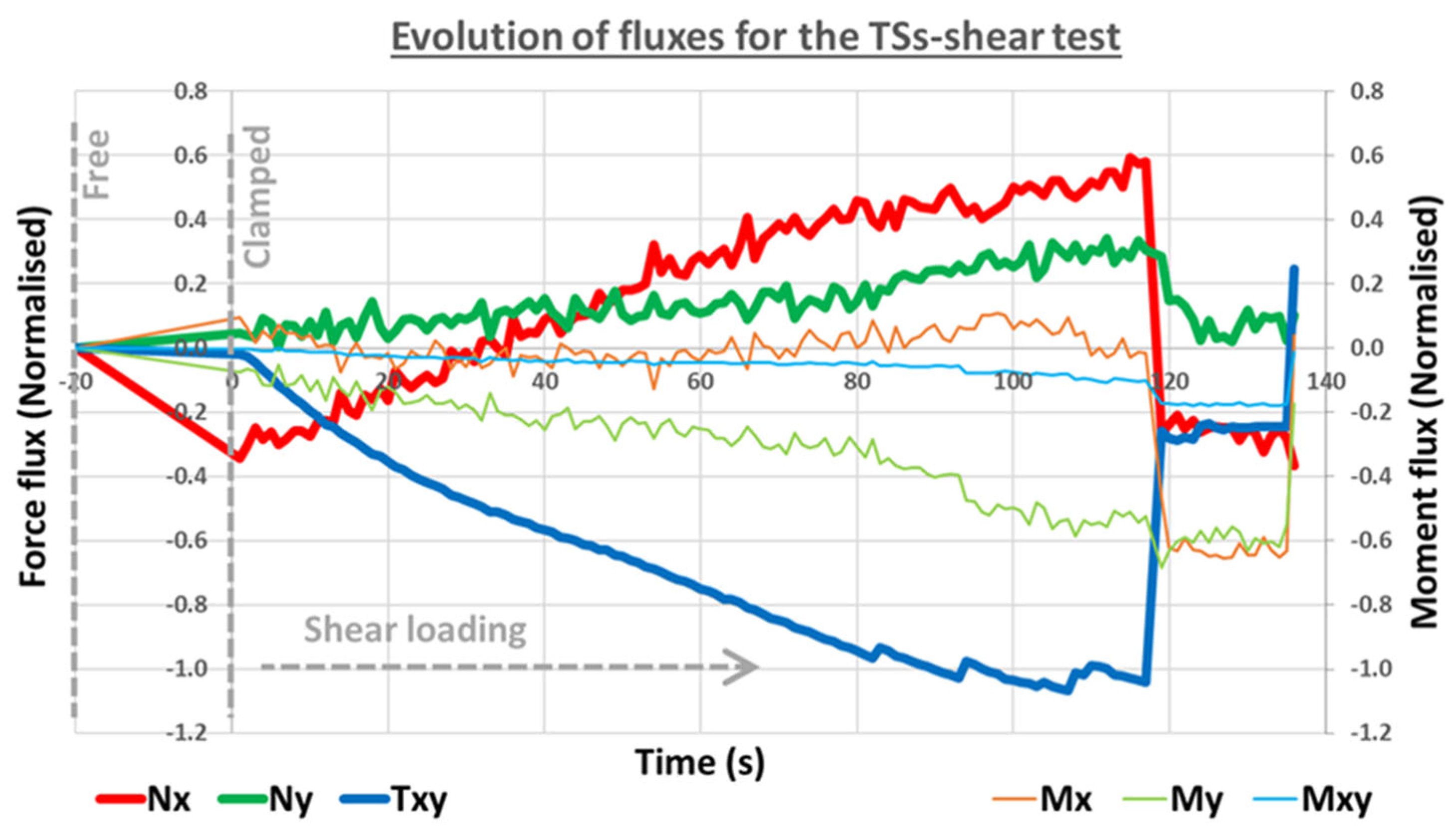
Figure 11.
Spatially averaged force and moment fluxes over time for the TSs-shear test [
47].
Figure 11.
Spatially averaged force and moment fluxes over time for the TSs-shear test [
47].
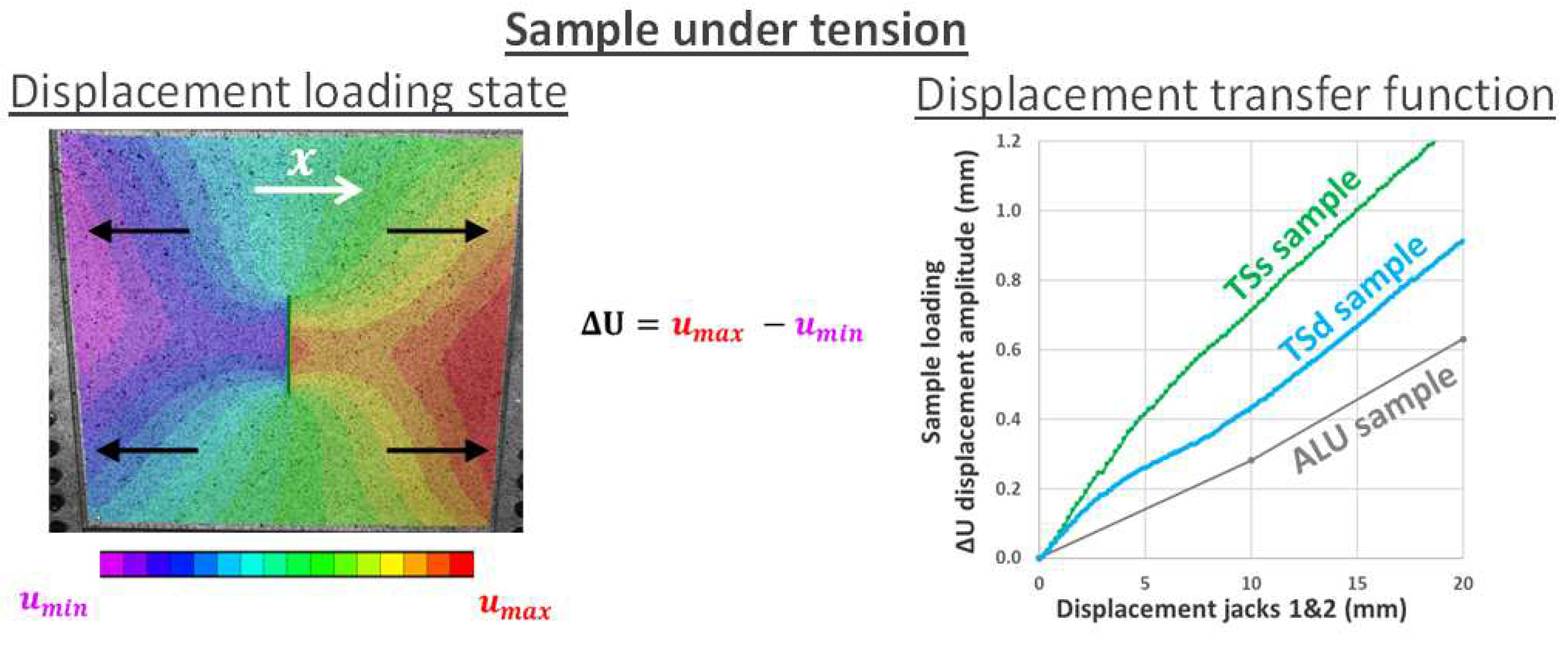
Figure 12.
Sample displacement amplitude in response to jack displacements, for three different samples under tension before failure - illustration of the bench loading dependency on the sample stiffness.
Figure 12.
Sample displacement amplitude in response to jack displacements, for three different samples under tension before failure - illustration of the bench loading dependency on the sample stiffness.
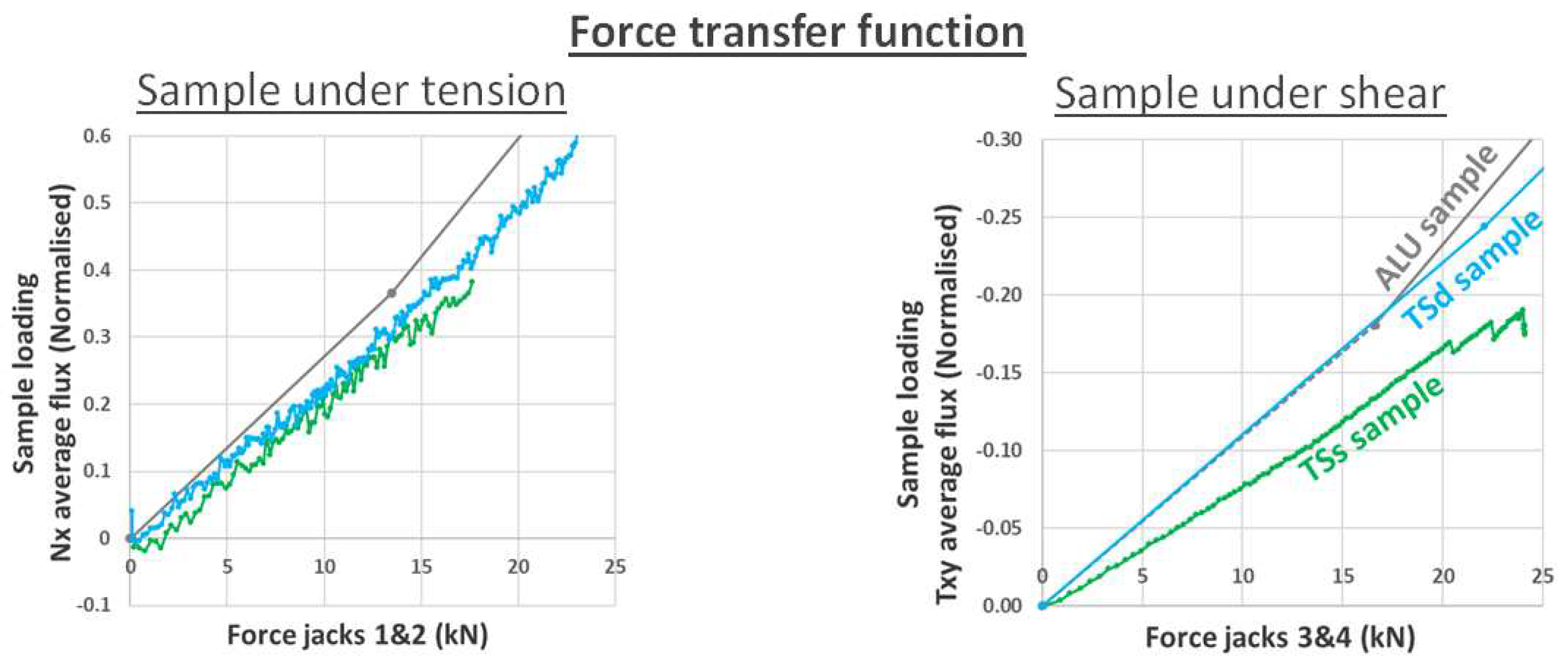
Figure 13.
Sample average force flux resulting from jack forces (referred to as force transfer function), for three different samples under tension and shear.
Figure 13.
Sample average force flux resulting from jack forces (referred to as force transfer function), for three different samples under tension and shear.
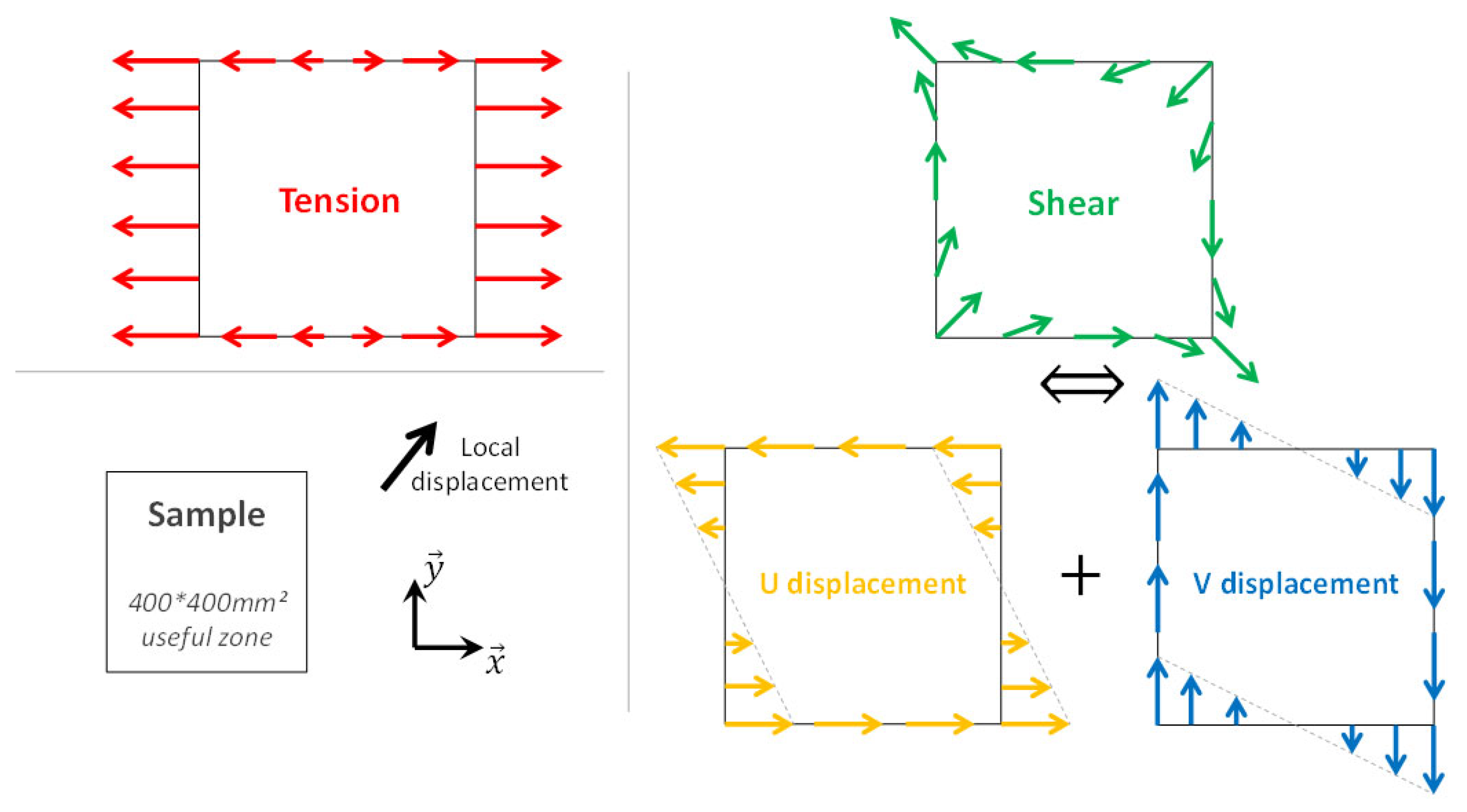
Figure 14.
Tension and shear idealized as homogeneous displacements imposed on the entire contour of a square panel.
Figure 14.
Tension and shear idealized as homogeneous displacements imposed on the entire contour of a square panel.
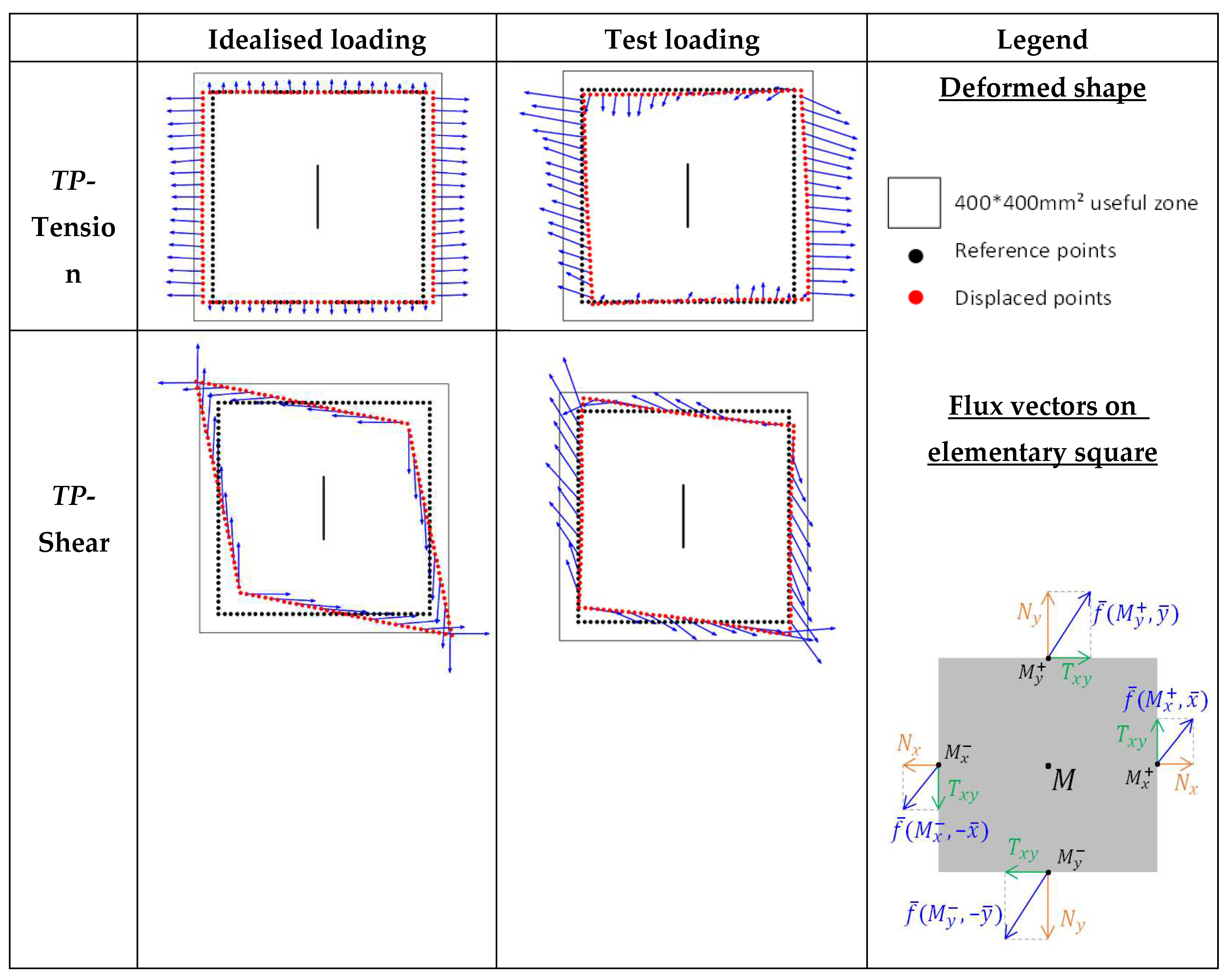
Figure 15.
Force flux (blue arrows) shapes with the VERTEX test rig (just before first failure) compared with ideal tension and shear, for a TP sample [
47].
Figure 15.
Force flux (blue arrows) shapes with the VERTEX test rig (just before first failure) compared with ideal tension and shear, for a TP sample [
47].
Figure 16.
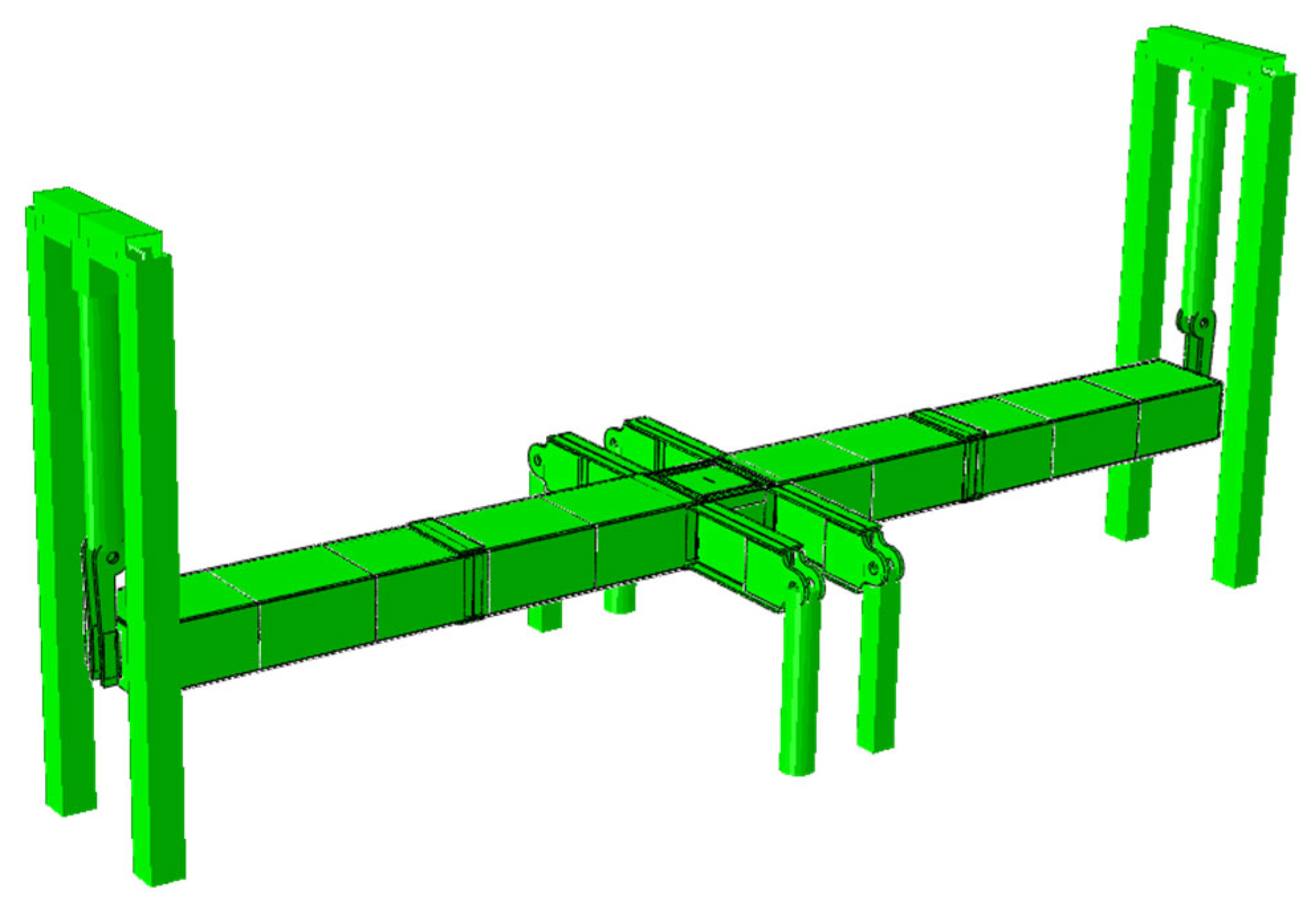
Finite element modelling of the VERTEX test rig, composed of thin shell and beam elements (shell-thickness and beam-section rendering enabled).
Figure 16.
Finite element modelling of the VERTEX test rig, composed of thin shell and beam elements (shell-thickness and beam-section rendering enabled).
Figure 17.
View of the model meshed parts, with the main occulting panels removed to appreciate the internal structure serving the parts assembly (shell-thickness and beam-section rendering enabled).
Figure 17.
View of the model meshed parts, with the main occulting panels removed to appreciate the internal structure serving the parts assembly (shell-thickness and beam-section rendering enabled).
Figure 18.
Picture showing the many bolts (black dots) composing the VERTEX test rig up to the sample, focusing on the central box (open-hole VERTEX sample, not presented here).
Figure 18.
Picture showing the many bolts (black dots) composing the VERTEX test rig up to the sample, focusing on the central box (open-hole VERTEX sample, not presented here).
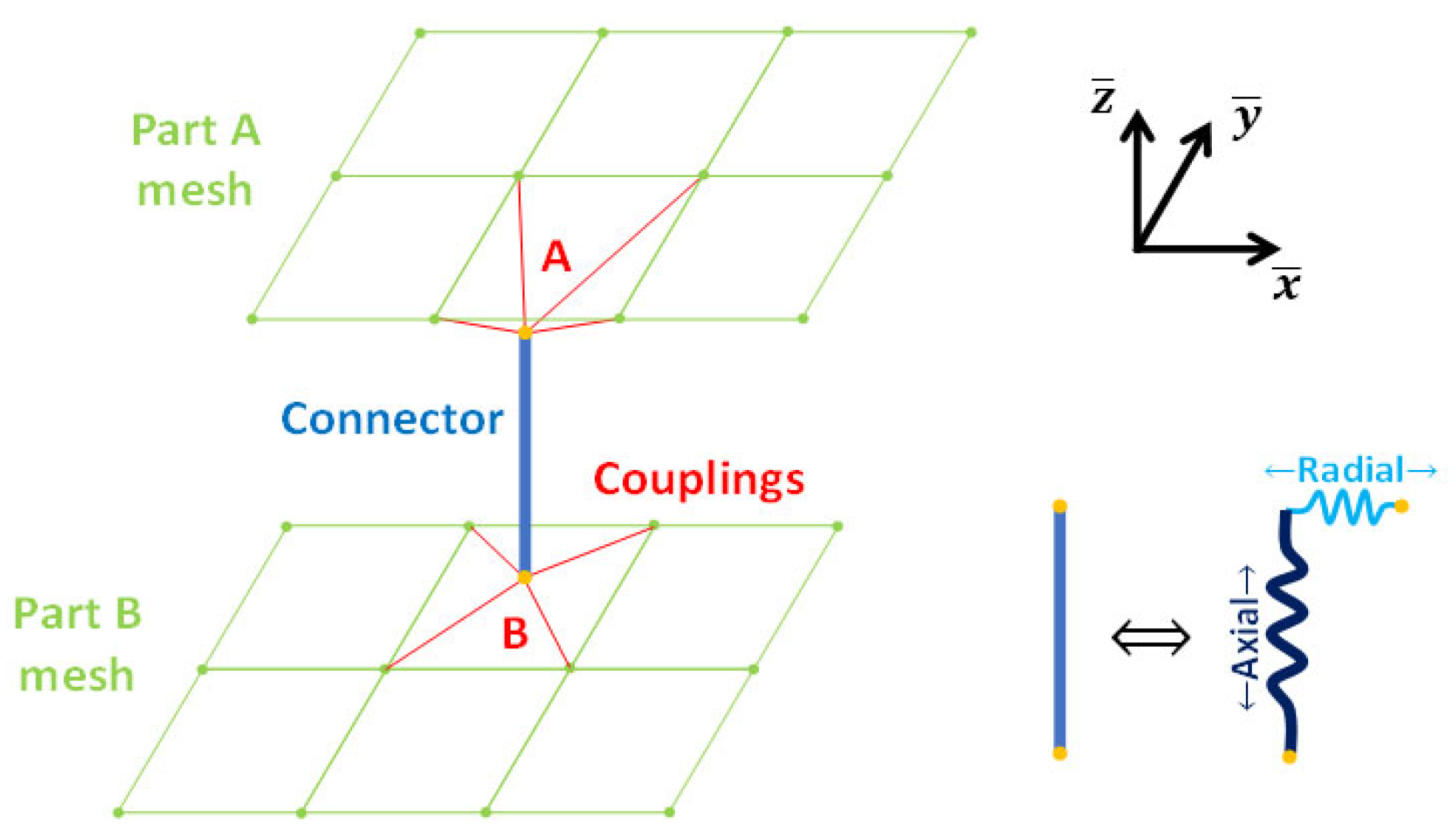
Figure 19.
Working principle of the modelling of bolted joint binding two parts, thanks to an intermediate connector tied to each part's nodes with a coupling.
Figure 19.
Working principle of the modelling of bolted joint binding two parts, thanks to an intermediate connector tied to each part's nodes with a coupling.
Figure 20.
Finite element meshing of the sample with only one element in the thickness to implement thick shell elements.
Figure 20.
Finite element meshing of the sample with only one element in the thickness to implement thick shell elements.
Figure 21.
Exploded view around the sample to illustrate the connector-coupling modelling of bolted joints – only a few couplings are plotted to avoid visualization overload.
Figure 21.
Exploded view around the sample to illustrate the connector-coupling modelling of bolted joints – only a few couplings are plotted to avoid visualization overload.
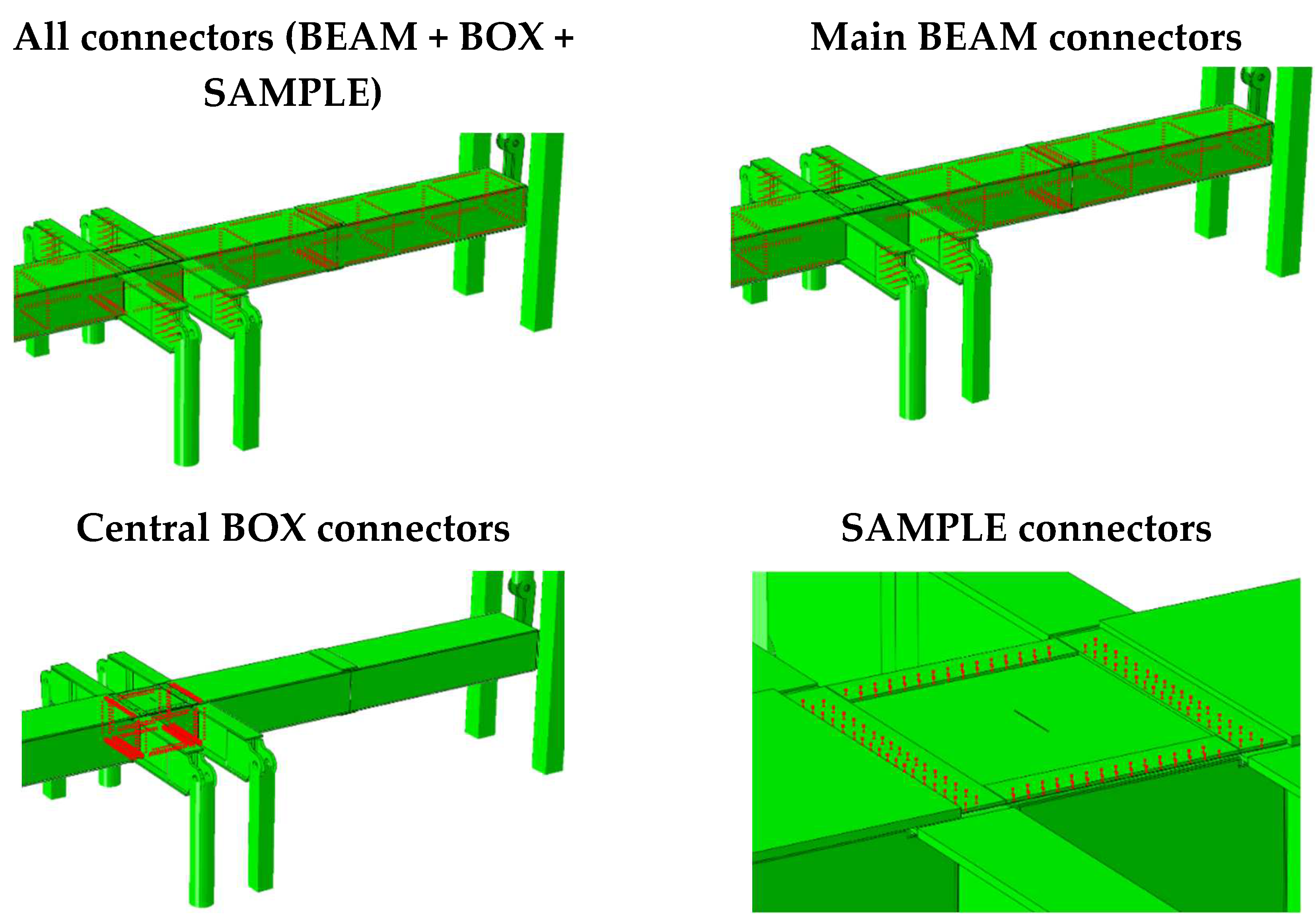
Figure 22.
Separation of all bolts of the VERTEX bench into three sets (main beam, central box, sample) to differentiate the stiffnesses of the connectors.
Figure 22.
Separation of all bolts of the VERTEX bench into three sets (main beam, central box, sample) to differentiate the stiffnesses of the connectors.
Figure 23.
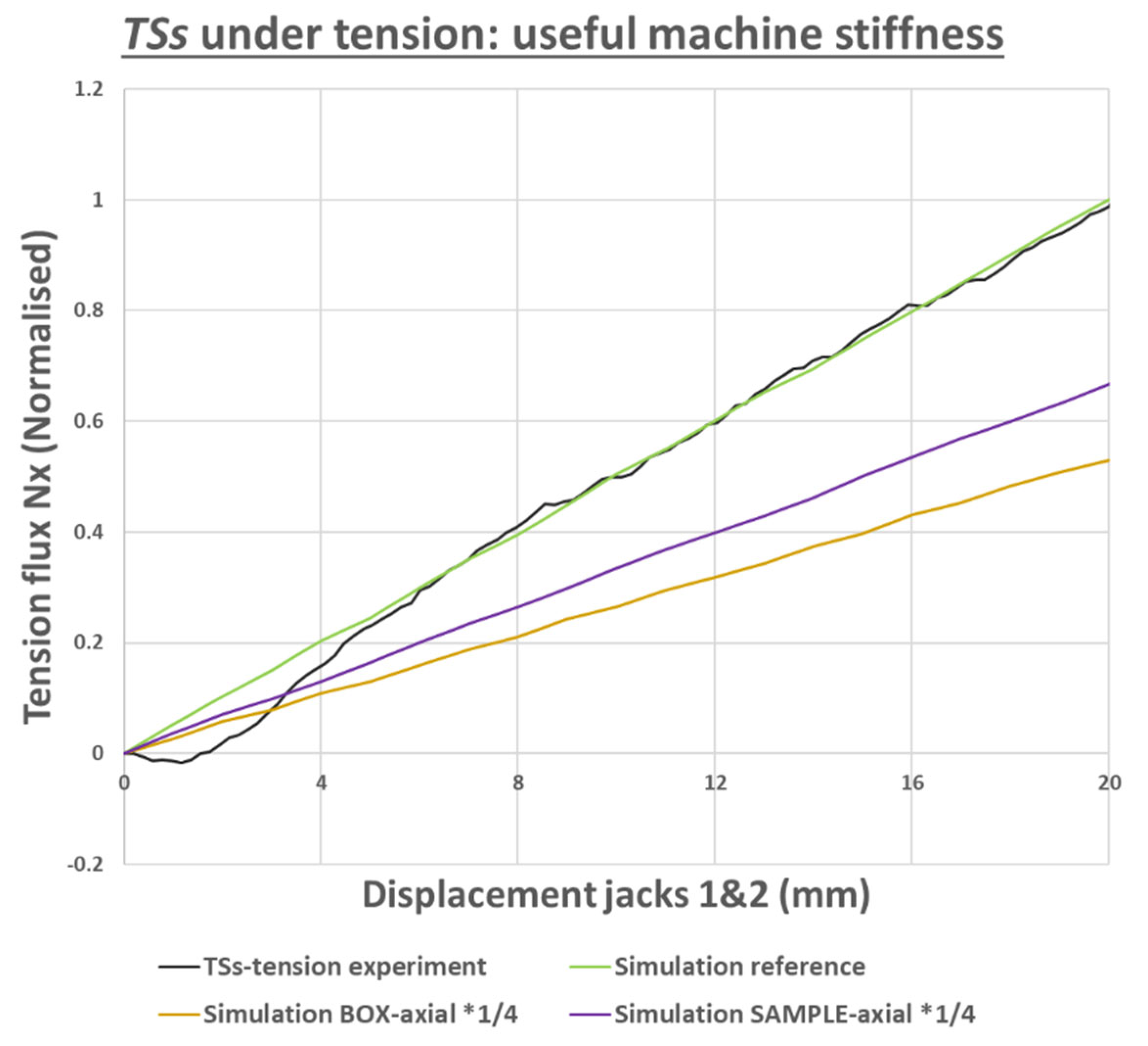
TSs sample under tension: effect of the variation of a few parameters on the machine useful stiffness and comparison with experiment.
Figure 23.
TSs sample under tension: effect of the variation of a few parameters on the machine useful stiffness and comparison with experiment.
Figure 24.
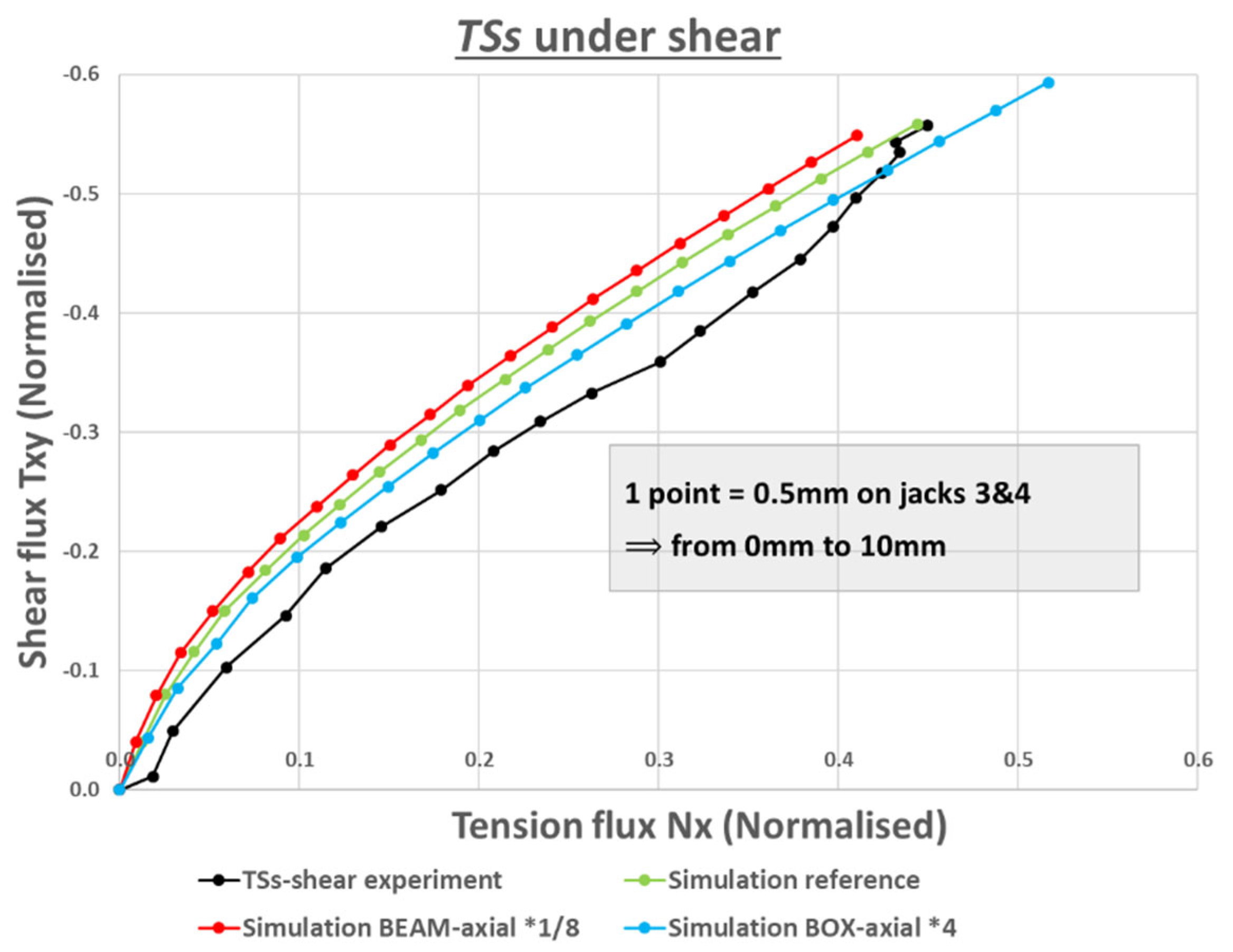
TSs sample under shear: effect of the variation of a few parameters on the machine tension shear coupling and the useful stiffness - comparison with experiment.
Figure 24.
TSs sample under shear: effect of the variation of a few parameters on the machine tension shear coupling and the useful stiffness - comparison with experiment.
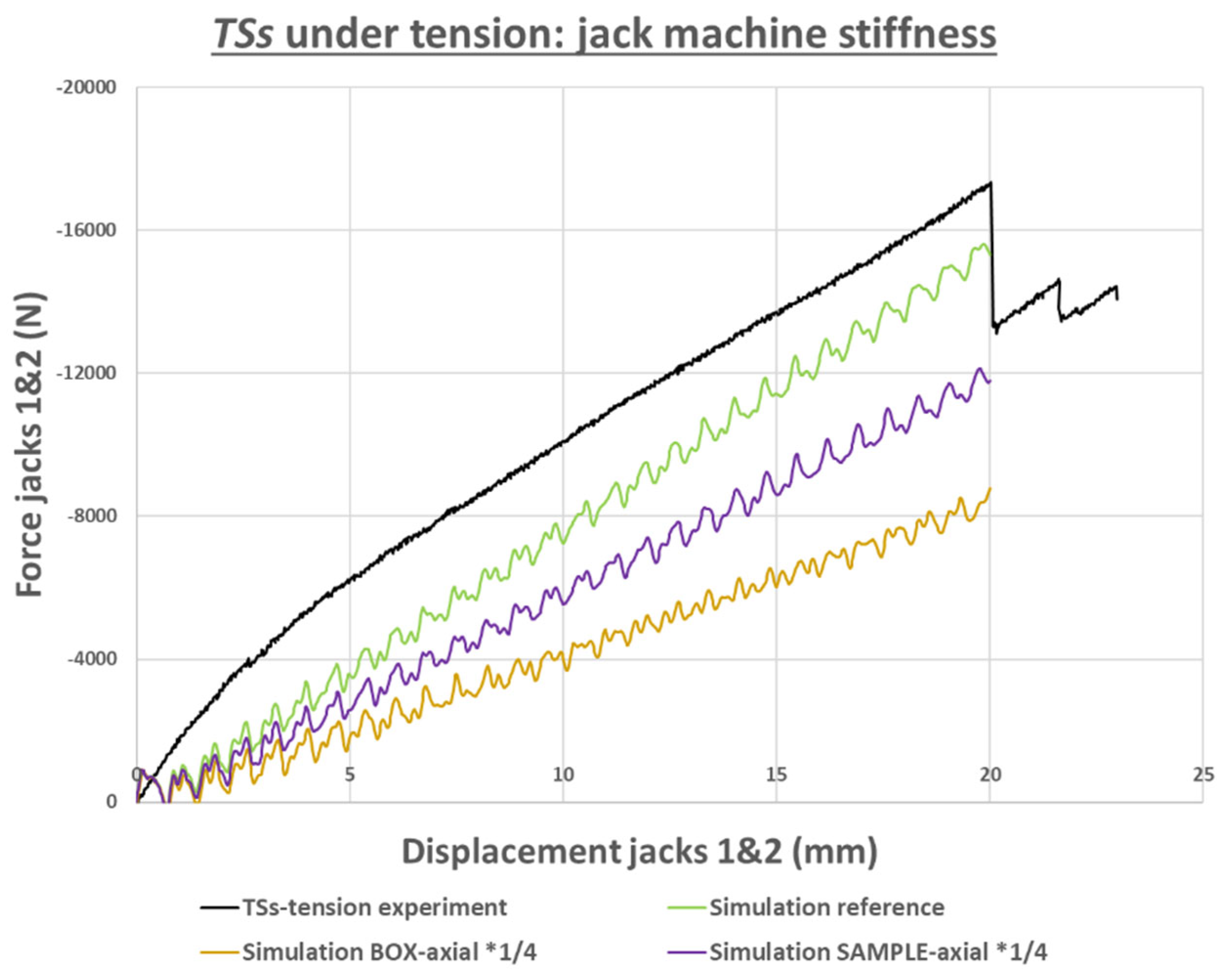
Figure 25.
TSs sample under tension: effect of the variation of a few parameters on the machine jack stiffness and comparison with experiment.
Figure 25.
TSs sample under tension: effect of the variation of a few parameters on the machine jack stiffness and comparison with experiment.
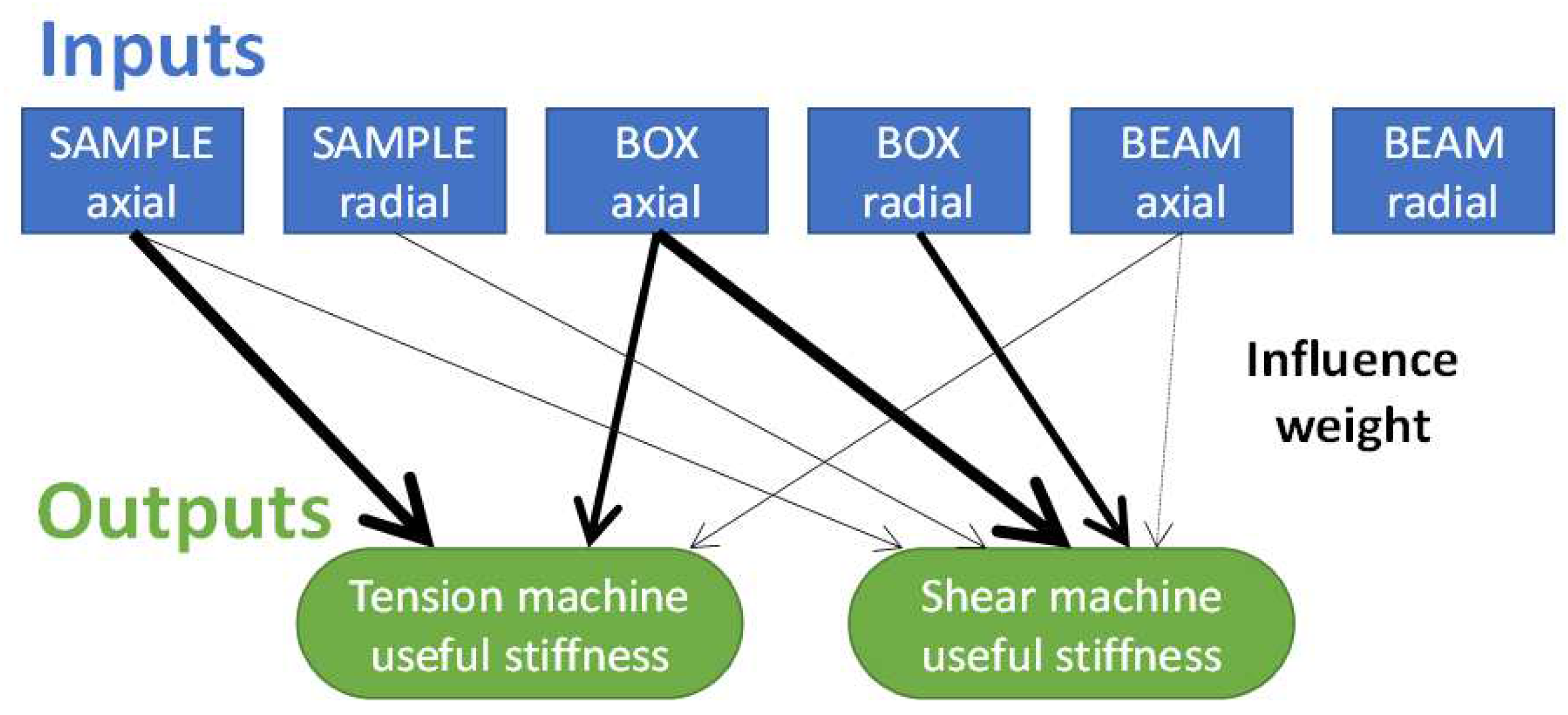
Figure 26.
Weight of influence (illustrated by the thickness of the arrows) of the input parameters on the main output features, obtained thanks to a sensitivity analysis on the VERTEX model with TSs and ALU samples.
Figure 26.
Weight of influence (illustrated by the thickness of the arrows) of the input parameters on the main output features, obtained thanks to a sensitivity analysis on the VERTEX model with TSs and ALU samples.
Figure 27.
Numerical prediction of the machine useful stiffness – experiment and simulation of the VERTEX bench loading a TP sample under tension.
Figure 27.
Numerical prediction of the machine useful stiffness – experiment and simulation of the VERTEX bench loading a TP sample under tension.
Figure 28.
Displacement fields of the TP sample under tension, before failure for the same Nx flux - (left) experiment with VERTEX test rig, (center) simulation with the VERTEX model, (right) simulation with ideal boundary conditions.
Figure 28.
Displacement fields of the TP sample under tension, before failure for the same Nx flux - (left) experiment with VERTEX test rig, (center) simulation with the VERTEX model, (right) simulation with ideal boundary conditions.
Figure 29.
Displacement fields of the TP sample under shear, before failure for the same Txy flux - (left) experiment with VERTEX test rig, (center) simulation with the VERTEX model, (right) simulation with ideal boundary conditions.
Figure 29.
Displacement fields of the TP sample under shear, before failure for the same Txy flux - (left) experiment with VERTEX test rig, (center) simulation with the VERTEX model, (right) simulation with ideal boundary conditions.
Figure 30.
Longitudinal tension test simulated on the bench model – the sample has been removed from the view and y displacements are highly exaggerated to visualize transverse compression caused by the bending of the bench's flanks towards the center.
Figure 30.
Longitudinal tension test simulated on the bench model – the sample has been removed from the view and y displacements are highly exaggerated to visualize transverse compression caused by the bending of the bench's flanks towards the center.
Figure 31.
Tension-shear coupling for numerical simulations of "shear" tests, coming from the Wagner effect and the machine behavior. (Yellow) Shear on a TP sample with the ideal boundary condition model, (red/grey) shear on a TP/ALU sample with the VERTEX bench model.
Figure 31.
Tension-shear coupling for numerical simulations of "shear" tests, coming from the Wagner effect and the machine behavior. (Yellow) Shear on a TP sample with the ideal boundary condition model, (red/grey) shear on a TP/ALU sample with the VERTEX bench model.
Figure 32.
Bolted joints of the VERTEX bench for a TSs sample under shear: radial force passing through each connector element, indicative of the bearing load of associated bolted joints. See
Figure 18 for a picture of the bolts with the same view.
Figure 32.
Bolted joints of the VERTEX bench for a TSs sample under shear: radial force passing through each connector element, indicative of the bearing load of associated bolted joints. See
Figure 18 for a picture of the bolts with the same view.
Figure 33.
Development of a corner-filleted sample geometry: investigation of the impact on the load shape, and refined hole meshing to assess conservative bearing loads.
Figure 33.
Development of a corner-filleted sample geometry: investigation of the impact on the load shape, and refined hole meshing to assess conservative bearing loads.
Figure 34.
Notch tip of a TSs sample under shear. Field of strain in the fiber direction of a specific ply: quantification of strain localization on the notch tip to evaluate failure criterion.
Figure 34.
Notch tip of a TSs sample under shear. Field of strain in the fiber direction of a specific ply: quantification of strain localization on the notch tip to evaluate failure criterion.
Figure 35.
Load shape severity on a TSs notched panel under tension: comparison of the simulated VERTEX bench and simulated ideal boundaries – maximum fiber strain against equivalent flux.
Figure 35.
Load shape severity on a TSs notched panel under tension: comparison of the simulated VERTEX bench and simulated ideal boundaries – maximum fiber strain against equivalent flux.
Figure 36.
First buckling modes and associated critical displacements of a TP sample for a VERTEX shear loading, obtained from a linear buckling analysis of the VERTEX model.
Figure 36.
First buckling modes and associated critical displacements of a TP sample for a VERTEX shear loading, obtained from a linear buckling analysis of the VERTEX model.
Table 1.
Samples considered, drawn from previous studies [
35,
36,
47,
51].
Table 1.
Samples considered, drawn from previous studies [
35,
36,
47,
51].
| Sample reference |
Material |
Central damage |
Thickness
(mm) |
| ALU |
aluminium AU4G1 |
None |
5 mm |
| TSs |
unidirectional CFRP tapes, thermoset |
100 mm notch |
~1 mm |
| TSd |
Same CFRP tapes as TSs |
100 mm notch |
double that of TSs |
| TP |
unidirectional CFRP tapes, thermoplastic |
100 mm notch |
~1 mm |
Table 2.
Connector stiffnesses identified for the VERTEX numerical model and behavior sensitivity to each parameter for the TSs test.
Table 2.
Connector stiffnesses identified for the VERTEX numerical model and behavior sensitivity to each parameter for the TSs test.
Parameter |
SAMPLE |
BOX |
BEAM |
| Axial |
Radial |
Axial |
Radial |
Axial |
Radial |
| Value (N/mm) |
10 000 |
5 000 |
10 000 |
10 000 |
80 000 |
100 000 |
| Influence on Tension |
+++ |
--- |
+++ |
--- |
+ |
--- |
| Influence on Shear |
+ |
+ |
++ |
++ |
- |
-- |