Discrete-Analog Low-Pass Filter Using Switched Capacitors With Resistive Pole Frequency Control

1. Introduction

Despite the fact that the digital transformation of industrial production makes extensive use of digital analog signal processing methods, they are redundant in some cases. As a consequence, discrete-analog processing, which combines the main advantages of analog-digital methods, is very promising. Thus, discrete-analog filters on switched capacitors (DAF), produced by dozens of leading microelectronic companies in the world, incl. Texas Instruments (USA), Maxim (USA), CYPRESS (USA), Analog Devices (USA), etc., provide a significant gain (in comparison with classic digital and analog filters) in size, cost, accuracy, functionality and are an effective means construction of frequency selection circuits and processing of analog signals in science and technology.

Discrete-analog switched capacitor filters and their practical applications have become the subject of intense intellectual property protection in almost every country in the world over the past 30 years [1,2,3,4,5,6]. The most promising DAF solutions [1,2,3,4,5,6] are patented by companies in the USA, Japan, France, Taiwan, China, Germany, Great Britain, Italy, etc.

The main goal and novelty of the article is to create and study a discrete-analog low-pass filter (LPF) based on switched capacitors [7], with adjustment of the pole frequency by changing the resistance ratio of additional resistors at a fixed switching frequency of electronic switches.

2. Discrete-Analog Low-Pass Filter with Resistive Pole Frequency Adjustment

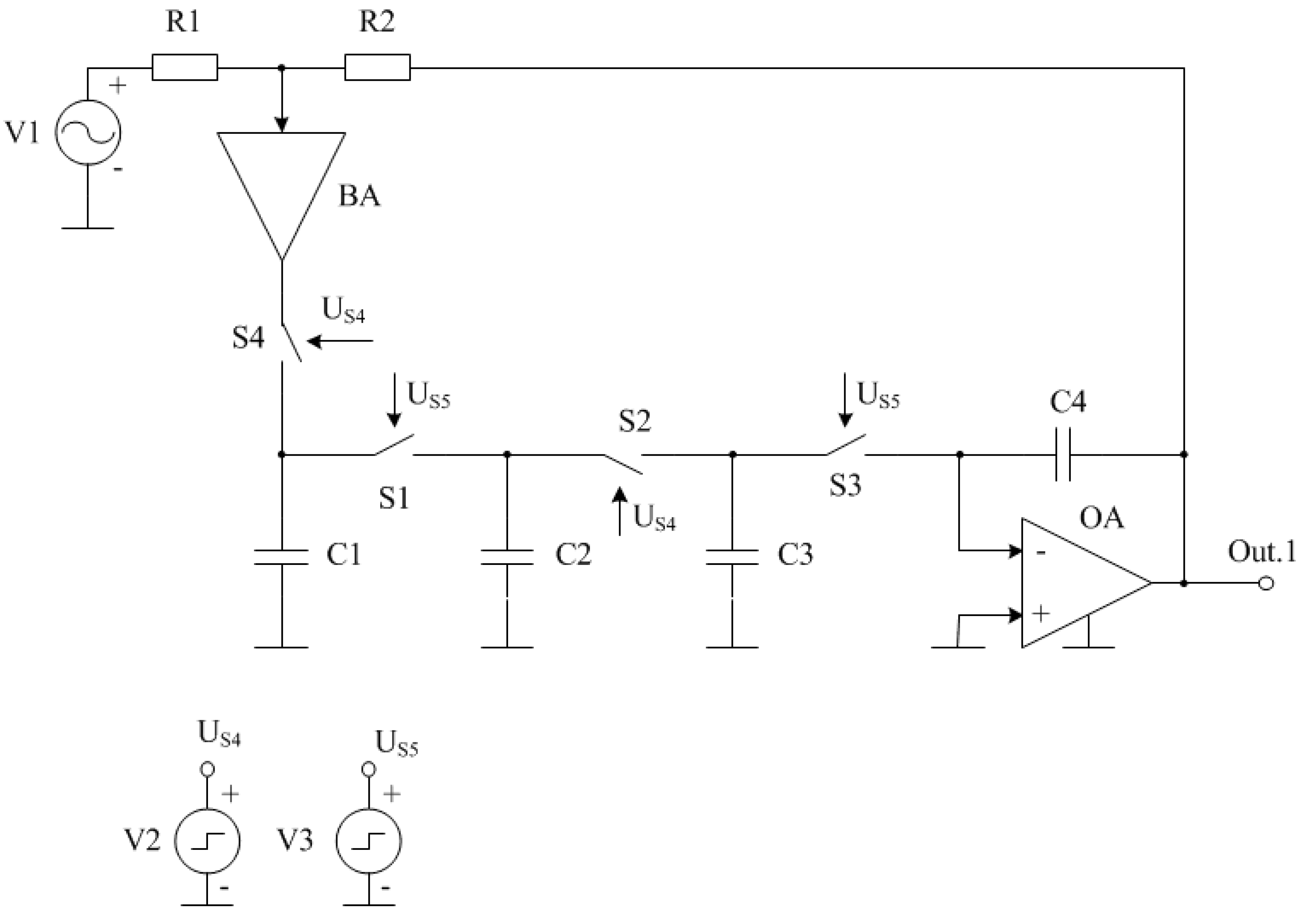
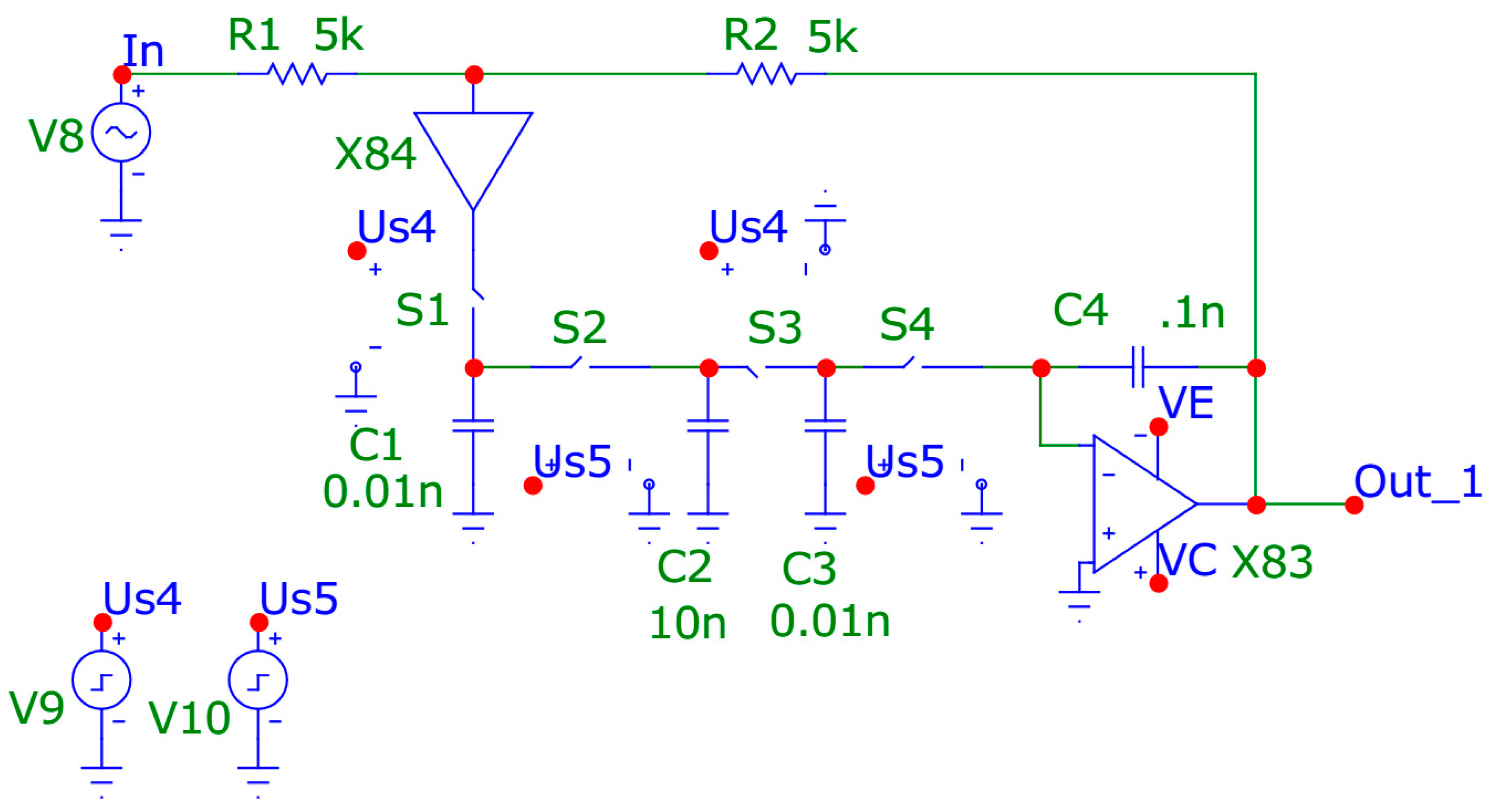
Figure 1 shows the developed DAF [7], where three frequency-setting capacitors C1, C2 and C3 are connected to a common bus, which increases the manufacturability of the DAF in microelectronic design. On Figure 1 designated is BA - buffer amplifier, OA – operational amplifier, Us4, Us5 – voltage applied to electronic keys.

With sequential and periodic closure of the first S1 and third S3, as well as the second S2 and fourth S4 electronic keys, in conditions where the frequency switching frequency of electronic keys $f_s$ much higher than the pole frequency $f_p=\frac{{\omega }_p}{2\pi }$ of the second-order link, as a result of mathematical analysis of the DAF circuit in Figure 1 it can be shown that this circuit implements the transfer function of a second-order low-pass filter (LPF) in the low-frequency region.

$$F\left(p\right)=\frac{M_0{\omega }_p}{p^2+{\mathit{pd}}_p{\omega }_p+{\omega }_p^2}\hspace{0.17em}\hspace{0.17em},$$

(1)

the main parameters of which are found using the following formulas:

-

LPF transmission coefficient at zero frequency

$$M_0=-\frac{R_2}{R_1}\hspace{0.17em}\hspace{0.17em},$$

(2)

-

LPF transmission coefficient at the pole frequency

$${\mathrm{M}}_{{\omega }_p}=-\frac{\frac{R_2}{R_1}\sqrt{\frac{R_1}{R_1+R_2}}}{\sqrt{\frac{C_1{C}_4}{C_2{C}_3}}+\sqrt{\frac{C_3{C}_4}{C_2{C}_1}}}\hspace{0.17em}\hspace{0.17em},$$

(3)

-

pole frequency

$${\omega }_p=f_s\sqrt{\frac{C_1{C}_3}{C_2{C}_4}}\sqrt{\frac{R_1}{R_1+R_2}}=\frac{1}{T}\sqrt{\frac{C_1{C}_3}{C_2{C}_4}}\sqrt{\frac{R_1}{R_1+R_2}}\hspace{0.17em}\hspace{0.17em},$$

(4)

-

pole attenuation

$$d_p=\sqrt{1+\frac{R_2}{R_1}}\left(\sqrt{\frac{C_1{C}_4}{C_2{C}_3}}+\sqrt{\frac{C_3{C}_4}{C_2{C}_1}}\right)\hspace{0.17em}\hspace{0.17em}.$$

(5)

In formula (4), $f_s$ is the switching frequency of electronic keys, and $T=1/f_s$ is their switching period, R₁ and R₂ are the resistances of the first R1 and second R2 additional resistors, C₁, C₂, C₃ and C₄ are the capacitances of the first C1, the second C2, third C3 and fourth C4 frequency-setting capacitors, respectively.

Thus, the frequency of the low-pass filter pole (formula (4)) depends both on the ratio of the capacitances of the frequency-setting capacitors and on the ratio of the resistances of additional resistors R1 and R2. Consequently, with constant C1, C2, C3, C4 and $f_s$, the frequency of the low-pass filter pole can be changed by the ratio of resistances R2 to R1.

On Figure 2 shows the developed filter circuit (Figure 1) in the Micro-Cap program [8].

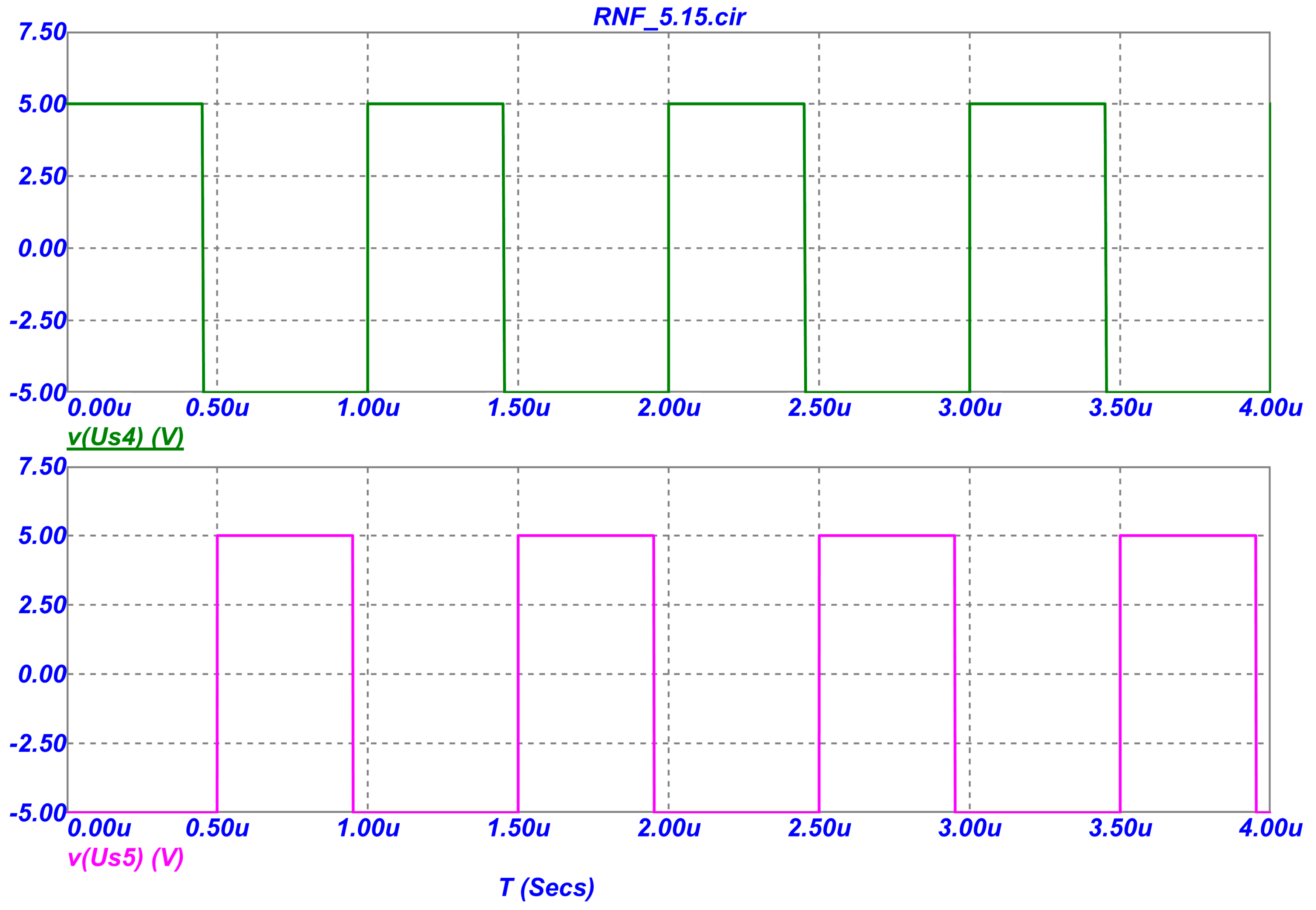
As control signals, the first S1, second S2, third S3 and fourth S4 electronic keys of DAF (Figure 1) use sequences of rectangular pulses, the oscillograms of which are shown in Figure 3.

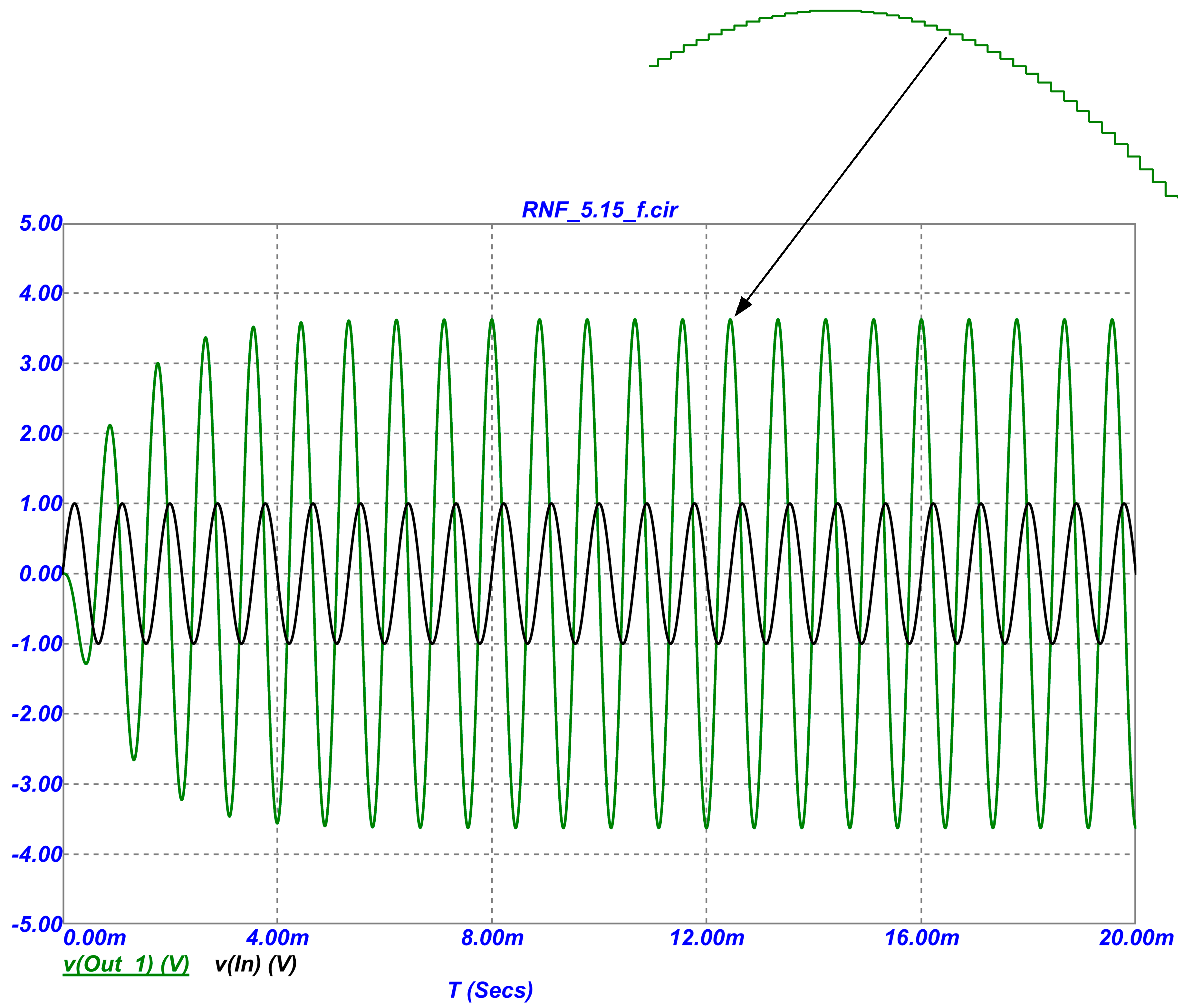
Figure 4 shows the response of the circuit in Figure 2 (its output voltage v(Out_1)) to the input sinusoidal signal v(In) with an amplitude of 1V and a frequency of 1125 Hz, which, with the parameters of the elements indicated in the diagram in Figure 2 and the switching frequency of electronic keys is 1 MHz (their period is 1μs) is equal to the pole frequency $f_p$, implemented by the circuit. In accordance with formula (3), at this frequency with the selected parameters of the elements, the transmission coefficient of the DAF is equal to $M_{{\omega }_p}=$-3.53. To obtain smaller absolute values of $M_{{\omega }_p}$, the parameters of the elements included in formula (3) should be selected accordingly. In the case of constructing a high-order filter, the numerical values of $M_{{\omega }_p}$ for each link included in such a filter structure may be chosen differently, incl. $M_{{\omega }_p}$=-1.

In Figure 4 also shows (on an enlarged scale) the graph of the DAF output signal Figure 2, which is “stepwise” in nature. The stepwise nature of the DAF output signal corresponds to the physical processes of signal conversion in filters of the class under consideration.

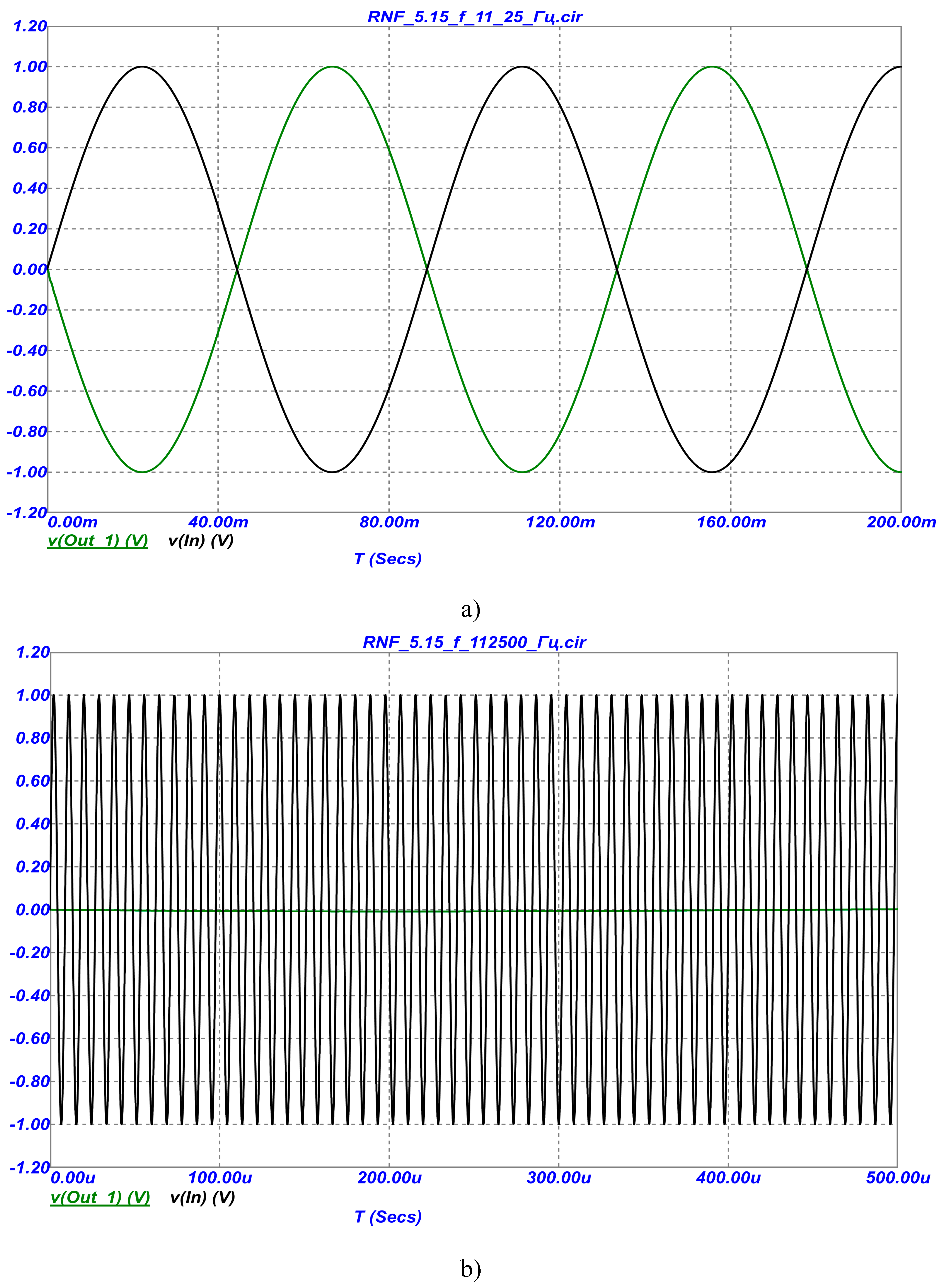
Figure 5 (a, b) shows the results of modeling the developed DAF in the range of very low (100 times lower than the pole frequency, Figure 5(a)) and high (100 times higher than the pole frequency, Figure 5(b)) frequencies (compared to pole frequency (4)).

3. Conclusion

The developed discrete-analog filter [7] has significant advantages in comparison with the well-known DAF [9] - in it, the pole frequency depends not only on the ratio of the capacitances of the frequency-setting capacitors, but also on the ratio of additional resistors in the feedback circuit. At constant values of the frequency-setting capacitors, the pole frequency can be set by changing the ratio of the resistances of the additional resistors. In addition, in the considered circuit, the first C1 and third C3 frequency-setting capacitors are connected with one output to a common power supply bus, which simplifies its microelectronic design.

The studied DAF [7] has the properties of a low-pass filter - it has a transmission coefficient close to minus one at very low frequencies (M₀=-1 at R₁=R₂) and a transmission coefficient close to zero at higher frequencies.

Computer simulation performed in the Micro-Cap environment confirms the performance of the proposed DAF as a second-order low-pass filter.

The research has been carried out at the expense of the Grant of the Russian Science Foundation (project No. 23-79-10023).