Submitted:
13 November 2023
Posted:
14 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Definitions
| initial and final population size | |
| r | growth rate |
| marker mutation rate of wildtype | |
| marker mutation rate of mutator | |
| rate of mutation from wildtype to mutator | |
| m | factor by which wildtype and mutator mutation rates differ: |
| recruitment rate of mutations; e.g. for marker recruitment rate on the wildtype background | |
| probability that a mutation appearing at time t leaves k mutants in the final population | |
| expected number of mutations of “type k”, i.e., that leave k mutants in the final population | |
| time at which population attains its maximum size: | |
| total number of marker mutations that occur on the wildtype background: | |
| total number of mutator mutations that occur on the wildtype background: | |
| pgf for the total number of mutants observed in the final population, given that a total of mutations occurred during growth. | |
| fast Fourier transform of function f. | |
| likelihood function for the i-th growth cycle. | |
2.2. Experimental Protocol
- Grow a bacterial population from initial size to a large (known) number, N, at time T.
-
At time T:
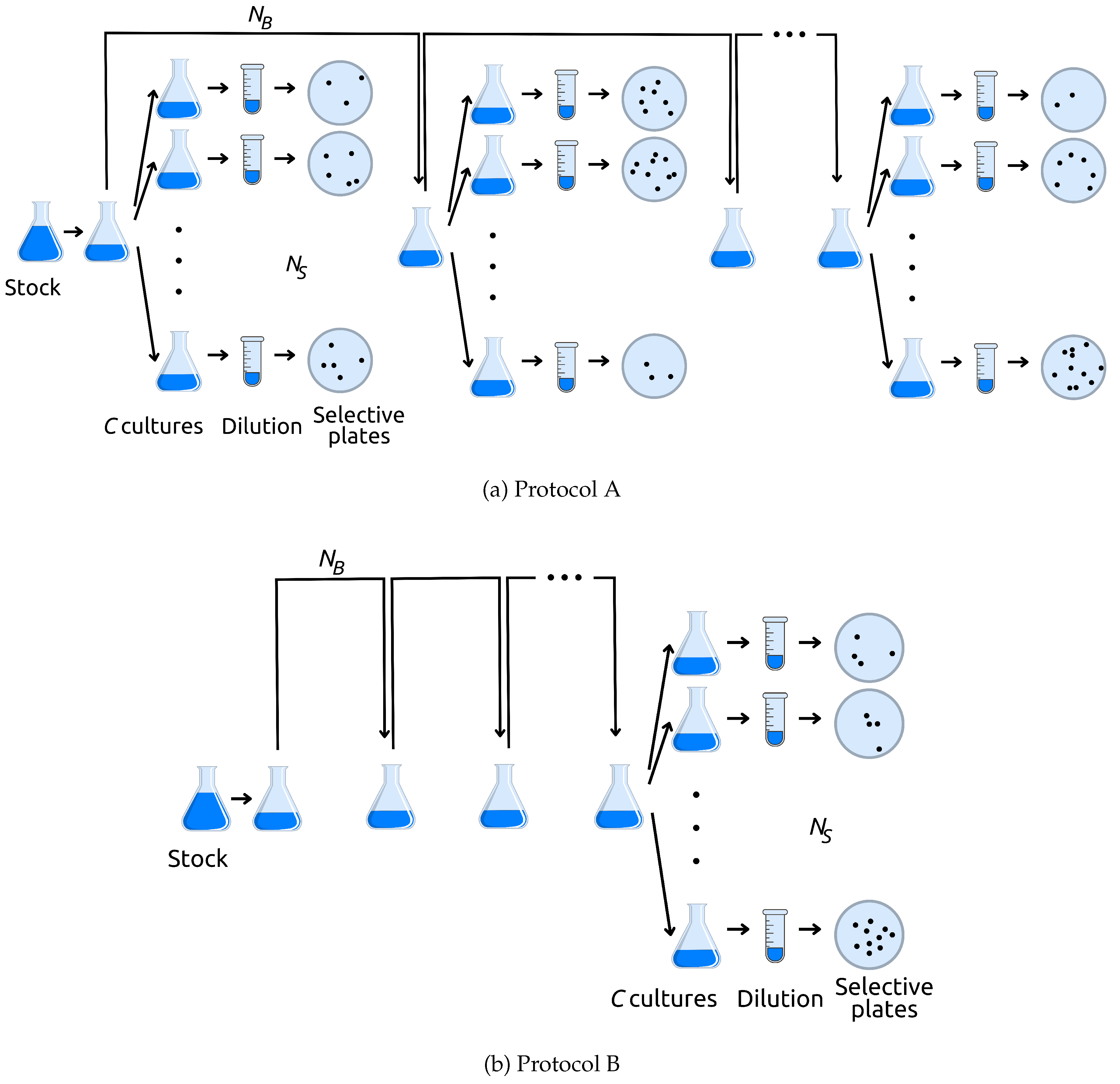
- Protocol A: Take two random samples of size and , where (S for sample, and B for bottleneck). Use the sample of size to inoculate a number c of flasks with fresh media; these independent cultures grow and each is then screened for marker mutants. Record the number of marker mutants observed in each of the c cultures. Use the sample of size to inoculate fresh media in a single flask to start the next growth cycle.
- Protocol B: Take one random sample of size to inoculate fresh medium to start the next growth cycle.
- Repeat Step 2 times (for n growth cycles)
- After the final growth cycle, take one random sample of size . Use this sample to inoculate a number c of flasks with fresh media; these independent cultures grow and each is then screened for marker mutants. Record the number of marker mutants observed in each of the c cultures.
2.3. Analysis
| Numbers of marker mutants | |||
| Growth cycle | |||
| Culture | 1 | 2 | 3 |
| 1 | 1 | 6 | 9 |
| 2 | 1 | 9 | 13 |
| 3 | 4 | 8 | 19 |
| 4 | 23 | 8 | 15 |
| 5 | 5 | 8 | 13 |
| 6 | 3 | 5 | 14 |
| 7 | 12 | 3 | 9 |
| 8 | 1 | 7 | 7 |
| 9 | 8 | 8 | 13 |
| 10 | 4 | 5 | 7 |
| 11 | 1 | 7 | 8 |
| 12 | 3 | 10 | 12 |
2.3.1. Incorporating mutators
2.4. Model fitting and validation
3. Results
3.1. Model reliability
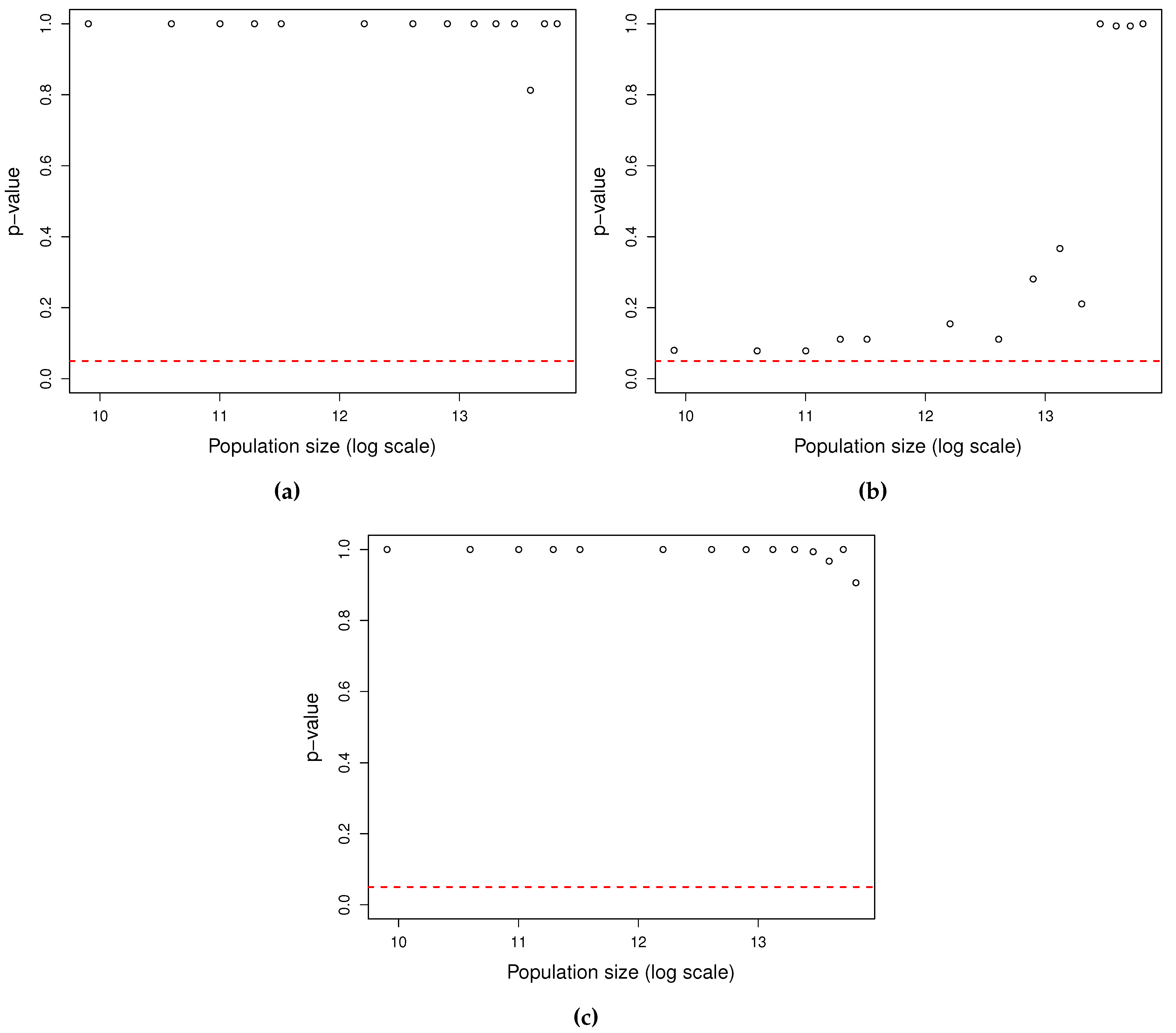
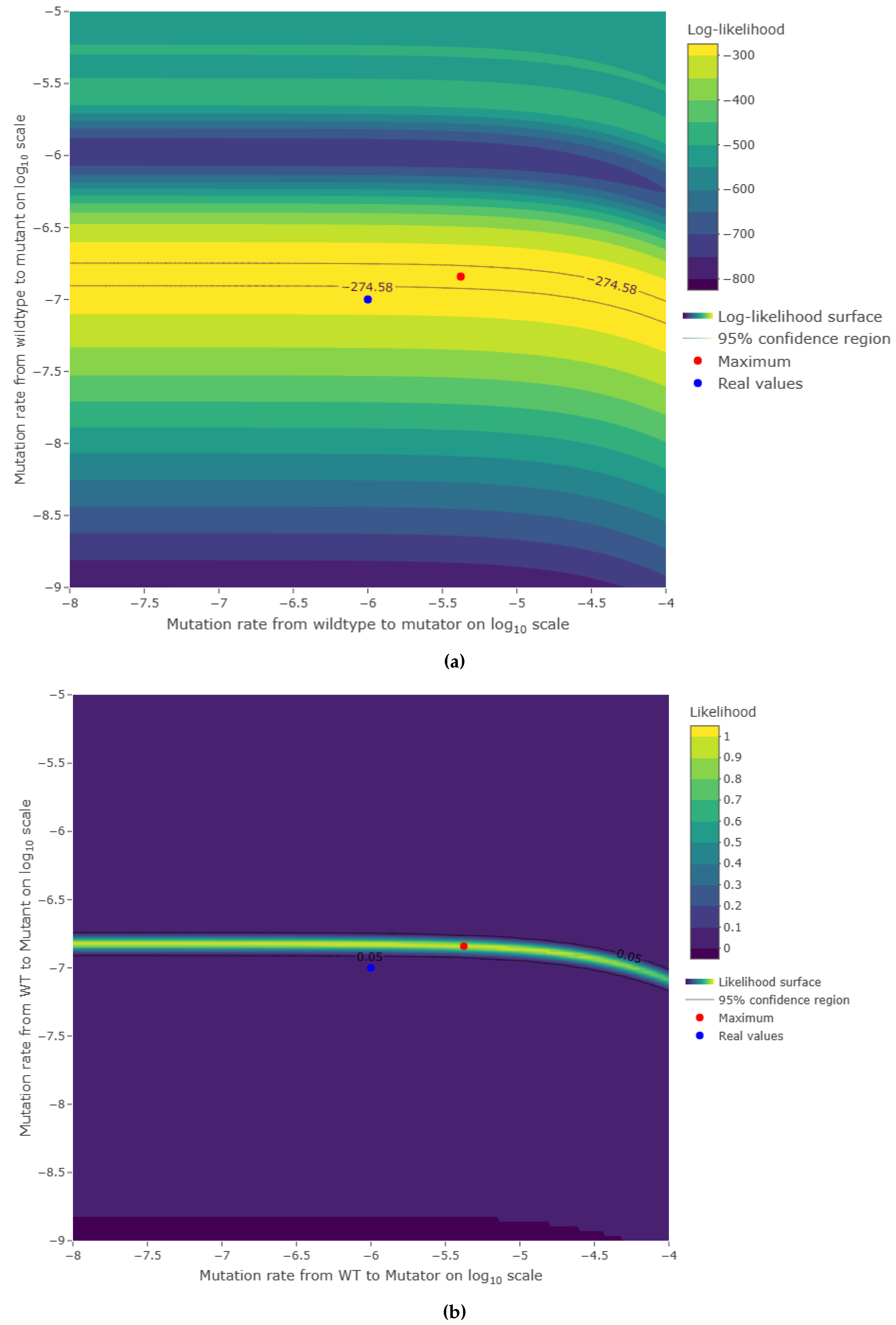
3.2. Estimations reliability
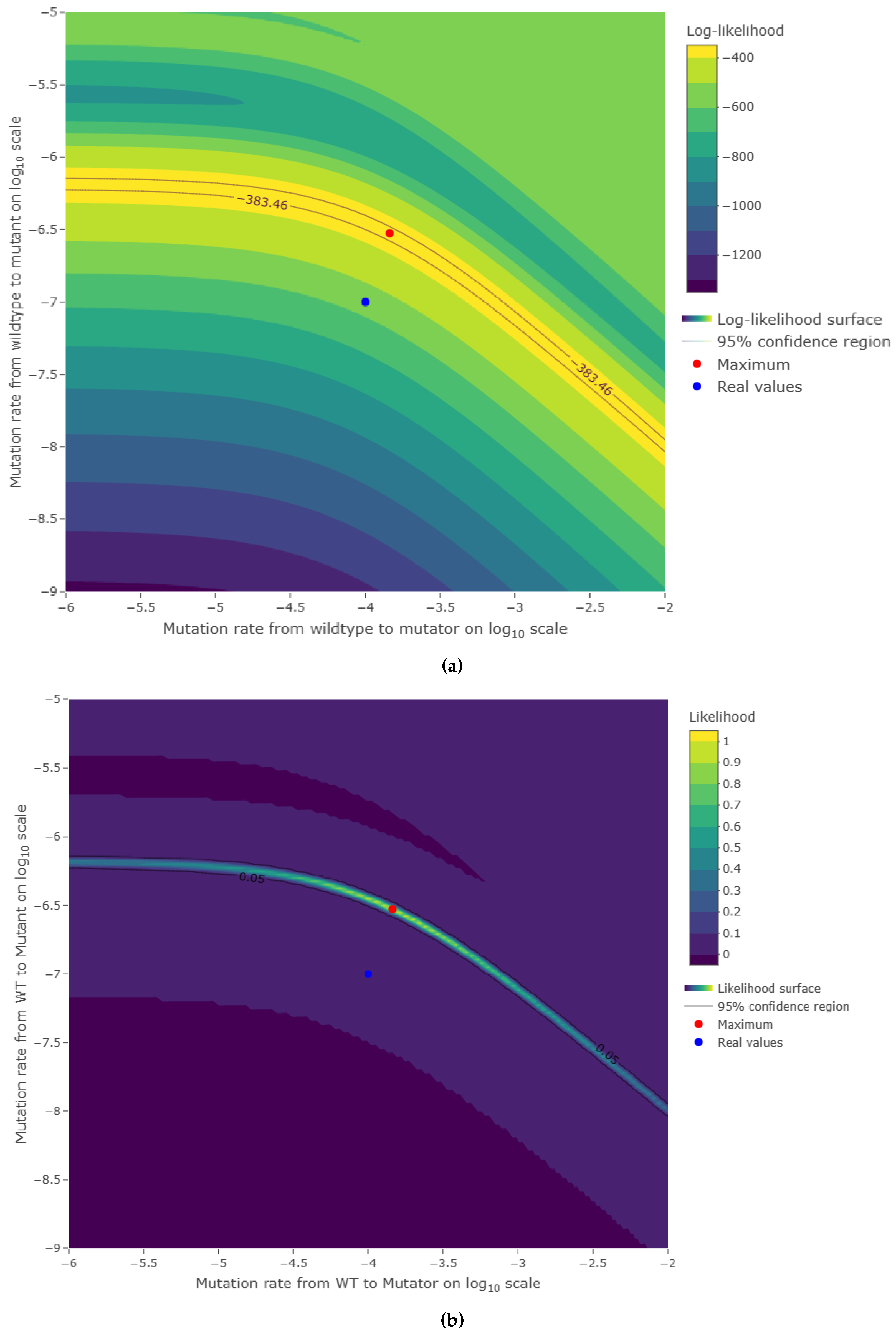
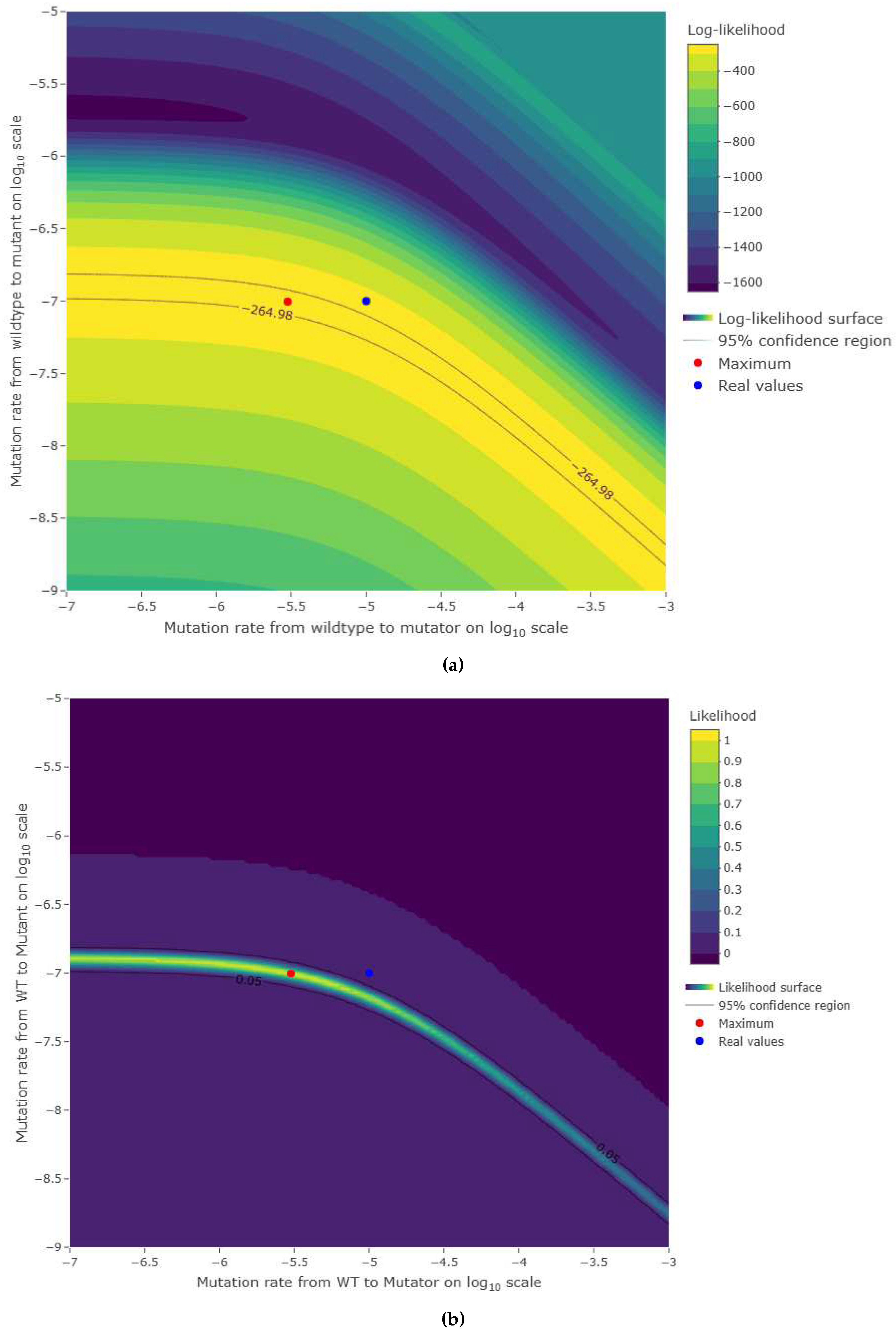
4. Discussion
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MLE | maximum likelihood estimation |
| pgf | probability generating function |
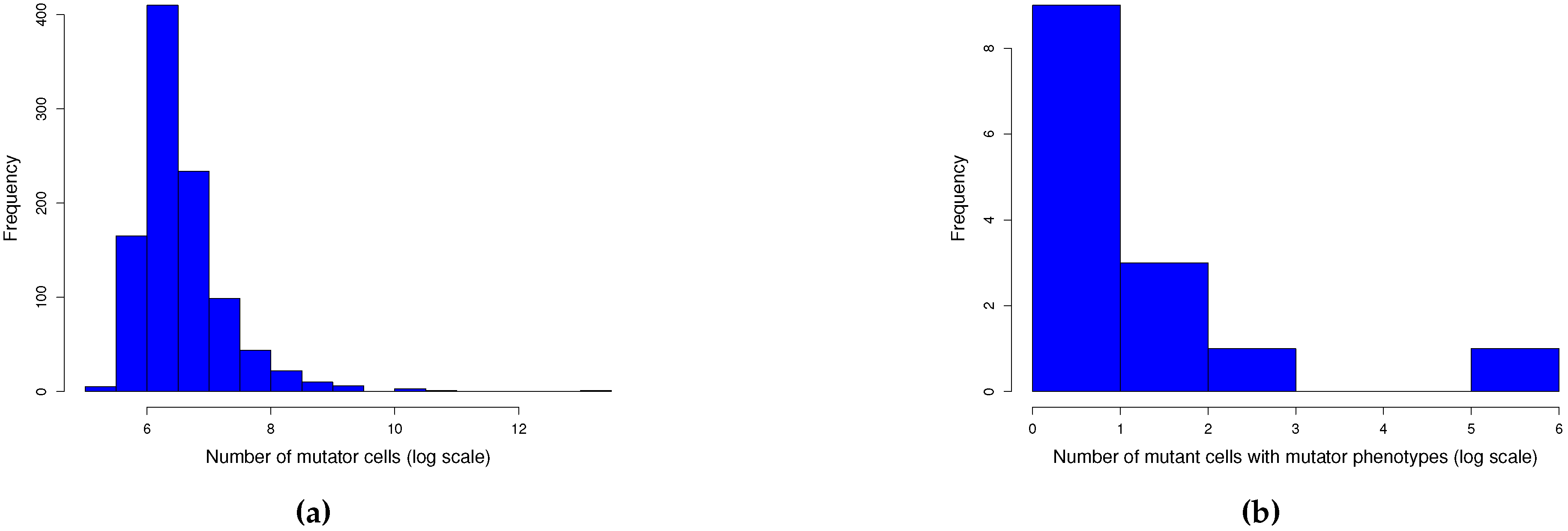
Appendix A. Simulations
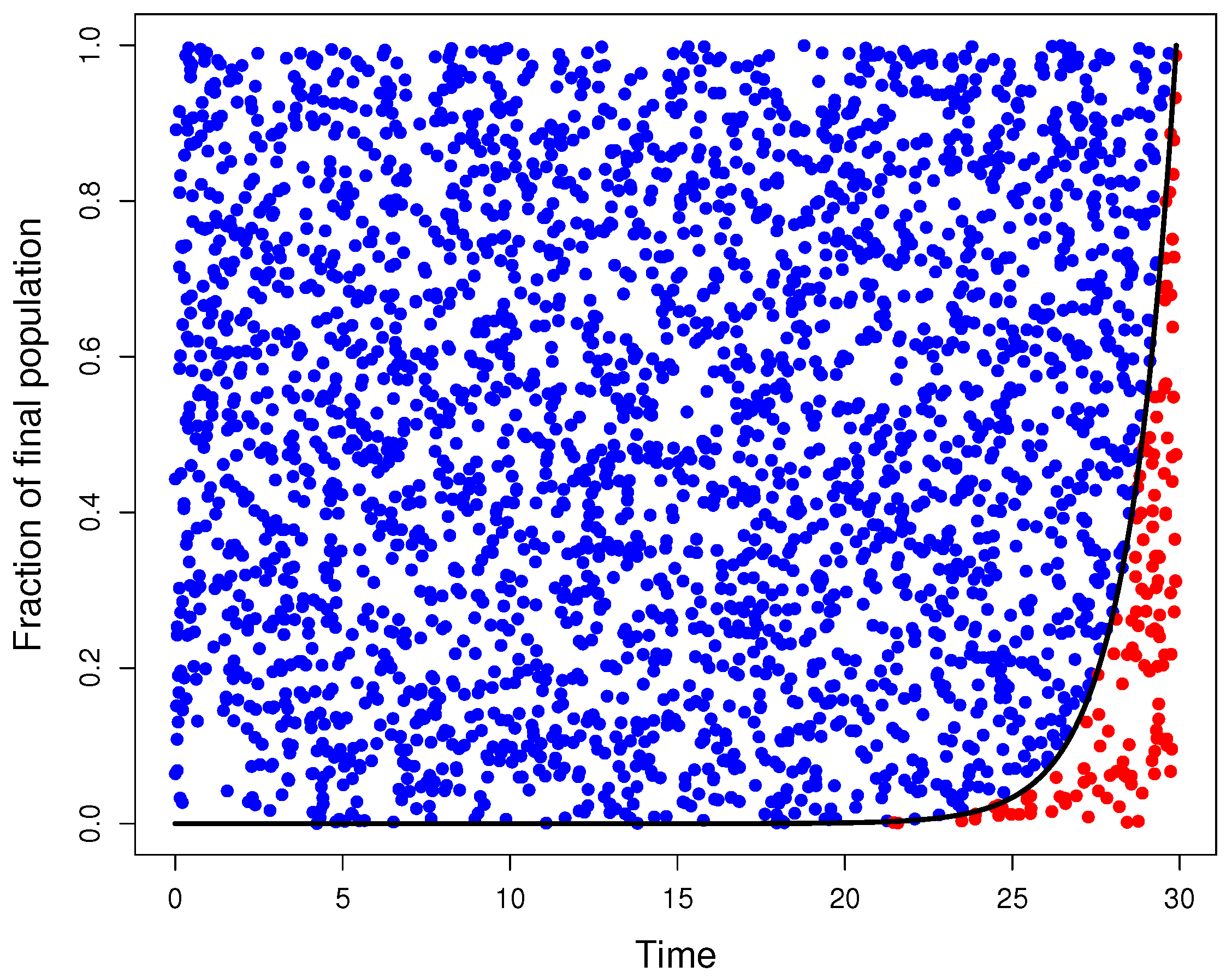
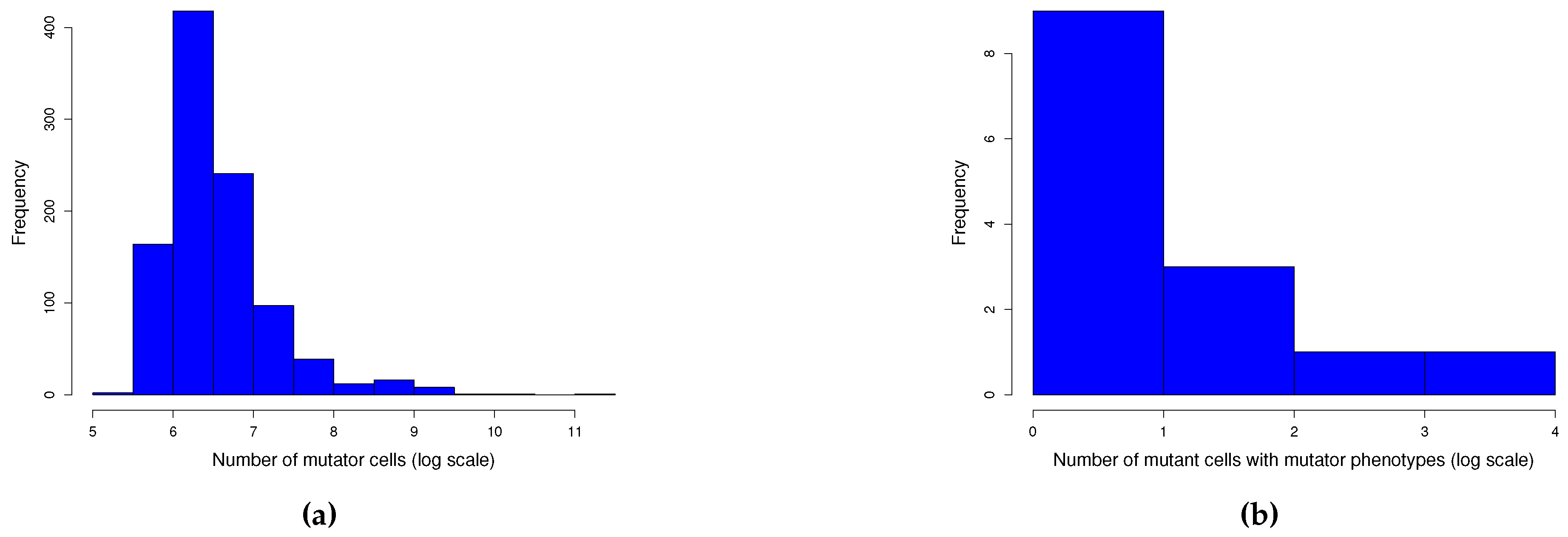
Appendix A.1. Graphical model
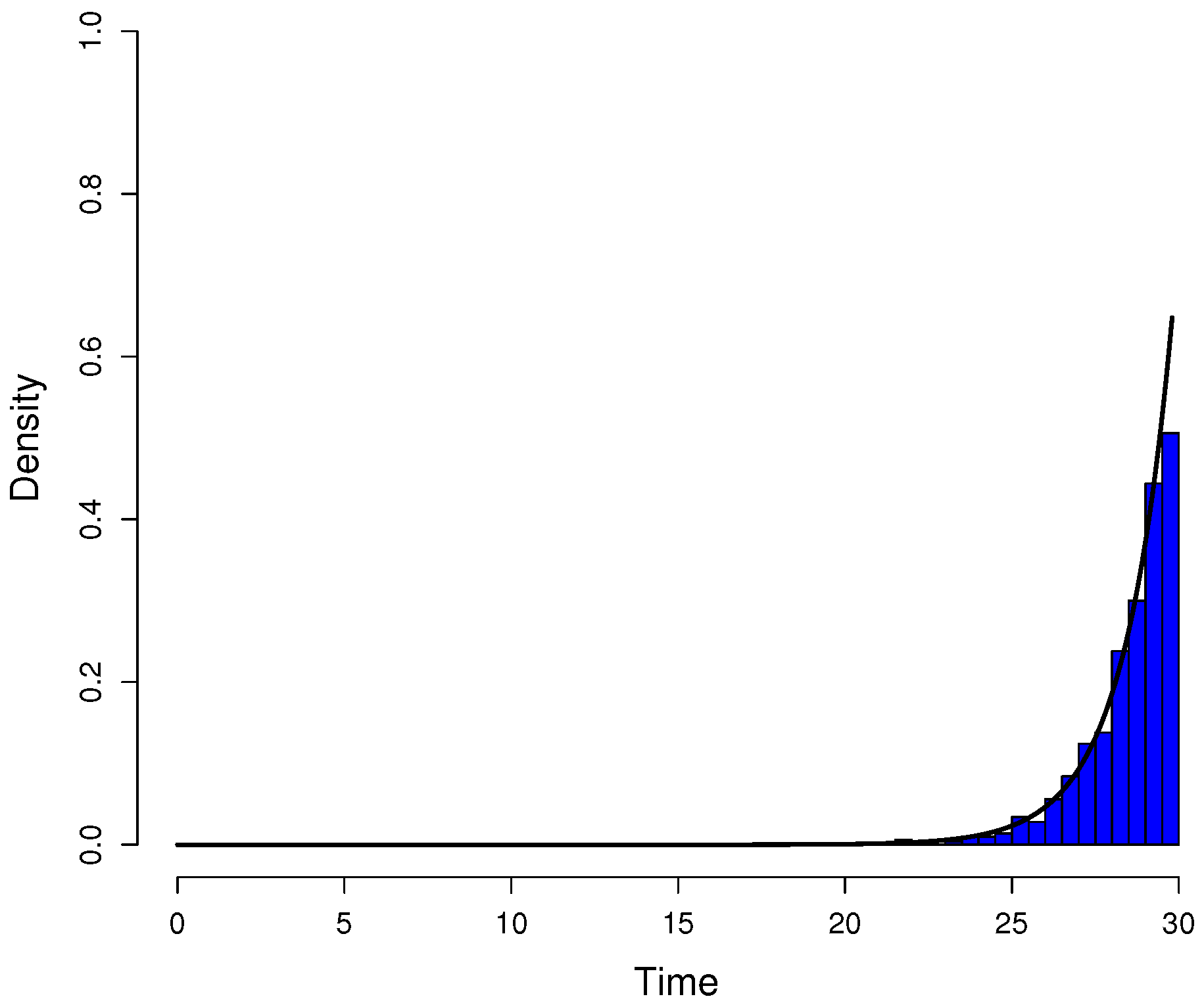
Appendix A.2. Quantile function model
Appendix A.3. Description of the Moran model
| Algorithm 1: Moran model definitions |
|
Input:
|
| Algorithm 2: Moran model pseudocode |
 |
| Algorithm 3: Moran model pseudocode, continued. |
 |
| Algorithm 4: Graphical model pseudocode. |
 |
| Algorithm 5: Quantile function model pseudocode. |
 |
Appendix B. Estimation methods
Appendix B.1. Direct estimations
Appendix B.2. Maximum likelihood estimations
References
- Eigen, M.; Schuster, P. The hypercycle. Naturwissenschaften 1978, 65, 7–41. [Google Scholar] [CrossRef]
- Jeancolas, C.; Malaterre, C.; Nghe, P. Thresholds in Origin of Life Scenarios. iScience 2020, 23, 101756. [Google Scholar] [CrossRef]
- Drake, J.W. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. U. S. A. 1991, 88, 7160–7164. [Google Scholar] [CrossRef]
- Biebricher, C.K.; Eigen, M. The error threshold. Virus Res. 2005, 107, 117–127. [Google Scholar] [CrossRef]
- Sniegowski, P.D.; Gerrish, P.J.; Johnson, T.; Shaver, A. The evolution of mutation rates: separating causes from consequences. Bioessays 2000, 22, 1057–1066. [Google Scholar] [CrossRef]
- Richard, G.F.; Kerrest, A.; Lafontaine, I.; Dujon, B. Comparative Genomics of Hemiascomycete Yeasts: Genes Involved in DNA Replication, Repair, and Recombination. Mol. Biol. Evol. 2005, 22, 1011–1023. [Google Scholar] [CrossRef] [PubMed]
- Barr, J.N.; Fearns, R. How RNA viruses maintain their genome integrity. J. Gen. Virol. 2010, 91, 1373–1387. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.W.; Charlesworth, B.; Charlesworth, D.; Crow, J.F. Rates of spontaneous mutation. Genetics 1998, 148, 1667–1686. [Google Scholar] [CrossRef] [PubMed]
- Jiang, P.; Ollodart, A.R.; Sudhesh, V.; Herr, A.J.; Dunham, M.J.; Harris, K. A modified fluctuation assay reveals a natural mutator phenotype that drives mutation spectrum variation within Saccharomyces cerevisiae. Elife 2021, 10, e68285. [Google Scholar] [CrossRef] [PubMed]
- Singh, T.; Hyun, M.; Sniegowski, P. Evolution of mutation rates in hypermutable populations of Escherichia coli propagated at very small effective population size. Biol. Lett. 2017, 13. [Google Scholar] [CrossRef]
- Harpak, A.; Bhaskar, A.; Pritchard, J.K. Mutation Rate Variation is a Primary Determinant of the Distribution of Allele Frequencies in Humans. PLoS Genet. 2016, 12, e1006489. [Google Scholar] [CrossRef] [PubMed]
- Gerrish, P. A simple formula for obtaining markedly improved mutation rate estimates. Genetics 2008, 180, 1773–1778. [Google Scholar] [CrossRef] [PubMed]
- Jones, M.E. An algorithm accounting for plating efficiency in estimating spontaneous mutation rates. Comput. Biol. Med. 1993, 23, 455–461. [Google Scholar] [CrossRef]
- Jones, M.E.; Thomas, S.M.; Rogers, A. Luria-Delbrück fluctuation experiments: design and analysis. Genetics 1994, 136, 1209–1216. [Google Scholar] [CrossRef] [PubMed]
- Amicone, M.; Borges, V.; Alves, M.J.; Isidro, J.; Zé-Zé, L.; Duarte, S.; Vieira, L.; Guiomar, R.; Gomes, J.P.; Gordo, I. Mutation rate of SARS-CoV-2 and emergence of mutators during experimental evolution. Evol Med Public Health 2022, 10, 142–155. [Google Scholar] [CrossRef]
- Biebricher, C.K.; Eigen, M. What is a quasispecies? Curr. Top. Microbiol. Immunol. 2006, 299, 1–31. [Google Scholar]
- Ancel, L.W.; Fontana, W. Plasticity, evolvability, and modularity in RNA. J. Exp. Zool. 2000, 288, 242–283. [Google Scholar] [CrossRef]
- Nowak, M.; Schuster, P. Error thresholds of replication in finite populations mutation frequencies and the onset of Muller’s ratchet. J. Theor. Biol. 1989, 137, 375–395. [Google Scholar] [CrossRef]
- Sardanyés, J.; Elena, S.F. Error threshold in RNA quasispecies models with complementation. J. Theor. Biol. 2010, 265, 278–286. [Google Scholar] [CrossRef]
- Wiehe, T. Model dependency of error thresholds: the role of fitness functions and contrasts between the finite and infinite sites models. Genet. Res. 1997, 69, 127–136. [Google Scholar] [CrossRef]
- Baake, E.; Wagner, H. Mutation–selection models solved exactly with methods of statistical mechanics. Genet. Res. 2001, 78, 93–117. [Google Scholar] [CrossRef]
- Boerlijst, M.C.; Bonhoeffer, S.; Nowak, M.A. Viral Quasi-Species and Recombination. Proc. Biol. Sci. 1996, 263, 1577–1584. [Google Scholar]
- Gardner, A.; Welch, J.J. A formal theory of the selfish gene. J. Evol. Biol. 2011, 24, 1801–1813. [Google Scholar] [CrossRef]
- Dawkins, R. The Selfish Gene; Oxford University Press, 1989.
- Mao, E.F.; Lane, L.; Lee, J.; Miller, J.H. Proliferation of mutators in A cell population. J. Bacteriol. 1997, 179, 417–422. [Google Scholar] [CrossRef] [PubMed]
- Neinavaie, F.; Kramer, A. Does mutation rate of cancer cells change as the stage of the disease advances? Cancer Res. 2022, 82, A038–A038. [Google Scholar] [CrossRef]
- Hao, D.; Wang, L.; Di, L.J. Distinct mutation accumulation rates among tissues determine the variation in cancer risk. Sci. Rep. 2016, 6, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Tomlinson, I.P.M.; Novelli, M.R.; Bodmer, W.F. The mutation rate and cancer. Proceedings of the National Academy of Sciences 1996, 93, 14800–14803. [Google Scholar] [CrossRef]
- Fox, E.J.; Prindle, M.J.; Loeb, L.A. Do mutator mutations fuel tumorigenesis? Cancer Metastasis Rev. 2013, 32, 353–361. [Google Scholar] [CrossRef] [PubMed]
- Russo, M.; Pompei, S.; Sogari, A.; Corigliano, M.; Crisafulli, G.; Puliafito, A.; Lamba, S.; Erriquez, J.; Bertotti, A.; Gherardi, M.; et al. A modified fluctuation-test framework characterizes the population dynamics and mutation rate of colorectal cancer persister cells. Nat. Genet. 2022, 54, 976–984. [Google Scholar] [CrossRef]
- Bielas, J.H.; Loeb, K.R.; Rubin, B.P.; True, L.D.; Loeb, L.A. Human cancers express a mutator phenotype. Proc. Natl. Acad. Sci. U. S. A. 2006, 103, 18238–18242. [Google Scholar] [CrossRef]
- Natali, F.; Rancati, G. The Mutator Phenotype: Adapting Microbial Evolution to Cancer Biology. Front. Genet. 2019, 10, 713. [Google Scholar] [CrossRef] [PubMed]
- Nowell, P.C. The clonal evolution of tumor cell populations. Science 1976, 194, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Sprouffske, K.; Merlo, L.M.F.; Gerrish, P.J.; Maley, C.C.; Sniegowski, P.D. Cancer in Light of Experimental Evolution. Curr. Biol. 2012, 22, R762–R771. [Google Scholar] [CrossRef] [PubMed]
- Stewart, F.M. Fluctuation analysis: the effect of plating efficiency. Genetica 1991, 84, 51–55. [Google Scholar] [CrossRef] [PubMed]
- Bokes, P.; Singh, A. A modified fluctuation test for elucidating drug resistance in microbial and cancer cells. Eur. J. Control 2021, 62, 130–135. [Google Scholar] [CrossRef]
- Luria, S.E.; Delbrück, M. Mutations of Bacteria from Virus Sensitivity to Virus Resistance. Genetics 1943, 28, 491–511. [Google Scholar] [CrossRef] [PubMed]
- Hamon, A.; Ycart, B. Statistics for the Luria-Delbrück distribution. EJSS 2012, 6, 1251–1272. [Google Scholar] [CrossRef]
- Ycart, B. Fluctuation analysis: can estimates be trusted? PLoS One 2013, 8, e80958. [Google Scholar] [CrossRef]
- Feller, W. An Introduction to Probability Theory and Its Applications; New York; Chapman & Hall: London, 1957. [Google Scholar]
- Brunetti, M.; Mackey, M.; Craig, M. Understanding normal and pathological hematopoietic stem cell biology using mathematical modelling. Current Stem Cell Reports 2021, 7, 109–120. [Google Scholar] [CrossRef]
- Arnold, T.; Emerson, J. Nonparametric goodness-of-fit tests for discrete null distributions. R Journal 2011, 3. [Google Scholar] [CrossRef]
- Ycart, B. Fluctuation Analysis: Can Estimates Be Trusted? PLoS ONE 2013, 8, e80958. [Google Scholar] [CrossRef]
- Lea, D.; Coulson, C. The distribution of the numbers of mutants in bacterial populations. Journal of Genetics 1949, 49, 264–285. [Google Scholar] [CrossRef] [PubMed]
- Gillet-Markowska, A.; Louvel, G.; Fischer, G. bz-rates: A Web Tool to Estimate Mutation Rates from Fluctuation Analysis. G3 Genes|Genomes|Genetics 2015, 5, 2323–2327. [Google Scholar] [CrossRef] [PubMed]
- Ramachandran, K.; Tsokos, C. Mathematical Statistics with Applications; Elsevier Science, 2009.
- Zheng, Q. New algorithms for Luria-Delbrück fluctuation analysis. Mathematical Biosciences 2005, 196, 198–214. [Google Scholar] [CrossRef] [PubMed]
- Feng, Z.; McCulloch, C.E. Statistical inference using maximum likelihood estimation and the generalized likelihood ratio when the true parameter is on the boundary of the parameter space. Statistics & Probability Letters 1992, 13, 325–332. [Google Scholar] [CrossRef]
- Ross, S. Introduction to probability models; Academic press, 2007.
- Luria S.E., D. M. Mutations of bacteria from virus sensitivity to virus resistance. Genetics 1943, 28, 491. [Google Scholar] [CrossRef] [PubMed]
- Chiang, C.L. . Introduction to Stochastic Processes in Biostatistics; John Wiley & Sons, Inc., 1968.
- Waller, J.H.; Rao, B.R.; Li, C.C. Heterogeneity of childless families. Social Biology 1973, 20, 133–138. [Google Scholar] [CrossRef] [PubMed]
- R Core Team. R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing: Vienna, Austria, 2022.
- Embrechts, P.; Hofert, M. A note on generalized inverses. Mathematical Methods of Operations Research 2013, 77, 423–432. [Google Scholar] [CrossRef]
- Crane, G. A modified Luria-Delbrück fluctuation assay for estimating and comparing mutation rates. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 1996, 354, 171–182. [Google Scholar] [CrossRef]
- de la Iglesia, F.; Martínez, F.; Hillung, J.; Cuevas, J.M.; Gerrish, P.J.; Daròs, J.A.; Elena, S.F. Luria-Delbrück Estimation of Turnip Mosaic Virus Mutation Rate In Vivo. Journal of Virology 2012, 86, 3386–3388. [Google Scholar] [CrossRef]
- Hall, B.M.; Ma, C.X.; Liang, P.; Singh, K.K. Fluctuation AnaLysis CalculatOR: a web tool for the determination of mutation rate using Luria–Delbrück fluctuation analysis. Bioinformatics 2009, 25, 1564–1565, [https://academic.oup.com/bioinformatics/article-pdf/25/12/1564/482426/btp253.pdf]. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.L. Mutation and growth rates from Luria-Delbrück fluctuation tests. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 1982, 95, 129–143. [Google Scholar] [CrossRef]
- Kosterlitz, O.; Tirado, A.M.; Wate, C.; Elg, C.; Bozic, I.; Top, E.M.; Kerr, B. Estimating the rate of plasmid transfer with an adapted Luria–Delbrück fluctuation analysis. bioRxiv, 2022; pp. 2021–01. [Google Scholar]
- Lang, G.I. Measuring Mutation Rates Using the Luria-Delbrück Fluctuation Assay. In Methods in Molecular Biology; Springer New York, 2017; pp. 21–31. [CrossRef]
- Zheng, Q. A new practical guide to the Luria–Delbrück protocol. Mutation Research/Fundamental and Molecular Mechanisms of Mutagenesis 2015, 781, 7–13. [Google Scholar] [CrossRef]
- Zheng, Q. New approaches to mutation rate fold change in Luria–Delbrück fluctuation experiments. Mathematical Biosciences 2021, 335, 108572. [Google Scholar] [CrossRef]
- Nakamura, M.; Pérez-Abreu, V. Empirical probability generating function: An overview. Insurance: Mathematics and Economics 1993, 12, 287–295. [Google Scholar] [CrossRef]
- Hamon, A.; Ycart, B. Statistics for the Luria-Delbrück distribution. Electronic Journal of Statistics 2012, 6, 1251–1272. [Google Scholar] [CrossRef]
- Alexander, H.K. Conditional Distributions and Waiting Times in Multitype Branching Processes. Advances in Applied Probability 2013, 45, 692–718. [Google Scholar] [CrossRef]
- Lange, K. Calculation of the Equilibrium Distribution for a Deleterious Gene by the Finite Fourier Transform. Biometrics 1982, 38, 79–86. [Google Scholar] [CrossRef]
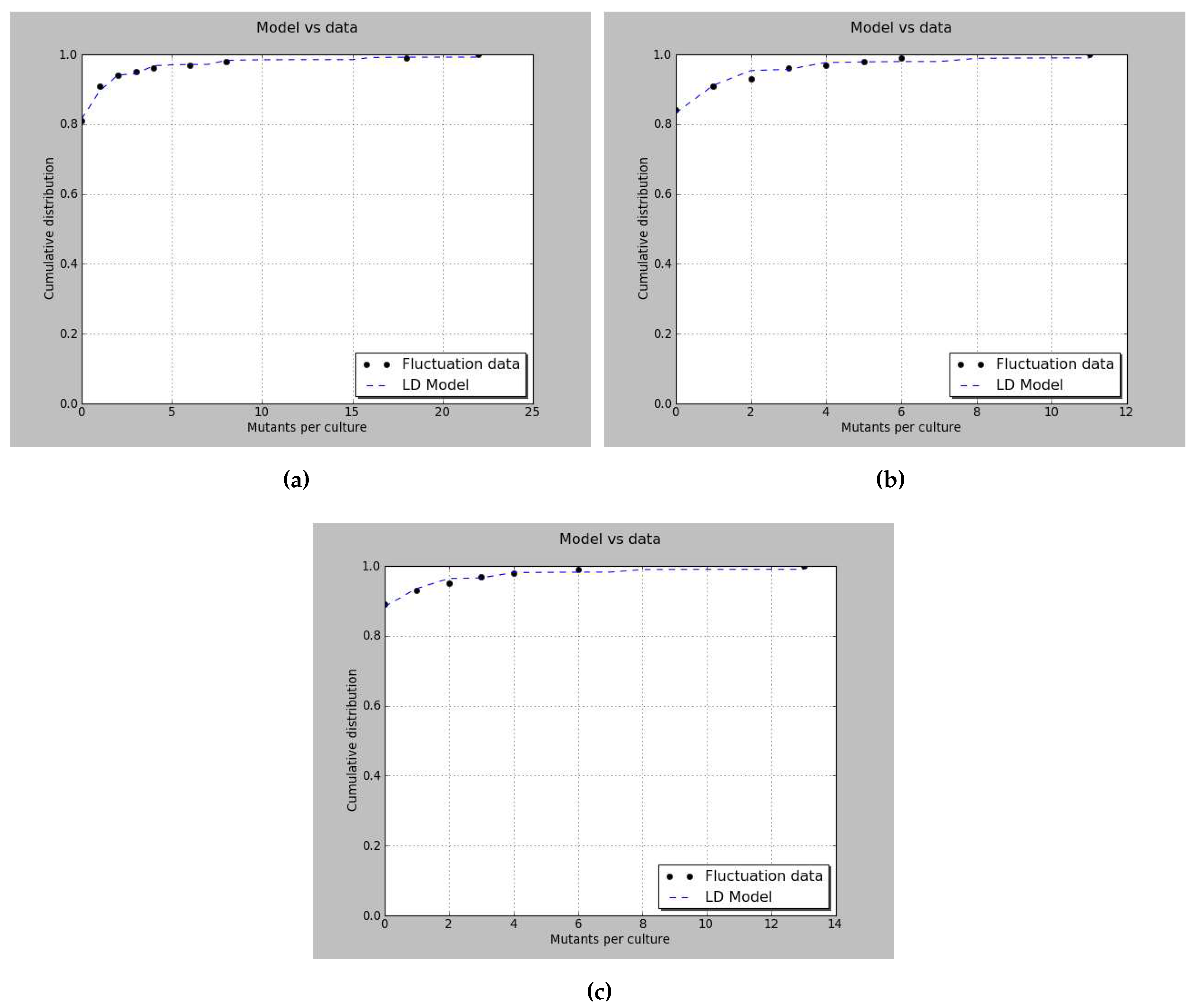
| Moran | Graphical | Quantile function | |
|---|---|---|---|
| Estimate of | |||
| Estimation error | |||
| 95% confidence interval lower bound | |||
| 95% confidence interval upper bound | |||
| Pearson’s value | 1.6333 | 4.1370 | 1.0446 |
| p-value | 0.8027 | 0.3877 | 0.9029 |
| Method | Estimate of | 95% confidence interval |
|---|---|---|
|
Direct estimations bootstrap |
||
| MLE | ||
|
Two-variable MLE |
| Method | Estimate of | 95% confidence interval |
|---|---|---|
|
Direct estimations bootstrap |
||
| MLE | ||
|
Two-variable MLE |
| Method | Estimate of | 95% confidence interval |
|---|---|---|
|
Direct estimations bootstrap |
||
| MLE | ||
|
Two-variable MLE |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





