The feasibility of recovering bioactive antioxidants from Phyllantus emblica leaves using ethanol -water mixture (0 – 100%) and heat-assisted extraction technology (HAE-T) was investigated in this present study. To this effect, the process parameter of operating temperature (OT: 30 -50 oC), solid -to-liquid ratio (S:L: 1:20 - 1:60 g/mL) and extraction time (ET: 45 - 180 min) were investigated on the extract total phenolic content (TPC, mg GAE/g d.w), yield (EY, %) and antioxidant activity (μM AAE/g d.w) by employing the Box-Behnken experimental design (BBD) available in response surface methodology (RSM). Multi-objective process optimization using the desirability function algorithm to determine set of process variables that simultaneously optimize process responses of TPC, EY and AA was also investigated. The recovery process was thereafter modeled with BBD-RSM and multi gene genetic programming (MGGP) algorithm and model reliability assessment via Monte Carlo simulation were conducted for the best performing set of models for predicting TPC, EY and AA values. The HPLC characterization of the recovered extract was carried out to ascertain the phenolic compound constituents of the Phyllantus emblica leaf extract. The 50% ethanol solution was found to be the best for the optimal extraction of antioxidants from Phyllantus emblica leaves. The HAE-T was suitable for recovering bioactive extract from Phyllantus emblica leaves and investigated process parameters have impacts on the recovery process. The process parameters that simultaneously gave the optimum EY of 21.6565%, TPC of 67.116 mg GAE/g and AA of 3.68583 µM AAE/g were OT of 41.61 oC, S:L of 1:60 g/mL and ET of 180 min. The HPLC extract profiling revealed that the bioactive constituents present in the recovered extract were betulinic acid, gallic acid, chlorogenic acid, caffeic acid, ellagic acid, and ferulic acid. Both the developed BBD-RSM and evolved MGGP-based models predicted the observed process response of TPC, EY and AA satisfactorily with BBD-RSM models marginally better in their predictions. The reliability results showed that the BBD-RSM models predicted TPC, EY and AA values with high certainty of 99.985%, 97.569% and 98.661%, respectively.

Keywords:

Subject: Engineering - Chemical Engineering

1.0. Introduction

Phyllanthus emblica, also known as Emblica officinalis or Indian gooseberry, is a plant widely recognized for its medicinal properties. P. emblica is native to tropical south-eastern Asia and it is one of the most extensively studied plants. All parts of P. emblica, including its fruits, have medicinal effects and are used to treat diarrhea, jaundice, inflammation, and act as a strong rasayana (techniques for lengthening lifespans) in Ayurveda [1]. There are documented reports of the applications of P. emblica in memory enhancement, respiratory, skin and ophthalmic disorders, and detoxification, including snake venom [2]. P. emblica holds a unique position in Indian (Ayurvedic), Turkish, Unani, and Tibetan medicinal systems and has therapeutic and healing potentials, making it a valid research option for the development of novel drug formulations with low side effects [1]. The plant is widely used for its nutritional and therapeutic properties, including antioxidant, antidiabetic, and antimicrobial effects [3]. However, the diverse activities of the polyphenols that are present in medicinal plants to a greater extent are responsible for their disease ameliorating properties [4] and these make them essential components of bioactive extracts. Phenolic compounds of plant origins have gained significant attention due to their numerous health-promoting properties and potential therapeutic benefits [5,6]. Hence there arises the need for the recovery of high quality of this class of bioactive compounds from P. emblica which could find applications in diverse fields of endeavor.

Heat-assisted extraction (HAE) technology has been a subject of interest and is among the commonly used conventional technologies in the extraction of bioactive compounds from various plant sources [7,8,9,10]. HAE technology (HAE-T) utilizes heat to enhance the extraction efficiency and improve the yield of desired compounds. Other frequently employed traditional techniques include maceration, Soxhlet extraction, and hydro-distillation [8]. Several parameters significantly influence the HAE efficiency in terms of yield and quality. These parameters include temperature, time, particle size, solid to liquid ratio, solvent type and extraction cycle [11]. Polar solvents such as water, methanol, ethanol, and acetone are commonly used for extracting polar bioactive compounds like phenolics and flavonoids [12]. On the other hand, non-polar solvents like hexane, ethyl acetate, and chloroform are preferred for extracting non-polar compounds such as essential oils and lipids [13]. In many cases, a single solvent may not be sufficient to extract the full range of bioactive compounds from a complex matrix. Therefore, solvent mixtures are often employed to improve extraction efficiency and broaden the spectrum of extracted compounds. Commonly used mixtures include ethanol-water, methanol-water, and ethyl acetate-methanol-water. These mixtures take advantage of the varying solvent polarities to extract a wider range of bioactive compounds with different polarities.

Literature searches have revealed several documented works on the use of HAE for the recovery of bioactive compounds from different plant sources. For instance, phenolic-rich extracts have been successfully recovered from Carica papaya leaves, Azadirachta indica leaves, Parkia speciosa pod Senna alata and Enantia chlorantha stem bark [4,9,14,15] using the HAE-T. HAE-T offer certain advantages, such as improved extraction efficiency and higher yields, however, may require longer extraction times, higher energy demands, and increased solvent requirements [14]. The HAE-T is notwithstanding, of interest from industrial-point of view because of its relative scalability, vessel availability and ease of maintenance [16]. HAE-T is among the most affordable extraction technologies in developing countries because of its low initial purchase cost and simplicity of operation. Hence there is a need to optimize the HAE process, enhance the yield of bioactive compounds, and improve the overall efficiency of bioactive extract recovery from P. emblica and other plant sources. Proper control and optimization of the HAE parameters are necessary to maximize the extraction efficiency and overcome the potential draw backs associated with this technology.

Response Surface Methodology (RSM) has been widely applied in various fields to optimize processes and reduce experimentation costs. RSM, coupled with factorial designs, offers a statistical approach to efficiently explore and optimize multiple process variables [17]. RSM is an effective approach for optimizing processes when multiple factors and interactions influence the desired outcomes [18,19]. One of the primary advantages of RSM is its ability to generate valuable insights from a relatively small number of experiments, providing significant information with reduced costs compared to traditional one-variable-at-a-time optimization methods [20]. RSM has found applications in areas such as solvent extraction, engineering optimization, machining process parameters, fermentation processes, and hydrogen production from ethanol thermochemical conversion [21,22]. RSM also aids in identifying optimal conditions and understanding the relationships between process variables and responses, facilitating process optimization and modelling of complex systems [23]. RSM experimental designs such as Box-Behnken design have ability to efficiently identify the curvature of the response surface and provide robustness against potential errors in the estimation of the model parameters. Its balance between accuracy and cost-effectiveness makes it a popular choice in designing experiments and optimizing process parameters [9].

Process modelling helps engineers design and analyze complex systems, improve efficiency, reduce costs, optimize resource allocation, and make informed decisions during the design and operation of engineering processes. Multi-gene genetic programming (MGGP) is one of the promising machine learning techniques that are available for creating mathematical or computational representations of physical processes or systems. MGGP is a variant of genetic programming that offers promising capabilities for behavioral modeling and engineering system analysis. MGGP combines the model structure selection ability of standard genetic programming with the parameter estimation power of classical regression to capture nonlinear relationships between input and output variables [24,25]. It effectively searches for suitable relationships between input and output datasets, independent of the physical background of the data [26] and generates mathematical models of predictor response data that are "multi-gene" in nature, involving linear combinations of low-order non-linear transformations of input variables[25]. MGGP has been successfully applied to various engineering problems, such as behavioral modeling of structural engineering systems [24], identifying the dynamic prediction model for an overhead crane [27], and short-term load forecasting in power systems [28]. However, works on the application of MGGP in modelling extraction processes are very scarce in the literature.

Predictive models are widely used in various fields to make informed decisions and forecasts based on available data. However, assessing the reliability of a predictive model is crucial to ensure its accuracy, robustness, and generalizability. Reliability assessment involves evaluating the performance, stability, and limitations of the model [29]. One of the popular techniques of assessing predictive model reliability and robustness is via Monte Carlo simulation. Monte Carlo simulation involves randomly sampling values from probability distributions of input variables to generate multiple simulated scenarios. This technique provides a comprehensive assessment of the reliability and uncertainty of predictive models by considering the variability in input variables. It also allows for a thorough understanding of the model’s behavior under different scenarios and helps in making informed decisions based on the range of predicted outcomes. Monte Carlo simulation is widely used in various fields, including finance, engineering, physics, economics, and many others. Its ability to handle complexity and uncertainty makes it an invaluable tool for assessing the reliability and robustness of models, allowing decision-makers to make more informed choices and manage risks effectively. This technique has been found useful in the assessment of the robustness and sensitivity evaluation of polymer composite BBD-RSM predictive models [4], GPR and ANN compressive strength predictive models [30], biodiesel yield CCD-RSM predictive model [16] and techno-economic MGGP predictive models [30].

Despite interesting bioactivities displayed by P. emblica leaf extracts in the management of broad scope of ailments, the protocol for its bioactive recovery which is necessary for product standardization has not been reported. Also, the engineering works which include process parameter optimization, process modelling and prediction; and model reliability assessment of the extract recovery process are still not available in the literature at present. These engineering works, however, form the basis for the design, optimization, scale-up, and techno-economic feasibility analysis of an integrated plant for commercial production of P. emblica extracts and which are presently lacking to the best of authors’ knowledge. Therefore, the objectives of this work are to (i) investigate the effects of process parameters on the recovery of bioactive extracts from P. emblica leaves using the Box-Benhken design (ii) optimize the bioactive recovery process with the assistance of desirability function algorithm and characterize the bioactive extract with HPLC (iii) model the recovery process with BBD-RSM and MGGP (iv) conduct a comprehensive model reliability assessment and process variable sensitivity analysis of the better predictive model between BBD-RSM and MGGP.

2. Materials and Methods

2.1. Materials and Chemical Reagents

Fresh leaves of P. emblica were harvested from a medicinal farm plantation and were rinsed with running water in order to remove all the dirt when received in the laboratory. The P. emblica leaves were afterward spread on a tray in the laboratory for about 2 weeks to allow them dry by natural convection. The dried P. emblica leaves were latter ground and sieves to particle size of 0.1 mm and the screened samples were kept inside a black polythene bag before experimentation. All the chemicals used in the laboratory, including absolute ethanol (99%), sodium carbonate, (Na₂CO₃), ascorbic acid, Folin Ciocateu phenol reagent, glacial acetic acid, 2, 4, 6-tripyridyl-s-triazine, sodium acetate trihydrate, HCl, and FeCl₃.6H₂O, were of analytical grade and were purchased from Sigma Aldrich located in Poole, England. Additionally, the HPLC standards employed in the study consisted of betulinic acid, gallic acid, caffeic acid, ellagic acid, chlorogenic acid, ferulic acid, rutin, and quercetin. Distilled water was used though out the laboratory investigations.

2.2. Preliminary Selection of Extraction Solvent

The selection of the best solvent for the heat-assisted extraction (HAE) of antioxidant phytochemicals from P. emblica leaf sample was investigated here. The two extreme pure solvents that were considered were the absolute ethanol (99%) and 100% distilled water. Other solvent mixtures investigated included the 20%, 40%, 50% and 80% ethanol solutions. The heat-assisted extraction of bioactive compounds from P. emblica leaves was conducted at fixed HAE parameters of 40 ^oC operating temperature (OT), 45 min extraction time (ET) and solid to liquid ratio (S:L) of 1:20 g/mL. P. emblica leaf particle size of 0.1 mm was used for all investigations. The responses selected for these investigations were the bioactive extract yield (EY), total phenolic content (TPC) and antioxidant activity (AA) of the extracts. The procedures for the HAE and EY; and TPC and AA quantifications are detailed in Section 2.3 and Sections 2.6 - 2.8 respectively. All investigations were carried out in duplicates and the results were reported as mean ± standard deviation.

2.3. Heat-assisted Extraction of Bioactive Compounds

In the laboratory, the heat-assisted extraction (HAE) of bioactive compounds from P. emblica leaves followed a procedure similar to the method described by Adeyi et al. [16], utilizing a water bath. The process involved placing a known quantity of P. emblica leaf sample and solvent into a beaker and subjecting it to elevated temperature for a specific duration while continuously stirring. To prevent solvent loss, the beaker was covered with foil during the experiment. The HAE experiments were conducted at OT of 40 ^oC, ET of 45 min and S:L of 1:20 g/mL as described in Section 2.2 for the preliminary selection of the best HAE solvent/mixture for the recovery of antioxidant phytochemicals from P. emblica leaves. However, for the study of the interactive effects of the HAE parameters on the extractability of bioactive antioxidants from P. emblica leaves and subsequent process optimization, the solvent used was the best mixture selected according to Section 2.2 and each extraction experiment was conducted based on the experimental conditions outlined in the Box-Benhken design, as explained in Section 2.4. After the designated residence time, the P. emblica leaves fiber was separated from the extracts through centrifugation (at 25 ^oC, 500 rpm, for 10 min). The resulting P. emblica leaves extract was then poured off and stored in plastic bottles for subsequent analysis.

2.4. Box-Behnken Experimental Design and Modeling

The design and investigation of HAE process for extracting bioactive compounds from P. emblica leaves were conducted using the Box-Behnken design-response surface methodology (BBD-RSM). The HAE process involved three key parameters: operating temperature (OT/X₁), solid-to-liquid ratio (S: L/X₂), and extraction time (ET/X₃). These parameters were studied at three levels (-1, 0, +1) in the BBD-RSM. The specific values for OT were 35, 45, and 55 ^oC, for S: L were 20, 35, and 50 mL, and for ET were 100, 150, and 200 min. These levels served as the independent HAE parameters in the study. The measured responses included the total phenolic content (TPC, mg GAE/g d.w), extract antioxidant activity (AA, μM AAE/g d.w), and extract yield (EY, %). The relationships between the HAE parameters and the responses were defined using Eq. (1), where the response parameter is denoted as Y.

Y = b_{o} + \sum_{i = 1}^{3} b_{i} X_{i} + \sum \sum_{i < j = 1}^{3} b_{i j} X_{i} X_{j} + \sum_{i = j}^{3} b_{i i} X_{i}^{2}

(1)

The coefficients

b_{o}

b_{i}

b_{i j}

and

b_{i i}

represent the linear, cross-product, and quadratic model coefficients. The HAE parameters in coded form are represented as

X_{i}

and

X_{j}

The statistical significance of all model coefficients was determined at a 95% confidence level using the Design-Expert software. The adequacy of the models was evaluated using

R^{2}

R_{a d j}^{2}

and Pred

R^{2}

as measures of model performance.

2.5. MGGP-Based Predictive Modeling Theory and Model Development

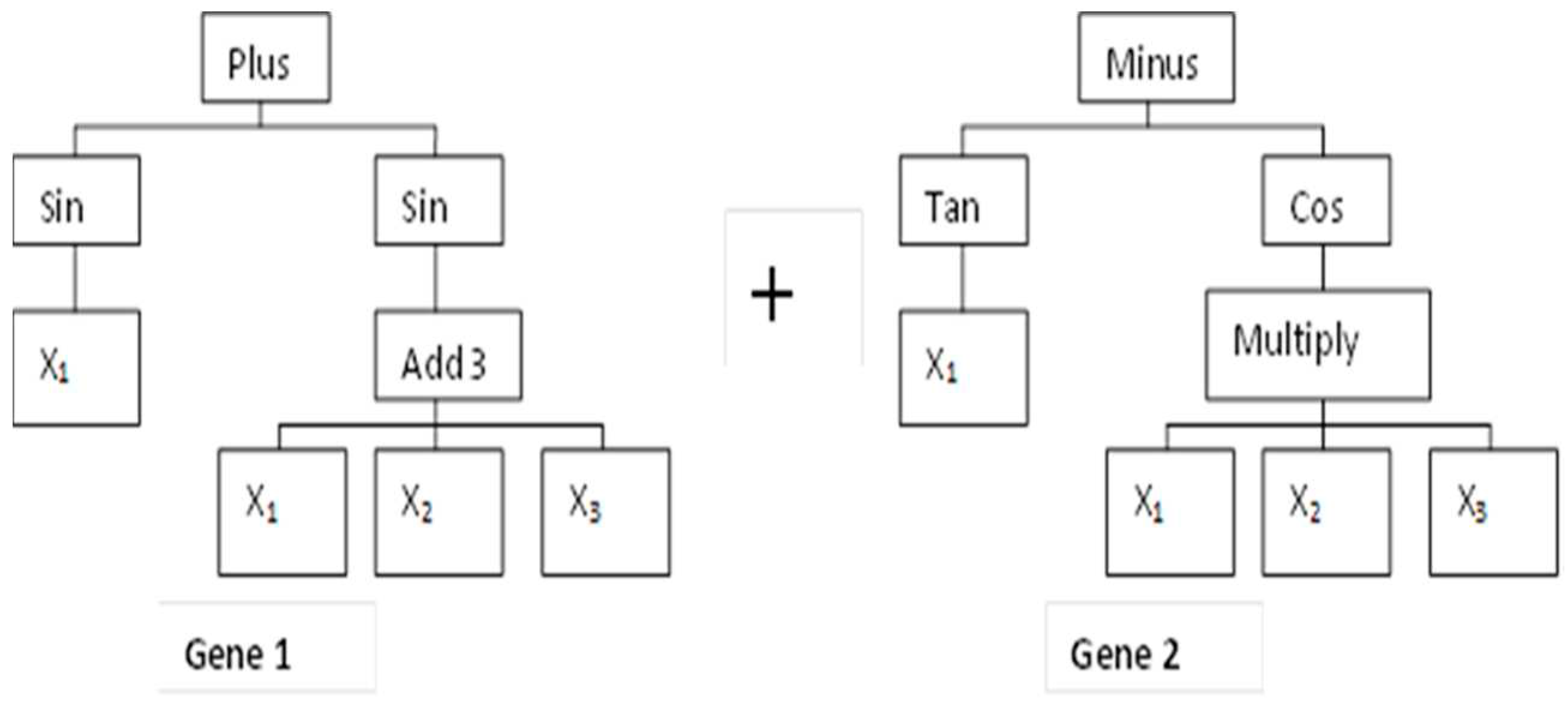
2.5.1. MGGP Theory

Multi-gene genetic programming modelling (MGGP) is a computational approach that combines multiple genetic programming sub-models to evolve complex models capable of capturing the intricacies of the system under investigation. The theory behind MGGP encompasses various aspects, including the representation of individuals, the evolution operators, and the fitness evaluation [4].

One of the key elements in MGGP is the representation of individuals. In MGGP, each individual consists of a collection of sub-models, also known as genes, which are combined to form the overall model. Each gene represents a different aspect of the system and contributes to the overall functionality and performance of the model. The combination of these genes allows MGGP to capture the interactions and dependencies among various variables in the system. Figure 1 illustrates a typical MGGP gene structure.

The model structure consists of independent variables denoted as X₁, X₂, and X₃, as shown in Figure 1. These variables are linked together using mathematical node functions such as subtraction, cosine, tangent, and addition. The mathematical representation of an MGGP regression model is given by Eq. (2).

Y = X₀ + X₁ × tree1 + … + x_k × treeK

(2)

In the equation, the constant term or bias is denoted as x₀, while x₁,..., x_M represent the gene coefficients or weights. The value of M corresponds to the number of genes present in the current or i^th set of inputs.

The evolution operators in MGGP play a crucial role in the creation and modification of individuals over successive generations. These operators include crossover and mutation. Crossover involves the exchange of genetic material between individuals, specifically the sub-models or genes, to create offspring with a combination of characteristics from the parent individuals. Mutation introduces small random changes in the sub-models or genes, allowing for exploration of the search space and potentially discovering new and improved models. Fitness evaluation is an essential component in MGGP to guide the evolution process. The fitness function assesses the performance of individuals based on their ability to solve the problem at hand. It is typically defined based on the specific objectives of the modelling task, such as accuracy, prediction error, or fitness criteria specific to the problem domain. Individuals with higher fitness values are more likely to be selected for reproduction and contribute to the next generation. The overall goal of MGGP is to iteratively evolve individuals with improved fitness through the application of evolution operators and fitness evaluation. This iterative process aims to search for optimal or near-optimal models that provide accurate representations of the system under study.

2.5.2. MGGP Model Development

A Genetic Programming Toolbox for Identification of Physical Systems (GPTIPs), which is open-source software, was utilized in Matlab R2014b® to construct an appropriate MGGP model that captures the relationships within the observed data. The configuration and settings for the modelling parameters of MGGP employed in this study were optimized for the prediction and are as detailed in Table 1. In the course of model development, the experimental data sets (each for TPC, EY and AA) were divided into training (50%) and testing (50%) data subsets.

The best model was selected on the basis of providing minimum fitness value on the training data and developed model simplicity. The effectiveness of the mathematical models developed using MGGP was assessed by calculating the coefficient of determination (R²) and root mean square error (RMSE) values as indicated in Eq. (3) and Eq. (4) respectively.

R^{2} = 1 - \frac{\sum_{i = 1}^{n} (x i - y_{i}) 2}{\sum_{i = 1}^{n} {(x_{i} - x)}^{2}}

(3)

RMSE = \sqrt{\frac{1}{n} \sum_{i = 1}^{n} {(x_{i} - y_{i})}^{2}}

(4)

where,

x_{i}

y_{i}

, x and n are observed, predicted output, mean of the observed and number of observations respectively.

2.6. Numerical Process Optimization and Validation

The optimal HAE conditions for recovering bioactive antioxidants from P. emblica leaves were determined using the numerical optimizer provided by the Design-Expert software. The desirability function algorithm, following the method of Adeyi et al., [4], was utilized for this purpose. The optimization criteria involved manually selecting the optimization goal, weight, and importance for both the dependent and independent variables.

In order to find an optimum solution, the goals are combined into an overall composite function D (x), called desirability function. The value of desirability function for n responses can be defined as:

D (x) = (d_{1} \times d_{2} \times d_{3} \dots \dots \dots \dots \dots \dots \dots \dots \dots . d_{n})^{1 / n}

(5)

For any response, the desirability varied from zero to one. A value of one represents the ideal case, while zero indicates that one or more responses fall outside the desirable limits.

In this study, the goal was to simultaneously maximize the total phenolic content (TPC), extract antioxidant activity (AA), and extract yield (EY). To validate the predicted optimal HAE conditions, laboratory experiments were conducted. The predicted results were compared to the validated data using the relative standard deviation (RSD) defined by Eq. (6).

% R S D = \frac{{S D}_{1 - 2}}{M_{v}} * 100

(6)

The RSD calculates the standard deviation (

{S D}_{1 - 2}

) and determines the similarity or dissimilarity between the predicted and validated data by comparing the mean value (

M_{v}

) obtained from both datasets.

2.7. Determination of Extract Yield

The determination of the extract yield (EY) followed the procedure outlined by Alara et al. [22]. In summary, the decanted extracts obtained from the separation of P. emblica leaves fiber and extracts in Section 2.3 were collected. These extracts were then concentrated and dried in a convective oven dryer until a constant weight of P. emblica leaves extracts was achieved. The EY (%) was calculated using Eq. (7).

% E Y = \frac{W_{1}}{W_{2}} * 100

(7)

In Eq. (7), the EY represent the percentage yield of P. emblica leaves extracts,

W_{1}

refers to the weight of P. emblica leaves extracts (in grams), and

W_{2}

represents the weight of P. emblica leaves (in grams) used in the HAE process.

2.8. Determination Total Phenolic Content

To determine the TPC of aqueous extracts, the Folin-Ciocalteu method was used following [31]. To a tube containing 1 mL of ECBEs, which had been diluted with distilled water at a ratio of 1:10, approximately 1.8 mL of Folin-Ciocalteu reagent was added, and the mixture was allowed to stand for 5 minutes. Then, 1.2 mL of 7.5% (w/v) sodium carbonate was added, and the mixture was stirred and incubated at room temperature of 20 ^oC for 1 hour. The TPC (mg GAE/g d.w) was measured spectrophotometrically at an absorbance of 765 nm and calculated using the pre-constructed gallic acid curve (y = 0.037x + 0.0025, R² = 0.997) according to Eq. (8).

T P C = \frac{C * V}{M}

(8)

In this equation, C (mg/mL) represents the concentration of gallic acid as interpreted from the calibration curve, V (mL) is the volume of the solvent, and m (g) is the weight of the dried P. emblica leaves used in the laboratory experimentation.

2.9. Determination of Antioxidant Activity

To evaluate the antioxidant activity of extracts, the ferric ion reducing antioxidant power (FRAP) method was used, as described by Uddin et al. (2016). The FRAP methodology is based on the ability of an antioxidant to reduce a ferric ion, and was used in this study to measure the reducing capacity of P. emblica leaf extracts. To carry out the FRAP assay, a FRAP reagent was prepared by mixing 0.1 M acetate buffer, 0.01 M TPTZ solution, and 0.02 M FeCl₃*6H₂O solution in a 10:1:1 ratio. Then, 50 µL of extract (diluted with distilled water at 1:10) was mixed with 1.5 mL of the FRAP reagent to create a reaction mixture. The mixture was incubated for 30 minutes at 25 °C, and then the absorbance of the reaction mixture was measured at 593 nm using a UV-Vis spectrophotometer. To determine the AA (expressed as µM AAE/g d.w.), a calibration curve of ascorbic acid standard was used, with equation y = 0.0051x + 0.0015 and R² = 0.995.

2.10. High Performance Liquid Chromatography Profiling of Extract

For the characterization of P. emblica leaves extracts, HPLC analysis was performed following the procedure outlined by Mirunalini [3]. The HPLC analysis was conducted using the bioactive extract obtained under optimized process conditions. Prior to the analysis, the extract was filtered using a 0.45 µm membrane to remove any unwanted particulate matter, such as fiber particles. The filtered extract (approximately 10 µL) was then injected into an HPLC system equipped with a UV diode array detector (UV-DAD) set to a wavelength range of 190-800 nm. The HPLC system, a Shimadzu Corporation instrument from Kyoto, Japan, utilized a VP-ODS column (150 × 4.6 mm, 5 µm particle size) to separate the bioactive compounds. The detection of these compounds occurred at a wavelength of 220 nm. The elution of the compounds from the column was achieved using a mobile phase consisting of 0.2% v/v formic acid and acetonitrile. During the analysis, the resulting chromatogram was recorded. To process the HPLC data, Windows LC solution software was utilized. This software facilitated the identification and quantification of the bioactive compounds present in the extract. The retention times and peak areas of the compounds were compared to those of known reference materials to verify their identity. Furthermore, a chromatographic fingerprint of the bioactive plant extract was generated by plotting the retention times and peak areas of the identified compounds.

2.11. Reliability Assessment of BBD-RSM-based Predictive Models

The BBD-RSM-based models were selected as marginally better models for the prediction of bioactive extract recovery from P. emblica leaves based on the statistical evaluation parameters and hence their reliability and robustness will be investigated in this section. Therefore, the reliability of the predictive equations developed using the BBD-RSM approach to estimate the TPC (mg GAE/g d.w), AA (μM AAE/g d.w) and EY (%) of P. emblica leaves extract, was assessed through Monte Carlo simulations performed in the Oracle Crystal Ball software (OCBS). Additionally, the sensitivity of the models to each process variable was examined. In the OCBS, the uncertainty and sensitivity analyses were conducted by assigning the input variables, including ET (min), OT (^oC), and S/L (g/mL), to the assumption cells. On the other hand, the forecast cells were set as TPC (mg GAE/g d.w), AA (μM AAE/g d.w) and EY (%). Uniform distributions were assumed for all the input variables, and a total of approximately 30,000 iterations were executed to ensure a low mean standard error in TPC (mg GAE/g d.w), AA (μM AAE/g d.w) and EY (%).

3. Results

3.1. Preliminary solvent mixture selection for the bioactive compound’s extraction

The selection of ethanol as a co-solvent for recovering bioactive extracts from P. emblica leaves stems from its versatility and effectiveness in extracting bioactive compounds from medicinal plants. These advantages include cost-effectiveness, safety, efficiency, preservation of bioactivity, scalability, eco-friendliness, and regulatory approval, among others. Table 2 presents the relative ability of different solvent mixtures in the recovery of bioactive compounds from P. emblica leaves. As shown in the table, all ethanol-water mixtures including the 100% absolute ethanol and distilled water were able to recover bioactive antioxidants from P. emblica leaves. This shows that a good number of bioactive compounds in P. emblica leaves are polar in nature. The mean values of the extract yield (EY), Total phenolic content (TPC) and Antioxidant activity (AA) were in the range 5.87 – 12.07 %, 13.67 – 24.25 mg GAE/g d.w and 1.98 – 3.76 μM AAE/g d.w respectively for investigations conducted at OT = 40 ^oC, ET = 45 min and S:L = 1:20 g/mL. Close examination of Table 1 revealed that the bioactive extract obtained with absolute ethanol as solvent possessed the least EY, TPC and AA is (EY = 5.87%, TPC = 13.67 mg GAE/g d.w, AA = 1.98 μM AAE/g d.w) while the bioactive extract recovered with 50% ethanol-water mixture demonstrated highest bioactive EY, TPC and AA (EY = 12.07%, TPC = 24.25 mg GAE/g d.w, AA = 3.76 μM AAE/g d.w). Although, the 100% distilled water (EY = 8.33%, TPC = 19.11 mg GAE/g d.w, AA = 2.81 μM AAE/g d.w) did not perform very badly, it was still far below the 80% ethanol-water (EY = 8.41%, TPC = 20.10 mg GAE/g d.w, AA = 2.99 μM AAE/g d.w), 60% ethanol-water (EY = 11.36%, TPC = 23.76 mg GAE/g d.w, AA = 3.66 μM AAE/g d.w), 40% ethanol-water (EY = 11.11%, TPC = 22.98 mg GAE/g d.w, AA = 3.52 μM AAE/g d.w) and 20% ethanol-water (EY = 8.67%, TPC = 19.73 mg GAE/g d.w, AA = 3.31 μM AAE/g d.w) solvent mixtures in the recovery of bioactive extract from P. emblica leaves.

These results clearly demonstrated varied solubility of bioactive compounds, TPC and AA in different ethanol concentrations (40 - 60% ethanol solutions). This work is in close agreement with previous works [32]. Huaman-Castilla et al., [32] pointed out that solvent polarity and ability of solvents to form hydrogen bonds with plant metabolite significantly impact the solvation capacity of solvents which consequently determines the extractability of polyphenols in plant matrices. This present study has however, shown that ethanol concentrations within 40 - 60% range enhanced the extraction of phenolic compounds due to the optimal solubility and stability of these compounds compared with the solvent extremes (absolute ethanol and 100% distilled water). Although the interesting range of ethanol-water solvent concentration for high bioactive solubility is 40 – 60%, the 50% ethanol-water solvent mixture demonstrated the best phytochemical extractability from P. emblica leaves. However, the literature has documented various optimal ethanol-mixture concentrations for the recovery of bioactive extracts from different medicinal origins. For example, a study conducted by Altıok et al. [33] on the extraction of bioactive compounds from olive oil demonstrated that a 70% ethanol solution optimized the extractability of total polyphenols, resulting in extracts with the highest antioxidant capacity. In the same vein, Cheaib et al. [34] concluded that 50% ethanol solution was best for the recovery of bioactive compounds from apricot pomace. Regardless, the addition of ethanol to water as solvent mixture greatly improved the polyphenol-rich antioxidant extraction from P. emblica leaves. This observation was attributed to the impact of ethanol on cell permeability, brought about by alterations in the phospholipid bilayer of the cell membranes, resulting in both chemical and biophysical modifications to the cell membrane [34]. Therefore, the 50% ethanol-water solvent mixture was hence forth used for the selection of the best set of process parameters for the recovery of bioactive compounds from P. emblica leaves in the subsequent Section.

3.2. Effects of process parameters on the recovery of bioactive extract form P. emblica leaves

The BBD-RSM was used to investigate the effects of process variables on the process responses. The variables selected for this investigation were the operating temperature (OT, solid to liquid ratio (S:L) and extraction time (ET). The ranges of their respective investigations are: OT = 40 - 50 ^oC, S:L = 1:20 - 1:60 and ET = 45 - 180 min. Likewise, the responses considered were the extract yield (EY), total phenolic content (TPC) and antioxidant activity (AA). The selected process parameters and investigated responses are consistent with similar works on bioactive antioxidant extractions from plant sources [4,7]. Table 3 shows the different experimental runs (OT, S:L and ET) prescribed by the BBD-RSM and their corresponding values of EY, TPC and AA.

It should be noted that the 3³ BBD produced 17 experimental runs. The range of values of EY = 9.28 – 21.39%, TPC = 18.58 - 69.35 mg GAE/g d.w and AA = 3.51 - 3.77 µM AAE/g. The experimental run 11 (OT = 40 ^oC, S:L = 1:60 and ET = 45 min), run 2 (OT = 30 ^oC, S:L = 1:20 and ET = 112.50 min) and run 4 (OT = 30 ^oC, S:L = 1:60 and ET = 112.50 min) possessed the least EY, TPC and AA respectively. Conversely, the highest EY and TPC and AA belonged to run 5 (OT = 40 ^oC, S:L = 1:60 and ET = 180 min), run 11 (OT = 40 ^oC, S:L = 1:60 and ET = 45 min) respectively. Experimental runs 6, 7 and 16 possessed AA of 3.67 µM AAE/g. The reported range of EY, TPC and AA are consistent with previous studies on HAE-T[7].

3.3. BBD-RSM modelling, model adequacies and statistical analysis

The BBD-RSM was employed to describe the relationship between the studied process parameters and the responses investigated. Hence, predictive mathematical models were developed for EY, TPC and AA as function of OT, S:L and ET with the assistance of Design Expert software. The coded form of the BBD-RSM quadratic predictive equations that relate the TPC, EY and AA with the operating parameters of OT (denoted as A in the equations), S:L (denoted as B) and ET (denoted as C) are presented in Eq. (9), Eq. (10) and Eq. (11) respectively.

\begin{array}{l} T P C = + 39.16 - 0.66 A - 1.18 B + 22.92 C - 0.90 A^{2} + 2.33 B^{2} + 4.15 C^{2} - 1.72 A B - \\ 1.45 A C + 0.38 B C \end{array}

(9)

\begin{array}{l} E Y = + 15.94 - 2.20 A + 4.08 B + 1.13 C - 1.29 A^{2} + 0.047 B^{2} - 1.25 C^{2} - 1.03 A B - \\ 0.75 A C + 2.38 B C \end{array}

(10)

\begin{array}{l} A A = + 3.70 + 0.055 A + 7.25 x 10^{- 3} B - 0.055 C - 0.040 A^{2} + 0.030 B^{2} - \\ 9.85 x 10^{- 3} C^{2} + 9.75 x 10^{- 3} A B + 0.025 A C - 2.5 x 10^{- 4} B C \end{array}

(11)

Table 4 contains the ANOVA results for the developed predictive quadratic equations. The models’ coefficients and parameters for assessing their adequacies are as well presented in the table. Table 3 shows that the F-values of the developed EY (32.58), TPC (4947.4) and AA (22.86) models are significant (p values < 0.05). These models also possessed non-significant (p values >0.05) lack of fit indicating they are well-developed and are all capable of predicting the observed experimental data with high accuracy. The R² values for the developed models are also appreciably high (EY = 0.9998. TPC = 0.9767 and AA = 0.9671) and hence indicate high effectiveness and capability of the models in describing the laboratory data. The Pred. R² values of all the models (EY = 0.7077, TPC = 0.9994 and AA = 0.8009) were in close agreement with their respective Adj R² values (EY = 0.9467, TPC =0.9996 and AA =0.9248).

Table 4 further shows the contributions of each term in the equation to the overall predictability of the developed models. The negative (-) and positive (+) sign in the model equations indicated a decrease and increase contributions respectively. Therefore, in the EY BBD-RSM predictive model, the linear terms of OT, S:L and ET are all significant (p < 0.05) and contributed negatively, positively and positively respectively to the overall predictability of the model. The quadratic term of OT (OT X OT) and ET (ET X ET) are significant and they both caused a reduction in the EY model. The quadratic effect of S:L resulted to an insignificant (p > 0.05) increase in EY model. The interactive effect of OT and S:L (OT X S:L) was insignificantly (p > 0.05) negative, however both OT X ET (AC) and S:L X ET (BC) produced a positive contribution in EY model, although the OT X ET effect was not significant (p > 0.05). Regarding the TPC and AA BBD-RSM models, the linear effect of OT, S:L and ET were positive, negative, negative and positive, positive, negative in the TPC and AA models respectively. The linear effects of OT, S:L and ET were significant (p < 0.05) in the TPC model, however, only the linear effects of OT and ET contributed significantly in the AA model. The OT X OT, S:L X S:L and ET X ET significantly (p < 0.05) caused reduction, increment and increment respectively in the developed TPC model. However, the ET X ET was the only insignificant (p > 0.05) quadratic effect in the AA BBD-RSM model. The OT X OT and S:L X S:L effects were significantly (p < 0.05) negative and positive respectively in the AA model. All the interactive effects of OT X S:L, OT X ET and S:L X ET were significant in the TPC model and the respectively produced a negative, negative and positive contributions in the model. Among all the interactive effects, only the OT X ET was significantly (p < 0.05) positive, other interactions such OT X S:L and S:L X ET were insignificant (p > 0.05) negative in the AA BBD-RSM model.

The prediction of the observed experimental data by the developed TPC, EY and AA BBD-RSM models are presented in Figure 2 (a), (b) and (c) respectively. The parity graphs showed excellent prediction of the observed data since the observed experimental and model predicted data fell close to the diagonal line [7].

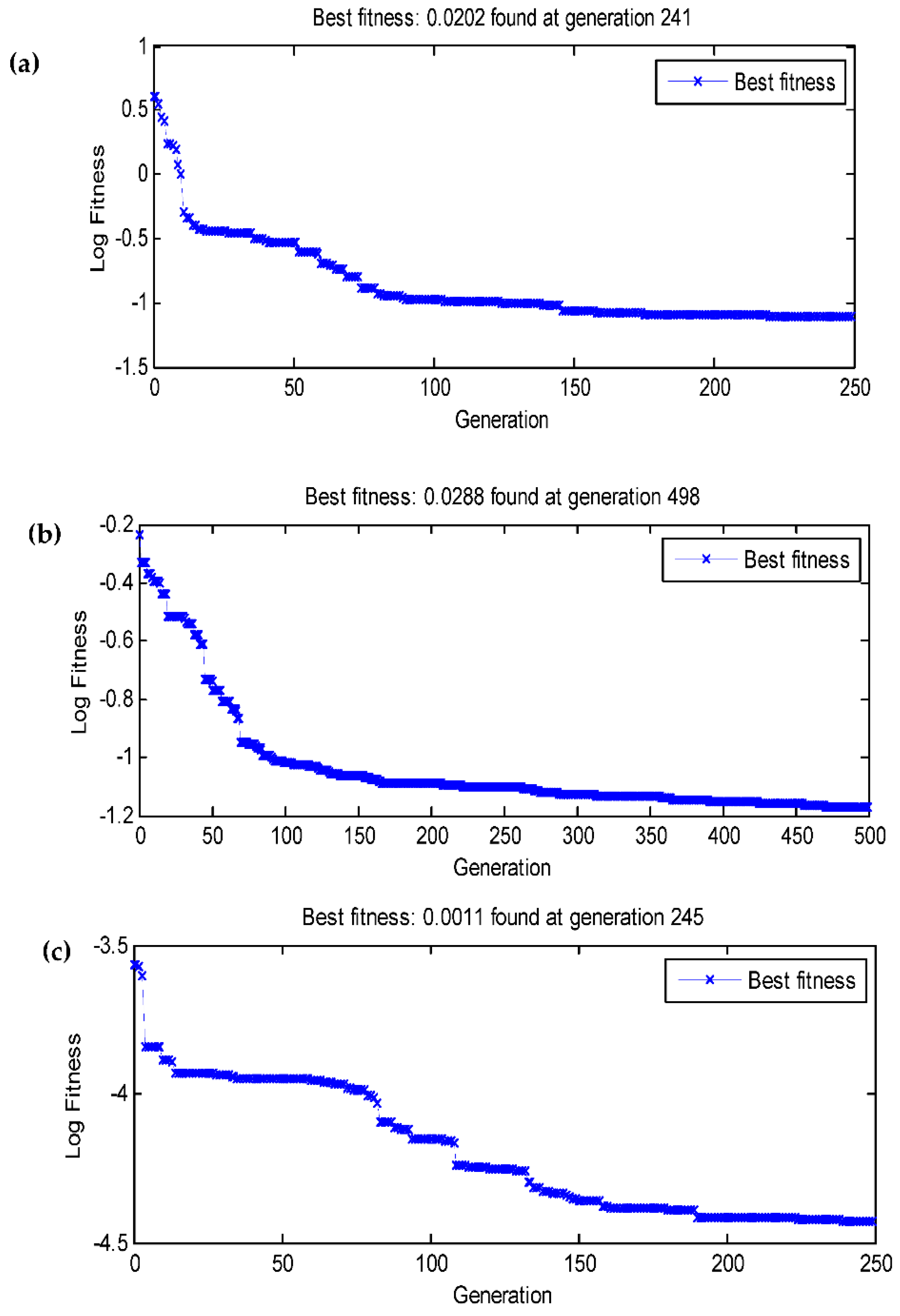
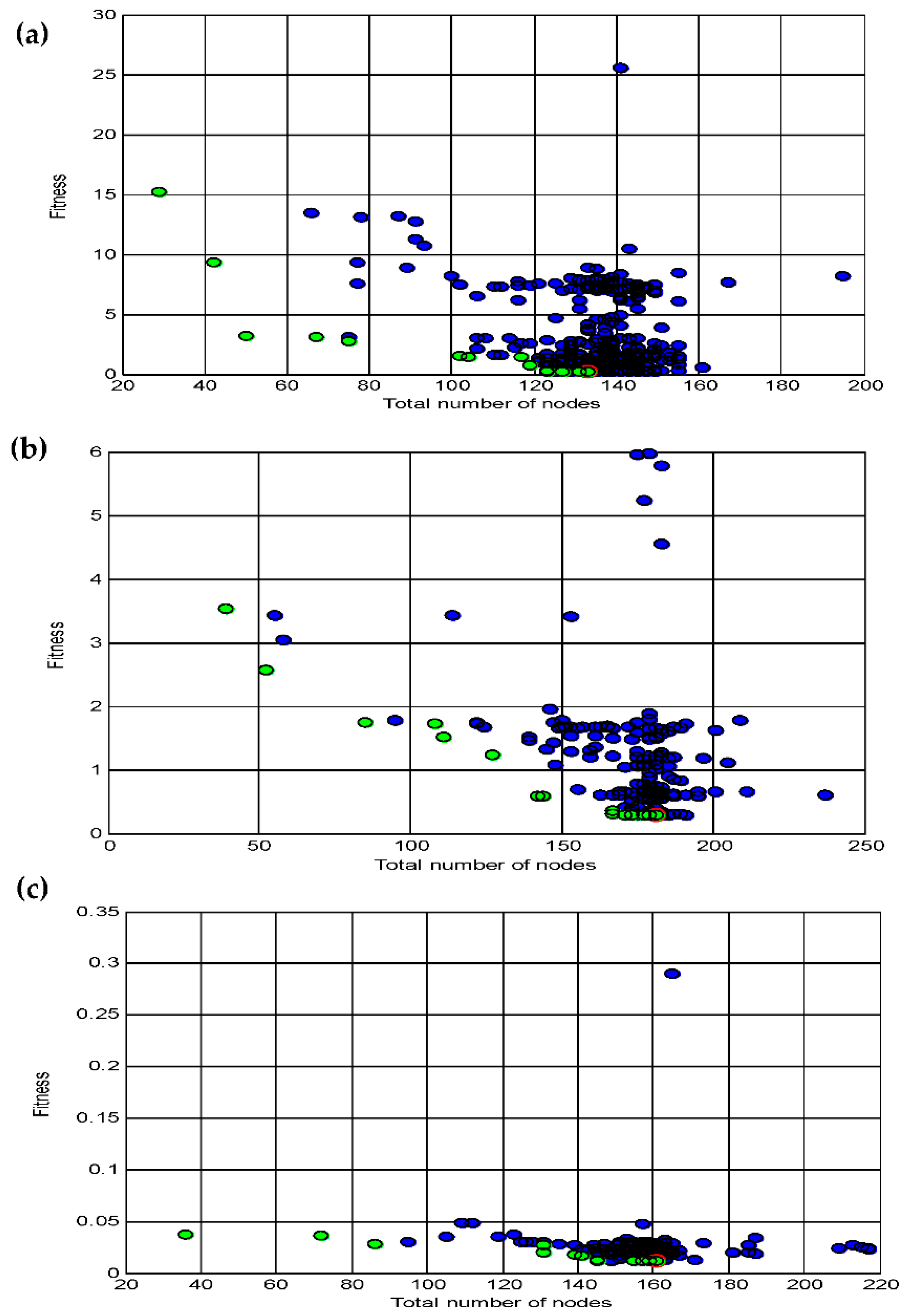
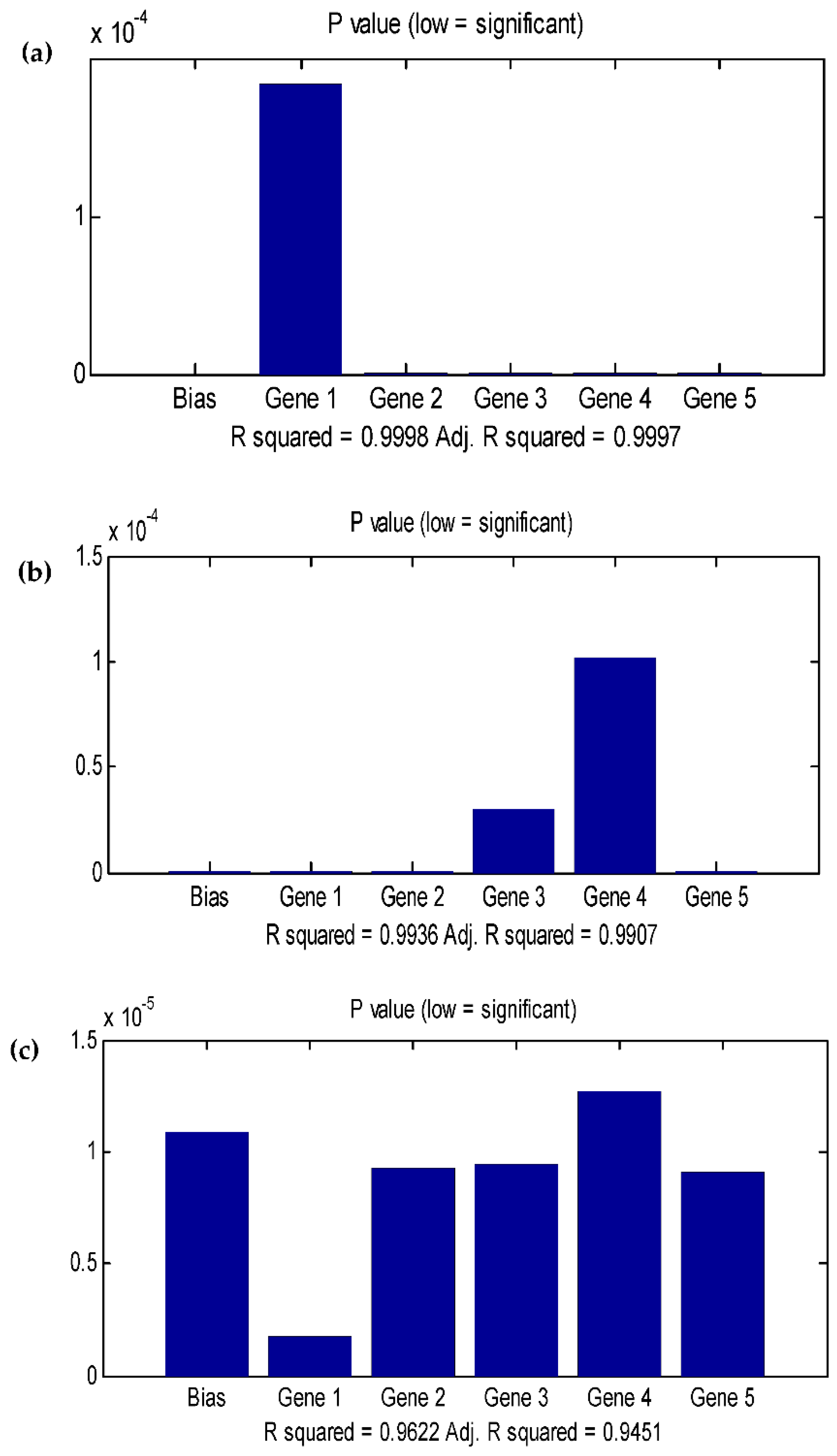
3.4. Data statistics and multi-gene genetic programming modelling

The properties and variability of both the input and output data were determined prior to MGGP modelling via descriptive statistical analysis. The input and output data were the heat-assisted extraction operating parameters and response parameters respectively as presented in Table 3. Therefore, the input parameters were the OT (^oC), S:L (g/mL) and ET (min) while the output response parameters were the EY (w/w %), TPC (mg GAE/g d.w) and AA (µM AAE/g). The relevant data characteristics that were assessed include data mean, standard error, median, mode, and standard deviation. Others were sample variance, data kurtosis, skewness, range, minimum, maximum, and sum. Seventeen (17) data points of each process parameters (OT, S:L and ET) and response parameters (EY, TPC and AA) (which totaled 102 data population) were used for the construction of the MGGP-based models. Table 5 showed the summary of the descriptive statistics of the data used for the MGGP modelling.

The mean of the data set ranged from 3.6905882 to 41.7864705 with the minimum and maximum belonging to AA and TPC respectively. Also, the mean value of OT, S: L, ET and EY are 40^oC, 40 g/mL, 112.5 min and 14.7682352% respectively. Similarly, the standard error, median, mode, and standard deviation are in the range of 0.0153745 - 11.5761544, 3.69 - 112.5, 3.67 - 112.5, 0.0633907 - 47.7297077 and 0.0040183 - 47.7297077 respectively. The sample variance of both the input and output parameters was between 0.0040183 and 2278.1250. The sample variance of 0.0040183 belonged to AA and it indicated minimal variation while variance of 2278.1250 for ET indicated wide variation. The variance of 271.2990492, 200, and 50 for TPC, S:L and OT also implied wide data variations. The data kurtosis, a statistical parameter that measures the peaked or flatness of a data distribution, was in the range of -0.4367377 - 3.1818297. The kurtosis of - 0.4367377, - 0.6261143, - 0.7428571, - 0.7428571, and -0.7428571 for EY, TPC, OT, S:L and ET respectively, indicated that the data were normally distributed (kurtosis value < +1)) while a value of +3.1818297 for AA implied that the sample population is peaked (kurtosis value > +1) [4]. Similarly, the data skewness (a measure of symmetry of data distribution) was in the range of -1.2675914 - 0.4519267 for all sample population. The skewness coefficients of zero (0) for OT, S:L and ET indicated that the data distributions for these variables were not skewed while a coefficient of -1.2675914 for AA indicated a negatively skewed data distribution. Numerical values of other statistical parameters such as the range, minimum, maximum and sum of the input and output data populations are also indicated in Table 5 and are in the range of 0.26 - 135, 3.51 - 45, 3.77 - 180, and 62.74 - 1912.5 respectively.

The MGGP model structures were optimized for the prediction of TPC, EY and AA as a function of processes extraction variables of operating temperature (OT), solid to liquid ratio (S:L) and extraction time (ET). The MGGP model structure optimization study was purposely carried out to achieve optimum model parameter settings that enable robust learning of the heat-assisted extraction process data (both input and output data presented in Table 3) for finest prediction. Therefore, the population size (PS) and number of generation (NG), which were the two significant parameters that determine the model structural predictive effectiveness to a very large extent [9], were each investigated in the range of 100 – 500. The reported ranges for the parameters investigation were determined based on several attempts of simulation experiments in the preliminary studies. Other model settings are as displayed in Table 1. Table 6 presents the summary of the results of the MGGP modeling optimization studies for the prediction of responses TPC, EY and AA. The R² values for the prediction of TPC, EY and AA were in the range of 0.9858 - 0.9998, 0.9157 - 0.9936 and 0.7595 - 0.9622, respectively.

The parameter settings combination for the optimum prediction of TPC, EY and AA are population size and number of generation of 500 and 250 (R² = 0.9998), 250 and 500 (R² = 0.9936) and 250 and 250 (0.9622), respectively. Therefore, these determined optimum parameter settings for the MGGP model prediction of TPC, EY and AA were henceforth used for the simulation.

Figure 3 presents the graphs (in the form of log Fitness vs. number of generation) of the training process for the best MGGP model structure of TPC (PS = 500; NG = 250), EY (PS = 500; NG = 250) and AA (PS = 250; NG = 250).

It is clear from the figure that the best fitness for the training of the models occurred at approximately 241^th, 498^th, and 245^th generation for the TPC, EY and AA simulations respectively. The fitness function assesses the evolved expressions to determine the most optimal encoded expressions [35] and was obtained by minimizing the root mean square error (RMSE). The prediction errors (also refers to as the fitness) for TPC, EY and AA models were found to reduce as a function of number of generation (NG) and were eventually stable at the optimum NG for each model. The decreases observed in prediction error as training progresses is an indication that the MGGP algorithm learnt from the training data rather than memorizing it and hence no data over-fitting occurred in the course of algorithm training [4]. Also, the ability of all the models to regain permanently decrease in fitness indicated that respective MGGP was able to overcome local minimum and adequately settled in global minimum during training process simulations [4]. The best prediction error for the TPC, EY and AA models were 0.0202, 0.0288, and 0.0011, respectively.

The set of possible solutions capable of predicting the process responses of TPC, EY and AA as a function of set of process variables of OT, S:L and ET are presented in Figure 4 (a), (b) and (c) respectively. Figure 4 showed that Pareto fronts (the circles with green coloration) existed for TPC, EY and AA responses.

The Pareto front represents solutions that outperform all other solutions in both model effectiveness and complexity (measured by the number of nodes in the genetic programming tree) simultaneously. Figure 4 revealed that there are 13, 15 and 14 Pareto solutions for the TPC, EY and AA responses, respectively. However, the green circles with red scribes in Figure 4a, b, and c represent the best Pareto front solutions for the TPC, EY and AA responses respectively, since they possessed the required minimum prediction error which is an indication of high effectiveness in process responses prediction. The mathematical models (best Pareto front solutions) relating the TPC, EY and AA responses to the investigated process variables of OT, S:L and ET are represented by Eq. (12), (13) and (14), respectively. All of the MGGP equations are non-linear in nature and each consisted of five genes and one bias.

\begin{array}{l} T P C = 7.048 * 10^{- 4} (B^{2} - 8.811 C (A - 5.1)) (9.149 A + B - 32.2) - 6.21 * 10^{- 3} B \\ - 7.657 * 10^{- 2} A + 5.215 * 10^{3} C (15.51 C - 1.455) - 9.833 \\ * 10^{- 3} A (9.027 A C^{2} + 33.11 A C + B) + 4.509 \\ * 10^{- 3} C (A + 1.8 B - C (9.149 A + B) - 14.52) (- C^{2} + A C + 5.1 A - B) \\ + 7.048 * 10^{- 3} A B C - 11.17 C (8.811 C - 3.876) (A - 12.55 A C^{2}) + 163.7 \end{array}

(12)

\begin{array}{l} E Y = 12.09 C (B C - B + C (B - 9.6870)) - 12.09 C - 1.633 \\ * 10^{- 4} A^{2} (B + C - 9.6870) - 2.198 * 10^{- 2} \\ + 1.616 C (A + 5 B + C - 2.3823) - 1.099 * 10^{- 2} A^{2} \\ + 1.616 C^{2} (A + 4 B) 1.099 * 10^{- 2} A (B - 2.382) \\ - \frac{4.127 A^{2} C (C - 4 B + A (A + 5.5470) (C + A C - 3.5975))}{10^{5}} - 6.532 \\ * 10^{- 4} B C (A + 4 B + 5 B C) - 1.099 * 10^{- 2} B C (C - A + 2 B C) + 11.22 \end{array}

(13)

\begin{array}{l} A A = 2.085 * 10^{- 1} A + 205.6 C - 2.815 A^{2} C^{2} - 6.469 * {10^{- 2} A}^{2} C^{2} + 4.448 * \\ 10^{- 2} A^{3} C^{2} + 7.491 * 10^{- 2} A^{3} C^{3} - 1.022 * 10^{- 2} A^{4} C^{3} - 6.272 A C + 2.942 * 10^{- 3} B C + \\ 30.93 A C^{2} - 2.942 * 10^{- 3} A^{2} C - 3.178 B C^{2} - 3.178 B C^{2} - 1.783 * 10^{- 3} A^{2} - 1679.0 C^{2} - \\ 3.178 * 10^{- 2} C^{3} - 3.386 \end{array}

(14)

The significance (p < 0.05) of each gene in the developed MGGP-based mathematical models for the prediction of TPC, EY and AA values can be visualized in Figure 5 (p-value vs. genes and bias). The structures of the equations, as well as their respective statistical model adequacy parameters are presented alongside in Figure 5.

Figure 5 showed the relative importance (based on the measure of probability values) of each gene and bias that made up the structure of the evolved MGGP equations. All the predictive MGGP-based models for TPC, EY and AA prediction of bioactive antioxidants from P. emblica leaves, possessed interestingly high R² (model R² for TPC, EY and AA are 0.9998, 0.9936 and 0.9622 respectively) and Adj R² (Adj R² for TPC, EY and AA are 0.9997, 0.9907 and 0.9451) values which indicate that the models are a good fit for the observed data and that they explain a significant portion of the variability in the dependent variables. Considering the evolved MGGP equation for the prediction of TPC (Eq. (11)), the probability all the genes and the bias were less than 0.0002 which implied that they are all significant (p < 0.05). However, the most important genes are genes 2, 3, 4 and 5. The bias was also a significant model term for MGGP-based predictive model for TPC as indicated in the figure. Similarly in Figure 5 (b), all the genes and the bias were significant part of MGGP-based predictive model structure for EY prediction since all the probability values of the evolved genes and bias were less than 0.00015. However, of significantly high importance in the evolved EY MGGP-based predictive model are the bias, gene 1, gene 2 and gene 5. Analysis of Figure 5 (c) also showed that the MGGP-based AA model have significant structure (genes and bias) for the prediction of AA values. As indicated on the graph (Figure 5 (c)), the probability values of all genes and bias in the structure are less than 0.000015, however, gene 1 is the most significant gene in the structure.

The ability of the MGGP-based models to predict the laboratory observed TPC, EY and AA data as function of process variables of OT, S:L and ET are presented in Figure 6 (a), (b) and (c), respectively.

It is obvious from Figure 6 that the MGGP-based models were able to predict the observed laboratory data for TPC, EY and AA satisfactorily. The parity graphs showed that both the observed and predicted data were clustered on the diagonal line which is an indication of good data predictive strengths of the MGGP-based models [4]. The models’ RMSE statistical parameter values were minimal (RMSE for TPC, EY and AA MGGP-developed models are 0.0202, 0.0288 and 0.0011) while all the models’ R² values were close to unity which implied perfect prediction of the models [4].

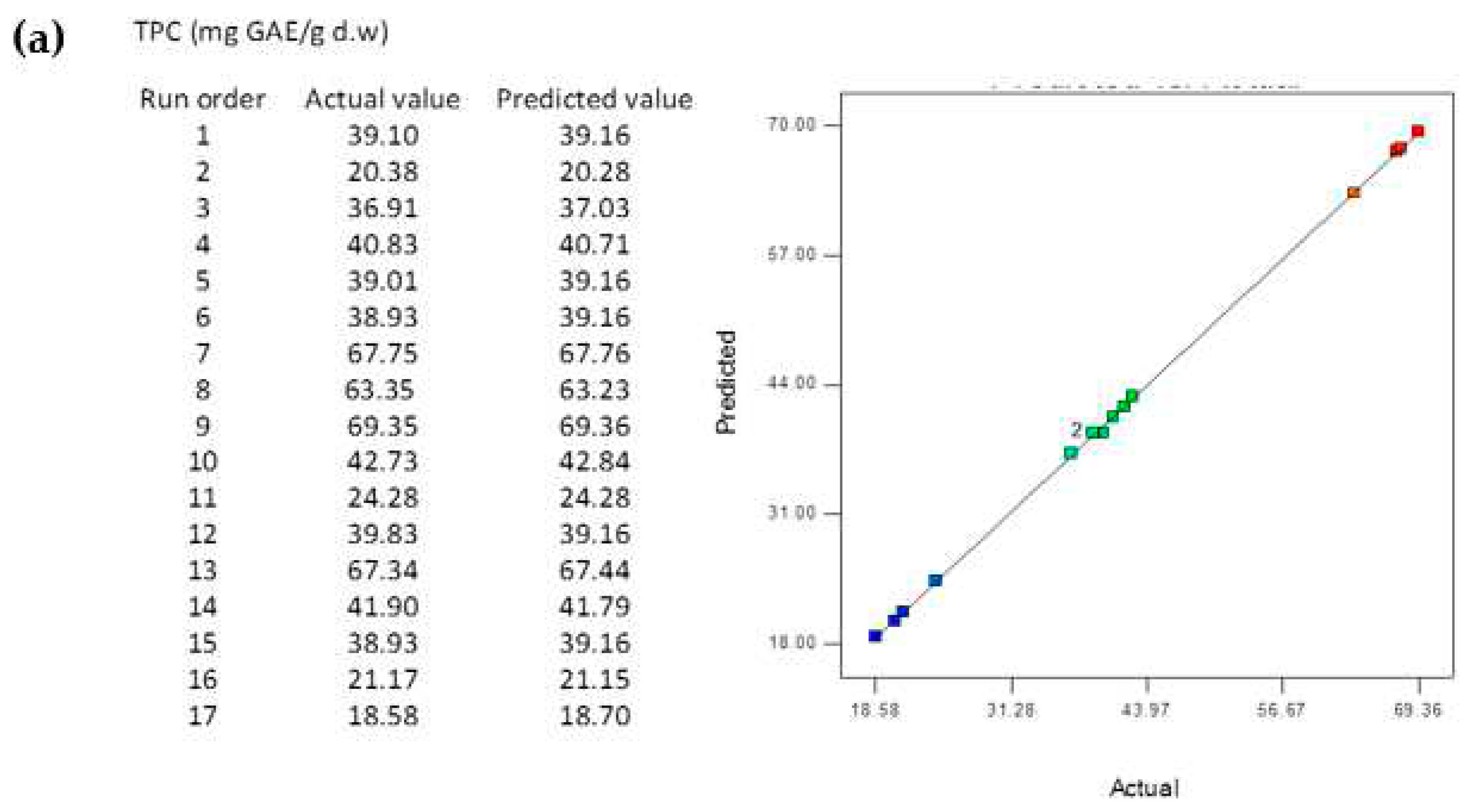
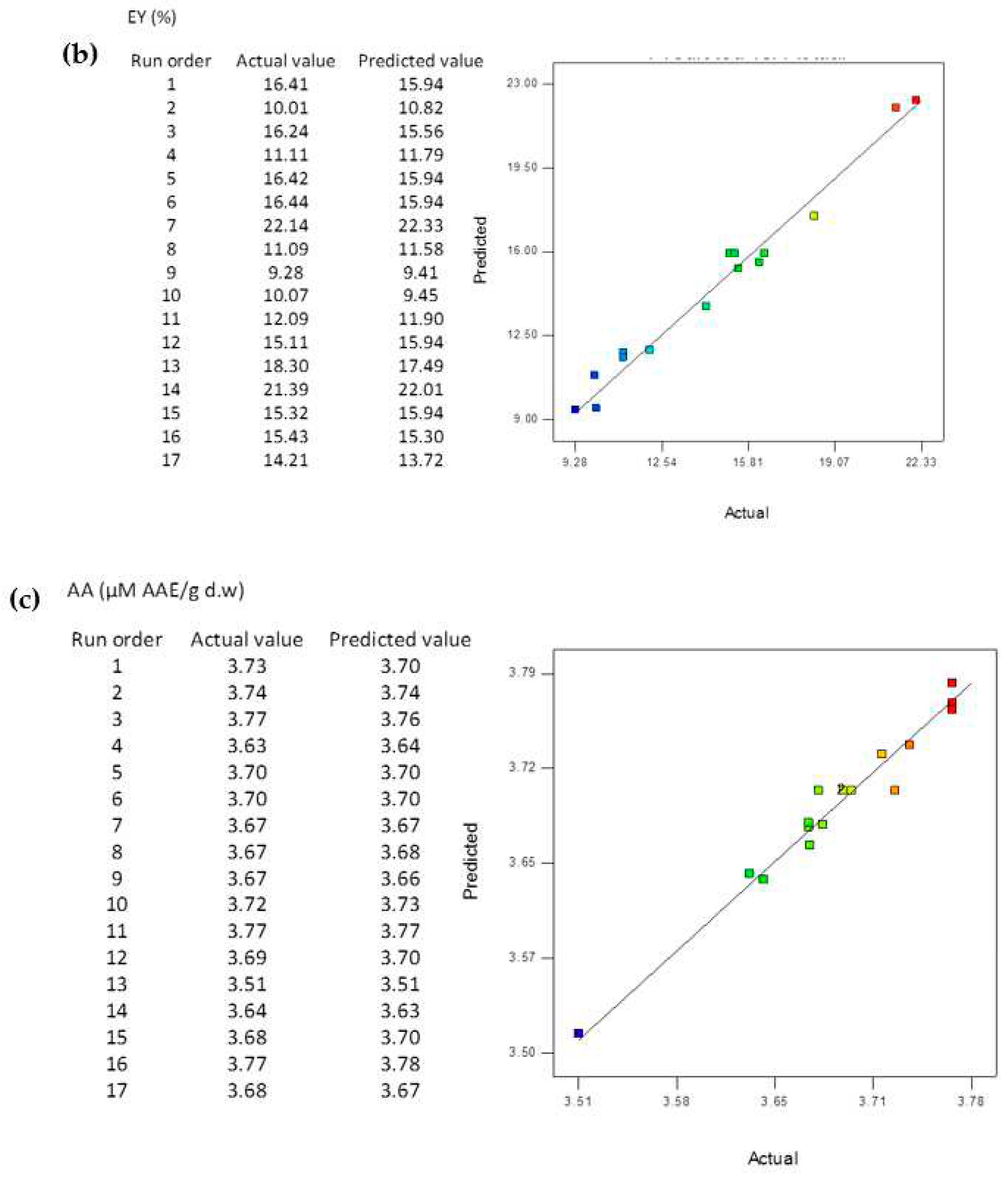
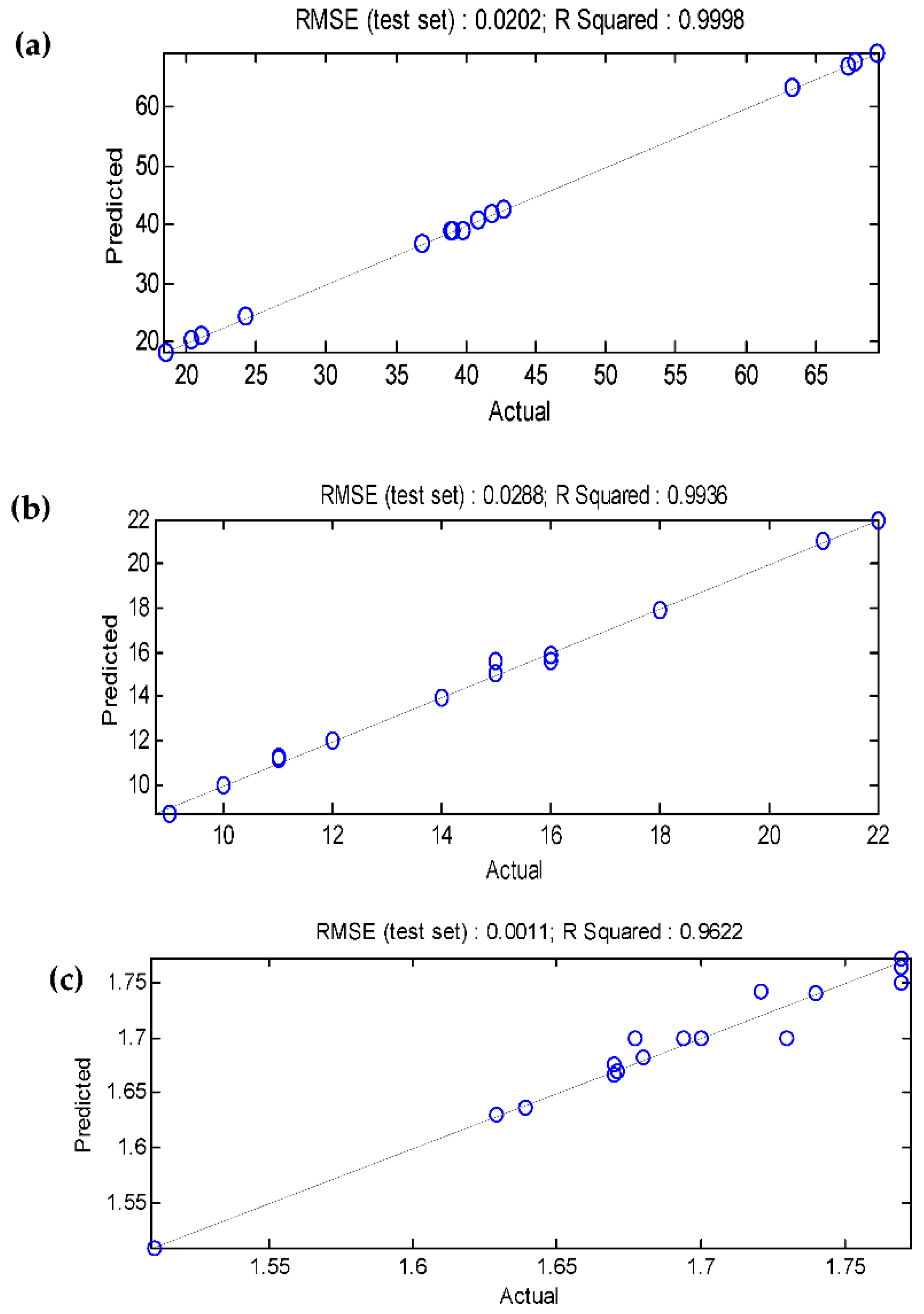
3.5. Comparison of the BBD-RSM and MGGP - based predictive models

The efficiency of RSM and MGGP is compared using their respective statistical indicators and the result is summarized in Table 9.

Adeyi et al. [4] reported that models with higher R² value implied better performances. Here, Table 9 depicts that the two models (i.e. RSM and MGGP model) performed well, however, the R² – value of RSM model is marginally greater than that of MGGP model and means a better model performance. RSM models are statistical models derived from regression analysis to fit a model to the data. It means that RSM models are parametric and therefore requires a priori knowledge of the functional form of the model [36]. However, parametric models are computationally efficient and can be utilized to model complex systems with a small number of data. On the other hand, MGGP is non-parametric and thus not require a priori knowledge of the functional form of the model, however, it is computationally intensive and evolves more accurate models as data utilized increased [37]. Therefore, the slightly improved performance of RSM model to MGGP model can be well related to small data set utilized, hence, RSM modeling approach is recommended for further model implementation.

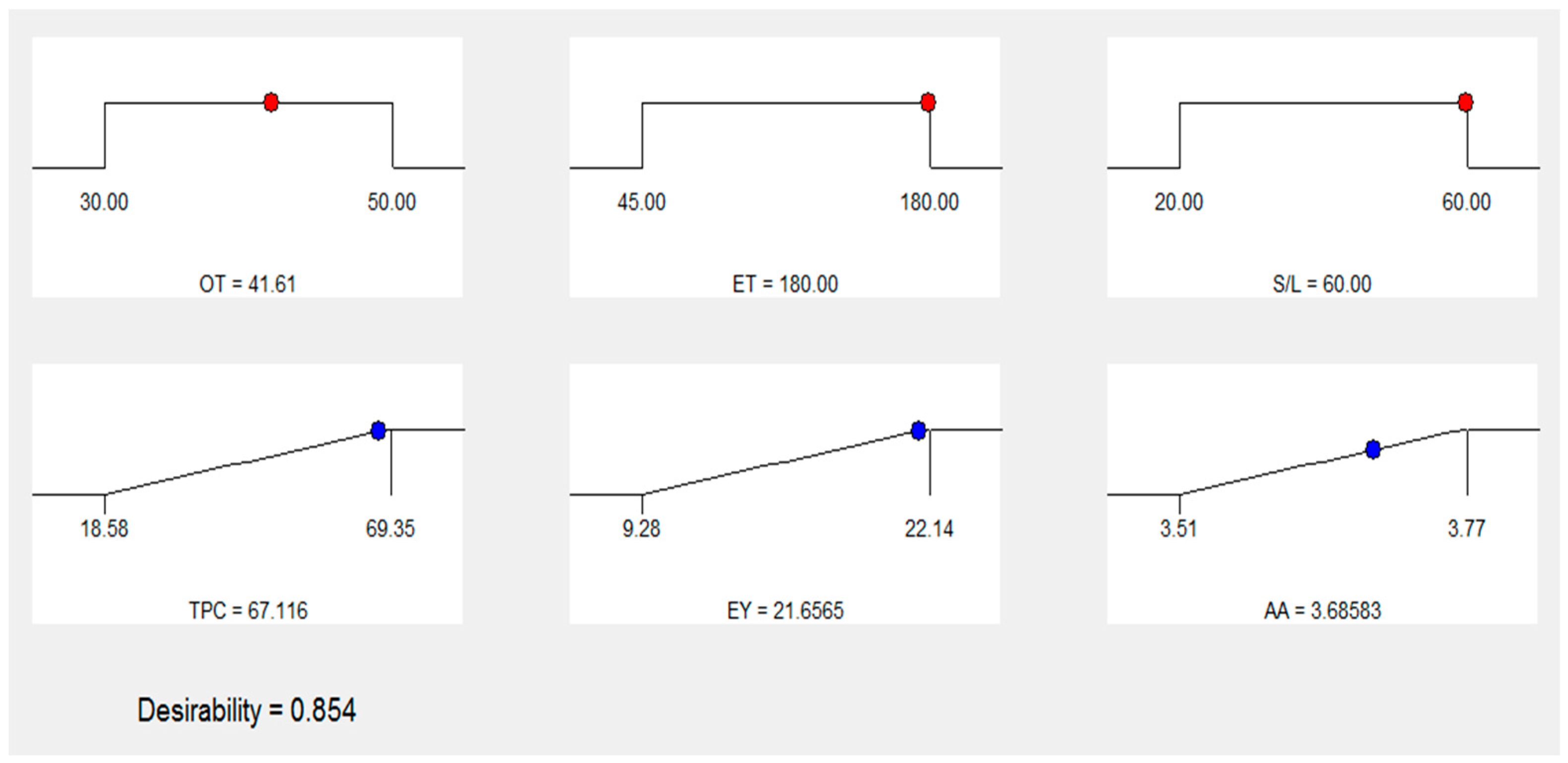
3.6. Numerical optimization and validation

The desirability algorithm that is present in the Design Expert software was used for achieving the optimization of the process parameter for the recovery of bioactive antioxidants from P. emblica leaves. The optimization procedure is in accordance with the work of Adeyi et al. [16]. The goal of the optimization scheme was to determine a set of process parameters that maximized the TPC, EY and AA of the bioactive extract. Table 5 presents the selected goal, weight, and importance for both the process parameters and responses. The table further shows the numerical range of search for the global optimum parameters of processing bioactive antioxidants recovery from P. emblica leaves.

Table 6 summarized all the thirteen (13) solutions presented based on the combined desirability values. The scale of the desirability is between 0 and 1, with desirability value of 1 adjudged the best [4].

The desirability values of the all the presented solutions ranged from 0.766 to 0.854. These solutions were ranked in ascending order of preference by the software with the first solution on the list, the best and selected. The 13^th solution on the table was the least preferred, although the solution also possessed appreciably high desirability value (0.766), the value was the least among the solutions provided by the algorithm. Hence, the first solution on the list with desirability value of 0.854 was selected as the best optimum solution. This desirability value of 0.854 compares well with other desirability values of selected optimum solutions in the literature. For instance this present desirability value is higher that than the desirability value of selected optimum solution in the work of Adeyi et al., [4] during the HAE process optimization of bioactive extract recovery from Carica papaya leaves.

Figure 3 is the optimization ramp for the best suggested solution (first) with combined desirability value of 0.854. The figure shows that the optimization search was within the range of investigated process parameters and observed laboratory response data. Therefore, the process parameters that simultaneously gave the optimum EY of 21.6565%, TPC of 67.116 mg GAE/g and AA of 3.68583 µM AAE/g were OT of 41.61 ^oC, S:L of 1:60 g/mL and ET of 180 min.

The validation experiment was conducted in the laboratory to ascertain the selected predicted optimum in the laboratory. Therefore, 1 g of P. emblica leaves was mixed with 60 mL of 50% ethanol-water mixture in a beaker and heated to approximately 42 ^oC by utilizing a water bath for the duration of 180 min. After the completion of the experiment, the leave fibers were separated from the extract through centrifugation and the EY, TPC and AA were quantified according to Section 2.7, 2.8 and 2.9 respectively. The results obtained for the validation experiment were EY = 22.31 %, TPC = 69.612 mg GAE/g and 3.72 µM AAE/g. The relative standard deviation (RSD) was computed to compare the experimental validated result with the predicted response result. It was found that the RSD between the validated and predicted values of EY, TPC and AA were 2.67%, 7.45% and 4.68% respectively. This indicated that these values are similar since the RSD between the validated and predicted response values are less than 10 [16]. This similarity in the validated and predicted results showed that the developed BBD-RSM models for EY, TPC and AA are effective, well-fitted, robust and capable of predicting the process of bioactive extract recovery from P. emblica leaves.

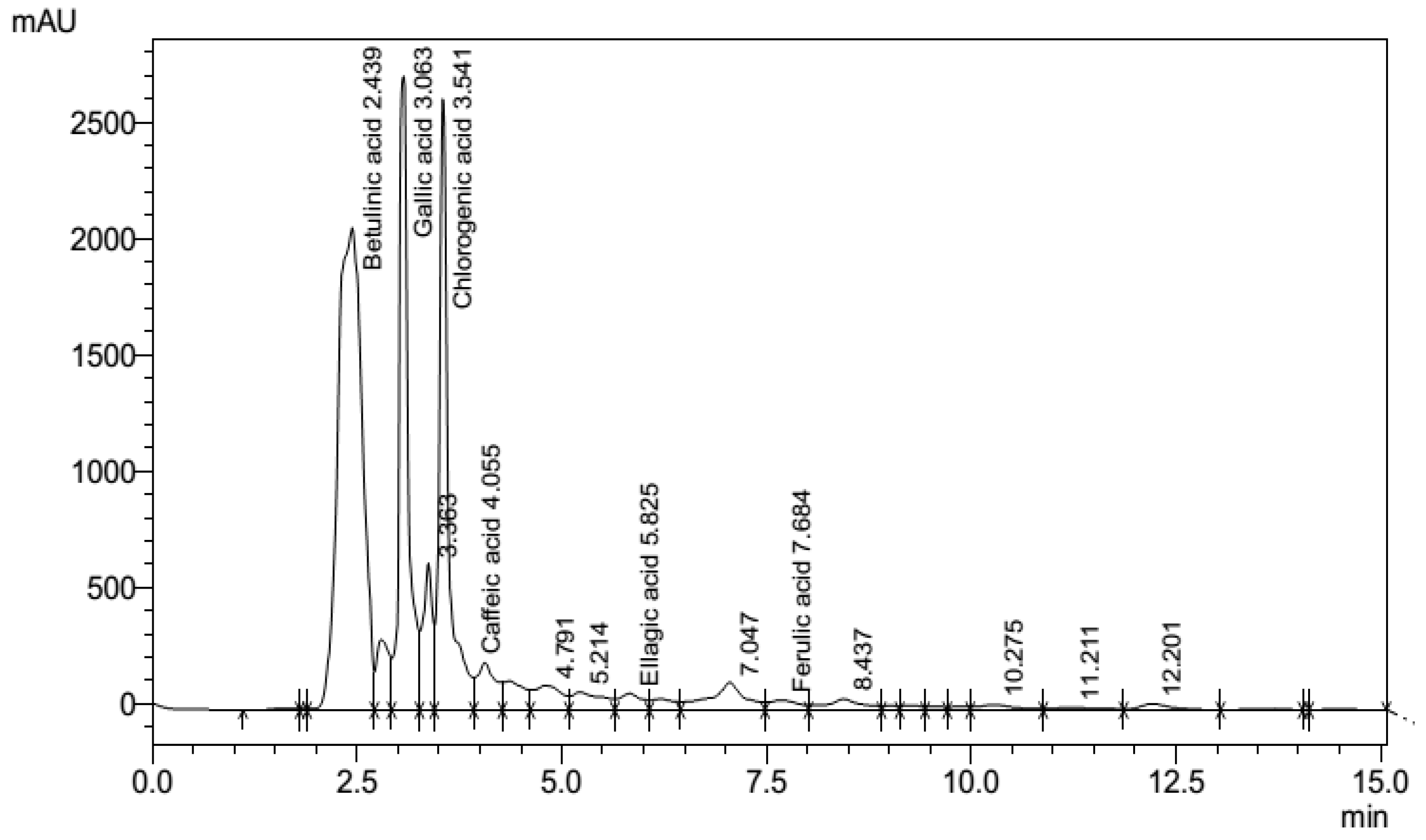
3.7. Phenolic fingerprints of P. emblica leaf extract

HPLC profiling of phenolic compounds in plant extracts is of paramount importance for the identification, and characterization of these bioactive compounds. It provides valuable insights into the chemical composition, quality, and therapeutic potential of plant extracts. Additionally, HPLC profiling can aid in the evaluation of the stability and degradation kinetics of phenolic compounds under different conditions, ensuring the preservation of their bioactivity. Therefore, the HPLC profiling of phenolic compounds in P. emblica leaf extract was for the purpose of identifying the phenolic compounds with potential therapeutic effects for the basis of future industrial production and techno-economic analysis of the P. emblica leaf extract. Hence to this end, eight (8) phenolic compounds with established bioactivities were used as standards for the HPLC profiling of the P. emblica leaf extract. These compounds were compared with the content of the extract using the similarities in retention factor (RF). Figure 4 is the HPLC fingerprints of P. emblica leaf extract. As shown, Figure 4 is characterized by different phenolic compounds and wide disparities in their corresponding areas. The figure revealed six (6) phenolic compounds that have comparable RT with the HPLC phenolic standards used as the baseline of identification. The identified phenolic compounds in the P. emblica leaf extract with corresponding RT are betulinic acid (RT = 2.439 min), gallic acid (RT = 3.063 min), chlorogenic acid (RT = 3.541 min), caffeic acid (RT = 4.055 min), ellagic acid (RT = 5.825 min), and ferulic acid (RT = 7.684 min).

The bioactivities of the identified phenolic compounds in the extract were interesting and pointing to the overall therapeutic potential of P. emblica leaf extract. For instance, betulinic acid exhibits a wide range of therapeutic properties and studies have shown that it induces apoptosis (programmed cell death) in cancer cells, making it a promising candidate for cancer treatment [38]. Gallic acid possesses numerous health benefits and recent investigations showed that it has potentials to inhibit tumor growth, reduce oxidative stress, and exert protective effects against various diseases [39]. Chlorogenic acid has been studied for its potential in preventing skin tumorigenesis, modulating MAPK and NF-κB pathways, and ameliorating oxidative stress [40] while caffeic acid has been investigated for its potential in inhibiting atopic dermatitis-like skin inflammation and synergistic antioxidant activity when combined with other phenolic acids [39]. Both ellagic acid and ferulic acid have been shown to exhibit antioxidant, anti-inflammatory, anticancer, antimicrobial, and antimutagenic effects [41,42].

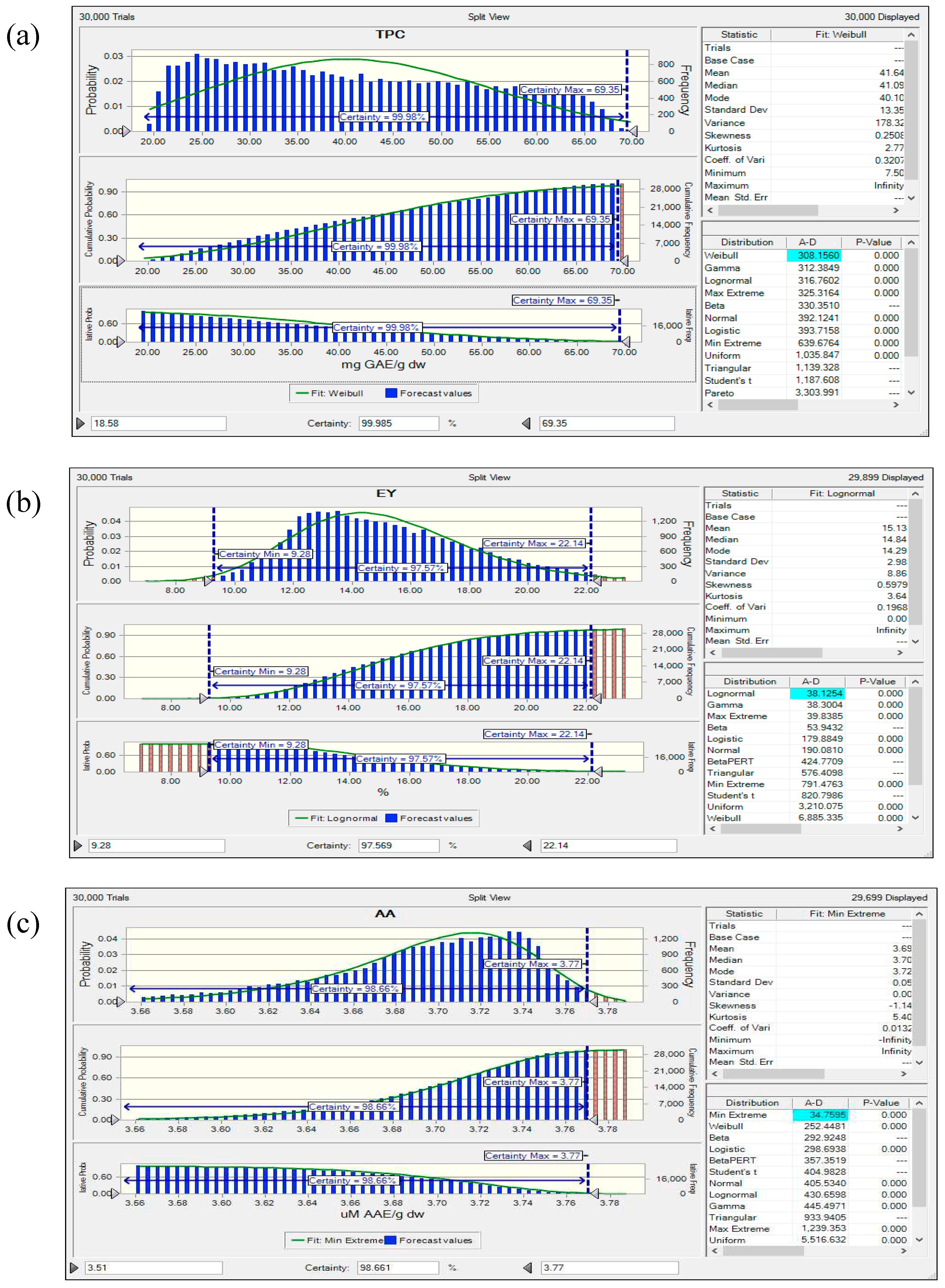
3.8. Reliability Assessment of BBD-RSM based Predictive Models

Model reliability assessment is the process of evaluating and determining the trustworthiness and accuracy of a model’s predictions or outputs. One of the various available techniques and methodologies to gauge the model’s performance and identify its strengths and limitations is via Monte Carlo simulation. The main purpose of Monte Carlo simulation in the context of model reliability assessment is to quantify uncertainty, validate model performance, and estimate the potential range of outcomes. Another key aspect of Monte Carlo simulation is its ability to conduct robust sensitivity assessment where various inputs are systematically varied to determine their impact on the model’s outputs which helps in identifying which input parameters have the most significant influence on the results and helps in understanding the robustness of the model. In the present investigation, the developed BBD-RSM based predictive models were used for this analysis due to their relative superiority in predicting the heat-assisted extraction process outputs of TPC, EY and AA, relative to the MGGP-based models as explained in Section 3.5. Figure 7 (a), (b) and (c) show the split views of the probability distributions, cumulative frequency and reverse cumulative frequency curves of the analyses conducted in Oracle Crystal ball software for the prediction of experimental observed data (in Table 3) of TPC, EY and AA respectively, as function of input variables of OT, S:L and ET in order to ascertain the robustness of the constructed BBD-RSM based predictive models. The outcomes’ data statistics and the best fit model for the distribution were also incorporated in the presented split view figures and positioned at the upper right and down respectively. Figure 7 shows that the BBD-RSM models for TPC, EY and AA are capable of predicting the respective outcomes as function of OT, S:L and ET within the range of their respective experimental outcomes. The data outcomes kurtosis and skewness (statistical measures that provide information about the shape and distribution of a dataset) for TPC, EY and AA are 2.77 and 0.2508; 3.64 and 0.5979; and 5.40 and -1.14, respectively. The distribution curves for the TPC, EY and AA were excellently modeled by Weibull (Anderson-Darling coefficient = 308.1560), Lognormal (Anderson-Darling coefficient = 38.1254) and Min Extreme (Anderson-Darling coefficient = 34.7595), respectively. As indicated in Figure 7, the percentage certainty of the developed BBD-RSM models in predicting the observed experimental data range of 18.58 – 69.35 mg GAE/g, 9.28 – 22.14% and 3.51 - 3.77 µM AAE/g (in Table 3) for TPC, EY and AA, is 99.985%, 97.569% and 98.661%, respectively. The high BBD-RSM models’ individual prediction certainty is an indication of their respective high reliability and robustness.

These values compare well with the prediction certainty of the Sierrathrissaleonensis cracker drying effective moisture diffusivity D-Optimal-RSM predictive model (99.831%) [14], biodiesel yield CCD-RSM predictive model (73.509%) (Oke et al., 2022) and techno-economic MGGP predictive models (MGGP-CAnysP APR = 99.980% and MGGP-CAnysP UPC = 98.477%) [14]. The dynamic sensitivity charts, which identify input parameters that have the most significant influence on the predictions of the developed BBD-RSM models, are presented in Figure 8. Here, the contribution of process variables of OT, S:L and ET to the variance in the prediction of BBD-RSM models for TPC, EY and AA were assessed. Figure 8 shows that process variables contributed differently to the perturbation in the developed BBD-RSM models predictions. In the dynamic sensitivity graphs, all the bars to the right hand side indicate positive contributions (increase in response variable value with an increase in process variable value) while the bars to the left hand side signify negative contributions (increase in process variable value with decrease in response variable value).

Also the length (measured by percentage) of a sensitivity bar determines its magnitude and relative importance. Hence, a long bar (to either side) is relatively significant than correspondingly shorter bar, with 0% assigned to a no-significant effect. A high significant parameter should be better controlled (or more accurately measured) in order to improve the model’s predictability. Therefore, analysis of Figure 8 (a) showed that S:L was the process variable with the most significant importance to the variance in TPC BBD-RSM model prediction. The ET and OT did not seem to influence profoundly the predictability of TPC BBD-RSM model. In the same vain, Figure 8 (b) showed that the ET and S:L were the process variables with highest and least significance, respectively to the variance in the EY BBD-RSM model prediction. Also the order of process variable significance (Figure 8 (c)) to the perturbation in the predictability of AA BBD-RSM model is S:L > OT > ET. In numerical terms however, S:L had positive contribution (+99.7%), ET had negative contribution (-0.28%) while OT did not contribute significantly (+ 0.02%) to the perturbation in the predictability of TPC BBD-RSM. Likewise, ET contributed positively (+76.2%), OT contributed negatively (-19.8%) while S:L contributed positively (+4%) to the variance in EY data prediction by the EY BBD-RSM model. The S:L, OT and ET contributed -52%, +46.7 and +1.3% respectively to the variance in AA value predictability by the constructed AA BBD-RSM model.

4.0. Conclusion

It is feasible to recover bioactive antioxidants from Phyllantus emblica leaves using the heat-assisted extraction technology and water-ethanol solvent mixture. The best ethanol-water mixture ratio for optimal recovery of bioactive extract was 50:50. All the investigated heat-assisted extraction process parameters had notable impacts on the bioactive extract’s total phenolic compound (TPC), yield (EY) and antioxidant activity (AA). The process parameters that simultaneously gave the optimum EY of 21.6565%, TPC of 67.116 mg GAE/g and AA of 3.68583 µM AAE/g were OT of 41.61 ^oC, S:L of 1:60 g/mL and ET of 180 min. The HPLC extract characterization revealed that the bioactive constituents of the recovered extract were betulinic acid, gallic acid, chlorogenic acid, caffeic acid, ellagic acid, and ferulic acid. Both response surface methodology (RSM) and multi gene genetic programing algorithm (MGGP) were able to model the relationships between the investigated heat-assisted extraction process parameters and observed process responses of TPC, EY and AA with high satisfaction. The developed RSM models (BBD-RSM) were however, marginally better than their corresponding MGGP based models for the prediction of TPC, EY and AA data. The BBD-RSM based models were highly reliable and were able to predict the laboratory observed data of TPC, EY and AA as function process variables with high certainty. The certainty values for the developed BBD-RSM models to predict observed TPC, EY and AA values were 99.985%, 97.569% and 98.661%, respectively. The process parameter of S:L had strong positive contribution (+99.7%) while OT, and ET did not seem to have strong effect (+ 0.02% for OT and -0.28% for ET) on the TPC values prediction of the BBD-RSM model. In the same manner, ET contributed positively (+76.2%), OT contributed negatively (-19.8%) while S:L contributed positively (+4%) to the variance in EY data prediction by the EY BBD-RSM model. The order of contribution of the process variables to the variance in AA value prediction by the constructed AA BBD-RSM model was S:L > OT > ET.

Author Contributions

Conceptualization, O.A. and A.J.A; methodology, H.A.; software, E.O; validation, H.A., O.A., A.J.A and Z.Z.; formal analysis, H.A., O.A., A.J.A and Z.Z.;; investigation, O.A.,A.J.A.; resources, H.A., H.A.; data curation, O.A.O; writing—original draft preparation, O.A., A.J.A’, H.A.; writing—review and editing, O.A.O; visualization, E.O., C.Y.G.; supervision, O.A.O, C.Y.G, O.A.; project administration, O.A., O.A.O; funding acquisition, H.A¹, H.A². All authors have read and agreed to the published version of the manuscript.

Funding

Please add: The APC was funded by Dr Hamdan Alanzi. Department of Chemical Engineering Technology, College of Technological Studies. The Public Authority for Applied Education and Training, Kuwait

Data Availability Statement

All data will be provided upon request.

Acknowledgments

The author acknowledges The Public Authority for Applied Education and Training, Kuwait

Conflicts of Interest

The authors declare no conflict of interest.

References

Saini, R., Sharma, N., Oladeji, O. S., Sourirajan, A., Dev, K., Zengin, G., ... & Kumar, V. (2022). Traditional uses, bioactive composition, pharmacology, and toxicology of Phyllanthus emblica fruits: A comprehensive review. Journal of ethnopharmacology, 282, 114570.
Ahmad, B., Hafeez, N., Rauf, A., Bashir, S., Linfang, H., Rehman, M. U., ... & Rengasamy, K. R. (2021). Phyllanthus emblica: A comprehensive review of its therapeutic benefits. South African Journal of Botany, 138, 278-310.
Mirunalini, S., & Krishnaveni, M. (2010). Therapeutic potential of Phyllanthus emblica (amla): the ayurvedic wonder. Journal of basic and clinical physiology and pharmacology, 21(1), 93-105.
Adeyi, O., Adeyi, A. J., Oke, E. O., Ajayi, O. K., Oyelami, S., Otolorin, J. A., ... & Isola, B. F. (2022). Adaptive neuro fuzzy inference system modeling of Synsepalum dulcificum L. drying characteristics and sensitivity analysis of the drying factors. Scientific Reports, 12(1), 13261.
Olalere, O. A., Abdurahman, H. N., & Gan, C. Y. (2019). Microwave-enhanced extraction and mass spectrometry fingerprints of polyphenolic constituents in Sesamum indicum leaves. Industrial Crops and Products, 131, 151-159.
Olalere, O. A., Abdurahman, N. H., bin Mohd Yunus, R., Alara, O. R., & Ahmad, M. M. (2019). Mineral element determination and phenolic compounds profiling of oleoresin extracts using an accurate mass LC-MS-QTOF and ICP-MS. Journal of King Saud University-Science, 31(4), 859-863.
Olalere, O. A., Gan, C. Y., Taiwo, A. E., Nour, A. H., Dominguez, B. C., Adeyi, O., ... & Adiamo, O. Q. (2023). Heat-reflux processing of black peppercorn into bioactive antioxidant oleoresins: a three-functioned Taguchi-based grey relational grading. Journal of Food Measurement and Characterization, 1-9.
Chuo, S. C., Nasir, H. M., Mohd-Setapar, S. H., Mohamed, S. F., Ahmad, A., Wani, W. A., ... & Alarifi, A. (2022). A glimpse into the extraction methods of active compounds from plants. Critical reviews in analytical chemistry, 52(4), 667-696.
Oke, E. O., Adeyi, O., Okolo, B. I., Adeyi, J. A., Ayanyemi, J., Osoh, K. A., & Adegoke, T. S. (2020). Phenolic compound extraction from Nigerian Azadirachta indica leaves: response surface and neuro-fuzzy modelling performance evaluation with Cuckoo search multi-objective optimization. Results in Engineering, 8, 100160.
Pinela, J., Prieto, M. A., Pereira, E., Jabeur, I., Barreiro, M. F., Barros, L., & Ferreira, I. C. (2019). Optimization of heat-and ultrasound-assisted extraction of anthocyanins from Hibiscus sabdariffa calyces for natural food colorants. Food chemistry, 275, 309-321.
Tchabo, W., Ma, Y., Kwaw, E., Xiao, L., Wu, M., & T. Apaliya, M. (2018). Impact of extraction parameters and their optimization on the nutraceuticals and antioxidant properties of aqueous extract mulberry leaf. International Journal of Food Properties, 21(1), 717-732.
Olalere, O. A., & Gan, C. Y. (2021). Investigating the heat stability, calorimetric degradations and chromatographic polyphenolic profiling of edible macerated hog-tree apple leaf (Morinda lucida Benth). Chemical Papers, 75, 1291-1299.
Alara, O. R., Abdurahman, N. H., Afolabi, H. K., & Olalere, O. A. (2018). Efficient extraction of antioxidants from Vernonia cinerea leaves: Comparing response surface methodology and artificial neural network. Beni-Suef University Journal of Basic and Applied Sciences, 7(3), 276-285.
Adeyi, A. J., Adeyi, O., Oke, E. O., Olalere, O. A., Oyelami, S., & Ogunsola, A. D. (2021). Effect of varied fiber alkali treatments on the tensile strength of Ampelocissus cavicaulis reinforced polyester composites: Prediction, optimization, uncertainty and sensitivity analysis. Advanced Industrial and Engineering Polymer Research, 4(1), 29-40.
Adeyi, O., Adeyi, A. J., Oke, E. O., Okolo, B. I., Olalere, A. O., Otolorin, J. A., & Taiwo, A. E. (2021). Techno-economic and uncertainty analyses of heat-and ultrasound-assisted extraction technologies for the production of crude anthocyanins powder from Hibiscus sabdariffa calyx. Cogent Engineering, 8(1), 1947015.
Adeyi, O., Adeyi, A. J., Oke, E. O., Okolo, B. I., Olalere, O. A., Taiwo, A. E., ... & Ogunsola, A. D. (2023). Heat-assisted extraction of phenolic-rich bioactive antioxidants from Enantia chlorantha stem bark: multi-objective optimization, integrated process techno-economics and profitability risk assessment. SN Applied Sciences, 5(6), 153.
Olalere, O. A., & Gan, C. Y. (2023). Process optimisation of defatted wheat germ protein extraction in a novel alkaline-based deep eutectic solvent (DES) via Box–Behnken experimental design (BBD). Food Chemistry, 409, 135224.
Rajewski, J., & Dobrzyńska-Inger, A. (2021). Application of response surface methodology (RSM) for the optimization of chromium (III) synergistic extraction by supported liquid membrane. Membranes, 11(11), 854.
Alenezi, H., & Al-Qabandi, O. (2023). Prediction of adsorption parameters for hydrogen sulfide removal from synthetic wastewater using Box-Behnken design. Journal of Engineering Research, 11(2), 100067.
Bezerra, M. A., Santelli, R. E., Oliveira, E. P., Villar, L. S., & Escaleira, L. A. (2008). Response surface methodology (RSM) as a tool for optimization in analytical chemistry. Talanta, 76(5), 965-977.
Breig, S. J. M., & Luti, K. J. K. (2021). Response surface methodology: A review on its applications and challenges in microbial cultures. Materials Today: Proceedings, 42, 2277-2284.
Alara, O. R., Abdurahman, N. H., & Olalere, O. A. (2018). Optimization of microwave-assisted extraction of flavonoids and antioxidants from Vernonia amygdalina leaf using response surface methodology. Food and bioproducts processing, 107, 36-48.
Kumari, M., & Gupta, S. K. (2019). Response surface methodological (RSM) approach for optimizing the removal of trihalomethanes (THMs) and its precursor’s by surfactant modified magnetic nanoadsorbents (sMNP)-An endeavor to diminish probable cancer risk. Scientific Reports, 9(1), 1-11.
Gandomi, A. H., & Alavi, A. H. (2012)a. A new multi-gene genetic programming approach to non-linear system modeling. Part II: geotechnical and earthquake engineering problems. Neural Computing and Applications, 21, 189-201.
Gandomi, A. H., & Alavi, A. H. (2012)b. A new multi-gene genetic programming approach to nonlinear system modeling. Part I: materials and structural engineering problems. Neural Computing and Applications, 21, 171-187.
Niazkar, M. (2023). Multigene genetic programming and its various applications. Handbook of Hydroinformatics, 321-332.
Kusznir, T., & Smoczek, J. (2022). Multi-Gene Genetic Programming-Based Identification of a Dynamic Prediction Model of an Overhead Traveling Crane. Sensors, 22(1), 339.
Ghareeb, W. T., & El Saadany, E. F. (2013, October). Multi-gene genetic programming for short term load forecasting. In 2013 3rd International Conference On Electric Power And Energy Conversion Systems (pp. 1-5). IEEE.
Haroonabadi, H., & Haghifam, M. R. (2011). Generation reliability assessment in power markets using Monte Carlo simulation and soft computing. Applied Soft Computing, 11(8), 5292-5298.
Dao, D. V., Adeli, H., Ly, H. B., Le, L. M., Le, V. M., Le, T. T., & Pham, B. T. (2020). A sensitivity and robustness analysis of GPR and ANN for high-performance concrete compressive strength prediction using a Monte Carlo simulation. Sustainability, 12(3), 830.
Olalere, O. A., & Gan, C. Y. (2021). Microwave-assisted extraction of phenolic compounds from Euphorbia hirta leaf and characterization of its morphology and thermal stability. Separation Science and Technology, 56(11), 1853-1865.
Huaman-Castilla, N. L., Martínez-Cifuentes, M., Camilo, C., Pedreschi, F., Mariotti-Celis, M., & Pérez-Correa, J. R. (2019). The impact of temperature and ethanol concentration on the global recovery of specific polyphenols in an integrated HPLE/RP process on Carménère pomace extracts. Molecules, 24(17), 3145.
Altıok, E., Bayçın, D., Bayraktar, O., & Ülkü, S. (2008). Isolation of polyphenols from the extracts of olive leaves (Olea europaea L.) by adsorption on silk fibroin. Separation and Purification Technology, 62(2), 342-348.
Cheaib, D., El Darra, N., Rajha, H. N., Maroun, R. G., & Louka, N. (2018). Systematic and empirical study of the dependence of polyphenol recovery from apricot pomace on temperature and solvent concentration levels. The Scientific World Journal, 2018.
Mohammadi Bayazidi, A., Wang, G. G., Bolandi, H., Alavi, A. H., & Gandomi, A. H. (2014). Multigene genetic programming for estimation of elastic modulus of concrete. Mathematical Problems in Engineering, 2014.
Noh, H., Kwon, S., Seo, I. W., Baek, D., & Jung, S. H. (2020). Multi-gene genetic programming regression model for prediction of transient storage model parameters in natural rivers. Water, 13(1), 76.
Ghattas, B., & Manzon, D. (2023). Machine Learning Alternatives to Response Surface Models. Mathematics, 11(15), 3406.
Yu, M., Gouvinhas, I., Rocha, J., & Barros, A. I. (2021). Phytochemical and antioxidant analysis of medicinal and food plants towards bioactive food and pharmaceutical resources. Scientific reports, 11(1), 10041.
Tsang, M.S., Jiao, D., Chan, B.C., Hon, K.L., Leung, P.C., Lau, C.B., Wong, E.C., Cheng, L., Chan, C.K., Lam, C.W. and Wong, C.K., (2016). Anti-inflammatory activities of pentaherbs formula, berberine, gallic acid and chlorogenic acid in atopic dermatitis-like skin inflammation. Molecules, 21(4), p.519.
Ranjha, M.M.A.N., Shafique, B., Wang, L., Irfan, S., Safdar, M.N., Murtaza, M.A., Nadeem, M., Mahmood, S., Mueen-ud-Din, G. and Nadeem, H.R., (2021). A comprehensive review on phytochemistry, bioactivity and medicinal value of bioactive compounds of pomegranate (Punica granatum). Advances in Traditional Medicine, pp.1-21.
Gupta, A., Atanasov, A.G., Li, Y., Kumar, N. and Bishayee, A., (2022). Chlorogenic acid for cancer prevention and therapy: Current status on efficacy and mechanisms of action. Pharmacological Research, p.106505.
Manivel, P., & Chen, X. (2021). Chlorogenic, Caffeic, and Ferulic Acids and Their Derivatives in Foods. Handbook of Dietary Phytochemicals, 1033-1063.

Figure 1. Representation of genes with tree structures [4].

Figure 2. Experimental Vs. predicted data for (a) TPC (b) EY (c) AA.

Figure 3. Training process for best MGGP model for (a) TPC (b) EY (c) AA.

Figure 4. Pareto model solutions for (a) TPC (b) EY and (c) AA.

Figure 5. MGGP-based model structure, adequacies and gene significance for the prediction of (a) TTPC, (b) EY and (c) AA values.

Figure 6. Parity graphs for the MGGP-based model prediction for (a) TPC (b) EY and (c) AA.

Figure 3. Optimization ramp for the suggested best solution.

Figure 4. HPLC fingerprints of P. emblica leaf extract.

Figure 7. Split views of Monte Carlo outcome prediction of the BBD-RSM models for (a) TPC (b) EY and (c) AA.

Figure 8. Contribution of process variable to variance in prediction of the BBD-RSM models for (a) TPC (b) EY (c) AA .

Table 1. Parameter settings of MGGP.

Parameter	Value
Population size range	100, 250, 500
Number of generation range	100, 250, 500
Tournament size Maximum tree depth	4
Elitism fraction	0.25 of population
Termination value	0.001
Maximum gene Crossover event Mutation event Subtree mutation	5
Node Function	Minus, times , rdivide, plus, plog, psqroot, tanh, square, pdivide, iflte, exp, sin, cos

Table 2. Selection of best solvent for extraction^a.

S/N	Solvent	Extract yield (%)	Total phenolic content (mg GAE/g d.w)	Antioxidant activity (μM AAE/g d.w)
1	Absolute ethanol	5.87±0.01	13.67±0.04	1.98±0.11
2	80% ethanol solution	8.41±0.25	20.10±0.12	2.99±0.05
3	60% ethanol solution	11.36±0.08	23.76±0.04	3.66±0.09
4	50% ethanol solution	12.07±0.02	24.25±0.03	3.76±0.01
5	40% ethanol solution	11.11±0.03	22.98±0.12	3.52±0.11
6	20% ethanol solution	8.67±0.13	19.73±0.02	3.31±0.10
7	100% distilled water	8.33±0.19	19.11±0.02	2.81±001

^aAll experiments were duplicated.

Table 3. 3³ Box-Behnken design and measured responses^b .

Run	Extraction conditions			Response values
Run	OT (^oC)	S:L (g/mL)	ET (min)	EY (w/w %)	TPC (mg GAE/g d.w)	AA (µM AAE/g)
1	40.00	1:40	112.50	15.11	39.83	3.69
2	30.00	1:20	112.50	14.21	18.58	3.68
3	40.00	1:40	112.50	16.41	39.10	3.73
4	30.00	1:60	112.50	18.30	67.34	3.51
5	40.00	1:60	180.00	22.14	67.75	3.67
6	40.00	1:20	45.00	12.09	24.28	3.77
7	40.00	1:20	180.00	15.43	21.17	3.77
8	50.00	1:20	112.50	10.01	20.38	3.74
9	40.00	1:40	112.50	15.32	38.93	3.68
10	30.00	1:40	180.00	21.39	41.90	3.64
11	40.00	1:60	45.00	9.28	69.35	3.67
12	30.00	1:40	45.00	11.11	40.83	3.63
13	40.00	1:40	112.50	16.42	39.01	3.70
14	50.00	1:60	112.50	11.09	63.35	3.67
15	40.00	1:40	112.50	16.44	38.93	3.70
16	50.00	1:40	180.00	16.24	36.91	3.77
17	50.00	1:40	45.00	10.07	42.73	3.72

^b OT represents operating temperature; S:L represent solid to liquid ratio; ET represent extraction time; EY represents extract yield; TPC represents total phenolic content ; AA represents antioxidant activity.

Table 4. Analysis of variance (ANOVA) for TPC, EYs and AA quadratic models^{c .}

Source	TPC (mg GAE/g d.w)				EY (%)				AA (µM AAE/g d.w)
	Sum of squares	df	F-value	P-value P>F	Sum of squares	df	F-value	P-value P>F	Sum of squares	df	F-value	P-value P>F
Model	4340.17	9	4947.4	<0.0001	225.75	9	32.58	<0.0001	0.062	9	22.86	0.0002
A - OT	3.48	1	35.71	0.0006	38.72	1	50.29	0.0002	0.025	1	80.77	<0.0001
B – S:L	11.21	1	115.01	<0.0001	133.25	1	173.1	< 0.0001	4 E-004	1	1.38	0.2778
C - ET	4203.67	1	4203.6	<0.0001	10.28	1	13.35	0.0081	0.024	1	79.32	<0.0001
A²	3.38	1	34.66	0.0006	6.95	1	9.03	0.0198	6 E-003	1	22.57	0.0021
B²	22.64	1	234.31	<0.0001	9.5E-003	1	0.012	0.9147	3 E-003	1	12.39	0.0097
C²	72.45	1	743.32	<0.0001	6.61	1	8.58	0.0221	4 E-004	1	1.35	0.2842
AB	11.88	1	121.86	<0.0001	4.22	1	5.48	0.0517	3 E-004	1	1.25	0.3001
AC	8.38	1	85.98	<0.0001	2.27	1	2.94	0.1300	2 E-003	1	8.23	0.0240
BC	0.58	1	5.90	0.0455	22.66	1	29.43	0.0010	2 E-007	1	8.2E-004	0.9779
Residual	0.68	7			5.39	7			2 E-003	7
Lack of fit	0.10	3	0.23	0.8693	3.62	3	2.72	0.1793	6 E-004	3	0.60	0.6473
Pure error	0.58	4			1.77	4			1 E-003	3
Cor. Total	4340.85	16			231.14	16			0.065	16
CV%	0.75				5.94				0.47
PRESS	2.53				60.62				0.013
Adeq Precision	211.576				19.201				20.041
R²	0.9998				0.9967				0.9671
Adj R²	0.9996				0.9467				0.9248
Pred R²	0.9994				0.7077				0.8009

^c OT is operating temperature; S:L is solid to liquid ratio; ET is extraction time; EY is extract yield; TPC is total phenolic content ; AA is antioxidant activity; df is degree of freedom; CV is coefficient of variation; Adeq Precision is adequate precision; Adj R² is adjusted R²; Pred R² is predicted R^2.

Table 5. Descriptive statistics of the process and response variables^d.

Statistical parameters	OT (^oC)	S:L (g/mL)	ET (min)	EY (w/w %)	TPC (mg GAE/g d.w)	AA (µM AAE/g)
Mean	40	40	112.5	14.7682352	41.7864705	3.6905882
Standard error	1.7149858	3.4299717	11.5761544	0.9218337	3.9948426	0.0153745
Median	40	40	112.5	15.32	39.1	3.69
Mode	40	40	112.5	N/A	38.93	3.67
Standard Deviation	7.0710678	14.1421356	47.7297077	3.8008177	16.4711581	0.0633907
Sample Variance	50	200	2278.1250	14.4462154	271.2990492	0.0040183
Kurtosis	-0.7428571	- 0.7428571	- 0.7428571	- 0.4367377	- 0.6261143	3.1818297
Skewness	6.2912E-17	0	0	0.3321146	0.4519267	-1.2675914
Range	20	40	135	12.86	50.77	0.26
Minimum	30	20	45	9.28	18.58	3.51
Maximum	50	60	180	22.14	69.35	3.77
Sum	680	680	1912.5	251.06	710.37	62.74
Count	17	17	17	17	17	17

^dOT is operating temperature; S:L is solid to liquid ratio; ET is extraction time; EY is extract yield; TPC is total phenolic content ; AA is antioxidant activity.

Table 6. MGGP parameter settings optimization for the prediction of TPC, EY and AA.

Population size	No of generation	R² (TPC)	R² (EY)	R² (AA)
100	100	0.9859	0.9157	0.7595
100	250	0.9858	0.9285	0.8290
100	500	0.9861	0.9480	0.8758
250	100	0.9859	0.9187	0.8350
250	250	0.9858	0.9382	0.9622
250	500	0.9858	0.9936	0.8291
500	100	0.9861	0.9291	0.8713
500	250	0.9998	0.9511	0.8416
500	500	0.9921	0.9351	0.8732

Table 9. Statistical metrics of MGGP and RSM.

Statistics	RSM			MGGP
Statistics	TPC	EY	AA	TPC	EY	AA
R²	0.9998	0.9967	0.9671	0.9998	0.9936	0.9622
RMSE	0.2005	0.0171	0.0113	0.0202	0.0288	0.0011

Table 5. Optimization goal, weight and importance^e.

Name	Goal	Lower limit	Upper limit	Lower weight	Upper weight	Importance
OT (^oC)	is in range	30	50	1	1	3
S : L (g/mL)	is in range	1:20	1:50	1	1	3
ET (min)	is in range	45	180	1	1	3
TPC (mg GAE/g)	maximize	18.58	69.35	1	1	3
EY (w/w %)	maximize	9.28	21.39	1	1	3
AA (µM AAE/g)	maximize	3.51	3.77	1	1	3

^e OT is operating temperature; S:L is solid to liquid ratio; ET is extraction time; EY is extract yield; TPC is total phenolic content ; AA is antioxidant activity.

Table 6. Numerical optimization solutions^f.

Number	OT (^oC)	ET (min)	S:L (g/mL)	TPC (mg GAE/g)	EY (%)	AA (µM AAE/g)	Desirability
1	41.61	180.00	1:60	67.116	21.6565	3.68583	0.854	Selected
2	41.83	180.00	1:60	67.0228	21.5575	3.68754	0.854
3	41.32	180.00	1:60	67.2314	21.7801	3.68361	0.854
4	42.33	180.00	1:60	66.8119	21.3312	3.69121	0.853
5	40.53	180.00	1:60	67.5498	22.1155	3.67704	0.852
6	41.71	179.49	1:60	67.0487	21.5654	3.68607	0.852
7	40.47	180.00	1:59	66.9680	22.1220	3.67791	0.850
8	43.18	180.00	1:59	66.4113	20.9343	3.69702	0.850
9	40.78	180.00	1:59	66.3632	21.9771	3.68168	0.850
10	41.80	177.66	1:60	66.9172	21.3518	3.68495	0.844
11	45.68	180.00	1:60	65.2926	19.6570	3.71053	0.830
12	36.67	180.00	1:51	55.7064	22.7236	3.67233	0.770
13	37.44	180.00	1:48	51.4708	22.1397	3.69064	0.766

^fOT = operating temperature; S:L = solid to liquid ratio; ET = extraction time; EY = extract yield; TPC = total phenolic content ; AA = antioxidant activity.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Process Optimization, Genetic Programming Modeling and Reliability Assessment of Bioactive Extracts Recovery From Phyllantus Emblica

Abstract