Submitted:
05 November 2023
Posted:
06 November 2023
You are already at the latest version
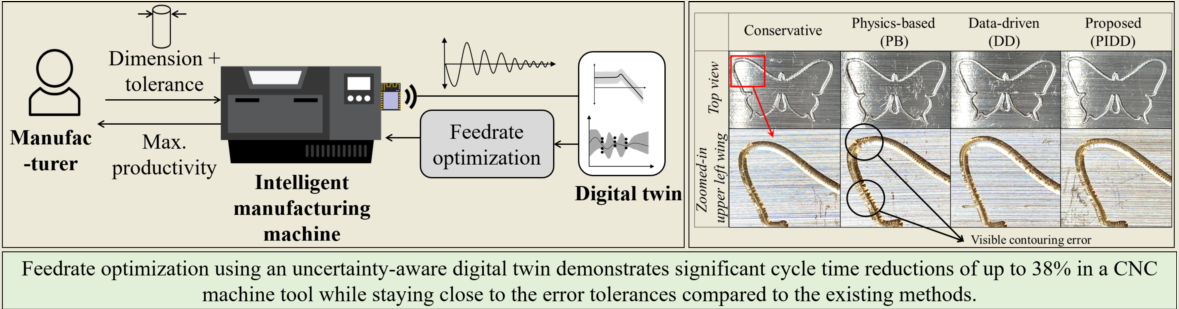
Abstract
Keywords:
1. Introduction
- It uses a novel physics-informed data-driven digital twin to predict the contour error and its uncertainty, where the digital twin incorporates the known uncertainty in the physics-based models and learns the unknown uncertainty by correcting the data-driven model on-the-fly using sensor feedback.
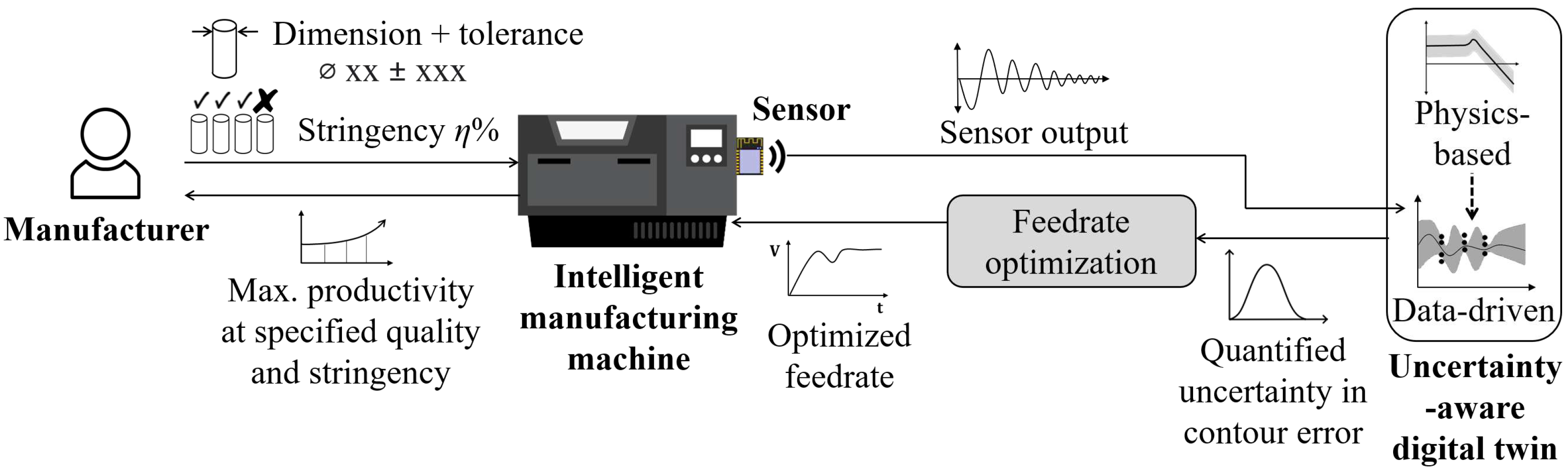
- It formulates an intelligent feedrate optimization framework capable of maximizing feedrate while accurately constraining contour error under desired tolerance and stringency, based on the uncertainty estimation from the digital twin using a model predictive control framework.
- It demonstrates the effectiveness of the proposed method by validating its performance in simulations and experiments using a desktop CNC machine tool and 3D printer.
2. Framework for Feedrate Optimization with Uncertainty-Aware Digital Twin
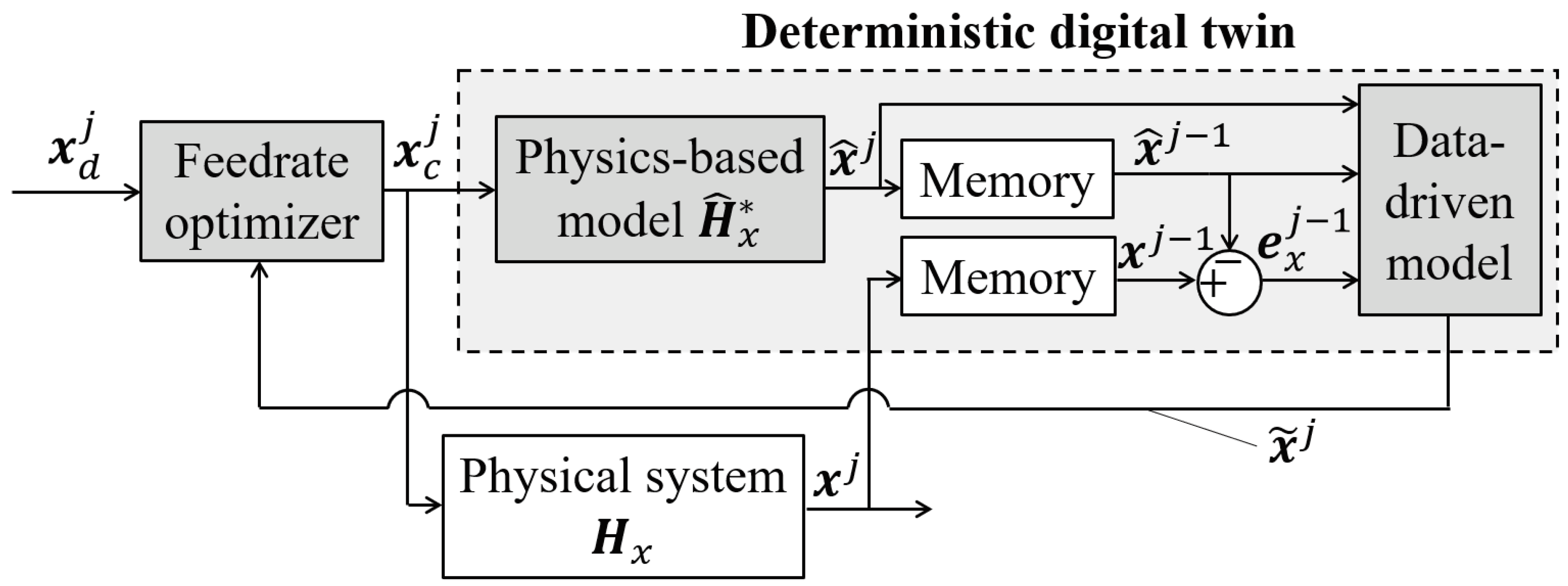
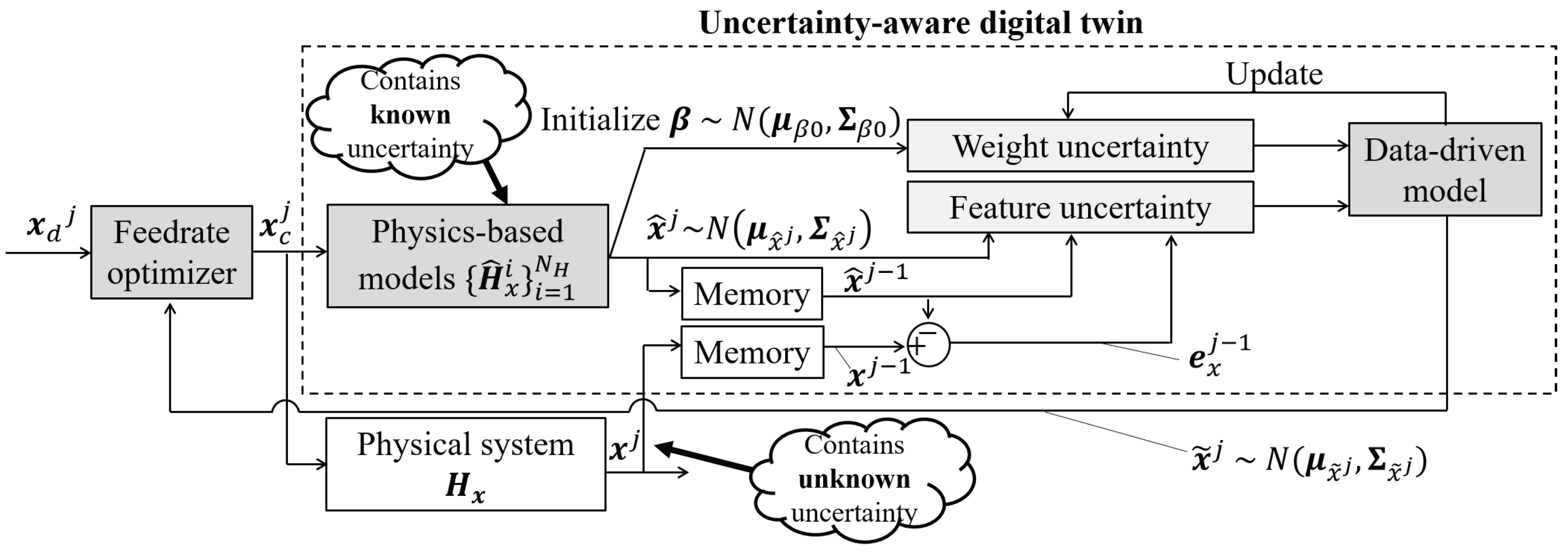
3. Contour Error Prediction with a Real-Time Uncertainty-Aware Digital Twin
3.1. Overview of Contour Error Prediction Using a Deterministic Digital Twin
3.2. Prediction and Uncertainty Quantification of Contour Error Using Uncertainty-Aware Digital Twin
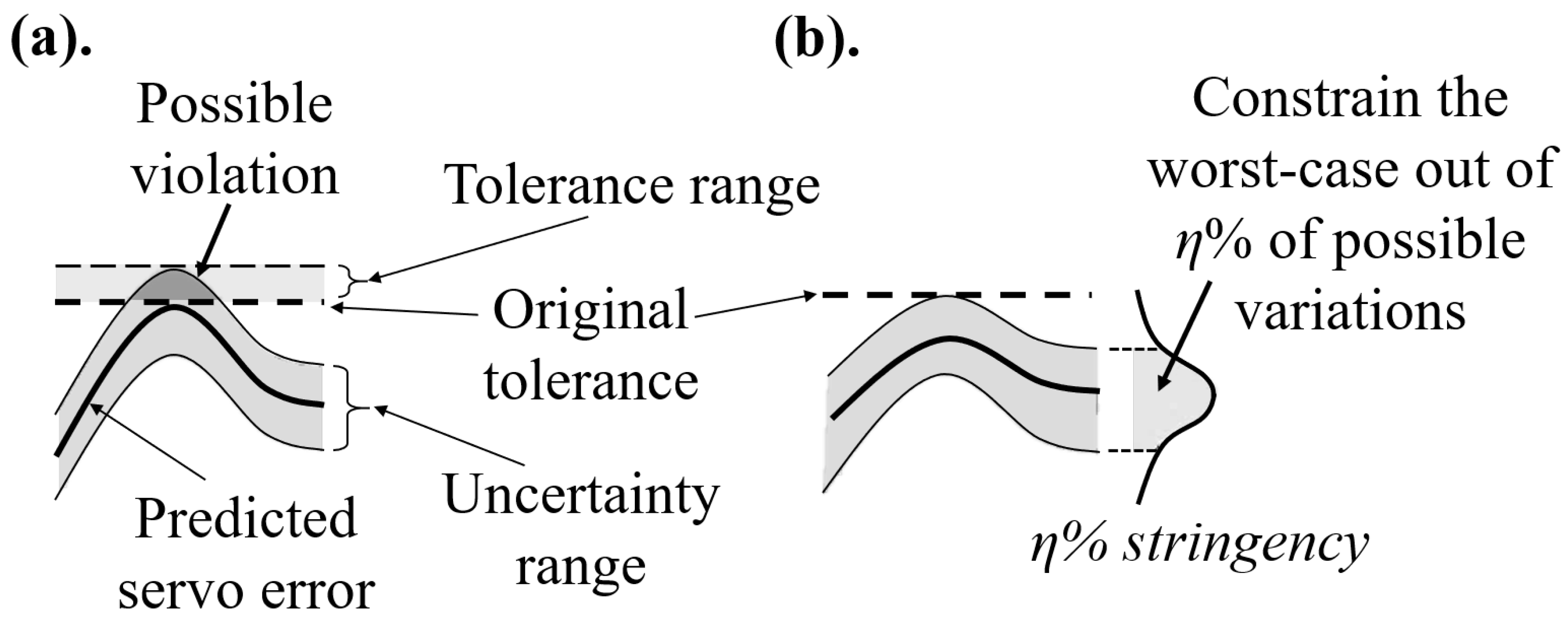
4. Methodology for Intelligent Feedrate Optimization with Contour Error Constraints
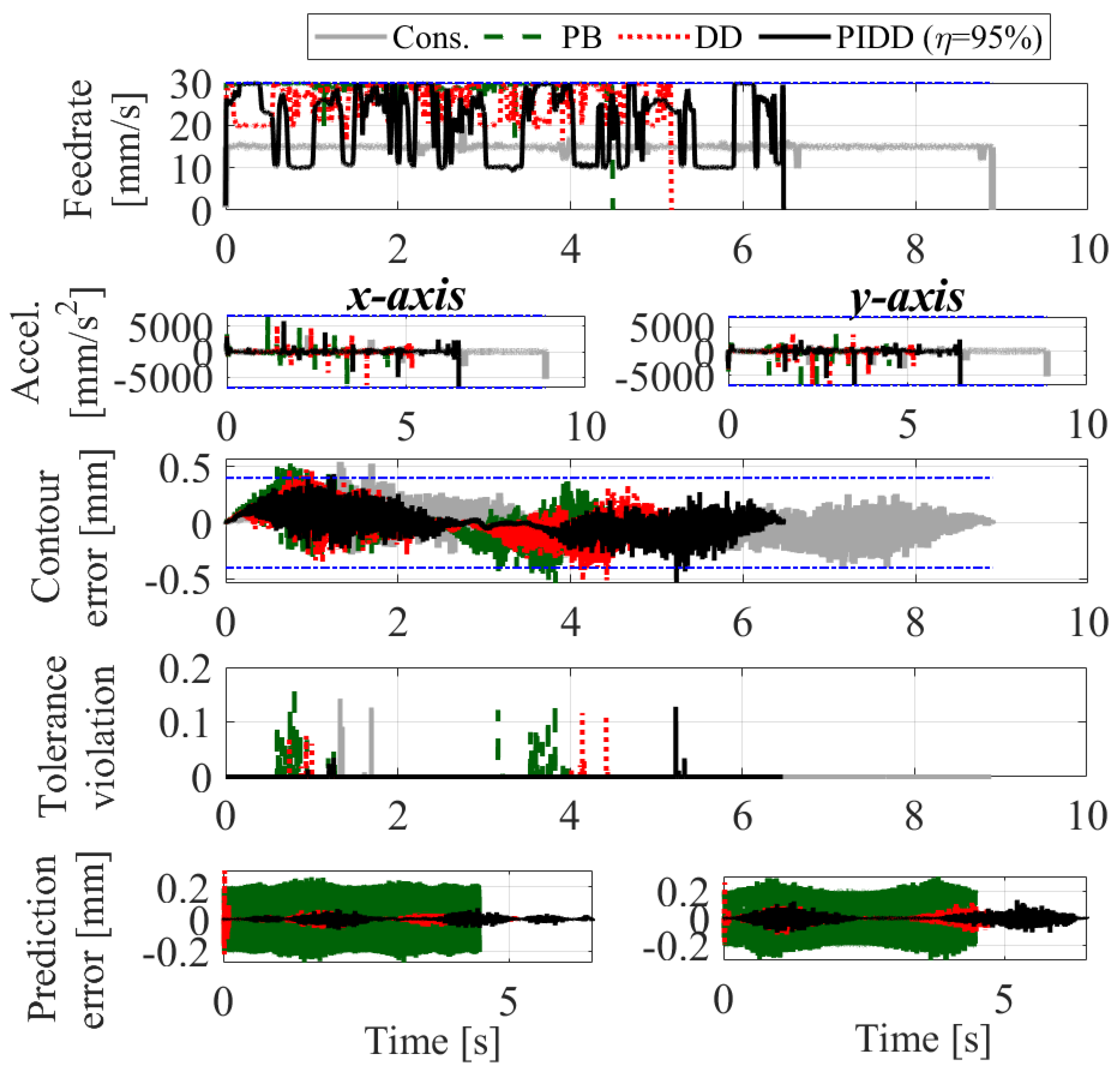
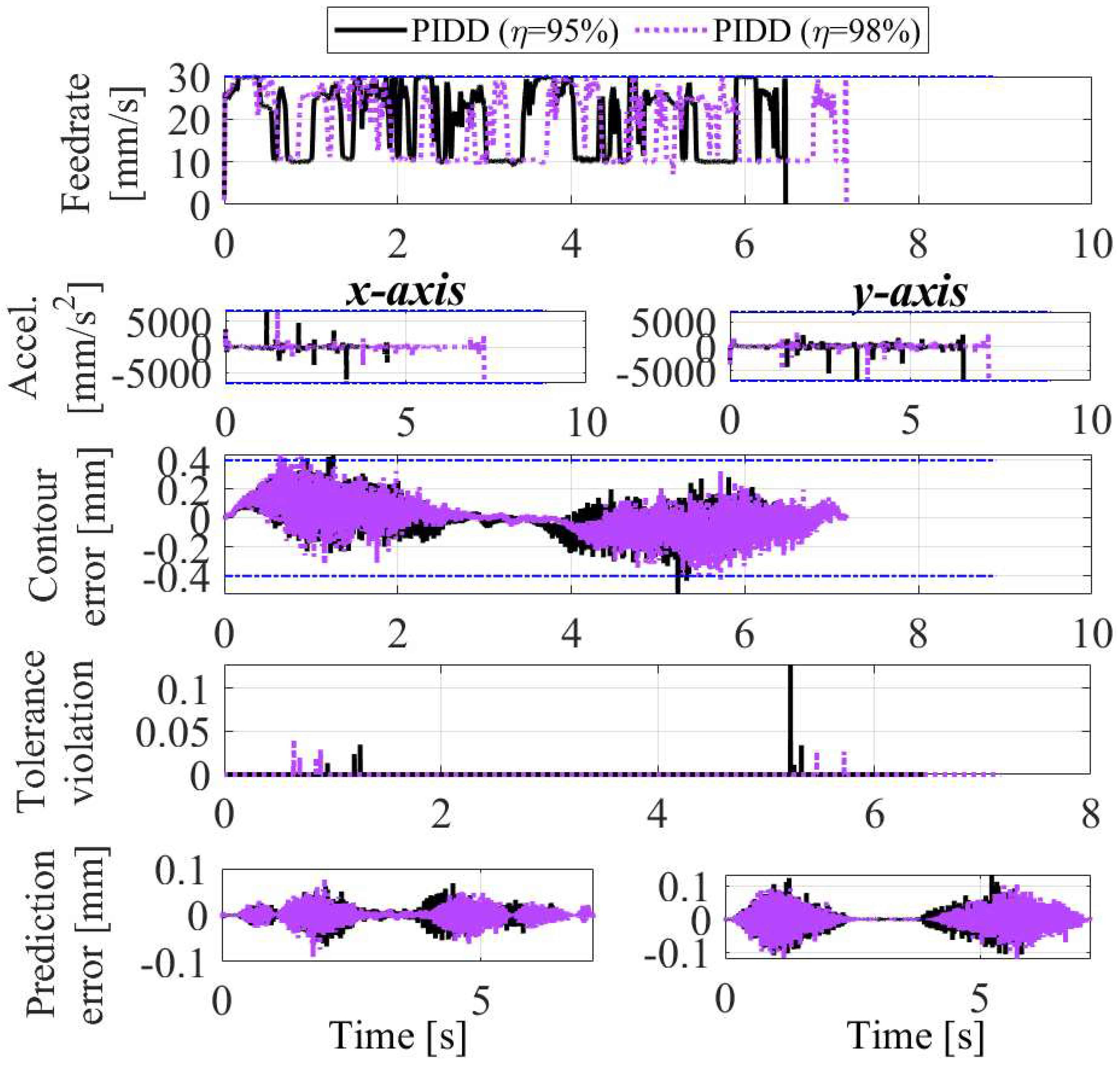
5. Numerical Validation of the Intelligent Feedrate Optimization Using Uncertainty-Aware Digital Twin
- Conservative method, which is defined as the benchmark generated using a trapezoidal acceleration profile [7] with kinematic limits tuned by trial-and-error to achieve the contour error tolerance with % stringency, by allowing up to % RMS violation normalized by defined in Section 4
- Physics-based (PB) method, which predicts the output position and its uncertainty using only the known uncertainty obtained from the set of physics-based models and
- Data-driven (DD) method, which predicts the output position and its uncertainty by learning the unknown uncertainty without incorporating any known uncertainties, i.e., the prior , , and are initialized as zero at the 0-th batch, and and are learned via Bayesian linear regression for deterministic features in Eq. (19). Note that both the PB and DD methods are subsets of the proposed uncertainty-aware digital twin. However, we have separated them out to highlight the effect of introducing uncertainty in both the PB and the DD models through the PIDD method used in the uncertainty aware digital twin
6. Experimental Validation
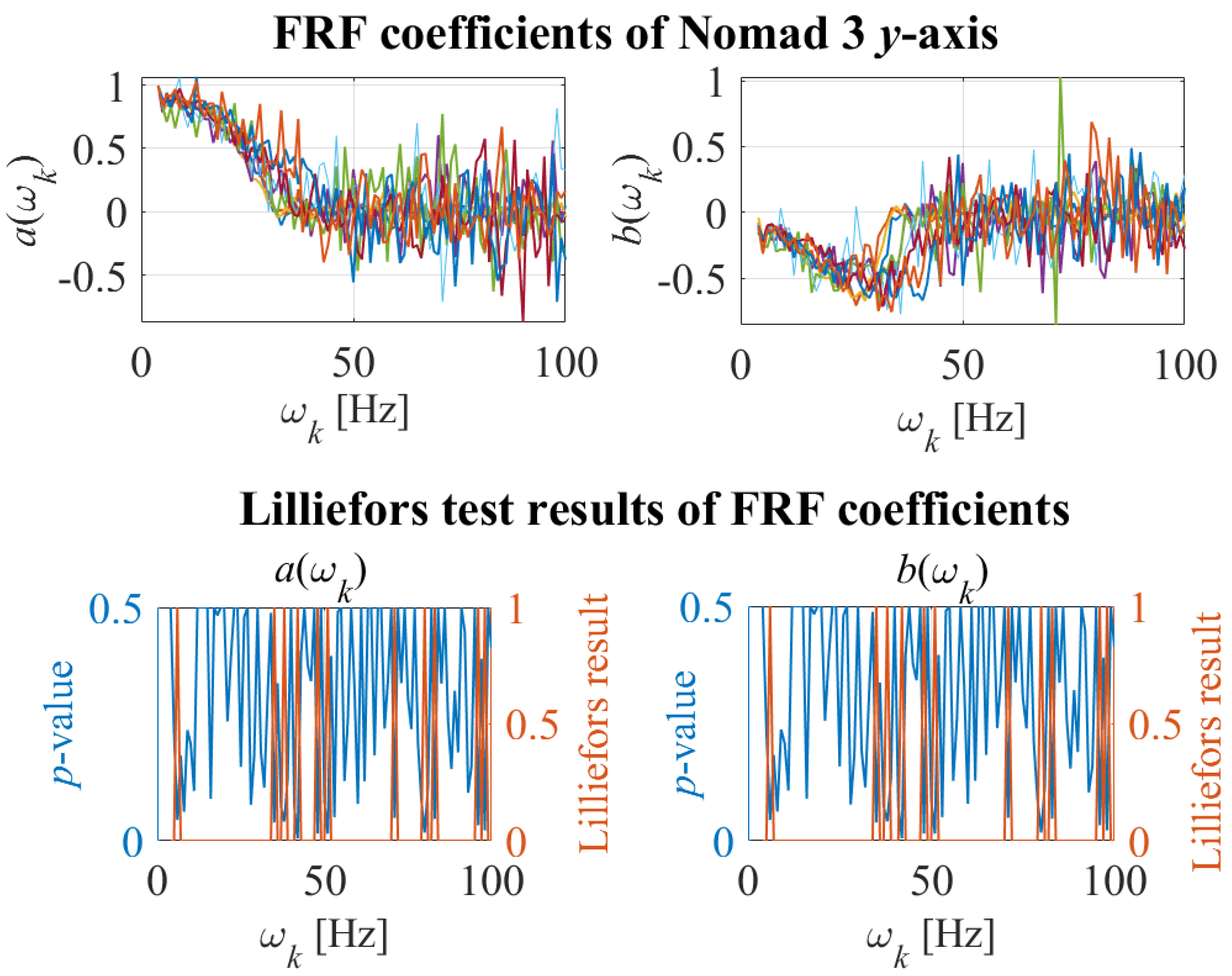
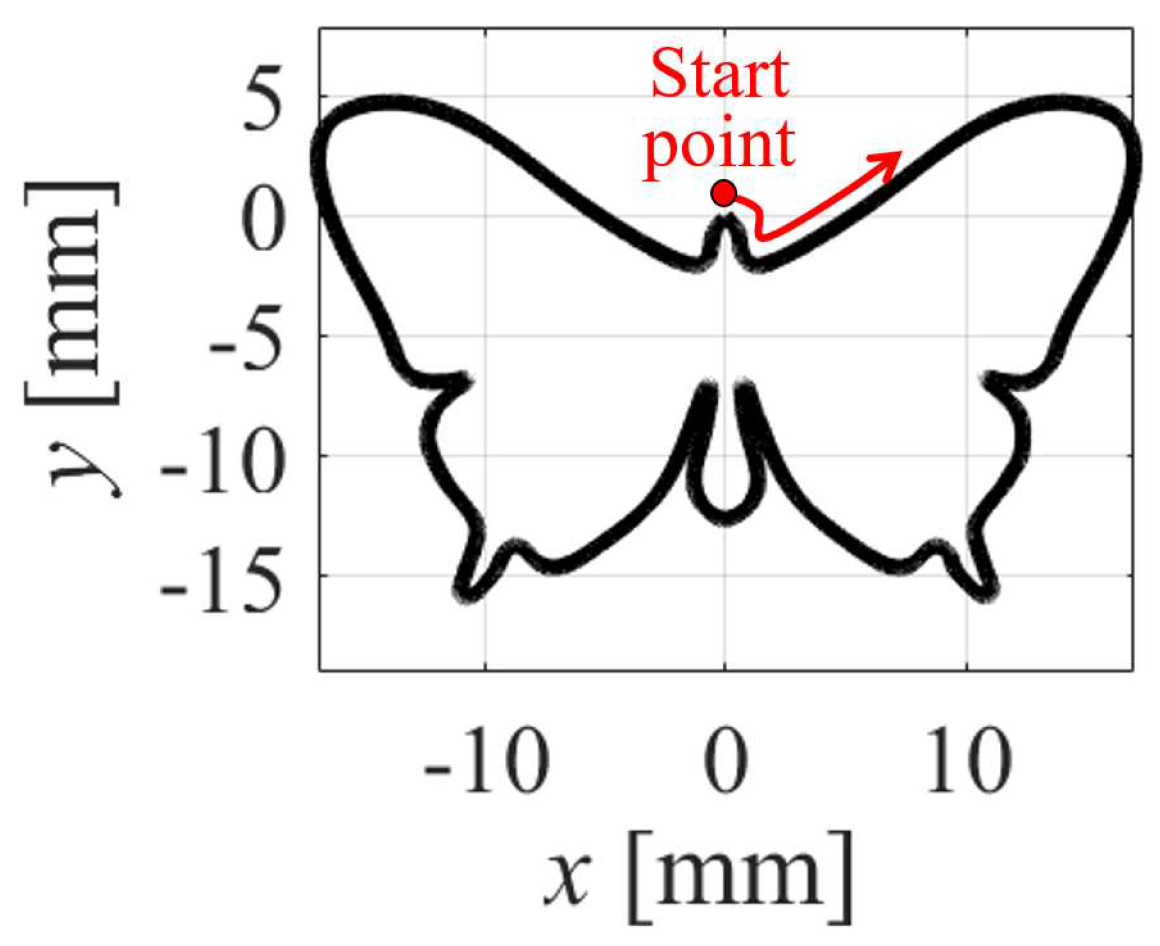
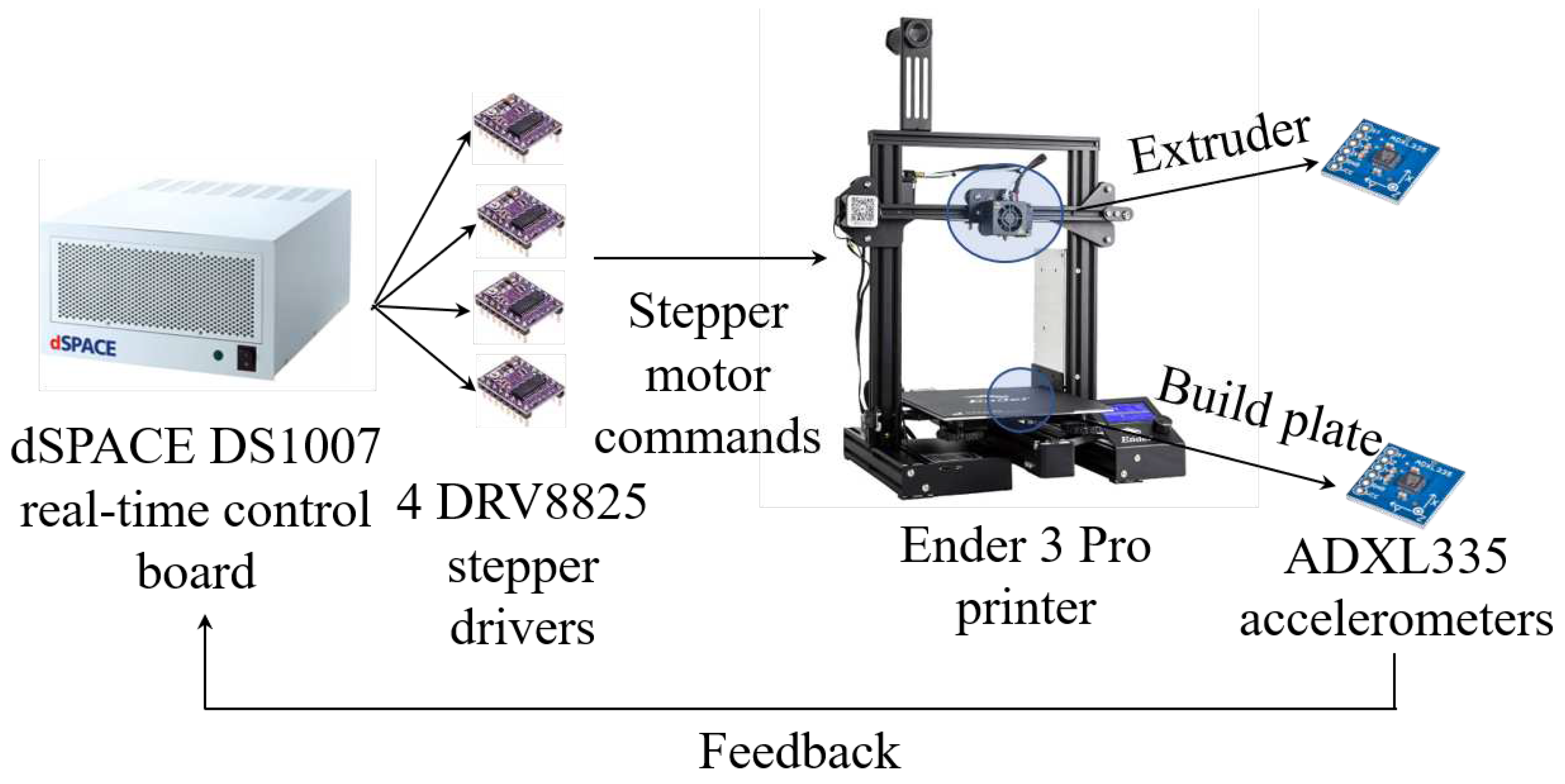
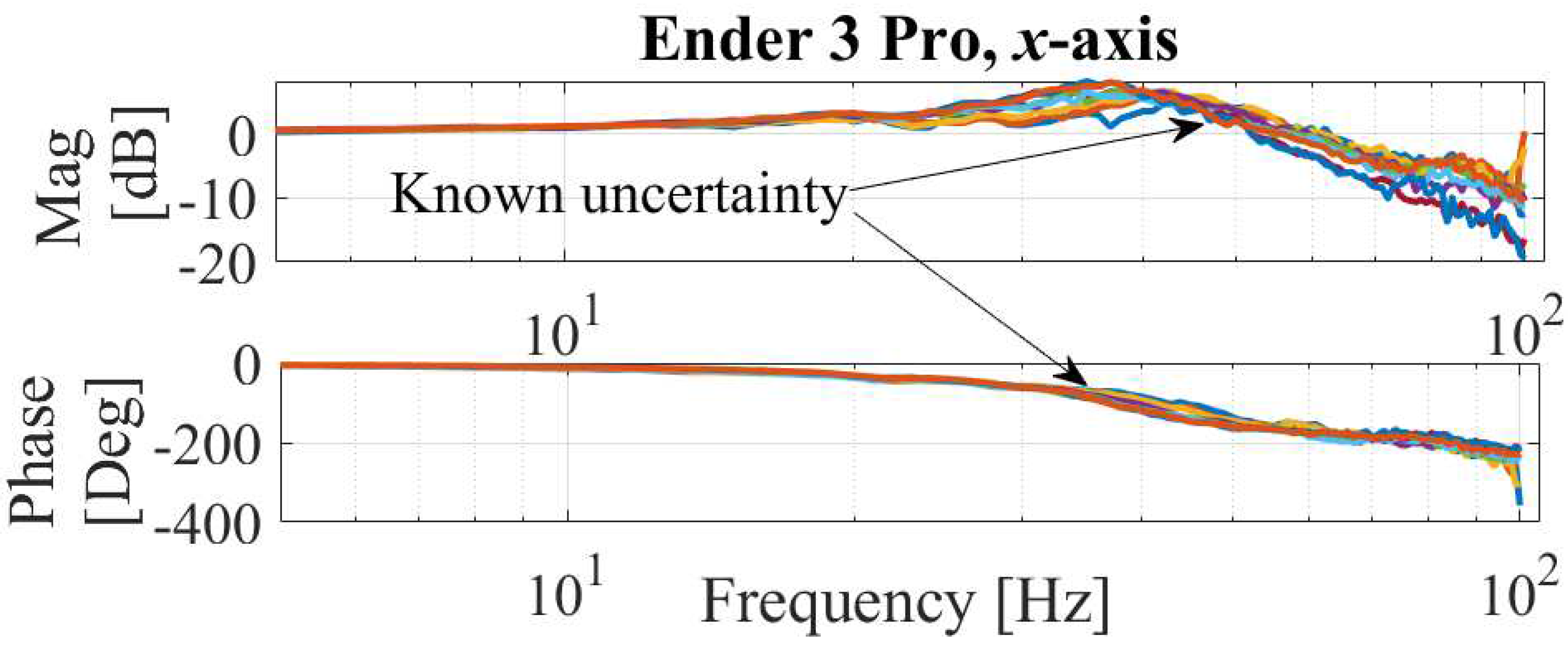
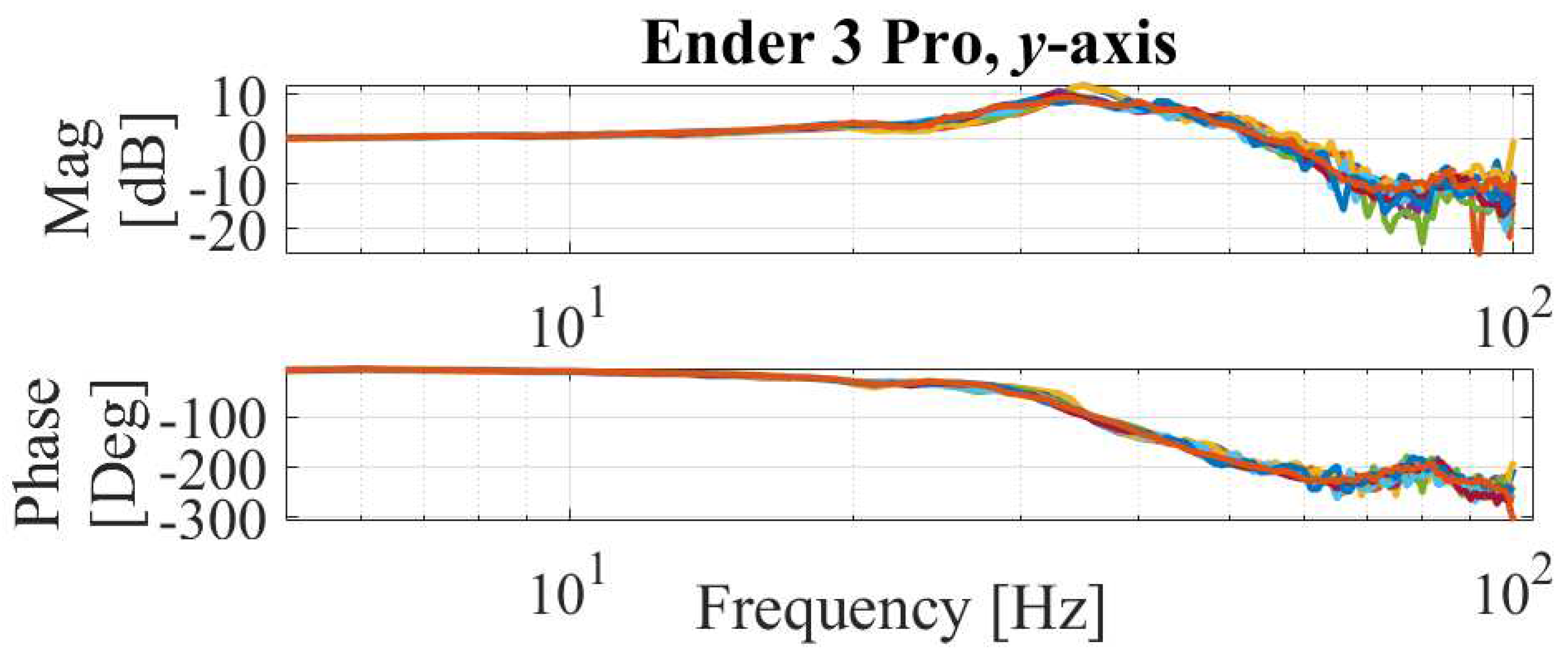
6.1. Desktop 3D Printer
6.1.1. Experimental Setup
6.1.2. Experimental Results
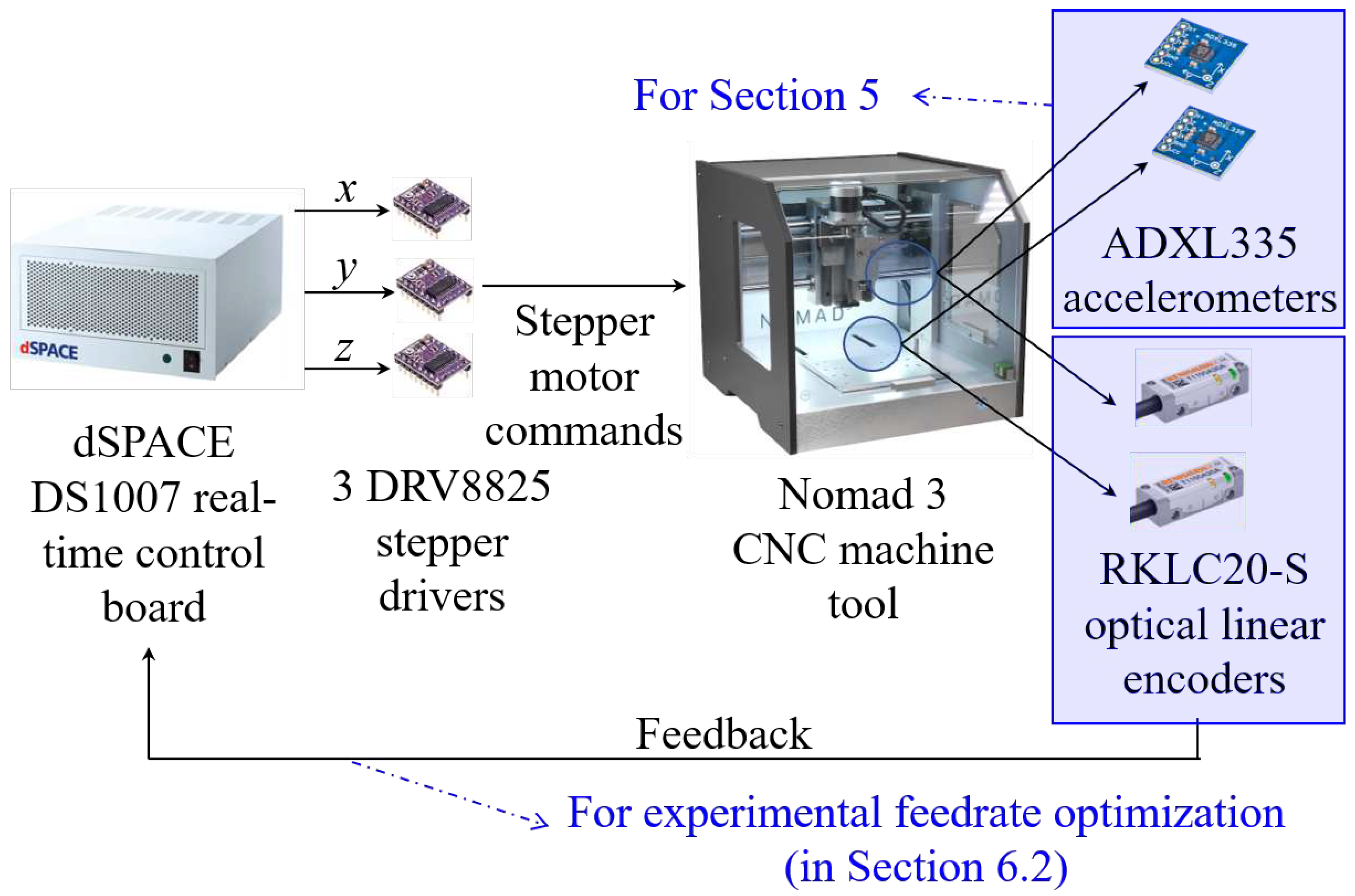
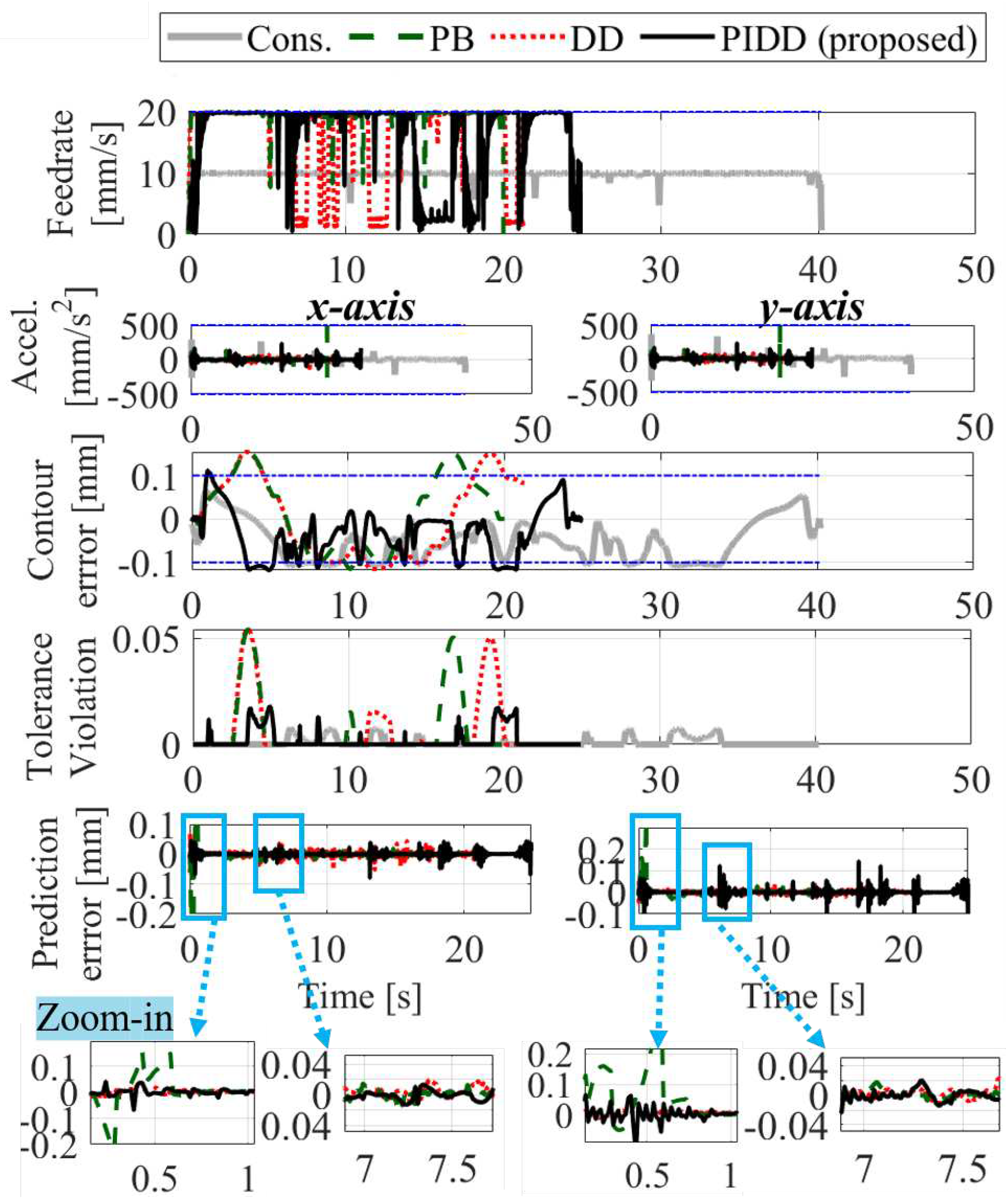
6.2. CNC Machine Tool
6.2.1. Experimental Setup
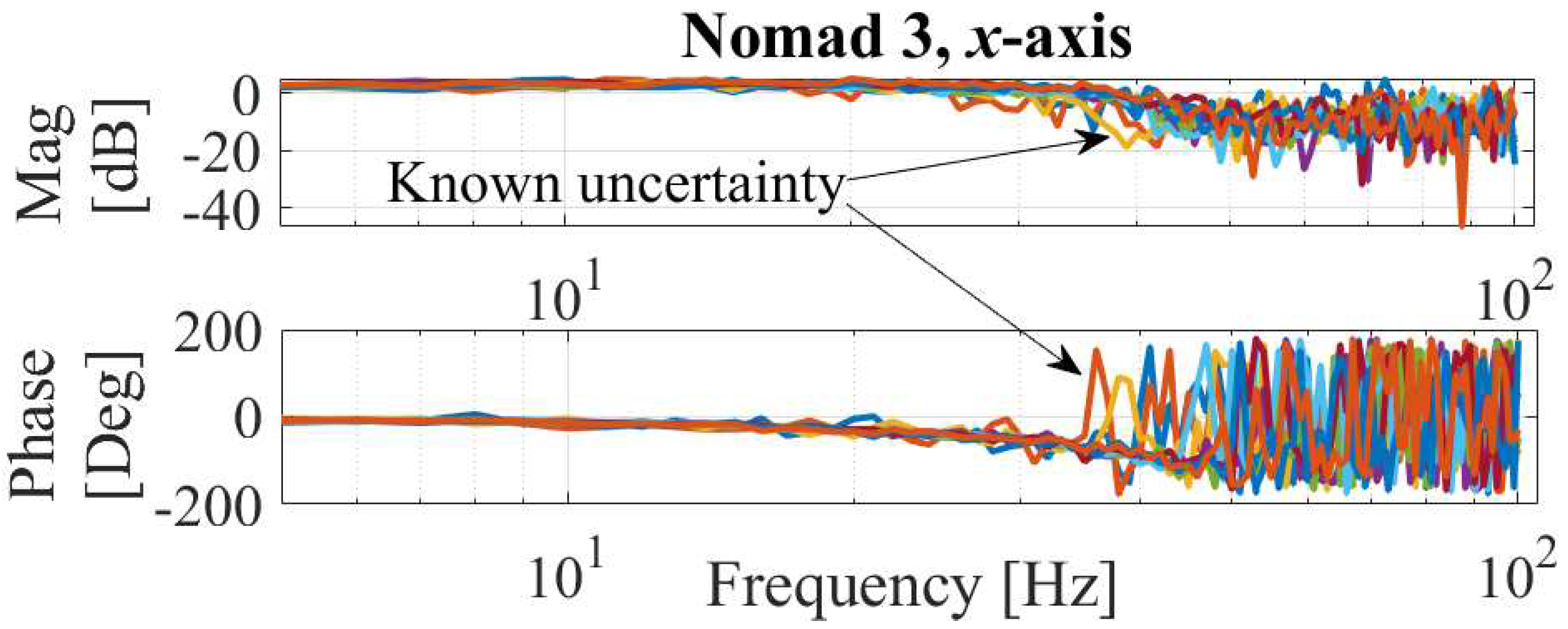
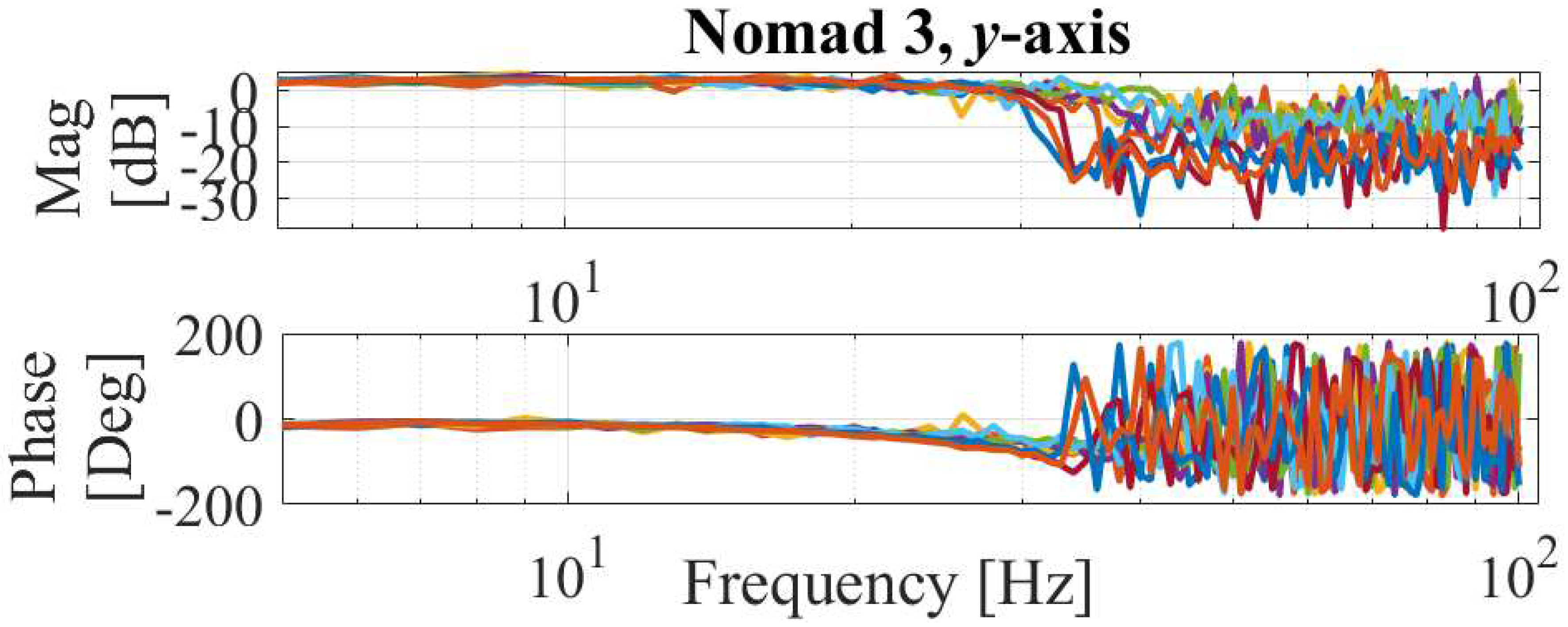
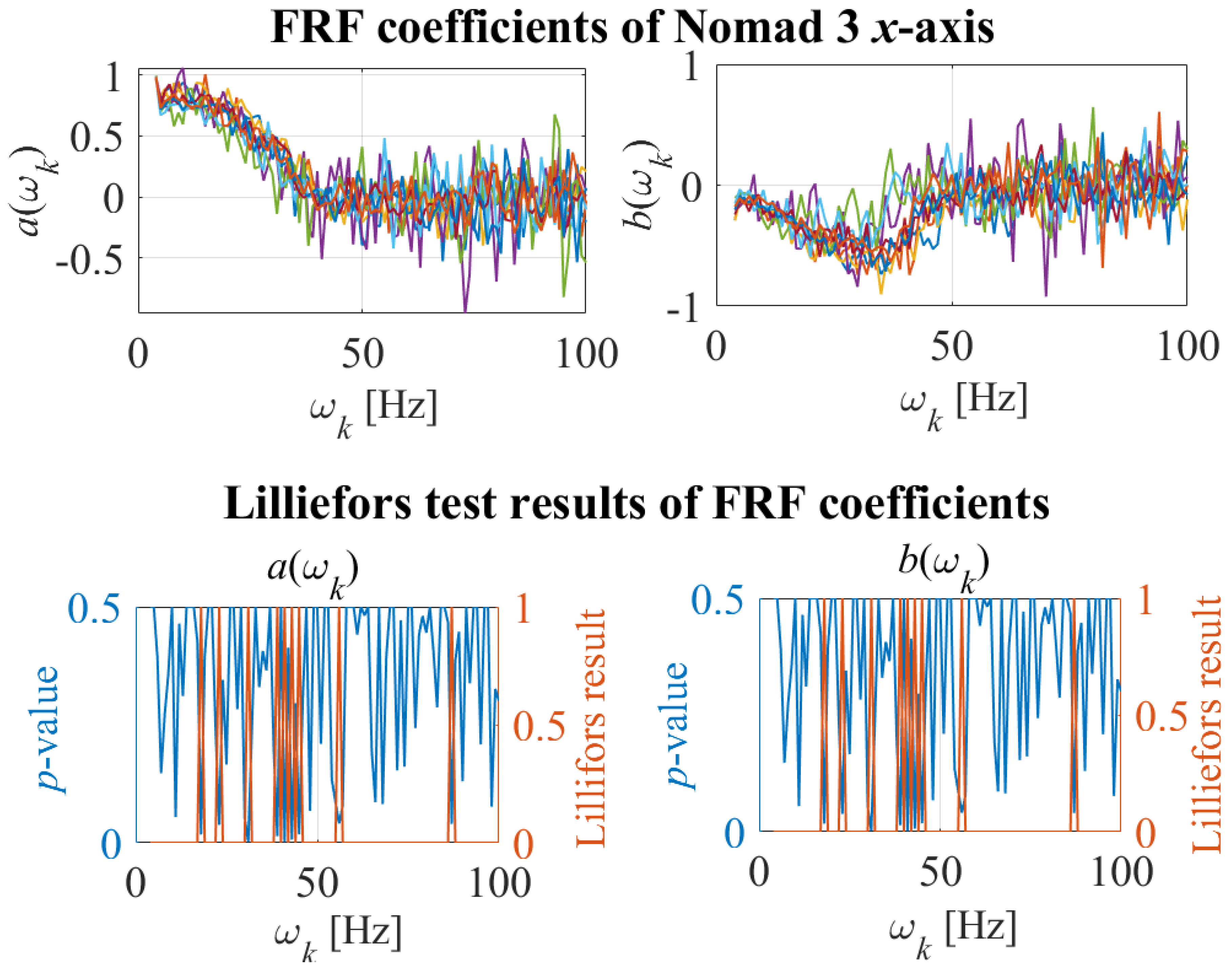
6.2.2. Experimental Results
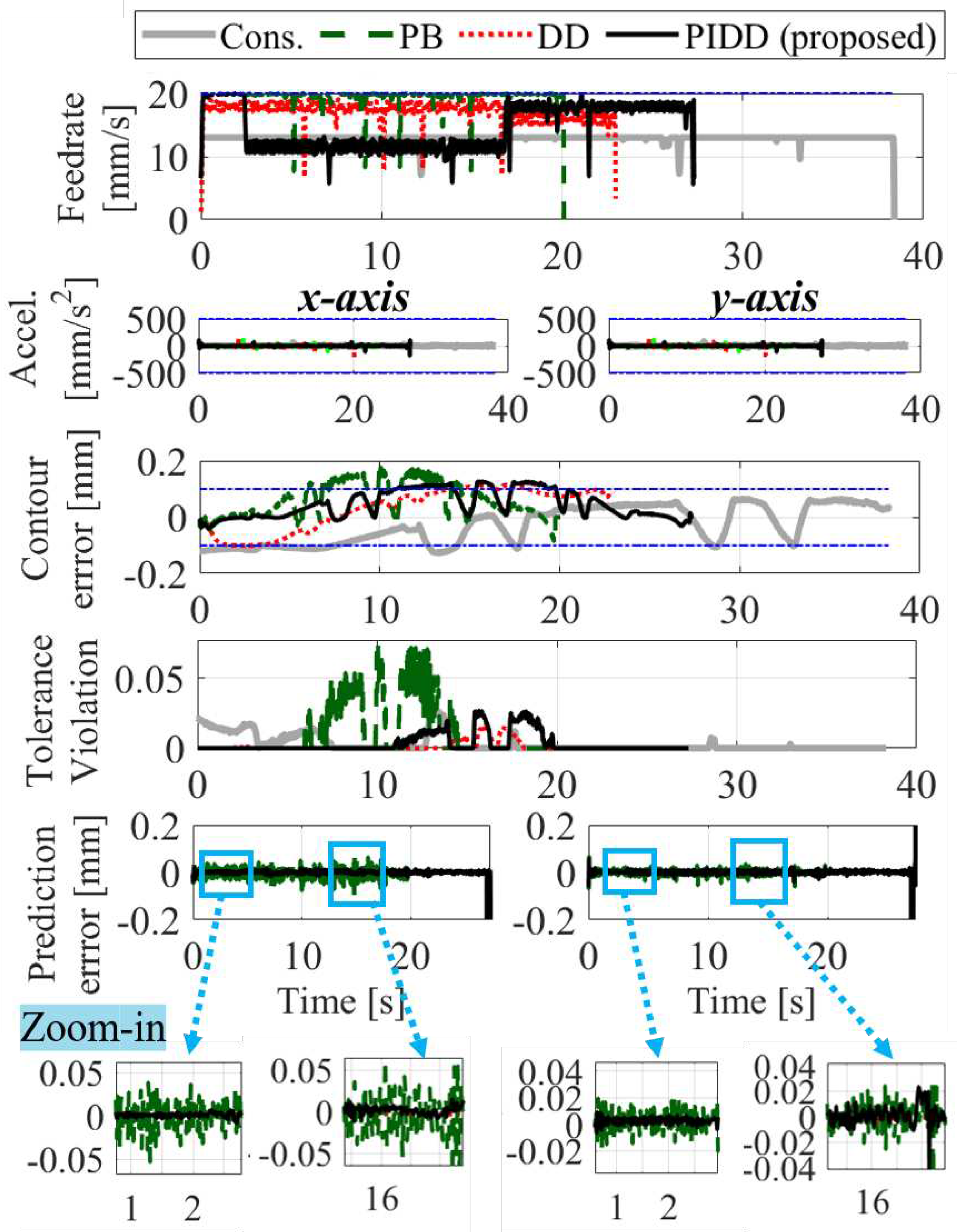
| Cons. | PB | DD | PIDD | ||
|---|---|---|---|---|---|
| Air-cutting | x Pred. Error [μm] | N/A | 17.8 | 17.5 | 10.2 |
| y Pred. Error [μm] | N/A | 25.4 | 15.7 | 7.2 | |
| Cycle time [s] | 40.2 | 20.0 | 21.1 | 24.9 | |
| RMS of [μm] | 5.0 | 16.7 | 16.5 | 2.3 | |
| Cutting | x Pred. Error [μm] | N/A | 47.2 | 17.3 | 16.7 |
| y Pred. Error [μm] | N/A | 34.2 | 17.7 | 18.1 | |
| Cycle time [s] | 39.4 | 20.0 | 23.0 | 27.2 | |
| RMS of [μm] | 6.8 | 22.2 | 3.7 | 7.4 |
7. Conclusion and Future Work
- A novel uncertainty-aware digital twin that predicts contour error is proposed. The digital twin is able to incorporate known uncertainty from physics-based models and learn unknown uncertainty using an online data-driven model to predict contour error’s distribution.
- For the first time, a feedrate optimization with constraints on kinematics and contour error using quantified uncertainty is introduced. The contour error’s uncertainty using digital twin enables the manufacturer to impose stringency constraints, which can replace trial-and-error approach of tuning the tolerance used in practice.
- We have demonstrated the effectiveness of the intelligent feedrate optimization using uncertainty-aware digital twin, to show up to 38% and 17% cycle time reduction using a desktop CNC machine tool and a desktop 3D printer, respectively, while achieving similar stringency of tolerance to that of the a conservative trial-and-error approach similar to those used in practice.
- The proposed intelligent feedrate optimization is expected to bring impact in achieving desired quality with higher productivity, using less trial-and-error. It is applicable to any machines that use feed drives, such as coordinate measurement machines (CMMs), and precision machine tools.
Acknowledgments
Appendix A. Initialization of μβ and Σβ in Section 3.2
Appendix B. Derivation of Coefficients c0 ,c1 and C2 in Eq. (16) in Section 3.2
Appendix C. Linearization of Contour Error Constraint in Eq. (27) in Terms of and
References
- Bharathi, A.; Dong, J. Feedrate optimization for smooth minimum-time trajectory generation with higher order constraints. Int J Adv Manuf Technol 2016, 82, 1029–1040. [Google Scholar] [CrossRef]
- Fussell, BK.; Jerard, RB.; Hemmett, JG. Robust feedrate selection for 3-axis NC machining using discrete models. J. Manuf. Sci. Eng. 2001, 123, 214–224. [Google Scholar] [CrossRef]
- Chou CH, Duan M, and Okwudire CE. A linear hybrid model for enhanced servo error pre-compensation of feed drives with unmodeled nonlinear dynamics. CIRP Annals 2021, 70, 301–304. [Google Scholar] [CrossRef]
- Bort CM, Leonesio M, and Bosetti P. A model-based adaptive controller for chatter mitigation and productivity enhancement in cnc milling machines. Robotics and Computer-Integrated Manufacturing 2016, 40, 34–43. [Google Scholar] [CrossRef]
- Lam D, Manzie C, and Good MC. Model predictive contouring control for biaxial systems. IEEE Transactions on Control Systems Technology 2012, 2, 552–559. [Google Scholar] [CrossRef]
- Luenberger, DG. An introduction to observers. IEEE Trans. On Automatic Control 1971, 16, 596–602. [Google Scholar] [CrossRef]
- Gordon DJ and Erkorkmaz, K. Accurate control of ball screw drives using pole-placement vibration damping and a novel trajectory prefilter. Precision Engineering 2013, 37, 308–322. [Google Scholar] [CrossRef]
- MacKay, DJ. Information theory, inference and learning algorithms; Cambridge university press, 2003. [Google Scholar]
- Erdim H, Lazoglu I, and Ozturk B. Feedrate scheduling strategies for free-form surfaces. International Journal of Machine Tools and Manufacture 2006, 46, 747–757. [Google Scholar] [CrossRef]
- Erdim H, Lazoglu I, and Kaymakci M. Free-form surface machining and comparing feedrate scheduling strategies. Machining Science and Technology 2007, 11, 117–133. [Google Scholar] [CrossRef]
- Kim H and Okwudire, C. Intelligent feedrate optimization using a physics-based and data-driven digital twin. CIRP Annals. 2023, 308–322. [Google Scholar] [CrossRef]
- Kim H and Okwudire, CE. Simultaneous servo error pre-compensation and feedrate optimization with tolerance constraints using linear programming. Int J Adv Manuf Technol 2020, 109, 809–821. [Google Scholar] [CrossRef]
- Kim H and Okwudire, CE. Accurate and computationally efficient approach for simultaneous feedrate optimization and servo error pre-compensation of long toolpaths—with application to a 3D printer. The International Journal of Advanced Manufacturing Technology 2021, 115, 2069–2082. [Google Scholar] [CrossRef]
- Möhring HC, Wiederkehr P, Erkorkmaz K; Kakinuma, Y. Self-optimizing machining systems. CIRP Annals 2020, 69, 740–763. [Google Scholar] [CrossRef]
- Park HS, Qi B, Dang DV; Park, D.Y. Development of smart machining system for optimizing feedrates to minimize machining time. Journal of Computational Design and Engineering 2018, 5, 299–304. [Google Scholar] [CrossRef]
- Lee HU and Cho, DW. An intelligent feedrate scheduling based on virtual machining. The International Journal of Advanced Manufacturing Technology, 2003; 22, 873–882. [Google Scholar] [CrossRef]
- Lilliefors, HW. On the kolmogorov-smirnov test for normality with mean and variance unknown. Journal of the American Statistical Association 1967, 62, 339–402. [Google Scholar] [CrossRef]
- Feng HY and Su, N. Integrated tool path and feed rate optimization for the finishing machining of 3D plane surfaces. International Journal of Machine Tools and Manufacture 2000, 40, 1557–1572. [Google Scholar] [CrossRef]
- Zagbani I and Songmene, V. Estimation of machine-tool dynamic parameters during machining operation through operational modal analysis. International Journal of Machine Tools and Manufacture 2009, 49, 945–957. [Google Scholar] [CrossRef]
- Dong J and Stori, JA. Optimal feed-rate scheduling for high-speed contouring. J. Manuf. Sci. Eng. 2007, 129, 63–76. [Google Scholar] [CrossRef]
- Yang J, Aslan D, and Altintas Y. A feedrate scheduling algorithm to constrain tool tip position and tool orientation errors of five-axis CNC machining under cutting load disturbances. CIRP journal of Manufacturing Science and Technology 2018, 23, 78–90. [Google Scholar] [CrossRef]
- Rawlings, JB. Model predictive control technology. 1999, 1, 662–676. [Google Scholar] [CrossRef]
- Rawlings JB, Maye DQ, and Diehl M. Model predictive control: theory, computation, and design; Nob Hill Publishing: Madison, WI; volume 2.
- Ko JH, Yun WS, and Cho DW. Off-line feed rate scheduling using virtual cnc based on an evaluation of cutting performance. Computer-Aided Design 2003, 35, 383–393. [Google Scholar] [CrossRef]
- Erkorkmaz K, Chen QGC, Beudaert X Zhao MY; Gao, X.S. Linear programming and windowing based feedrate optimization for spline toolpaths. CIRP Annals 2017, 66, 393–396. [Google Scholar] [CrossRef]
- Rattunde L, Laptev I, Klenske ED; Möhring, H.C. Safe optimization for feedrate scheduling of power-constrained milling processes by using Gaussian processes. Procedia CIRP 2021, 99, 127–132. [Google Scholar] [CrossRef]
- Zhang L, Feng J, Wang Y; Chen, M. Feedrate scheduling strategy for free-form surface machining through an integrated geometric and mechanistic model. International Journal of Advanced Manufacturing Technology 2009, 40, 740–763. [Google Scholar] [CrossRef]
- Chen M, Xu J, and Sun Y. Adaptive feedrate planning for continuous parametric tool path with confined contour error and axis jerks. The International Journal of Advanced Manufacturing Technology 2017, 89, 1113–1125. [Google Scholar] [CrossRef]
- Richards ND, Fussell BK, and Jerard RB. Efficient NC machining using off-line optimized feedrates and on-line adaptive control. 2002, 3641, 181–191. [Google Scholar] [CrossRef]
- Qin P, Wang M, and Sun L. Feed rate variation strategy for semi-conical shell workpiece in ball head end milling process. Applied Sciences 2020, 10, 9135. [Google Scholar] [CrossRef]
- Zhang Q and Li, SR. Efficient computation of smooth minimum time trajectory for cnc machining. Int J Adv Manuf Technol 2013, 68, 683–692. [Google Scholar] [CrossRef]
- Kontar R, Raskutti G, and Shiyu Z. Minimizing negative transfer of knowledge in multivariate gaussian processes: A scalable and regularized approach. IEEE Transactions on Pattern Analysis and Machine Intelligence 2020, 43, 3508–3522. [Google Scholar] [CrossRef]
- Balula S, Liao-McPherson D, Rupenyan A; Lygeros, J. Data-driven reference trajectory optimization for precision motion systems. arXiv 2022, arXiv:2205.15694. [Google Scholar] [CrossRef]
- Tajima S and Sencer, B. Real-time trajectory generation for 5-axis machine tools with singularity avoidance. CIRP Annals 2020, 69, 349–352. [Google Scholar] [CrossRef]
- Tajima S and Sencer, B. Online interpolation of 5-axis machining toolpaths with global blending. International Journal of Machine Tools and Manufacture 2022, 175, 103862. [Google Scholar] [CrossRef]
- Yang S, Ghasemi AH, Lu X; Okwudire, C.E. Pre-compensation of servo contour errors using a model predictive control framework. Int J Mach Tool Manu 2015, 98, 50–60. [Google Scholar] [CrossRef]
- Merdol SD and Altintas, Y. Virtual simulation and optimization of milling applications—part II : optimization and feedrate scheduling. [CrossRef]
- Merdol SD and Altintas, Y. Virtual cutting and optimization of three-axis milling processes. International Journal of Machine Tools and Manufacture 2008, 48, 1063–1071. [Google Scholar] [CrossRef]
- Fan W, Gao XS, Lee CH; Zhang, K.; Zhang, Q. Time-optimal interpolation for five-axis cnc machining along parametric tool path based on linear programming. Int J Adv Manuf Technol 2013, 69, 1373–1388. [Google Scholar] [CrossRef]
- Fan W, Gao XS, Lee CH; Zhang, K.; Zhang, Q. Time-optimal interpolation for five-axis cnc machining along parametric tool path based on linear programming. The International Journal of Advanced Manufacturing Technology 2013, 69, 1373–1388. [Google Scholar] [CrossRef]
- Altintas Y, Yang J, and Kilic ZM. Virtual prediction and constraint of contour errors induced by cutting force disturbances on multi-axis cnc machine tools. CIRP Annals 2019, 68, 377–380. [Google Scholar] [CrossRef]
- Altintas Y, Biermann D Kersting P, Budak E; Denkena, B.; Lazoglu, I. Virtual process systems for part machining operations. CIRP Annals 2014, 63, 585–605. [Google Scholar] [CrossRef]
- Altintas Y and Merdol, SD. Virtual high performance milling. CIRP annals 2007, 56, 81–84. [Google Scholar] [CrossRef]
- Chang YC, Chen CW, and Tsao TC. Near time-optimal real-time path following under error tolerance and system constraints. CIRP Annals 2018, 140, 071004. [Google Scholar] [CrossRef]

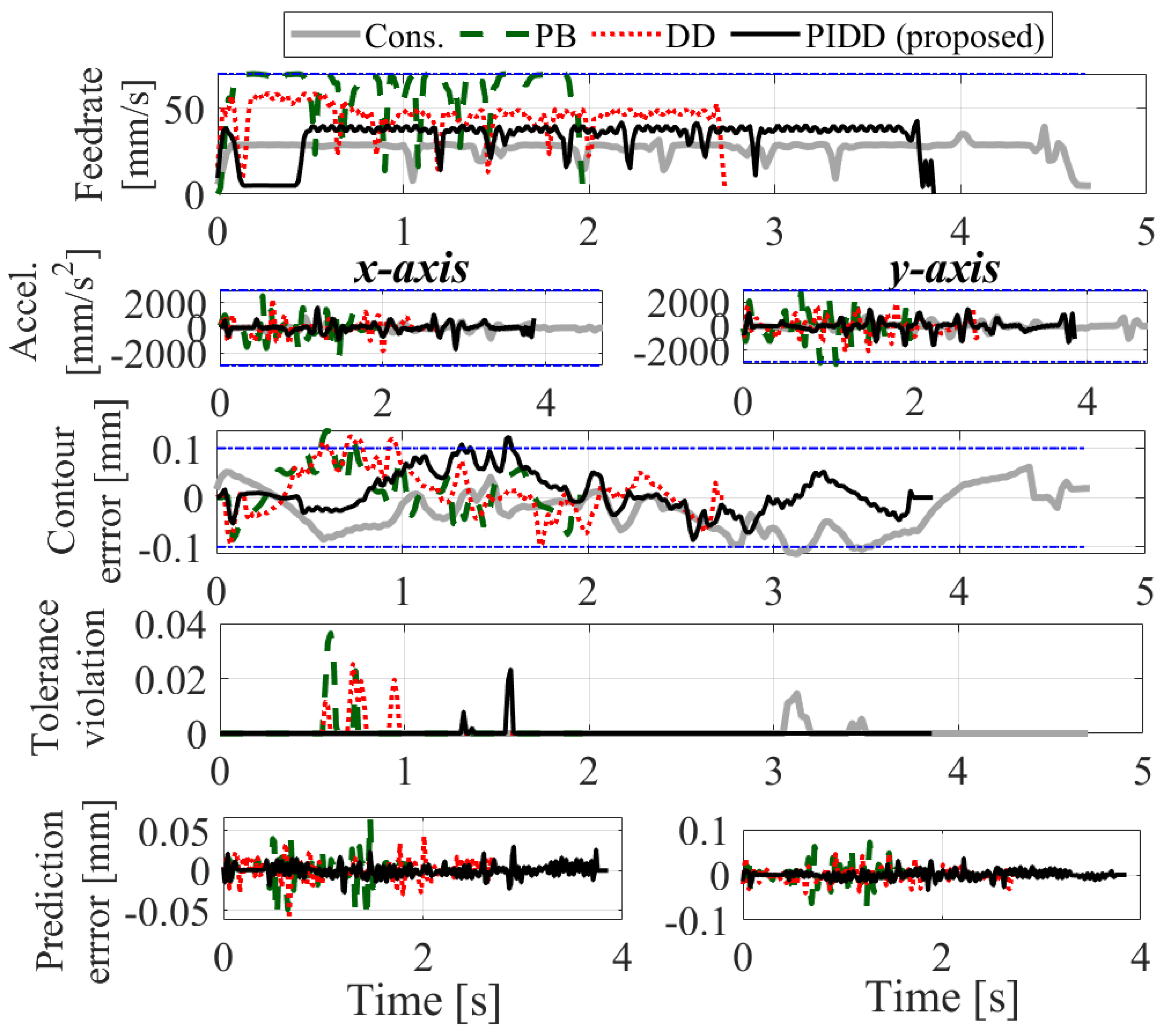
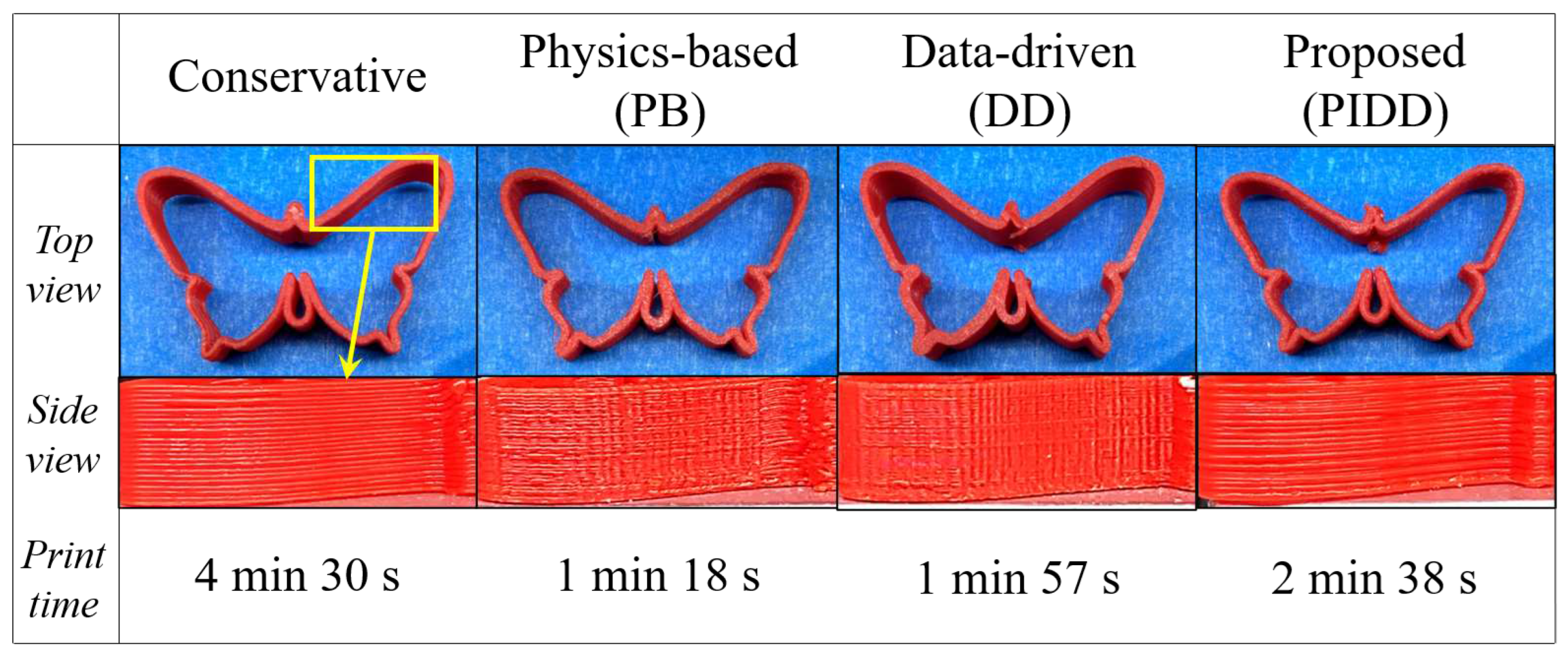

| Cons. | Physics. | Data. | Proposed | |
|---|---|---|---|---|
| x Pred. Error [m] | N/A | 37.4 | 22.1 | 18.1 |
| y Pred. Error [m] | N/A | 31.7 | 23.9 | 19.3 |
| Cycle time [s] | 4.70 | 1.97 | 2.73 | 3.86 |
| RMS of [m] | 1.8 | 5.5 | 3.9 | 1.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





