Submitted:
31 October 2023
Posted:
01 November 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Methods
2.1. Basic Notions
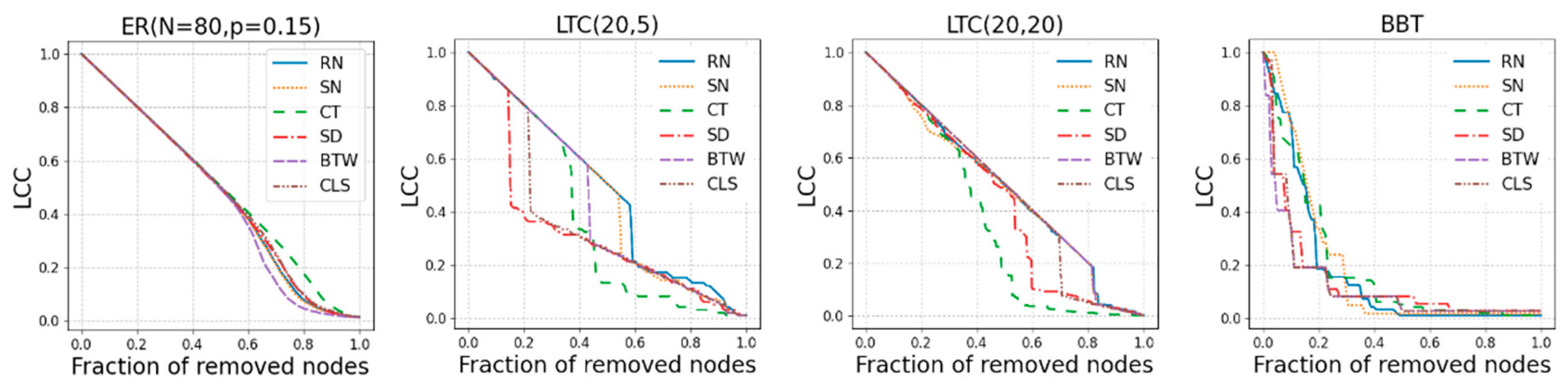
2.2. Synthetic Networks
- ER: classical Erdös-Rényi (ER) random graph [26]. In the ER model, each edge has a fixed probability of being present or absent, independently of the other edges. The ER graph is defined by two parameters only, the number of nodes and the probability of drawn links . We indicate of nodes, and probability of link between each pair of vertices. We investigate ER network with and .
- LTC: rectangular (or square) lattice (LTC) complex network. In graph theory, a lattice graph is called a mesh or grid graph. The LTC is a specific lattice graph where nodes form a grid with square meshes. The LTC can be defined with two parameters, , and , indicating the number of nodes along each side. We simulate two networks by choosing and [27].
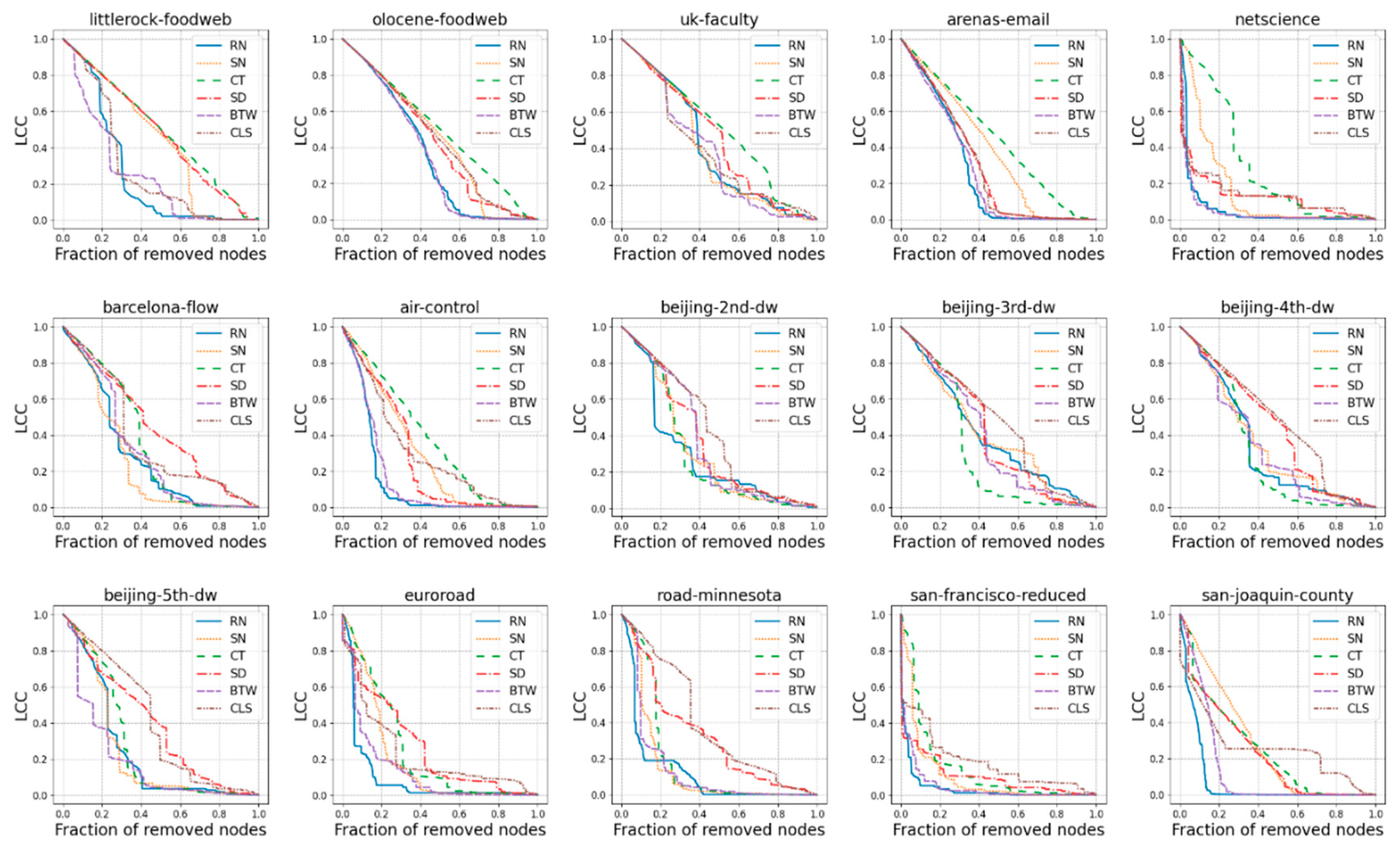
2.3. Real-World Complex Networks
- Air Control: This network was constructed from the USA’s FAA (Federal Aviation Administration) National Flight Data Center (NFDC), Preferred Routes Database (Preferred Routes Database: http://www.fly.faa.gov/). Nodes in this network represent airports or service centers, and links are created from strings of preferred routes recommended by the NFDC [32].
- Arenas Email: email communications among people working within a medium-sized university (i.e., Universitat Rovira i Virgily, Spain) with about employees [21]. Nodes are employees, and links describe mailing among them.
- Barcelona Flow: models the traffic flow in Barcelona (Spain). Nodes represent intersections among roads, and links represent roads (Transportation Networks, https://github.com/bstabler/TransportationNetworks).
- Uk Faculty: personal friendship network within a faculty at a university in the UK. This network comprises 81 vertices representing individuals and edges representing their friendship relations [34].
- Netscience: a coauthorship network focusing on scientists involved in network science. The network represents collaborations among these scientists [25]. Nodes are scientists, and links depict the coauthorship in scientific papers.
- represents the second ring road of Beijing city, China’s capital. Nodes and links represent road intersections and roads, respectively [35].
- Beijing : represents the third ring road of Beijing city, China’s capital. Nodes and links represent road intersections and roads, respectively [35].
- Beijing : represents the fourth ring road of Beijing city, China’s capital. Nodes and links represent road intersections and roads, respectively [35].
- Beijing : represents the fifth ring road of Beijing city, China’s capital. Nodes and links represent road intersections and roads, respectively [35].
- Euroroad: a topological representation of international European roads in which nodes represent intersections among roads and links represent roads [36].
- Littlerock food-web: a model of trophic interactions among species of the Little Rock Lake ecosystem in Wisconsin. In this ecological network, nodes represent living species, and links represent the transfer of nutrients between them [37].
- Olocene: the Olocene food web ecological network is the basis of the 48 million years old uppermost early Eocene Messel Shale food web. Nodes are biological species, and links represent trophic relationships among them [38].
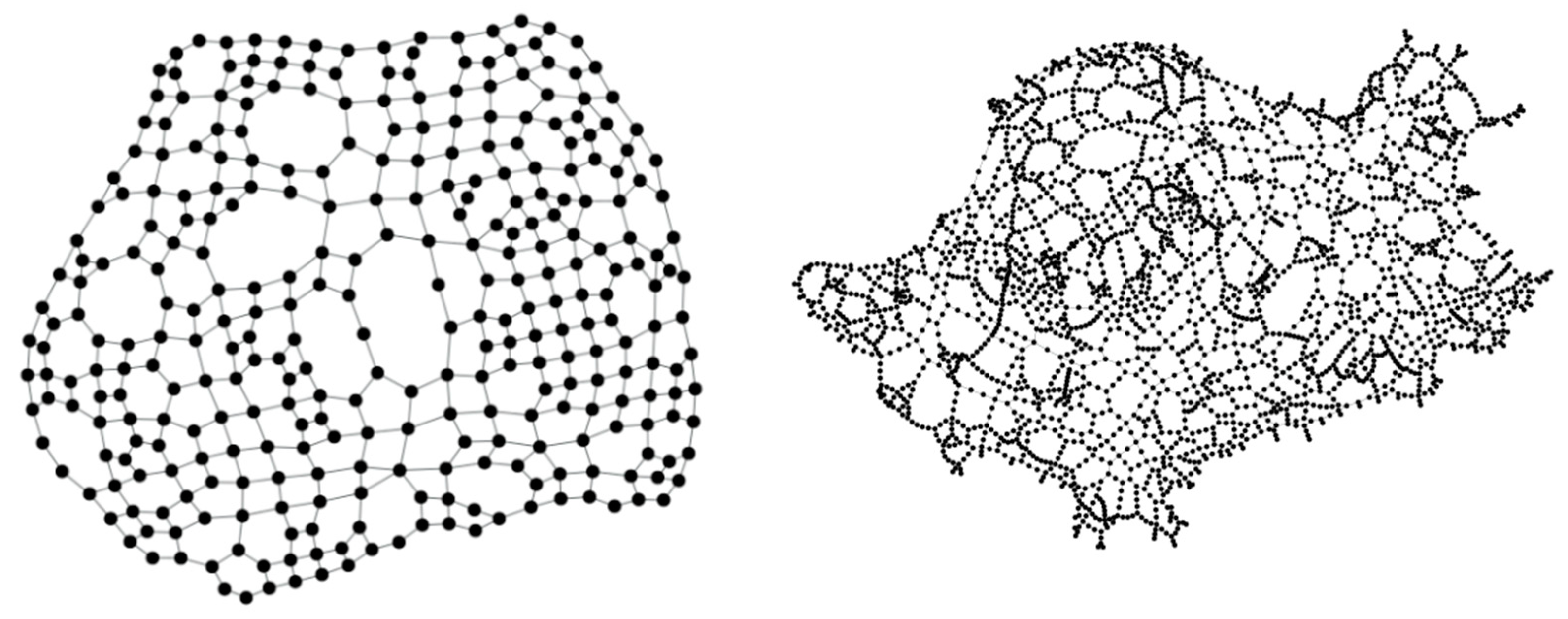
- San-Francisco Reduced: represents a reduced version of the San Francisco road network [31] (Real Datasets for Spatial Databases, https://users.cs.utah.edu/~lifeifei/SpatialDataset.htm ), obtained by applying a simple spatial-partitioning algorithm, resulting in a smaller, computationally affordable graph for the scope of this work.
- Road Minnesota: the road map of Minnesota (US) [40]. Nodes represent intersections among roads, and links represent roads.
- San Joaquin County: California (US) city road map [31](Real Datasets for Spatial Databases, https://users.cs.utah.edu/~lifeifei/SpatialDataset.htm). Nodes are the intersections among roads, and links represent roads.
2.4. Network Structural Indicators
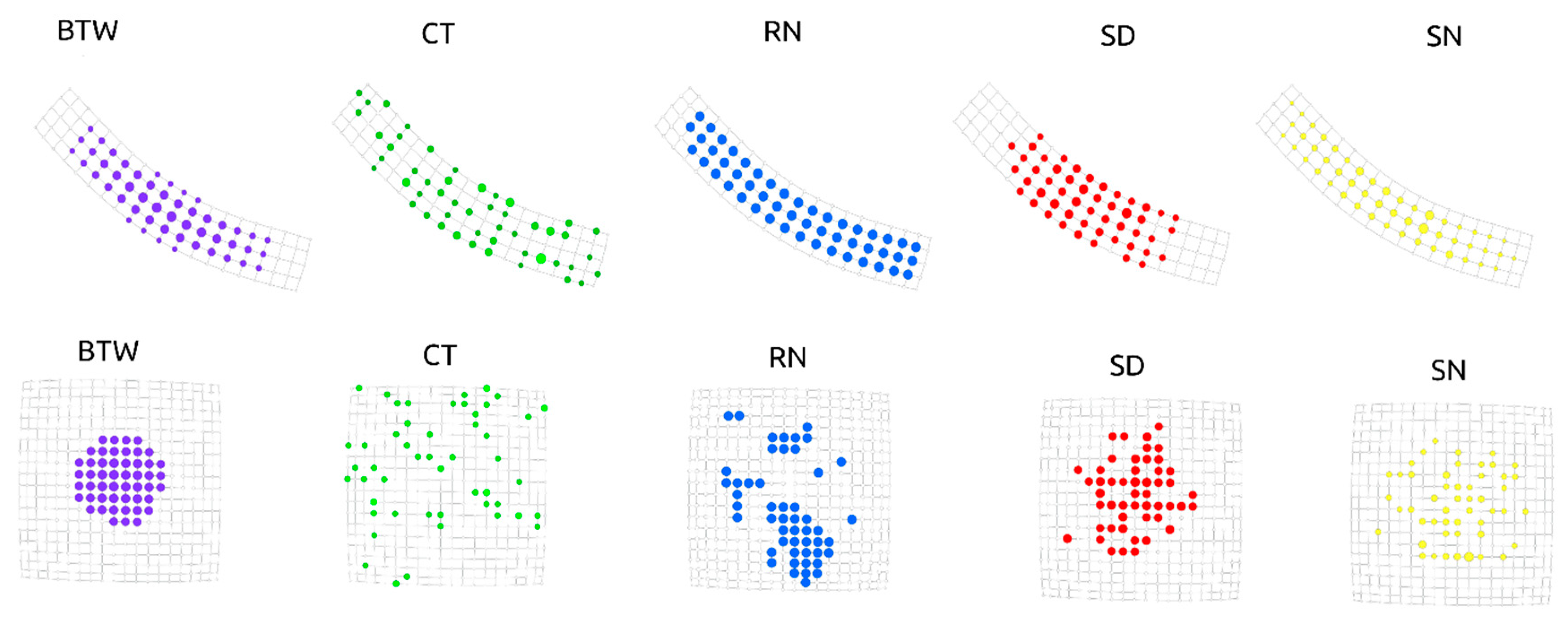
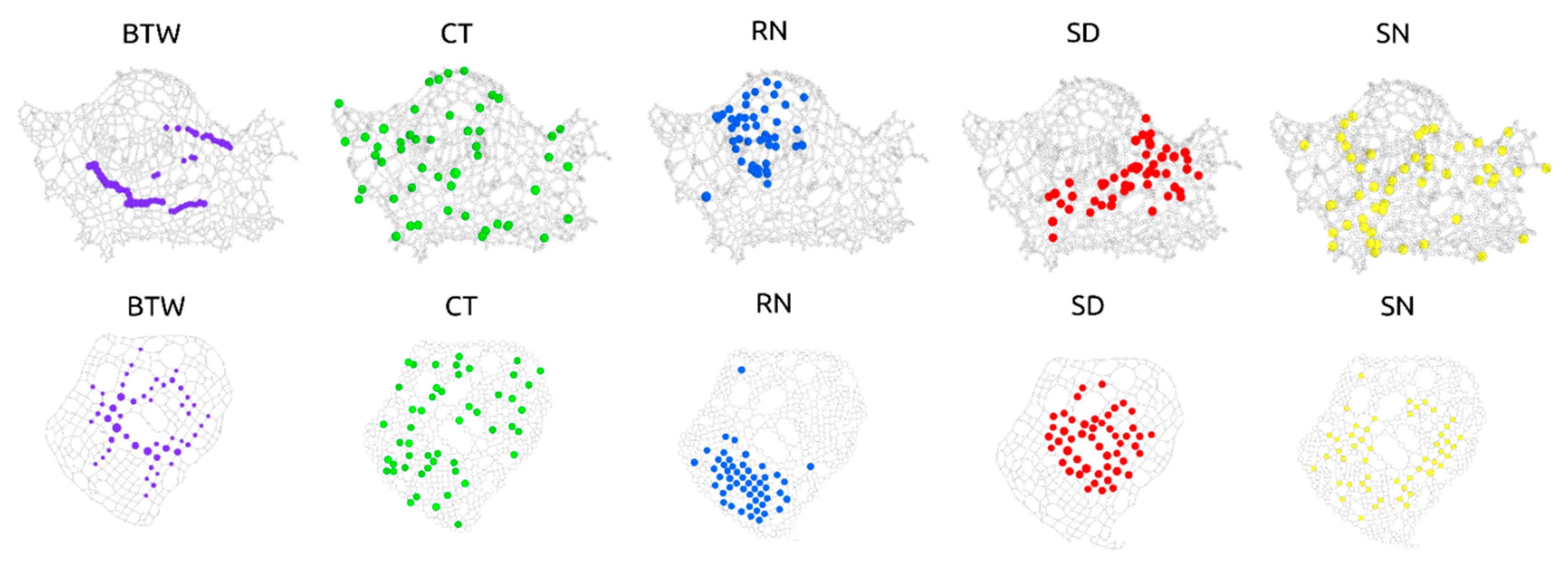
2.5. Node Removal Strategies
2.6. Betweenness Centrality
2.7. Closeness Centrality
2.8. Random Walk Based Strategies
2.9. Recurrence Number
2.10. Stop Node
2.11. Cover Time
2.11. Stop Distance
| Algorithm 1: Methodology of the RW analysis. |
| RW(G(V,E), start_node): |
| rec |
| rec_number 1 |
| cov_time 1 |
| stop |
| v |
| while ∃ x ∊ V | rec_num[x] == 0 do |
| u randomly chose a neighbor of v |
| rec_num[u] rec_num[u] + 1 |
| stop_node u |
| cov_time cov_time + 1 |
| v u |
| end while |
| stop_distanced(start_node, stop_node) |
2.12. Network Robustness Indicator
2.12.1. Largest Connected Component
2.12.2. Robustness
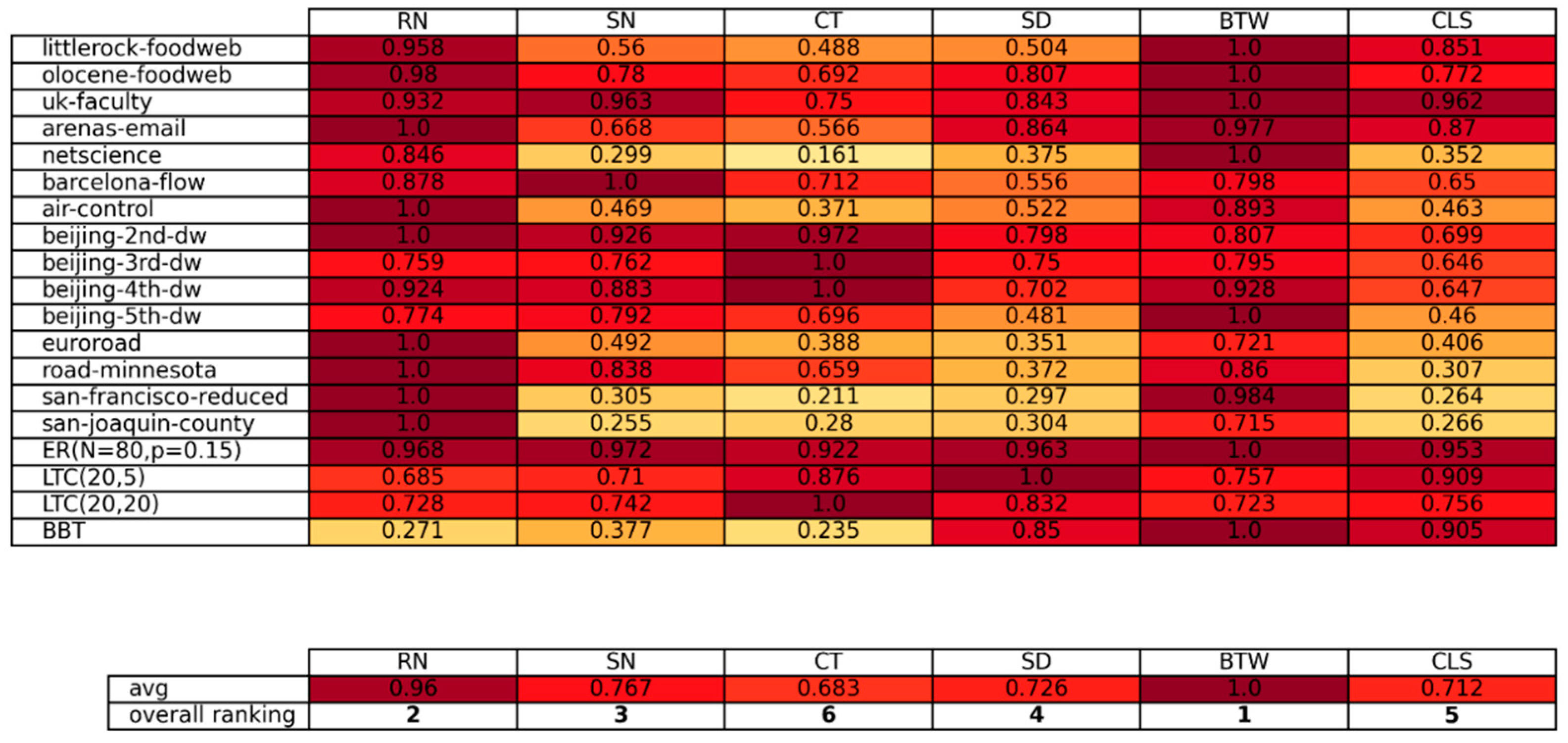
3. Results and Discussion
4. Conclusions
Acknowledgments
References
- Cohen, R.; Havlin, S. Complex Networks: Structure, Robustness and Function. Cambridge university press, 2010. [Google Scholar]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Resilience of the Internet to Random Breakdowns. Phys Rev Lett 2000, 85, 4626. [Google Scholar] [CrossRef] [PubMed]
- Morone, F.; Makse, H.A. Influence Maximization in Complex Networks through Optimal Percolation. Nature 2015, 524, 65–68. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Newman, M.E.J.; Strogatz, S.H.; Watts, D.J. Network Robustness and Fragility: Percolation on Random Graphs. Phys Rev Lett 2000, 85, 5468. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Cassi, D.; Vincenzi, S. Efficiency of Attack Strategies on Complex Model and Real-World Networks. Physica A: Statistical Mechanics and its Applications 2014, 414, 174–180. [Google Scholar] [CrossRef]
- Huang, X.; Gao, J.; Buldyrev, S.V.; Havlin, S.; Stanley, H.E. Robustness of Interdependent Networks under Targeted Attack. Phys Rev E 2011, 83, 65101. [Google Scholar] [CrossRef] [PubMed]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.-M. New Attack Strategies for Complex Networks. Physica A: Statistical Mechanics and its Applications 2015, 424, 248–253. [Google Scholar] [CrossRef]
- Pagani, A.; Mosquera, G.; Alturki, A.; Johnson, S.; Jarvis, S.; Wilson, A.; Guo, W.; Varga, L. Resilience or Robustness: Identifying Topological Vulnerabilities in Rail Networks. R Soc Open Sci 2019, 6, 181301. [Google Scholar] [CrossRef] [PubMed]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Breakdown of the Internet under Intentional Attack. Phys Rev Lett 2001, 86, 3682. [Google Scholar] [CrossRef] [PubMed]
- Bassett, D.S.; Bullmore, E.D. Small-World Brain Networks. The neuroscientist 2006, 12, 512–523. [Google Scholar] [CrossRef]
- Bullmore, E.; Sporns, O. Complex Brain Networks: Graph Theoretical Analysis of Structural and Functional Systems. Nat Rev Neurosci 2009, 10, 186–198. [Google Scholar] [CrossRef]
- Borgatti, S.P.; Mehra, A.; Brass, D.J.; Labianca, G. Network Analysis in the Social Sciences. Science (1979) 2009, 323, 892–895. [Google Scholar] [CrossRef] [PubMed]
- Boldi, P.; Rosa, M.; Vigna, S. Robustness of Social and Web Graphs to Node Removal. Soc Netw Anal Min 2013, 3, 829–842. [Google Scholar] [CrossRef]
- Sartori, F.; Turchetto, M.; Bellingeri, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.-K.-K.; Le, T.-T.; Nguyen, Q.; Cassi, D. A Comparison of Node Vaccination Strategies to Halt SIR Epidemic Spreading in Real-World Complex Networks. Sci Rep 2022, 12, 21355. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-K.-K.; Nguyen, T.-T.; Nguyen, T.-A.; Sartori, F.; Turchetto, M.; Scotognella, F.; Alfieri, R.; Cassi, D.; Nguyen, Q.; Bellingeri, M. Effective Node Vaccination and Containing Strategies to Halt SIR Epidemic Spreading in Real-World Face-to-Face Contact Networks. In Proceedings of the 2022 RIVF International Conference on Computing and Communication Technologies (RIVF); 2022; pp. 1–6. [Google Scholar]
- Michele Bellingeri Massimiliano Turchetto, D.B. Modeling the Consequences of Social Distancing over Epidemics Spreading in Complex Social Networks: From Link Removal Analysis to SARS-CoV-2 Prevention. Front Phys 2021, 9, 681343. [Google Scholar]
- Wandelt, S.; Sun, X.; Feng, D.; Zanin, M.; Havlin, S. A Comparative Analysis of Approaches to Network-Dismantling. Sci Rep 2018, 8, 1–15. [Google Scholar] [CrossRef] [PubMed]
- Iyer, S.; Killingback, T.; Sundaram, B.; Wang, Z. Attack Robustness and Centrality of Complex Networks. PLoS ONE 2013, 8, e59613. [Google Scholar] [CrossRef] [PubMed]
- Burioni, R.; Cassi, D. Random Walks on Graphs: Ideas, Techniques and Results. J Phys A Math Gen 2005, 38, R45. [Google Scholar] [CrossRef]
- Masuda, N.; Porter, M.A.; Lambiotte, R. Random Walks and Diffusion on Networks. Phys Rep 2017, 716, 1–58. [Google Scholar] [CrossRef]
- Guimer, R.; Danon, L.; Diaz-Guilera, A.; Giralt, F.; Arenas, A. Self-Similar Community Structure in a Network of Human Interactions. Phys. Rev. E 2003, 68, 65103. [Google Scholar] [CrossRef] [PubMed]
- Agliari, E. Exact Mean First-Passage Time on the T-Graph. Phys Rev E 2008, 77, 11128. [Google Scholar] [CrossRef]
- Noh, J.D.; Rieger, H. Random Walks on Complex Networks. Phys Rev Lett 2004, 92, 118701. [Google Scholar] [CrossRef] [PubMed]
- Rocha, L.E.C.; Masuda, N. Random Walk Centrality for Temporal Networks. New J Phys 2014, 16, 63023. [Google Scholar] [CrossRef]
- Newman, M.E.J. Analysis of Weighted Networks. Phys Rev E 2004, 70, 56131. [Google Scholar] [CrossRef] [PubMed]
- RENYI, E. On Random Graph. Publicationes Mathematicate 1959, 6, 290–297. [Google Scholar]
- Acharya, B.D.; Gill, M.K. On the Index of Gracefulness of a Graph and the Gracefulness of Two-Dimensional Square Lattice Graphs. Indian J. Math 1981, 23, 14. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Book: Introduction to Algorithms. 2009. [Google Scholar]
- Van Steen, M. Graph Theory and Complex Networks. An introduction 2010, 144. [Google Scholar]
- Chen, G.; Wang, X.; Li, X. Fundamentals of Complex Networks: Models, Structures and Dynamics. 2014; Volume 96. [Google Scholar]
- Preferred Routes Database.
- Kunegis, J. Konect: The Koblenz Network Collection. In Proceedings of the 22nd international conference on world wide web; 2013; pp. 1343–1350. [Google Scholar]
- Transportation Networks.
- Nepusz, T.; Petróczi, A.; Négyessy, L.; Bazsó, F. Fuzzy Communities and the Concept of Bridgeness in Complex Networks. Phys Rev E 2008, 77, 16107. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.-L.; Lu, Z.-M. Urban Road Network and Taxi Network Modeling Based on Complex Network Theory. J. Inf. Hiding Multim. Signal Process. 2016, 7, 558–568. [Google Scholar]
- Šubelj, L.; Bajec, M. Robust Network Community Detection Using Balanced Propagation. Eur Phys J B 2011, 81, 353–362. [Google Scholar] [CrossRef]
- Martinez, N.D. Artifacts or Attributes? Effects of Resolution on the Little Rock Lake Food Web. Ecol Monogr 1991, 61, 367–392. [Google Scholar] [CrossRef]
- Dunne, J.A.; Labandeira, C.C.; Williams, R.J. Highly Resolved Early Eocene Food Webs Show Development of Modern Trophic Structure after the End-Cretaceous Extinction. Proceedings of the Royal Society B: Biological Sciences 2014, 281, 20133280. [Google Scholar] [CrossRef] [PubMed]
- Real Datasets for Spatial Databases.
- Rossi, R.A.; Ahmed, N.K. The Network Data Repository with Interactive Graph Analytics and Visualization. In Proceedings of the AAAI; 2015. [Google Scholar]
- Bellingeri, M.; Montepietra, D.; Cassi, D.; Scotognella, F. The Robustness of the Photosynthetic System I Energy Transfer Complex Network to Targeted Node Attack and Random Node Failure. J Complex Netw 2021, 10, cnab050. [Google Scholar] [CrossRef]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.-U. Complex Networks: Structure and Dynamics. Phys Rep 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Gleeson, J.P.; Melnik, S.; Hackett, A. How Clustering Affects the Bond Percolation Threshold in Complex Networks. Phys Rev E 2010, 81, 66114. [Google Scholar] [CrossRef] [PubMed]
- Dunne, J.A.; Williams, R.J.; Martinez, N.D. Network Structure and Biodiversity Loss in Food Webs: Robustness Increases with Connectance. Ecol Lett 2002, 5, 558–567. [Google Scholar] [CrossRef]
- Bellingeri, M.; Vincenzi, S. Robustness of Empirical Food Webs with Varying Consumer’s Sensitivities to Loss of Resources. J Theor Biol 2013, 333, 18–26. [Google Scholar] [CrossRef]
- Nguyen, Q.; Pham, H.-D.; Cassi, D.; Bellingeri, M. Conditional Attack Strategy for Real-World Complex Networks. Physica A: Statistical Mechanics and its Applications 2019, 530, 121561. [Google Scholar] [CrossRef]
- Albert, R.; Barabási, A.-L. Statistical Mechanics of Complex Networks. Rev Mod Phys 2002, 74, 47. [Google Scholar] [CrossRef]
- Tiago, P. Peixoto Graph-Tool, Efficient Network Analysis. https://Graph-Tool.Skewed.De/.
- Siek, J.G.; Lee, L.-Q.; Lumsdaine, A. The Boost Graph Library: User Guide and Reference Manual, The; Pearson Education, 2001. [Google Scholar]
- Freeman, L.C. A Set of Measures of Centrality Based on Betweenness. Sociometry 1977, 35–41. [Google Scholar] [CrossRef]
- Marchiori, M.; Latora, V. Harmony in the Small-World. Physica A: Statistical Mechanics and its Applications 2000, 285, 539–546. [Google Scholar] [CrossRef]
- Campari, R.; Cassi, D. Random Collisions on Branched Networks: How Simultaneous Diffusion Prevents Encounters in Inhomogeneous Structures. Phys Rev E 2012, 86, 21110. [Google Scholar] [CrossRef] [PubMed]
- Xia, F.; Liu, J.; Nie, H.; Fu, Y.; Wan, L.; Kong, X. Random Walks: A Review of Algorithms and Applications. IEEE Trans Emerg Top Comput Intell 2019, 4, 95–107. [Google Scholar] [CrossRef]
- Lovász, L. Random Walks on Graphs. Combinatorics, Paul erdos is eighty 1993, 2, 4. [Google Scholar]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.; Cassi, D. The Heterogeneity in Link Weights May Decrease the Robustness of Real-World Complex Weighted Networks. Sci Rep 2019, 9, 10692. [Google Scholar] [CrossRef]
- Zhang, Y.; Ng, S.T. Identification and Quantification of Node Criticality through EWM–TOPSIS: A Study of Hong Kong’s MTR System. Urban Rail Transit 2021, 7, 226–239. [Google Scholar] [CrossRef]
- Schneider, C.M.; Moreira, A.A.; Andrade Jr, J.S.; Havlin, S.; Herrmann, H.J. Mitigation of Malicious Attacks on Networks. Proceedings of the National Academy of Sciences 2011, 108, 3838–3841. [Google Scholar] [CrossRef]
- Levin, D.A.; Peres, Y. Markov Chains and Mixing Times. American Mathematical Soc., 2017; Volume 107. [Google Scholar]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of Influential Spreaders in Complex Networks. Nat Phys 2010, 6, 888–893. [Google Scholar] [CrossRef]
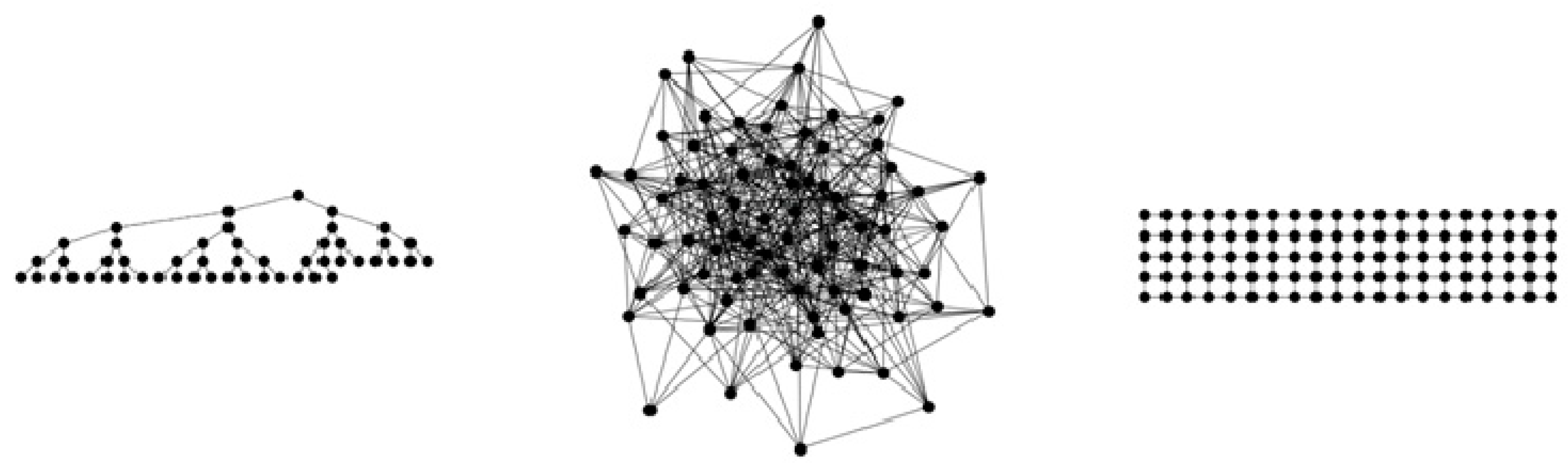
| Network | |||||||
|---|---|---|---|---|---|---|---|
| air-control | 1226 | 2410 | 17 | 3.931 | 5.924 | 0.064 | 0.003 |
| arenas-email | 1133 | 5451 | 8 | 9.622 | 3.603 | 0.166 | 0.009 |
| barcelona-flow | 930 | 1798 | 27 | 3.867 | 12.721 | 0.084 | 0.004 |
| beijing-2th | 144 | 233 | 19 | 3.236 | 7.813 | 0.011 | 0.023 |
| beijing-3rd | 322 | 544 | 27 | 3.379 | 11.030 | 0.018 | 0.011 |
| beijing-4th | 547 | 926 | 33 | 3.386 | 13.904 | 0.019 | 0.006 |
| beijing-5th | 815 | 1308 | 48 | 3.210 | 17.246 | 0.024 | 0.004 |
| euroroad | 1039 | 1305 | 62 | 2.512 | 18.377 | 0.035 | 0.002 |
| littlerock-foodweb | 183 | 2452 | 4 | 26.798 | 2.135 | 0.332 | 0.147 |
| netscience | 379 | 914 | 17 | 4.823 | 6.026 | 0.431 | 0.013 |
| olocene-foodweb | 700 | 6425 | 6 | 18.357 | 2.629 | 0.074 | 0.026 |
| road-minnesota | 2641 | 3303 | 100 | 2.501 | 35.349 | 0.028 | 0.001 |
| san-francisco-reduced | 435 | 440 | 41 | 2.023 | 17.461 | 0.000 | 0.005 |
| san-joaquin-county | 7087 | 9793 | 50 | 2.764 | 13.939 | 0.000 | 0.000 |
| uk-faculty | 81 | 577 | 4 | 14.247 | 2.072 | 0.473 | 0.178 |
| LTC(20,5) | 100 | 175 | 23 | 3.500 | 8.250 | 0.000 | 0.035 |
| LTC(20,20) | 400 | 760 | 38 | 3.800 | 13.300 | 0.000 | 0.010 |
| BBT | 100 | 99 | 12 | 1.980 | 7.654 | 0.000 | 0.020 |
| ER(N=80,p=0.15) | 80.0 | 474.52 | 3.1 | 11.863 | 1.969 | 0.148 | 0.150 |
| LCC | network largest connected component |
| |𝑽| | number of nodes in the network |
| |𝑬| | Number of links in the network |
| Diam | Diameter of the network |
| Average node degree | |
| Average length of shortest path among all node pairs | |
| 𝑪𝑪 | Clustering coefficient, i.e., number of closed triples |
| 𝝆 | Network density, i.e., fraction of realized links in the network among all possible links |
| R | Robustness of the network |
| Inverse of the network robustness | |
| among all networks | |
| RN | Recurrence Number |
| CT | Covering Time |
| SN | Stop Node |
| SD | Stop Distance |
| BTW | Betweenness Centrality |
| CLS | Closeness Centrality |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





