Submitted:
30 October 2023
Posted:
30 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. The Matrix Low-Rank Constrained Inpainting Model and Its Solution Algorithm
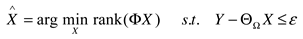
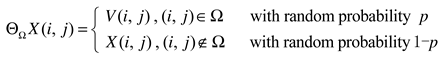
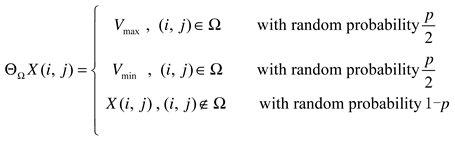
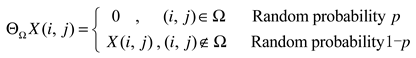
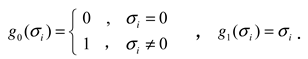
2.1. Nuclear norm ‖X‖∗
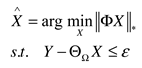
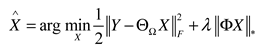
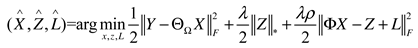
2.2. Weighted nuclear norm
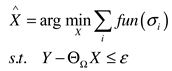
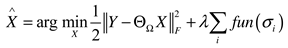
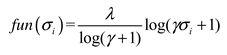
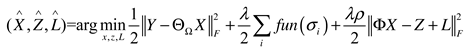
2.3. Truncated nuclear norm
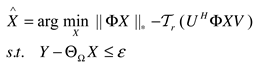
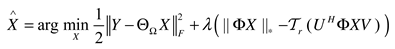
2.4. The F norm of UV matrix factorization
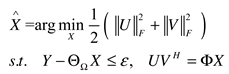
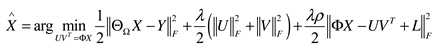
3. Comparative Experiments
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
| 1 | The interference rate is the percentage of the number of interference pixels in the total number of image pixels. |
References
- Kyong, H.; Jong, C. Sparse and Low-Rank Decomposition of a Hankel Structured Matrix for Impulse Noise Removal. IEEE Trans. Image Process. 2018, 27, 1448–1461. [Google Scholar] [CrossRef]
- Kyong, H.; Ye, J. Annihilating filterbased lowrank Hankel matrix approach for image inpainting. IEEE Trans. Image Process. 2015, 24, 3498–511. [Google Scholar] [CrossRef]
- Balachandrasekaran, A.; Magnotta, V.; Jacob, M. Recovery of damped exponentials using structured low rank matrix completion. IEEE Trans. Med. Imaging 2017, 36, 2087–2098. [Google Scholar] [CrossRef] [PubMed]
- Haldar, J. Low-rank modeling of local-space neighborhoods (LORAKS) for constrained MRI. IEEE Trans. Med. Imaging 2014, 33, 668–680. [Google Scholar] [CrossRef] [PubMed]
- Ren, W.; Cao, X.; Pan, J.; et al. Image deblurring via enhanced low-rank prior. IEEE Trans. Image Process. 2016, 25, 3426–3437. [Google Scholar] [CrossRef]
- Xu, Z.; Sun, J. Image inpainting by patch propagation using patch sparsity. IEEE Trans. Image Process. 2010, 9, 1153–1165. [Google Scholar] [CrossRef]
- Zhao, B.; Haldar, J.; Christodoulou, A.; et al. Image reconstruction from highly undersampled (k, t)-space data with joint partial separability and sparsity constraints. IEEE Trans. Med. Imaging 2012, 31, 1809–20. [Google Scholar] [CrossRef]
- Kyong, H.; Jong, C. Annihilating Filter-Based Low-Rank Hankel Matrix Approach for Image Inpainting. IEEE Trans. Image Process. 2018, 27, 1448–1461. [Google Scholar] [CrossRef]
- Long, Z.; Liu, Y.; Chen, L.; et al. Low rank tensor completion for multiway visual data. Signal Process. 2019, 155, 301–316. [Google Scholar] [CrossRef]
- Kolda, T.; Bader, B. Tensor decompositions and applications. SIAM Review 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Oseledets, I. Tensor-train decomposition. SIAM J. Scien. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Shi, Q.; Cheung, M.; Lou, J. Robust Tensor SVD and Recovery With Rank Estimation. IEEE Trans. Cyber. 2022, 52, 10667–10682. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Li, C.; Li, Y.; Tang, N. Robust low-rank tensor completion via new regularized model with approximate SVD. Inform. Sciences 2023, 629, 646–666. [Google Scholar] [CrossRef]
- Huang, J.; Yang, F. Compressed magnetic resonance imaging based on wavelet sparsity and nonlocal total variation. IEEE 9th International Symposium on Biomedical Imaging: From Nano to Macro, 2012, 5, 968–971. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, T. Wavelet inpainting by nonlocal total variation. Inverse Problems and Imaging 2010, 4, 191–210. [Google Scholar] [CrossRef]
- Wang, W.; Chen, J. Adaptive rate image compressive sensing based on the hybrid sparsity estimation model. Digit. Signal Process. 2023, 139, 104079. [Google Scholar] [CrossRef]
- Ou, Y.; Li, B.; Swamy, M. Low-rank with sparsity constraints for image denoising. Information Sciences 2023, 637, 118931. [Google Scholar] [CrossRef]
- Lingala, S.; Hu, Y.; Dibella, E.; et al. Accelerated dynamic MRI exploiting sparsity and lowrank structure: kt SLR. IEEE Trans. Med. Imaging 2011, 30, 1042–1054. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Huang, L.; Li, Y.; Zhang, K.; Yin, C. Low-Rank and Sparse Matrix Recovery for Hyperspectral Image Reconstruction Using Bayesian Learning. Sensors 2022, 22, 343. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Li, M.; Nie, T.; Han, C.; Huang, L. An Innovative Approach for Removing Stripe Noise in Infrared Images. Sensors 2023, 23, 6786. [Google Scholar] [CrossRef]
- Tremoulheac, B.; Dikaios, N.; Atkinson, D.; et al. Dynamic MR image reconstructionseparation from undersampled (k, t)space via lowrank plus sparse prior. IEEE Trans. Med. Imaging 2014, 33, 1689–1701. [Google Scholar] [CrossRef] [PubMed]
- Kyong, H.; Ye, J. Annihilating filter-based low-rank Hankel matrix approach for image inpainting. IEEE Trans. Image Process. 2015, 24, 3498–511. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Q.; Zhou, G.; Xie, S.; et al. Tensor ring decomposition. 2016, arXiv:1606.05535. [Google Scholar] [CrossRef]
- Kilmer, M.; Braman, K.; Hao, N. Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. Siam J. Matrix Anal. A. 2013, 34, 148–172. [Google Scholar] [CrossRef]
- Zhang, Z.; Aeron, S. Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Bengua, J. Efficient tensor completion for color image and video recovery: Lowrank tensor train. IEEE Trans. Image Process. 2017, 26, 1057–7149. [Google Scholar] [CrossRef] [PubMed]
- Ma, S.; Du, H.; Mei, W. Dynamic MR image reconstruction from highly undersampled (k, t)-space data exploiting low tensor train rank and sparse prior. IEEE Access 2020, 8, 28690–28703. [Google Scholar] [CrossRef]
- Ma, S.; Ai, J.; Du, H.; Fang, L.; Mei, W. Recovering low-rank tensor from limited coefficients in any ortho-normal basis using tensor-singular value decomposition. IET Signal Process. 2021, 19, 162–181. [Google Scholar] [CrossRef]
- Tang, T.; Kuang, G. SAR Image Reconstruction of Vehicle Targets Based on Tensor Decomposition. Electronics 2022, 11, 2859. [Google Scholar] [CrossRef]
- Gross, D. Recovering low-rank matrices from few coefficients in any basis. IEEE Trans. Infor. Theory 2011, 57, 1548–1566. [Google Scholar] [CrossRef]
- Jain P.; Oh S. Provable tensor factorization with missing data. In: Proceedings of the 27th International Conference on Neural Information Processing Systems (NIPS) 2014, 1: 1431–1439.
- Zhang, Z.; Aeron, S. Exact tensor completion using t-SVD. IEEE Trans. Signal Process. 2017, 65, 1511–1526. [Google Scholar] [CrossRef]
- Vetterli, M.; Marziliano, P.; Blu, T. Sampling signals with finite rate of innovation. IEEE trans. Signal Process. 2002, 50, 1417–1428. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image denoising by sparse 3-D transform-domain collaborative filtering. IEEE Trans. Image Process. 2007, 16, 2080–209. [Google Scholar] [CrossRef] [PubMed]
- Lou, Y.; Zhang, X.; Osher, S.; Bertozzi, A. Image recovery via nonlocal operators. Journal of Scientific Computing 2010, 42, 185–197. [Google Scholar] [CrossRef]
- Filipovi, M.; Juki´, A. Tucker factorization with missing data with application to low-n-rank tensor completion. Multidim Syst. Sign. Process. 2015, 26, 677–692. [Google Scholar] [CrossRef]
- Wang, X.; Kong, L.; Wang, L.; Yang, Z. High-Dimensional Covariance Estimation via Constrained Lq-Type Regularization. Mathematics 2023, 11, 1022. [Google Scholar] [CrossRef]
- Candès, E.; Wakin, M.; Boyd, S. Enhancing sparsity by reweighted l1 minimization. J. Fourier Anal. Appl. 2008, 14, 877–905. [Google Scholar] [CrossRef]
- Lu, C.; Tang, J.; Yan, S.; et al. Nonconvex Nonsmooth Low-Rank Minimization via Iteratively Reweighted Nuclear Norm. IEEE Trans. Image Process. 2015, 25, 829–839. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, J.; Wang, C.; Li, S. Hyperspectral and multispectral image fusion via superpixel-based weighted nuclear norm minimization. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–12. [Google Scholar] [CrossRef]
- Li, Z.; Yan, M.; Zeng, T.; Zhang, G. Phase retrieval from incomplete data via weighted nuclear norm minimization. Pattern Recognition. 2022, 125, 108537. [Google Scholar] [CrossRef]
- Cao, F.; Chen, J.; Ye, H.; et al. Recovering low-rank and sparse matrix based on the truncated nuclear norm. Neural Networks 2017, 85, 10–20. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, D.; Ye, J.; et al. Fast and accurate matrix completion via truncated nuclear norm regularization. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2117–2130. [Google Scholar] [CrossRef] [PubMed]
- Fan, Q.; Liu, Y.; Yang, T.; Peng, H. Fast and accurate spectrum estimation via virtual coarray interpolation based on truncated nuclear norm regularization. IEEE Signal Process. Lett. 2022, 29, 169–173. [Google Scholar] [CrossRef]
- Yadav, S.; George, N. Fast direction-of-arrival estimation via coarray interpolation based on truncated nuclear norm regularization. IEEE Trans. Circuits Syst. II, Exp. Briefs 2021, 68, 1522–1526. [Google Scholar] [CrossRef]
- Cai, J.; Candès, E.; Shen, Z. A singular value thresholding algorithm for matrix completion. Siam J. Optimiz. 2010, 20, 1956–1982. [Google Scholar] [CrossRef]
- Xu, J.; Fu, Y.; Xiang, Y. An edge map-guided acceleration strategy for multi-scale weighted nuclear norm minimization-based image denoising. Digit. Signal Process. 2023, 134, 103932. [Google Scholar] [CrossRef]
- Jain P.; Meka R. Guaranteed rank minimization via singular value projection. Available online: http://arxiv.org/ abs/0909.5457, 2009. [CrossRef]
- Stephen, B. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends in Mach. Le. 2010, 3, 1–122. [Google Scholar] [CrossRef]
- Zhao, Q.; Lin, Y.; Wang, F. Adaptive weighting function for weighted nuclear norm based matrix/tensor completion. Int. J. Mach. Learn. Cyber. 2023. [Google Scholar] [CrossRef]
- Liu, X.; Hao, C.; Su, Z. Image inpainting algorithm based on tensor decomposition and weighted nuclear norm. Multimed Tools Appl. 2023, 82, 3433–3458. [Google Scholar] [CrossRef]
- Fan, J.; Li, R. Variable selection via nonconcave penalized likelihood and its oracle properties. J. Amer. Statist. Assoc. 2001, 96, 1348–1360. [Google Scholar] [CrossRef]
- Friedman, J. Fast sparse regression and classification. Int. J. Forecasting 2012, 28, 722–738. [Google Scholar] [CrossRef]
- Zhang, C.-H. Nearly unbiased variable selection under minimax concave penalty. Ann. Statist. 2010, 38, 894–942. [Google Scholar] [CrossRef]
- Geman, D.; Yang, C. Nonlinear image recovery with half-quadratic regularization. IEEE Trans. Image Process. 1995, 4, 932–946. [Google Scholar] [CrossRef] [PubMed]
- Trzasko, J.; Manduca, A. Highly undersampled magnetic resonance image reconstruction via homotopic 0-minimization. IEEE Trans. Med. Imag. 2009, 28, 106–121. [Google Scholar] [CrossRef] [PubMed]
- Liu, Q. A truncated nuclear norm and graph-Laplacian regularized low-rank representation method for tumor clustering and gene selection. BMC Bioinformatics. 2021, 22, 436. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, X.; Mao, H.; Huang, Z.; Xiao, Y.; Chen W., g; Xian, J.; Bi, Y. Improved sparse low-rank model via periodic overlapping group shrinkage and truncated nuclear norm for rolling bearing fault diagnosis. Measurement Sci. Technol. 2023, 34. [Google Scholar] [CrossRef]
- Ran, J.; Bian, J.; Chen, G.; Zhang, Y.; Liu, W. A truncated nuclear norm regularization model for signal extraction from GNSS coordinate time series. Adv. Space Res. 2022, 70, 336–349. [Google Scholar] [CrossRef]
- Signoretto M.; Cevher V.; Suykens J. An SVD-free approach to a class of structured low rank matrix optimization problems with application to system identification. In: IEEE Conference on Decision and Control, EPFL-CONF-184990, 2013.
- Srebro N. Learning with matrix factorizations. Cambridge, MA, USA: Massachusetts Institute of Technology, 2004.
- Recht, B.; Fazel, M.; Parrilo, P. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM review 2010, 52, 471–501. [Google Scholar] [CrossRef]
- Ma, S.; Du, H.; Mei, W. A two-step low rank matrices approach for constrained MR image reconstruction. Magn. Reson. Imaging 2019, 60. [Google Scholar] [CrossRef]
- Yang, G.; Zhang, L.; Wan, M. Exponential Graph Regularized Non-Negative Low-Rank Factorization for Robust Latent Representation. Mathematics 2022, 10, 4314. [Google Scholar] [CrossRef]
- Wen, Z.; Yin, W.; Zhang, Y. Solving a low-rank factorization model for matrix completion by a nonlinear successive over-relaxation algorithm. Math. Program. Comput. 2012, 4, 333–361. [Google Scholar] [CrossRef]
- Daubechies, I.; Defrise, M.; Mol, C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint. Commun. Pure Appl. Math. 2004, 57, 1413–1457. [Google Scholar] [CrossRef]
- Goldstein, T.; Osher, S. The split Bregman method for L1regularized problems. Siam J. Imaging Sci. 2009, 2, 323–343. [Google Scholar] [CrossRef]
- Jacobson, M.; Fessler, J. An Expanded Theoretical Treatment of IterationDependent MajorizeMinimize Algorithms. IEEE Trans. Image Process. 2007, 16, 2411–2422. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.; Sheikh, H.; et al. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]

| Input: Y, ΘΩ, ρ, λ, the maximum number of iteration tmax, and convergence condition ηtol = e − 6. |
| Initialization: (m, n) = size(Y), X(0) = zeros(m, n), = Y, t = 1. |
|
While t < tmax and η(t) < ηtol do [U, S, V] = SVD(). δ0 = diag(S), τ = , δ = 1 – min(, 1), δ0 = δ0 ∗ δ. Update X(t) = |U ∗ diag(δ0) ∗ VH|. Update = | + λ(Y − X(t))|. Update η(t) = . t = t + 1. End while X∗ = X(t), ΘΩX∗ = ΘΩY. |
| Output: X∗. |
| Input: Y, ΘΩ, τ = 0.01, the rank r, the maximum number of iteration tmax, and convergence condition ηtol = e − 6. |
| Initialization: (m, n) = size(Y), X(0) = zeros(m, n), = Y, t = 1. |
|
While t < tmax and η(t) < ηtol do = X(t−1) – τ(X(t−1) – Y). ΘΩ = ΘΩY. [U, S, V] = SVD() δ0 = diag(S), δ0 = δ0(1:r,1). Update X(t) = |U(:,1:r) ∗ diag(δ0) ∗ V(:,1:r)H|. Update η(t) = . ΘΩX(t) = ΘΩY, t = t + 1. End while X∗ = X(t). |
| Output: X∗. |
| Input: Y, ΘΩ, ρ, λ, the maximum number of iteration tmax, and convergence condition ηtol = e − 6. |
| Initialization: (m, n) = size(Y), X(0) = zeros(m, n), = Y, Z(0) = zeros(m, n), L(0) = zeros(m, n), t = 1. |
|
While t < tmax and η(t) < ηtol do Update X(t) = ( + λρ(Z(t−1) − L(t−1)))./(ΘΩ + λρ). [U, S, V] = SVD(X(t) + L(t−1)). δ0 = diag(S) − , δ0(find(δ0)) < 0) = 0. Update Z(t) = U ∗ diag(δ0) ∗ VH. Update L(t) = L(t−1) + X(t) − Z(t). Update η(t) = . t = t + 1. End while ΘΩX(t) = ΘΩY, X∗ = |X(t)|. |
| Output: X∗. |
| Input: Y, ΘΩ, ρ, θ, λ, γ, the maximum number of iteration tmax, decay factor , and convergence condition ηtol = e − 6. |
| Initialization: (m, n) = size(Y), X(0) = zeros(m, n), L(0) = zeros(m, n), = Y, λ = ∗ max(|Y(:)|), t = 1. |
|
While t < tmax and η(t) < ηtol do [U, S, V] = SVD(). δ0 = diag(S), w = fun(δ0, γ, λ), δ0 = δ0 – w ∗ , δ0(find(δ0)) < 0) = 0. Update X(t) = U ∗ diag(δ0) ∗ VH. Update = | + θ(Y − X(t))|. Update η(t) = . λ = ∗ λ, ΘΩX(t) = ΘΩY, t = t + 1. End while X∗ = X(t). |
| Output: X∗. |
| Input: Y, ΘΩ, ρ, λ, the maximum number of iteration tmax,, the truncated rank r, and convergence condition ηtol = e − 6. |
| Initialization: (m, n) = size(Y), X(0) = zeros(m, n), = Y, Z(0) = zeros(m, n), L(0) = zeros(m, n), t = 1. |
|
While t < tmax and η(t) < ηtol do τ = , T = Z(t−1) – τ ∗ L(t−1), [U, S, V] = SVD(T). δ0 = diag(S), δ = 1 – min(, 1), δ0 = δ0 ∗ δ. Update X(t) = U ∗ diag(δ0) ∗ VH. [Uz, Sz, Vz] = SVD(Z(t−1)), B = Uz(:,1:r).H∗ Vz(:,1:r). Update Z(t) = X(t) + τ ∗ (Z(t−1) + B), ΘΩZ(t) = ΘΩY. Update L(t) = L(t−1) + ρ(X(t) – Z(t)). Update η(t) = . t = t + 1. End while ΘΩX(t) = ΘΩY, X∗ = X(t). |
| Output: X∗. |
| Input: Y, ΘΩ, ρ, λ, the maximum number of iteration tmax, and convergence condition ηtol. |
| Initialization: and by the LMaFit method [65], (m, n) = size(Y), X(0) = zeros(m, n), = Y, L(0) = zeros(m, n), t = 1. |
|
While t < tmax and η < ηtol do Update X(t) = (Y(t) + λρ ∗ (U(t−1)V(t−1)H − L(t−1)))./(ΘΩ + λρ). Update U(t) = ρ ∗ (X(t) + L(t−1)) ∗ V(t−1) ∗ inv(eye(r) + ρV(t−1)V(t−1)H). Update V(t) = ρ ∗ (X(t) + L(t−1)) ∗ U(t) ∗ inv(eye(r) + ρU(t)HU(t)). Update L(t) = L(t−1) + X(t) − U(t)V(t)H. Update ηt+1 = . t = t + 1. End while ΘΩX(t) = ΘΩY, X∗ = X(t). |
| Output: X∗. |
| Constrained Modeling | Nuclear Norm | Truncated Nuclear Norm | Weighted Nuclear Norm | Matrix Decomposition F Norm | ||
| Solution algorithm | SVT | SVP | ADMM | ADMM | ADMM | ADMM |
| Method abbreviation | SVT | SVP | n_ADMM | TSVT_ADMM | WSVT_ADMM | UV_ADMM |
| Noise forms | Methods | Untreated | SVT | SVP | n_ADMM | TSVT_ ADMM |
WSVT_ ADMM |
UV_ ADMM |
|
| Indices | |||||||||
| Random impulse | RLNE (%) | 45.88 | 18.36 | 9.83 | 19.70 | 8.43 | 8.19 | 20.01 | |
| SSIM (%) | 34.77 | 77.50 | 92.19 | 74.96 | 94.25 | 94.49 | 74.30 | ||
| Running time (s) | / | 11.7357 | 0.5484 | 1.3883 | 1.0401 | 2.0523 | 0.3375 | ||
| Salt and pepper noise | RLNE (%) | 69.72 | 19.96 | 9.76 | 19.73 | 8.41 | 8.22 | 20.29 | |
| SSIM (%) | 18.63 | 74.18 | 92.25 | 74.79 | 94.21 | 94.39 | 73.80 | ||
| Running time(s) | / | 5.34 | 0.4793 | 1.1451 | 1.2996 | 2.216 | 0.1993 | ||
| Pixel missing | RLNE (%) | 54.77 | 12.96 | 9.84 | 8.73 | 8.43 | 8.19 | 8.9 | |
| SSIM (%) | 32.46 | 87.91 | 92.25 | 94.02 | 94.25 | 94.49 | 93.69 | ||
| Running time (s) | / | 9.9569 | 0.5418 | 0.5194 | 0.9842 | 2.3475 | 0.2543 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





