Submitted:
25 October 2023
Posted:
26 October 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Field of a loop current
2.1. Circular current loop
2.2. General current loop on a plane
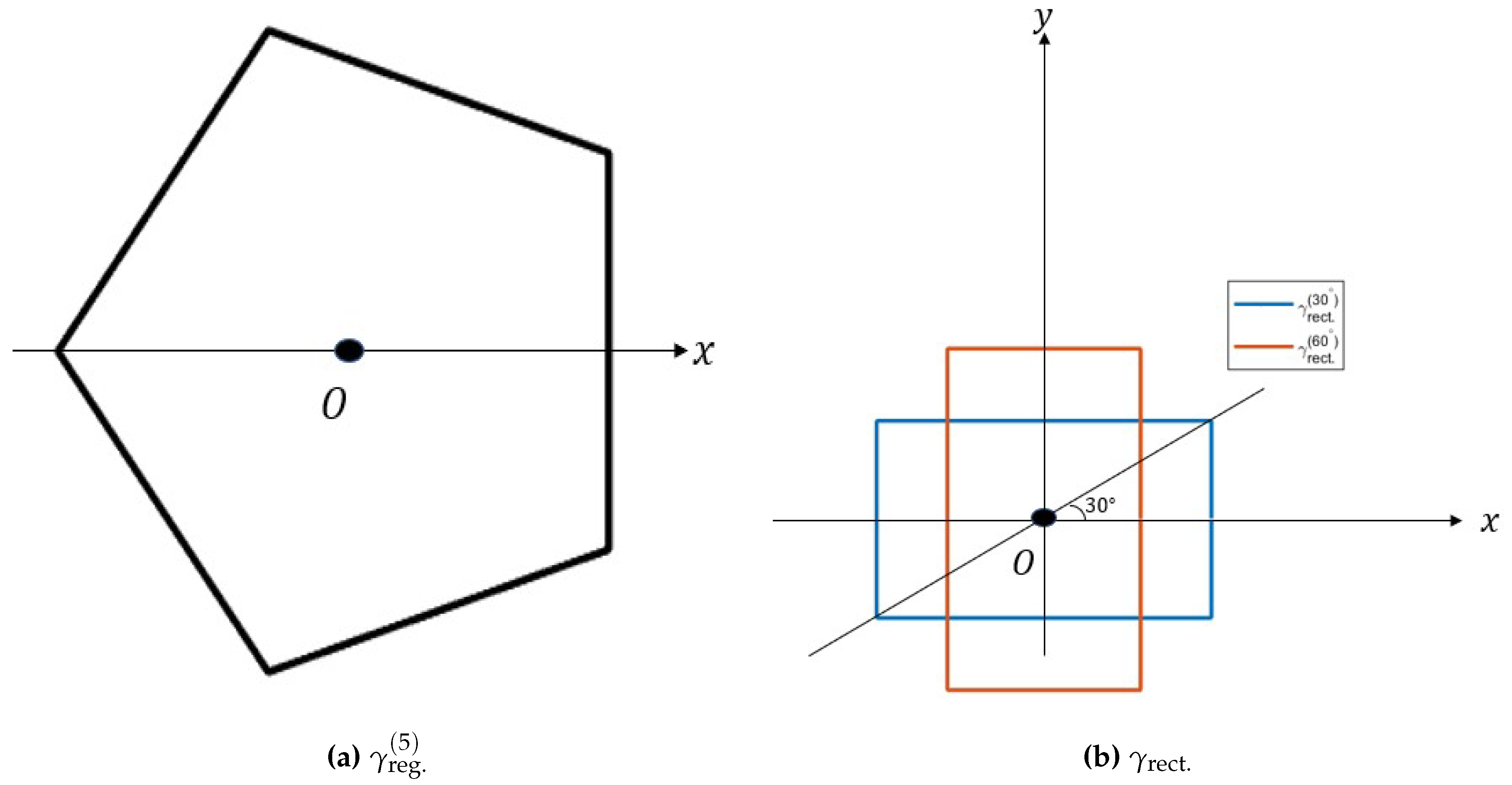
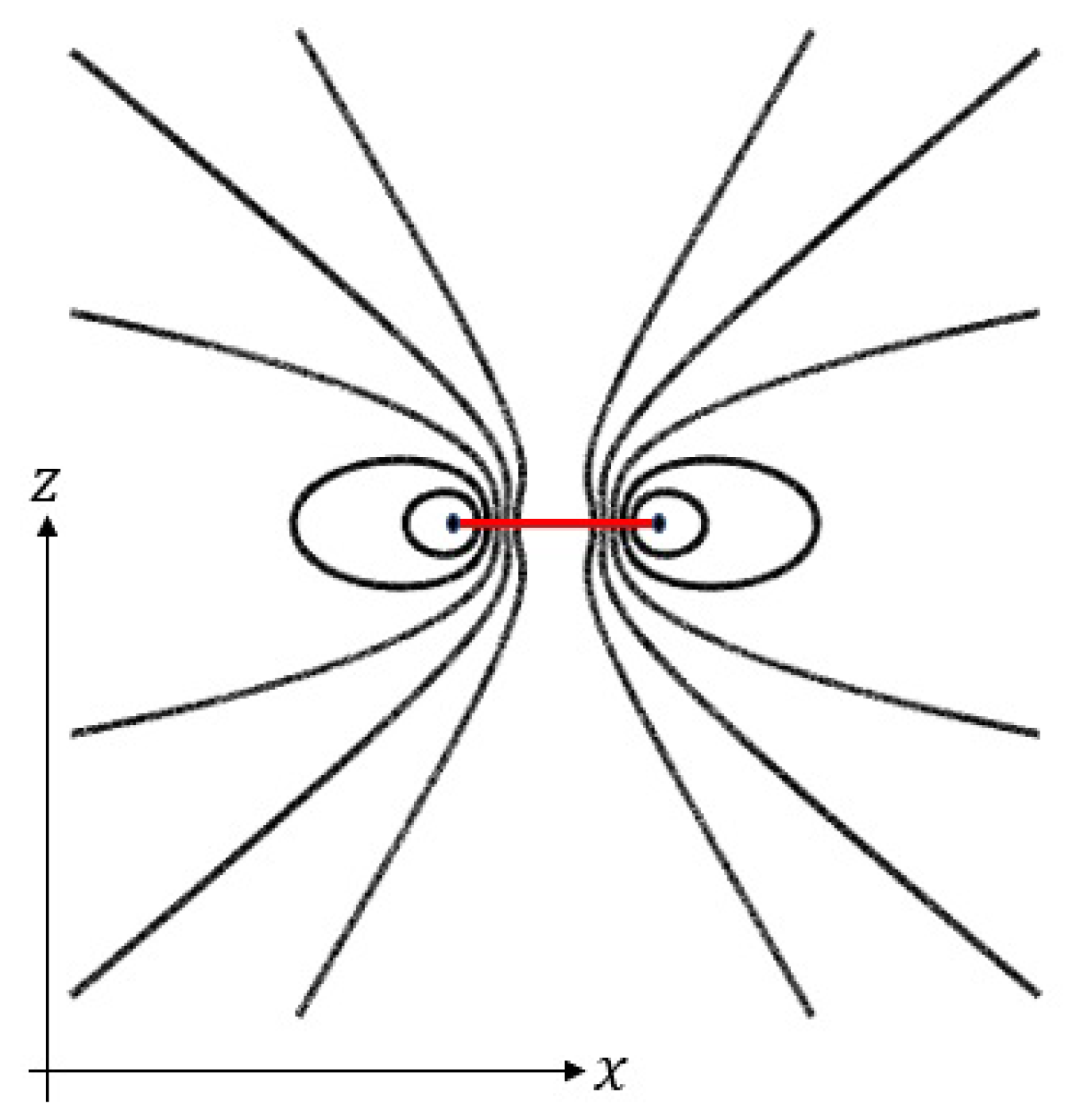
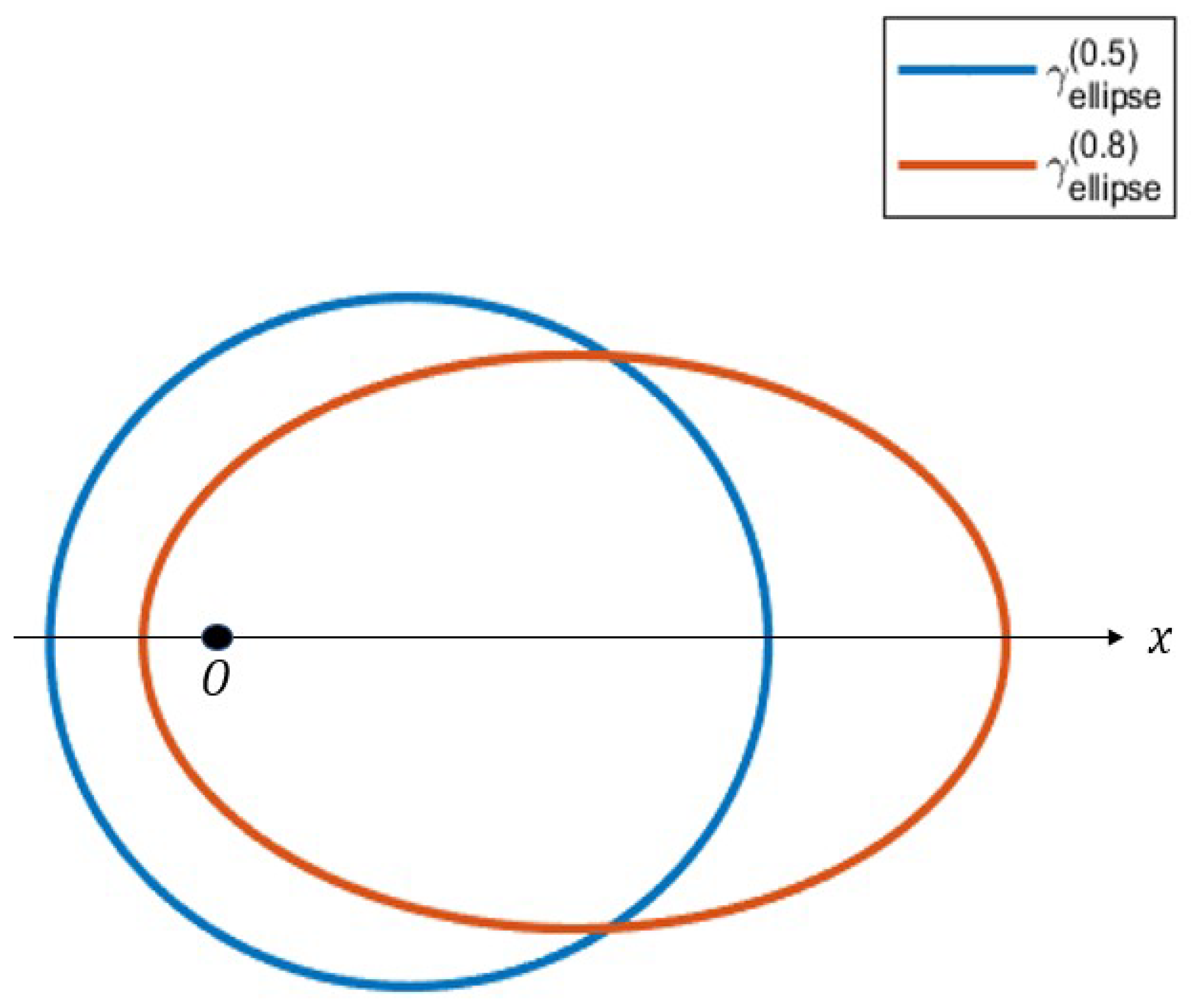
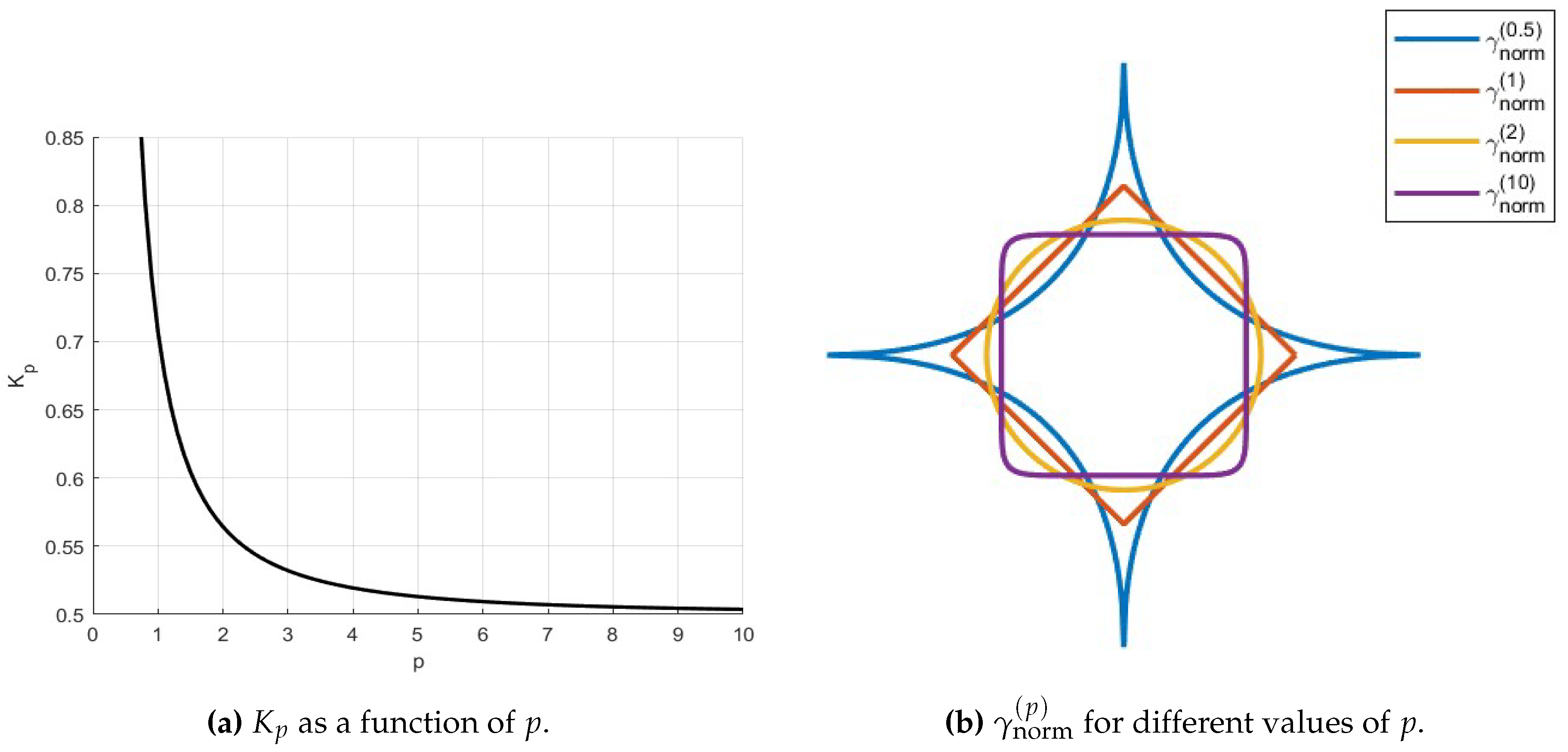
3. Current loop to ideal magnetic dipole
3.1. Circular loop
3.2. Arbitrary loop
4. Discussions
References
- H. C. Ørsted, “Experiments on the effect of a current of electricity on the magnetic needles”, Annals of Philosophy 16:273, 1820.
- Brian Baigrie, Electricity and Magnetism: A Historical Perspective (Greenwood Press, 2007), pp. 7–8.
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Coding for Asymmetric Channels and Channels with State”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1367–1372, 2021. [CrossRef]
- Étienne Du Trémolet de Lacheisserie, Damien Gignoux, and Michel Schlenker, Magnetism: Fundamentals (Springer, 2005), pp. 3–6.
- G. A. G. Bennet, Electricity and Modern Physics (2nd Ed.) (UK:Edward Arnold, 1974).
- James Clerk Maxwell, On Physical Lines of Force (New York: Dover Publications, 1890). [CrossRef]
- Shouvik Ganguly and Young-Han Kim, “Capacity Scaling for Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1472–1476, 2019. [CrossRef]
- James Clerk Maxwell, “A dynamical theory of the electromagnetic field”, Philosophical Transactions of the Royal Society of London, 155, pp. 459–512, 1865. [CrossRef]
- Damian, P. Hampshire, “A derivation of Maxwell’s equations using the Heaviside notation”, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences 376(2134), 2018. [CrossRef]
- Herbert Goldstein, Classical Mechanics (2nd ed.) (Addison–Wesley Publishing Co., 1980), Chap. 7: “Special Relativity in Classical Mechanics”.
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Coding for Network Communication”, IEEE Trans. Inf. Theory (early access), doi 10.1109/TIT.2023.3323839, 2023. [CrossRef]
- Albert Einstein, Relativity: The Special and the General Theory: Reprint of 1920 translation by Robert W. Lawson ed. (Routledge, 2001). [CrossRef]
- Roald, K. Wangsness, Electromagnetic Fields (2nd Ed.) (New York:Wiley, 1986).
- Harvey R. Brown, “The origins of length contraction–I: the FitzGerald-Lorentz deformation hypothesis”, Amer. Journ. Phys. 69(10), pp. 1044–1054, 2001. [CrossRef]
- Shaul Katzir, “Poincaré’s Relativistic Physics: Its Origins and Nature”, Phys. Perspect. 7(3), pp. 268–292, 2005. [CrossRef]
- S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Nonparametric Sequential Detection”, Proceedings of the National Conference on Communications (NCC), India, pp. 1–6, 2014. [CrossRef]
- Charles Coulston Gillispie, The Edge of Objectivity: An Essay in the History of Scientific Ideas (Princeton University Press, 1960), p. 408. [CrossRef]
- Jakob Laub, “Über die experimentellen Grundlagen des Relativitätsprinzips”, Jahrbuch der Radioaktivität und Elektronik 7, pp. 405–463, 1960.
- David Mattingly, “Modern Tests of Lorentz Invariance”, Living Rev. Relativ. 8(3):5, 2005. [CrossRef]
- Ch. Eisele, A. Yu. Nevsky, and S. Schillerv, “Laboratory Test of the Isotropy of Light Propagation at the 10-17 level”, Phys. Review Lett. 103(9):090401, 2009. [CrossRef]
- Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Functional Construction of Codes for Multiple Access and Broadcast Channels”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1581–1586, 2020. [CrossRef]
- Albert A. Michelson and Edward W. Morley, “On the Relative Motion of the Earth and the Luminiferous Ether”, Amer. Journ. Science 34(203), pp. 333–345, 1887. [CrossRef]
- B. P. Abbott et al. (LIGO Scientific Collaboration and Virgo Collaboration), “GW151226: Observation of Gravitational Waves from a 22-Solar-Mass Binary Black Hole Coalescence”, Phys. Rev. Lett. 116(24):241103, 2016. [CrossRef]
- T. S. Jaseja, A. Javan, J. Murray, and C. H. Townes, “Test of Special Relativity or of the Isotropy of Space by Use of Infrared Masers”, Phys. Rev. 133(5a), pp. 1221–1225, 1964. [CrossRef]
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Lossy Source Coding”, Proceedings of the 17th Canadian Workshop on Information Theory (CWIT), pp. 45–50, 2022. [CrossRef]
- S. Chowla and A. Selberg, “On Epstein’s Zeta Function (I)”, Proceedings of the National Academy of Sciences 35(7):373, 1949. [CrossRef]
- R. C. Gupta, “The Madhava–Gregory series”, The Mathematics Education 7, pp. B67–B70, 1973.
- H. L. Royden, Real Analysis (Prentice Hall, 1988).
- Murray H. Protter and Charles B. Morrey, Jr., Intermediate Calculus (2nd Ed.) (New York: Springer, 1985), pp. 421–426.
- Shouvik Ganguly and Lele Wang, “Sliding-Window Gelfand–Pinsker Coding: General K-User Broadcast Channels”, Proceedings of the IEEE Information Theory Workshop (ITW), pp. 1–5, 2020. [CrossRef]
- A. E. Taylor, “L’Hospital’s rule”, Amer. Math. Monthly 59(1), pp. 20–24, 1952.
- David J. Griffiths, Introduction to Electrodynamics (Boston:Pearson, 2013).
- Shouvik Ganguly and Young-Han Kim, “On the Capacity of Cloud Radio Access Networks”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 2063–2067, 2017. [CrossRef]
- J. D. Jackson, Classical Electrodynamics (3rd ed.) (New York:Wiley, 1999).
- John W. Morgan, “Recent progress on the Poincaré conjecture and the classification of 3-manifolds”, Bull. Amer. Math. Soc. (N.S.) 42(1), pp. 57–78, 2005.
- Jongha Jon Ryu, Shouvik Ganguly, Young-Han Kim, Yung-Kyun Noh, and Daniel D. Lee, “Nearest Neighbor Density Functional Estimation based on Inverse Laplace Transform”, IEEE Trans. Inf. Theory 68(6), pp. 3511–3551, June 2022. [CrossRef]
- Tai L. Chow, Introduction to electromagnetic theory: a modern perspective (Jones & Bartlett Learning, 2006).
- E. W. Lee, Magnetism, An Introductory Survey (Dover Publications Inc., 1970).
- Richard P. Feynman, “Space–Time Approach to Quantum Electrodynamics”, Phys. Rev. 76(6), pp. 769–789, 1949.
- Shouvik Ganguly, Seung-Eun Hong, and Young-Han Kim, “On the Capacity Regions of Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, IEEE Trans. Inf. Theory 67(5), pp. 2958–2988, May 2021. [CrossRef]
- R. Courant and D. Hilbert, “Methods of Mathematical Physics”, Interscience, New York, 1966.
- C. Castelnovo, R. Moessner, and S. L. Sondhi, “Magnetic monopoles in spin ice”, Nature 451(7174), pp. 42–45, 2008. [CrossRef]
- Xiao-Gang Wen and Edward Witten, “Electric and magnetic charges in superstring models”, Nuclear Phys. B 261, pp. 651–677, 1985. [CrossRef]
- S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Distributed Nonparametric Sequential Detection”, Proceedings of the IEEE International Conference on Communications (ICC), pp. 1409–1415, 2014. [CrossRef]
- M. W. Ray, E. Ruokokoski, S. Kandel, M. Möttönen, and D. S. Hall, “Observation of Dirac monopoles in a synthetic magnetic field”, Nature 505(7485), pp. 657–660, 2014. [CrossRef]
- Erwin Kreyszig, Advanced Engineering Mathematics (3rd ed.) (New York: Wiley, 1972). [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




