Prerpints.org logo
Preprint
Article

Network Inference from Cancer and Epithelial Cell Co-Culture Reveal Microenvironmental Configurations That Drives Population Dynamics

Altmetrics

Downloads

325

Views

477

Comments

0

Submitted:

23 October 2023

Posted:

25 October 2023

Read the latest preprint version here

Alerts
Abstract
Cellular Automata and Boolean Networks are generalizations of one another because algorithms to compute the preimage of cellular automata reveal the underlying network, i.e., the global dynamics in terms of the basins of attraction. Therefore, we hypothesize we can reveal the local dynamics of cellular automata from the basin of attraction of an inferred boolean network. Our motivation was the observation that human keratinocytes and melanoma can stick together to form clusters after eight days in co-culture. This cluster formation would be the attractor of population dynamics, and cell seeding would be the initial condition of the basin of attraction. Hence, we propose a method to estimate the rules of cellular automata, which consist of comparing the density states within each state transition and reaching a consensus among state transitions belonging to a basin of attraction. Therefore, we aim: (1) to infer a boolean network from the \emph{in vitro} co-culture growth curve; (2) to estimate the rules of cellular automata; and (3) to implement a cellular automata for spatial dynamics simulations. The binarization of the growth curve shows high population density after four days; the estimated cellular automata rules were compatible with cell proliferation and migration in agreement with experimental observations. Spatial dynamics shows that: (1) keratinocytes exhibit higher density in neighborhoods where melanoma is present; (2) the chance of keratinocyte migration increases until the fourth day, but the probability of survival increases; and (3) space is freed for cells with maximum proliferation capacity through proliferation compensated by death. Our approach suggests that the attractor state of cell co-culture would be induced by an increase in keratinocyte migration and survival, as well as the balance of proliferation and death concerning melanoma. Our approach has the potential to offer valuable clues about microenvironmental interactions or configurations that drive population dynamics.
Keywords: 
Subject: Computer Science and Mathematics  -   Mathematical and Computational Biology

1. Introduction

In cells co-culture experiments, after eight days, keratinocytes surround the melanoma clusters, limiting the growth of the melanoma cells. To be more specific, the keratinocytes are denser near the melanoma clusters and less dense farther away [1]. It’s interesting that when keratinocytes are cultured with melanoma, they become less differentiated and connect with the melanoma instead of other keratinocytes nearby [2] [3]. These observations may explain biologically the different levels of tolerance to high density, which is called allelophilia, between melanoma and keratinocytes [1].
As in concepts about discrete dynamic system modeling, this spatial characteristic observed on the eighth day of the experiment would correspond to an equilibrium state or attractor of the population dynamics. Conversely, the initial distribution of cells on the cell culture plate would be the initial condition of the basin of attraction. Thus, the system moves from the initial condition towards its attractor through state transitions like proliferation, migration, survival, and cell death, etc, causing changes in the spatial pattern of the population.
Herein, discrete dynamic system modeling approaches enables the modeling and analysis of the mechanisms governing the regulation of population density. Cellular Automata (CA) is a computational model where the cells are placed on the lattice and the state of each cell is updated at time t + 1 , based on logical rules that consider the state of the neighborhood cells at time t such that the outcome is the emergence of spatial patterns at any given moment [4] [5] [6]. Boolean networks (BN), in turn, are models commonly used in gene expression or signaling pathway studies. They consist of a collection of variables (the nodes), with binary states determined by other variables in the network through Boolean functions [7] [8]. There are algorithms that calculate the preimage of the CA trajectory in a backward direction, thereby unveiling the network of CA dynamics also called global dynamics [9][10]. For this reasons, CA and BN are considered instances of discrete dynamical systems composed of parallel-acting components [10,11]. The dynamics of both are driven by transition functions that determine the state transitions culminating in the system’s trajectory which is a path within the basin of attraction. Hence, CA are generalizations of BN one another in terms of basins of attraction [9,10,11,12,13,14,15].
The Square-Lattice Cellular Automata (SLCA) and a two-dimensional version of Elementary Cellular Automata (ECA) has been successfully used to simulate avascular and vascular tumor growth [16,17,18,19,20,21,22,23] and invasion [24,25,26,27], tumor interactions with environmental cues [28,29,30,31,32,33,34], stromal composition [34,35,36,37,38] and tissue architecture [39,40,41,42]. Similarly, BN has been applied in many fields, including quantitative System Pharmacology [43], competition in microbiome [44], stability of apoptosis [45,46], epithelial-mesenchymal transition [47] and target therapy [48].
Here, we argue that once one can find the global dynamics of an CA in terms of basin of attraction, through an inferred boolean network (IBN) basin of attraction, one could discover the local dynamics of a CA to model a given population dynamic. The primary dimensional unit in a cell culture plate is the cell density ( c e l l s / m m 2 ), and one can qualitatively characterize it as "high" or "low," like the confluence in cell plate culture. Given that CA dynamics are based on logical rules about the configuration of neighborhoods, the changing of these qualitative density states ("low" or "high") in the IBN basin of attraction could be the substrate for estimating CA rules. Given the above we aim (1) to infer a BN from the growth curve time series obtained from in vitro co-culture, (2) to estimate the rules of CA dynamics from the IBN basin of attraction by comparing the density states within each state transition and reaching a consensus among state transitions, and (3) to implement a CA to simulate spatial dynamics.
We observed that the binarization of the time series points to a high population density after the fourth day. The IBN functions let us choose a regulator for each node that is supported by the literature, and the CA rules estimated from the IBN basin suggest a condition for cells to migrate or proliferate that is consistent with what has been seen experimentally [1][3]. The migration of keratinocytes increases smoothly until the fourth day of the simulation, making them denser near melanoma clusters and limiting melanoma proliferation, so that the melanoma survival probability curve shape looks like a normal distribution depending on the proliferation capacity. Therefore, the simulation suggests that the attractor state of cell co-culture population dynamics would be induced by an increase in keratinocyte migration and survival, as well as the balance of proliferation and death concerning melanoma.

2. Material and Methods

In this section, we present the methodological approach used for data inference and modeling. We shall highlight that the modeling process is contingent upon the outcomes derived from the inference. Figure 1 illustrates the workflow for data analysis and modeling. The source code link can be found at S5 Source code.

2.1. Experimental Data

We use previously published cell proliferation data measured in co-culture [1]. The data are the density ( c e l l s / m m 2 ) of normal human keratinocytes (HaCaT), metastatic melanoma (SK-MEL-147), at co-culture with the initial proportion of 1:10 (SK-MEL-147:HaCaT) [49] measured along 8 days in triplicate. To quantify the cell density necessary to achieve the carrying capacity, we introduced the variable S to express the difference between the carrying capacity (K) and the population density at each specific time point. This additional variable is justified because the space has a significant impact on the population dynamics. Hence, the more cells need to reach carrying capacity, less space is available, and the fewer cells need to reach carrying capacity, more space is available. Consequently, this variable serves as an initial arithmetic approximation of the space availability. Throughout this paper T will represent melanoma, H keratinocyte, and S space availability.

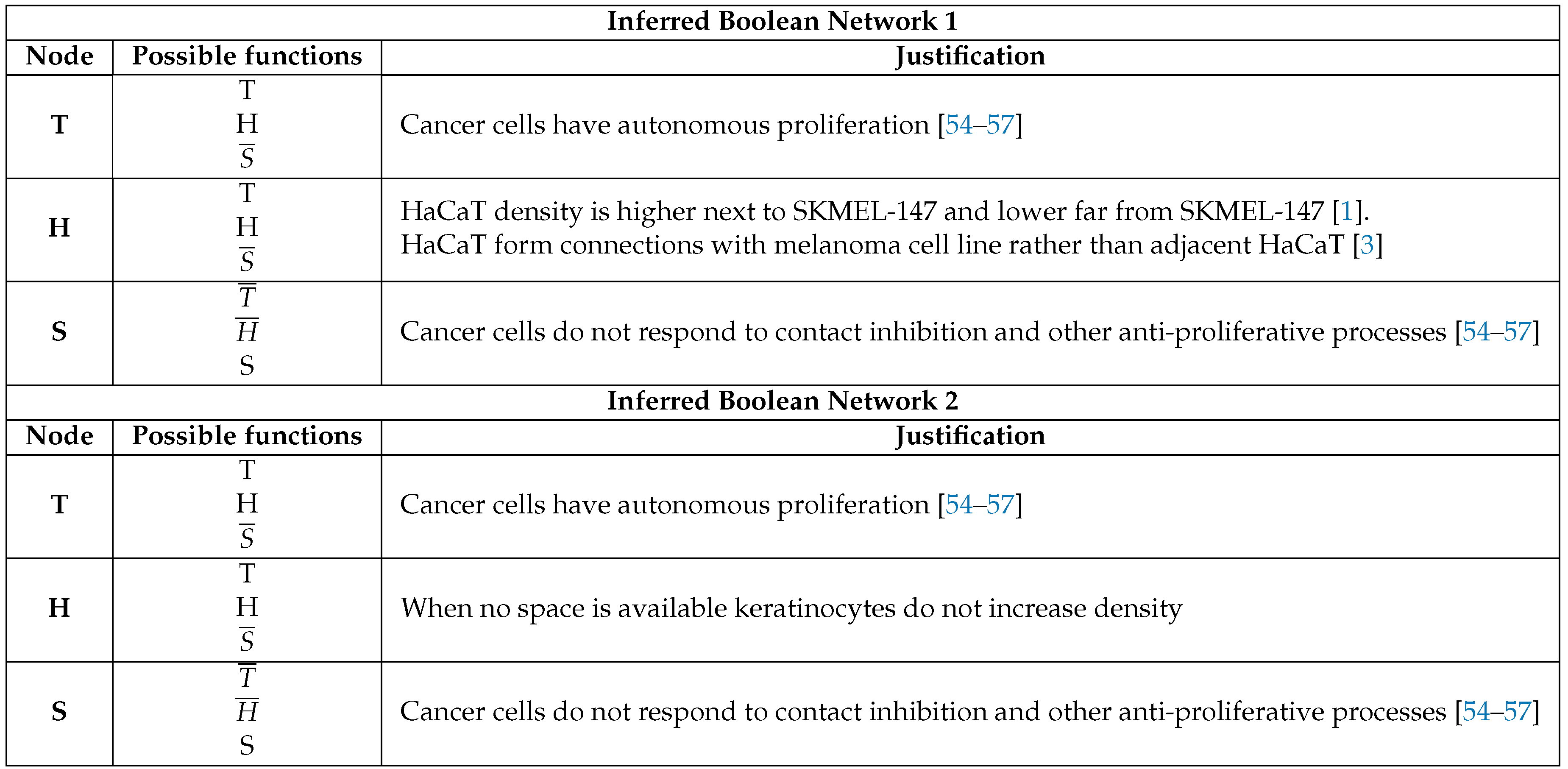
2.2. Boolean Network Inference

BN inference involves two steps: 1) binarization, which transforms cell counts per day in binary discrete data, and 2) network learning. We evaluated three different binarization methods: (1) k-means, (2) iterative k-means [50] [44] and (3) BASC [51]. The binarization outcome chosen to network learning shall be the one which point highest density after confluence onset in agreement with Morais et al [1]. We used BoolNet 2.1.8 from R 4.2 [52] to implement the binarization by BASC and k-means, and Python 3.10.2 to implement the binarization by iterative k-means, adapted from Steinway et al [44]. In the context of this work, the number 0 denotes low density, and the number 1 denotes high density. We performed BN learning using the BestFit algorithm [53] through the BoolNet package 2.1.8 from R 4.2 [52].

2.3. Estimating the Cellular Automata Dynamic Rules from BN Basins through Consensus of State Transition Comparison

Here propose a simple method to estimate CA rules from BN basin of attraction. The proposed approach involves three steps. First, we compare the density states among variables within all individual transition belonging to a given basin of attraction. Second, we obtain a consensus of all comparison among state transitions. For instance, while analyzing six state transitions, it is observed that a specific variable A = 1 and variable B = 0 ( A ≥ B ) in three of them, while A = 0 and B = 1 ( A ≤ B ) in one of them, and A = 0 and B = 0 ( A = B ) in two of them. The most observed inequalities are A ≥ B and A = B , and we define the CA rule as A ≥ B . We determine absence of regulation between variables when >, = and <, have the same frequencies such in case.

2.4. Implementation of Square-Lattice Cellular Automata

The Square-Lattice Cellular Automata (SLCA) was built based on the estimation of CA dynamic rules from the BN basin (Figure 1). The model consists of a tissue scale, resulting in a single discrete variable, namely the cells. The model encompasses a dynamic process involving cell proliferation, death, migration, and survival. This process runs on a two-dimensional lattice ( n × n with n = 200). The criteria for determining lattice size was based on the spatial model developed by Morais et al [1]. Each vertex can accommodate only one tumor cell. During each iteration, all cells undergo the actions outlined in Figure 5. The cells were randomly distributed over the lattice in a ratio of 1 T to 10 H according to [1]. We assume a time-step of 12 hours resulting in a total of 16 iteration, corresponding to 8 days-culture, for each simulation. Section 3.3 describes in detail the state transition rules.

2.5. Spatial Configuration, Parameter Estimation, and Population Dynamics Process Probabilities

We applied a convolutional Gaussian filter of size k = 5 × 5 and standard deviation σ 2 to estimate the relative local density of H cells (arbitrary units) in the simulation domain. To calculate the growth curve of both cell lines we fitted the logistic model (Eq. 1) using the curve fit function of the optimize module of the Scipy library (version 1.7.1) in Python (version 3.10.2)
N ( t ) = K 1 − e − ρ ( t − τ ) ,
where K denotes carrying capacity, ρ denotes proliferation rates and τ denotes time for half asymptote.
Throughout the simulations, we calculate the probability of the cells going through those tumor growth dynamic processes described in Section 2.4. Denote i = 1 , . . . , n as an element of the list ω = (Proliferation, Death, Migration, Survive) and f the frequency of occurrence of one of the processes in the list ω , thus
P r ( ω i ) = f ω i ∑ i = 1 n f ω i ,
for both T and H.

3. Results

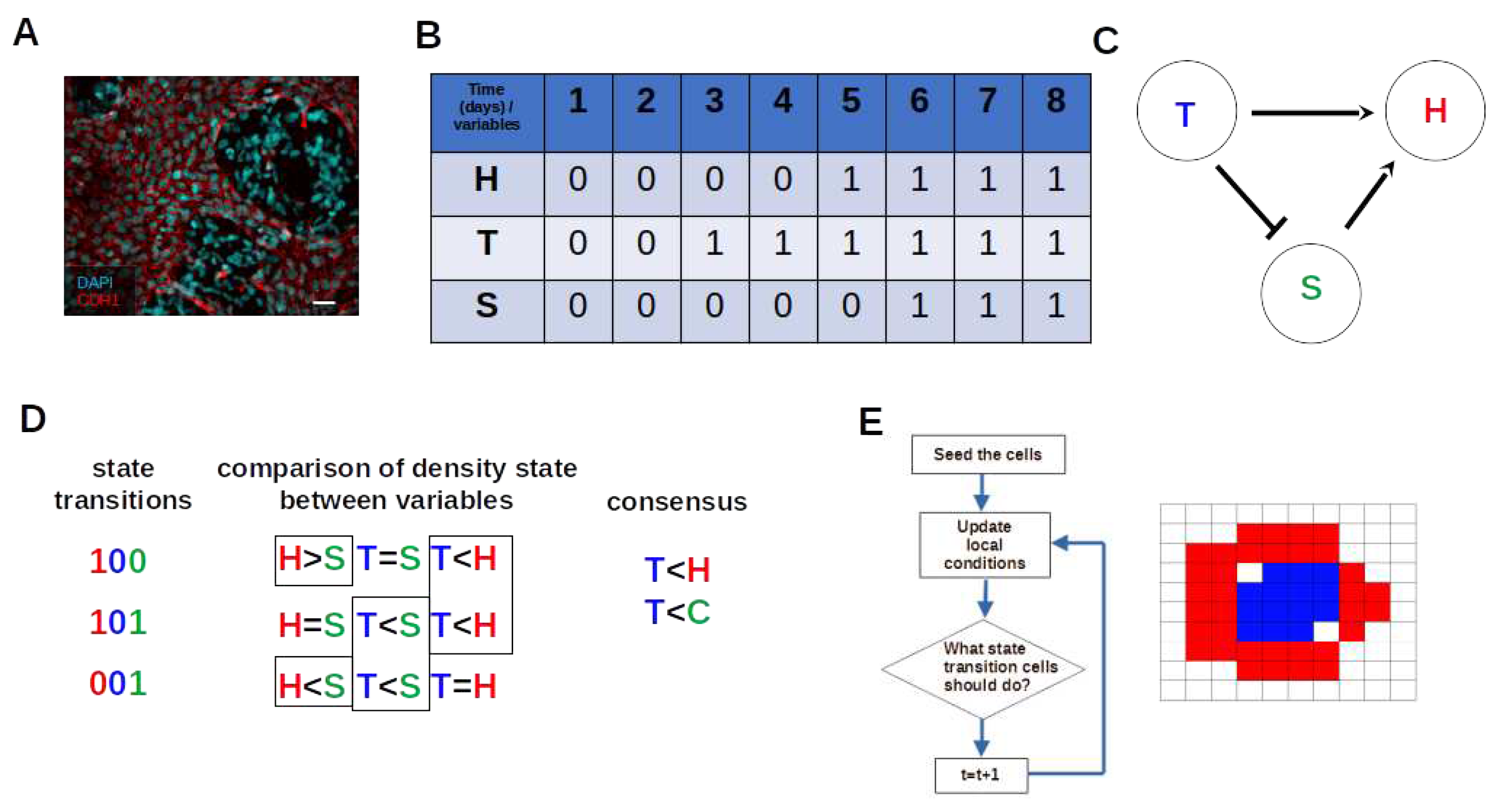
3.1. The Iterative k-Means Binarization Method Demonstrated That Both Populations Are in High Density after 4 Days

As described in Section 2.2, the time series was binarized, and then we learned a BN. The binarization by iterative k-means showed a high density of H and T and a low availability of S, after four days (Figure 1 and in S1 Figure).
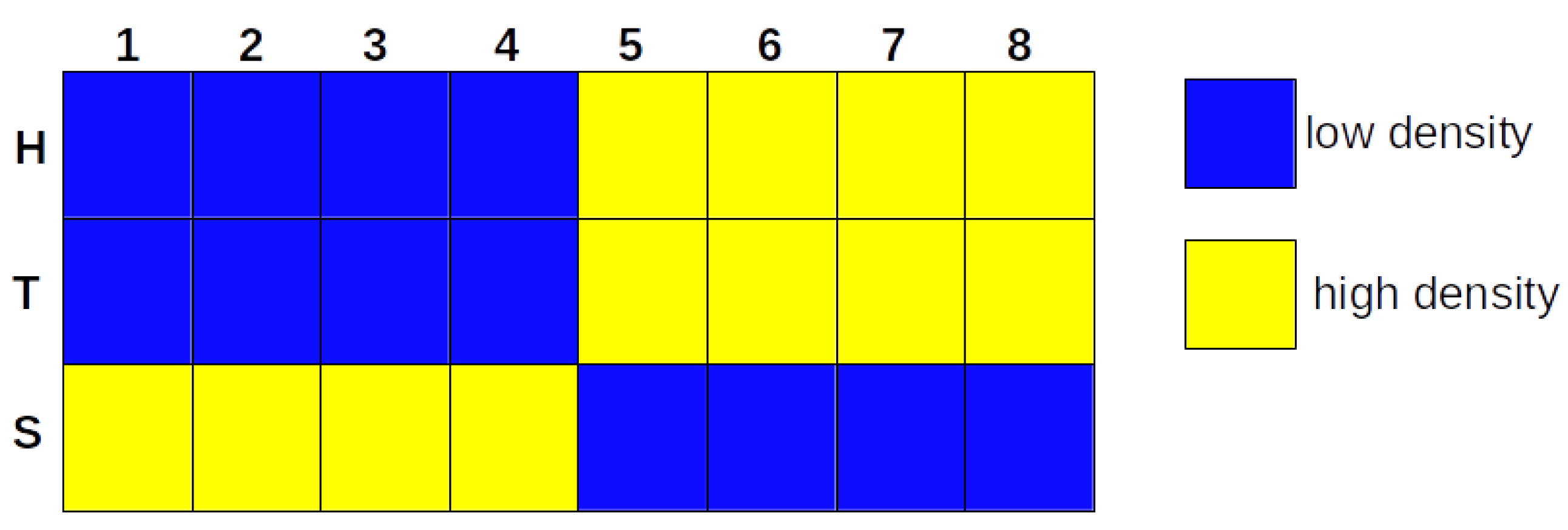
Preprints 88563 g002
Figure 2. The heatmap represents the binarization of co-culture time series by iterative k-means. The yellow cells represent 1, which means high density, and the blue cells represent 0, which means low density. Each row represents the binarized trajectories of H, T, and S, and each column represents the state transition of the network over eight days.
Figure 2. The heatmap represents the binarization of co-culture time series by iterative k-means. The yellow cells represent 1, which means high density, and the blue cells represent 0, which means low density. Each row represents the binarized trajectories of H, T, and S, and each column represents the state transition of the network over eight days.
Preprints 88563 g002
Table 1 shows the possible Boolean functions for each variable. The possible function for each variable is highlighted in yellow with its justification. The intention of showing two different biologically reasonable networks would be to ascertain possible plasticity in the estimated rules for CA as the BN basin topologies change once a BN has 2 n possible state transitions, here n=3 (H, T, and S).

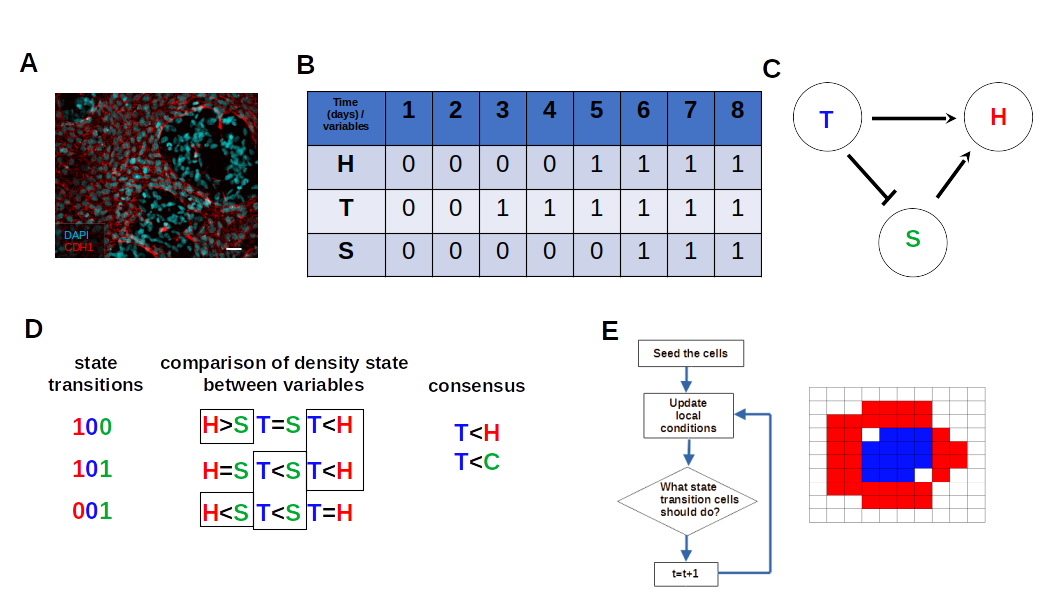
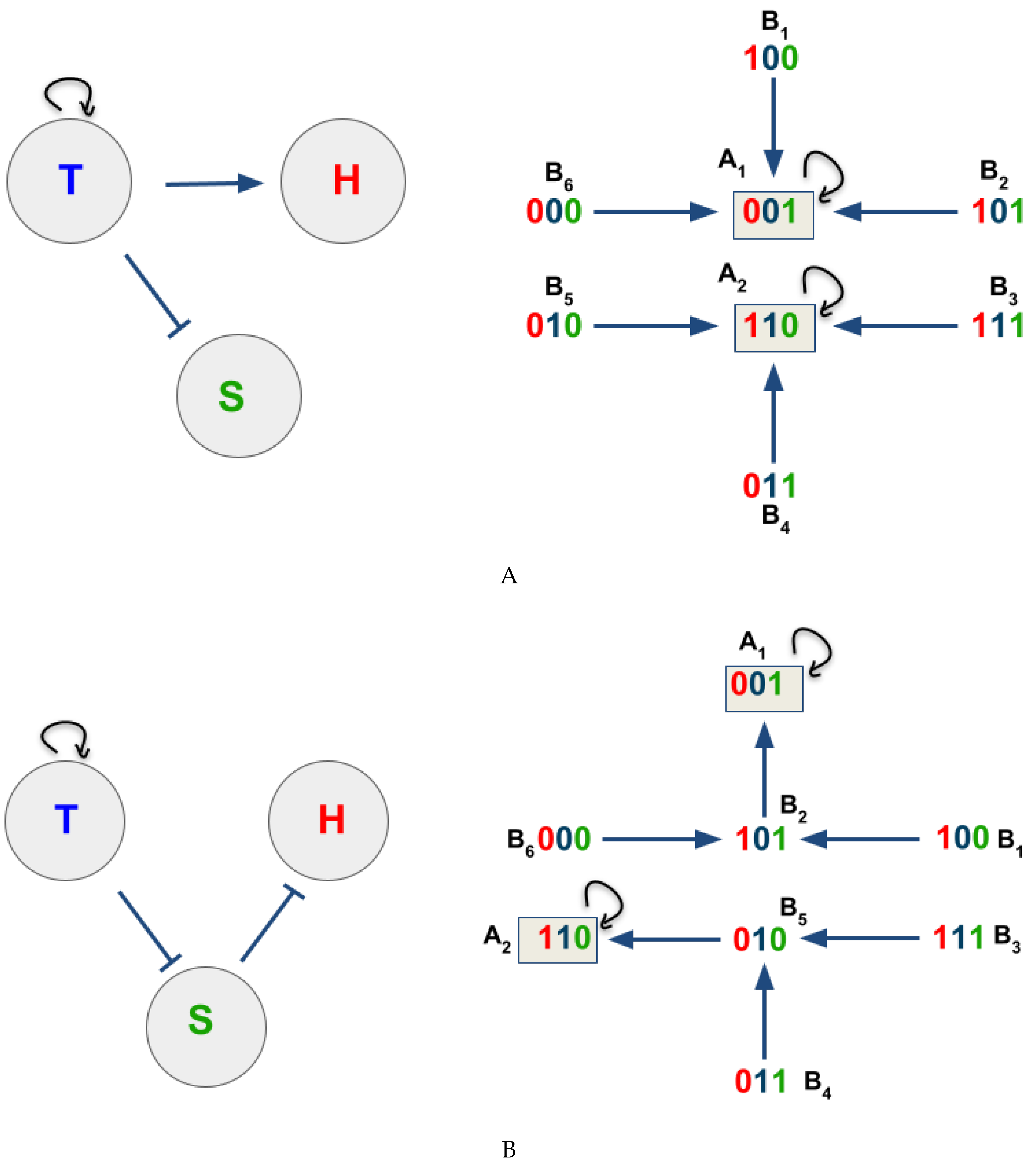
3.2. The Network Dynamics Exhibit Two Singleton Attractors

After we binarized the time series and applied a method of network learning, we generated the state graph, and observed two singletons (fix points) attractors in both IBN 1 (Figure 3A) and 2 (Figure 3B). Before evaluating the attractors and proceeding with the estimation of CA dynamics rules, we labeled each transition state as B 1 , B 2 , B 3 , B 4 , B 5 , B 6 , A 1 , A 2 . These IDs belongs to the same state transition in both IBN 1 and 2. The attractor A 1 shows T and H in low density, while S is in high density, which ultimately means high space availability or the population is scattered. The attractor A 2 shows H and T in high density and S in low density, which ultimately means low space availability or that the population is in high density. The IBN 1 has no predecessor state transition from initial condition among basins of attraction, while the IBN 2 present an small sequence of state transition not.

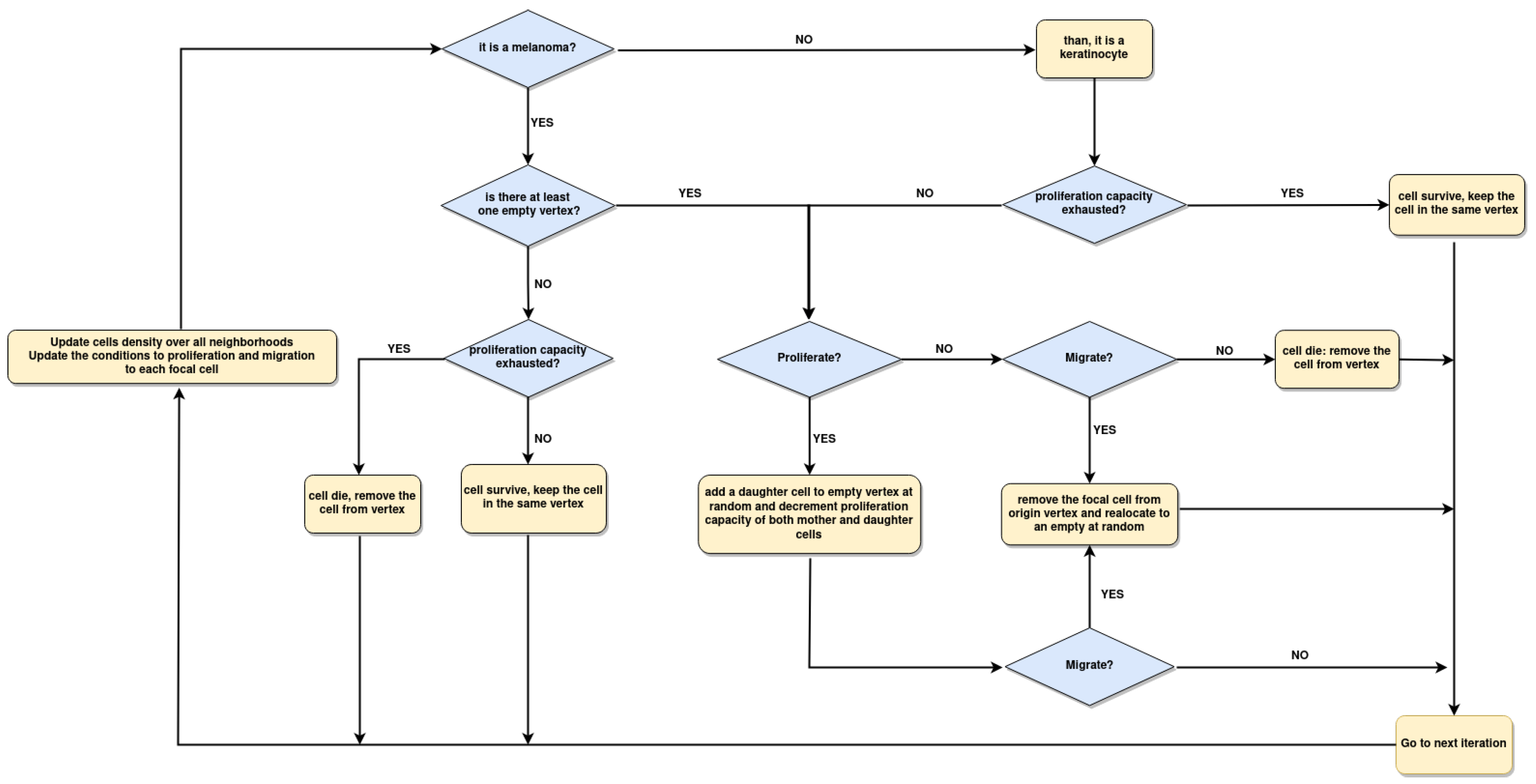
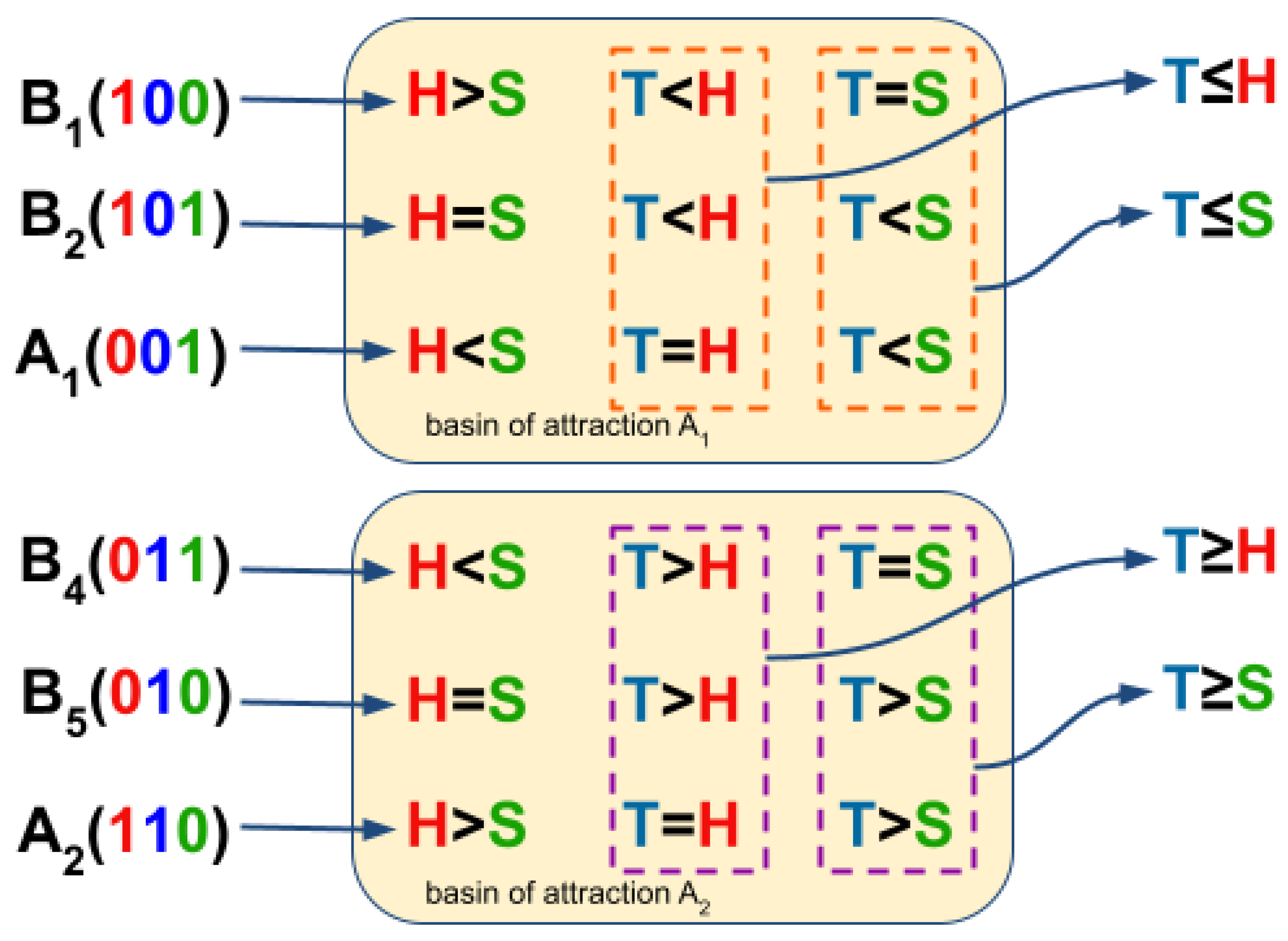
3.3. Boolean Network Basin Provide Cellular Automata Dynamic Rules for Proliferation and Migration

To estimate the CA dynamic rules from BN basins, we analyze the state transitions in terms of density comparison. We ignore the state transitions that do not have a reasonable biological meaning. B 3 presents a low cell density and low space availability, and B 6 presents a high cell density and high space availability. When we compare the density states between T and S among state transitions B 1 , B 2 , and A 1 , T < S in two-thirds of these state transitions (orange-dash rectangle at Figure 4). Additionally, T < H in 2/3 of the aforementioned state transitions (orange-dash rectangle at Figure 4). Thus, from the consensus of the density state comparisons among these state transitions, we obtained two inequalities: T ≤ S and T ≤ H (Figure 4). In contrast, upon comparing the density states between T and S among transition states B 4 , B 5 , and A 2 , T ≥ S in two-thirds of these state transitions (purple-dash rectangle at Figure 4). Furthermore, T ≥ H in 2/3 of those state transitions (purple-dash rectangle at Figure 4), so by consensus among these state transitions, we obtained two new inequalities: T ≥ S and T ≥ H (Figure 4).
The inequalities T ≤ S and T ≤ H represent a condition in which there is a low amount of T and a high amount of H or S, which do not favor an increase in density, and according to [3], we determine that it favors migration. Thus, we set eq. 3 where M T , H denotes migration.
M T , H = ( T ≤ S ) ∨ ( T ≤ H )
The inequalities T ≥ S and T ≥ H represent a condition where a higher density of T and a lower density H or S, favors density increase. Thus, P T and P H denotes proliferation of T and H in equations 4 and 5, respectively. Due to the lack of data about the resources present in the cell culture media, we decided to augment equations 4 and 5 with the probability of instantaneous proliferation 1 − N K [58], since the logistic model fitted to the growth curves present in Morais et al [1]. If the probability of instantaneous proliferation is satisfied ( 1 − N K ≥ r , where r is a random number) then the cells can proliferate. Another important condition to simulate cell dynamics is cell death, represented by the death term D ¯ T in eq. 4 and 5, and the survive term S V ¯ H that blocks H cell proliferation, as explained in Section 3.4.
P H = 1 − N K ∨ ( ( T ≥ S ) ∨ ( T ≥ H ) ) ∧ S V ¯ H
P T = 1 − N K ∨ ( ( T ≥ S ) ∨ ( T ≥ H ) ) ∧ D ¯ T

3.4. Data from Cell Lines and Growth Curves Allow us to Propose a Simple Rule to Describe Survival and Death Dynamics

Here, we only could estimate CA rules that are compatible with migration and proliferation. So to describe the survival and death of cells, we turn to Hayflick’s limit [59,60,61] concept to H and cancer stem cell hypothesis [62,63,64,65,66,67] to T because both can embrace the so-called parameter proliferation capacity ( ρ m a x ). Thus, with each cell division, the proliferation capacity of T and H will decrease by one unit, ρ m a x = ρ m a x − 1 . It is well documented that H undergoes a limited number of duplications in the cell culture plate and does not always reach 100% confluence; thus, once H reaches ρ m a x = 0 , they survive ( S V H ), as proposed in eq. 6. We assume that when T reaches ρ m a x = 0 and in circumstances where there is no space ( D T ), the crowding situations might yield cell de-adherence and death [68], as in eq. 7.
S V H = ρ m a x = 0
D T = ρ m a x = 0 ∧ S = 0
Once H does not migrate, proliferate, or survive, they die, as in eq. 8. Alternately, once T does not migrate, proliferate, and die, they survive, eq. 9.
D H = M ¯ H ∧ P ¯ H ∧ S V ¯ H
S V T = M ¯ T ∧ D ¯ T ∧ P ¯ T
Preprints 88563 g005
Figure 5. Flowchart of the CA implementation. First, we set the initial density of cells and a random initial distribution of them over Lattice. At each iteration, the algorithm updates the amount of T, H, and empty vertex (S) in all focal cell neighborhoods. The conditions described in eqs. 3 to 9 are updated in each cell. When there is at least one empty vertex, the cells proliferate or migrate, but when the proliferation capacity is exhausted, the cells survive or die.
Figure 5. Flowchart of the CA implementation. First, we set the initial density of cells and a random initial distribution of them over Lattice. At each iteration, the algorithm updates the amount of T, H, and empty vertex (S) in all focal cell neighborhoods. The conditions described in eqs. 3 to 9 are updated in each cell. When there is at least one empty vertex, the cells proliferate or migrate, but when the proliferation capacity is exhausted, the cells survive or die.
Preprints 88563 g005

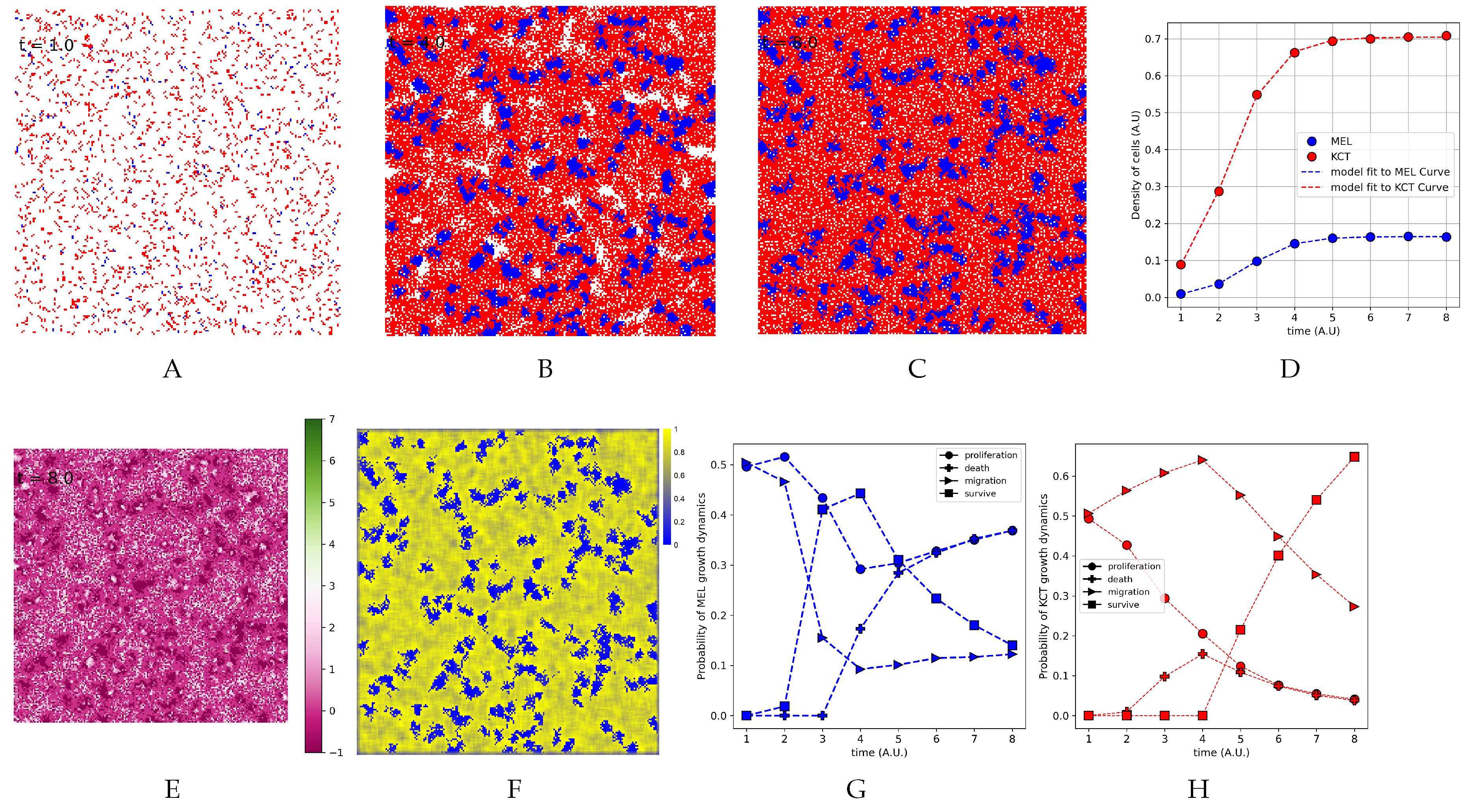
3.5. The Parameter Estimation Are in Agreement with Experimental Data

The values of cells density and the frequency of proliferating, migrating, surviving, and dying cell in the overall simulation were used to evaluate if the growth curve fit to the logistic model (eq. 1). The growth curves fit the logistic model (Figure 6G) and the estimated values for the parameter K, ρ , and τ are presented at Table 2. Considering each iteration as a Δ t = 12 hours favored the estimation of ρ T ≈ ρ H and τ T ≈ τ H . We shall recall that the results in Figure 6 concern ρ m a x T = 7 and ρ m a x H = 6 . According to Morais et al [1] the values estimated to ρ T and ρ H are equal as well those estimated to τ T and τ H .

3.6. The Density of H Indeed is Higher Close to T Cluster

We implemented the spatial model using CA (Section 2.4, Section 3.3 and Section 3.4) and, starting from a given an initial distribution of cells, on the fourth day we can already see some T clusters surrounded by H, so this spatial pattern is consolidated on the eighth day (Figure 6A–C and animation in S3 Video). The heat map shows H density in the neighborhood of each focal cell (Figure 6F) points to higher yellow intensity around T clusters. This can be explained by the smooth increase in H migration probability from the beginning of the simulation (Figure 6H) as well as the increase in T survival probability from day 4 onward (Figure 6G). Therefore, as T clusters consolidate, more of the H neighborhood lacks T; hence the probability of migration decrease mostly because the probability of H survive increase substantially after four days (Figure 6H).
Preprints 88563 g006
Figure 6. The spatial population and tumor growth dynamics. (A), (B), and (C) frames correspond to days 1, 4, and 8. Blue represents T, and red represents H. (D) Growth curves of T and H. E Spatial distribution of the cells according to the values of ρ m a x at day 8. In the bar of color at right, the shades of green to pink represent the ρ m a x values. (F) Heatmap representing H density over all focal cell neighborhoods at day 8. In the bar of color at right, the shades of blue to yellow represent the percentage of occupied vertex by H in all focal cell neighborhoods. (G) Probabilities of T tumor growth dynamics (H) Probabilities of H tumor growth dynamics.
Figure 6. The spatial population and tumor growth dynamics. (A), (B), and (C) frames correspond to days 1, 4, and 8. Blue represents T, and red represents H. (D) Growth curves of T and H. E Spatial distribution of the cells according to the values of ρ m a x at day 8. In the bar of color at right, the shades of green to pink represent the ρ m a x values. (F) Heatmap representing H density over all focal cell neighborhoods at day 8. In the bar of color at right, the shades of blue to yellow represent the percentage of occupied vertex by H in all focal cell neighborhoods. (G) Probabilities of T tumor growth dynamics (H) Probabilities of H tumor growth dynamics.
Preprints 88563 g006

4. Discussion

In this study, we used the time series of the growth curve in the co-culture of T and H to infer a BN. Through BN inference, we were able to determine the boolean functions that led to network dynamics. These dynamics were shown in a state graph, where we arranged the state transitions according to the basin of attraction and estimated the CA rules. These estimated CA rules were biologically sound; hence, they could represent neighborhood or microenvironmental configurations that drive population dynamics toward the attractor state, as mentioned before.
The binarization of the growth curve data reveals that the population attained a high density after 4 days. This observation aligns with the findings of Morais et al [1], who reported that the population achieves confluence after the same 4-day period. The proposed methodology captured the relationship between the confluence observed on the cell culture plate and the corresponding cell density. A boolean network of n nodes exhibits 2 n state transitions; hence, our time series, consisting of a sequence of 8 data points, can fully define the system. The occurrence of non-null error rates in the inferred boolean network arises due to the similarity of the H and T binarized trajectories, also known an identifiability, nevertheless, this issue can be solved by prior biological knowledge or by pruning the network nodes according to the context [43].
The BestFit BN learning paradigm searches for possible boolean functions that describe the state of a given variable (node) at time t + 1 as a function of the network state (the states of all nodes) at time t. In the heatmap (Figure 2), S is ON when both T and H are OFF, and vice versa, which means that S inhibits both T and H, which in turn inhibits S, and finally both T and H can "activate" each other.
The IBN 1 in Table and Table 1 shows a canalizing node and a initial condition with no predecessor state transiton throughout basin of attraction. The IBN 2 in table Table and Figure 3A, on the other hand, shows a small number of states before reaching the attractor. However, both networks (Figure 3A,B) have the same attractor. Hence, different BNs can lead to the same attractors. This indicates that the estimation of CA rules was not affected by changes in the topology of the state graph, suggesting a system plastic capacity, as in the genetic networks [69].
Indeed melanoma affects keratinocytes phenotypes [2] [3], our approach only captured an equilibrium state concerning local density of both melanoma and keratinocyte. By comparing the density states of state transitions B 4 , B 5 , and A 2 , we could estimate the logical sentence ( T ≥ S ) ∨ ( T ≥ H ) , suggesting that T will only proliferate where there is more T, since experiments with model organisms like zebrafish have shown that melanoma tends to cluster [70]. Likewise, we could estimate the logical sentence ( T ≤ S ) ∨ ( T ≤ H ) based on how the density states of states transition B 1 , B 2 , and A 1 , meaning that either H or T will move away [1] [3]. It is worth highlighting that these Boolean expressions can be concurrently satisfied in a dynamic context. So, the potential for cell proliferation and migration is inherently incorporated, which reduces any challenges in modeling associated with the go-or-grow phenomenon [71,72,73,74,75].
The spatial dynamic shows H more denser nearby T clusters than close to themselves (Figure 6A,B); moreover, the values estimated for ρ T , H and τ T , H are very similar, corroborating the results of Morais et al [1] despite the dependence of estimated ρ T , H on the initial condition. The growth curve certainly did not emerge from the dynamics itself, but it is likely hardwired to the instantaneous probability term present in eqs. 5 and 6 that was employed to represent the resources in the culture medium.
We could only estimate CA rules for proliferation and migration, then adopt an intrinsic condition for cells to survive and die. Normal cells like H undergo a limited number of duplications in the cell culture plate and do not always reach 100% confluence because at each duplication the telomeres shorten, yielding to the onset of replicative senescence [59,60,61]. In the case of cancer cells, i.e., T, the telomeres shorten with doublings, and the cells will enter a state of crisis or death. Both normal and cancer cells could die whenever there is no space, because in vitro crowding situations lead some cells to undergo de-adherence and die [68]. Moreover, crowding-induced elimination would facilitate the expansion of the malignant clones [76,77,78,79]. Due to the duration of the in vitro experiment (see Section 2.1), for simplification, we discarded stem cells with ρ m a x = ∞ in the model.
The proliferation capacity parameter ( ρ m a x ) as a measure of T death shows that cells with a lower ρ m a x value tend to be at the edges of the clusters, competing for space with cells with a higher ρ m a x value (Figure 6E). As soon as the cells on the periphery die, the others proliferate and thus decrease their proliferation capacity. In this respect, the ignition of stem cells by space release and/or their capacity to proliferate more than those with no stemness are in agreement with previously published theoretical models [62,63,64,65,66,67], experimental evidence [80], and the amalgamation of experimental data with mathematical modeling [81] [82].
Probably, if we had implemented a Lattice Gas Cellular Automata (LGCA), by considering that proliferating T cells could pile up due to the lack of contact inhibition, T proliferation would naturally be counterbalanced by their death because of mass action in the growth dynamics. Even though we used a simple SLCA, which doesn’t let us include more than one cell per lattice vertex, this makes it harder to include the lack of contact inhibition, which is typical of cancer cells. However, even if cancer cells present a low contact inhibition degree, mechanical factors could restrict their proliferation [83]. The approach using proliferation capacity as a simpler rule to distinguish death from survival allowed us to observe a decrease in the H T density ratio, which we hypothesize to be due to death-induced proliferation (Figure 6G). It is biologically sound because pathways involved in contact inhibition might go through a transition towards the regulation of autophagy, which in turn can yield survival and proliferation [84].
Our results suggest that the inference of BN from the co-culture growth curve time series provides a path to estimate specifics microenvironmental conditions for proliferation and migration in terms of CA dynamic rules, despite the tumor microenvironment being considered a complex regulatory network that shapes tumor architecture and growth law [57,85,86,87,88]. Even though the spatial population dynamics model was made using a mix of estimated data from IBN dynamics and observations from the literature, the results are in line with experimental data. Hitherto, we simulate local dynamics by running the CA forward for space-time patterns and this was enough to reach our goals, but as future perspective our approach could be coupled with the software DDLAB (www.ddlab.org) in order to develop a pipeline to evaluate the dynamic upon or on the network [9,10].
Since either model-driven experimentation or data-driven modeling are important ways to improve and integrate mathematical, biological, and clinical models, unraveling CA rules from BN dynamics could be useful to capture any interaction between cells in terms of density patterns and it deserve room for further refinement. This is mainly because a discrete approach can be linked with a continuous one [89,90], and important parameters beyond the local or global dynamics can be estimated. Cell co-culture is an experimental system that can comprise diverse time points, images of spatial features, and different cell types and densities. This makes it much easier to figure out how networks work at the tissue scale, especially when it comes to figuring out how to reconstruct population dynamics.

5. Conclusion

In this work, we introduce a novel approach to cell proliferation dynamics. We present a approach to estimate the rules of the dynamics of a cellular automaton from the basins of attraction of a Boolean network and, also, align them with experimental conditions. By establishing a direct connection between our theoretical model and experimentally observed spatial patterns, we attain a significant milestone in the field of cellular analysis by effectively connecting computation and experimental methods. This modeling approach can make a significant advancement in our ability to comprehend and predict complex biological phenomena.

Supplementary Materials

The following supporting information can be downloaded at the website of this paper posted on Preprints.org

Acknowledgments

We would like to thank NPAD/UFRN for computational resources. MCCM is supported by São Paulo State Research Foundation (FAPESP process n. 2020/12017-9). ASQ thanks Prof. Dr. Roger Chammas, who read the very first version of the article and assured him that the idea was coherent. The authors are thankful for anonymous reviewers whose comments enhanced manuscript’s quality.

References

  1. Morais MCC, Stuhl I, Sabino AU, Lautenschlager WW, Queiroga AS, Tortelli Jr TC, et al. Stochastic model of contact inhibition and the proliferation of melanoma in situ. Sci. Rep. 2017, 7, 8026. [Google Scholar] [CrossRef]
  2. Kodet O, Lacina L, Krejčí E, Dvořánková B, Grim M, Štork J, et al. Melanoma cells influence the differentiation pattern of human epidermal keratinocytes. Mol. Cancer 2015, 14, 1–12. [Google Scholar] [CrossRef]
  3. Mazurkiewicz J, Simiczyjew A, Dratkiewicz E, Kot M, Pietraszek-Gremplewicz K, Wilk D, et al. Melanoma stimulates the proteolytic activity of HaCaT keratinocytes. Cell Commun. Signal. 2022, 20, 1–17. [Google Scholar]
  4. Neumann, JV. Theory of self-reproducing automata. Edited by Arthur W Burks. 1966.
  5. Wolfram, S. Statistical mechanics of cellular automata. Rev. Mod. Phys. 1983, 55, 601. [Google Scholar] [CrossRef]
  6. Wolfram, S. A new kind of science. vol. 5. Wolfram media Champaign, IL; 2002.
  7. Kauffman, S. Homeostasis and differentiation in random genetic control networks. Nature 1969, 224, 177–178. [Google Scholar] [CrossRef]
  8. Bornholdt, S. Boolean network models of cellular regulation: prospects and limitations. Journal of the royal society interface. 2008, 5 (Suppl. 1), S85–S94. [Google Scholar] [CrossRef] [PubMed]
  9. Wuensche A, Lesser M. Global dynamics of cellular automata: An atlas of basin of attraction fields of one-dimensional cellular automata. vol. 1. Colorado: Westview Press; 1992.
  10. Wuensche, A. Exploring discrete dynamics. Luniver Press; 2011.
  11. Wuensche, A. Attractor basins of discrete networks. Cognitive science research paper. 1997;461.
  12. Wuensche, A. The Ghost in the Machine: Basin of Attraction Fields of Disordered Cellular Automata Networks. In: Artificial Life III Conference; 1992.
  13. Wuensche, A. The ghost in the machine: Basins of attraction of random boolean networks. Artificial Life III: SFI Studies in the Sciences of Complexity, vol ëVII Addison-Wesley. 1994.
  14. Jeras I, Dobnikar A. Algorithms for computing preimages of cellular automata configurations. Phys. Nonlinear Phenom. 2007, 233, 95–111. [Google Scholar] [CrossRef]
  15. Soto JMG. Computation of explicit preimages in one-dimensional cellular automata applying the De Bruijn diagram. J. Cell. Autom. 2008, 3, 219–230. [Google Scholar]
  16. Dormann S, Deutsch A. Modeling of self-organized avascular tumor growth with a hybrid cellular automaton. Silico Biol. 2002, 2, 393–406. [Google Scholar]
  17. Spencer SL, Gerety RA, Pienta KJ, Forrest S. Modeling somatic evolution in tumorigenesis. Plos Comput. Biol. 2006, 2, e108. [Google Scholar]
  18. Enderling H, Hlatky L, Hahnfeldt P. Migration rules: tumours are conglomerates of self-metastases. Br. J. Cancer 2009, 100, 1917–1925. [Google Scholar] [CrossRef]
  19. Enderling H, Anderson AR, Chaplain MA, Beheshti A, Hlatky L, Hahnfeldt P. Paradoxical dependencies of tumor dormancy and progression on basic cell kinetics. Cancer Res. 2009, 69, 8814–8821. [Google Scholar] [CrossRef] [PubMed]
  20. Kansal A, Torquato S, Chiocca E, Deisboeck T. Emergence of a subpopulation in a computational model of tumor growth. J. Theor. Biol. 2000, 207, 431–441. [Google Scholar] [CrossRef]
  21. Zhang L, Strouthos CG, Wang Z, Deisboeck TS. Simulating brain tumor heterogeneity with a multiscale agent-based model: linking molecular signatures, phenotypes and expansion rate. Math. Comput. Model. 2009, 49, 307–319. [Google Scholar] [CrossRef] [PubMed]
  22. Wcisło R, Dzwinel W, Yuen DA, Dudek AZ. A 3-D model of tumor progression based on complex automata driven by particle dynamics. J. Mol. Model. 2009, 15, 1517–1539. [Google Scholar] [CrossRef] [PubMed]
  23. Wang Z, Deisboeck TS. Computational modeling of brain tumors: discrete, continuum or hybrid? Scientific modeling and simulations 2009; pp. 381–393.
  24. Anderson AR, Rejniak KA, Gerlee P, Quaranta V. Microenvironment driven invasion: a multiscale multimodel investigation. J. Math. Biol. 2009, 58, 579–624. [Google Scholar] [CrossRef] [PubMed]
  25. Zhang L, Wang Z, Sagotsky JA, Deisboeck TS. Multiscale agent-based cancer modeling. J. Math. Biol. 2009, 58, 545–559. [Google Scholar] [CrossRef] [PubMed]
  26. Anderson, AR. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Math. Med. Biol. J. IMA 2005, 22, 163–186. [Google Scholar] [CrossRef]
  27. Sottoriva A, Verhoeff JJ, Borovski T, McWeeney SK, Naumov L, Medema JP, et al. Cancer stem cell tumor model reveals invasive morphology and increased phenotypical heterogeneity. Cancer Res. 2010, 70, 46–56. [Google Scholar] [CrossRef]
  28. Gatenby RA, Smallbone K, Maini PK, Rose F, Averill J, Nagle RB, et al. Cellular adaptations to hypoxia and acidosis during somatic evolution of breast cancer. Br. J. Cancer 2007, 97, 646–653. [Google Scholar] [CrossRef]
  29. Gerlee P, Anderson A. Evolution of cell motility in an individual-based model of tumour growth. J. Theor. Biol. 2009, 259, 67–83. [Google Scholar] [CrossRef]
  30. Silva AS, Yunes JA, Gillies RJ, Gatenby RA. The potential role of systemic buffers in reducing intratumoral extracellular pH and acid-mediated invasion. Cancer Res. 2009, 69, 2677–2684. [Google Scholar] [CrossRef]
  31. Zhang L, Chen LL, Deisboeck TS. Multi-scale, multi-resolution brain cancer modeling. Math. Comput. Simul. 2009, 79, 2021–2035. [Google Scholar] [CrossRef] [PubMed]
  32. Gerlee P, Anderson AR. A hybrid cellular automaton model of clonal evolution in cancer: the emergence of the glycolytic phenotype. J. Theor. Biol. 2008, 250, 705–722. [Google Scholar] [CrossRef]
  33. Smallbone K, Gatenby RA, Gillies RJ, Maini PK, Gavaghan DJ. Metabolic changes during carcinogenesis: potential impact on invasiveness. J. Theor. Biol. 2007, 244, 703–713. [Google Scholar] [CrossRef] [PubMed]
  34. Anderson AR, Hassanein M, Branch KM, Lu J, Lobdell NA, Maier J, et al. Microenvironmental independence associated with tumor progression. Cancer Res. 2009, 69, 8797–8806. [Google Scholar] [CrossRef] [PubMed]
  35. Anderson AR, Weaver AM, Cummings PT, Quaranta V. Tumor morphology and phenotypic evolution driven by selective pressure from the microenvironment. Cell 2006, 127, 905–915. [Google Scholar] [CrossRef]
  36. Basanta D, Strand DW, Lukner RB, Franco OE, Cliffel DE, Ayala GE, et al. The role of transforming growth factor-β–mediated tumor-stroma interactions in prostate cancer progression: An integrative approach. Cancer Res. 2009, 69, 7111–7120. [Google Scholar] [CrossRef] [PubMed]
  37. de Pillis LG, Mallet DG, Radunskaya AE. Spatial tumor-immune modeling. Comput. Math. Methods Med. 2006, 7, 159–176. [Google Scholar] [CrossRef]
  38. Enderling H, Alexander NR, Clark ES, Branch KM, Estrada L, Crooke C, et al. Dependence of invadopodia function on collagen fiber spacing and cross-linking: computational modeling and experimental evidence. Biophys. J. 2008, 95, 2203–2218. [Google Scholar] [CrossRef]
  39. Bankhead A, Magnuson NS, Heckendorn RB. Cellular automaton simulation examining progenitor hierarchy structure effects on mammary ductal carcinoma in situ. J. Theor. Biol. 2007, 246, 491–498. [Google Scholar] [CrossRef]
  40. Gevertz J, Torquato S. Growing heterogeneous tumors in silico. Phys. Rev. 2009, 80, 51–91. [Google Scholar]
  41. Anderson AR, Basanta D, Gerlee P, Rejniak KA. Evolution, regulation, and disruption of homeostasis, and its role in carcinogenesis. Multiscale cancer modeling. 2011; p. 1–30.
  42. Silva AS, Gatenby RA, Gillies RJ, Yunes JA. A quantitative theoretical model for the development of malignancy in ductal carcinoma in situ. J. Theor. Biol. 2010, 262, 601–613. [Google Scholar] [CrossRef]
  43. Putnins M, Campagne O, Mager D, Androulakis I. From data to QSP models: a pipeline for using Boolean networks for hypothesis inference and dynamic model building. J. Pharmacokinet. Pharmacodyn. 2022, 49, 101–115. [Google Scholar] [CrossRef]
  44. Steinway SN, Biggs MB, Loughran Jr TP, Papin JA, Albert R. Inference of network dynamics and metabolic interactions in the gut microbiome. Plos Comput. Biol. 2015, 11, e1004338. [Google Scholar]
  45. Schlatter R, Schmich K, Avalos Vizcarra I, Scheurich P, Sauter T, Borner C, et al. ON/OFF and beyond-a Boolean model of apoptosis. Plos Comput. Biol. 2009, 5, e1000595. [Google Scholar]
  46. Mai Z, Liu H. Boolean network-based analysis of the apoptosis network: irreversible apoptosis and stable surviving. J. Theor. Biol. 2009, 259, 760–769. [Google Scholar] [CrossRef] [PubMed]
  47. Steinway SN, Zañudo JG, Ding W, Rountree CB, Feith DJ, Loughran Jr TP, et al. Network modeling of TGFβ signaling in hepatocellular carcinoma epithelial-to-mesenchymal transition reveals joint sonic hedgehog and Wnt pathway activation. Cancer Res. 2014, 74, 5963–5977. [Google Scholar] [CrossRef] [PubMed]
  48. Fumia HF, Martins ML. Boolean network model for cancer pathways: predicting carcinogenesis and targeted therapy outcomes. PLoS ONE 2013, 8, e69008. [Google Scholar]
  49. Cichorek M, Wachulska M, Stasiewicz A, Tymińska A. Skin melanocytes: biology and development. Adv. Dermatol. Allergol. 2013, 30, 30–41. [Google Scholar]
  50. Berestovsky N, Nakhleh L. An evaluation of methods for inferring boolean networks from time-series data. PLoS ONE 2013, 8, e66031. [Google Scholar]
  51. Hopfensitz M, Mussel C, Wawra C, Maucher M, Kuhl M, Neumann H, et al. Multiscale binarization of gene expression data for reconstructing Boolean networks. Ieee/Acm Trans. Comput. Biol. Bioinform. 2011, 9, 487–498. [Google Scholar]
  52. Müssel C, Hopfensitz M, Kestler HA. BoolNet—an R package for generation, reconstruction and analysis of Boolean networks. Bioinformatics 2010, 26, 1378–1380. [Google Scholar] [CrossRef]
  53. Lähdesmäki H, Shmulevich I, Yli-Harja O. On learning gene regulatory networks under the Boolean network model. Mach. Learn. 2003, 52, 147–167. [Google Scholar] [CrossRef]
  54. Hanahan D, Weinberg RA. The hallmarks of cancer. Cell 2000, 100, 57–70. [Google Scholar] [CrossRef]
  55. Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell 2011, 144, 646–674.
  56. Weinberg, RA. The biology of cancer. 2013. [Google Scholar]
  57. Hanahan, D. Hallmarks of cancer: new dimensions. Cancer Discov. 2022, 12, 31–46. [Google Scholar] [CrossRef]
  58. Benzekry S, Lamont C, Beheshti A, Tracz A, Ebos JM, Hlatky L, et al. Classical mathematical models for description and prediction of experimental tumor growth. Plos Comput. Biol. 2014, 10, e1003800. [Google Scholar]
  59. Hayflick L, Moorhead PS. The serial cultivation of human diploid cell strains. Exp. Cell Res. 1961, 25, 585–621. [Google Scholar] [CrossRef]
  60. Hayflick, L. The limited in vitro lifetime of human diploid cell strains. Exp. Cell Res. 1965, 37, 614–636. [Google Scholar] [CrossRef] [PubMed]
  61. Blackburn EH, Gall JG. A tandemly repeated sequence at the termini of the extrachromosomal ribosomal RNA genes in Tetrahymena. J. Mol. Biol. 1978, 120, 33–53. [Google Scholar] [CrossRef] [PubMed]
  62. Poleszczuk J, Hahnfeldt P, Enderling H. Biphasic modulation of cancer stem cell-driven solid tumour dynamics in response to reactivated replicative senescence. Cell Prolif. 2014, 47, 267–276. [Google Scholar] [CrossRef]
  63. Poleszczuk J, Enderling H. A high-performance cellular automaton model of tumor growth with dynamically growing domains. Appl. Math. 2014, 5, 144. [Google Scholar] [CrossRef] [PubMed]
  64. Poleszczuk J, Hahnfeldt P, Enderling H. Evolution and phenotypic selection of cancer stem cells. Plos Comput. Biol. 2015, 11, e1004025. [Google Scholar]
  65. Poleszczuk J, Enderling H. Cancer stem cell plasticity as tumor growth promoter and catalyst of population collapse. Stem Cells Int. 2016, 2016, 3923527. [Google Scholar]
  66. Morton CI, Hlatky L, Hahnfeldt P, Enderling H. Non-stem cancer cell kinetics modulate solid tumor progression. Theor. Biol. Med. Model. 2011, 8, 1–13. [Google Scholar]
  67. Shyntar A, Patel A, Rhodes M, Enderling H, Hillen T. The Tumor Invasion Paradox in Cancer Stem Cell-Driven Solid Tumors. Bull. Math. Biol. 2022, 84, 139. [Google Scholar]
  68. Topman G, Sharabani-Yosef O, Gefen A. A method for quick, low-cost automated confluency measurements. Microsc. Microanal. 2011, 17, 915–922. [Google Scholar] [CrossRef]
  69. Martin S, Zhang Z, Martino A, Faulon JL. Boolean dynamics of genetic regulatory networks inferred from microarray time series data. Bioinformatics 2007, 23, 866–874. [Google Scholar] [CrossRef]
  70. Campbell NR, Rao A, Hunter MV, Sznurkowska MK, Briker L, Zhang M, et al. Cooperation between melanoma cell states promotes metastasis through heterotypic cluster formation. Dev. Cell 2021, 56, 2808–2825. [Google Scholar] [CrossRef] [PubMed]
  71. Hatzikirou H, Basanta D, Simon M, Schaller K, Deutsch A. ‘Go or grow’: the key to the emergence of invasion in tumour progression? Math. Med. Biol. J. Ima 2012, 29, 49–65. [Google Scholar] [CrossRef] [PubMed]
  72. Gallaher J, Anderson AR. Evolution of intratumoral phenotypic heterogeneity: the role of trait inheritance. Interface Focus 2013, 3, 20130016. [Google Scholar] [CrossRef] [PubMed]
  73. Kimmel GJ, Dane M, Heiser LM, Altrock PM, Andor N. Integrating mathematical modeling with high-throughput imaging explains how polyploid populations behave in nutrient-sparse environments. Cancer Res. 2020, 80, 5109–5120. [Google Scholar] [CrossRef] [PubMed]
  74. Garay T, Juhász É, Molnár E, Eisenbauer M, Czirók A, Dekan B, et al. Cell migration or cytokinesis and proliferation?–revisiting the “go or grow” hypothesis in cancer cells in vitro. Exp. Cell Res. 2013, 319, 3094–3103. [Google Scholar] [CrossRef] [PubMed]
  75. Vittadello ST, McCue SW, Gunasingh G, Haass NK, Simpson MJ. Examining go-or-grow using fluorescent cell-cycle indicators and cell-cycle-inhibiting drugs. Biophys. J. 2020, 118, 1243–1247. [Google Scholar] [CrossRef] [PubMed]
  76. Kon S, Ishibashi K, Katoh H, Kitamoto S, Shirai T, Tanaka S, et al. Cell competition with normal epithelial cells promotes apical extrusion of transformed cells through metabolic changes. Nat. Cell Biol. 2017, 19, 530–541. [Google Scholar] [CrossRef]
  77. Hill W, Zaragkoulias A, Salvador-Barbero B, Parfitt GJ, Alatsatianos M, Padilha A, et al. EPHA2-dependent outcompetition of KRASG12D mutant cells by wild-type neighbors in the adult pancreas. Curr. Biol. 2021, 31, 2550–2560. [Google Scholar] [CrossRef]
  78. Martins VC, Busch K, Juraeva D, Blum C, Ludwig C, Rasche V, et al. Cell competition is a tumour suppressor mechanism in the thymus. Nature 2014, 509, 465–470. [Google Scholar] [CrossRef]
  79. Wagstaff L, Goschorska M, Kozyrska K, Duclos G, Kucinski I, Chessel A, et al. Mechanical cell competition kills cells via induction of lethal p53 levels. Nat. Commun. 2016, 7, 11373. [Google Scholar] [CrossRef]
  80. Alowaidi F, Hashimi SM, Alqurashi N, Alhulais R, Ivanovski S, Bellette B, et al. Assessing stemness and proliferation properties of the newly established colon cancer ‘stem’cell line, CSC480 and novel approaches to identify dormant cancer cells. Oncol. Rep. 2018, 39, 2881–2891. [Google Scholar]
  81. Gao X, McDonald JT, Hlatky L, Enderling H. Acute and fractionated irradiation differentially modulate glioma stem cell division kinetics. Cancer Res. 2013, 73, 1481–1490. [Google Scholar] [CrossRef]
  82. Tang J, Fernandez-Garcia I, Vijayakumar S, Martinez-Ruis H, Illa-Bochaca I, Nguyen DH, et al. Irradiation of juvenile, but not adult, mammary gland increases stem cell self-renewal and estrogen receptor negative tumors. Stem Cells 2014, 32, 649–661. [Google Scholar] [CrossRef]
  83. Grimes DR, Fletcher AG. Close encounters of the cell kind: The impact of contact inhibition on tumour growth and cancer models. Bull. Math. Biol. 2020, 82, 1–13. [Google Scholar]
  84. Pavel M, Renna M, Park SJ, Menzies FM, Ricketts T, Füllgrabe J, et al. Contact inhibition controls cell survival and proliferation via YAP/TAZ-autophagy axis. Nat. Commun. 2018, 9, 2961. [Google Scholar] [CrossRef] [PubMed]
  85. West J, Newton PK. Cellular interactions constrain tumor growth. Proc. Natl. Acad. Sci. USA 2019, 116, 1918–1923. [Google Scholar] [CrossRef] [PubMed]
  86. Hanahan D, Coussens LM. Accessories to the crime: functions of cells recruited to the tumor microenvironment. Cancer Cell 2012, 21, 309–322. [Google Scholar] [CrossRef] [PubMed]
  87. Quail DF, Joyce JA. Microenvironmental regulation of tumor progression and metastasis. Nat. Med. 2013, 19, 1423–1437. [Google Scholar] [CrossRef]
  88. Maley CC, Aktipis A, Graham TA, Sottoriva A, Boddy AM, Janiszewska M, et al. Classifying the evolutionary and ecological features of neoplasms. Nat. Rev. Cancer 2017, 17, 605–619. [Google Scholar] [CrossRef] [PubMed]
  89. Wittmann DM, Krumsiek J, Saez-Rodriguez J, Lauffenburger DA, Klamt S, Theis FJ. Transforming Boolean models to continuous models: methodology and application to T-cell receptor signaling. Bmc Syst. Biol. 2009, 3, 1–21. [Google Scholar]
  90. Krumsiek J, Pölsterl S, Wittmann DM, Theis FJ. Odefy-from discrete to continuous models. Bmc Bioinform. 2010, 11, 1–10. [Google Scholar]
Preprints 88563 g001
Figure 1. Workflow of data inference and population dynamic modeling. (A) Cell co-culture model of keratinocytes and melanoma cells Scale bar: 50 μ m [1]. (B) Population growth time-series binarization. Number 0 indicates a low density of cells (OFF state), and number 1 indicates a high density of cells (ON state). (C) Inferred Boolean Network Topology Arrows indicate activation and blunt arrows indicate inhibition. (D) Estimating cellular automata rules from a state graph or transition table. (E) Implementation of simulation through cellular automata.
Figure 1. Workflow of data inference and population dynamic modeling. (A) Cell co-culture model of keratinocytes and melanoma cells Scale bar: 50 μ m [1]. (B) Population growth time-series binarization. Number 0 indicates a low density of cells (OFF state), and number 1 indicates a high density of cells (ON state). (C) Inferred Boolean Network Topology Arrows indicate activation and blunt arrows indicate inhibition. (D) Estimating cellular automata rules from a state graph or transition table. (E) Implementation of simulation through cellular automata.
Preprints 88563 g001
Preprints 88563 g003
Figure 3. The dynamics of IBN 1 and 2. (A) the topology of the network is shown on the left, and the state graph of IBN 1 on the right. (B) The topology of the network is shown on the left, and the state graph of IBN 2 on the right. A 1 and A 2 denote singleton attractors 1 and 2, respectively, and the letter B denotes state transitions. The red number represents the density state of H, the blue number represents the density state of T, and the green number, the space availability state of S.
Figure 3. The dynamics of IBN 1 and 2. (A) the topology of the network is shown on the left, and the state graph of IBN 1 on the right. (B) The topology of the network is shown on the left, and the state graph of IBN 2 on the right. A 1 and A 2 denote singleton attractors 1 and 2, respectively, and the letter B denotes state transitions. The red number represents the density state of H, the blue number represents the density state of T, and the green number, the space availability state of S.
Preprints 88563 g003
Preprints 88563 g004
Figure 4. Estimate of the CA dynamic rule from the BN basin. One can observe the comparison within each state transition ( B 1 , B 2 , B 4 , B 5 , A 1 and A 2 ) where the number in red indicating the density state of H, blue indicating T, and green indicating S. The dashed rectangles marks the comparisons among state transitions belonging to a basin of attraction, and the arrow points to the comparison consensus among state transitions. The orange-dash rectangle concerns the basin of attraction A 1 , while the purple-dash rectangle to A 2 .
Figure 4. Estimate of the CA dynamic rule from the BN basin. One can observe the comparison within each state transition ( B 1 , B 2 , B 4 , B 5 , A 1 and A 2 ) where the number in red indicating the density state of H, blue indicating T, and green indicating S. The dashed rectangles marks the comparisons among state transitions belonging to a basin of attraction, and the arrow points to the comparison consensus among state transitions. The orange-dash rectangle concerns the basin of attraction A 1 , while the purple-dash rectangle to A 2 .
Preprints 88563 g004
Table 1. Inferred boolean functions through the Best Fit algorithm.
Table 1. Inferred boolean functions through the Best Fit algorithm.
Preprints 88563 i001
All functions inferred showed non-null error rates. The highlighted functions set the state graph in Figure 3A,B. The bar over the node symbol denotes the NOT logical operator. All the inferred boolean functions have error rates equal to 1. The highlighted functions set the state graph in Figure 3A,B. The bar over the node symbol denotes the NOT logical operator. All the inferred boolean functions have error rates equal to 1.
Table 2. Table of estimated values for the parameters of the logistic model.
Table 2. Table of estimated values for the parameters of the logistic model.
Parameters Melanoma Keratinocytes
K 0.16 0.7
rho 1.63 1.20
tau 2.7 2.2
These estimated values for K, ρ , and τ refer to simulations with N 0 = 2000 , ρ m a x T = 6 , and ρ m a x H = 7 .
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated