Algorithm for the Accelerated Calculation of Conceptual Distances in Massive Graphs

1. Introduction

The spread of information and communication technologies has significantly increased the available information. Thus, we can interpret this information through concepts. Conceptual matching is essential for human and machine reasoning, enabling problem-solving and data-driven inference. Researchers studying the human brain use the term "concept" to describe a unit of meaning stored in memory. The ability to relate concepts and generate knowledge is inherent to humans. Giving computers this capability is a significant advance in computer science.

Transferring the relationship between concepts from the human domain to the computational domain is complex. Sociocultural and language aspects are closely related to the types of concepts an individual acquires. Determining the similarity between concepts so that a computer can process them is one of the most basic and relevant problems in various research fields.

Over time, people have explored various structures and methods to represent the semantic relationships underlying conceptual distance. The graph is one of the most used abstract data types to represent this information, designed to model connections between people, objects, or entities. Nodes and edges are the two main elements of a graph. In addition, graphs have specific properties that make them unique and valuable in different applications.

In recent years, conceptual graphs generated from ontologies have gained relevance. These graphs are strongly connected, where each concept is a vertex, and two edges represent each relationship (one in each direction). Consequently, applying different graph theory search algorithms to study and analyze the relations represented in the conceptual graph is possible. The shortest-path algorithms are crucial in solving different optimization problems. The primary purpose of these algorithms is to find the path with the minimum cost or distance between a given pair of vertices in a graph or network. The study of the shortest path algorithms and proposing different approaches to reduce computational cost have been deeply studied, considering the research works proposed by Dreyfus (1969) [1], Gallo and Pallottino (1988) [2], Magzhan and Jani (2013) [3], Madkour et al. (2017) [4].

Some research works offer different techniques and optimizations for efficiently applying the shortest path algorithm to handle massive data. Fuhao and Jiping (2009) [5] proposed a novel adjacent node algorithm that is more suitable for analyzing networks with massive spatial data. Chakaravarthy et al. (2016) [6] introduced a scalable parallel algorithm that significantly reduced inter-node communication traffic and achieved high processing rates on large-scale graphs. Yang et al. (2019) [7] focused on routing optimization algorithms based on node-compression in big data environments, addressing the common problem of finding the shortest path within a limited time and limited nodes passing through. Liu et al. (2019) [8] presented a navigation algorithm based on a navigator data structure, which effectively navigates the shortest path with high probability in massive complex networks.

Unfortunately, the shortest path algorithm can propagate local distances to determine the distance between two not directly connected concepts by a relation in the ontology. This process is applied to each pair of concepts, making establishing semantic closeness possible. However, calculating these distances has a high computational cost since traditional algorithms have a complexity of around $\mathcal{O}\left(n^3\right)$, which is disadvantageous with massive graphs. In this paper, we use the DIS-C algorithm Quintero et al. (2019) [9] as a basis for computing the conceptual distance, which has a complexity $\mathcal{O}\left(n^{2}log\left(n\right)\right)$ to try to make it more efficient.

According to Mejia Sanchez-Bermejo (2013) [10], measuring the conceptual distance between words has been the object of study for many years within the areas of linguistic computing and artificial intelligence because it represents a generic procedure in a wide variety of applications, such as natural language processing, word disambiguation, detection and error correction in text documents, text classification, among others. Reducing the computational cost of calculating conceptual distances for each pair of concepts in massive graphs will accelerate semantic similarity computation. Consequently, it will have practical benefits and contribute to developing more efficient applications to solve practical problems, for instance, reducing the computational time required to search pairs of documents with high semantic similarity in large data sets composed of millions of documents. Additionally, it expands the understanding of the phenomenon of semantic similarity in computing systems based on conceptual graphs. Research and developing efficient algorithms that reduce computing time by combining approximation or analytical techniques is vital to advance the study of semantic similarity.

The manuscript is organized as follows: Section 2 comprises the state-of-the-art that refers to this field. Section 3 presents an analysis of the complexity of the DIS-C algorithm to reference the parts to be improved accurately, the algorithms proposed to improve performance, and the demonstration of its accuracy and the associated computational complexity. In Section 4, we establish the execution scenarios, which include the total number and type of tests. Section 5 presents the experimental results and their discussion. Finally, Section 6 outlines the conclusion and future work.

2. Related work

2.1. Semantic Similarity

Conceptual distance is closely related to semantic relationship and semantic similarity. The semantic relationship, on the other hand, is not necessarily conditioned by a taxonomic relationship; in general terms, these relationships are given by any relationship between concepts, such as meronymy, antonymy, functionality, cause-effect, holonymy, hyponymy, hyperonymy, and so on. On the other hand, we define conceptual distance as the space that separates two concepts within a conceptualization; in other words, it is the degree of proximity between the concepts Quintero et al. (2023) [11]. We can define a rule that indicates conceptual closeness about how close to 0 (in terms of distance) the assigned value is. However, computing such distance depends entirely on the context of the concepts. However, to calculate it, the concepts must first be represented in a model that allows expressing the semantic relationships and defining the measurement metric from the different underlying structures and representations.

In the network model, ontologies are used to face the problem of formally representing the semantics of the information and its relationships Meersman (1999) [12]. The above structures assess the conceptual distance between terms. The present work considers the assumption that we can represent an ontology as a strongly connected graph (conceptual graph); in this context, some authors have proposed many approaches to evaluate the closeness between concepts.

In the literature, authors employ four groups of methods, models, and techniques to compute semantic similarity: a) edge counting-based, b) feature-based, c) information content-based, and d) hybrids. In this work, we use information content-based methods due to their direct relationship with calculating conceptual distance as a measure to determine semantic similarity. The underlying knowledge base offers these methods a structured representation of terms or concepts connected by semantic relationships, also offering a semantic measure free of ambiguity since we consider the terms’ real meaning Sanchez et al. (2012) [13].

2.1.1. Edge counting-based methods

Edge-counting methods consider an ontology a connected graph, where the nodes are concepts, and the edges are relations (almost always taxonomic). The number of edges separating two concepts establishes the similarity between them. Rada et al. (1989) [14] presented one of the first outcomes, proposing a metric called “Distance” defined as ${\mathrm{dis}}_{rada}(a,b)=$minimum number of edges that separate a and b. Despite the effectiveness of its algorithm, one of its most significant drawbacks is its inefficiency when using relationships other than “is-a”.

Wu and Palmer (1994) [15] proposed a measure based on a semantic representation, where they define each verb by a set of concepts in different conceptual domains. Thus, they organized such representation in a hierarchy, formally demarcating its measurement.

In the study presented by Hirst and Stonge (1995) [16], the edge-counting method is extended by considering non-taxonomic semantic links in lexical strings. Such an idea was based on considering all types of relationships found on the WordNet [17], along with the intuition that the longer the path and the more direction the relationship changes, the less the similarity. In such work, authors interpreted the directions in the relationship of the lexical chain as ascending (hypernymy and meronymy), descending (hyponymy and holonymy), and horizontal (antonymy).

Li et al. (2003) [18] proposed a similarity measure as a function that considers the attributes of the shortest path length, depth of ontological information, and local density in a nonlinear function. This research employed a hierarchical structure with relationships of the type “is-a” or “is a type of”.

More recent investigations within the edge count method are mainly based on already established measures, such as those mentioned above with slight variations or the addition of penalty factors to calculate the shortest distance between concepts. An example is the work proposed by fullciteshenoy2012new, inspired by the measure developed by Wu and Palmer (1994) [15].

Thus, Table 1 summarizes the methods based on edge counting we have mentioned; the table contains the expression used to compute the similarity/distance and a brief explanation of the variables involved.

While this method’s class performs well and enjoys simplicity, several limitations hinder their performance. First, they only consider the shortest path between pairs of concepts. It applied to large and detailed ontologies that incorporate multiple taxonomic inheritances; the result is only sometimes the best because the users need to consider several taxonomic paths. Other characteristics that influence the semantics of the concept, such as the number and distribution of common and uncommon taxonomic ancestors, are not considered either. Another problem with edge count measures is that they are based on the notion that all links in the taxonomy represent a uniform distance. In practice, the semantic distance will depend on the granularity and taxonomic detail implemented by the knowledge engineer Sanchez et al. (2012) [13].

2.1.2. Feature-based methods

Feature-based methods are based on the Tversky (1977) [20] similarity model, which in turn derives from set theory, assesses the similarity between concepts based on their properties, subtracting the common and uncommon features of the terms, and attempts to overcome the limitations of edge count-based measures concerning the fact that taxonomic links in an ontology do not necessarily represent uniform distances Sanchez et al. (2012) [13]. These types of measures have the potential to be applied in the calculation of semantic similarity supported by crossed ontological structures, that is, when the pairs of concepts belong to two different ontologies, a milestone that methods based on edge counting are not capable of reaching.

The idea is quite simple: if we imagine three concepts such as “dog”, “bird”, and “sofa”, we can almost instinctively realize that “dog” and “bird” are more similar to each other. This reasoning may be associated with the fact that we identify a “dog” and a “bird” as animals despite not having a direct relationship of kinship. Someone can argue that “dog” and “bird” have more characteristics in common than they would with a “couch”.

One of the first studies to develop a semantic similarity measure based on the hypothesis that the more common characteristics two words have, the more related they are, the research by Lesk (1986) [21] proposed the homonymous measure. The algorithm for calculating this Lesk measure aims to search for the disambiguation of words in texts. The work presented by Banerjee and Pedersen (2003) [22] is an extension of the Lesk measure. It took as reference the terms or synsets provided by WordNet. The idea of performing multiple comparisons sets it apart from the original algorithm. His measure seeks overlaps between the glosses of the synsets themselves, hyperonyms, hyponyms, meronyms, holonyms, and troponyms.

In the modern world, there are multiple sources of information, such as social networks and internet blogs, among others, that provide a large amount of information daily, including terms or concepts (new words, brands, acronyms, among others) uncaptured in domain ontologies or formal taxonomic structures. For this reason, there are works where other sources of knowledge are used, such as Wikipedia. In this aspect, the study of Jiang et al. (2015) [23] evaluates specific existing methods, based on characteristics, under a formal representation of concepts extracted from said source. In general, there is an excellent human correlation, and there are some practical ways to determine the similarity between Wikipedia concepts.

The main drawback of the feature-based approach is its reliance on ontologies or knowledge sources with semantic features such as glosses, and most ontologies rarely incorporate semantic features other than relations [13]. It significantly restricts its use for computing the similarity between concepts; however, this approach has been adopted to calculate the similarity between other data types, such as images or videos.

2.1.3. Information content-based methods

Information content-based approaches arose from the need to improve some of the limitations of edge-counting-based methods. Specifically, Resnik (1995) [24] proposed to complement the taxonomic structure of an ontology with the information distribution of concepts evaluated in the input corpus. Similarly, the author framed the notion of information content (IC) by associating probabilities of the appearance of each concept in the taxonomy. The IC was computed from its occurrences in a given corpus. Therefore, a high IC value indicates that the word is more specific and clearly describes a concept with less ambiguity.

In contrast, lower IC values indicate that the words have a more abstract meaning [25]. The Resnik measure calculates the IC of a concept a according to the negative logarithm of its probability of occurrence $P\left(a\right)$, $I_C\left(a\right)=-logP\left(a\right)$. This measure is closely related to the notion of LCS (Least Common Subsumer) because, according to Resnik’s research, semantic similarity depends on the information shared between 2 terms and a way that represents such measure in a taxonomy. This way, if two terms do not share an LCS, they are considered significantly different.

It is evident that if any pair of terms share the same LCS, the result of semantic similarity is the same; this is one of the main drawbacks of the measure. For this basis, over time, research focused on the notion of the IC, combining the main reasoning of the IC with other ideas that complement its calculation and, in its entirety, semantic similarity.

An example of the above is the work of Jiang and Conrath (1997) [26] based on the notion of IC proposed by Resnik (1995) [24]. The measure proposed by Jiang and Conrath (1997) [26] is a combined model derived from the method based on edge counting by adding the information content as a decision factor. The results showed that a combined approach outperforms the IC approach alone. Thanks to the practical results, such outcomes gave credibility to using the IC as a factor for calculating the semantic similarity and as reinforcement in the computation of the conceptual distance based on finding the shortest path between two terms.

Gao et al. (2015) [27] considered the basis of edge counting methods, that is, the shortest path length between two concepts, and combines it with the IC of the LCS. This way of interpreting relations is close to the work of Jiang and Conrath (1997) [26], and in general terms, this approach is mainly accepted in many research investigations; however, the fundamental difference is in the model used to describe the semantic similarity. Jiang et al. (2017) [28] proposed computing the IC of a concept from Wikipedia. They suggested diverse methods for IC calculation that aim to test which IC calculation method and which underlying similarity measurement approach are suitable for concept similarity calculation in the Wikipedia category structure. The first technique presented the computing of IC using the category structure and the extension of methods founded on Jiang and Conrath (1997) [26] corpus. Table 2 summarizes the IC-based methods. Moreover, we present the expressions used to calculate IC and briefly explain the variables involved.

2.1.4. Hybrid methods

While some of the above mentioned investigations use a hybrid approach, where authors combine two or more techniques for calculating semantic similarity, This section explains the work on which this is based. In [9], we proposed the DIS-C method to calculate the conceptual distance between two concepts in an ontology based on a fundamental approach that uses the topology of ontology to compute the weight of relationships between concepts. Unlike other methods, DIS-C can incorporate various relationships between concepts, such as meronymy, hyponymy, antonymy, functionality, and causation, without needing to represent the source of knowledge in taxonomic or hierarchical structures.

The theoretical foundation of the DIS-C method considers the conceptual distance as the space that separates two concepts within a conceptualization represented as a directed graph. We assumed that the distance is related to the difference in information content provided by the concepts in their definitions. The method assigns a distance value to each relationship type and transforms this into a weighted directed graph, allowing the conceptual structure not to matter. This characteristic means that DIS-C can be applied to any conceptual structure. The only requirement for the algorithm is that the conceptualization be a 3-tuple of elements $K=(C,\Re ,R)$, where C is a set of concepts, ℜ is the set of types of relations, and R is the set of relations in the conceptualization. With this information, the method can calculate the conceptual distance between each pair of concepts, the weight each type of relationship contributes, and a marginal measure called generality closely related to the IC. The DIS-C algorithm includes a method for the automatic weighting of the graph. In the literature, the weighting in methods based on graphs is too specific to the type of conceptualization, so proposing a general method allows independence concerning the domain.

Thus, we consider DIS-C a hybrid approach because, as we have seen, the computing of the IC (characterized by generality) is used and combined with the calculation of the shortest path between all pairs of nodes to find all the most critical concepts, close to each of the concepts themselves. Section 3.1 presents the analysis of the DIS-C algorithm in more detail. In summary, the method is described through the following steps:

• Assign to each relation $\rho \in \Re$ an arbitrary conceptual weight defined in each direction of the relationship.
• A directed and weighted graph (conceptual graph) is created where the vertices are the concepts contained in the conceptualization and the edges are the relationships that connect each pair of concepts. Each edge has its counterpart in the opposite direction with different weighting. Finally, to compute the weighting, the generality of each concept is necessary.
• Calculate the length of the shortest paths between each pair of vertices, i.e., diffuse the conceptual distance to all concepts.

2.2. All pair shortest path problem

In the conceptual graph, each node is a concept, and each relation is an edge connecting a pair of nodes. Graph theory techniques can extract the underlying knowledge encoded in the ontology. The natural step is to compute the shortest path to find the distance between concepts that are not directly related. In this step, we find one of the leading technical drawbacks of the approach, and it is the specific issue to be dealt with in this work. When dealing with large graphs, calculating the shortest path between each pair of concepts is computationally expensive. This type of problem in graph theory is known as “All Pair Shortest Path” (APSP) [31].

In [9], we used two well-known algorithms to solve this problem: the Floyd-Warshall and Johnson-Dijkstra algorithms. Floyd-Warshall is based on transitive Boolean matrix closure [32] with computational complexity of $\mathcal{O}\left(n^3\right)$1. At the same time, Johnson-Dijkstra has complexity $\mathcal{O}\left(mn+n^{2}log\left(n\right)\right)$ (when using Fibonacci heaps as a priority queue); however, it requires that there is no negative cycle in the graph and when $m\in \mathcal{O}\left(n^2\right)$ the complexity is equal to $\mathcal{O}\left(n^3\right)$ [33].

The APSP is widely related to the matrix multiplication problem (MM); for this explanation, people often use accelerated matrix multiplication algorithms where, in general, there is a cost of $\mathcal{O}\left(n^{2+ϵ}\right),ϵ<1$ [34]. Techniques like divide and conquer [35] or metaheuristic algorithms [36] are also used to optimize the computational cost. Another approach uses new-generation hardware, such as the GPU, to parallelize existing algorithms and thus reduce runtime [37].

Thus, the complexity of the APSP problem has remained open even though it is executed in polynomial time. According to Reddy (2016) [38], most of the algorithms are based on the following two types of computational models:

• Addition comparison model: The shortest path algorithms in this model assume that the inputs are real weighted graphs, where the only operations allowed on reals are comparisons and additions.
• Random Access Machine (RAM) model: In this model, shortest path algorithms assume that the inputs are weighted graphs of integers manipulated by addition, subtraction, comparison, shift, and various logical operations [39].

Most algorithms that solve the APSP problem work on the RAM model. Unfortunately, some of the algorithms are far from practical. We must consider the characteristics of the graph (directed, weighted, complete, among others) to face this problem; the effectiveness of most algorithms depends directly on their properties.

2.2.1. Analytic solutions

The algorithm presented by Johnson (1977) [40] was one of the first to use Dikjstra’s algorithm as a subprocess, in addition to the Bellman-Ford algorithm to remove negative edge weights, thus achieving a total computational complexity of $\mathcal{O}\left(mn+n^{2}logn\right)$. This complexity improves on the Floyd-Warshall algorithm described by Bernard Roy in 1959, which has a $\mathcal{O}\left(n^3\right)$ complexity.

Chan (2010) [41] presented an algorithm for the APSP problem with real-weighted general dense graphs. It has a computational complexity of $\mathcal{O}\left(\frac{n^3{log}^{3}logn}{lo{g}^{2}n}\right)$. The base of such an algorithm is on calculating the distance product of two square matrices, and the efficiency is obtained through computational geometry and using rectangular matrix multiplications instead of square matrix multiplications.

Moreover, Peres et al. (2013) [42] studied a specific case of graphs achieving a theoretical time limit of $\mathcal{O}\left(n^2\right)$. However, the limitation of the proof is the dependency on the class of complete and directed graphs with an edge weight independently and uniformly at random between $[0,1]$. The algorithm proposed by Peres et al. (2013) [42] is considered a variant of Demetrescu and Italiano (2004) [43]. The notion of local shortest paths (LSP) is the base of such algorithms.2 Roughly speaking, the algorithm presented by Demetrescu and Italiano (2004) [43] is a parallel implementation of Dijkstra’s algorithm from each node of the graph, with the difference that it only examines the LSP, following a series of specific rules using a priority queue. This algorithm correctly finds all the shortest paths in the graph in time $\mathcal{O}\left(n^{2}log\left(n\right)+\left|LSP\right|\right)$.

Williams (2018) [44] proposed the fastest known algorithm for the APSP problem with dense graphs. The computational complexity is $\mathcal{O}\left(\frac{n^3}{2^{\Omega \sqrt{log\left(n\right)}}}\right)$. The algorithm uses Monte Carlo and algebraic techniques to reduce the computation time in multiplying rectangular matrices. It is a non-deterministic algorithm. However, the investigation also showed that the APSP could be solved deterministically in a time $\mathcal{O}\left(\frac{n^3}{2^{log{\left(n\right)}^{\delta }}}\right)$ for a $\delta >0$ using a suitable deterministic polynomial transformation. Later, Chan and Williams (2016) [45] showed that the problem can be solved deterministically in time $\mathcal{O}\left(\frac{n^3}{2^{\Omega \sqrt{log\left(n\right)}}}\right)$.

Brodnik and Grgurovic (2017) [46] developed an algorithm that sub-processes any other single source the shortest path (SSSP) algorithm, which solves APSP with an asymptotic limit $\mathcal{O}\left((m^{\ast }n+mlog\left(n\right)+n{T}_{\psi }(m^{\ast },n))\right)$; where $m^{\ast }$ is the number of different edges in the shortest paths, and $T_{\psi }(m^{\ast },n)$ is the time the algorithm, $\psi$ solves the SSSP problem. This approach is very similar to the hidden path algorithm [47], which is essentially a modification of Dijkstra’s algorithm to make it more efficient in solving APSP. The primary difference between the two methods is that the hidden path method only works with Dijkstra’s algorithm, while the Brodnik and Grgurovic (2017) [46] algorithm works for any arbitrary algorithm that solves SSSP. The authors used the Johnson weighting technique, topological ordering, and the propagation algorithm to solve the APSP in time $\mathcal{O}\left(m^{\ast }n+mlog\left(n\right)\right)$ for directed acyclic graphs with arbitrary weighting.

Kratsch and Nelles (2020) [48] considered the APSP within the framework of efficient parameterized algorithms (FPT in P). Specifically, the authors investigated the influence of two parameters: clique-width ($cw$) and modular-width ($mw$). The result is an efficient and combinatorial algorithm for graphs with non-negative weighting in the vertices, such that the algorithm is executed in time $\mathcal{O}\left(c{w}^2+n^2\right)$ using the parameter $cw$ and $\mathcal{O}\left(m{w}^{2}n+n^2\right)$ for $mw$. In addition, when fast matrix multiplication can be used, the time is reduced to $\mathcal{O}\left(m{w}^{1.842}n+n^2\right)$ using the algorithm defined by Yuster (2009) [49] as a black box for the matrix multiplication. One of the differences with other algorithms is the particularity of working with graphs weighted in the vertices and not in the edges.

In summary, despite the great interest in the APSP problem, there are only minor advances in computational complexity over $\mathcal{O}\left(n^3\right)$ for general graphs based on the computation of the distance product, closely related to matrix multiplication. Although subcubic algorithms exist, they only take advantage of properties of specific graphs or benefit from sparse graphs, so up to now, there is no genuinely subcubic combinatorial algorithm. Table 3 describes the algorithms developed with their computational complexity over time, and Figure 1 shows the execution time comparison of each algorithm.

2.2.2. Approximation solutions

Although we can solve the APSP problem in polynomial time, its application for large graphs is not feasible in practice. For this basis, it is interesting to analyze heuristic and metaheuristic methods and approximation algorithms in this class of problems. The clear advantage of this approach is the speed gain, while its disadvantage is the accuracy of the computation. In the literature, authors use a few relevant investigations of this class of algorithms in the APSP problem: genetic, evolutionary, and optimization algorithms per ant colony.

Attiratanasunthron and Fakcharoenphol (2008) [59] presented a rigorous analysis of the running time for ACO in a shortest-path problem. Its n-ANT algorithm is inspired by the 1-ANT [60] and the AntNet [61] algorithm. In Horoba and Sudholt (2009) [62], the n-ANT algorithm to solve APSP is formalized and optimized. We will call this algorithm $M_{APSP}$ that is a generalization of $M_{SDSP}$ presented in the same research study. This algorithm solves the single source shortest path problem. The computational complexity of $M_{APSP}$ is $\mathcal{O}\left(\Delta l{l}^{\ast }+\frac{llog\left(\Delta l\right)}{p}\right)$, where $\Delta$ is the maximum degree of the graph, l the maximum number of edges in any shortest path, and $l^{\ast }:=max\{l,ln\left(n\right)\}$.

On the other hand, Chou et al. (1998) [63] used a hierarchical approach to decompose a network (graph) into several smaller subnets. In this way, when it is necessary to search for a shorter path, it is evaluated in a smaller graph. However, the shortest path may be different. The shortest paths of all pairs of nodes can be approximated through various constraint mechanisms by exploring a search space smaller than that of the original graph. The authors compare the computational complexity between Dijkstra’s algorithm and two versions of the algorithm called HA: Best HA, which obtained the best results regarding the error of the shortest paths, and the Nearest HA, the fastest execution instance. Dijkstra had no error percentage, while the Nearest HA had 21.5% and Best HA had 4.68%. Concerning runtime, Nearest HA was 15 times faster than Dijkstra and Best HA only twice. Mohring et al. (2007) [64] presented a similar work; however, their study only focuses on the shortest path to a single source. So, the hypothesis that it can be generalized for APSP is supported.

Other works that do not focus on graph partitioning but do speed up the asymptotic limit concerning $\mathcal{O}\left(n^3\right)$ are Baswana et al. (2009) [65] and Yuster (2012) [66]. The first one points to unweighted and undirected graphs, where the merit lies in presenting the first algorithm $\left(n^2\right)$ to calculate APSP with a 3-approximation, this means that for each pair of vertices $u,v\in V$, the distance reported by the algorithm is not greater than $3\ast \delta (u,v)$, such that $\delta (u,v)$ is the actual shortest distance of the path. The article also presents two more algorithms for a 2-approximation, specifically, the first corresponds with complexity $\mathcal{O}\left(m^{2/3}nlog\left(n\right)+n^2\right)$ and $2\delta (u,v)+1$, the second, $\mathcal{O}\left(n^{2}log{\left(n\right)}^{3/2}\right)$ and $2\delta (u,v)+3$. The clear advantage is that there is a defined limit of error.

Finally, there is the Sketch-based approach. Multiple investigations have been considered, but two extensive processes can be identified globally. The first is pre-processing, where the result is a data structure that allows consulting the distance between two nodes. This data structure, a distance oracle, was introduced in [67]. The second process is related to queries, where it is a question of making queries to the oracle and for it to return, in a specific time limit, the result of the shortest distance between two nodes.

Unlike exact algorithms, these algorithms reduce time by several orders of magnitude. Das Sarma et al. (2010) [68] is one of the first studies to adopt this approach for complex graphs with hundreds of millions of nodes and billions of edges. The description of the algorithm is simple: sample a small number of node sets from the graph, called seed node sets. Then, for each node of the graph, the nearest seed is searched in each of these sets of seeds. The sketch of a node is the set of closest seeds and the distance to them. Thus, given a pair of nodes u and v, the distance between them can be estimated by looking for a common seed in their sketches. Although there are no theoretical guarantees of the degree of optimization of the method for directed graphs, the results showed a better average, close to the actual distance, when applied to directed graphs than to undirected graphs.

Wang et al. (2021) [69] centered on finding all shortest paths in huge-scale undirected graphs. Despite having practically the same approach, what makes it different from the work of Das Sarma et al. (2010) [68] is that Wang et al. (2021) [69] considered the computational complexity to perform the preliminary calculation. This task’s standard method applies a BFS algorithm to the seed node sets. It is well known that the complexity of BFS is $\mathcal{O}\left(m+n\right)$ when using an adjacency list or $\mathcal{O}\left(n^2\right)$ for an adjacency matrix. This complexity is a drawback when processing extensive graphs. For this reason, they considered whether it is possible to speed up the preliminary computation with the [70] pruned reference point labeling technique, that is, applying a pruned BFS. The specific results for this stage showed a linear time for its construction, that is, $\mathcal{O}\left(m\right)$. The results showed a notable improvement, especially in runtime, for large graphs.

3. Methods and materials

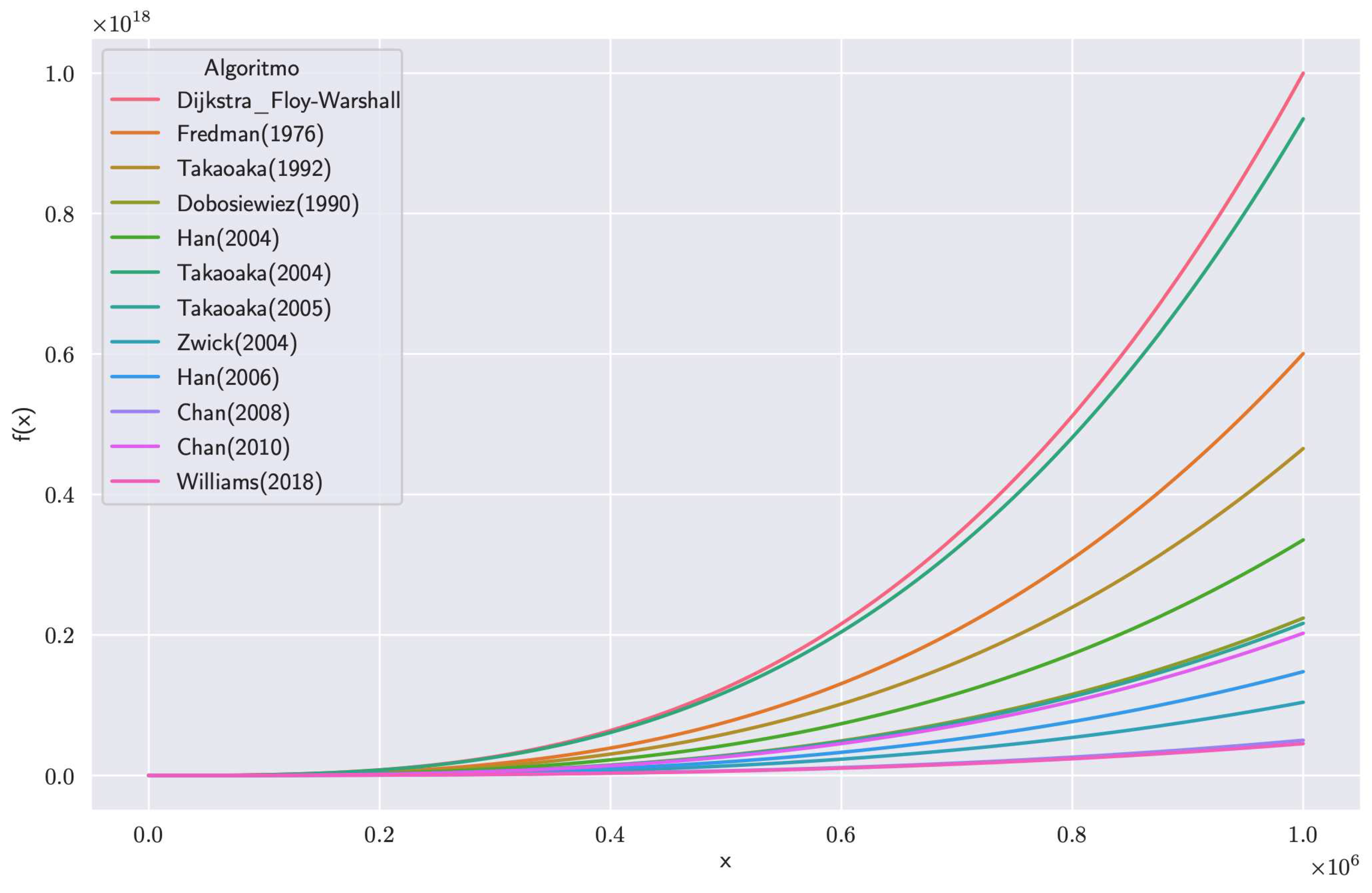
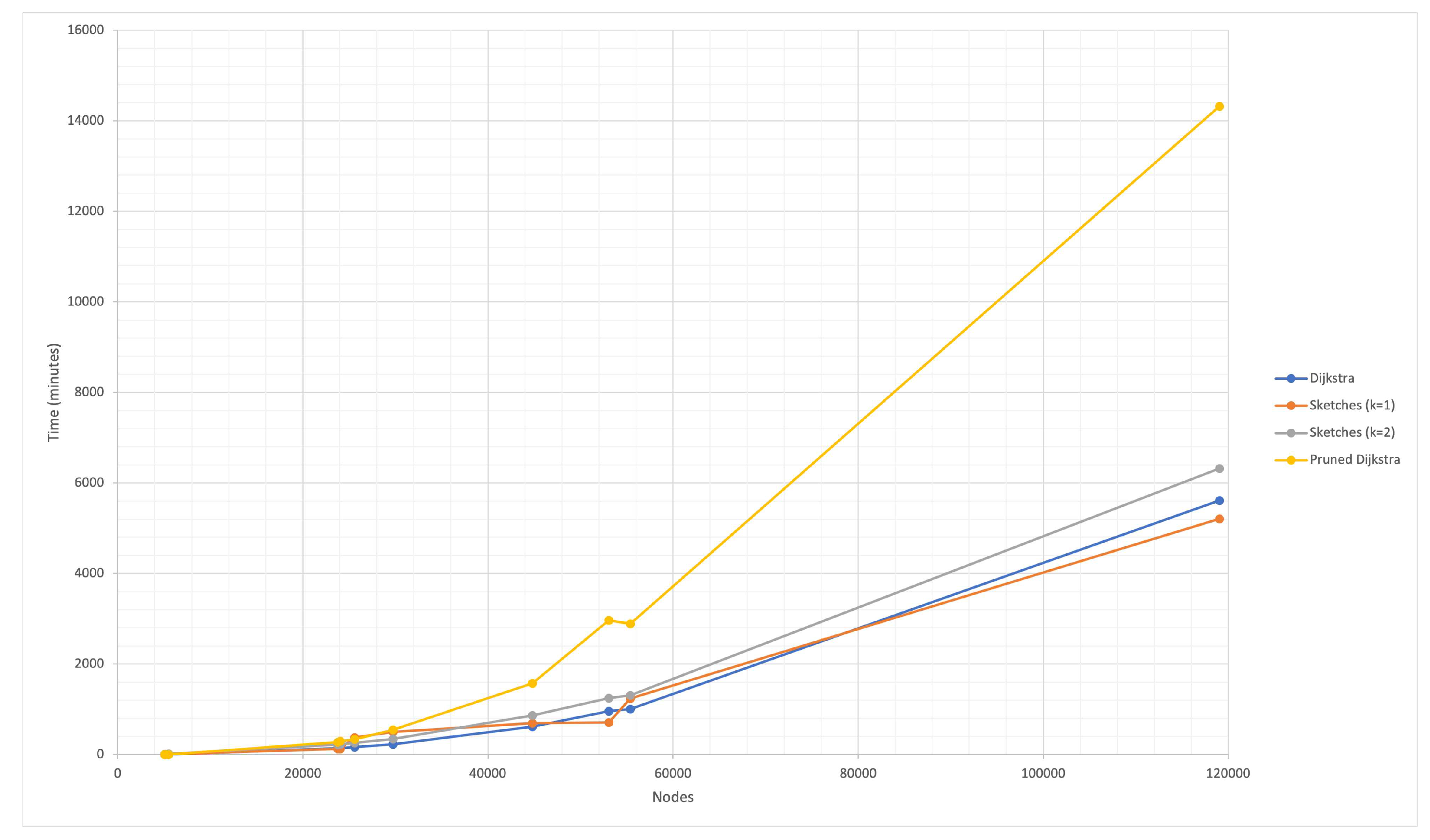
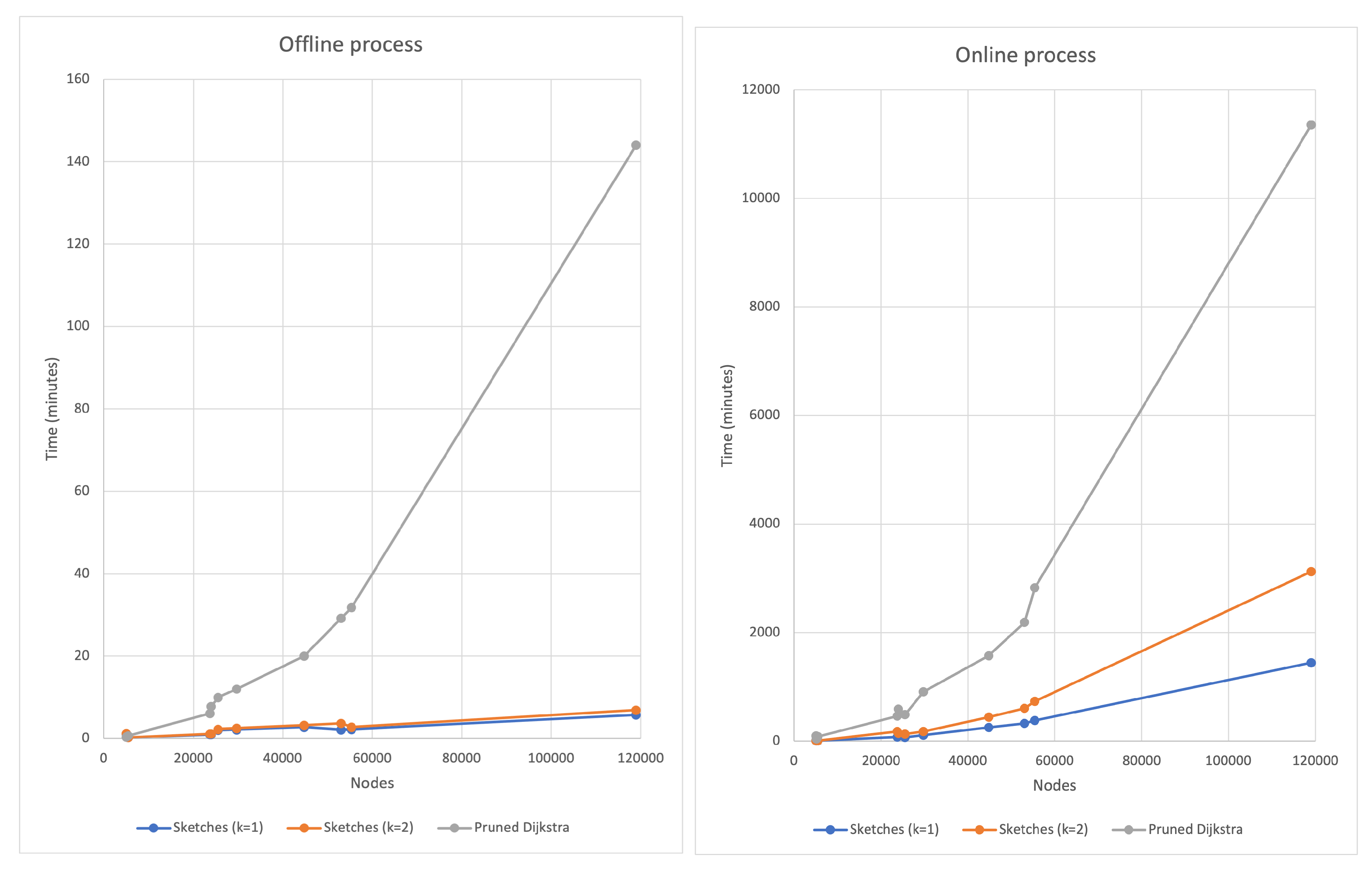
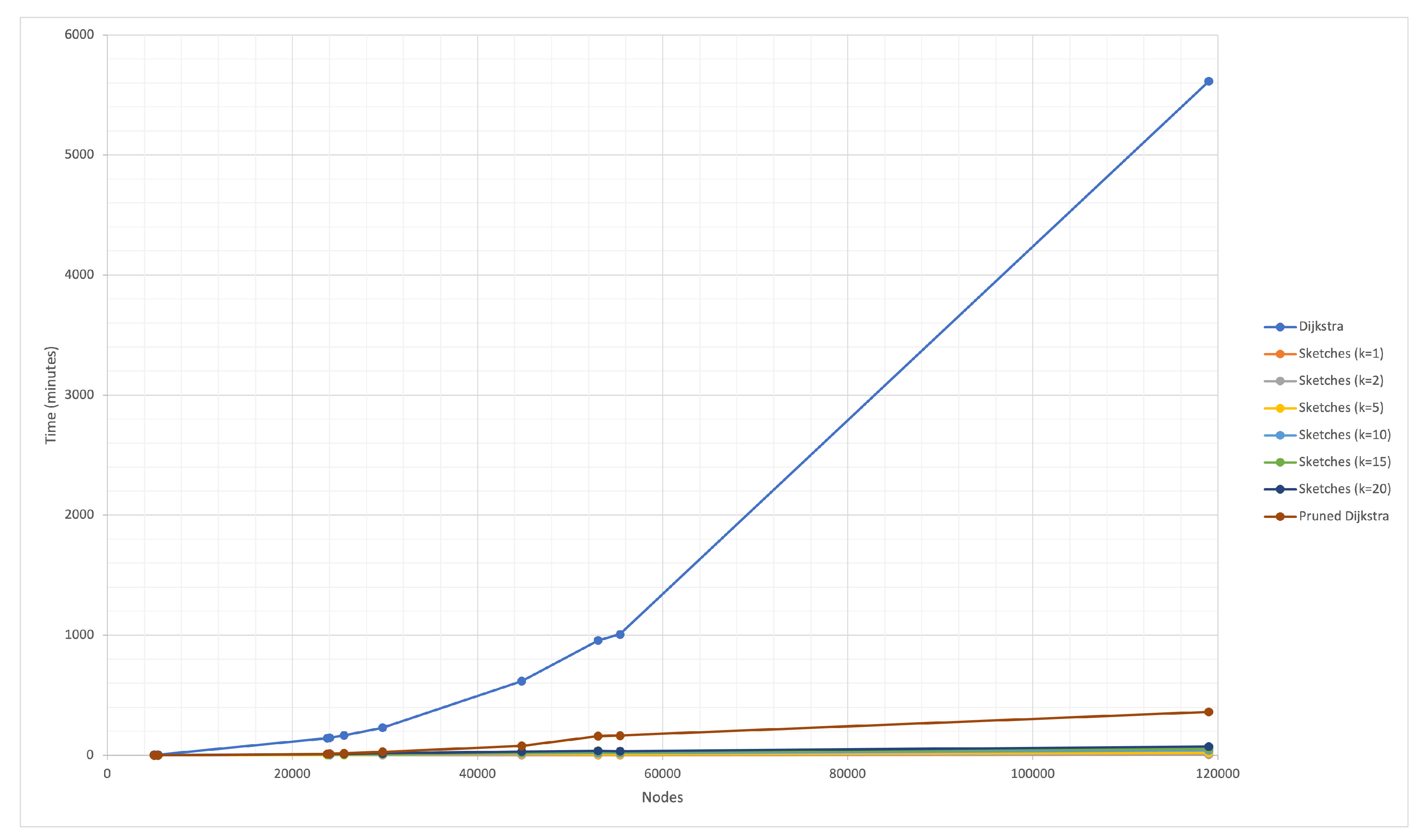
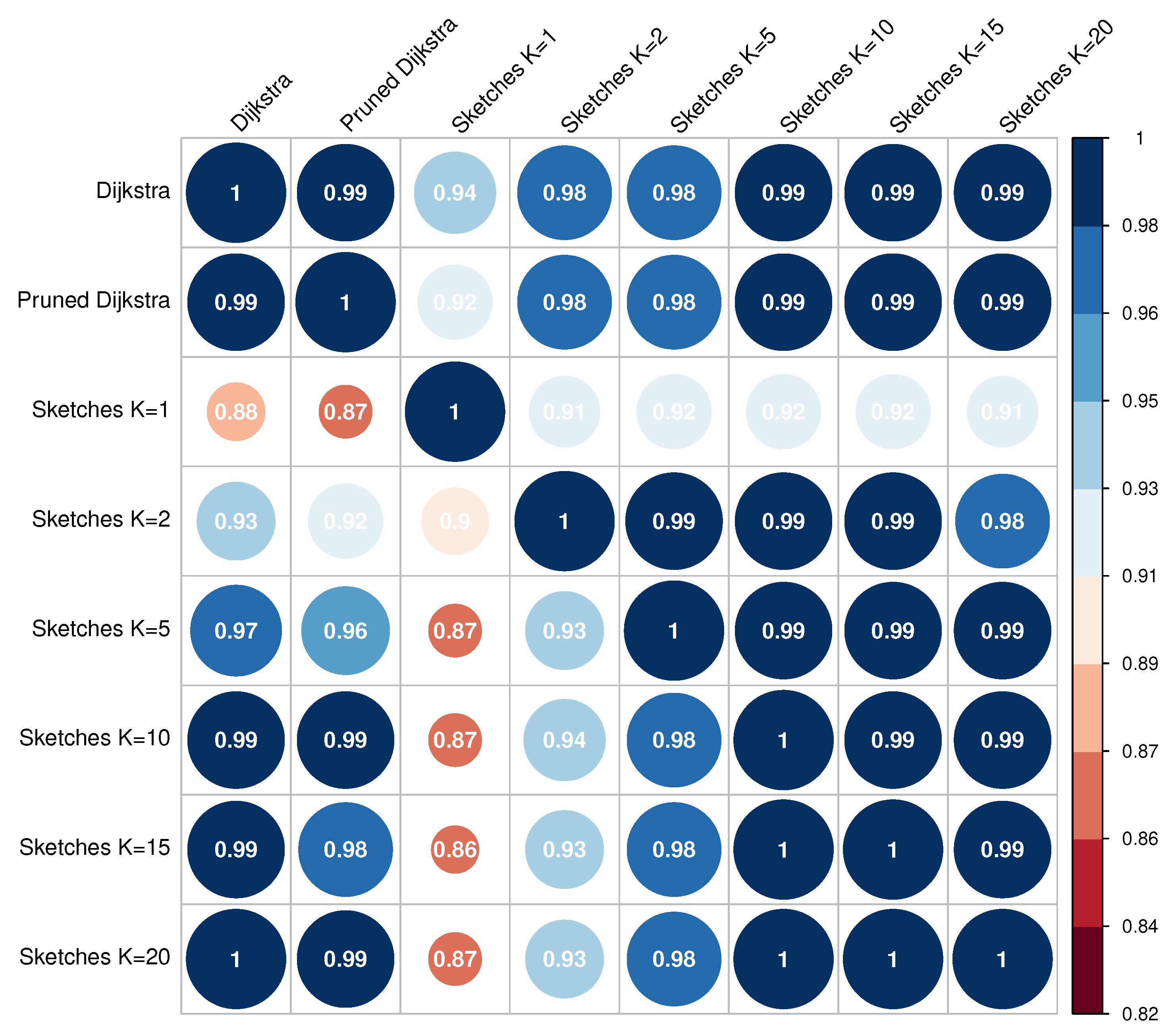
The solution presented combines several approaches to solve the APSP, although the DIS-C algorithm consists of other processes whose computational cost is non-significant.

3.1. Analysis of the DIS-C algorithm

Quintero et al. (2019) [9] detailed two algorithms; the basic one, which calculates the conceptual distance given a conceptualization $K=\left(C,\Re ,R\right)$ and the weights ${\delta }^{\rho }$ for each relationship type $\rho \in Re$. Such an algorithm consists of converting the conceptualization K into a graph $G=(V_G,A_G)$ with $V_G=C$ and $A_G=R$ through which we compute the conceptual distance by calculating the APSP in the graph G. The second algorithm enables automatic weighting, which allows the conceptual distance to be computed automatically without providing the weights of the relationship types. It is precisely this algorithm that we want to speed up. Figure 2 shows the flowchart corresponding to the DIS-C algorithm with automatic weighting3, which will subsequently be referred to simply as DIS-C.

As mentioned, the APSP algorithm has the most significant influence on computational complexity. Up to this point, we can set that the computational complexity of the DIS-C algorithm is $\mathcal{O}\left(n^{2}logn\right)$ for a conceptualization with n concepts4.

3.2. The pruned Dijkstra

The pruned Dijkstra algorithm is an optimized version of Dijkstra’s algorithm in which unnecessary paths are removed in the search, keeping a list of pending nodes and choosing to expand the one with the minimum distance in the list. If we find a path longer than the currently known shortest path to any node during expansion, then that path is discarded and not considered again. In this way, the pruned Dijkstra algorithm reduces the number of paths to be considered. It is a generalization of the PLL (Pruned Landmark Labeling) method for undirected weighted graphs [70]. The PLL method is based on the idea of 2-hop coverage [72], which is an exact method. It is defined as follows: let $G=(V,E)$ be an undirected and weighted graph; for each node $v\in V$, the cover $L\left(v\right)$ is a set of pairs $(u,{\delta }_{uv})$, where u is a node and ${\delta }_{uv}$ is the distance from u to v in the graph G. All covers are denoted as indexed $L{\left(v\right)}_{v\in V}$. To calculate the distance between two vertices, s and t, we use the search function (Q), as shown in Eqn. 1. L is a two-hop cover of G if $Q(s,t,L)={\delta }_{st}$ for any $s,t\in V$.

$$Q(s,t,L)=\left\{\begin{array}{cc}\infty \hfill & L\left(s\right)\cap L\left(t\right)=\varnothing \hfill \\ min\left\{{\delta }_{vs}+{\delta }_{vt}|(v,{\delta }_{vs})\in L\left(s\right),(v,{\delta }_{vt}\in L\left(t\right)\right\}\hfill & L\left(s\right)\cap L\left(t\right)\ne \varnothing \hfill \end{array}\right.$$

(1)

In the case of weighted directed graphs, it is necessary to calculate two indexes; the first $L^{in}$ contains the coverage of all the nodes, considering the incoming edges. The second $L^{out}$ considers the outgoing edges. The way to consult the distances has a minor modification, but the idea remains the same. Such change can be observed in Eqn. 2.

$$Q(s,t,L)=\left\{\begin{array}{cc}\infty \hfill & L{\left(s\right)}^{in}\cap L{\left(t\right)}^{out}=\varnothing \hfill \\ min\left\{{\delta }_{vs}+{\delta }_{vt}|(v,{\delta }_{vs})\in L{\left(s\right)}^{in},(v,{\delta }_{vt}\in L{\left(t\right)}^{out}\right\}\hfill & L{\left(s\right)}^{in}\cap L{\left(t\right)}^{out}\ne \varnothing \hfill \end{array}\right.$$

(2)

A naive way to build these indexes is through two executions of Dijkstra’s algorithm. Although this method needs to be more obvious and effective, we will explain the details to discuss the next method. Let $V=\{v_1,v_1,...,v_n\}$, start with an empty index $L_0^{in}$, where $\forall u\in V,L_0^{in}\left(u\right)=\varnothing$. Suppose Dijkstra is used on each vertex in the order $v_1,v_2,...,v_n$. After the k-th Dijskstra on a vertex $v_k$, the distances of $v_k$ are added to the coverages of the vertices reached, whereby $L_k^{in}\left(u\right)=L_{k-1}^{in}\left(u\right)\cup \left\{(v_k,d_G(v_k,u))\right\}$ for each $u\in V$ with $d_G(v_k,u)\ne \infty$, where $d_G(u,v)$ is the distance from node u to node v within the graph G. It is important to mention that the coverages of the vertices reached are not changed, which implies $L_k^{in}\left(u\right)=L_{k-1}^{in}\left(u\right)$ for each $u\in V$ with $d_G(v_k,u)=\infty$. By performing this procedure starting with $L_0^{out}$, the same result can be obtained but considering the output edges.

Thus, $L_n^{in}$ and $L_n^{out}$ are the final indices contained in $L_n$. Obviously, $Q(s,t,L)=d_G(s,t)$ for any pair of vertices, therefore $L_n^{in}$ and $L_n^{out}$ are the 2-hop covers of G. This is because, if s and t are reachable, then $(s,0)\in L_n^{in}\left(s\right)$ and $(s,d_G(s,t))\in L_n^{out}\left(t\right)$.

As mentioned at the beginning of the description, this way of creating indexes could be more efficient. For this reason, pruning is added to the naive method. This technique reduces the search space considerably. Like the naive method, a pruned search is conducted with Dijkstra’s algorithm starting from the vertices in the following order: $v_1,v_2,...,v_n$. Start with a pair of indices $L_0^{in}$, $L_0^{out}$ and create indices $L_k^{in}$, $L_k^{out}$ from $L_{k-1}^{in}$ and $L_{k-1}^{out}$, respectively, using the information obtained by the k-th execution of pruned Dijkstra for vertex $v_k$.

The pruning process is as follows: suppose we have the indices $L_{k-1}^{out}$ and $L_{k-1}^{in}$ and we execute the pruned Dijkstra from $v_k$ to create a new index $L_k^{out}$. Assuming that we are visiting a vertex u with distance $\delta$. If $Q(s,t,L_{k-1})\le \delta$, then we prune u, that is, we do not add $(u_k,\delta )$ to $L_k^{out}\left(u\right)$ and we do not add any neighbors of u to the priority queue. If the condition is not met, then $(u_k,\delta )$ is added to the cover of u, and Dijkstra is executed as normal. As with the naive method, we set $L_k^{in}\left(u\right)=L_{k-1}^{in}\left(u\right)$ and $L_k^{out}\left(u\right)=L_{k-1}^{out}\left(u\right)$ for all vertices that were not reached in the k-th execution of the pruned Dijkstra. In the end, $L_k^{out}$ and $L_k^{in}$ are the final indices contained in $L_k^{{}^{\prime }}$.

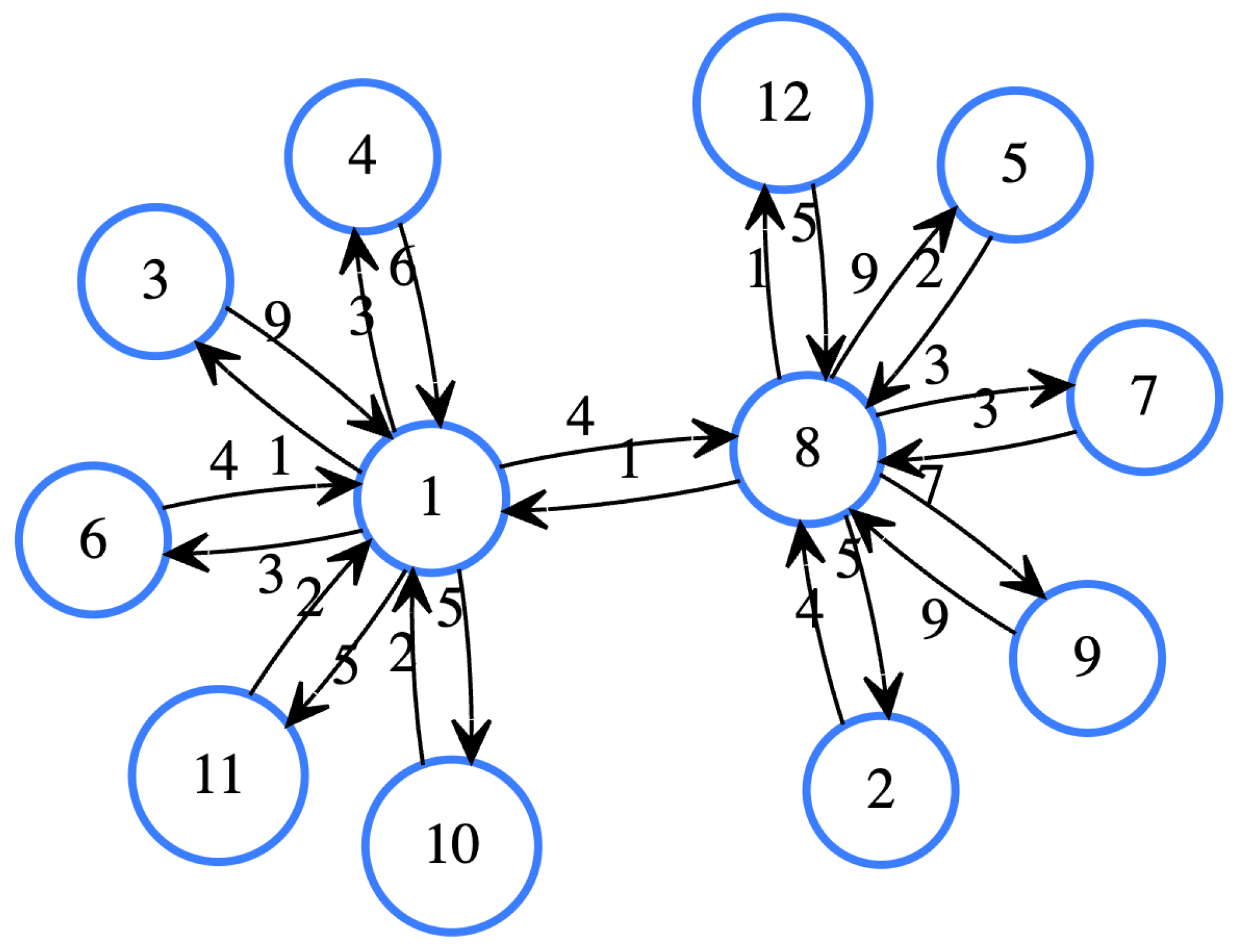
Figure 3 shows an example of the algorithm acting on the graph represented in the figure, taking the order of execution as $1,8,2,3,4,5,6,7,9,10,11,12$. The first pruned Dijkstra from vertex one visits all other vertices, forward and reverse (see Figure 4a and Figure 4b). During the next iteration from vertex 8 (Figure 5e), when node one is visited, given that $Q(8,1,L_1^{{}^{\prime }})=1=\delta (8,1)=$1, vertex one is pruned and none of its neighbors are visited anymore; the same occurs in the opposite direction (see Figure 5f). With these two executions, it is possible to cover all the shortest paths, and once the process is executed on the remaining vertices, they will only refer to themselves. The pruned Dijkstra algorithm is described in Algorithm 2, and the whole algorithm for constructing indices is presented in Algorithm 1.

Algorithm 1:APSP_PDijkstra

We executed the pruned Dijkstra in order $v_1,v_2,...,v_n$; and arbitrarily chose the order of the vertices; however, it is relevant for a good algorithm performance. Ideally, start from central vertices so that many shortest paths pass through them. There are many strategies to order the vertices; some of the most used ones apply to order by centralities. In this work, we choose the order of the vertices by the degree of centrality. The graphs generated by semantic networks behave like networks without scale, where high-degree vertices provide high connectivity to the network. In this way, the shortest path between two vertices will likely pass through those nodes.

Algorithm 2:The Pruned Dijkstra

Algorithm 3: Check distance from source to target nodes according a 2-hop cover

3.2.1. The pruned Dijkstra analysis

To prove the correctness of the method, it suffices to show that the algorithm computes a two-hop coverage, that is, $Q(s,t,L_k^{{}^{\prime }})=d_G(s,t)$ for any $s,t\in V$. Let $L_k$ be the index built without the pruning process, so it is a two-hop coverage; $L_k^{{}^{\prime }}$ is the index built by applying the pruning process. Since there exists a node $v_j$ such that $(v_j,d_G(v_j,s))\in L_k{\left(s\right)}^{in}$, $(v_j,d_G(v_j,t))\in L_k{\left(t\right)}^{out}$ and ${\delta }_{v_j,s}+{\delta }_{v_j,t}=d_G(s,t)$, the goal is to show that $v_j$ also exists in $L_k^{{}^{\prime }}{\left(s\right)}^{in}$ and $L_k^{{}^{\prime }}{\left(t\right)}^{out}$.

Theorem 1.

For $k=1,...,n$, and $s,t\in V$, $Q(s,t,L_k^{{}^{\prime }})=Q(s,t,L_k)$

Proof. 

Let $s,t\in V$, assume there is a path between them, j the smallest number such that $(v_j,d_G(v_j,s))\in L_k{\left(s\right)}^{in}$ , $(v_j,d_G(v_j,t))\in L_k{\left(t\right)}^{out}$ and ${\delta }_{v_j,s}+{\delta }_{v_j,t}=d_G(s,t)$. We must show that $(v_j,d_G(v_j,s))$ and $(v_j,d_G(v_j,t))$ also lie in $L_k^{{}^{\prime }}{\left(s\right)}^{in}$ and $L_k^{{}^{\prime }}{\left(t\right)}^{out}$ respectively; that is to say that $Q(s,t,L_k^{{}^{\prime }})=Q(s,t,L_k)$. To prove that $v_j\in L_k^{{}^{\prime }}{\left(t\right)}^{out}$, first, for any $i<j$, suppose $v_i\in P_G(s,v_j)$, where $P_G(a,b)$ is a path between a and b. If we assume that $v_i\in P_G(v_j,t)$, by inequality:

$$\begin{array}{cc}\hfill Q(s,t,L_k)& =d_G(s,v_j)+d_G(v_j,t)\hfill \\ \hfill & =d_G(s,v_j)+d_G(v_j,v_i)+d_G(v_i,t)\hfill \\ \hfill & \ge d_G(s,v_i)+d_G(v_i,t)\hfill \end{array}$$

Since $(v_i,d_G(v_i,s))\in L_k{\left(s\right)}^{in}$ and $(v_i,d_G(v_i,t))\in L_k{\left(t\right)}^{out}$, it contradicts the fact that j is the smallest number. Therefore, $v_i\notin P_G(v_j,t)$ for no $i<j$.

Now, we prove that $(v_j,d_G(v_j,t))\in L_k^{{}^{\prime }}{\left(t\right)}^{out}$. Suppose we execute the j-th Dijkstra pruned from node $v_j$ to construct index $L_j^{{}^{\prime }out}$. Let $t\in P_G(v_j,t)$. Since there is no $v_i\in P_G(v_j,t)$ for $i<j$, it means that there is no vertex in the i-th pruned Dijkstra iteration that covers the shortest path of $v_j$ to t, therefore $Q(v_j,t,L_{j-1}^{{}^{\prime }})>d_G(v_j,t)$. Consequently, vertex t is visited without pruning and $(v_j,d_G(v_j,t))\in L_j{\left(t\right)}^{out}\subseteq L_k{\left(t\right)}^{out}$ is added.

Finally, suppose we execute the j-th Dijkstra pruned from $v_j$, but this time to build $L_j^{{}^{\prime }in}$. If s and t are reachable in G, it means that there is a path between $v_j$ and s taking into account the input edges, or what is the same, there is $P_G(s,v_j)$. Since we already proved that $v_i\notin P_G(v_j,t)$ for $i<j$, it means that $v_j$ is a neighbor of s or $v_j=s$, and since $v_j$ is the initial vertex of the path $P_G(v_j,t)$, then $v_j$ is the least distance neighbor sharing s. In any of the cases $Q(s,v_j,L_{j-1}^{{}^{\prime }})>d_G(s,v_j)$, therefore the node s is visited without pruning (remember that it is considering the input edges). Consequently $(v_j,d_G(v_j,s))\in L_j{\left(s\right)}^{in}\subseteq L_k{\left(s\right)}^{in}$ is added.    □

As mentioned, the order in which the nodes are processed influences the algorithm’s performance. Is there an order of execution such that the construction time is the minimum possible? The answer is yes; however, finding such an order is challenging. So, there are two approaches: the first is to find the minor nodes that cover all the shortest paths, which is a much bigger problem since this is an instance of the minimum vertex coverage problem that is NP-hard. The second approach is a parameterized perspective; specifically, the explored parameter is the width of the tree. It also relies on the process of centroid decomposition of the tree [73]. This approach deduces the following lemma; the formal proof is made in [70].

Lemma 1.

Let w be the width of the graph of G. There is a vertex order with which the pruned Dijkstra method executes in time $\mathcal{O}\left(wmlog\left(n\right)+w^{2}n{log}_2\left(n\right)\right)$ for preprocessing, stores an index with space $BigOwnlog\left(n\right)$ and answers each query in $\mathcal{O}\left(wlog\left(n\right)\right)$ time.

Considering that this research study does not look for minimum two-hop coverage, using the upper bound of $\mathcal{O}\left(wmlog\left(n\right)+w^{2}n{log}_2\left(n\right)\right)$ for the algorithm can be considered an inconsistency. Since there is no guarantee that the chosen order (degree centrality) is the same as the order necessary to achieve such computational complexity, however, what we concluded for our implementation is that it cannot be faster than the one theoretically obtained using the order with which $\mathcal{O}\left(wmlog\left(n\right)+w^{2}nisachieved.lo{g}_2\left(n\right)\right)$. That is, our implementation has a lower bound $\Omega (wmlog\left(n\right)+w^{2}n{log}_2\left(n\right))$. Also, in terms of Dijkstra’s algorithm, we can hypothesize that the construction of the coverage using the pruned process, regardless of the order of execution, is much smaller than for the construction of the naive coverage in highly connected graphs, that is to say, that $\mathcal{O}\left(mn+n^{2}log\left(n\right)\right)$.

3.3. The sketches

Sketch-based algorithms are methods comprising two general processes: offline and online. In the offline process, the sketches (that are crucial nodes, initially random) are computed from which the shortest path to all the other nodes is calculated. In the online process, we compute the closest distance between a pair of nodes $u,v\in V$ from the closest common sketch between them.

The offline process consists of sampling $log\left(n\right)$ sets of seed nodes, each containing a subset $S\subseteq V$ of size $2^i,i=1,2,3,...,log\left(n\right)$. From each set, the closest seed $s\in S$ of each node is stored together with its distance; that is, for each node u, a sketch of the form SKETCH$\left(u\right)=\left\{(s,{\delta }_{s,u})\right\}$ is created. Therefore, the final size of the sketch for each node is $log\left(n\right)$. This construction can be made with Dijkstra’s algorithm. The node $s\in S$ closest to u is called the seed of u. This procedure is executed k times with different sample sizes. At the end of the k iterations, we obtain $klog\left(n\right)$ seeds for each node.

As with the previous algorithm, we must compute two sketches for each node. The first SKETCH${}^{out}\left(u\right)$ and SKETCH${}^{in}\left(u\right)$ representing the distance from node $u\in V$ to the nearest seed and vice versa. We do this by running the search algorithm twice; one considering the input edges, the other with the output edges.

We can randomly choose S, using some criteria to bias our choice. For example, we can discard those nodes whose degree is less than two. We can also take advantage of the graph’s structure, and its specific properties5. In the Algorithm 4, the proposed pseudocode is shown to generate the sketches of each node.

Algorithm 4:Sketches_DIS-C: offline sampling

For each sample, we obtain the closest seed node and its distance for each node. This process is done with the classical Dijkstra multi-source algorithm. In this way, the seed nodes for each $u\in V$ are computed (see Algorithm 5).

Algorithm 5:Sketches_DIS-C: k sketches offline

In each iteration, we generated a sketch from an offline sample; therefore, at the end of the algorithm, there will be $klog\left(n\right)$ seeds for each node.

The second process of the method is the online one. The calculation of the approximate minimum distance between nodes u and v is done by looking at the distance from u and v to any node w that appears in both ${\mathcal{S}}_u^{in}$ as in ${\mathcal{S}}_v^{out}$. So, we compute the path length from u to v by adding the distance from u to w plus the distance from w to v. The minimum distance is taken if there are two or more common nodes w. Algorithm 6 shows the proposal to perform said calculation.

Algorithm 6:Sketches_DIS-C: k sketches online

Finally, to solve the APSP problem, it is necessary to create another algorithm that it executes for each pair of nodes (Algorithm 7).

Algorithm 7:Sketches_DIS-C: k sketches online APSP

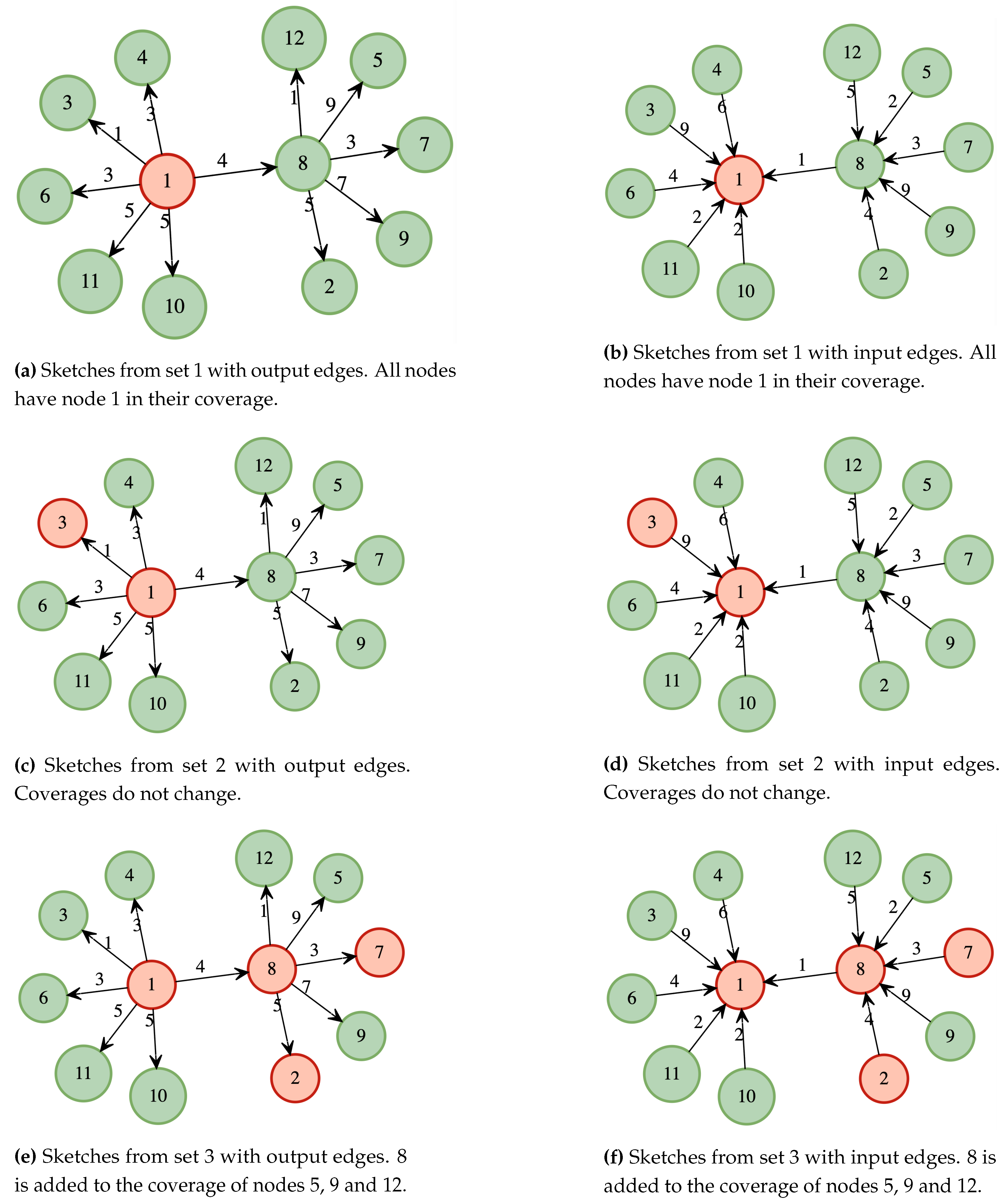
Figure 5 shows an example of the described procedure. The graph of Figure 3 is taken as a reference. Since there are 12 nodes, the number of seed sets is 3 (${log}_2\left(12\right)=3$), and the size of the sets are 1, 2, and 4, respectively. The nodes in each set are 1; for the first, $3.1$; for the second, and $8,1,2,7$, for the last.

In the first iteration (Figure 5a), all the nodes have node 1 in their coverage; this also happens for the input edges (see Figure 5b). In the second iteration (Figure 5c and Figure 5d), the coverages do not change since node three does not cover any path shorter than those already covered by node 1, finally, in the last iteration (Figure 5e and Figure 5f), we have node 8 in the seed set, this covers the shortest path of its neighbors, except those that are also in the set; therefore, nodes 5, 12 and 9 will have 8 in their coverage. On the other hand, nodes 2 and 7 are contained in their respective coverage.

3.3.1. Sketches analysis

In the sketches-based method, there is no accuracy test for general graphs. It means that the method does not guarantee exact node labeling to answer the exact distance between all pairs of vertices. As far as computational complexity is concerned, it is easy to determine.

Theorem 2.

For a set of nodes $S\subseteq V$ such that the size of said set is $2^w$ for $0\le w\le n$, the computational complexity of the algorithm is $\mathcal{O}\left(w(m+nlog(n\left)\right)\right)$.

Proof. 

We know that the sketch-based method selects a number w founded on the number of nodes in the graph, that is, $w=f\left(V\right)\le \left|V\right|$. Then, given w, $Q_i$ subsets of nodes are created for $i=0,1,2,...,logn$ such that the size of each one is $|Q_i|=2^i|i=0,1,...,w$. It can be seen that $S={\bigcup }_{i=0}^w{Q}_i$. For each of the $Q_i$ subsets, the multi-source Dijkstra algorithm is executed, with the aim of finding, for all the nodes of G, the closest node of the $Q_i$ set. Dijkstra’s algorithm from multiple sources has a complexity of $\mathcal{O}\left(m+nlog\left(n\right)\right)$; for each subset of nodes, it is necessary to apply (independent of size) a single execution of Dijkstra’s algorithm. Therefore, since there are w subsets of nodes, w Dijkstra processes from multiple sources must be executed; that is to say, in total, we reach a complexity of $\mathcal{O}\left(w(m+nlog(n\left)\right)\right)$. □

In the implementation carried out in this work, we determined w by a logarithmic function $w={log}_2\left(n\right)$, where $n=\left|V\right|$. In this way, we ensured that $\left|S\right|<\left|V\right|$. Therefore, for the implementation made, the method has a complexity of $\mathcal{O}\left({log}_2\left(n\right)(m+n{log}_2\left(n\right))\right)$.

4. Experiments and execution scenarios

This section specifies the different experiments carried out, the proposed datasets, and the execution environments.

4.1. The datasets

Datasets are pairs of words to which, through human judgment, a numerical value is assigned. We divide these sets into two families: those that measure semantic similarity and those that measure semantic relatedness. These sets are described in Table 4.

Therefore, we run the process through a script that, for each data set, takes a couple of words, generates the conceptual graph that connects them, and applies the DIS-C algorithm to find the conceptual distance. We repeat this process with all the pairs of words, and in the end, all the graphs generated from a set of words are unified to obtain a graph with all the pairs of words in the set. We also apply the DIS-C algorithm to the unified graph from this last execution, where the conceptual distances are registered. The objective of applying DIS-C to graphs that connect only a couple of words is to measure the runtime with different sizes of graphs and thus have a much more extensive record.

4.2. Evaluation metrics

We divide the evaluation metrics for this research work into performance and semantics. The first corresponds to the running time measurement, related to the graph’s number of nodes and edges. Semantic metrics measure the precision in estimating similarity, using the Pearson correlation factor (Equation 3), the Spearman rank correlation factor (Equation 4), and the harmonic score (Equation 5).

$$r=\frac{{\sum }_{i=1}^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_{i=1}^n{(X_i-\overline{X})}^2}\sqrt{{(Y_i-\overline{Y})}^2}}$$

(3)

$$p=1-\frac{6{\sum }_{i=1}^n{d}_i^2}{n(n^2-1)},d_i=(x_i-y_i)$$

(4)

$$h=\frac{2rp}{r+p}$$

(5)

Pearson’s correlation compares human similarity vectors and has been widely used to evaluate similarity estimation methods between words and concepts. Spearman’s rank correlation ranks invariants and allows comparison of the intrinsic power of word similarity measures. In addition, we used harmonic scoring, which combines Pearson and Spearman correlations to provide a single weighted score for assessing word similarity methods. These correlation measurements are essential for evaluating and comparing similarity methods in the literature.

5. Experimental results

In this section, we describe the results of the different experiments. In the first part, we analyze the performance metrics on the generated graphs; also, we compare the control algorithm and those proposed. The second section analyzes the results of the semantic metrics.

5.1. Generated graphs and performance

We generated a graph connecting each pair of words for each dataset to generate the corresponding unified graphs later. Table 5 shows the size of these graphs. The last row of the table (labeled ’All’) refers to the union of all graphs; additionally, algorithms were applied to this graph.

Below are a series of graphs related to each proposed algorithm’s runtime. Figure 6 shows the runtime of the control algorithm, the pruned Dijkstra algorithms, and Sketches. At specific points, the runtime is increased in a “abnormal” way; this is due to a parameter other than the size of the graph; specifically, it is the convergence threshold of the algorithm. It indicates that more iterations were necessary for this dataset, particularly the graph structure, to reach the threshold.

The convergence threshold is a function of the total generality of the graph, that is, the sum of all the generalities of each node. The total generality of the graph depends on the distance value between each pair of nodes provided by the APSP algorithm; for this reason, the algorithms that obtain the shortest actual distance always reach the convergence threshold in the same number of iterations. In this case, there is the control algorithm and the pruned Dijkstra. On the other hand, the Sketches algorithm varies in the number of iterations to reach the threshold; however, as a general rule, such many iterations cannot be less than the number reached by the control algorithm. The reason for this is that the control algorithm obtains the exact shortest distances, so the total generality of the graph is the minimum possible. Since it is known that the Sketches algorithm (and any other approximation algorithm) cannot compute the shortest distance less than the real one, then the generality of the graph cannot be less than the minimum generality.

In the same Figure 6, it can be seen that most of the proposed algorithms have a longer runtime than the control algorithm; this is mainly due to the density of the graphs, that is, the generated graphs have few edges and can be considered sparse graphs. It is noted that only the Sketches algorithm with $k=1$ stays below the time of the control algorithm. However, it is not a considerable acceleration. For the acceleration to be significant, it must be reduced by at least one order of magnitude, considering that the runtime is in the order of days in the results analyzed. Since the proposed algorithms are divided into two significant processes (construction and query), we break down the runtime these two processes take separately. Figure 7 illustrates this particular task.

The query time is the bottleneck in the algorithms. In the complexity analysis of the query process, we established that the complexity of the Sketches algorithm depends on the size of the coverages, and these are a function of k, so the behavior when increasing the value of k is predictable, as shown in Figure 7. In the case of the pruned Dikstra algorithm, the size of the coverages is enormous for more general nodes and decreases as a function of such generality. It motivates some nodes to find their shortest distance, which will take longer; this behavior speeds up the total query time. Although a binary search can be used instead of a linear one, it does not underestimate the quadratic factor inherent to APSP and whose behavior is reflected in the results. This inconvenience led us to conjecture that it is possible to calculate the generality of the graph only with the coverages of the nodes. It means that solving APSP to calculate the generality is unnecessary, so the quadratic factor of APSP is eliminated.

Due to the last basis, a framework was established for computing generality, only considering the coverage of the nodes, because we defined generality as the average of the conceptual distances from concept x to all other concepts, divided by the sum of the average conceptual distances and all concepts in the ontology. In the case of the pruned Dijkstra, the more general concepts contain a more significant coverage; their area of influence is much larger than the less general concepts. The area of influence can be used in such a way that the generality of a node depends on it. The insight of generality is respected, given that the information provided by other concepts to the concept x (the distances of the coverage $L_x^{in}$) and the information that the concept x itself provides to its related concepts (the distances of the coverage $L_x^{out}$). We can see it as a generality calculation based on the extended neighborhood of the nodes represented through their coverage. We can perform this since the covers map the graph’s topology. So, we performed the generality computation as in Equation 6, and from now on, versions of DIS-C that use this type of generality are referred to as simple algorithm.

$$g\left(x\right)=\frac{{\sum }_{b\in L_x^{out}}\delta (b,x)}{{\sum }_{b\in L_x^{in}}\delta (b,x)}$$

(6)

In Figure 8, we can see the total cost of running the simple algorithms compared to the others. An apparent acceleration is observed concerning the proposed algorithms’ first versions.

There is a considerably higher speed for the simple pruned Dijkstra algorithm, which means reducing one order of magnitude for the most extensive graph from days to hours. In the case of Sketches algorithms, there is a more predictable, linear behavior concerning k; that is, the runtime for $k=2$ is two times less than for $k=1$, and so on.

We identified a significant speedup when using the simple version of the algorithms. Likewise, the use of the proposed algorithms in their original form is ruled out, at least in a practical sense. The practical utility of conceptual distance is put on trial in the following section: how much precision is lost in the calculation and if it is compensated by the acceleration achieved.

5.2. Conceptual distance results

In this section, we analyzed the results of the conceptual distance obtained in the different datasets evaluated, considering the metrics previously proposed.

Before analyzing the group of sets, we only analyzed the results of one set individually, the MC30. The results of the pruned Dijkstra algorithm correspond directly to the results of the control algorithm because the process obtains the exact shortest distances. The Sketches algorithm adjusts satisfactorily to the conceptual control distance results; the closeness of these results depends, in the first instance, on the value of k; the higher it is, the smaller the difference with the original results. This behavior allows us to notice a high correlation with the control algorithm and, in general, with the other versions of the algorithms.

Figure 9 and Figure 10 show the correlation matrix of Person and Spearman, respectively. The upper part of the diagonal represents the correlation between the words in the $a-b$ sense (conceptual distance from the word “a” to the word “b”). In contrast, the lower diagonal is the correlation of $b-a$.

The matrices showed a very high correlation among all the algorithms. Although the results in all cases are excellent, the correlation values of the algorithms concerning the control are the most relevant for the analysis; these are those represented in row 1 and column 1, with values of $a-b$ and $b-a$, respectively. In the first case, the lowest correlation value (0.94) corresponds to the Sketches algorithm with $k=1$; however, the correlation growth can be observed depending on the increase in the value of k. This same behavior is replicated in the Spearman matrix and the results of the sense $b-a$ of the concepts. Regarding the pruned Disjktra algorithms, in its standard version, the correlation is 1, while in its simple version, it reaches values very close to 1 (0.99). These results suggest that the use of the algorithms in its standard version or its simple version is indifferent since, in both cases, the correlation gained is quite similar and identical in some instances.

We also performed experiments with different datasets (with diverse amounts of nodes, paths, and edges). In this sense, Table 6 and Table 7 show the results of the Pearson correlation obtained by all the algorithms and their configurations in the eleven datasets. Moreover, Table 8 and Table 9 show the Spearman correlation.

All the algorithms obtained a correlation that is considered high (greater than 0.7). In both types of correlation, the algorithm with the best performance was the pruned Dijkstra. The one that obtained the lowest correlation was the Sketches algorithm with $k=1$, with values ranging from 0.77 to 0.81; although they cannot be considered bad results, they do show a disparity with all the others. If the analysis is focused on the Sketches algorithm with its different configurations, the behavior observed individually in the MC30 dataset can be confirmed; that is, increasing the value of k also increases the probability of getting a better correlation.

Finally, the harmony values are shown in Table 10; these values unify the performance obtained by both correlations. As mentioned in the previous sections, this table demonstrates that the pruned Dijkstra algorithm achieves the highest correlation values. In contrast, the Sketches algorithm performs better depending on the given value of its k parameter.

With these results, we can conclude that any proposed algorithms can replace Dijkstra’s algorithm regarding the conceptual values between each concept, considering the function of solving the APSP problem. However, if we include the runtime results, the practical use of the algorithms, the pruned Dijkstra and Sketches in their regular (or standard) version can be immediately ruled out since their growth exceeds Dijkstra’s speed, at least with the graphs used. In this way, the algorithms in their simple version are the most useful in practice; if the highest precision is required in computing the distance, the best option is the simple version of the pruned Dijkstra.

On the other hand, if speed is the priority, the simple version of Sketches with moderate values (greater than one but less than 20) in the k parameter is a better alternative. We must also consider the size of the conceptualization; for sizes, less than a thousand concepts, the type of algorithm is indifferent, and the use of Dijkstra is a better option since the computation time is not excessive and ensures the calculation as proposed in the DIS-C model. An exciting way to take advantage of the speed of the Sketches algorithm with low parameters (less than 5) in k is when it is required to carry out tests quickly on systems that use DIS-C or directly when we desire to compare the method with others. In this sense, the implementation of sketches can provide a behavior guide; that is to say, if good results are obtained with the simple version, it is pretty confident that by implementing the model as it was proposed at the beginning (with Dijkstra’s algorithm) it achieves, at least, the same results as its simple version. The preceding considers that precision is the most crucial thing and computation time is not a priority, and even if time is a limitation, the pruned Dijkstra algorithm can be used as a replacement for Dijkstra, given its very high correlation.

6. Conclusions

With the development of the present research work, we obtained several implementations for computing the conceptual distance based on the DIS-C method that considerably reduces the processing time up to $2,381$ times faster, according to the experiments carried out. One of the main interests is maintaining a reduced loss of precision in distance computing concerning the original version of DIS-C, which was more than achieved given the experimental results, reaching correlation values of $1.0$ with specific implementations.

Moreover, we achieved the acceleration obtained by replacing the use of APSP as a sub-process for the propagation of conceptual distances between all pairs of concepts and the main factor for the calculation of generality by the application of the concept of coverage of a node, which is built from the proposed algorithms. This milestone marks the elimination of the most costly process in the method.

Likewise, the results achieved thanks to the simple implementations of the proposed algorithms confirmed that the use of the complete topology of a graph for the calculation of conceptual distance in the DIS-C model is excessive and supposes a high computational cost. In this sense, we experimentally demonstrated that the coverage can be a reliable approximation for generality computing.

Regarding the APSP problem, using two-hop coverages generated through Dijkstra’s pruned and sketches algorithm can be a slower method than Dijkstra’s algorithm, at least in weighted, directed graphs and with a low density. However, in undirected graphs, the hypothesis is supported that the coverage method can surpass, at runtime, traditional algorithms (such as BFS) for the same purpose because, within the literature, there are multiple specific optimizations for these graphs.

Finally, the proposed methodology allows a logical order, oriented to practice, of the process of design, analysis, implementation, and experimentation of the algorithms. Such an order lets us verify that it is possible to reduce the runtime of the DIS-C method without losing caution in computing the conceptual distance without the need to use the APSP problem as a basis for the calculation of generality.