Submitted:
09 October 2023
Posted:
11 October 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Method
3. Results and Discussion
| IC | GLM | GLMM (group-random effect) | ||||||
| logit | Probit | cloglog | cauchit | logit | probit | cloglog | cauchit | |
| AIC | 132.678 | 130.395 | 154.461 | 149.267 | 134.678 | 132.395 | 156.461 | 151.267 |
| BIC | 173.625 | 171.342 | 195.407 | 190.214 | 180.174 | 177.892 | 201.957 | 196.763 |
| AICc | 132.939 | 130.656 | 154.722 | 149.528 | 134.998 | 132.715 | 156.780 | 151.587 |
| CAIC | 182.625 | 180.342 | 204.407 | 199.214 | 190.174 | 187.892 | 211.957 | 206.763 |
| GLMM (id-random effect) | GLMM (id and group-random effect) | |||||||
| logit | Probit | cloglog | cauchit | logit | probit | cloglog | cauchit | |
| AIC | 98.550 * | 119.813 | 121.752 | 149.044 | 99.962 | 117.486 | 120.208 | 151.044 |
| BIC | 144.047 * | 165.309 | 167.248 | 194.541 | 150.008 | 167.532 | 170.254 | 201.090 |
| AICc | 98.870 * | 120.133 | 122.071 | 149.364 | 100.346 | 117.870 | 120.592 | 151.428 |
| CAIC | 154.047 * | 175.309 | 177.248 | 204.541 | 161.008 | 178.532 | 181.254 | 212.090 |
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aalaei, S.; Shahraki, H.; Rowhanimanesh, A.; Eslami, S. Feature selection using genetic algorithm for breast cancer diagnosis: experiment on three different datasets. Iranian journal of basic medical sciences 2016, 19, 476.
- Kadhim, R. R.; Kamil, M. Y. Comparison of breast cancer classification models on Wisconsin dataset. Int J Reconfigurable & Embedded Syst ISSN 2022, 2089, 4864. [CrossRef]
- Roser, M.; Ritchie, H. "Cancer". Published online at OurWorldInData.org. 2015. Available online: https://ourworldindata.org/cancer (accessed 16 August 2023).
- Our World in Data. Cancer Deaths by Type, World, 2019. Available online: https://ourworldindata.org/cancer (accessed 16 August 2023).
- Desantis, C. E.; Ma, J.; Gaudet, M. M.; Newman, L. A.; Miller, K. D.; Goding Sauer, A.; Siegel, R. L. Breast cancer statistics, 2019. CA: a cancer journal for clinicians, 2019, 69, 438-451.
- Jain, R.; Abraham, A. A comparative study of fuzzy classification methods on breast cancer data. Australasian Physics & Engineering Sciences in Medicine 2004, 27, 213-218. [CrossRef]
- Karabatak, M.; Ince, M. C. An expert system for detection of breast cancer based on association rules and neural network. Expert systems with Applications 2009, 36, 3465-3469. [CrossRef]
- Fallahi, A.; Jafari, S. An expert system for detection of breast cancer using data preprocessing and bayesian network. International Journal of Advanced Science and Technology 2011, 34, 65-70.
- Kumar, G. R.; Ramachandra, G. A.; Nagamani, K. An efficient prediction of breast cancer data using data mining techniques. International Journal of Innovations in Engineering and Technology (IJIET) 2013, 2, 139.
- Borges, L. R. Analysis of the Wisconsin breast cancer dataset and machine learning for breast cancer detection. Group 2015, 1, 15-19.
- Dubey, A. K.; Gupta, U.; Jain, S. Analysis of k-means clustering approach on the breast cancer Wisconsin dataset. International journal of computer assisted radiology and surgery 2016, 11, 2033-2047. [CrossRef]
- Banerjee, C.; Paul, S.; Ghoshal, M. A Comparative study of different ensemble learning techniques using wisconsin breast cancer dataset. In 2017 International Conference on Computer, Electrical & Communication Engineering (ICCECE), (22-23, December, 2017).
- Alshayeji, M. H.; Ellethy, H.; Gupta, R. Computer-aided detection of breast cancer on the Wisconsin dataset: An artificial neural networks approach. Biomedical Signal Processing and Control 2022, 71, 103141. [CrossRef]
- Mumtaz, K.; Sheriff, S. A.; Duraiswamy, K. Evaluation of three neural network models using Wisconsin breast cancer database. In 2009 International Conference on Control, Automation, Communication and Energy Conservation. (June 2009).
- Sarvestani, A. S.; Safavi, A. A.; Parandeh, N. M.; Salehi, M. Predicting breast cancer survivability using data mining techniques. In 2010 2nd International Conference on Software Technology and Engineering. (2010, October).
- Marcano-Cedeño, A.; Quintanilla-Domínguez, J.; Andina, D. WBCD breast cancer database classification applying artificial metaplasticity neural network. Expert Systems with Applications 2011, 38, 9573-9579. [CrossRef]
- Salama, G. I.; Abdelhalim, M.; Zeid, M. A. E. Breast cancer diagnosis on three different datasets using multi-classifiers. Breast Cancer (WDBC), 2012, 32, 2.
- Shajahaan, S. S.; Shanthi, S.; ManoChitra, V. Application of data mining techniques to model breast cancer data. International Journal of Emerging Technology and Advanced Engineering 2013, 3, 362-369.
- Vig, L. Comparative analysis of different classifiers for the wisconsin breast cancer dataset. Open Access Library Journal 2014, 1, 1. [CrossRef]
- Sivakami, K.; Saraswathi, N. Mining big data: breast cancer prediction using DT-SVM hybrid model. International Journal of Scientific Engineering and Applied Science (IJSEAS), 2015, 1, 418-429.
- Kumari, M.; Singh, V. Breast cancer prediction system. Procedia computer science 2018, 132, 371-376. [CrossRef]
- Obaid, O. I.; Mohammed, M. A.; Ghani, M. K. A.; Mostafa, A.; Taha, F. Evaluating the performance of machine learning techniques in the classification of Wisconsin Breast Cancer. International Journal of Engineering & Technology, 2018, 7, 160-166.
- Sultana, J.; Jilani, A. K. Predicting breast cancer using logistic regression and multi-class classifiers. International Journal of Engineering & Technology 2018, 7, 22-26. [CrossRef]
- Mohammed, S. A.; Darrab, S.; Noaman, S. A.; Saake, G. Analysis of breast cancer detection using different machine learning techniques. In Data Mining and Big Data: 5th International Conference, DMBD 2020, Belgrade, Serbia, (14–20 July 2020).
- Mushtaq, Z.; Yaqub, A.; Sani, S.; Khalid, A. Effective K-nearest neighbor classifications for Wisconsin breast cancer data sets. Journal of the Chinese Institute of Engineers 2020, 43, 80-92. [CrossRef]
- MurtiRawat, R.; Panchal, S.; Singh, V. K.; Panchal, Y. Breast Cancer detection using K-nearest neighbors, logistic regression and ensemble learning. In 2020 international conference on electronics and sustainable communication systems (ICESC). (July 2020).
- Seddik, A. F.; Shawky, D. M. Logistic regression model for breast cancer automatic diagnosis. In 2015 SAI Intelligent Systems Conference (IntelliSys). (November 2015).
- Mathew, T. E; Kumar, K. A. A logistic regression based hybrid model for breast cancer classification. Indian Journal of Computer Science and Engineering (IJCSE) 2020, 11, 899-903.
- Li, Y.; Chen, Z. Performance evaluation of machine learning methods for breast cancer prediction. Appl Comput Math 2018, 7, 212-216.
- Magboo, V. P. C.; Magboo, M. S. A. Machine learning classifiers on breast cancer recurrences. Procedia Computer Science 2021, 192, 2742-2752. [CrossRef]
- Haziemeh, F. A.; Darawsheh, S. R.; Alshurideh, M.; Al-Shaar, A. S. Using logistic regression approach to predicating breast cancer dataset. In The Effect of Information Technology on Business and Marketing Intelligence Systems. Cham: Springer International Publishing, 2023, pp. 581-591.
- Mathew, T. E. A logistic regression with recursive feature elimination model for breast cancer diagnosis. International Journal on Emerging Technologies 2019, 10(3), 55-63.
- Basunia, M. R.; Pervin, I. A.; Mahmud, M.; Saha, S.; Arifuzzaman, M. On predicting and analyzing breast cancer using data mining approach. In 2020 IEEE Region 10 Symposium (TENSYMP). (June 2020).
- Al-Azzam, N.; Shatnawi, I. Comparing supervised and semi-supervised machine learning models on diagnosing breast cancer. Annals of Medicine and Surgery 2021, 62, 53-64. [CrossRef]
- Khairunnahar, L.; Hasib, M. A.; Rezanur, R. H. B.; Islam, M. R.; Hosain, M. K. Classification of malignant and benign tissue with logistic regression. Informatics in Medicine Unlocked 2019, 16, 100189. [CrossRef]
- Islam, M. M.; Haque, M. R.; Iqbal, H.; Hasan, M. M.; Hasan, M.; Kabir, M. N. Breast cancer prediction: a comparative study using machine learning techniques. SN Computer Science 2020, 1, 1-14.
- Mushtaq, Z.; Yaqub, A.; Hassan, A.; Su, S. F. Performance analysis of supervised classifiers using PCA based techniques on breast cancer. In 2019 international conference on engineering and emerging technologies (ICEET), (February 2019).
- Hossin, M. M.; Shamrat, F. J. M.; Bhuiyan, M. R.; Hira, R. A.; Khan, T.; Molla, S. Breast cancer detection: an effective comparison of different machine learning algorithms on the Wisconsin dataset. Bulletin of Electrical Engineering and Informatics 2023, 12, 2446-2456.
- Rekha, R.; Vinoci, K. L. Wisconsin Breast Cancer Detection Using L1 Logistic Regression. In 2023 International Conference on Intelligent Systems for Communication, IoT and Security (ICISCoIS). (February, 2023).
- Mangasarian, O. L.; Wolberg, W. H. Cancer diagnosis via linear programming. SIAM News 1990, 23, 1 -18.
- Wolberg, W. H.; Mangasarian, O. L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology, Proceedings of the National Academy of Sciences USA, Applied Mathematics 1990, 87, 9193-9196. [CrossRef]
- Wolberg, W. H.; Mangasarian, O. L.; Setiono, R. Pattern recognition via linear programming: Theory and application to medical diagnosis, University of Wisconsin-Madison Department of Computer Sciences. SIAM Workshop on Optimization, Society for Industrial and Applied Mathematics, 1989.
- Bennett, K. P.; Mangasarian, O. L. Robust linear programming discrimination of two linearly inseparable sets, Optimization Methods and Software 1992, 1, 23-34. [CrossRef]
- Wolberg W. Breast Cancer Wisconsin (Original). UCI Machine Learning Repository. 1992. Available online: http://archive.ics.uci.edu/dataset/15/breast+cancer+wisconsin+original. [CrossRef]
- Wickham, H.; Bryan, J.; Kalicinski, M.; Valery, K.; Leitienne, C.; Colbert, B.; Bryan, M. J. 2019. Package ‘readxl’. Version, 1.3, 1.
- Team, R. C.; Team, M. R. C.; Suggests, M.; Matrix, S.; 2018, Package stats, The R Stats Package.
- Wickham, H., Chang, W. and Wickham, M. H., 2016, Package ‘ggplot2’, Create elegant data visualisations using the grammar of graphics. Version, 2 (1), 1-189.
- Hardin, J. W.; Hilbe, J. M., Generalized linear models and extensions, 2. ed.; A Stata Press Publication : Texas, 2007.
- Agresti, A. Foundations of linear and generalized linear models, John Wiley & Sons: New Jersey, 2015.
- Fox, J. Applied regression analysis and generalized linear models, 3. ed.; Sage Publications: USA, 2015.
- İyit, N., Yonar, H., & Yonar, A. An application of generalized linear model approach on econometric studies. In: İyit N., Doğan H.,H., Akgül H, editors. Research & reviews in science and mathematics-II. Ankara: Gece Publishing; 2021; 201–16.
- Nelder, J. A.; Wedderburn, R. W. Generalized linear models. Journal of the Royal Statistical Society Series A: Statistics in Society 1972, 135, 370-384.
- Salinas Ruíz, J.; Montesinos López, O. A.; Hernández Ramírez, G.; Crossa Hiriart, J. Generalized linear models. In Generalized linear mixed models with applications in agriculture and biology Cham: Springer International Publishing: 2023, (43-84).
- Özaltın, Ö.; İyit, N. Modelling the US diabetes mortality rates via generalized linear model with the Tweedie distribution. Int. J. Sci. Res, 2018, 7, 1326-1334.
- Goldburd, M.; Khare, A.; Tevet, D.; Guller, D. Generalized linear models for insurance rating. 2. ed.; Casualty Actuarial Society: CAS Monographs Series, 5, 2016.
- Dunn, P. K.; Smyth, G. K. Generalized linear models with examples in R, Springer, 2018.
- Dunteman, G. H.; Ho, M. H. R. An introduction to generalized linear models . Sage Publication: 2006.
- İyit, N., Yonar, H.; Genç, A. Generalized linear models for European Union countries energy data. Acta Physica Polonica A, 2016, 130, 397-400. [CrossRef]
- Myers R. H.; Montgomery D. C.; Vining G. G.; Robinson T. J. Generalized linear models: with applications in engineering and the sciences. John Wiley & Sons: 2012.
- İyit, N. Modelling world energy security data from multinomial distribution by generalized linear model under different cumulative link functions. Open Chemistry, 2018, 16, 377-385.
- McCulloch, C. E.; Searle, S. R. Generalized, linear, and mixed models. John Wiley & Sons: 2004.
- Stroup W. W. Generalized linear mixed models: modern concepts, methods and applications. 1st ed. Florida: CRC press; 2012.
- İyit, N.; Sevim, F.; Kahraman, Ü. M. Investigating the impact of CO2 emissions on the COVID-19 pandemic by generalized linear mixed model approach with inverse Gaussian and gamma distributions. Open Chemistry, 2023a, 21, 20220301. [CrossRef]
- Morgan, B. J.; Smith, D. A note on Wadley's problem with overdispersion, Journal of the Royal Statistical Society: Series C (Applied Statistics), 1992, 41, 349-354.
- Olsson, U. Generalized linear models: an applied approach, Lund, Studentlitteratur, 2002.
- Koenker, R.; Yoon, J. Parametric links for binary choice models: A Fisherian–Bayesian colloquy, Journal of Econometrics, 2009, 152, 120-130. [CrossRef]
- Hilbe, J. M. Logistic regression models, Boca Raton, CRC press, 2009.
- İyit, N.; Sarı, E.; Sevim, F. Modeling COVID-19 Binary Data in the Aspect of Neoplasms as a Potential Indicator of Cancer by Logit and Probit Regression Models. International Journal of Advanced Natural Sciences and Engineering Researches 2023b, 7, 400-407.
- İyit N.; Al Mashhadani, A.A. An application of generalized linear model (GLM) to child mortality data in Iraq based on socioeconomic indicators. In: Ugur A, Tozak K, Yatbaz A, editors. Turkish World Socio Economic Strategies. Beau Bassin, Mauritius: LAP Lambert, 2017,195–203.
- Jiang J. Linear and generalized linear mixed models and their applications. 1st ed. New York: Springer; 2007.
- Faraway J.J. Extending the linear model with R: Generalized linear, mixed effects and nonparametric regression models. 2nd ed. New York: Chapman and Hall/CRC; 2016.
- Tekin, K.U.; Mestav, B.; İyit N. Robust logistic modelling for datasets with unusual points. Journal of New Theory 2021, 36, 49–63. [CrossRef]
- İyit, N.; Sevim, F. A novel statistical modeling of air pollution and the COVID-19 pandemic mortality data by Poisson, geometric, and negative binomial regression models with fixed and random effects. Open Chemistry 2023, 21(1), 20230364.
- Fawcett, T. An introduction to ROC analysis. Pattern recognition letters, 2006, 27(8), 861-874. [CrossRef]
- Piryonesi, S. M.; El-Diraby, T. E. Data analytics in asset management: Cost-effective prediction of the pavement condition index. Journal of infrastructure systems 2020, 26, 04019036. [CrossRef]
- Powers, D. M. Evaluation: from precision, recall and F-measure to ROC, informedness, markedness and correlation. 2020, arXiv preprint arXiv:2010.16061.
- Sammut, C.; Webb, G. I. (Eds.) Encyclopedia of machine learning. Springer Science & Business Media, 2011.
- Brooks, H.; Brown, B.; Ebert, B.; Ferro, C.; Jolliffe, I.; Koh, T. Y.; Stephenson, D. WWRP/WGNE joint working group on forecast verification research. Collab. Aust. Weather Clim. Res. World Meteorol. Organ, 2015.
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC genomics 2020, 21, 1-13.
- Tharwat, A. Classification assessment methods. Applied computing and informatics 2020, 17, 168-192.
- Fallahi, A.; Jafari, S. An expert system for detection of breast cancer using data preprocessing and bayesian network. International Journal of Advanced Science and Technology 2011, 34, 65-70.
- Jain, R.; Abraham, A. A comparative study of fuzzy classification methods on breast cancer data. Australasian Physics & Engineering Sciences in Medicine 2004, 27, 213-218.
- Übeyli, E. D. Implementing automated diagnostic systems for breast cancer detection. Expert systems with Applications, 2007, 33, 1054-1062.
- Metz, C. E. Basic principles of ROC analysis. In Seminars in nuclear medicine, 1978, 8, 283-298.
- British Standards Institution (BSI). Accuracy (trueness and precision) of measurement methods and results—Part 1: General principles and definitions, 1994.
- Yerushalmy, J. Statistical problems in assessing methods of medical diagnosis, with special reference to X-ray techniques. Public Health Reports (1896-1970), 1947, 1432-1449.
- Lewis, D. D. Representation quality in text classification: An introduction and experiment. In Speech and Natural Language: Proceedings of a Workshop Held at Hidden Valley, Pennsylvania, June 24-27, 1990.
- Lewis, D. D. Evaluating text categorization i. In Speech and Natural Language: Proceedings of a Workshop Held at Pacific Grove, California, February 19-22, 1991.
- Chinchor, N.; Hirschman, L.; Lewis, D. D. Evaluating message understanding systems: an analysis of the third message understanding conference (MUC-3). Computational linguistics, 1993,19, 409-450.
- Akaike H. A new look at the statistical model identification. IEEE Transactions on Automatic Control. 1974;19, 716-23. [CrossRef]
- Cavanaugh J. E. Unifying the derivations for the Akaike and corrected Akaike information criteria. Statistics & Probability Letters 1997, 33, 201-8. [CrossRef]
- Schwarz M. Estimating the dimensions of a model. Annals of Statistics 1978, 6, 461-4.
- Bozdogan H. Model selection and Akaike's Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika 1987, 52, 345-70. [CrossRef]
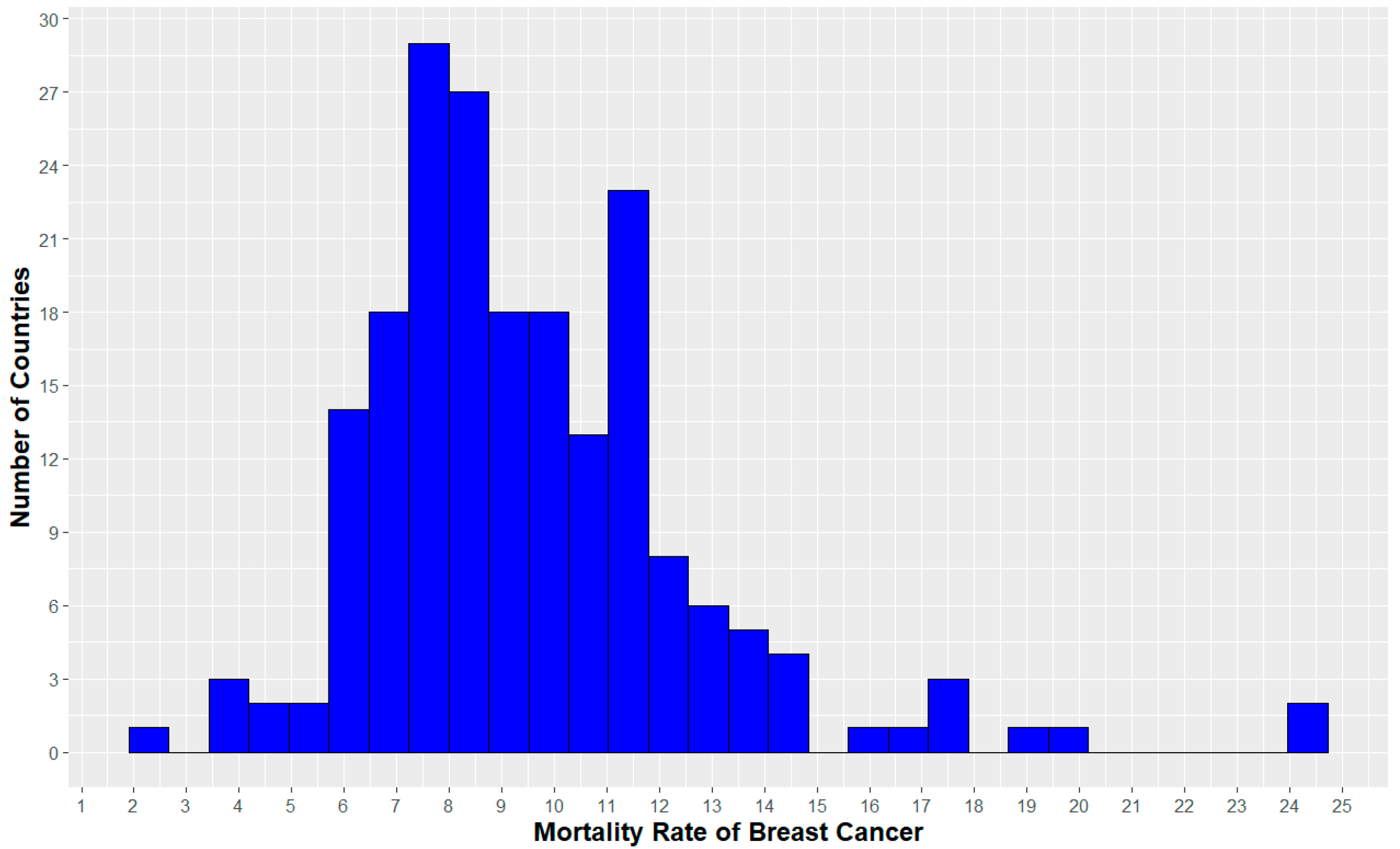
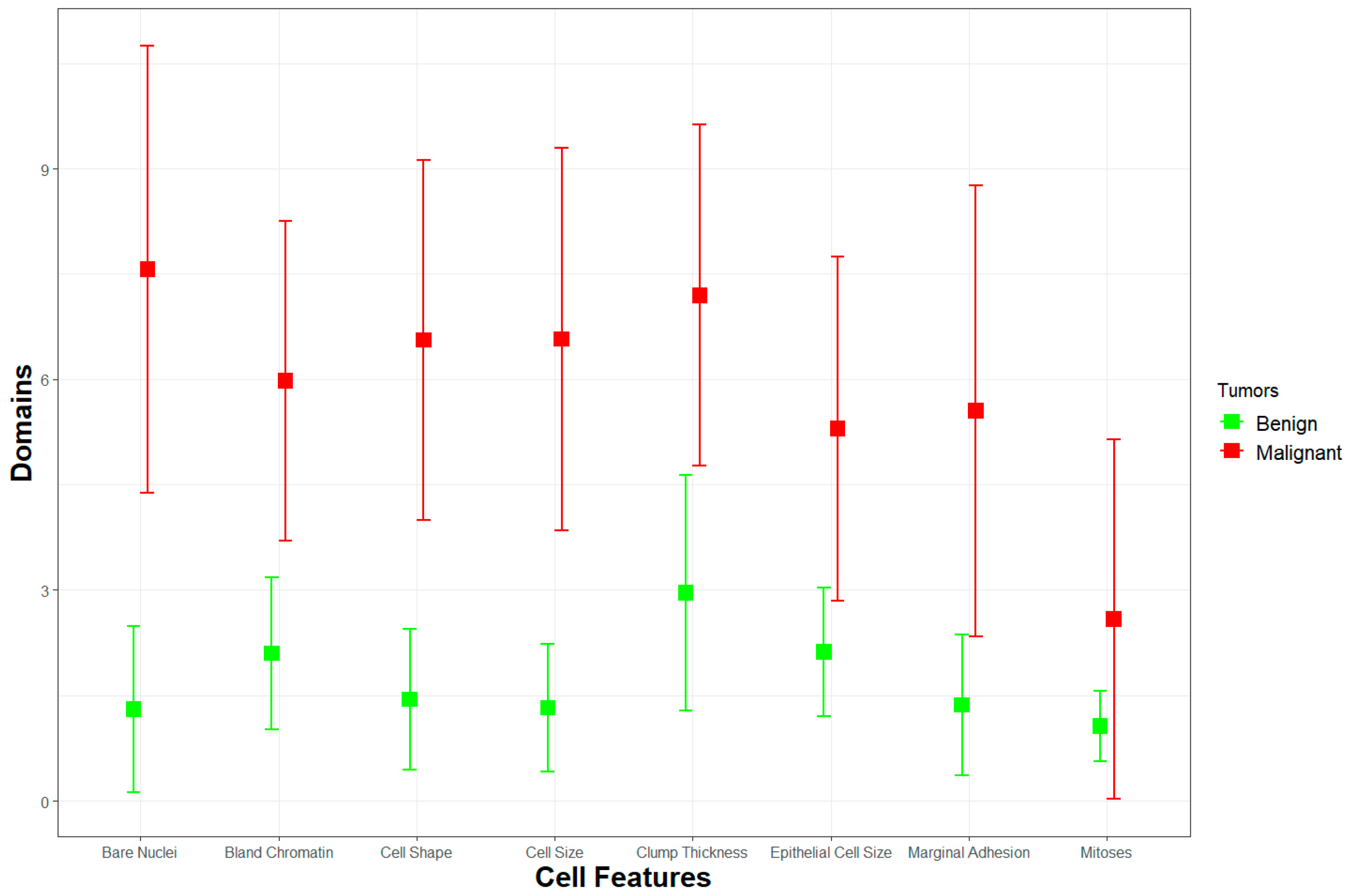
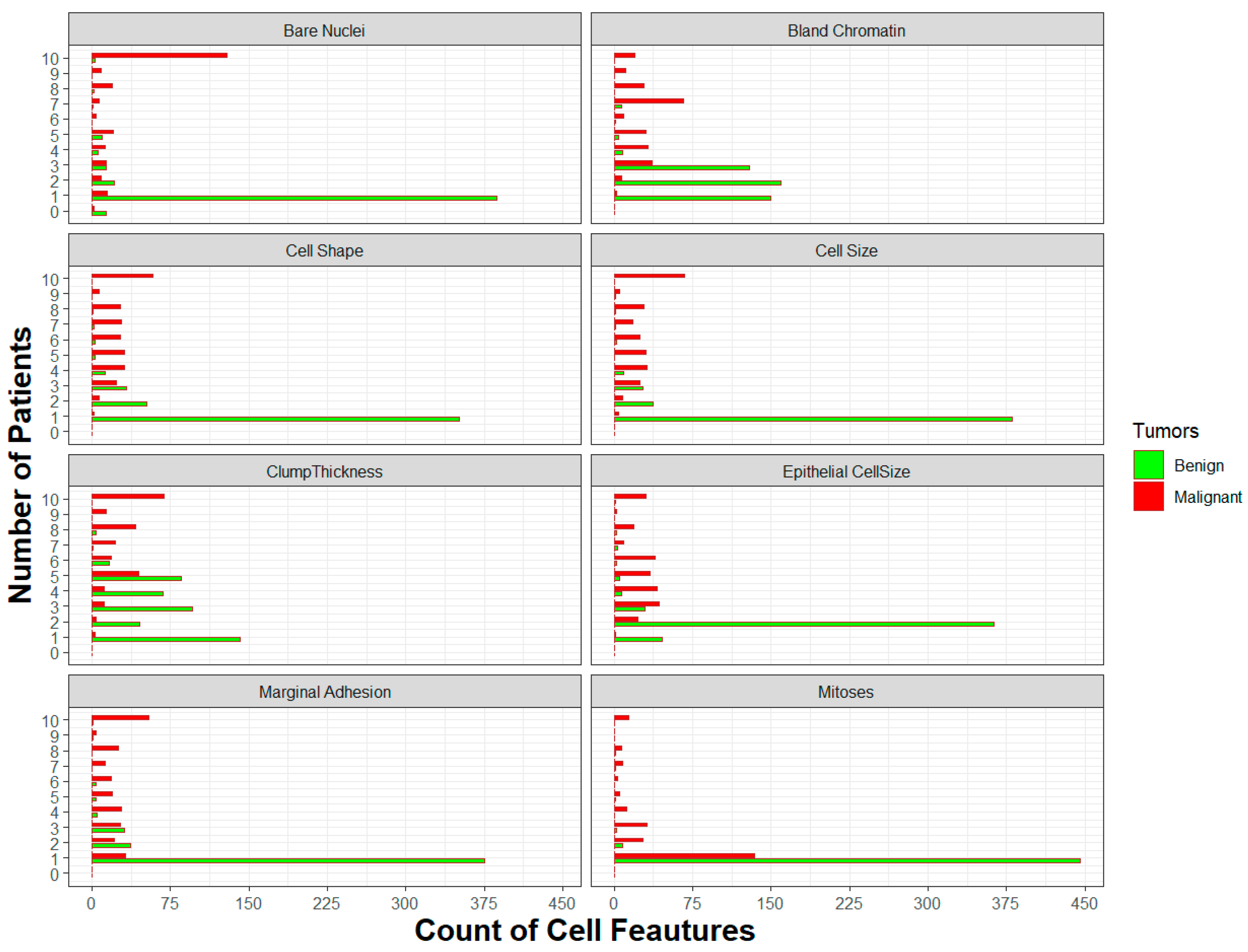
| Variables | Benign | Malignant | ||||||
|---|---|---|---|---|---|---|---|---|
| Min. | Median | Mean Sd. | Max. | Min. | Median | Mean Sd. | Max. | |
| Clump Thickness |
1 | 3 | 2.9563 1.6743 | 8 | 1 | 8 | 7.195 2.4288 | 10 |
| Cell Size | 1 | 1 | 1.3253 0.9077 | 9 | 1 | 6 | 6.5726 2.7195 | 10 |
| Cell Shape | 1 | 1 | 1.4432 0.9978 | 8 | 1 | 6 | 6.5602 2.562 | 10 |
| Marginal Adhesion |
1 | 1 | 1.3646 0.9968 | 10 | 1 | 5 | 5.5477 3.2105 | 10 |
| Epithelial Cell Size | 1 | 2 | 2.1201 0.9171 | 10 | 1 | 5 | 5.2988 2.4516 | 10 |
| Bare Nuclei | 0 | 1 | 1.3057 1.1827 | 10 | 0 | 10 | 7.5643 3.1802 | 10 |
| Bland Chromatin |
1 | 2 | 2.1004 1.0803 | 7 | 1 | 7 | 5.9793 2.2739 | 10 |
| Mitoses | 1 | 1 | 1.0633 0.5020 | 8 | 1 | 1 | 2.5892 2.5579 | 10 |
| Clump Thickness | Cell Size | Cell Shape | Marginal Adhesion | Epithelial Cell Size | Bare Nuclei | Bland Chromatin | Mitoses | ||||||||||
| Malign | Benign | Malign | Benign | Malign | Benign | Malign | Benign | Malign | Benign | Malign | Benign | Malign | Benign | Malign | Benign | ||
| Group 1 | Min. | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| Median | 2 | 8 | 1 | 6 | 1 | 6 | 1 | 4 | 2 | 5 | 1 | 10 | 3 | 5 | 1 | 1 | |
| Mean Sd. | 2.675 1.7333 | 7.3054 2.434 | 1.375 1.0439 | 6.1257 2.7685 | 1.475 1.1384 | 6.2575 2.5197 | 1.33, 0.9674 |
5.1796 3.2157 | 2.24 1.1658 |
5.4072 2.6255 | 1.43 1.5154 |
7.6168 3.1215 | 2.6 1.1988 |
5.3892 2.0648 | 1.08 0.5432 |
2.8204 2.6826 | |
| Max. | 8 | 10 | 8 | 10 | 8 | 10 | 9 | 10 | 10 | 10 | 10 | 10 | 7 | 10 | 7 | 10 | |
| Group 2 | Min. | 1 | 3 | 1 | 5 | 1 | 3 | 1 | 1 | 1 | 2 | 0 | 1 | 1 | 2 | 1 | 1 |
| Median | 3 | 9 | 1 | 8 | 1 | 8 | 1 | 5 | 2 | 5 | 1 | 10 | 2 | 7 | 1 | 1 | |
| Mean Sd. | 2.7544 1.5616 | 8.3077 2.213 | 1.6842 1.27 |
8.0769 1.801 | 1.7895 1.2209 | 8 2.1213 |
1.4737 1.0369 | 4.9231 3.0947 | 2.2105 0.7731 | 5.6923 2.9264 | 1.2807 1.0816 | 8.1538 3.3874 | 1.9298 0.7526 | 6.8462 2.035 | 1.0526 0.2941 | 1.9231 2.06 | |
| Max. | 6 | 10 | 9 | 10 | 7 | 10 | 6 | 10 | 5 | 10 | 8 | 10 | 4 | 10 | 3 | 8 | |
| Group 3 | Min. | 1 | 4 | 1 | 2 | 1 | 2 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 1 | 1 |
| Median | 4 | 10 | 1 | 6 | 1 | 6 | 1 | 7 | 2 | 5 | 1 | 10 | 1 | 8 | 1 | 1 | |
| Mean Sd. | 3.6364 1.6197 | 8.1111 2.4721 | 1.1364 0.4676 | 5.8889 2.0883 | 1.2727 0.6311 | 5.8889 2.4721 | 1.9091 1.377 | 6.1111 2.9768 | 2 0.4364 |
4.7778 1.3944 | 1.4545 1.101 | 8.1111 2.9345 | 1.0909 0.2942 | 7.7778 2.8186 | 1 0 |
1.4444 0.7265 | |
| Max. | 6 | 10 | 3 | 9 | 3 | 9 | 6 | 10 | 3 | 6 | 5 | 10 | 2 | 10 | 1 | 3 | |
| Group 4 | Min. | 1 | 4 | 1 | 7 | 1 | 7 | 1 | 5 | 1 | 4 | 1 | 5 | 1 | 7 | 1 | 1 |
| Median | 4.5 | 8 | 1 | 8 | 1 | 8 | 1 | 10 | 2 | 5 | 1 | 10 | 1 | 9 | 1 | 1 | |
| Mean Sd. | 4.2857 1.326 | 7 2.6458 |
1.2143 0.5789 | 8.3333 1.5275 | 1.2857 0.4688 | 8.3333 1.5275 | 1.3571 0.9288 | 8.3333 2.8868 | 1.7857 0.4258 | 6.3333 3.2146 | 1 0 |
8.3333 2.8868 | 1.1429 0.3631 | 8.6667 1.5275 | 1 0 |
4 5.1962 |
|
| Max. | 6 | 9 | 3 | 10 | 2 | 10 | 4 | 10 | 2 | 10 | 1 | 10 | 2 | 10 | 1 | 10 | |
| Group 5 | Min. | 1 | 3 | 1 | 3 | 1 | 2 | 1 | 1 | 1 | 3 | 1 | 3 | 1 | 3 | 1 | 1 |
| Median | 3.5 | 6 | 1 | 6.5 | 1 | 6.5 | 1 | 8.5 | 2 | 3.5 | 1 | 10 | 1.5 | 6.5 | 1 | 1 | |
| Mean Sd. | 3.1389 1.5703 | 6.25 2.2613 |
1.1111 0.3984 | 6.9167 2.6443 | 1.1389 0.4245 | 6.5833 2.811 | 1.4167 1.5376 | 6.8333 3.5633 | 1.8333 0.6547 | 4.0833 1.4434 | 1.25 0.8742 |
8.0833 2.8749 | 1.6111 0.6878 | 6.3333 2.0151 | 1 0 |
2 1.954 |
|
| Max. | 6 | 10 | 3 | 10 | 3 | 10 | 10 | 10 | 4 | 7 | 5 | 10 | 3 | 9 | 1 | 7 | |
| Group 6 | Min. | 1 | 5 | 1 | 4 | 1 | 3 | 1 | 1 | 1 | 3 | 1 | 2 | 1 | 2 | 1 | 1 |
| Median | 3.5 | 7 | 1 | 8 | 1 | 8 | 1 | 6 | 2 | 5 | 1 | 10 | 2 | 7 | 1 | 1 | |
| Mean Sd. | 3.425 1.534 | 7.3333 1.8708 | 1.225 0.6597 | 7.8889 2.0883 | 1.275 0.5541 | 7.3333 2.958 | 1.15 0.4267 |
6.2222 3.3082 | 1.925 0.2667 | 5 1.5 |
1.175 0.7121 | 8 3.1225 |
2.225 0.7675 | 7.4444 2.4037 | 1.025 0.1581 | 1.3333 0.5 |
|
| Max. | 6 | 10 | 4 | 10 | 3 | 10 | 3 | 10 | 2 | 8 | 5 | 10 | 4 | 10 | 2 | 2 | |
| Group 7 | Min. | 1 | 2 | 1 | 3 | 1 | 2 | 1 | 3 | 1 | 3 | 1 | 1 | 1 | 4 | 1 | 1 |
| Median | 4 | 5.5 | 1 | 8 | 1 | 7.5 | 1 | 8 | 2 | 4.5 | 1 | 10 | 1 | 7.5 | 1 | 1 | |
| Mean Sd. | 3.7647 1.5219 | 6.5 2.6239 |
1.0588 0.2425 | 7.1429 2.9576 | 1.4118 0.8703 | 7.0714 2.8138 | 1.3529 1.2217 | 7.2857 2.7012 | 1.9412 0.4287 | 4.9286 1.7744 | 1 0 |
7.5 3.8381 |
1.5294 0.6243 | 7.5714 2.0273 | 1 0 |
1.9286 2.4008 | |
| Max. | 5 | 10 | 2 | 10 | 4 | 10 | 6 | 10 | 3 | 10 | 1 | 10 | 3 | 10 | 1 | 10 | |
| Group 8 | Min. | 1 | 3 | 1 | 6 | 1 | 4 | 1 | 1 | 1 | 3 | 0 | 1 | 1 | 4 | 1 | 1 |
| Median | 3 | 5 | 1 | 10 | 1 | 8 | 1 | 6 | 2 | 5 | 1 | 5 | 1.5 | 7 | 1 | 2.5 | |
| Mean Sd. | 2.8889 1.5883 | 5.7143 2.1989 | 1.2083 0.5799 | 8.8571 1.4601 | 1.4167 0.9154 | 7.8571 2.2483 | 1.3056 0.6846 | 6.2857 2.8401 | 2.1111 0.7792 | 5.3571 1.9057 | 1.1667 0.7121 | 5.2143 3.2148 | 1.6528 0.8419 | 7.6429 2.0979 | 1.125 0.8381 | 2.8571 2.627 | |
| Max. | 7 | 10 | 4 | 10 | 5 | 10 | 3 | 10 | 8 | 10 | 5 | 10 | 6 | 10 | 8 | 10 | |
| Quantities | Domain | ||||||||||
| Type | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Clump Thickness | Benign | 142 (31 %) | 46 (10.04 %) | 96 (20,96 %) | 68 (14,85 %) | 85 (18,56 %) | 16 (3,49 %) | 1 (0,22 %) | 4 (0,87 %) | 0 (0 %) |
0 (0 %) |
| Malign | 3 (1,24 %) | 4 (1,66 %) | 12 (4,98 %) | 12 (4,98 %) | 45 (18,67 %) | 18 (7,47 %) | 22 (9,13 %) | 42 (17,43 %) | 14 (5,81 %) | 69 (28,63 %) | |
| Both | 145 (20,74 %) | 50 (7,15 %) | 108 (15,45 %) | 80 (11,44 %) | 130 (18,6 %) | 34 (4,86 %) | 23 (3,29 %) | 46 (6,58 %) | 14 (2 %) | 69 (9,87 %) | |
| Cell Size | Benign | 380 (82,97 %) | 37 (8,08 %) | 27 (5,9 %) | 9 (1,97 %) | 0 (0 %) |
2 (0,44 %) | 1 (0,22 %) | 1 (0,22 %) | 1 (0,22 %) | 0 (0 %) |
| Malign | 4 (1,66 %) | 8 (3,32 %) | 25 (10,37 %) | 31 (12,86 %) | 30 (12,45 %) | 25 (10,37 %) | 18 (7,47 %) | 28 (11,62 %) | 5 (2,07 %) | 67 (27,8 %) | |
| Both | 384 (54,94 %) | 45 (6,44 %) | 52 (7,44 %) | 40 (5,72 %) | 30 (4,29 %) | 27 (3,86 %) | 19 (2,72 %) | 29 (4,15 %) | 6 (0,86 %) | 67 (9,59 %) | |
| Cell Shape | Benign | 351 (76,64 %) | 52 (11,35 %) | 33 (7,21 %) | 13 (2,84 %) | 3 (0,66 %) | 3 (0,66 %) | 2 (0,44 %) | 1 (0,22 %) | 0 (0 %) |
0 (0 %) |
| Malign | 2 (0,83 %) | 7 (2,9 %) | 23 (9,54 %) | 31 (12,86 %) | 31 (12,86 %) | 27 (11,2 %) | 28 (11,62 %) | 27 (11,2 %) | 7 (2,9 %) | 58 (24,07 %) | |
| Both | 353 (50,5 %) | 59 (8,44 %) | 56 (8,01 %) | 44 (6,29 %) | 34 (4,86 %) | 30 (4,29 %) | 30 (4,29 %) | 28 (4,01 %) | 7 (1 %) |
58 (8,3 %) | |
| Marginal Adhesion | Benign | 375 (81,88 %) | 37 (8,08 %) | 31 (6,77 %) | 5 (1,09 %) | 4 (0,87 %) | 4 (0,87 %) | 0 (0 %) |
0 (0 %) |
1 (0,22 %) | 1 (0,22 %) |
| Malign | 32 (13,28 %) | 21 (8,71 %) | 27 (11,2 %) | 28 (11,62 %) | 19 (7,88 %) | 18 (7,47 %) | 13 (5,39 %) | 25 (10,37 %) | 4 (1,66 %) | 54 (22,41 %) | |
| Both | 407 (58,23 %) | 58 (8,3 %) | 58 (8,3 %) | 33 (4,72 %) | 23 (3,29 %) | 22 (3,15 %) | 13 (1,86 %) | 25 (3,58 %) | 5 (0,72 %) | 55 (7,87 %) | |
| Epithelial Cell Size | Benign | 46 (10,04 %) | 363 (79,26 %) | 29 (6,33 %) | 7 (1,53 %) | 5 (1,09 %) | 2 (0,44 %) | 3 (0,66 %) | 2 (0,44 %) | 0 (0 %) |
1 (0,22 %) |
| Malign | 1 (0,41 %) | 23 (9,54 %) | 43 (17,84 %) | 41 (17,01 %) | 34 (14,11 %) | 39 (16,18 %) | 9 (3,73 %) | 19 (7,88 %) | 2 (0,83 %) | 30 (12,45 %) | |
| Both | 47 (6,72 %) | 386 (55,22 %) | 72 (10,3 %) | 48 (6,87 %) | 39 (5,58 %) | 41 (5,87 %) |
12 (1,72 %) | 21 (3 %) |
2 (0,29 %) | 31 (4,43 %) | |
| Bare Nuclei | Benign | 387 (84,5 %) | 21 (4,59 %) | 14 (3,06 %) | 6 (1,31 %) | 10 (2,18 %) | 0 (0 %) |
1 (0,22 %) | 2 (0,44 %) | 0 (0 %) |
3 (0,66 %) |
| Malign | 15 (6,22 %) | 9 (3,73 %) | 14 (5,81 %) | 13 (5,39 %) | 20 (8,3 %) | 4 (1,66 %) | 7 (2,9 %) |
19 (7,88 %) | 9 (3,73 %) | 129 (53,53 %) | |
| Both | 402 (57,51 %) | 30 (4,29 %) | 28 (4,01 %) | 19 (2,72 %) | 30 (4,29 %) | 4 (0,57 %) | 8 (1,14 %) | 21 (3 %) |
9 (1,29 %) | 132 (18,88 %) | |
| Bland Chromatin | Benign | 150 (32,75 %) | 159 (34,72 %) | 129 (28,17 %) | 8 (1,75 %) | 4 (0,87 %) | 1 (0,22 %) | 7 (1,53 %) | 0 (0 %) |
0 (0 %) |
0 (0 %) |
| Malign | 2 (0,83 %) | 7 (2,9 %) | 36 (14,94 %) | 32 (13,28 %) | 30 (12,45 %) | 9 (3,73 %) | 66 (27,39 %) | 28 (11,62 %) | 11 (4,56 %) | 20 (8,3 %) | |
| Both | 152 (21,75 %) | 166 (23,75 %) | 165 (23,61 %) | 40 (5,72 %) | 34 (4,86 %) | 10 (1,43 %) | 73 (10,44 %) | 28 (4,01 %) | 11 (1,57 %) | 20 (2,86 %) | |
| Mitoses | Benign | 445 (97,16 %) | 8 (1,75 %) | 2 (0,44 %) | 0 (0 %) |
1 (0,22 %) | 0 (0 %) |
1 (0,22 %) | 1 (0,22 %) | 0 (0 %) |
0 (0 %) |
| Malign | 134 (55,6 %) | 27 (11,2 %) | 31 (12,86 %) | 12 (4,98 %) | 5 (2,07 %) | 3 (1,24 %) | 8 (3,32 %) | 7 (2,9 %) |
0 (0 %) |
14 (5,81 %) | |
| Both | 579 (82,83 %) | 35 (5,01 %) | 33 (4,72 %) | 12 (1,72 %) | 6 (0,86 %) | 3 (0,43 %) | 9 (1,29 %) | 8 (1,14 %) | 0 (0 %) |
14 (2 %) |
|
| Predicted | |||
| Total Population |
Positive | Negative | |
| Actual | Positive | True Posisite | False Negative |
| Negative | False Positive | True Negative | |
| Performance Metrics | Abbreviations | Formulas | References |
| Accuracy | ACC | Metz [84], BSI [85] |
|
| Sensitivity (Recall, True Positive Rate) | TPR | Yerushalmy [86], Lewis [87], Lewis [88] |
|
| Specificity (Selectivity, True Negative Rate) | TNR | Yerushalmy [86] | |
| Precision (Positive Predictive Value) | PPV | Lewis [87], Lewis [88] |
|
| F1 Score | F1 | Chinchor et al. [89] |
| Link Functions | Explanatory Variables | ||||||
|---|---|---|---|---|---|---|---|
| Lower | Upper | ||||||
| logit | Intercept | -9.7417 | 1.0620 | <2e-16 * | 0.0001 | 0.0000 | 0.0005 |
| Clump Thickness | 0.5374 | 0.1354 | 7.23e-05 * | 1.7116 | 1.3126 | 2.2320 | |
| Cell Size | 0.0669 | 0.1821 | 0.71327 | 1.0692 | 0.7483 | 1.5278 | |
| Cell Shape | 0.3681 | 0.2038 | 0.07092 | 1.4449 | 0.9691 | 2.1544 | |
| Marginal Adhesion | 0.2398 | 0.1145 | 0.03625 * | 1.2710 | 1.0155 | 1.5909 | |
| Epithelial Cell Size | 0.0897 | 0.1517 | 0.55464 | 1.0938 | 0.8124 | 1.4726 | |
| Bare Nuclei | 0.4222 | 0.0899 | 2.61E-06 | 1.5253 | 1.2790 | 1.8191 | |
| Bland Chromatin | 0.4490 | 0.1568 | 0.00418 * | 1.5668 | 1.1523 | 2.1303 | |
| Mitoses | 0.5416 | 0.3110 | 0.08157 | 1.7187 | 0.9344 | 3.1616 | |
| probit | Intercept | -5.1152 | 0.4863 | <2e-16* | 0.0060 | 0.0023 | 0.0156 |
| Clump Thickness | 0.2689 | 0.0659 | 4.51e-05* | 1.3085 | 1.1499 | 1.4890 | |
| Cell Size | 0.0297 | 0.0927 | 0.7491 | 1.0301 | 0.8589 | 1.2355 | |
| Cell Shape | 0.2215 | 0.1008 | 0.0280* | 1.2480 | 1.0242 | 1.5207 | |
| Marginal Adhesion | 0.1093 | 0.0592 | 0.0648 | 1.1155 | 0.9933 | 1.2528 | |
| Epithelial Cell Size | 0.0553 | 0.0773 | 0.4742 | 1.0569 | 0.9083 | 1.2297 | |
| Bare Nuclei | 0.2195 | 0.0430 | 3.26e-07* | 1.2454 | 1.1448 | 1.3549 | |
| Bland Chromatin | 0.2313 | 0.0771 | 0.0027* | 1.2602 | 1.0835 | 1.4658 | |
| Mitoses | 0.2592 | 0.1393 | 0.0628 | 1.2959 | 0.9863 | 1.7027 | |
| cloglog | Intercept | -6.99164 | 0.60571 | <2e-16* | 0.0009 | 0.0003 | 0.0030 |
| Clump Thickness | 0.31983 | 0.06462 | 7.44e-07* | 1.3769 | 1.2131 | 1.5628 | |
| Cell Size | -0.01662 | 0.08392 | 0.84298 | 0.9835 | 0.8343 | 1.1594 | |
| Cell Shape | 0.32819 | 0.09544 | 0.00058* | 1.3885 | 1.1516 | 1.6741 | |
| Marginal Adhesion | 0.07062 | 0.05742 | 0.21871 | 1.0732 | 0.9589 | 1.2010 | |
| Epithelial Cell Size | 0.14707 | 0.07803 | 0.05945 | 1.1584 | 0.9941 | 1.3499 | |
| Bare Nuclei | 0.23099 | 0.03901 | 3.21e-09* | 1.2598 | 1.1671 | 1.3600 | |
| Bland Chromatin | 0.27925 | 0.07608 | 0.00024* | 1.3221 | 1.1390 | 1.5347 | |
| Mitoses | 0.26686 | 0.1283 | 0.03753* | 1.3059 | 1.0155 | 1.6792 | |
| cauchit | Intercept | -34.0342 | 9.2132 | 0.00022* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 1.6139 | 0.5607 | 0.00400* | 5.0224 | 1.6735 | 15.0725 | |
| Cell Size | 1.2674 | 0.6981 | 0.069441 | 3.5516 | 0.9040 | 13.9527 | |
| Cell Shape | 2.5983 | 0.9536 | 0.00644* | 13.4409 | 2.0735 | 87.1261 | |
| Marginal Adhesion | 0.5877 | 0.3087 | 0.056899 | 1.7998 | 0.9828 | 3.2961 | |
| Epithelial Cell Size | -0.4612 | 0.3948 | 0.242818 | 0.6305 | 0.2908 | 1.3670 | |
| Bare Nuclei | 2.2314 | 0.6716 | 0.00089* | 9.3129 | 2.4969 | 34.7346 | |
| Bland Chromatin | 0.8428 | 0.5632 | 0.13454 | 2.3229 | 0.7702 | 7.0053 | |
| Mitoses | 2.2195 | 1.1861 | 0.06131 | 9.2027 | 0.9001 | 94.0904 | |
| Link Functions | Explanatory Variables | 95% Confidence Level for | |||||
| Lower | Upper | ||||||
| logit | Intercept | -9.7417 | 1.0620 | <2e-16* | 0.0001 | 0.0000 | 0.0005 |
| Clump Thickness | 0.5374 | 0.1354 | 7.23e-05* | 1.7116 | 1.3126 | 2.2320 | |
| Cell Size | 0.0669 | 0.1821 | 0.71327 | 1.0692 | 0.7483 | 1.5278 | |
| Cell Shape | 0.3681 | 0.2038 | 0.0709 | 1.4449 | 0.9691 | 2.1544 | |
| Marginal Adhesion | 0.2398 | 0.1145 | 0.03625* | 1.2710 | 1.0155 | 1.5909 | |
| Epithelial Cell Size | 0.0897 | 0.1517 | 0.55464 | 1.0938 | 0.8124 | 1.4726 | |
| Bare Nuclei | 0.4222 | 0.0899 | 2.61e-06* | 1.5253 | 1.2790 | 1.8191 | |
| Bland Chromatin | 0.4490 | 0.1568 | 0.00418* | 1.5668 | 1.1523 | 2.1303 | |
| Mitoses | 0.5416 | 0.3110 | 0.08157 | 1.7187 | 0.9344 | 3.1616 | |
| probit | Intercept | -5.11523 | 0.48457 | <2e-16* | 0.0060 | 0.0023 | 0.0155 |
| Clump Thickness | 0.26891 | 0.06747 | 6.73e-05* | 1.3085 | 1.1464 | 1.4935 | |
| Cell Size | 0.02967 | 0.09444 | 0.75343 | 1.0301 | 0.8560 | 1.2396 | |
| Cell Shape | 0.22152 | 0.10487 | 0.03466* | 1.2480 | 1.0161 | 1.5328 | |
| Marginal Adhesion | 0.10932 | 0.0574 | 0.05682 | 1.1155 | 0.9968 | 1.2484 | |
| Epithelial Cell Size | 0.0553 | 0.07852 | 0.48124 | 1.0569 | 0.9061 | 1.2327 | |
| Bare Nuclei | 0.21947 | 0.04211 | 1.87e-07* | 1.2454 | 1.1468 | 1.3526 | |
| Bland Chromatin | 0.2313 | 0.07684 | 0.00261* | 1.2602 | 1.0840 | 1.4651 | |
| Mitoses | 0.25921 | 0.14433 | 0.0725 | 1.2959 | 0.9766 | 1.7196 | |
| cloglog | Intercept | -6.9915 | 0.5798 | <2e-16* | 0.0009 | 0.0003 | 0.0029 |
| Clump Thickness | 0.3198 | 0.0681 | 2.66e-06* | 1.3769 | 1.2048 | 1.5735 | |
| Cell Size | -0.0166 | 0.0894 | 0.85262 | 0.9835 | 0.8255 | 1.1719 | |
| Cell Shape | 0.3282 | 0.1087 | 0.00252* | 1.3885 | 1.1221 | 1.7180 | |
| Marginal Adhesion | 0.0706 | 0.0614 | 0.25013 | 1.0732 | 0.9515 | 1.2104 | |
| Epithelial Cell Size | 0.1471 | 0.0855 | 0.08532 | 1.1584 | 0.9797 | 1.3697 | |
| Bare Nuclei | 0.2310 | 0.0396 | 5.39e-09* | 1.2598 | 1.1658 | 1.3615 | |
| Bland Chromatin | 0.2792 | 0.0726 | 0.00012* | 1.3221 | 1.1467 | 1.5244 | |
| Mitoses | 0.2669 | 0.1434 | 0.0628 | 1.3058 | 0.9858 | 1.7297 | |
| cauchit | Intercept | -34.0344 | 9.7337 | 0.00047* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 1.6140 | 0.5278 | 0.00223* | 5.0229 | 1.7852 | 14.1327 | |
| Cell Size | 1.2679 | 0.6157 | 0.03947* | 3.5534 | 1.0630 | 11.8778 | |
| Cell Shape | 2.5982 | 1.0076 | 0.00992* | 13.4395 | 1.8651 | 96.8435 | |
| Marginal Adhesion | 0.5877 | 0.3256 | 0.0711 | 1.7998 | 0.9508 | 3.4071 | |
| Epithelial Cell Size | -0.4612 | 0.4024 | 0.25178 | 0.6305 | 0.2865 | 1.3875 | |
| Bare Nuclei | 2.2315 | 0.6837 | 0.00110* | 9.3138 | 2.4387 | 35.5718 | |
| Bland Chromatin | 0.8427 | 0.5186 | 0.10421 | 2.3226 | 0.8405 | 6.4183 | |
| Mitoses | 2.2184 | 1.0522 | 0.03501* | 9.1926 | 1.1689 | 72.2919 | |
| Link Functions | Explanatory Variables | 95% Confidence Level for | |||||
| Lower | Upper | ||||||
| logit | Intercept | -35.7502 | 0.0012 | <2e-16* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 2.0682 | 0.0012 | <2e-16* | 7.9104 | 7.8911 | 7.9296 | |
| Cell Size | 0.3343 | 0.0013 | <2e-16* | 1.3970 | 1.3934 | 1.4006 | |
| Cell Shape | 1.4162 | 0.0013 | <2e-16* | 4.1212 | 4.1107 | 4.1318 | |
| Marginal Adhesion | 0.7265 | 0.0012 | <2e-16* | 2.0679 | 2.0629 | 2.0729 | |
| Epithelial Cell Size | 0.6289 | 0.0013 | <2e-16* | 1.8755 | 1.8707 | 1.8803 | |
| Bare Nuclei | 1.6063 | 0.0013 | <2e-16* | 4.9842 | 4.9717 | 4.9967 | |
| Bland Chromatin | 1.7385 | 0.0013 | <2e-16* | 5.6888 | 5.6746 | 5.7031 | |
| Mitoses | 1.7342 | 0.0012 | <2e-16* | 5.6643 | 5.6506 | 5.6781 | |
| probit | Intercept | -9.5614 | 0.0019 | <2e-16* | 0.0001 | 0.0001 | 0.0001 |
| Clump Thickness | 0.5102 | 0.0019 | <2e-16* | 1.6657 | 1.6596 | 1.6718 | |
| Cell Size | 0.2569 | 0.0020 | <2e-16* | 1.2929 | 1.2879 | 1.2979 | |
| Cell Shape | 0.2526 | 0.0020 | <2e-16* | 1.2874 | 1.2824 | 1.2924 | |
| Marginal Adhesion | 0.1723 | 0.0019 | <2e-16* | 1.1880 | 1.1836 | 1.1924 | |
| Epithelial Cell Size | 0.1059 | 0.0020 | <2e-16* | 1.1117 | 1.1074 | 1.1161 | |
| Bare Nuclei | 0.4757 | 0.0019 | <2e-16* | 1.6092 | 1.6031 | 1.6153 | |
| Bland Chromatin | 0.4538 | 0.0019 | <2e-16* | 1.5743 | 1.5684 | 1.5803 | |
| Mitoses | 0.4191 | 0.0019 | <2e-16* | 1.5206 | 1.5150 | 1.5262 | |
| cloglog | Intercept | -13.7073 | 0.0017 | <2e-16* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 0.5358 | 0.0016 | <2e-16* | 1.7088 | 1.7036 | 1.7141 | |
| Cell Size | 0.2359 | 0.0017 | <2e-16* | 1.2660 | 1.2618 | 1.2703 | |
| Cell Shape | 0.5402 | 0.0017 | <2e-16* | 1.7164 | 1.7107 | 1.7221 | |
| Marginal Adhesion | 0.1428 | 0.0016 | <2e-16* | 1.1535 | 1.1500 | 1.1571 | |
| Epithelial Cell Size | 0.3906 | 0.0017 | <2e-16* | 1.4778 | 1.4729 | 1.4827 | |
| Bare Nuclei | 0.5884 | 0.0016 | <2e-16* | 1.8011 | 1.7956 | 1.8067 | |
| Bland Chromatin | 0.6811 | 0.0016 | <2e-16* | 1.9761 | 1.9700 | 1.9822 | |
| Mitoses | 0.5726 | 0.0017 | <2e-16* | 1.7729 | 1.7669 | 1.7788 | |
| cauchit | Intercept | -41.3991 | 11.5252 | 0.00033* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 2.9538 | 0.9066 | 0.00112* | 19.1787 | 3.2442 | 113.3790 | |
| Cell Size | 0.3683 | 0.8930 | 0.68004 | 1.4453 | 0.2511 | 8.3193 | |
| Cell Shape | -0.2457 | 0.8710 | 0.77789 | 0.7822 | 0.1419 | 4.3123 | |
| Marginal Adhesion | 1.9768 | 0.6551 | 0.00255* | 7.2196 | 1.9993 | 26.0703 | |
| Epithelial Cell Size | 0.4090 | 0.5235 | 0.434632 | 1.5053 | 0.5395 | 4.1999 | |
| Bare Nuclei | 2.3869 | 0.7747 | 0.00206* | 10.8797 | 2.3833 | 49.6656 | |
| Bland Chromatin | 1.9481 | 0.7656 | 0.01094* | 7.0153 | 1.5644 | 31.4587 | |
| Mitoses | 3.3792 | 1.0396 | 0.00115* | 29.3473 | 3.8251 | 225.1611 | |
| Link Functions | Explanatory Variables | 95% Confidence Level for | |||||
| Lower | Upper | ||||||
| logit | Intercept | -37.3782 | 0.0025 | <2e-16* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 2.1253 | 0.0025 | <2e-16* | 8.3754 | 8.3338 | 8.4172 | |
| Cell Size | 0.3621 | 0.0027 | <2e-16* | 1.4364 | 1.4288 | 1.4440 | |
| Cell Shape | 1.5250 | 0.0026 | <2e-16* | 4.5951 | 4.5717 | 4.6186 | |
| Marginal Adhesion | 0.7773 | 0.0025 | <2e-16* | 2.1756 | 2.1649 | 2.1864 | |
| Epithelial Cell Size | 0.6156 | 0.0026 | <2e-16* | 1.8508 | 1.8414 | 1.8603 | |
| Bare Nuclei | 1.6801 | 0.0025 | <2e-16* | 5.3661 | 5.3395 | 5.3928 | |
| Bland Chromatin | 1.7540 | 0.0025 | <2e-16* | 5.7774 | 5.7488 | 5.8062 | |
| Mitoses | 2.1798 | 0.0025 | <2e-16* | 8.8443 | 8.8009 | 8.8879 | |
| probit | Intercept | -11.1554 | 0.0013 | <2e-16* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 0.6323 | 0.0013 | <2e-16* | 1.8820 | 1.8772 | 1.8868 | |
| Cell Size | 0.2335 | 0.0014 | <2e-16* | 1.2630 | 1.2596 | 1.2664 | |
| Cell Shape | 0.3308 | 0.0014 | <2e-16* | 1.3921 | 1.3884 | 1.3959 | |
| Marginal Adhesion | 0.2271 | 0.0013 | <2e-16* | 1.2549 | 1.2517 | 1.2582 | |
| Epithelial Cell Size | 0.0988 | 0.0014 | <2e-16* | 1.1039 | 1.1009 | 1.1068 | |
| Bare Nuclei | 0.5542 | 0.0013 | <2e-16* | 1.7406 | 1.7360 | 1.7452 | |
| Bland Chromatin | 0.5370 | 0.0013 | <2e-16* | 1.7109 | 1.7064 | 1.7154 | |
| Mitoses | 0.5032 | 0.0013 | <2e-16* | 1.6540 | 1.6496 | 1.6583 | |
| cloglog | Intercept | -15.1586 | 0.0015 | <2e-16* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 0.6358 | 0.0015 | <2e-16* | 1.8885 | 1.8830 | 1.8939 | |
| Cell Size | 0.1922 | 0.0016 | <2e-16* | 1.2119 | 1.2082 | 1.2156 | |
| Cell Shape | 0.6651 | 0.0016 | <2e-16* | 1.9446 | 1.9387 | 1.9505 | |
| Marginal Adhesion | 0.2313 | 0.0015 | <2e-16* | 1.2603 | 1.2567 | 1.2639 | |
| Epithelial Cell Size | 0.4966 | 0.0016 | <2e-16* | 1.6432 | 1.6382 | 1.6482 | |
| Bare Nuclei | 0.5542 | 0.0015 | <2e-16* | 1.7405 | 1.7355 | 1.7456 | |
| Bland Chromatin | 0.7217 | 0.0015 | <2e-16* | 2.0579 | 2.0520 | 2.0639 | |
| Mitoses | 0.6025 | 0.0015 | <2e-16* | 1.8267 | 1.8213 | 1.8322 | |
| cauchit | Intercept | -41.3991 | 11.5111 | 0.00032* | 0.0000 | 0.0000 | 0.0000 |
| Clump Thickness | 2.9538 | 0.9057 | 0.00111* | 19.1787 | 3.2499 | 113.1792 | |
| Cell Size | 0.3683 | 0.8930 | 0.68003 | 1.4453 | 0.2511 | 8.3193 | |
| Cell Shape | -0.2457 | 0.8709 | 0.77786 | 0.7822 | 0.1419 | 4.3114 | |
| Marginal Adhesion | 1.9768 | 0.6546 | 0.00253* | 7.2196 | 2.0013 | 26.0447 | |
| Epithelial Cell Size | 0.4090 | 0.5235 | 0.4346 | 1.5053 | 0.5395 | 4.1999 | |
| Bare Nuclei | 2.3869 | 0.7739 | 0.00204* | 10.8797 | 2.3870 | 49.5878 | |
| Bland Chromatin | 1.9481 | 0.7651 | 0.01089* | 7.0153 | 1.5660 | 31.4279 | |
| Mitoses | 3.3792 | 1.0384 | 0.00114* | 29.3473 | 3.8341 | 224.6321 | |
| GLM | GLMM (group-random effect) | |||||||||||||||
| Link Functions | logit | probit | cloglog | cauchit | logit | probit | cloglog | cauchit | ||||||||
| Conf. Matrix | 447 | 11 | 448 | 10 | 449 | 9 | 448 | 10 | 453 | 5 | 444 | 14 | 447 | 11 | 448 | 10 |
| 11 | 230 | 13 | 228 | 18 | 223 | 16 | 225 | 7 | 234 | 12 | 229 | 16 | 225 | 6 | 235 | |
| ACC (Accuracy) | 0.96853 | 0.96710 | 0.96137 | 0.96280 | 0.9828326 | 0.96280 | 0.96137 | 0.97711 | ||||||||
| TPR (Sensitivity, Recall) | 0.97598 | 0.97817 | 0.98035 | 0.97817 | 0.989083 | 0.96943 | 0.97598 | 0.97817 | ||||||||
| TNR (Specificity) | 0.95436 | 0.94606 | 0.92531 | 0.93361 | 0.9709544 | 0.95021 | 0.93361 | 0.97510 | ||||||||
| PPV (Precision) | 1.85477 | 1.85892 | 1.86307 | 1.85892 | 1.879668 | 1.84232 | 1.85477 | 1.85892 | ||||||||
| F1 Score | 0.97598 | 0.97497 | 0.97081 | 0.97180 | 0.9869281 | 0.97155 | 0.97068 | 0.98246 | ||||||||
| GLMM (id-random effect) | GLMM (id and group random effects) | |||||||||||||||
| Link Functions | logit | probit | cloglog | cauchit | logit | probit | cloglog | cauchit | ||||||||
| Conf. Matrix | 456 | 4 | 447 | 11 | 446 | 12 | 440 | 18 | 451 | 7 | 450 | 8 | 450 | 8 | 445 | 13 |
| 3 | 238 | 9 | 232 | 10 | 231 | 14 | 227 | 4 | 237 | 13 | 228 | 4 | 237 | 5 | 236 | |
| ACC (Accuracy) | 0.98999* | 0.97139 | 0.96853 | 0.95422 | 0.9842632 | 0.969957 | 0.982833 | 0.974249 | ||||||||
| TPR (Sensitivity, Recall) | 0.99127* | 0.97598 | 0.97380 | 0.96070 | 0.9847162 | 0.982533 | 0.982533 | 0.971616 | ||||||||
| TNR (Specificity) | 0.98755* | 0.96266 | 0.95851 | 0.94191 | 0.9834025 | 0.946058 | 0.983402 | 0.979253 | ||||||||
| PPV (Precision) | 1.88382* | 1.85477 | 1.85062 | 1.82573 | 1.871369 | 1.86722 | 1.86722 | 1.846473 | ||||||||
| F1 Score | 0.99235* | 0.97812 | 0.97593 | 0.96491 | 0.9879518 | 0.977199 | 0.986842 | 0.980176 | ||||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





