Für einen Organismus muß die Welt voraussagbar sein,
sonst kann er in ihr nicht leben.1
Irinäus Eibl-Eibesfeldt, 1998
The theory of life is a theory for the generation of information.
Manfred Eigen, 2013
1. Introduction
Life on Earth emerged by
self-organisation. Following Eibl-Eibesfeld (1998), the ability of prediction
is a necessary condition for life; no organisms are known without this ability.
Forms of “honorary life” (Dawkins 1996) such as human apparatuses that are part
of the human culture also belong to the realm of life (Donald 2008). If we
include those, there exists no prediction outside that realm, so that
prediction is also a sufficient condition for life. From this perspective, the
self-organisation of prediction is a process equivalent to the
self-organisation of life. In contrast to the various chemical and
environmental ingredients to the beginning of life, however, prediction may be
understood as a merely physical technique, based on causality and natural laws,
independent of any specific biological or biochemical details. According to
Eigen (1971, 1976, 1994, 2013, Eigen and Schuster 1977), life is a process of
generation and accumulation of information by means of repeated trial and
error.
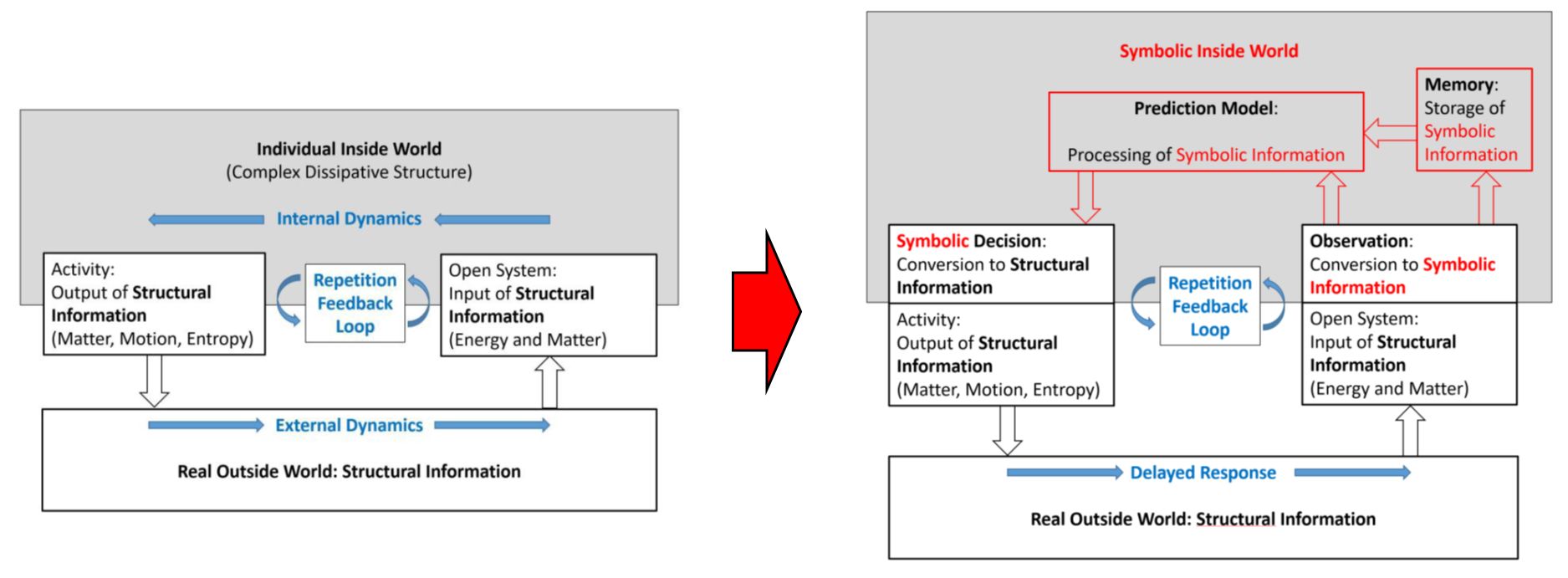
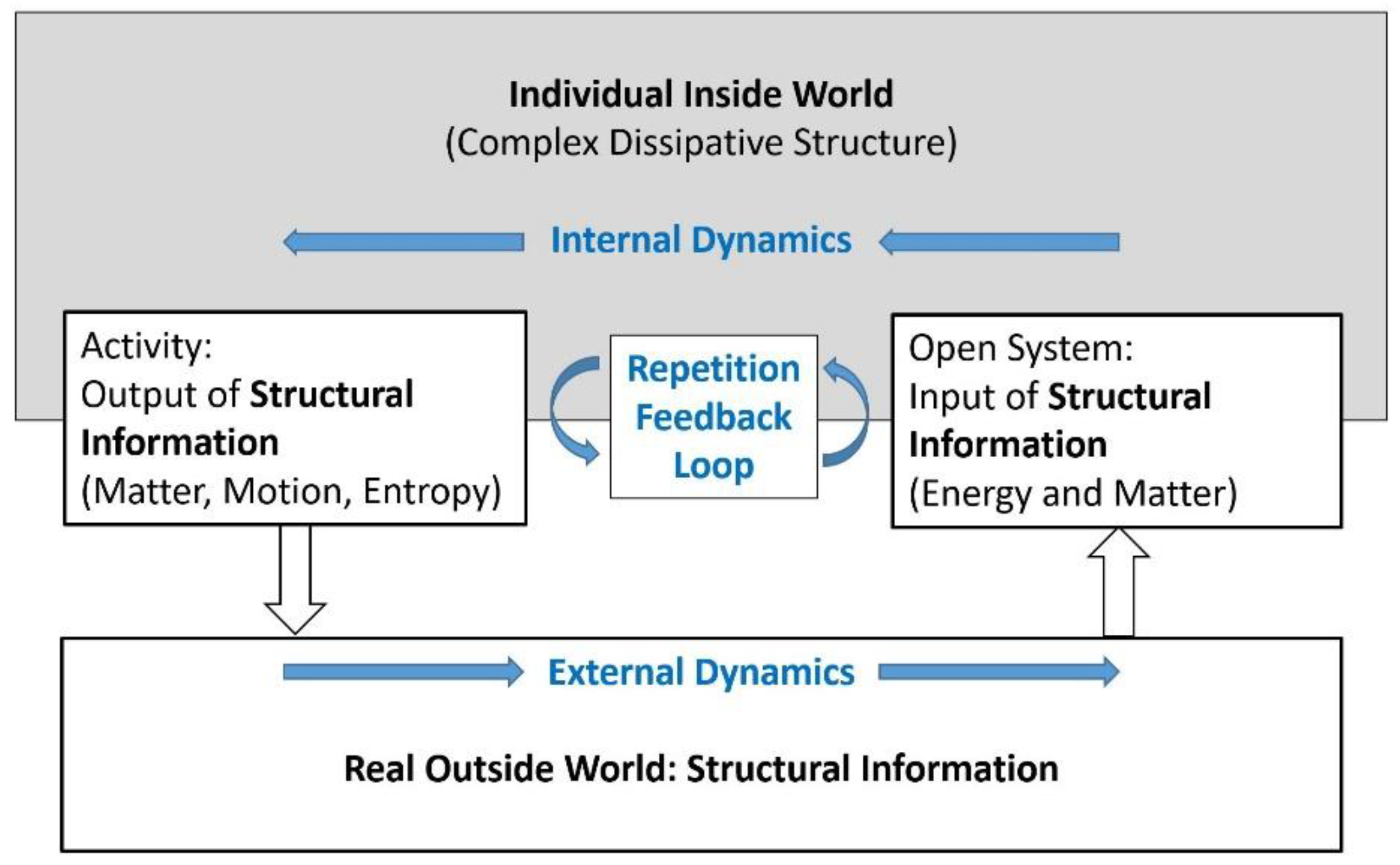
Fig. f1.1 shows schematically a simple conceptual model of a trial-and-error system
interacting with its outside world, representing this way also any arbitrary
organism from its perspective of prediction. “The ability to learn and form
memories allows animals to adapt their behavior based on previous experiences”
(Botton-Amiot et al. 2023).
Trial, in particular random trial,
is an elementary, precursory version of prediction. The self-organisation of
prediction may be understood as the transition from blind trial to sophisticated
prediction based on causal models. Conventional physical systems such as a heat
engine do not possess any prediction abilities.
Fig. f1.2 shows a conceptual
model of such an inanimate open physical system, possessing internal
non-equilibrium dissipative structures and performing related processes,
interacting across an interface with its environment.
A striking distinction between
Figure f1.1 and
Figure f1.2 is the one between
symbolic information and
structural
information (Ebeling and Feistel 1994, Feistel and Ebeling 2011, Feistel
2017a, 2023),
see Section 5 and
Section 6.
Entropy may serve as an example demonstrating the
difference. By the “negentropy principle of information” (Brillouin 2013: p.
153), entropy is often described as a quantitative measure for the amount of
information contained in a certain physical structure. Introduced empirically
by Clausius (1865, 1876) and statistically by Planck (1906, 1966), thermal
entropy is a measure of the amount of
structural information (or
physically bound information). Its value depends on the physical nature and on
the state of a given object; for example, the entropy of a mass of liquid water
is different from that of the same mass of ice, even at the same temperature
and pressure (Feistel and Wagner 2006). Entropy of Shannon and Weaver (1964),
by contrast, is a measure of the amount of
symbolic information (or
physically free information); it does not depend on the physical nature of the
particular information carriers, be those neural nerve pulses, electronic
computer bits or ink-printed letters (Brillouin 2013, Feistel 2017a, 2019).
“From the perspective of evolution
theory, the world of sign-likes appears as a stage of evolution that was
preceded by a world of not yet sign-likes“ (Nöth 2000: p. 135). “Semiosis is
the process in which the sign (and meaning) emerges. In other terms, semiosis
is interpretation” (Kull 2018: p. 455). The schematic transition process from
Fig. f1.2
to f1.1 is a
self-organised replacement of a structural process by a symbolic process. At
the transition point, which will be described here as a
ritualisation
transition, the two processes are actually identical. Such a transition has
occurred at the beginning of life, as will be considered in more detail in
Section 7
. A similar
transition has also happened in recent time in the technical world, such as the
transition from cybernetic systems using mechanical or electrical feedback
circuits and relays (Wiener 1948, Kämmerer 1974, 1977), functioning as in
Fig. f1.2
, to artificial
intelligence which is learning by the trial-and-error method of
Fig. f1.1
, and is much more
flexible by using of symbolic information.
Clearly, in the end, any symbolic
process is also some physical process, similar to the “naked” structural
process, but in the symbolic one the physical aspect is not the essential
contribution. If a task needs to be solved on a computer, this is performed
physically by certain mechanical or electronic switches or relays, but the kind
of (structural) hardware is not crucial for the task, while the (symbolic)
software implemented on the hardware is the significant aspect for the solution
of the problem. The arbitrariness of the particular hardware platform had been
formulated by Turing (1950) as the universality principle of digital
computers. With respect to symbolic information processing, this principle implies
the code symmetry (Feistel 1990, 2017a,b), or the semiotic arbitrariness
(Nöth 2000), or the principle of code plurality (Kull 2007), of
symbols in representing a certain meaning.
In this paper it will be assumed
that any symbolic information, in distinction to its structural counterpart,
has a purpose, and that this purpose consists in its influence on future
decisions and physical actions taken by the receiver of the symbolic
information. Purpose is something meaningless in the lifeless world. Symbolic
information in its own right is futile; it gets its relevance only after
subsequent conversion to structural information within the associated
information-processing context. In the understanding of this paper, models, and
in particular prediction models, are special symbols themselves. The
self-organisation of prediction models, suggested here as a transition between
the models of Figures F1.2 and f1.1, requires the emergence of symbols, requires
the transition from the transfer of structural information to the transfer of
symbolic information in repeated interaction with an outside world.
By humans or any other living
beings, decisions made now will matter only later on in the future.
Beneficial decisions require good prognoses. Causal models can exploit
past experience to predict upcoming events or circumstances. By appropriate
receptors, after suitable conversion to symbolic information, structural
information received from the environment may be filtered and stored in
suitable symbolic form. After having passed through a symbol-processing model,
the symbolic result needs to be transformed back into structural information
transmitted to the environment, such as by triggered mechanical activity,
incarnating the actual decision.
Living organisms are self-organised
dissipative structures. To stay alive and multiply, they need permanent supply
of high-valued energy to compensate the inevitable production and export of
entropy, to assemble and accumulate energy-rich molecules that make up the
body, as well as to supply internal energy stocks to be exploited for driving
active behaviour. The latter is ruled by a series of decisions of what needs to
be done when and how, being permanently made by any living being, from the
simplest singe-cell up to human life and labour. The future fate of an organism
is affected by any decision derived from experience made in the past and
triggered by suitably adjusted prediction models, estimating what is expected
to come. By trial and error, symbolically stored sensational experience is used
to evaluate the success of previous decisions and to modify the prediction
model accordingly.
The self-organisation of
prediction models requires several qualitative steps, although not necessarily
in this temporal sequence:
- (i)
Symbols need to emerge from non-symbolic, structural information processing,
- (ii)
Sensors need to emerge which convert received structural information into symbolic information,
- (iii)
Experience in the form of symbolic information needs to be stored in memory,
- (iv)
Symbols need to be combined in networks to form symbol-processing models,
- (v)
Symbols produced by models represent the evaluation result of the processed experience, and
- (vi)
Decision-making models convert symbolic values back into structural information of activity.
In natural evolution, this process
is typically rolled out from the end. Internal information processing developed
and advanced any already existing activities to become more and more diverse,
sophisticated, effective and beneficial with respect to survival. Simple organisms
perform certain mechanical or chemical activities without recognising any
environmental signals. “Lower animals often possess a richer embodiment of
their activity system as compared to a poor perception system” (von Uexküll
1973: p. 161). Subsequently, structural information from the surrounding, such
as temperature or brightness, may affect the organism’s metabolism. If this
enhances the fitness, direct physical impact may develop into specialised
reception of selected external signals. Direct physical links (structural
information) between receptor and effector may turn into more versatile
symbolic information transfer by the ritualisation transition. Chemical
symbols, such as specific indicator molecules, may be processed by logical
gates such as NOT or AND, as this is known from properties of allosteric
enzymes (Oubrahim and Boon Chock 2016), similar to information processing in
electronic computers. Networks of this kind may recognise signals of a certain
duration rather than just instantaneously happening conditions, that is, they
may build up memory devices.
The paper is organised as follows.
Prediction models emerge and work between sensual perception and decided action
of individuals, between input of structural information converted to symbolic
one, and output of structural information after conversion from symbolic one.
In
Section 2
, the
terms “symbol” and “model” are specified and compared with other common similar
words. In
Section 3
, the relation of causality and final causality to prediction models
is discussed. The role of decisions, physical as well as symbolic decisions, as
a transformer of symbolic to structural information is considered with simple
physical examples, such as homoclinic orbits, in
Section 4
. Symbolic
information is compared to structural information in greater detail in
Section 5
, and the
self-organised emergence of novel symbolic information out of existing
structural information by the ritualisation transition, as the key process for
the self-organisation of prediction models, is characterised by selected
contrasting properties in
Section 6
. The paper is discussed from a more general perspective in
Section 7
. To assist the
reading,
Appendix A
reviews selected general properties of self-organisation processes
and phase transitions. With respect to the origin of life,
Appendix B
explains briefly a
conceptional ritualisation scenario.
2. Symbols and Models
Computer bits, feather colours or
printed letters are symbols. Words like “energy”, “entropy”, “information” or
“symbol” are also symbols. In the literature, in particular in semiotics,
symbols may also be regarded as “signs”, “icons”, “displays” or “signals”
(Oehler 1995, Deacon 1997, Nöth 2000, Pattee 2001, Feistel 2023). Within some
external context,
symbols are physical structures that represent
something else than themselves, namely, the symbol’s
meaning. The
relation between the symbol’s structure and its meaning is arbitrary and
assigned by convention (Nöth 2000, Lacková et al. 2017). Arbitrariness, that
is, neutral stability with respect to fluctuations among any arbitrary suitable
carriers, is a specific functional symmetry of symbol-processing systems
(Feistel 1990, 2017a,b, Feistel and Ebeling 2016). Accordingly, the
self-organised emergence of arbitrariness has properties of a kinetic phase
transition of the 2
nd kind, see
Appendix A
. The corresponding
fundamental character of this arbitrariness, of the purely conventional
character of the relation between the physical structure of a symbol and its
meaning, was proposed to be termed the
central dogma of semiotics by
Deacon (2021).
Models do exist for the climate, for a steam engine or for sailing
vessels. Construction plans, cooking recipes or genetic strands are also models
for the physical structures that appear by execution of those symbolic
instruction sets. Some authors understand models as opposed to theories; not so
here. Following Stachowiak (1973: p. 56), “a model is likewise … the most
elementary item of perception as well as the most complex, most comprehensive
theory.” “The word ‘model’ … is used … to mean an approximate description of an
aspect of reality, with this description being developed for a specific
purpose“ (Willink 2013: p. 16).
Models represent something else than they
physically constitute in their own right. This property specifies models to be
a special class of symbols. Typically, models are complex, consisting of
structured sets of simpler, more elementary symbols. Similar to symbols, which
may also represent other symbols rather than directly any physical reality,
models may also represent other symbols or models. The text of this paragraph,
for example, is a model of a model, similar to any other scientific article
which consists of ordered sets of symbols (letters, words, numbers, figures)
representing the research object, be that an observed or measured physical
structure or another model (theory, hypothesis, simulation). Similarly, the
notion of entropy is a model for certain fundamental properties of a
macroscopic physical object, rather than being any kind of real physical
“substance” itself. Sets of mutually consistent models are not necessarily
pairwise reducible to one another, as if they were forming this way a connected
group or semigroup of models. Irreducible such models are often described as emergent
models, quantities or properties (Butterfield 2012, Fuentes 2014, Feistel and Ebeling 2016).
A particularly important group of models is that of
mental models (Craik 1943) implemented in brains of higher animals,
especially of humans. Mental models result from the combination of phylogenetic
(inherited) experience and ontogenetic (individually undergone) experience.
Highly relevant for physicists and philosophers is the human model of naïve
realism (Born 1965a, b). “The reality of a simple, untaught human is what
he/she [immediately] feels and recognises. … The reality of those things which
surround him/her is self-evident to him/her. … This attitude is termed naïve
realism. The large majority of humans remains with that” (Born 1965a: p. 53,
54). “Naïve realism is a natural attitude expressing the biological situation
of humans and all animals” (Born 1965b: p. 106). Naïve realism is a
self-organised mental model as the result of successful Darwinian survival of
all ancestors in the past (Hoffman 2020, Feistel 2021, 2022, 2023), rather than
an a-priori principle of human understanding (Kant 1956), possibly of divine
origin.
Most models serve as prediction models, directly or
indirectly. In symbolic form, they provide estimates for expected future
observations, derived from similar experience already stored symbolically in
memory, in combination with recent input, such as sensation suitably converted
to symbols (
Fig. f1.1). In turn,
observationally successful predictions serve as criteria for the reliability of
the responsible model, to be used again in the future upon repetition of
similar sensations. By repetition, models accumulate information about
properties of the represented object, such as the real outside world.
Causality, as a hypothetically lawful link between repeatedly observed
correlated events, is an established construction principle for empirical
prediction models. “Only after an activity has been performed and therefore
belongs to the past, are we entitled to an attempt of understanding it from the
perspective of causality”
2
(Planck 1937: p. 29).
Causal models are the most successful prediction
tools. “The validity of the causal law is connected with the
possibility of making correct predictions for the future” (Planck 1948b: p. 3).
“If it is the task of science to look for lawful relations in all what happens
in Nature and in human life, an inevitable prerequisite for that is … that such
a relation in fact exists, and may be described in clear words. In this sense
we tend to talk about the validity of a general causal law and about the determination
of all processes in the natural and the mental world by this law. However, what
does it mean that a process, an event, an activity occurs with lawful
necessity, is causally determined, and how can the lawful necessity of a
process be detected? I have no better idea to provide a clearer and more
convincing proof for the necessity of a process than by the possibility of
predicting the occurrence of the particular process”
3(Planck 1937: p.5).
Sudden deadly risks cannot be learned by individual
ontogenetic experience because the killed organism cannot store this
information in its memory for later. Organisms, however, which due to randomly
modified prediction models instinctively avoid related risky situations, can
inherit their survival strategy as phylogenetic experience. Such warnings may
appear emotionally as a diffuse “fear” without causal justification. This
indirect feedback mechanism is related to the psychological phenomenon of
biased recognition known as silent evidence (Taleb 2008). When
after an earthquake a few survivors praise their god for saving their lives,
while the many killed victims fail to oppose, than the earthquake finally
appears as a convincing reason to trust in god. Winners write history.
Prediction models may exploit information about never-experienced events.
Symbols and especially models have two conjugate
aspects, on the one hand the way they emerge by self-organisation, and on the
other hand the way they are used in systems processing symbolic information
(Feistel 2023). The first aspect may be denoted as the design time of a
symbol; this process is described here as the ritualisation transition.
The second aspect may be denoted as run time of a symbol which is
denoted as a symbolisation process that takes place, e.g., during an
observation or a measurement that extracts symbols such as nerve pulses or
measured numbers from structural information of the given external object or
measurand. “Measurement is a form of symbolisation. It consists in assigning
numerals to objects or quantities” (Craik 1943: p. 75).
3. Causality and Finality
Although causality cannot be
perceived in nature (Hume 1758, Russel 1919), it is an extremely useful concept
for the construction of prediction models, especially of human mental models
(Kant 1956, Planck 1948b, Feistel 2023). The physical concept of causality is a
strictly irreversible one (Prigogine 2000, Riek 2020): a cause always precedes
its effect in time. In the literature of philosophy, biology and semiotics,
however, also a final causality, or finality, or retrocausation
is extensively discussed as the phenomenon by which the final result of a
process is actually assumed to be its “cause” (Sapper 1928, Nöth 2000, Nomura
et al. 2019, Pink 2021, Deichmann 2023). Actually, prediction models may
provide a logical link between the two disjunct causalities.
Why at all are there symbols?
Darwinian selection demands the use of prediction models by the competitors in
order to gain selective advantage. In turn, causal prediction models require
the prior emergence of symbols. In this sense, the “purpose” or “final cause”
for the existence of symbols and for the self-organisation of the ritualisation
phenomenon is the need for prediction that arose from the possibility of
prediction by gradually modifying random trial activities. Symbol processing
makes prediction faster, energetically cheaper, more effective, more reliable
and more flexible, similar to digital technology as compared to its analogue
forerunner. Concerning systems that are equipped with an appropriate prediction
model, finality is consistent with causality. However, not the system’s future
state is controlling and “causing” the system’s development but rather the
inherited prediction model which is attempting to repeat the previous success
of its predecessor’s mature structure and processing. This successful
repetition is possible under the requirement of environmental continuity, of
persistent boundary conditions. If, otherwise, the system’s external conditions
change so quickly and dramatically beyond some critical tolerance limit, the
system will fail to achieve the expected mature state because the prediction
model becomes unable to properly predict the result of the development under
the altered boundary conditions.
Darwinian evolution relies on such
a continuity principle (Feistel 2023): “the world must be predictable for an
organism to live therein” (Eibl-Eibesfeldt 1998). “For any form of life, from
unicellular organisms to large-brained mammals, living in a predictable
environment is essential for increasing its chances for survival” (Nomura et
al. 2019: p. 267). If the parental genetic survival recipe suddenly turns
inappropriate to also ensure offspring survival because of environmental
discontinuity, evolution cannot take place by trial and error and by gradual
accumulation of symbolic information in successively improving prediction
models. While, say, cyanobacteria have a wide tolerance range to survive under
strongly varying conditions, highly specialised species such as dinosaurs or
humans run a higher risk of extinction. The pace by which the global human
population is currently overturning the terrestrial ecosystem has become
intolerably fast for numerous other recent species; they can no longer adapt
their genetic prediction model by the traditional mutation-and-selection
mechanism. Final causality as fitness for purpose may not function in those
cases.
Evolution established deliberation
as a prediction method of mammals which permits quick reactions and decisions
about their immediate activity under circumstances never experienced before
(LeDoux 2021). Evolution established sex (Smith 1988, Margulis 2017) as
the most successful method to survive unpredictable situations, especially
during population bottlenecks, by keeping available a variety of alternative
genetic prediction models. Sexual reproduction and selection gave rise to the
evolution of a spectacular wealth of new symbols used in mating activities
(Darwin 1859, Prum 2017). The price to pay for the benefits of sex, however, is
the individual death (Margulis 2017).
Physical causality is an
asymmetric binary relation between certain pairs of events. For a network of
events, causality represents a mathematical semigroup rather than a group as
not necessarily each pair of events is mutually linked. If events are
represented by nodes and their causal links by arrows, a causal network may be
described by a directed graph or a non-negative adjacency matrix (Frobenius
1912, Lancaster 1969, Gantmacher 1971, Feistel and Ebeling 1978b, Feistel 1979,
Ebeling and Feistel 1982, Bornholdt and Schuster 2003). Final causality, if
understood as a cause appearing later than its effect, violates the semigroup
model of physical causality. Similarly, in science-fiction films and novels,
fictitious time travel, the heroes carry their mental prediction models along
with their stored experience back to the past, so that the memory can
symbolically “remember the future”. This is inconsistent with the causality
semigroup properties and implies logical contradictions.
Likely, prediction models are
physical systems that causally combine and connect symbols of events as
semigroups in a similar way as those had been observed of real, structural
events. It may be assumed that the expected sequence of symbolic events in the model
is represented also by an irreversible structural process, percussing previous
experience in a simplified form.
4. Physical and Symbolic Decisions
A popular example for a decision
is the millennium-old parable of “Buridan’s Ass”, named after the French
philosopher Jean Buridan: a donkey placed exactly amid two equal stacks of hay
is unable to decide for one and will eventually die of hunger. Mathematically,
the donkey is located at a saddle point of a fictitious “surface of happiness”
with two equal maxima to the left and right. Tiny fluctuations may suffice to
break this symmetry at the initial unstable steady state and to trigger a
decision toward one of the heaps.
Decisions
play a key role in human personal and social life. Back to Adam
Smith (1776), disciplines such as “decision theory” or “best-choice theory”
typically investigate problems related to reasons for, and consequences of,
individual decisions in the society. In the case of human decisions, those are
often regarded as “free will” (Planck 1937) and are widely and controversially
disputed in the literature (Pauen and Roth 2008, Pink 2009, Maldonato 2012).
However, decisions, in the particular sense as specified below, are more
fundamental acts for biology in general than just those of humans. “Decision
theory provides a means to find the optimum response given uncertain
information by weighing appropriately the costs and benefits of each potential
response” (Perkins and Swain 2009: p.1). Prediction models are built to deliver
symbolic information which leads to decisions by evaluating and comparing the
expected benefits; asking for the physical roots of the self-organisation of
such models implies the question for physical roots of the self-organisation of
decisions. Here, we shall discuss certain aspects of
physical decisions
and of
symbolic decisions, assuming that those represent a physical
basis of biological behaviour from the very beginnings up to human interests
and related activities. The importance of decision (or choice) for symbolic
information processing (or semiotics) in combination with prediction,
experience and memory has already been emphasised previously by Kull (2018),
who quoted Viktor von Weizsäcker’s (1940: p. 126) statement that “the process
of life is a decision rather than a succession of cause and effect“
4. “By ‘semiosis’ we mean the process of choice-making between
simultaneously alternative options” (Kull 2018: p. 454).
“There is a large number of new
phenomena which are associated to irreversibility, and appear only in systems
far from equilibrium. … In front of a bifurcation, you have many possibilities,
many branches. The system ‘chooses’ one branch” (Prigogine 2000: p. 5). When a
straight elastic column is put under pressure, beyond a critical load it will
suddenly bend, a phenomenon known as Euler buckling (Zeeman 1976). In
the simplest case, the column has two options, to bend to the left or to the
right. The decision to which side to bend depends on small fluctuations,
asymmetric structures or boundary conditions. Typically, the physical process
initiating the decision occurs at an energy level much lower than that of the
amplified processes that “explode” due to feedback processes in accelerated
manner after the decision was made. In this sense, a physical decision is a
macroscopic amplification of a chosen option out of a microscopic manifold of
those.
Let a physical decision be
a macroscopic process triggered by a microscopic event, such as an avalanche
released by a tiny tremor, a bomb exploding after a slide touch of its
detonator, or the sudden freezing-over of a supercooled liquid after a local
thermal fluctuation. The fertilisation of an egg cell to form a zygote is a
physical decision to start pregnancy. A physical decision is an apple that
suddenly falls from a tree, or a spark igniting a wildfire. Physical decisions
occur at unstable or metastable states (Summers 2023); they are irreversible
and produce entropy.
An instructive dynamical model for
a system capable of physical decisions is a homoclinic orbit (Shilnikov
1969, Gaspard et al. 1984, Drysdale 1994).
"Shilnikov homoclinic orbits are
trajectories that depart from a fixed saddle-focus point … and return to it
after an infinity time" (Medrano et al. 2005: p.1).
If several different homoclinic orbits start from the same
stationary point, a system may, by microscopic fluctuations, “decide” which
orbit to follow, performing the orbit’s macroscopic dynamics as an “activity”,
before returning asymptotically to the initial waiting state. The simplest model
for such a decision is a saddle-type homoclinic orbit (Drysdale 1994) with two
leaves representing alternative decisions and performed activities.
A simple saddle-type homoclinic
orbit is shown in
Fig. f4.1
. A related possible system of canonical-dissipative equations
(Graham 1973, 1981, Feistel and Ebeling 1989) is,
with the functions
and
. The dissipation inequality
implied,
shows that the system possesses a
homoclinic orbit (
Fig. f4.1) of the shape of a lemniscate,
. The steady state at (0, 0) is a
saddle point. Fluctuations in its stable directions let the system immediately
return to the origin. Fluctuations in either of the unstable directions trigger
macroscopic excursions after which the system finally returns to the original
state. Such a model may conceptionally reflect decisions such as those being
made by an animal confronted with an enemy. The animal may either hide and do
nothing, or decide to take the flight, or to attack.
Let a symbolic decision be
a physical decision in the form of structural information that is triggered by
symbolic information, see the following section. For example, for humans, the
consequences of speech acts which are “doing things with words” (Austin
1962, Bühler 1965) are typical symbolic decisions. When at her wedding the
bride declares “yes, I will”, then this symbolic message of just three words
given to the audience will dramatically change her future social and personal
life. When on a market some bargain ends with “deal”, then the offered goods
will instantaneously exchange their owners and will face an altered fate. Such
a deal is usually the result of a cost-benefit analysis performed by mental
prediction models of the participants. As an aside, the German word for “to
exchange” is “tauschen”, a word that has common roots with “täuschen”, meaning
“to deceive”, to mislead the opponent’s prediction model.
Mechanical switches used to start
or stop engines are devices for making physical decisions, releasing
significant amounts of energy upon a minor energetic effort such as pushing a
button. Those become symbolic decisions as soon as the switch is operated
electronically by symbolic computer bits rather than mechanically by human
fingers. By virtue of its effect, a symbolic decision assigns a
structural
meaning to a symbol. While observation translates external structural
information into internal symbolic information,
Fig. f1.1
, decision is the
counterpart that translates symbolic information into structural information of
action, physically affecting the external world. Symbolic information in its
own right is useless; it gains its relevance only in connection with associated
structural information that ultimately appears as a result of a symbolic
decision. Such a “magic power” of symbols is marvelled in numerous legends and
fairy tales.
5. Structural and Symbolic Information
Prediction models are used to
transform available information about the past and present into yet unavailable
information about the future. However, the meaning of the term information
varies widely in the scientific and other literature. Here, information
is a term used for special physical processes or structures, or for certain
properties of those. Information carriers are structures requisite for
any transfer, storage and processing of information. There is no information
without a physical carrier, quite in contrast to the understanding of some
authors who assume information to be the substance of which the world
ultimately consists. With respect to the physical carrier structures,
information itself is an emergent quantity, something assigned to those
structures by an external context or agent. Occasionally, information itself is
regarded as some physical quantity similar to entropy, as it may obey
conservation and dissipation laws, and it may possess an amount and a value.
When receiving the honorary
citizenship of Pescara in Italy, Ilya Prigogine (2000) said in his inauguration
speech with respect to certain physical information theories that “the pleasure
of being invited to this beautiful ceremony, and my friendship with Professor
Ruffini, would have been included in the information at the big bang. But that
seems very strange, and I could never accept this view.” In this quotation, by
“information”, physical structural information is meant that may (or
rather, may not) had been preformed already at the big bang, in absence of any
symbols, and has nonetheless been perfectly conserved from then on to the
present day, and to any future yet to come. Such a putative conservation of
structural quantum information, known as »Hawking’s information paradox«, is
subject to recent gravity research (Almheiri et al. 2020). It is well known,
however, that the macroscopic loss of information as a consequence of Clausius’
law of irreversibly increasing entropy is inconsistent with the microscopic
reversibility of classical mechanics (Feistel and Ebeling 2016), and a similar
inconsistency can neither be excluded for quantum effects. All these physical
laws apply to structural information.
In this paper, structural
information is distinguished from symbolic information. It is
understood that any physical structure carries structural information just by
its very existence. Symbols, the way they are introduced here, are
physical structures which additionally carry symbolic information. The latter
is assigned to the structure in the context of an external
information-processing system by convention, not reducible to the
symbol’s intrinsic structural information. For example, a printed word carries
a certain meaning as its conventional symbolic information which is independent
of the word’s structural information such as the kind of ink or paper used for
printing. Symbols represent something else than themselves. Physically, the conventionality
or arbitrariness of the symbol’s meaning corresponds to a Goldstone
mode, expressed by a vanishing Lyapunov coefficient of the system’s
dynamical equations with respect to fluctuations that replace the given
structure by a different one with the same meaning. For example, if a text is
typed in “Sans-serif” letter font and is replaced by the same text in “Arial”,
the meaning of the text remains unaffected, and there is no physical
restauration or relaxation force that tends to return the text to “Sans-serif”.
The discovery of planet Neptune
may serve as an example for the relation between structural and symbolic
information. Observational data of planet Uranus published by Bouvard in 1821
deviated significantly from values predicted by Kepler’s mathematical model. Le
Verrier could explain the discrepancies mathematically by the existence of a
yet unknown planet, Neptune, which could indeed be observed near the suggested
position by Galle in 1846. This famous history can be understood in a way that
the perturbation of Uranus’ orbit represents structural information that was
transferred from Neptune to Uranus by gravity interaction. The existence and
certain properties of Neptune are physically present in Uranus’ trajectory. By
measuring Uranus’ motion, this information was converted to symbolic
information in the form of numerical tables. By exploiting this experience, a
mathematical prediction model then provided the hypothetical position of
Neptune in the sky. By the decision of pointing a telescope to that spot, the
symbolic model result was converted back to structural information. The light
observed from that star, again as structural information, could be observed and
converted again into symbolic information in the form of scientific
communication about the new discovery, as a validation of the prediction.
Great apes can learn to use some
words. They never did that themselves, but were always taught by humans. By
contrast, nobody had ever taught early humans to use words to speak or write.
The human use of language is definitely self-organised. In the course of the
natural evolution of life, including humans, symbols emerged by
self-organisation in a ritualization process. Similarly, the emergence of the
genetic code and the symbolic information it represents can be assumed to have
occurred by self-organisation. A simple conceptional model for the origin of
life understood as a ritualisation transition is briefly presented in
Appendix B
.
6. Properties of the Ritualisation Transition
Prediction models are special symbols; the self-organisation of prediction models became possible only along with the self-organisation of symbols. This relation makes ritualisation, as the key process for the emergence of symbols, a crucial event also for the evolution of prediction models. Ritualisation had previously been defined to be (Feistel 2017b)
- -
“the gradual change of a useful action into a symbol and then into a ritual; or in other words, the change by which the same act which first subserved a definite purpose directly comes later to subserve it only indirectly (symbolically) and then not at all” (Huxley 1914),
- -
a process by which behavioural or physical forms, or both, that had originally developed to serve certain different purposes for communication within a population (Lorenz 1970),
- -
the modification of an animal behavioural pattern to a pure symbolic activity (Eibl-Eibesfeldt 1970),
- -
the development of signal-activity from use-activity (Tembrock 1977), or as
- -
the self-organised emergence of systems capable of processing symbolic information (Feistel and Ebeling 2011).
Typically, in the course of
evolution, three stages of a ritualisation transition are observed: before,
during and after the transition (Feistel 1990, Feistel and Ebeling 2011). Initially,
the existing structure is only slightly variable in order to maintain the
system’s essential functionality. Successively, involved structures may
gradually reduce to some rudimentary, simplified version of themselves, to
“icons” or “pictograms”, which represent the minimum complexity requisite for
the actual task (Klix 1980). As a kind of caricature this may be a modified, a
skeleton representation of the original structure in a way that emphasises some
relevant characteristics and simplifies or omits others, irrelevant ones.
Redundant partial structures are no longer supported by restoring forces, and
related fluctuations may increase substantially. At the transition point, the
“icons” turn into mere symbols that may be modified arbitrarily, thus expressing
the emerging code symmetry, and permit divergent, macroscopic fluctuations, see
Appendix A
. As a
result, the kind and pool of symbols may quickly enlarge and adjust to new
external requirements or functions. Later, in a maturation phase, the code becomes
standardised to maintain intrinsic consistency and compatibility of the newly
established information-processing system. Fluctuations are increasingly
suppressed, the code becomes frozen-in and preserves in its remaining arbitrary
structural details a record of its own evolution history. For example, in the
ritualisation of spoken and written language, of numbers or of gestures, all
these stages appear in similar, more or less pronounced form (Feistel 2017a,b,
2023). “In all aboriginal languages, vestiges of these sounds of nature are
still to be heard; though, to be sure, they are not the principal fibres of
human speech” (von Herder 1772).
Symbolic information has some
general properties (Feistel and Ebeling 2011):
- (i)
Symbolic information systems possess a new symmetry, the carrier invariance. Information may loss-free be copied to other carriers or multiplied in the form of an unlimited number of physical instances. The information content is independent of the physical carrier system used.
- (ii)
Symbolic information systems possess a new symmetry, the coding invariance. The functionality of the processing system is unaffected by substitution of symbols by other symbols as long as unambiguous bidirectional conversion remains possible. In particular, the stock of symbols can be extended by the addition of new symbols or the differentiation of existing symbols. At higher functional levels, code invariance applies similarly also to the substitution of groups of symbols, synonymous words or of equivalent languages.
- (iii)
Within the physical relaxation time of the carrier structure, discrete symbols represent quanta of information that do not degrade and can be refreshed unlimitedly.
- (iv)
Redundant copies of symbolic information may be carried along for error correction in cases of loss or damage of the original.
- (v)
Imperfect functioning or external interference may destroy symbolic information but only biological processing systems can generate new or recover lost information.
- (vi)
Symbolic information systems consist of complementary physical components that are capable of producing the structures of each of the symbols in an arbitrary sequence upon writing, of keeping the structures intact over the duration of transmission or storage, and of detecting each of those structures upon reading the message. If the stock of symbols is subject to evolutionary change, a consistent co-evolution of all components is required.
- (vii)
Symbolic information is an emergent property; its governing laws are beyond the framework of physics, even though the supporting structures and processes do not violate physical laws.
- (viii)
Symbolic information is extracted from structural information by observation or measurement processes.
- (ix)
Symbolic information has a meaning or purpose beyond the scope of physics which becomes revealed by conversion to structural information, such as by symbolic decisions.
- (x)
In their structural information, the constituents of the symbolic information system preserve a frozen history (“fossils”) of their evolutionary pathway.
- (xi)
Symbolic information processing is an irreversible, non-equilibrium processes that produces entropy and requires free-energy supply.
- (xii)
Symbolic information is encoded in the form of structural information of its carrier system. Source, transmitter and destination represent and transform physical structures.
- (xiii)
Symbolic information exists only in the realm of life.
Structural information has a number of different general properties (Feistel and Ebeling 2011):
- (i)
Structural information is inherent to its carrier substance or process. Information cannot loss-free be copied to any other carrier or identically multiplied in the form of additional physical instances. The physical carrier is an integral constituent of the information, meaning and structure cannot be separated from one another. The state of the physical context of the system is an integral part of the information.
- (ii)
There is no invariance of structural information with respect to structure transformations. Different structures represent different structural information.
- (iii)
Structural information emerges and exists on its own, without being produced or supported by any kind of separate information source. No coding rules are involved when the structure is formed by natural processes.
- (iv)
Over the relaxation time of the carrier structure, structural information degrades systematically as a consequence of the Second Law, and disappears when the equilibrium state is approached.
- (v)
Internal physical processes or external interference may destroy structural information; it cannot be regenerated or recovered. Periodic processes can rebuild similar structures but never exactly the same, in particular because the surrounding world will never be exactly the same again at any later point of time.
- (vi)
Structural information is not represented in the form of codes. No particular coding rule or language is required or distinguished to decipher a structure.
- (vii)
Structural information is a physical property; it is represented by the spatial and temporal configuration of matter, its governing laws are the laws of physics.
- (viii)
Structural information is of physical nature and is independent of life.
7. Discussion
Key aspects of seemingly unrelated
scientific topics such as Leibniz’ (1765) “Final Cause”, Hume’s (1758)
“Scepticism”, Darwin’s (1859) “Natural Selection”, Peirce’s “Semiotics” (Nöth
2000), Huxley’s (1914) “Ritualisation”, Born’s (1965a,b) “Naïve Realism”,
Prigogine’s (1969) “Dissipative Structures”, Gilbert’s (1986) “RNA World”,
Pattee’s (2001) “Physics of Symbols” or Hoffman’s (2020) “Relative Reality” may
jointly be considered from a common perspective of self-organised prediction
models. Active decisions governed by prediction models may be regarded as a
universal property of life, independent of specific biochemical details or
terrestrial conditions, and also including non-Darwinian forms of “honorary
life” such as market economy, scientific or technological artefacts such as
computers or artificial intelligence. First prediction models emerged by
self-organisation in the course of coevolution of sensual reception, symbol
processing and memory, and decisions on activities. Typically,
self-organisation is characterised by a spontaneous formation of novel,
“dissipative” structures or functions induced by symmetry-breaking kinetic
phase transitions far from thermodynamic equilibrium, such as oscillations of a
hydrothermal geyser. Symbols may emerge in a similar manner by a universal
kinetic transition that had been termed “ritualisation” in ethology,
introducing arbitrariness as a new additional symmetry into information
processing. Ain
Appendix B
, a conceptual model for the origin of life is painting a simplified
picture of the primordial ritualisation transition to the very first symbols
and models. A similarly fundamental success of the self-organised emergence of
symbols such as language and numbers, and of causal mental prediction models is
characteristic also for the historical ascent of humans.
Here are some widely known but
rather different examples, related to selected features of prediction models:
- -
Phylogenetic experience: When Darwin (1859) wrote his famous book “On the Origin of Species”, he mentioned in his Chapter 1 various examples for the variability of phenotypic properties between parents and offspring: “When among individuals … any very rare deviation … appears in the parent … and it reappears in the child, the mere doctrine of chances almost compels us to attribute its reappearance to inheritance. … Perhaps the correct way of viewing … would be, to look at the inheritance … as a rule, and non-inheritance as the anomaly. The laws governing inheritance are for the most part unknown”. Despite that, only a few years later, Mendel’s (1866) empirical inheritance rules went largely unnoticed by the scientific community. It took another century until Watson and Crick (1953) as well as Nirenberg and Matthaei (1961) revealed the molecular symbolic memory behind biological inheritance, known today as the “genetic code”. In this paper, the genetic information is considered as an inherited prediction model, self-organised previously in the course of Darwinian selection by the long and unbroken track of successful ancestors, this way keeping their accumulated phylogenetic experience available for the offspring as a predicted instruction set for the offspring’s subsequent survival and multiplication. This process may be regarded as Darwinian evolution of prediction models in the sense of Dawkins’ (1976) “selfish genes”.
- -
Ontogenetic experience: When Pavlov in 1905 measured the salivation of a dog in the lab, he noticed that already the sound of the walking technician started watering the dog’s mouth in expectation of the food the same person had always been providing. This classical conditioning (Denny-Brown 1928) is controlled by a mental prediction model that had been established before by repeated recognition of correlated events during the individual ontogenetic experience in the past. To make this happen, sensual impressions must be recorded symbolically in memory. Triggered by a repeated event, this information must be recalled and processed by the model in order to predict and await the yet missing events of the formerly observed scenario. “Brains are … essentially prediction machines” (Clark 2013: p. 181). The concept of mental models was developed by Craik (1943).
- -
Scientific prediction laws: When Clausius (1876) studied cyclic thermal processes of heat engines, he mutually compared numerous measured values of heat supply,
, at temperatures,
. He found that cycles with
are technically impossible: „Die
algebraische Summe aller in einem Kreisprocesse vorkommenden Verwandlungen kann
nur positiv oder als Grenzfall Null sein“
5.
As a fundamental theorem, he concluded that “ein Wärmeübergang aus einem
kälteren in einen wärmeren Körper kann nicht ohne Compensation stattfinden“
6. This
natural
law is a prediction model for, say, the maximum efficiency of any modern
heat pump. Clausius (1865: p. 390, 1876: p. 94, 111) proposed a new
thermodynamic state quantity,
,
termed “entropy” (“Verwandlung”, transformation, greek “τροπή”) by him (Feistel
and Ebeling 2011, 2016). His most famous prediction was: “Die Energie der Welt
ist constant. Die
Entropie der Welt strebt einem Maximum zu”
7. Physical “natural” laws are
symbolically formulated human models (Feistel 2023), derived from past
observations in order to predict results of future observations or
measurements.
- -
Observation-prediction-action cycle: Brahe’s meticulous observation of stars between 1586 and 1597 enabled Kepler to discover his pioneering laws of planetary motion, published in the books Astronomia nova of 1609 and Harmonices mundi of 1619. In 1687, Newton could demonstrate that his fundamental physical laws of bodily motion and of universal gravity were sufficient to correctly derive Kepler’s findings mathematically. Kepler’s laws allowed successful predictions of the solar transits of Mercury in 1631 and of Venus in 1639, and later even the discovery of Neptune in 1846. In remote space regions never directly experienced by humans before, predictions by those laws gave rise to the first successful flight of an artificial celestial body, “Sputnik”, in 1957, confirming the merely symbolic predictions of astronomers in the form of structural information. Newton’s dynamical differential equations offer more comprehensive predictions than Kepler’s conservation laws of energy and angular momentum provide. “The ultimate goal of celestial mechanics [was] to resolve the great problem of determining if Newton’s law alone explains all astronomical phenomena” (Poincaré and Goroff 1993: p. I17).
- -
Causal prediction models: “Mathematically, the law of causality is expressed by the fact that physical quantities obey differential equations of a certain kind. The causal law of classical physics implies that the knowledge of the state of a closed system at some point of time determines its behaviour for all of its future” (Born 1966: p.7). Causality is a key element of the human mental model of naïve realism. Causality does not exist in reality (Russell 1919: p. 180) nor can it be observed: “Through its sensational properties, no object may ever reveal the causes that produced it nor the effects that will result from it” (Hume 1758: p. 44). However, causality is an unrivalled human mental prediction tool (Orcutt 1952). The historical success of causal mental models made humans addicted to causal explanations for their personal observations, such as by superstition, religion or science (Planck 1948a: p. 23, Feistel 2023). “The human brain is the most advanced tool ever devised for managing causes and effects. … Causal explanations, not dry facts, make up the bulk of our knowledge” (Pearl and Mackenzie 2019: p. 2, 24). „We struggle for attributing cause and effect. Seeing events causally connected is an outstanding strategy to master our daily life“ (Mast 2020: p. 32).
- -
Mental prediction models: The neuronally implemented, inherited prediction model of naïve realism emerged by self-organisation in the course of Darwinian evolution (Hoffman 2020, Feistel 2023). By introspection, Kant (1956) painted a detailed picture of human naïve realism. Eighty years before Darwin (1859), lacking a better explanation, Kant described causality as an a-priori principle of reason rather than an empirical conclusion from phylogenetic experience. The alternative advantages either of exploiting intergenerational, phylogenetic experience stored in genetic information, or of fast and flexible individual, ontogenetic experience stored in brain memory, became combined by socially distributed prediction models of science and technology of humans, permitted by the self-organisation of spoken and written language (Logan 1986, Pinker 1994, Deacon 1997). Sagan (1978: p. 39) regarded this kind of accumulated symbolic information as an “extrasomatic-cultural” one.
- -
Non-causal prediction models: Scientific prediction models are not necessarily causal ones. For the description of technical or natural processes, for example, the quantitative knowledge of certain properties of physical objects may be required. Typically, a finite set of such properties is carefully measured and symbolically tabulated, similar to Brahe’s star-gazing, and subsequently represented mathematically by a continuous function, similar to Kepler’s and Newton’s laws, which predicts the properties under any other, not yet measured conditions. This way, as a special case, properties of water, seawater, ice and humid air are described in the form of empirical thermodynamic potentials by the international standard TEOS-10, the “Thermodynamic Equation of Seawater - 2010”, for use in numerical models for climate, oceanography or desalination (IOC et al. 2010, Feistel 2018, Harvey et al. 2023). Such predicted property values should always be associated with estimated uncertainties (GUM 2008, Willink 2013, Feistel et al. 2016). The method of mathematical inter- and extrapolation, generalising locally observed situations to previously unexplored ones, is a powerful non-causal mental prediction tool that likely evolved from first geometric measurements in agriculture (Hilbert 1903) and is still successfully applied in latest science.
Appendix A. Self-Organisation and Phase Transitions
The term self-organisation
describes a macroscopic phenomenon by which the system’s uniform elements
spontaneously exhibit some cooperative behaviour. “We use the term
cooperative in the physico-chemical sense as referring to systems with
correlated molecular motions. Order-disorder processes and phase
transformations are familiar examples of cooperative phenomena” (Kirkaldy 1965:
p. 966). As a special case, at certain conditions, thermodynamic equilibrium
systems may start separating into different phases or de-mixing of its
constituents, such as an ice cover forming on a lake. Equilibrium phase
transitions are traditionally classified into ones of the 1st kind,
such as liquid water at the freezing point, and of the 2nd kind,
such as the loss of ferromagnetism at the Curie point (Landau and Lifschitz
1966).
Phase transitions of the 1st
kind
are characterised by the possible coexistence
of the two phases which are well distinguished from one another (such as liquid
and vapour) and may or may not possess different symmetries (such as liquid and
ice). In case of equal symmetries, the transition jump may be bypassed smoothly
(such as fluid water above the critical point). The actual transition process
is typically passing an intermediate metastable state by developing nucleation
and hysteresis phenomena (Schmelzer 2005, 2019, Hellmuth et al. 2020). Phase
transitions of the 2nd kind are continuous and characterised by
the identity of the two phases at the transition point, by the impossibility of
their coexistence and a necessary difference in their symmetries away from the
transition. Because of the latter, transitions of the 2nd kind can
never be circumvented. Infinitely large systems exhibit a sharp transition
point while small, finite systems possess a narrow transition region within
which the microscopic fluctuations between the two phases increase toward the
critical point, where fluctuations become mesoscopic or macroscopically large
or may even diverge mathematically (Hill 1962, Stanley 1971).
Note that the distinction between
those two kinds is not necessarily axiomatically rigorous. The transformation
of homogeneous liquid water into homogeneous ice is a transition of the 1st
kind. But, during the transition from one single phase to the other, a
two-phase composite state may appear, such as ice on a lake. The transition
from a homogeneous single-phase state to an inhomogeneous two-phase state is
breaking the system’s spatial symmetry and may itself be considered as a
transition of the 2nd kind.
In non-equilibrium systems,
transition phenomena qualitatively similar to those at equilibrium may be
observed which are then often termed kinetic phase transitions, bifurcations
or catastrophes. However, there exist various additional new phenomena
such as self-organised criticality (Bak and Chen 1991), multistability
(Ebeling and Schimansky-Geier 1979), strange attractors (Schuster 1984,
Ruelle 1994, Anishchenko et al. 2009) or homoclinic orbits (Shilnikov
1969, Gaspard et al. 1984, Drysdale 1994). From the thermodynamic point of
view, self-organisation may spontaneously create dissipative structures
(Prigogine 1969, Glansdorff and Prigogine 1971, Ebeling 1976, Prigogine and
Stengers 1981, Nicolis and Prigogine 1987), while from the kinetic perspective,
self-organisation is seen as a cooperative phenomenon of synergetics
(Haken 1977, Haken et al. 2016). The numerous degrees of freedom of a
macroscopic system may be classified with respect to their characteristic time
scales. Model parameters that vary on the time scale of interest are order
parameters, those which vary much slower or are externally imposed
constitute control parameters, and finally, the fastest degrees of
freedom may be replaced by their statistically averaged values as functions of
the slower modes, a method known as the quasi-steady-state hypothesis
(Hahn 1974, Haken 1977). Self-organisation is typically indicated by a
qualitative change in the properties of order parameters where the control
parameters pass critical threshold values of a kinetic phase transition.
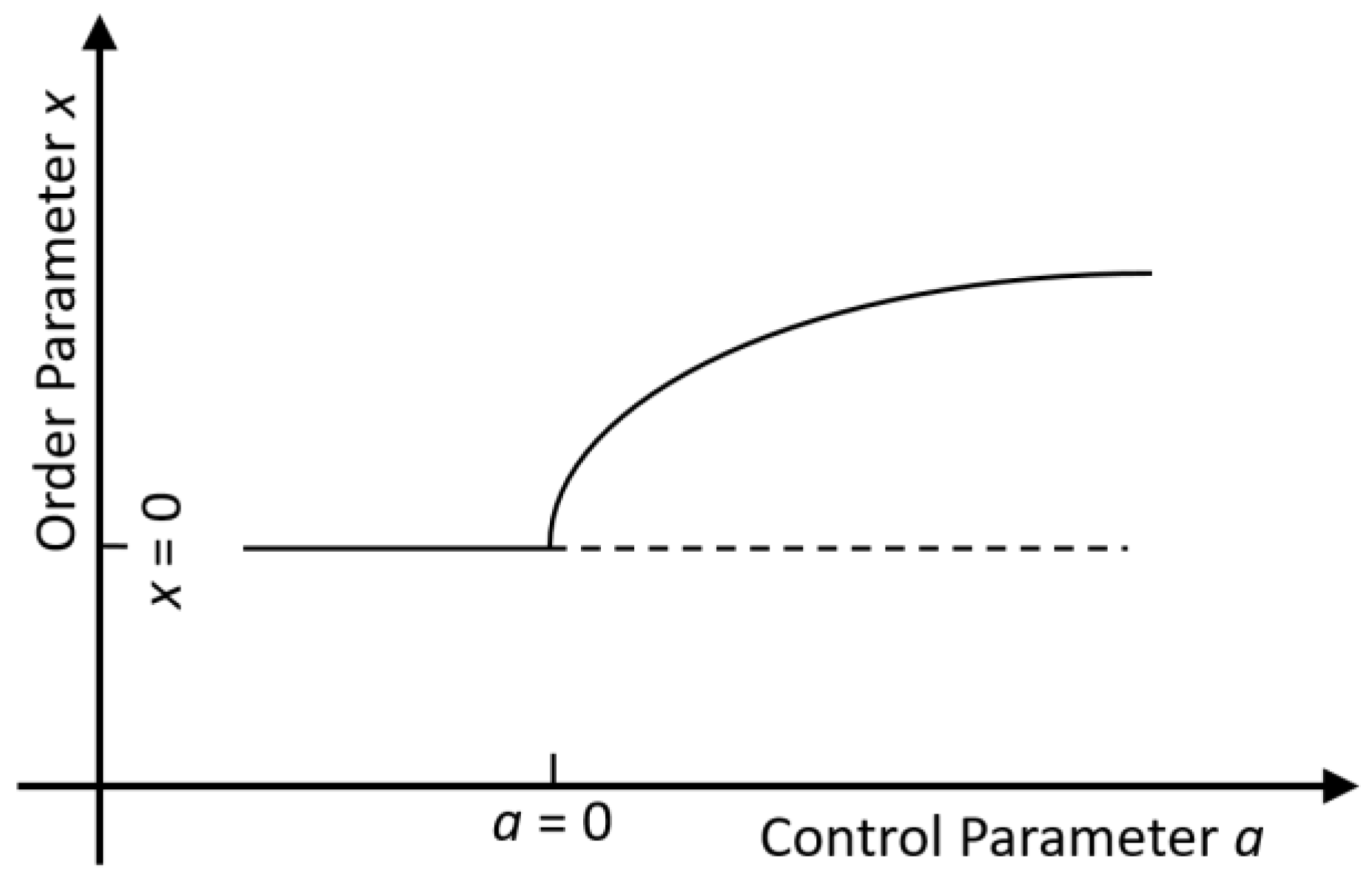
The transition between whispering
and speaking may serve as just one simple example for a kinetic phase transition
of the 2
nd kind, namely, a so-called
Hopf bifurcation.
Mathematically, the process may be modelled as a friction oscillator (Ebeling
1976). Let
as a control parameter describe
the air flow rate, so that
is the critical value for the
onset of voicing, and
, as the order parameter, be the
amplitude of the vocal cord oscillation, which may build up following the
differential equation
At subcritical conditions,
, the state
is stable and the only steady
state. This state becomes unstable at
, and the new stable state
corresponds to a finite
oscillation amplitude. At the critical point,
, the two regimes coincide at
. The two regimes have different
symmetries as
is time-independent while
represents periodic behaviour of
the vocal cord. A related stochastic model for chemical oscillations (Feistel
and Ebeling 1978a, 1989) demonstrates the significant fluctuation growth near
the transition at
. A bifurcation diagram (
Fig. fA.1) shows the
stationary value of
as a function of
.
Fig. fA.1.
Bifurcation diagram of the model (A.1) for a kinetic phase transition of 2nd kind.
Fig. fA.1.
Bifurcation diagram of the model (A.1) for a kinetic phase transition of 2nd kind.
Prigogine and Wiaume (1946) were
the first to draw attention to the role of irreversible thermodynamics in the
self-organised emergence of macroscopic structures. They found that stable
stationary non-equilibrium states are characterised by least production of
entropy per mass unit and suspected this principle to hold also for living
organisms. It turned out later (Glansdorff and Prigogine 1971, Prigogine et al.
1972, Ebeling 1976), however, that Prigogine’s law of minimum entropy
production is rigorously valid only for linear irreversible thermodynamics
below a critical distance from equilibrium, such as Fourier heat conduction of
a fluid at rest, while the self-organisation of dissipative structures requires
super-critical conditions far from equilibrium, such as thermal convection or
turbulence of a fluid. This thermodynamic theory of dissipative structures
eventually resolved the century-long lingering apparent contradiction between
Clausius’ law of growing entropy and Darwin’s law of improving fitness. This
insight inspired a wealth of further studies regarding self-organisation in
biology and related fields (Eigen 1971, 2013, Romanovsky et al. 1975, Ebeling
and Feistel 1979, 1982, 1994, 2018b, Ebeling and Ulbricht 1986, Ebeling et al.
1990, Feistel and Ebeling 1989, 2011, Haken et al. 2016).
Here, self-organised structures
are certain non-equilibrium attractor states which possess lower entropies than
the associated equilibrium state with the same values of total mass, energy and
volume. According to Clausius’ law, after isolation from the surrounding any
such system will relax spontaneously to equilibrium by producing additional
entropy. Note, however, that entropy of non-equilibrium states is not always
uniformly defined (Gibbs 1902, Planck 1906, 1948a, Shannon and Weaver 1964,
Subarev 1976, Alberti and Uhlmann 1981, Klimontovich 1982, Ebeling 1992, 2017,
Volkenstein 2009, Feistel 2019).
Appendix B. A Model for the Ritualisation Transition to Early Life
The conceptual model very briefly
presented here had originally been developed in 1979 at the Lomonosov Moscow
State University in cooperation with Yuri M. Romanovsky and Vladimir A.
Vasiliev (Feistel et al. 1980), and became first published by Ebeling and
Feistel (1982). The model considers qualitative properties of catalytic networks
rather than biochemical details of certain molecules or reactions. It aims at a
plausible stepwise evolution scenario of minimum complexity from random
catalysis to the emergence of first molecular symbols (Deacon 2021) by the
ritualisation transition. This symmetry-breaking transition may be considered
as the beginning of life (Ebeling and Feistel 1992, 1994, Matsuno 2008, Feistel
and Ebeling 2011, Pattee and Rączaszek-Leonardi 2012).
By definition, symbols do not need
to express their meaning by their own physical structure. For the mutual
connection between structure and meaning, an arbitrary convention must be
implemented physically which is capable of identifying the symbol on the one
hand, and, on the other hand, of expressing the symbol’s meaning by some
physical structure or activity. In real life, t-RNA molecules take this
interpreter role (Rich 1962, Eigen and Winkler-Oswatitsch 1981). All parts of
this complicated machinery need to emerge subsequently within a
self-reproducing catalytic cycle of minimum complexity to represent the very
first life form. Hardly, this may occur in just a few simple steps.
Step 1: Catalytic networks
. The chemical process of catalysis is a non-equilibrium process
accompanied by permanent entropy production. There is no catalysis at
thermodynamic equilibrium. Complex molecules, in particular specific catalysts,
may appear under non-equilibrium conditions in low concentrations. Submarine
hydrothermal vents are preferred candidates as relatively stable sources providing
the required energy over large scales of time and space (Van Dover 2019). Let
be the coordination number of a
directed random graph, expressing the ratio of the number of molecule pairs
with a catalytic link between them, to the total number of molecules regardless
of their mutual interaction. If this network is sparsely occupied (Kaplan
1978), , then the probability for the
occurrence of random cycles of length is proportional to (Austin et al. 1959). Pure
autocatalysis () excluded, binary cycles may have
the highest realistic chance for spontaneous emergence in a “primary soup”
(Feistel 1979, Ebeling and Feistel 1979, 1982, Sonntag et al. 1981, Eigen
2013). Such a hypothetical, initial self-replicating catalytic cluster may be
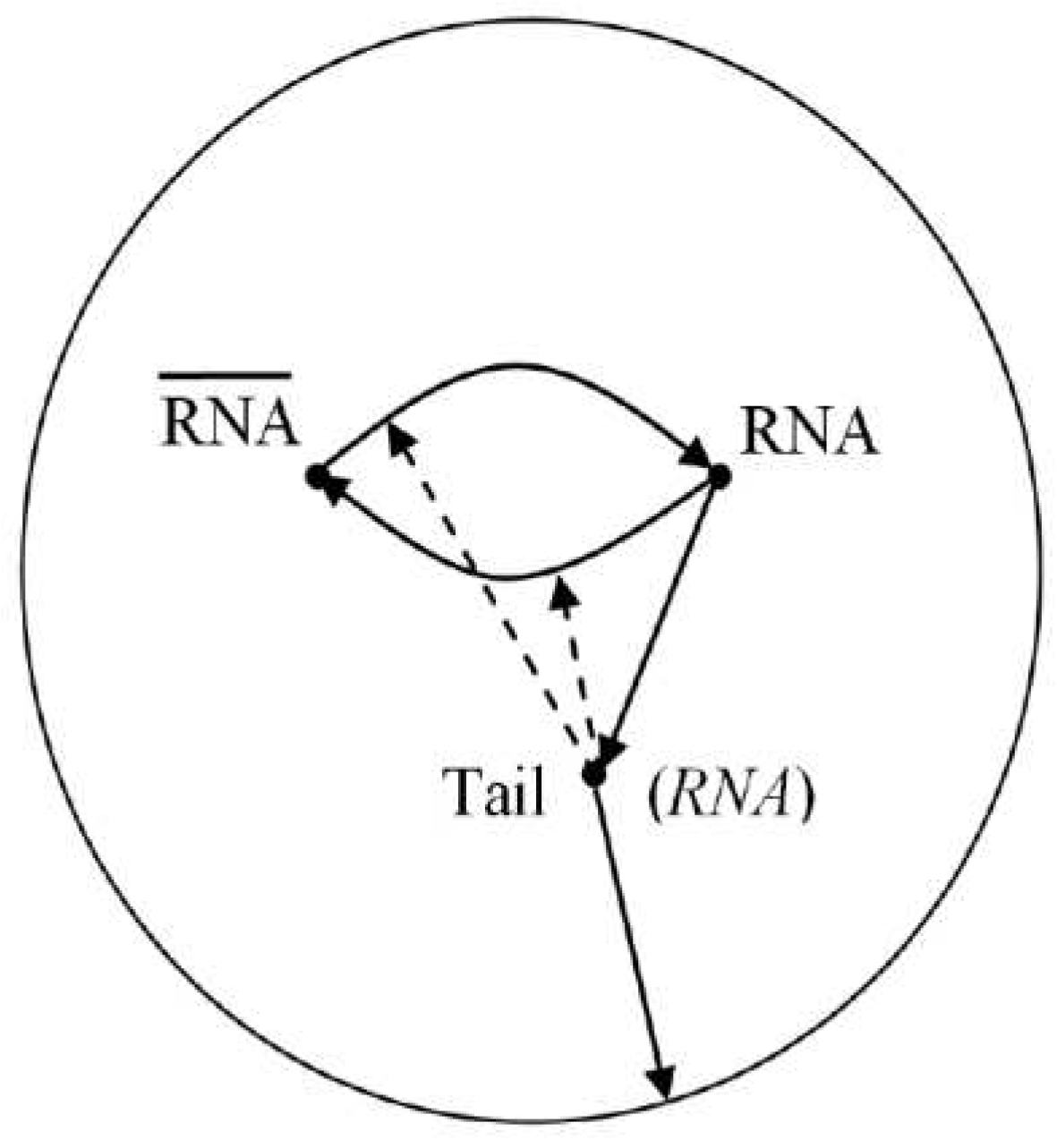
termed an “RNA-Replicase Cycle” (Ebeling and Feistel 1979), where “RNA” stands
for some chain molecule and “replicase” for a suitable catalyst, self-assembled
under support of the 3D configuration of the same or a complementary RNA
(Gilbert 1986).
Step 2: Spatial compartments
: Due to their nonlinear kinetics, catalytic cycles in homogeneous
solution exhibit once-forever selection (Eigen and Schuster 1977) and cannot
gradually compete and improve in chemical selection processes. The latter may
happen, however, as soon as the central cycle develops “parasitic side chains”
which form certain lipid-like membranes, individual droplets or coacervates
(Ebeling and Feistel 1979, 2018a, Feistel et al. 1980, Feistel 1983, Feistel
and Ebeling 2011). For each such droplet a reproduction rate and a selective
value may be calculated from its internal reaction network. A droplet contains
multiple copies of each molecular species. If the molecules are densely packed,
their stoichiometry will adjust in such way that all species reproduce at the
same rate so that the composition of a growing droplet remains fixed. Large
droplets may split up randomly into equally composed “daughter droplets”.
Darwinian chemical selection may eliminate ineffective individuals. Side chains
do not affect the primary cycle catalytically but enhance its reproduction
indirectly by providing a supporting local environment.
Fig. A.1.
Conceptual model of an RNA-replicase cycle enclosed in a self-assembled coacervate, formed from a “parasitic” tail of the central catalytic loop (Ebeling and Feistel 2018b). (RNA) denotes a catalytically active configuration of the chain molecule RNA. This doplet is imagined as the simplest self-replicating individual entity being subject to molecular Darwinian evolution (Feistel et al. 1980). However, lacking yet any symbolic information processing, this coacervate is still considered as a physico-chemical precursor of the first life form.
Fig. A.1.
Conceptual model of an RNA-replicase cycle enclosed in a self-assembled coacervate, formed from a “parasitic” tail of the central catalytic loop (Ebeling and Feistel 2018b). (RNA) denotes a catalytically active configuration of the chain molecule RNA. This doplet is imagined as the simplest self-replicating individual entity being subject to molecular Darwinian evolution (Feistel et al. 1980). However, lacking yet any symbolic information processing, this coacervate is still considered as a physico-chemical precursor of the first life form.
Step 3: Stoichiometric
diversification
: Error copies occurring in the
reproduction of the central cycle may coexist within the same droplet if the
new cycle is catalytically coupled to the primary cycle, forming a special side
chain. Coexisting cycles offer the possibility of specialising the encoded
catalysts, for example into one supporting the reproduction of the chain (RNA
“transcription”) and a different one supporting the reading of the chain
(“translation” to form the replicase).
Step 4: Building-block assembly
lines
: Different small catalysts present in the
same droplet may self-assembly to larger, more effective catalysts. As an
example, the modern highly effective porphyrine molecule may be imagined as a
composite of four simpler proline amino acids. Such a composed catalyst is
initially translated from separate pieces of chain molecules, but the correct
mounting of pieces may become more precise and effective by concatenating the
responsible chain molecules in the required sequence of mounting. This
procedure demands additional auxiliary catalysts. To produce n final
catalysts, each from m different parts, catalytic support of all immediate
steps would require auxiliary catalysts. This way,
the need for different catalysts would grow faster that the possibilities to
assemble those within the given droplet. A way out is standardisation –
different catalysts may be assembled from a small set of elementary building
blocks but in varying sequences. Accordingly, few elementary, coding chain
molecules (say, “segments”) need to be assembled to longer chain sequences
(say, “strands”), each such sequence responsible for assembling a particular
composite catalyst. Up to this point, we still talk about self-organising
chemical networks, yet at the threshold to proper life.
Step 5: Ritualisation
transition
: Strands with many repeated identical
segments are highly redundant, error-prone and ineffective in the execution of
their catalytic activity. A segment catalysing the assembly of a particular
building block needs to exist only once, and if the same block is required
again, reference to its segment is sufficient rather than full repetition of the
segment. In other words, the production of building blocks may be separated
from mounting them together in a certain sequence. Repeated segments in a
strand may then by reduced to shorter “stenographic” identifiers, to mere
symbols prescribing the way of mounting the blocks. The initial symbol for a
segment is the segment itself, but the symbol may then become arbitrary, and
subsequently, become simplified and diversified. This is a new symmetry,
distinguishing first life, native “biology”, from previous catalytic clusters,
from mere “chemistry”.
Step 6: Code evolution
: Because of their arbitrariness, symbols emerged by ritualisation
are neutral, so-called Goldstone modes with vanishing Lyapunov coefficients, so
that random fluctuations may modify the symbol’s physical structure without
affecting its meaning, and without back-driving forces trying to return to a
previous structure. This property permits neutral drift or “weathering” of the
code. On the other hand, this neutrality after the ritualization transition
preserves details of the evolution history in the physical structure of the
symbols (Feistel 1990, 2017a,b, 2023, Feistel and Ebeling 2011). Analysing its
physical structure, the modern genetic code offers various opportunities for
studies of its likely original form and later development (Woese 1965, Crick
1968, Ebeling and Feistel 1982, Jiménez-Montaño et al. 1996, Béland and Allen
1994, Carter 2008, Jiménez-Montaño 2009, José et al. 2017, Xie 2021, Wills
2023).
Symbolically stored genetic
information constitutes a prediction model
to be
exploited by an organism to ensure its survival and reproduction, provided that
similar external conditions prevail under which this information had been
gathered and stored by surviving and reproducing precursors in the past.
References
- Alberti, P.M., Uhlmann, A. (1981): Dissipative Motion in State Spaces. Teubner, Leipzig.
- Almheiri, A.; Hartman, T.; Maldacena, J.; Shaghoulian, E.; Tajdini, A. Replica wormholes and the entropy of Hawking radiation. J. High Energy Phys. 2020, 2020, 1–42,. [CrossRef]
- Anishchenko, V.S., Astakhov, V., Neiman, A., Vadivasova, T., Schimansky-Geier, L. (2009): Nonlinear Dynamics of Chaotic and Stochastic Systems. Springer, Berlin, Heidelberg.
- Austin, J.L. (1962): How to Do Things with Words. Analysis 23, 58-64. [CrossRef]
- Austin, T.L.; Fagen, R.E.; Penney, W.F.; Riordan, J. The Number of Components in Random Linear Graphs. Ann. Math. Stat. 1959, 30, 747–754,. [CrossRef]
- Bak, P., Chen, K. (1991): Self-Organized Criticality. Scientific American 264, No. 1, 46-53. Available online: https://www.jstor.org/stable/24936753.
- Béland, P.; Allen, T. The Origin and Evolution of the Genetic Code. J. Theor. Biol. 1994, 170, 359–365. [CrossRef]
- Born, M. Symbol und Wirklichkeit I: Ein Versuch, auf naturwissenschaftliche Weise zu philosophieren — nicht eine Philosophie der Naturwissenschaften. Phys. J. 1965, 21, 53–63,. [CrossRef]
- Born, M. Symbol und Wirklichkeit II. Phys. J. 1965, 21, 106–108,. [CrossRef]
- Born, M. (1966): Physik im Wandel meiner Zeit. Vieweg & Sohn, Braunschweig.
- Bornholdt, S., Schuster, H.G. (2003): Handbook of Graphs and Networks. Wiley VCH, Weinheim.
- Botton-Amiot, G.; Martinez, P.; Sprecher, S.G. Associative learning in the cnidarian Nematostella vectensis. Proc. Natl. Acad. Sci. 2023, 120, e2220685120. [CrossRef] [PubMed]
- Brillouin, L. (2013): Science and Information Theory. Dover Publications, Mineola, New York.
- Bühler, K. (1965): Sprachtheorie. Gustav Fischer, Stuttgart.
- Butterfield, J. Laws, causation and dynamics at different levels. 2012, 2, 101–114. [CrossRef]
- Carter, C.W. Whence the genetic code?: Thawing the ‘Frozen Accident’. Heredity 2008, 100, 339–340. [CrossRef]
- Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 2013, 36, 181–204. [CrossRef]
- Clausius, R. Ueber verschiedene für die Anwendung bequeme Formen der Hauptgleichungen der mechanischen Wärmetheorie.
-
Ann. der Phys. 1865, 201, 353–400. [CrossRef]
- Clausius, R. (1876): Die mechanische Wärmetheorie. Friedrich Vieweg und Sohn, Braunschweig.
- Craik, K.J.W. (1943): The Nature of Explanation. Cambridge University Press, Cambridge, UK, reprint 1967.
- Crick, F. The origin of the genetic code. J. Mol. Biol. 1968, 38, 367–379,. [CrossRef]
- Darwin, C. (1859): On the origin of species by means of natural selection, or the preservation of favoured races in the struggle for life. John Murray, London.
- Dawkins, R. (1976): The Selfish Gene. Oxford University Press, Oxford.
- Dawkins, R. (1996): The Blind Watchmaker. W.W. Norton & Co., New York.
- Deacon, T.W. (1997): The Symbolic Species. W.W. Norton, New York, London.
- Deacon, T.W. How Molecules Became Signs. Biosemiotics. 2021, 14, 537–559. [CrossRef]
- Deichmann, U. Self-Organization and Genomic Causality in Models of Morphogenesis. Entropy. 2023, 25, 873. [CrossRef]
- Denny-Brown, D. Conditioned Reflexes: an Investigation of the Physiological Activity of the Cerebral Cortex. Nature. 1928, 121, 662–664. [CrossRef]
- Donald, M. (2008): Triumph des Bewusstseins. Klett-Cotta, Stuttgart. American original (2001): A Mind so Rare: The Evolution of Human Consciousness. W.W. Norton & Co., New York.
- Drysdale, D.M. (1994): Homoclinic Bifurcations. Thesis for Doctor of Philosophy, University of Oxford, Jesus College, Oxford, UK.
- Ebeling, W. (1976): Strukturbildung bei irreversiblen Prozessen. Teubner, Leipzig.
- Ebeling, W. On the relation between various entropy concepts and the valoric interpretation. Phys. A: Stat. Mech. its Appl. 1992, 182, 108–115. [CrossRef]
- Ebeling, W. Physical basis of information and the relation to entropy٭. Eur. Phys. J. Spéc. Top. 2017, 226, 161–176. [CrossRef]
- Ebeling, W., Engel, A., Feistel, R. (1990): Physik der Evolutionsprozesse. Akademie-Verlag, Berlin.
- Ebeling, W., Feistel, R. (1979): On the Evolution of Biological Macromolecules. I: Physico-Chemical Self-Organization. Studia biophysica 75, 131-146.
- Ebeling, W., Feistel, R. (1982): Physik der Selbstorganisation und Evolution. Akademie-Verlag, Berlin.
- Ebeling, W., Feistel, R. Theory of Selforganization and Evolution: The Role of Entropy, Value and Information. J. Non-Equilibrium Thermodyn. 1992, 17, 303–332. [CrossRef]
- Ebeling, W., Feistel, R. (1994): Chaos und Kosmos. Spektrum-Verlag, Wiesbaden.
- Ebeling, W, Feistel, R. (2018a): On Models of the Self-Organization of Information Processing. Preprint,. [CrossRef]
- Ebeling, W.; Feistel, R. Studies on Manfred Eigen's model for the self-organization of information processing. Eur. Biophys. J. 2018, 47, 395–401,. [CrossRef]
- Ebeling, W.; Schimansky-Geier, L. Stochastic dynamics of a bistable reaction system. Phys. A: Stat. Mech. its Appl. 1979, 98, 587–600,. [CrossRef]
- Ebeling, W., Ulbricht, H. (1986): Selforganization by Nonlinear Irreversible Processes. Springer, Berlin, Heidelberg.
- Eibl-Eibesfeldt, I. (1970): Liebe und Haß. Piper, München.
- Eibl-Eibesfeldt, I. (1998): Ernst Haeckel – Der Künstler im Wissenschaftler. In: Haeckel, E. (1904): Kunstformen der Natur. Neudruck 1988, München, S. 19-30.
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Sci. Nat. 1971, 58, 465–523. [CrossRef]
- Eigen, M. Wie entsteht Information? Prinzipien der Selbstorganisation in der Biologie. 1976, 80, 1059–1081. [CrossRef]
- Eigen, M. The origin of genetic information. Space Life Sci. 1994, 24, 241–262,. [CrossRef]
- Eigen, M. (2013): From Strange Simplicity to Complex Familiarity: A Treatise on Matter, Information, Life and Thought. Oxford University Press, Oxford.
- Eigen, M.; Winkler-Oswatitsch, R. Transfer-RNA, an early gene? Naturwissenschaften. 1981, 68, 282–292. [CrossRef]
- Eigen, M.; Schuster, P. A principle of natural self-organization. Part A: Emergence of the Hypercycle. Die Naturwissenschaften. Sci. Nat. 1977, 64, 541–565. [CrossRef]
- Feistel, R. (1979): Selektion und nichtlineare Oszillationen in chemischen Modellsystemen. Thesis, Rostock University.
- Feistel, R. (1983): On the Evolution of Biological Macromolecules. IV: Holobiotic Competition. Studia biophysica 93, 121-128.
- Feistel, R. (1990): Ritualisation und die Selbstorganisation der Information. In: Niedersen, U., Pohlmann, L. (eds): Selbstorganisation. Jahrbuch für Komplexität in den Natur-, Sozial- und Geisteswissenschaften, Band 1. Duncker & Humblot, Berlin. [CrossRef]
- Feistel, R. Self-organisation of symbolic information. Eur. Phys. J. Spéc. Top. 2017, 226, 207–228,. [CrossRef]
- Feistel, R. (2017b): Chapter 4: Emergence of Symbolic Information by the Ritualisation Transition. In: Burgin, M., Hofkirchner, W. (eds.): Information Studies and the Quest for Transdisciplinarity. World Scientific, Singapore, pp. 115-164. [CrossRef]
- Feistel, R. Thermodynamic properties of seawater, ice and humid air: TEOS-10, before and beyond. Ocean Sci. 2018, 14, 471–502,. [CrossRef]
- Feistel, R. Distinguishing between Clausius, Boltzmann and Pauling Entropies of Frozen Non-Equilibrium States. Entropy. 2019, 21, 799,. [CrossRef]
- Feistel, R. (2021): Life, Symbols, and Causality. Preprint,. [CrossRef]
- Feistel, R. (2022): Dynamics, Symbols, and Prediction. Preprint,. [CrossRef]
- Feistel, R. On the Evolution of Symbols and Prediction Models. Biosemiotics. 2023, 16, 1–61,. [CrossRef]
- Feistel, R.; Ebeling, W. Deterministic and stochastic theory of sustained oscillations in autocatalytic reaction systems. Phys. A: Stat. Mech. its Appl. 1978, 93, 114–137,. [CrossRef]
- Feistel, R., Ebeling, W. (1978b): On the Eigen-Schuster Concept of Quasispecies in the Theory of Natural Self-Organization. Studia biophysica 71, 139.
- Feistel, R., Ebeling, W. (1989): Evolution of Complex Systems. Self-Organization, Entropy and Development. Kluwer, Dordrecht, Boston, London.
- Feistel, R., Ebeling, W. (2011): Physics of Self-Organization and Evolution. Wiley-VCH, Weinheim.
- Feistel, R.; Ebeling, W. Entropy and the Self-Organization of Information and Value. Entropy. 2016, 18, 193. [CrossRef]
- Feistel, R.; Lovell-Smith, J.W.; Saunders, P.; Seitz, S. Uncertainty of empirical correlation equations. Metrologia. 2016, 53, 1079–1090. [CrossRef]
- Feistel, R., Romanovsky, Yu.M., Vasiliev, V.A. (1980): Evolution of Eigen's Hypercycles Existing in Coacervates (in Russian). Biofizika XXV, 882-887.
- Feistel, R.; Wagner, W. A New Equation of State for H2O Ice Ih. J. Phys. Chem. Ref. Data. 2006, 35, 1021–1047. [CrossRef]
- Frobenius, G. (1912): Über Matrizen aus nicht negative Elementen. Sitzung der physikalisch-mathematischen Classe vom 23. Mai 1912, Königliche Gesellschaft der Wissenschaften, Göttingen, 456-477. [CrossRef]
- Fuentes, M.A. Complexity and the Emergence of Physical Properties. Entropy. 2014, 16, 4489–4496. [CrossRef]
- Gantmacher, F.R. (1971): Matrizenrechnung II. Deutscher Verlag der Wissenschaften, Berlin. Russian original (1954): Teoriya Matrits. Moscow.
- Gaspard, P.; Kapral, R.; Nicolis, G. Bifurcation phenomena near homoclinic systems: A two-parameter analysis. J. Stat. Phys. 1984, 35, 697–727. [CrossRef]
- Gibbs, J.W. (1902): Elementary Principles of Statistical Mechanics. Charles Scribner’s Sons, New York, Edward Arnold, London.
- Gilbert, W. Origin of life: The RNA world. Nature. 1986, 319, 618. [CrossRef]
- Glansdorff, P., Prigogine, I. (1971): Thermodynamic Theory of Structure, Stability and Fluctuations. Wiley-Interscience, London, New York, Sydney, Toronto.
- Graham, R. (1973): Statistical Theory of Instabilities in Stationary Nonequilibrium Systems with Applications to Lasers and Nonlinear Optics. In: Höhler, G. (ed): Springer Tracts in Modern Physics. Springer, Berlin, Heidelberg, pp. 1-97. [CrossRef]
- Graham, R. (1981): Models of Stochastic Behavior in Non-Equilibrium Steady States. In: Chen, SH., Chu, B., Nossal, R. (eds.): Scattering Techniques Applied to Supramolecular and Nonequilibrium Systems. NATO Advanced Study Institutes Series, vol 73. Springer, Boston, MA, pp. 559–612. [CrossRef]
- GUM (2008): Guide to the Expression of Uncertainty in Measurement. JCGM.
- Hahn, H. (1974): Geometrical Aspects of the Pseudo Steady State Hypothesis in Enzyme Reactions. In: Conrad, M., Güttinger, W., Dal Cin, M. (eds): Physics and Mathematics of the Nervous System. Springer, Berlin, Heidelberg, pp. 546-582. [CrossRef]
- Haken, H. (1977): Synergetics. An Introduction. Nonequilibrium Phase Transitions and Self-Organization in Physics, Chemistry and Biology. Springer, Berlin, Heidelberg, New York.
- Haken, H., Plath, P.J., Ebeling, W., Romanovsky, Yu.M. (2016): Beiträge zur Geschichte der Synergetik, Allgemeine Prinzipien der Selbstorganisation in Natur und Gesellschaft. Springer Spektrum, Wiesbaden.
- Harvey, A.H.; Hrubý, J.; Meier, K. Improved and Always Improving: Reference Formulations for Thermophysical Properties of Water. J. Phys. Chem. Ref. Data. 2023, 52, 011501. [CrossRef]
- Hellmuth, O.; Schmelzer, J.W.P.; Feistel, R. Ice-Crystal Nucleation in Water: Thermodynamic Driving Force and Surface Tension. Part I: Theoretical Foundation. Entropy. 2020, 22, 50. [CrossRef]
- Hilbert, D. (1903): Grundlagen der Geometrie. Teubner, Leipzig.
- Hill, T.L. Thermodynamics of Small Systems. J. Chem. Phys. 1962, 36, 3182–3197. [CrossRef]
- Hoffman, D.D. (2020): Relativ Real. Warum wir die Wirklichkeit nicht erfassen können und wie die Evolution unsere Wahrnehmung geformt hat. dtv, München. English original: A Case Against Reality. W.W. Norton.
- Hume, D. (1758): An Enquiry Concerning Human Understanding. German edition (1967): Eine Untersuchung über den menschlichen Verstand. Reclam, Ditzingen.
- Huxley, J.S. 33. The Courtship - habits * of the Great Crested Grrebe (Podiceps cristatus); with an addition to the Theory of Sexual Selection. J. Zoöl. 1914, 84, 491–562. [CrossRef]
- IOC, SCOR, IAPSO (2010): The International Thermodynamic Equation of Seawater—2010: Calculation and Use of Thermodynamic Properties. Intergovernmental Oceanographic Commission, Manuals and Guides No. 56, UNESCO (English), p. 196, Paris. Available online: http://www.TEOS-10.org (accessed on 26 November 2022).
- Jiménez-Montaño, M.A. The fourfold way of the genetic code. Biosystems. 2009, 98, 105–114. [CrossRef]
- Jiménez-Montaño, M.A.; de la Mora-Basáñez, C.R.; Pöschel, T. The hypercube structure of the genetic code explains conservative and non-conservative aminoacid substitutions in vivo and in vitro. Biosystems. 1996, 39, 117–125. [CrossRef]
- José, M.V.; Zamudio, G.S.; Morgado, E.R. A unified model of the standard genetic code. R. Soc. Open Sci. 2017, 4, 160908. [CrossRef]
- Kämmerer, W. (1974): Einführung in die mathematischen Methoden der Kybernetik. Akademie-Verlag, Berlin.
- Kämmerer, W. (1977): Kybernetik. Akademie-Verlag, Berlin.
- Kant, I. (1956): Kritik der reinen Vernunft. Felix Meiner, Hamburg. Original editions A: 1781, B: 1787.
- Kaplan, R.W. (1978): Der Ursprung des Lebens. Thieme, Stuttgart.
- Kirkaldy, J. Thermodynamics of Terrestrial Evolution. Biophys. J. 1965, 5, 965–979. [CrossRef]
- Klimonotovich, Yu.L. (1982): Statistical Physics (in Russian). Nauka, Moscow.
- Klix, F. (1980): Erwachendes Denken. Eine Entwicklungsgeschichte der menschlichen Intelligenz. Deutscher Verlag der Wissenschaften, Berlin.
- Kull, K. (2007): Biosemiotics and Biophysics – the Fundamental Approaches to the Study of Life. In: Barbieri, M. (ed.): Introduction to Biosemiotics. Springer, Dordrecht, pp. 167-177. [CrossRef]
- Kull, K. Choosing and learning: Semiosis means choice. Sign Syst. Stud. 2018, 46, 452–466. [CrossRef]
- Lacková,.; Matlach, V.; Faltýnek, D. Arbitrariness is not enough: towards a functional approach to the genetic code. Theory Biosci. 2017, 136, 187–191. [CrossRef]
- Lancaster, P. (1969): Theory of Matrices. Academic Press, London, New York.
- Landau, L.D., Lifschitz, E.M. (1966): Lehrbuch der Theoretischen Physik Band V, Statistische Physik. Akademie-Verlag, Berlin.
- LeDoux, J. (2021): Bewusstsein. Die ersten vier Milliarden Jahre. Klett-Cotta, Stuttgart.
- Leibniz, G.W. (1765): Nouveaux essais sur l‘entendement humain. Amsterdam/Leipzig. German edition (1904): Neue Abhandlungen über den menschlichen Verstand. Dürr, Leipzig.
- Logan, R.K. (1986): The Alphabet Effect. The Impact of the Phonetic Alphabet on the Development of Western Civilisation. William Morrow, New York.
- Lorenz, K. (1970): Foreword to Koenig, O.: Kultur und Verhaltensforschung. Deutscher Taschenbuch-Verlag, München.
- Maldonato, M. (2012): The Decisions of Consciousness and the Consciousness of Decisions. Humana.Mente 15, 99-120.
- Margulis, L. (2017): Der symbiotische Planet. Westend Verlag, Frankfurt/Main. English original (1998): Symbiotic Planet. Basic Books, New York.
- Mast, F. (2020): Black Mamba oder die Macht der Imagination. Verlag Herder, Freiburg i. B.
- Matsuno, K. Molecular Semiotics toward the Emergence of Life. Biosemiotics. 2008, 1, 131–144. [CrossRef]
- Medrano-T., R.O.; Baptista, M.S.; Caldas, I.L. Basic structures of the Shilnikov homoclinic bifurcation scenario. Chaos: Interdiscip. J. Nonlinear Sci. 2005, 15, 33112. [CrossRef]
- Mendel, G. (1866): Versuche über Pflanzenhybriden. Verhandlungen des naturforschenden Vereines in Brünn, Bd. IV für das Jahr 1865, Abhandlungen, 3–47.
- Nicolis, G., Prigogine, I. (1987): Die Erforschung des Komplexen. Piper, München.
- Nirenberg, M.W.; Matthaei, J.H. The dependence of cell-free protein synthesis in E. coli upon naturally occurring or synthetic polyribonucleotides. Proc. Natl. Acad. Sci. USA. 1961, 47, 1588–1602. [CrossRef]
- Nöth, W. (2000): Handbuch der Semiotik, 2nd edition. J.B. Metzler, Stuttgart.
- Nomura, N.; Matsuno, K.; Muranaka, T.; Tomita, J. How Does Time Flow in Living Systems? Retrocausal Scaffolding and E-series Time. Biosemiotics. 2019, 12, 267–287. [CrossRef]
- Oehler, K. (1995): Sachen und Zeichen. Zur Philosophie des Pragmatismus. Vittorio Klostermann, Frankfurt am Main.
- Orcutt, G.H. Actions, Consequences, and Causal Relations. Rev. Econ. Stat. 1952, 34, 305. [CrossRef]
- Oubrahim, H, Boon Chock, P. (2016): Chemical and Physical Principles. Encyclopedia of Cell Biology (Second Edition) 1, 3-11,. [CrossRef]
- Pattee, H.H. The physics of symbols: bridging the epistemic cut. Biosystems. 2001, 60, 5–21,. [CrossRef]
- Pattee, H.H.; Rączaszek-Leonardi, J. Historical Introduction to Laws Language and Life. Springer, Dordrecht, 2012. [CrossRef]
- Pauen, M., Roth, G. (2008): Freiheit, Schuld und Verantwortung. Grundzüge einer naturalistischen Theorie der Willensfreiheit. Suhrkamp, Frankfurt am Main.
- Pearl, J., Mackenzie, D. (2019): The Book of Why. The New Science of Cause and Effect. Penguin Books.
- Perkins, T.J.; Swain, P.S. Strategies for cellular decision-making. Mol. Syst. Biol. 2009, 5, 326–326. [CrossRef]
- Pink, T. (2009): Free Will and Consciousness. In: Bayne, T., Cleeremans, A., Wilken, P. (eds): The Oxford Companion to Consciousness. Oxford University Press, Oxford.
- Pink, T. (2021): Final Causation. In: Braun, H.E., De Born, E., Astorri, P. (eds): The Companion to the Spanish Scholastics (Brill's Companions to the Christian Tradition). Brill, Leiden.
- Pinker, S. (1994): The Language Instinct. How the Mind Creates Language. William Morrow, New York.
- Planck, M. (1906): Vorlesungen über die Theorie der Wärmestrahlung. Johann Ambrosius Barth, Leipzig.
- Planck, M. (1937): Vom Wesen der Willensfreiheit. Nach einem Vortrag in der Ortsgruppe Leipzig der Deutschen Philosophischen Gesellschaft am 27. November 1936. Johann Ambrosius Barth, Leipzig.
- Planck, M. (1948a): Wissenschaftliche Selbstbiographie. Johann Ambrosius Barth, Leipzig.
- Planck, M. (1948b): Der Kausalbegriff in der Physik. Johann Ambrosius Barth, Leipzig.
- Planck, M. (1966): Theorie der Wärmestrahlung. Johann Ambrosius Barth, Leipzig.
- Poincaré, H., Goroff, D.L. (1993): New Methods of Celestial Mechanics. American Institute of Physics.
- Prigogine, I. (1969): Structure, Dissipation and Life. North-Holland Publ. Company, Amsterdam.
- Prigogine, I. (2000): The Arrow of Time. Inaugural Lecture at the Bestowal of the Honorary Citizenship of the City of Pescara. In: Gurzadyan, V.G., Ruffini, R. (eds): The Chaotic Universe: Proceedings of the Second Icra Network Workshop: Rome, Pescara, Italy 1-5 February 1999 (Advanced Series in Astrophysics and Cosmology, Band 10). World Scientific, Singapore, pp. 1-15. [CrossRef]
- Prigogine, I.; Nicolis, G.; Babloyantz, A. Thermodynamics of evolution. Phys. Today. 1972, 25, 23–28,. [CrossRef]
- Prigogine, I., Stengers, I. (1981): Dialog mit der Natur. Piper, München.
- Prigogine, I.; Wiame, J.M. Biologie et thermodynamique des phénomènes irréversibles. Cell. Mol. Life Sci. 1946, 2, 451–453. [CrossRef]
- Prum, R.O. (2017): The Evolution of Beauty. Doubleday, New York.
- Rich, A. (1962): On the Problems of Evolution and Biochemical Information Transfer. In: Kasha, M., Pullman, B. (eds): Horizons in Biochemistry. Academic Press, London, New York, pp. 103-126.
- Riek, R. Entropy Derived from Causality. Entropy. 2020, 22, 647,. [CrossRef]
- Romanovsky, Yu.M., Stepanova, N.V., Chernavsky, D.S. (1975): Mathematical Modelling in Biophysics (in Russian). Nauka, Moscow.
- Ruelle, D. (1994): Zufall und Chaos. Springer, Berlin, Heidelberg.
- Russell, B. (1919): Mysticism and Logic and Other Essays. Chapter IX: On the Notion of Cause. Longmans, Green and Co., London, p. 180-208. Available online: https://en.wikisource.org/wiki/Mysticism_and_Logic_and_Other_Essays.
- Sagan, C. (1978): Die Drachen von Eden. Das Wunder der menschlichen Intelligenz. Droemer/Knaur, München/Zürich.
- Sapper, K. (1928): Kausalität und Finalität. Annalen der Philosophie und philosophischen Kritik 7, 205-212. Available online: https://www.jstor.org/stable/20018075.
- Schmelzer, J.W.P. (2005): Nucleation Theory and Applications. Wiley-VCH, Berlin.
- Schmelzer, J.W.P. Application of the Nucleation Theorem to Crystallization of Liquids: Some General Theoretical Results. Entropy. 2019, 21, 1147. [CrossRef]
- Schuster, H.G. (1984): Deterministic Chaos. An Introduction. Physik Verlag, Weinheim.
- Shannon, C.E., Weaver, W. (1964): The Mathematical Theory of Communication. The University of Illinois Press, Urbana.
- Shilnikov, L.P. (1969): A certain new type of bifurcation of multidimensional dynamic systems (in Russian). Doklady Akademii Nauk SSSR 189, 59–62.
- Smith, A. (1776): An Inquiry into the Nature and Causes of the Wealth of Nations. German edition (2013): Der Wohlstand der Nationen. Eine Untersuchung seiner Natur und seiner Ursachen. Deutscher Taschenbuch Verlag, München.
- Smith, J.M. (1988): Games, Sex and Evolution. Harvester Wheatsheaf, New York.
- Sonntag, I.; Feistel, R.; Ebeling, W. Random Networks of Catalytie Biochemical Reactions. Biom. J. 1981, 23, 501–515. [CrossRef]
- Stachowiak, H. (1973): Allgemeine Modelltheorie. Springer-Verlag, Wien.
- Stanley, H.E. (1971): Introduction to Phase Transitions and Critical Phenomena. Clarendon Press, Oxford.
- Subarev, D.N. (1976): Statistische Thermodynamik des Nichtgleichgewichts. Akademie-Verlag, Berlin.
- Summers, R.L. Lyapunov Stability as a Metric for Meaning in Biological Systems. Biosemiotics. 2023, 16, 1–14. [CrossRef]
- Taleb, N.N. (2008): The Black Swan: The Impact of the Highly Improbable. Penguin Books, London.
- Tembrock, G. (1977): Grundlagen des Tierverhaltens. Akademie-Verlag, Berlin.
- Turing, A.M. (1950): Computing machinery and intelligence. Mind 59, 433-460. Available online: http://www.jstor.org/stable/2251299.
- Van Dover, C.L. Forty years of fathoming life in hot springs on the ocean floor. Nature. 2019, 567, 182–184. [CrossRef]
- Volkenstein, M.V. (2009): Entropy and information. Birkhäuser, Basel.
- von Herder, J.G. (1772): Abhandlung über den Ursprung der Sprache, welche den von der Königl. Academie der Wissenschaften für das Jahr 1770 gesezten Preis erhalten hat. Christian Friedrich Voß, Berlin. Available online: http://www.deutschestextarchiv.de/book/show/herder_abhandlung_1772.
- English translation: Gode, A. (1966): Essay on the Origin of Language. In: Two Essays On the Origin of Language, Jean-Jacques Rousseau and Johann Gottfried Herder. The University of Chicago Press, Chicago, London, pp. 85-166.
- von Uexküll, J. (1973): Theoretische Biologie. Suhrkamp, Frankfurt am Main.
- von Weizsäcker, V. (1940): Der Gestaltkreis: Theorie der Einheit von Wahrnehmen und Bewegen. Georg Thieme Verlag, Leipzig.
- Watson, J.D.; Crick, F.H.C. Molecular Structure of Nucleic Acids: A Structure for Deoxyribose Nucleic Acid. Nature. 1953, 171, 737–738. [CrossRef]
- Wiener, N. (1948): Cybernetics. Wiley, New York.
- Willink, R. Measurement Uncertainty and Probability; Cambridge University Press (CUP): Cambridge, United Kingdom, 2013. ISBN 9781107021938.
- Woese, C.R. On the evolution of the genetic code. Proc. Natl. Acad. Sci. 1965, 54, 1546–1552. [CrossRef]
- Wills, P.R. Origins of Genetic Coding: Self-Guided Molecular Self-Organisation. Entropy. 2023, 25, 1281. [CrossRef]
- Xie, P. Who is the missing “matchmaker” between proteins and nucleic acids? Innov. 2021, 2, 100120. [CrossRef]
- Zeeman, E.C. (1976): Euler buckling. In: Hilton, P. (ed.): Structural Stability, the Theory of Catastrophes, and Applications in the Sciences. Lecture Notes in Mathematics, vol. 525. Springer, Berlin, Heidelberg. [CrossRef]
Notes
|
1 Eibl-Eibesfeld (1998): p. 21. English: “For an organism the world must be predictable, otherwise it cannot live therein.” |
|
2 Original text: “Erst wenn eine Handlung vollzogen ist und somit der Vergangenheit angehört, sind wir zu dem Versuch berechtigt, sie von rein kausalem Gesichtspunkten aus zu verstehen“ |
|
3 Original text: “Wenn es die Aufgabe der Wissenschaft ist, bei allem Geschehen in der Natur oder im menschlichen Leben nach gesetzlichen Zusammenhängen zu suchen, so ist … eine unerläßliche Voraussetzung dabei, daß ein solcher Zusammenhang wirklich besteht, und daß er sich in deutliche Worte fassen läßt. In diesem Sinne sprechen wir auch von der Gültigkeit des allgemeinen Kausalgesetzes und von der Determinierung sämtlicher Vorgänge in der natürlichen und in der geistigen Welt durch dieses Gesetz. |
|
4 Original text: “Der Lebensvorgang ist nicht eine Sukzession von Ursache und Wirkung, sondern eine Entscheidung.” |
|
5 Clausius (1876): p. 223: English: “The algebraic sum of all transformations in a cyclic process can only be positive or, as a limiting case, zero.” |
|
6 Clausius (1876): p. 82, 364: English: „Heat transfer from a colder to a warmer body cannot occur without compensation.” |
|
7 Clausius (1865): p. 400: English: „The energy of the world is constant. The entropy of the world aspires to a maximum.” |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).