Dark Energy and Dark Matter from Extra Dimensional Symmetry as Different Manifestations of Vacuum Energy

1. Introduction

Dark energy is a mysterious energy component that have been observed to be driving the accelerated expansion of the universe, and have defied several explanations since its discovery in supernova observations [1]. Its existence has since been confirmed by several independent observations like the Planck measurements of the Cosmic Microwave Background (CMB), indicating that it accounts for about 68.3% of the gravitating energy content of the universe [2]. This is in addition to the existing mystery [3,4] of a gravitationally attractive but invisible matter component known as dark matter which now constitutes about 26.8% of the gravitating energy content of the universe. Only about 4.6% is in the form of visible baryonic matter.

The cosmological constant (Λ) earlier introduced into Einstein’s Field Equations, which appears to be the simplest solution, results in a serious conflict between measured density of dark energy and the 120 orders of magnitude larger value predicted from Quantum Field Theory [5]. The Λ problem has defied logical solutions from supersymmetric cancellation approaches, relaxation of vacuum energy [6] and anthropic approach [7]. It also defies an approach that simply makes the spacetime metric insensitive to Λ [8].

Slowly evolving scalar field models like quintessence [9,10] is one of the many alternative approaches to solve the dark energy mystery without the Λ route. We also have modified gravity models [11] and unification of dark energy and dark matter [12]. See Ref. [13] for detailed review and Refs. [14,15] for recent review.

The amount of theoretical and observational efforts that has been applied to understand dark energy and dark matter suggests that they require new physics beyond the existing standard model of cosmology and particle physics.

Attempts to resolve the dark matter mystery can be mainly classified as either a modification of gravity or introduction of new particles beyond the standard model of particle physics. However, both approaches of modified gravity and particle dark matter tends to fail in providing consistent explanations to the dark matter mystery as each approach tends to succeed in explaining some observations and fail at some others. But recent observations have largely ruled out modified gravity models [16,17,18].

There is an approach that explains dark matter as gravitational polarization of vacuum energy by baryonic matter without invoking new particle or modifying gravity in the traditional sense [19]. It is based on the idea that matter and antimatter have opposite gravitational charges. Preliminary findings from measurements of antiproton to proton charge to mass ratio imply that matter and antimatter gravitate the same way [20]. In addition, the recent result from the ALPHA collaboration has ruled out the possibility of gravitationally repulsive antimatter [21].

In this paper, the dark energy and dark matter puzzle are approached using the new framework of Extra Dimension Symmetry (EDS) that doubles the number of large extra dimensions with microscopic partners of opposite handedness. EDS provides a possible solution to the dark energy puzzle by placing vacuum energy in a gravitationally inert state where the actual gravitational constant is zero G. Due to an asymptotically evolving speed limit asymmetry between the two states and an energy density constraint, a small component of vacuum energy is constrained to the gravitationally active state, manifesting as dark energy. For dark matter, it relies on the background effect of neutrinos which induces non-zero gravitational constant in the inert state, enabling the gravitation of the dense component of vacuum energy which appears as dark matter and neutrino mass generation mechanism. See Ref [22] for a review on neutrino mass which is still an open question.

While neutrino interaction with dark energy produces light neutrino mass, chiraly inverted neutrino interaction with the bulk of vacuum energy produces heavy neutrino mass which manifests as cold dark matter. Transition to the heavy state can be enabled by the gravitational expansion of microscopic dimensions by shear stress. This neutrino substrate approach for dark matter while similar, does not require the polarization of the quantum vacuum or opposite gravitational charges for particles and antiparticles like in [19].

In this paper, distinction is made between ordinary baryonic matter and neutrino baryonic matter as neutrinos are required to be domiciled in the left handed microscopic extra dimensional partners of the visible spatial dimensions which gives them unique gravitational properties different from ordinary baryons.

This paper is organized as follows. Section 2 discusses the key dimensional symmetry in which spatial dimensions are grouped as a set of dimension(s) with dimensional partners having opposite dimension numbers that determines either a positive or negative response to the stress energy tensor. It also discusses the possible relationship between the fine structure constant and the minimum path lengths in microscopic extra dimensions as well as the response of theses extra dimensions to the components of the stress energy tensor. It further discusses the speed constraint, the two gravitationally inert and active states, their speed limit asymmetry and density constraint, which is then applied in Section 4 to provide a possible solution to the Λ problem of dark energy. Section 3 discusses General Relativity in two set of these extra dimensions with negative dimension numbers, which determines the dynamics of expansion and contraction. Section 4 discusses the emergence of an asymptotically evolving Λ dark energy due to the speed limit asymmetry and energy density constraint discussed in section 2. It also briefly discusses dynamics of the resulting dark energy and the cyclic universe scenario that can result from the reversal of a dimensionality parameter that reverses the dimension number signs. Section 5 discusses neutrino gravitational properties including the induced gravitation of virtual particles which appears as dark matter, neutrino mass as well as stress enabled chiral transition. Section 6 discusses observational and experimental probes of this form of dark matter. Discussion and conclusion follows in Section 7.

2. Extra Dimensional Symmetry Framework

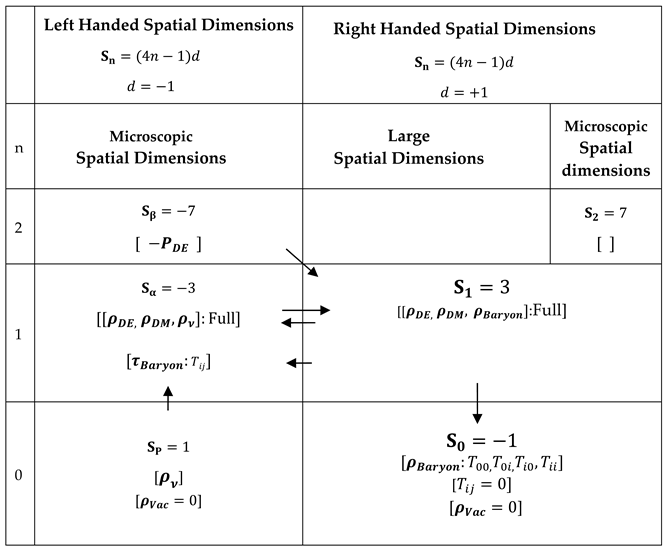
In this framework, the spatial dimensions are grouped, with the number of large spatial dimensions described by the dimension number ${\mathrm{S}}_n$ (analogous to baryon number) with a dimensionality parameter d that is an indication of handedness that can either be positive or negative (right handed or left handed) and oscillates on cosmological time scale such that

$${\mathrm{S}}_n=(4n-1)d,$$

(1)

where $n=0,1,2,3,\dots$, and $d=+1$ for right handed dimensions in the present universe. A dimension with $n=0,$ corresponds to ${\mathrm{S}}_0=-1$ which is a 1D large spatial dimension that is invisible due to a speed constraint consistent with special relativity discussed later in Section 2.2. Dimensions with $n=1,$ corresponds to ${\mathrm{S}}_1=3$ which is the visible 3D set of spatial dimensions. Ref [23] discusses right handedness of space time although in the context of the geometry of the Euclidean version of twistor space in understanding the symmetries of the standard model.

Gravitational interaction in ${\mathrm{S}}_1$ is not diluted by a large ${\mathrm{S}}_0$ as they are compartmentalized partly by their opposite dimension number and response to components of the stress energy tensor. While the positive dimension number (gravitational charge) of ${\mathrm{S}}_1$ denotes positive response to the components of the stress energy tensor where mass energy is seen as positive and therefore attractive, the negative dimension number of ${\mathrm{S}}_0$ denotes a negative response where mass energy appears negative and therefore repulsive.

The EDS framework further doubles these large set of right handed spatial dimensions (${\mathrm{S}}_1=3d$ and ${\mathrm{S}}_0=-1d$) with left handed microscopic partners that have opposite dimension numbers where $d=-1$, such that the total dimension number of the universe can be zero. While the dimensional partner of ${\mathrm{S}}_0$, is a Planck size ${\mathrm{S}}_{\mathrm{P}}$ dimension, the dimensional partner of ${\mathrm{S}}_1$ is denoted ${\mathrm{S}}_{\mathsf{\alpha }}$.

Table 1. Periodic table of spatial dimensions indicating dimension number symmetry between the sets of right handed spatial and left handed spatial dimensions within the EDS framework. With positive dimensionality parameter d, the right handed spatial dimensions ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ expanded in the early universe while their left handed partners of opposite dimensionality parameter, collapsed to their minimum length scales.

	Microscopic Spatial dimensions (Left Handed)	Large Spatial dimensions (Right Handed)
	$d=-1$	$d=+1$
n	${\mathbf{S}}_{\mathbf{n}}=(4n-1)d$	${\mathbf{S}}_{\mathbf{n}}=(4n-1)d$
1	${\mathbf{S}}_{\mathsf{\alpha }}=-3$	${\mathbf{S}}_1=3$
0	${\mathbf{S}}_{\mathbf{P}}=1$	${\mathbf{S}}_0=-1$

Table 1. Periodic table of spatial dimensions indicating dimension number symmetry between the sets of right handed spatial and left handed spatial dimensions within the EDS framework. With positive dimensionality parameter d, the right handed spatial dimensions ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ expanded in the early universe while their left handed partners of opposite dimensionality parameter, collapsed to their minimum length scales.

	Microscopic Spatial dimensions (Left Handed)	Large Spatial dimensions (Right Handed)
	$d=-1$	$d=+1$
n	${\mathbf{S}}_{\mathbf{n}}=(4n-1)d$	${\mathbf{S}}_{\mathbf{n}}=(4n-1)d$
1	${\mathbf{S}}_{\mathsf{\alpha }}=-3$	${\mathbf{S}}_1=3$
0	${\mathbf{S}}_{\mathbf{P}}=1$	${\mathbf{S}}_0=-1$

The opposite dimension numbers of right handed spatial and left handed spatial dimensions implies opposite gravitational charges with the inversion of the sign of the stress energy tensor in which expansion becomes contraction while contraction becomes expansion. As a result of this, the right handed spatial dimensions ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ expanded to cosmic scales in the early universe while their left handed dimensional partners collapsed to their various minimum microscopic length scales. This was partly enabled by the absence of vacuum energy in ${\mathrm{S}}_0-{\mathrm{S}}_{\mathrm{P}}$ dimensions. Instead, all vacuum energy fluctuations are restricted to ${\mathrm{S}}_1-{\mathrm{S}}_{\mathsf{\alpha }}$ dimensions. In addition, while ordinary baryonic matter are domiciled in the large right handed ${\mathrm{S}}_1-{\mathrm{S}}_0$ dimensions, neutrinos are domiciled in the microscopic left handed dimensions.

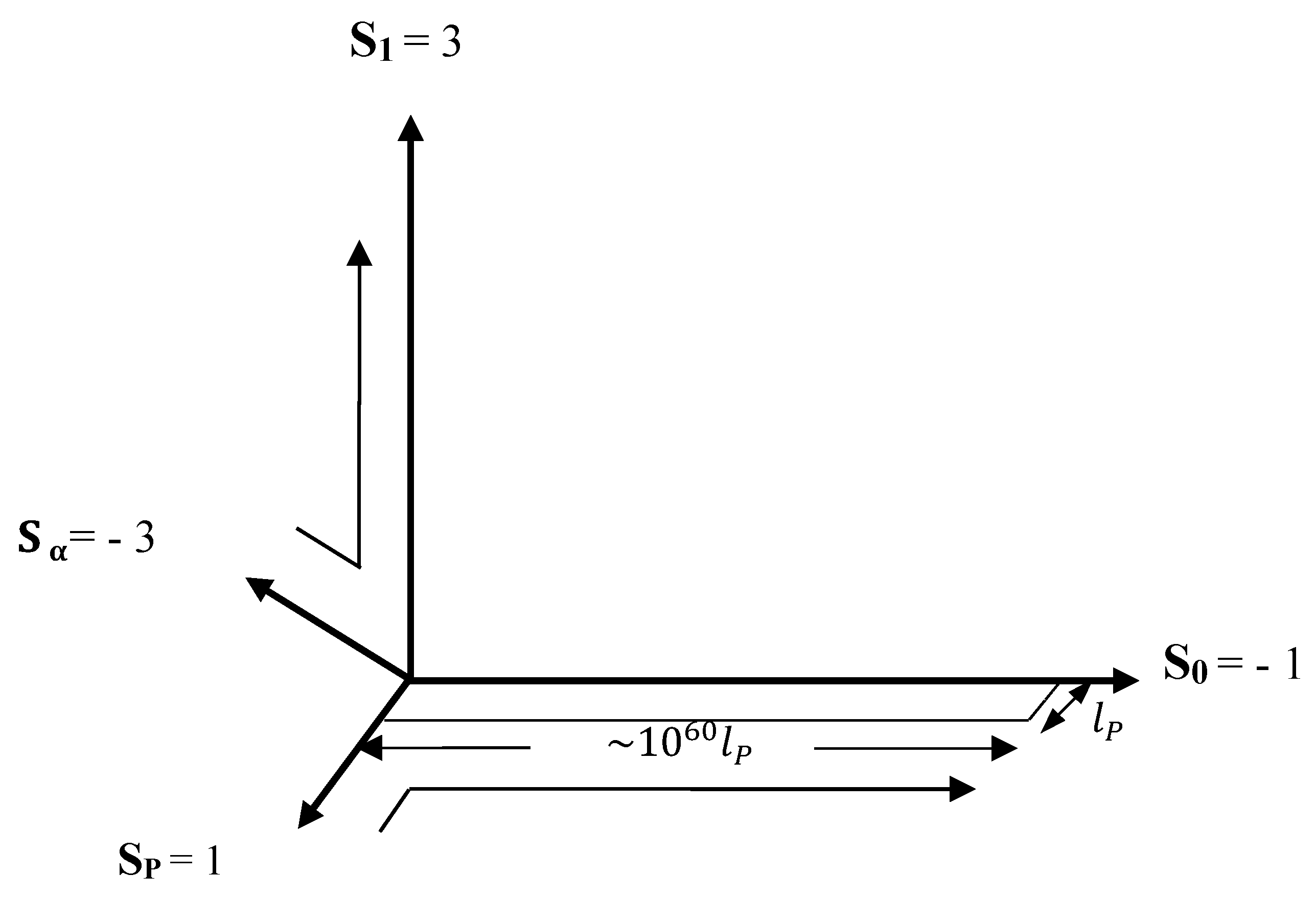
Figure 1. Large spatial dimensions ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ and their microscopic dimensional partners ${\mathrm{S}}_{\mathsf{\alpha }}$ and ${\mathrm{S}}_{\mathrm{P}}$. The opposite dimension numbers which inverts the sign of the stress energy tensor implies that ${\mathrm{S}}_{\mathrm{P}}$ and ${\mathrm{S}}_{\mathsf{\alpha }}$ collapsed toward their minimum microscopic sizes during the inflation of ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ in the early universe. The sizes of ${\mathrm{S}}_{\mathrm{P}}$ and ${\mathrm{S}}_0$ are constrained to the Planck length $l_P$ and 10⁶⁰$l_P$ respectively as their ratio determines the value dark energy density as discussed later in Section 4.

Figure 1. Large spatial dimensions ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ and their microscopic dimensional partners ${\mathrm{S}}_{\mathsf{\alpha }}$ and ${\mathrm{S}}_{\mathrm{P}}$. The opposite dimension numbers which inverts the sign of the stress energy tensor implies that ${\mathrm{S}}_{\mathrm{P}}$ and ${\mathrm{S}}_{\mathsf{\alpha }}$ collapsed toward their minimum microscopic sizes during the inflation of ${\mathrm{S}}_1$ and ${\mathrm{S}}_0$ in the early universe. The sizes of ${\mathrm{S}}_{\mathrm{P}}$ and ${\mathrm{S}}_0$ are constrained to the Planck length $l_P$ and 10⁶⁰$l_P$ respectively as their ratio determines the value dark energy density as discussed later in Section 4.

2.1. Minimum Toroidal Path Lengths Along the Component Dimensions and $\alpha$

The minimum path length $(l_{min}$) along the component dimension(s) ($l_{n1}, l_{n2} and l_{n3}$) of the dimension groups up to 3D can be linked to torus topology and expressed as,

$$l_{min}=(4{\pi }^3+{\pi }^2+\mathsf{\pi })l_P,$$

(2)

where $l_P$ is the Planck length in Planck unit. This cumulative sequence in path lengths, is due to the toriodal relationship between the component dimensions of each group of dimension(s). As such, the minimum path length ($l_{01})$ along the only component dimesion of $S_P$ is $\pi l_P$.

For $S_{\alpha }$ dimensions, the minimum path length of the component dimensions ($S_{\alpha 1}, S_{\alpha 2} and S_{\alpha 3})$ are $l_{\alpha 1}=\pi l_P$, $l_{\alpha 2}={(\pi }^2+\pi )l_P$ and $l_{\alpha 3}=\left(4{\pi }^3+{\pi }^2+\pi \right)l_P\approx 137.0363$ in Planck unit, a value that remarkably matches the inverse value of the fine structure constant $\alpha$ to about one part in ${10}^6$.

The geometric interpretation of this cumulative sequence in path length, is that for 1D motion in 1D, $\pi l_P$ is the minimum path along the circumference of a circle with a diameter $l_P$. For 2D, ${(\pi }^2+\pi )l_P$ is the minimum path length along a torus with minor circumference $\pi l_P$ and a major radius ${\displaystyle \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}\pi l_P$. For 3D, $(4{\pi }^3+{\pi }^2+\pi )l_P$, is the minimum path length along a torus with a minor circumference ${\pi }^2{l}_P$ and a major radius ${2\pi }^2{l}_P$.

Attempts have been made to determine the value of $\alpha$ from first principle [24] including geometric approaches such as in [25] suggesting the golden ratio as the mathematical basis.

Any potential link between the value of $\alpha$ and minimum path length in $S_{\alpha 3}$ (one of the component dimensions in $S_{\alpha }$) should have measurable consequences from the resulting dent in $\alpha$ wherever there is high concentration of dark matter beyond a threshold density. This is because, in EDS, as discussed in the next subsection, components like dark matter density ${\rho }_{DM}$ and baryonic stress ${\tau }_{Baryon}$, expands the $S_{\alpha }$ dimensions while contracting the visible spatial dimensions $S_1$.

This potential link between the minimum toroidal path length along the component dimensions of $S_{\alpha }$ and the value of $\alpha$, is a crucial determinant of some of the properties of concentrated EDS form of dark matter discussed later in Section 5.4.

2.2. Responses of Extra Dimensions to Components of the Stress Energy Tensor

As mentioned earlier, the symmetry in EDS requires that every response of the visible spatial dimensions to components of $T_{\mu \nu }$ has to be balanced in extra dimensions with opposite dimension numbers such as ${\mathrm{S}}_0$ and ${\mathrm{S}}_{\mathsf{\alpha }}.$ However, not all the extra dimensions are responsive to all components. For instance shear stress requires two spatial dimensions and therefore cannot exist in ${\mathrm{S}}_0$ with only one spatial dimension where stress is meaningless. With this, baryonic shear stress response branches into ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions (3D). The absence of vacuum energy fluctuations in ${\mathrm{S}}_0$ also makes it insensitive to $T_{\mu \nu }$ contributions from dark matter and dark energy which are different manifestations of vacuum energy in EDS. Instead, vacuum energy is limited to the ${\mathrm{S}}_1-{\mathrm{S}}_{\mathsf{\alpha }}$ dimensions.

While the $T_{\mu \nu }$ contribution from ordinary baryonic matter are domiciled in the right handed (large) ${\mathrm{S}}_1-{\mathrm{S}}_0$ dimensions except for stress components that appears in ${\mathrm{S}}_{\mathsf{\alpha }}$ due to the 1D constraint, neutrino are domiciled in the left handed ${\mathrm{S}}_{\mathsf{\alpha }}-{\mathrm{S}}_{\mathrm{P}}$ dimensions that had collapsed to their minimum length scale. There are two primary restrictions that arises from this ${\mathrm{S}}_{\mathsf{\alpha }}$ collapse. Neutrinos are unable to undergo chiral transition to sterile neutrinos unless there is a stress driven expansion of ${\mathrm{S}}_{\mathsf{\alpha }}$. Secondly, the collapse of the component dimensions of ${\mathrm{S}}_{\mathsf{\alpha }}$ to their minimum length scales implies a null response to the negative pressure from vacuum energy. To match the gravitational expansion of the universe by negative pressure, there have to be another set of spatial dimensions with negative dimension number undergoing gravitational collapse. From Eq. (1), this comes from $n=2$, which corresponds to ${\mathrm{S}}_2=7$ and ${\mathrm{S}}_{\mathsf{\beta }}=-7$. This is the only justification for extra dimensions beyond $n=1$. With existing constraints on the size of extra dimensions, ${\mathrm{S}}_{\mathsf{\beta }}$ and ${\mathrm{S}}_2$ must be microscopic, unable to inflate in the early universe.

Table 2. Periodic table of right and left handed spatial dimensions showing their content and response to the stress energy tensor (gravitational channel of expansion and contraction).

Table 2. Periodic table of right and left handed spatial dimensions showing their content and response to the stress energy tensor (gravitational channel of expansion and contraction).

The right handed spatial dimensions contain ordinary baryonic matter and their gravitational responses except for shear stress which branches into ${\mathrm{S}}_{\mathsf{\alpha }}$ due to the one dimensional limitation of ${\mathrm{S}}_0$. Neutrinos and their gravitational responses on the other hand, are restricted to the left handed spatial dimensions where their gravitational channel is the collapse of ${\mathrm{S}}_{\mathrm{P}}$ for the expansion of ${\mathrm{S}}_{\mathsf{\alpha }}$. The vacuum energy components (dark energy and dark matter are restricted to the ${\mathrm{S}}_1-{\mathrm{S}}_{\mathsf{\alpha }}$ dimensions except for the negative pressure of dark energy which has to extend into ${\mathrm{S}}_{\mathsf{\beta }}$ due to the collapse of the component dimensions of ${\mathrm{S}}_{\mathsf{\alpha }}$ to the minimum length scales.

2.3. Speed Constraint and Invisibility of S₀ Dimension

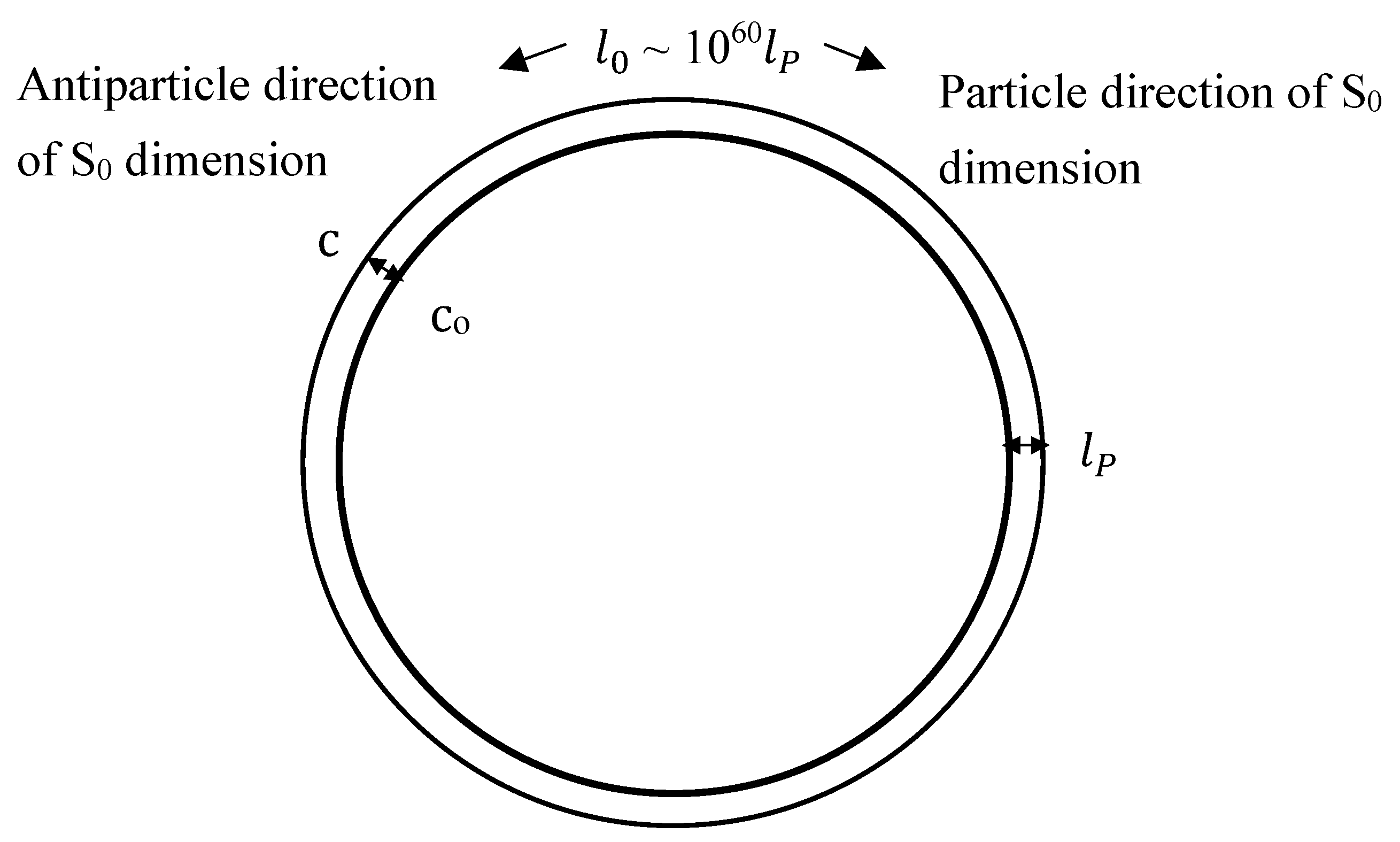
Despite its cosmic size, the ${\mathrm{S}}_0$ dimension is invisible due to its time like behavior from the speed constraint in the EDS framework. Consistent with Special Relativity, the speed constraint requires that a particle’s velocity must always equal the maximum speed limit c in the ${\mathrm{S}}_1$—${\mathrm{S}}_0$ dimensions.

Massless particles like photons have zero velocity component along ${\mathrm{S}}_0$, while massive particles and antiparticles travel in opposite directions along ${\mathrm{S}}_0$ as illustrated in Figure 2. This motion along ${\mathrm{S}}_0$ can be quantitatively equivalent to the passage of time such that,

$$c^2={\mu }^2+{\nu }^2.$$

(3)

where µ is particle velocity along ${\mathrm{S}}_0$, and ν is particle velocity along visible spatial dimensions ${\mathrm{S}}_1$.

When $\nu \to 0,$ for massive particles, $\mu \to c$ and conversely, when ν $=c$, for massless particles, $\mu =0$, to satisfy the speed constraint. This suggests that time can be an emergent temporal dimension driven by the velocity of particles along ${\mathrm{S}}_0$ dimension. How fast time appears to pass for a massive particle can be equivalent to the ratio of its ${\mathrm{S}}_0$ component of velocity $\mu$ to the speed limit c as,

$${\displaystyle \frac{1}{{\gamma }^0}}={\displaystyle \frac{\mu }{c}}.$$

(4)

where ${\gamma }^0$ is the equivalent Lorentz factor for the ${\mathrm{S}}_0$ dimension. Since ${\mu }^2=c^2-{\nu }^2$,

$${\gamma }^0={\displaystyle \frac{1}{\sqrt{1-\frac{v^2}{c^2}}}}.$$

(5)

2.4. Speed Limit Asymmetry

The asymmetry in speed limits c and ${\mathrm{c}}_0$ is described by the asymmetry parameter $\mathsf{\Gamma }$ which is the ratio of the Planck size of ${\mathrm{S}}_{\mathrm{P}}$ to the size of ${\mathrm{S}}_0$ dimension, illustrated in Figure 2. $0<\mathsf{\Gamma }<1$ such that,

$$\mathsf{\Gamma }={\displaystyle \frac{2\pi }{l_o}}.$$

(6)

where $l_o$ ($~{10}^{60}$) is the size of ${\mathrm{S}}_0$ in Planck unit which expands with the gravitational contraction of ${\mathrm{S}}_1$ as discussed in the previous subsections and further explained later in Section 3, which implies a slightly larger value of $l_o$ in deep gravitational potential wells and hence smaller value of $\mathsf{\Gamma }$.

The asymmetry between the two speed limits $\mathrm{c}$ and ${\mathrm{c}}_0$ in Figure 2 can be expressed as,

$$C_o=C\left[1-\mathsf{\Gamma }\right].$$

(7)

2.5. Gravitational States and Particle Chirality Oscillation

In the EDS framework, the opposite speed limit states discussed in the previous subsection as illustrated in Figure 2, are also opposite gravitational on and off states which corresponds to opposite particle chirality. Thus, for ordinary baryonic particles undergoing chirality oscillation, they also oscillate between the two G and zero G states with slightly different speed limits c and ${\mathrm{c}}_0$ respectively. They still however experience an average gravitational constant value of 1G.

2.6. Planck Energy Density Constraint

The Planck energy density constraint essentially constrains the total energy density in a given volume of spacetime to always equal the upper limit of the Planck density ${\rho }_P$. This density constraint is analogous to the speed constraint in Section 2.3 and can be expressed as,

$${\rho }_P={\rho }_m+{\rho }_{Vac}.$$

(8)

where ${\rho }_{vac}$ is the vacuum energy density, and ${\rho }_m$ is the total baryonic matter density.

However, Planck density is only obtainable in the gravitational active state where the speed limit is c while the bulk of the vacuum energy component exists in the inert state with lower speed limit and hence lower Planck density. The key significance of this, is in the emergence of a small Λ dark energy component in Section 4. However, such energy density constraint implies a Planck density limit to the density of black holes like that suggested in [26], where Planck stars replace black hole singularities.

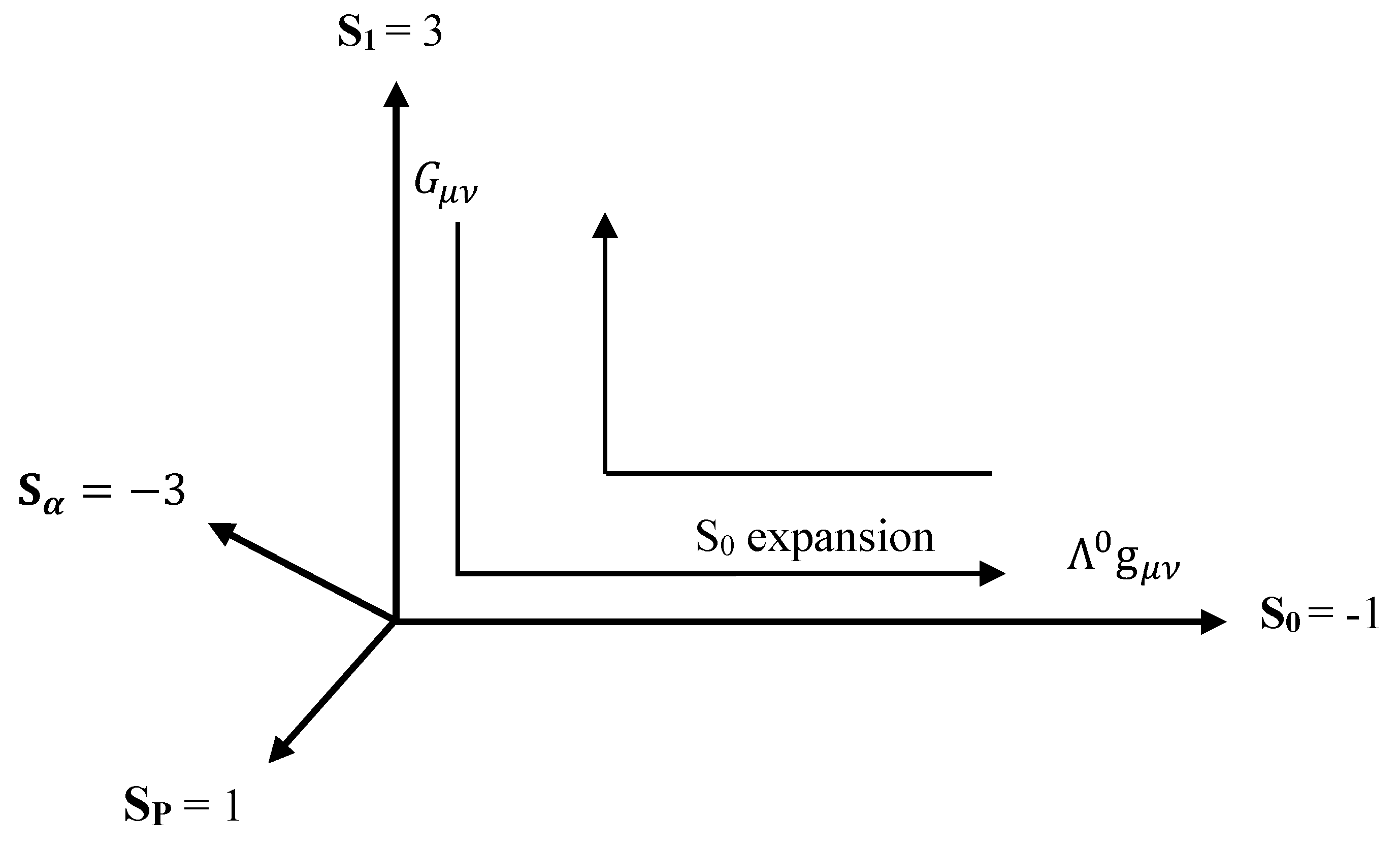
3. General Relativity in ${\mathbf{S}}_0$ and ${\mathbf{S}}_{\mathsf{\alpha }}$ Dimensions

3.1. General Relativity in S₀ Dimension

In 1+1 dimensionality the curvature term in Einstein Field Equations is zero [27]. In ${\mathrm{S}}_0$ dimension where the dimension number is negative, it can be expressed as,

$${{\mathsf{\Lambda }}^0\mathrm{g}}_{\mu \nu }=-{\displaystyle \frac{8\pi G}{c^4}}{T}_{\mu \nu }.$$

(9)

where ${\mathsf{\Lambda }}^0$ is the equivalent cosmological constant in S₀ dimension, ${\mathrm{g}}_{\mu \nu }$ is the metric tensor and $T_{\mu \nu }$ is the stress energy tensor. The negative dimension number of the ${\mathrm{S}}_0$ dimension which inverts the sign of the stress energy tensor, confers on it some unique features such as:

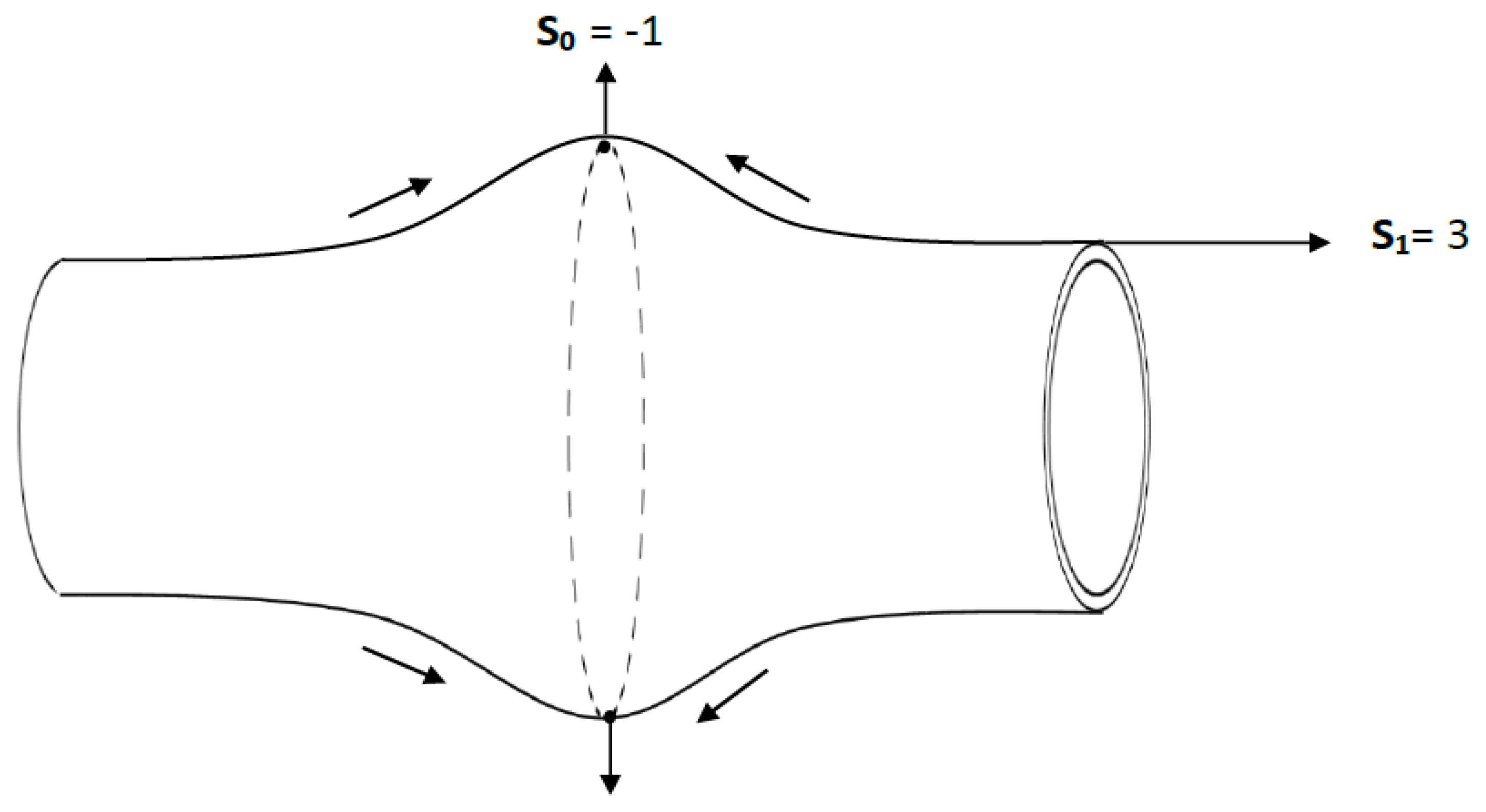
i.

Positive energy density in ${\mathrm{S}}_1$ is equivalent to negative energy density everywhere in ${\mathrm{S}}_0$.

An energy density associated with a given Planck volume of 3d space ${\mathrm{S}}_1$ appears as an equivalent negative energy density everywhere along the corresponding ${\mathrm{S}}_0$ dimension as illustrated in Figure 3.

ii.

Positive pressure in ${\mathrm{S}}_1$ is equivalent to negative pressure in ${\mathrm{S}}_0$

Any form of positive pressure in ${\mathrm{S}}_1$ appears as negative pressure in ${\mathrm{S}}_0$ for the same reason of negative dimensionality. The result is a positive cosmological constant expansion of ${\mathrm{S}}_0$ that is equivalent to the curvature of ${\mathrm{S}}_1$ ($G_{\mu \nu }$) as illustrated in Figure 4, such that,

$$G_{\mu \nu }+{{\mathsf{\Lambda }}^0\mathrm{g}}_{\mu \nu }=0,$$

(10)

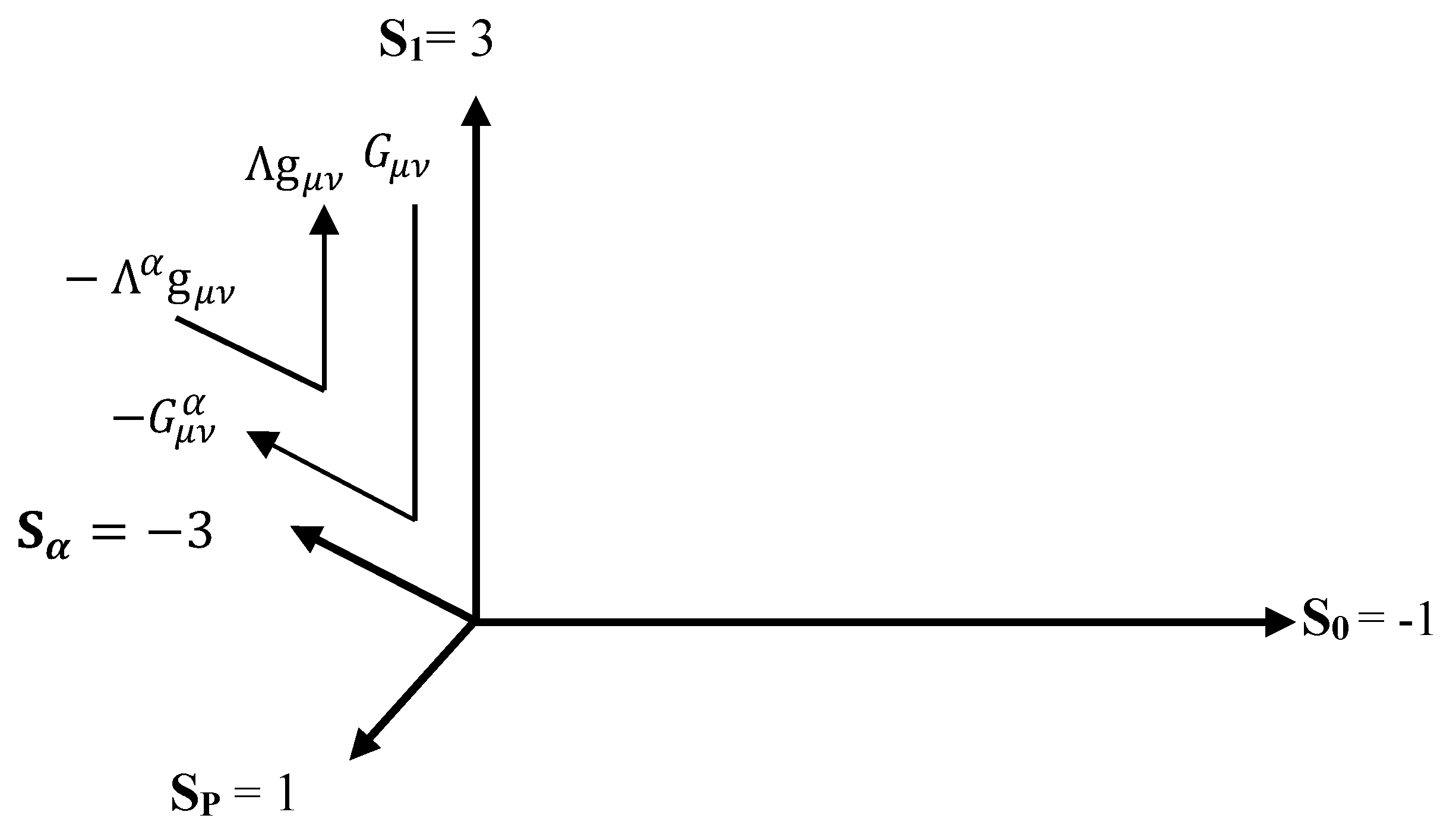
3.2. General Relativity in $S_{\alpha }$ Dimensions

In 3D ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions, the Einstein tensor is not zero unlike in 1D ${\mathrm{S}}_0$ dimension. In addition, ${\mathrm{S}}_{\mathsf{\alpha }}$ only responds to baryonic shear stress and vacuum energy components (dark energy and dark matter) as discussed in Section 2.2. The result is that on one hand, the positive curvature effect ($G_{\mu \nu }$) of shear stress and vacuum energy density contributions from dark matter and dark energy on ${\mathrm{S}}_1$ dimensions is equivalent to their negative curvature effect ($-G_{\mu \nu }^{\alpha }$) on the ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions. Therefore,

$$G_{\mu \nu }-G_{\mu \nu }^{\alpha }=0.$$

(11)

On the other hand, the positive cosmological constant ($\mathsf{\Lambda }$) expansion of ${\mathrm{S}}_1$ due to negative pressure form dark energy, is equivalent to the negative cosmological constant (${-\mathsf{\Lambda }}^{\alpha }$) contraction of ${\mathrm{S}}_{\alpha }$.

$${\mathsf{\Lambda }\mathrm{g}}_{\mu \nu }-{{\mathsf{\Lambda }}^{\alpha }\mathrm{g}}_{\mu \nu }=0.$$

(12)

The gravitational inversions in ${\mathrm{S}}_1$-${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions as illustrated in Figure 5 results in the negative pressure driven collapse of ${\mathrm{S}}_{\mathsf{\alpha }}$ until all its component dimensions have completely collapsed to their minimum length scale.

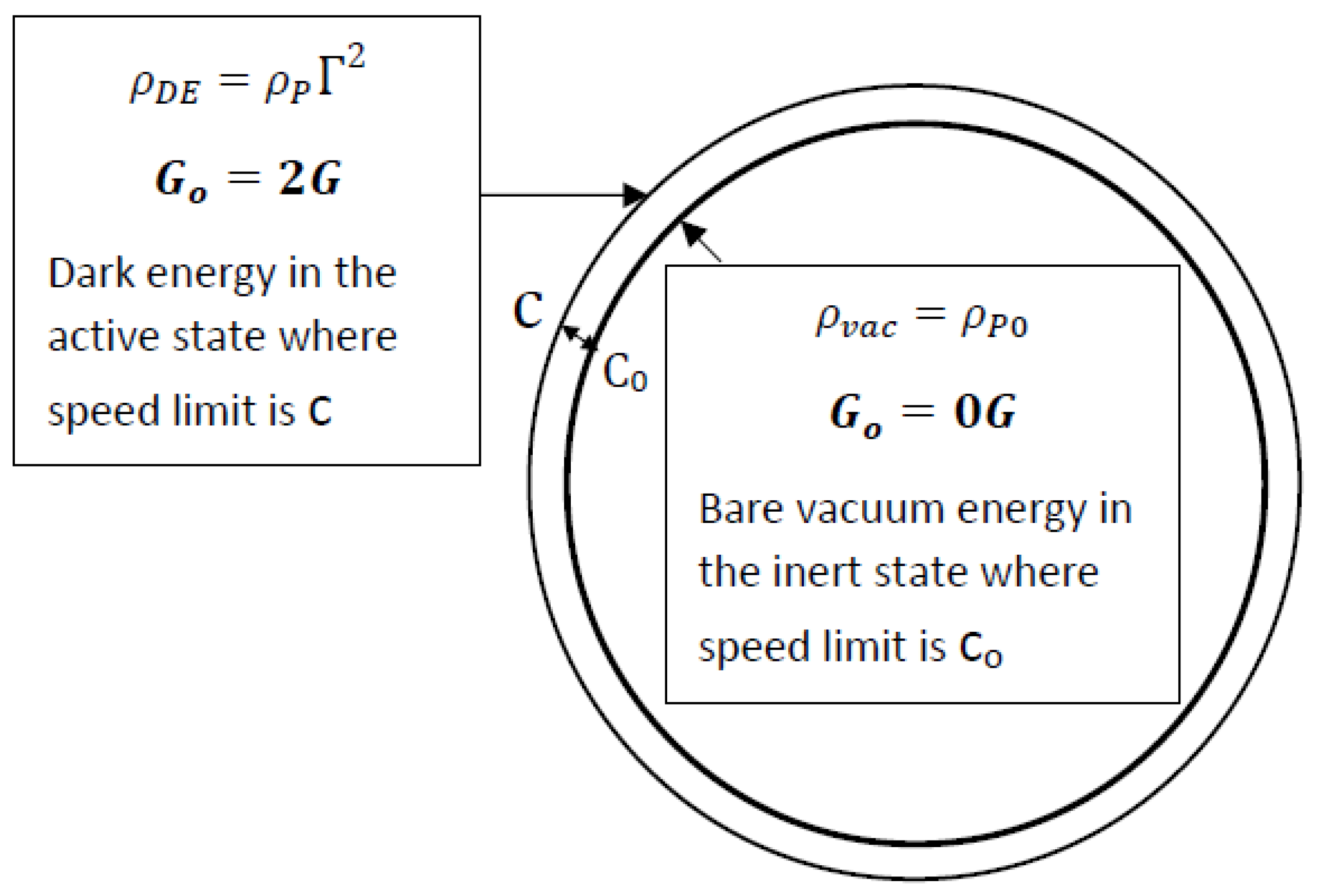
4. Emergence of an Asymptotically Evolving Cosmological Constant

The asymmetry in speed limit described in Equation (6) between the two gravitational states also reflects in the values of their Planck densities such that (Since $E=m{c}^2$),

$${\rho }_{Vac}={\rho }_P(1-{\mathsf{\Gamma }}^2)$$

(13)

Where ${\rho }_{Vac}$ is the vacuum energy density and equals the lower Planck density in ${\mathrm{C}}_0$ state. ${\rho }_P$ is the Planck density in the $\mathrm{C}$ state. $\mathsf{\Gamma }$ is the asymmetry parameter that asymptotically approaches zero with the baryonic gravity driven growth of ${\mathrm{S}}_0$ as discussed in the previous section.

In the presence of Baryons with energy density ${\rho }_m$, Eq. (12) can be expressed as,

$${\rho }_P={\rho }_m+{\rho }_{Vac}+{\rho }_P{\mathsf{\Gamma }}^2.$$

(14)

Since the gravitationally inert (lower speed) state is unable to contain the total vacuum energy components, the small component ${\rho }_P{\mathsf{\Gamma }}^2$ in Eq. (13) is therefore constrained to the gravitationally active state as a cosmological constant dark energy ${\rho }_{DE}$ with an equation of state parameter $\omega =-1$ as illustrated in Figure 6. That is,

$${\rho }_{DE}={\rho }_P{\mathsf{\Gamma }}^2.$$

(15)

4.1. Dynamics of $\Lambda$ Dark Energy in a Cyclic Universe

Despite maintaining a constant equation of state, this form of $\mathsf{\Lambda }$ dark energy varies spatially and with time since it depends on $\mathsf{\Gamma }$ as discussed in the previous section. In turn depends on the size of ${\mathrm{S}}_0$ dimension ($l_o$) according to Eq. (6) and Figure (3) illustration. The value of $l_o$ is entirely driven by the gravity of the baryonic component (Table 2) and therefore, much larger in deep gravitational potential wells. This can show up in the precision measurement of the Integrated Sachs Wolf effect. With the resulting asymptotic evolution of dark energy density, a smaller $l_o$ in the early universe can result in $\mathsf{\Gamma }\lesssim 1$ with ${\rho }_{DE }\lesssim {\rho }_P$ capable of driving an inflationary universe before asymptotically falling close to its current value. The recent result from the DESI collaboration indicates possible evolution of dark energy density [28,29].

Due to the gravitational symmetry in this framework, the positive $\mathsf{\Lambda }$ expansion of the visible spatial dimensions is equivalent to the negative $\mathsf{\Lambda }$ contraction of ${\mathrm{S}}_{\mathsf{\alpha }}$ until all its 3D components completely collapsed to their characteristic minimum length scales. The existence and contraction of an extra dimension with negative dimension number (${\mathrm{S}}_{\mathsf{\beta }}=-7$) is the required to sustain the continued expansion of the universe.

However, the dimensionality parameter in Eq. (1) is required to chiraly oscillate in a similar way chirality oscillation of particles occur but on cosmological time scale. When the dimensionality parameter is eventually reversed, a reverse cycle of the universe begins in which dimension number signs of the dimensions are reversed as well as their various responses to components of the stress energy tensor. In this scenario, in which the visible spatial dimensions ${\mathrm{S}}_1$, illustrated in Table 1 and Table 2 as right handed becomes left handed and their ${\mathrm{S}}_{\mathsf{\alpha }}$ partners become right handed, the dark energy equation of state still remains constant. Rather, it is the response of the visible spatial dimensions to positive energy density that becomes negative while its response to negative pressure becomes negative as well.

The result is that baryonic matter and dark matter becomes repulsive with black holes becoming white holes until complete evaporation, while dark energy becomes attractive, driving the collapse of the visible universe while expanding the ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions. Associated with an expanding ${\mathrm{S}}_{\mathsf{\alpha }}$, is the fall in the value of the fine structure constant since it is coupled to the size of one of its 3 component dimensions in this framework as discussed in Section 2.1 and later in Section 5. The corresponding contraction of ${\mathrm{S}}_0$ increases the density of dark energy in reverse towards the Planck density scale, while the ${\mathrm{S}}_{\mathrm{P}}$ dimension begins to expand due to neutrino energy density. This results in an accelerated collapse of the visible right handed spatial dimensions with the inflation of the left handed ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions in a cyclic scenario which gets reversed with continued chiral oscillation of the dimensionality parameter on cosmological time scale.

5. Dark Matter from Neutrino Enabled Gravitation of Virtual Particles

In the EDS framework, the existence of most of the vacuum energy component in the gravitationally inert state ensures that virtual particles in such state are gravitationally inert. However, neutrinos have some unique gravitational properties, one of which is the ability to induce small component of the gravitational constant in this inert state. It enables virtual particles to gravitate with positive pressure and appear as dark matter.

5.1. Gravitational Properties of Neutrinos in EDS

As mentioned earlier and ilustrated in Table 2, neutrino energy density is domiciled in the left handed spatial dimensions ($S_{\alpha }-S_P$) while ordinary baryons exists in the right handed spatial dimensions ($S_1-S_0$). As a result of this, the channel of neutrino gravitational interaction is restricted to the left handed dimensions while that of baryons are restricted to the right except for baryonic stress which branches into the $S_{\alpha }$ dimensions due to the 1D limitation of $S_{\alpha }$ as explained in Section 2.2.

The result of this different gravitational channels for neutrino and other bayic matter, is the insenitivity of light neutrinos to baryonic gravitational potential. Therefore EDS predicts non gravitational lensing of of neutrinos even around black holes.

In addition to the left handedness of neutrino gravitational response in EDS, as mentioned earlier, neutrinos also induce some gravitational constant component restricted to the internal structure of neutrinos without a radiative term. It can be expressed as,

$$G_{\nu }=\beta \varphi rG$$

(16)

where $\varphi$ is the dimensionless phase parameter. It oscillates such that $0\le \varphi \le 1$. $r$ is a hierarchical dimensionless term with a bound $0<r<1$ and it is different for each of the neutrino flavours. $\beta$ is a dimensionless energy scale parameter. It is the ratio of neutrino energy to Planck energy such that $0<\beta <1$.

$$\beta ={\displaystyle \frac{E_{\nu }}{E_P}}$$

(17)

where $E_{\nu }$ is neutrino energy and $E_P$ is Planck energy.

5.2. Neutrino Mass Generation Mechanism

When neutrinos are in the gravitationally active state as left handed neutrinos and right handed antineutrinos, they interact with dark energy through their induced gravitational constant component $G_{\nu }$ from Eq. 16 such that,

$${\mu }_{\nu }=G_{\nu }{V_{\nu }\rho }_{DE}$$

(18)

where ${\mu }_{\nu }$ is the resulting neutrino gravitational parameter, ${\rho }_{DE}$ is the mass density of dark energy and $V_{\nu }$ is the spatial volume under the influence of the neutrino gravitational constant component.

The generated neutrino mass $m_{\nu }$ from ordinary neutrino interaction with dark energy can therefore be expressed as,

$$m_{\nu }=\beta \varphi r{V_{\nu }\rho }_{DE.}$$

(19)

It is therefore expected that maximum light neutrino masses obtainable when $\varphi =1$, should coincide and track the mass scale of dark energy at about 10^-3 eV. Indeed, an attempt was made in [30] to justify a possible coincidence between the mass scale of dark energy to what we expect of the neutrino mass. However, since light neutrino mass in this framework is coupled to the mass density of dark energy, it should track the time evolution of dark energy and should be slightly lower in deep gravitational potential wells which also suppresses dark energy density as discussed in Section 4.1.

When light neutrinos chiraly transition to right handed neutrinos and left handed antineutrinos, they interact with the dense component of vacuum energy in the otherwise gravitationally inert state. The mass of the resulting sterile neutrinos becomes increasingly heavy as $\varphi \to 1$ and begins to behave as cold dark matter since Eq. (19) becomes,

$$m_{\nu s}=\beta \varphi r{V_{\nu }\rho }_{Vac},$$

(20)

where $m_{\nu s}$ is the mass of sterile neutrinos and ${\rho }_{Vac}$ is the mass density of vacuum energy which is a mass scale of 30 orders of magnitude greater than that of dark energy. The value of $r$ for the various neutrino flavours in Eq. (16) and by extension, Eq. (19), determines the neutrino mass hierarchy. For experimental determination of neutrino mass hierarchy, see Ref [31].

5.3. Neutrino Chiral Transition

In this framework neutrino chiral transition depends on the size the ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions which have collapsed to microscopic scales below the required transition threshold under the influence of negative pressure from dark energy as discussed in Section 3. However, the gravitational effect of shear stress expands these ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions as discussed in the same Section 3. Once neutrinos pass through regions of spacetime with shear stress above a certain threshold, ${\mathrm{S}}_{\mathsf{\alpha }}$ dimensions can expand beyond the transition threshold, allowing light neutrino chiral transition to heavy neutrinos which manifests as cold dark matter.

5.4. Properties of Neutrino Dependent Dark Matter

i. 

Formation of $\alpha$-dent by Concentrated Dark Matter

Astrophysical spatial variations in the fine structure constant α have been reported in [32]. In this subsection, one of the possible effect of concentrated EDS form of dark on the value of $\alpha$ is breifly discussed.

Since the gravitational channel of vacuum energy is across $S_1{-S}_{\alpha }$ dimensions, the dark matter energy density ${\rho }_{DM}$ contracts $S_1$ to expand $S_{\alpha }$. As a result of this gravitational channel of ${\rho }_{DM}$, beyond a certain threshold density and associated term $G_{\mu \nu }^{\alpha }$ in Eq. (11), concentrated forms of EDS dark matter should cause the largest component dimension of $S_{\alpha }$ ($S_{\alpha 3}$) to expand beyond the 137$l_P$ size which determines the value of the fine structure constant $\alpha$ as discussed in Section 2.1. Concentrated forms of EDS dark matter should readily form from fast transitioning neutrino species around intense stress generating materials, tectonically active Planets and stellar corona and supernova. When this ocure, it forms a dent in the value of $\alpha$ with sharp boundries at the point where $G_{\mu \nu }^{\alpha }$ crosses the threshold value. This dent in alpha should have reflective properties at the boundary and should cause the lowering of atomic energy levels which in turn should cause release of atomic energy. This concentrated dark matter induced dent in $\alpha$ can manifest as glowing orbs in fluid medium such as the earth’s atmosphere, stellar corona and reflective orbs in the vacuum of space.

ii. 

Hierarchical Cold Dark Matter Halo Formation Around Baryons

When light neutrinos pass through shear stress generating baryonic structures such as planets and stars, their probability of chiral transition increases with the magnitude of shear stress and duration in the shallow stress gravitational potential. When chiral transition to sterile neutrinos eventualy occure, the phase parameter $\varphi$ oscillates from zero to one over a transition period $t_{\varphi }$ in the neutrino refrence frame. The transition distance therefore, will depend on neutrino energy scale and specie, resulting in a spectrum of transion distances that may range from a less than a centimeter for some non relativistic cosmic neutrinos to several light years for ultra-relativistic neutrinos. While low energy neutrinos with short transition distances should have relatively short life time 2$t_{\varphi }$, medium and high energy neutrinos, when they transition can have relativley long sterile life time on cosmological timescale.

The result is the formation of a herarchical halo profile around stress generating baryonic structures reflecting the spectrum of transition distances of the various neutrino specie, energies and the stress profile of the baryonic structure. It is also possible that neutrinos and anti neutrinos as well as diferent neutrino flavours, have different transition periods which can cause sterile neutrino flavour dispersion and contribute to the halo profile of this form of dark matter. See Ref [33] on Navaro-Frenk-White hierarchical halo profile.

iii. 

Response to Baryonic Gravitational Potential

Unlike ordinary neutrinos in EDS, this form of dark matter responds to the gravitational potential of baryonic matter. Its gravitational potential connects neutrinos on the lefthand gravitational channel with baryonic matter on the right. This because, as illustrated earlier in Table 2, the gravitational channel of dark matter is horizontal, cutting across and connecting the left and right channels ($S_1{-S}_{\alpha }$). However when the gravitational potential of dark matter is very shallow (like a few isolated particles or very small structure of neutrino-dark mater), this coupling can be very weak and the neutrino-dark matter can appear weakly responsive to baryonic gravitational potential.

6. Observational and Experimental Probe of Sterile Neutrino Dependent Dark Matter

6.1. Stress Activation and Indirect Detection of Sterile Cosmic Neutrinos

Since cosmic neutrinos have become non relativistic in the present universe they should have shorter transition distance. If there are cosmic neutrino species with transition distance of less than a millimeter, they may readily clump up and form a transient dent in $\mathsf{\alpha }$ within their relatively short lifetime. The effect of such transient dent in $\mathsf{\alpha }$ may manifest in the mechanism of Mechanoluminescence (ML). ML is still one of the largely unresolved issues in Material Science [34]. If indeed ML have anything to do with cosmic neutrinos and dark matter, then this would present a readily achievable probe of the very early universe among other potentially exotic applications.

6.2. Probe of Earth Quake Light from Possible Dent in $\mathsf{\alpha }$

As previously mentioned there is a possibility that geo-neutrino have relatively shorter transition distance compared to their neutrino counterpart. On passing through regions of high tectonic stress, such geo neutrinos should transition to sterile neutrinos that may clump up, showing up above the surface not just as anomalies in measurements of the gravitational constant but as dent in $\alpha$. Such dent in $\alpha$ should be observable as slight drop in atomic energy levels and possible glow resulting from energy level transitions in atoms of air within the dent. Spectral analysis of Earth Quake Lights (EQL) [35,36] can be of potential interest in this regard. There is also the possibility of MeV neutrinos such as solar neutrinos and Geo-neutrinos, transitioning over hundreds of thousands of kilometers to form halos of dark matter around the planet which can be the target of future probes.

If indeed EQLs are caused by dents in the value of $\mathsf{\alpha }$ from concentrated dark matter which in turn are caused by stressed geo-neutrinos, then this will suggest that anti neutrinos have relatively shorter transition distance compared to their neutrino counterpart. Furthermore, attempts can be made to reverse engineer EQLs by using an underground stress field lensing array of stress cells. Such an array of stress cell can be made of tough steel alloys under tremendous stress. Such stress field lensing approach will ensure that heavy neutrinos that may form from stressed geo-neutrinos passes through a focus for possible accumulation and formation of concentrated dark matter.

6.3. Probe of Little Red Dots in JWST Data

Given the stress based production mechanism of dark matter in EDS, it is assumed that most of the dark matter in the early universe where formed from stressed cosmic neutrinos which transitioned into heavy sterile neutrinos with relatively long life time. It is expected that a lot of these cold sterile neutrinos could have condensed into dense clouds of dark matter beyond the required threshold density for the formation of dents in the value of $\alpha$ where atomic energy levels are lowered. Atomic and molecular hydrogen gas that falls into such dent can only glow as they fall into the lower ground state energies. These could appear as glowing star-like gas clouds in the early universe before the onset of star formation. If they really existed in the early universe, these $\alpha$-stars (for want of a better name) can behave like the dark stars described in [37,38]. Unlike dark stars where the glow energy comes from dark matter annihilation, the glow energy from $\alpha$-stars comes from hydrogen and helium atoms falling into lower ground state energies in the $\alpha$-dents caused by the dense dark matter structures. However, $\alpha$-stars still have similar end of life phase with dark stars when they run out of gas falling into the $\alpha$-dent as they stop glowing, allowing the gas cloud to collapse to form real stars. The Little Red Dots (LRDs) observed by JWST [39], though earlier attributed to Active Galactic Nuclei (AGN), may be $\alpha$-stars if they really exist and further detailed data analysis will be required to discern between the various possibilities.

6.4. Measurement of the Strength of Gravity During Solar Eclipse

There is the possibility of sterile transition of solar neutrinos after passing through regions of shear stress in the lunar interior, mostly from tidal forces and possible moon quakes which are usually stronger during solar eclipse. The resulting sterile neutrinos from coincident lunar quake and solar eclipse event on reaching Earth can be observed as anomalies in measurements of the gravitational constant. Moreover, there have been various reports of anomalies in measurements of the gravitational constant during some solar eclipse events [40,41]. This is in addition to other reports of anomalies in measurements of the gravitational constant such as in [42] that appears to be correlated with length of day variation. Neutrino detectors can also be used to look out for expected deficit in the detection rate of light neutrino flavours under the moon’s shadow during solar eclipse.

7. Discussion and Conclusions

EDS as a symmetry framework of spatial dimensions, doubles large spatial dimensions with microscopic partners of opposite handedness and dimension number which inverts the sign of gravitational interactions in these extra dimensions. It provides a framework for the possible resolution of the mysteries of dark energy, dark matter and neutrino mass. In doing so, it provides some potential insights into the dimensional structure of spacetime, gravity, the value of the fine structure constant and the dynamics of a cyclic universe. It also implies that time could be an emergent property of a large right handed extra spatial dimension ${\mathrm{S}}_0$ with negative dimension number.

Specifically, it places the bare vacuum energy component in a state where the gravitational field is switched off while real massive standard model particles chiraly oscillate between these gravitationally inert and active states. It also places ordinary baryonic matter in the right handed spatial dimensions while neutrinos are restricted to the left handed spatial dimensions which predicts the inability of neutrinos to respond to the gravitational potential of ordinary baryonic matter.

Due to a Planck energy density constraint and a speed limit asymmetry described by the asymptotically evolving asymmetry parameter $\mathsf{\Gamma }$, a small component of vacuum energy is constrained to exist in the gravitationally active state and appear as dark energy. The density of this $\mathsf{\Lambda }$ form of dark energy with a constant equation of state parameter $\omega$, asymptotically approaches zero with the gravity driven growth of ${\mathrm{S}}_0$ dimension as explained in Section 3. However, the chiral oscillation of the dimensionality parameter from Eq. (1) on a cosmological timescale can still result in a cyclic universe scenario as discussed in Section 4.1.

Furthermore, EDS describes dark matter as resulting from neutrino enabled gravitation of virtual particles, in which neutrinos induce small component of the gravitational constant in the gravitationally inert state. The induced gravitational constant also serves as a mass generation mechanism for neutrinos through this gravitational coupling to vacuum energy. While light neutrino mass arises from interaction with dark energy, heavy sterile neutrino mass arises from its interaction with the bulk of vacuum energy. However, chiral transition to sterile neutrino phase is suppressed by negative pressure driven collapse of the ${\mathrm{S}}_{\mathsf{\alpha }}$ dimension, but can be activated with the extra degree of freedom from shear stress driven expansion of ${\mathrm{S}}_{\mathsf{\alpha }}$.

Due to various transition distances which depends on neutrino specie and energy scale, the resulting sterile neutrinos and cold dark matter readily form hierarchical halos, exhibiting hybrid particle and modified gravity behaviour like the gravitational polarization of vacuum energy approach [15] and superfluid dark matter [43]. Another unique property of this form of dark matter, is that, above a threshold density, they can cause dents in the value of $\mathsf{\alpha }$. Such dents should have reflective boundaries and cause the release of atomic energies manifesting as reflective orbs and glowing orbs in fluid medium like the earth’s atmosphere or gas clouds. Experimental and observational probes for this sterile neutrino dependent form of cold dark matter were briefly discussed in Section 6.

Expected results from the trio of the JWST, Euclid, Vera Rubin Observatory and upcoming Nancy Grace Roman Telescope, are expected to provide precision measurements of dark energy density as well as the dynamics of dark matter. Such precision measurements should glean out the predicted suppression of dark energy density in the deep gravitational potential wells of baryonic matter.

EDS also provides a way to view baryon asymmetry even though it does not provide a solution. Since spin in opposite directions of ${\mathrm{S}}_0$ dimension as illustrated in Figure 2 represents particle and antiparticle states, a matter dominated universe like ours can be seen as having a net spin with respect to the ${\mathrm{S}}_0$ dimension in a Multiverse scenario.

In conclusion, the EDS framework offers new physics explanations for dark energy and dark matter as different manifestations of vacuum energy with potential insights into a number of other unsolved problems. While dark energy is the small repulsive component of vacuum energy in the active state, dark matter is simply virtual particles in the inert state that are enabled to gravitationally attract with neutrino induced gravitational constant and also serves as mass generation mechanism for neutrinos. The predicted dynamics of dark energy, stress based production of dark matter as well as some of its predicted properties, provides observational and experiment tests.