Submitted:
08 September 2023
Posted:
13 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
1.1. Background
1.2. Related review studies
1.3. This review
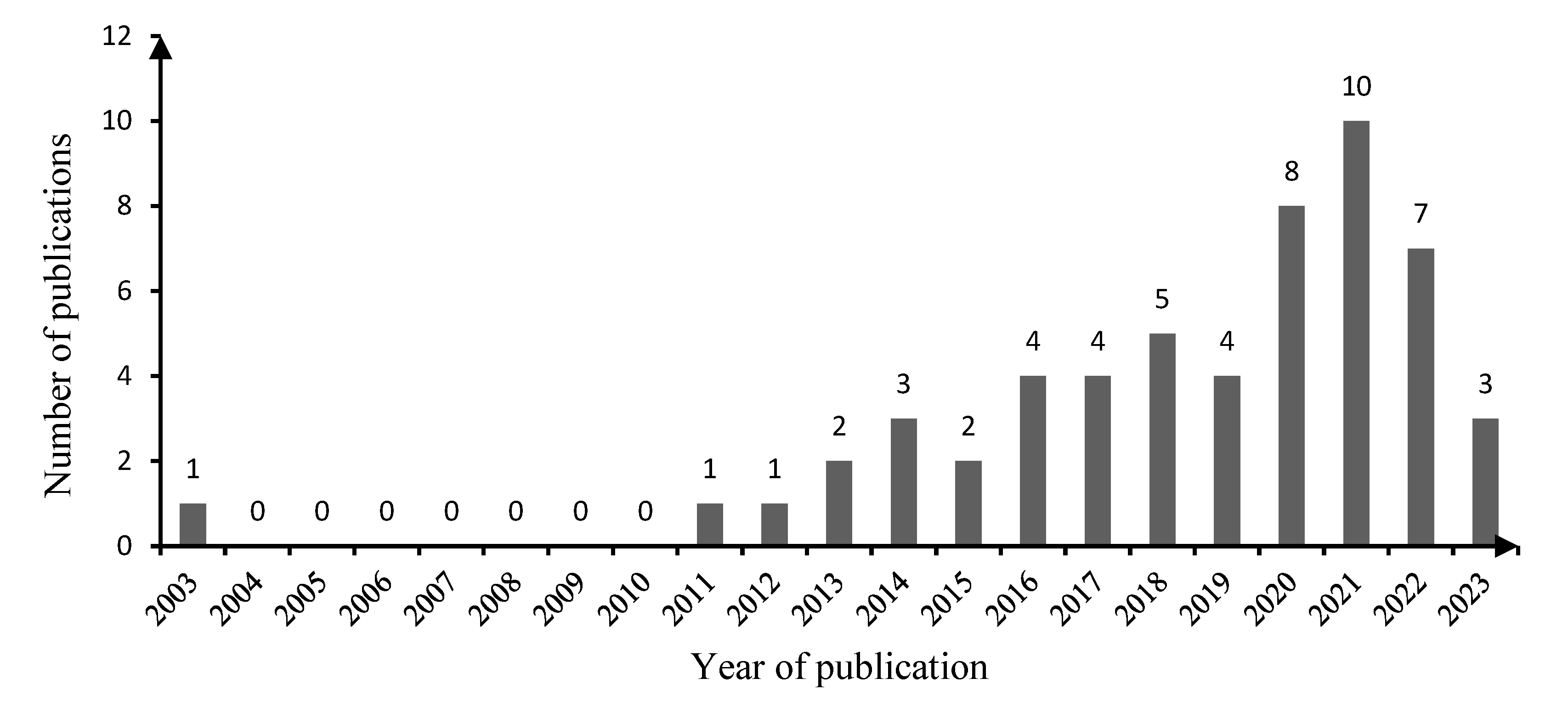
2. Systematic literature review on multi-objective optimization for high-performance building facade design
2.1. Search strategy and systematic literature review process
2.1.1. Term occurrences and co-occurrence links
2.1.2. Title and abstract screening
- i.
- Only publications containing building façade design strategies or related keywords (such as passive design strategy) were included.
- ii.
- Publications that explicitly used multi-objective optimization strategies were included.
- i.
- Review papers related to multi-objective building design optimization were excluded in order to focus only on publications focused on building façade design.
- ii.
- Publications that did not provide sufficient information to directly contribute to the understanding of multi-objective building facade design optimization were excluded.
- iii.
- In order to focus on building facade design strategies, publications related to multi-objective optimization for passive design strategies or building retrofitting that potentially include building façade design parameters but also include building geometry, floor plans, roofs, or active systems were excluded.
- iv.
- To maintain a specific focus on the impact of comprehensive façade optimization on building performance, publications on optimization for specific building façade elements or technologies, such as PV panel placement or implementation of specific movable shading techniques, as well as those on fenestration and wall materials were excluded.
2.1.3. Full-text screening
| Author (s) | Year | Type * | Method | Objectives | Design parameters | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| R | O | E | H | T | Energy | Eco | Env | Daylight | Thermal | Orientation | Window | Shading | Wall | Glazing | Airtightness | ||||
| [21] | Caldas and Norford | 2003 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [22] | Zemella et al. | 2011 | ✓ | ENN | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [23] | Gagne and Andersen | 2012 | ✓ | GA | ✓ | ✓ | |||||||||||||
| [24] | Bogar et al. | 2013 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [25] | Gossard et al. | 2013 | ✓ | ANN+GA | ✓ | ✓ | |||||||||||||
| [26] | Wright et al. | 2014 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [27] | Jayedi et al. | 2014 | ✓ | ANN+GA | ✓ | ✓ | |||||||||||||
| [28] | Kasinalis et al. | 2014 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [29] | Echenagucia et al. | 2015 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [30] | Chatzikonstantinou et al. | 2015 | ✓ | DE | ✓ | ✓ | ✓ | ||||||||||||
| [31] | Wu et al. | 2016 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [32] | Ascione et al. | 2016 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [33] | Xu et al. | 2016 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [34] | Azari et al. | 2016 | ✓ | ANN+GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [35] | Karaman et al. | 2017 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [36] | Fan and Xia | 2017 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [37] | Narangerel et al. | 2017 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [38] | Bingham et al. | 2017 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [39] | Kang et al. | 2018 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [40] | Chen et al. | 2018 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [41] | Cascone et al. | 2018 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [42] | Grygierek et al. | 2018 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [43] | Shen | 2018 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [44] | Shahbazi et al. | 2019 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ||||||||||||
| [45] | Yi | 2019 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ||||||||||||
| [46] | Ascione et al. | 2019 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [47] | Torres-Rivas et al. | 2019 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [48] | Jalali et al. | 2020 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ||||||||||||
| [49] | Kim and Clayton | 2020 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ||||||||||||
| [50] | Chang et al. | 2020 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [51] | Zhao and Du | 2020 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [52] | Yilmaz et al. | 2020 | ✓ | PS+PSO+HJ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [53] | Pilechiha et al. | 2020 | ✓ | SPEA-2 | ✓ | ✓ | |||||||||||||
| [54] | Ciardiello et al. | 2020 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [55] | Wang et al. | 2020 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||
| [56] | Acar et al. | 2021 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [57] | Naji et al. | 2021 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [58] | Lin et al. | 2021 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [59] | Nasrollahzadeh | 2021 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [60] | Abdou et al. | 2021 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [61] | Belhous et al. | 2021 | ✓ | NSGA-II | ✓ | ✓ | |||||||||||||
| [62] | Xu et al. | 2021 | ✓ | NSGA-II/MOPSO | ✓ | ✓ | ✓ | ||||||||||||
| [63] | Lin and Yang | 2021 | ✓ | ANN+GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [64] | Mashaly et al. | 2021 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ||||||||||||
| [65] | Albatayneh | 2021 | ✓ | GA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||
| [66] | Yao et al. | 2022 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [67] | Seghier et al. | 2022 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [68] | Wu and Zhang | 2022 | ✓ | SPEA-2 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [69] | Xu et al. | 2022 | ✓ | ANN+GA | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [70] | Semahi et al. | 2022 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [71] | Xu et al. | 2022 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||
| [72] | Zong et al. | 2022 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [73] | Himmetoglu | 2022 | ✓ | ANN+GA | ✓ | ✓ | ✓ | ✓ | ✓ | ||||||||||
| [74] | Nazari et al. | 2023 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | |||||||||||
| [75] | Wang et al. | 2023 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
| [76] | Elsheikh et al. | 2023 | ✓ | NSGA-II | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |||||||||
3. Features of building façade optimization
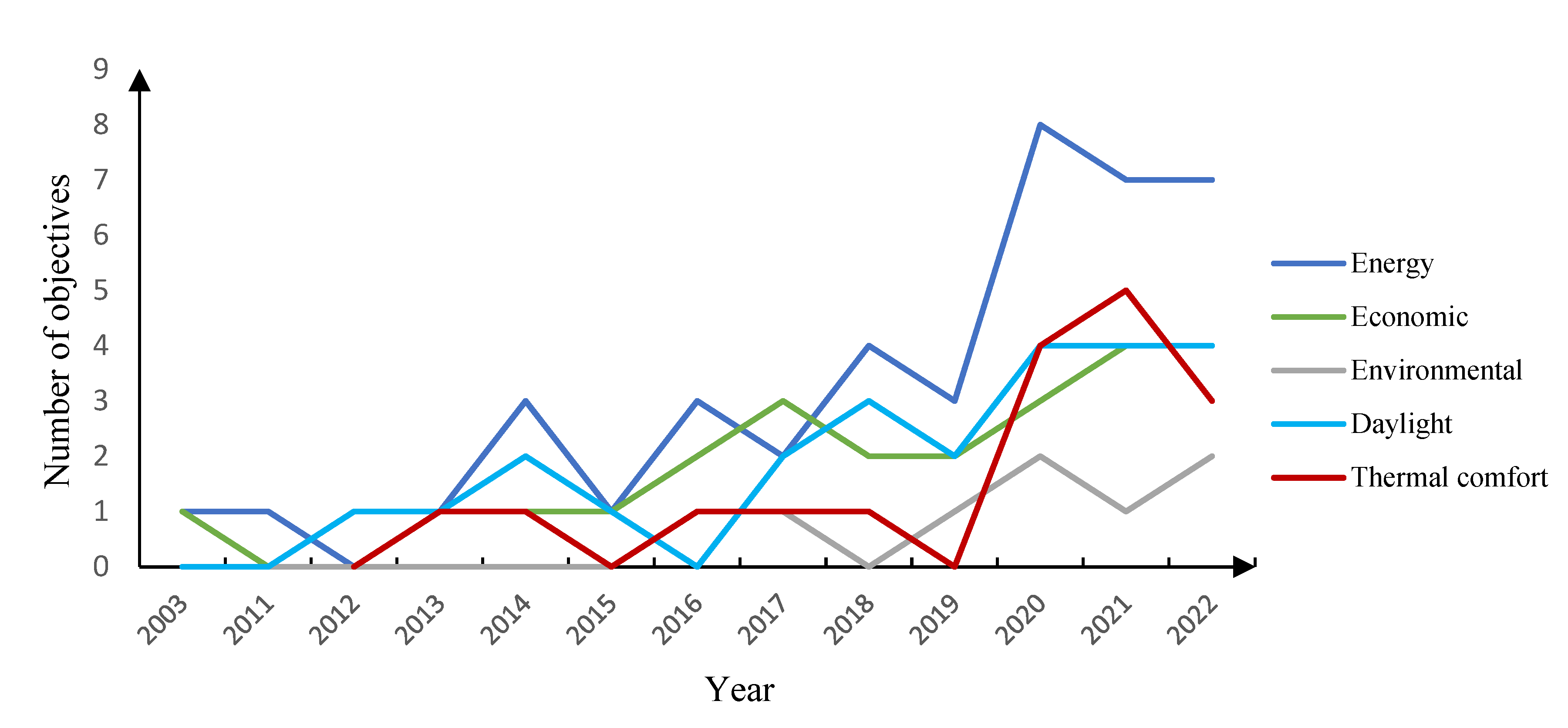
3.1. Optimization objectives
3.2. Design variables
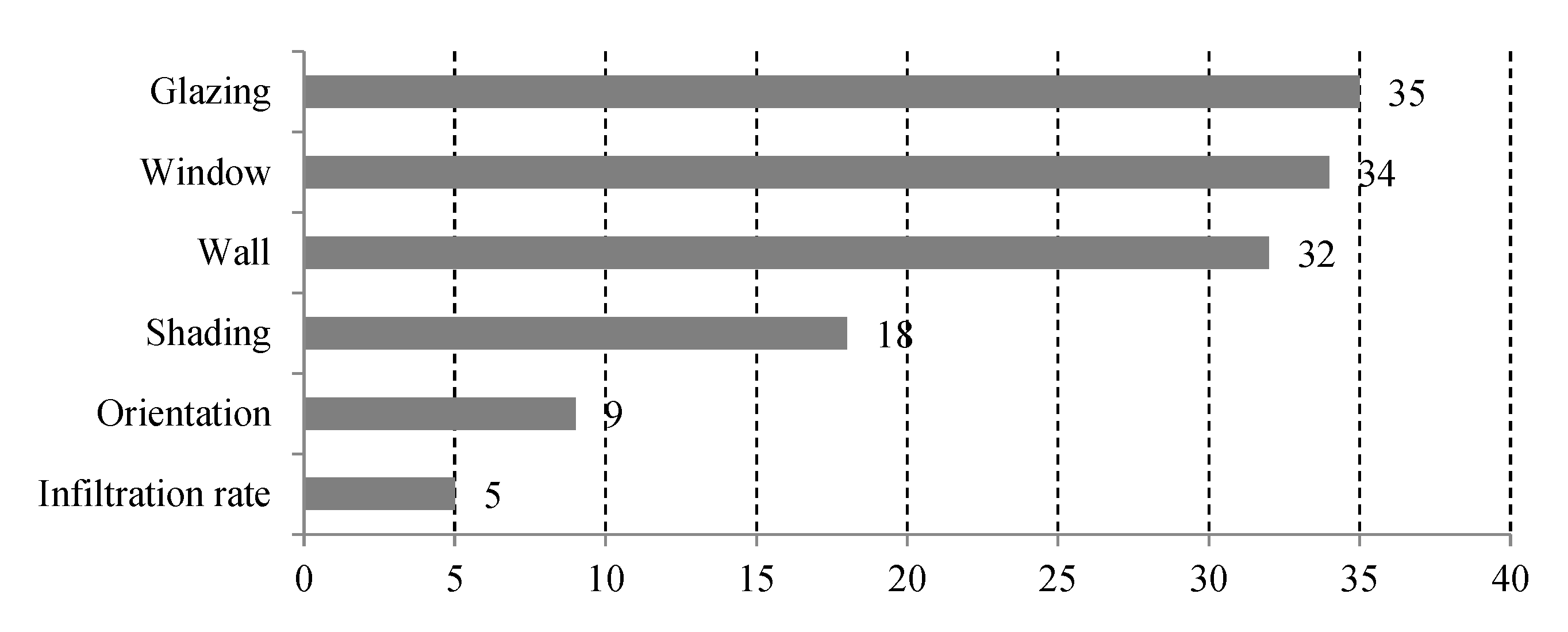
| Design variables | Continuous | Discrete |
|---|---|---|
| Building orientation | ✓ | |
| Window system | ||
| Window area | ✓ | |
| length | ✓ | |
| width | ✓ | |
| Shading system | ||
| shading depth; | ✓ | |
| distance between fins or shading blinds; | ✓ | |
| tilt angle of fins and blinds; | ✓ | |
| solar absorptance; | ✓ | |
| reflectance of the shading material | ✓ | |
| Building façade (exterior wall and roof) | ||
| thermal transmittance of material | ✓ | |
| solar absorbance of material | ✓ | |
| thickness of layer | ✓ | |
| Glazing system | ||
| glazing properties (U-value, τ-value, SHGC) | ✓ | |
| Infiltration rate | ✓ |
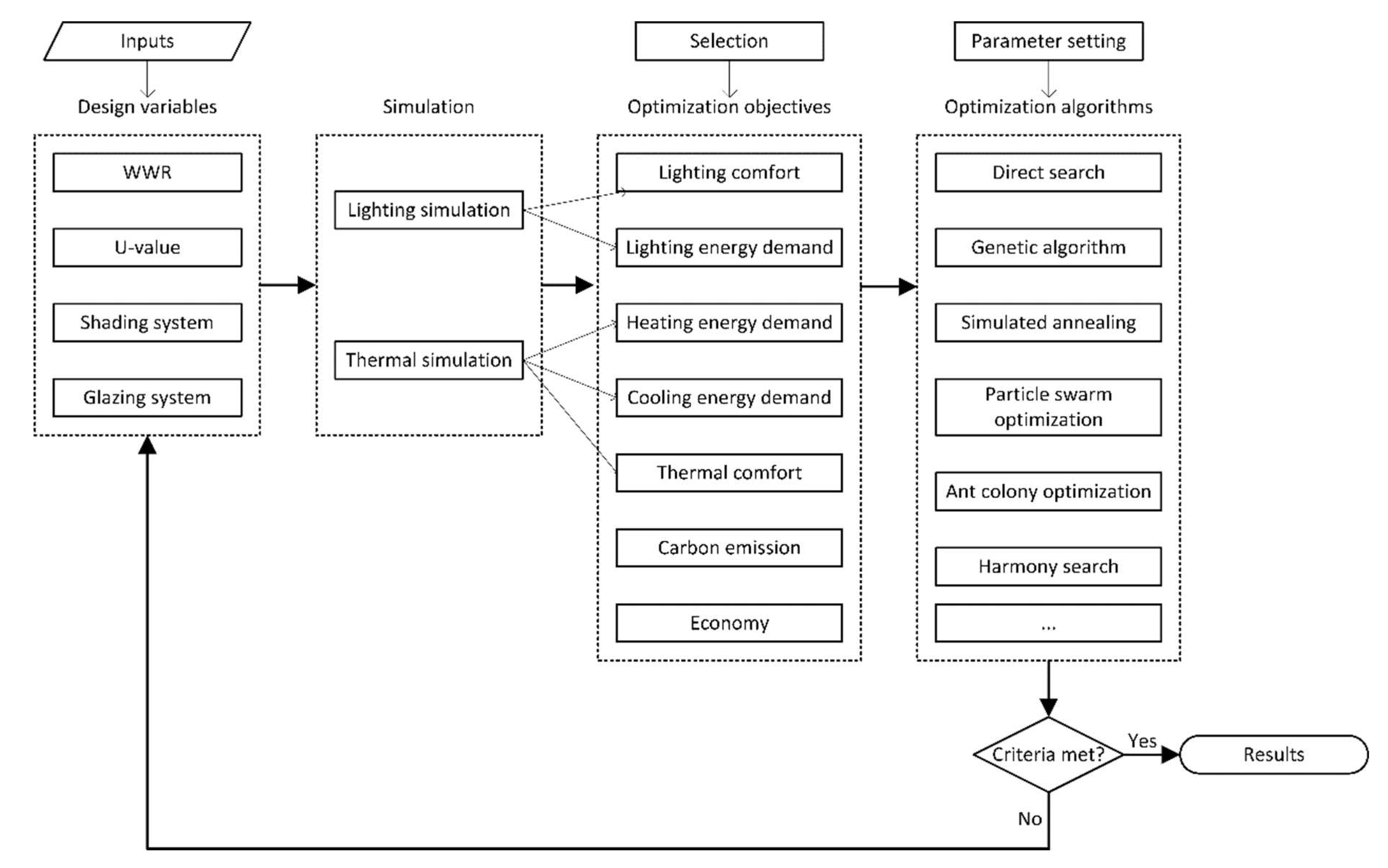
4. Optimization algorithms for multi-objective building façade optimization
4.1. Hooke-Jeeves
4.2. Heuristic algorithms
- Most optimization problems are complex multi-model problems with discrete design variables. Derivative-free heuristic algorithms have a strong ability to solve such problems.
- The procedure of BFO usually needs to satisfy the time constraint in the early design stage. Heuristic algorithms can run parallel simulations more efficiently, thus greatly reducing the computational cost.
- Building façade design needs to maintain the diversity of different design parameters and techniques. Therefore, the heuristic algorithms, especially the evolutionary algorithms with niche methods, which can collect a variety of different design variables, are more feasible for solving BFO problems.
- GA effectively handles multidimensional, non-differentiable, and non-continuous problems.
- GA quickly provides Pareto optimal solutions early in the optimization process through parallel simulations.
- GA’s niching method provides multiple solutions during evolution.
- GA runs reach acceptable optima in reasonable time.
4.3. MLA/ANN-integrated based heuristic algorithms
| Author (s) | Year | Method | Simulation Tool | Optimization Tool | |
|---|---|---|---|---|---|
| [21] | Caldas and Norford | 2003 | NSGA | DOE-2 | N/A |
| [22] | Zemella et al. | 2011 | Evolutionary Neural Network Design (ENN-Design) | EnergyPlus | N/A |
| [23] | Gagne and Andersen | 2012 | Micro-GA | Lightsolve Viewer (LSV) | N/A |
| [24] | Bogar et al. | 2013 | NSGA-II | EnergyPlus | ePlusOpt + MATLAB |
| [25] | Gossard et al. | 2013 | ANN+NSGA-II | TRNSYS | GenOpt |
| [26] | Wright et al. | 2014 | NSGA-II | EnergyPlus | N/A |
| [27] | Jayedi et al. | 2014 | ANN+GA | TRNSYS | GenOpt |
| [28] | Kasinalis et al. | 2014 | NSGA-II | TRNSYS; DAYSIM | MATLAB |
| [29] | Echenagucia et al. | 2015 | NSGA-II | EnergyPlus | Python |
| [30] | Chatzikonstantinou et al. | 2015 | Differential Evolution(DE) | DIVA for Rhinoceros | MATLAB |
| [31] | Wu et al. | 2016 | NSGA-II | EnergyPlus | MATLAB |
| [32] | Ascione et al. | 2016 | NSGA-II | EnergyPlus | jEPlus+EA |
| [33] | Xu et al. | 2016 | NSGA-II | EnergyPlus | Jmetal package (Java based) |
| [34] | Azari et al. | 2016 | ANN+NSGA-II | eQuest | N/A |
| [35] | Karaman et al. | 2017 | NSGA-II; jE_DEMO | N/A | N/A |
| [36] | Fan and Xia | 2017 | GA | N/A | N/A |
| [37] | Narangerel et al. | 2017 | GA | N/A | N/A |
| [38] | Bingham et al. | 2017 | NSGA-II | EnergyPlus | jEPlus+EA |
| [39] | Kang et al. | 2018 | NSGA-II | TRNSYS | RcmdrPlugin of DOE |
| [40] | Chen et al. | 2018 | NSGA-II | EnergyPlus | N/A |
| [41] | Cascone et al. | 2018 | NSGA-II | EnergyPlus | Python |
| [42] | Grygierek et al. | 2018 | NSGA-II | EnergyPlus | MATLAB |
| [43] | Shen | 2018 | SPEA-2 | DIVA for Grasshopper | Octopus plugin for Grasshopper |
| [44] | Shahbazi et al. | 2019 | SPEA-2 | DIVA for Grasshopper | Octopus plugin for Grasshopper |
| [45] | Yi | 2019 | NSGA-II | DIVA for Grasshopper | MATLAB |
| [46] | Ascione et al. | 2019 | GA | EnergyPlus | MATLAB |
| [47] | Torres-Rivas et al. | 2019 | NSGA-II | EnergyPlus | MOBO |
| [48] | Jalali et al. | 2020 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [49] | Kim and Clayton | 2020 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [50] | Chang et al. | 2020 | GA | EnergyPlus (Honeybee for Grasshopper) | MATLAB |
| [51] | Zhao and Du | 2020 | NSGA-II | EnergyPlus | jEPlus+EA |
| [52] | Yilmaz et al. | 2020 | Pattern Search+PSO+HJ | GenOpt | |
| [53] | Pilechiha et al. | 2020 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [54] | Ciardiello et al. | 2020 | aNSGA-II | EnergyPlus | Python (eppy library) |
| [55] | Wang et al. | 2020 | NSGA-II | EnergyPlus | Python |
| [56] | Acar et al. | 2021 | NSGA-II | EnergyPlus | MATLAB |
| [57] | Naji et al. | 2021 | NSGA-II | EnergyPlus | jEPlus+EA |
| [58] | Lin et al. | 2021 | NSGA-II | MOBELM | MATLAB |
| [59] | Nasrollahzadeh | 2021 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [60] | Abdou et al. | 2021 | NSGA-II | TRNSYS | MOBO |
| [61] | Belhous et al. | 2021 | NSGA-II | TRNSYS | MOBO |
| [62] | Xu et al. | 2021 | ANN+NSGA-II/MOPSO | EnergyPlus | Python |
| [63] | Lin and Yang | 2021 | ANN+GA | DesignBuilder | MATLAB |
| [64] | Mashaly et al. | 2021 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [65] | Albatayneh | 2021 | GA | EnergyPlus | DesignBuilder-jEPlus link package |
| [66] | Yao et al. | 2022 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [67] | Seghier et al. | 2022 | NSGA-II | N/A | MATLAB |
| [68] | Wu and Zhang | 2022 | SPEA-2 | EnergyPlus (Honeybee for Grasshopper) | Octopus plugin for Grasshopper |
| [69] | Xu et al. | 2022 | ANN+MOGA/NSGA-II/MOPSO | EnergyPlus | N/A |
| [70] | Semahi et al. | 2022 | NSGA-II | EnergyPlus | jEPlus+EA |
| [71] | Xu et al. | 2022 | NSGA-II | EnergyPlus | Python |
| [72] | Zong et al. | 2022 | NSGA-II | N/A | Python |
| [74] | Nazari et al. | 2023 | ANN+GA | EnergyPlus | N/A |
| [75] | Wang et al. | 2023 | NSGA-II | EnergyPlus (Honeybee for Grasshopper) | Wallacei plugin for Grasshopper |
| [76] | Elsheikh et al. | 2023 | NSGA-II | EnergyPlus | DesignBuilder-jEPlus link package |
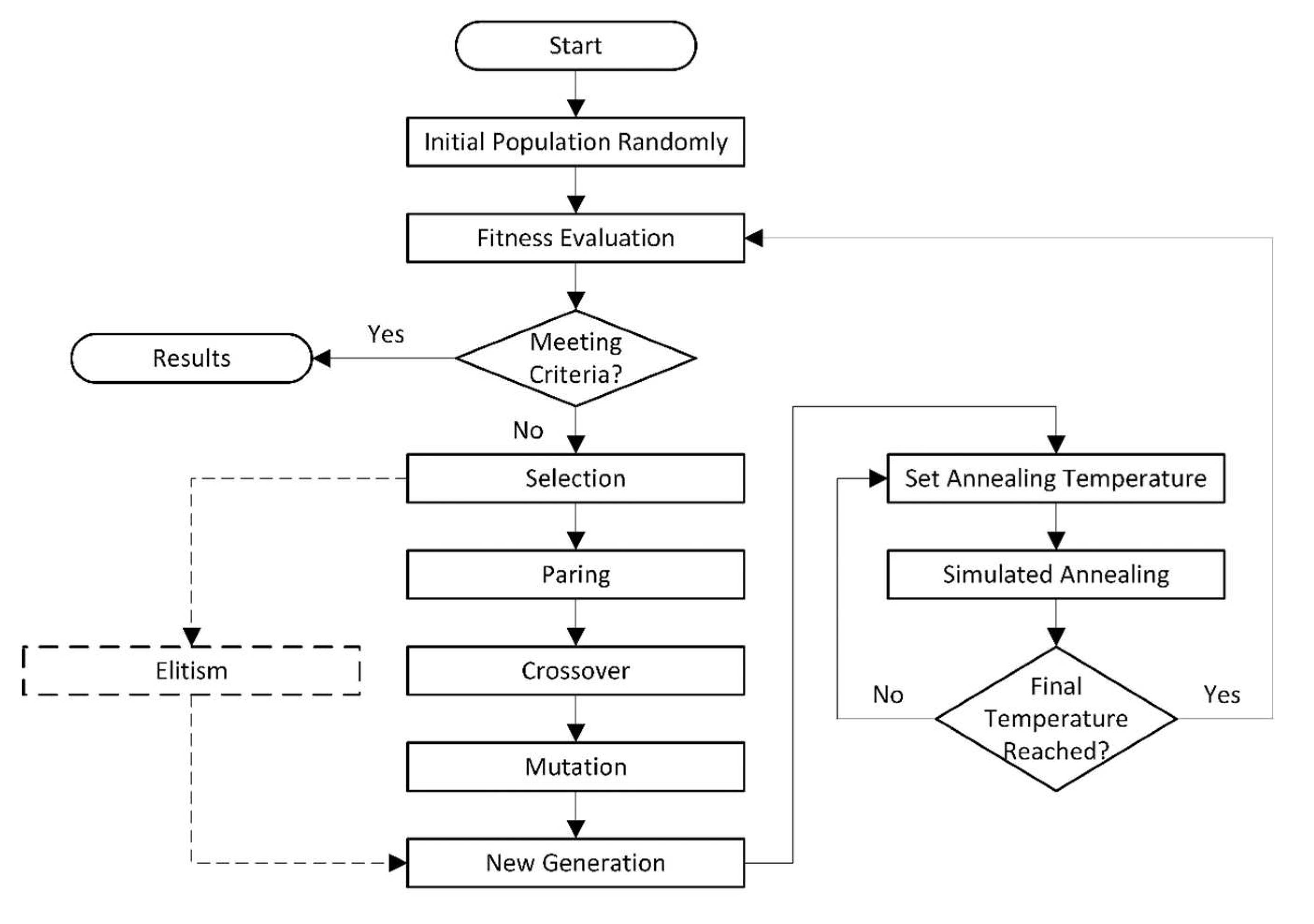
5. Simulation-based building optimization technique
- Input Design Parameters: Architects provide essential design parameters such as window-to-wall ratio (WWR), U-value, shading system, and glazing types. These serve as design variables for the Building Facade Optimization (BFO) problem.
- Define Design Objectives: Architects desine the design objectives for the BFO problem, outlining what needs to be optimized in terms of building facade performance.
- Optimization Algorithm Selection: Architects select an appropriate optimization algorithm and configure its parameters to meet the requirements of the problem.
- Optimization Algorithm Execution: The selected optimization algorithm begins its actions, initiating computational modeling and simulations.
- Simulation Engine Execution: The lighting/thermal simulation engine performs in dynamic simulations, producing results that meet the specified design objectives.
- Result Selection Mechanism: The optimization algorithm selection mechanism evaluates the simulation results and determines the results that meet the optimization objectives.
- Post-Processing Module: A post-processing module kicks in and extracts the Pareto fronts from the simulation results. These fronts represent the optimal trade-off solutions between conflicting objectives.
| Platform | BPS engine integration | 3D Visualize | Algorithm selection | Custom | 3D model Interact | |
|---|---|---|---|---|---|---|
| Thermal | Lighting | |||||
| Matlab | ✓ | ✓ | ✓ | ✓ | ✓ | × |
| GenOpt | ✓ | × | ✓ | ✓ | ✓ | × |
| ModelCenter | ✓ | × | ✓ | ✓ | ✓ | × |
| modeFRONTIER | ✓ | × | ✓ | ✓ | ✓ | × |
| jEPlus + EA | ✓ | × | ✓ | × | × | × |
| MOBO | ✓ | × | ✓ | × | × | × |
| Octopus | ✓ | ✓ | ✓ | × | ✓ | ✓ |
6. Discussion and conclusion
6.1. Summary of main findings
6.2. Suggestions for further work
- Delving deeper into the analysis and comparison of evaluation criteria tailored to optimization algorithms, specifically addressing the challenges posed by building facade optimization.
- Uncovering the intricate interplay between design variables and the effectiveness of optimization algorithms, offering insights into how design choices impact algorithm performance.
- Crafting research endeavors that align with the practical constraints confronting architectural firms, acknowledging time limitations during the early design stages that frequently dictate decision-making timelines.
- Pioneering the creation of comprehensive platforms that integrate architectural design, simulation, and optimization tools seamlessly, promoting a cohesive design process.
- Addressing compatibility issues through optimization platforms that integrate seamlessly with 3D CAD software improves user-friendliness for architects.
- Creation of optimization tools designed for integration with popular 3D architectural design platforms, revolutionizing architects’ communication with clients through visualized and optimized design solutions.
- Empowering architects with the ability to develop and incorporate bespoke algorithms within optimization processes, fostering innovation and tailoring algorithms to specific design challenges.
- Further refining and expanding architect-friendly environments is crucial in harmoniously blending in-depth building performance simulation with real-time reflection of 3D design models.
- A concerted focus on optimization algorithms will enhance their selection, adaptation, and enhancement, addressing unique challenges that arise in diverse building optimization scenarios.
- Advancing algorithms and ATC approaches is key to harnessing the strengths of multiple algorithms and achieving improved optimization outcomes.
- Additionally, formulating systematic optimization frameworks that can handle the intricacies of complex multi-objective building facade optimization problems is essential.
- This ensures architects can harness the full potential of optimization beyond simulation surrogates. Advocating for the integration of optimization concepts into architectural education to equip architects with the ability to utilize optimization for data analysis, form exploration, and fine-tuning building design parameters to enhance overall performance.
References
- Gossard, D.; Lartigue, B.; Thellier, F. Multi-objective optimization of a building envelope for thermal performance using genetic algorithms and artificial neural network. Energy Build. 2013, 67, 253–260. [Google Scholar] [CrossRef]
- Tuhus-Dubrow, D.; Krarti, M. Genetic-algorithm based approach to optimize building envelope design for residential buildings. J. Affect. Disord. 2010, 45, 1574–1581. [Google Scholar] [CrossRef]
- Lomas, K.J.; Eppel, H. Sensitivity analysis techniques for building thermal simulation programs. Energy Build. 1992, 19, 21–44. [Google Scholar] [CrossRef]
- Caldas, L.G.; Norford, L.K. Genetic Algorithms for Optimization of Building Envelopes and the Design and Control of HVAC Systems. J. Sol. Energy Eng. 2003, 125, 343–351. [Google Scholar] [CrossRef]
- Sadineni, S.B.; Madala, S.; Boehm, R.F. Passive building energy savings: A review of building envelope components. Renew. Sustain. Energy Rev. 2011, 15, 3617–3631. [Google Scholar] [CrossRef]
- Pacheco, R.; Ordóñez, J.; Martínez, G. Energy efficient design of building: A review. Renew. Sustain. Energy Rev. 2012, 16, 3559–3573. [Google Scholar] [CrossRef]
- Kaynakli, O. A review of the economical and optimum thermal insulation thickness for building applications. Renew. Sustain. Energy Rev. 2012, 16, 415–425. [Google Scholar] [CrossRef]
- Kheiri, F. A review on optimization methods applied in energy-efficient building geometry and envelope design. Renew. Sustain. Energy Rev. 2018, 92, 897–920. [Google Scholar] [CrossRef]
- Nguyen, A.-T.; Reiter, S.; Rigo, P. A review on simulation-based optimization methods applied to building performance analysis. Appl. Energy 2014, 113, 1043–1058. [Google Scholar] [CrossRef]
- Attia, S.; Hamdy, M.; O’brien, W.; Carlucci, S. Assessing gaps and needs for integrating building performance optimization tools in net zero energy buildings design. Energy Build. 2013, 60, 110–124. [Google Scholar] [CrossRef]
- Evins, R. A review of computational optimisation methods applied to sustainable building design. Renew. Sustain. Energy Rev. 2013, 22, 230–245. [Google Scholar] [CrossRef]
- Machairas, V.; Tsangrassoulis, A.; Axarli, K. Algorithms for optimization of building design: A review. Renew. Sustain. Energy Rev. 2014, 31, 101–112. [Google Scholar] [CrossRef]
- Huang, Y.; Niu, J.-L. Optimal building envelope design based on simulated performance: History, current status and new potentials. Energy Build. 2016, 117, 387–398. [Google Scholar] [CrossRef]
- Costa-Carrapiço, I.; Raslan, R.; González, J.N. A systematic review of genetic algorithm-based multi-objective optimisation for building retrofitting strategies towards energy efficiency. Energy Build. 2019, 210, 109690. [Google Scholar] [CrossRef]
- Manni, M.; Nicolini, A. Multi-Objective Optimization Models to Design a Responsive Built Environment: A Synthetic Review. Energies 2022, 15, 486. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lamont, G.B.; Ray, T.; Farina, M.; Di Barba, P.; Reed, P.; Devireddy, V.; Luna, E.H.; Furukawa, T.; Dissanayake, G.; et al. Applications of Multi-Objective Evolutionary Algorithms. 2004. [CrossRef]
- Kitchenham, B.; Brereton, O.P.; Budgen, D.; Turner, M.; Bailey, J.; Linkman, S. Systematic literature reviews in software engineering – A systematic literature review. Inf. Softw. Technol. 2009, 51, 7–15. [Google Scholar] [CrossRef]
- Xiao, Y.; Watson, M. Guidance on Conducting a Systematic Literature Review. J. Plan. Educ. Res. 2017, 39, 93–112. [Google Scholar] [CrossRef]
- N. J. van Eck and L. Waltman, “Software survey: VOSviewer, a computer program for bibliometric mapping,” Scientometrics, vol. 84, no. 2, pp. 523–538, Dec. 2010. [CrossRef]
- Hashempour, N.; Taherkhani, R.; Mahdikhani, M. Energy performance optimization of existing buildings: A literature review. Sustain. Cities Soc. 2019, 54, 101967. [Google Scholar] [CrossRef]
- Caldas, L.G.; Norford, L.K. Genetic Algorithms for Optimization of Building Envelopes and the Design and Control of HVAC Systems. J. Sol. Energy Eng. 2003, 125, 343–351. [Google Scholar] [CrossRef]
- Zemella, G.; De March, D.; Borrotti, M.; Poli, I. Optimised design of energy efficient building façades via Evolutionary Neural Networks. Energy Build. 2011, 43, 3297–3302. [Google Scholar] [CrossRef]
- Gagne, J.; Andersen, M. A generative facade design method based on daylighting performance goals. J. Build. Perform. Simul. 2012, 5, 141–154. [Google Scholar] [CrossRef]
- D. Bogar, G. D. Bogar, G. Rapone, A. Mahdavi, and O. Saro, “GA-optimisation of a curtain wall façade for different orientations and climates,” in Building Simulation Applications, 2013. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2. 8504. [Google Scholar]
- Gossard, D.; Lartigue, B.; Thellier, F. Multi-objective optimization of a building envelope for thermal performance using genetic algorithms and artificial neural network. Energy Build. 2013, 67, 253–260. [Google Scholar] [CrossRef]
- Wright, J.A.; Brownlee, A.; Mourshed, M.M.; Wang, M. Multi-objective optimization of cellular fenestration by an evolutionary algorithm. J. Build. Perform. Simul. 2013, 7, 33–51. [Google Scholar] [CrossRef]
- Jayedi, N. Tabassum, J. Hopfenblatt, J. B. Kim, and M. O. Haque, “Optimizing container housing units for informal settlements: A parametric simulation & visualization workflow for architectural resilience,” in Projections - Proceedings of the 26th International Conference of the Association for Computer-Aided Architectural Design Research in Asia, CAADRIA 2021, 2021, pp. 51–60. [CrossRef]
- Kasinalis, C.; Loonen, R.; Cóstola, D.; Hensen, J. Framework for assessing the performance potential of seasonally adaptable facades using multi-objective optimization. Energy Build. 2014, 79, 106–113. [Google Scholar] [CrossRef]
- Echenagucia, T.M.; Capozzoli, A.; Cascone, Y.; Sassone, M. The early design stage of a building envelope: Multi-objective search through heating, cooling and lighting energy performance analysis. Appl. Energy 2015, 154, 577–591. [Google Scholar] [CrossRef]
- Chatzikonstantinou, B. Ekici, I. S. Sariyildiz, and B. K. Koyunbaba, “Multi-objective diagrid facąde optimization using differential evolution,” in 2015 IEEE Congress on Evolutionary Computation, CEC 2015 - Proceedings, 2015. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84963612041&doi=10.1109%2FCEC.2015.7257170&partnerID=40&md5=369f0e7cf66aea8b08ce21e68db02d8c.
- M. H. Wu, T. S. Ng, and M. R. Skitmore, “Sustainable building envelope design by considering energy cost and occupant satisfaction,” Energy Sustain. Dev., 2016, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84957671952&doi=10.1016%2Fj.esd.2015.12.003&partnerID=40&md5=9cd1f38c375e0711ac6577274920bb16.
- Ascione, F.; De Masi, R.F.; de Rossi, F.; Ruggiero, S.; Vanoli, G.P. Optimization of building envelope design for nZEBs in Mediterranean climate: Performance analysis of residential case study. Appl. Energy 2016, 183, 938–957. [Google Scholar] [CrossRef]
- W. Xu, K. P. W. Xu, K. P. Lam, A. Chong, and O. T. Karaguzel, “Multi-objective optimization of building envelope, lighting and HVAC systems designs,” in ASHRAE and IBPSA-USA Building Simulation Conference, 2016, pp. 110–117.
- Azari, R.; Garshasbi, S.; Amini, P.; Rashed-Ali, H.; Mohammadi, Y. Multi-objective optimization of building envelope design for life cycle environmental performance. Energy Build. 2016, 126, 524–534. [Google Scholar] [CrossRef]
- S. Karaman, B. Ekici, C. Cubukcuoglu, B. K. Koyunbaba, and I. Kahraman, “Design of rectangular façade modules through computational intelligence,” in 2017 IEEE Congress on Evolutionary Computation, CEC 2017 - Proceedings, 2017. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85028509112&doi=10.1109%2FCEC.2017.7969420&partnerID=40&md5=7d89d539e179acdd51e9576e64ed7d88.
- Fan, Y.; Xia, X. A multi-objective optimization model for energy-efficiency building envelope retrofitting plan with rooftop PV system installation and maintenance. Appl. Energy 2017, 189, 327–335. [Google Scholar] [CrossRef]
- Narangerel, J.-H. Lee, and R. Stouffs, “Thermal and Daylighting Optimization of Complex 3D Faceted Façade for Office Building,” in Proceedings of the International Conference on Education and Research in Computer Aided Architectural Design in Europe, 2017, pp. 209–218.
- R. Bingham, M. Agelin-Chaab, and M. A. Rosen, “Multi-objective optimization of a residential building envelope in the Bahamas,” in 2017 5th IEEE International Conference on Smart Energy Grid Engineering, SEGE 2017, 2017. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85032352094&doi=10.1109%2FSEGE.2017.8052815&partnerID=40&md5=77671c2a5a2310bfda6d5e7563ecda63.
- Kang, S.; Yong, S.-G.; Kim, J.; Jeon, H.; Cho, H.; Koo, J. Automated processes of estimating the heating and cooling load for building envelope design optimization. Build. Simul. 2017, 11, 219–233. [Google Scholar] [CrossRef]
- Chen, K.W.; Janssen, P.; Schlueter, A. Multi-objective optimisation of building form, envelope and cooling system for improved building energy performance. Autom. Constr. 2018, 94, 449–457. [Google Scholar] [CrossRef]
- Cascone, Y.; Capozzoli, A.; Perino, M. Optimisation analysis of PCM-enhanced opaque building envelope components for the energy retrofitting of office buildings in Mediterranean climates. Appl. Energy 2018, 211, 929–953. [Google Scholar] [CrossRef]
- Grygierek, K.; Ferdyn-Grygierek, J. Multi-Objective Optimization of the Envelope of Building with Natural Ventilation. Energies 2018, 11, 1383. [Google Scholar] [CrossRef]
- X. Shen, “Environmental parametric multi-objective optimization for high performance facade design,” in CAADRIA 2018 - 23rd International Conference on Computer-Aided Architectural Design Research in Asia: Learning, Prototyping and Adapting, 2018, pp. 103–112.
- Shahbazi, Y.; Heydari, M.; Haghparast, F. An early-stage design optimization for office buildings’ façade providing high-energy performance and daylight. Indoor Built Environ. 2019, 28, 1350–1367. [Google Scholar] [CrossRef]
- Yi, Y.K. Building facade multi-objective optimization for daylight and aesthetical perception. J. Affect. Disord. 2019, 156, 178–190. [Google Scholar] [CrossRef]
- Ascione, F.; Bianco, N.; Mauro, G.M.; Napolitano, D.F. Building envelope design: Multi-objective optimization to minimize energy consumption, global cost and thermal discomfort. Application to different Italian climatic zones. Energy 2019, 174, 359–374. [Google Scholar] [CrossRef]
- Torres-Rivas, A.; Palumbo, M.; Haddad, A.; Cabeza, L.F.; Jiménez, L.; Boer, D. Multi-objective optimisation of bio-based thermal insulation materials in building envelopes considering condensation risk. Appl. Energy 2018, 224, 602–614. [Google Scholar] [CrossRef]
- Jalali, Z.; Noorzai, E.; Heidari, S. Design and optimization of form and facade of an office building using the genetic algorithm. Sci. Technol. Built Environ. 2019, 26, 128–140. [Google Scholar] [CrossRef]
- Kim, H.; Clayton, M.J. A multi-objective optimization approach for climate-adaptive building envelope design using parametric behavior maps. J. Affect. Disord. 2020, 185, 107292. [Google Scholar] [CrossRef]
- Chang, S.; Castro-Lacouture, D.; Yamagata, Y. Decision support for retrofitting building envelopes using multi-objective optimization under uncertainties. J. Build. Eng. 2020, 32, 101413. [Google Scholar] [CrossRef]
- Zhao, J.; Du, Y. Multi-objective optimization design for windows and shading configuration considering energy consumption and thermal comfort: A case study for office building in different climatic regions of China. Sol. Energy 2020, 206, 997–1017. [Google Scholar] [CrossRef]
- Yılmaz, Y.; Yılmaz, B. . A weighted multi-objective optimisation approach to improve based facade aperture sizes in terms of energy, thermal comfort and daylight usage. J. Build. Phys. 2020, 44, 435–460. [Google Scholar] [CrossRef]
- Pilechiha, P.; Mahdavinejad, M.; Pour Rahimian, F.; Carnemolla, P.; Seyedzadeh, S. Multi-objective optimisation framework for designing office windows: quality of view, daylight and energy efficiency. Appl. Energy 2020, 261, 114356. [Google Scholar] [CrossRef]
- Ciardiello, A.; Rosso, F.; Dell'Olmo, J.; Ciancio, V.; Ferrero, M.; Salata, F. Multi-objective approach to the optimization of shape and envelope in building energy design. Appl. Energy 2020, 280, 115984. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A three-stage optimization methodology for envelope design of passive house considering energy demand, thermal comfort and cost. Energy 2019, 192, 116723. [Google Scholar] [CrossRef]
- Acar, U.; Kaska, O.; Tokgoz, N. Multi-objective optimization of building envelope components at the preliminary design stage for residential buildings in Turkey. J. Build. Eng. 2021, 42, 102499. [Google Scholar] [CrossRef]
- S. Naji, L. Aye, and M. Noguchi, “Multi-objective optimisations of envelope components for a prefabricated house in six climate zones,” Appl. Energy, 2021, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85096001686&doi=10.1016%2Fj.apenergy.2020.116012&partnerID=40&md5=01f711dc9b6b47931823df8686e4978e.
- Y.-H. Lin, M.-D. Lin, K.-T. Tsai, M.-J. Deng, and H. Ishii, “Multi-objective optimization design of green building envelopes and air conditioning systems for energy conservation and CO2 emission reduction,” Sustain. Cities Soc., 2021, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85094197524&doi=10.1016%2Fj.scs.2020.102555&partnerID=40&md5=b7be83cc7b54a2c744afa0286f6cc834.
- Nasrollahzadeh, N. Comprehensive building envelope optimization: Improving energy, daylight, and thermal comfort performance of the dwelling unit. J. Build. Eng. 2021, 44, 103418. [Google Scholar] [CrossRef]
- N. Abdou, Y. El Mghouchi, S. Hamdaoui, and M. Mhamed, “Optimal Building Envelope Design and Renewable Energy Systems Size for Net-zero Energy Building in Tetouan (Morocco),” in Proceedings of 2021 9th International Renewable and Sustainable Energy Conference, IRSEC 2021, 2021.
- M. Belhous, H. Mastouri, H. Radoine, S. I. Kaitouni, and B. Benhamou, “Multi-objective Optimization of the Thickness of the Thermal Insulation and the Windows Area of a House in Benguerir, Morocco,” in Proceedings of 2021 9th International Renewable and Sustainable Energy Conference, IRSEC 2021, 2021. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85128017241&doi=10.1109%2FIRSEC53969.2021.9741150&partnerID=40&md5=4edcf510153e6102ffd9b6177130cc4c.
- Xu, Y.; Zhang, G.; Yan, C.; Wang, G.; Jiang, Y.; Zhao, K. A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China. J. Affect. Disord. 2021, 204, 108142. [Google Scholar] [CrossRef]
- Y. Lin and W. Yang, “An ANN-exhaustive-listing method for optimization of multiple building shapes and envelope properties with maximum thermal performance,” Front. Energy, 2021, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85060017171&doi=10.1007%2Fs11708-019-0607-1&partnerID=40&md5=1c6ce8b0dbaaeb764f5c1b961c4e37dd.
- Mashaly, I.A.; Garcia-Hansen, V.; Cholette, M.E.; Isoardi, G. A daylight-oriented multi-objective optimisation of complex fenestration systems. J. Affect. Disord. 2021, 197, 107828. [Google Scholar] [CrossRef]
- Albatayneh, A. Optimising the Parameters of a Building Envelope in the East Mediterranean Saharan, Cool Climate Zone. Buildings 2021, 11, 43. [Google Scholar] [CrossRef]
- Yao, S.; Jiang, Z.; Yuan, J.; Wang, Z.; Huang, L. Multi-objective optimization of transparent building envelope of rural residences in cold climate zone, China. Case Stud. Therm. Eng. 2022, 34. [Google Scholar] [CrossRef]
- Seghier, T.E.; Lim, Y.-W.; Harun, M.F.; Ahmad, M.H.; Samah, A.A.; Majid, H.A. BIM-based retrofit method (RBIM) for building envelope thermal performance optimization. Energy Build. 2022, 256. [Google Scholar] [CrossRef]
- H. Wu and T. Zhang, “Multi-objective optimization of energy, visual, and thermal performance for building envelopes in China’s hot summer and cold winter climate zone,” J. Build. Eng., 2022, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85136006394&doi=10.1016%2Fj.jobe.2022.105034&partnerID=40&md5=796014f21bfdc366e11c6ba37b13290e.
- Xu, Y.; Yan, C.; Pan, Y.; Zhao, K.; Li, M.; Zhu, F.; Jiang, Y. A three-stage optimization method for the classroom envelope in primary and secondary schools in China. J. Build. Eng. 2022, 52. [Google Scholar] [CrossRef]
- Semahi, S.; Zemmouri, N.; Hamdy, M.; Attia, S. Passive envelope design optimization of residential buildings using NSGA-II in different Algerian climatic zones. 2021, 17, 760–767. [CrossRef]
- Xu, Y.; Yan, C.; Wang, D.; Li, J.; Shi, J.; Lu, Z.; Lu, Q.; Jiang, Y. Coordinated optimal design of school building envelope and energy system. Sol. Energy 2022, 244, 19–30. [Google Scholar] [CrossRef]
- Zong, C.; Margesin, M.; Staudt, J.; Deghim, F.; Lang, W. Decision-making under uncertainty in the early phase of building façade design based on multi-objective stochastic optimization. J. Affect. Disord. 2022, 226. [Google Scholar] [CrossRef]
- Himmetoğlu, S.; Delice, Y.; Aydoğan, E.K.; Uzal, B. Green building envelope designs in different climate and seismic zones: Multi-objective ANN-based genetic algorithm. Sustain. Energy Technol. Assessments 2022, 53. [Google Scholar] [CrossRef]
- Nazari, S.; Sajadi, B.; Sheikhansari, I. Optimisation of commercial buildings envelope to reduce energy consumption and improve indoor environmental quality (IEQ) using NSGA-II algorithm. Int. J. Ambient. Energy 2023, 44, 918–928. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Fan, B.; Yin, Z.; Li, W.; Wang, H.; Chi, F. Multi-Objective Optimization of Envelope Design of Rural Tourism Buildings in Southeastern Coastal Areas of China Based on NSGA-II Algorithm and Entropy-Based TOPSIS Method. Sustainability 2023, 15, 7238. [Google Scholar] [CrossRef]
- Elsheikh, A.; Motawa, I.; Diab, E. Multi-objective genetic algorithm optimization model for energy efficiency of residential building envelope under different climatic conditions in Egypt. Int. J. Constr. Manag. 2021, 23, 1244–1253. [Google Scholar] [CrossRef]
- Chang, S.; Castro-Lacouture, D.; Yamagata, Y. Decision support for retrofitting building envelopes using multi-objective optimization under uncertainties. J. Build. Eng. 2020, 32, 101413. [Google Scholar] [CrossRef]
- Sharif, S.A.; Hammad, A. Simulation-Based Multi-Objective Optimization of institutional building renovation considering energy consumption, Life-Cycle Cost and Life-Cycle Assessment. J. Build. Eng. 2019, 21, 429–445. [Google Scholar] [CrossRef]
- F. Flager, J. F. Flager, J. Basbagill, M. Lepech, and M. Fischer, “Multi-objective building envelope optimization for life-cycle cost and global warming potential,” eWork Ebus. Archit. Eng. Constr. - Proc. Eur. Conf. Prod. Process Model. 2012, ECPPM 2012, no. Cross 2004, pp. 193–200, 2012. [CrossRef]
- Wu, H.; Zhang, T. Multi-objective optimization of energy, visual, and thermal performance for building envelopes in China's hot summer and cold winter climate zone. J. Build. Eng. 2022, 59, 105034. [Google Scholar] [CrossRef]
- G. Zemella, D. De March, M. Borrotti, and I. Poli, “Optimised design of energy efficient building façades via Evolutionary Neural Networks,” Energy Build., 2011, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-80755163157&doi=10.1016%2Fj.enbuild.2011.10.006&partnerID=40&md5=9cb64b50c0a204ab8a5723d5afbd3afe.
- Acar, U.; Kaska, O.; Tokgoz, N. Multi-objective optimization of building envelope components at the preliminary design stage for residential buildings in Turkey. J. Build. Eng. 2021, 42, 102499. [Google Scholar] [CrossRef]
- Seghier, T.E.; Lim, Y.-W.; Harun, M.F.; Ahmad, M.H.; Samah, A.A.; Majid, H.A. BIM-based retrofit method (RBIM) for building envelope thermal performance optimization. Energy Build. 2022, 256. [Google Scholar] [CrossRef]
- Chang, S.; Castro-Lacouture, D.; Yamagata, Y. Decision support for retrofitting building envelopes using multi-objective optimization under uncertainties. J. Build. Eng. 2020, 32, 101413. [Google Scholar] [CrossRef]
- Yao, S.; Jiang, Z.; Yuan, J.; Wang, Z.; Huang, L. Multi-objective optimization of transparent building envelope of rural residences in cold climate zone, China. Case Stud. Therm. Eng. 2022, 34. [Google Scholar] [CrossRef]
- Naji, S.; Aye, L.; Noguchi, M. Multi-objective optimisations of envelope components for a prefabricated house in six climate zones. Appl. Energy 2020, 282, 116012. [Google Scholar] [CrossRef]
- Jalali, Z.; Noorzai, E.; Heidari, S. Design and optimization of form and facade of an office building using the genetic algorithm. Sci. Technol. Built Environ. 2019, 26, 128–140. [Google Scholar] [CrossRef]
- Yılmaz, Y.; Yılmaz, B. . A weighted multi-objective optimisation approach to improve based facade aperture sizes in terms of energy, thermal comfort and daylight usage. J. Build. Phys. 2020, 44, 435–460. [Google Scholar] [CrossRef]
- de Weck, O.; Agte, J.; Sobieszczanski-Sobieski, J.; Arendsen, P.; Morris, A.; Spieck, M. State-of-the-Art and Future Trends in Multidisciplinary Design Optimization. Collect. Tech. Pap. - AIAA/ASME/ASCE/AHS/ASC Struct. Struct. Dyn. Mater. Conf. [CrossRef]
- N. M. Alexandrov, M. Y. N. M. Alexandrov, M. Y. Hussaini, and others, “Multidisciplinary design optimization: State of the art,” 1997.
- Choudhary, R.; Papalambros, P.Y.; Malkawi, A. A Hierarchical Design Optimization Approach for Meeting Building Performance Targets. Arch. Eng. Des. Manag. 2005, 1, 57–76. [Google Scholar] [CrossRef]
- Burer, S.; Letchford, A.N. Non-convex mixed-integer nonlinear programming: A survey. Surv. Oper. Res. Manag. Sci. 2012, 17, 97–106. [Google Scholar] [CrossRef]
- Jung, Y.; Heo, Y.; Lee, H. Multi-objective optimization of the multi-story residential building with passive design strategy in South Korea. J. Affect. Disord. 2021, 203, 108061. [Google Scholar] [CrossRef]
- Dutta, A.; Samanta, A.; Neogi, S. Influence of orientation and the impact of external window shading on building thermal performance in tropical climate. Energy Build. 2017, 139, 680–689. [Google Scholar] [CrossRef]
- Monteiro, H.; Freire, F.; Soares, N. Life cycle assessment of a south European house addressing building design options for orientation, window sizing and building shape. J. Build. Eng. 2021, 39, 102276. [Google Scholar] [CrossRef]
- F. Flager, J. Basbagill, M. Lepech, and M. Fischer, “Multi-objective building envelope optimization for life-cycle cost and global warming potential,” in eWork and eBusiness in Architecture, Engineering and Construction - Proceedings of the European Conference on Product and Process Modelling 2012, ECPPM 2012, 2012, pp. 193–200. [CrossRef]
- Grygierek, K.; Ferdyn-Grygierek, J. Multi-Objective Optimization of the Envelope of Building with Natural Ventilation. Energies 2018, 11, 1383. [Google Scholar] [CrossRef]
- Evins, R. Configuration of a genetic algorithm for multi-objective optimisation of solar gain to buildings. Proc. 12th Annu. Genet. Evol. Comput. Conf. GECCO ’10 - Companion Publ, 2006. [Google Scholar] [CrossRef]
- Delgarm, N.; Sajadi, B.; Kowsary, F.; Delgarm, S. Multi-objective optimization of the building energy performance: A simulation-based approach by means of particle swarm optimization (PSO). Appl. Energy 2016, 170, 293–303. [Google Scholar] [CrossRef]
- C. Coello, “Evolutionary multiobjective optimisation: a historical view of the field,” IEEE Comput. Intell. Mag., no. 1, pp. 28–36, 2006.
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239. [Google Scholar] [CrossRef]
- R. Hooke and T. A. Jeeves, “‘Direct Search’ Solution of Numerical and Statistical Problems*”.
- Wetter, M.; Polak, E. Building design optimization using a convergent pattern search algorithm with adaptive precision simulations. Energy Build. 2005, 37, 603–612. [Google Scholar] [CrossRef]
- Peippo, K.; Lund, P.; Vartiainen, E. Multivariate optimization of design trade-offs for solar low energy buildings. Energy Build. 1999, 29, 189–205. [Google Scholar] [CrossRef]
- Wetter, M.; Wright, J. A comparison of deterministic and probabilistic optimization algorithms for nonsmooth simulation-based optimization. Build. Environ. 2004, 39, 989–999. [Google Scholar] [CrossRef]
- Futrell, B.J.; Ozelkan, E.C.; Brentrup, D. Bi-objective optimization of building enclosure design for thermal and lighting performance. J. Affect. Disord. 2015, 92, 591–602. [Google Scholar] [CrossRef]
- J. H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology. Control & Artificial Intelligence University of Michigan Press, 1975.
- Shan, R.; Junghans, L. “Adaptive radiation” optimization for climate adaptive building facade design strategy. Build. Simul. 2017, 11, 269–279. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Fan, B.; Yin, Z.; Li, W.; Wang, H.; Chi, F. Multi-Objective Optimization of Envelope Design of Rural Tourism Buildings in Southeastern Coastal Areas of China Based on NSGA-II Algorithm and Entropy-Based TOPSIS Method. Sustainability 2023, 15, 7238. [Google Scholar] [CrossRef]
- Echenagucia, T.M.; Capozzoli, A.; Cascone, Y.; Sassone, M. The early design stage of a building envelope: Multi-objective search through heating, cooling and lighting energy performance analysis. Appl. Energy 2015, 154, 577–591. [Google Scholar] [CrossRef]
- Bingham, R.; Agelin-Chaab, M.; Rosen, M.A. Multi-objective optimization of a residential building envelope in the Bahamas. In Proceedings of the 2017 IEEE International Conference on Smart Energy Grid Engineering (SEGE), Oshawa, ON, Canada, 14–17 August 2017; pp. 294–301. [Google Scholar]
- D. E. Goldberg, “Genetic Algorithms in Search, Optimization & Machine Learning (p. 126) Addison-Wesley,” Reading, Mass, 1989.
- Xu, Y.; Yan, C.; Pan, Y.; Zhao, K.; Li, M.; Zhu, F.; Jiang, Y. A three-stage optimization method for the classroom envelope in primary and secondary schools in China. J. Build. Eng. 2022, 52. [Google Scholar] [CrossRef]
- Junghans, L.; Darde, N. Hybrid single objective genetic algorithm coupled with the simulated annealing optimization method for building optimization. Energy Build. 2015, 86, 651–662. [Google Scholar] [CrossRef]
- J. Kennedy, “Particle swarm optimization,” IEEE Int. Conf. Neural Networks, pp. 129–132, 1995.
- Wang, J.; Li, H. Particle Swarm Optimization with Enhanced Global Search and Local Search. J. Intell. Syst. 2016, 26, 421–432. [Google Scholar] [CrossRef]
- 117. Y. Yılmaz and B. Ç. Yılmaz, “A weighted multi-objective optimisation approach to improve based facade aperture sizes in terms of energy, thermal comfort and daylight usage,” https://doi.org/10.1177/1744259120930047, vol. 44, no. 5, pp. 435–460, Jun. 2020. [CrossRef]
- Y. Xu, G. Y. Xu, G. Zhang, C. Yan, G. Wang, Y. Jiang, and K. Zhao, “A two-stage multi-objective optimization method for envelope and energy generation systems of primary and secondary school teaching buildings in China,” Build. Environ., 2021, [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-85111072847&doi=10.1016%2Fj.buildenv.2021.108142&partnerID=40&md5=8606461b7f5641db3f05bf3fa3aad686.
- Vera, S.; Uribe, D.; Bustamante, W.; Molina, G. Optimization of a fixed exterior complex fenestration system considering visual comfort and energy performance criteria. Build. Environ. 2017, 113, 163–174. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- V. Cerny, “Minimization of continuous functions by simulated annealing.” Dec. 10, 1984. Accessed: Jan. 03, 2023. [Online]. Available: https://cds.cern.ch/record/156608.
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Suman, B.; Kumar, P. A survey of simulated annealing as a tool for single and multiobjective optimization. J. Oper. Res. Soc. 2006, 57, 1143–1160. [Google Scholar] [CrossRef]
- Czyzżak, P.; Jaszkiewicz, A. Pareto simulated annealing—a metaheuristic technique for multiple-objective combinatorial optimization. J. Multi-Criteria Decis. Anal. 1998, 7, 34–47. [Google Scholar] [CrossRef]
- M. Dorigo, “Optimization, learning and natural algorithms,” Ph. D. Thesis, Politec. di Milano, 1992.
- Bamdad, K.; Cholette, M.E.; Guan, L.; Bell, J. Ant colony algorithm for building energy optimisation problems and comparison with benchmark algorithms. Energy Build. 2017, 154, 404–414. [Google Scholar] [CrossRef]
- K. Shea, A. K. Shea, A. Sedgwick, and G. Antonuntto, “Multicriteria optimization of paneled building envelopes using ant colony optimization,” Lect. Notes Comput. Sci. (including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics), vol. 4200 LNAI, pp. 627–636, 2006. [CrossRef]
- Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [Google Scholar] [CrossRef]
- Fesanghary, M.; Asadi, S.; Geem, Z.W. Design of low-emission and energy-efficient residential buildings using a multi-objective optimization algorithm. Build. Environ. 2012, 49, 245–250. [Google Scholar] [CrossRef]
- Asadi, E.; da Silva, M.G.; Antunes, C.H.; Dias, L.; Glicksman, L. Multi-objective optimization for building retrofit: A model using genetic algorithm and artificial neural network and an application. Energy Build. 2014, 81, 444–456. [Google Scholar] [CrossRef]
- Khoroshiltseva, M.; Slanzi, D.; Poli, I. A Pareto-based multi-objective optimization algorithm to design energy-efficient shading devices. Appl. Energy 2016, 184, 1400–1410. [Google Scholar] [CrossRef]
- Chegari, B.; Tabaa, M.; Simeu, E.; Moutaouakkil, F.; Medromi, H. Multi-objective optimization of building energy performance and indoor thermal comfort by combining artificial neural networks and metaheuristic algorithms. Energy Build. 2021, 239. [Google Scholar] [CrossRef]
- Ayata, T.; Arcaklıoğlu, E.; Yıldız, O. Application of ANN to explore the potential use of natural ventilation in buildings in Turkey. Appl. Therm. Eng. 2007, 27, 12–20. [Google Scholar] [CrossRef]
- J. Yang, H. J. Yang, H. Rivard, and R. Zmeureanu, “BUILDING ENERGY PREDICTION WITH ADAPTIVE ARTIFICIAL NEURAL NETWORKS,” 2005.
- Magnier, L.; Haghighat, F. Multiobjective optimization of building design using TRNSYS simulations, genetic algorithm, and Artificial Neural Network. J. Affect. Disord. 2010, 45, 739–746. [Google Scholar] [CrossRef]
- Nourkojouri, H.; Shafavi, N.S.; Tahsildoost, M.; Zomorodian, Z.S. Development of a Machine-Learning Framework for Overall Daylight and Visual Comfort Assessment in Early Design Stages. J. Daylighting 2021, 8, 270–283. [Google Scholar] [CrossRef]
- “MATLAB - MathWorks - MATLAB Simulink.” Accessed: Aug. 14, 2022. [Online]. Available: https://www.mathworks.com/products/matlab.html.
- Bushnell, D. GENOPT—a program that writes user-friendly optimization code. Int. J. Solids Struct. 1990, 26, 1173–1210. [Google Scholar] [CrossRef]
- Giouri, E.D.; Tenpierik, M.; Turrin, M. Zero energy potential of a high-rise office building in a Mediterranean climate: Using multi-objective optimization to understand the impact of design decisions towards zero-energy high-rise buildings. Energy Build. 2019, 209, 109666. [Google Scholar] [CrossRef]
- F. Flager, J. Basbagill, M. Lepech, and M. Fischer, “Multi-objective building envelope optimization for life-cycle cost and global warming potential,” in eWork and eBusiness in Architecture, Engineering and Construction - Proceedings of the European Conference on Product and Process Modelling 2012, ECPPM 2012, 2012. [Online]. Available: https://www.scopus.com/inward/record.uri?eid=2-s2.0-84863524280&doi=10.1201%2Fb12516-32&partnerID=40&md5=4f93403d25f00c06c25753cdbee6458b. 1201. [Google Scholar]
- Wahid, A.; Gao, X.; Andreae, P. Multi-objective clustering ensemble for high-dimensional data based on Strength Pareto Evolutionary Algorithm (SPEA-II). 2015, 1–9. [CrossRef]
- Bader, J.; Zitzler, E. HypE: An Algorithm for Fast Hypervolume-Based Many-Objective Optimization. Evol. Comput. 2011, 19, 45–76. [Google Scholar] [CrossRef] [PubMed]
- Winkelmann, F.; Birdsall, B.; Buhl, W.; Ellington, K.; Erdem, A.; Hirsch, J.; Gates, S. DOE-2 supplement: Version 2. 1E. 1993. [Google Scholar] [CrossRef]
- Beckman, W.A.; Broman, L.; Fiksel, A.; Klein, S.A.; Lindberg, E.; Schuler, M.; Thornton, J. TRNSYS The most complete solar energy system modeling and simulation software. Renew. Energy 1994, 5, 486–488. [Google Scholar] [CrossRef]
- Crawley, D.B.; Lawrie, L.K.; Winkelmann, F.C.; Buhl, W.; Huang, Y.; Pedersen, C.O.; Strand, R.K.; Liesen, R.J.; Fisher, D.E.; Witte, M.J.; et al. EnergyPlus: creating a new-generation building energy simulation program. Energy Build. 2001, 33, 319–331. [Google Scholar] [CrossRef]
- J. K. Kissock, J. S. Haberl, and D. E. Claridge, “Development of a Toolkit for Calculating Linear, Change-Point Linear and Multiple-Linear Inverse Building Energy Analysis Models, ASHRAE Research Project 1050-RP, Final Report.” Energy Systems Laboratory, Texas A&M University, Nov. 2002. [Online]. Available: https://oaktrust.library.tamu.edu/handle/1969.1/2847.
- Bingham, R.D.; Agelin-Chaab, M.; Rosen, M.A. Whole building optimization of a residential home with PV and battery storage in The Bahamas. Renew. Energy 2018, 132, 1088–1103. [Google Scholar] [CrossRef]
- Zhao, J.; Du, Y. Multi-objective optimization design for windows and shading configuration considering energy consumption and thermal comfort: A case study for office building in different climatic regions of China. Sol. Energy 2020, 206, 997–1017. [Google Scholar] [CrossRef]
- Negendahl, K.; Nielsen, T.R. Building energy optimization in the early design stages: A simplified method. Energy Build. 2015, 105, 88–99. [Google Scholar] [CrossRef]
- Zani, A.; Andaloro, M.; Deblasio, L.; Ruttico, P.; Mainini, A.G. Computational Design and Parametric Optimization Approach with Genetic Algorithms of an Innovative Concrete Shading Device System. Procedia Eng. 2017, 180, 1473–1483. [Google Scholar] [CrossRef]
- Zani, A.; Tagliabue, L.C.; Poli, T.; Ciribini, A.L.; De Angelis, E.; Manfren, M. Occupancy Profile Variation Analyzed through Generative Modelling to Control Building Energy Behavior. Procedia Eng. 2017, 180, 1495–1505. [Google Scholar] [CrossRef]
- Agirbas, A. Multi-objective building design optimisation using acoustics and daylighting. Indoor Built Environ. 2021, 31, 853–867. [Google Scholar] [CrossRef]
- Lakhdari, K.; Sriti, L.; Painter, B. Parametric optimization of daylight, thermal and energy performance of middle school classrooms, case of hot and dry regions. J. Affect. Disord. 2021, 204, 108173. [Google Scholar] [CrossRef]

| Database | Keywords | Results |
|---|---|---|
| WOS | (TS=(building facade) OR TS=(building envelope) OR TS=(building skin)) AND (TS=(multi-objective) OR TS=(two-objective) OR TS=(triple-objective)) AND (TS=(optimization) OR TS=(optimize)) | 376 |
| Scopus | TITLE-ABS-KEY (building AND (facade OR envelope OR skin) AND (multi-objective OR two-objective OR triple-objective) AND (optimization OR optimize) ) | 326 |
| Total After Deduplication | 459 | |
| Total After Title Screening | 266 | |
| Total After Abstract Screening | 110 | |
| Total After Full-text Screening | 56 |
| Building type | Number in the reviewed literatures |
|---|---|
| Office | 26 |
| Residential | 19 |
| Education | 3 |
| Hospital | 1 |
| Tourism | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).




