Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis

Preprint

Article

Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis

Altmetrics

Downloads

Views

Comments

A peer-reviewed article of this preprint also exists.

This version is not peer-reviewed

Submitted:

04 September 2023

Posted:

05 September 2023

You are already at the latest version

Alerts

Abstract

The flow field around a straight chain of multiple slip spherical particles rotating steadily in an incompressible Newtonian fluid about their line of centers is analyzed at low Reynolds numbers. The particles may vary in radius, slip coefficient, and angular velocity, and they are permitted to be unevenly spaced. Through the use of a boundary collocation method, the Stokes equation governing the fluid flow is solved semi-analytically. The interaction effects among the particles are found to be noteworthy under appropriate conditions. For the rotation of two spheres, our collocation results for their hydrodynamic torques are in good agreement with the analytical asymptotic solution in the literature obtained by using a method of twin multipole expansions. For the rotation of three spheres, the particle interaction effect indicates that the existence of the third particle can influence the torques exerted on the other two particles noticeably. The interaction effect is stronger on the smaller or less slippery particles than on the larger or more slippery ones. Torque results for the rotation of chains of many particles visibly show the shielding effect among the particles.

Keywords:

Subject: Engineering - Chemical Engineering

1. Introduction

The translation and rotation of small particles in Newtonian fluids at low Reynolds numbers play important roles in a variety of technological and industrial processes such as centrifugation, sedimentation, aggregation, microfluidics, suspension rheology, and aerosol technology. The analysis of this subject was initiated by Stokes [1,2] on the motions of an isolated nonslip spherical particle in a viscous fluid. The phenomena that viscous fluids in creeping flow can frictionally slip at particle surfaces occur for numerous situations such as a colloidal particle with lyophobic surface [3,4,5,6,7], an aerosol particle in low-density gas [8,9,10], and a porous particle [11,12]. The slip velocity is presumably proportional to the shear stress of the fluid at the particle surface with the proportionality constant

β^{- 1}

as the slip coefficient [13,14,15].

The hydrodynamic torque exerted on a slip sphere of radius

a

rotating with angular velocity

Ω

in a fluid of viscosity

η

was obtained by Basset [13] as

T^{(0)} = - 8 π η a^{3} Ω \frac{1}{1 + 3 η / β a},

(1)

where

η / β

signifies a slip length. In the limiting case of the stickiness/slip parameter

β a / η = 0

, the particle is perfectly slip (like a gas bubble in a liquid) and

T^{(0)} = 0

. In the other limit

β a / η \to \infty

, the particle is nonslip and Eq. (1) becomes the Stokes result. More recently, the creeping-flow rotation of slip particles has been examined for a slightly deformed sphere [16], an axisymmetric particle such as spheroid [17,18,19], and a circular cylinder [20].

In many technical applications, slip particles are not isolated. Thus, it is imperative to determine if the attendance of adjoining particles meaningfully affects the particle movement [21,22]. Through an exact representation in spherical bipolar coordinates, the axisymmetric slow translation of two slip spherical particles was investigated semi-analytically and numerical results were calculated for the cases of identical spheres with equal magnitude of velocities [23] and arbitrary spheres with arbitrary velocities [24]. On the other hand, the translational and rotational motions of two arbitrarily oriented spheres with arbitrary radii and slip coefficients were analyzed using a method of twin multipole expansions [25]. Subsequently, the creeping flow around two arbitrary slip spheres translating along and rotating about their line of centers was studied by using a boundary collocation method [26]. It was found from these investigations that the two-sphere interaction effect decreases with increasing slip coefficients of the particles, may be pronounced as the distance between particle surfaces approaches zero, and is greater on the smaller particles than on the larger ones.

For a concentrated suspension, the interaction amongst multiple particles may be important. The objective of this article is to analyze the slow rotation of a chain of coaxial slip spherical particles about the axis. The particles may vary in radius, slip coefficient, and angular velocity, and they are permitted to be unevenly spaced. Through the use of the boundary collocation method, the Stokes equation is solved semi-analytically and the torques exerted on the particles by the fluid are obtained with excellent convergence. For the simple case of rotation of two spherical particles, our collocation solutions for the torques agree well with the asymptotic solutions resulted from the method of twin multipole expansions [25] and with some numerical calculations [26].

2. Analysis

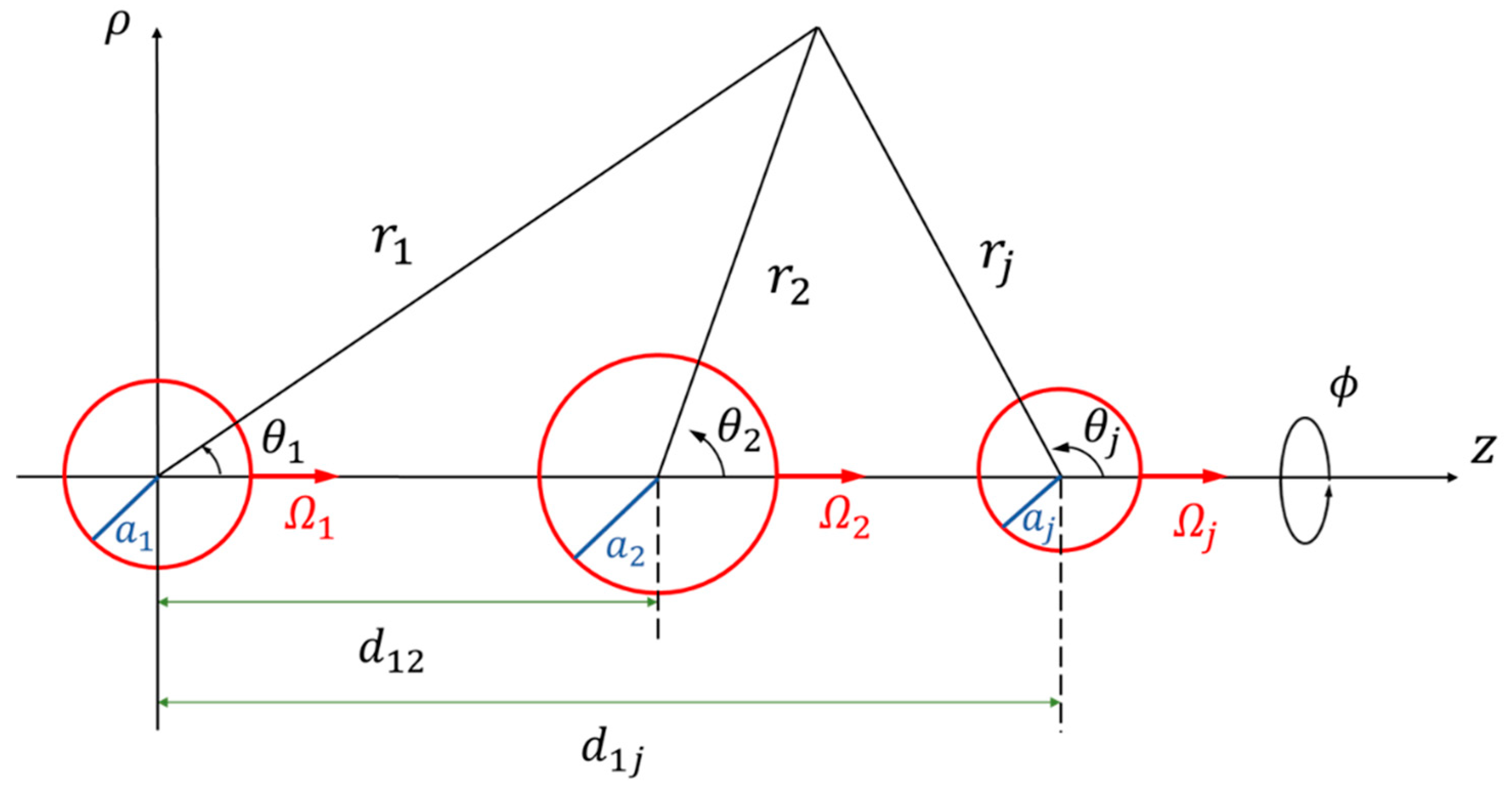
As shown in Figure 1, we consider the steady slow rotation of a straight chain of

N

neutrally-buoyant spherical particles in a boundless, quiescent, incompressible Newtonian fluid of viscosity

η

about the line through their centers (

z

axis), where the fluid may slip frictionally at the particle surfaces. The spherical coordinates

(r_{i}, θ_{i}, ϕ)

are measured from the center of particle

i

(with radius

a_{i}

) for

i = 1

, 2, …, and

N

, and the origin of the circular cylindrical coordinates

(ρ, ϕ, z)

is set at the center of particle 1. The particles may vary in size, surface slippage, and angular velocity, and they are permitted to be unevenly spaced. The purpose is to obtain the correction to Eq. (1) for the rotational motion of each particle owing to the presence of the other ones.

The Stokes equation governing the creeping flow around the rotating particles is

(\nabla^{2} - ρ^{- 2}) v_{ϕ} = \frac{1}{r_{i}^{2}} {\frac{\partial}{\partial r_{i}} (r_{i}^{2} \frac{\partial v_{ϕ}}{\partial r_{i}}) + \frac{\partial}{\partial θ_{i}} [\frac{1}{\sin θ_{i}} \frac{\partial}{\partial θ_{i}} (v_{ϕ} \sin θ_{i})]} = 0,

(2)

where

v_{φ} (r_{i}, θ_{i})

v_{ϕ} (ρ, z)

is the

φ

(only nontrivial) component of the fluid velocity distribution (with

r_{1} \geq a_{1}

r_{2} \geq a_{2}

, …, and

r_{N} \geq a_{N}

), the continuity equation is satisfied, and the dynamic pressure is constant everywhere. In Eq. (2), any coordinate system

(r_{i}, θ_{i}, ϕ)

can be chosen. Because the slip velocity is proportional to the nontrivial tangential stress locally at each particle surface [13], the fluid velocity satisfies the boundary conditions

r_{i} = a_{i} : v_{ϕ} = Ω_{i} a_{i} \sin θ_{i} + \frac{1}{β_{i}} τ_{r_{i} ϕ}, i = 1, 2, \dots, and N,

(3)

{(ρ^{2} + z^{2})}^{1 / 2} \to \infty : v_{ϕ} = 0,

(4)

where

Ω_{i}

is the angular velocity of particle

i

τ_{r_{i} φ} = η r_{i} \frac{\partial}{\partial r_{i}} (\frac{v_{φ}}{r_{i}}),

(5)

which is the relevant shear stress, and

1 / β_{i}

is the Navier slip coefficient about the particle

i

We can express a sufficiently general solution of the fluid velocity in the form

v_{ϕ} = \sum_{j = 1}^{N} \sum_{n = 1}^{\infty} A_{j n} r_{j}^{- n - 1} P_{n}^{1} (\cos θ_{j}),

(6)

where

P_{n}^{1}

is the associated Legendre function of the first kind of order

n

and degree 1, and

A_{j n}

are the unknown constants to be determined. The boundary condition (4) is satisfied immediately by Eq. (6), in which the solutions in

N

spherical coordinate systems can be superimposed due to the linearity of Eq. (2). Substituting Eq. (6) into Eq. (3), we obtain

\sum_{j = 1}^{N} \sum_{n = 1}^{\infty} A_{j n} {r_{j}^{- n - 1} [1 + (n + 2) \frac{η}{β_{i} r_{j}}] P_{n}^{1} (\cos θ_{j})}_{r_{i} = a_{i}} = Ω_{i} a_{i} \sin θ_{i}, i = 1, 2, \dots, and N .

(7)

To express Eqs. (6) and (7) in a single coordinate system, one can use the conversion formulas between the coordinates

(r_{j}, θ_{j})

and

(ρ, z)

r_{j} = {[ρ^{2} + {(z - d_{1 j})}^{2}]}^{1 / 2},

(8)

\cos θ_{j} = (z - d_{1 j}) / r_{j},

(9)

where

d_{i j}

denotes the distance between the centers of particles

i

and

j

(thus

d_{j j} = 0

The satisfaction of the boundary conditions in Eq. (7) on the particle surfaces requires the solution of the unknown constants

A_{j n}

. The collocation technique [27,28,29] permits these boundary conditions to be imposed at

M

points along the longitudinal arc of each sphere and the infinite series in Eq. (6) is truncated after the

M

terms, leading to

N M

simultaneous algebraic equations in the truncated form of Eq. (7). For sufficiently large number of

M

, these equations can be numerically solved to yield the

N M

constants

A_{j n}

required in the truncated form of Eq. (6). The details of the adopted boundary collocation arrangement were given in an early article on the translation of a chain of fluid spheres along their line of centers [30].

The hydrodynamic torque acting on the particle

i

is the integral of the product of the shear force

τ_{r_{i} ϕ} (r_{i} = a_{i}) a_{i}^{2} \sin θ_{i} d θ_{i} d ϕ

exerted on a differential surface element and the lever arm

a_{i} \sin θ_{i}

of that element over the particle surface, resulting in

T_{i} = 8 π η A_{i 1}, i = 1, 2, \dots, and N .

(10)

The previous formula shows that only the lowest-order constants

A_{i 1}

contribute to the hydrodynamic torques

T_{i}^{}

The torque results can be expressed as

T_{i} = \sum_{j = 1}^{N} g_{i j} T_{j}^{(0)},

(11)

with

T_{j}^{(0)} = - 8 π η a_{j}^{3} Ω_{j} \frac{β_{j} a_{j}}{β_{j} a_{j} + 3 η},

(12)

which is the torque acting on the isolated particle

j

given by Eq. (1). The torque correction parameters

g_{i j}

are functions of the scaled radii, separation distances, and surface slippages of the particles. When the separation distances are infinite, obviously,

g_{i j}

equals unity if

j = i

and zero if

j \neq i

3. Results for Two Particles

In this section, we present the boundary collocation results for the rotation of two slip spheres (

N = 2

) about their line of centers. Once the unknown constants

A_{1 n}

and

A_{2 n}

in Eq. (6) for the fluid velocity are solved from the truncated form of Eq. (7), Eq. (10) can be used to calculate the torque exerted by the fluid on each particle. Numerical results of the four torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

in Eq. (11) are presented in Table 1 for the case of two identical spheres (

a_{1} = a_{2} = a

β_{1} = β_{2} = β

g_{11} = g_{22}

, and

g_{12} = g_{21}

) with various values of the stickiness/slip parameter

β a / η

and spacing parameter

2 a / d_{12}

. In Table 2, collocation solutions of the torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two nonslip spheres (

β_{1} = β_{2} \to \infty

) with different radii (choosing

a_{2} / a_{1}

equal to 2 and 5) at various values of the spacing parameter

(a_{1} + a_{2}) / d_{12}

are given. In Table 3, we list typical collocation results of these torque correction parameters for cases of two slip spheres differing in either size or slippage at various values of the spacing parameter

(a_{1} + a_{2}) / d_{12}

. All of our results converge to at least five digits after the decimal point.

In Table 1, Table 2 and Table 3, for all values of

a_{2} / a_{1}

β_{1} a_{1} / η

, and

β_{2} a_{2} / η

, the parameters

g_{11}

and

g_{22}

are positive and increase with an increase in

(a_{1} + a_{2}) / d_{12}

from unity at

(a_{1} + a_{2}) / d_{12} = 0

, while

g_{12}

and

g_{21}

are negative and whose magnitudes also increase with an increase in

(a_{1} + a_{2}) / d_{12}

but from zero at

(a_{1} + a_{2}) / d_{12} = 0

. These results manifest that the particles’ interaction rises with diminishing gap thickness between them. In general, this interaction can be significant as

(a_{1} + a_{2}) / d_{12} \to 1

and its influence is stronger on a smaller or less slippery (stickier) particle than on a larger or more slippery (less sticky) one for any given value of

(a_{1} + a_{2}) / d_{12}

Using a method of twin multipole expansions, Keh and Chen [25] analytically obtained the following power-series formulas of the torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axial rotation of two spheres with

β_{1} a_{1} = β_{2} a_{2} = β a

g_{11} (s, λ) = g_{22} (s, λ^{- 1}) = \sum_{k = 0}^{\infty} f_{2 k} (λ) {(1 + λ)}^{- 2 k} s^{- 2 k},

(13)

g_{12} (s, λ) = g_{21} (s, λ^{- 1}) = - 8 \sum_{k = 0}^{\infty} f_{2 k + 1} (λ) {(1 + λ)}^{- 2 k - 4} s^{- 2 k - 1},

(14)

where

s = \frac{2 d_{12}}{a_{1} + a_{2}},

(15)

λ = \frac{a_{2}}{a_{1}},

(16)

f_{1} = f_{2} = f_{4} = f_{5} = f_{7} = 0,

(17)

f_{0} = 1, f_{3} = 8 λ^{3} \frac{β a}{β a + 3 η}, f_{6} = 64 λ^{3} {(\frac{β a}{β a + 3 η})}^{2} .

(18)

Thus, there are two independent torque correction parameters to be determined for

0 \leq λ < \infty

and

2 \leq s < \infty

. Alternatively, we could determine all four parameters in the range

1 \leq λ < \infty

and

2 \leq s < \infty

. In the particular case of

β_{1} = β_{2} \to \infty

(two nonslip spheres), more terms of

f_{k} (λ)

are available [31]:

f_{8} = 768 λ^{5}, f_{9} = 512 λ^{6}, f_{10} = 6144 λ^{7}, f_{11} = 6144 (λ^{6} + λ^{8}) .

(19)

The asymptotic solutions for the torque correction parameters obtained from the previous formulas are also listed in Table 1 and Table 2 for comparison. It is found that our collocation results are in good agreement with these asymptotic solutions as

(a_{1} + a_{2}) / d_{12}

is small. However, the errors of these asymptotic solutions become significant when

(a_{1} + a_{2}) / d_{12}

gets close to unity.

Using the reciprocal theorem of Lorentz [15] for the axisymmetric rotation of any two slip spheres with

β_{1} a_{1} = β_{2} a_{2}

, we obtain

\frac{g_{21}}{g_{12}} = {(\frac{a_{2}}{a_{1}})}^{3} .

(20)

The collocation results in Table 1 and Table 2 satisfy Eq. (20) and the relations

g_{11} + g_{21} \leq 1

and

g_{12} + g_{22} \leq 1

(with

g_{11}

and

g_{22}

being positive and

g_{12}

and

g_{21}

negative), indicating that the rotation of one particle is enhanced (its hydrodynamic torque is reduced) by another nearby particle rotating with a comparable or larger angular velocity in the same direction but is hindered (the resisting torque is augmented) by another particle rotating with an arbitrary angular velocity in the opposite direction.

4. Results for Multiple Particles

We now present the boundary collocation results for the rotation of a chain of three or more slip spheres about their line of centers. From Eq. (11), the general problem requires nine torque correction parameters to represent the hydrodynamic torques on the three-sphere chain. For the sake of brevity, here we only consider the rotation of three coaxial spheres with the same slip coefficient (

β_{1} = β_{2} = β_{3} = β

) in a symmetric configuration, i.e. the spheres at both ends have equal radii (

a_{3} = a_{1}

) and are equally distant from the central sphere (

d_{23} = d_{12} = d

). For this symmetric case, it is clear that the torque correction coefficients

g_{11} = g_{33}, g_{12} = g_{32}, g_{23} = g_{21}, g_{31} = g_{13} .

(21)

In Table 4, collocation results of the torque correction parameters in Eq. (11) for the axisymmetric rotation of three identical slip spheres (

a_{1} = a_{2} = a_{3} = a

) with different values of the stickiness parameter

β a / η

and spacing parameter

2 a / d

are offered. In Table 5, the numerical results of the torque correction parameters for the rotation of three nonslip spheres (

β \to \infty

) for two typical cases of relative particle sizes (

a_{2} / a_{1}

equal to 2 and 1/2) at various values of the spacing parameter

(a_{1} + a_{2}) / d

are given. In Table 6, we list results of the torque correction parameters for the rotation of three slip spheres (with

β a_{2} / η = 1

and

a_{2} / a_{1}

equal to 2 and 1/2) at various values of

(a_{1} + a_{2}) / d

. In general, particle interactions increase with decreasing gap thickness between two adjacent particles. When the central particle is greater than the end ones, however, the torque correction parameters

g_{13}

and

g_{31}

are not always monotonical functions of

(a_{1} + a_{2}) / d

. Again, Eq. (20) holds in Tables IV and V for the axisymmetric rotation of the three-sphere chain and the effect of particle interactions on the hydrodynamic torques is greater for smaller or less slippery particles than for larger or more slippery ones for a given value of

(a_{1} + a_{2}) / d

It may be interesting to realize how much the presence of a third particle influences the hydrodynamic torques of its two neighbors. The normalized torques

T_{i}^{} / T_{}^{(0)}

of three identical spheres (

a_{1} = a_{2} = a_{3} = a

β_{1} = β_{2} = β_{3} = β

, and

T_{1}^{(0)} = T_{2}^{(0)} = T_{3}^{(0)} = T_{}^{(0)}

) rotating at equal angular velocities (

Ω_{1} = Ω_{2} = Ω_{3} = Ω

) about their line of centers at equal spacings (

d_{12} = d_{23} = d

) are plotted versus the spacing parameter

2 a / d

by solid curves for various values of the stickiness parameter

β a / η

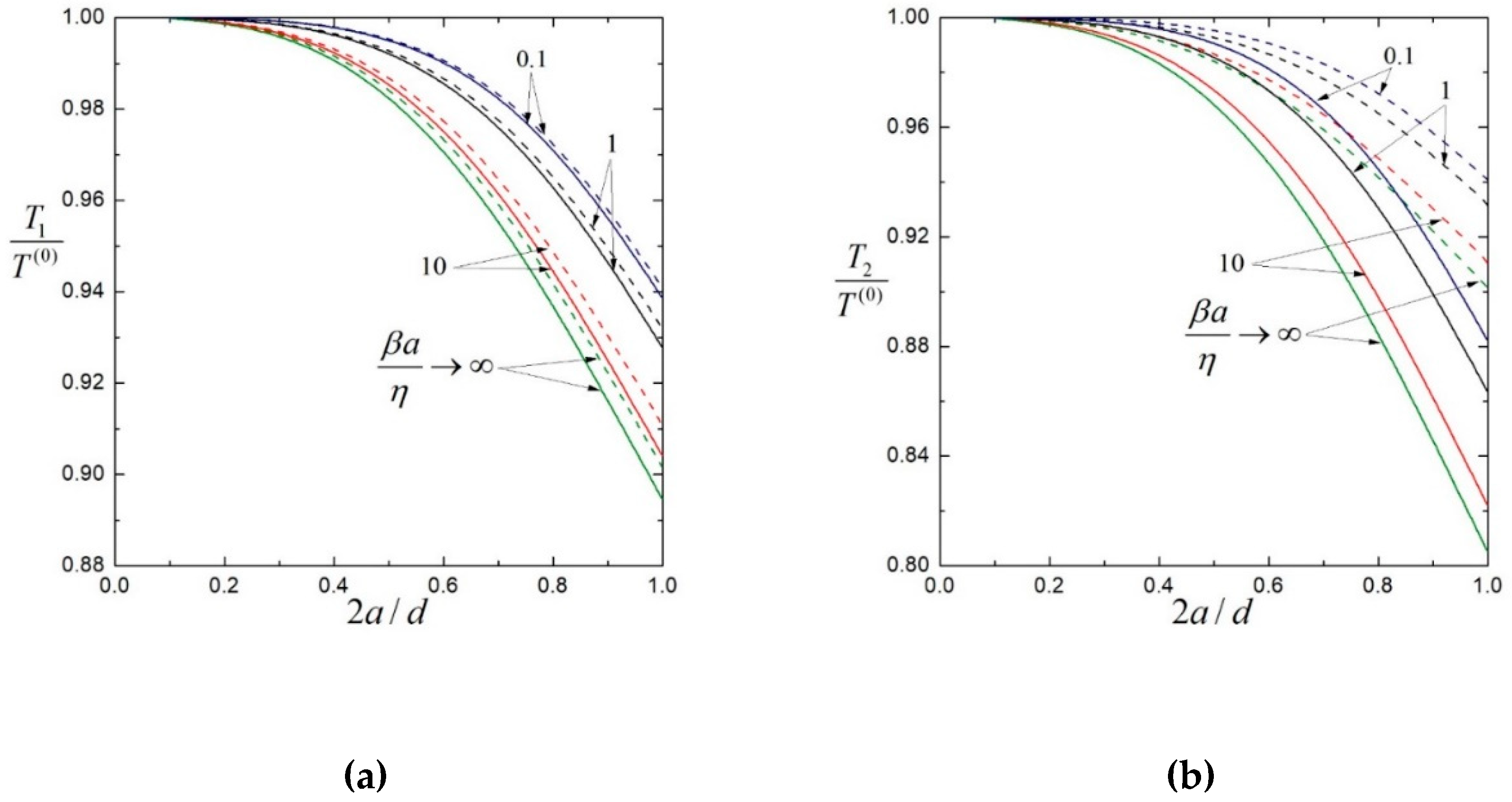
in Figure 2. For comparison, the corresponding results of normalized torques of the first and second particles in the absence of the third one, which agree well with those obtained by Saad [26], are plotted in the same figure by dashed curves. Clearly, the presence of the third particle reduces the torques of the other two particles. As expected, the reduction in torque is much more pronounced on the center particle than on the end ones. When the particles are in contact with each other (

2 a / d = 1

), the presence of the third particle reduces the torque on the first (end) particle by merely about 0.8% in the case of no-slip particles (

β a / η \to \infty

) and about 0.3% in the case of slip particles with

β a / η = 1

, as shown in Figure 2a (and Table 1 and Table 4). In contrast, as shown in Figure 2b (and Table 1 and Table 4), the torque on the second (center) particle is reduced by 10.7% in the case of no-slip particles and by 7.3% in the case of slip particles with

β a / η = 1

when the particles touch each other. Note that, due to the configurational symmetry, the torque results presented in Table 1 and Figure 2 for two identical slip spheres a distance

d

apart and rotating at identical angular velocity are the same as those for an isolated slip sphere rotating at equal angular velocity at a distance

d / 2

from a large planar free surface (with vanishing shear stress) normal to the axis of rotation.

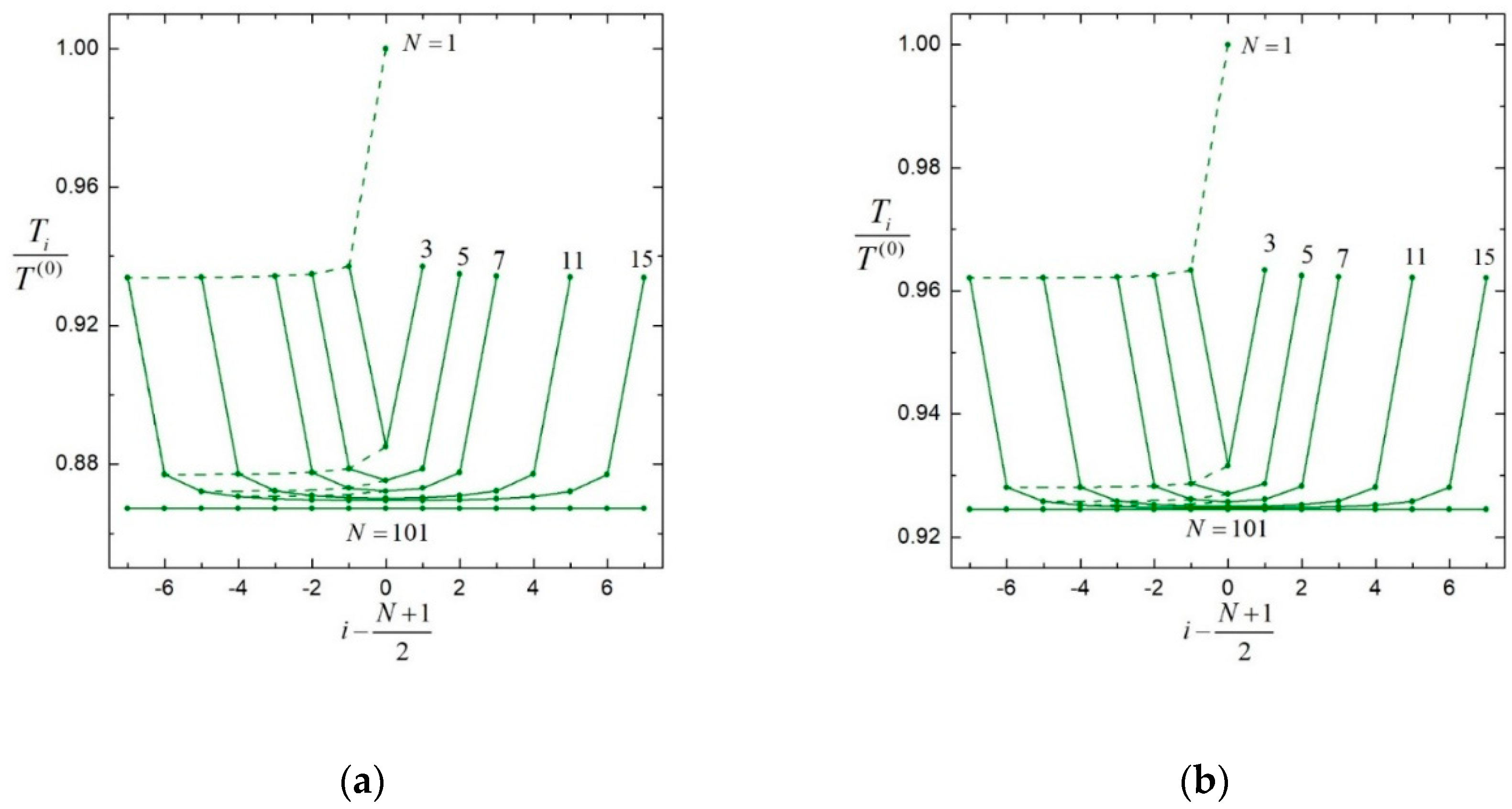
The solution to the problem of chains consisting of different numbers of

N

(up to 101) identical slip spheres (

a_{i} = a

β_{i} = β

, and

T_{i}^{(0)} = T_{}^{(0)}

) with equal spacings (

d_{i (i + 1)} = d

), rotating about their line of centers with equal angular velocities (

Ω_{i} = Ω

), has also been obtained by the boundary collocation method. Results of the normalized torques

T_{i}^{} / T_{}^{(0)}

for these chains with

2 a / d = 0.8

are plotted against the particle number

i

in Figure 3. It can be seen that the torques on the central particles decrease with increasing chain length, indicating a shielding effect of the particle chain. When approaching the ends of the chain, the relative torques of neighboring particles change rapidly, demonstrating a strong end effect. As the chain length increases for a relatively long chain, the torques on the central particles change slowly. The torque on each particle will be the same in the limit of an infinite chain. The dashed curves in Figure 3 represent the change in torque of the ith particle in the chain as more particles are added to the chain. These curves are leveled out as the chain length is increased, again demonstrating the shielding effect exhibited by particle chains.

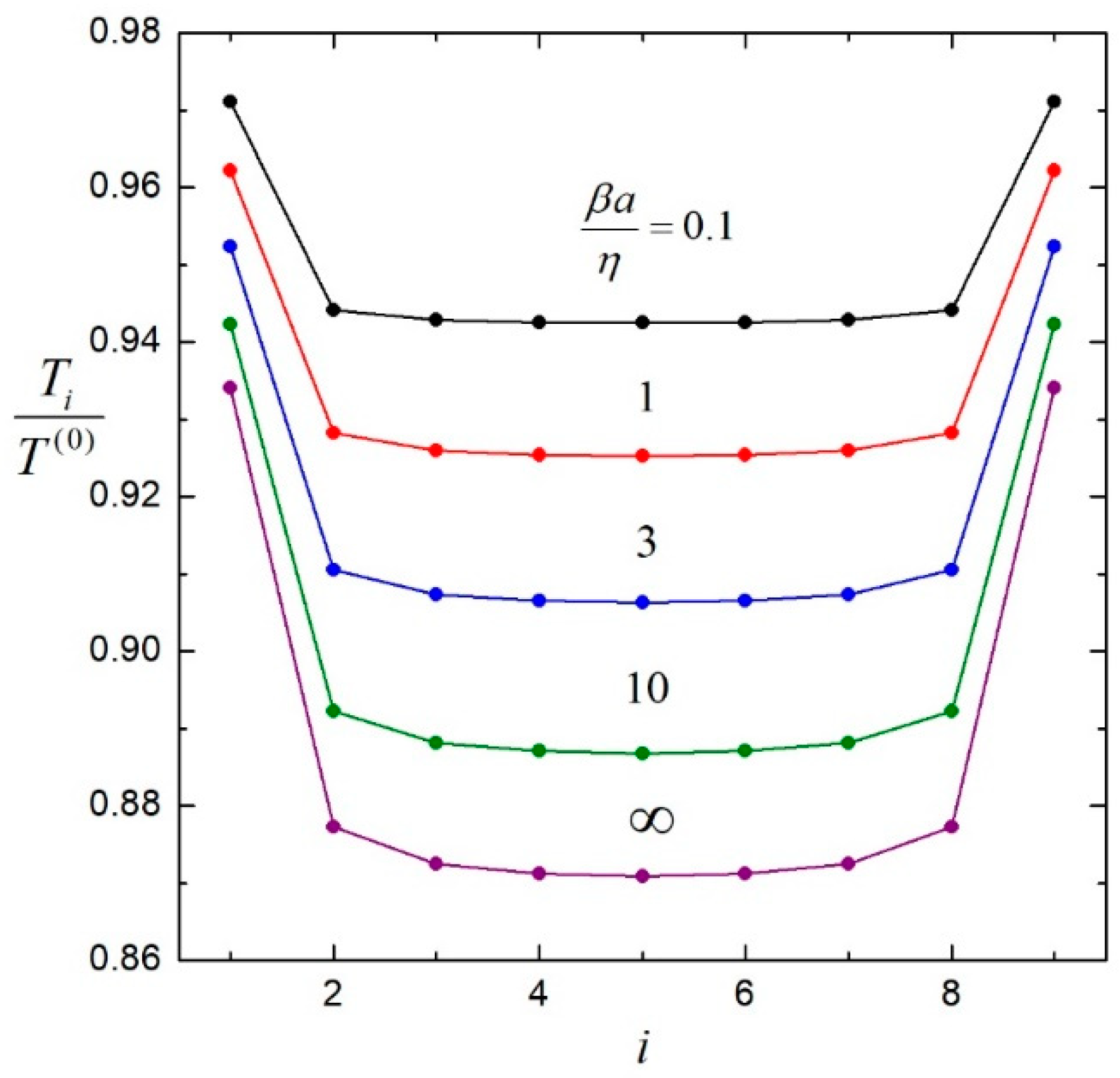
Figure 4 represents a plot of the normalized torques

T_{i}^{} / T_{}^{(0)}

versus the particle number

i

for a chain of nine identical and equally spaced slip particles with

2 a / d = 0.8

rotating with equal angular velocities at different values of the stickiness parameter

β a / η

. These results show that as

β a / η

increases, the torque on each particle in the chain decreases. Particle interactions are strictest for no-slip particle chains and weaker for corresponding more slippery particle chains.

To examine the effect of particle spacing, the normalized torques

T_{i}^{} / T_{}^{(0)}

versus the particle number

i

are plotted in Figure 5 for the chain containing nine identical and equally spaced particles rotating at equal angular velocities with

2 a / d

as a parameter. Both the case of no-slip (

β a / η \to \infty

) particle chains and a case of partly slip (with

β a / η = 1

) particle chains are shown. The results in this figure illustrate that end effects decrease with increasing spacing (decreasing

2 a / d

). As expected, the torque of each particle in the chain decreases as the particles get closer together.

5. Concluding Remarks

The slow rotation of a straight chain of multiple slip spheres about their line of centers in a Newtonian fluid is analyzed in this article. The spheres may vary in radius, slip coefficient, and angular velocity, and they are permitted to be unevenly spaced. The boundary collocation method has been employed to obtain the fluid velocity field semi-analytically. The solutions of the hydrodynamic torques exerted on the particles can be obtained even when the number of particles is large and the particles touch one another. Section 2 presents the linear algebraic collocation formulations for solving the general axisymmetric problem of multi-sphere rotations, and numerical results of the torques for two-sphere, three-sphere, and multi-sphere systems to correct Eq. (1) are given in Section 3 and Section 4. The interaction effects among the particles are found to be noteworthy under appropriate conditions.

The results for the resistance problem are presented in previous sections, in which the hydrodynamic torques

T_{i}

experienced by a chain of particles are calculated for specified angular velocities

Ω_{i}

according to Eqs. (11) and (12). In a mobility problem, on the other hand, the applied torques on the particles are specified and the resultant angular velocities need to be determined. For the axisymmetric rotation of

N

slip spheres, the angular velocity of particle

i

can be expressed as

Ω_{i} = \sum_{j = 1}^{N} m_{i j} Ω_{j 0}, i = 1, 2, \dots, and N,

(22)

with

Ω_{j 0} = - \frac{β_{j} a_{j} + 3 η}{8 π η a_{j}^{3} β_{j} a_{j}} T_{j},

(23)

which is the angular velocity of particle

j

subject to an applied torque

- T_{j}

in the absence of the other particles, and the mobility parameters

m_{i j}

are functions of the scaled radii, separation distances, and surface slippages of the particles. For the case of two particles (

N = 2

), one can use Eqs. (11), (12), (22), and (23) to obtain

m_{11} = {(g_{11} - g_{12} g_{21} / g_{22})}^{- 1},

(24)

m_{12} = {(\frac{a_{2}}{a_{1}})}^{3} \frac{β_{2} a_{2} (β_{1} a_{1} + 3 η)}{β_{1} a_{1} (β_{2} a_{2} + 3 η)} {(g_{21} - g_{11} g_{22} / g_{12})}^{- 1},

(25)

where the corresponding expressions for

m_{22}

and

m_{21}

can be determined from the previous formulas by interchanging subscripts 1 and 2. The mobility parameters

m_{11}

m_{12}

m_{21}

, and

m_{22}

can thus be calculated from using the torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

obtained in Section 3 for its resistance problem.

Author Contributions

Conceptualization, H.J.K.; methodology, H.J.K. and M.J.T.; investigation, H.J.K. and M.J.T.; writing—original draft preparation, H.J.K. and M.J.T.; writing—review and editing, H.J.K.; supervision, H.J.K.; funding acquisition, H.J.K. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by the Ministry of Science and Technology, Taiwan (Republic of China) grant number MOST 110-2221-E-002-017-MY3.

Data Availability Statement

Not applicable.

Conflicts of Interest

The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.

References

Stokes, G.G. On the theories of the internal friction of fluids in motion and of the equilibrium and motion of elastic solids. Trans. Camb. Phil. Soc. 1845, 8, 287-319.
Stokes, G.G. On the effect of the internal friction of fluids on the motion of pendulums. Trans. Cambridge Phil. Soc. 1851, 9, 8-106. [CrossRef]
Pit, R.; Hervet, H.; Leger, L. Direct experimental evidence of slip in hexadecane: solid interfaces. Phys. Rev. Lett. 2000, 85, 980-983. [CrossRef]
Tretheway, D.C.; Meinhart, C.D. Apparent fluid slip at hydrophobic microchannel walls. Phys. Fluids 2002, 14, L9-L12. [CrossRef]
Neto, C.; Evans, D.R.; Bonaccurso, E.; Butt, H.J.; Craig, V.S.J. Boundary slip in Newtonian liquids: a review of experimental studies. Rep. Prog Phys. 2005, 68, 2859-2897. [CrossRef]
Choi, C.H.; Ulmanella, U.; Kim, J.; Ho, C.M.; Kim, C.J. Effective slip and friction reduction in nanograted superhydrophobic microchannels. Phys. Fluids 2006, 18, 087105. [CrossRef]
Cottin-Bizonne, C.; Steinberger, A.; Cross, B.; Raccurt, O.; Charlaix, E. Nanohydrodynamics: the intrinsic flow boundary condition on smooth surfaces. Langmuir 2008, 24, 1165-1172. [CrossRef]
Hutchins, D.K.; Harper, M.H.; Felder, R.L. Slip correction measurements for solid spherical particles by modulated dynamic light scattering. Aerosol Sci. Technol. 1995, 22, 202-218. [CrossRef]
Sharipov, F.; Kalempa, D. Velocity slip and temperature jump coefficients for gaseous mixtures. I. Viscous slip coefficient. Phys. Fluids 2003, 15, 1800-1806. [CrossRef]
Myong, R.S.; Reese, J.M.; Barber, R.W.; Emerson, D.R. Velocity slip in microscale cylindrical Couette flow: the Langmuir model. Phys. Fluids 2005, 17, 087105. [CrossRef]
Saffman, P.G. On the boundary condition at the surface of a porous medium. Studies Appl. Math. 1971, 50, 93-101. [CrossRef]
Nir, A. Linear shear flow past a porous particle. Appl. Sci. Res. 1976, 32, 313-325. [CrossRef]
Basset, A.B. A Treatise on Hydrodynamics, vol 2; Deighton, Bell and Co.: Cambridge, UK, 1888. [CrossRef]
Felderhof, B.U. Hydrodynamic interaction between two spheres Physica 1977, 89A, 373-384.
Happel, J.; Brenner, H. Low Reynolds Number Hydrodynamics; Nijhoff: Dordrecht, Netherlands, 1983.
Chang, Y.C.; Keh, H.J. Translation and rotation of slightly deformed colloidal spheres experiencing slip. J. Colloid Interface Sci. 2009, 330, 201-210. [CrossRef]
Loyalka, S.K.; Griffin, J.L. Rotation of non-spherical axi-symmetric particles in the slip regime. J. Aerosol Sci. 1994, 25, 509-525. [CrossRef]
Wan, Y.W.; Keh, H.J. Slow rotation of an axisymmetric slip particle about its axis of revolution. Comp. Mod. Eng. Sci. 2009, 53, 73-93.
Chang, Y.C.; Keh, H.J. Creeping-flow rotation of a slip spheroid about Its axis of revolution. Theor. Comput. Fluid Dyn. 2012, 26, 173-183. [CrossRef]
Yariv, E.; Siegel, M. Rotation of a superhydrophobic cylinder in a viscous liquid. J. Fluid Mech. 2019, 880, R4. [CrossRef]
Tekasakul, P.; Tompson, R.V.; Loyalka, S.K. A numerical study of two coaxial axisymmetric particles undergoing steady equal rotation in the slip regime. Z. Angew. Math. Phys. 1999, 50, 387-403. [CrossRef]
Luo, H.; Pozrikidis, C. Interception of two spheres with slip surfaces in linear Stokes flow. J. Fluid Mech. 2007, 581, 129-156. [CrossRef]
Reed. L.D.; Morrison, F.A. Particle interactions in viscous flow at small values of Knudsen number. J. Aerosol Sci. 1974, 5, 175-89.
Chen, S.H.; Keh, H.J. Axisymmetric motion of two spherical particles with slip surfaces. J. Colloid Interface Sci. 1995, 171, 63-72. [CrossRef]
Keh, H.J. Chen, S.H. Low Reynolds number hydrodynamic interactions in a suspension of spherical particles with slip surfaces. Chem. Eng. Sci. 1997, 52, 1789-1805. [CrossRef]
Saad, E.I. Motion of two spheres translating and rotating through a viscous fluid with slip surfaces. Fluid Dyn. Res. 2012, 44, 055505. [CrossRef]
Gluckman, M.J.; Pfeffer, R.; Weinbaum, S. A new technique for treating multi-particle slow viscous flow: axisymmetric flow past spheres and spheroids. J. Fluid Mech. 1971, 50, 705-740.
Chou, C.Y.; Keh, H.J. Slow rotation of a spherical particle in an eccentric spherical cavity with slip surfaces. Eur. J. Mech. B Fluids 2021, 86, 150-156. [CrossRef]
Chang, C.L.; Keh, H.J. Slow rotation of a soft colloidal sphere normal to two plane walls. Colloids Interfaces 2023, 7, 18. [CrossRef]
Chen, L.S.; Keh, H.J. The slow motion of coaxial droplets along their line of centers. J. Chinese Inst. Chem. Engrs. 1992, 23, 53-66.
Jeffrey, D.J.; Onishi, Y. Calculation of the resistance and mobility functions for two unequal rigid spheres in low-Reynolds-number flow. J. Fluid Mech. 1984, 139, 261-290. [CrossRef]

Figure 1. Geometric sketch for the rotation of a chain of coaxial slip spheres about their axis.

Figure 2. Normalized torques on three coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the separation parameter

2 a / d

with various values of the stickiness parameter

β a / η

: (a) the first (end) sphere; (b) the second (center) sphere. For comparison, the dashed curves are plotted for the torques when only two spheres are present.

Figure 2. Normalized torques on three coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the separation parameter

2 a / d

with various values of the stickiness parameter

β a / η

: (a) the first (end) sphere; (b) the second (center) sphere. For comparison, the dashed curves are plotted for the torques when only two spheres are present.

Figure 3. Normalized torques on

N

coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the sphere number

i

with

2 a / d = 0.8

: (a)

β a / η \to \infty

; (b)

β a / η = 1

Figure 3. Normalized torques on

N

coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the sphere number

i

with

2 a / d = 0.8

: (a)

β a / η \to \infty

; (b)

β a / η = 1

Figure 4. Normalized torques on nine coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the sphere number

i

with

2 a / d = 0.8

and various values of the stickiness parameter

β a / η

Figure 4. Normalized torques on nine coaxial, identical, equally spaced, slip spheres rotating at equal angular velocities about their axis versus the sphere number

i

with

2 a / d = 0.8

and various values of the stickiness parameter

β a / η

Figure 5. Normalized torques on nine coaxial, identical, equally spaced, no-slip spheres (

β a / η \to \infty

, solid curves) and slip spheres (with

β a / η = 1

, dashed curves) rotating at equal angular velocities about their axis versus the sphere number

i

with various values of the separation parameter

2 a / d

Figure 5. Normalized torques on nine coaxial, identical, equally spaced, no-slip spheres (

β a / η \to \infty

, solid curves) and slip spheres (with

β a / η = 1

, dashed curves) rotating at equal angular velocities about their axis versus the sphere number

i

with various values of the separation parameter

2 a / d

Table 1. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two identical spheres (

a_{1} = a_{2} = a

β_{1} = β_{2} = β

). The asymptotic solution is calculated from Eqs. (13)-(19) for comparison.

Table 1. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two identical spheres (

a_{1} = a_{2} = a

β_{1} = β_{2} = β

). The asymptotic solution is calculated from Eqs. (13)-(19) for comparison.

$\frac{β a}{η}$	$\frac{2 a}{d_{12}}$	Collocation solution		Asymptotic solution
$\frac{β a}{η}$	$\frac{2 a}{d_{12}}$	$g_{11} = g_{22}$	$g_{12} = g_{21}$	$g_{11} = g_{22}$	$g_{12} = g_{21}$
1	0.2	1.00000	-0.00033	1.00000	-0.00025
	0.3	1.00000	-0.00123	1.00000	-0.00084
	0.4	1.00001	-0.00322	1.00000	-0.00200
	0.5	1.00006	-0.00691	1.00002	-0.00391
	0.6	1.00023	-0.01306	1.00005	-0.00675
	0.7	1.00079	-0.02260	1.00011	-0.01072
	0.8	1.00247	-0.03676	1.00026	-0.01600
	0.9	1.00738	-0.05761	1.00052	-0.02278
	0.99	1.02224	-0.08900	1.00092	-0.06064
	1.0	1.02693	-0.09567	1.00098	-0.06250
10	0.2	1.00000	-0.00079	1.00000	-0.00077
	0.3	1.00001	-0.00271	1.00001	-0.00260
	0.4	1.00005	-0.00653	1.00004	-0.00615
	0.5	1.00020	-0.01295	1.00014	-0.01202
	0.6	1.00068	-0.02273	1.00043	-0.02077
	0.7	1.00199	-0.03674	1.00109	-0.03298
	0.8	1.00529	-0.05612	1.00242	-0.04923
	0.9	1.01351	-0.08313	1.00491	-0.07010
	0.99	1.03508	-0.12286	1.00870	-0.01971
	1.0	1.04120	-0.13103	1.00925	-0.02031
∞	0.2	1.00000	-0.00100	1.00000	-0.00100
	0.3	1.00001	-0.00338	1.00001	-0.00338
	0.4	1.00007	-0.00800	1.00007	-0.00800
	0.5	1.00030	-0.01563	1.00030	-0.01563
	0.6	1.00097	-0.02704	1.00096	-0.02703
	0.7	1.00273	-0.04306	1.00268	-0.04301
	0.8	1.00702	-0.06485	1.00669	-0.06451
	0.9	1.01727	-0.09494	1.01539	-0.09280
	0.99	1.04336	-0.13974	1.03082	-0.12569
	1.0	1.05097	-0.14943	1.03320	-0.12988

Table 2. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two no-slip spheres (

β_{1} = β_{2} \to \infty

). The values in parentheses are the asymptotic solution calculated from Eqs. (13)-(19) for comparison.

Table 2. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two no-slip spheres (

β_{1} = β_{2} \to \infty

). The values in parentheses are the asymptotic solution calculated from Eqs. (13)-(19) for comparison.

$\frac{a_{2}}{a_{1}}$	$\frac{a_{1} + a_{2}}{d_{12}}$	g₁₁	g₁₂	g₂₁	g₂₂
2	0.5	1.00024	-0.00463	-0.03705	1.00019
	0.5	(1.00024)	(-0.00463)	(-0.03705)	(1.00019)
	0.6	1.00086	-0.00801	-0.06406	1.00058
	0.6	(1.00084)	(-0.00801)	(-0.06406)	(1.00058)
	0.7	1.00271	-0.01275	-0.10197	1.00153
	0.7	(1.00250)	(-0.01273)	(-0.10187)	(1.00152)
	0.8	1.00795	-0.01917	-0.15335	1.00363
	0.8	(1.00673)	(-0.01908)	(-0.15262)	(1.00358)
	0.9	1.02335	-0.02800	-0.22396	1.00809
	0.9	(1.01667)	(-0.02737)	(-0.21897)	(1.00769)
	0.99	1.06197	-0.04126	-0.33012	1.01787
	0.99	(1.03560)	(-0.03691)	(-0.29532)	(1.01444)
	1.0	1.09395	-0.04449	-0.35606	1.02075
	1.0	(1.03861)	(-0.03812)	(-0.30497)	(1.01544)
5	0.5	1.00007	-0.00058	-0.07234	1.00004
	0.5	(1.00007)	(-0.00058)	(-0.07234)	(1.00004)
	0.6	1.00030	-0.00100	-0.12504	1.00013
	0.6	(1.00027)	(-0.00100)	(-0.12503)	(1.00013)
	0.7	1.00110	-0.00159	-0.19873	1.00033
	0.7	(1.00086)	(-0.00159)	(-0.19862)	(1.00033)
	0.8	1.00412	-0.00238	-0.29764	1.00074
	0.8	(1.00247)	(-0.00237)	(-0.29679)	(1.00074)
	0.9	1.01743	-0.00344	-0.43050	1.00156
	0.9	(1.00653)	(-0.00339)	(-0.42353)	(1.00152)
	0.99	1.09830	-0.00508	-0.63487	1.00318
	0.99	(1.01468)	(-0.00453)	(-0.56594)	(1.00274)
	1.0	1.14324	-0.00556	-0.69390	1.00368
	1.0	(1.01601)	(-0.00467)	(-0.58361)	(1.00291)

Table 3. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two spheres differing in size or slippage.

Table 3. The torque correction parameters

g_{11}

g_{12}

g_{21}

, and

g_{22}

for the axisymmetric rotation of two spheres differing in size or slippage.

$\frac{a_{1} + a_{2}}{d_{12}}$	$g_{11}$	$g_{12}$	$g_{21}$	$g_{22}$
$a_{2} / a_{1} = 1$ , $β_{1} a_{1} / η = 1$ , $β_{2} \to \infty$
0.2	1.00000	-0.00033	-0.00100	1.00000
0.3	1.00000	-0.00123	-0.00338	1.00000
0.4	1.00003	-0.00322	-0.00800	1.00003
0.5	1.00014	-0.00691	-0.01563	1.00013
0.6	1.00049	-0.01307	-0.02702	1.00046
0.7	1.00155	-0.02263	-0.04298	1.00140
0.8	1.00449	-0.03688	-0.06453	1.00387
0.9	1.01258	-0.05814	-0.09382	1.01021
0.99	1.03642	-0.09147	-0.13622	1.02710
1.0	1.04514	-0.09962	-0.14624	1.03280
$a_{2} / a_{1} = 2$ , $β_{1} a_{1} / η = 3$ , $β_{2} = β_{1}$
0.2	1.00000	-0.00016	-0.00169	1.00000
0.3	1.00000	-0.00055	-0.00588	1.00000
0.4	1.00002	-0.00134	-0.01438	1.00002
0.5	1.00011	-0.00271	-0.02901	1.00009
0.6	1.00042	-0.00482	-0.05184	1.00028
0.7	1.00143	-0.00788	-0.08532	1.00079
0.8	1.00459	-0.01216	-0.13272	1.00201
0.9	1.01496	-0.01813	-0.20015	1.00479
0.99	1.05306	-0.02690	-0.30147	1.01124
1.0	1.06789	-0.02888	-0.32475	1.01311

Table 4. The torque correction parameters for the axisymmetric rotation of three identical slip spheres (

a_{1} = a_{2} = a_{3} = a

and

β_{1} = β_{2} = β_{3} = β

) with equal spacings (

d_{23} = d_{12} = d

Table 4. The torque correction parameters for the axisymmetric rotation of three identical slip spheres (

a_{1} = a_{2} = a_{3} = a

and

β_{1} = β_{2} = β_{3} = β

) with equal spacings (

d_{23} = d_{12} = d

$β a / η$	$\frac{2 a}{d}$	$g_{22}$	$g_{11} = g_{33}$	$\begin{array}{l} g_{12} = g_{32} \\ = g_{21} = g_{23} \end{array}$	$g_{13} = g_{31}$
1	0.2	1.00000	1.00000	-0.00033	-0.00004
	0.3	1.00000	1.00000	-0.00123	-0.00013
	0.4	1.00002	1.00001	-0.00322	-0.00032
	0.5	1.00012	1.00006	-0.00691	-0.00063
	0.6	1.00046	1.00023	-0.01305	-0.00110
	0.7	1.00158	1.00080	-0.02256	-0.00171
	0.8	1.00493	1.00247	-0.03666	-0.00244
	0.9	1.01473	1.00739	-0.05740	-0.00322
	0.99	1.04441	1.02225	-0.08866	-0.00392
	1.0	1.05330	1.02724	-0.09501	-0.00399
10	0.2	1.00000	1.00000	-0.00079	-0.00010
	0.3	1.00002	1.00001	-0.00271	-0.00032
	0.4	1.00010	1.00005	-0.00652	-0.00075
	0.5	1.00040	1.00020	-0.01293	-0.00142
	0.6	1.00136	1.00069	-0.02267	-0.00232
	0.7	1.00396	1.00200	-0.03660	-0.00341
	0.8	1.01054	1.00531	-0.05582	-0.00461
	0.9	1.02693	1.01355	-0.08259	-0.00586
	0.99	1.06996	1.03511	-0.12204	-0.00695
	1.0	1.08354	1.04192	-0.13082	-0.00707
∞	0.2	1.00000	1.00000	-0.00100	-0.00012
	0.3	1.00002	1.00001	-0.00337	-0.00041
	0.4	1.00014	1.00007	-0.00799	-0.00094
	0.5	1.00059	1.00030	-0.01560	-0.00175
	0.6	1.00193	1.00098	-0.02695	-0.00282
	0.7	1.00545	1.00275	-0.04286	-0.00409
	0.8	1.01397	1.00705	-0.06445	-0.00546
	0.9	1.03439	1.01732	-0.09423	-0.00687
	0.99	1.08644	1.04341	-0.13864	-0.00812
	1.0	1.10321	1.05182	-0.14909	-0.00826

Table 5. The torque correction parameters for the axisymmetric rotation of three no-slip spheres (

β_{1} = β_{2} = β_{3} \to \infty

) with

a_{3} = a_{1}

and

d_{23} = d_{12} = d

Table 5. The torque correction parameters for the axisymmetric rotation of three no-slip spheres (

β_{1} = β_{2} = β_{3} \to \infty

) with

a_{3} = a_{1}

and

d_{23} = d_{12} = d

$a_{1} : a_{2} : a_{3}$	$\frac{a_{1} + a_{2}}{d}$	$g_{22}$	$g_{11} = g_{33}$	$g_{12} = g_{32}$	$g_{21} = g_{23}$	$g_{13} = g_{31}$
1:2:1	0.2	1.00000	1.00000	-0.00030	-0.00237	-0.00004
	0.3	1.00002	1.00001	-0.00100	-0.00800	-0.00012
	0.4	1.00009	1.00006	-0.00237	-0.01896	-0.00026
	0.5	1.00037	1.00024	-0.00463	-0.03703	-0.00045
	0.6	1.00116	1.00087	-0.00800	-0.06402	-0.00067
	0.7	1.00306	1.00271	-0.01273	-0.10188	-0.00088
	0.8	1.00726	1.00795	-0.01915	-0.15320	-0.00103
	0.9	1.01616	1.02335	-0.02797	-0.22373	-0.00110
	0.99	1.03572	1.07433	-0.04123	-0.32982	-0.00110
	0.999	1.04058	1.09059	-0.04397	-0.35177	-0.00110
	1.0	1.04136	1.09376	-0.04445	-0.35557	-0.00110
2:1:2	0.2	1.00000	1.00000	-0.00237	-0.00030	-0.00030
	0.3	1.00002	1.00001	-0.00799	-0.00100	-0.00099
	0.4	1.00011	1.00005	-0.01892	-0.00236	-0.00233
	0.5	1.00049	1.00021	-0.03685	-0.00461	-0.00447
	0.6	1.00172	1.00064	-0.06346	-0.00793	-0.00756
	0.7	1.00536	1.00169	-0.10038	-0.01255	-0.01165
	0.8	1.01568	1.00396	-0.14971	-0.01871	-0.01681
	0.9	1.04600	1.00872	-0.21645	-0.02706	-0.02308
	0.99	1.14694	1.01894	-0.31689	-0.03961	-0.02980
	0.999	1.17932	1.02142	-0.33813	-0.04227	-0.03054
	1.0	1.18582	1.02188	-0.34194	-0.04274	-0.03062

Table 6. The torque correction parameters for the axisymmetric rotation of three slip spheres with

β_{1} = β_{2} = β_{3} = β

a_{3} = a_{1}

β a_{2} / η = 1

, and

d_{23} = d_{12} = d

Table 6. The torque correction parameters for the axisymmetric rotation of three slip spheres with

β_{1} = β_{2} = β_{3} = β

a_{3} = a_{1}

β a_{2} / η = 1

, and

d_{23} = d_{12} = d

$a_{1} : a_{2} : a_{3}$	$\frac{a_{1} + a_{2}}{d}$	$g_{22}$	$g_{11} = g_{33}$	$g_{12} = g_{32}$	$g_{21} = g_{23}$	$g_{13} = g_{31}$
1:2:1	0.2	1.00000	1.00000	-0.00006	-0.00083	-0.00001
	0.3	1.00000	1.00000	-0.00023	-0.00322	-0.00002
	0.4	1.00001	1.00001	-0.00061	-0.00865	-0.00006
	0.5	1.00006	1.00004	-0.00133	-0.01896	-0.00011
	0.6	1.00021	1.00017	-0.00254	-0.03657	-0.00017
	0.7	1.00069	1.00067	-0.00442	-0.06463	-0.00024
	0.8	1.00202	1.00254	-0.00720	-0.10748	-0.00030
	0.9	1.00549	1.00977	-0.01125	-0.17256	-0.00033
	0.99	1.01456	1.04047	-0.01731	-0.27461	-0.00030
	0.999	1.01694	1.05118	-0.01849	-0.29502	-0.00030
	1.0	1.01726	1.05328	-0.01864	-0.29841	-0.00030
2:1:2	0.2	1.00000	1.00000	-0.00114	-0.00009	-0.00013
	0.3	1.00000	1.00000	-0.00417	-0.00033	-0.00046
	0.4	1.00002	1.00001	-0.01070	-0.00083	-0.00113
	0.5	1.00011	1.00005	-0.02252	-0.00174	-0.00228
	0.6	1.00047	1.00017	-0.04185	-0.00320	-0.00406
	0.7	1.00175	1.00052	-0.07142	-0.00541	-0.00658
	0.8	1.00619	1.00141	-0.11479	-0.00855	-0.00995
	0.9	1.02229	1.00358	-0.17814	-0.01300	-0.01428
	0.99	1.08748	1.00878	-0.27514	-0.01954	-0.01910
	0.999	1.10984	1.01016	-0.29470	-0.02083	-0.01964
	1.0	1.11423	1.01033	-0.29798	-0.02096	-0.01970

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Slow Rotation of Coaxial Slip Colloidal Spheres about Their Axis

Abstract

1. Introduction

2. Analysis

3. Results for Two Particles

4. Results for Multiple Particles

5. Concluding Remarks

Author Contributions

Funding

Data Availability Statement

Conflicts of Interest

References

MDPI Initiatives

Important Links

Subscribe