Submitted:
05 September 2023
Posted:
06 September 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Structure Concept in Identification Tasks
3. Structural Identification Problem Statement
4. Requirements for Model Structure
5. On SI Difficulties of Static Systems
6. Model order estimation
- Bayesian information criterion or Schwartz criterion [46]where is the maximum likelihood function value for the estimated model;
- Hannan-Quinn Information Criterion [47]where is the squared deviation sum.
- There know modifications of criteria (6) - (9), which are used for the synthesis of various models.
7. System nonlinearity degree
8. LPS structural identification
9. Structural identifiability of systems
- The set provides a solution to the parametric identification problem.
- Input provides an informative framework .
10. Identification and identifiability of Lyapunov exponents
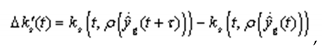
11. Identification of parametric constraints in static systems under uncertainty
12. Approaches to choosing model structure
13. Conclusion
References
- Ljung, L. System identification: Theory for the User. Prentice Hall PTR, 1999.
- Box, G.P.; Jenkins, G.M Time series analysis: Forecasting and control. Holden-Day, 1976.
- Eickhoff P. Fundamentals of identification of control systems. John Wiley and Sons Ltd, 1974.
- Raibman N.S., Chadeev V.M. Construction of models of production processes. Moscow: Energiya, 1975.
- Graupe D. Identification of systems. Litton Educational Co., 1975.
- Kashyap R. Rao A. Dynamic stochastic models from empirical data. New York: Academic Press, 1976.
- Perelman, I.I. Model structure selection Methodology in control objects identification. Automation and telemechanics. 1983, 11, 5–29. [Google Scholar]
- Raibman, N.S. Identification of control objects (Review). Automation and telemechanics. 1978, 6, 80–93. [Google Scholar]
- Giannakis, G.B.; Serpedin, E. A bibliography on nonlinear system identification. Signal Process. 2001, 81, 533–580. [Google Scholar] [CrossRef]
- Ljung L. System Identification Toolbox User’s Guide. Computation. Visualization. Programming. Version 5. The MathWorks Inc., 2000.
- Greene B.R. The fabric of the cosmos: space, time and the texture of reality. New York: Random House, Inc., 2004.
- New Philosophical Encyclopedia: In 4 volumes / Edited by V.S. Stepin. Moscow: Mysl, 2001.
- Mathematical Encyclopedia / Edited by I. M. Vinogradov, vol. 2, D–Koo. Moscow: Soviet Encyclopedia, 1979.
- Besekersky V.A., Popov E.P. Theory of automatic control systems. Third edition, revised. Moscow: Nauka, 1975. N: Moscow, 1975.
- Aho A.V., Hopkroft V., Ulman D.D. Data structures and algorithms. Addison-Wesley, 2004.
- Van Gig J. Applied general systems theory. Harper & Row, 1978.
- Modern Identification Methods. Ed. by P. Eykhoff. John Wiley and Sons 1974.
- Karabutov, N.N. About structures of state systems identification of static object with hysteresis. International journal sensing, computing and control. 2012, 2, 59–69. [Google Scholar]
- Koh C. G., Perry M.J. Structural identification and damage detection using genetic algorithms. CRC Press, 2010.
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.-C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Sirca, G.F., Jr.; Adeli, H. System identification in structural engineering. Sci. Iran. 2012, 19, 1355–1364. [Google Scholar] [CrossRef]
- Karabutov, N. Geometrical Frameworks in Identification Problem. Intell. Control. Autom. 2021, 12, 17–43. [Google Scholar] [CrossRef]
- Isermann R., Münchhof M. Identification of dynamic systems. Springer-Verlag Berlin Heidelberg. 2011. ISBN 978-3-540-78878-2.
- Kuntsevich V.M., Lychak M.M. Synthesis of optimal and adaptive control systems: A game approach. Kiev: Naukova dumka, 1985.
- Karabutov N.N. Structural identification of systems: Analysis of information structures. Мoscow: URSS, 2016.
- Karabutov N.N. Structural identification of static objects: Fields, structures, methods. Moscow: URSS, 2016.
- Karabutov, N. About structures of state systems identification of static object with hysteresis. Int. J. Sensing, Computing and Control. 2012, 2, 59–69. [Google Scholar]
- Mosteller F., Tukey J.W. Data Analysis and Regression: A Second Course in Statistics. Addison-Wesley. 197.
- Boguslavsky I.A. Polynomial approximation for nonlinear estimation and control problems. Moscow: Fizmatlit, 2006.
- Johnston J. Econometric Methods. McGraw-Hill, 197.
- Draper N.R., Smith H. Applied Regression Analysis. John Wiley & Sons. 2014.
- Proceedings of the IX International Conference “System Identification and Control Problems” SICPRO’12 Moscow January 28-31, 2008. V.A. Trapeznikov Institute of Control Sciences. Moscow: V.A. Trapeznikov Institute of Control Sciences. 2012. 28 January.
- Britenkov A.K., Dedus F.F. Prediction of time sequences using a generalized spectral-analytical method. Mathematical modelling. Optimal control. Bulletin of the Nizhny Novgorod University named after N.I. Lobachevsky. 2012; 28-32.
- Marple Jr S. L. Digital spectral analysis: With applications. Prentice-Hall, 1987.
- Prokhorov S.A., Grafkin V.V. Structural and spectral analysis of random processes. Moscow: SNC RAS, 2010.
- Woodside, С.М. Estimation of the order of linear systems. Automatica 1971, 7, 727–733. [Google Scholar] [CrossRef]
- Lee R. Optimal estimation, identification, and control. MIT Press, 1964.
- Jenkins G.M., Watts D.G. Spectral analysis and its applications. Holden-Day, 1969.
- Goldenberg L., Matiushkin B.D., Poliak M. Digital signal processing: Handbook. Moscow: Radio and Communications, 1990.
- Berryman, J.G. Choice of operator length for maximum entropy spectral analysis. Geophysics 1978, 43, 1384–1391. [Google Scholar] [CrossRef]
- Jones, R.H. Autoregression order selection. Geophysics 1976, 41, 771–773. [Google Scholar] [CrossRef]
- Kay S.M. Modern spectral estimation: Theory and application. N. J.: Prentice-Hall, Inc., Englewood Cliffs. 1999. 543 p.
- Kashyap, R.L. Inconsistency of the aic rule for estimation the order of autoregressive models. IEEE Trans. Autom. Control 1980, AC-25, 996–998. [Google Scholar] [CrossRef]
- Hastie T., Tibshirani R., Friedman J. The elements of statistical learning. Springer, 2001.
- Stoica, P.; Selen, Y. Model-order selection: a review of information criterion rules. Signal Processing Magazine. 2004, 21, 36–47. [Google Scholar] [CrossRef]
- Wagenmakers, E.-J. A practical solution to the pervasive problems of p values. Psychonomic Bulletin and Review. 2007, 14, 779–804. [Google Scholar] [CrossRef]
- Hannan, E.J.; Quinn, B.G. The Determination of the Order of an Autoregression. J. R. Stat. Soc. Ser. B (Methodological) 1979, 41, 190–195. [Google Scholar] [CrossRef]
- Dubrovsky A.M., Mkhitaryan V.S., Troshin L.I. Multidimensional statistical methods. M.: Finance and Statistics 200.
- Hamilton J.D. Time Series Analysis. Princeton University Press, 1994. 813 p.
- Malinvaud E. Statistical methods in econometrics. 3d ed. Amsterdam: North-Holland Publishing Co, 1980.
- Almon, S. The Distributed Lag Between Capital Appropriations and Expenditures. Econometrica 1965, 33, 178. [Google Scholar] [CrossRef]
- Karabutov, N. Structures, Fields and Methods of Identification of Nonlinear Static Systems in the Conditions of Uncertainty. Intell. Control. Autom. 2010, 1, 59–67. [Google Scholar] [CrossRef]
- Mehra, R.K. Optimal input signals for parameter estimation in dynamic systems. A survey and new results. IEEE Trans. Automatic Control 1974, AC-19, 753–768. [Google Scholar] [CrossRef]
- Soderstrom, T. Comments on “Order assumption and singularity of information matrix for pulse transfer function models”. IEEE Trans. Autom. Control 1975, 20, 445–447. [Google Scholar] [CrossRef]
- Stoica, P.; Söderström, T. On non-singular information matrices and local identifiability. Int. J. Control. 1982, 36, 323–329. [Google Scholar] [CrossRef]
- Young, P.С.; Jakeman, A.J.; McMurtrie, R. An instrumental variable method for model order identification. Automatica. 1980, 16, 281–294. [Google Scholar] [CrossRef]
- Karabutov N.N. Introduction to the structural identifiability of nonlinear systems. Moscow: URSS/LENAND, 2021.
- Karabutov N.N. Adaptive identification of systems: Information synthesis. Moscow: URSS, 2016.
- Raibman, N.S.; Terekhin, A.T. Dispersion methods of random functions and their application for the study of nonlinear control objects. Automation Telemechanics 1965, 26, 500–509. [Google Scholar]
- Billings S.A. Structure Detection and Model Validity Tests in the Identification of Nonlinear Systems. Research Report. ACSE Report 196. Department of Control Engineering, University of Sheffield, 1982. [CrossRef]
- Haber, R. Nonlinearity Tests for Dynamic Processes. IFAC Proc. Vol. 1985, 18, 409–414. [Google Scholar] [CrossRef]
- Hosseini, S.M.; Johansen, T.A.; Fatehi, A. Comparison of nonlinearity measures based on time series analysis for nonlinearity detection. Modeling Identification and Control 2011, 32, 123–140. [Google Scholar] [CrossRef]
- Malinvaud E. Méthodes statistiques de l’économétrie. Deuxième édition. London-Paris, 1969.
- Demetriou, I.C.; Vassiliou, E.E. An algorithm for distributed lag estimation subject to piecewise monotonic coefficients. International Journal of Applied Mathematics 2009, 39, 1–10. [Google Scholar]
- Dhrymes P.J. Distributed Lags: Problems of estimation and formulation. San Francisco: Holden-Day, 1971.
- Gershenfeld N. The Nature of Mathematical Modelling. Cambridge: Cambridge University Press, 1999.
- Linear Least-Squares Estimation, Stroudsburg / Ed. Kailath T. Pennsylvania: Dowden, Hutchinson and Ross, Inc., 1977.
- Armstrong, B. Models for the relationship between ambient temperature and daily mortality. Epidemiology. 2006, 17, 624–631. [Google Scholar] [CrossRef]
- Nelson, C.R.; Schwert, G.W. Estimating the parameters of a distributed lag model from cross-section data: The Case of hospital admissions and discharges. Journal of the American Statistical Association 1974, 69, 627–633. [Google Scholar] [CrossRef]
- Gasparrini, A.; Armstrong, B.; Kenward, M.G. Distributed lag non-linear models. Stat. Med. 2010, 29, 2224–2234. [Google Scholar] [CrossRef]
- Karabutov, N.; Moscow, R. System with Distributed Lag: Adaptive Identification and Prediction. Int. J. Intell. Syst. Appl. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Fisher, I. Note on a Short-cut Method for Calculating Distributed Lags. Bulletin de l’Institut International de Statistique 1937, 29. [Google Scholar]
- Кoуск L.M. Distributed Lags and Investment Analysis. North-Holland Publishing Company, 1954.
- Solow, R. On a family of lag distributions. Econometrica. 1960, 28, 393–406. [Google Scholar] [CrossRef]
- Theil, H.; Stern, R.M. A simple unimodal lag distribution. Metroeconomica 1960, 12, 111–119. [Google Scholar] [CrossRef]
- Jorgenson, D.W. Minimum variance, linear, unbiased seasonal adjustment of economic time series. Journal of the American Statistical Association 1964, 59, 681–724. [Google Scholar] [CrossRef]
- Demetriou I.C., Vassiliou E. E. A distributed lag estimator with piecewise monotonic coefficients. Proceedings of the World Congress on Engineering. 2008. V. 2. WCE 2008, July 2 - 4, 2008, London, U.K. 2008. 2 July.
- Yoder J. Autoregressive distributed lag models. WSU Econometrics II. 2007;91-115.
- Karabutov, N. Structural identification of systems with distributed lag. International journal of intelligent systems and applications. 2013, 5, 1–10. [Google Scholar] [CrossRef]
- Karabutov, N. Structural Identification of Static Systems with Distributed Lags. Int. J. Control. Sci. Eng. 2012, 2, 136–142. [Google Scholar] [CrossRef]
- Kalman R., Falb P.L., Arbib M.A. Topics in mathematical system theory. McGraw-Hill, 1969.
- Aguirregabiria V., Mira P. Dynamic Discrete Choice Structural Models: A Survey. Working Paper 297. University of Toronto, 2007.
- Elgerd O.I. Control Systems Theory, New York: McGraw-Hill, 1967.
- Walter E. Identifiability of state space models. Berlin. Germany: Springer-Verlag. 1982. [CrossRef]
- Audoly, S.; D’Angio, L.; Saccomani, M.; Cobelli, C. Global identifiability of linear compartmental models-a computer algebra algorithm. IEEE Trans. Biomed. Eng. 1998, 45, 36–47. [Google Scholar] [CrossRef]
- Avdeenko, T.V. Identification of linear dynamical systems using concept of parametric space separators. Automation and Software Engineering 2013, 1, 16–23. [Google Scholar]
- Bodunov, N.A. Introduction to theory of local parametric identifiability. Differential Equations and Control Processes 2012, 1–137. [Google Scholar]
- Balonin, N.A. Identifiability theorems. St. Petersburg: Publishing house "Polytechnic", 2010.
- Handbook of the theory of automatic control. Edited by A. A. Krasovsky. Moscow: Nauka, 1987.
- Stigter J.D., Peeters R.L.M. On a geometric approach to the structural identifiability problem and its application in a water quality case study. Proceedings of the European Control Conference 2007 Kos, Greece, July 2-5, 2007. 2007; 3450-3456.
- Chis, O.-T.; Banga, J.R.; Balsa-Canto, E. Structural Identifiability of Systems Biology Models: A Critical Comparison of Methods. PLOS ONE 2011, 6, e27755. [Google Scholar] [CrossRef]
- Saccomani M.P., Thomaseth K. Structural vs practical identifiability of nonlinear differential equation models in systems biology. Bringing mathematics to life. In: Dynamics of mathematical models in biology. Ed. A. Rogato, V. Zazzu, M. Guarracino. Springer. 2010; 31-42.
- Ayvazyan S.A. (ed.), Enyukov I.S., Meshalkin L.D. Applied Statistics: Dependency Research. Reference edition, Moscow: Finansy i Statistika, 1985.
- Karabutov, N. Structural identification of dynamic systems with hysteresis. International journal of intelligent systems and applications. 2016, 8, 1–13. [Google Scholar] [CrossRef]
- Karabutov N. Structural methods of design identification systems. Nonlinearity problems, solutions and applications. V. 1. Ed. L.A. Uvarova, A. B. Nadykto, A.V. Latyshev. New York: Nova Science Publishers, Inc. 2017;233-274.
- Karabutov, N. Structural identification of nonlinear dynamic systems. International Journal of Intelligent Systems and Applications 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Thamilmaran, K.; Senthilkumar, D.V.; Venkatesan, A.; Lakshmanan, M. Experimental realization of strange nonchaotic attractors in a quasiperiodically forced electronic circuit. Phys. Rev. E 2006, 74, 036205. [Google Scholar] [CrossRef] [PubMed]
- Porcher, R.; Thomas, G. Estimating Lyapunov exponents in biomedical time series. Phys. Rev. E 2001, 64, 010902. [Google Scholar] [CrossRef] [PubMed]
- Hołyst, J.A.; Urbanowicz, K. Chaos control in economical model by time-delayed feedback method. Physica A: Statistical Mechanics and Its Applications. 2000, 287, 587–598. [Google Scholar] [CrossRef]
- Macek, W.M.; Redaelli, S. Estimation of the entropy of the solar wind flow. Phys. Rev. E 2000, 62, 6496–6504. [Google Scholar] [CrossRef]
- Skokos, C. The Lyapunov Characteristic Exponents and Their Computation. Lect. Notes Phys. 2010, 790, 63–135. [Google Scholar]
- Gencay, R.; Dechert, W.D. An algorithm for the n Lyapunov exponents of an n-dimensional unknown dynamical system. Physica D. 1992, 59, 142–157. [Google Scholar] [CrossRef]
- Takens F. Detecting strange attractors in turbulence. Dynamical Systems and Turbulence. Lecture Notes in Mathematics /Eds D. A. Rand, L.-S. Young. Berlin: Springer-Verlag, 1980; 898;366–381.
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets Source. Physica D. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Bespalov, A.V.; Polyakhov, N.D. Comparative analysis of methods for estimating first Lyapunov exponent. Modern Problems of Science and Education 2016, 6. [Google Scholar]
- Golovko V.A. Neural network methods of processing chaotic processes. In: Scientific session of MEPhI-2005. VII All-Russian Scientific and Technical Conference "Neuro-Informatics-2005": Lectures on neuroinformatics. Moscow: MIPhI, 2005; 43-88.
- Perederiy, Y.A. Method for calculation of lyapunov exponents spectrum from data series. Izvestiya VUZ Applied Nonlinear Dynamics 2012, 20, 99–104. [Google Scholar]
- Benettin, G.; Galgani, L.; Giorgilli, A.; Strelcyn, J.-M. Lyapunov characteristic exponents for smooth dynamical systems and for Hamiltonian systems; a method for computing all of them. Part. I: Theory. Pt. II: Numerical applications. Meccanica 1980, 15, 9–30. [Google Scholar] [CrossRef]
- Lyapunov A. M. General problem of motion stability. CRC Press, 1992.
- Dieci, L.; Russell, R.D.; Van Vleck, E.S. On the Compuation of Lyapunov Exponents for Continuous Dynamical Systems. SIAM J. Numer. Anal. 1997, 34, 402–423. [Google Scholar] [CrossRef]
- Filatov, V.V. Structural characteristics of anomalies of geophysical fields and their use in forecasting. Geophysics Geophysical Instrumentation 2013, 4, 34–41. [Google Scholar]
- Bylov, F., Vinograd, R.E., Grobman, D.M. and Nemytskii, V.V. Theory of Lyapunov exponents and its application to problems of stability. Moscow: Nauka, 1966.
- Karabutov, N. Structural Methods of Estimation Lyapunov Exponents Linear Dynamic System. Int. J. Intell. Syst. Appl. 2015, 7, 1–11. [Google Scholar] [CrossRef]
- Karabutov N.N. Structures in identification problems: Construction and analysis. Moscow: URSS. 20.
- Karabutov, N.N. Identifi ability and Detectability of Lyapunov Exponents for Linear Dynamical Systems. Mekhatronika, Avtom. Upr. 2022, 23, 339–350. [Google Scholar] [CrossRef]
- Karabutov N. Chapter 9. Identifiability and Detectability of Lyapunov Exponents in Robotics. In: Design and Control Advances in Robotics/ Ed. Mohamed Arezk Mellal. IGI Globalss Publisher of Timely Knowledge. 2023;152-174.
- Gagliardini P., Gouriéroux C., Renault E. Efficient Derivative Pricing by Extended Method of Moments. National Centre of Competence in Research Financial Valuation and Risk Management, 2005.
- Rossi, B. Optimal tests for nested model selection with underlying parameter instability. Econ. Theory 2005, 21, 962–990. [Google Scholar] [CrossRef]
- Giacomini R., Rossi B. Model comparisons in unstable environments. ERID Working Paper 30, Duke. 2009. [CrossRef]
- Magnusson L., Mavroeidis S. Identification using stability restrictions. 2012. Available online: http://econ.sciences-po.fr/sites/default/files/SCident32s.pdf.
- Bardsley J.M. A Bound-Constrained Levenburg-Marquardt Algorithm for a Parameter Identification Problem in Electromagnetics, 2004. Available online: http://www.math.umt.edu/bardsley/papers/EMopt04.pdf.
- Palanthandalam-Madapusia, H.J.; van Peltb, T.H.; Bernstein, D.S. Parameter consistency and quadratically constrained errors-in-variables least-squares identification. International Journal of Control 2010, 83, 862–877. [Google Scholar] [CrossRef]
- Van Pelt T.H., Bernstein D.S. Quadratically constrained least squares identification. Proceedings of the American Control Conference, Arlington, VA June 25-27. 2001. 2001;3684-3689. [CrossRef]
- Correa, M.; Aguirre, L.; Saldanha, R. Using steady-state prior knowledge to constrain parameter estimates in nonlinear system identification. IEEE Trans. Circuits Syst. I Regul. Pap. 2002, 49, 1376–1381. [Google Scholar] [CrossRef]
- Chadeev V.М., Gusev S.S. Identification with restrictions. determining a static plant parameters estimate. Proceedings of the VII International Conference “System Identification and Control Problems” SICPRO ‘OS Moscow January 28-31, 2008. V.A. Trapeznikov Institute of Control Sciences. Moscow: V.A. Trapeznikov Institute of Control Sciences. 2012; 261-269.
- Chia, T.L.; Chow, P.C.; Chizeck, H.J. Recursive parameter identification of constrained systems: an application to electrically stimulated muscle. IEEE Trans Biomed Eng. 1991, 38, 429–42. [Google Scholar] [CrossRef]
- Shi, W.-M. Parameter estimation with constraints based on variational method. J. Mar. Sci. Appl. 2010, 9, 105–108. [Google Scholar] [CrossRef]
- Vanli, O.A.; Del Castillo, E. Closed-Loop System Identification for Small Samples with Constraints. Technometrics 2007, 49, 382–394. [Google Scholar] [CrossRef]
- Hametner, C.; Jakubek, S. Nonlinear Identification with Local Model Networks Using GTLS Techniques and Equality Constraints. IEEE Trans. Neural Networks 2011, 22, 1406–1418. [Google Scholar] [CrossRef] [PubMed]
- Mead, J.L. ; Renaut R.A. Least squares problems with inequality constraints as quadratic constraints. Linear Algebra and Its Applications 2010, 432, 1936–1949. [Google Scholar] [CrossRef]
- Mazunin, V.P. ; Dvoinikov D.A. Parametric constraints in nonlinear control systems of mechanisms with elasticity. Electrical engineering 2010, 5, 9–13. [Google Scholar]
- Karabutov, N. Identification of parametrical restrictions in static systems in conditions of uncertainty. International journal of intelligent systems and applications. 2013, 5, 43–54. [Google Scholar] [CrossRef]
- Karabutov, N.N. Structural identification of a static object by processing measurement data. Meas. Tech. 2009, 52, 7–15. [Google Scholar] [CrossRef]
- Gabor, D.; Wiby, W.P.L.; Woodcock, R.A. A universal nonlinear filter, predictor and simulator which optimizes itself by learning processes. Proceedings of the IEEE - Part B: Electronic and Communication Engineering 1961, 108, 422–438. [Google Scholar]
- Ivakhnenko A.G. Long-term forecasting and management of complex systems. Kiev: Technika, 1975.
- Goodman, T.P.; Reswick, J.B. Determination of system characteristics from normal operating records. Trans. ASME 1956, 2, 259–271. [Google Scholar] [CrossRef]
- Parsen, E. Some recent advances in time series modelling. IEEE Trans. Automat. Control 1974, AC-19, 723–730. [Google Scholar] [CrossRef]
- Graupe, D.; Сline, W.K. Derivation of ARMA parameters and orders from pure AR models. Int. J. Syst. ScL. 1975, 10, 101–106. [Google Scholar] [CrossRef]
- Isermann, R.; Baur, U.; Bamberger, W.; Kneppo, P.; Siebert, H. Comparison of six on-line identification and parameter estimation methods. Automatica 1974, 10, 81–103. [Google Scholar] [CrossRef]
- F., Tukey J. Data analysis and regression: A second course in statistics 1st edition. Pearson, 1977.
- Karabutov, N.N. Frameworks application for estimation of Lyapunov exponents for systems with periodic coefficients. Mekhatronika Avtomatizatsiya, Upravlenie. 2020, 21, 3–13, (In Russ.). [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



