Submitted:
06 September 2023
Posted:
07 September 2023
Read the latest preprint version here
Abstract
Keywords:
0. Introduction
1. Loop equation
1.1. Loop operators
1.2. Dimensional reduction
1.3. Random global vorticity
1.4. Decay or fixed point
2. Fractal curve in complex space
2.1. Random walk
2.2. Constraints imposed on a random step
2.3. Closure condition
2.4. Mirror pairs of solutions
2.5. The degenerate fixed point and its statistical meaning
3. Exact analytic solution
3.1. Random walk on a circle
3.2. The Euler ensemble
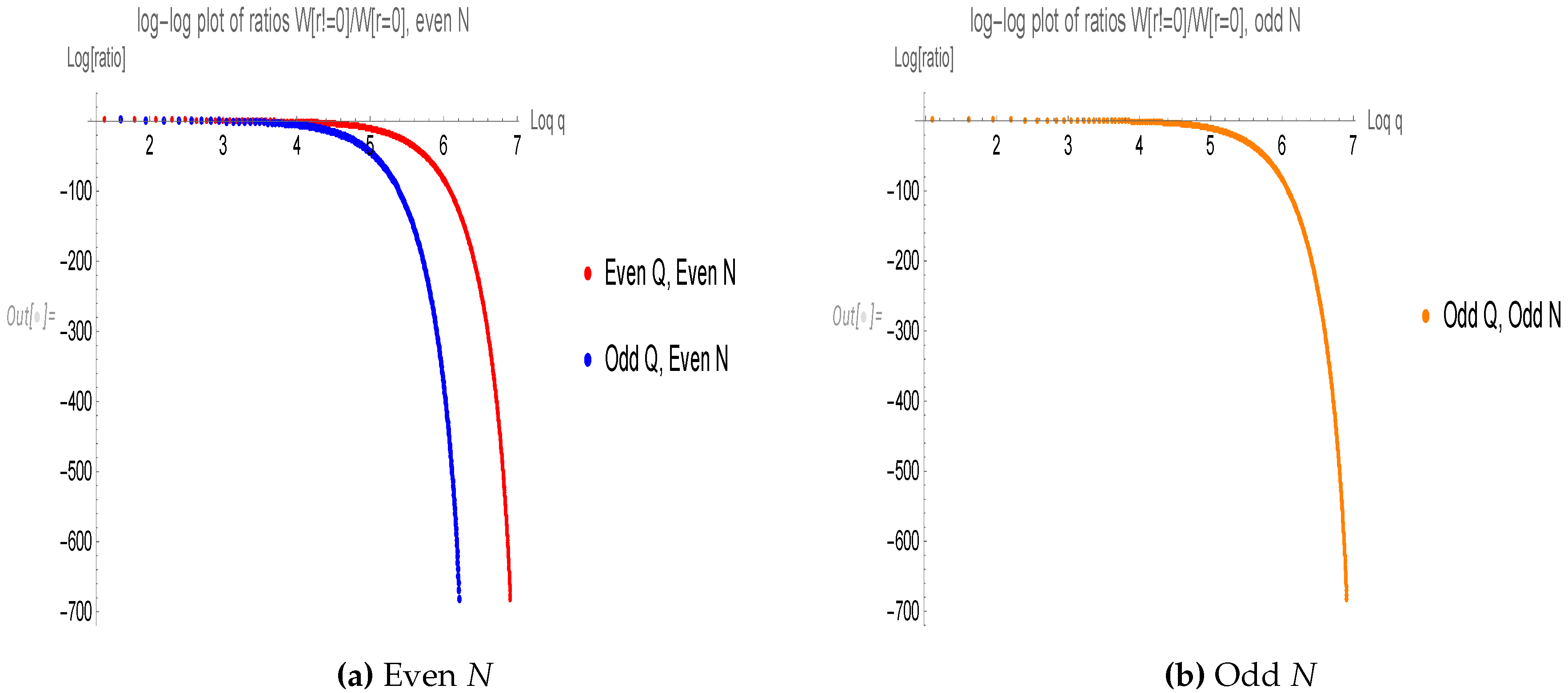
3.3. Grand canonical ensemble
4. Correlation functions
4.1. General formulas
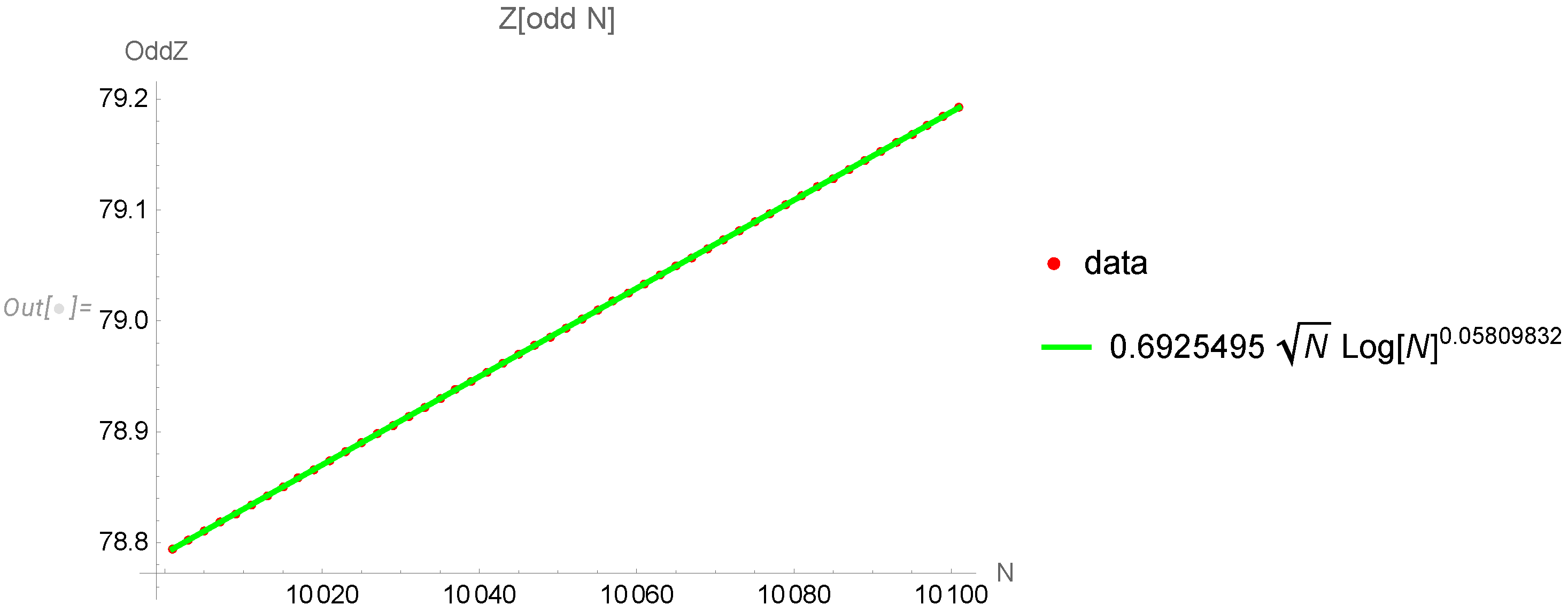
4.2. Critical phenomena in statistical limit
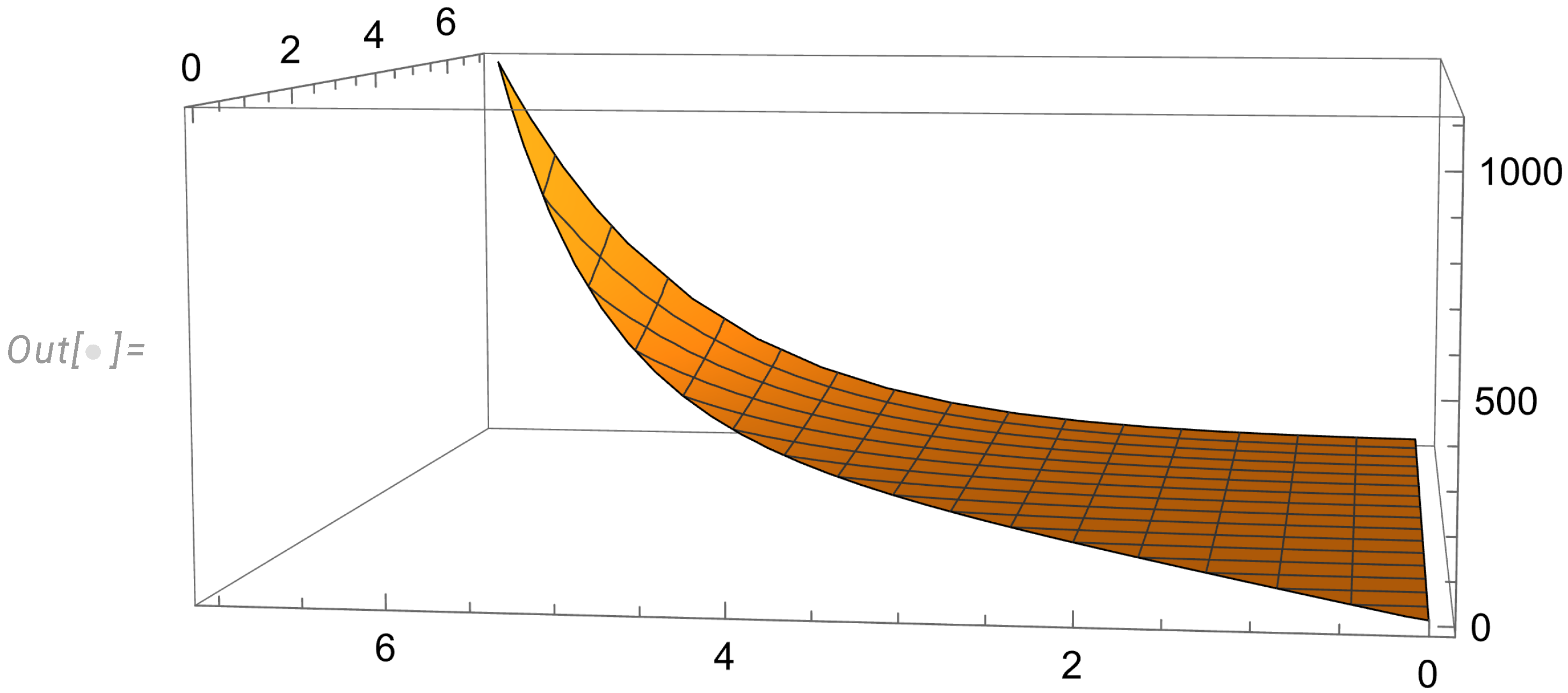
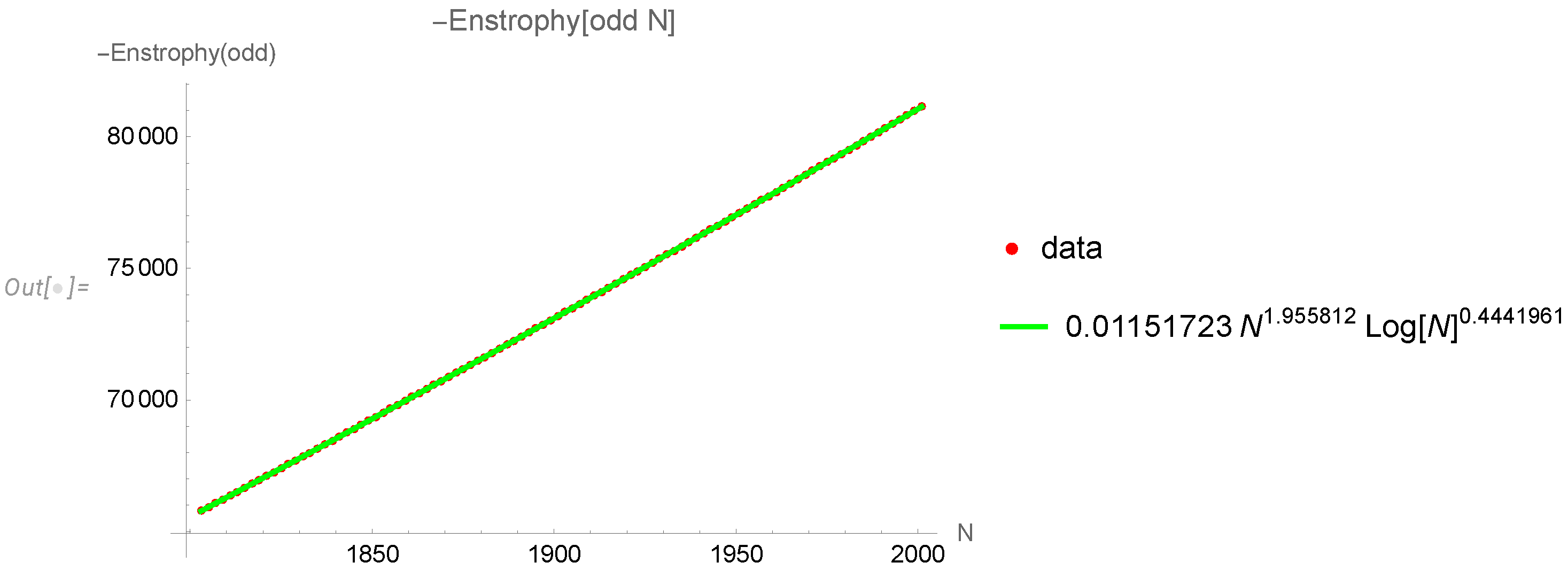
4.3. Analytic solution for the enstrophy
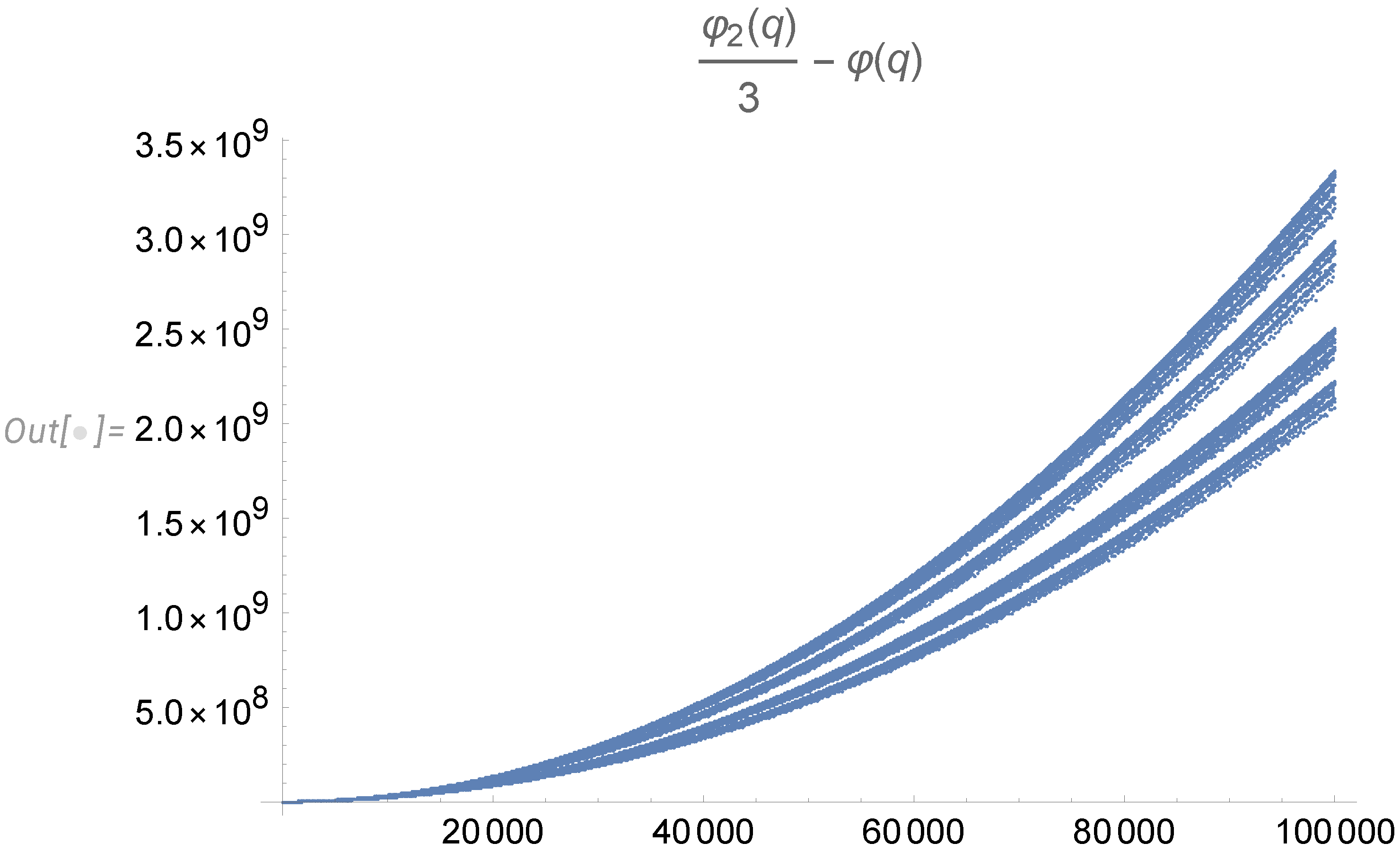
4.4. The local limit of the energy dissipation

4.5. The higher moments of the enstrophy
5. The decay index spectrum
5.1. Linearized loop equation
5.2. The circulation distribution
5.3. The spectral identity and Wilson loop asymptotics
6. Discussion
6.1. The Duality of Turbulence
6.2. Classical flow and quantum geometry
6.3. Stokes-type functionals and vorticity correlations
6.4. Relation of our solution to the weak turbulence
6.5. Continuum spectrum of anomalous dimensions and multifractality
6.6. Conclusion
Data Availability Statement
Acknowledgments
Appendix A Euler averages as multitotient functions
References
- Migdal, A.A. Random Surfaces and Turbulence. Proceedings of the International Workshop on Plasma Theory and Nonlinear and Turbulent Processes in Physics, Kiev, April 1987; Bar’yakhtar, V.G., Ed. World Scientific, 1988, p. 460. 19 April.
- Migdal, A. Loop Equation and Area Law in Turbulence. In Quantum Field Theory and String Theory; Baulieu, L.; Dotsenko, V.; Kazakov, V.; Windey, P., Eds.; Springer US, 1995; pp. 193–231. [CrossRef]
- Makeenko, Y.; Migdal, A. Exact equation for the loop average in multicolor QCD. Physics Letters B 1979, 88, 135–137. [Google Scholar] [CrossRef]
- Migdal, A. Loop equations and 1N expansion. Physics Reports 1983, 201. [Google Scholar] [CrossRef]
- Migdal, A. Momentum loop dynamics and random surfaces in QCD. Nuclear Physics B 1986, 265, 594–614. [Google Scholar] [CrossRef]
- Migdal, A. Second quantization of the Wilson loop. Nuclear Physics B - Proceedings Supplements 1995, 41, 151–183. [Google Scholar] [CrossRef]
- Migdal, A.A. Hidden symmetries of large N QCD. Prog. Theor. Phys. Suppl. 1998, 131, 269–307. [Google Scholar] [CrossRef]
- Anderson, P.D.; Kruczenski, M. Loop equations and bootstrap methods in the lattice. Nuclear Physics B 2017, 921, 702–726. [Google Scholar] [CrossRef]
- Kazakov, V.; Zheng, Z. Bootstrap for lattice Yang-Mills theory. Phys. Rev. D 2023, arXiv:hep-th/2203.11360]107, L051501. [Google Scholar] [CrossRef]
- Ashtekar, A. New variables for classical and quantum gravity. Physical Review Letters 1986, 57, 2244–2247. [Google Scholar] [CrossRef] [PubMed]
- Rovelli, C.; Smolin, L. Knot Theory and Quantum Gravity. Phys. Rev. Lett. 1988, 61, 1155–1158. [Google Scholar] [CrossRef] [PubMed]
- Iyer, K.P.; Sreenivasan, K.R.; Yeung, P.K. Circulation in High Reynolds Number Isotropic Turbulence is a Bifractal. Phys. Rev. X 2019, 9, 041006. [Google Scholar] [CrossRef]
- Iyer, K.P.; Bharadwaj, S.S.; Sreenivasan, K.R. The area rule for circulation in three-dimensional turbulence. Proceedings of the National Academy of Sciences of the United States of America 2021, 118, e2114679118. [Google Scholar] [CrossRef] [PubMed]
- Apolinario, G.; Moriconi, L.; Pereira, R.; valadão, V. Vortex Gas Modeling of Turbulent Circulation Statistics. PHYSICAL REVIEW E 2020, 102, 041102. [Google Scholar] [CrossRef] [PubMed]
- Müller, N.P.; Polanco, J.I.; Krstulovic, G. Intermittency of Velocity Circulation in Quantum Turbulence. Phys. Rev. X 2021, 11, 011053. [Google Scholar] [CrossRef]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence Turbulence and Predictability. Geophysical Fluid Dynamics: Proc. Intl School of Physics E. Fermi; M Ghil, R.B., Ed.; Parisi, G., Eds. Amsterdam: North-Holland, 1985; pp. 84–88. [Google Scholar]
- Migdal, A. Statistical Equilibrium of Circulating Fluids. Physics Reports 2023, arXiv:physics.flu-dyn/2209.12312]1011C, 1–117. [Google Scholar] [CrossRef]
- Migdal, A. Symmetric Fixed Point. https://www.wolframcloud.com/obj/sasha.migdal/Published/SymmetricFixedPoint.nb, 2023.
- Gross, D.J.; Migdal, A.A. Nonperturbative two-dimensional quantum gravity. Phys. Rev. Lett. 1990, 64, 127–130. [Google Scholar] [CrossRef] [PubMed]
- AGISHTEIN, M.; MIGDAL, A. SIMULATIONS OF FOUR-DIMENSIONAL SIMPLICIAL QUANTUM GRAVITY AS DYNAMICAL TRIANGULATION. Modern Physics Letters A 1992, 07, 1039–1061. [Google Scholar] [CrossRef]
- Wikipedia contributors. Euler’s totient function — Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Euler%27s_totient_function&oldid=1163400966, 2023. [Online; accessed 6-August-2023].
- Migdal, A. Enstrophy Computations. https://www.wolframcloud.com/obj/sasha.migdal/Published/Enstrophy.
- Maxim Bulatov, A.M. Numerical Simulations of Fractal Curve in Decalying Turbulence Theory. to be submitted to Fractal and Fractions.
- Lehmer, D.N. Asymptotic Evaluation of Certain Totient Sums. American Journal of Mathematics 1900, 22, 293–335. [Google Scholar] [CrossRef]
- Migdal, A. Sum Cotangent Squared. https://www.wolframcloud.com/obj/sasha.migdal/Published/TestMultitotients.nb, 2023.
- Migdal, A. Topological Vortexes, Asymptotic Freedom, and Multifractals. MDPI Fractals and Fractional, Special Issue 2023, [arXiv:physics.flu-dyn/2212.13356].
- Migdal, A. Multifractal Spectrum. https://www.wolframcloud.com/obj/sasha.migdal/Published/MultifractalSpectrum.nb, 2023.
- Migdal, A. Corr Function Integrals. https://www.wolframcloud.com/obj/sasha.migdal/Published/CorrFunctionIntegrals.nb, 2023.
- Migdal, A. Analytic Solution for Enstrophy. https://www.wolframcloud.com/obj/sasha.migdal/Published/AnalyticSolutionEnstrophy.nb, 2023.
- Migdal, A. Euler Partition Function. https://www.wolframcloud.com/obj/sasha.migdal/Published/EnstrophyEuler.nb, 2023.
- Wikipedia contributors. Inclusion–exclusion principle — Wikipedia, The Free Encyclopedia. https://en.wikipedia.org/w/index.php?title=Inclusion%E2%80%93exclusion_principle&oldid=1170123427, 2023. [Online; accessed 22-August-2023].
- Franke, J. Rational functions, cotangent sums and Eichler integrals. Research in Number Theory 2021, 7, 23. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).



