The Implied Views of Bond Traders on the Spot Equity Market

1. Introduction

In this paper, we will explore the relationships between a zero-coupon bond’s implied daily return $\mu$, implied natural upturn probability p, and implied daily volatility $\sigma$ and the zero-coupon bond’s time to maturity. Additionally, based on the data visualization, we will obtain a general conclusion, and thus we can give bond traders some suggestions.

First, we will provide the theoretical support of this research, so that readers can understand the foundational theorems that we will use. Additionally, two important ideas are described in the next section: first, we consider a zero-coupon bond as a European contingent claim (ECC), so that we can use the binomial option pricing algorithm to calculate its theoretical fair value, and second, we explain that we cannot just assume that the risk-neutral probability $(\tilde{p},\tilde{q})=(\frac{1}{2},\frac{1}{2})$, since this will lead to an unrealistic natural probability $(p,q)$; a detailed explanation of this can be found in [1]. Thus, we need to calculate the real risk-neutral probability $(\tilde{p},\tilde{q})$ by building an equation that relates the market value of a zero-coupon bond and the theoretical value of the zero-coupon bond.

Second, we will perform empirical research. Before doing this, we will do some preparation—we need to extract the values of the related parameters from the raw data we obtained from the internet. Then, we will follow the form of the Black-Derman-Toy (BDT) model to find new coefficients to calibrate the model. After completing these steps, we can find the implied daily return, implied natural upturn probability, and implied daily volatility with respect to the zero-coupon bond’s time to maturity.

Lastly, we will provide a general conclusion about the three relationships described above and give some suggestions to bond traders.

2. Theoretical Support

2.1. Underlying Asset $\mathcal{S}$

Consider a Black-Scholes-Merton market model consisting of a risky asset $\mathcal{S}$, a riskless bank account $\mathcal{B}$, and an ECC $\mathcal{C}$ that has $\mathcal{S}$ as the underlying asset. We also assume that $t=0$ is the current time and $t=T$ is the terminal time of the ECC.

Now, we will divide the time period $[0,T]$ into N intervals, where $N=\frac{T}{\Delta }$ and $\Delta =\frac{1}{252}$1, so that $0=t_0<t_1<\cdots <t_N=T$. If $S_{t_n}=S_{n\Delta }$2 represents the risky asset’s price at time $t_n$, then based on the binomial model, the randomness of the price $S_{(n+1)\Delta }$ is given by

$$\begin{array}{c}\hfill S_{(n+1)\Delta }=\left\{\begin{array}{cc}{S}_{(n+1)\Delta }^{\left(u\right)}\hfill & =S_{n\Delta }(1+u\Delta )\mathrm{w}.\mathrm{p}.p\in (0,1)\hfill \\ S_{(n+1)\Delta }^{\left(d\right)}\hfill & =S_{n\Delta }(1+d\Delta )\mathrm{w}.\mathrm{p}.1-p\in (0,1)\hfill \end{array}\right..\end{array}$$

(1)

Next, we define the arithmetic stock return in the sub-time period $[n\Delta ,(n+1)\Delta )$:

$$\begin{array}{c}\hfill R_{(n+1)\Delta }=\frac{S_{(n+1)\Delta }-S_{n\Delta }}{S_{n\Delta }}.\end{array}$$

(2)

By combining (2) and (1), we can obtain, for $n=0,1,\cdots ,N-1$,

$$\begin{array}{c}\hfill R_{(n+1)\Delta }=\left\{\begin{array}{cc}u\Delta \hfill & \mathrm{w}.\mathrm{p}.p\in (0,1)\hfill \\ d\Delta \hfill & \mathrm{w}.\mathrm{p}.1-p\in (0,1)\hfill \end{array}\right..\end{array}$$

(3)

Then, we let the mean of $R_{(n+1)\Delta }$ be $\mathbf{E}{R}_{(n+1)\Delta }={\mu }_{(n+1)\Delta }=\mu \Delta$, where $\mu$ is the instantaneous mean return. We let the variance of $R_{(n+1)\Delta }$ be $\mathbf{Var}{R}_{(n+1)\Delta }=\mathbf{E}{\left(R_{(n+1)\Delta }\right)}^2-{\left(\mathbf{E}{R}_{(n+1)\Delta }\right)}^2={\sigma }_{(n+1)\Delta }^2={\sigma }^2\Delta$, where ${\sigma }^2$ is the instantaneous variance. Thus, we will have the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\mu }_{(n+1)\Delta }\hfill & =\mu \Delta =pu\Delta +(1-p)d\Delta \hfill \\ {\sigma }_{(n+1)\Delta }^2\hfill & ={\sigma }^2\Delta ={(u-d)}^{2}p(1-p){\Delta }^2\hfill \end{array}\right..\end{array}$$

(4)

Based on (4),

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}u\hfill & =\mu +\sqrt{\frac{1-p}{p}}\frac{\sigma }{\sqrt{\Delta }}\hfill \\ d\hfill & =\mu -\sqrt{\frac{p}{1-p}}\frac{\sigma }{\sqrt{\Delta }}\hfill \end{array}\right..\end{array}$$

(5)

By combining (4) and (1), we can obtain

$$\begin{array}{c}\hfill S_{(n+1)\Delta }=\left\{\begin{array}{cc}{S}_{(n+1)\Delta }^{\left(u\right)}\hfill & =S_{n\Delta }(1+\mu \Delta +\sqrt{\frac{1-p}{p}}\sigma \sqrt{\Delta })\mathrm{w}.\mathrm{p}.p\in (0,1)\hfill \\ S_{(n+1)\Delta }^{\left(d\right)}\hfill & =S_{n\Delta }(1+\mu \Delta -\sqrt{\frac{p}{1-p}}\sigma \sqrt{\Delta })\mathrm{w}.\mathrm{p}.1-p\in (0,1)\hfill \end{array}\right..\end{array}$$

(6)

Thus, the up factor of the underlying asset $\mathcal{S}$ in the time period $[n\Delta ,(n+1)\Delta )$ is $1+\mu \Delta +\sqrt{\frac{1-p}{p}}\sigma \sqrt{\Delta }$, and the down factor is $1+\mu \Delta -\sqrt{\frac{p}{1-p}}\sigma \sqrt{\Delta }$.

2.2. European contingent claim $\mathcal{C}$

In [2], we can find a basic type of binomial option pricing algorithm. If we let $f_{n\Delta }$ represent the price of the ECC at time $t_n=n\Delta$, then the recursive pricing algorithm will be

$$\begin{array}{c}\hfill f_{n\Delta }=\frac{1}{1+r\Delta }\left(\tilde{p}{f}_{(n+1)\Delta }^{\left(u\right)}+(1-\tilde{p})f_{(n+1)\Delta }^{\left(d\right)}\right),\end{array}$$

(7)

where $f_{(n+1)\Delta }^{\left(u\right)}$ and $f_{(n+1)\Delta }^{\left(d\right)}$ represent two possible prices of the ECC at time $t_{(n+1)}=(n+1)\Delta$, r is the riskless rate, and $\tilde{p}$ is the upturn risk-neutral probability.

In the previous subsection, we do not have any information about the risk-neutral probability, and thus we hope to find a connection between the natural probability and risk-neutral probability. Suppose that we want to construct a riskless portfolio

$$\begin{array}{c}\hfill P_{n\Delta }=D{S}_{n\Delta }-f_{n\Delta }.\end{array}$$

(8)

From [2], we can find that

$$\begin{array}{c}\hfill D=\frac{f_{(n+1)\Delta }^{\left(u\right)}-f_{(n+1)\Delta }^{\left(d\right)}}{S_{(n+1)\Delta }^{\left(u\right)}-S_{(n+1)\Delta }^{\left(d\right)}}=\frac{f_{(n+1)\Delta }^{\left(u\right)}-f_{(n+1)\Delta }^{\left(d\right)}}{S_{n\Delta }\left(\sqrt{\frac{1-p}{p}}+\sqrt{\frac{p}{1-p}}\right)\sigma \sqrt{\Delta }}=\frac{f_{(n+1)\Delta }^{\left(u\right)}-f_{(n+1)\Delta }^{\left(d\right)}}{S_{n\Delta }\sigma \sqrt{\Delta }}\sqrt{p(1-p)}.\end{array}$$

(9)

Then, by combining (8) and (9), we can obtain

$$\begin{array}{c}\hfill f_{n\Delta }=\frac{1}{1+r\Delta }\left((p-\theta \sqrt{p(1-p)\Delta })f_{(n+1)\Delta }^{\left(u\right)}+(1-p+\theta \sqrt{p(1-p)\Delta }{f}_{(n+1)\Delta }^{\left(d\right)}\right),\end{array}$$

(10)

where $\theta =\frac{\mu -r}{\sigma }$.

By combining (10) and (7), we find that the relationship between the natural upturn probability p and risk-neutral upturn probability $\tilde{p}$ is

$$\begin{array}{c}\hfill \tilde{p}=p-\theta \sqrt{p(1-p)\Delta }.\end{array}$$

(11)

Observe that we can consider the zero-coupon bond $B(t,T)$ as a kind of ECC with a final payoff of $1 regardless of the path in the binomial tree.3 Thus, the recursive pricing algorithm for the zero-coupon bond should be

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}B(n\Delta ,T)\hfill & =\frac{1}{1+r\Delta }\left[\tilde{p}B{((n+1)\Delta ,T)}^{\left(u\right)}+(1-\tilde{p})B{((n+1)\Delta ,T)}^{\left(d\right)}\right](n=0,1,\cdots ,N-1)\hfill \\ B(T,T)\hfill & =B(N\Delta ,T)=1\hfill \end{array}\right..\end{array}$$

(12)

3. Empirical Research

3.1. Preparation

The main purpose of this research is to find the implied values of the daily return $\mu$, upturn probability p, and volatility $\sigma$. To do this, we need to build an equation that relates the theoretical value of the zero-coupon bond $B(t,T;\mathrm{Theoretical}\mathrm{Value})$ and the market value of the zero-coupon bond $B(t,T;\mathrm{Market}\mathrm{Value})$ for different time-to-maturity values.

To calculate the market value of the zero-coupon bond, we can use the formula given in [3], where the value of the yield to maturity $Y(t,T)$ satisfies

$$\begin{array}{c}\hfill B(t,T;\mathrm{Market}\mathrm{Value})exp\left\{(T-t)Y(t,T)\right\}=1.\end{array}$$

(13)

Based on (13),

$$\begin{array}{c}\hfill B(t,T;\mathrm{Market}\mathrm{Value})=exp\left\{-(T-t)Y(t,T)\right\},\end{array}$$

(14)

and from (14), we can easily obtain the market values of zero-coupon bonds with different time-to-maturity values since the parameters in (14) can be found on the internet.4

To obtain the theoretical value of the zero-coupon bond, we can use the recursive algorithm in (12). With different time-to-maturity values, we expect to get different values of the risk-neutral upturn probability $\tilde{p}$, and based on (11), the theoretical value can be written as $B(t,T,\mu ,p,\sigma ;\mathrm{Theoretical}\mathrm{Value})$.

To find the implied $\mu$, p, and $\sigma$ values, we should let

$$\begin{array}{c}\hfill B(t,T,\mu ,p,\sigma ;\mathrm{Theoretical}\mathrm{Value})=B(t,T;\mathrm{Market}\mathrm{Value})\end{array}$$

(15)

and fix the other two parameters. In this research, we chose data concerning the SPDR S&P 500 ETF Trust (SPY) from June 16, 2022 to June 16, 2023 (this time period has exactly 252 business days) as a sample.5 The initial estimates for $\mu$, p, and $\sigma$ are ${\widehat{\mu }}_0=8.0037\times {10}^{-4}$, ${\widehat{p}}_0=0.4821$, and ${\widehat{\sigma }}_0=0.0126$, respectively.

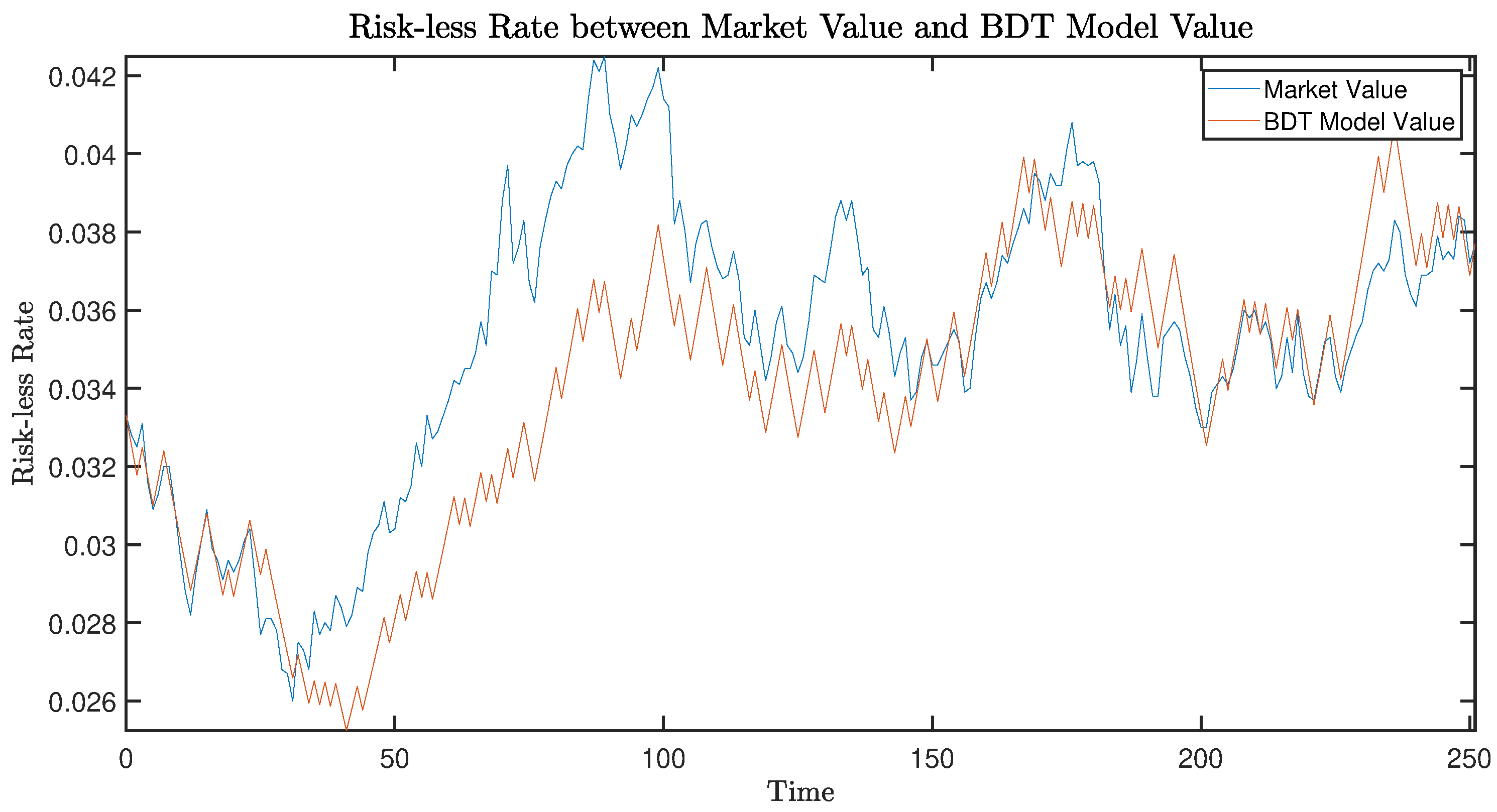
Because we cannot consider the riskless rate r to be constant, especially for a long period of time, we will use the BDT model6 to predict the future riskless rate. In this process, we set June 16, 2023, as the start date and use 252 days of back data7 to find the coefficient sequences $\left\{a_n\right\}$ and $\left\{b_n\right\}$ to calibrate the model. Figure 1 shows the fitting effect of the BDT model.

The mathematical expression of this model, if we consider June 16, 2023, to be the start date, is

$$\begin{array}{c}\hfill R_n({\omega }_1{\omega }_2\cdots {\omega }_n)=a_n·b_n^{\#H({\omega }_1{\omega }_2\cdots {\omega }_n)}=\frac{0.0377}{1.{0236}^n}·1.{0464}^{\#H({\omega }_1{\omega }_2\cdots {\omega }_n)}(n=0,1,\cdots ),\end{array}$$

(16)

where ${\omega }_i\in \{H,T\}$, H indicates that the riskless rate is strictly increasing, T indicates that the riskless rate is decreasing, and $\#H({\omega }_1{\omega }_2\cdots {\omega }_n)$ is the number of periods in which the riskless rate is strictly increasing.

3.2. Data Visualization and Explanation

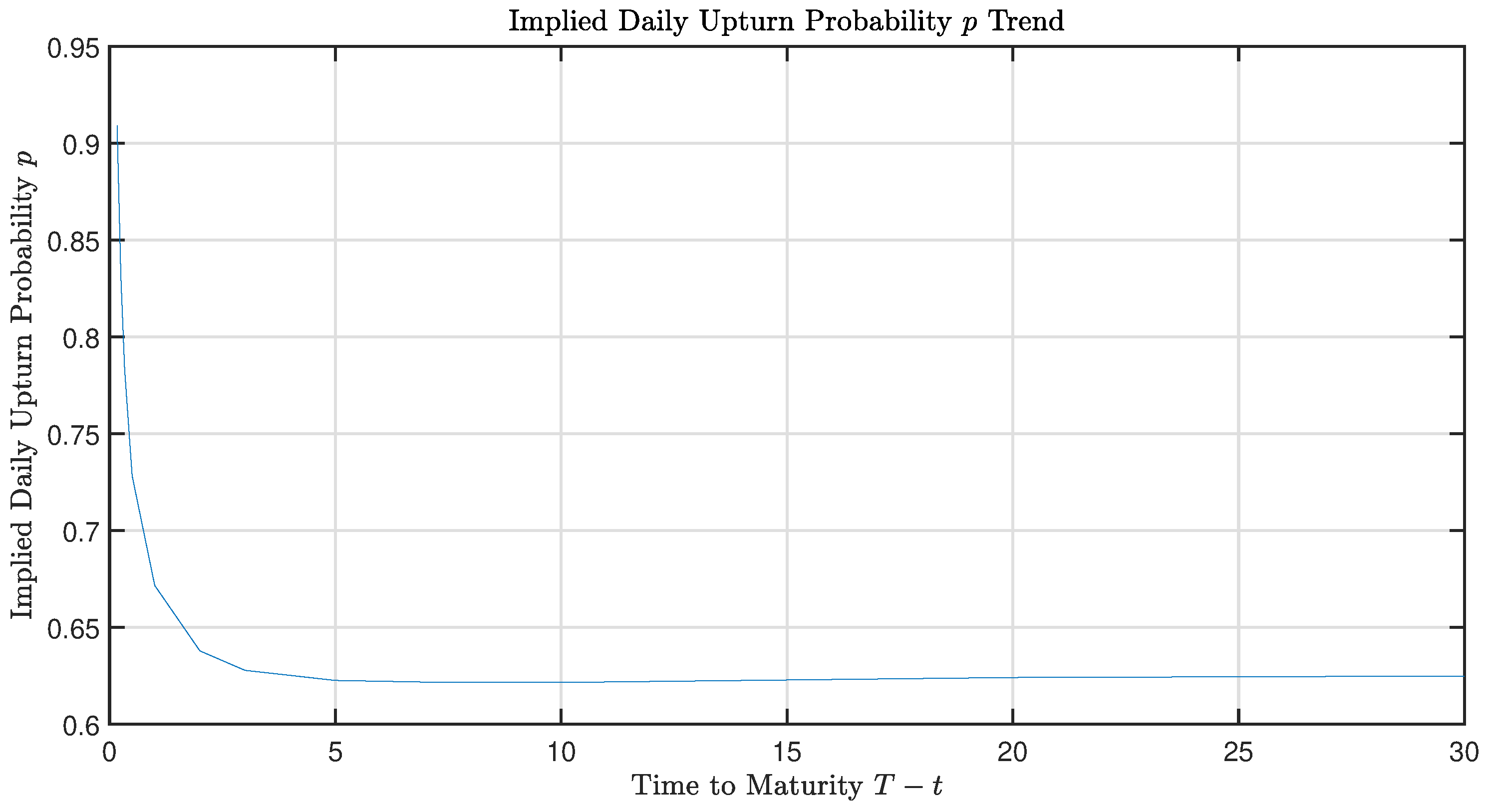
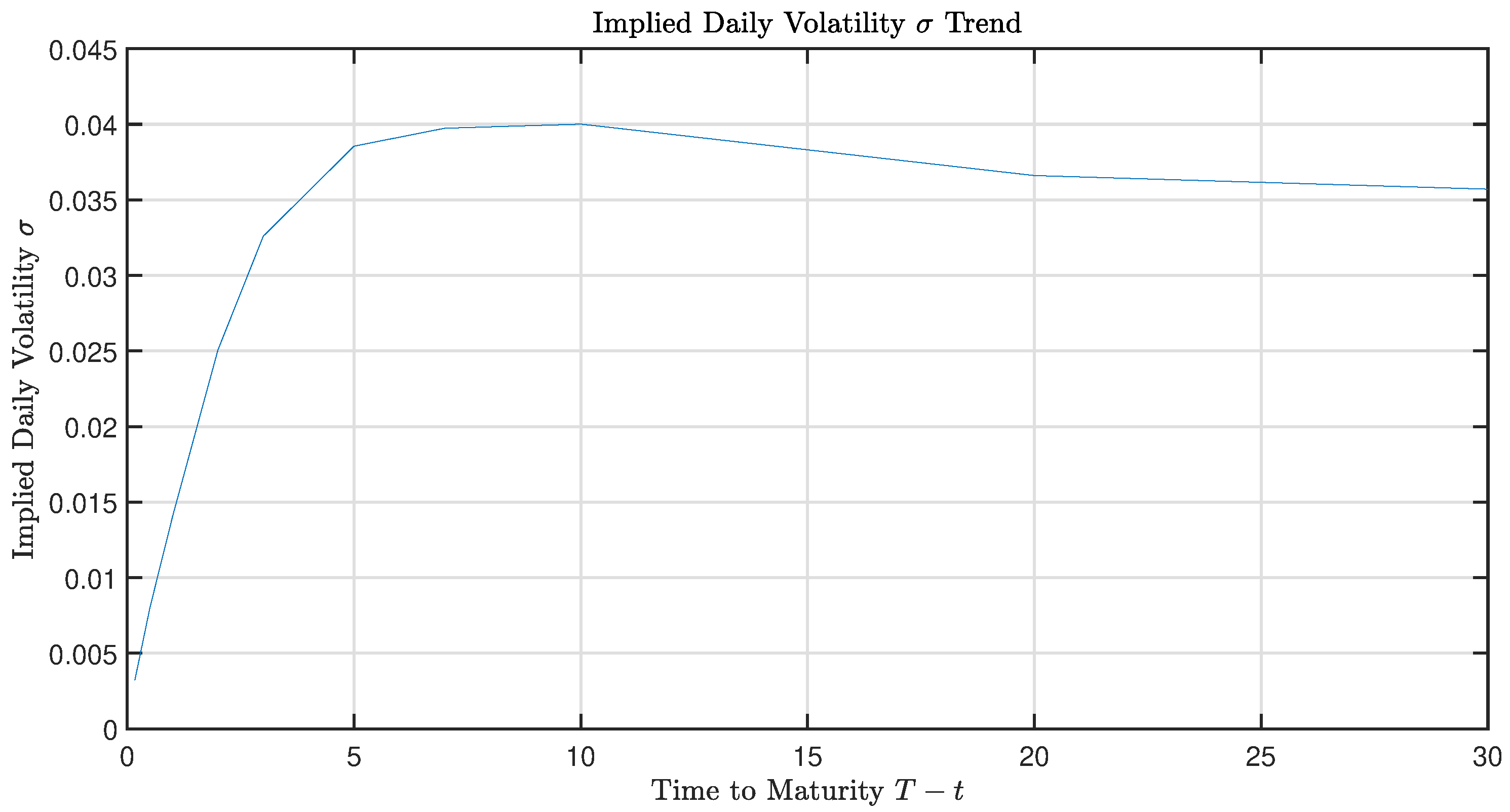
As we have previously stated, we will treat June 16, 2023, as the start date, and we choose different time-to-maturity values8 for the zero-coupon bonds to find the implied $\mu$, p, and $\sigma$ values. Figure 2, Figure 3, and Figure 4 show the implied $\mu$, p, and $\sigma$ values, respectively.

Based on these figures, we can obtain the following observations:

• In Figure 2, we can see that the value of the implied daily return increases sharply at first, from about -0.11, and then it begins to increase more slowly; finally, the value converges to about 0.025.
• In Figure 3, we can see that the value of the implied daily upturn probability decreases sharply at first, from about 0.9, and then it begins to decrease more slowly; finally, the value converges to about 0.62.
• In Figure 4, we can see that the daily volatility will increase at first and attain its peak value of 0.04 in year 10; then, the value of the daily volatility will slightly decrease to about 0.035.

4. Conclusion

Based on the three graphs that we constructed, it is clear that if the time to maturity is short, even if the natural upturn probability is high and the daily volatility is low, the daily return is strictly negative. However, the daily return will become positive quickly, and then its value will converge to a constant. Similarly, the natural upturn probability and daily volatility will change sharply in a short amount of time, but on a longer time scale, they will attain stable levels. Thus, based on the graphs, our suggestion to bond traders is to focus on zero-coupon bonds with a time to maturity of about 2 years, since at this level, the bond trader has a large probability of obtaining a high return, the upturn probability is about 65%, and the daily volatility is also not very high (at least, it does not attain its peak).

Of course, there are many factors that should affect bond traders’ choices. They cannot rely only on the factors that we analyze in this paper when they make decisions; they also need to consider other factors.