1. Introduction
Data analysis of an association between clinical class outcomes, such as patient versus controls, or responders versus non-responders, and complex underlying information, such as omics data, is often performed using classical methods such as binary logistic regression, or in case of k > 2 classes, multinomial logistic regression. These methods are believed to be effective in achieving the desired goals, making it unnecessary to broaden the methodological spectrum on the data analysis side. Hence, reviewers and editors of scientific papers occasionally require restricting the data analysis to this perceived standard, up to demanding deletion of alternative approaches on the grounds these would merely produce confusion without adding relevant information. This is in stark contrast to the demand for a wider range of data analysis methods covering different facets of a disease and the use of more laboratory methods to address complex clinical or preclinical questions.
However, restricting data analysis to, for example, calculating differential expression and performing a regression makes implicit assumptions such as (i) the relevant information is fully contained in the statistically significant variables, and (ii) the regression always adequately captures the relevant structure in a data set, and therefore analysis of which variables were relevant in the regression model is sufficient. In the dynamic and rapidly evolving field of data science, which encompasses diverse experts ranging from biomedical researchers to computer scientists and fosters collaborative efforts among individuals driven by their shared passion for data, it becomes apparent that the above assumptions are only partially valid. First, and it can be shown that the best predictive variables for subgroup assignment, such as a medical diagnosis, are not necessarily the variables that differ most significantly between subgroups or may not even show statistically significant group differences at all [
1]. Second, the assertion that regression necessarily adequately describes data sets with a class structure, and therefore can always provide a reliable basis for identifying relevant variables, is challenged by a canonical example presented below.
2. Introductory example case
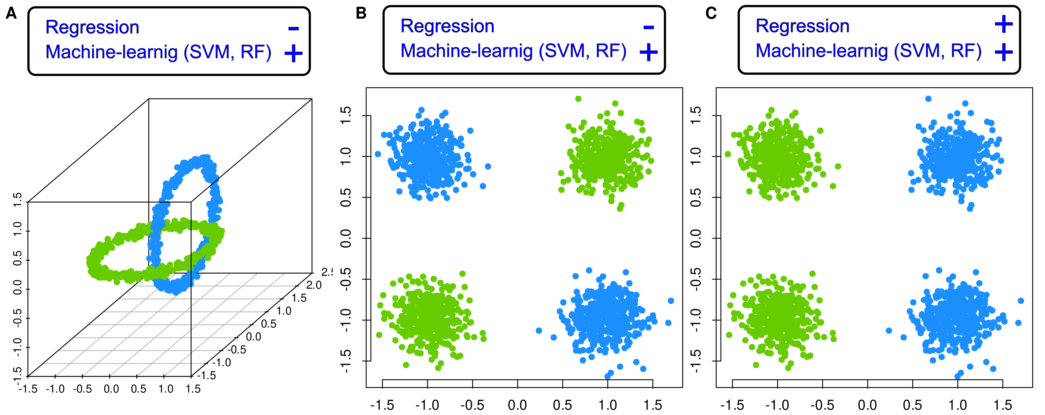
As an example of the limitations of relying solely on a regression model, consider a data set consisting of two classes that form two orthogonally intertwined rings in three dimensions (variables) (“X”, “Y”, and “Z”) [
2]. These rings are clearly visually distinguishable, and the variables are independent (Pearson’s correlation [
3] r = -0.064 to r = 0.026). Logistic regression analysis produced a highly significant result indicating that the variable “Y” carried the relevant information for class membership of the data points, with a p-value of p < 2 • 10
-16 (
Table 1).
Regression was run on 80% of the n = 1000 data points (400 of each class), while a 20% class-proportional holdout sample of the data (100 data points of each class) was separated as a validation data subset prior to analysis. When applying the fitted regression model on this validation sample, it becomes clear that the model captured the class structure in the data set with only 65% accuracy. In contrast, there are alternative algorithms, such as random forests [
9], that can much better separate the two classes (
Figure 1).
This raises the question of whether a research result in terms of relevant variables should be based on a model that incompletely describes the data, in particular when an obviously better model is available. By contrast, it seems preferable to validate several models on data not used for model fitting, and then to use the best models for identification of relevant variables on which the main conclusions of a research project can be based. It will be shown this problem applies not only to the artificial data set chosen here as an introductory example because its true class structure is known by design, but also to real biomedical data sets.
3. Materials and Methods
3.1. Sample data sets
The introductory example data set is an artificial data set published as part of the “Fundamental Clustering Problems Suite (FCPS)” [
2]. It is freely available at
https://www.mdpi.com/2306-5729/5/1/13/s1 or in the similarly named R library “FCPS” (
https://cran.r-project.org/package=FCPS [
10]). The “ChainLink” data set contains two distinct classes arranged as interlinked rings in the variables X, Y and Z, each class containing n = 500 members. Two other data sets from the FCPS collection, “Atom” and “Tetra”, were additionally used. The “Atom” data set contains 3D data visually resembling an atomic nucleus and its hull, each composed of n = 200 data points. The “Tetra” data set consists of four classes of n = 100 points each, and each point has three variables indicating the position in a three-dimensional space and drawn independently and uniformly distributed. Additionally, a canonical machine learning data set was generated consisting of 4 normal distributions with means [(5,-5), (-5,5), (-5,-5), (5,5)] and standard deviations of 1 in both x and y directions with n = 400 observations in each Gaussian. This results in four heaps of points in an xy coordinate system. In both dimensions, the variables were normalized, i.e., standardized to mean 0 and unit variance. The upper left and lower right corners belong to class 1, and the lower left and upper right corners belong to class 2. This “Four Gaussians” data set provides a classic “XOR” structured data set [
11]. That is, in this two-dimensional group of data, one group is characterized by either high values in both variables or low values. Otherwise, the case belongs to the other group.
A large biomedical data set was from a multiomics data analysis in the context of non-small cell lung cancer [
12]. The data set contained information from a total of n = 566 patients, including 672 differentially expressed mRNAs, 9 microRNAs, 719 gene methylation data, and 153 protein expression data. In the original study, spectral clustering was used to identify k = 5 clusters that correlated with patient survival. For the present analysis, we downloaded Supplementary Table S17 from the publication site at
https://static-content.springer.com/esm/art%3A10.1038%2Fs41598-023-31426-w/MediaObjects/41598_2023_31426_MOESM2_ESM.xlsx. The file contains cluster membership information and preprocessed omics data used by the authors of the original paper to train and validate machine learning-based classifiers. In the present demonstration, the data set was used to test the sufficiency of regression as an analysis method of biomedical data sets in comparison to alternative methods, with no intention to replicate or challenge the published results.
3.2. Experimentation
These included regression methods, specifically binary or multinomial logistic regression for data sets with k = 2 or k > 2 classes, respectively. Additionally, linear discriminant analysis (LDA) [
17], a commonly applied statistical procedure, was employed. Furthermore, a non-compressive collection of supervised machine learning algorithms was utilized, chosen methods often used for biomedical data analysis and generally known to usually well perform classification tasks. These included random forests [
9,
18] as a robust tree-based bagging classifier, support vector machines (SVM) [
19] as a hyperplane separation-based method, k-nearest neighbors [
20] as a distance-based classifier, naïve Bayes [
21] as a posterior probabilities-based method, and furthermore, decision rules were created based on repeated incremental clipping for error reduction (RIPPER [
22]). Hyperparameter tuning, such as kernel shape for SVM, number of trees for random forests, and others, was done in a grid search, and classifier training and validation was done using nested cross-validation. Details of the R code are available at
https://github.com/JornLotsch/MisClassificationRegressionNN/blob/main/MisClassificationAnaylsis_MainFunctions_paper.R.
The methods were then compared in terms of their classification performance based on balanced accuracy [
23] in a 20% hold-out validation sample separated from the data set before the analysis. In addition, the area under the receiver operator curve (roc-auc) was calculated [
24]. A “mixture of experts” approach was used to identify the most suitable variables based on the best-performing classification algorithms. These were identified by item categorization into subsets labeled “A,” “B,” and “C”, implemented as computed ABC analysis (cABC) [
25]. Algorithms falling in category “C”, which is generally considered as “the trivial many” [
26], were rejected as a basis of variable selection
. The informative variables were then selected for the best models using generic permutation importance as a feature selection method applicable to any type of classifier.
Since this was not a feature selection benchmarking assessment, other methods (for an overview, see [
28]) were not considered. Finally, the selected variables were used to train algorithms in a 5 x 20 nested cross-validation scenario using randomly selected subsets of 67% of the original training data set and applied to each 80% of the hold-out validation data subset.
4. Results
4.1. Regression occasionally generalizes poorly compared to alternative
methods
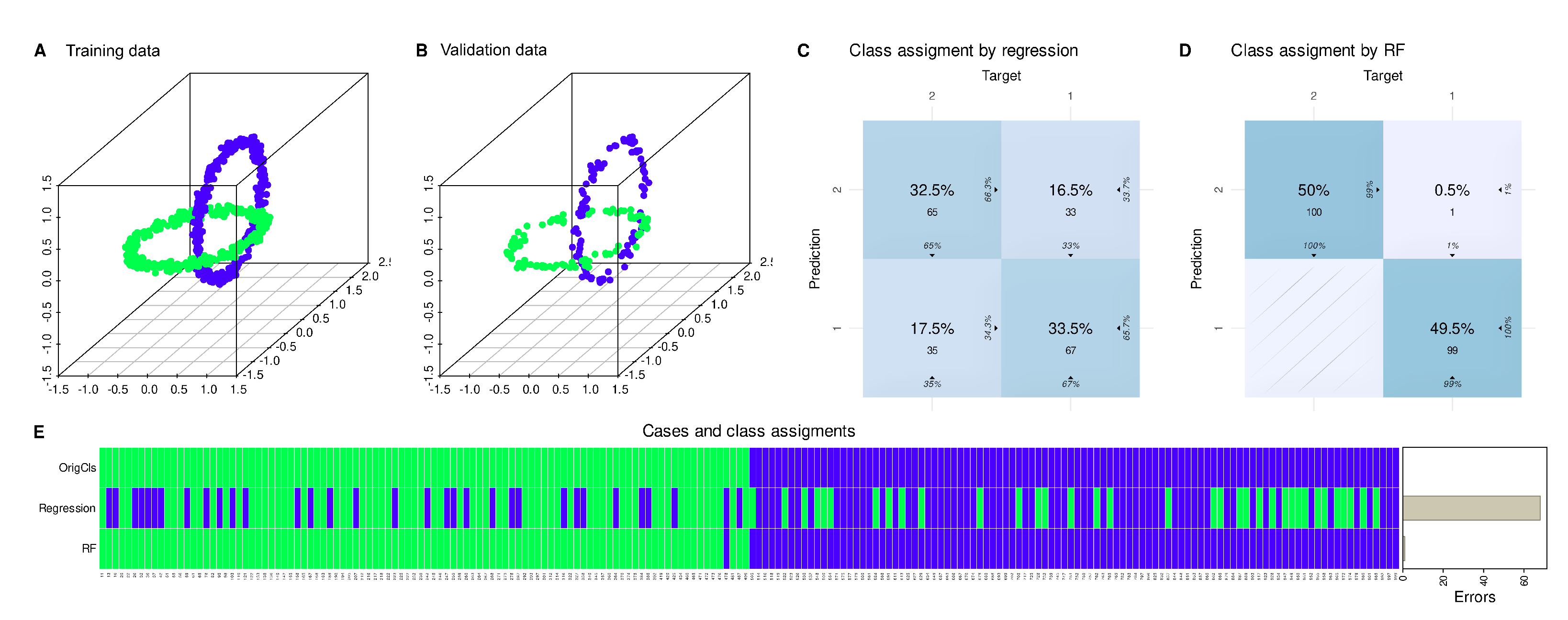
As shown in the introductory example, the regression result for the variable “Y” in the “ChainLink” data set was highly statistically significant (
Table 1). However, cautious interpretation is needed when considering “Y” as the primary determinant of class membership since regression had only modest ability to assign class membership of new cases, not seen during regression model building (
Figure 1).
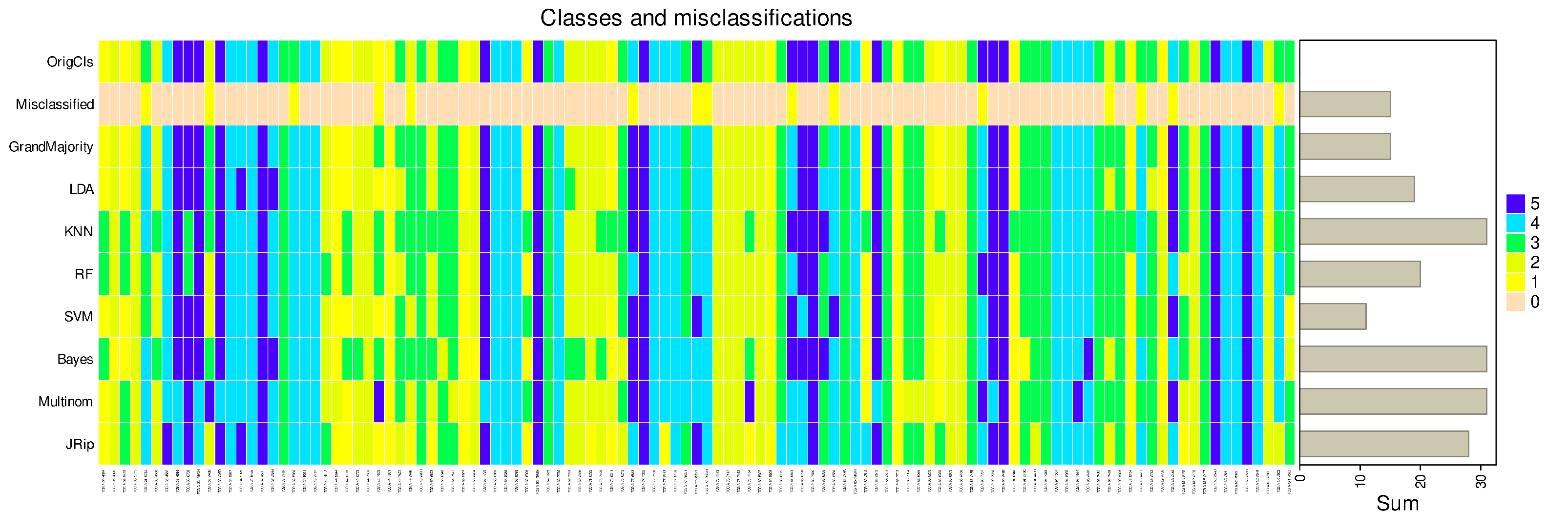
To further validate this, six different models were trained on all possible combinations of preserved and randomly permuted variables (
Figure 2). The results showed that most algorithms successfully classified unseen data when trained on the three variables, with regression and LDA performing worst as mentioned in the introductory example. By contrast, classification constantly failed when all variables were randomly permuted as the expected outcome in this scenario (
Figure 2 G and H, respectively). Surprisingly when considering the statistical results of regression analysis, training with only the variable “Y”, i.e., the variable emerging as a highly significant result from regression analysis, resulted in poor classification performance for new data across all algorithms (
Figure 2 B).
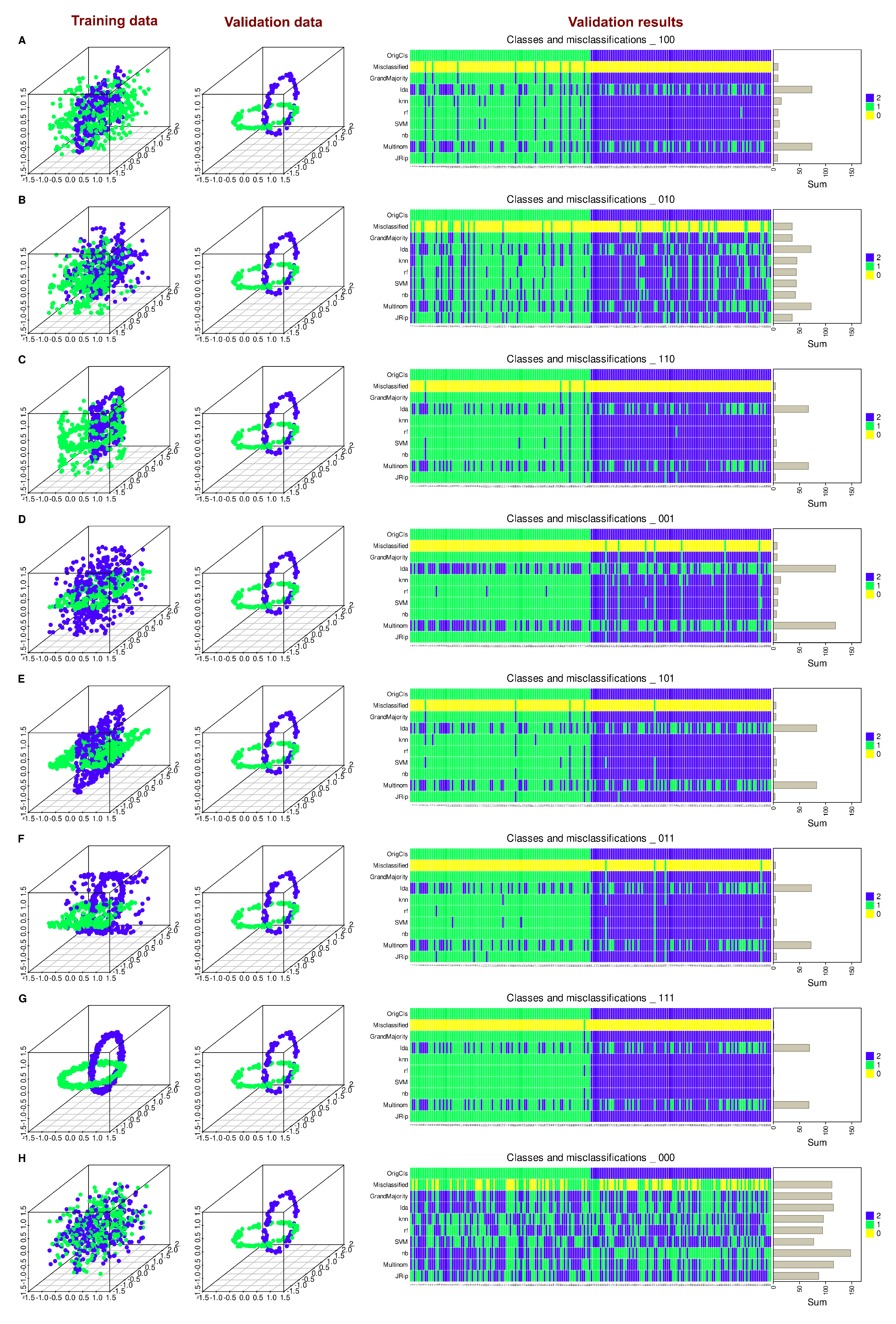
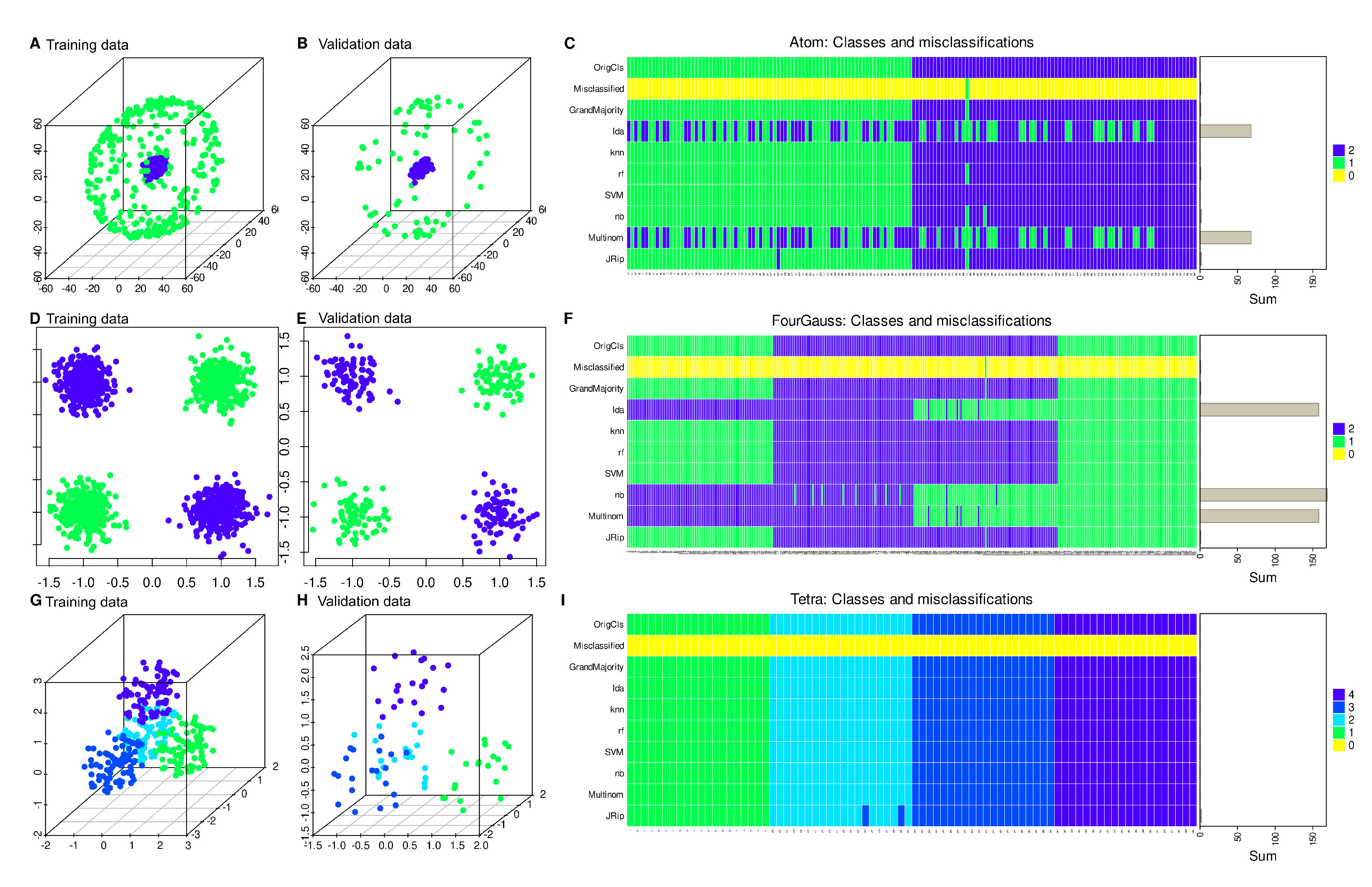
Regression was also found to be inferior to machine learning algorithms in the FCPS based “Atom” data set as well as in the “Four Gaussians” data set (
Figure 3). However, to highlight that regression can be a successful method, the FCPS based “Tetra” data set was included in which it expectedly provided a perfect classification similar to the other methods (
Figure 3).
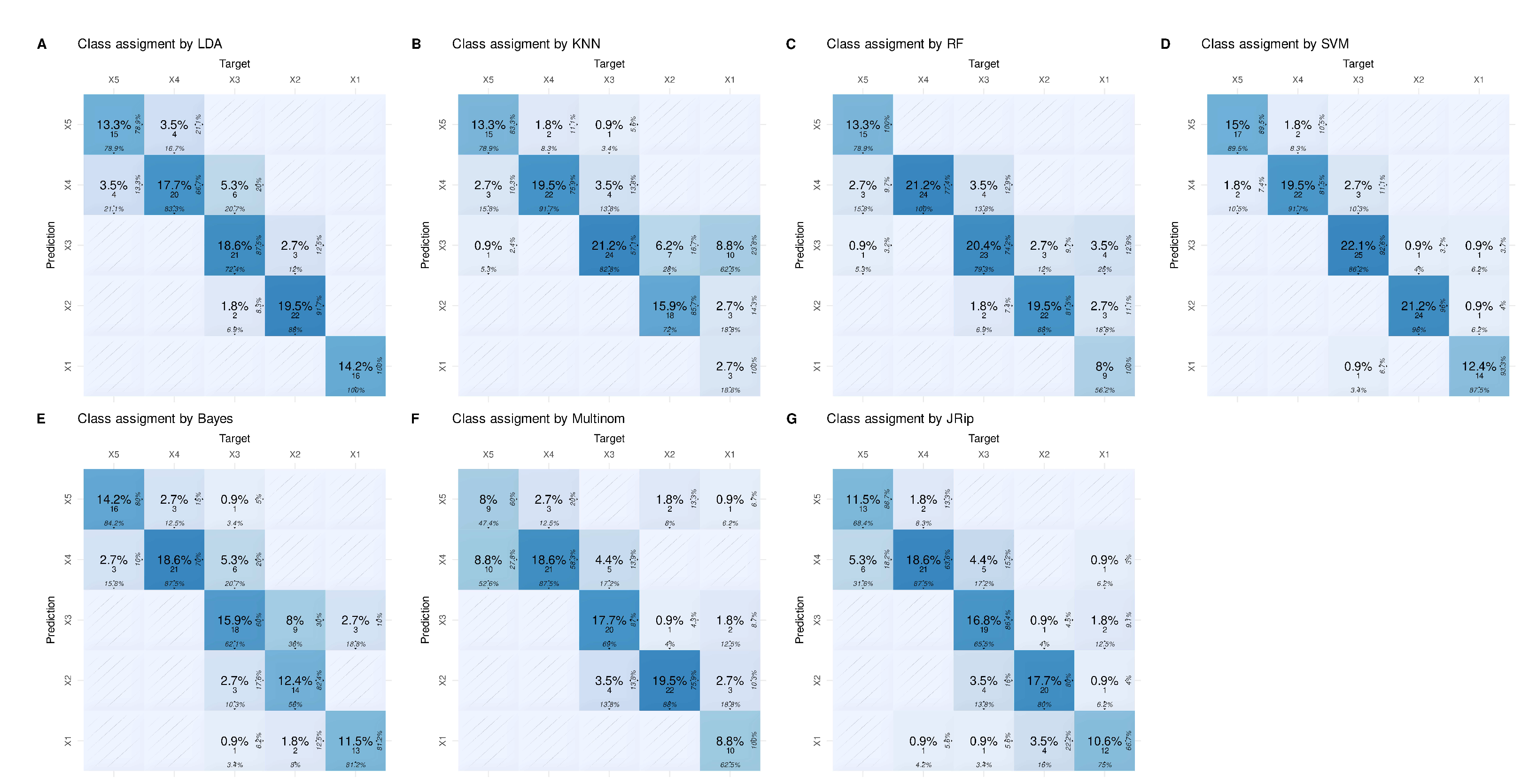
The weakness of regression was not arbitrarily produced by the actual choice of artificial data sets expected to pose problems, but extends to real-life data sets, such as a large multiomics data set from cancer research (
Figure 4).
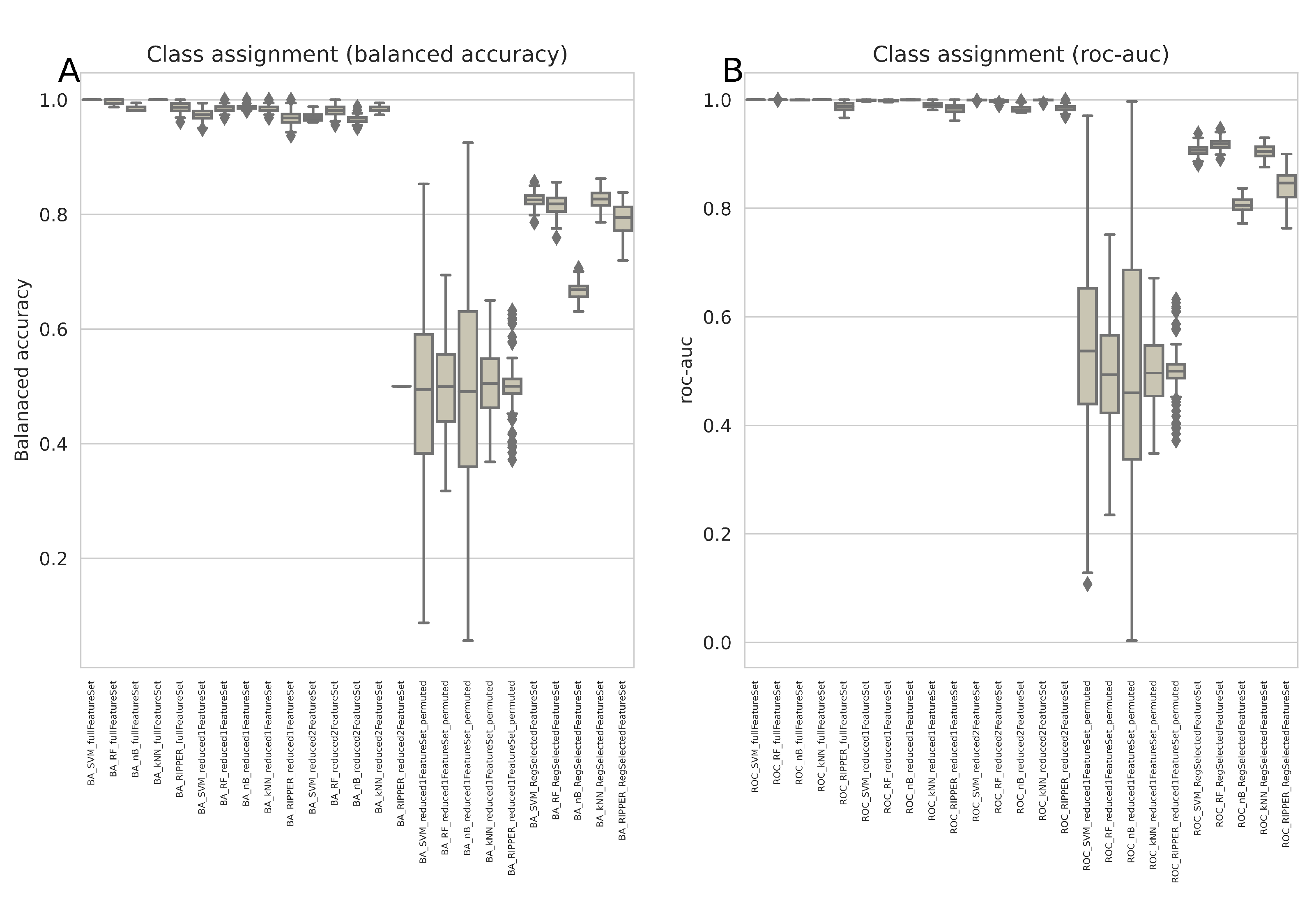
There, for example support vector machines outperformed regression considerably. This data set identified once again regression as one of the weakest predictors producing least accurate class assignment of unseen (validation) cases (
Figure 5).
4.2. Regression inadequately captures the structural characteristics of
certain data sets
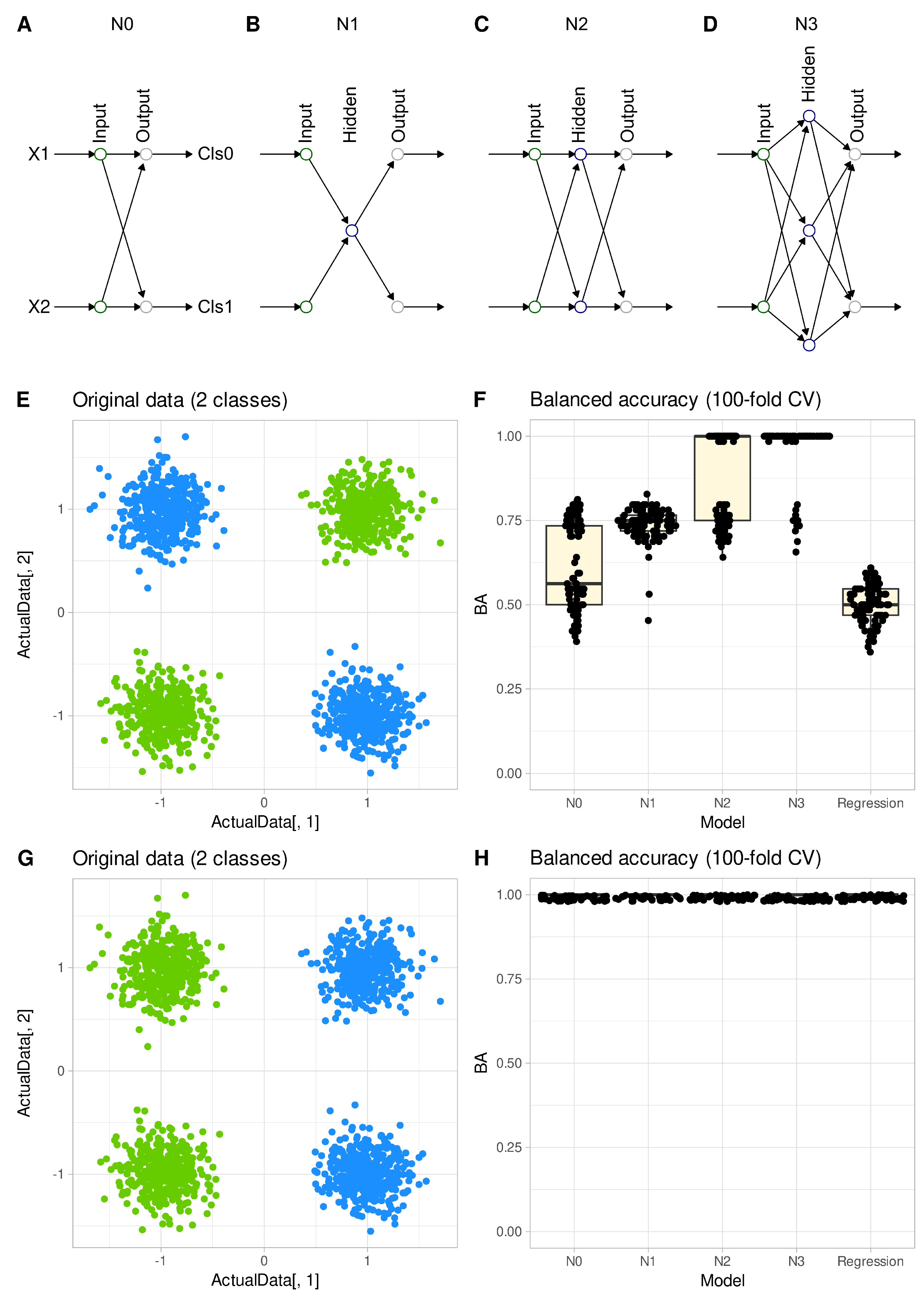
In the “Four Gaussians” data set, regression analysis failed to provide the correct classification when the classes in the data set are linear non-separable (
Figure 6 E and F). Its inability to draw a line between the two original classes was shared by a single-layer neural network (
Figure 6 A). The balanced accuracy obtained with binary logistic regression or with a single-layer perceptron was about 50%, i.e., guessing level in two classes. Only the addition of a hidden layer with at least 1 and up to 3 neurons (
Figure 6 B - D) enabled the algorithms to perform the classification successfully, eventually reaching 100% accuracy. When the class labels were changed so that the classes were linearly separable (
Figure 6 G), both regression and simple artificial neural networks were able to perform classification with 100% accuracy (
Figure 6 H). The R code for this experiment can be is available at
https://github.com/JornLotsch/MisClassificationRegressionNN.
4.3. Variables chosen by the most successful algorithms are more
generalizable
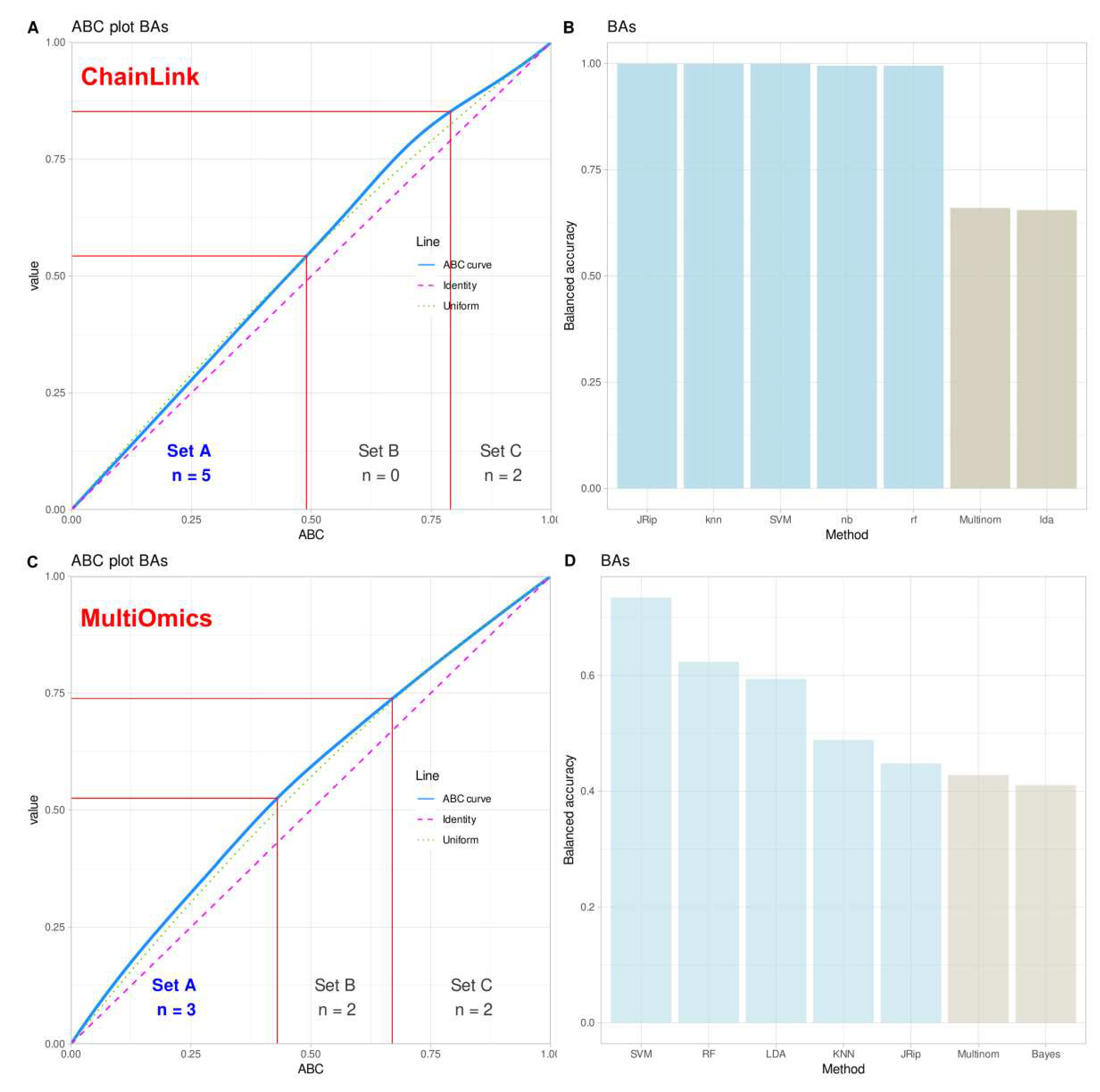
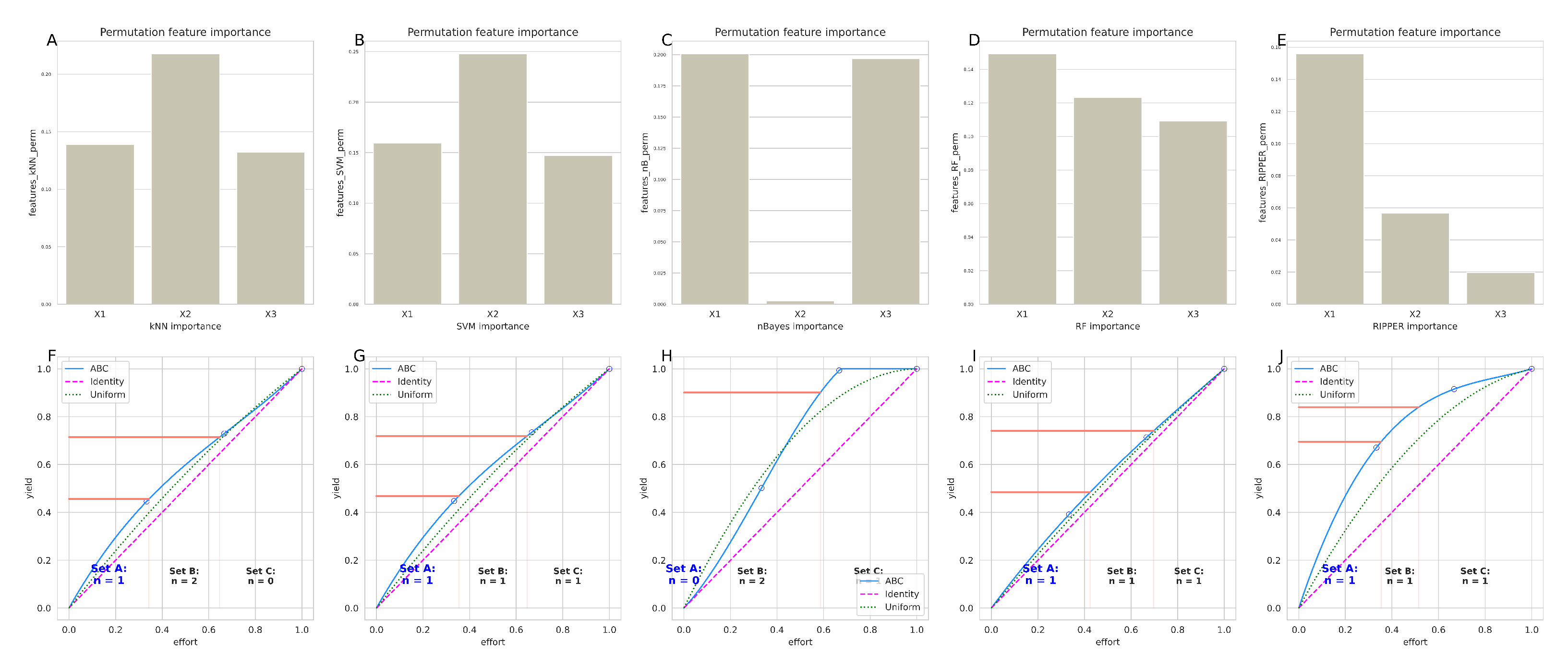
Above experiments cast doubt on the validity of the statistically significant result of the logistic regression analysis identifying the variable ’Y’ in the FCPS “ChainLink” data set as the relevant variable for class assignment. Regression was the poorest model for assigning new cases to the correct classes based on the available variables, and therefore may not be the most reliable “expert” to indicate which variables are relevant in the data set. Using cABC analysis and the permutation importance method on the balanced accuracy, LDA and regression were placed in category “C” by cABC analysis, indicating that these methods provided the poorest description of the “ChainLink” data set and should therefore not be explored further for important variables (
Figure 7).
The brute force experiment reported above suggested that variable “Y” was consistently worse than other combinations as a basis for training any model to perform the classification task on new data. When this issue was addressed using feature selection based on permutation variable importance, variable “X” was consistently found to be important for most of the (well-performing) algorithms, while “Y” and “Z” were each important for three out of five algorithms (
Figure 8), which was further addressed by testing classifiers when trained with different combinations of variables. Training the models with all variables or combinations of “XZ” or “XY” resulted in good classification performance (
Figure 9), but with “XZ” slightly better than “XY”. More importantly, using only variable “Y” for training resulted in significantly worse classification performance on new data. As a control, training the algorithms with permuted and thus nonsensical information led, as expected, to guessing class membership (balanced accuracy in the median around 50%), supporting that observed correct classification was not due to overfitting.
In the real-life multi-omics data set, the highest balanced accuracies of the k = 5 classes identified by the authors of the original paper [
12] were support vector machines, along with random forest, k-nearest neighbors, LDA and RIPPER (
Figure 7). In fact, the first two algorithms currently identified as the best (SVM, random forests) were used by the authors of the original report [
12]. Thus, from the range of methods available, these should be used to identify the variables relevant to the cluster structure in this data set. This will not be done again here, as it is not the intention of this report to verify the original results, but rather to use this data set as an example to discourage reliance on regression alone in this type of data set.
5. Discussion
Present findings challenge the traditional reliance on regression as the standard for multivariate data analysis in biomedical research aimed at identifying variables most relevant for a given class structure. The widespread use of regression in the past may have been due to the lack of alternatives or computational limitations. However, with the advancement of machine learning techniques and the availability of computational power, it is now possible to employ a collection of different methods for data analysis and select those that accurately capture the underlying structure of the data.
This paper attempts to clarify a common misconception about regression, namely that regression algorithms for classification are as powerful as machine learning methods and therefore, suffice all requirements of the analysis of biomedical data. This is not true. By contrast, this paper points out a structural weakness of regression in separating classes in data sets, comparable to early neural networks. The breakthrough to address linear non-separable classifications of data sets was the introduction of hidden layers. In this context, regression provides the equivalent of a simple perceptron, which for good reasons has been discarded for data analysis in favor of more sophisticated model architectures. One can show that a single artificial neuron of a neural network can be described as nonlinear (logistic) regression and vice versa. However, to generalize this to “machine learning is nothing more than the application of regression models under a different name” is a mistake. Regression models can handle the same type of classification problems as neural networks without hidden layers. This type of model was proposed by Rosenblatt in 1958 under the name “Perceptron” [
30]. These algorithms were used until 1970 for many problems, including classification. In 1969, Minsky and Papert published a book showing that single-layer neural networks are, in principle, incapable of classifying data sets that are linearly non-separable [
11].
The data set “Four Gaussians” illustrates this property for empirical data in a nutshell: for this type of data sets (
Figure 6) there is no single straight line, i.e., a “hyperplane in two dimensions”, that can correctly separate the two classes. Regression models used for classification (e.g., logistic regression) can only achieve a classification accuracy of about 50%, which is a guessing level as shown in the present analyses. Current experiments emphasize that regression is equivalent to a simple perceptron with respect to classification. A practical example of such data is a normal versus abnormal body mass index (BMI): a person is in the “normal BMI” (the green group in
Figure 6) group if they have either a high weight and height or a low weight and height, otherwise they are in the “abnormal BMI” group (the blue group in
Figure 6).
Thus, regression models, which are computationally equivalent to neural networks with one layer, are in principle unable to classify data sets that are linearly non-separable. Indeed, the other algorithms used in this report, except LDA, were well able to classify the “Four Gausian” data set (
Figure 3 D - F). However, testing whether a given empirical multivariate data set is linearly non-separable is not an easy task and often requires the use of more powerful machine learning algorithms [
31]. A simple example to demonstrate this is the “ChainLink” data set used in the present experiments (see introductory example and
Figure 2. Machine learning (ML) models such as deep learning, i.e., hidden layer networks, support vector machines (SVN), random forests, and other ML algorithms can easily handle linear, non-separable data. Some of these algorithms, such as SVN, are specifically designed to handle linearly non-separable classification problems.
The current experiments have shown that relying on a single algorithm to select informative variables in a data set has potential risks in scientific findings. If the chosen algorithm fails for any reason to capture the class structure, although statistics may deliver highly significant p-values the results could be unreliable. Regression can of course be successful, as in the “Tetra” data set and many other reported in the scientific literature, however, this should not be assumed as a given fact but verified in every actual data set. The present workflow included alternative methods creating a “mixture of experts” on which conclusions can be relied with greater confidence that on a single model that has not even been tested in unseen data, as it is a frequent approach in biomedical research. This is likely to provide a result closer to the ground truth than when relying on a single model and basing research results on a particular model architecture. Furthermore, the addition of other methods provides internal validation, and there is major no disadvantage compared to a pure regression analysis.
However, the abandonment of an apparent standard that provided reassurance about the results of data analysis could be perceived as a disadvantage. In fact, selecting relevant variables requires more effort than simply accepting the statistical results of a regression. There are many methods for selecting features, of which the permutation importance method chosen here is only one [
28]. These include univariate feature selection methods such as effect size calculations, the false positive rate, the family-wise error rate, selection of the k best variables based on F-statistics and others, available for example in the “sklearn.feature_selection” module of the “scikit-learn” Python package (
https://scikit-learn.org/stable/modules/feature_selection.html [
16]). Model-based methods are applied after training the algorithms and include methods such as “ SelectFromModel” (SFM), which selects features based on importance weights in the trained algorithm, and (vii) Recursive Feature Elimination (RFE), which selects features by recursively considering smaller and smaller feature sets and generating a feature ranking, and many others. Neural network based feature selection was not even considered in these experiments [
32]. The choice of algorithms also influences the final result. Currently, algorithms of different types have been compiled, but alternatives are certainly possible. In addition, as shown in a simple biomedical case [
33], the current setting of the hyperparameters can directly affect the classification performance and thus the ranking of the algorithms, resulting in different sets of algorithms from which to derive the relevant features. While this may be a difficult task to test, reverting to a simple single method, with the uncertainty of whether dise even captures the class structure in a dataset, does not seem to be a better solution.
The mixture of experts makes the model predictions more robust. In the present experiments, a majority vote was always included in the presentation of the results (“grand majority” columns in
Figure 2,
Figure 3 and
Figure 4), showing that occasional weakness of one or the other model can often be compensated by the votes contributed by stronger models, although this might not be a general rule. In fact, research has shown that using a “mixture of experts” (MOE) approach, where multiple models are combined, can yield more accurate results in the analysis of biomedical data. The cited multiomics example paper was produced using support vector machines, random forests, and additionally a feed-forward neural network [
12], but not regression, consistent with the present observations in other data sets and the referenced examples. Further examples include, a customized electrocardiogram (ECG) beat classifier combined with a global classifier to form an MOE classifier structure, which provided significant performance improvement over single method approaches [
34]. Similarly, a wide variety of machine learning algorithms have been proposed to select the best combination of biomarkers to predict categorical outcomes from highly unbalanced (biomedical) data sets [
35,
36,
37], and own molecular research also points to the advantage of using multiple models, of which regression can be one, but should not be the only one [
38].
6. Conclusions
Regression is only one of several possible mathematical models to describe a data set; it can be valid, as in the present “Tetra” data set, but this cannot be taken for granted and used to demand that scientific reports be based on regression analysis. Regression is not necessarily always the best and most correct model, as shown in other data sets where it failed completely, as in three artificial data sets, or was one of the poorest predictors in an actual real-life multiomics data set from cancer research. This means that regression has been outperformed by most alternative machine-learning based algorithms on almost every dataset, yet it is still considered a standard that can be requested in scientific publications. A regression model needs to be validated like any other model, although many scientific papers do not do this, so it cannot be taken for granted that the results reported are valid. In contrast, this paper highlights a structural problem with logistic regression that it has in common with early neural network architectures (perceptrons), which were abandoned for good reason. Since it is difficult or even impossible to judge whether a given real-life data set is linearly non-separable, this paper calls for the use of a mixture of experts (MOE) of machine learning models, which may include regression, to handle classification problems in biomedical data. Requiring authors of scientific reports to use regression to classify a biomedical dataset, or even limiting the analysis to regression without considering alternatives, is clear malpractice.
Author Contributions
JL – Conceptualization of the project, programming, performing the experiments, writing of the manuscript, data analyses and creation of the figures, funding acquisition. AU – Theoretical background, mathematical implementation, writing of the manuscript.
Funding
JL was supported by the Deutsche Forschungsgemeinschaft (DFG LO 612/16-1).
Institutional Review Board Statement
Not applicable. All data sets have been taken from public sources.
Informed Consent Statement
Not applicable. All data sets have been taken from public sources.
Data Availability Statement
Data sets except the 4-Gaussians-example have been taken from public sources that are precisely referenced in the report. The data of the 4-Gaussians example and the R code for this experiment can be is available at
https://github.com/JornLotsch/MisClassificationRegressionNN. Please note that the unmodified R code runs only on Unix-like systems (e.g., Linux, MacOS) due to the particular kind of implementation of parallel processing.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Sample Availability
Not applicable.
References
- Lo, A.; Chernoff, H.; Zheng, T.; Lo, S.H. Why significant variables aren’t automatically good predictors. Proceedings of the National Academy of Sciences of the United States of America 2015, 112, 13892–13897. [Google Scholar] [CrossRef] [PubMed]
- Ultsch, A.; Lötsch, J. The Fundamental Clustering and Projection Suite (FCPS): A Dataset Collection to Test the Performance of Clustering and Data Projection Algorithms. Data 2020, 5, 13. [Google Scholar] [CrossRef]
- Pearson, K. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 1901, 2, 559–572. [Google Scholar] [CrossRef]
- Team, R.D.C. R: A Language and Environment for Statistical Computing; 2008.
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis; Springer-Verlag: New York, 2009. [Google Scholar]
- Ligges, U.; Mächler, M. Scatterplot3d - an R Package for Visualizing Multivariate Data. Journal of Statistical Software 2003, 8, 1–20. [Google Scholar] [CrossRef]
- Olsen, L.R.; Zachariae, H.B. cvms: Cross-Validation for Model Selection, 2023.
- Gu, Z.; Eils, R.; Schlesner, M. Complex heatmaps reveal patterns and correlations in multidimensional genomic data. Bioinformatics 2016, 32, 2847–9. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Thrun, M.; Stier, Q. Fundamental clustering algorithms suite. SoftwareX 2021, 13, 100642–100642. [Google Scholar] [CrossRef]
- Minsky, M.; Papert, S. Perceptrons; an Introduction to Computational Geometry; MIT Press, 1969. [Google Scholar]
- Khadirnaikar, S.; Shukla, S.; Prasanna, S.R.M. Machine learning based combination of multi-omics data for subgroup identification in non-small cell lung cancer. Sci Rep 2023, 13, 4636. [Google Scholar] [CrossRef]
- Ihaka, R.; Gentleman, R. R: A Language for Data Analysis and Graphics. Journal of Computational and Graphical Statistics 1996, 5, 299–314. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake Jr, F.L. Python tutorial; Vol. 620, Centrum voor Wiskunde en Informatica Amsterdam, 1995.
- Kuhn. ; Max. Building Predictive Models in R Using the caret Package. Journal of Statistical Software 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; Perrot, M.; Duchesnay, E. Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research 2011, 12, 2825–2830. [Google Scholar]
- Fisher, R.A. The use of multiple measurements in taxonomic problems. Annals of Eugenics 1936, 7, 179–188. [Google Scholar] [CrossRef]
- Ho, T.K. Random decision forests. Proceedings of 3rd International Conference on Document Analysis and Recognition, 1995, Vol. 1, pp. 278–282 vol.1. [CrossRef]
- Cortes, C.; Vapnik, V. Support-Vector Networks. Machine Learning 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theor. 1967, 13, 21–27. [Google Scholar] [CrossRef]
- Bayes, M.; Price, M. An Essay towards Solving a Problem in the Doctrine of Chances. By the Late Rev. Mr. Bayes, F. R. S. Communicated by Mr. Price, in a Letter to John Canton, A. M. F. R. S. Philosophical Transactions 1763, 53, 370–418. [Google Scholar] [CrossRef]
- Cohen, W.W. Fast Effective Rule Induction. ICML, 1995.
- Brodersen, K.H.; Ong, C.S.; Stephan, K.E.; Buhmann, J.M. The Balanced Accuracy and Its Posterior Distribution. Pattern Recognition (ICPR), 2010 20th International Conference on, 2010, pp. 3121–3124. [CrossRef]
- Peterson, W.; Birdsall, T.; Fox, W. The theory of signal detectability. Transactions of the IRE Professional Group on Information Theory 1954, 4, 171–212. [Google Scholar] [CrossRef]
- Ultsch, A.; Lötsch, J. Computed ABC Analysis for Rational Selection of Most Informative Variables in Multivariate Data. PLoS One 2015, 10, e0129767. [Google Scholar] [CrossRef]
- Juran, J.M. The non-Pareto principle; Mea culpa. Quality Progress 1975, 8, 8–9. [Google Scholar]
- Venables, W.N.; Ripley, B.D. Modern Applied Statistics with S, fourth ed.; Springer: New York, 2002; ISBN 0-387-95457-0. [Google Scholar]
- Guyon, I. An introduction to variable and feature selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Waskom, M.L. seaborn: statistical data visualization. Journal of Open Source Software 2021, 6, 3021. [Google Scholar] [CrossRef]
- Rosenblatt, F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review 1958, 65, 386–408. [Google Scholar] [CrossRef] [PubMed]
- Elizondo, D. The linear separability problem: some testing methods. IEEE Transactions on Neural Networks 2006, 17, 330–344. [Google Scholar] [CrossRef]
- Verikas, A.; Bacauskiene, M. Feature selection with neural networks. Pattern Recognition Letters 2002, 23, 1323–1335. [Google Scholar] [CrossRef]
- Lötsch, J.; Mayer, B. A Biomedical Case Study Showing That Tuning Random Forests Can Fundamentally Change the Interpretation of Supervised Data Structure Exploration Aimed at Knowledge Discovery. BioMedInformatics 2022, 2, 544–552. [Google Scholar] [CrossRef]
- Hu, Y.H.; Palreddy, S.; Tompkins, W.J. A patient-adaptable ECG beat classifier using a mixture of experts approach. IEEE Trans Biomed Eng 1997, 44, 891–900. [Google Scholar] [CrossRef] [PubMed]
- Leclercq, M.; Vittrant, B.; Martin-Magniette, M.L.; Scott Boyer, M.P.; Perin, O.; Bergeron, A.; Fradet, Y.; Droit, A. Large-Scale Automatic Feature Selection for Biomarker Discovery in High-Dimensional OMICs Data. Front Genet 2019, 10, 452. [Google Scholar] [CrossRef]
- Miettinen, T.; Nieminen, A.I.; Mäntyselkä, P.; Kalso, E.; Lötsch, J. Machine Learning and Pathway Analysis-Based Discovery of Metabolomic Markers Relating to Chronic Pain Phenotypes. Int J Mol Sci 2022, 23. [Google Scholar] [CrossRef]
- Kringel, D.; Kaunisto, M.A.; Kalso, E.; Lötsch, J. Machine-learned analysis of global and glial/opioid intersection-related DNA methylation in patients with persistent pain after breast cancer surgery. Clin Epigenetics 2019, 11, 167. [Google Scholar] [CrossRef]
- Lötsch, J.; Schiffmann, S.; Schmitz, K.; Brunkhorst, R.; Lerch, F.; Ferreiros, N.; Wicker, S.; Tegeder, I.; Geisslinger, G.; Ultsch, A. Machine-learning based lipid mediator serum concentration patterns allow identification of multiple sclerosis patients with high accuracy. Sci Rep 2018, 8, 14884. [Google Scholar] [CrossRef]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).