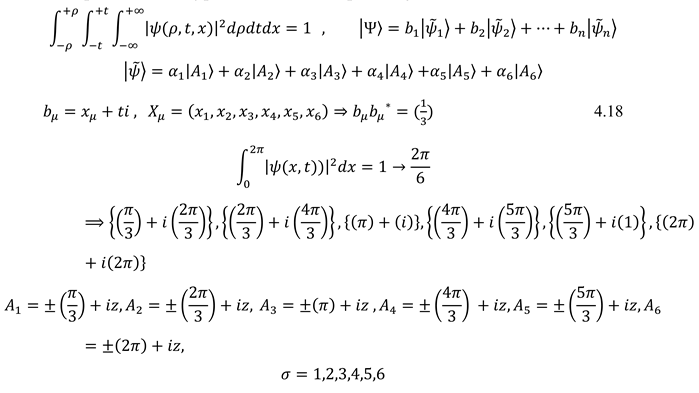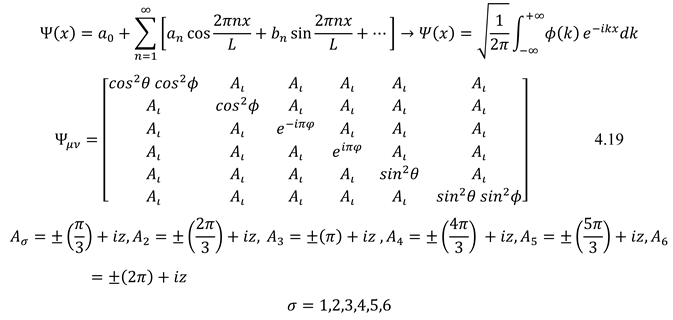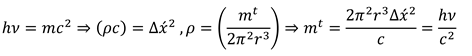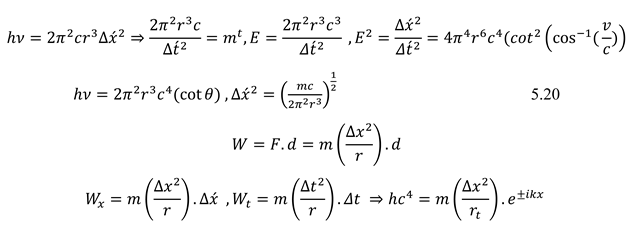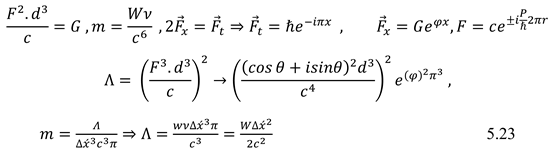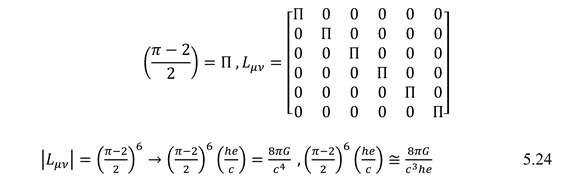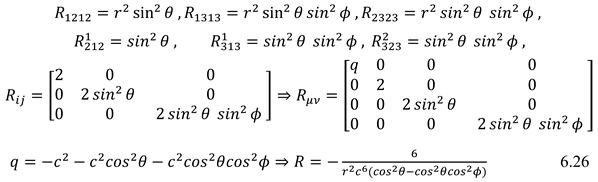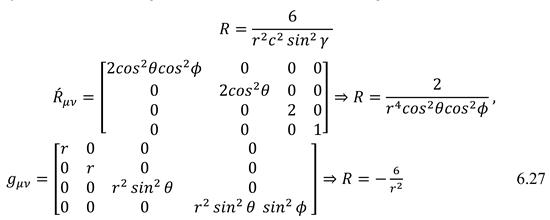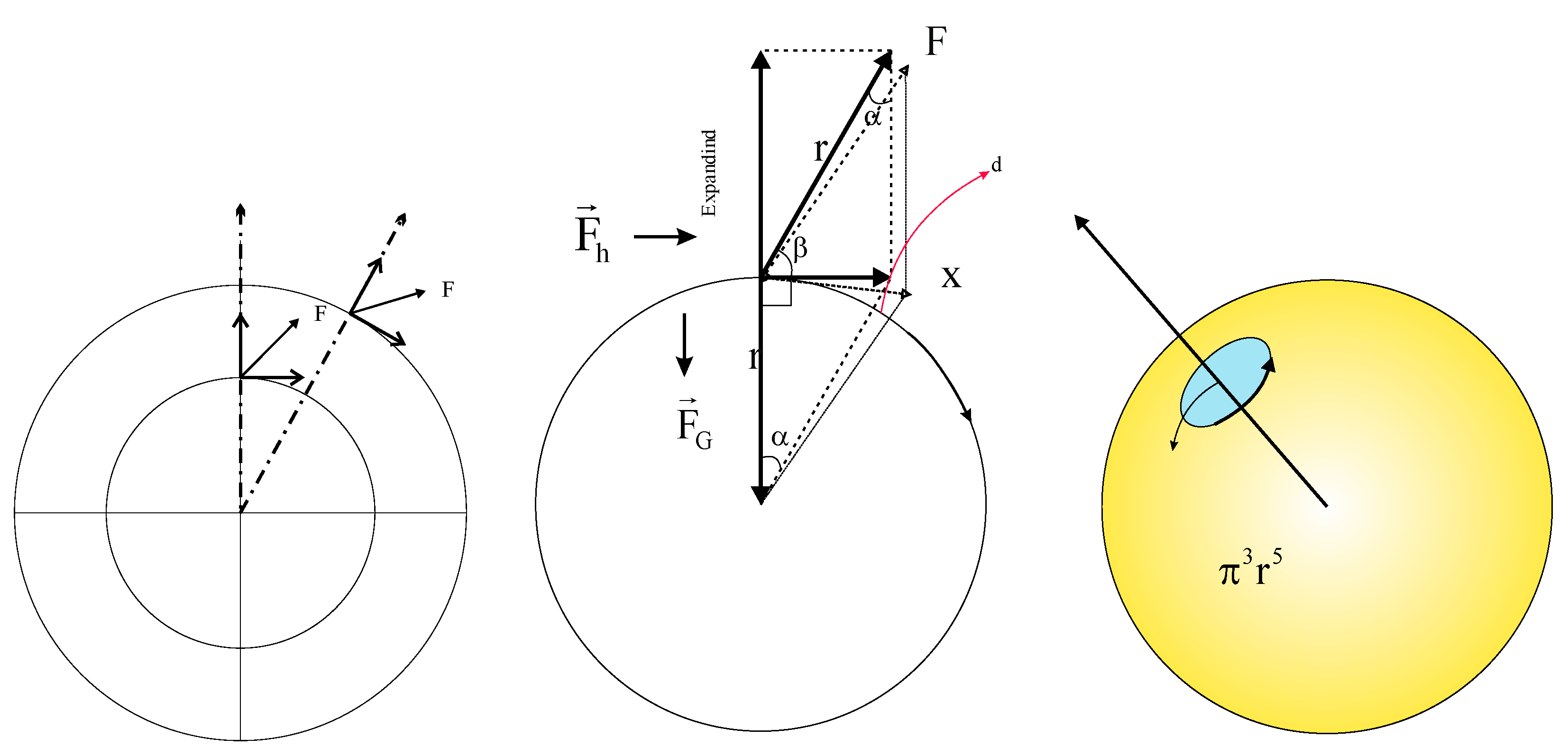The General Balance in the Six Dimensional of Space-Time

1. Introduction

In the past century, significant efforts have been dedicated to reconciling quantum mechanics and general relativity. The inherent non-deterministic nature of quantum mechanical phenomena has posed a fundamental challenge to the compatibility of these two pillars of modern physics. At the heart of this incompatibility lies the unreality of quantum mechanical phenomena, which stands in stark contrast to the deterministic framework of general relativity. This discrepancy has been a subject of intense theoretical and experimental investigation, reflecting the profound implications for our understanding of the fundamental nature of reality. Albert Einstein, a key figure in the development of both quantum mechanics and general relativity, articulated a perspective that sheds light on this fundamental issue. According to Einstein, the reality of a physical quantity is contingent upon the ability to predict that reality with certainty, without inducing any disruption or disorder within the system. This criterion, rooted in the classical determinism of physics, underscores the challenge posed by the inherently probabilistic nature of quantum mechanics [1].

To unite two theories, the two theories must share identical attitudes towards physical quantities. Understanding the phenomenon of quantum mechanics can be achieved through a comprehensive knowledge of the origins of mass, spin, electric charge, and other related factors. This understanding is crucial for the integration of theories and the advancement of scientific knowledge in the field. [2,3,4,5,6]. The exploration of time's nature has become increasingly crucial in the ongoing development of the theory of everything, particularly in light of the remarkable successes of quantum mechanics. As we strive towards a comprehensive understanding of the universe, it is imperative to consider the fundamental nature of time and its role in shaping the fabric of reality. By delving into the intricacies of temporal dynamics, we can gain valuable insights that may ultimately lead to a more unified and comprehensive theoretical framework. This endeavor holds great promise for advancing our understanding of the cosmos and represents a pivotal strategy in the evolution of scientific thought [7]

A new approach to understanding quantum mechanics phenomena involves reexamining the nature of space-time. Describing events outside of the constraints of time is a novel area of study that offers a fresh perspective in the field of physics. This new outlook provides a different vantage point from which to explore the universe. Research and scholarly work in this area is centered on defining different metrics within a six-dimensional space. This shift in perspective opens up new possibilities for comprehending the fundamental principles that govern the behavior of particles at the quantum level [8,9,10,11,12]. The incorporation of six-dimensional space as a framework for understanding space-time presents certain challenges, yet it proves to be highly advantageous in elucidating various phenomena within the realm of quantum mechanics [13]. The concept of space-time metric, described in terms of elliptical eccentricity, offers a compelling solution to several longstanding problems in the field of astrophysics and cosmology. This innovative approach provides a new framework for understanding the fundamental nature of space-time and its impact on the behavior of celestial bodies. One of the key advantages of employing elliptical eccentricity in the metric description of space-time is its ability to account for the non-uniform distribution of mass and energy throughout the universe. Traditional models often struggle to accurately represent the complex gravitational interactions that occur in systems with significant asymmetry or irregularity. By incorporating elliptical eccentricity into the metric, scientists can more effectively capture the dynamic and intricate nature of these systems, leading to more accurate predictions and explanations of observed phenomena.

Furthermore, this approach has the potential to address discrepancies between theoretical predictions and observational data related to the motion of celestial bodies. The incorporation of elliptical eccentricity into the space-time metric offers a more nuanced understanding of gravitational effects, allowing for better alignment between theoretical calculations and empirical evidence. This has significant implications for our ability to model and interpret the behavior of objects ranging from individual stars to entire galaxies. In addition, the use of elliptical eccentricity in the metric description of space-time has implications for our understanding of the fundamental structure of the universe. By providing a more comprehensive framework for incorporating the effects of mass and energy distribution, this approach has the potential to shed light on longstanding mysteries such as dark matter and dark energy. It may also offer new insights into the behavior of black holes and other exotic astronomical phenomena. Overall, the incorporation of elliptical eccentricity into the metric description of space-time represents a promising avenue for advancing our understanding of the cosmos. By providing a more accurate and comprehensive model of gravitational interactions, this approach has the potential to revolutionize our ability to explain and predict a wide range of astrophysical phenomena. As researchers continue to explore and refine this innovative framework, it is likely to yield discoveries and deepen our appreciation for the intricate interplay between space, time, and the forces that shape the universe [14,15]. In this six-dimensional space-time framework, quantum mechanics offers a comprehensive and elegant way to describe the behavior of particles and their interactions. By incorporating both the three dimensions of space and the three dimensions of time, this approach provides a more complete picture of the dynamics of quantum systems. The concept of six-dimensional space-time has profound implications for our understanding of phenomena such as quantum entanglement, particle-wave duality, and the behavior of subatomic particles. It allows for a more nuanced and sophisticated description of these phenomena, shedding light on the underlying principles that govern the behavior of the quantum world [16]. The concept of time as an independent dimension from space allows for the definition of a unique type of 'motion' in time itself. When considering extrinsic geometry, this motion in time can be understood as a 'real' distance. The unidirectional nature of time is expressed by the time arrow, and it is observed that objects move at varying speeds within this dimension. The rate of an object's movement through time is directly related to its mass, with denser objects moving more slowly in the time dimension. This relationship between mass and movement through time is further exemplified by phenomena such as gravitational time dilation and time dilation for moving objects. These occurrences express the change in density of an object within the space-time continuum, resulting in a slower movement through time for denser objects. The balance theory delves into the equilibrium of events and quantities across the three dimensions of time and the three dimensions of space within the six dimensions of space-time [17]. This theory provides a framework for understanding the interplay between temporal and spatial dimensions, offering insights into the dynamic nature of the universe. In conclusion, the consideration of time as an independent dimension opens up new avenues for understanding motion and the interplay between mass, space, and time. It provides a framework for exploring the intricacies of the universe and offers valuable insights into the fundamental nature of reality. The paper addresses several key defects in a particular theory, aiming to establish a balance and parity between time, space, and physical quantities. Its theories the concept of mass resulting from movement in both time dimensions and space, emphasizing the interconnectedness of these fundamental aspects. The proposition that time can be disregarded in the sub-atomic realm is explored, with examples illustrating particle behavior within different time dimensions. Furthermore, the paper discusses the relationship between particle state entanglement and higher dimensions, highlighting the intriguing closeness of particles despite spatial separation. Additionally, the article explores the potential independence of three-time dimensions from three space dimensions and their deep interconnections for analyzing quantum mechanics and general relativity phenomena. The nature and cause of quantum mechanical phenomena are attributed to the relationship between fundamental constants and key mathematical numbers. Finally, the paper emphasizes the significance of a geometrical interpretation for unifying quantum mechanics with general relativity.

2. Six-Dimensional Space-Time

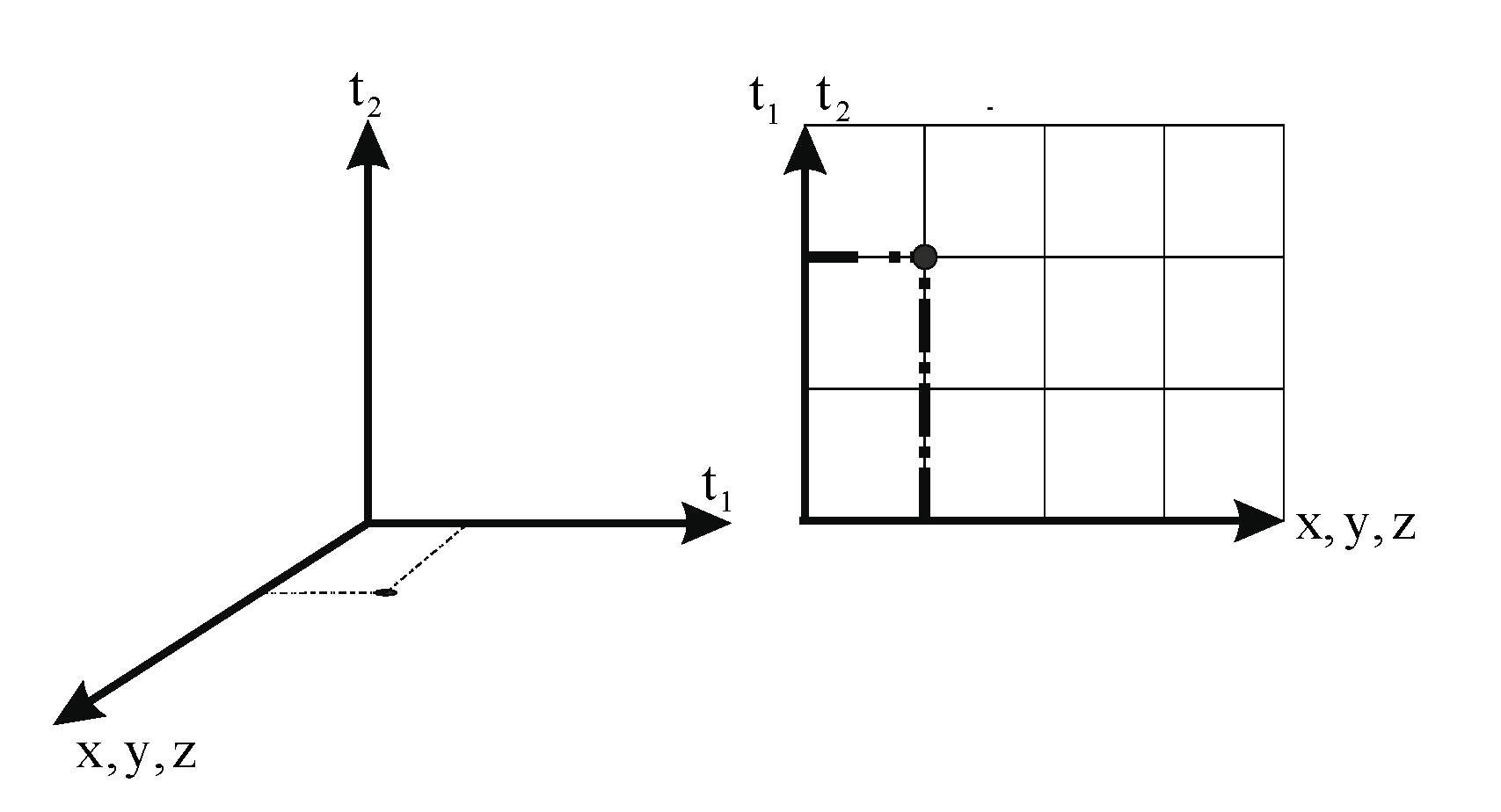
The space-time framework considered in this study is a Euclidean 6-dimensional manifold, denoted as 3+3, comprising three spatial coordinates (x,y,z) and three temporal coordinates (t−,t, t+) (2.1) From the standpoint of an external observer, time is structured as a three-dimensional imaginary vector space, although it is directly perceived as a single observable dimension. (1.2) (2.2)

$$X=\left(x_1,x_2,x_3,t_1,t_2,t_3\right)\in R^6 \left(1.2\right)$$

$$d{s}^2=d{x_1}^2+d{x_2}^2+d{x_3}^2-{(c}^{2}d{t_1}^2+c^{2}d{t_2}^2+c^{2}d{t_3}^2) (2.2)$$

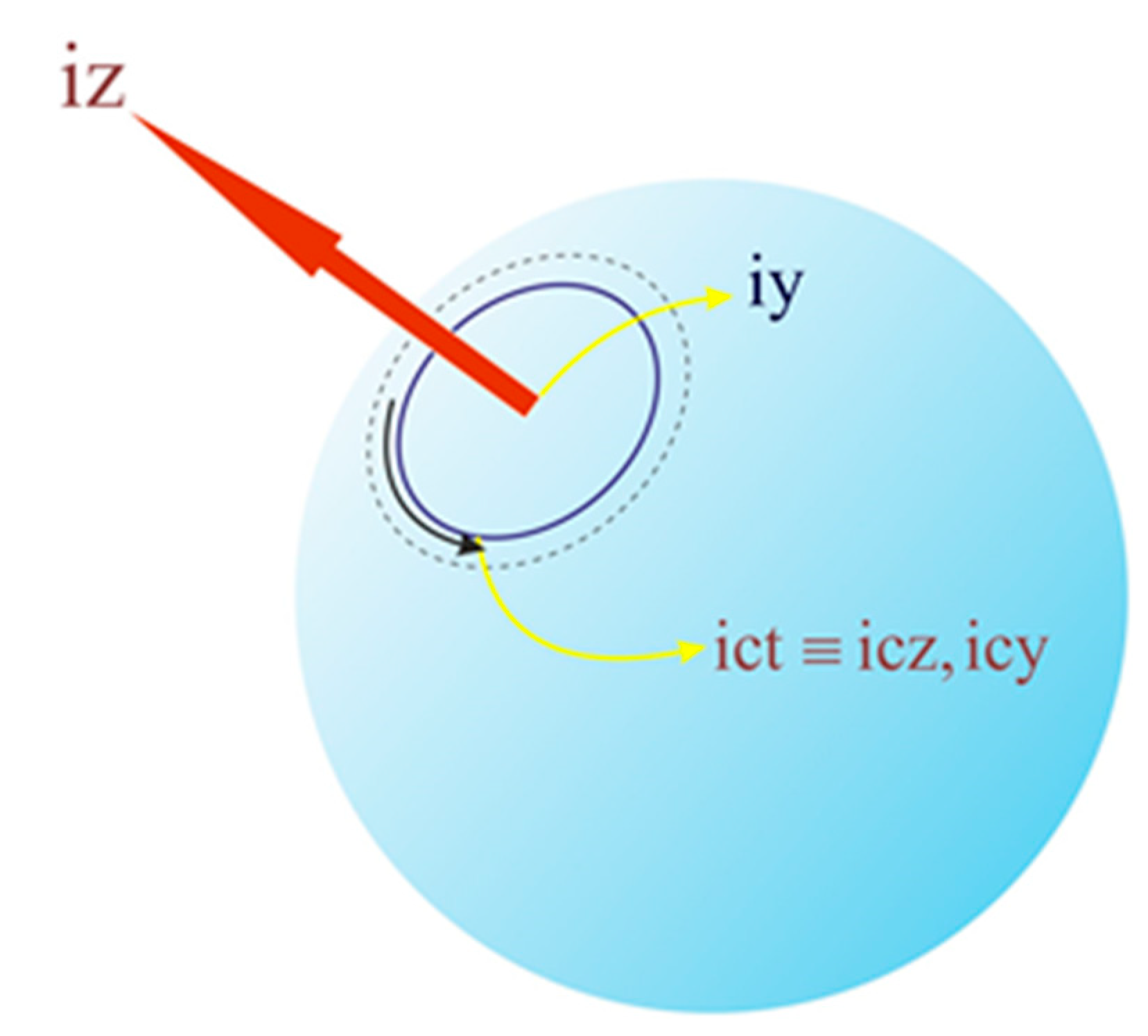
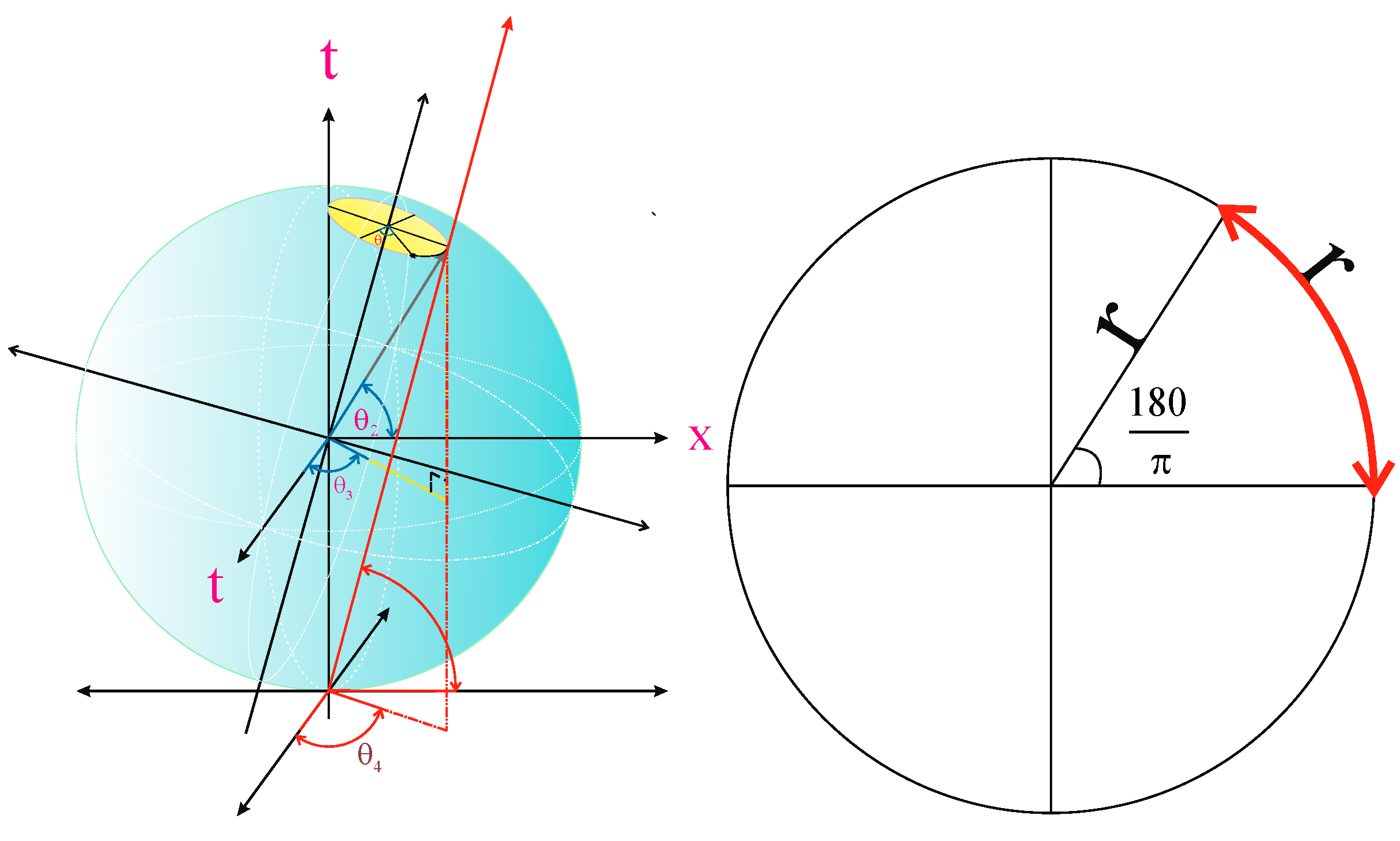
The y and z spatial dimensions are imaginary from the perspective of one-dimensional entities confined to motion along a circular path. This circle is situated on the surface of a three-dimensional sphere that undergoes continuous expansion (see Figure 1). As a result of their limited frame of reference, these one-dimensional observers perceive two imaginary dimensions projected onto a single imaginary direction due to parallax effects. Additionally, the temporal structure includes an internal dimension.

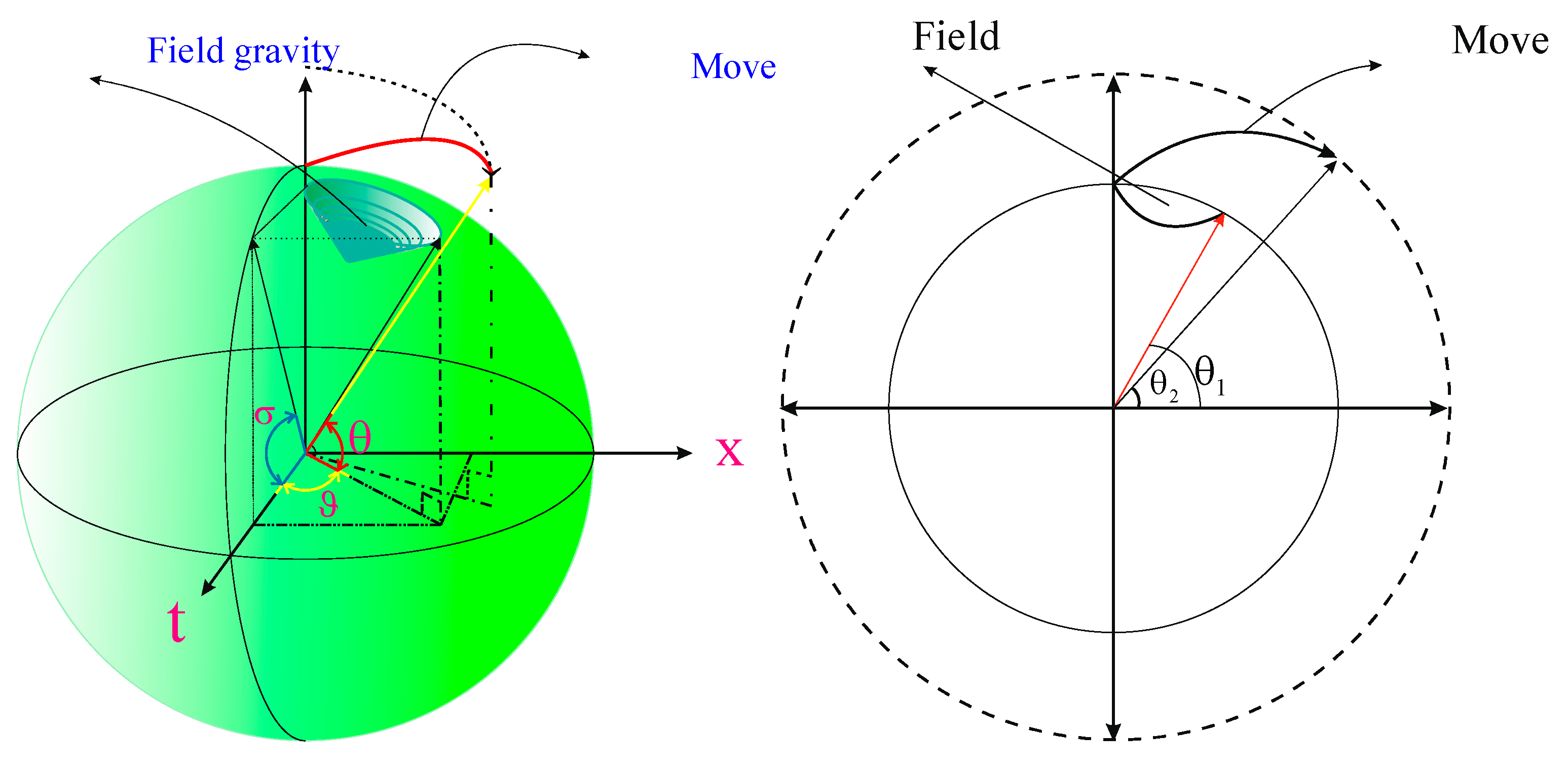
Time dilation the rate of progression through the time dimension is influenced by both the mass and velocity of the observer. These two factors are directly associated with the eccentricity of the ellipse describing the observer's trajectory in space-time (Figure 2). The eccentricity defined in spatial dimensions affects the temporal dimensions as well. From the standpoint of extrinsic geometry, both relativistic time dilation due to motion and gravitational time dilation in a gravitational field can be formulated as a function of the angle θ (2.3). Variations in density or speed contribute to changes in eccentricity across the dimensions of space-time.

$$\sqrt{1-{\displaystyle \frac{v^2}{c^2}}}=\sin ({\cos }^{-1}\left({\displaystyle \frac{v}{c}}\right)) t={\displaystyle \frac{t_0}{\sin \theta }} t=t_0\sqrt{1-{\displaystyle \frac{2GM }{r{c}^2}}} \left(2.3\right)$$

The passed distance in space is real six-dimensional from the perspective of space-time. But the distance from the perspective of 4 or 5-dimensional space-time is expressed in hyperbolic geometry. (2.4) (2.5)

$$\mathit{i}\mathit{n}\mathit{t}\mathit{r}\mathit{i}\mathit{n}\mathit{s}\mathit{i}\mathit{c} \mathit{g}\mathit{e}\mathit{o}\mathit{m}\mathit{e}\mathit{t}\mathit{r}\mathit{y},\mathit{d}{\mathit{s}}^2=\mathit{d}{{\mathit{x}}_1}^2+\mathit{d}{{\mathit{x}}_2}^2+\mathit{d}{{\mathit{x}}_3}^2+{\mathit{c}}^2\mathit{d}{{\mathit{t}}_1}^2+{\mathit{c}}^2\mathit{d}{{\mathit{t}}_2}^2-{\mathit{c}}^2\mathit{d}{{\mathit{t}}_3}^2\left(2.4\right)$$

$$\mathit{e}\mathit{x}\mathit{t}\mathit{r}\mathit{i}\mathit{n}\mathit{s}\mathit{i}\mathit{c} \mathit{g}\mathit{e}\mathit{o}\mathit{m}\mathit{e}\mathit{t}\mathit{r}\mathit{y},\mathit{d}{\mathit{s}}^2=\mathit{d}{{\mathit{x}}_1}^2+\mathit{d}{{\mathit{x}}_2}^2+\mathit{d}{{\mathit{x}}_3}^2+\mathit{d}{{\mathit{t}}_1}^2+\mathit{d}{{\mathit{t}}_2}^2+\mathit{d}{{\mathit{t}}_3}^2 \left(2.5\right)$$

Eccentricity in one axis causes eccentricity in other axes. As a result of this eccentricity, the path traversed in space-time has a rotation equal to ¼ of the circumference of the hypothetical circle with the radius of the density (field). Figure 3

As a result of defining the passed distance in space-time, is dependent on the space-time expansion, the light speed as well as eccentricity in six-dimensional space-time. (2.6)

$$\eta =\mathit{sin}({\mathit{cos}}^{-1}({\displaystyle \frac{\mathsf{\Delta }x}{c}})) ,\mu =\mathit{cos}({\mathit{cos}}^{-1}\begin{array}{c}({\displaystyle \frac{\Delta x}{c}})) \\ \end{array}$$

$$\mu =\mathit{sin}({\mathit{cos}}^{-1}({\displaystyle \frac{\Delta t}{c}})) ,\eta =\mathrm{c}\mathrm{o}\mathrm{s}({\mathit{cos}}^{-1}({\displaystyle \frac{\Delta t}{c}})) (2.6)$$

$$\mathsf{\theta }+\mathsf{\varphi }=90\Rightarrow {\sin }^2\theta {\mathit{sin}}^2\varphi =(\sin \theta \cos \varphi \left)\right(\sin \varphi cos\theta )={\mathit{cos}}^2\theta {\mathit{cos}}^2\varphi$$

$${\mathit{cos}}^2\theta ={\mathit{sin}}^2\left(90-\theta \right)\Rightarrow \varphi =90-\theta$$

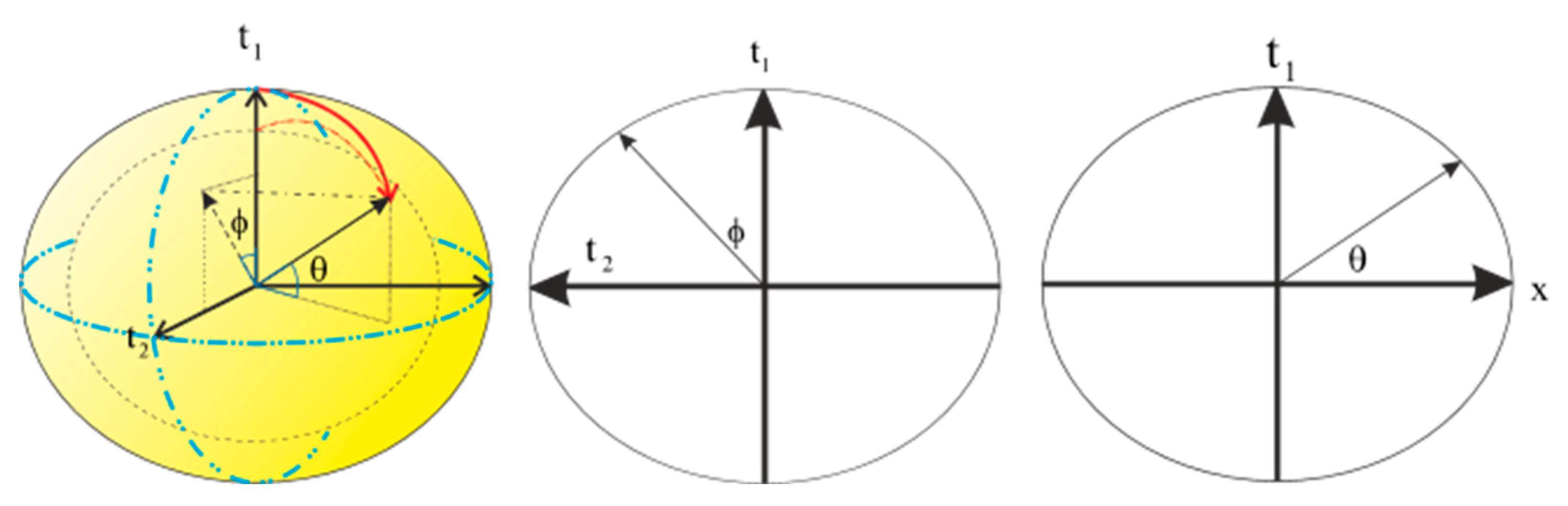
In six-dimensional space, there are five degrees of freedom. From the perspective of 4–dimensional space-time, two-time dimensions are observed in one dimension. Consequently, the two angles, related to eccentricity are expressed by the angle θ. The angle κ is also for expansion and final movement in time. Figure 4

While moving the rigid object in space, the radius of the field and object lengths change which is proportional to density. The angles related to eccentricity exist in equilibrium in the two-time dimensions. (2.7)

$$\theta ={\displaystyle \frac{180}{\pi }}, \varphi =90-{\displaystyle \frac{180}{\pi }} \left(2.7\right)$$

$$\sin \left(90-{\displaystyle \frac{180}{\pi }}\right)=\mathrm{c}\mathrm{o}\mathrm{s}({\displaystyle \frac{180}{\pi }} ) ,\mathit{cos}\left(90-{\displaystyle \frac{180}{\pi }}\right)=sin\left({\displaystyle \frac{180}{\pi }}\right)$$

With consideration of the two-time axles, the matter is stressed by space–time. The exerted stress on the matter from time dimensions is twice the exerted stress from space dimensions. This twice proportion has a direct connection with the golden constant. (2.8)

$$\phi ={\displaystyle \frac{x+\sqrt{x^2+(2{x)}^2}}{2x}}={\displaystyle \frac{{\overrightarrow{F}}_X+\sqrt{{{\overrightarrow{F}}_X}^2+{{\overrightarrow{F}}_t}^2}}{{\overrightarrow{F}}_t}} (2.8)$$

Figure 5. Two dimensions of time are seen from the perspective of three-dimensional space in one dimension, and as a result, this causes the material to experience double stress from the time dimensions.

Figure 5. Two dimensions of time are seen from the perspective of three-dimensional space in one dimension, and as a result, this causes the material to experience double stress from the time dimensions.

From the perspective of extrinsic geometry, the imaginary dimension of time is a real dimension. And the distance traveled in space-time is a real path over time. (2.9)

$$(r\left(\cos \left(\theta \right)\right)+isin(\theta \left)\right)\left)\right(r\left(\cos \left(\theta \right)\right)-isin\left(\theta \right)\left)\right)=r^2 \left(2.9\right)$$

$$\eta c=\Delta t , \mu c=\mathsf{\Delta }x \Rightarrow {\Delta x}^2+\Delta t^2=c^2\Rightarrow d{s}^2=c^{2}d{t}^2-d{x}_1^2-d{x}_2^2-d{x}_3^2$$

The angles θ and ϕ indicate the extent of eccentricity. The metric of space-time is expressed based on the two angles of θ, according to the surface metric of the sphere (3sphere). (2.10)

The matter with a 3-dimensional nature creates heterogeneity in the space density with higher dimensions. As a result of this heterogeneity, matter moves in space–time. Meanwhile, heterogeneity is a factor in creating eccentricity and stress to the material. Based on creating heterogeneity in space–time structure by matter and energy, density can be expressed in the form of passed distance in space–time. The oscillation of heterogeneity in space-time creates gravitational mass. Mass cannot exist in the past or future; therefore, expressing negative density is necessary for the Energy momentum tensor (2.11).

$$\sin 0=0\Rightarrow x,t\ne c \xi =\mathrm{s}\mathrm{i}\mathrm{n}({\cos }^{-1}\left({\displaystyle \frac{∆x}{c}}\right))+sin({\mathit{cos}}^{-1}\left({\displaystyle \frac{∆y}{c}}\right))+sin({\mathit{cos}}^{-1}\left({\displaystyle \frac{∆z}{c}}\right))$$

$$t={\displaystyle \frac{t_0}{\xi }}\equiv t=t_0\sqrt{1-{\displaystyle \frac{2GM}{r{c}^2}}}\Rightarrow c\left({{\eta }^2}_1+{{\eta }^2}_2+{{\eta }^2}_3\right)=r_{x,\rho }c\Rightarrow \mathrm{s}\mathrm{i}\mathrm{n}\left({\cos }^{-1}({\displaystyle \frac{\sqrt{2GM}}{c\sqrt{r}}}\right))\equiv sin\varphi$$

$$t={\displaystyle \frac{t_0}{\eta }} , l={\displaystyle \frac{l_0}{\eta }} , m={\displaystyle \frac{m_0}{\eta }} m^t={\displaystyle \frac{h\nu }{c^2}} ,{\left( \rho c\right)}^{{\displaystyle \frac{1}{2}}}=∆\acute{x} ,r_{x,\rho }=∆x+∆\acute{x} ,$$

$$\left(m^t+m_x\right)={\displaystyle \frac{m^t}{\eta }} \to sin\theta ={\displaystyle \frac{m^t}{m^t+m_x}} (2.11)$$

$$\left(\rho c\right)={∆\acute{x}}^2 , \left({\displaystyle \frac{c}{\rho }}\right)={∆\acute{t}}^2$$

$$\rho =\left({\displaystyle \frac{m^t}{2{\pi }^2{r}^3}}\right) ,m/\rho ={\displaystyle \frac{2{\pi }^2{r}^3}{\eta }}$$

$$T_{\mu \nu }=\left[\begin{array}{cccccc}-\rho & 0& 0& 0& 0& 0\\ 0& -\rho & 0& 0& 0& 0\\ 0& 0& \rho & 0& 0& 0\\ 0& 0& 0& P& 0& 0\\ 0& 0& 0& 0& P& 0\\ 0& 0& 0& 0& 0& P\end{array}\right] \left(2.11\right)$$

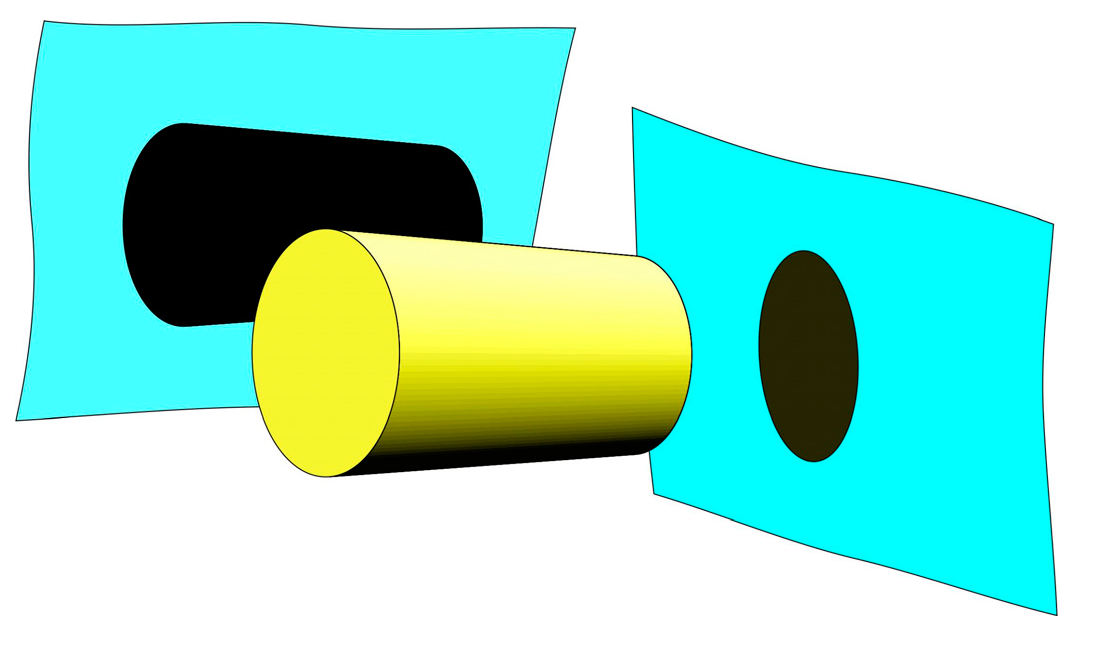
Möbius space extends the properties of lower-dimensional systems into higher-dimensional contexts. This idea draws from the well-known Möbius strip a two-dimensional surface embedded in three-dimensional space formed by applying a half-twist to a strip before joining its ends. In a similar fashion, Möbius space enables properties associated with lower dimensions to be preserved and transformed through rotational operations, resulting in nontrivial and often counterintuitive behaviors. This framework offers a novel lens for examining the structure of space, time, and the physical universe.

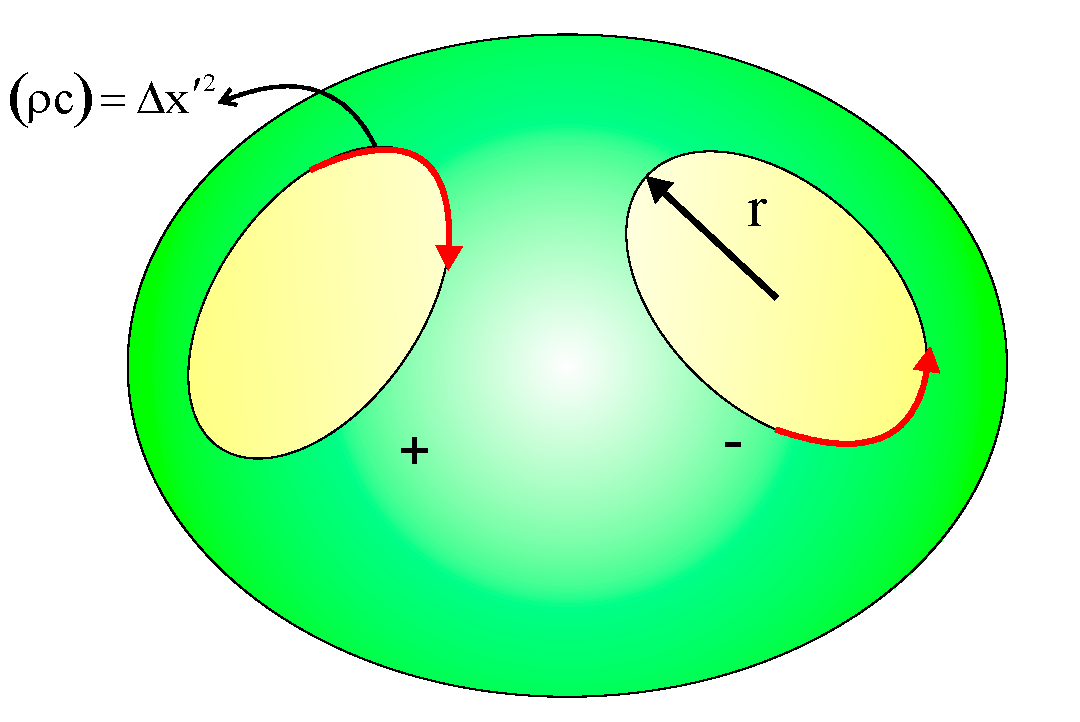
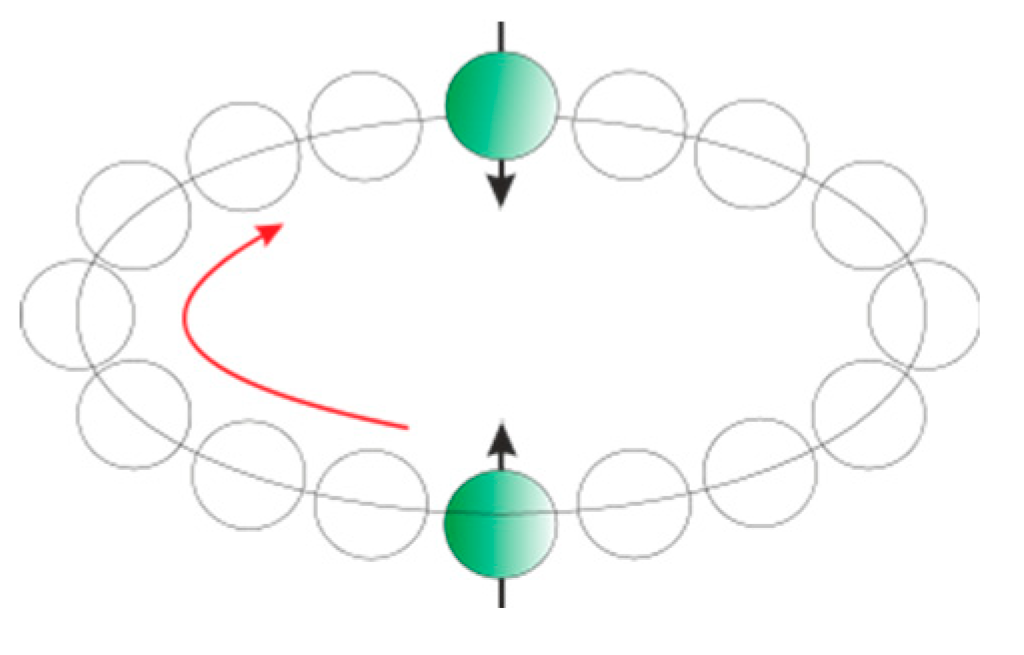
In this context, objects within space-time are modeled as rotating around a field whose radius corresponds to their density-defined radius in higher dimensions. This radius is defined such that it represents the two-dimensional density distributed over an arc of one radian (Figure 6). The matter field undergoes simultaneous rotation and displacement, with the radius of rotation evolving along with cosmic expansion (Figure 7). The measure of density or spatial heterogeneity is analogized to the arc length of one radian on a circular path. The sum of a density value and its inverse (or negative counterpart) across two dimensions equals one-quarter of a full circular perimeter.

As illustrated in Figure 3, an object’s trajectory in one dimension may be altered along the geodesic path of space-time in another. This interaction results in a quarter-turn rotation across three-dimensional space, and the principle is extended to higher dimensions as stated in (2.12). This rotation is attributed to the conservation of object density and leads to eccentricity along other axes in the expanding space-time geometry.

$$M\left\{1,-1,-\mathrm{1,0},-\mathrm{1,1}\right\}$$

$$L=\left({\displaystyle \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$360$}\right.}\right)2\pi r \theta =90\Rightarrow L=\left({\displaystyle \frac{1}{4}}\right)2\pi r\Rightarrow \left({\displaystyle \frac{1}{2\pi }}\right)=\left({\displaystyle \raisebox{1ex}{$\raisebox{1ex}{$180$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.$}\!\left/ \!\raisebox{-1ex}{$360$}\right.}\right)=1Rad$$

$$\left({\displaystyle \frac{90-\frac{180}{\pi }}{360}}\right)=\left({\displaystyle \frac{1}{4}}\right)-1Rad=\left({\displaystyle \frac{\pi -2}{4\pi }}\right)\Rightarrow \left({\displaystyle \frac{\pi -2}{4\pi }}\right)+\left({\displaystyle \frac{1}{2\pi }}\right)=\left({\displaystyle \frac{1}{4}}\right) \left(2.12\right)$$

$${\left({\displaystyle \frac{1}{2}}\right)}^{2}2\pi r {\left({\displaystyle \frac{1}{2}}\right)}^{3}4\pi r^2 {\left({\displaystyle \frac{1}{2}}\right)}^{4}2{\pi }^2{r}^3 {\left({\displaystyle \frac{1}{2}}\right)}^5{\displaystyle \frac{8}{3}}{\pi }^2{r}^4 {\left({\displaystyle \frac{1}{2}}\right)}^6{\pi }^3{r}^5$$

$$a_{\mu \nu }=\left[\begin{array}{ccc}{cos}^2\theta {cos}^2\varphi & 0& 0\\ 0& {cos}^2\theta & 0\\ 0& 0& 1\end{array}\right]\Rightarrow \left|a_{\mu \nu }\right|={cos}^2\left(60\right){cos}^2\left(120\right){cos}^2\left(120\right)={\left({\displaystyle \frac{1}{2}}\right)}^6$$

3. Geometry and Fundamental Constants of Physics

The rotation of objects in five-dimensional space is described by the Golden proportion. (3.13) The Golden ratio, π, and e are geometrically connected to the fundamental constants of physics, such as the gravitational constant and Planck’s constant, within a six-dimensional space-time.

. (3.13)

$${\pi }^3{r}^5\in \left({\displaystyle \frac{1}{6}}\right){\pi }^3{r}^6 , \ln \left(\phi \right)\approx {\left({\displaystyle \frac{1}{2}}\right)}^6{\pi }^3$$

$$\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3\left(\frac{1}{6}\right){\pi }^3\left(\frac{\left(\frac{3\pi -6}{2\pi }\right) }{360}\right){\phi }^3}{c}}\right)\cong 6.6765834\times {10}^{-11}\cong G \left(3.13\right)$$

$${\left({\displaystyle \frac{{\left(\frac{1}{2\pi }\right)}^3+{\left(\frac{1}{2}\right)}^6{\pi }^3{e}^{\tan \left(\frac{180}{\pi }\right)}}{c^2}}\right)}^2=6.5693903027\times {10}^{-34}\cong h$$

$$\left({\displaystyle \frac{{{\left(\frac{3\pi -6}{2\pi }\right)}^2\left(\frac{\pi \phi }{3}\right)}^2}{c^4}}\right)=1.05597784887\times {10}^{-34}=\hslash , \left({\displaystyle \frac{90-\raisebox{1ex}{$180$}\!\left/ \!\raisebox{-1ex}{$\pi $}\right.}{1÷6}}\right)=\left({\displaystyle \frac{3\pi -6}{2\pi }}\right)$$

The resulting force from rotating objects around the field and then the performed work in six-dimensional space were calculated by the Planck constant coefficient. (3.14) The Planck constant relates to object motion in space-time, while the gravitational constant describes resistance to the expansion of space-time. Figure 7

$$F=m\left({\displaystyle \frac{{\partial }^{2}x}{\partial t^2}}\right)=m\left({\displaystyle \frac{{∆x}^2}{r}}\right) , E=m\left({∆x}^2+{∆t}^2\right) , W_x=F.d_x , W^t=F.d^t$$

$${\displaystyle \frac{h\nu }{c^2}}=m^t , {\displaystyle \frac{F}{a}}=m_x , h={\displaystyle \frac{W}{c^4}} \Rightarrow m^t={\displaystyle \frac{W\nu }{c^6}} \left(3.14\right)$$

$$F=m\left({\displaystyle \frac{v^2}{r}}\right)\Rightarrow W=F.∆L\to L=\left({\displaystyle \raisebox{1ex}{$\theta $}\!\left/ \!\raisebox{-1ex}{$360$}\right.}\right)2\pi r , F=a{e}^{\pm i\theta }=a(cos\theta +isin\theta )$$

Two forces are exerted on the rigid object by the higher dimensions. One force causes the object to move perpendicular to the axis of expansion, and the other force opposes the direction of space-time expansion of space-time. As a whole, the object is rotating around a field, and the field is also rotating around an expanding sphere. Changing angles of ɑ and β indicate rigid object motion around a field with higher dimensions. (3.15)

$$\left({\displaystyle \frac{\overrightarrow{{\mathit{F}}_{\mathit{x}}}+\mathit{c}}{\overrightarrow{{\mathit{F}}_{\mathit{t}}}}}\right)=\mathit{\phi }\Rightarrow {\mathbf{tan}}^{-1}\left(2\right)={63.4349488}^{°}, \left({\displaystyle \frac{{\left(\mathbf{cos}\mathit{\theta }+\mathit{i}\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }\right)}^2{\mathit{d}}^3}{{\mathit{c}}^4}}\right)=\mathit{h}\Rightarrow \mathit{d}=\mathit{c}\mathit{o}\mathit{t}\left(30.50389\right)$$

$$90-63.43=26.57\Rightarrow 30.50389-26.57=3.933\Rightarrow \mathit{\alpha }=26.57\to \mathit{\alpha }+{3.933}^{\circ }$$

$$\left({\displaystyle \frac{{\left(\mathit{cos}\mathit{\theta }+\mathit{i}\mathit{s}\mathit{i}\mathit{n}\mathit{\theta }\right)}^3{\mathit{d}}^3}{\mathit{c}}}\right)=\mathit{G}\Rightarrow \mathit{d}=\mathbf{cos}\left(59.99\right),63.43-59.99=3.4346\left(3.15\right)$$

Cosmology constant has a direct connection with the Planck constant, the gravity constant, and 3 natural numbers. (3.16)

$$h^2{G}^2{e}^{{\left(\phi \right)}^2{\pi }^3}=\mathsf{\Lambda }\left(3.16\right)$$

Observations related to the planet's movement express a deep geometrical relationship between fundamental constants. (3.17)

$${\left({\displaystyle \frac{\mathit{\pi }-2}{2}}\right)}^6\left({\displaystyle \frac{\mathit{h}\mathit{e}}{\mathit{c}}}\right)={\displaystyle \frac{8\mathit{\pi }\mathit{G}}{{\mathit{c}}^4}}\Rightarrow {\left({\displaystyle \frac{\mathit{\pi }-2}{2}}\right)}^6\cong {\displaystyle \frac{8\mathit{\pi }\mathit{G}}{{\mathit{c}}^3\mathit{h}\mathit{e}}} \left(3.17\right)$$

The radius of the object field in space–time has a direct relationship with exerted force by the higher dimensions. Due to this direct relationship, the proportions between these forces have a constant with density. These proportions follow the golden constant, Euler's number, and π.

Figure 8

.

4. Wave Function

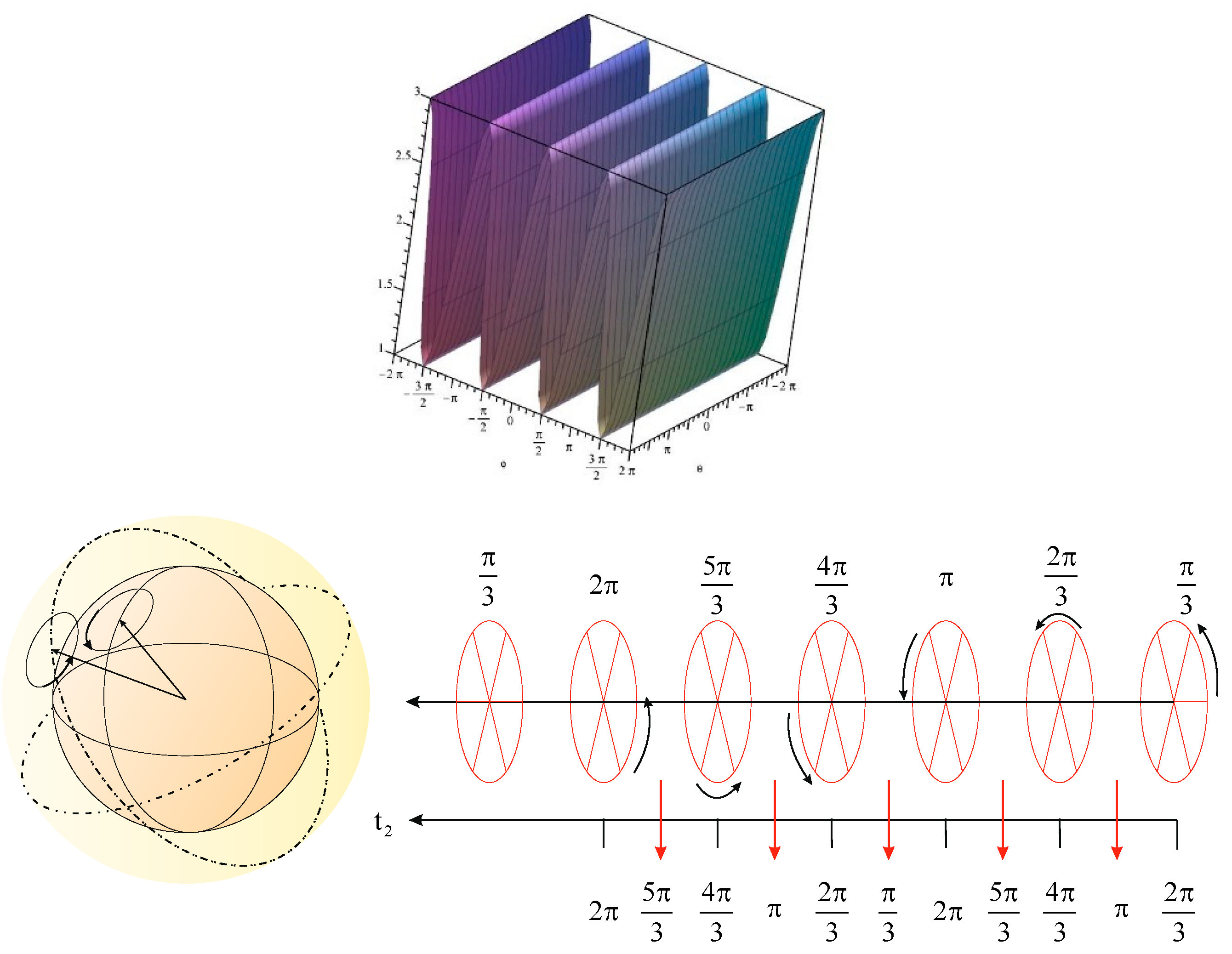
The wave function in quantum mechanics has expanded over time. Concerning the object field, the eccentricity of space-time dimensional, negative density, object rotation around the field, and field rotation, the structure of wave function was expressed in the 6-dimensional space-time (4.18) Quantization depends on two types of rotations in space. Figure 9

Concerning affine transformation, elliptic parametric equation, Fourier Series eccentricity of elliptic, and metric of 6-dimensional space-time, the relationship between wave function and wave tensor was expressed. (4.19) Meanwhile, the tensor Ψ expresses the created rotation stress by space-time to the matter. (4.19). Positive and negative amounts that have a relationship with object rotation in higher dimensions are variable depending on the phase, speed, and density.

5. Field Structure and Force

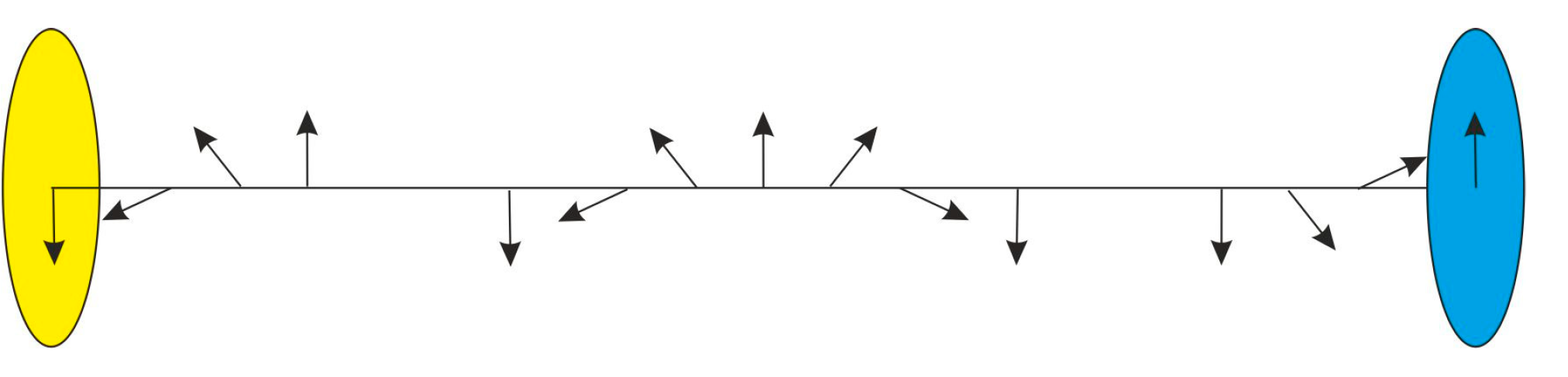
The electrical load has a direct relationship with the phase of object field rotation. Particles with no mass or without loads have two opposite rotation phases. Photons transport energy and follow from the geodesics of quantized space-time. the photons can be decomposed into a pair couple of electron-positron fields. Each pack of energy has a particular geometric structure, and on this basis, the field radius and the 2nd radius can be calculated with consideration of the performed work in space and time. (5.20) Electrical load has a direct relationship with the phase of the field in higher dimensions. Figure 10

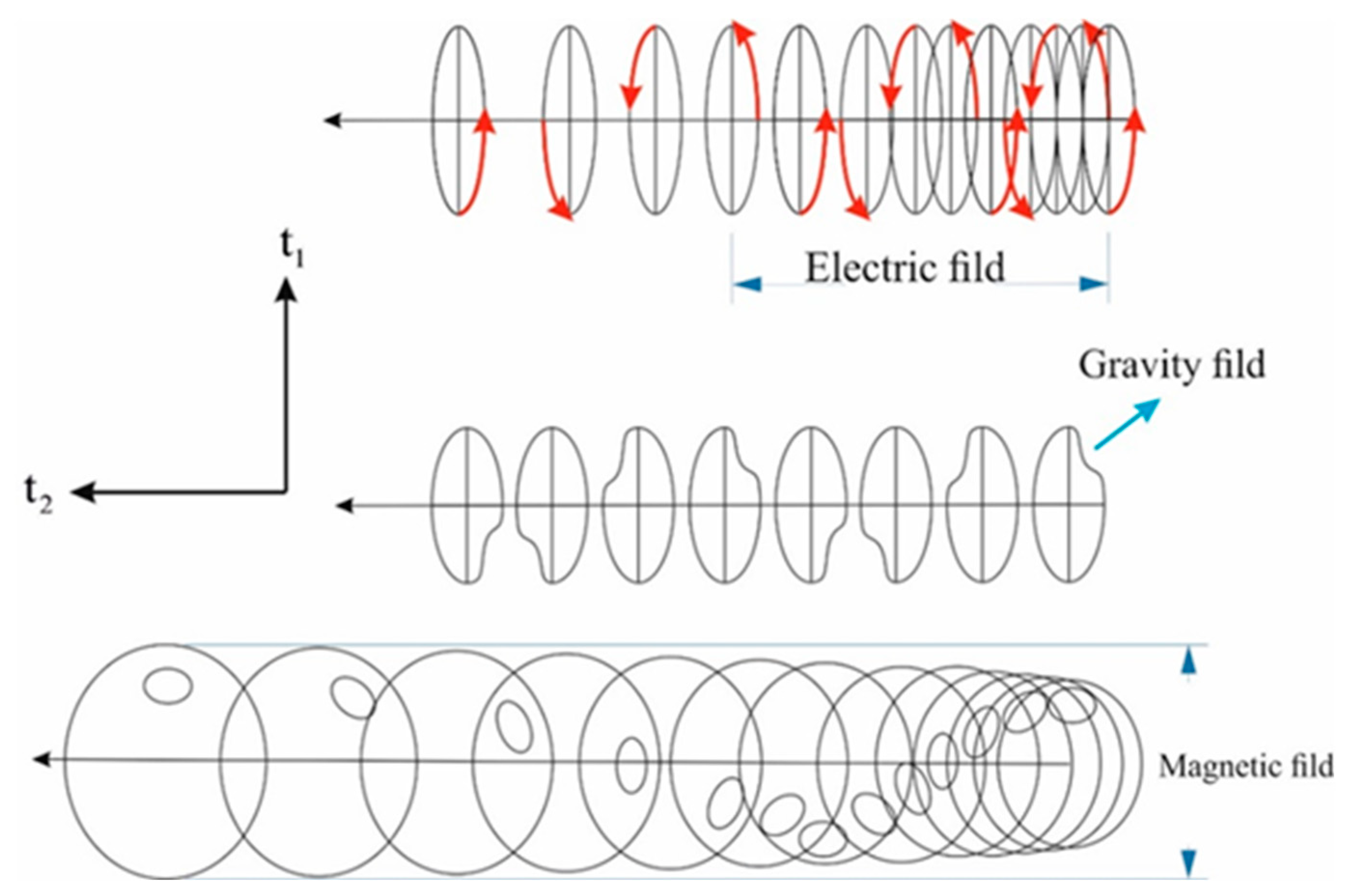
Changing the speed of rotation phases in the electromagnetic field is more than other space-time points. Each particle follows space-time geodesics within the limits of an electrical field. Eccentricity, in the gravitational field and electromagnetic fields, creates phase-changing speed. Figure 11

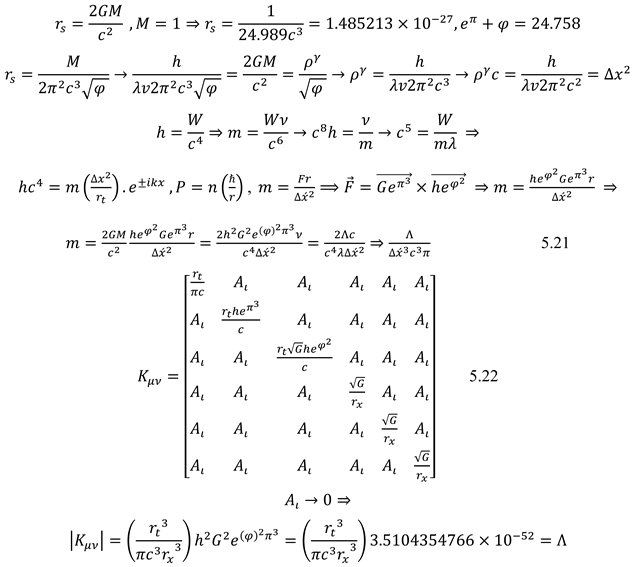
The mass obtained from motion in space is (inertial mass) and the mass obtained from motion in time is (gravitational mass). The exerted stress from space-time to matter concerns the Planck constant and gravitation constant. This stress intensity is very insignificant. However, the exerted stress is observable concerning the rotation around the field and the passage of time. Tensor for space-time stress based on Planck constant, gravitation constant, and cosmology constant indicate the quantum Structure of space-time. (5.21) (5.22). The “K” tensor expresses the exerted stress to matter in space-time with higher dimensions. This Stress is, therefore, a factor in producing spin, electrical load & electromagnetic fields. K tensor has a direct relationship with wavelength and cosmology constant. (5.22) The radius equal to density length (field radius) is ‘r x’ and the radius for the variable of field rotation is ‘r t’. It is not able to be greater than a specific amount that is dependent on the object's mass. Consequently, 'r t’ is periodic.

Based on Movement in time dimensions and also work definition, the relationship of the Planck constant and gravitational constant is specified with the cosmology constant. (5.23)

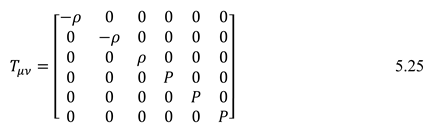
The type and intensity of electrical load and magnetic field depend on other components of the k tensor. Momentum tensor and energy with new coefficient make the general relativity equation more complete. (5.24). Mass in space-time can cause inhomogeneity, which is represented by negative density. (5.25)

6. Curvature in Six-Dimensional Space-Time

Ricci tensor expresses curvature in 4-dimensional space-time; by adding two Dimensions of time another definition of curvature is formed. Expression of the sphere surface curvature by Riemann tensor and Ricci tensor in six-dimensional space-time may not be comprehensive. (6.26)

Concerning space rotation, the Ricci tensor expresses curvature in the time dimension length, and space dimensions. Curvature in time means changing wavelength in higher dimensions and becoming closer or farther the states of space-time from each other. Generally, Ricci's 6-dimensional tensor can only be defined during the time in the case of existing various masses. (6.27)

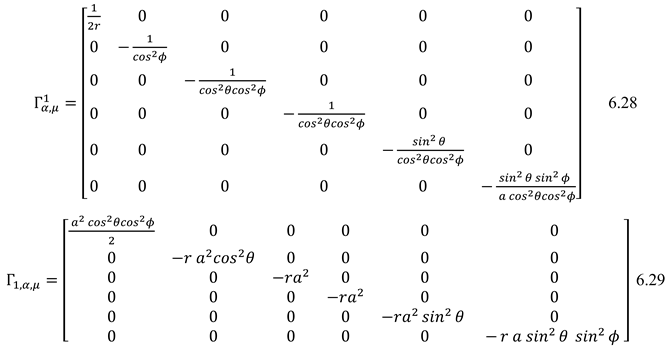
Using the introduced metric, two types of Christoffel symbols were expressed in 6-dimensional space. (6.28) (6.29)

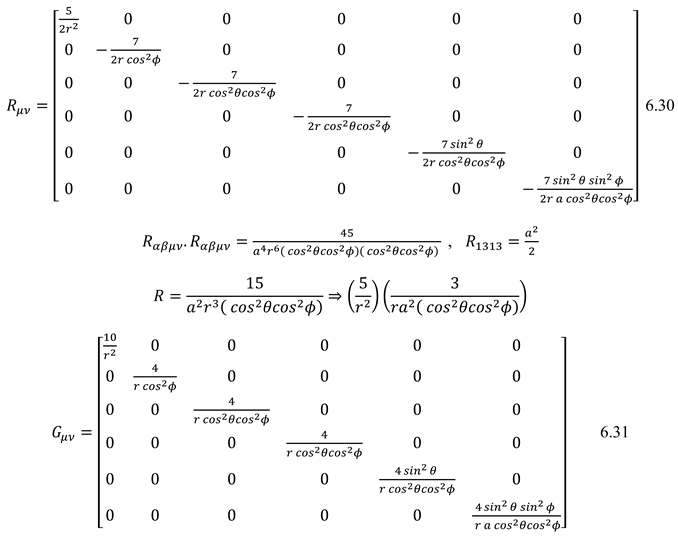
Einstein tensor, Scalar Ricci, and Ricci tensor were obtained using Christoffel symbols. (6.30) (6.31) Geometrical connection is hidden between space curvature and time length curvature in Scalar Ricci. (6.30)

The general equation was obtained for general relativity and quantum mechanics. (6.32) that Whenever mass is high (not in the scale of black holes), wave function and electromagnetic field are disappeared, and whenever mass and density are low, quantum behavior is observed (6.32)

$$\mathsf{\mu },\nu =\mathrm{1,2},\mathrm{3,4},\mathrm{5,6}$$

$${\mathsf{\Psi }}_{\mathit{\mu }\mathit{\nu }}+{\mathit{R}}_{\mathit{\mu }\mathit{\nu }}-{\displaystyle \frac{1}{2}}\mathit{R}{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}+\mathsf{\Lambda }{\mathit{g}}_{\mathit{\mu }\mathit{\nu }}={\left({\displaystyle \frac{\mathit{\pi }-2}{2}}\right)}^6\left({\displaystyle \frac{\mathit{h}\mathit{e}}{\mathit{c}}}\right){\mathit{T}}_{\mathit{\mu }\mathit{\nu }}+{\mathit{K}}_{\mathit{\mu }\mathit{\nu }}\left(6.32\right)$$

7. Quantum Mechanics

Hilbert space is a complex of various states for a particle in a time loop. A particle rotates around the field with a density radius in higher dimensions. In a moment a particle can have two upper and lower spins. Measurement reduces the dimensions of a particle to four dimensions. Figure 12

Measuring a phenomenon in higher dimensions causes the wave function to collapse to the lower dimensions, resulting in different observable states. Figure 13

Despite the distance of the two objects from each other, they can have similar states. Regarding the masses with similar densities, these states are contrariwise. Figure 14

Due to direct relationship of mass and momentum with wave function and direct relationship of wave function with space-time structure, the whole similar particles like electrons, photons, and protons,... follow space geodesics. When one of the entangled particles is measured, another particle’s all states can be predicted with certainty. Figure 15

Before measuring a particle, there is no orientation in 3-dimensional space. Measuring in the time state π/3 causes the particle’s dimension collapses into a four-dimensional space; for this reason, we select the states from the tensor Ψ which are constant for all the particles with a specific momentum. As a result, entanglement will never occur between two particles in the coordinate system of relativistic. Entanglement has been institutionalized in the space-time structure. Bell's Inequality defect is due to the existence of similar states in the space-time rotating structure. (7.33)

$$\left|\mathit{\gamma }⟩={\mathit{c}}_0\left|{\mathit{a}}_0\right.⟩\right.+{\mathit{c}}_1\left|{\mathit{a}}_1\right.⟩,\left|\mathit{\tau }⟩={\mathit{d}}_0\left|{\mathit{b}}_0\right.⟩\right.+{\mathit{d}}_1\left|{\mathit{b}}_1\right.⟩$$

$$\left|\mathit{\gamma }\right.⟩⨂\left|\mathit{\tau }\right.⟩={(\mathit{c}}_0{\mathit{d}}_0\left|{\mathit{a}}_0\right.⟩\left|{\mathit{b}}_0\right.⟩+{\mathit{c}}_0{\mathit{d}}_1\left|{\mathit{a}}_0\right.⟩\left|{\mathit{b}}_1\right.⟩)+{(\mathit{c}}_1{\mathit{d}}_0\left|{\mathit{a}}_1\right.⟩\left|{\mathit{b}}_0\right.⟩+{\mathit{c}}_1{\mathit{d}}_1\left|{\mathit{a}}_1\right.⟩\left|{\mathit{b}}_1\right.⟩)$$

$$\left|00\right.⟩=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right],\left|01\right.⟩=\left[\begin{array}{c}0\\ 1\\ 0\\ 0\\ 0\\ 0\end{array}\right],\left|10\right.⟩=\left[\begin{array}{c}0\\ 0\\ 1\\ 0\\ 0\\ 0\end{array}\right],\left|11\right.⟩=\left[\begin{array}{c}0\\ 0\\ 0\\ 1\\ 0\\ 0\end{array}\right],\left|01\right.⟩=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 1\\ 0\end{array}\right],\left|00\right.⟩=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\\ 0\\ 1\end{array}\right]$$

$$\left|\tilde{\mathit{\psi }}⟩={\mathit{\alpha }}_1\left|{\mathit{A}}_1⟩+{\mathit{\alpha }}_2\left|{\mathit{A}}_2⟩+{\mathit{\alpha }}_3\left|{\mathit{A}}_3⟩+{\mathit{\alpha }}_4\left|{\mathit{A}}_4⟩+\right.\right.\right.\right.\right.{\mathit{\alpha }}_5\left|{\mathit{A}}_5⟩+{\mathit{\alpha }}_6\left|{\mathit{A}}_6⟩\right.\right.$$

$${\mathit{b}}_1=\mathit{c}\mathit{o}\mathit{s}\left({\displaystyle \frac{\mathit{\theta }}{2}}\right),{\mathit{b}}_2={\mathit{e}}^{\mathit{i}\mathsf{\Phi }}\mathit{s}\mathit{i}\mathit{n}\left({\displaystyle \frac{\mathit{\theta }}{2}}\right),\sqrt{1-{\displaystyle \frac{{\mathit{v}}^2}{{\mathit{c}}^2}}}=\mathbf{sin}\left({\mathit{c}\mathit{o}\mathit{s}}^{-1}\left({\displaystyle \frac{\mathit{v}}{\mathit{c}}}\right)\right)=\mathit{s}\mathit{i}\mathit{n}\mathit{\theta },\mathit{v}\equiv ∆\mathit{x}$$

$$∆{\mathit{x}}^2\equiv \left(\mathit{\rho }\mathit{c}\right)\Rightarrow \mathit{\rho }\equiv \mathit{E}\equiv \mathit{\theta },\mathsf{\Phi }$$

$${\int }_0^{2\mathit{\pi }}{\left|\mathit{\psi }(\mathit{x},\mathit{t}))\right|}^2\mathit{d}\mathit{x}=1\to {\displaystyle \frac{2\mathit{\pi }}{6}}⟹\left({\displaystyle \frac{\mathit{\pi }}{3}}\right),\left({\displaystyle \frac{2\mathit{\pi }}{3}}\right),\left(\mathit{\pi }\right),\left({\displaystyle \frac{4\mathit{\pi }}{3}}\right),\left({\displaystyle \frac{5\mathit{\pi }}{3}}\right),\left(2\mathit{\pi }\right)$$

$${\mathit{A}}_1=\pm \left({\displaystyle \frac{\mathit{\pi }}{3}}\right),{\mathit{A}}_2=\pm \left({\displaystyle \frac{2\mathit{\pi }}{3}}\right),{\mathit{A}}_3=\pm \left(\mathit{\pi }\right),{\mathit{A}}_4=\pm \left({\displaystyle \frac{4\mathit{\pi }}{3}}\right),{\mathit{A}}_5=\pm \left({\displaystyle \frac{5\mathit{\pi }}{3}}\right),{\mathit{A}}_6=\pm \left(2\mathit{\pi }\right),$$

$$\left|\mathit{\Psi }⟩={\mathit{b}}_1\left|0⟩+{\mathit{b}}_2\left|1⟩\Rightarrow \right.\right.\right.\left|\mathit{\Psi }⟩={\mathit{b}}_1\left|0⟩+{\mathit{b}}_2\left|1⟩+{\mathit{b}}_3\left|0⟩+{\mathit{b}}_4\left|1⟩\right.\right.\right.\right.\right.$$

$$⟹{\displaystyle \frac{1}{\sqrt{2}}}(\left|00\right.⟩+\left|11\right.⟩$$

$$\left|\mathit{\eta }⟩={\mathit{z}}_0\left|{\mathit{a}}_0\right.⟩\right.+{\mathit{z}}_1\left|{\mathit{a}}_1\right.⟩+\acute{{\mathit{z}}_0}\left|{\mathit{a}}_0\right.⟩+\acute{{\mathit{z}}_1}\left|{\mathit{a}}_1\right.⟩,\left|\mathit{\mu }⟩={\mathit{d}}_0\left|{\mathit{b}}_0\right.⟩\right.+{\mathit{d}}_1\left|{\mathit{b}}_1\right.⟩+\acute{{\mathit{d}}_0}\left|{\mathit{b}}_0\right.⟩+\acute{{\mathit{d}}_1}\left|{\mathit{b}}_1\right.⟩$$

$$\left|\mathit{\eta }\right.⟩⨂\left|\mathit{\mu }\right.⟩={(\mathit{z}}_0{\mathit{d}}_0\acute{{\mathit{d}}_0}\acute{{\mathit{z}}_0}\left|{\mathit{a}}_0\right.⟩\left|{\mathit{a}}_0\right.⟩\left|{\mathit{b}}_0\right.⟩\left|{\mathit{b}}_0\right.⟩+\dots$$

$$\Rightarrow \left({\mathit{A}}_1+{\mathit{B}}_0\right)\mathit{\alpha }+\left({\mathit{A}}_0+{\mathit{B}}_1\right)\mathit{\beta }-\left({\mathit{A}}_1+{\mathit{B}}_1\right)\mathit{\gamma }\le 2$$

$$\left|〈\left({\mathit{A}}_1+{\mathit{B}}_0\right)\mathit{\alpha }+\left({\mathit{A}}_0+{\mathit{B}}_1\right)\mathit{\beta }-\left({\mathit{A}}_1+{\mathit{B}}_1\right)\mathit{\gamma }〉\right|\ge 2\left(7.33\right)$$

$${\mathit{c}\mathit{o}\mathit{s}}^2\left({\displaystyle \frac{\mathit{\pi }}{3}}\right)={\displaystyle \frac{1}{4}}\Rightarrow \mathit{S}\mathit{a}\mathit{m}\mathit{e}\mathit{r}\mathit{e}\mathit{s}\mathit{u}\mathit{l}\mathit{t}\le {\displaystyle \frac{1}{3}}$$

8. Results and Discussion

As a result of this research, the relationship between the three numbers π, the golden ratio, and Euler’s number defines the geometric structure of space and time in relation to matter and energy. The geometric and classical interpretation of spin, polarization, mass, and charge is one of the major achievements of this perspective. The intrinsic expansion of space within itself is the driving factor behind the arrow of time, and time represents the geometric potential difference arising from inhomogeneity in the spatial geometry.

The inhomogeneity caused by the presence of mass and energy within the fabric of space-time establishes a connection between Möbius space, the wav function, and spin. The existence of two orthogonal time dimensions and the resulting tension between them leads to the formation of the golden spiral within material structures. The violation of Bell’s inequality over time indicates the presence of these two orthogonal dimensions.

Entanglement, in its simplest interpretation, can be visualized as a boat positioned atop the peak of waves in the present moment. Based on this principle, the correlation between information within the structure of space-time gives rise to the phenomenon of entanglement. The rotation of electromagnetic and gravitational fields, as well as the direct connection between gravity and electromagnetism in Möbius space, is dependent on dimensional attributes. Möbius coils and capacitors have the ability to convert gravitational field fluctuations into electrical current and vice versa.

The physical verification of this relationship provides an experimental framework for researchers to test this theory. The deep connection between fundamental constants and geometric relations involving the three irrational numbers π, φ, and Euler’s number—as well as their relation to the cosmological constant—establishes a mathematical proof for the six-dimensional geometric structure of the universe.

Every mass possesses three spatial dimensions but also includes informational dimensions across time. Information concerning the past, present, and future forms a six-dimensional framework through the spatial rotation of matter and energy over time within a unified theory incorporating quantum mechanics. Based on this foundation, a classical interpretation of quantum mechanical events becomes possible.