Prerpints.org logo

You are currently viewing a beta version of our website. If you spot anything unusual, kindly let us know.

Leave Feedback
Preprint
Article

Improving Photovoltaic MPPT Performance through PSO Dynamic Swarm Size Reduction

Altmetrics

Downloads

190

Views

153

Comments

0

A peer-reviewed article of this preprint also exists.

Submitted:

07 August 2023

Posted:

08 August 2023

You are already at the latest version

Alerts
Abstract
Efficient energy extraction in photovoltaic (PV) systems relies on the effective implementation of Maximum Power Point Tracking (MPPT) methods. Conventional MPPT techniques often suffer from slow convergence speeds and suboptimal tracking performance, particularly under dynamic variation of environmental conditions. Smart optimization algorithms (SOA) using metaheuristic optimization algorithms can avoid this limitation inherent in the conventional MPPT methods. The problem of slow convergence of the SOA is avoided in this paper using a novel strategy called Swarm Size Reduction (SSR) utilized with Particle Swarm Optimization (PSO) algorithm, specifically designed to achieve short convergence time (CT) while maintaining exceptional tracking accuracy. The novelty of the proposed MPPT method introduced in this paper is the dynamic reduction of the swarm size of the PSO for improved performance of the MPPT of the PV systems. This adaptive reduction approach allows the algorithm to efficiently explore the solution space of PV systems and rapidly exploit to identify the global maximum power point (GMPP) even under fast fluctuation of uneven solar irradiance and temperature. This pioneering ultra-fast MPPT method represents a significant advancement in PV system efficiency and promotes the wider adoption of solar energy as a reliable and sustainable power source. The novel adaptive PSO algorithm also opens new possibilities for further innovations in optimization-driven applications, extending its potential impact on a diverse range of real-world challenges. The results obtained from this proposed strategy are compared with several optimization algorithms to validate its superiority.
Keywords: 
Subject: Engineering  -   Electrical and Electronic Engineering

1. Introduction

The demand for renewable energy sources has risen significantly in recent years, with solar energy being one of the most popular and widely used options. Photovoltaic (PV) systems are widely adopted for converting solar energy into usable electrical power. One of the critical aspects of PV systems is the efficient extraction of maximum power under varying environmental and partial shading conditions. Partial shading not only adversely impacts the shaded modules/arrays themselves but also diminishes the total power output captured from the entire PV system [1]. Maximum power point tracker (MPPT) techniques play a pivotal role in enhancing the performance of PV systems by ensuring that the operating point of the system stays close to the maximum power point (MPP) [2]. Conventional MPPT methods including perturb and observe (P&O) [3], incremental conductance [4], and hill climbing (HC) [5], and others, have been successful in tracking the MPP under steady-state conditions, they may exhibit slow convergence and poor performance under rapidly changing environmental conditions, such as variable irradiance and temperature [6]. For this reason, it is required to have smart optimization algorithms (SOA) to overcome this shortcoming. Several soft computing techniques have been used to track the GMPP of PV system such as particle swarm optimization (PSO) [7], genetic algorithm (GA) [8], gray wolf optimization (GWO) [9], cuckoo search algorithm (CSA) [10], bat algorithm (BA) [11], ant colony algorithm (ACA) [12], etc. These approaches diverge in aspects such as intricacy, cost, performance, reaction time, and robustness [13]. All these soft computing techniques showed an effective tracking of GMPP of the PV array [14].
PSO is a population-based optimization algorithm inspired by the social behavior of bird flocks or fish schools [15]. The PSO technique is recognized as one of the strongest and most effective search algorithms for tackling non-linear optimization problems [16]. It has been extensively applied to various optimization problems, including MPPT. The PSO method is widely recognized as a robust, simple, effective, and highly popular swarm optimization technique, which has consequently found extensive use as a means of MPPT for PV systems [17,18,19,20]. The primary advantage of using PSO for MPPT in the PV system applications is its ability to converge quickly to the global optimum without getting trapped in local optima, which is common in gradient-based optimization techniques [21]. The convergence time (CT) and failure rate (FR) of PSO-based MPPT methods are critical factors that determine the overall effectiveness of the algorithm [22]. CT refers to the duration required for the algorithm to reach an acceptable proximity to the global optimum, while the FR represents the likelihood of the algorithm not converging to the optimal solution [23]. The CT and FR are influenced by several factors, including the initial population, parameter settings, and the termination criteria of the PSO algorithm.
Several studies have been conducted to analyze and improve the CT and FR of PSO-based MPPT methods. For instance, new adaptive PSO (NA-PSO) which reduced the CT by 50% and zero FR [14]. Similarly, a newly proposed strategy uses two nested PSO (NESTPSO) which shows its supercity in reducing the CT from 442.7% to 86.9% [24]. Another study showed a reduction of the CT up to 650% by applying the anticipated peaks idea [25]. In the research conducted by [26], an enhanced particle swarm optimization (EPSO) method is proposed that demonstrates a remarkable improvement in CT. Also, PSO with targeted position-mutated elitism (PSO-TPME) technique exhibits a 45% enhancement in CT [27]. This improvement in CT can be attributed to the utilization of hybrid techniques, which have been employed in various studies to enhance the performance of MPPT algorithms. For instance, [28] introduces an incremental conductance based particle swarm optimization (ICPSO) algorithm, a unique PSO-PID algorithm is proposed in [29], while grey wolf optimization and PSO (GWO–PSO) technique is discussed in [30], PSO and salp swarm optimization (PSO-SSO) is presented in [31], and incremental conductance with PSO and model predictive control (IncCond-PSO-MPC) is introduced in [32], The tunicate swarm algorithm with the PSO technique (TSA-PSO) is detailed in [33], and PSO and incremental conductance (PSO-IC) is described in [34]. All these hybrid techniques can achieve MPP in just a fraction of a second, exhibiting a marked improvement in comparison to conventional PSO algorithm.
The starting population size plays a crucial role in determining the CT. A larger population size may require more time to converge, as there are more individuals to evaluate and update. Conversely, a smaller population size could lead to a faster convergence but at the risk of getting trapped in local optima, which are suboptimal solutions. Therefore, this study aims to investigate the delicate balance between CT and population size, as striking the right equilibrium is essential for efficient optimization.
In this research article, an innovative PSO-based MPPT algorithm was presented, designed to overcome the limitations of existing methods by incorporating a smart optimization strategy. The approach was specifically geared toward significantly improving CT and minimizing FRs, allowing the algorithm to promptly adapt to changing irradiance and temperature conditions. Comprehensive simulation results indicated that the proposed technique surpassed other PSO-based MPPT algorithms in terms of tracking speed, accuracy, and dependability, establishing it as a practical solution for real-world PV applications. The primary innovation in the method was the employment of a SSR strategy in each iteration to attain a fast-converging system. The reduction was implemented by decreasing one particle per iteration, and then comparing the outcomes with those achieved using conventional PSO. The objective was to demonstrate the effectiveness of the proposed system. Ultimately, the aim was to identify the optimal swarm size for achieving the best performance in real-world PV applications.
The remainder of this paper is structured to present the methodology of our research, which includes a detailed discussion of both the conventional particle swarm optimization (C-PSO) and the newly proposed PSO when employed as MPPT techniques for PV systems. Next, a comprehensive description of the PV system components and their operational principles is provided. Following this, a simulation study that aims to compare the performance of our proposed PSO method with that of C-PSO when used for MPPT in PV systems is introduced. Through this comparative analysis, the advantages and improvements offered by our novel approach are presented. Lastly, the conclusions drawn from this research and offer recommendations for future work in this area, providing insights and suggestions for further enhancements and exploration in the field of MPPT for PV systems are demonstrated.

2. Methodology

In this section, a comprehensive examination of the PSO technique is introduced. Initially, the intricacies of the C-PSO are explored, followed by an in-depth presentation of the novel proposed PSO method. Figure 1 illustrates the PV system utilized in this research, composed of a series configuration of three PV panels, a DC-DC converter, and a the PSO-based MPPT is used to follow the GMPP via controlling the duty ratio of the boost converter. To facilitate understanding of the proposed method, a flowchart illustrating the sequence of steps involved in the proposed approach is provided, elucidating the workflow and its underlying principles is shown in Figure 2.

2.1. PSO technique in PV MPPT applications

The PSO technique is a type of metaheuristic approaches that imitates the behavior of animals or fish when searching for food. In this technique, particles explore the search space randomly, and the particle that discovers the most food shares its experience with others to guide their movements towards the best feeding location [25]. This method can be employed as a MPPT strategy for PV systems. Initially, particles acquire duty ratio values and then evaluate the corresponding output power. The particle with the highest power output becomes a reference for the other particles, which adjust their movements to move towards this optimal position. Each particle keeps track of its best solution, known as personal best, achieved during its journey. The particles' path and movement speed to reach their new positions can be calculated using Equation (1), and the new position of the particles can be obtained by adding the particle's velocity calculated from Equation (1) to its current position as shown in Equation (2) [35].
v i + 1 k = ω i v i k + c 1 r 1 P b e s t , i K − d i k + c 2 r 2 ( G b e s t , i − d i k )
d i + 1 k = d i k + v i + 1 k
where, ω is the inertia weight, c 1 and c 2 are the acceleration coefficients, P b e s t , i K is the personal best solution of particle k at iteration i , G b e s t , i is the global best at iteration i, k is the particle order within the swarm, and r 1 and r 2 are random values in between [0,1].
The classical PSO algorithm typically employed a fixed value for the inertia weight [36]. However, to enhance its performance, researchers introduced the concept of time-varying inertia weight (TVIM) in [37-38]. This approach involves a linear decrease of the inertia weight with respect to time. Specifically, a larger inertia weight is recommended during the initial stages of the search process to facilitate global exploration, while a smaller inertia weight is used during the final stages for fine-tuning the current search area (local exploitation) [36]. The PSO-TVIM formula is expressed mathematically as follows:
ω = ( ω 1 − ω 2 ) ( N − T N ) + ω 2
where ω 1   is initial value of the inertia weight, ω 2 is final value of the inertia weight, T current iteration, and N the maximum number of allowable iterations.
The PSO-TVIW approach can rapidly identify a favorable solution compared to other evolutionary optimization techniques, it may have difficulty fine-tuning the optimal solution due to a lack of diversity towards the end of the search process [14]. In previous studies, researchers have emphasized the importance of problem-based parameter tuning in the PSO algorithm to achieve precise and efficient solutions [39]. To overcome these limitations, [40] proposes the Time-Varying Acceleration Coefficients (TVAC) approach to enhance the performance of the PSO as shown in Equations (4) and (5).
c 1 = c 1 f − c 1 i T N + c 1 i
c 2 = c 2 f − c 2 i T N + c 2 i
where c 1 i , c 1 f , c 2 i and c 2 f are constants, T is the current iteration number and N is the maximum number of allowable iterations.
Several research studies have proposed diverse approaches for estimating the optimal values of the PSO control parameters [41-45]. Many of these strategies involve adjusting the parameters through a trial-and-error process or using empirical formulas to enhance the PSO performance. However, some approaches have been succeeded in specific application but have failed to deliver desirable results in others. As a result, there is a growing need to fine-tune the PSO control parameters for different applications [24].
In this paper, the values have been chosen to ensure the best performance of the PSO operation across all examined case studies, as; c 1 i =1, c 1 f =0.0015, c 2 i =0.3, c 2 f =1.4, ω 1 = 0.1, ω 2 = 0.2 & N =50,
Moreover, randomly initializing the swarms can result in longer CT and a higher probability of failure. To overcome this issue, the swarms can be equally distributed within the range of [0.1,0.9], as demonstrated in Equation (6) [14].
d 0 k = k ( s s + 1 )
where d 0 k is the initial particle (duty ratio) with number k in the swarm, s s is the swarm-size, k is the counter used to represent the number of the particle in the swarm ( k =1, 2, …. s s ). The suffix 0 in d 0 k is used to represent that this initial values of particles.

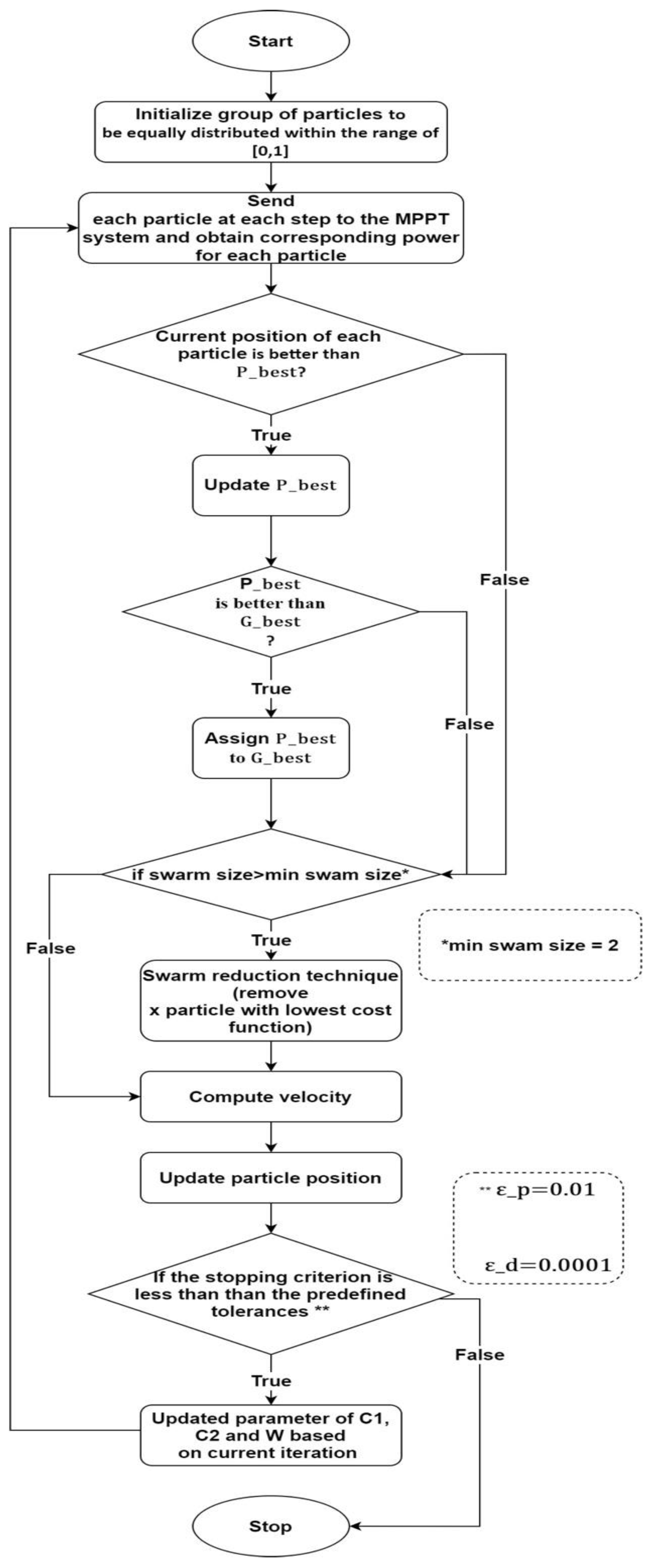
2.2. Proposed Strategy (New adaptive PSO technique)

The main contribution of the new adaptive PSO approach is the gradual reduction of the swarm size during each iteration, leading to faster CT. However, reducing the swarm size may increase the FR, so the optimal swarm size value will be carefully analyzed and discussed in the results section. This approach enables a fast tracker to be implemented under fluctuating and uneven irradiance, as well as fast temperature change conditions, which, to the authors' knowledge, has not been achieved in previous research. The proposed technique can benefit not only the PSO method but also other metaheuristic techniques facing similar challenges. In this study, the proposed approach involves reducing the swarm size, which leads to a faster CT to the MPP compared to existing methods. The higher number of search agents at the beginning of the optimization process supports the exploration of the convergence. Meanwhile, with the continual reduction of the number of search agents (particles) supports the exploitation and improve the accuracy of the GMPP value. The performance parameters and initialization of the PSO and the termination criteria are critical factors that need to be carefully considered to ensure effective implementation of the approach.
The stopping criterion was discussed in literature [24], in this study two conditions need to be satisfied to calculate the CT. The difference in power should be less than a predefined tolerance ε p = 0.01 , and the duty cycle difference at each iteration should be less than another predefined tolerance ε d = 0.0001 . These values have been chosen empirically after studying the performance of the convergence of the proposed PSO. Figure 2 illustrates the adaptive PSO's logic in a flowchart, which can be described in the following steps:
  • Step 1: Initialize the particle, to be equally distributed within the range of [0.1,0.9].
  • Step 2: Send each particle at each step to the MPPT system and obtain corresponding power for each particle.
  • Step 3: Check current position of each particle if better than P b e s t update P b e s t else go to Step 4.
  • Step 4: Check each P b e s t with G b e s t if G b e s t is less than P b e s t , then update G b e s t else go to Step 5.
  • Step 5: Apply Reduction technique if swarm size >min swam size, remove particle with lowest cost function else go to Step 6.
  • Step 6: Update velocity of each particle.
  • Step 7: Update the position of the particle based on the global and personal best.
  • Step 8: Updated parameter of c 1 , c 2 & ω based on current iteration, go to Step 2.

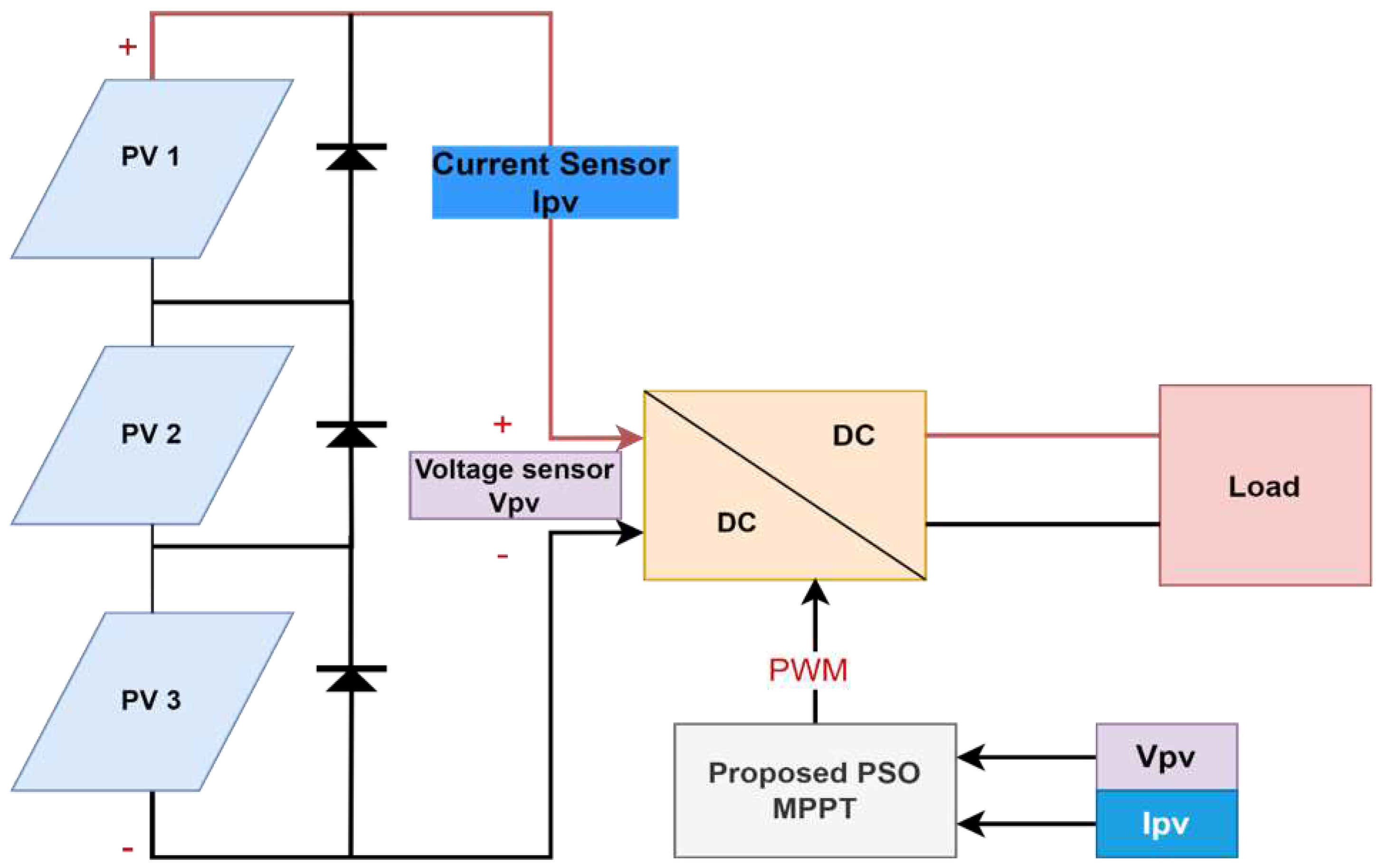
3. Modeling of PV system

The suggested setup includes PV arrays connected to a DC-DC boost converter to optimize power output under varying irradiance conditions. The boost converters, commonly used in PV systems with MPPT which can be implemented in either a single or interleaved configuration [7]. The PV system insulated for the simulation consist of 3 PV panels connected in series with each having maximum power generation capacity of 83.28 W. In this system, a control mechanism ensures that a PSO-based MPPT algorithm is used to track the GMPP by regulating the duty ratio of the boost converter, as depicted in Figure 1. The connection between the PV output power and the output voltage under both uniform and non-uniform conditions is shown in Figure 3. In a similar manner, Figure 4 illustrates the relationship between PV output power and the duty ratio of the boost converter for both uniform and non-uniform irradiance scenarios. The Power-Voltage (P-V) curve shows a clear MPP under uniform irradiance (SPO [1000 1000 1000]), which can be easily tracked using conventional MPPT techniques. However, under non-uniform irradiance (SP1 [700 1000 1000]), the P-V curve exhibits multiple Local Peaks (LPs) and the Global Peak (GP), as shown in Figures 3.

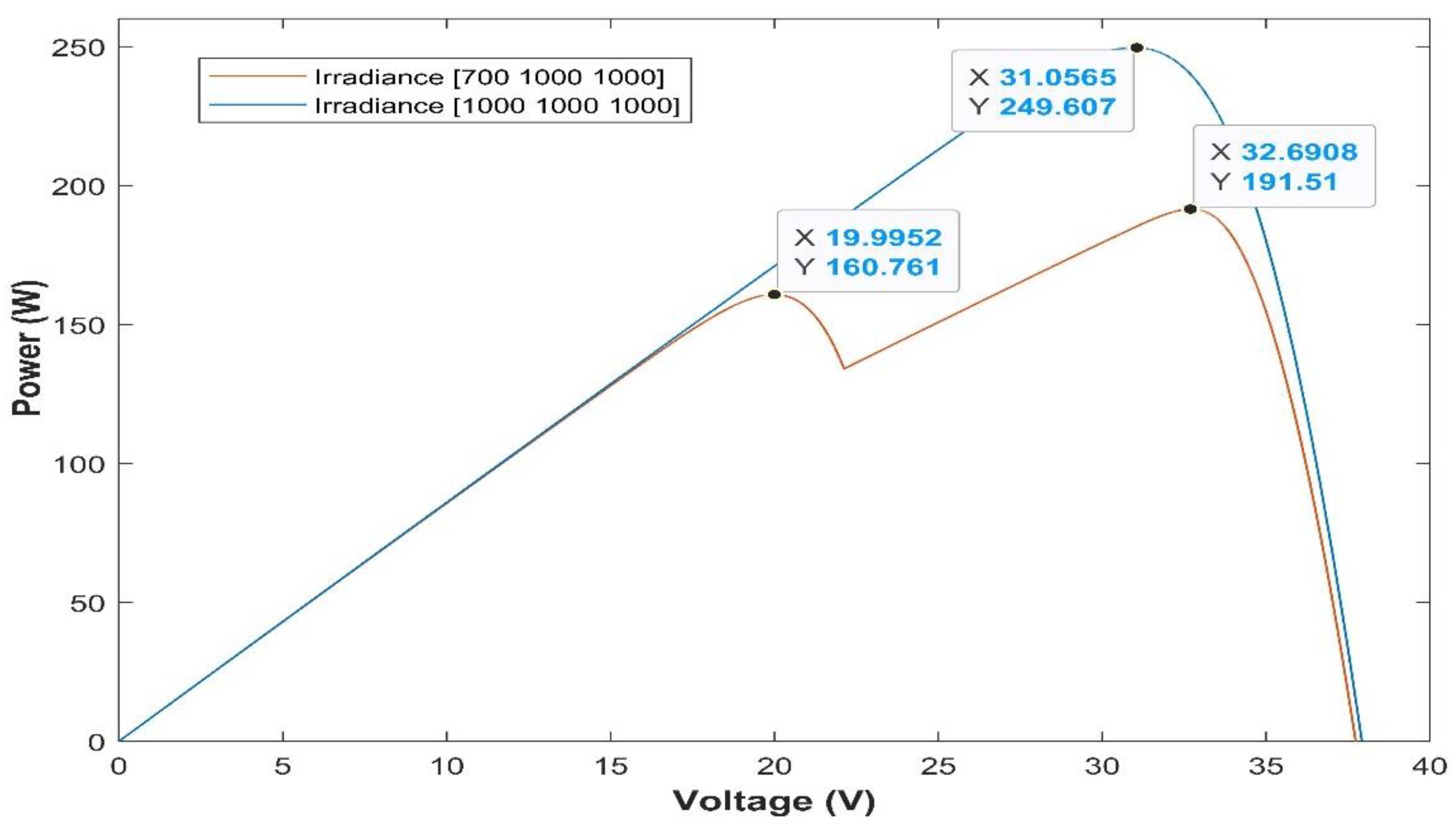
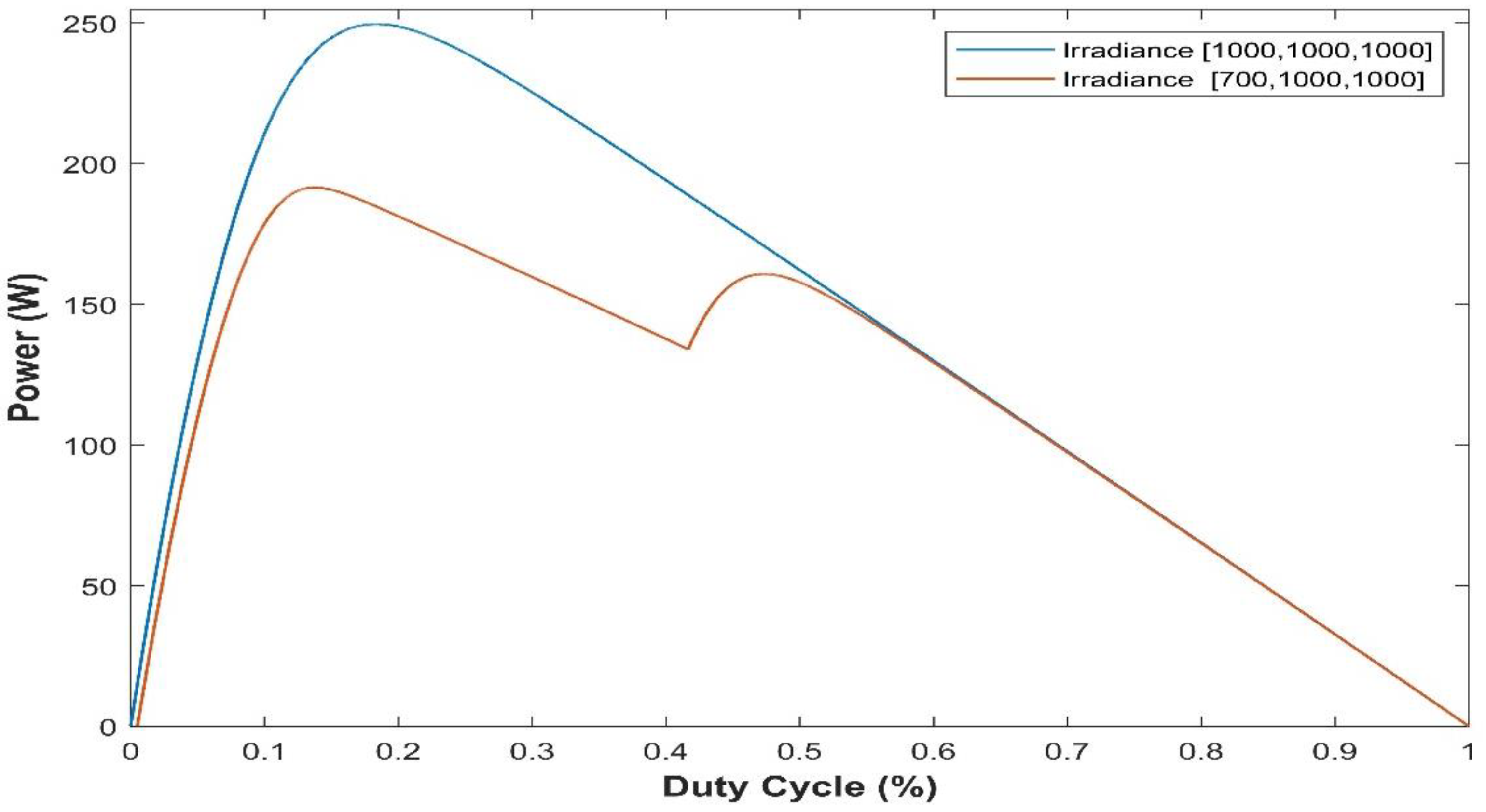
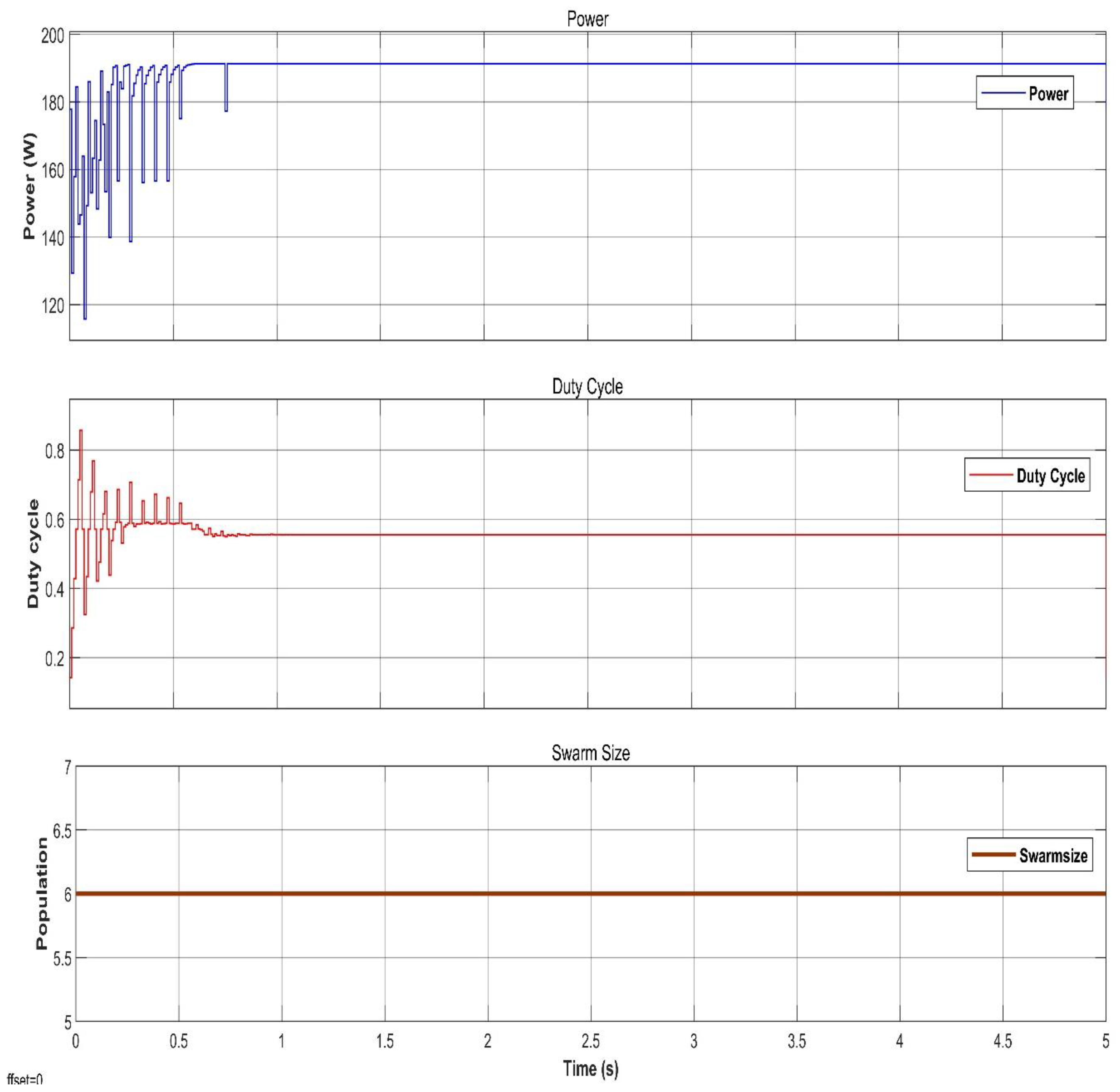
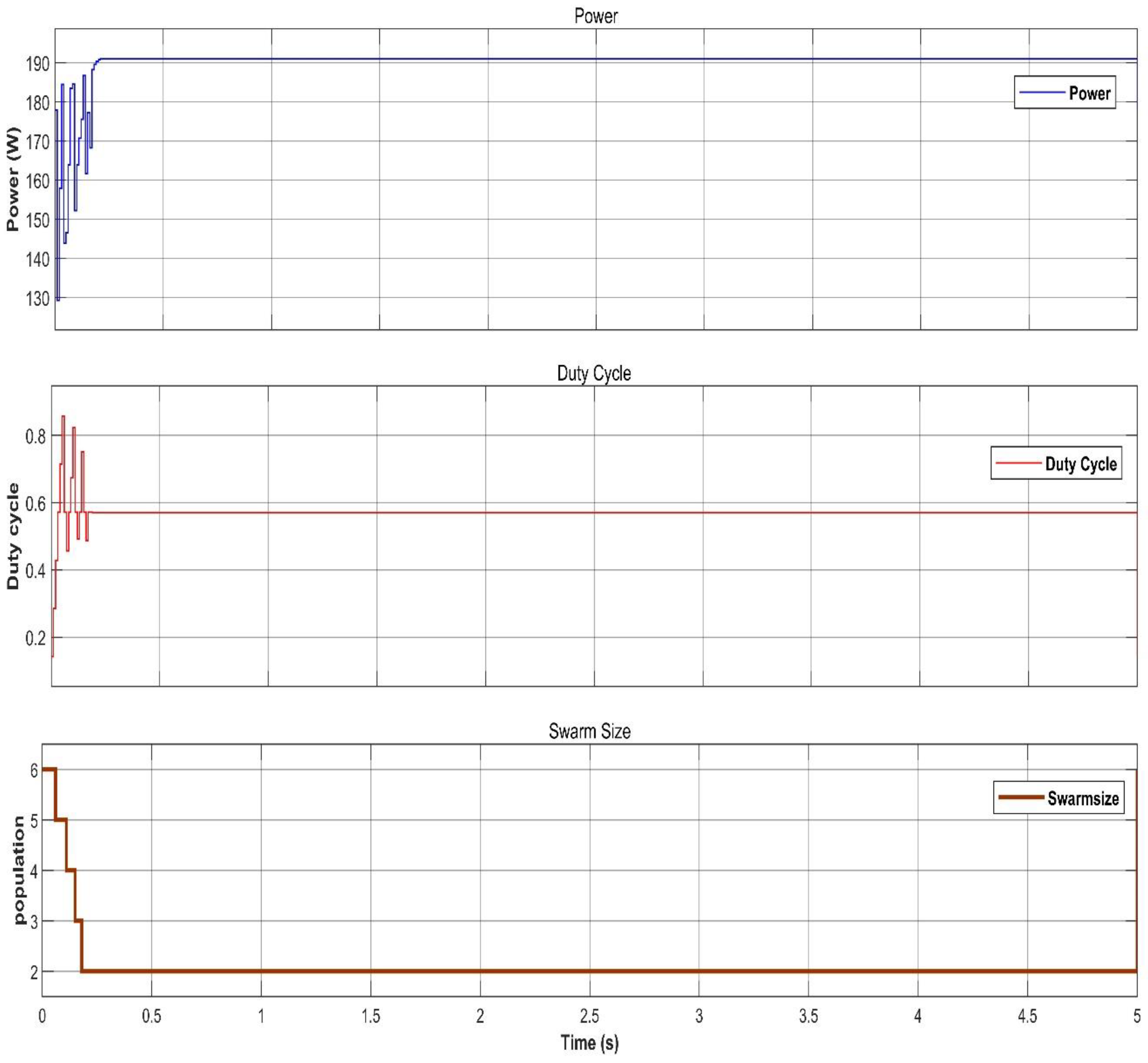
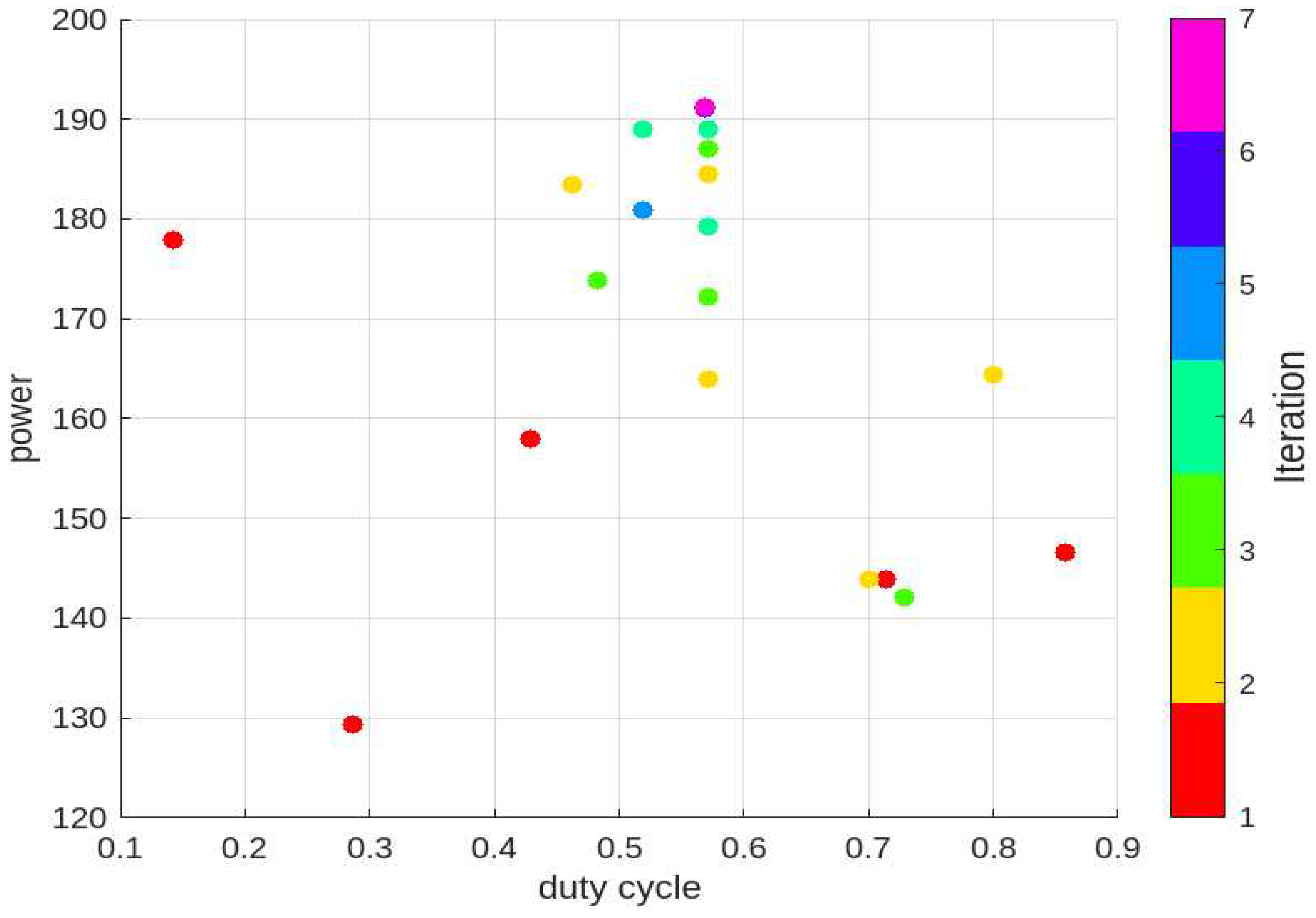
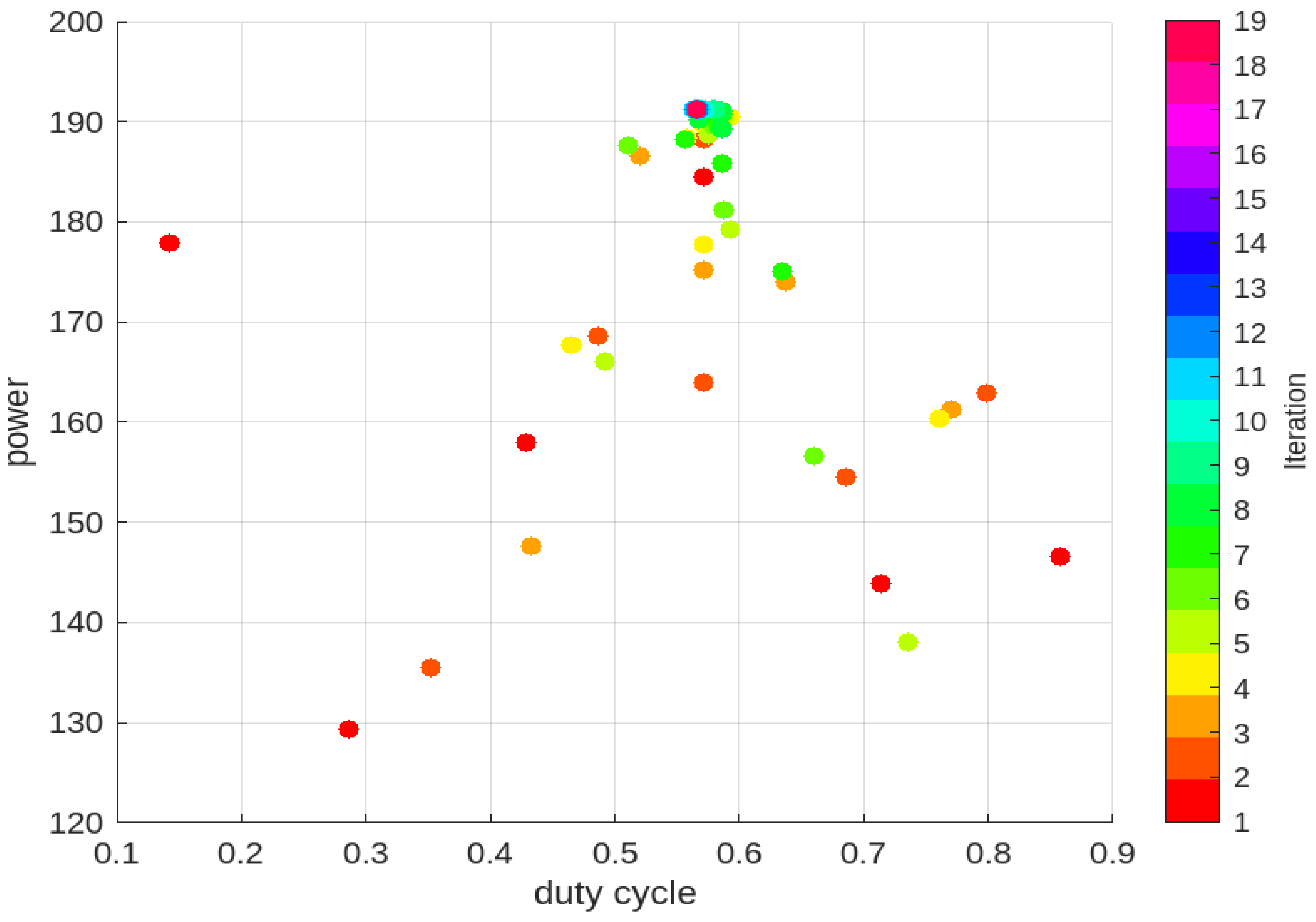
4. Simulation Results

In this section, the simulation of the suggested PV system employing the novel adaptive approach for the PSO method, which functioned as an MPPT system is demonstrated and discussed. The simulation was carried out by integrating MATLAB code, which includes the PSO algorithm, with Simulink that houses the PV system, and the DC-DC converter. The module parameters used in the simulation are displayed in Table 1. The system featured three series-connected PV modules. Each module had differing radiation levels, with the set-up being [700, 1000, 1000]. The objective of the study is to implement a swarm size reduction technique in each iteration. Two different scenarios were examined: first, the C-PSO without reduction; second, the application of the reduction method with a step of 1. In both cases, the Initial Swarm Size (ISS) starts from 20 until 3, with results collected at each swarm size. As a result, the optimum swarm size of the two cases was selected based on the optimum CT & FR percentage. Table 2 shows the results of CT & FR for the two scenarios.
As demonstrated in Table 2, a consistent and systematic decrease in CT is observed when executing the algorithm with varying swarm sizes. This trend is to be expected, given that a smaller number of particles in the swarm would typically result in faster computation. The impact of reducing the swarm size is particularly prominent in the case of the proposed PSO algorithm, as the CT continues to exhibit a decreasing pattern until the swarm is reduced to a mere two particles.
Upon conducting a detailed analysis of the results, it becomes evident that when the swarm size lies within the range of 20 to 6 particles, the algorithm exhibits an impressive zero-FR across 10 separate executions. However, when the swarm size is further reduced to 5, 4, or 3 particles, the FRs begin to appear. This can primarily be attributed to a decline in the exploration efficiency of the C-PSO algorithm. The consequences of this diminished exploration efficiency become even more pronounced in the context of the newly proposed PSO algorithm, as the limited number of particles available for exploration hinders the algorithm's ability to effectively locate the MPP. Despite these challenges, it is crucial to highlight that the CT remains consistently shorter when using the proposed PSO algorithm, as compared to the conventional method. The limitation linked to the utilization of the SSR strategy was pronounced when the swarm size was minimized, consequently affecting the performance of exploration. As detailed in this research, a rigorous assessment of 18 different swarm sizes was performed to pinpoint the ideal size for optimal exploration.
The findings presented in Table 2 offer valuable insights into the relationship between swarm size and CT for both the C-PSO and the proposed PSO algorithms. Furthermore, they underscore the potential advantages of the newly proposed PSO algorithm, particularly about achieving faster CTs, while also emphasizing the need for an optimal balance between swarm size and exploration efficiency to ensure reliable performance in locating the MPP.
In the current study, it has been determined that the optimal swarm size for the algorithm being examined is 6 particles, accompanied by a reduction size of 1. This configuration leads to a CT of just 0.258 seconds, which constitutes a substantial 75% improvement when compared to the 1.02-second CT observed with the C-PSO method. This significant reduction in CT serves as a testament to the effectiveness of the proposed PSO algorithm and emphasizes its potential for delivering enhanced performance across a variety of applications. The discovery of the optimal swarm size for improved performance offers valuable insights into the underlying dynamics of the proposed PSO algorithm. By meticulously adjusting the swarm size to consist of 6 particles and adopting a reduction size of 1, researchers have been able to achieve a remarkable improvement in the algorithm's CT, rendering it more efficient and effective compared to the conventional approach. The optimization of swarm size, as evidenced by the notable 75% improvement in CT, demonstrates the potential of the proposed PSO algorithm to provide superior performance in diverse applications, especially those that require swift convergence towards an optimal solution. This accomplishment not only contributes to the growing body of research on PSO techniques but also lays the groundwork for future investigations aimed at further refining and enhancing the performance of PSO algorithms in various contexts.
Figure 5 and Figure 6 display the outcomes for power, duty cycle, and swarm size in both scenarios, emphasizing the use of a swarm size consisting of 6 particles. Figure 7 illustrates the behavior of particles converging towards the MPP using the C-PSO method with a swarm size of 6. It is evident from the figure that particle traffic is a significant factor, as the algorithm requires 19 iterations to achieve convergence. In each iteration, 6 particles are dispatched to search for the MPP, resulting in a combined count of 114 calling the objective function (the PV system) for the search process, which leads to increased particle traffic surrounding the MPP as the iterative process progresses. In contrast, Figure 8 presents the particle behaviors converging towards the MPP when employing the proposed particle reduction PSO algorithm. This method requires only 7 iterations to achieve convergence and incorporates a swarm size of 6. In this scenario, the number of particles decreases with each iteration, resulting in diminished particle traffic and expedited convergence, necessitating fewer iterations overall. The approach utilizes 6 particles in the first iteration, followed by 5 in the second, 4 in the third, 3 in the fourth, and 2 in both the fifth and sixth iterations, as well as the seventh iteration, this results in a total of 24 particles for searching. Clearly, the SSR strategy utilizes a substantially reduced number of particles in comparison to the C-PSO approach for reaching the MPP, resulting in swifter convergence. To facilitate improved visualization of the graphical representations, a color scale is employed, which assigns a unique color to each iteration, thereby enabling a more effective interpretation of the convergence process and the associated particle traffic patterns.

5. Conclusions

Maximum Power Point Tracker (MPPT) methods based on PSO demonstrate considerable benefits compared to traditional MPPT approaches, particularly in dynamic environmental varying and partial shading conditions. Factors such as CT and FR significantly influence the efficacy of PSO-based MPPT techniques. In this research, a novel PSO method involving the reduction of swarm size is employed to track the GMPP of PV systems under partial shading conditions. Various swarm sizes, ranging from 20 to 3, were tested in two scenarios each, to obtain a comprehensive understanding of the system and select the optimal swarm size based on the shortest conversion time (CT) and zero failure rate (FR) criteria.
To the best of the author's experience, this marks the inaugural instance where the idea of diminishing swarm size has been employed to enhance the performance of PSO. In this study, the optimal swarm size is determined to be 6, as it exhibited excellent CT and a zero-FR. The results highlight the superiority of this innovative technique, achieving up to an 75% reduction in time compared to conventional PSO method. However, some failures were observed at the swarm size of 5, 4 & 3 in both cases, and this is due to fewer particles are available for exploration to find the MPP. Future research will compare this proposed method with other metaheuristic techniques, as well as explore the applicability of swarm size reduction to other metaheuristic approaches.

References

  1. Farh, H.M.; Eltamaly, A.M.; Al-Saud, M.S. Interleaved boost converter for global maximum power extraction from the photovoltaic system under partial shading. IET Renew. Power Gener. 2019, 13, 1232–1238. [Google Scholar] [CrossRef]
  2. Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Convers. 2007, 22, 439–449. [Google Scholar] [CrossRef]
  3. Ahmed, J.; Salam, Z. An Enhanced Adaptive P&O MPPT for Fast and Efficient Tracking Under Varying Environmental Conditions. IEEE Trans. Sustain. Energy 2018, 9, 1487–1496. [Google Scholar] [CrossRef]
  4. Ilyas, M. Ayyub, M. R. Khan, A. Jain and M. A. Husain, "Realization of Incremental Conductance MPPT Algorithm for Solar Photovoltaic System," International Journal of Ambient Energy, vol. 39, no. 8, pp. 873-884, 2017. [CrossRef]
  5. Zhu, W.; Shang, L.; Li, P.; Guo, H. Modified hill climbing MPPT algorithm with reduced steady-state oscillation and improved tracking efficiency. J. Eng. 2018, 2018, 1878–1883. [Google Scholar] [CrossRef]
  6. Subudhi, B.; Pradhan, R. A Comparative Study on Maximum Power Point Tracking Techniques for Photovoltaic Power Systems. IEEE Trans. Sustain. Energy 2012, 4, 89–98. [Google Scholar] [CrossRef]
  7. Farh, H.M.H.; Othman, M.F.; Eltamaly, A.M.; Al-Saud, M.S. Maximum Power Extraction from a Partially Shaded PV System Using an Interleaved Boost Converter. Energies 2018, 11, 2543. [Google Scholar] [CrossRef]
  8. Hadji, S.; Gaubert, J.-P.; Krim, F. Real-Time Genetic Algorithms-Based MPPT: Study and Comparison (Theoretical an Experimental) with Conventional Methods. Energies 2018, 11, 459. [Google Scholar] [CrossRef]
  9. Eltamaly, A.M.; Farh, H.M. Dynamic global maximum power point tracking of the PV systems under variant partial shading using hybrid GWO-FLC. Sol. Energy 2018, 177, 306–316. [Google Scholar] [CrossRef]
  10. Ahmed, J.; Salam, Z. A Maximum Power Point Tracking (MPPT) for PV system using Cuckoo Search with partial shading capability. Appl. Energy 2014, 119, 118–130. [Google Scholar] [CrossRef]
  11. Tey, K.S.; Mekhilef, S.; Seyedmahmoudian, M. Implementation of BAT Algorithm as Maximum Power Point Tracking Technique for Photovoltaic System Under Partial Shading Conditions. IEEE Energy Conversion Congress and Exposition (ECCE) 2018, 2531–2535. [Google Scholar] [CrossRef]
  12. Priyadarshi, N.; Ramachandaramurthy, V.K.; Padmanaban, S.; Azam, F. An Ant Colony Optimized MPPT for Standalone Hybrid PV-Wind Power System with Single Cuk Converter. Energies 2019, 12, 167. [Google Scholar] [CrossRef]
  13. Eltamaly, A.M. Performance of MPPT Techniques of Photovoltaic Systems Under Normal and Partial Shading Conditions," in Advances in Renewable Energies and Power Technologies, Elsevier,2018, 115–161. 2018. [CrossRef]
  14. A. M. Eltamaly, H. M. H. Farh and A. G. Abokhalil, "A novel PSO strategy for improving dynamic change partial shading photovoltaic maximum power point tracker," ENERGY SOURCES, PART A: RECOVERY, UTILIZATION, AND ENVIRONMENTAL EFFECTS, 2020. [CrossRef]
  15. J. Kennedy and R. Eberhart, "Particle Swarm Optimization," International Conference on Neural Networks (ICNN’95), p. 1942–1948, 1995.
  16. Eltamaly, A.M.; Farh, H.M.; Al-Saud, M.S. Grade point average assessment for metaheuristic GMPP techniques of partial shaded PV systems. IET Renew. Power Gener. 2019, 13, 1215–1231. [Google Scholar] [CrossRef]
  17. Chao, K.-H.; Lin, Y.-S.; Lai, U.-D. Improved particle swarm optimization for maximum power point tracking in photovoltaic module arrays. Appl. Energy 2015, 158, 609–618. [Google Scholar] [CrossRef]
  18. Eltamaly, A.M. Performance of smart maximum power point tracker under partial shading conditions of photovoltaic systems. J. Renew. Sustain. Energy 2015, 7. [Google Scholar] [CrossRef]
  19. Eltamaly, A.M.; Farh, H.M.H.; Al Saud, M.S. Impact of PSO Reinitialization on the Accuracy of Dynamic Global Maximum Power Detection of Variant Partially Shaded PV Systems. Sustainability 2019, 11, 2091. [Google Scholar] [CrossRef]
  20. Ahmed, J.; Salam, Z. A critical evaluation on maximum power point tracking methods for partial shading in PV systems. Renew. Sustain. Energy Rev. 2015, 47, 933–953. [Google Scholar] [CrossRef]
  21. Elgendy, M.A.; Zahawi, B.; Atkinson, D.J. Assessment of Perturb and Observe MPPT Algorithm Implementation Techniques for PV Pumping Applications. IEEE Trans. Sustain. Energy 2011, 3, 21–33. [Google Scholar] [CrossRef]
  22. Eltamaly, A.M.; Al-Saud, M.; Abokhalil, A.G. A novel scanning bat algorithm strategy for maximum power point tracker of partially shaded photovoltaic energy systems. Ain Shams Eng. J. 2020, 11, 1093–1103. [Google Scholar] [CrossRef]
  23. Askarzadeh, A.; Rezazadeh, A. Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 2013, 102, 943–949. [Google Scholar] [CrossRef]
  24. Eltamaly, A.M. A Novel Strategy for Optimal PSO Control Parameters Determination for PV Energy Systems. Sustainability 2021, 13, 1008. [Google Scholar] [CrossRef]
  25. Eltamaly, A.M.; Al-Saud, M.S.; Abo-Khalil, A.G. Performance Improvement of PV Systems’ Maximum Power Point Tracker Based on a Scanning PSO Particle Strategy. Sustainability 2020, 12, 1185. [Google Scholar] [CrossRef]
  26. Kamil, A.; University of Babylon; Nasr, M. ; Alwash, S. Maximum Power Point Tracking Method for Photovoltaic System Based on Enhanced Particle Swarm Optimization Algorithm Under Partial Shading Condition. Int. J. Intell. Eng. Syst. 2020, 13, 241–254. [Google Scholar] [CrossRef]
  27. Shaqarin, T. Particle Swarm Optimization with Targeted Position-Mutated Elitism (PSO-TPME) for Partially Shaded PV Systems. Sustainability 2023, 15, 3993. [Google Scholar] [CrossRef]
  28. Chawda, G.; Mahela, O.; Gupta, N.; Khosravy, M.; Senjyu, T. Incremental Conductance Based Particle Swarm Optimization Algorithm for Global Maximum Power Tracking of Solar-PV under Nonuniform Operating Conditions. Appl. Sci. 2020, 10, 4575. [Google Scholar] [CrossRef]
  29. Al-Muthanna, G.; Fang, S.; Al-Wesabi, I.; Ameur, K.; Kotb, H.; AboRas, K.M.; Al Garni, H.Z.; Mas’ud, A.A. A High Speed MPPT Control Utilizing a Hybrid PSO-PID Controller under Partially Shaded Photovoltaic Battery Chargers. Sustainability 2023, 15, 3578. [Google Scholar] [CrossRef]
  30. Chtita, S.; Motahhir, S.; El Hammoumi, A.; Chouder, A.; Benyoucef, A.S.; El Ghzizal, A.; Derouich, A.; Abouhawwash, M.; Askar, S.S. A novel hybrid GWO–PSO-based maximum power point tracking for photovoltaic systems operating under partial shading conditions. Sci. Rep. 2022, 12, 1–15. [Google Scholar] [CrossRef]
  31. Dagal, I.; Akın, B.; Akboy, E. MPPT mechanism based on novel hybrid particle swarm optimization and salp swarm optimization algorithm for battery charging through simulink. Sci. Rep. 2022, 12, 1–17. [Google Scholar] [CrossRef]
  32. N. Kacimi, A. Idir, S. Grouni and M. S. Boucherit, "Improved MPPT Control Strategy for PV Connected to Grid Using IncCond-PSO-MPC Approach," CSEE JOURNAL OF POWER AND ENERGY SYSTEMS, vol. 9, no. 3, pp. 1008-1020, 2023. [CrossRef]
  33. Sharma, A.; Sharma, A.; Jately, V.; Averbukh, M.; Rajput, S.; Azzopardi, B. A Novel TSA-PSO Based Hybrid Algorithm for GMPP Tracking under Partial Shading Conditions. Energies 2022, 15, 3164. [Google Scholar] [CrossRef]
  34. Ibrahim, M.H.; Ang, S.P.; Dani, M.N.; Rahman, M.I.; Petra, R.; Sulthan, S.M. Optimizing Step-Size of Perturb & Observe and Incremental Conductance MPPT Techniques Using PSO for Grid-Tied PV System. IEEE Access 2023, 11, 13079–13090. [Google Scholar] [CrossRef]
  35. A. M. Eltamaly and H. M. H. Farh, "Maximum Power Extraction from the Photovoltaic System Under Partial Shading Conditions," pp. 107-129, 2019. [CrossRef]
  36. Umapathy, P.; Venkataseshaiah, C.; Arumugam, M.S. Particle Swarm Optimization with Various Inertia Weight Variants for Optimal Power Flow Solution. Discret. Dyn. Nat. Soc. 2010, 2010, 1–15. [Google Scholar] [CrossRef]
  37. M. Abido, "Multiobjective particle swarm optimization technique for environmental/economic dispatch problem," IEEE, 2008.
  38. Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1945–1950. [Google Scholar] [CrossRef]
  39. Y. Shi and R. C. Eberhart, "Parameter Selection in Particle Swarm Optimization," in Lecture Notes in Computer Science—Evolutionary Programming VII, vol. 1447, pp. 591-600, 1998.
  40. Ratnaweera, A.; Halgamuge, S.; Watson, H. Self-Organizing Hierarchical Particle Swarm Optimizer With Time-Varying Acceleration Coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
  41. Clerc, M.; Kennedy, J. The particle swarm - explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef]
  42. Clerc, M. The swarm and the queen: Towards a deterministic and adaptive particle swarm optimization. In Proceedings of the ICEC, Washington, DC, USA, 6–9 July 1999; pp. 1951–1957. [Google Scholar]
  43. M. Jiang, Y. P. Luo and S. Y. Yang, "Particle swarm optimization-stochastic trajectory analysis and parameter selection,". In Swarm Intelligence, Focus on Ant and Particle Swarm Optimization; p. 179–198, 2007.
  44. Zhang, W.; Ma, D.; Wei, J.-J.; Liang, H.-F. A parameter selection strategy for particle swarm optimization based on particle positions. Expert Syst. Appl. 2014, 41, 3576–3584. [Google Scholar] [CrossRef]
  45. K. R. Harrison, A. P. Engelbrecht and B. . M. Ombuki-Berman, "An adaptive particle swarm optimization algorithm based on optimal parameter regions," IEEE, pp. 1-8, 2017. [CrossRef]
Preprints 81817 g001
Figure 1. PV system with proposed PSO-based MPPT.
Figure 1. PV system with proposed PSO-based MPPT.
Preprints 81817 g001
Preprints 81817 g002
Figure 2. Flowchart of the proposed PSO.
Figure 2. Flowchart of the proposed PSO.
Preprints 81817 g002
Preprints 81817 g003
Figure 3. P-V curve under full irradiance [1000 1000 1000], and partial shading [700 1000 1000].
Figure 3. P-V curve under full irradiance [1000 1000 1000], and partial shading [700 1000 1000].
Preprints 81817 g003
Preprints 81817 g004
Figure 4. P-D curve under full irradiance [1000 1000 1000], and partial shading [700 1000 1000].
Figure 4. P-D curve under full irradiance [1000 1000 1000], and partial shading [700 1000 1000].
Preprints 81817 g004
Preprints 81817 g005
Figure 5. Simulation Results of the optimum ISS = 6 with no reduction
Figure 5. Simulation Results of the optimum ISS = 6 with no reduction
Preprints 81817 g005
Preprints 81817 g006
Figure 6. Simulation Results of the optimum ISS = 6 with reduction = 1
Figure 6. Simulation Results of the optimum ISS = 6 with reduction = 1
Preprints 81817 g006
Preprints 81817 g007
Figure 7. Particles behaviors towards the MPP at each iteration, optimum ISS = 6 with reduction = 1
Figure 7. Particles behaviors towards the MPP at each iteration, optimum ISS = 6 with reduction = 1
Preprints 81817 g007
Preprints 81817 g008
Figure 8. Particles behaviors towards the MPP at each iteration, optimum ISS = 6 with reduction = 0
Figure 8. Particles behaviors towards the MPP at each iteration, optimum ISS = 6 with reduction = 0
Preprints 81817 g008
Table 1. Specifications of PV module used in this study.
Table 1. Specifications of PV module used in this study.
Specification Value
maximum power per module 83.28 W
open-circuit voltage 12.64 V
short-circuit current 8.62 A
voltage at MPP 10.32 V
current at MPP 8.07 A
Table 2. Simulation results of the CT and FR at each Initial swarm size (ISS).
Table 2. Simulation results of the CT and FR at each Initial swarm size (ISS).
ISS Reduction = 0 Reduction = 1
CT FR CT FR
20 3.66 0% 1.972 0%
19 3.591 0% 1.809 0%
18 3.456 0% 1.667 0%
17 3.043 0% 1.51 0%
16 2.976 0% 1.324 0%
15 2.73 0% 1.182 0%
14 2.688 0% 1.06 0%
13 2.379 0% 0.91 0%
12 2.172 0% 0.824 0%
11 1.958 0% 0.682 0%
10 1.79 0% 0.584 0%
9 1.602 0% 0.472 0%
8 1.36 0% 0.422 0%
7 1.065 0% 0.342 0%
6 1.02 0% 0.258 0%
5 0.97 43% 0.2 67%
4 0.915 61% 0.11 93%
3 0.708 84% 0.07 98%
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.
Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.
Incremental Conductance Based Particle Swarm Optimization Algorithm for Global Maximum Power Tracking of Solar-PV under Nonuniform Operating Conditions

Gajendra Singh Chawda

et al.

Applied Sciences,

2020

Improved PSO: A Comparative Study in MPPT Algorithm for PV System Control under Partial Shading Conditions

Wafa Hayder

et al.

Energies,

2020

Accelerated Particle Swarm Optimization for Photovoltaic Maximum Power Point Tracking under Partial Shading Conditions

Muhannad Alshareef

et al.

Energies,

2019

Prerpints.org logo

Preprints.org is a free preprint server supported by MDPI in Basel, Switzerland.

facebook logotwitter logolinkedin logo
MDPI Initiatives
Important Links
Subscribe

Disclaimer

Terms of Use

Privacy Policy

© 2024 MDPI (Basel, Switzerland) unless otherwise stated