Submitted:
06 August 2023
Posted:
08 August 2023
Read the latest preprint version here
Abstract
Keywords:
1. Introduction
2. Laplace’s Equation and Electric Fields
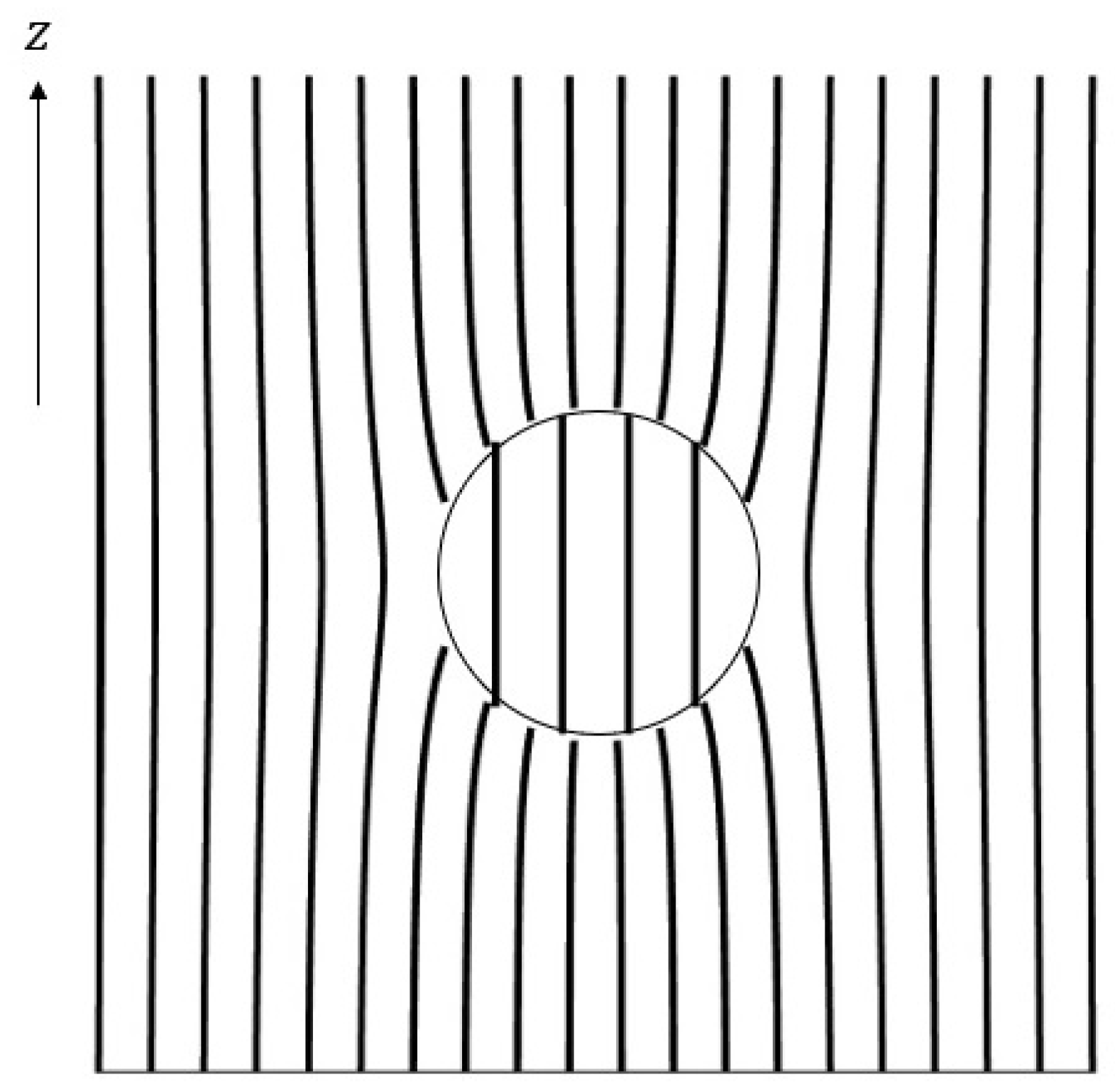
2.1. Conducting Sphere in Uniform Electric Field
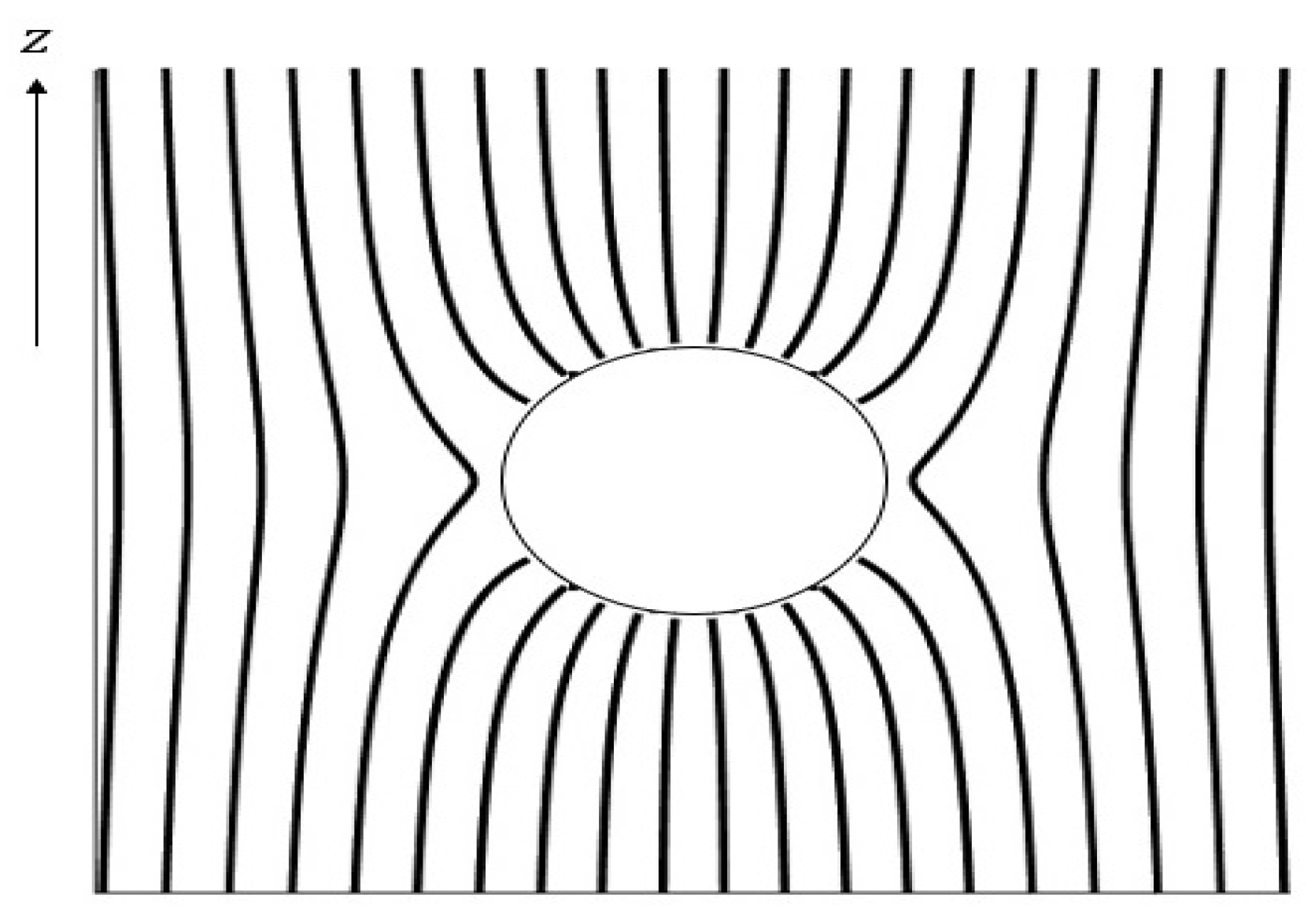
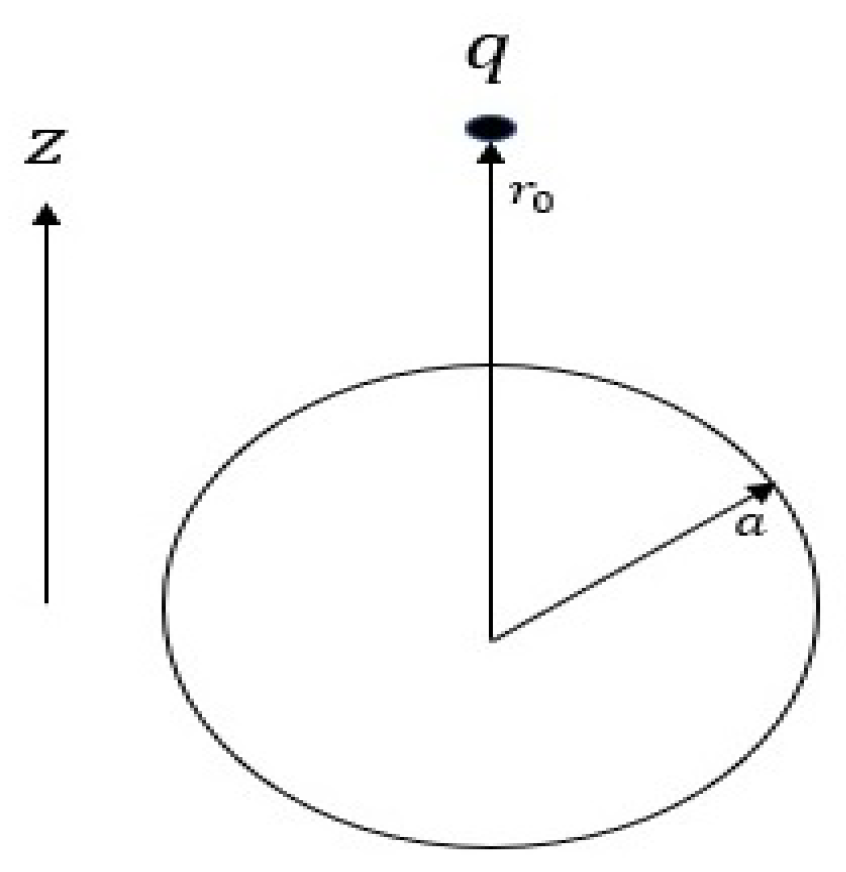
2.2. Conducting Sphere Near a Point Charge
2.3. Uniform Dielectric Sphere in Uniform Electric Field
3. Discussion
Appendix A. Proofs
References
- Brian Baigrie, Electricity and Magnetism: A Historical Perspective (Greenwood Press, 2007), pp. 7–8.
- Charles–Augustin de Coulomb, “Premier mémoire sur l’électricité et le magnétisme”, Histoire de l’Académie Royale des Sciences, 1785.
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Coding for Asymmetric Channels and Channels with State”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1367–1372, 2021.
- Charles–Augustin de Coulomb, “Second mémoire sur l’électricité et le magnétisme”, Histoire de l’Académie Royale des Sciences, pp. 578–611, 1785.
- Shouvik Ganguly and Young-Han Kim, “Capacity Scaling for Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1472–1476, 2019.
- Carl, F. Gauss, “Theoria attractionis corporum sphaeroidicorum ellipticorum homogeneorum methodo nova tractata”, Gauss, Werke V, p. 1.
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Coding for Network Communication”, arXiv:2211.07208v3 [cs.IT], 2022.
- James Clerk Maxwell(1865), “A dynamical theory of the electromagnetic field”, Philosophical Transactions of the Royal Society of London, 155, pp. 459–512.
- Shouvik Ganguly and Sridip Pal, “Bounds on the Density of States and the Spectral Gap in CFT–2”, Phys. Rev. D 101(14):106022, pp. 1–4, May 2020.
- Richard, P. Feynman, “Space–Time Approach to Quantum Electrodynamics”, Phys. Rev. 76(6), pp. 769–789, 1949.
- Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Functional Construction of Codes for Multiple Access and Broadcast Channels”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 1581–1586, 2020.
- P. R. Garabedian and M. Schiffer, “On existence theorems of potential theory and conformal mapping”, Annals of Mathematics 52(1), pp. 164–187, 1950.
- Shouvik Ganguly and Lele Wang, “Sliding-Window Gelfand–Pinsker Coding: General K-User Broadcast Channels”, Proceedings of the IEEE Information Theory Workshop (ITW), pp. 1–5, 2020.
- Siméon Denis Poisson, “Mémoire sur la théorie du magnétisme en mouvement”, Mémoires de l’Académie Royale des Sciences de l’Institut de France 6, pp. 441–570, 1823.
- Shouvik Ganguly and Young-Han Kim, “On the Capacity of Cloud Radio Access Networks”, Proceedings of the International Symposium on Information Theory (ISIT), pp. 2063–2067, 2017.
- R. Courant and D. Hilbert, “Methods of Mathematical Physics”, Interscience, New York, 1966.
- Shouvik Ganguly, Seung-Eun Hong, and Young-Han Kim, “On the Capacity Regions of Cloud Radio Access Networks with Limited Orthogonal Fronthaul”, IEEE Trans. Inf. Theory 67(5), pp. 2958–2988, May 2021.
- Richard, P. Feynman, Robert B. Leighton, and Matthew Sands, The Feynman Lectures on Physics, Vol. 2, Chap. 12 (Addison-Wesley, 1964).
- David, J. Griffiths, Introduction to Electrodynamics (Boston:Pearson, 2013).
- S. Persides, “The Laplace and Poisson equations in Schwarzschild’s space–time”, Journal of Mathematical Analysis and Applications 43(3), pp. 571–578, 1973.
- David Gilbarg and Neil, S. Trudinger, Elliptic Partial Differential Equations of Second Order (Berlin: Springer, 2015).
- G. Barton, Elements of Green’s Functions and Propagation: Potentials, Diffusion and Waves (Oxford: Oxford Science Publications, 1989).
- Augusto, B. d’Oliveira, Ed Gerck, and Jason A. C. Gallas, “Solution of the Schrödinger equation for bound states in closed form”, Phys. Rev. A 26:1(1), June 1982.
- S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Distributed Nonparametric Sequential Detection”, Proceedings of the IEEE International Conference on Communications (ICC), pp. 1409–1415, 2014.
- Erwin Kreyszig, Advanced Engineering Mathematics (3rd ed). New York: Wiley, 1972.
- George, B. Arfken and Hans J. Weber, Mathematical Methods for Physicists (Elsevier Academic Press, 2005).
- Richard Courant, Differential and Integral Calculus, Vol. 1 London: Blacktie & Son Limited, 1961.
- Jongha Jon Ryu, Shouvik Ganguly, Young-Han Kim, Yung-Kyun Noh, and Daniel D. Lee, “Nearest Neighbor Density Functional Estimation based on Inverse Laplace Transform”, IEEE Trans. Inf. Theory 68(6), pp. 3511–3551, June 2022.
- J. D. Jackson, Classical Electrodynamics (3rd ed.) (New York:Wiley, 1999).
- S. Ganguly, K. Sahasranand, and V. Sharma, “A New Algorithm for Nonparametric Sequential Detection”, Proceedings of the National Conference on Communications (NCC), India, pp. 1–6, 2014.
- P. M. Morse and H. Feshbach, Methods of Theoretical Physics, Part I (New York: McGraw–Hill, 1953), p. 658.
- Nadim Ghaddar, Shouvik Ganguly, Lele Wang, and Young-Han Kim, “A Lego-Brick Approach to Lossy Source Coding”, Proceedings of the 17th Canadian Workshop on Information Theory (CWIT), pp. 45–50, 2022.
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).




