Adaptive Control of M3C-Based Variable Speed Drive for Multiple PMSM-Driven Centrifugal Pumps

Preprint

Article

Adaptive Control of M3C-Based Variable Speed Drive for Multiple PMSM-Driven Centrifugal Pumps

Altmetrics

Downloads

100

Views

Comments

A peer-reviewed article of this preprint also exists.

Rodrigo Mendoza-Becker,

Juan Carlos Travieso-Torres^*,

Matías Díaz

Rodrigo Mendoza-Becker,

Juan Carlos Travieso-Torres^*,

Matías Díaz

This version is not peer-reviewed

Submitted:

02 August 2023

Posted:

03 August 2023

You are already at the latest version

Alerts

Abstract

There has been growing interest in using permanent magnet synchronous motors (PMSMs) for pumping applications to improve energy efficiency. One promising approach for powering these motors in variable speed applications is using modular multilevel cascaded converters based on a Triple-Star Bridge Cell (M3C) due to their inherent fault tolerance capability. However, M3C converters require a more complex control system than simpler converters. For instance, A basic M3C control system for power transmission requires seventeen (17) PI controllers, whose adjustment depends on the M3C’s dynamical model parameters’ value knowledge needing extensive and time-consuming testing to obtain them. To solve this control system issue, we propose an adaptive M3C control system for variable speed drives powering multiple PMSM-driven centrifugal pumps that reduces the number of controllers to six (6). Furthermore, the proposal does not require knowledge of the converter, motor, or load parameters, making it more practical and versatile. The proposal introduces an ad-hoc hybrid passivity-based model reference adaptive controller in cascade with a passivity-based control. It has been validated through theoretical stability proof and comparative simulation results with a basic control system under normal and fault operations. As a result, the proposal effectively follows the required rotor speed while enhancing performance by decreasing the current consumption and recovering from a 10% input phase imbalance, a cell short circuit, and an open cell.

Keywords:

Subject: Engineering - Electrical and Electronic Engineering

1. Introduction

In recent years, a growing emphasis has been on utilizing permanent magnet synchronous motors (PMSM) to enhance energy efficiency in pumping applications [1]. Compared to traditional induction motors (IM), PMSM motors have demonstrated superior efficiency, as evidenced by [1, Figure 3]. The work [2] proposes customizing PMSM design for this application, while [3,4] study a variable speed PMSM for water pumps powered by AC-AC converter fed by photovoltaic panels. The works [3,4] use a two-level voltage source inverter controlled by model reference adaptive control (MRAC).

However, the work [5] proposes several fault-tolerant multilevel converters. In this sense, the use of modular multilevel cascaded converter (MMCC) obtained popularity due to its many benefits, such as redundancy, high efficiency, robustness, lower output voltage TDH, and low maintenance [6,7,8]. Among these converters, the triple-star bridge cells (M3C) topology is particularly noteworthy. M3C employs smaller floating capacitors [6,9].

What sets M3C apart is its inherent fault tolerance characteristics, allowing it to continue proper operations even after having a power supply phase imbalance or a power cell failure [6,9]. It ensures energy balancing with low impact on the output currents [9]. Furthermore, it reduces current harmonics, enhances power factor and efficiency, [6,8,10], eliminates voltage fluctuations and ensures optimal operation at low output frequencies [11,12]. There are even several studies that propose fault detection and control under fault of M3C [13,14,15]. This manuscript focuses on controlling fault-tolerant M3C-based variable speed drive for PMSM-driven centrifugal pumps.

Figure 1 shows a commonly used M3C. It has modularity, the ability to reach high-voltage levels, power quality, bidirectional power conversion, and redundancy [16,17]. It has nine clusters (three per phase) that link the input phases (a, b, c) with the output phases (r, s, t), each consisting of three cells. Additionally, each cell has a full-bridge monophasic inverter. It has been widely utilized [18]; examples are to inject wind energy into an electrical network [17,19], and feed general loads [20].

However, while having these fault-tolerant capabilities, controlling M3C is complex compared to simpler converters. Figure 2 describes how the control system of an M3C involves:

Complex managing feedback signals that rearrange nine-dimensional measurement vectors $i_{i j}$ , $V_{C i j}$ , into matrixes form to work with variables at the intricate coordinate system called $2 α β γ$ , and later rearrange them back to their vector form to allow the control [9,22,23].
Controlling the average capacitor voltage (ACV) $V_{C a v g}$ in cascade with the input currents amplitude $I_{i n}$ control, through the required input voltage $v_{i n - c l}^{*}$ .
Keeping zero imbalance of the cluster capacitor voltage (CCV) in cascade with the circulating current $i_{c i r}$ control via the needed cluster voltage $v_{c l}^{*}$ . It considers reducing to zero the Inter-CCV imbalances (CCV imbalance among clusters of different Sub-Converters) and the Intra-CCV imbalances (CCV imbalance among clusters inside the same Sub-Converters).
Controlling a required output variable by adjusting the output voltage $v_{o u t - c l}^{*}$ amplitude and frequency.

The control diagram of Figure 2 uses Park transform P[24],

α β γ

transform

C

[22], doble

α β γ

transform

C X C^{T}

of different matrix variables X[22], and the combined components transformation matrix

C_{D}

[25]. Furthermore, the local cell balancing (LCB) and modulation block may use a phase-shifted (PS) pulse-wide modulation (PWM) technique [12,26], a space vector modulation (SVM) [27] or Predictive Control [11,21]. This manuscript controls an M3C with the most extensively used PS-PWM [6].

Regarding the controllers, the works [17,21,25,28,29] consider M3C has several single-input and single-output (SISO) subsystems and use Proportional Integer (PI) controllers for all variables except for the circulating current. Most reported control strategies for the circulating current regulation are based on a simple P controller [17,25,28]. However, some authors use a P-resonant (PR) controller [21,29] as described in [6]. As a result, there are thirteen (13) PI controllers and four (4) PR or P controllers. One (1) PI regulates the ACV direct component in cascade with two (2) PIs for the input current amplitude direct and quadrature components. Eight (8) PIs aim to reduce the CCV imbalance in cascade with four (4) PR or P circulating current controllers. Finally, two (2) PIs regulate the load output current amplitude direct and quadrature components for energy transfer applications between the power supply and the load [6].

Figure 2. Basic control system of an M3C for transferring energy between the power supply and the load, which is based on [6,17,22,29].

The M3C has also been powering electrical motors with an output control strategy that differs from the one shown in Figure 2 and uses a speed control loop. The works [12,22,30] power IMs with an M3C, while [26] drives PMSMs. However, [12,22,26,30] do not describe the used output control strategy. In contrast, [31] clearly identifies a field-oriented control (FOC) strategy for an MMCC converter feeding IMs. Moreover, it presents multiple-input and multiple-output (MIMO) controllers, significantly reducing the number of controllers. All control systems proposed in [12,22,26,30,31] require knowledge of the plant parameters for their adjustment, which is typically obtained through extensive and time-consuming testing.

To overcome this issue and as the main contribution, this manuscript proposes a MIMO adaptive control of an M3C-based variable speed drive. It operates multiple PMSM-driven centrifugal pumps using a scalar control scheme (

V / f

) [32] for the output control, as FOC is unnecessary in pumping applications. Our proposal involves the following novelties:

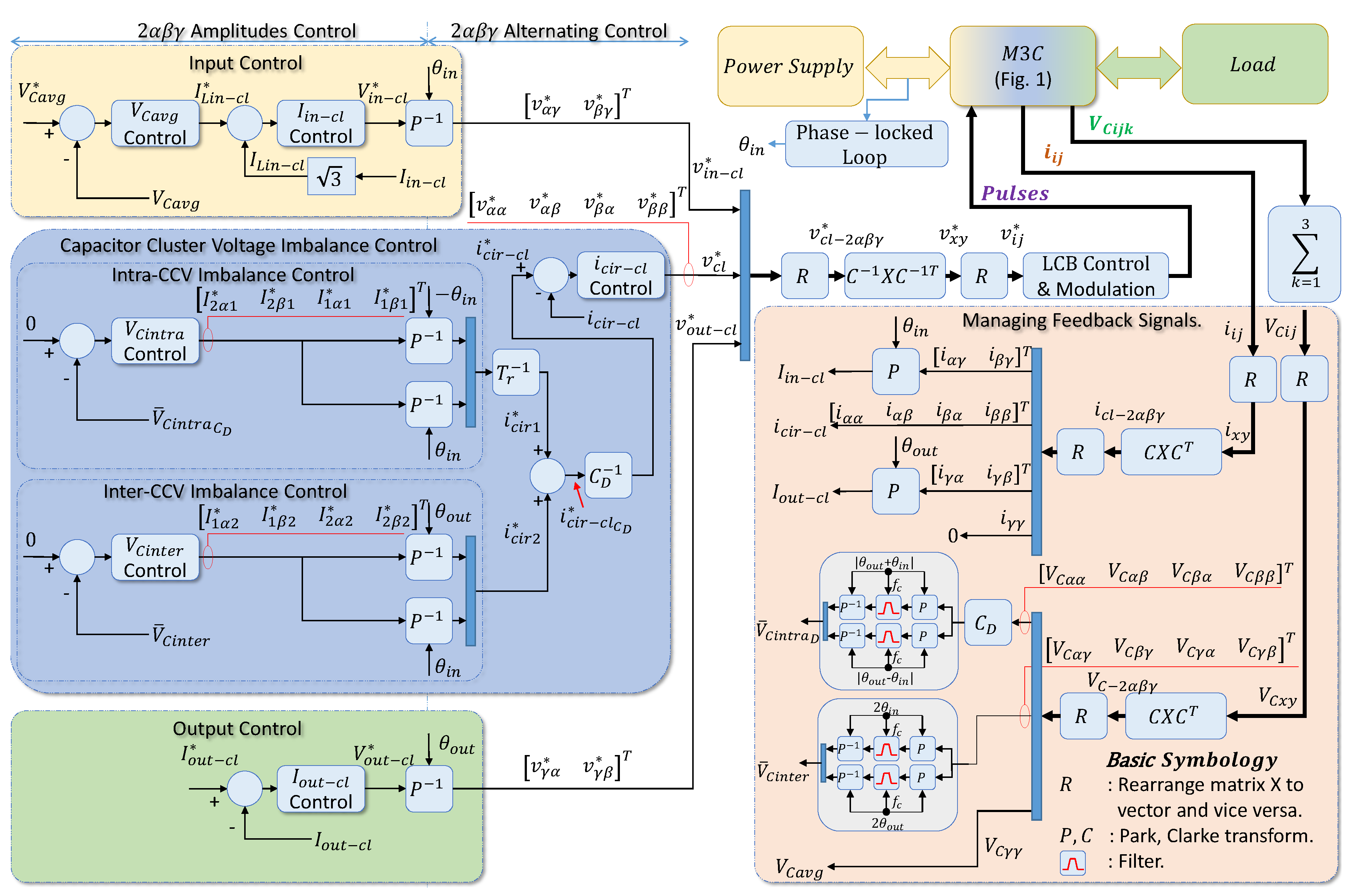
Obtaining the multivariable M3C state-space model for control. It is a MIMO dynamical system with a currents inner loop, a voltages outer loop, and an inner-outer interface. Appendix A of this manuscript details the model obtaining, which complements, describes, rearranges, and summarizes elements taken from [6,22,23,33]. In contrast to [6,22,23,33], herein we give details for control implementation, such as the matrix and vector operations (please see, for instance, the Managing feedback signals details given in Figure 2), and identify the state-space model form with inner and outer loops.
Using MIMO adaptive controllers instead of non-adaptive SISO controllers [17,21,25,28,29,31]. We show it is a viable and more straightforward solution. The proposal gains the benefits discussed in [31] of reducing the number of controllers by using a MIMO approach for an MMCC but herein for the M3C. In contrast to the works [17,21,25,28,29,31], tuning adaptive controllers does not require plant parameters knowledge, decreasing the commissioning time. Moreover, they adapt to plant changes without compromising their effectiveness.
Proposing a passivity-based hybrid MRAC called PBMRAC. In contrast to [3,4,34], it uses the MRAC as a low-pass filter for the noisy reference input signals. Moreover, PBMRAC introduces to MRAC a term of an adaptive passivity-based controller (APBC) [35] to attend to the closed-loop system response time. M3C control particularly needs it after having inner reference input noise periods more than sixty times distant from the M3C inner time constant.
Presenting APBC in cascade with PBMRAC. It expands the Cascade MRAC [36] and the cascade APBC [37]. The first uses an outer SISO controller, whereas the M3C outer loop requires a MIMO controller. Moreover, as Figure 2 shows, the M3C has zero or constant outer references eliminating the need for the outer reference model; therefore, an outer APBC [37] ensures a faster outer loop’s time response.

The following manuscript sections describe the control preliminaries in Section 2. Section 3 details the proposed adaptive control algorithm. Section 4 exhibits the experimental setup and obtained results illustrating the proposal’s effectiveness. Finally, the Authors present concluding remarks in Section 5.

2. Preliminaries

This section commences by introducing the M3C state-space dynamical model. Subsequently, it presents the conventional PI tuning methods. Finally, it gives the requisite background information of the cascade MRAC to be extended with the proposal.

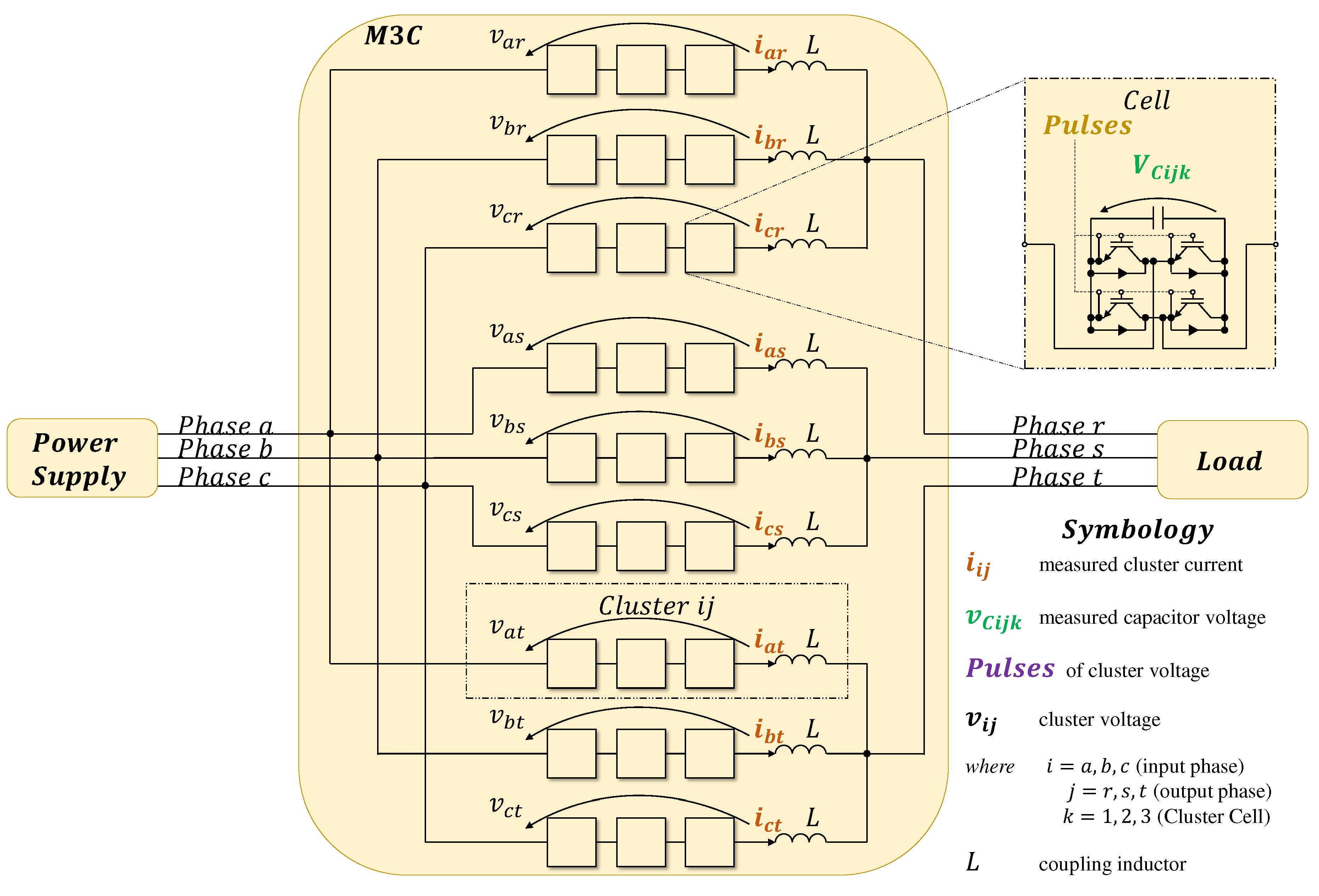
2.1. M3C State-Space Model

The M3C state-space model obtaining is detailed in Appendix A, resulting in the equations (A7) and (A13). The following dynamical equations describe it:

2 α β γ Currents Inner Loop

\begin{matrix} {\dot{I_{L i n}}}_{- c l} (t) = - \frac{\sqrt{3}}{L} V_{i n - c l} (t) + Δ_{i n - c l} (t), & Input current amplitude \\ {\dot{i_{c i r}}}_{- c l} (t) = - \frac{1}{L} v_{c l} (t), & Circulating alternating current \\ {\dot{I_{o u t}}}_{- c l} (t) = - \frac{1}{L} V_{o u t - c l} (t) + Δ_{o u t - c l} (t), & Output current amplitude \end{matrix}

(1)

2 α β γ Inner - Outer Interface

\begin{matrix} I_{L i n - c l} (t) = {[I_{L i n - c l_d} (t) 0]}^{T}, \\ i_{c i r - c l} (t) = C_{D}^{- 1} \{T_{r}^{- 1} [\begin{matrix} P {(- θ_{i n})}^{- 1} \\ P {(θ_{i n})}^{- 1} \end{matrix}] I_{c i r 1} (t) + [\begin{matrix} P {(- θ_{o u t})}^{- 1} \\ P {(θ_{i n})}^{- 1} \end{matrix}] I_{c i r 2} (t)\}, \end{matrix}

(2)

2 α β γ Voltages Outer Loop

\begin{matrix} {\dot{V}}_{C a v g} (t) = \frac{V_{a v g} (t)}{3 C ϵ (t) V_{C}^{*}} {I_{L i n}}_{- c l_d} (t) + Δ_{a v g} (t), & ACV amplitude \\ {\dot{V}}_{C i n t r a} (t) = \frac{V_{i n t r a} {(t)}^{T}}{\sqrt{6} C ϵ (t) V_{C}^{*}} T_{r} I_{c i r 1} (t) + Δ_{i n t r a_{C_{D}}} (t), & Intra - CCV imbalance amplitude \\ {\dot{V}}_{C i n t e r} (t) = \frac{V_{i n t e r} {(t)}^{T} (t)}{\sqrt{3} C ϵ (t) V_{C}^{*}} I_{c i r 2} (t) + Δ_{i n t e r} (t), & Inter - CCV imbalance amplitude \end{matrix}

(3)

where in the inner loop, the output variables to control are the amplitudes of the input and output cluster currents

I_{i n - c l} \in ℜ^{2 \times 1}

and

I_{o u t - c l} \in ℜ^{2 \times 1}

, and the instantaneous circulating current

i_{c i r - c l} \in ℜ^{4 \times 1}

. Here, the input variables are the amplitudes of the input and output voltages

V_{i n - c l} \in ℜ^{2 \times 1}

and

V_{o u t - c l} \in ℜ^{2 \times 1}

, and the instantaneous cluster voltage

v_{c l} \in ℜ^{4 \times 1}

. The parameter is the coupling inductors inductance L. Finally, the time-varying and bounded disturbance terms for the input are

Δ_{i n - c l} (t) = \frac{3}{L} ϵ_{i n} (t) V_{i n_r a t e d} \in ℜ^{2 \times 1}

and

Δ_{o u t - c l} (t) = - \frac{\sqrt{3}}{L} ϵ_{o u t} (t) V_{o u t_r a t e d} \in ℜ^{2 \times 1}

for the output currents, where

ϵ_{i n} (t)

and

ϵ_{o u t} (t)

are rated voltages fluctuations.

For the outer loop, the output variables are the ACV

V_{C a v g} \in ℜ

, the intra-CCV imbalance

V_{C i n t r a} \in ℜ^{4 \times 1}

, and the inter-CCV imbalance

V_{C i n t e r} \in ℜ^{4 \times 1}

. The input variables are the amplitudes of the cluster input direct component

I_{i n - c l_d} \in ℜ

, and the circulating currents

I_{c i r 1} \in ℜ^{4 \times 1}

and

I_{c i r 2} \in ℜ^{4 \times 1}

. There are also time-varying bounded disturbance terms

Δ_{a v g} (t) \in ℜ

Δ_{i n t r a_{C_{D}}} (t) \in ℜ^{4 \times 1}

, and

Δ_{i n t e r} (t) \in ℜ^{4 \times 1}

. Finally, the fixed parameters are the cells capacitor capacitance C and required capacitor voltage

V_{C}^{*} \in ℜ

; while the time-varying parameters are the cluster voltages amplitudes

V_{i n t r a} (t) \in ℜ^{4 \times 1}

V_{i n t e r} (t) \in ℜ^{4 \times 1}

V_{a v g} (t) \in ℜ

, and the capacitor voltage fluctuations

ϵ (t)

The inner-outer interface links the direct component of the line input cluster current

I_{L i n - c l_d}

with the input cluster current

I_{i n - c l}

. Moreover, it relates the circulating current amplitudes

I_{c i r 1}

and

I_{c i r 2}

with the instantaneous circulating current

i_{c i r - c l}

, after using the auxiliary transformation matrix

C_{D}

[25] and the Park transformation matrix P[24] with the corresponding input

θ_{i n}

and output

θ_{o u t}

angles dependence. Please see Appendix A and Figure 2 for details.

Regarding the operating points in this

2 α β γ

coordinate, the outer loops consider an ACV setpoint of

V_{C a v g}^{*} = 3 V_{C}^{*}

[22, Definition given bellow Equation (26)], working at zero intra-CCV Imbalance

V_{C i n t r a_{C_{D}}}^{*} = 0

and zero inter-CCV Imbalance

V_{C i n t e r}^{*} = 0

[18]. Moreover, the output current reference would be

I_{o u t - c l}^{*} = \frac{s q r t (3)}{3} I_{o u t}

for applications of energy transference between the power supply and the load [6].

The following section describes the PI controllers design for the M3C converter.

2.2. Basic Control Based PI Controllers

PI controllers design starts by assuming that plant parameters are constant, thus

ϵ_{i n} (t) = ϵ_{o u t} (t) = ϵ (t) = 1

. Later, the method splits every equation (1) to (3) in scalar subsystems having each one the general form

\dot{y} (t) = b \cdot u (t) + δ (t)

. Here,

y (t) \in ℜ

is the output variable,

u (t) \in ℜ

is the input, b represents the fixed subsystems parameter, and

δ (t)

is the disturbance.

Then, Laplace transform is applied obtaining

Y (S) = (\frac{b}{S}) (U (S) + b^{- 1} Δ (S)

, not including the circulating current working in alternating current. Here, the corresponding open-loop transfer function is

F T_{L A} (S) = \frac{b}{S}

, after neglecting the disturbance term, i.e.,

Δ (S) = 0

After considering the PI transfer function

(K_{p} + \frac{K_{i}}{S})

acting in series with the

F T_{L A}

, the feed forward transfer function is

G (S) = (K_{p} + \frac{K_{i}}{S}) (\frac{b}{S})

. Later, considering the feedback transfer function

H (S)

, you may obtain the following closed-loop transfer function as [38]:

F T_{L C} = \frac{G (S)}{1 + G (S) H (S)} = \frac{K_{p} b \cdot S + K_{i} b}{S^{2} + K_{p} b \cdot S + K_{i} \cdot b} = \frac{2 ξ ω_{n} S + ω_{n}^{2}}{S^{2} + 2 ξ ω_{n} S + ω_{n}^{2}},

(4)

where

ξ

is the damping coefficient, and

ω_{n}

is the natural frequencies in

r a d / s

The feedback sensor transfer function

H (S)

is often considered a unitary gain. Moreover, we can identify in (4) the equivalence terms

2 ξ ω_{n} = K_{p} b

and

ω_{n}^{2} = K_{i} b

, between the general second-order equation of the right side and the obtained result of the center side. It allows adjusting the PI controllers as follows:

\begin{matrix} K_{p} = \frac{2 ξ ω_{n}}{b}, K_{i} = \frac{ω_{n}^{2}}{b} . \end{matrix}

(5)

To tune all PI controllers based on (5),

ξ = \frac{\sqrt{2}}{2}

is usually considered [38, Section (5-3)]. However, there are different values of b,

ω_{n}

, and PI quantities for the distinct controlled variables, as Table 1 shows. Two (2) identical PI regulates the input and output current amplitude components d and q with

b = - \frac{\sqrt{3}}{L}

, as described in (1) and (A7). One (1) PI controls the ACV with

b = \frac{V_{a v g}}{3 C V_{C}^{*}}

as can be seen in (3) and (A14). Four (4) PIs control the intra-CCV imbalance, where

V_{i n t r a} = V_{i n_{α}} {[\begin{matrix} 1 & 1 & 1 & 1 \end{matrix}]}^{T}

from (A14); thus, all components of the vector

V_{i n t r a}

of are equal

V_{i n_{α}}

, having the same

b = \frac{V_{i n t r a}^{T}}{\sqrt{6} C V_{C}^{*}}

. Finally, also four (4) PI controls the inter-CCV imbalance. However, these have different values of b as described in Table 1, due to

V_{i n t e r} = {[\begin{matrix} - V_{o u t_{α}} & V_{o u t_{α}} & V_{i n_{α}} & V_{i n_{α}} \end{matrix}]}^{T}

from (A14).

The alternating circulating current controller often considers four (4) P controllers adjusted as in (5) but a

k_{i} = 0

[23], and our case

b = - \frac{1}{L}

and

ω_{n} = 2 π (10 f_{o u t})

Finally, for applications of energy transference between the power supply and the load [6,17,22,29], the output current amplitude control

d q

would have two PI controllers adjusted as in (5) and considering

b = - \frac{1}{L}

and

ω_{n} = 2 π (f_{o u t})

Remark 1.

It is imperative to know the plant parameters value to adjust the PI controllers, as can be seen in equation (5) and Table 1. This knowledge is usually obtained through extensive testing, which can be time-consuming. It’s also crucial for the controllers to handle plant changes without compromising their effectiveness.

Finally, the output controller must be adjusted as we study pumping applications. Thus, the following P controller called scalar control scheme (

V / f

) is commonly used for a two-level voltage source inverter feeding PMSD-driven centrifugal pumps [32]:

V_{o u t - c l_d}^{*} = \{\begin{matrix} 0 & for 0 < ω_{r} < ω_{r_m i n} \\ P_{1} ω_{r}^{*} + \sqrt{2} V_{b o o s t}, with P_{1} = \sqrt{2} (\frac{V_{s_r a t e d}}{ω_{r_r a t e d}} - \frac{V_{b o o s t}}{ω_{r_c}}) & for ω_{r_m i n} < ω_{r} < ω_{r_c} . \\ P_{2} ω_{r}^{*}, with P_{2} = \sqrt{2} \frac{V_{s_r a t e d}}{ω_{r_r a t e d}} & for ω_{r_c} < ω_{r} < ω_{r_r a t e d} \end{matrix}

(6)

Here,

V_{s_r a t e d}

is the rated phase voltage from the motor data plate.

ω_{r_r a t e d}

is the motor-rated rotor speed in

r a d / s

. The

V_{b o o s t}

is a controller bias or offset (with a value up to

50 %

V_{s_r a t e d}

allowing the PMSM to deliver a certain amount of starting torque. The

V_{b o o s t}

operates from minimum frequency

ω_{r_m i n}

(with a value up to

6 %

ω_{r_r a t e d}

to the cut-frequency

ω_{r_c}

(with a value up to

50 %

ω_{r_r a t e d}

) [32].

Remark 2.

In order to attain the desired rotor angular frequency

ω_{r}^{*}

with a ramp-up, a two-level voltage source inverter necessitates a phase stator voltage amplitude of

V_{o u t - c l}^{*} = {[V_{o u t - c l_d}^{*} 0]}^{T}

. However, the output voltage required for the M3C is in

d o u b l e α β γ

coordinates, utilizing a Power invariant transformation in lieu of Clarke’s transformation that preserves the amplitude [39]. This paper proposes utilizing equation (6) [32, Equation (1)] in conjunction with the subsequent equation:

V_{o u t - c l}^{*} = \sqrt{3} {[V_{o u t - c l_d}^{*} 0]}^{T}

(7)

The following section will give an overview of an adaptive controller that can maintain optimal performance while adapting to plant changes without requiring knowledge of plant parameters.

2.3. Cascade Adaptive Control Background

M3C modeled as (1) to (3) needs a cascade control system and the following cascade MRAC [36, Equations (14) - (22)] ensures the outputs

y_{o}

and

y_{i}

tracks the references

y_{o}^{*}

and

y_{i}^{*}

\begin{matrix} {\dot{y}}_{r o} (t) = - a_{r o} y_{r o} (t) + b_{r o} y_{o}^{*} (t), & Outer reference model \\ u_{o} (t) = - θ_{o} {(t)}^{T} ω_{o} (t), & Outer adaptive control law \\ ω_{o} (t) = {[\begin{matrix} y_{o} (t) & f_{2} (u; I, y_{i}) & y_{o}^{*} (t) \end{matrix}]}^{T}, & MRAC outer information vector \\ {\dot{θ}}_{o} {(t)}^{T} = - (s i g n (b_{o}) e_{o} (t) ω_{o} {(t)}^{T} + σ_{o} θ_{o} {(t)}^{T}) Γ_{o}, & Outer adaptive law for MRAC \\ θ_{o}^{*} {(t)}^{T} = [\begin{matrix} b_{o}^{- 1} (t) a_{r o} & b_{o}^{- 1} (t) a_{o} & - b_{o}^{- 1} (t) b_{r o} \end{matrix}], & Ideal outer MRAC parameter \end{matrix}

(8)

\begin{matrix} y_{i}^{*} (t) = f_{1} (u_{o} (t)), & Inner - outer loop interface \end{matrix}

(9)

\begin{matrix} {\dot{y}}_{r i} (t) = - A_{r i} y_{r i} (t) + B_{r i} y_{i}^{*} (t), & Inner reference model \\ u_{i} (t) = - θ_{i} {(t)}^{T} ω_{i} (t), & Inner adaptive control law \\ ω_{i} (t) = {[\begin{matrix} y_{i} {(t)}^{T} & 1_{m}^{T} & y_{i}^{*} {(t)}^{T} \end{matrix}]}^{T}, & MRAC inner information vector \\ {\dot{θ}}_{i} {(t)}^{T} = - (s i g n (B_{i}) e_{i} (t) ω_{i} {(t)}^{T} + σ_{i} θ_{i} {(t)}^{T}) Γ_{i}, & Inner adaptive law for MRAC \\ θ_{i}^{*} {(t)}^{T} = [\begin{matrix} B_{i}^{- 1} A_{r i} & B_{i}^{- 1} A_{i} (t) & - B_{i}^{- 1} B_{r i} \end{matrix}] . & Ideal inner MRAC parameter \end{matrix}

(10)

Here, the outer tracking error is

e_{o} (t) = y_{r o} (t) - y_{o} (t) \in ℜ

and the inner tracking error is

e_{i} (t) = y_{r i} (t) - y_{i} (t) \in ℜ^{m}

. The variables

y_{r o} (t) \in ℜ

y_{r i} (t) \in ℜ^{m}

are the outer and inner reference model outputs. The set point are

y_{o}^{*} (t) \in ℜ

and

y_{i}^{*} (t) \in ℜ^{m}

. The reference model parameters are

a_{r o}, b_{r o} \in ℜ

and

A_{r i}, B_{r i} \in ℜ^{(m \times m - D i a g o n a l)}

made equal (

a_{r o} = b_{r o}

and

A_{r i} = B_{r i}

) for an exact set point tracking without scaling. The adaptive external and internal controllers

u_{o} (t) \in ℜ

and

u_{i} (t) \in ℜ^{m}

depends on their adaptive parameters

θ_{o} (t) \in ℜ^{3}

and

θ_{i} (t) \in ℜ^{(m \times 3 m)}

and their corresponding information vectors

ω_{o} (t) \in ℜ^{3}

and

ω_{i} (t) \in ℜ^{3 m}

. The ideal adaptive parameters are

θ_{o}^{*} (t) \in ℜ^{3}

and

θ_{i}^{*} (t) \in ℜ^{(m \times 3 m)}

. The term

1_{m} \in ℜ^{m}

refers to a vector with all its components equal to one. Besides the model reference parameters, the cascade MRAC has the following tuning parameters: adaptive law fixed-gains

Γ_{o} \in ℜ^{(3 \times 3 - D i a g o n a l)}

and

Γ_{i} \in ℜ^{(3 m \times 3 m - D i a g o n a l)}

, and adaptive law modification factors

σ_{o} \in ℜ

and

σ_{i} \in ℜ^{(3 m \times 3 m - D i a g o n a l)}

Cascade MRAC (8)-(10) applies to time-varying cascade systems of the following form [36]:

\begin{matrix} {\dot{y}}_{i} (t) = A_{i} (t) + B_{i} (t) \cdot u_{i} (t), & Inner loop \\ y_{i} (t) = f_{1} (u_{o} (t)), & Inner - outer interface \\ {\dot{y}}_{0} (t) = a_{o} (t) f_{2} (u; I, y_{i}) + b_{o} (t) \cdot u_{o} (t), & Outer loop \end{matrix}

(11)

where

y_{o} (t) \in ℜ

and

y_{i} (t) \in ℜ^{m}

are the outer and inner output variables, respectively. The inputs are

u_{o} (t) \in ℜ

for the outer loop and

u_{i} (t) \in ℜ^{m}

for the inner loop. Moreover,

a_{o} (t), b_{o} (t) \in ℜ

and

A_{i} (t), B_{i} (t) \in ℜ^{m \times m}

are time-varying plant parameters, where

B_{i} (t) = | B_{i} (t) | S i g n (B_{i} (t))

and

b_{0} (t) = | b_{0} (t) | S i g n (b_{0} (t))

with

| B_{i} (t) |

and

| b_{0} (t) |

the modulus of each element of

B_{i} (t)

and

b_{0} (t)

Remark 3.

It is important to note that the cascade MRAC (8)-(10) uses an outer SISO controller, whereas the M3C outer loop (3) requires a MIMO controller. Additionally, Figure 2 shows that M3C has zero or constant outer references, eliminating the need for the outer reference model of (8), which would slow down the outer loop’s time response. Finally, the inner control loop receives noisy reference input signals with certain switching noise periods. Although the inner reference model of (10) could filter these signals, it would disregard the required inner loop response time, failing to ensure both needs.

These issues are solved by the controller proposed in the following section.

3. Proposal

This section proposes an adaptive controller for the following system that encompasses the M3C state-space model (1)-(3):

\begin{matrix} \dot{y_{i}} (t) = B_{i} (t) u_{i} (t) + Δ_{i} (t), & Inner loop \\ y_{i} (t) = f_{1} (u_{o} (t)), & Inner - outer interface \\ \dot{y_{0}} (t) = B_{o} (t) u_{o} (t) + Δ_{o} (t), & Outer loop \end{matrix}

(12)

where

y_{o} (t) \in ℜ^{n}

and

y_{i} (t) \in ℜ^{m}

are the outer and inner output variables, respectively. The outer control input is

u_{o} (t) \in ℜ^{n}

and the inner is

u_{i} (t) \in ℜ^{m}

. Moreover,

B_{o} (t) \in ℜ^{n \times n}

and

B_{i} (t) \in ℜ^{m \times m}

are time-varying and unknown plant parameters, where

B_{i} (t) = | B_{i} (t) | S i g n (B_{i} (t))

and

B_{0} (t) = | B_{0} (t) | S i g n (B_{0} (t))

. Here, the matrix

| B_{i} (t) |

and

| B_{0} (t) |

are compose by the modulus of each element of

B_{i} (t)

and

B_{0} (t)

and are unknown. Furthermore, the matrix

S i g n (B_{i} (t))

and

S i g n (B_{0} (t))

are compose by the sign of each element of

B_{i} (t)

and

B_{0} (t)

and are known. The known interface nonlinear function is

f_{1} \in ℜ^{m \times n}

. Finally,

Δ_{i} (t)

and

Δ_{o} (t)

are the inner and outer bounded and unknown disturbances, respectively.

The following Theorem describes the proposal:

Theorem 1.

For systems of the form (12), the following adaptive controller ensures the outputs

y_{o}

and

y_{i}

tends to the constant references

y_{o}^{*}

and

y_{i}^{*}

, respectively:

\begin{matrix} u_{o} (t) = - θ_{o} {(t)}^{T} ω_{o} (t), & Outer control law \\ ω_{o} (t) = {[\begin{matrix} Δ_{o_b}^{T} & u_{o}^{p} {(t)}^{T} \end{matrix}]}^{T}, with u_{o}^{p} (t) = K_{o} \nabla V_{e_{o}} (t), & APBC outer information vector \\ \dot{θ_{o}} {(t)}^{T} = - (s i g n (b_{o}) \nabla V_{e_{o}} (t) ω_{o} {(t)}^{T} + σ_{o} θ_{o} {(t)}^{T}) Γ_{o}, & APBC outer adaptive law \\ θ_{o}^{*} {(t)}^{T} = [\begin{matrix} B_{o}^{- 1} (t) & B_{o}^{- 1} (t) \end{matrix}], & Ideal outer APBC parameter \end{matrix}

(13)

\begin{matrix} y_{i}^{*} (t) = f_{1} (u_{o} (t)), & Inner - outer loop interface \end{matrix}

(14)

\begin{matrix} {\dot{y}}_{r i} (t) = - A_{r i} y_{r i} (t) + B_{r i} y_{i}^{*} (t), & Inner reference model \\ u_{i} (t) = - θ_{i} {(t)}^{T} ω_{i} (t), & Inner control law based \\ ω_{i} (t) = {[\begin{matrix} y_{i} {(t)}^{T} & y_{i}^{*} {(t)}^{T} & Δ_{i_b}^{T} & u_{i}^{p} {(t)}^{T} \end{matrix}]}^{T}, & PBMRAC inner inform . vector \\ with u_{i}^{p} (t) = K_{i} \nabla V_{e_{i}} (t), \\ \dot{θ_{i}} {(t)}^{T} = - (s i g n (B_{i}) \nabla V_{e_{i}} (t) ω_{i} {(t)}^{T} + σ_{i} θ_{i} {(t)}^{T}) Γ_{i}, & PBMRAC inner adaptive law \\ θ_{i}^{*} {(t)}^{T} = [\begin{matrix} B_{i}^{- 1} A_{r i} & - B_{i}^{- 1} B_{r i} & B_{i}^{- 1} \end{matrix}] . & Ideal inner PBMRAC parameter \end{matrix}

(15)

Here, the outer tracking error is

e_{o} (t) = y_{r o} (t) - y_{o} (t) \in ℜ^{n}

and the inner tracking error is

e_{i} (t) = y_{r i} (t) - y_{i} (t) \in ℜ^{m}

. The variables

y_{r o} (t) \in ℜ^{n}

and

y_{r i} (t) \in ℜ^{m}

are the outer and inner reference model outputs, respectively. The set points are

y_{o}^{*} (t) \in ℜ^{n}

and

y_{i}^{*} (t) \in ℜ^{m}

. The inner and outer controllers

u_{o} (t) \in ℜ^{n}

and

u_{i} (t) \in ℜ^{m}

depends on their adaptive parameters

θ_{o} (t) \in ℜ^{n \times 2 n}

and

θ_{i} (t) \in ℜ^{(m \times 3 m)}

and their corresponding information vectors

ω_{o} (t) \in ℜ^{2 n}

and

ω_{i} (t) \in ℜ^{3 m}

. The unknown ideal adaptive parameters are defined as

θ_{o}^{*} (t) \in ℜ^{n \times 2 n}

and

θ_{i}^{*} (t) \in ℜ^{(m \times 3 m)}

. Moreover,

V_{e_{o}} (t)

and

V_{e_{i}} (t)

are Lyapunov-type energy terms.

Following, the adaptive controller tuning parameters settings are described. The outer APBC loop tunes the outer PB gain as

K_{o} = \frac{5 δ_{1 o}}{T_{s}^{*}} I_{n} \in ℜ^{(n \times n - D i a g o n a l)}

, where

5 T_{s}^{*}

is the process required stabilization time [32]. The adaptive law modification term is

σ_{o} = δ_{2 o} I_{n} \in ℜ^{(n \times n - D i a g o n a l)}

, depending on the identity matrix

I_{n}

of order n. The adaptive law fixed-gain is

Γ_{o} \in ℜ^{(2 n \times 2 n - D i a g o n a l)}

. Moreover, the fine-tuning scalar factors are

0 < α_{o 1 l}

α_{o 2 l} < 10

and

0 < δ_{1 o}, δ_{2 o} < 10

, with

l = 1, 2, 3, . . ., n

[36, Theorem 1]. Finally, APBC adjusts the adaptive law fixed-gain [32, Equation (11)] as follows:

\begin{matrix} \begin{matrix} Γ_{o} = D i a g [\begin{matrix} \frac{α_{o 11} Δ_{o 1_b}}{1 + Δ_{o 1_b}^{2}} & \dots & \frac{α_{o 1 n} Δ_{o n_b}}{1 + Δ_{o n_b}^{2}} & \frac{α_{o 21} u_{o 1_b}^{p}}{1 + u_{{o 1_b}^{2}}^{p}} & \dots & \frac{α_{o 2 n} u_{o n_b}^{p}}{1 + u_{{o n_b}^{2}}^{p}} \end{matrix}] \end{matrix} . \end{matrix}

(16)

The inner PBMRAC loop adjusts the model reference parameter as

A_{r i} = \frac{f_{n o i s e} δ_{1 i}}{20} I_{n} \in ℜ^{(n \times n - D i a g o n a l)}

. The PB gain

K_{i}

is computed as

(A_{r i} + K_{i}) = 15 K_{o}

(over fifteen times faster than the outer loop), and the adaptive law modification terms

σ_{i} = δ_{2 i} I_{m} \in ℜ^{(m \times m - D i a g o n a l)}

. Here,

0 < δ_{1 i}, δ_{2 i} < 10

are fine-tuning scalar adjusting factors, toguether with

0 < α_{i 1 l}

α_{i 2 l}

α_{i 3 l}

α_{i 4 l} < 10

where

l = 1, 2, 3, . . ., n

. Finally, the adaptive law fixed-gain

Γ_{i} \in ℜ^{(2 m \times 2 m - D i a g o n a l)}

is adjusted via the following equation [36]:

\begin{matrix} Γ_{i} = D i a g [\frac{α_{i 11} y_{i 1_b}}{1 + {y_{i 1_b}}^{2}} \dots \frac{α_{i 1 n} y_{i n_b}}{1 + {y_{i n_b}}^{2}} \frac{α_{i 21} y_{i 1_b}^{*}}{1 + {y_{i 1_b}^{*}}^{2}} \dots \frac{α_{i 2 n} y_{i n_b}^{*}}{1 + {y_{i n_b}^{*}}^{2}} \\ \frac{α_{i 31} Δ_{i 1_b}}{1 + Δ_{i 1_b}^{2}} \dots \frac{α_{i 3 n} Δ_{i n_b}}{1 + Δ_{i n_b}^{2}} \frac{α_{i 41} u_{i 1_b}^{p}}{1 + u_{{i 1_b}^{2}}^{p}} \dots \frac{α_{i 4 n} u_{i n_b}^{p}}{1 + u_{{i n_b}^{2}}^{p}}] . \end{matrix}

(17)

Following is the Theorem Proof.

Proof of Theorem 1.

As a result of applying the adaptive controllers (13) and (15) to the corresponding dynamical equation of (11), we obtain the closed-loop dynamical error equations whose require verification of their stability.

In detail, the term

u_{o}^{p} (t)

is added and subtracted to the right side of the outer loop equation of (11). The outer control law of (13) is then applied, the outer tracking error definition

e_{o} (t) = y_{o}^{*} (t) - y_{i} (t)

considered, and the terms regrouped conveniently. In regards to the inner loop, we subtract the inner reference model of (15) from the inner loop equation of (11). Later, we add and subtract the term

A_{r i} y_{i} (t)

to the right side and consider the inner tracking error definition

e_{i} (t) = y_{r i} (t) - y_{i} (t)

. Moreover, we apply the inner control law of (15) and regroup terms. As a result, the following control error dynamical equations is obtained:

\begin{matrix} \begin{matrix} {\dot{e}}_{o} (t) = u_{o}^{p} (t) - B_{o} (t) ϕ_{o} {(t)}^{T} ω_{o} (t), \\ {\dot{e}}_{i} (t) = - A_{r i} e_{i} (t) + u_{i}^{p} (t) - B_{i} (t) ϕ_{i} {(t)}^{T} ω_{i} (t), \end{matrix} \end{matrix}

(18)

where

ϕ_{o} {(t)}^{T} = θ_{o} {(t)}^{T} - θ_{o}^{*} {(t)}^{T}

and

ϕ_{i} {(t)}^{T} = θ_{i} {(t)}^{T} - θ_{i}^{*} {(t)}^{T}

are the adaptive parameters errors. Obtaining now the first-time derivative of

ϕ_{o} {(t)}^{T}

and

ϕ_{i} {(t)}^{T}

, considering the definitions given in Theorem 1 for

θ_{o} {(t)}^{T}

θ_{o}^{*} {(t)}^{T}

θ_{i} {(t)}^{T}

, and

θ_{i}^{*} {(t)}^{T}

, these errors dynamical equations give:

\begin{matrix} \begin{matrix} {\dot{ϕ}}_{o} {(t)}^{T} = - (s i g n (B_{o}) \nabla V_{e_{o}} (t) ω_{o} {(t)}^{T} + σ_{o} θ_{o} {(t)}^{T}) Γ_{o} - {\dot{θ}}_{o}^{*} {(t)}^{T}, \\ {\dot{ϕ}}_{i} {(t)}^{T} = - (s i g n (B_{i}) \nabla V_{e_{i}} (t) ω_{i} {(t)}^{T} + σ_{i} θ_{i} {(t)}^{T}) Γ_{i} - {\dot{θ}}_{i}^{*} {(t)}^{T} . \end{matrix} \end{matrix}

(19)

These closed-loop dynamical error equations (18) and (19) have the following associated Lyapunov function:

\begin{matrix} V (e_{i}, e_{0}, ϕ_{i}, ϕ_{o}) = V_{e_{i}} + V_{e_{0}} + T r a c e (\frac{1}{2} | B_{i} | ϕ_{i}^{T} Γ_{i}^{- 1} ϕ_{i}) + \frac{1}{2} | b_{o} | ϕ_{o}^{T} Γ_{o}^{- 1} ϕ_{o} . \end{matrix}

(20)

Taking the first-time derivative of (20), considering the derivative property of the product in the trace, and replacing the control errors dynamical equations (18), we obtain:

\begin{matrix} \dot{V} (e_{i}, e_{0}, ϕ_{i}, ϕ_{o}) = - \nabla V_{e_{i}}^{T} A_{r i} e_{i} - \nabla V_{e_{i}}^{T} u_{i}^{p} + \nabla V_{e_{i}}^{T} B_{i} ϕ_{i}^{T} ω_{i} - \nabla V_{e_{o}}^{T} u_{o}^{p} + \nabla V_{e_{o}}^{T} B_{o} ϕ_{o}^{T} ω_{o} \\ + T r a c e (| B_{i} | {\dot{ϕ}}_{i}^{T} Γ_{i}^{- 1} ϕ_{i}) + | B_{o} | {\dot{ϕ}}_{o}^{T} Γ_{o}^{- 1} ϕ_{o} . \end{matrix}

(21)

Moreover, using the vector property

a^{T} b = T r a c e (a b^{T})

, we can rewrite the following term

(\nabla V_{e_{o}}^{T} B_{o}) (ϕ_{o}^{T} ω_{o}) = T r a c e ((B_{o}^{T} \nabla V_{e_{o}}) (ω_{o}^{T} ϕ_{o}))

. Moreover, we can also re express the term

(\nabla V_{e_{i}}^{T} B_{i}) (ϕ_{i}^{T} ω_{i}) = T r a c e ((B_{i}^{T} \nabla V_{e_{i}}) (ω_{i}^{T} ϕ_{i}))

. Finally, considering that

B_{o} = | B_{o} | S i g n (B_{0})

and

B_{i} = B_{i}^{T} = | B_{i} (t) | S i g n (B_{i} (t))

(due to

B_{i}

is diagonal), it gives the following expression:

\begin{matrix} \dot{V} (e_{i}, e_{0}, ϕ_{i}, ϕ_{o}) - \nabla V_{e_{i}}^{T} A_{r i} e_{i} - \nabla V_{e_{i}}^{T} u_{i}^{p} - \nabla V_{e_{o}}^{T} u_{o}^{p} \\ + T r a c e (| B_{i} | s i g n (B_{i}) \nabla V_{e_{i}}) (ω_{i}^{T} ϕ_{i})) + | B_{i} | {\dot{ϕ}}_{i}^{T} Γ_{i}^{- 1} ϕ_{i}) \\ + T r a c e (| B_{o} | s i g n (B_{o}) \nabla V_{e_{o}}) (ω_{o}^{T} ϕ_{o})) + | B_{o} | {\dot{ϕ}}_{i}^{T} Γ_{o}^{- 1} ϕ_{o}) . \end{matrix}

(22)

Here, replacing the control parameters errors dynamical equation (19), canceling terms, and taking into account the expressions

θ_{o} {(t)}^{T} = ϕ_{o} {(t)}^{T} + θ_{o}^{*} {(t)}^{T}

and

θ_{i} {(t)}^{T} = ϕ_{i} {(t)}^{T} + θ_{i}^{*} {(t)}^{T}

, the Lyapunov function first-time derivative becomes:

\begin{matrix} \dot{V} (e_{i}, e_{0}, ϕ_{i}, ϕ_{o},) = - \nabla V_{e_{i}}^{T} A_{r i} e_{i} - \nabla V_{e_{i}}^{T} u_{i}^{p} - \nabla V_{e_{o}}^{T} u_{o}^{p} \\ - T r a c e (| B_{i} | σ_{i} ϕ_{i}^{T} ϕ_{i}) - T r a c e (| B_{o} | σ_{o} ϕ_{o}^{T} ϕ_{o}) \\ - T r a c e (| B_{i} | σ_{i} θ_{i}^{*^{T}} ϕ_{i}) - T r a c e (| B_{i} | {\dot{θ}}_{i}^{*^{T}} Γ_{i}^{- 1} \\ - T r a c e (| B_{o} | σ_{o} θ_{o}^{*^{T}} ϕ_{o}) - T r a c e (| B_{o} | {\dot{θ}}_{o}^{*^{T}} Γ_{o}^{- 1} . \end{matrix}

(23)

Here, we have that

A_{r i}

| B_{i} |

σ_{i}

| B_{o} |

, and

σ_{o}

are positives; therefore the first five terms of (23) are negatives. However, although the terms

Γ_{i}

and

Γ_{o}

are also positives, there is nothing we can say about the sign of the last fourth terms of (23) at first sight. Therefore, we re-express equation (23) using some modulus and norm properties.

Using the Frobenius norm definition and the Cauchy–Schwarz inequality, we have that

| T r a c e (A B C) | \leq {∥ A ∥}_{F} {∥ B ∥}_{F} {∥ C ∥}_{F}

[40, Section 11.2.2]. Moreover, considering a positive A,

T r a c e (A B^{T} B) = | T r a c e (A B^{T} B) {| \leq ∥ A ∥}_{F} {∥ B ∥}_{F}^{2}

. Therefore, the following terms become

- T r a c e ((| B_{i} | σ_{i}) ϕ_{i}^{T} ϕ_{i}) \leq - ∥ (| B_{i} | σ_{i} {) ∥}_{F} {∥ ϕ_{i} ∥}_{F}^{2}

and

- T r a c e ((| B_{o} | σ_{o}) ϕ_{o}^{T} ϕ_{o}) \leq - ∥ (| B_{o} | σ_{o} {) ∥}_{F}

∥ ϕ_{o} ∥_{F}^{2}

. Also, the last fourth terms fulfill

- T r a c e (| B_{i} | σ_{i} θ_{i}^{*^{T}} ϕ_{i}) \leq - ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ θ_{i}^{*^{T}} ∥_{F} {∥ ϕ_{i} ∥}_{F}

- T r a c e (| B_{o} | σ_{o} θ_{o}^{*^{T}} ϕ_{o}) \leq - ∥ (| B_{o} | σ_{o} {) ∥}_{F} ∥ θ_{o}^{*^{T}} ∥_{F} {∥ ϕ_{o} ∥}_{F}

- T r a c e (| B_{i} | {\dot{θ}}_{i}^{*^{T}} Γ_{i}^{- 1} ϕ_{i}) \leq - ∥ (| B_{i} {|) ∥}_{F}

∥ {\dot{θ}}_{i}^{*} ∥_{F} ∥ ϕ_{i} ∥_{F} {∥ Γ_{i}^{- 1} ∥}_{F}

, and

- T r a c e (| B_{o} | {\dot{θ}}_{o}^{*^{T}} Γ_{o}^{- 1} ϕ_{o}) \leq - ∥ (| B_{o} {|) ∥}_{F} ∥ {\dot{θ}}_{o}^{*} ∥_{F} ∥ ϕ_{o} ∥_{F} {∥ Γ_{o}^{- 1} ∥}_{F}

. Finally, using the property

2 a b \leq a^{2} + b^{2}

[40, Section 11.2.2], and conveniently adding the term

r^{2}

to the right side of equation (23), the Lyapunov function first-time derivative (23) becomes:

\begin{matrix} \dot{V} (e_{i}, e_{0}, ϕ_{i}, ϕ_{o},) = - \nabla V_{e_{i}}^{T} A_{r i} e_{i} - \nabla V_{e_{i}}^{T} u_{i}^{p} - \nabla V_{e_{o}}^{T} u_{o}^{p} \\ + r^{2} - ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ ϕ_{i} ∥_{F}^{2} - ∥ (| B_{o} | σ_{o} {) ∥}_{F} {∥ ϕ_{o} ∥}_{F}^{2} \\ - \frac{1}{2} ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ (θ_{i}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) - \frac{1}{2} ∥ (| B_{o} | σ_{o} {) ∥}_{F} ∥ (θ_{o}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) \\ - \frac{1}{2} ∥ (| B_{i} {|) ∥}_{F} (∥ {\dot{θ}}_{i}^{*} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) ∥ Γ_{i}^{- 1} ∥_{F} - \frac{1}{2} ∥ (| B_{o} {|) ∥}_{F} (∥ {\dot{θ}}_{o}^{*} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) ∥ Γ_{o}^{- 1} ∥_{F}, \end{matrix}

(24)

where the plant parameters and their first-time derivatives are bounded. Therefore,

\dot{V} \leq - \nabla V_{e_{i}}^{T} u_{i}^{p} - \nabla V_{e_{o}}^{T} u_{o}^{p}

and closed-loop dynamical error equations (18) and (19) are passive outside the region

Ω

. This last, is the following instability hyper elliptical paraboloid that is compact, closed, and includes the origin:

\begin{matrix} Ω = [∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ ϕ_{i} ∥_{F}^{2} + ∥ (| B_{o} | σ_{o} {) ∥}_{F} {∥ ϕ_{o} ∥}_{F}^{2} \\ + \frac{1}{2} ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ (θ_{i}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) + \frac{1}{2} ∥ (| B_{o} | σ_{o} {) ∥}_{F} ∥ (θ_{o}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) \\ + \frac{1}{2} ∥ (| B_{i} {|) ∥}_{F} (∥ {\dot{θ}}_{i}^{*} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) ∥ Γ_{i}^{- 1} ∥_{F} + \frac{1}{2} ∥ (| B_{o} {|) ∥}_{F} (∥ {\dot{θ}}_{o}^{*} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) ∥ Γ_{o}^{- 1} ∥_{F}] < r^{2} . \end{matrix}

(25)

Furthermore, substituting into (25), the terms

u_{o}^{p} (t) = K_{o} \nabla V_{e_{o}} (t)

and

u_{i}^{p} (t) = K_{i} \nabla V_{e_{i}} (t)

defined in (13) and (15), and using Lyapunov’s second method, we can conclude that the closed-loop dynamical error equations (18) and (19) are bounded outside

Ω

. Suppose the errors are as minor as possible, resulting in

\dot{V} > 0

within the instability compact and closed region

Ω

, including the origin. In that case, they will be pushed back to a stable boundary. In practice, the values of

σ_{i}, σ_{o}, Γ_{i},

and

Γ_{o}

are chosen so the permanent errors are the possible lowest.

Thus,

e_{i} (t), e_{o} (t), ϕ_{i} (t)

, and

ϕ_{o} (t)

are bounded outside

Ω

, i.e.,

e_{i} (t), e_{o} (t), ϕ_{i} (t), ϕ_{o} (t) \in L^{\infty}

outside

Ω

. Since

e_{i} (t) = y_{i} (t) - y_{r i}

and

e_{o} (t) = y_{o} (t) - y_{r o}

are bounded, it implies that

y_{i} (t)

and

y_{o} (t)

are bounded, as

y_{r i}, y_{i}^{*}

and

y_{r o}, y_{0}^{*}

are bounded references. Moreover,

ϕ_{i} (t)

and

ϕ_{o} (t)

are bounded, and we have bounded plant parameters, then the adaptive parameters

θ_{i} (t)

and

θ_{o} (t)

are bounded, since

θ_{i} {(t)}^{T} = ϕ_{i} {(t)}^{T} + θ_{i}^{*} {(t)}^{T}

and

θ_{o} {(t)}^{T} = ϕ_{o} {(t)}^{T} + θ_{o}^{*} {(t)}^{T}

. Having all these bounded signals outside

Ω

, and that

V, e (t), ϕ (t) \in L^{\infty}

, from (18) and (19), we have that

{\dot{e}}_{i} (t), {\dot{e}}_{o} (t), {\dot{ϕ}}_{i} (t), {\dot{ϕ}}_{o} (t) \in L^{\infty} .

Integrating both sides of

\dot{V} (e_{i}, e_{0}, ϕ_{i}, ϕ_{o},)

in the interval

(0, \infty)

, it gives

\begin{matrix} V (\infty) - V (0) = \int_{0}^{\infty} (- \nabla V_{e_{i}}^{T} A_{r i} e_{i} - \nabla V_{e_{i}}^{T} K_{i} \nabla V_{e_{i}} (t) - \nabla V_{e_{o}}^{T} K_{o} \nabla V_{e_{o}} (t) \\ + r^{2} - ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ ϕ_{i} ∥_{F}^{2} - ∥ (| B_{o} | σ_{o} {) ∥}_{F} {∥ ϕ_{o} ∥}_{F}^{2} \\ - \frac{1}{2} ∥ (| B_{i} | σ_{i} {) ∥}_{F} ∥ (θ_{i}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) - \frac{1}{2} ∥ (| B_{o} | σ_{o} {) ∥}_{F} ∥ (θ_{o}^{*^{T}} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) \\ - \frac{1}{2} ∥ (| B_{i} {|) ∥}_{F} (∥ {\dot{θ}}_{i}^{*} ∥_{F}^{2} + ∥ ϕ_{i} ∥_{F}^{2}) ∥ Γ_{i}^{- 1} ∥_{F} - \frac{1}{2} ∥ (| B_{o} {|) ∥}_{F} (∥ {\dot{θ}}_{o}^{*} ∥_{F}^{2} + ∥ ϕ_{o} ∥_{F}^{2}) ∥ Γ_{o}^{- 1} ∥_{F}) d τ . \end{matrix}

(26)

As V is bounded outside

Ω,

from the right-hand side of this last equation; we have that

e (t) \in L^{2}

outside

Ω

. Furthermore, as

e_{i} (t), {\dot{e}}_{i} (t) \in L^{\infty}

and

e_{i} (t) \in L^{2},

and

e_{o} (t), {\dot{e}}_{o} (t) \in L^{\infty}

and

e_{0} (t) \in L^{2}

, all outside

Ω

, using Barbalat’s Lemma [34, Section 4.5.2] we have that

e_{i} (t)

and

e_{o} (t)

, both tend asymptotically to zero outside

Ω

. Hence,

y_{i} (t) \to y_{i}^{*}

and

y_{o} (t) \to y_{o}^{*}

outside

Ω^{c}

. We do not ensure parameter convergence. This concludes the proof. □

The following section applies the proposed controller to the M3C converter and describes the obtained results.

4. Simulation Results

This section applies the proposed control system shown in Figure 2 to the power topology of Figure 1 with three cells per cluster. It runs on a personal computer, in PLECS 4.7.2. The modeling settings are solver RADAU with variable-step, using a relative tolerance of

1 \times 10^{- 3}

The M3C load corresponds to four equal PMSMs electrically connected in parallel and moving a centrifugal pump each. Table 2 shows the motor-pump parameters.

Here,

V_{s_r a t e d}

and

I_{s_r a t e d}

are the rated stator voltage and current of the PMSM, respectively. The power factor is

f_{p}

and

f_{e}

is the electric required frequency of the PMSM for it to run at rated speed. P is the number of pole pairs and

ω_{r}

is the PMSM rated speed. The PMSM-rated torque and power are

T_{r a t e d}

and

P_{r a t e d}

, respectively. Moreover,

R_{s}

L_{d}

and

L_{q}

are the resistance and inductance of the motor,

Φ

is the magnetic flux induced by the motor magnets,

J_{m}

is the motor inertia,

J_{L o a d}

is the inertia of the load. On the other hand, the load parameters are the initial load torque

T_{0}

are zero speed and the constant

K_{l o a d}

, characterizing the pump model equation

T_{L o a d} = K_{l o a d} \cdot ω_{r}^{2} + T_{0}

The M3C is designed to power these PMSMs-driven centrifugal pumps, having the same

P_{r a t e d}

. Table 3 presents the plate data and parameters value of the M3C.

The reference capacitor voltage mean value

V_{C}^{*}

is defined based on the M3C input and output rated voltages

V_{i n_r a t e d}

and

V_{o u t_r a t e d}

and the number of cells. Here,

V_{C}^{*} \geq 1.2 \cdot \sqrt{2} \cdot (V_{i n_r a t e d} + V_{o u t_r a t e d})

, been divisible by 3 (number of cells per cluster). Therefore,

V_{C}^{*} \geq 1.2 \cdot \sqrt{2} \cdot (V_{i n_r a t e d} + V_{o u t_r a t e d}) = 3 \cdot 500 [V] = 1500 [V] \geq 1.2 \sqrt{2} \cdot (220 [V] + 400 [V]) \geq 1052 [V]

Moreover, the Power supply has the rated voltage

V_{i n_r a t e d}

, the input frequency

f_{i n}

, and an input inductance

L_{i n}

. The load has the rated voltage

V_{o u t_r a t e d}

equals the rated motor voltage

V_{s}_r a t e d

, and an output frequency

f_{o u t}

equals rated motor frequency

f_{e}

. Finally, we have the cells with switching frequency

f_{s w}

and a capacitance capacitor C. The cluster coupling inductance is L.

The following two control systems are applied to the M3C-based variable speed drive for multiple PMSM-driven centrifugal pumps for comparison purposes:

Basic Control System [23] .

The basic control includes sixteen (16) PI controllers, whose settings are calculated based on the definitions provided in equation (5) and Table 1:

Input Control:

-

One (1) PIs for the $2 α β γ$ ACV Control:

\begin{matrix} K_{p}_V_{C a v g} = \frac{8.485 π C V_{C}^{*}}{V_{a v g}} = 0.4241, K_{i}_V_{C a v g} = \frac{12 π^{2} C V_{C}^{*}}{V_{a v g}} = 1.8843, \end{matrix}

where the constant cluster voltage amplitude is

V_{a v g} = V_{i n_{d}} = \sqrt{2} V_{i n_r a t e d}

. The output of the ACV controller is the input cluster line current amplitude direct component reference

I_{L i n - c l_d}^{*}

. Here, the input cluster line current amplitude reference is

I_{L i n - c l}^{*} = {[I_{L i n - c l_d} 0]}^{T}

and is controlled by the following controllers.

-

Two (2) PIs for the $2 α β γ$ input cluster line current $I_{L i n - c l}$ amplitude direct and quadrature components:

\begin{matrix} K_{p}_I_{i n - c l_d} = K_{p}_I_{i n - c l_q} = - \frac{\sqrt{2} (2 π f_{i n}) L}{\sqrt{3}} = - 81.65 π L = - 0.2567, \\ K_{i}_I_{i n - c l_d} = K_{i}_I_{i n - c l_q} = - \frac{{(2 π f_{i n})}^{2} L}{\sqrt{3}} = - 5773.5 π^{2} L = - 56.98 . \end{matrix}

CCV Imbalance Control.

-

Four (4) PIs for the $2 α β γ$ Intra-CCV Imbalance Control [23, Outer controller of Figure 3]:

\begin{matrix} K_{p}_V_{C 1 α} = K_{p}_V_{C 1 β} = K_{p}_V_{C 2 α} = K_{p}_V_{C 2 β} = \frac{14.142 π \sqrt{6} C V_{C}^{*}}{V_{i n_{d}}} = 1.1541, \\ K_{i}_V_{C 1 α} = K_{i}_V_{C 1 β} = K_{i}_V_{C 2 α} = K_{i}_V_{C 2 β} = \frac{100 π^{2} \sqrt{6} C V_{C}^{*}}{V_{i n_{d}}} = 25.642 . \end{matrix}

-

Four (4) PIs for the $2 α β γ$ Inter-CCV Imbalance Control [23, Figure 4]:

\begin{matrix} K_{p}_V_{C α γ} = - \frac{14.142 π \sqrt{3} C V_{C}^{*}}{V_{o u t_{d}}} = - 0.6348, K_{p}_V_{C β γ} = \frac{14.142 π \sqrt{3} C V_{C}^{*}}{V_{o u t_{d}}} = 0.6348, \\ K_{p}_V_{C γ α} = K_{p}_V_{C γ β} = \frac{14.142 π \sqrt{3} C V_{C}^{*}}{V_{i n_{d}}} = 0.8161, \\ K_{i}_V_{C α γ} = - \frac{100 π^{2} \sqrt{3} C V_{C}^{*}}{V_{o u t_{d}}} = - 14.1031, K_{i}_V_{C β γ} = \frac{100 π^{2} \sqrt{3} C V_{C}^{*}}{V_{o u t_{d}}} = 14.1031, \\ K_{i}_V_{C γ α} = K_{i}_V_{C γ β} = \frac{100 π^{2} \sqrt{3} C V_{C}^{*}}{V_{i n_{d}}} = 18.1316, \end{matrix}

with the constant voltage

V_{o u t_{d}} = \sqrt{2} V_{o u t_r a t e d}

. Both of these controllers are in cascade with the following controller:

-

Four (4) PIs controllers for the $2 α β γ$ circulating current, considering only a P action [23, Inner controller of Figure 3]:

\begin{matrix} K_{p}_i_{c i r c - c l_α α} = K_{p}_i_{c i r c - c l_α β} = K_{p}_i_{c i r c - c l_β α} = K_{p}_i_{c i r c - c l_β β} \\ = - \sqrt{2} \sqrt{3} (2 π 10 f_{o u t}) = - 4242, 64 π L = - 13.3266, \\ K_{i}_i_{c i r c - c l_α α} = K_{i}_i_{c i r c - c l_α β} = K_{i}_i_{c i r c - c l_β α} = K_{i}_i_{c i r c - c l_β β} = 0 . \end{matrix}

Output control.

One (1) P for the $2 α β γ$ output voltage amplitude $V_{o u t - c l}^{*} = {[V_{o u t - c l_d} 0]}^{T}$ , with the $V_{o u t - c l_d}^{*} of equation (6)$ [32, Equation (1)] with (7).

Adaptive Control System .

The adaptive control system consists of the following six (6) controllers, which are configured according to the definitions given in equations (13)-(15). These controllers utilize the Lyapunov-type energy terms

V_{e_{o}} (t) = \frac{1}{2} e_{o}^{T} e_{o}

and

V_{e_{i}} (t) = \frac{1}{2} e_{i}^{T} e_{i}

. Moreover, all base disturbances

Δ_{o_b}

and

Δ_{i_b}

are computed based on the equations (1) and (3) in a stable state (zero first-time-derivatives), considering rated values from Table 3 and unitary parameter values (taking the known disturbance portion).

Input Control.

-

One (1) APBC (13) for the $2 α β γ$ ACV Control, with:

\begin{matrix} Δ_{o_b_V_{C a v g}} = - \frac{4 P_{r a t e d}}{9 V_{C}^{*}} = - 0.19, K_{o_V_{C a v g}} = \frac{K_{i_I_{i n - c l}}}{15} = 0.67, \\ Γ_{o_V_{C a v g}} = D i a g [\frac{1}{(1 + 0 . 19^{2})} \frac{1}{(1 + 10^{2})}] = D i a g [0.9649 0.0099], σ_{o_V_{C a v g}} = 1 . \end{matrix}

The output of this ACV controller is the input cluster line current amplitude direct component reference

I_{L i n - c l_d}^{*}

. Therefore the inner loop input cluster line current amplitude reference is

I_{L i n - c l}^{*} = {[I_{L i n - c l_d} 0]}^{T}

, having the following controller:

-: One (1) PBMRAC (15) for the $2 α β γ$ input cluster line current, and filtering a 2 KHz reference input noise:

\begin{matrix} A_{r i_i n} = B_{r i_i n} = \frac{2000}{20} I_{2} = 100 I_{2}, \\ K_{i_i n} = K_{i_I_{c i r c - c l}} (2 π f_{i n}) I_{2} - A_{r i_i n} = (3141.6 - 100) I_{2} = - 3041.6 I_{2}, \\ Δ_{i_b_i n} = 3 \sqrt{2} V_{i n_r a t e d} {[1 1]}^{T} = 933.6 {[1 1]}^{T}, σ_{i_i n} = I_{2}, \\ Γ_{i_i n} = D i a g [\frac{16}{(1 + 16^{2})} \frac{16}{(1 + 16^{2})} \frac{16}{(1 + 16^{2})} \frac{16}{(1 + 16^{2})} \frac{933.6}{(1 + 933 . 6^{2})} \frac{933.6}{(1 + 933 . 6^{2})} \frac{16}{(1 + 16^{2})} \frac{16}{(1 + 16^{2})}] \\ = D i a g [0.0623 0.0623 0.0623 0.0623 0.001 0.001 0.099 0.099] . \end{matrix}

CCV Imbalance Control.

-

One (1) APBC (13) for the $2 α β γ$ intra-CCV imbalance.

$\begin{matrix} Δ_{o_b_V_{C i n t r a}} = - \frac{\sqrt{2} V_{i n_r a t e d} I_{c i r_r a t e d}}{\sqrt{6} V_{C}^{*}} {[1 1 1 1]}^{T} = - 4.23 {[1 1 1 1]}^{T}, \\ K_{o_V_{C i n t r a}} = \frac{K_{i_I_{c i r c - c l}}}{15} I_{4} = 0.67 I_{4}, σ_{o_V_{C a v g}} = I_{4}, \\ Γ_{o_V_{C i n t r a}} = D i a g [\frac{1}{(1 + 10^{2})} \frac{1}{(1 + 10^{2})} \frac{1}{(1 + 4 . 23^{2})} \frac{1}{(1 + 4 . 23^{2})}] = D i a g [0.001 0.001 0.053 0.053] . \end{matrix}$

-

One (1) APBC (13) for the $2 α β γ$ inter-CCV imbalance.

$\begin{matrix} Δ_{o_b_V_{C i n t e r}} = - {[- \frac{\sqrt{2} V_{o u t_r a t e d} I_{c i r_r a t e d}}{\sqrt{3} V_{C}^{*}} \frac{\sqrt{2} V_{o u t_r a t e d} I_{c i r_r a t e d}}{\sqrt{3} V_{C}^{*}} \frac{\sqrt{2} V_{i n_r a t e d} I_{c i r_r a t e d}}{\sqrt{3} V_{C}^{*}} \frac{\sqrt{2} V_{i n_r a t e d} I_{c i r_r a t e d}}{\sqrt{3} V_{C}^{*}}]}^{T}, \\ = {[7.7 - 7.7 - 6 - 6]}^{T}, \\ K_{o_V_{C i n t e r}} = \frac{K_{i_I_{c i r c - c l}}}{15} I_{4} = 0.67 I_{4}, σ_{o_V_{C a v g}} = I_{4}, \\ Γ_{o_V_{C i n t e r}} = D i a g [\frac{1}{(1 + 7 . 7^{2})} \frac{1}{(1 + 7 . 7^{2})} \frac{1}{(1 + 6^{2})} \frac{1}{(1 + 6^{2})}] = D i a g [0.016 0.016 0.027 0.027] . \end{matrix}$

The inner controller is designed as follows

-

One (1) PBMRAC (15) for the $2 α β γ$ circulating cluster current, and filtering a 3.0 KHz reference input noise:

$\begin{matrix} A_{r i_c i r c - c l} = B_{r i_c i r c - c l} = 2 π \frac{3000}{20} I_{4} = 942.5 I_{4}, \\ K_{i_c i r c - c l} = K_{i_I_{c i r c - c l}} (2 π (2 f_{o u t}) I_{4} - A_{r i_c i r c - c l} = (9424.7 - 942.5) I_{4} = - 8482.3 I_{4}, \\ Δ_{i_b_c i r c - c l} = 0 σ_{i_c i r c - c l} = 0, Γ_{i_c i r c - c l} = \frac{10}{(1 + 10^{2})} I_{4} = 0.099 I_{4} . \end{matrix}$
Output control.

One (1) P for the output voltage amplitude $V_{o u t - c l}^{*} = {[V_{o u t - c l_d} 0]}^{T}$ , using the $V_{o u t - c l_d}^{*} of equation (6)$ [32, Equation (1)] joined to (7).

The following sections present the comparative results of the M3C feeding the four PMSMs, each moving a centrifugal pump. The results were obtained with a simulation time of

8 s

, under the following situations are described: normal operation, input phase imbalance, a cluster cell short-circuit, and an opened cluster cell.

For all cases, the set points in this

2 α β γ

coordinate are:

V_{C a v g}^{*} = 3 V_{C}^{*} = 4500 V

V_{C i n t r a_{C_{D}}}^{*} = 0

, and

V_{C i n t e r}^{*} = 0

. Moreover, the reference rotor angular speed

ω_{r}_{r a t e d}^{*} =

0 r a d / s

between

0 s

and

1 s

, having a ramp up reaching

ω_{r_r a t e d}

5 s

and kept constant the remaining time.

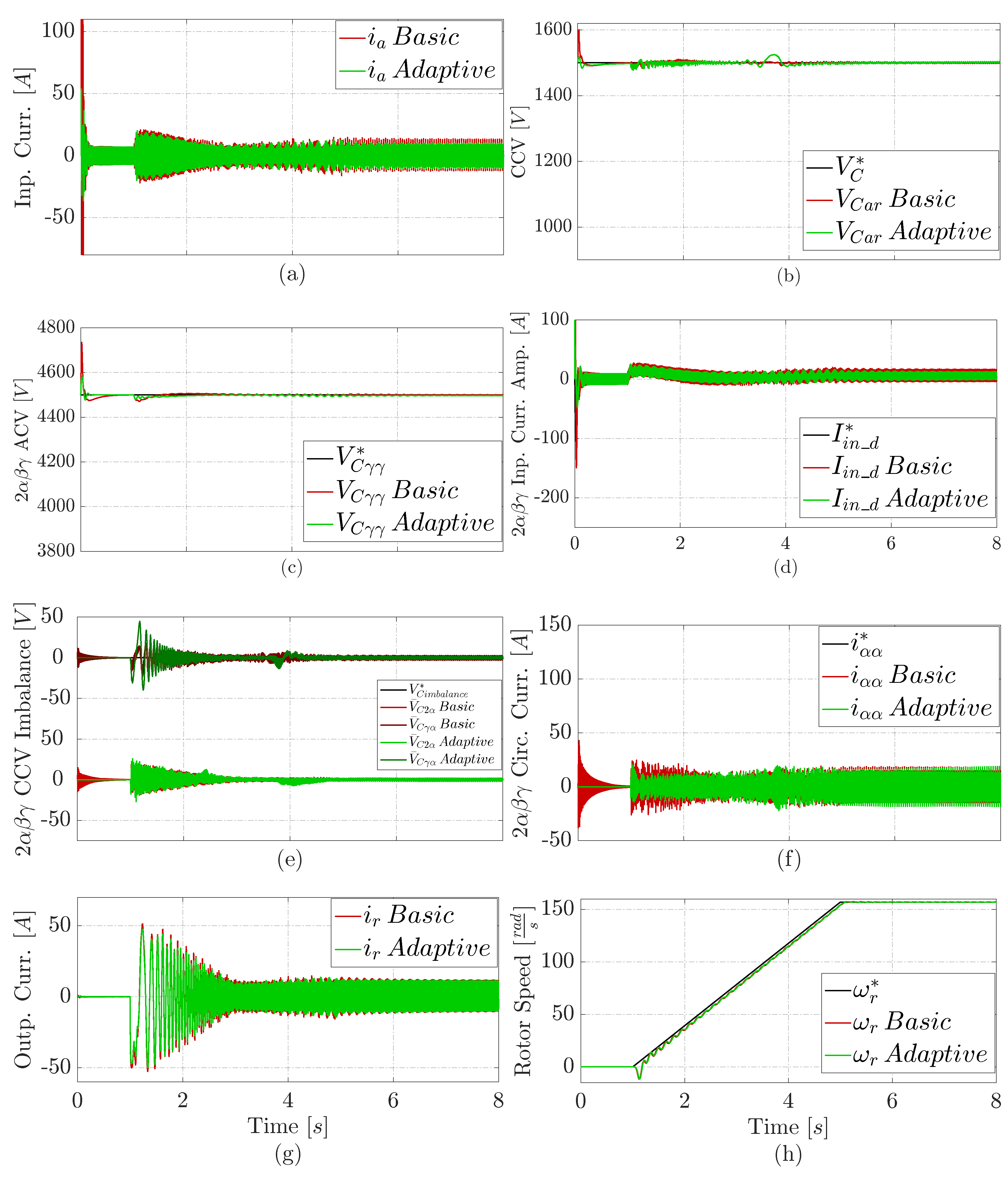
4.1. Results Under a Normal Operation

Figure 3 shows the comparative results under a normal operation. Here, we operate with the rated input and output voltages.

Figure 3 (a) and (g) demonstrate that the M3C adaptive proposal results in

25 %

lower input and output current consumption (with a reduction of

5 A

) compared to the basis control that utilizes PI controllers. Moreover, the adaptive controllers also exhibit less input current overshoot than the PI controllers.

Figure 3 (b) shows that the proposed M3C adaptive control has a

64 %

less CCV overshoot (with a

70 V

reduction) than the basic solution. Both adaptive and basic solutions ensure that the rotor speed follows the reference, as shown in Figure 3 (h).

Regarding the directly controlled variables in double-

α β γ

coordinates, both adaptive and basic solution also follow the reference. However, the adaptive solution has lower overshoots of ACV in Figure 3 (c), input current amplitude in Figure 3 (d), intra and inter CCV Imbalance in Figure 3 (e), circulating current in Figure 3 (f). Moreover the adaptive proposal consumes less input and circulation currents. As for the basic solution, the adaptive one has a

5 K H z

noisy input amplitude in double-

α β γ

4.2. Results Under an Input Phase Imbalance

Figure 4 displays the comparative results under an input phase imbalance. This first fault considers a drop of

10 %

of the

" a "

phase voltage, starting at 3 seconds.

Figure 4 (a) and (g) illustrates that prior to the fault, the M3C adaptive proposal results in

25 %

lower input and output current consumption, with a reduction of

5 A

compared to the basis control. The adaptive controllers also show less input current overshoot than the PI controllers. However, during the first second after the fault, the basic solution deteriorated while the adaptive approach recover its better performance faster.

Figure 4 (b) shows that the proposed M3C adaptive control has a

64 %

less CCV overshoot (with a

70 V

reduction) than the basic solution, similar to Figure 3 (b). However, the basic solution deteriorated after the fault while the adaptive approach tend to recover its performance.

Figure 4 (h) demonstrates that both the proposal and basic M3C controllers maintain the rotor speed in line with the reference, similar to Figure 3 (d). This is evident even when a fault occurs at the second 3, as it does not affect the pumping speed response.

Regarding the variables in double-

α β γ

coordinates; again, the adaptive solution has lower overshoots of ACV in Figure 3 (c), input current amplitude in Figure 3 (d), intra and inter CCV Imbalance in Figure 3 (e), circulating current in Figure 3 (f). Moreover, the adaptive proposal consumes less input and circulation currents before the fault. After the fault, the adaptive proposal completely recover its performance within

2 s

in contrast to the basic solution.

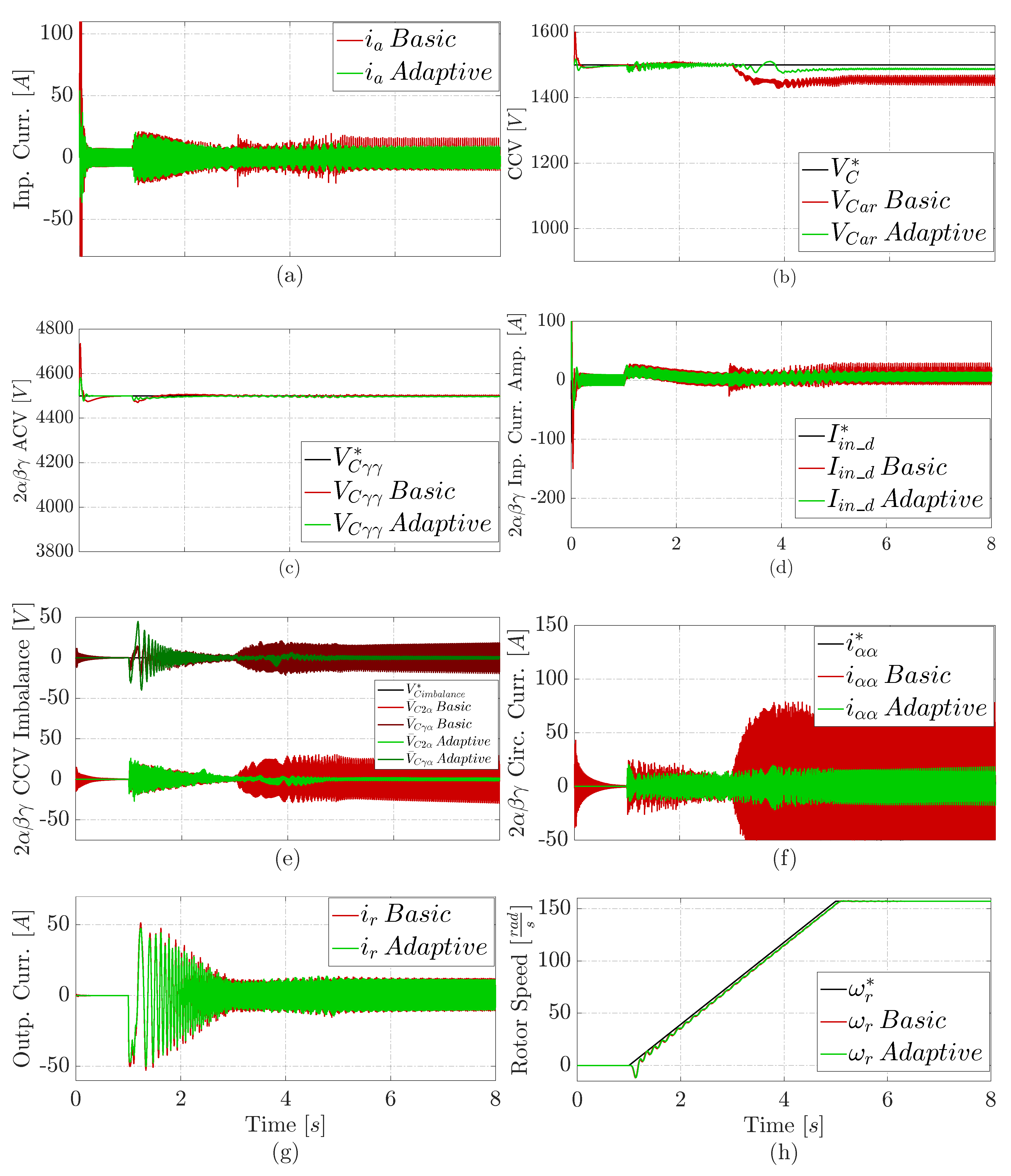
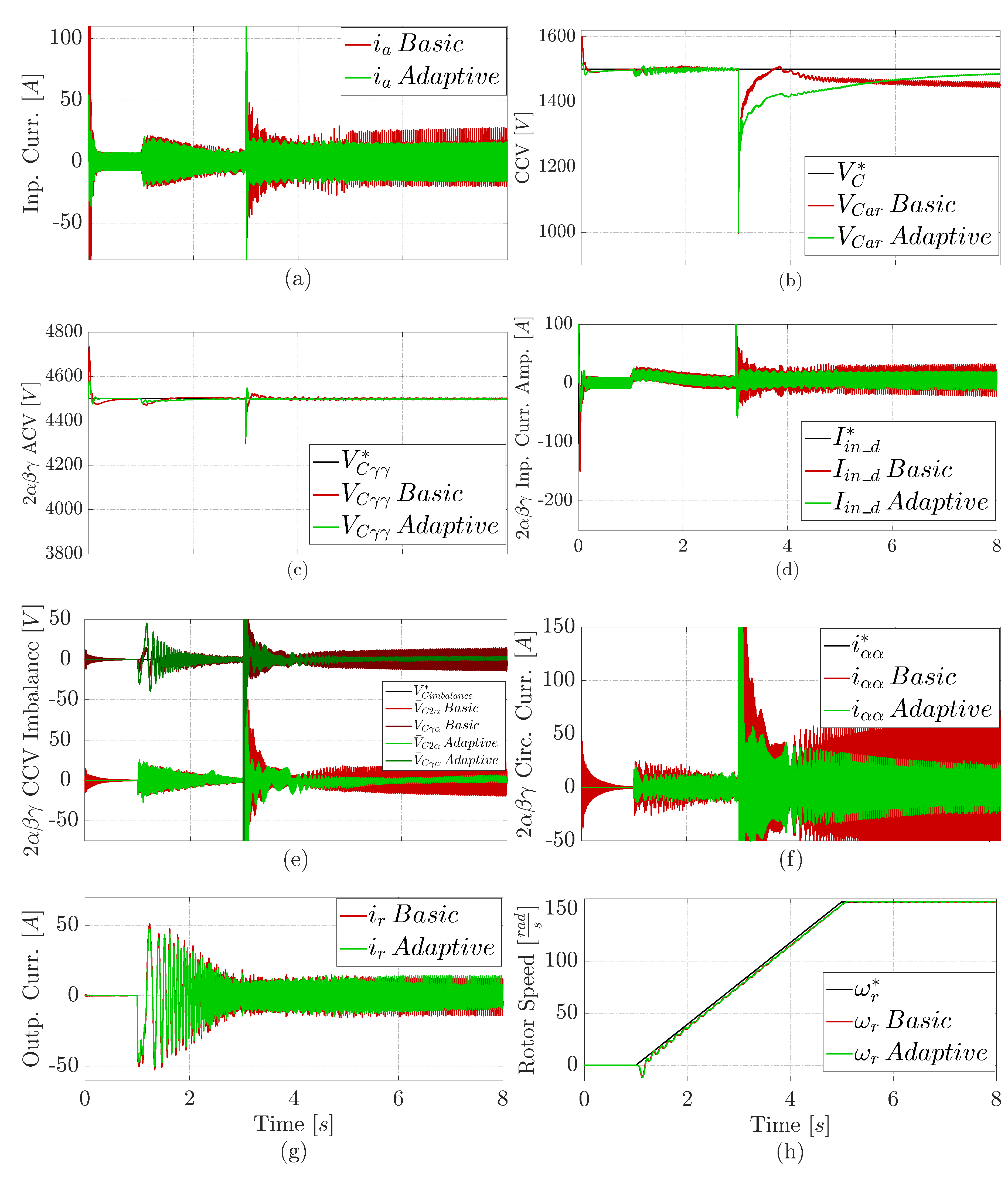
4.3. Results Under a Cluster Cell Short Circuit

Figure 5 exhibits the comparative results under a cluster cell short circuit. This fault happens in cell one of the cluster

a r

at 3 seconds.

Figure 5 (a) and (g) show that prior to the fault, the M3C adaptive proposal results in

25 %

lower input and output current consumption, with a reduction of

5 A

compared to the basis control. However, during the first two seconds after the fault, the basic solution deteriorated and had a

70 %

increase in input current consumption, increasing by

35 A

compared to the adaptive approach.

Figure 5 (b) shows that the M3C adaptive control method has a

64 %

reduction in CCV overshoot compared to the basic solution, reducing

70 V

. This reduction is similar to the one shown in Figure 3 (b). However, the basic solution demonstrates a quicker CCV to recovery after the fault tending towards the CCV reference of

1500 V

Figure 5 (h) demonstrates that both the proposal and basic M3C controllers maintain the rotor speed in line with the reference, similar to Figure 3 (d) and Figure 4 (d). Again. this is observed even after the fault happens at the second 3, which does not have an impact on the pumping speed’s response.

Regarding the variables in double-

α β γ

coordinates; a similar behaviour than shown in Figure 3 is obtained. The adaptive solution has lower overshoots of ACV in Figure 5 (c), input current amplitude in Figure 5 (d), intra and inter CCV Imbalance in Figure 5 (e), and circulating current in Figure 5 (f). After the fault, the adaptive solution completely recover its performance within

2 s

; while the basic solution does not.

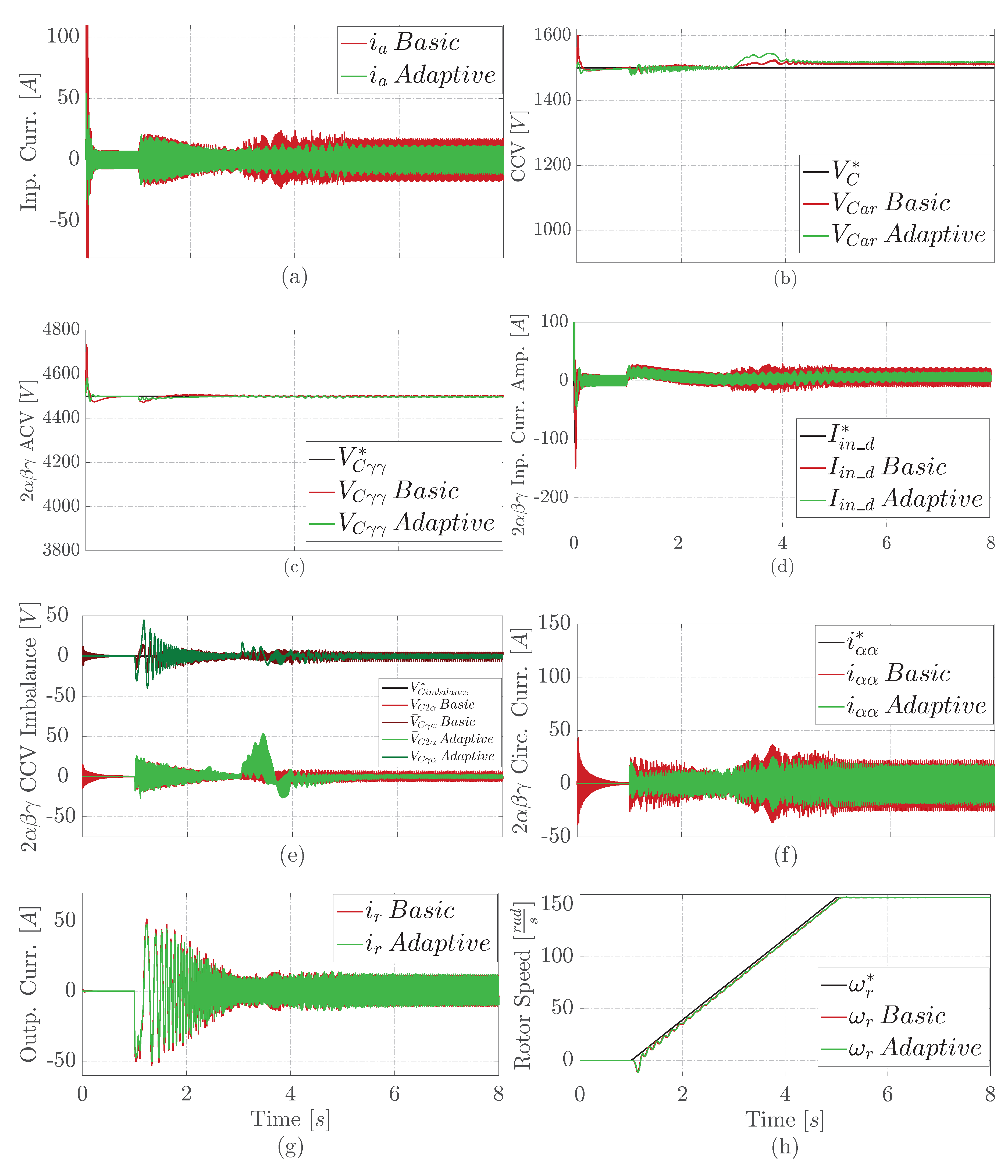
4.4. Results Under an Opened Cluster Cell

Figure 6 exhibits the comparative results under an opened cluster cell. This fault occurs in cell one of the cluster

a r

at 3 seconds.

Figure 6 describes a similar behaviour than in previously described faulty situations. However, both solutions have a lower degradation under this fault.

5. Conclusions

In this study, an adaptive control for an M3C-based variable speed drive powering multiple PMSM-driven centrifugal pumps was proposed. he study found that the adaptive proposal offers better performance and fault tolerance compared to the non-adaptive solution. The first step was to obtain the multivariable M3C state-space model for control, which allowed for the design and implementation of novel MIMO adaptive controllers.

Notably, the paper proposed and applied a novel cascade APBC-PBMRAC to the M3C. Simulation results demonstrate that the proposal and basic M3C controllers ensure the rotor speed follows the reference, even when a fault occurs. However, the proposal has several advantages over the basic solution:

It reduces the number of non-adaptive PI controllers from thirteen (16) to five (5) MIMO adaptive controllers.
It is a more straightforward solution that does not require plant parameters knowledge, reducing commissioning time.
The proposed adaptive control has less overshoots than the basic solution.
Additionally, it shows a more stable CCV response (less noisy), as expected due to the APBC-PBMRAC design.
Finally, the basic solution tends to remain degraded after a fault, while the adaptive approach tends to recover quickly from any studied fault.

Author Contributions

Conceptualization, methodology, writing—original draft preparation, and visualization, R.M.-B. and J.C.T.-T.; investigation, formal analysis, supervision, project administration, data curation, and resources and funding acquisition, J.C.T.-T. and M.D.; validation, software, and writing—review and editing; R.M.-B. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by FONDECYT Chile, grant 1220168; and FONDEQUIP Chile, grant EQM200234.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Not applicable.

Acknowledgments

The Authors thank Abdiel Ricaldi-Morales for its technical support in the adaptive control implementation

Conflicts of Interest

The authors declare no conflict of interest.

Sample Availability

Not applicable.

Appendix A

This section starts by describing the M3C state-space dynamical model obtaining.

Appendix A.1. Inner control Loop M3C Dynamical model

The M3C inner loop dynamical model involves the following equation, obtained after applying Kirchhoff’s voltage law to the power system of Figure 1 [22, Figure 2], [25] and rearranging terms in a matrix form (for details, please see Appendix A.3):

x - y Voltage - current model [Equation (9)]

v_{i n - x y} = L {\dot{i_{c l}}}_{- x y} + v_{c l - x y} + v_{o u t - x y} + v_{n N - x y},

(A1)

where L is the coupling inductor inductance shown in Figure 1. Moreover, the instantaneous input phase voltage

v_{i n - x y}

, cluster phase current

i_{c l - x y}

, cluster phase voltage

v_{c l - x y}

, output phase voltage

v_{o u t - x y}

, and neutral voltage

v_{n N - x y}

are defined as follows:

\begin{matrix} v_{i n - x y} = [\begin{matrix} v_{a} & v_{b} & v_{c} \\ v_{a} & v_{b} & v_{c} \\ v_{a} & v_{b} & v_{c} \end{matrix}], i_{c l - x y} & = [\begin{matrix} i_{a r} & i_{b r} & i_{c r} \\ i_{a s} & i_{b s} & i_{c s} \\ i_{a t} & i_{b t} & i_{c t} \end{matrix}], v_{c l - x y} = [\begin{matrix} v_{a r} & v_{b r} & v_{c r} \\ v_{a s} & v_{b s} & v_{c s} \\ v_{a t} & v_{b t} & v_{c t} \end{matrix}], \\ v_{o u t - x y} & = [\begin{matrix} v_{r} & v_{r} & v_{r} \\ v_{s} & v_{s} & v_{s} \\ v_{t} & v_{t} & v_{t} \end{matrix}], v_{n N - x y} = [\begin{matrix} 1 & 1 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & 1 \end{matrix}], \end{matrix}

(A2)

where

v_{a}

v_{b}

v_{c}

are the instantaneous phase voltages of the power supply. The instantaneous phase cluster currents and voltages are

i_{a r}

i_{b r}

i_{c r}

i_{a s}

i_{b s}

i_{c s}

i_{a t}

i_{b t}

i_{c t}

and

v_{a r}

v_{b r}

v_{c r}

v_{a s}

v_{b s}

v_{c s}

v_{a t}

v_{b t}

v_{c t}

respectively. Finally,

v_{r}

v_{s}

v_{t}

are the instantaneous load phase voltages.

For independent control, a double-

α β γ

transformation

C X C^{T}

[22] is applied to (A1). It consists in multiplying (A1) by the

α β γ

transform

C

[22] from the left and the right side, with matrix X representing each phase variable

v_{i n - x y}

i_{c l - x y}

v_{c l - x y}

v_{o u t - x y}

, and

v_{n N - x y}

. As a result, we have:

Double - α β γ Voltage - current model [Equation (18)]

\sqrt{3} v_{i n - 2 α β γ} = L {\dot{i_{c l}}}_{- 2 α β γ} + v_{c l - 2 α β γ} + \sqrt{3} v_{o u t - 2 α β γ} + 3 v_{n N - 2 α β γ},

(A3)

where the

α β γ

transform

C

[22], the input phase voltage

v_{i n - 2 α β γ}

, the cluster phase current

i_{c l - 2 α β γ}

, the cluster phase voltage

v_{c l - 2 α β γ}

, the output phase voltage

v_{o u t - 2 α β γ}

, and the neutral voltage

v_{n N - 2 α β γ}

are following defined:

\begin{matrix} C & = [\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} \\ 0 & \frac{\sqrt{2}}{2} & \frac{- \sqrt{2}}{2} \\ \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} \end{matrix}], v_{i n - 2 α β γ} = [\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ v_{i n_{α}} & v_{i n_{β}} & v_{i n_{γ}} \end{matrix}], i_{c l - 2 α β γ} = [\begin{matrix} i_{α α} & i_{β α} & i_{γ α} \\ i_{α β} & i_{β β} & i_{γ β} \\ i_{α γ} & i_{β γ} & i_{γ γ} \end{matrix}], \\ v_{c l - 2 α β γ} & = [\begin{matrix} v_{α α} & v_{β α} & v_{γ α} \\ v_{α β} & v_{β β} & v_{γ β} \\ v_{α γ} & v_{β γ} & v_{γ γ} \end{matrix}], v_{o u t - 2 α β γ} = [\begin{matrix} 0 & 0 & v_{o u t_{α}} \\ 0 & 0 & v_{o u t_{β}} \\ 0 & 0 & v_{o u t_{γ}} \end{matrix}], v_{n N - 2 α β γ} = [\begin{matrix} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \end{matrix}] . \end{matrix}

(A4)

Here,

v_{i n_{α}}

v_{i n_{β}}

v_{i n_{γ}}

are the phase voltages of the power supply in double-

α β γ

coordinates. The cluster phase currents and phase voltages in double-

α β γ

coordinates are

i_{α α}

i_{β α}

i_{γ α}

i_{α β}

i_{β β}

i_{γ β}

i_{α γ}

i_{β γ}

i_{γ γ}

and

v_{α α}

v_{β α}

v_{γ α}

v_{α β}

v_{β β}

v_{γ β}

v_{α γ}

v_{β γ}

v_{γ γ}

, respectively. Moreover,

v_{o u t_{α}}, v_{o u t_{β}}, v_{o u t_{γ}}

are the load phase voltages in double-

α β γ

coordinates.

Based on previous equations (A3) and (A4), the obtained decoupled state-space model for the input port, circulating currents, and output port is [6,25]:

Double - α β γ State - space model of instantaneous voltage - current [Equations (19) - - (21)]

\begin{matrix} {\dot{i_{i n}}}_{- c l} = - \frac{1}{L} v_{i n - c l} + \frac{\sqrt{3}}{L} v_{i n}, & Input phase current \\ {\dot{i_{c i r}}}_{- c l} = - \frac{1}{L} v_{c l}, & Circulating phase current \\ {\dot{i_{o u t}}}_{- c l} = - \frac{1}{L} v_{o u t - c l} - \frac{\sqrt{3}}{L} v_{o u t}, & Output phase current \end{matrix}

(A5)

with the instantaneous input phase voltage

v_{i n}

having an input frequency

ω_{i n}

, and the instantaneous output phase voltage

v_{o u t}

having an output frequency

ω_{o u t}

. These variables, joined the instantaneous cluster phase currents

i_{i n - c l}

i_{c i r - c l}

i_{o u t - c l}

, and the instantaneous cluster voltages

v_{i n - c l}

v_{c l}

v_{o u t - c l}

, are defined as:

\begin{matrix} i_{i n - c l} & = [\begin{matrix} i_{α γ} \\ i_{β γ} \end{matrix}], v_{i n} = [\begin{matrix} v_{i n_{α}} \\ v_{i n_{β}} \end{matrix}], v_{i n - c l} = [\begin{matrix} v_{α γ} \\ v_{β γ} \end{matrix}], \\ i_{c i r - c l} & = [\begin{matrix} i_{α α} & i_{β α} \\ i_{α β} & i_{β β} \end{matrix}], v_{c l} = [\begin{matrix} v_{α α} & v_{β α} \\ v_{α β} & v_{β β} \end{matrix}], \\ i_{o u t - c l} & = [\begin{matrix} i_{γ α} \\ i_{γ β} \end{matrix}], v_{o u t} = [\begin{matrix} v_{o u t_{α}} \\ v_{o u t_{β}} \end{matrix}], v_{o u t - c l} = [\begin{matrix} v_{γ α} \\ v_{γ β} \end{matrix}] . \end{matrix}

(A6)

Finally, multiplying the Park Transformation P[24] from the left by the input and output phase current equations of (A5), these are converted to their dq coordinates to allow their amplitudes control. The circulating phase current equation of (A5) remains the same for the control of this instantaneous variable. Moreover, we consider the input cluster line current control, related to the phase current as

I_{L i n - c l} = \sqrt{3} I_{i n - c l}

. As a result, the previous model (A5) takes the form:

Double - α β γ Voltage - current state - space model

\begin{matrix} {\dot{I_{L i n}}}_{- c l} = - \frac{\sqrt{3}}{L} V_{i n - c l} + \frac{3}{L} V_{i n}, & Input phase current amplitude \\ {\dot{i_{c i r}}}_{- c l} = - \frac{1}{L} v_{c l}, & Circulating phase current \\ {\dot{I_{o u t}}}_{- c l} = - \frac{1}{L} V_{o u t - c l} - \frac{\sqrt{3}}{L} V_{o u t}, & Output phase current amplitude \end{matrix}

(A7)

where the Park Transformation P, the amplitudes of the input phase voltage

V_{i n}

, output phase voltage

V_{o u t}

, cluster input line current

I_{L i n - c l}

, cluster output phase current

I_{o u t - c l}

, and cluster phase voltages

V_{i n - c l}

V_{o u t - c l}

, all in d-q coordinates, are defined as:

\begin{matrix} P = [\begin{matrix} c o s (θ) & s i n (θ) \\ - s i n (θ) & c o s (θ) \end{matrix}], I_{L i n - c l} = [\begin{matrix} I_{L i n - c l_d} \\ I_{L i n - c l_q} \end{matrix}], V_{i n} = [\begin{matrix} V_{i n_d} \\ V_{i n_q} \end{matrix}], \\ V_{i n - c l} = [\begin{matrix} V_{i n - c l_d} \\ V_{i n - c l_q} \end{matrix}], I_{o u t - c l} = [\begin{matrix} I_{o u t - c l_d} \\ I_{o u t - c l_q} \end{matrix}], V_{o u t} = [\begin{matrix} V_{o u t_d} \\ V_{o u t_q} \end{matrix}], V_{o u t - c l} = [\begin{matrix} V_{o u t - c l_d} \\ V_{o u t - c l_q} \end{matrix}], \end{matrix}

(A8)

where

I_{L i n - c l_d}

and

I_{L i n - c l_q}

are the amplitude components of the input coordinates of the cluster line currents.

V_{i n_d}

and

V_{i n_q}

are the amplitude components of the power supply phase voltage.

V_{i n - c l_d}

and

V_{i n - c l_q}

are the amplitude components of the input coordinates of the cluster phase voltages.

I_{o u t - c l_d}

and

I_{o u t - c l_q}

are the amplitude components of the output cluster phase currents.

V_{o u t_d}

and

V_{o u t_q}

are the amplitude components of the power supply phase voltage. Finally,

V_{o u t - c l_d}

and

V_{o u t - c l_q}

are the amplitude components of the output cluster phase voltages. The Park transformation uses

θ = θ_{i n} = \int ω_{i n} d τ

for the input signals and

θ = θ_{o u t} = \int ω_{o u t} d τ

for the output signals.

The following section describes the outer-loop M3C dynamical model obtaining.

Appendix A.2. Outer control Loop M3C Dynamical model

The outer loop M3C dynamical model considers the formula

I_{C} = C {\dot{V}}_{C i j k}

of an ideal capacitor instantaneous current

I_{C}

, depending on the capacitance C and the capacitor voltage variation

\dot{V_{C i j k}}

of a cell shown in Figure 1. Then, this last expression is re-expressed to obtain the variation rate of the cluster capacitor voltage

V_{C i j} = \sum_{k = 1}^{3} (V_{C i j k})

in terms of the power through a cluster

P_{c l}

\dot{V_{C i j}} = \frac{1}{C V_{C}} P_{c l}

[22, Equation (8)]. Finally, applying this concept to the M3C, assuming the clusters have three cells (summing their voltage variation expressions), are balanced, and all capacitors are the same, and that the average cluster capacitor voltage fluctuates

ϵ (t)

times around its required value

V_{C}^{*}

, the following matrix expression is obtained:

x - y Cluster capacitor voltage - power state - space model

{\dot{V}}_{C - x y} = \frac{1}{C ϵ (t) V_{C}^{*}} P_{c l - x y} .

(A9)

The reference cluster capacitor voltage mean value is

V_{C}^{*} \geq 1.2 \cdot \sqrt{2} \cdot (V_{i n_r a t e d} + V_{o u t_r a t e d})

, where

V_{C}^{*}

is a multiple of 3 (number of cells per cluster). Moreover, the instantaneous cluster capacitor voltage

V_{C - x y}

and cluster power

P_{c l - x y}

are defined as follows:

\begin{matrix} V_{C - x y} = [\begin{matrix} V_{C a r} & V_{C b r} & V_{C c r} \\ V_{C a s} & V_{C b s} & V_{C c s} \\ V_{C a t} & V_{C b t} & V_{C c t} \end{matrix}], P_{c l - x y} & = [\begin{matrix} P_{a r} & P_{b r} & P_{c r} \\ P_{a s} & P_{b s} & P_{c s} \\ P_{a t} & P_{b t} & P_{c t} \end{matrix}], \end{matrix}

(A10)

where the cluster capacitor instantaneous voltages are

V_{C a r}

V_{C b r}

V_{C c r}

V_{C a s}

V_{C b s}

V_{C c s}

V_{C a t}

V_{C b t}

V_{C c t}

Again, for independent control, a double-

α β γ

transformation

C X C^{T}

[22] is applied to (A9). Thus, (A9) is multiplied by the

α β γ

transform

C

[22] from the left and the right side, with matrix X representing the instantaneous cluster capacitor voltage

V_{C - x y}

and the cluster instantaneous power

P_{c l - x y}

(A10). Then, re-expressing the obtained result in a state space form, we have:

Double - α β γ state - space model of instantaneous voltage - power

\begin{matrix} {\dot{V}}_{C a v g} = \frac{1}{C ϵ (t) V_{C}^{*}} P_{a v g}, & ACV \\ {\dot{V}}_{C i n t r a} = \frac{1}{C ϵ (t) V_{C}^{*}} P_{i n t r a}, & Intra - CCV imbalance \\ {\dot{V}}_{C i n t e r} = \frac{1}{C ϵ (t) V_{C}^{*}} P_{i n t e r}, & Inter - CCV imbalance \end{matrix}

(A11)

having the following variables definitions:

\begin{matrix} V_{C a v g} = & V_{C γ γ}, P_{a v g} = P_{γ γ}, \\ V_{C i n t r a} = & {[\begin{matrix} V_{C α α} & V_{C α β} & V_{C β α} & V_{C γ α} \end{matrix}]}^{T}, P_{i n t r a} = {[\begin{matrix} P_{α α} & P_{α β} & P_{β α} & P_{γ α} \end{matrix}]}^{T}, \\ V_{C i n t e r} = & {[\begin{matrix} V_{C α γ} & V_{C β γ} & V_{C γ α} & V_{C γ β} \end{matrix}]}^{T}, P_{i n t e r} = {[\begin{matrix} P_{α γ} & P_{β γ} & P_{γ α} & P_{γ β} \end{matrix}]}^{T} . \end{matrix}

(A12)

Here, in double-

α β γ

coordinates are

v_{C α α}

, the cluster capacitor instantaneous voltages components,

v_{C β α}

v_{C γ α}

v_{C α β}

v_{C β β}

v_{C γ β}

v_{C α γ}

v_{C β γ}

v_{C γ γ}

and the instantaneous cluster power components are

P_{α α}

P_{β α}

P_{γ α}

P_{α β}

P_{β β}

P_{γ β}

P_{α γ}

P_{β γ}

P_{γ γ}

, which are clearly defined in [6]. However, there is an issue with the intra-CCV and inter-CCV imbalance control. Every power component could be controlled by controlling certain component of the circulating current

i_{c i r - c l}

(A6) but

P_{γ α}

[6] that would be controlled by

i_{α α}

P_{α γ}

[6]. Therefore, an extra auxiliary transformation is made after multiplying from the left the intra-CCV imbalance equation of (A11) by the matrix

C_{D}

[25] as a solution to allow control. Moreover, the power formulas are re-expressed as a function of the phase voltages and phase currents as detailed in [6] separating the control terms from the rest, which are considered as a disturbance. Finally, the state-space form for control takes the following form:

Double - α β γ voltage - power state - space model

\begin{matrix} {\dot{V}}_{C a v g} = \frac{V_{a v g} (t)}{3 C ϵ (t) V_{C}^{*}} I_{L i n - c l_d} + Δ_{a v g} (t), & ACV \\ {\dot{V}}_{C i n t r a D} = \frac{V_{i n t r a} {(t)}^{T}}{\sqrt{6} C ϵ (t) V_{C}^{*}} T_{r} I_{c i r 1} + Δ_{i n t r a_{C_{D}}} (t), & Intra - CCV imbalance \\ {\dot{V}}_{C i n t e r} = \frac{V_{i n t e r} {(t)}^{T}}{\sqrt{3} C ϵ (t) V_{C}^{*}} I_{c i r 2} + Δ_{i n t e r} (t), & Inter - CCV imbalance \end{matrix}

(A13)

where the auxiliary transformation matrix

C_{D}

[25], capacitor voltage

V_{C i n t r a}

V_{C i n t e r}

V_{C a v g}

, the cluster voltage

V_{i n t r a}

V_{i n t e r}

V_{a v g}

, the cluster current

I_{c i r 1}

I_{c i r 2}

I_{a v g}

, and the disturbances

Δ_{i n t r a}

Δ_{i n t e r}

Δ_{a v g}

, are following defined:

\begin{matrix} C_{D} = & \frac{1}{2} [\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & - 1 & 0 \\ 1 & 0 & 0 & - 1 \\ 0 & 1 & 1 & 0 \end{matrix}], T_{r} = [\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}], \\ V_{a v g} = V_{i n_{α}}, V_{C i n t r a D} = & C_{D} V_{C i n t r a} = {[\begin{matrix} V_{C 1 α} & V_{C 1 β} & V_{C 2 α} & V_{C 2 β} \end{matrix}]}^{T}, \\ V_{i n t r a} = & {[\begin{matrix} V_{i n_{α}} & V_{i n_{α}} & V_{i n_{α}} & V_{i n_{α}} \end{matrix}]}^{T}, \\ V_{i n t e r} = & {[\begin{matrix} - V_{o u t_{α}} & V_{o u t_{α}} & V_{i n_{α}} & V_{i n_{α}} \end{matrix}]}^{T}, \\ I_{c i r 1} = & {[\begin{matrix} I_{1 α_{1}} & I_{1 β_{1}} & I_{2 α_{1}} & I_{2 β_{1}} \end{matrix}]}^{T}, \\ I_{c i r 2} = & {[\begin{matrix} I_{1 α_{2}} & I_{1 β_{2}} & I_{2 α_{2}} & I_{2 β_{2}} \end{matrix}]}^{T}, \\ Δ_{a v g} = Δ_{γ γ}, Δ_{i n t r a_{C_{D}}} = & {[\begin{matrix} Δ_{2 α} & Δ_{2 β} & Δ_{1 α} & Δ_{1 β} \end{matrix}]}^{T}, \\ Δ_{i n t e r} = & {[\begin{matrix} Δ_{α γ} & Δ_{β γ} & Δ_{γ α} & Δ_{γ β} \end{matrix}]}^{T}, \end{matrix}

(A14)

where the disturbance terms are obtained from the power expressions [6, Equations (38)-(45)], [22, Equations (17)-(25)], after separating the control terms components. The result gives:

Δ_{γ γ} = \frac{1}{3} (V_{i n_{β}} I_{i n_{β}}) - \frac{1}{3} (V_{o u t_{α}} I_{o u t α} + V_{o u t_{β}} I_{o u t_{β}}) .

(A15)

\begin{matrix} Δ_{1 α} = \frac{1}{6} & [(V_{i n_{α}} I_{o u t_{α}} - V_{o u t_{α}} I_{i n_{α}}) + (V_{i n_{β}} I_{o u t_{β}} - V_{o u t_{β}} I_{i n_{β}})] \\ + \frac{1}{\sqrt{6}} & [(- V_{i n_{β}} I_{2 β}) + (- V_{o u t_{α}} I_{2 α} + V_{o u t_{β}} I_{2 β})] - V_{n} I_{1 α}, \\ Δ_{1 β} = \frac{1}{6} & [(V_{i n_{α}} I_{o u t_{β}} - V_{o u t_{β}} I_{i n_{α}}) - (V_{i n_{β}} I_{o u t_{α}} - V_{o u t_{α}} I_{i n_{β}})] \\ + \frac{1}{\sqrt{6}} & [(V_{i n_{β}} I_{2 α}) + (V_{o u t_{α}} I_{2 β} + V_{o u t_{β}} I_{2 α})] - V_{n} I_{1 β}, \\ Δ_{2 α} = \frac{1}{6} & [(V_{i n_{β}} I_{o u t_{α}} - V_{o u t_{α}} I_{i n_{β}}) - (V_{i n_{β}} I_{o u t_{β}} - V_{o u t_{β}} I_{i n_{β}})] \\ + \frac{1}{\sqrt{6}} & [(V_{i n_{β}} I_{1 β}) + (- V_{o u t_{α}} I_{1 α} + V_{o u t_{β}} I_{1 β})] - V_{n} I_{2 α}, \\ Δ_{2 β} = \frac{1}{6} & [(V_{i n_{β}} I_{o u t_{β}} - V_{o u t_{β}} I_{i n_{β}}) + (V_{i n_{β}} I_{o u t_{α}} - V_{o u t_{α}} I_{i n_{β}})] \\ + \frac{1}{\sqrt{6}} & [(- V_{i n_{β}} I_{1 α}) + (V_{o u t_{α}} I_{1 β} + V_{o u t_{β}} I_{1 α})] - V_{n} I_{2 β} . \end{matrix}

(A16)

\begin{matrix} Δ_{α γ} & = \frac{1}{3 \sqrt{2}} [(V_{i n_{α}} I_{i n_{α}} - V_{i n_{β}} I_{i n_{β}})] - \frac{1}{\sqrt{3}} [V_{o u t_{α}} (I_{2 α}) + V_{o u t_{β}} (I_{1 β} + I_{2 β}) - V_{n} I_{i n_{α}}], \\ Δ_{β γ} & = - \frac{1}{3 \sqrt{2}} [(V_{i n_{α}} I_{i n_{β}} + V_{i n_{β}} I_{i n_{α}})] - \frac{1}{\sqrt{3}} [V_{o u t_{α}} (I_{2 β}) + V_{o u t_{β}} (I_{1 α} - I_{2 α}) - V_{n} I_{i n_{β}}], \\ Δ_{γ α} & = - \frac{1}{3 \sqrt{2}} [(V_{o u t_{α}} I_{o u t_{α}} - V_{o u t_{β}} I_{o u t_{β}})] + \frac{1}{\sqrt{3}} [V_{i n_{α}} (I_{1 α}) + V_{i n_{β}} (- I_{1 β} + I_{2 β}) - V_{n} I_{o u t_{α}}], \\ Δ_{γ β} & = \frac{1}{3 \sqrt{2}} [(V_{o u t_{α}} I_{o u t_{β}} + V_{o u t_{β}} I_{o u t_{α}})] + \frac{1}{\sqrt{3}} [V_{i n_{α}} (I_{1 β}) + V_{i n_{β}} (I_{1 α} - I_{2 α}) - V_{n} I_{o u t_{β}}] . \end{matrix}

(A17)

The following section details the different vector and matrix transformations made in the previous state-space model obtaining.

Appendix A.3. Vector and Matrix Transformation Details

This section details the vector and matrix used transformations, starting from the managing feedback signals block located at the right lower side of Figure 2. First, the vector of the cluster capacitor voltages

V_{C i j}

is obtained after summing the capacitor voltages

\sum_{k = 1}^{3} (V_{i j k})

per cell k inside each cluster as follows:

\overset{V_{C i j k}}{\overset{︷}{[\begin{matrix} V_{C a r 1} V_{C a r 2} V_{C a r 3} \\ V_{C b r 1} V_{C b r 2} V_{C b r 3} \\ V_{C c r 1} V_{C c r 2} V_{C c r 3} \\ V_{C a s 1} V_{C a s 2} V_{C a s 3} \\ V_{C b s 1} V_{C b s 2} V_{C b s 3} \\ V_{C c s 1} V_{C c s 2} V_{C c s 3} \\ V_{C a t 1} V_{C a t 2} V_{C a t 3} \\ V_{C b t 1} V_{C b t 2} V_{C b t 3} \\ V_{C c t 1} V_{C c t 2} V_{C c t 3} \end{matrix}]}} \Rightarrow \sum_{k = 1}^{3} (V_{C i j k}) = \overset{\sum_{k = 1}^{3} V_{C i j k}}{\overset{︷}{[\begin{matrix} \sum_{k = 1}^{3} V_{C a r k} \\ \sum_{k = 1}^{3} V_{C b r k} \\ \sum_{k = 1}^{3} V_{C c r k} \\ \sum_{k = 1}^{3} V_{C a s k} \\ \sum_{k = 1}^{3} V_{C b s k} \\ \sum_{k = 1}^{3} V_{C c s k} \\ \sum_{k = 1}^{3} V_{C a t k} \\ \sum_{k = 1}^{3} V_{C b t k} \\ \sum_{k = 1}^{3} V_{C c t k} \end{matrix}]}} = \overset{V_{C i j}}{\overset{︷}{[\begin{matrix} V_{C a r} \\ V_{C b r} \\ V_{C c r} \\ V_{C a s} \\ V_{C b s} \\ V_{C c s} \\ V_{C a t} \\ V_{C b t} \\ V_{C c t} \end{matrix}]}} .

(A18)

Then, the following rearrangements R are made to convert vectors to the matrix form to allow implementation. It applies to the measurement vectors of the cluster currents

i_{i j}

and the cluster capacitor voltage

V_{C i j}

\overset{i_{i j}}{\overset{︷}{[\begin{matrix} i_{a r} \\ i_{b r} \\ i_{c r} \\ i_{a s} \\ i_{b s} \\ i_{c s} \\ i_{a t} \\ i_{b t} \\ i_{c t} \end{matrix}]}} \Rightarrow R (i_{i j}) = \overset{i_{x y}}{\overset{︷}{[\begin{matrix} i_{a r} & i_{b r} & i_{c r} \\ i_{a s} & i_{b s} & i_{c s} \\ i_{a t} & i_{b t} & i_{c t} \end{matrix}]}}, \overset{V_{C i j}}{\overset{︷}{[\begin{matrix} V_{C a r} \\ V_{C b r} \\ V_{C c r} \\ V_{C a s} \\ V_{C b s} \\ V_{C c s} \\ V_{C a t} \\ V_{C b t} \\ V_{C c t} \end{matrix}]}} \Rightarrow R (V_{C i j}) = \overset{V_{C x y}}{\overset{︷}{[\begin{matrix} V_{C a r} & V_{C b r} & V_{C c r} \\ V_{C a s} & V_{C b s} & V_{C c s} \\ V_{C a t} & V_{C b t} & V_{C c t} \end{matrix}]}} .

(A19)

The matrix X previously obtained results are double-

α β γ

transformed

C X C^{T}

[22]. The right lower side of Figure 2 shows these operations, multiplying X by the

α β γ

transform

C

[22] from the left and right sides. Following, for

X = i_{i j}

and

X = V_{C i j}

, it gives:

\overset{C}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} \\ 0 & \frac{\sqrt{2}}{2} & \frac{- \sqrt{2}}{2} \\ \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} \end{matrix}]}} \cdot \overset{i_{x y}}{\overset{︷}{[\begin{matrix} i_{a r} & i_{b r} & i_{c r} \\ i_{a s} & i_{b s} & i_{c s} \\ i_{a t} & i_{b t} & i_{c t} \end{matrix}]}} \cdot \overset{C^{T}}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & 0 & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2} & \frac{\sqrt{3}}{3} \end{matrix}]}} = \overset{i_{c l - 2 α β γ}}{\overset{︷}{[\begin{matrix} i_{α α} & i_{β α} & i_{γ α} \\ i_{α β} & i_{β β} & i_{γ β} \\ i_{α γ} & i_{β γ} & i_{γ γ} \end{matrix}]}},

(A20)

\overset{C}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} \\ 0 & \frac{\sqrt{2}}{2} & \frac{- \sqrt{2}}{2} \\ \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} \end{matrix}]}} \cdot \overset{V_{C x y}}{\overset{︷}{[\begin{matrix} V_{C a r} & V_{C b r} & V_{C c r} \\ V_{C a s} & V_{C b s} & V_{C c s} \\ V_{C a t} & V_{C b t} & V_{C c t} \end{matrix}]}} \cdot \overset{C^{T}}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & 0 & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2} & \frac{\sqrt{3}}{3} \end{matrix}]}} = \overset{V_{C - 2 α β γ}}{\overset{︷}{[\begin{matrix} V_{C α α} & V_{C β α} & V_{C γ α} \\ V_{C α β} & V_{C β β} & V_{C γ β} \\ V_{C α γ} & V_{C β γ} & V_{C γ γ} \end{matrix}]}} .

(A21)

Moreover, there are other rearrangements R made to convert the matrix obtained in (A20) and (A21) to their vector form to allow implementation. The resulting vectors are demultiplexed in managing feedback signals block of Figure 2. It delivers the cluster instantaneous phase currents and capacitor voltages defined in (A6) and (A14) (

i_{i n - c l}

i_{c i r c - c l}

i_{o u t - c l}

, and

V_{C i n t r a}

V_{C i n t e r}

V_{C a v g}

) as follows:

\overset{i_{c l - 2 α β γ}}{\overset{︷}{[\begin{matrix} i_{α α} & i_{β α} & i_{γ α} \\ i_{α β} & i_{β β} & i_{γ β} \\ i_{α γ} & i_{β γ} & i_{γ γ} \end{matrix}]}} \Rightarrow R (i_{c l - 2 α β γ}) = [\begin{matrix} i_{α γ} \\ i_{β γ} \\ i_{α α} \\ i_{α β} \\ i_{β α} \\ i_{β β} \\ i_{γ α} \\ i_{γ β} \\ i_{γ γ} \end{matrix}], \overset{V_{C - 2 α β γ}}{\overset{︷}{[\begin{matrix} V_{C α α} & V_{C β α} & V_{C γ α} \\ V_{C α β} & V_{C β β} & V_{C γ β} \\ V_{C α γ} & V_{C β γ} & V_{C γ γ} \end{matrix}]}} \Rightarrow R (V_{C - 2 α β γ}) = [\begin{matrix} V_{C α α} \\ V_{C α β} \\ V_{C β α} \\ V_{C β β} \\ V_{C α γ} \\ V_{C β γ} \\ V_{C γ α} \\ V_{C γ α} \\ V_{C γ γ} \end{matrix}] .

(A22)

Additionally, the cluster instantaneous capacitor voltage intra-components are multiplied by the matrix

C_{D}

[25]:

\overset{C_{D}}{\overset{︷}{\frac{1}{2} [\begin{matrix} 1 & 0 & 0 & 1 \\ 0 & 1 & - 1 & 0 \\ 1 & 0 & 0 & - 1 \\ 0 & 1 & 1 & 0 \end{matrix}]}} \overset{V_{C i n t r a}}{\overset{︷}{[\begin{matrix} V_{C α α} \\ V_{C α β} \\ V_{C β α} \\ V_{C β β} \end{matrix}]}} = \overset{V_{C i n t r a_{C_{D}}}}{\overset{︷}{[\begin{matrix} V_{C α α} + V_{C β β} \\ V_{C α β} - V_{C β α} \\ V_{C α α} - V_{C β β} \\ V_{C α β} + V_{C β α} \end{matrix}]}} = \overset{V_{C i n t r a_{C_{D}}}}{\overset{︷}{[\begin{matrix} V_{C 1 α} \\ V_{C 1 β} \\ V_{C 2 α} \\ V_{C 2 β} \end{matrix}]}} .

(A23)

The outer signals of the Intra-CCV imbalance control are located at the left-center side of Figure 2. These are multiplied by the

T_{r}^{- 1}

matrix to obtain

i_{c i r 1}

to be sumed with

i_{c i r 2}

. The result is multiplied by the inverse matrix

C_{D}^{- 1}

to obtain the circulating current

i_{c i r - c l}^{*}

as follows:

\overset{i_{c i r 1}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α 1}^{*} \\ i_{1 β 1}^{*} \\ i_{2 α 1}^{*} \\ i_{2 β 1}^{*} \end{matrix}]}} = \overset{T_{r}^{- 1}}{\overset{︷}{[\begin{matrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{matrix}]}} \overset{i_{c i r 1 D}^{*}}{\overset{︷}{[\begin{matrix} i_{2 α 1}^{*} \\ i_{2 β 1}^{*} \\ i_{1 α 1}^{*} \\ i_{1 β 1}^{*} \end{matrix}]}}, \overset{i_{c i r 1}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α 1}^{*} \\ i_{1 β 1}^{*} \\ i_{2 α 1}^{*} \\ i_{2 β 1}^{*} \end{matrix}]}} + \overset{i_{c i r 2}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α 2}^{*} \\ i_{1 β 2}^{*} \\ i_{2 α 2}^{*} \\ i_{2 β 2}^{*} \end{matrix}]}} = \overset{i_{C i n t r a_{C_{D}}}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α}^{*} \\ i_{1 β}^{*} \\ i_{2 α}^{*} \\ i_{2 β}^{*} \end{matrix}]}},

(A24)

\overset{i_{c i r - c l}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α}^{*} + i_{2 α}^{*} \\ i_{1 β}^{*} + i_{2 β}^{*} \\ - i_{1 β}^{*} + i_{2 β}^{*} \\ i_{1 α}^{*} - i_{2 α}^{*} \end{matrix}]}} = \overset{C_{D}^{- 1}}{\overset{︷}{[\begin{matrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & - 1 & 0 & 1 \\ 1 & 0 & - 1 & 0 \end{matrix}]}} \overset{i_{c i r - c l D}^{*}}{\overset{︷}{[\begin{matrix} i_{1 α}^{*} \\ i_{1 β}^{*} \\ i_{2 α}^{*} \\ i_{2 β}^{*} \end{matrix}]}} = \overset{i_{c i r - c l}^{*}}{\overset{︷}{[\begin{matrix} i_{α α}^{*} \\ i_{α β}^{*} \\ i_{β α}^{*} \\ i_{β β}^{*} \end{matrix}]}} .

(A25)

Later, the output signal of the controllers (

V_{i n - c l}^{*}

V_{c l}^{*}

V_{o u t - c l}^{*}

) are multiplexed, considering

v_{γ γ}^{*} = 0

, and the obtained vector is rearrangement R in the following matrix form:

[\begin{matrix} v_{α γ}^{*} \\ v_{β γ}^{*} \\ v_{α α}^{*} \\ v_{α β}^{*} \\ v_{β α}^{*} \\ v_{β β}^{*} \\ v_{γ α}^{*} \\ v_{γ β}^{*} \\ v_{γ γ}^{*} \end{matrix}] \Rightarrow R = \overset{v_{c l - 2 α β γ}^{*}}{\overset{︷}{[\begin{matrix} v_{α α}^{*} & v_{β α}^{*} & v_{γ α}^{*} \\ v_{α β}^{*} & v_{β β}^{*} & v_{γ β}^{*} \\ v_{α γ}^{*} & v_{β γ}^{*} & v_{γ γ}^{*} \end{matrix}]}} .

(A26)

The obtained matrix

X = v_{c l - 2 α β γ}^{*}

is then multiplied by the inverse

α β γ

transformation matrix

C^{- 1}

[22] from the left and right sides, obtaining the required cluster voltage as follows:

\overset{C^{- 1}}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & 0 & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{\sqrt{2}}{2} & \frac{\sqrt{3}}{3} \\ \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2} & \frac{\sqrt{3}}{3} \end{matrix}]}} \cdot \overset{v_{c l - 2 α β γ}^{*}}{\overset{︷}{[\begin{matrix} v_{α α}^{*} & v_{β α}^{*} & v_{γ α}^{*} \\ v_{α β}^{*} & v_{β β}^{*} & v_{γ β}^{*} \\ v_{α γ}^{*} & v_{β γ}^{*} & v_{γ γ}^{*} \end{matrix}]}} \cdot \overset{C^{- 1^{T}}}{\overset{︷}{[\begin{matrix} \frac{\sqrt{2}}{\sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} & \frac{- \sqrt{2}}{2 \sqrt{3}} \\ 0 & \frac{\sqrt{2}}{2} & \frac{- \sqrt{2}}{2} \\ \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} & \frac{\sqrt{3}}{3} \end{matrix}]}} = \overset{v_{x y}^{*}}{\overset{︷}{[\begin{matrix} v_{a r}^{*} & v_{b r}^{*} & v_{c r}^{*} \\ v_{a s}^{*} & v_{b s}^{*} & v_{c s}^{*} \\ v_{a t}^{*} & v_{b t}^{*} & v_{c t}^{*} \end{matrix}]}} .

(A27)

A final rearrangement R is made to convert the obtained matrix to the required voltage vector form as follows:

\overset{v_{x y}^{*}}{\overset{︷}{[\begin{matrix} v_{a r}^{*} & v_{b r}^{*} & v_{c r}^{*} \\ v_{a s}^{*} & v_{b s}^{*} & v_{c s}^{*} \\ v_{a t}^{*} & v_{b t}^{*} & v_{c t}^{*} \end{matrix}]}} \Rightarrow R (v_{x y}^{*}) = \overset{v_{i j}^{*}}{\overset{︷}{[\begin{matrix} v_{a r}^{*} \\ v_{b r}^{*} \\ v_{c r}^{*} \\ v_{a s}^{*} \\ v_{b s}^{*} \\ v_{c s}^{*} \\ v_{a t}^{*} \\ v_{b t}^{*} \\ v_{c t}^{*} \end{matrix}]}} .

(A28)

References

Beck, M.; Sperlich, A.; Blank, R.; Meyer, E.; Binz, R.; Ernst, M. Increasing energy efficiency in water collection systems by submersible PMSM well pumps. Water 2018, 10, 1310. [Google Scholar] [CrossRef]
Candelo-Zuluaga, C.; Riba, J.R.; Espinosa, A.G.; Blanch, P.T. Customized PMSM design and optimization methodology for water pumping applications. IEEE Transactions on Energy Conversion 2021, 37, 454–465. [Google Scholar] [CrossRef]
Kashif, M.; Singh, B. Reduced-Sensor-Based Multistage Model Reference Adaptive Control of PV-Fed PMSM Drive for Water Pump. IEEE Transactions on Industrial Electronics 2022, 70, 3782–3792. [Google Scholar] [CrossRef]
Kashif, M.; Singh, B. Modified Active-Power MRAS Based Adaptive Control with Reduced Sensors for PMSM Operated Solar Water Pump. IEEE Transactions on Energy Conversion 2022. [Google Scholar] [CrossRef]
Pires, V.F.; Cordeiro, A.; Foito, D.; Pires, A.J. Fault-tolerant multilevel converter to feed a switched reluctance machine. Machines 2022, 10, 35. [Google Scholar] [CrossRef]
Diaz, M.; Cardenas, R.; Ibaceta, E.; Mora, A.; Urrutia, M.; Espinoza, M.; Rojas, F.; Wheeler, P. An Overview of Modelling Techniques and Control Strategies for Modular Multilevel Matrix Converters. Energies 2020, 13. [Google Scholar] [CrossRef]
Kucka, J.; Karwatzki, D.; Mertens, A. AC/AC modular multilevel converters in wind energy applications: Design considerations 2016. pp. 1–10.
Miura, Y.; Mizutani, T.; Ito, M.; Ise, T. Modular multilevel matrix converter for low frequency AC transmission 2013. pp. 2013, 1079–1084. [Google Scholar]
Bontemps, P.; Milovanovic, S.; Dujic, D. Performance analysis of energy balancing methods for matrix modular multilevel converters. IEEE Transactions on Power Electronics 2022, 38, 2910–2924. [Google Scholar] [CrossRef]
Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. An optimal full frequency control strategy for the modular multilevel matrix converter based on predictive control. IEEE Transactions on Power Electronics 2017, 33, 6608–6621. [Google Scholar] [CrossRef]
Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. A branch current reallocation based energy balancing strategy for the modular multilevel matrix converter operating around equal frequency. IEEE Transactions on Power Electronics 2017, 33, 1105–1117. [Google Scholar] [CrossRef]
Kawamura, W.; Chen, K.L.; Hagiwara, M.; Akagi, H. A low-speed, high-torque motor drive using a modular multilevel cascade converter based on triple-star bridge cells (MMCC-TSBC). IEEE Transactions on Industry Applications 2015, 51, 3965–3974. [Google Scholar] [CrossRef]
Wang, C.; Zheng, Z.; Wang, K.; Li, Y. Fault detection and tolerant control of IGBT open-circuit failures in modular multilevel matrix converters. IEEE Journal of Emerging and Selected Topics in Power Electronics 2022, 10, 6714–6727. [Google Scholar] [CrossRef]
Wang, C.; Zheng, Z.; Wang, K.; Yang, B.; Zhou, P.; Li, Y. Analysis and control of modular multilevel matrix converters under branch fault conditions. IEEE Transactions on Power Electronics 2021, 37, 1682–1699. [Google Scholar] [CrossRef]
Wang, C.; Zheng, Z.; Wang, K.; Li, Y. Submodule Fault-Tolerant Control of Modular Multilevel Matrix Converters With Adaptive Optimum Common-Mode Voltage Injection. IEEE Transactions on Power Electronics 2022, 37, 7548–7554. [Google Scholar] [CrossRef]
Erickson, R.W.; Al-Naseem, O.A. A new family of matrix converters 2001. 2, 1515–1520.
Diaz, M.; Cardenas, R.; Espinoza, M.; Rojas, F.; Mora, A.; Clare, J.C.; Wheeler, P. Control of wind energy conversion systems based on the modular multilevel matrix converter. IEEE Transactions on Industrial Electronics 2017, 64, 8799–8810. [Google Scholar] [CrossRef]
Diaz, M.; Cárdenas Dobson, R.; Ibaceta, E.; Mora, A.; Urrutia, M.; Espinoza, M.; Rojas, F.; Wheeler, P. An overview of applications of the modular multilevel matrix converter. Energies 2020, 13, 5546. [Google Scholar] [CrossRef]
Guo, F.; Yu, J.; Ni, Q.; Zhang, Z.; Meng, J.; Wang, Y. Grid-forming control strategy for PMSG wind turbines connected to the low-frequency AC transmission system. Energy Reports 2023, 9, 1464–1472. [Google Scholar] [CrossRef]
Bravo, P.; Pereda, J.; Merlin, M.M.; Neira, S.; Green, T.C.; Rojas, F. Modular Multilevel Matrix Converter as Solid State Transformer for Medium and High Voltage AC Substations. IEEE Transactions on Power Delivery 2022, 37, 5033–5043. [Google Scholar] [CrossRef]
Mora, A.; Urrutia, M.; Cárdenas, R.; Angulo, A.; Espinoza, M.; Díaz, M.; Lezana, P. Model-predictive-control-based capacitor voltage balancing strategies for modular multilevel converters. IEEE Transactions on Industrial Electronics 2018, 66, 2432–2443. [Google Scholar] [CrossRef]
Kawamura, W.; Hagiwara, M.; Akagi, H. Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells. IEEE Transactions on Industry Applications 2014, 50, 3536–3548. [Google Scholar] [CrossRef]
Diaz, M.; Cardenas, R.; Espinoza, M.; Hackl, C.M.; Rojas, F.; Clare, J.C.; Wheeler, P. Vector control of a modular multilevel matrix converter operating over the full output-frequency range. IEEE Transactions on Industrial Electronics 2018, 66, 5102–5114. [Google Scholar] [CrossRef]
Park, R.H. Two-reaction theory of synchronous machines generalized method of analysis-part I. Transactions of the American Institute of Electrical Engineers 1929, 48, 716–727. [Google Scholar] [CrossRef]
Kammerer, F.; Gommeringer, M.; Kolb, J.; Braun, M. Energy balancing of the modular multilevel matrix converter based on a new transformed arm power analysis. 2014 16th European Conference on Power Electronics and Applications; IEEE, 2014; pp. 1–10. [Google Scholar]
Kawamura, W.; Chiba, Y.; Akagi, H. A broad range of speed control of a permanent magnet synchronous motor driven by a modular multilevel TSBC converter. IEEE Transactions on Industry Applications 2017, 53, 3821–3830. [Google Scholar] [CrossRef]
Gili, L.C.; Dias, J.C.; Lazzarin, T.B. Review, Challenges and Potential of AC/AC Matrix Converters CMC, MMMC, and M3C. Energies 2022, 15, 9421. [Google Scholar] [CrossRef]
Fan, B.; Wang, K.; Wheeler, P.; Gu, C.; Li, Y. An optimal full frequency control strategy for the modular multilevel matrix converter based on predictive control. IEEE Transactions on Power Electronics 2017, 33, 6608–6621. [Google Scholar] [CrossRef]
Duran, A.; Ibaceta, E.; Diaz, M.; Rojas, F.; Cardenas, R.; Chavez, H. Control of a modular multilevel matrix converter for unified power flow controller applications. Energies 2020, 13, 953. [Google Scholar] [CrossRef]
Kawamura, W.; Hagiwara, M.; Akagi, H.; Tsukakoshi, M.; Nakamura, R.; Kodama, S. AC-Inductors design for a modular multilevel TSBC converter, and performance of a low-speed high-torque motor drive using the converter. IEEE Transactions on Industry Applications 2017, 53, 4718–4729. [Google Scholar] [CrossRef]
Arias-Esquivel, Y.; Cardenas, R.; Urrutia, M.; Diaz, M.; Tarisciotti, L.; Clare, J.C. Continuous control set model predictive control of a modular multilevel converter for drive applications. IEEE Transactions on Industrial Electronics 2022, 70, 8723–8733. [Google Scholar] [CrossRef]
Travieso-Torres, J.C.; Vilaragut-Llanes, M.; Costa-Montiel, Á.; Duarte-Mermoud, M.A.; Aguila-Camacho, N.; Contreras-Jara, C.; Álvarez-Gracia, A. New adaptive high starting torque scalar control scheme for induction motors based on passivity. Energies 2020, 13, 1276. [Google Scholar] [CrossRef]
Zhang, Z.; Jin, Y.; Xu, Z. Modeling and Control of Modular Multilevel Matrix Converter for Low-Frequency AC Transmission. Energies 2023, 16, 3474. [Google Scholar] [CrossRef]
Narendra, K.S.; Annaswamy, A.M. Stable adaptive systems; Courier Corporation, 2012.
Travieso-Torres, J.C.; Duarte-Mermoud, M.A.; Sepuleveda, D.I. Passivity-based control for stabilization, regulation and tracking purposes of a class of nonlinear systems. International Journal of adaptive control and signal processing 2007, 21, 582–602. [Google Scholar] [CrossRef]
Travieso-Torres, J.C.; Ricaldi-Morales, A.; Véliz-Tejo, A.; Leiva-Silva, F. Robust Cascade MRAC for a Hybrid Grid-Connected Renewable Energy System. Processes 2023, 11, 1774. [Google Scholar] [CrossRef]
Travieso-Torres, J.C.; Duarte-Mermoud, M.A.; Estrada, J.L. Tracking control of cascade systems based on passivity: the non-adaptive and adaptive cases. ISA transactions 2006, 45, 435–445. [Google Scholar] [CrossRef] [PubMed]
Ogata, K.; et al. Modern control engineering; Prentice hall Upper Saddle River: NJ, 2010; Volume 5. [Google Scholar]
Clarke, E. Circuit analysis of AC power systems: symmetrical and related components; Wiley, 1943; Volume 1. [Google Scholar]
Eugene, L.; Kevin, W.; Howe, D. Robust and adaptive control with aerospace applications; Springer: London, England, 2013. [Google Scholar]

Figure 1. Basic power topology of an M3C for transferring energy between the power supply and the load, which is based on [6,9,19,21,22].

Figure 3. Comparative results under normal operation, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 3. Comparative results under normal operation, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 4. Comparative results under an input voltage imbalance, with a

10 %

voltage drop in phase a at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 4. Comparative results under an input voltage imbalance, with a

10 %

voltage drop in phase a at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 5. Comparative results under a cluster

a r

short circuit at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 5. Comparative results under a cluster

a r

short circuit at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 6. Comparative results under a cluster

a r

open circuit at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Figure 6. Comparative results under a cluster

a r

open circuit at 3 seconds, (a) Phase a input current, (b) Branch

a r

CCV, (c) Controlled

2 α β γ

ACV, (d) Controlled d component of the input current amplitude in

2 α β γ

, (e) Controlled intra and inter CCV imbalance in

2 α β γ

, (f) Controlled

α α

component of the circulating current in

2 α β γ

, (g) Phase r output current, (h) PMSM angular rotor speed.

Table 1. Values of b and

ω_{n}

for each controller.

Table 1. Values of b and

ω_{n}

for each controller.

Controller	b	$ω_{n}$	PI Quantity
Input Current Amplitude Control $d q$	$- \frac{\sqrt{3}}{L}$	$2 π (f_{i n})$	2
ACV Control d	$\frac{V_{a v g}}{3 C V_{C}^{*}}$	$2 π$ (1 Hz)	1
Intra-CCV Imbalance Control	$\frac{V_{i n_{α}}}{\sqrt{6} C V_{C}^{*}}$	$2 π$ (5 Hz)	4
Inter-CCV Imbalance Control $α γ$	$- \frac{V_{o u t_{α}}}{\sqrt{3} C V_{C}^{*}}$	$2 π$ (5 Hz)	1
Inter-CCV Imbalance Control $β γ$	$\frac{V_{o u t_{α}}}{\sqrt{3} C V_{C}^{*}}$	$2 π$ (5 Hz)	1
Inter-CCV Imbalance Control $γ α β$	$\frac{V_{i n_{α}}}{\sqrt{3} C V_{C}^{*}}$	$2 π$ (5 Hz)	2

Table 2. Motor-pump parameters.

Parameter	Value	Parameter	Value
$P_{r a t e d}$	644 [W]	$T_{r a t e d}$	4.1 [N-m]
$V_{s_r a t e d}$	165 [V]	$I_{s_r a t e d}$	2.65 [A]
$f_{e}$	75 [Hz]	$f_{p}$	0.95
P	3	$Φ$	0.305 [Wb]
$ω_{r}$	157.08[rad/s]	$J_{m}$	0.0036 [Nms $^{2}$ ]
$R_{s}$	6.2 [ $Ω$ ]	$J_{L o a d}$	0.0108 [Nms $^{2}$ ]
$L_{d}$	25.025 [mH]	$K_{l o a d}$	93.053 $\cdot 10^{- 6}$ [Kg m $^{2}$ ]
$L_{q}$	40.17 [mH]	$T_{0}$	0.41 [N-m]

Table 3. Plate data and parameters value of the M3C.

Parameter	Value	Parameter	Value
$P_{r a t e d}$	644 [W]	$V_{C}^{*}$	1500 [V]
$V_{i n_r a t e d}$	220 [V]	$V_{o u t_r a t e d}$	165 [V]
$f_{i n}$	50 [Hz]	$f_{o u t}$	75 [Hz]
$L_{i n}$	1.5 [mH]	L	1.0 [mH]
$f_{s w}$	10 [KHz]	C	3.3 [mF]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Adaptive Control of M3C-Based Variable Speed Drive for Multiple PMSM-Driven Centrifugal Pumps

Abstract

1. Introduction

2. Preliminaries

2.1. M3C State-Space Model

2.2. Basic Control Based PI Controllers

2.3. Cascade Adaptive Control Background

3. Proposal

4. Simulation Results

4.1. Results Under a Normal Operation

4.2. Results Under an Input Phase Imbalance

4.3. Results Under a Cluster Cell Short Circuit

4.4. Results Under an Opened Cluster Cell

5. Conclusions

Author Contributions

Funding

Institutional Review Board Statement

Informed Consent Statement

Data Availability Statement

Acknowledgments

Conflicts of Interest

Sample Availability

Appendix A

Appendix A.1. Inner control Loop M3C Dynamical model

Appendix A.2. Outer control Loop M3C Dynamical model

Appendix A.3. Vector and Matrix Transformation Details

References

MDPI Initiatives

Important Links

Subscribe