Redshift Drift in the Universe: Theoretical Features and Observational Constraints

In this paper, we investigate an exact Universe which is observational viable and filled with binary mixture of perfect fluid and cosmological constant $\Lambda$. Owning the non-uniform expansion of cosmos, we have considered redshift drift $\dot{z} = -(1+z)H_{0}+H(z)$ and performed statistical test to obtain the best fit value of model parameters of derived Universe with its observed values. Here $H_{0}$ and $z$ denote the present value of Hubble constant and redshift respectively. We estimate the best fit values of Hubble constant and density parameters are $H_{0} = 68.58 \pm 0.84$ km/s/Mpc, $(\Omega_{m})_{0} = 0.26 \pm 0.010$ and $(\Omega_{\Lambda})_{0} = 0.71 \pm 0.025$ by bounding the derived model with latest observational Hubble data (OHD) while with joint Pantheon data and OHD, its values are $H_{0} = 71.93 \pm 0.58$ km/s/Mpc, $(\Omega_{m})_{0} = 0.272 \pm 0.06$ and $(\Omega_{\Lambda})_{0} = 0.74 \pm 0.09$. The analysis of deceleration parameter and jerk parameter show that the Universe in derived model is compatible with $\Lambda$CDM model.

Keywords:

Subject: Physical Sciences - Nuclear and High Energy Physics

1. Introduction

Considering the discovery of Supernovae observations (SN Ia) in 1990 decade, it has been known that the distant supernovae are fainter and at long distant from us [1,2,3]. This result does not favour the matter dominated decelerating Universe and nailed down our belief in de sitter model of the Universe. In Refs. [4] and [5], the authors have investigated some cosmological models of the Universe with non baryon matter as the major part of the Universe. Thus, in order to explain the observed phenomenon of the current Universe, in particular the late time acceleration, one has to assumed some exotic type matter/energy to counter the gravitation pull of normal matter. This exotic energy have negative pressure and it is know as Dark Energy (DE). The cosmological constant

(Λ)

is a simple candidate of DE, however, it suffers mainly two problems on theoretical ground: i) cosmic coincidence and ii) fine tuning problems. In Refs. [6,7], the authors have constructed a cosmological model, assuming

Λ

as a source of dark energy in FRW space-time. This cosmological model is often known as

Λ

cold dark matter

(Λ

CDM) model or standard

(Λ

CDM) model of the Universe. It is worthwhile to note the FRW models of the Universe with absence of

Λ

exhibits a model that describes decelerated expansion phase of the Universe while these models have gained acceleration for some specific value of

Λ

. Later on, it has been observed that the

Λ

CDM model is in good agreement with recent astrophysical observations [8,9,10,11,12]. Further, we note that Wilkinson Microwave Anisotropy Probe (WMAP) [6] have nailed down the curvature of space and ordinary matter up to

0.4 %

and

4.6 %

respectively. Therefore

Λ

CDM cosmological model describes the Universe filled with two components baryon matter and cosmological constant with its density parameters

Ω_{m}

and

Ω_{Λ}

Seeing the success of

Λ

CDM model on observational ground, it is desirable to investigate its roll in early radiation dominated Universe. In Ref. [13], Sandage has given a clue about to obtain the present value of Hubble parameter (HP) and deceleration parameters (DP)

i . e .

H_{0}

and

q_{0}

) through observations. Now, it is widely accepted that

q_{0}

is negative and

H_{0}

is known to within 10% [14,15], making it one of the best measured quantities in modern cosmology. However, it is worthwhile to note that

Λ

CDM model persists some theoretical problems [16,17,18], which incite researchers to search other options that can explain the data and have some theoretical appeal as well. We also observe that many cosmological models have been investigated by introducing dynamical dark energy with negative pressure [19,20,21,22,23,24,26] or modification in general theory of relativity [27,28,29,30,31,32,33,34,35,36,37], where additional gravitational degree(s) may lead the accelerated expansion of the Universe at present epoch (see [38,39]). In recent time, a discrepancy of

H_{0}

value in measurement of Hubble parameter between Plank team and independent cosmological probes has been observed. This problem is known as

H_{0}

tension problem. In particular, the Plank collaboration [40] finds

H_{0} = 67.27 \pm 0.60

km/s/Mpc at

68 %

confidence level (CL) which is in

4.4 σ

tension with R19 [41] constraint,

H_{0} = 74.03 \pm 1.42

km/s/Mpc from the Hubble Space Telescope (HST) observations of 70 long-period Cepheids in the Large Magellanic Cloud. In Ref. [15], the authors have estimated

H_{0} = 69.8 \pm 1.1

km/s/Mpc in different way based on the Tip of the Red Giant Branch. Some other estimates of

H_{0}

are given in Refs. [42,43,44,45,46]. Recently, Bonilla et al. [47] have investigated a promising approach for measurements of

H_{0}

and reconstruction of DE properties from model independent joint analysis. The Refs. [48,49,50,51,52,53,54,55,56,57] are recorded as significant literature for developing new physics beyond the standard cosmological model to solve the

H_{0}

tension. Some other recent investigations [58,59,60,61,62,63,64] also suggest that the concordance model or

Λ

CDM model is in crisis.

The third order derivative of scale factor - jerk parameter (

j_{0}

) plays a significant role in describing the dynamics of the Universe as whole. For

Λ

CDM model, the present value of jerk parameter

j_{0}

is equal to 1. In this paper, we have performed

χ^{2}

test to obtain the best fit value of model parameters of derived model with its observed values. It is obtained that the best fit values of Hubble constant and density parameters are

H_{0} = 68.58 \pm 1.24

km/s/Mpc,

{(Ω_{m})}_{0} = 0.26 \pm 0.012

and

{(Ω_{Λ})}_{0} = 0.71 \pm 0.018

by bounding the derived model with latest

H (z)

data while with Pantheon data, its values are

H_{0} = 71.93 \pm 0.58

km/s/Mpc,

{(Ω_{m})}_{0} = 0.272 \pm 0.02

and

{(Ω_{Λ})}_{0} = 0.73 \pm 0.03

. The analysis of deceleration parameter and jerk parameter shows that the Universe in derived model is comparable to the

Λ

CDM model. Some important features of dark energy dominated Universe are given in Refs. [65,66,67,68,69,70,71,72,73,74]. In Refs. [75,76], the authors have studied the non interaction of dark energy and electromagnetic field and summarized that the late time evolution of the Universe is dominated with dark energy. It is worthwhile to note that the testing of anisotropy in the Universe with observational data is major challenge [77,78]. In Wang and Wang [77], the authors have studied a Bianchi type I Universe by using Joint Light-curve Analysis (JLA) sample of SNe Ia observations and investigated that there is no obvious evidence for a preferred direction of anisotropic axis in this model. Akarsu et al. [78] have generalized

Λ

CDM model in Bianchi type I space time and proposed a very informative method for constraining the current expansion anisotropy of the Universe. Some other sensible researches with extension of standard

Λ

CDM model in different physical contexts are given in Refs. [79,80,81]. Some useful applications of cosmological models in modified gravity are also given in Refs. [82,83,84,85].

Motivated by the above researches, in this paper, firstly we have investigated an exact solution of Einstein’s field equations in FRW space - time. Secondly, owning the non-uniform expansion of cosmos, we obtained the expressions of cosmological parameters for redshift drift

\dot{z} = - (1 + z) H_{0} + H (z)

and constrained the model parameters with OHD and joint Pantheon compilation of SN Ia data and OHD. The paper is structured as follows: Section 1 is introductory in nature. Section 2 deals with model and its basic formalism. In Section 3, we describe data and likelihoods. The physical as well as geometrical properties of the model are discussed in Section 4. In Section 5 we summarized the main findings of this paper.

2. The model and basic formalism

In standard spherical co-ordinates, a spatially homogeneous and isotropic FRW space-time is read as

d s^{2} = d t^{2} - a^{2} (t) [\frac{d r^{2}}{1 - k r^{2}} + r^{2} (d θ^{2} + s i n^{2} θ d ϕ^{2})]

(1)

where

a (t)

is the scale factor which describes how the scales change in an expanding Universe. k is the curvature of space-time and its values

k = - 1

, 0, 1 correspond to closed, flat and open Universe respectively. The co-ordinates r,

θ

and

ϕ

in space-time (1) are co-moving co-ordinates.

The Einstein’s field equation is read as

R_{i j} - \frac{1}{2} R g_{i j} - Λ g_{i j} = 8 π G T_{i j}

(2)

where the symbols have their usual meaning.

The energy-momentum tensor

(T_{i j})

of perfect fluid is read as

T_{i j} = (ρ + p) v_{i} v_{j} - p g_{i j}

(3)

where

v^{i}

is four velocity vector satisfying

v^{i} v_{i} = 1

. In Equation (3), p and

ρ

are the isotropic pressure and energy density of the perfect fluid.

Equations (2) and (1) lead the following system of equations

2 \frac{\ddot{a}}{a} + \frac{{\dot{a}}^{2}}{a^{2}} + \frac{k}{a^{2}} = - 8 π G p + Λ

(4)

3 \frac{{\dot{a}}^{2}}{a^{2}} + 3 \frac{k}{a^{2}} = 8 π G ρ + Λ

(5)

In addition to Equations (4) and (5), the energy conservation equation is given as

\dot{ρ} + 3 (1 + ω) ρ H = 0,

(6)

where, we have used the following barotropic equation of state for perfect fluid and

0 \leq ω \leq 1

is equation of state parameter.

p = ω ρ .

(7)

Equation (5) is written as

3 H^{2} = 8 π G (ρ + ρ_{Λ} + ρ_{k})

(8)

where

H = \frac{\dot{a}}{a}

ρ_{Λ} = \frac{Λ}{8 π G}

and

ρ_{k} = \frac{3 k}{8 π G a^{2}}

Using Equations (6) and (7), Equation (8) leads to

\frac{H^{2}}{H_{0}^{2}} = {(Ω_{m})}_{0} a^{- 3 (1 + ω)} + {(Ω_{k})}_{0} a^{- 2} + {(Ω_{Λ})}_{0}

(9)

where

{(Ω_{i})}_{0} = \frac{{(ρ_{i})}_{0}}{{(ρ_{c})}_{0}}

is the present day density parameter of the

i^{t h}

fluid.

{(ρ_{c})}_{0} = \frac{3 H_{0}^{2}}{8 π G}

denotes the critical density of the Universe at present epoch. Thus, we obtain that

{(Ω_{m})}_{0} + {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0} = 1

Defining red-shift z in terms of a

i . e .

z = - 1 + \frac{a_{0}}{a}

where

a_{0}

is the present values of scale factor. Then we obtain

H (z)

as following

H = H_{0} \sqrt{{(Ω_{m})}_{0} {(1 + z)}^{3 (1 + ω)} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}}

(10)

For

Λ

CDM model,

H (z)

is read as

H = H_{0} \sqrt{{(Ω_{m})}_{0} {(1 + z)}^{3} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}}

(11)

The luminosity distance (

D_{L}

) is defined as

D_{L} = r_{1} (1 + z) a_{0}

(12)

For determination of

r_{1}

, we consider a photon emitted by source with co-ordinate

(r, t)

and received at a time

t_{0}

by an observer located at

r = 0

. Then

r_{1} = \int_{t}^{t_{0}} \frac{d t}{a} \Rightarrow a_{0} r_{1} = - \int_{0}^{z} \frac{(1 + z) d z}{\dot{z}}

(13)

Owning the non-uniform expansion of cosmos, the redshift z is time dependent

z (t)

. As a result a second photon emitted by the same object at different instant of time

t + ▵ t = t^{'}

will corresponds to the redshift

z (t^{'})

. Therefore a redshift drift is defined as

\dot{z} = - (1 + z) H_{0} + H (z)

(14)

Using Equations (13) and (14) in Equation (12), we obtain

D_{L} (z) = \frac{(1 + z)}{H_{0}} \int_{0}^{z} \frac{(1 + z) d z}{(1 + z) - h (z)}; h (z) = \frac{H}{H_{0}}

(15)

Thus, the distance Modulus (

μ

) is obtained as

μ (z) = m_{b} - M = 5 l o g_{10} (\frac{D_{L} (z)}{M p c}) + μ_{0}

(16)

where

m_{b}

, M and

μ_{0}

denote apparent magnitude, absolute magnitude and zero point offset.

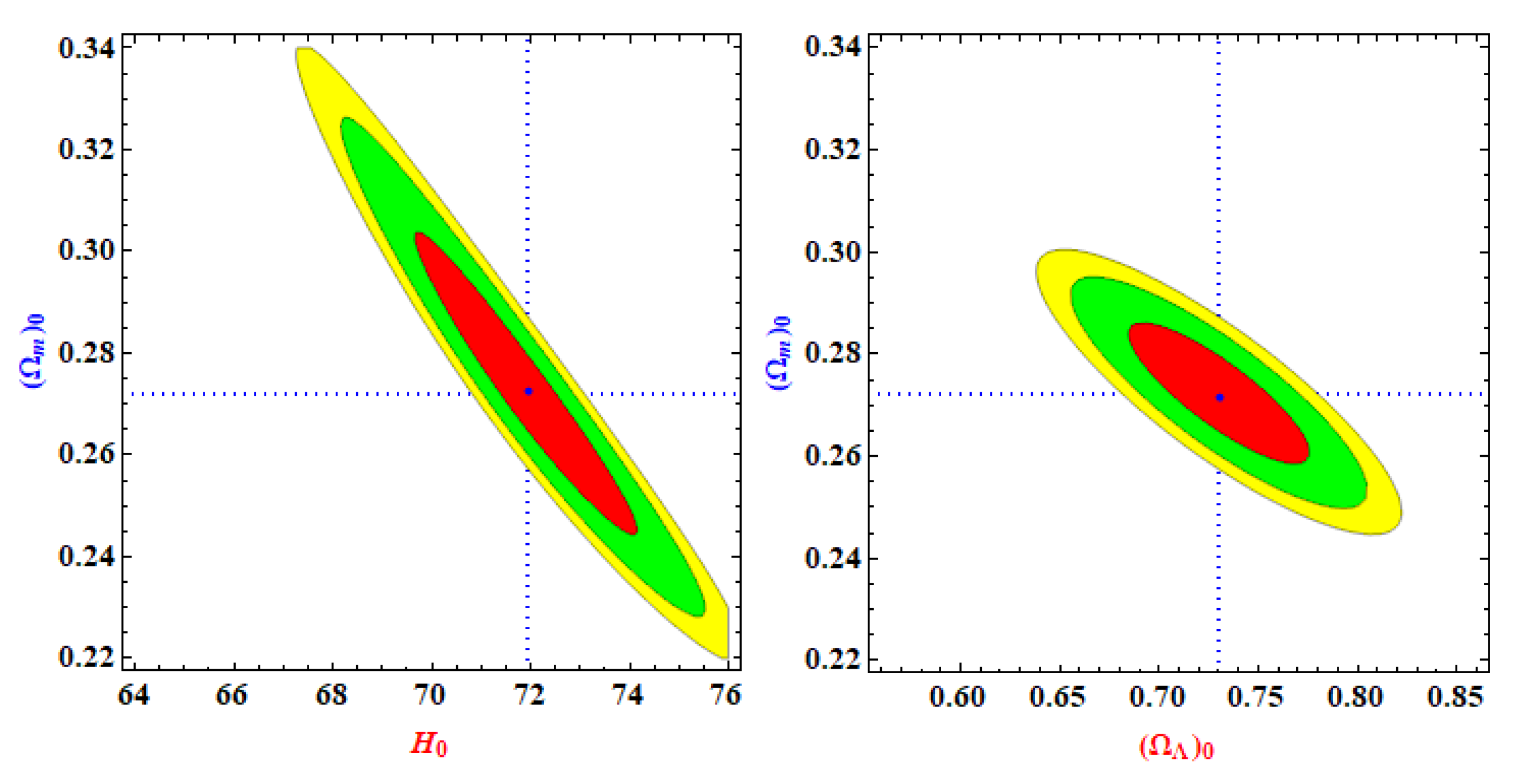
3. Observational constraints on the model parameters

In this section, we describe observation

H (z)

data, SN Ia Pantheon compilation data and the statistical methodological analysis for constraining various model parameters .

Observational Hubble Data (OHD): We have take over $46 H (z)$ observational datapoints in the range of $0 \leq z \leq 2.36$ , dominated from cosmic chronometric technique. These all $46 H (z)$ datapoints are compiled in Table 1 of Ref. [86].
Supernovae Type Ia (SN Ia): We have used Pantheon compilation of SN Ia data [87] which includes 1048 SN Ia apparent magnitude measurements in the redshift range $0.01 < z < 2.3$ . In Riess et al. [88], the authors have summarized the full sample of Pantheon in six model independent data points.

Now, we define

χ^{2}

as following:

χ^{2} = \sum_{i = 1}^{N} {[\frac{E_{t h} (z_{i}) - E_{o b s} (z_{i})}{σ_{i}}]}^{2}

(17)

where

E_{t h} (z_{i})

and

E_{o b s} (z_{i})

denote the theoretical values and observed values of corresponding parameter respectively.

σ_{i}

and N are standard errors in

E_{o b s} (z_{i})

and number of data points.

Figure 1 exhibits two dimensional (2D) contours at

1 σ

2 σ

and

3 σ

confidence levels by bounding the Universe in derived model with 46 observational Hubble data. The summary of statistical analysis is as follows:

H_{0} = 68.58 \pm 0.84 k m / s e c / M p c

{(Ω_{m})}_{0} = 0.26 \pm 0.010

and

{(Ω_{Λ})}_{0} = 0.71 \pm 0.025

. Figure 2 depicts the best fit curve of Hubble rate with red-shift of derived model with OHD.

Figure 1. Two dimensional contours at

1 σ

2 σ

and

3 σ

confidence regions by bounding our model with latest 46 observational Hubble data. The unit of

H_{0}

k m s^{- 1} M p c^{- 1}

Figure 1. Two dimensional contours at

1 σ

2 σ

and

3 σ

confidence regions by bounding our model with latest 46 observational Hubble data. The unit of

H_{0}

k m s^{- 1} M p c^{- 1}

Figure 3 depicts 2D contours at

1 σ

2 σ

and

3 σ

confidence regions by bounding our model with Pantheon data. The result of statistical analysis is as follows:

H_{0} = 71.93 \pm 0.58 k m / s e c / M p c

{(Ω_{m})}_{0} = 0.272 \pm 0.06

and

{(Ω_{Λ})}_{0} = 0.74 \pm 0.09

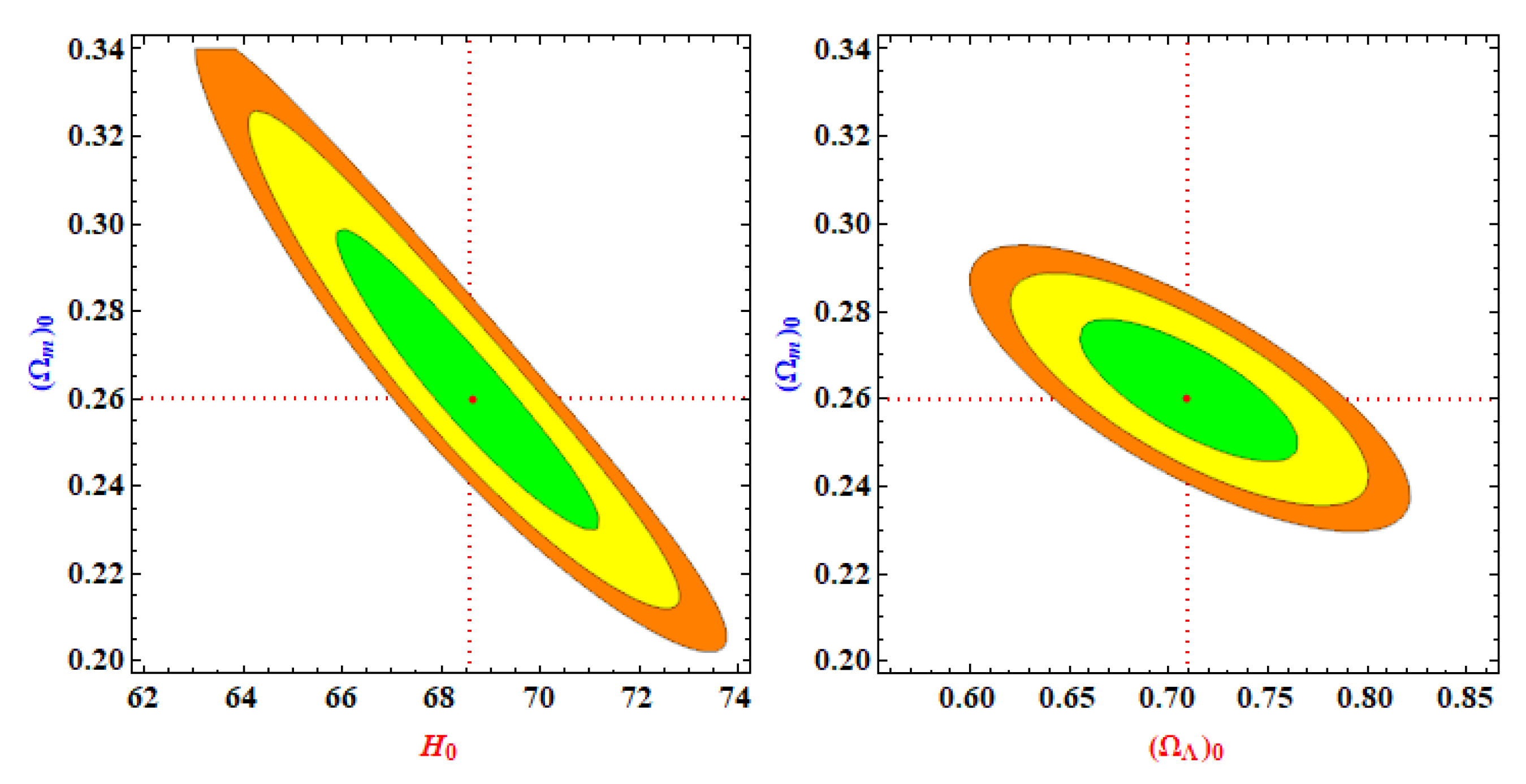
4. Physical properties of the model

4.1. Deceleration parameter

The deceleration parameter

(q)

is given by

\begin{matrix} q & = & - 1 - \frac{\dot{H}}{H^{2}} = - 1 - \frac{3 (ω + 1) {(Ω_{m})}_{0} {(1 + z)}^{(3 ω + 2)} + 2 (1 + z) {(Ω_{k})}_{0}}{2 {[{(Ω_{m})}_{0} {(1 + z)}^{3 (ω + 1)} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}]}^{3 / 2}} \times \\ \frac{\sqrt{{(Ω_{m})}_{0} {(1 + z)}^{3 (ω + 1)} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}} - (1 + z)}{2 {[{(Ω_{m})}_{0} {(1 + z)}^{3 (ω + 1)} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}]}^{3 / 2}} \end{matrix}

(18)

The behaviors of deceleration parameter versus redshift for OHD and joint Pantheon Data and OHD are shown in Figure 4. The solid gray curve in both panels of Figure 4 show the best fit curve of deceleration parameter. The sign of q indicates weather the model inflates or not. A positive sign of q corresponds the decelerated expansion of Universe while negative sign of q describes the present accelerated expansion of the Universe. Here, we observe that the Universe in derived model is in accelerated phase of expansion at present epoch [74,89,90,91,92,93]. The present value of q is obtained by putting

z = 0

in Equation (18)

i . e .

q_{0} = - 1 - \frac{(3 (ω + 1) {(Ω_{m})}_{0} + 2 {(Ω_{k})}_{0}) (\sqrt{{(Ω_{m})}_{0} + {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0}} - 1)}{2 {[{(Ω_{m})}_{0} + {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0}]}^{3 / 2}}

(19)

From Equation (19), we observe that

q_{0} \sim - 1

. It is worthwhile to note that

q_{0} = - 1

leads

{(\frac{d H}{d t})}_{t = t_{0}} = 0

which implies the greatest value of Hubble parameter and fastest rate of expansion of the Universe. Therefore, the Universe in derived model can be utilize to describe the dynamics of late time evolution of observed Universe. In Refs. [94,95,96,97,98], the authors have studied transitioning behaviour of deceleration parameter by assuming scale factor in hybrid form - a product of power-law and exponential type of functions.

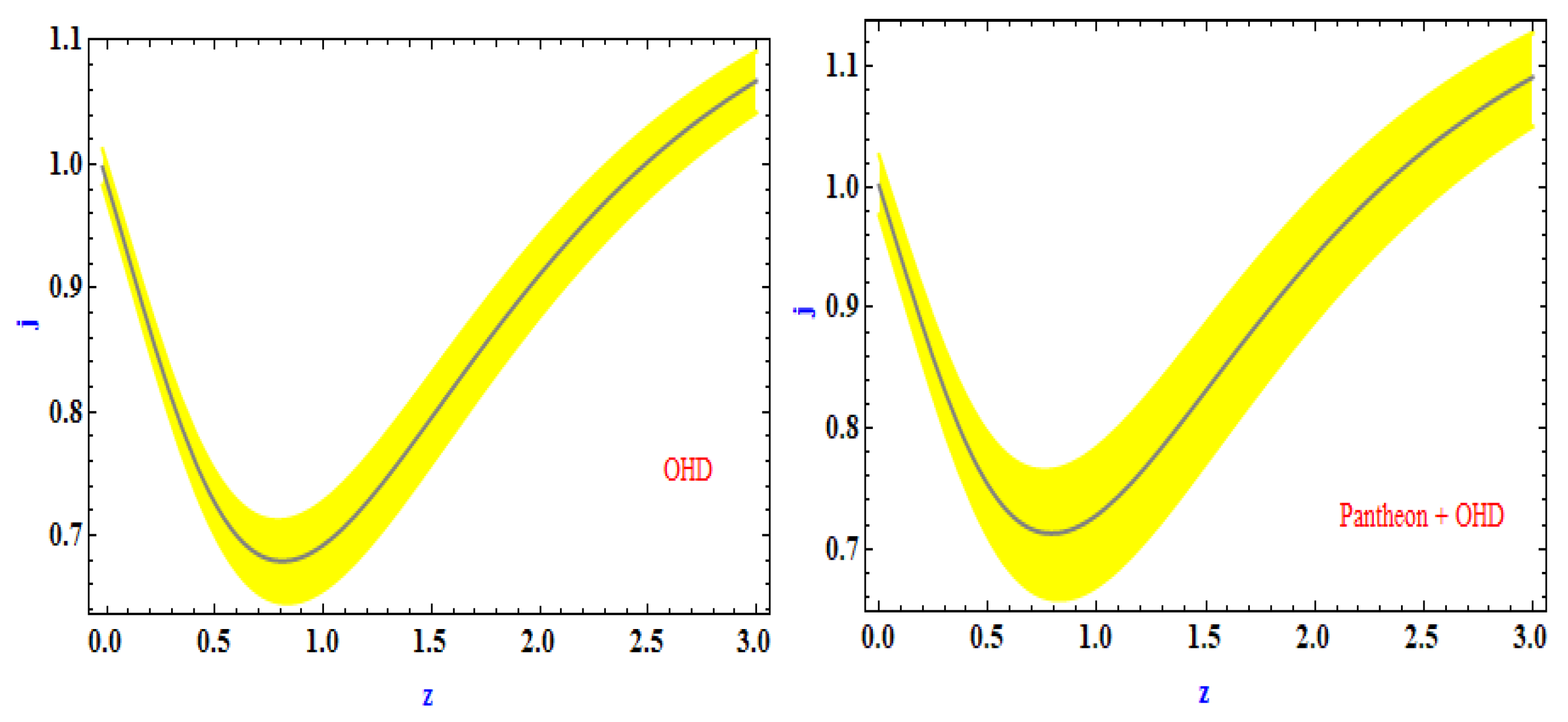
4.2. Jerk parameter

The jerk parameter

(j)

is a dimensionless quantity which measure departure of any cosmological model from concordance model or

Λ

CDM model [100]. It is defined as [101,102,103].

j = \frac{\overset{⃛}{a}}{a H^{3}}

(20)

where

\overset{⃛}{a} = \frac{d^{3} a (t)}{d t}

Using

\dot{z} = - (1 + z) H_{0} + H

, we obtain j as following

j = 2 q^{2} + q - [\frac{h (z) - (1 + z)}{h (z)}] \frac{d q}{d z}

(21)

We have not given the full expression for the jerk parameter

(j)

here, since this expression is too lengthy, and only plotted it in Figure 5 for both OHD (left panel) and joint Pantheon data and OHD (right panel). The present value of jerk parameter is obtained as

j_{0} = 2 q_{0}^{2} + q_{0}

(22)

Thus, we obtain

j_{0} \sim 1

in our analysis by assuming the red-shift drift. Some sensible researches on observational cosmology show that for

Λ

CDM model

j_{0} = 1

[95,104]. In Ref. [105], Luongo has carried out the reconstruction of a cosmological model through jerk parameter. In our analysis,

j_{0} \approx 1

, therefore the derived model exhibits the properties of

Λ

CDM model of the Universe. The usefulness of jerk parameter in discriminating the various dark energy models are given in Refs. [102,106,107,108,109,110,112,113,114,115]. In comparison of our model model with

Λ

CDM model, it is worthwhile to note that if we consider

ω = 0

(pressure-less matter) then

q_{0}

and

j_{0}

coincide with its corresponding values in

Λ

CDM model of the Universe.

4.3. Effective energy density and effective pressure

Effective energy density and pressure(DP) corresponds over all density parameter which includes both baryon and

Λ

energy density parameter. Thus, we define

ρ_{e f f} = ρ_{m} + ρ_{k} + ρ_{Λ}, p_{e f f} = p_{m} + p_{k} + p_{Λ}, p_{Λ} = - ρ_{Λ} = - Λ / 8 π G

Therefore, the field Equations (4) and (5) recast as

2 \frac{\ddot{a}}{a} + \frac{{\dot{a}}^{2}}{a^{2}} = - 8 π G p_{e f f}

(23)

3 \frac{{\dot{a}}^{2}}{a^{2}} = 8 π G ρ_{e f f}

(24)

Solving Equations (23) and (24), we obtain the expressions for

ρ_{e f f}

and

p_{e f f}

as follow:

ρ_{e f f} = {(ρ_{c})}_{0} ({(Ω_{m})}_{0} {(1 + z)}^{3 (1 + ω)} + {(Ω_{Λ})}_{0} + {(Ω_{k})}_{0} {(1 + z)}^{2})

(25)

p_{e f f} = ρ_{e f f} \times

[\frac{[2 (1 + z) {(Ω_{k})}_{0} + (ω + 1) {(Ω_{m 0})}_{0} {(1 + z)}^{ω}] (- \sqrt{{(1 + z)}^{2} {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0} + {(Ω_{m})}_{0} {(1 + z)}^{ω + 1}} + z + 1)}{3 {[{(1 + z)}^{2} {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0} + {(Ω_{m})}_{0} {(1 + z)}^{ω + 1}]}^{3 / 2}} - 1]

(26)

We also define an effective equation of state parameter

ω_{e f f}

as following

ω_{e f f} = p_{e f f} / ρ_{e f f} =

\frac{[2 (1 + z) {(Ω_{k})}_{0} + (ω + 1) {(Ω_{m 0})}_{0} {(1 + z)}^{ω}] (- \sqrt{{(1 + z)}^{2} {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0} + {(Ω_{m})}_{0} {(1 + z)}^{ω + 1}} + z + 1)}{3 {[{(1 + z)}^{2} {(Ω_{k})}_{0} + {(Ω_{Λ})}_{0} + {(Ω_{m})}_{0} {(1 + z)}^{ω + 1}]}^{3 / 2}} - 1

(27)

From Equations (25) - (27), we observe the following facts:

The present value of effective pressure and EoS parameter $ω_{e f f}$ is as below

$p_{e f f} = - {(ρ_{c})}_{0} {(Ω_{Λ})}_{0}, {(ω_{e f f})}_{0} = - {(Ω_{Λ})}_{0} \sim - 0.7$ .

Fortunately, these confirm that the Universe is expanding with acceleration at present epoch.
At radiation era, when the Universe was highly warm and turbulent, $p_{m} = ρ_{m} / 3 ω = 1 / 3$ . This was the period when red shift $z \geq 1100$ . During this span of time, $ω_{e f f}$ is as follow

$ω_{e f f} = 0.333 - \frac{1.333 {(Ω_{Λ})}_{0}}{[{(Ω_{m})}_{0} {(1 + z)}^{3 (1 + ω)} + {(Ω_{k})}_{0} {(1 + z)}^{2} + {(Ω_{Λ})}_{0}]}$

Thus $ω_{e f f} ≃ ω = 1 / 3$ and $p_{e f f} ≃ 1 / 3 ρ_{e f f},$ when $z \geq 1100$ .
It is evident that the inclusion of $Λ$ in the energy content of the Universe does not change the physics of early Universe but it is required to explain the late time acceleration of the Universe.

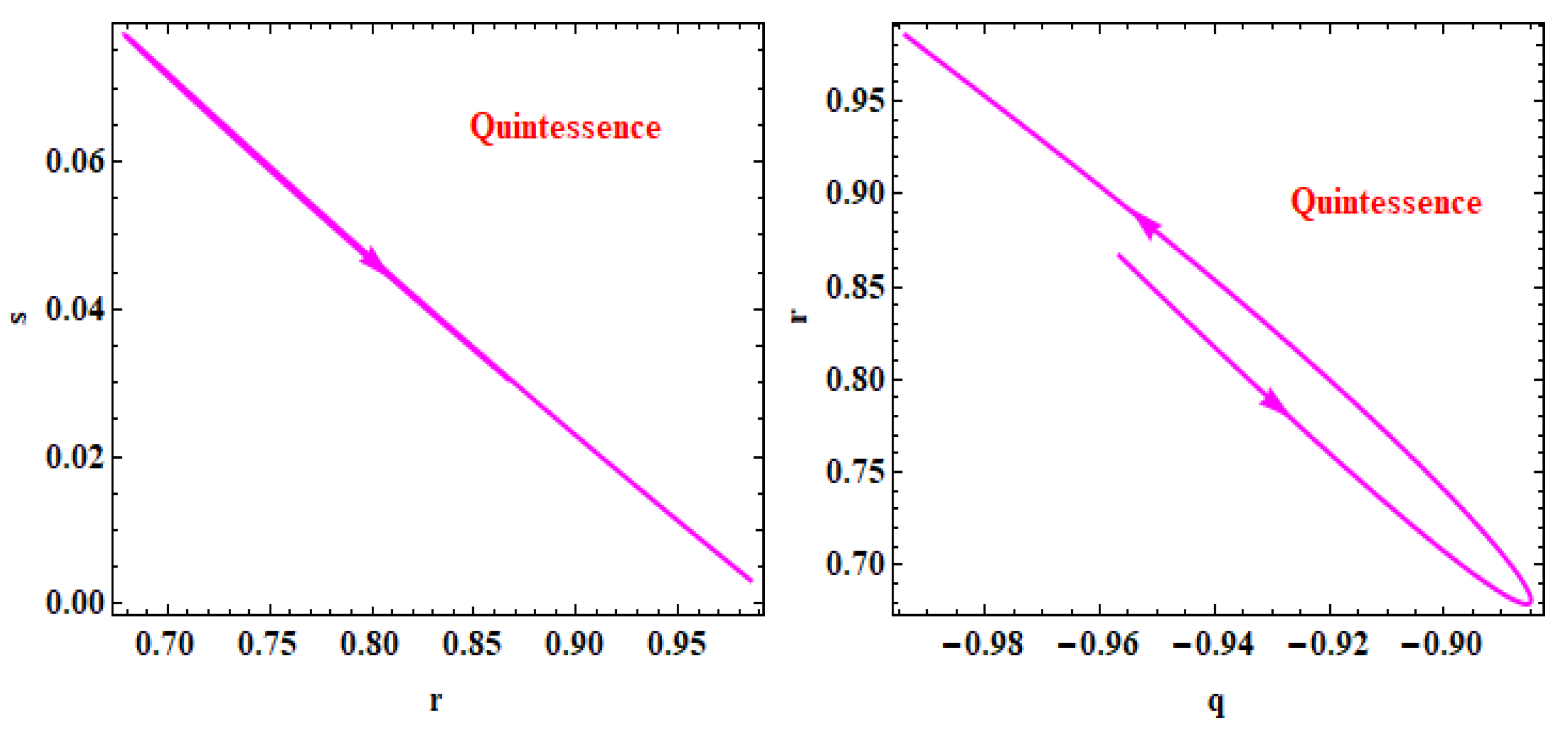
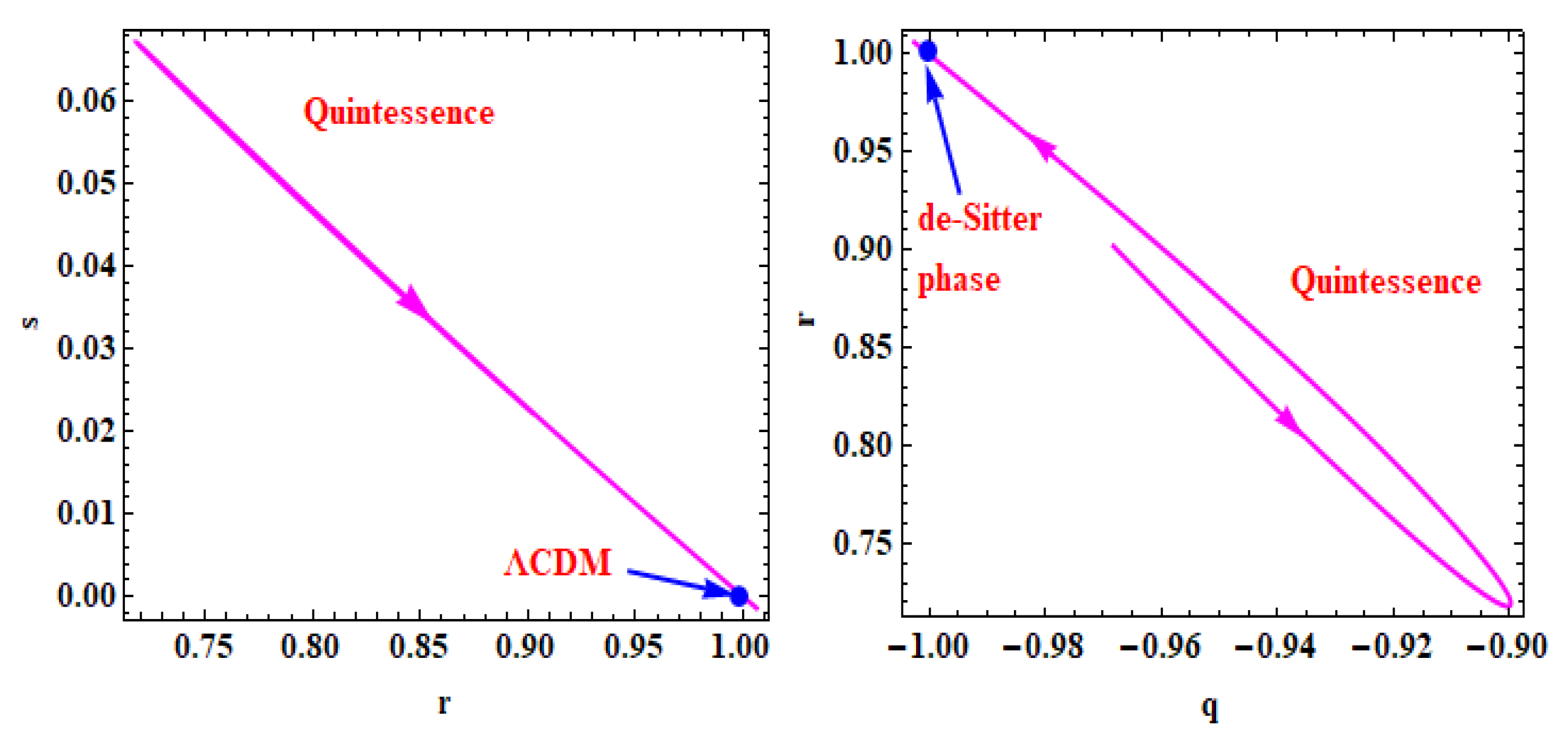
4.4. Statefinder diagnostics

The statefinder pairs

{r, s}

is the geometrical quantities which are directly obtained from metric and used to distinguish different dark energy models. Alam et al [116] have defined the statefinder parameters r and s as following

r = \frac{\overset{⃛}{a}}{a H^{3}}, s = \frac{r - 1}{3 (q - \frac{1}{2})} .

(28)

At present, we obtain that

r \sim 1

and

s \sim 0

for the constrained values of model parameters due to OHD and OHD + Pantheon compilation of SN Ia data. Therefore, the Universe in derived model approaches

Λ

CDM model at present. Figure 6 depicts the trajectories of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with OHD. Note that

r = 1

and

s = 0

correspond to the

Λ

CDM model. From Figure 6, we observe that the profile starts from quintessence and likely to approach

Λ

CDM model. Figure 7 shows the the trajectories of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with combined OHD and pantheon compilation of SN Ia data. From Figure 7, it is evident that profile in

r - s

plane starts from quintessence and evolves into

Λ

CDM model. We also observe from Figure 7 that the

q - r

plane is followed by the the region

r < 1

and

q < 0

and finally approaches to the de - Sitter phase with

r = 1

and

q = - 1

5. Conclusions

In this paper, we have investigated a cosmological model, filled with binary mixture of perfect fluid and cosmological constant

Λ

and constrained the present values of the model parameters by restricting the Universe in derived model with recent OHD and pantheon compilation of SN Ia data sets. We observe that our results are compatible with the concordance model or standard

Λ

CDM model of the Universe. We have examined the model parameters of the Universe with its observed values through

χ^{2}

minimization technique. The summary of numerical analysis is given in Table 1.

The main features of the Universe in derived model are as follows:

i): The Universe in derived model represents a model of accelerating Universe at present epoch with dominance of dark energy. The natural consequence of this research is that the cosmological constant $Λ$ is a promising candidate of dark energy.
ii): We have obtained the effective energy density and pressure of the Universe in derived model which describes the dynamics of the Universe from its beginning to present epoch.
iii): The present value of jerk parameter of the Universe in derived model is computed as $j \sim 1$ which confirms that the derived model is representing a $Λ$ CDM type Universe.
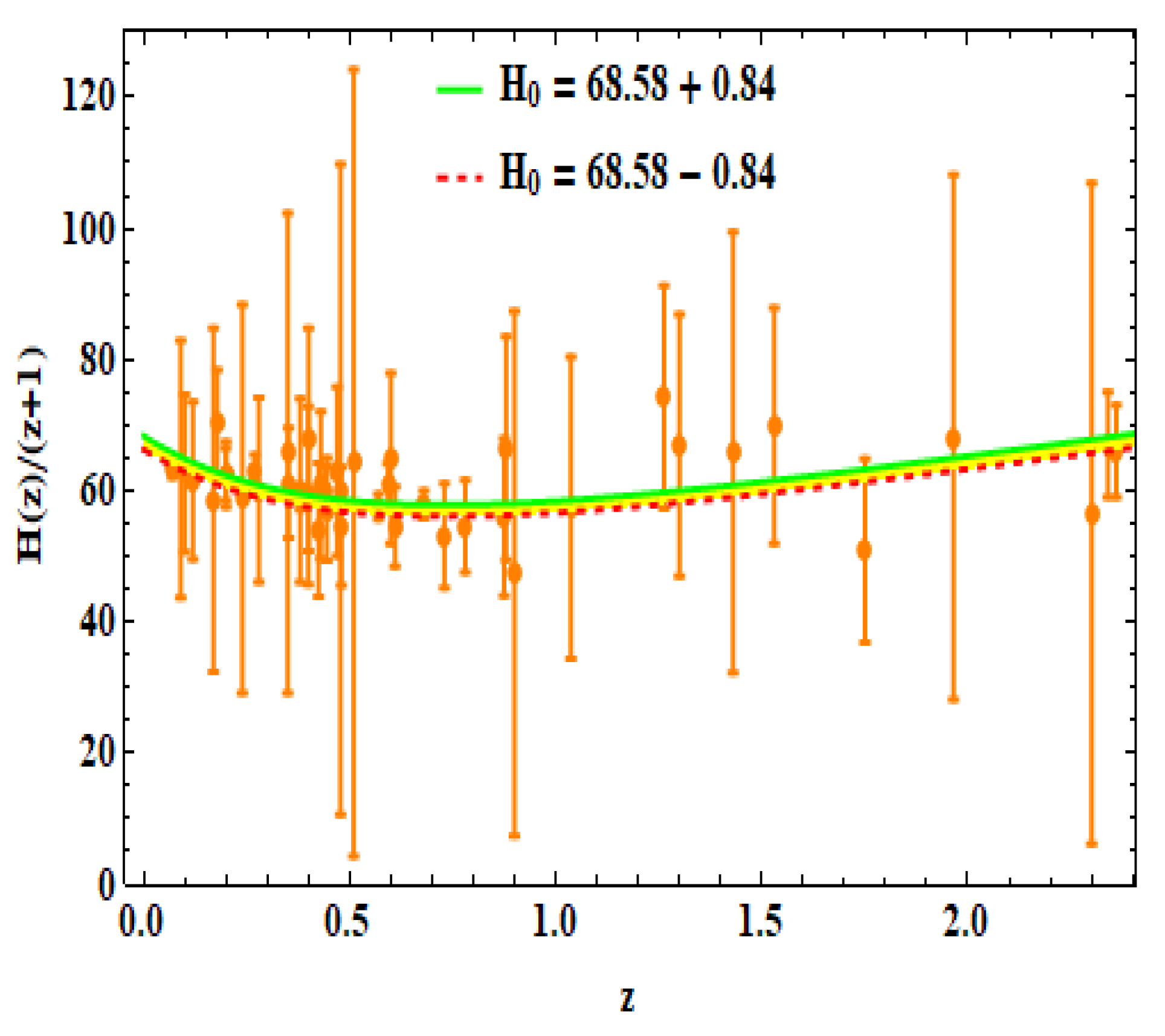
iv): We estimated $H_{0} = 68.58 \pm 0.84$ km/s/Mpc (OHD) and $H_{0} = 71.93 \pm 0.58$ km/s/Mpc (Pantheon + OHD). Comparing these results with what reported in R19 [40], we observe that $H_{0} = 68.58 \pm 0.84$ km/s/Mpc (OHD) is in $1.26 σ$ tension. Thus, we observe that the cosmological models owning redshift drift minimize $H_{0}$ tension.

References

S. Perlmutter et al, Nature 1998, 391, 51.
S. Perlmutter et al, Astrophys. J. 1999, 517, 5.
A. G. Riess et al, Astron. J. 1998, 116, 1009.
J. P. Ostriker and P. J. Steinhardt, Nature 1995, 377, 600.
M. S. Turner, G. Steigman and L. Krauss, Phys. Rev. Lett. 1984, 52, 2090.
D. N. Spergel et al. [WMAP Collaboration], Astrophys. J. Suppl. Ser. 2007, 170, 377.
M. Tegmark et al. [SDSS Collaboration], Phys. Rev. D 2004, 69, 103501.
E. J. Copeland, M. Sami, S. Tsujikawa, Int. J. Mod. Phys. D 2006, 15, 1753.
O. Gron and S. Hervik, Einstien’s General Theory of Relativity With Modern Application in Cosmology, (New York: Springer) (2007).
K. Abazajian et al. [SDSS Collaboration], Astron. J. 2004, 128, 502.
V. Sahni, A. A. Starobinsky, Int. J. Mod. Phys. D 2000, 9, 373.
W. L. Freedman et al., The Astrophys. J. 2001, 553, 47.
A. Sandage, Physics Today 1970, 23, 34.
K. C. Wong et al., arXiv:1907.04869 [astro-ph.CO].
W. L. Freedman et al., arXiv:1907.05922 [astro-ph.CO].
S. Weinberg, Rev. Mod. Phys. 1989, 61, 1.
T. Padmanabhan, Phys. Rept. 2003, 380, 235.
R. Bousso, Gen. Rel. Grav. 2008, 40, 607.
J. Martin, Mod. Phys. Lett. A 2008, 23, 1252.
R. R. Caldwell, M. Kamionkowski, N. N. Weinberg, Phys. Rev. Lett. 2003, 91, 071301.
M. C. Bento, O. Bertolami, A. A. Sen, Phys. Rev. D 2002, 66, 043507.
W. Zimdahl, D. Pavon, Gen. Relativ. Gravit. 2004, 36, 1483.
X. Zhang, Phys. Lett. B 2005, 611, 1.
X. Zhang, Commun. Theor. Phys. 2005, 44, 762.
M. R. Setare, A. Banijamali and B. Fazlpour, Int. J. Mod. Phys. D 2011, 20, 269.
H. Amirhashchi, Astrophys Space Sc. 2014, 351, 641.
A. K. Yadav, Phys. Rev. D 2020, 102, 108301.
T. P. Sotiriou and V. Faraoni, Rev. Mod. Phys. 2010, 82, 451.
R. Aldrovandi and J. G. Pereira, Teleparallel Gravity. vol. 173. Springer, Dordrecht (2013).
D. Blixt, M. Hohmann and C. Pfeifer, Phys. Rev. D 2019, 99, 084025.
R. Ferraro and F. Fiorini, Phys. Rev. D 2007, 75, 084031.
E. V. Linder, Phys. Rev. D 2010, 81, 127301.
D. Lovelock, J. Math. Phys. 1971, 12, 498.
S. Bahamonde, K. F. Dialektopoulos, and Said J. Levi, Phys. Rev. D 2019, 100, 064018.
A. K. Yadav et al., Phys. Dark Uni. 2021, 31, 100738.
H. Amirhashchi and A. K. Yadav, Phys. Dark Uni. 2020, 30, 100711.
R. Prasad, L. K. Gupta, A. K. Yadav, Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150029.
D. Huterer, D. L. Shafer, Rep. Prog. Phys. 2017, 81, 016901.
M. Ishak, Living Rev. Rel. 2019, 1, 22.
N. Aghanim et al. (Planck Collaboration), Planck 2018 results. VI. Cosmological parameters, arXiv: 1807.06209.
A. G. Riess et al., Astrophys. J. 2019, 876, 1.
D. Camarena, V. Marra, Phys. Rev. Res. 2020, 2, 013028.
D. Camarena, V. Marra, MNRAS 2020, 495, 3.
R. C. Nunes, A. Bernui, arXiv: 2008.03259.
N. Schoneberg, J. Lesgourgues, D. C. Hooper, J. Cosmol. Astrop Phys. 2019, 10, 029.
O. H. E. Philcox, B. D. Sherwin, G. S. Farren, E. J. Baxter, arXiv: 2008.08084.
A. Bonilla, S. Kumar, R. C. Nunes, arXiv: 2011.0714.
L. Verde, T. Treu, A. G. Riess, Nature Astronomy 2019, 3, 891.
V. Poulin, T. L. Smith, T. Karwal, M. Kamionkowski, Phys. Rev. Lett. 2019, 122, 221301.
R. C. Nunes, J. Cosmol. Astrop. Phys. 2018, 05, 052.
W. Yang et al., J. Cosmol. Astrop. Phys. 2018, 09, 019.
E. Di Valentino, A. Melchiorri, O. Mena, S. Vagnozzi, arXiv: 1908.04281.
S. Vagnozzi, arXiv: 1907.07569.
S. Vagnozzi, E. Di Valentino, S. Gariazzo, A. Melchiorri, O. Mena, J. Silk, arXiv: 2010.02230.
B. S. Haridasu, M. Viel, Mon. Not. Roy. Astron. Soc. 2020, 497, 2.
E. Di Valentino, arXiv: 2011.00246.
E. Di Valentino, A. Melchiorri, O. Mena, S. Pan, W. Yang, arXiv: 2011.00283.
E. Di Valentino, A. Melchiorri, J. Silk, arXiv: 2003.04935.
E. Di Valentino, A. Melchiorri, J. Silk, Nature Astronomy 2020, 4, 196.
G. B. Zhao et al., Nature Astronomy 2017, 1, 627.
S. Peirone, G. Benevento, N. Frusciante, S. Tsujikawa, Phys. Rev. D 2019, 100, 063540.
E. Di Valentino, A. Melchiorri, J. Silk, Phys. Rev. D 2016, 93, 023513.
L. Kazantzidis, L. Perivolaropoulos, arXiv: 1907.03176.
R. Prasad, L. K. Gupta, A. Beesham, G. K. Goswami, A. K. Yadav, Int. J. Geom. Meth. Mod. Phys. 2021, 18, 2150069.
G. K. Goswami, M. Mishra, A. K. Yadav & A. Pradhan, Mod. Phys. Lett. A 2020, 33, 2050086.
G. K. Goswami, A. K. Yadav & B. Mishra, Mod. Phys. Lett. A 2020, 35, 2050224.
N. Singla, A. K. Yadav, M. K. Gupta, G. K. Goswami & R. Prasad, Mod. Phys. Lett. A 2020, 35, 2050174.
S. Kumar, A. K. Yadav, Mod. Phys. Lett. A 2011, 26, 281.
A. K. Yadav, Astrophys. Space Sc. 2011, 335, 565.
A. K. Yadav, Astrophys. Space Sc. 361, 276 (2016).
A. K. Yadav, F. Rahaman, S. Ray & G. K. Goswami, Euro. Phys. J. Plus 2012, 127, 127.
H. Amirhashchi, A. K. Yadav, arXiv:2001.03775.
A. K. Yadav, V. Bhardwaj, Res. Astron. Astrophys. 2018, 18, 64.
R. Prasad, A. K. Yadav, & A. K. Yadav, Euro. Phys. J. Plus 2020, 135, 297.
P. P. Ray, B. Mishra, S. K. Tripathy, Int. J. Mod. Phys. D 2019, 28, 1950093.
B. Mishra, P. P. Ray, S. K. Tripathy, K. Bamba, Mod. Phys. Lett. A 2019, 34, 1950217.
Y. Y. Wang, F. Y. Wang, Mon. Not. Roy. Astron. Soc. 2018, 474, 3516.
Ö. Akarsu, S. Kumar, S. Sharma and L. Tedesco, Phys. Rev. D 2019, 100, 023532.
Ö. Akarsu, J. D. Barrow, N. M. Uzun, arXiv:2009.06517.
Ö. Akarsu, N. Katirci, S. Kumar, R. C. Nunes, B. Ozturk and S. Sharma, arXiv:2004.04074.
Ö. Akarsu, N. Katirci, N. Özdemir, J. A. Vazquez, Euro. Phys. J. C 2020, 80, 1.
V. K. Bhardwaj, M. K. Rana, ·A. K. Yadav, Astrophys. Space Sc. 2019, 364, 136.
A. K. Yadav, V. K. Bhardwaj, P. K. Sahoo, Mod. Phys. Lett. A 2019, 34, 1950145.
A. K. Yadav, A. M. Alshehri, N. Ahmad, G.K. Goswami, M. Kumar, Phys. Dark Uni. 2021, 31, 100738.
A. K. Yadav, V. K. Bhardwaj, Res. Astron. Astrophys. 2018, 18, 64.
P. Biswas, P. Roy, R. Biswas, arXiv: 1908.00408.
D. M. Scolnic et al, Astrophys. J. 2018, 859, 101.
A. G. Riess et al., Astrophys. J. 853, 126 (2018).
H. Amirhashchi and S. Amirhashchi, Phys. Rev. D 2019, 99, 023516.
H. Yu, B. Ratra and F.-Y. Wang, Astrophys. J. 2016, 856, 3.
O. Farooq, F. R. Madiyar, S. Crandall and B. Ratra, Astrophys. J. 2017, 835, 26.
C. E. Cunha et al., Mon. Not. R. Astron. Soc. 2009, 396, 2379.
A. K. Yadav, Euro Phys. J. Plus 2014, 129, 194.
A. K. Yadav, Braz. J. Phys. 2019, 49, 262.
Ö Akarsu, S. Kumar, R. Ayrzakulov, M. Sami & L. Xu, J. Cosmol. Astropart. Phys. 2014, 1, 022.
A. K. Yadav, P. K. Sahoo, V. K. Bhardwaj, Mod. Phys. Lett. A 2019, 34, 1950145.
A. K. Yadav, Res. Astron. Astrophys. 12, 1467 (2012).
A. Pradhan, H. Amirhashchi, Mod. Phys. Lett. A 2011, 26, 2261.
M. P. Hobson, G. P. Efstathiou and A. N. Lasenby, General Relativity: An Introduction for Physicists, Cambridge University Press (2006).
P. Mukherjee, S. Chakrabarti, Euro. Phys. J. C 2019, 79, 681.
D. Rapetti, S. W. Allen, M. A. Amin, R. D. Blandford, Mon. Not. R. Astron. Soc. 2007, 375, 1510.
O. Luongo, Mod. Phys. Lett. A 2013, 28, 1350080.
R. Prasad, M. Singh, A. K. Yadav, A. Beesham, arXiv: 2010.02728.
A. A. Mamon, K. Bamba, Eur. Phys. J. C 2018, 78, 862.
O. Luongo, Mod. Phys. Lett. A 2015, 19, 1350080.
S. Capozziello, R. D’Agostino, O. Luongo, Int. J. Mod. Phys. D 2019, 28, 1930016.
P. K. S. Dunsby and O. Luongo, Int. J. Geom. Meth. Mod. Phys. 2016, 13, 1630002.
M. Visser, Class. Quant. Grav. 2004, 21, 2603.
M. Dunajski, G. Gibbons, Class. Quant. Grav. 2008, 25, 235012.
Z. X. Zhai, M. J. Zhang, Z. S. Zhang, X. M. Liu, T. J. Zhang, Phys. Lett. B 2013, 727, 8.
O. Luongo, Mod. Phys. Lett. A 2013, 28, 1350080.
M. Dunajski,Gen. Relativ. Gravit. 2014, 46, 1814.
C. C. Dantas, A. L. B. Ribeiro, Phys. Rev. D 2016, 93, 043509.
A. Mukherjee, N. Banerjee, Phys. Rev. D 2016, 93, 043002.
L. Tedesco, Eur. Phys. J. Plus 2018, 133, 5.
U. Alam, V. Sahni, T. D. Saini, A. A. Starobinsky, Mon. Not. R. Astron. Soc. 2003, 344, 1057.

Figure 2. The plot of Hubble rate

H (z) / (1 + z)

versus z for

H_{0} = 68.58 \pm 0.84 k m s^{- 1} M p c^{- 1}

Figure 2. The plot of Hubble rate

H (z) / (1 + z)

versus z for

H_{0} = 68.58 \pm 0.84 k m s^{- 1} M p c^{- 1}

Figure 3. Two dimensional contours at

1 σ

2 σ

and

3 σ

confidence regions by bounding our model with joint Pantheon and OHD. The unit of

H_{0}

k m s^{- 1} M p c^{- 1}

Figure 3. Two dimensional contours at

1 σ

2 σ

and

3 σ

confidence regions by bounding our model with joint Pantheon and OHD. The unit of

H_{0}

k m s^{- 1} M p c^{- 1}

Figure 4. The behaviors of q versus z for OHD (left panel) and Pantheon Data (Right panel). The solid gray curve in both panels show the best fit curve of deceleration parameter.

Figure 5. Plot of jerk j versus z for OHD (left panel) and Pantheon Data (Right panel). The solid gray curve in both panels show the best fit curve of jerk parameter.

Figure 6. The behavior of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with OHD

Figure 6. The behavior of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with OHD

Figure 7. The behavior of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with combined OHD and pantheon compilation of SN Ia data

Figure 7. The behavior of

r - s

(left panel) and

q - r

(right panel) plane for the constrained values of model parameters along with combined OHD and pantheon compilation of SN Ia data

Table 1. The summary of numerical analysis

Model parameters	OHD	Pantheon + OHD
$H_{0}$	$68.58 \pm 0.84$	$71.93 \pm 0.58$
${(Ω_{m})}_{0}$	$0.26 \pm 0.010$	$0.272 \pm 0.06$
${(Ω_{Λ})}_{0}$	$0.71 \pm 0.025$	$0.74 \pm 0.09$
${(Ω_{k})}_{0}$	$0.0005 \pm 0.00035$	$0.0006 \pm 0.00028$

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Redshift Drift in the Universe: Theoretical Features and Observational Constraints

Abstract

1. Introduction

2. The model and basic formalism

3. Observational constraints on the model parameters

4. Physical properties of the model

4.1. Deceleration parameter

4.2. Jerk parameter

4.3. Effective energy density and effective pressure

4.4. Statefinder diagnostics

5. Conclusions

References

MDPI Initiatives

Important Links

Subscribe