Comparative Study of Magnetic Properties of (Mn$_{1-x}$A$_x^{IV}$)Bi2Te4 A$_x^{IV}$ = Ge, Pb, Sn

1. Introduction

The interest in investigating magnetic topological insulators (TIs) arise primarily from their potential to manifest the quantum anomalous Hall effect (QAHE) [1,2,3,4]. In the QAHE state, edge conduction occurs in magnetic TIs, which enables the transport of spin-polarised electrons over significant distances without scattering. The remarkable aspect of magnetic TIs is that the realization of the QAHE state does not require an external magnetic field, making them highly applicable in low-power electronics and quantum computing. Among various platforms, the intrinsic antiferromagnetic (AFM) TI MnBi${}_2$Te${}_4$ has emerged as the most promising candidate for investigating the interplay between magnetism and topology, as well as achieving the QAHE state [5,6,7,8,9]. Recent studies have confirmed the feasibility of attaining the QAHE state in thin films of MnBi${}_2$Te${}_4$, demonstrating its transition at considerably higher temperatures compared to magnetically doped TIs [10,11,12].

MnBi${}_2$Te${}_4$ is a layered van der Waals crystal composed of septuple-layer (SL) blocks with each SL block arranged in a Te-Bi-Te-Mn-Te-Bi-Te configuration [13,14]. The magnetic atoms are directly incorporated into the crystal structure. This allows to significantly increase the concentration of magnetic material in TI without disturbing the crystal structure and provides better interaction between magnetic atoms (Mn) and atoms (Bi, Te) on which topological surface states are localised. The magnetic properties of MnBi${}_2$Te${}_4$ turn out to be outstanding among other known magnetic TIs. The material exhibits A-type AFM ordering with Mn magnetic moments aligned ferromagnetically within each SL and antiferromagnetically along the c-axis between adjacent SLs. The Nèel temperature of MnBi${}_2$Te${}_4$ is approximately $24-25$ K [6,9,15,16,17]. The spin-flop transition field is approximately 3.5 T, and the ferromagnetic transition fields range from $7-8$ T [18].

The ability to manipulate the magnetic properties of MnBi${}_2$Te${}_4$ is an intriguing and practically significant area of research. For instance, in pure MnBi${}_2$Te${}_4$, a substantial external magnetic field of several Tesla is required to alter the current direction in the QAHE state, which ideally should be reduced. Currently, several approaches are being developed to achieve control over the magnetic properties of MnBi${}_2$Te${}_4$:

(1)

The first approach involves the insertion of additional (m-1) [Bi${}_2$Te${}_3$] QLs between one [MnBi${}_2$Te${}_4$] SL resulting in the series of compounds MnBi${}_{2m}$Te${}_{3m+1}$ with $m\ge 1$[14,19,20,21,22]. This series includes the homologous phases MnBi${}_2$Te${}_4$ (m=1: 124), MnBi${}_4$Te${}_7$ (m=2: 147), and MnBi${}_6$Te${}_{10}$ (m=3: 16$\overline{10}$), all of which can be classified as ${\mathbb{Z}}_2$ AFM TIs. However, as the number of [Bi${}_2$Te${}_3$] QLs increases, significant changes occur in the magnetic properties. For the 147 phase, T${}_{\mathrm{N}}$ is already 13 K and H${}_{\mathrm{SF}}$ does not exceed 0.3 T. The phase 16$\overline{10}$ possesses an uncertain type of magnetic ordering which can be either AFM or FM, depending on growth conditions and the presence of defects [23,24]. For phases with higher m, the system resembles non-interacting 2D ferromagnets formed by the [MnBi${}_2$Te${}_4$] SL [21].

(2)

The second approach is to substitute Bi atoms with Sb atoms, resulting in Mn(Bi${}_{1-y}$Sb${}_y$)${}_2$Te${}_4$ compounds [25]. This substitution generally leads to an increase in the number of anti-site defects, such as Mn${}_{\mathrm{Bi},\mathrm{Sb}}$ (Mn occupying the position of Bi or Sb atoms) [26,27]. Consequently, this substitution affects the magnetic order of the SL, transforming it from ferromagnetic to ferrimagnetic [18]. By adjusting the growth parameters, it is possible to further increase the number of anti-site defects and induce a transition from antiferromagnetic to ferromagnetic behavior in the ground state [27].

(3)

Another way is to dilute Mn atoms with non-magnetic atoms. The A${}^{\mathrm{IV}}$ = Ge, Pb, Sn elements can be chosen as suitable substituents. There are ternary TI compounds, such as A${}^{\mathrm{IV}}$Bi${}_2$Te${}_4$, with the same $R\overline{3}m$ symmetry group as MnBi${}_2$Te${}_4$ [13,28], allowing for arbitrary ratios of Mn substitution. Several studies [29,30,31,32,33] have demonstrated the synthesis of these crystals and confirmed the absence of additional substitution defects, as in the case of s substitution of Sb for Bi atoms.

The latter approach offers several intriguing advantages. For instance, in manganese tellurides (TeMn), the partial substitution of Mn atoms with nonmagnetic atoms (such as Ge) has been shown to increase the critical temperature of magnetic ordering [34,35]. Furthermore, introducing an additional element into the central layer can reduce structural strains in the crystal lattice. This effect is exemplified by the compound BiSbTeSe${}_2$, in which the combination of four elements results in an enhanced surface conductivity [36,37]. This suggests that it may be possible to produce higher-quality crystals of MnBi${}_2$Te${}_4$-based magnetic TI through the partial substitution of Mn atoms with nonmagnetic elements. In general, such approach may have promise for further study and exploration.

In this study, we investigated the magnetic properties of (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_2$Te${}_4$ compounds with substitution of Mn atoms by A${}^{\mathrm{IV}}$ = Ge, Pb, Sn atoms. Hereafter, the concentration x refers to the molar ratio of A${}^{\mathrm{IV}}$/(A${}^{\mathrm{IV}}$+Mn). Crystals with nominal concentrations x equal to 10%, 20%, 50%, 60%, and 80% were synthesized. Using SQUID magnetometry, we analyzed various magnetic properties including the type and temperature of magnetic ordering, magnetic saturation and spin-flop transition fields for all samples. Additionally, for the (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ sample with a nominal Pb concentration of 10%, which exhibited increased critical parameters, we conducted ARPES studies. These studies allow us to estimate the local magnetic ordering temperature by analyzing the temperature-dependent changes in the electronic structure, following the approach described in [17].

2. Materials and Methods

The bulk crystals of doped MnBi${}_2$Te${}_4$ (i.e. (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_2$Te${}_4$ where A${}^{\mathrm{IV}}$ = Ge, Pb, Sn) were prepared by a modified Bridgman method [38,39]. The elementary Mn, Bi, Te, Ge, Pb, Sn of 4N purity were loaded into conically shaped quartz ampoules and sealed under vacuum 10${}^{-2}$ torr. The charge was synthesized by heating the ampoule to 1050 ${}^{\circ }$C directly in the growth furnace. The compositions were taken according to proportions (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_2$Te${}_4$$+2\times$Bi${}_2$Te${}_3$. After a day of homogenization the ampoule was transferred to the cold zone (600 ${}^{\circ }$C) with a speed 10 mm/day.

Thin films obtained from the ingot were initially characterized by XPS (X-ray tube with Al cathode, $h\nu =1486$ eV). It is important to note that the characterization was performed only for the film surface, as oriented crystals were required for SQUID magnetometry measurements. The total molar fraction of Mn and A${}^{\mathrm{IV}}$ = Ge, Pb, Sn exceeded 10%, indicating the prevalence of the 124 phase. Magnetic properties (i.e. the temperature dependences of the magnetic susceptibility $\chi \left(T\right)$ and magnetization as a function of applied magnetic field M(H) at various temperatures) were assessed using a Quantum Design MPMS 3 SQUID VSM instrument. The measurements were conducted at temperatures as low as 1.8 K, with an external magnetic field range of ±7 T and a sensitivity of $1\times {10}^{-8}$ emu at 0 T. The samples were oriented such that the external magnetic field was applied perpendicular to the crystal surface (0001), aligning with the crystallographic axis c.

ARPES measurements of a single crystal of (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ (Pb 10% nominally) were performed at the Laser ARPES facility of the HiSOR synchrotron centre [40]. A clean surface was prepared by tape-cleavage inside a vacuum chamber with a pressure below 10${}^{-9}$ torr. The measurements were performed using a photon energy of $h\nu =6.3$ eV with liquid helium cooling. The base pressure during the measurements remained below $5\times {10}^{-11}$ torr. To obtain the dispersion dependencies at a certain temperature (temperature dependence), the sample was heated by means of an integrated heating element in the manipulator with keeping the sample position unchanged.

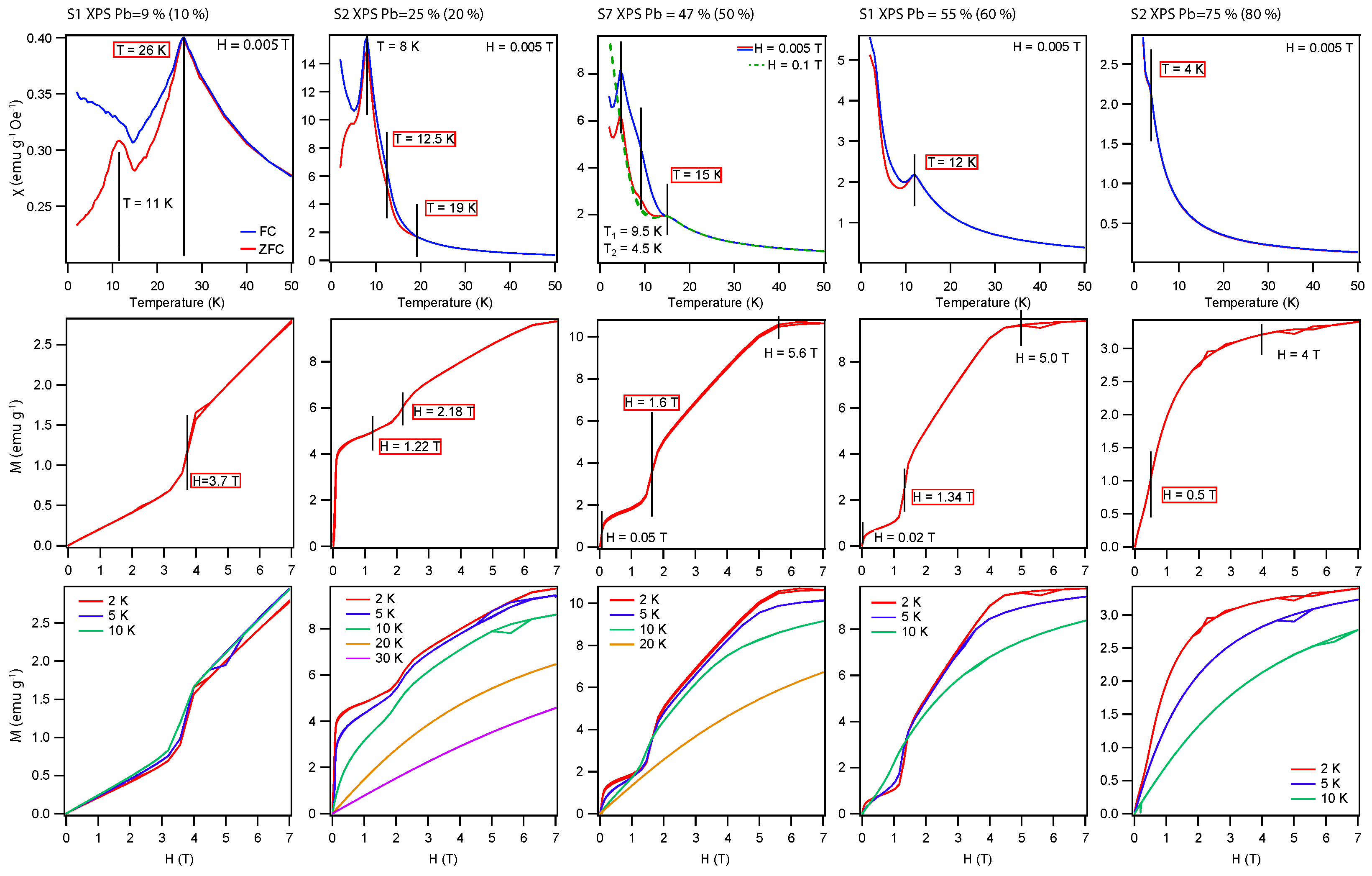
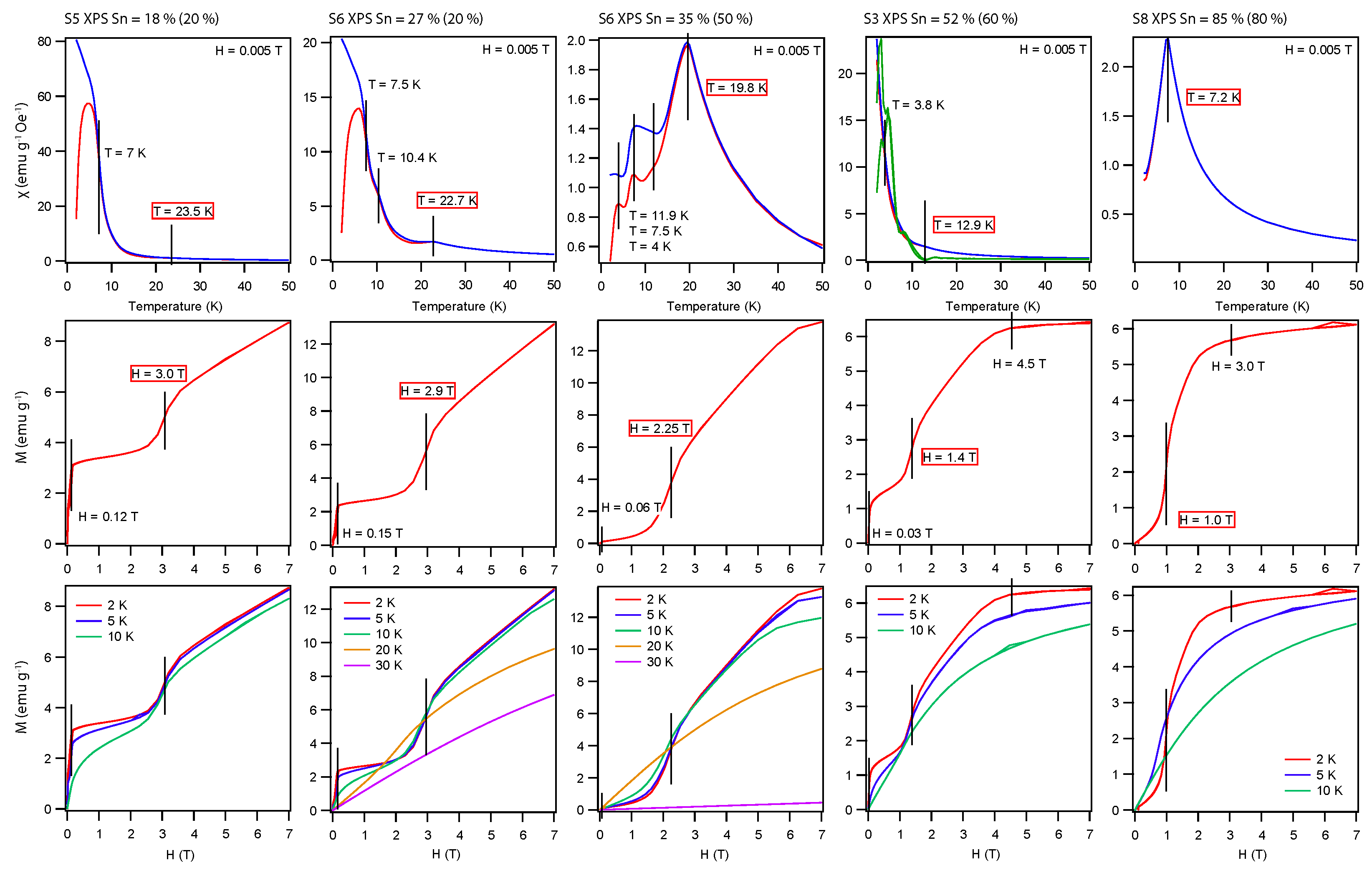
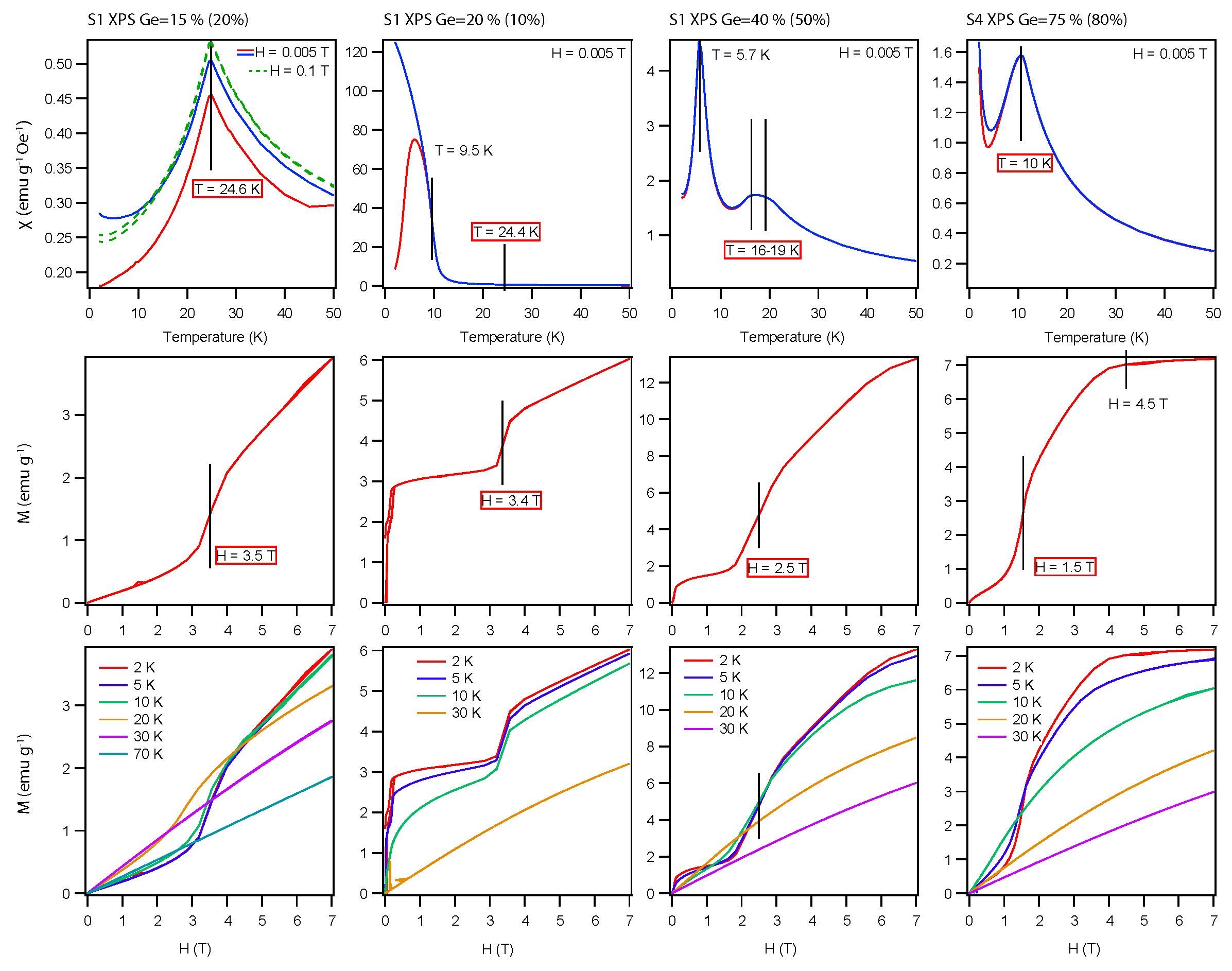
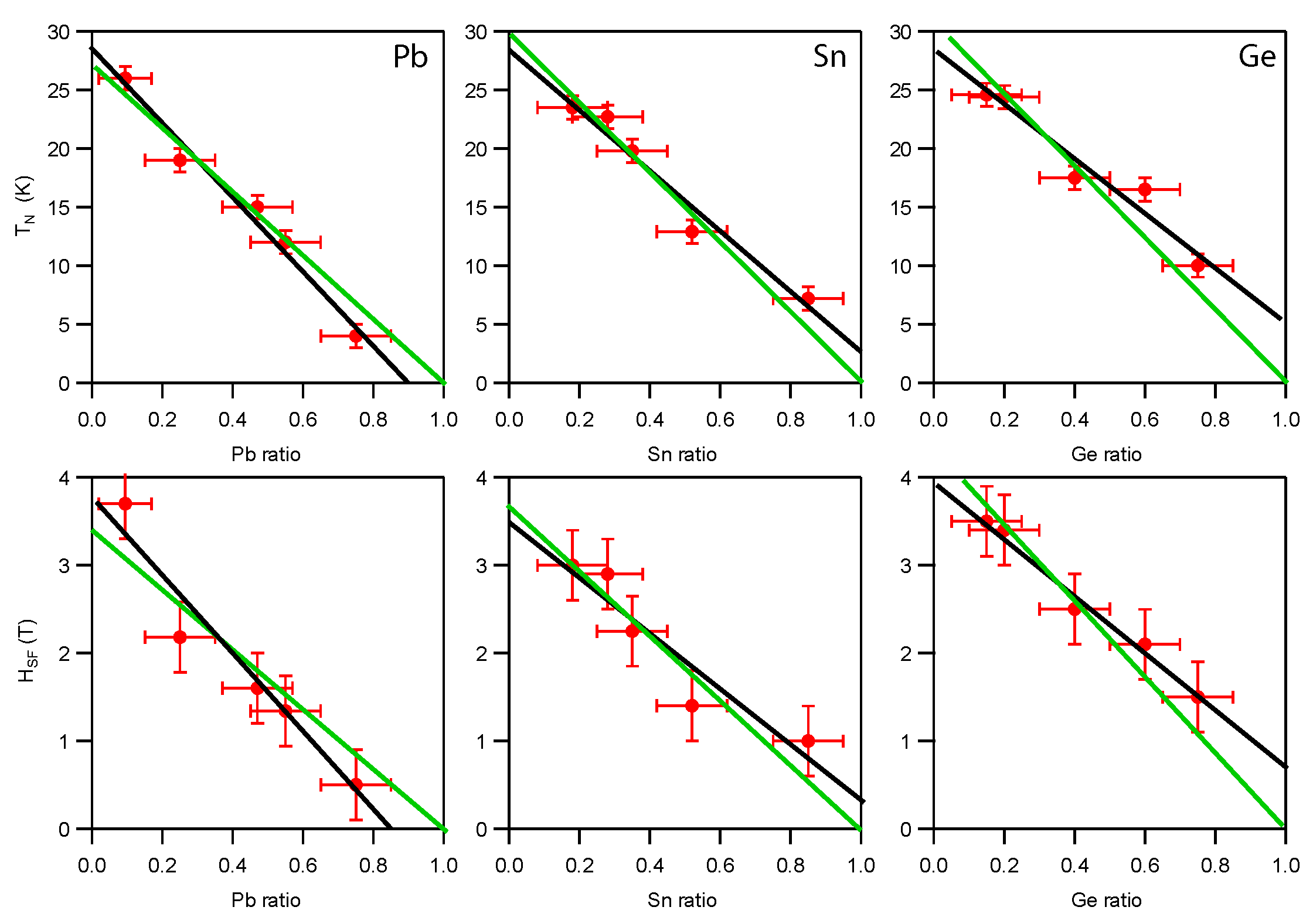
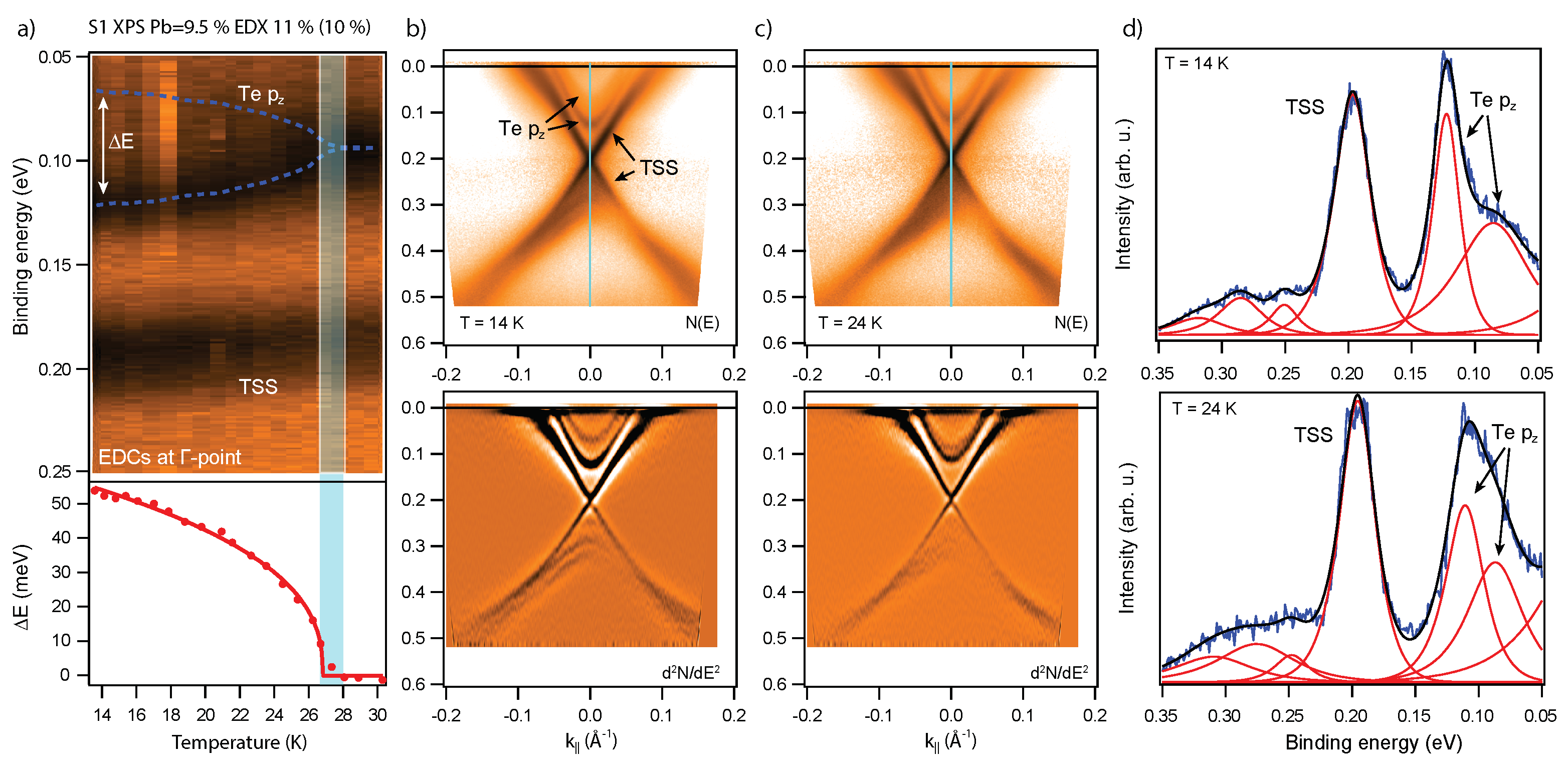
3. Results and Discussion

Figure 1 depicts the investigation of magnetic properties in (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ samples, specifically the magnetic susceptibility as a function of temperature, $\chi \left(T\right)$, and the magnetization as a function of applied magnetic field, M(H). The nominal and actual concentrations of Pb are indicated at the top of the figure. The actual concentrations were determined by XPS method for the cleaved (0001) surface of the single-crystal. It is important to note that the crystal may exhibit volume inhomogeneity with regions containing excess/deficient elements or regions with different phases of the homologous series (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_{2m}$Te${}_{3m+1}$. The SQUID method, being sensitive to bulk properties, can reveal additional features in the measurements, such as multiple critical temperatures, multiple spin-flop transitions, or ferromagnetic hysteresis loops. It is expected that the different phases of the (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_{2m}$Te${}_{3m+1}$ series do not influence each other within the crystal volume, and their magnetization signals are superimposed. The samples investigated in this study exhibited various combinations of magnetization signals arising from different phases. In each sample the highest observed magnetic transition temperature and the maximum spin-flop transition field were attributed to the 124 phase. When the M(H) or $\chi \left(T\right)$ signals were relatively weak in the examined region, their derivatives ($dM\left(H\right)/dH$ and $d\chi \left(T\right)/dT$) were analyzed to identify distinctive features in the dependencies.

The sample with a nominal Pb concentration of 10% exhibits a $\chi \left(T\right)$ dependence that reveals the Nèel temperature of 26 K. Below this temperature, a divergence is observed between the magnetic susceptibility curves measured in ZFC conditions (red curve) and FC conditions (blue curve). This divergence arises from the presence of individual [MnBi${}_2$Te${}_4$] SL inside the crystal. The magnetic moments of these SLs can exhibit a disordered orientation along the crystallographic axis c, which corresponds to the easy magnetization axis [21]. Another AFM transition is observed at a temperature of approximately 11 K, which likely corresponds to the phase 16$\overline{10}$. Analysis of the magnetization dependence M(H) revealed that the maximum (i.e. corresponding to the 124 phase) spin-flop transition field for this sample is determined to be 3.7 T. In the low-field region another transition is detected at approximately 0.15 T (can be seen when zooming in), which rather corresponds to the 16$\overline{10}$ phase and is consistent with the results obtained from the $\chi \left(T\right)$ data.

At higher concentrations of Pb (20% nominally), the Nèel temperature of phase 124 decreases. In the investigated sample, other phases were present within the volume, and their signals dominated the measurements. However, by analyzing the derivative $d\chi \left(T\right)/dT$, it was possible to determine the Nèel temperature associated with phase 124 which is approximately 19 K. Additional AFM transition peaks were observed at temperatures of 12.5 K and 8 K. The Nèel temperature of 12.5 K is likely related to phase 147, where the Mn layer is partially diluted with Pb atoms, resulting in a slightly lower temperature compared to phase 147 without Pb atoms (13 K) [21]. However, this transition temperature may be characteristic of crystal regions with a high substitution of Mn atoms by Pb atoms (approximately $50-60$%). Furthermore, several spin-flop transition fields were determined from the magnetization dependence M(H): 1.22 T and 2.18 T. Hence, the investigated sample likely contains two phases of 124 with different Pb concentrations.

In the sample with a Pb concentration of 47% (50% nominally), the Nèel temperature for the 124 phase is approximately 15 K. The presence of other phases is also observed in the sample. However, in measurements with a 0.1 T applied magnetic field, the signals from these phases become less pronounced, indicating that they correspond to phases 147 and higher. The spin-flop transition field for the 124 phase is determined to be 1.6 T. Additionally, magnetization saturation is observed at 5.6 T at this concentration. For the previous samples, the saturation fields were outside the measured range of ±7 T. For the sample with a nominal Pb concentration of 60%, the Nèel temperature is 12 K, the spin-flop transition field is 1.34 T, and the saturation field is approximately 5 T. At a Pb concentration of 75%, the Nèel temperature decreases to 4 K, the spin-flop transition field is 0.5 T, and the saturation field is 4 T. The obtained data clearly demonstrates that the AFM type of ordering is maintained for 124 phase across all Pb concentrations up to 75%.

It is noteworthy that the AFM peak in the $\chi \left(T\right)$ dependence and the step observed in the spin-flop transition region of the M(H) dependence exhibit sharp characteristics. This suggests a homogeneous level of Mn substitution within the investigated samples. In cases where a certain range of substitution concentrations exists, one would expect a broader and more extended peak (step). Therefore, it is likely that the samples possess discrete values of substitution concentration, which can be estimated through XPS measurements conducted on the sample surface.

Further, we studied (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_2$Te${}_4$ samples where Mn atoms were substituted with Sn and Ge atoms (Figure 2 and Figure 3). Overall, similar trends as observed for (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ samples are preserved for (Mn${}_{1-x}$Sn${}_x$)Bi${}_2$Te${}_4$ and (Mn${}_{1-x}$Ge${}_x$)Bi${}_2$Te${}_4$: the critical temperature and spin-flop transition field gradually decrease, while the AFM type of magnetic ordering is maintained. However, some peculiarities may occur due to deficiencies of the investigated crystals. The samples also exhibit different phases from the homologous series (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_{2m}$Te${}_{3m+1}$.

No additional features were found in the $\chi \left(T\right)$ and M(H) dependencies for (Mn${}_{1-x}$Sn${}_x$)Bi${}_2$Te${}_4$ compared to (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$. However, when Mn is substituted with Ge in the sample with a nominal concentration of 20%, an additional feature appears in the $\chi \left(T\right)$ dependence. Unusually, a divergence between the ZFC and FC curves is observed both above and below the Nèel temperature. We attribute this to the presence of the MnTe phase in the studied sample, which also exhibits the AFM type of magnetic ordering with a critical temperature up to 300 K [41]. Interestingly, these features disappear when measurements are conducted with the application of a larger field (0.1 T). The observed spin-flop transition at a field of 3.5 T corresponds to the 124 phase. This is supported by the absence of this transition in the M(H) dependence above 30 K (see Figure 3, bottom line). Furthermore, in the (Mn${}_{1-x}$Ge${}_x$)Bi${}_2$Te${}_4$ sample with a nominal Ge concentration of 50%, the AFM transition peak appears relatively broad compared to other samples where the peaks are sharper. This indicates that the Ge concentration in this particular sample varies within a certain range. As a result, a range of Nèel temperatures from 16 to 19 K is observed for this sample.

To compare the obtained data, the experimental values of the Nèel temperature (T${}_{\mathrm{N}}$, upper line) and spin-flop transition field (H${}_{\mathrm{SF}}$, lower line) are plotted as a function of the concentration of A${}^{\mathrm{IV}}$ = Ge, Pb, Sn in Figure 4. As mentioned previously, the concentration was estimated for the surface of single crystals, which may have slight variations compared to the average element concentration in the bulk. However, for the majority of samples, a relatively sharp AFM peak is observed, suggesting a relatively homogeneous distribution of A${}^{\mathrm{IV}}$ = Ge, Pb, Sn within the volume. This allows evaluations to be carried out using XPS from surface of a single-crystal. Nevertheless, a sufficiently large error interval of ±0.05 fraction was chosen for the concentration, which is expected to include the actual concentration value. The error in determining the Nèel temperature is ±1 K, and the error in determining the spin-flop transition field is ±0.4 T. The observed changes in the magnetic parameters for samples with adjacent concentrations are generally larger than the associated errors.

A clear monotonic decrease of T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$ with increasing substitution concentration can be observed for all elements. The experimental data points can be approximated by linear dependencies [30]. The black line represents a linear approximation of the experimental points, while the green line takes into account the expectation that the Nèel temperature and spin-flop transition field reach zero at 100% of A${}^{\mathrm{IV}}$ = Ge, Pb, Sn.

In the case of (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$, it is evident that the black line reaches zero for both T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$ at Pb concentrations around $80-90$%. This suggests that Mn-doped PbBi${}_2$Te${}_4$ does not exhibit magnetic properties at Mn concentration $(1-x)<15-20$%. Thus, it is important to note that a doping level of approximately 2% (the ratio of impurity in total, which corresponds to a Mn fraction of $(1-x)\approx 15$% in the notation used) appears to be sufficient for TIs to demonstrate magnetic properties and transition to the QAHE state, as demonstrated in the case of Cr${}_{0.1}$(Bi,Sb)${}_{1.9}$Te${}_3$[42]. This difference could be attributed to the fact that in magnetically doped TIs, the magnetic impurity replaces Bi atoms in both layers, resulting in close proximity of magnetic atoms. In the case of (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$, however, Mn atoms preferentially replace Pb in the central layer, leading to weaker interaction between Mn atoms across the layers, which prevents the formation of magnetic order.

Regarding (Mn${}_{1-x}$Sn${}_x$)Bi${}_2$Te${}_4$ and (Mn${}_{1-x}$Ge${}_x$)Bi${}_2$Te${}_4$, the approximation reveals non-zero values of T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$ even at zero Mn concentration. This could indicate either (i) the possibility of nonlinear behavior in the region of high Sn/Ge concentration, resulting in more rapid decrease of T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$ towards zero in that region, or (ii) a potential overestimation of the Sn/Ge concentration in the estimations obtained using XPS from surface of a single-crystal.

From the analysis of the obtained dependencies, it can be observed that the slope of the approximating (black) lines is different for different elements. The steepest slope is observed for (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$, followed by (Mn${}_{1-x}$Sn${}_x$)Bi${}_2$Te${}_4$, and the smallest slope is seen for (Mn${}_{1-x}$Ge${}_x$)Bi${}_2$Te${}_4$. This indicates that the magnetic parameters change at different rates when Mn is substituted by the corresponding elements. This discrepancy could be attributed to the different rates of increase in the crystal cell size for the different elements. As PbBi${}_2$Te${}_4$ has the largest cell size among the three compounds, the change in cell parameters is likely to be most significant for (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$. Hence, the magnetic properties are influenced by the magnetic dilution effect and the changes in cell parameters, as also was analyzed in a previous study [30,43].

Another notable feature is that, based on the linear approximation at zero substitution concentration (i.e., pure MnBi${}_2$Te${}_4$), the expected values for T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$ are approximately $27-30$ K and $3.5-4$ T, respectively. These values are higher than the experimentally measured values for pure MnBi${}_2$Te${}_4$: T${}_{\mathrm{N}}$ = 24.5 K and H${}_{\mathrm{SF}}$ = 3.5 T. Indeed, for (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ with a nominal Pb concentration of 10%, the critical parameters exceed those of pure MnBi${}_2$Te${}_4$. These results suggest a non-monotonic dependence of the magnetic parameters in the low Pb concentration region. Specifically, adding a small amount of Pb to pure MnBi${}_2$Te${}_4$ leads to an increase in T${}_{\mathrm{N}}$ and H${}_{\mathrm{SF}}$, which then reach a maximum value before starting to decrease.

Hence, the inclusion of a small amount of Pb enhances the magnetic properties of the system. Several explanations can be proposed for this phenomenon. The presence of Pb atoms can decrease the occurrence of Mn${}_{\mathrm{Bi}}$ anti-site defects. In this case Pb atoms occupy the Bi positions instead of Mn since Pb${}_{\mathrm{Bi}}$ anti-site defects may be more energetically favorable due to the similar sizes of Bi and Pb atoms. Consequently, the ferrimagnetic properties of the [MnBi${}_2$Te${}_4$] SL can be mitigated. Additionally, the introduction of a small amount of impurity enables structural relaxation, resulting in a more favorable ordering of Mn atoms in the central layer. The obtained results provide evidence supporting such behavior for (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$. In general, similar enhancements in magnetic properties can be expected when Mn is substituted with Sn or Ge.

For the (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ sample with a nominal concentration of 10%, which exhibited increased magnetic parameters, the temperature-dependent changes in the electronic structure near the Néel temperature region were investigated using ARPES (Figure 5). The analysis of the splitting of Te $p_z$ states can provide insight into the local magnetic properties of the MnBi${}_2$Te${}_4$-related system [17]. Figure 5a illustrates the temperature-dependent distribution of states at the $\Gamma$-point. Similar to pure MnBi${}_2$Te${}_4$, a splitting of the Te $p_z$ states at the edge of the conduction band is observed (indicated by blue dashed lines). The lower part of the panel presents the dependence of the splitting [$\Delta E\left(T\right)$] of this state. The experimental data points were fitted with a power law: $\Delta E\sim {(1-T/T_0)}^{\beta }$, where $\beta$ is the critical exponent and $T_0$ is the onset temperature of the splitting. The obtained values are $T_0=26.6$ K and $\beta =0.38$, which is close to the critical exponent for the 3D Heisenberg case.

In Figure 5b, the dispersion relations measured at 14 K are presented. Panel d (top part) displays the decomposition of the EDC at the $\Gamma$-point into spectral components. The splitting of the Te $p_z$ states is clearly observed. Notably, even at T = 24 K (panel c), the states remain split, although the splitting becomes smaller. This can be seen from the EDC decomposition in panel d (bottom part). Overall, the obtained data provide clear evidence for an elevated magnetic ordering temperature of the 124 phase in (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ at a Pb concentration of approximately 10%.

4. Conclusions

A series of (Mn${}_{1-x}$A${}_x^{\mathrm{IV}}$)Bi${}_2$Te${}_4$ samples with different levels of Mn substitution by nonmagnetic A${}^{\mathrm{IV}}$ = Ge, Pb, Sn elements was studied in this work. Overall, similar trends were observed for all elements: the magnetic ordering temperature and spin-flop transition field decreased with increasing A${}^{\mathrm{IV}}$ = Ge, Pb, Sn concentration for the 124 phase. The magnetic ordering remained AFM for all substitution levels. However, different rates of change in the magnetic parameters were observed for different elements, with the highest rate for Pb, followed by Sn, and the lowest for Ge. This behavior can be attributed to the combined effects of magnetic dilution and lattice parameter increase, which is most pronounced in the (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ compound. Furthermore, the linear approximation of the experimental data indicated that pure MnBi${}_2$Te${}_4$ could exhibit higher values of the critical parameters than those observed experimentally. This suggests a potential non-monotonic behavior of the magnetic parameters at low substitution concentrations and the possibility of enhancing the magnetic properties through the doping of MnBi${}_2$Te${}_4$ with a small amount of nonmagnetic impurity. Indeed, we found (Mn${}_{1-x}$Pb${}_x$)Bi${}_2$Te${}_4$ sample with a nominal concentration of 10% that exhibited higher critical parameters compared to MnBi${}_2$Te${}_4$, with T${}_{\mathrm{N}}\approx 26$ K and H${}_{\mathrm{SF}}\approx 3.7$ T. The increased Nèel temperature was further confirmed through the analysis of electronic structure changes using the ARPES method.