1. Introduction
There have been many public discussions about issues related to prize money distributions in professional snooker [
1], or whether the tour is perhaps too UK-centric. To address these issues more quantitatively, a detailed analysis of snooker prize money rankings is presented here. In particular, this analysis focuses on (1) how dominated the rankings are by the top players, and (2) the share of prize money earned by UK players. Seasonal ranking data over a time range of more than four decades (1980-2023) is considered. These analyses and results aim at providing a more objective and quantitative basis for any further discussions on the mentioned issues.
2. Methods
2.1. Data
All data was obtained online from
CueTracker [
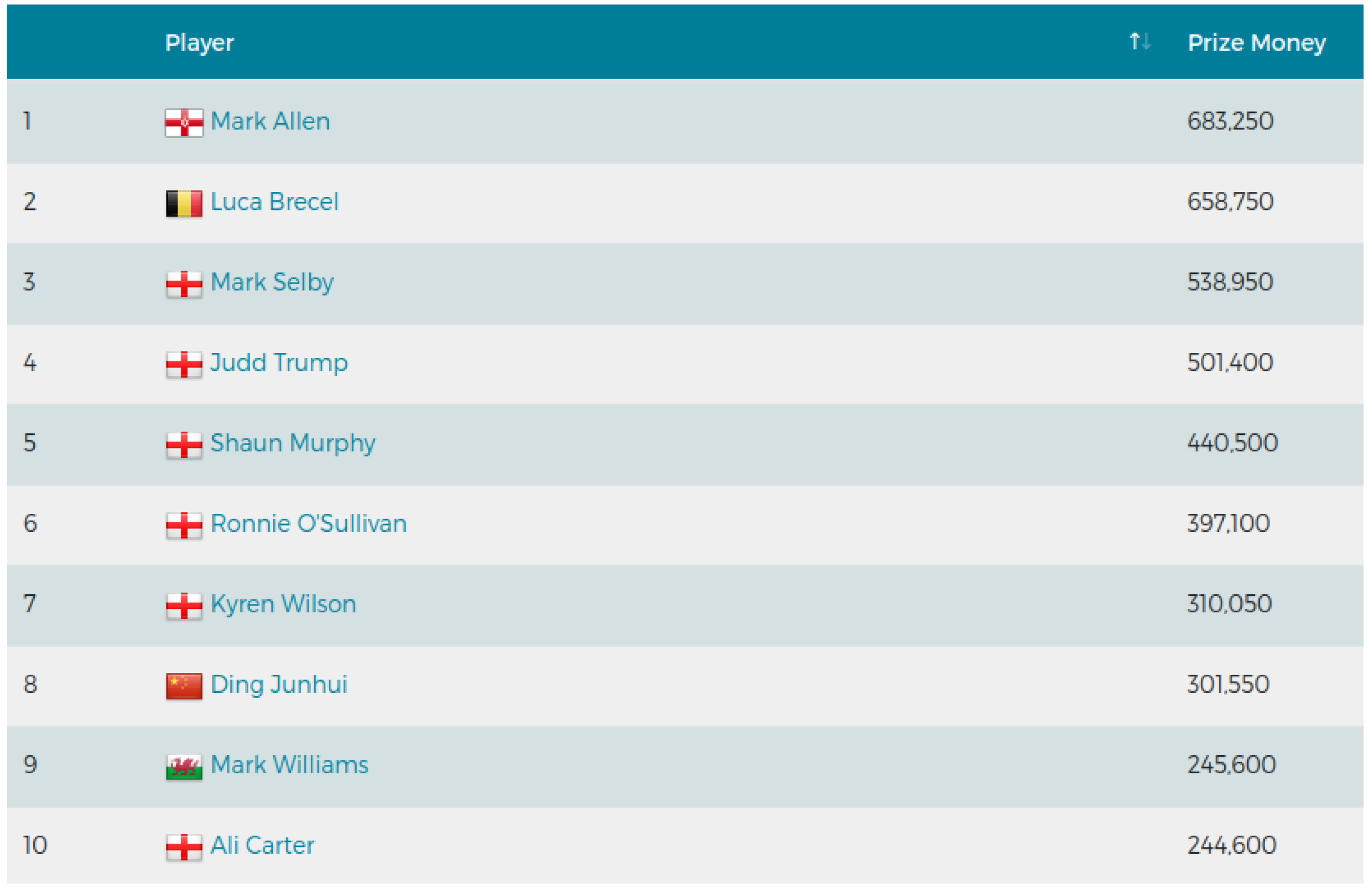
2]. In particular, the prize money ranking at the end of each season starting from the 1980-1981 season up to and including the most recent completed season (2022-2023) were used. For each season, the full list of players who earned any prize money in a professional tournament during that season (ranked from largest to smallest amount) was retrieved. To illustrate,
Figure 1 shows the top 10 of the prize money ranking for the 2022-2023 season.
In addition, a list of the total number of professional tournaments held in each season was retrieved. Besides presenting various basic statistics such as averages and min-max ranges, the two main results are based on calculating an 80% rank and performing a t-test, respectively. These analyses are explained in detail next.
2.2. 80% Rank
As a measure of how much the rankings are dominated by the top players, an
80% prize money rank, or simply referred to as an
80% rank here, is calculated for each season. The 80% rank is directly related to the Pareto principle, more commonly known as the 80-20 rule [
3]. This principle is based on the observation that, for example, roughly 80% of the wealth of a country is owned by the (richest) 20% of people, or 80% of the revenue of a company is generated by 20% of its customers. To find out whether this principle also holds for snooker rankings, one can ask what percentage of the (top) players it takes to earn 80% of the available prize money.
To calculate the 80% rank for a given prize money ranking, first express each player’s earnings as a percentage of the total amount of prize money earned. Next, add up these percentages, starting at rank 1 and going down the ranking (i.e., up in rank number), until this subtotal becomes equal to or larger than 80%.
Table 1 shows a simple (hypothetical) example with just ten players, where the 80% rank (indicated in blue) is equal to four.
Finally, calculate a relative 80% rank by expressing the (absolute) 80% rank as a percentage of the length of the full ranking. In the example above, the relative 80% rank would be 40% (rank four out of a total of ten players). In other words, it takes the top 40% of players to earn 80% or more of the available prize money.
2.3. t-Test
To determine if (and how much) the rankings are dominated by players from the UK, the percentage of players from the UK (i.e., from England, Scotland, Wales, or Northern Ireland) is compared to the percentage of available prize money that is earned by those UK players in each season. A
t-test [
4] is then performed to determine whether the averages (over the 43 seasons considered) of these two percentages are statistically significantly different or not.
The result of a t-test is generally presented in the form of a p-value, which is calculated from the actual data. This p-value indicates the probability that the difference between two sample averages is at least as large as observed in the actual data, under the hypothesis that the two samples come from the same underlying probability distribution. If the calculated p-value is very small, e.g. less than 1% (0.01), then this hypothesis can be rejected with high confidence, and the sample averages can be considered to be statistically significantly different.
All data analyses presented here were performed with the
R language for statistical computing [
5].
3. Results
3.1. Number of Tournaments
Figure 2 shows the number of professional tournaments held in each season for the four decades considered. This number fluctuates between 15 and 35, but without any particular trend.
3.2. Total Prize Money
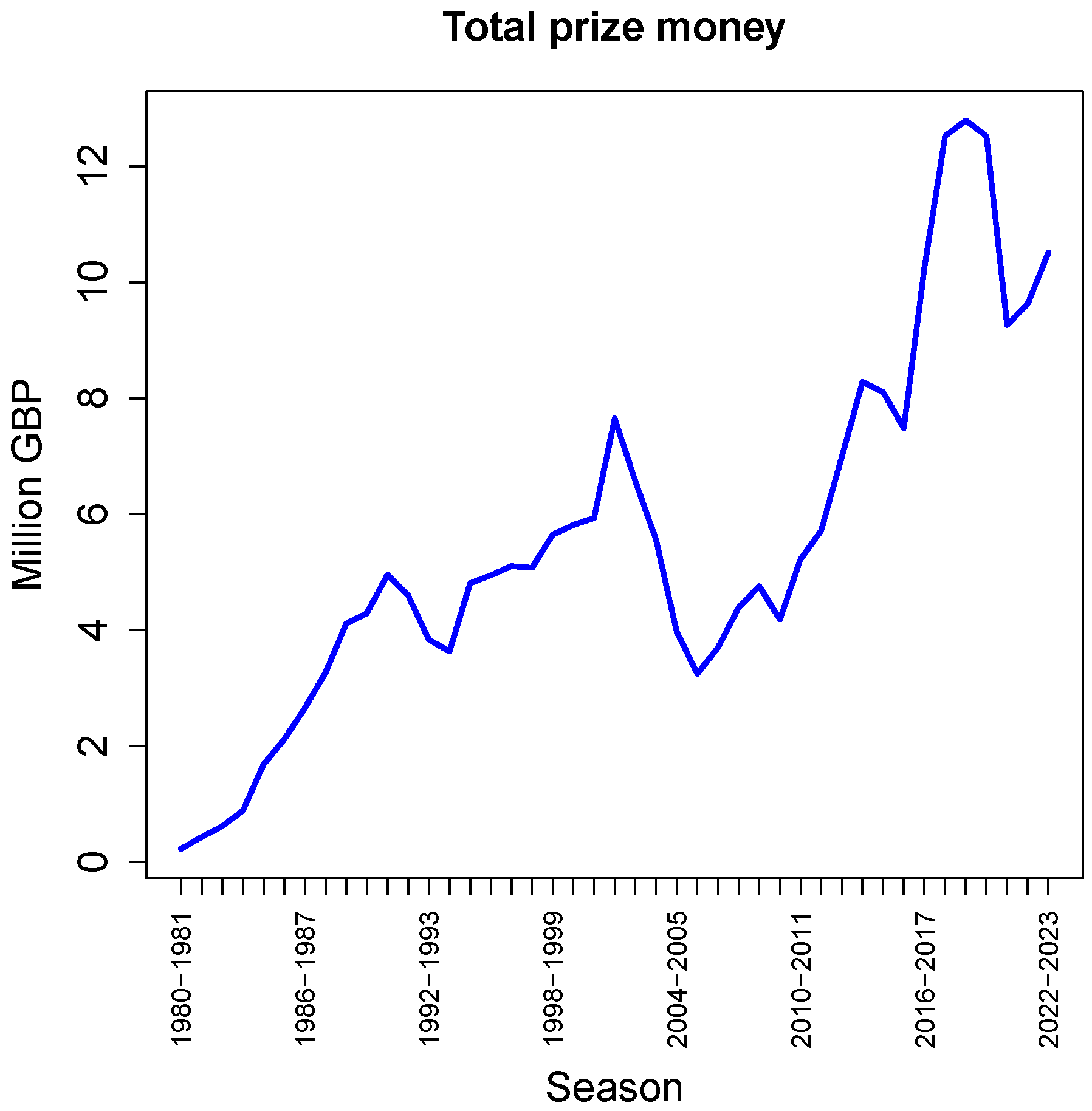
Figure 3 shows the total amount of prize money earned in each season (combined over all players), in million GBP. There clearly is an overall upward trend, but with two notable exceptions: shortly after the turn of the millennium, and in recent years as a result of lockdowns and other restrictions.
3.3. Number of Players
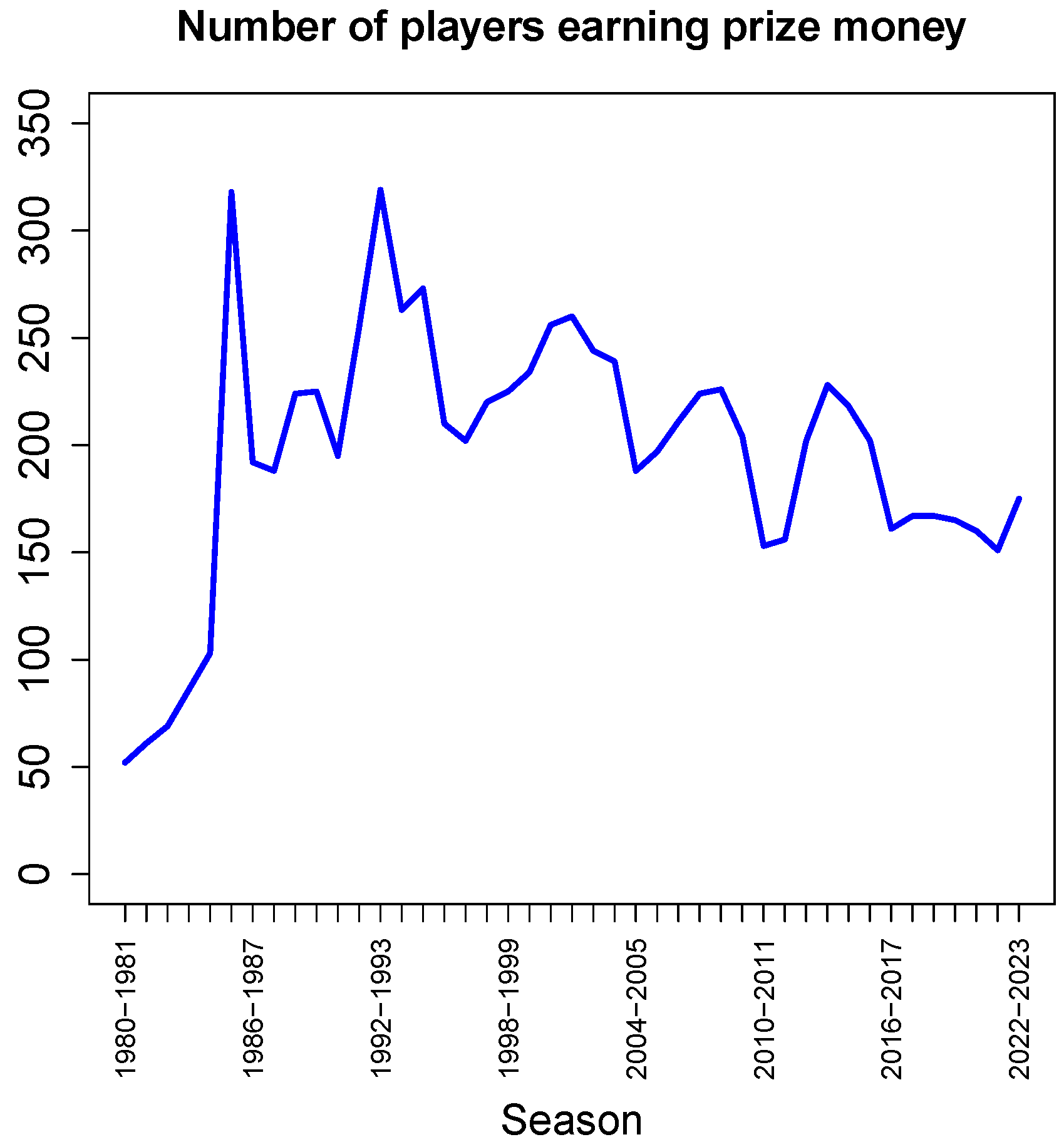
Figure 4 shows the number of players that have earned any prize money in a professional tournament in a given season (no matter how much or little). After a drastic increase in the early 1980s, the number has steadily declined again, but with some fluctuations.
3.4. Player Earnings Range
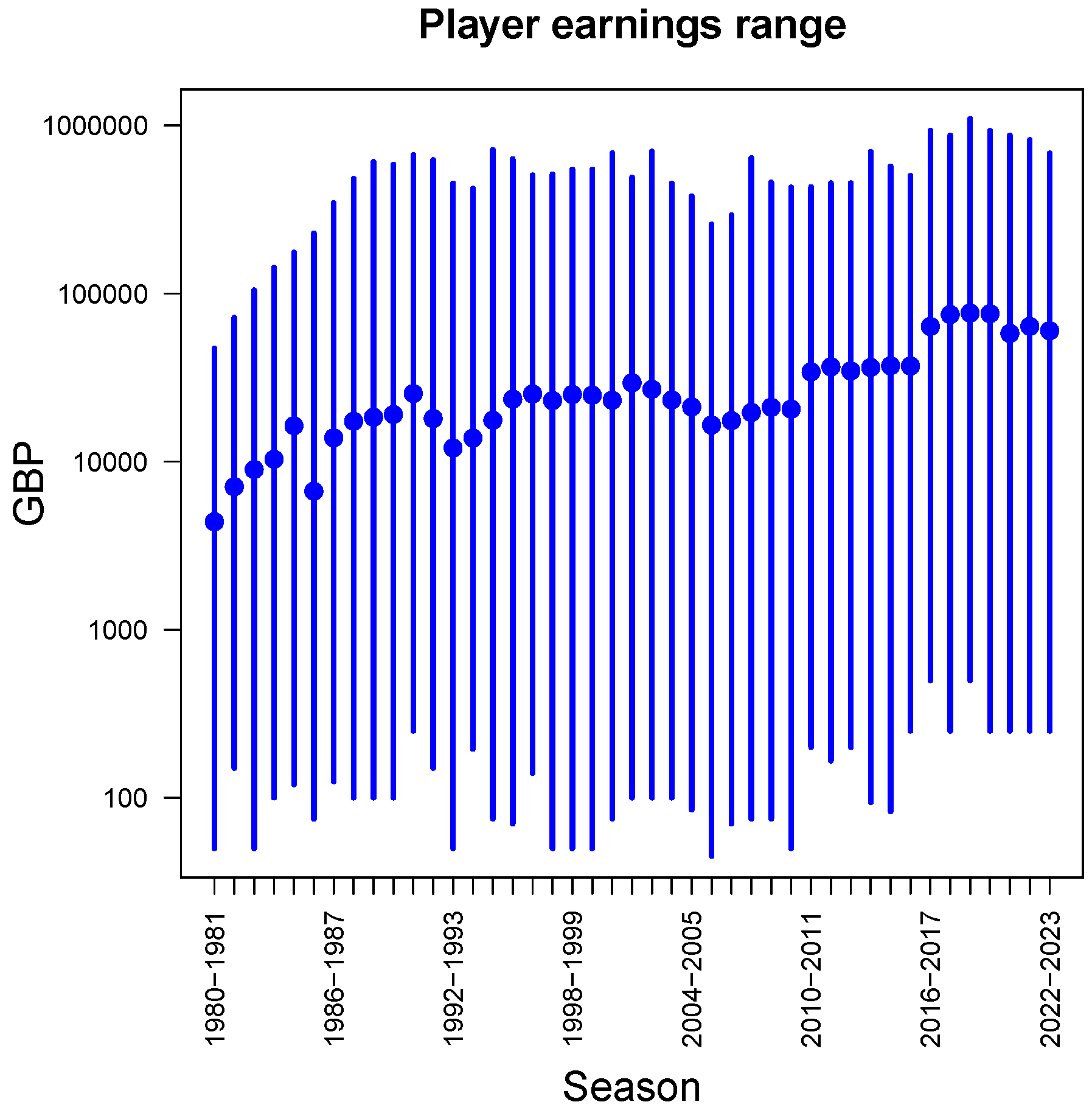
Figure 5 shows the average (dots) and range (bars) of prize money earned by individual players in each season. These amounts range from a minimum of 50 GBP to a maximum of just over one million GBP. Note that the vertical axis is on a
logarithmic scale: every next value going up along the vertical axis is
ten times larger than the previous one. Therefore, although the fluctuations at the low and high ends of the range seem visually similar, in absolute value they are several orders of magnitude larger at the high end. The average amount of prize money earned per player (dots) has increased by about one order of magnitude, from around 5,000 to around 50,000 GBP, over the four decades considered.
3.5. Prize Money Distribution
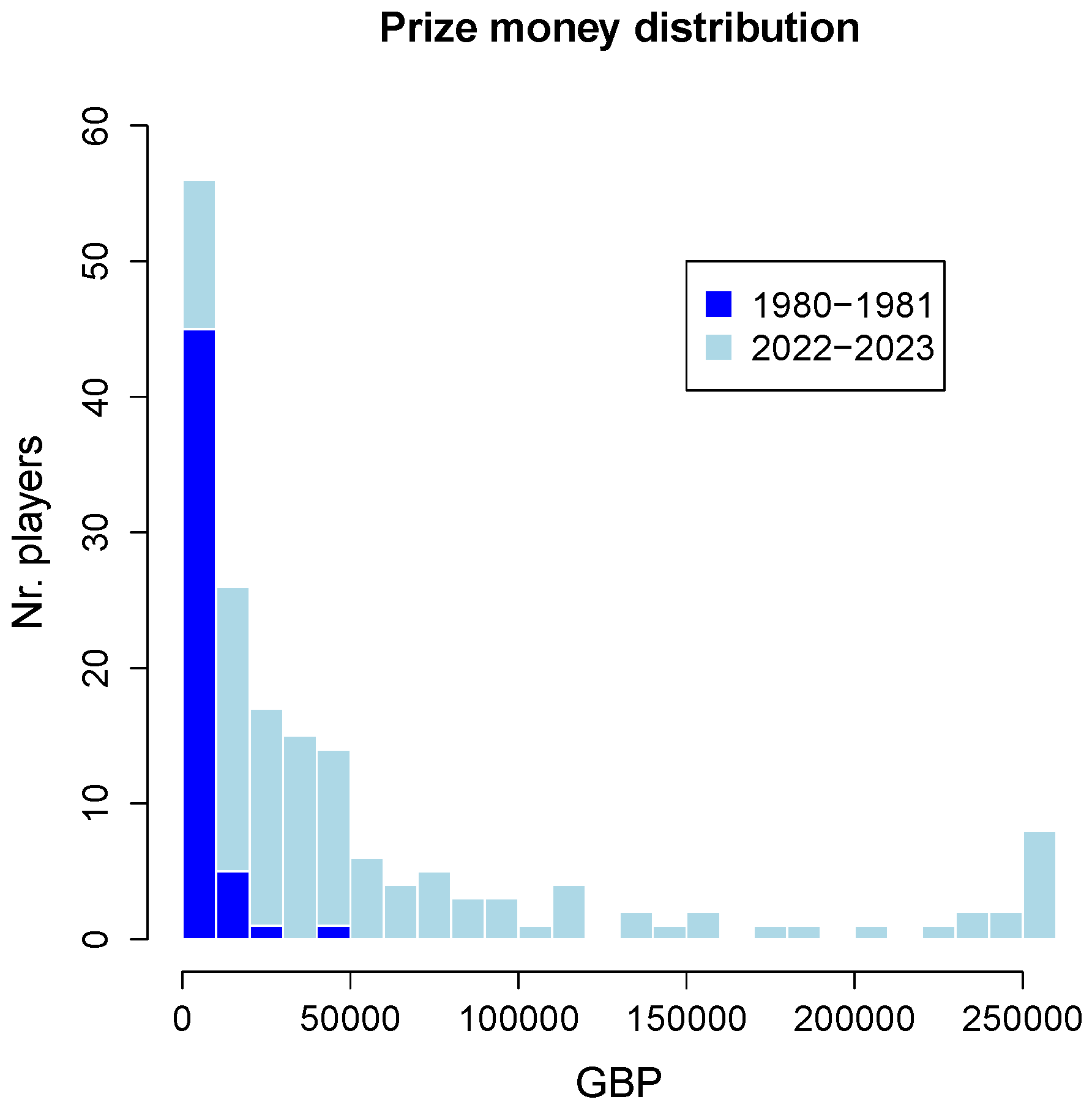
Given the highly skewed distribution of prize money among the players, though, with many players earning very little and a few players earning a large amount, a simple average is unfortunately rather meaningless.
Figure 6 shows these skewed distributions in a histogram for the first season (1980-1981) and the last season (2022-2023) considered. The bin width is 10,000 GBP, with the rightmost bar representing the eight players earning more than 250,000 GBP during the most recent season (see the image of the top ten in the
Section 2 above). Note that all presented data is for
actual prize money earned,
not including the 20,000 GBP minimum income guarantee introduced in the last season.
3.6. 80% Rank
With such a skewed distribution, a more informative statistic (instead of a simple average) is a measure of how much a prize money ranking is dominated by the top players. One such measure is the 80% rank introduced in
Section 2.
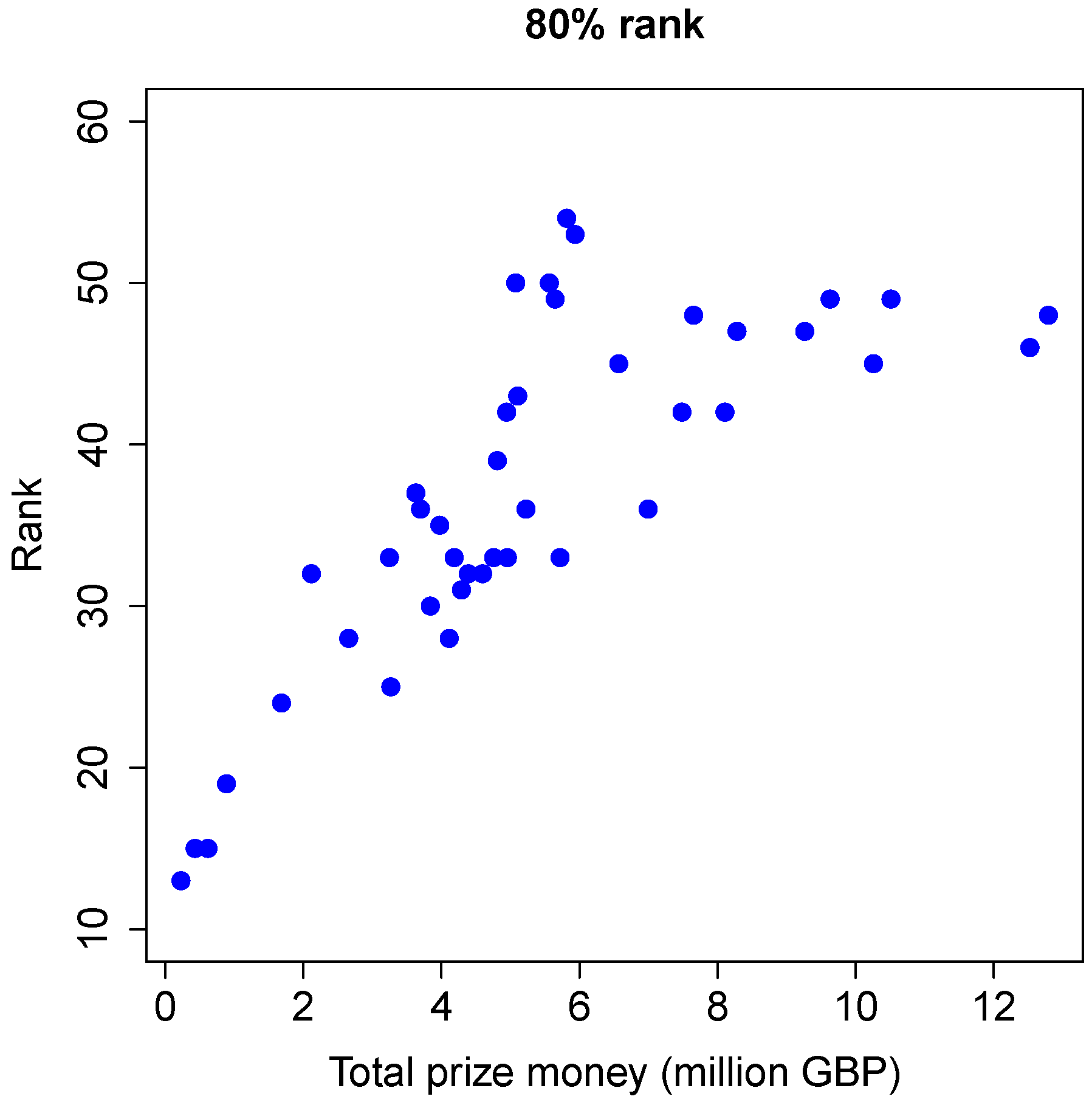
Figure 7 shows these 80% ranks (vertical axis) against the amount of available prize money (horizontal axis) for each season. Clearly there is an upward trend: if the amount of available prize money increases, the 80% rank also becomes larger. This, in turn, means that the ranking becomes
less dominated by the top players. For example, if the total prize money is less than one million GBP, it takes fewer than the top 20 players to earn 80% of it. However, with a total amount of six million GBP in prize money, it may take more than the top 50 players to earn 80% of it. This trend seems to level out, though, once the total amount of prize money becomes more than about nine or ten million GBP.
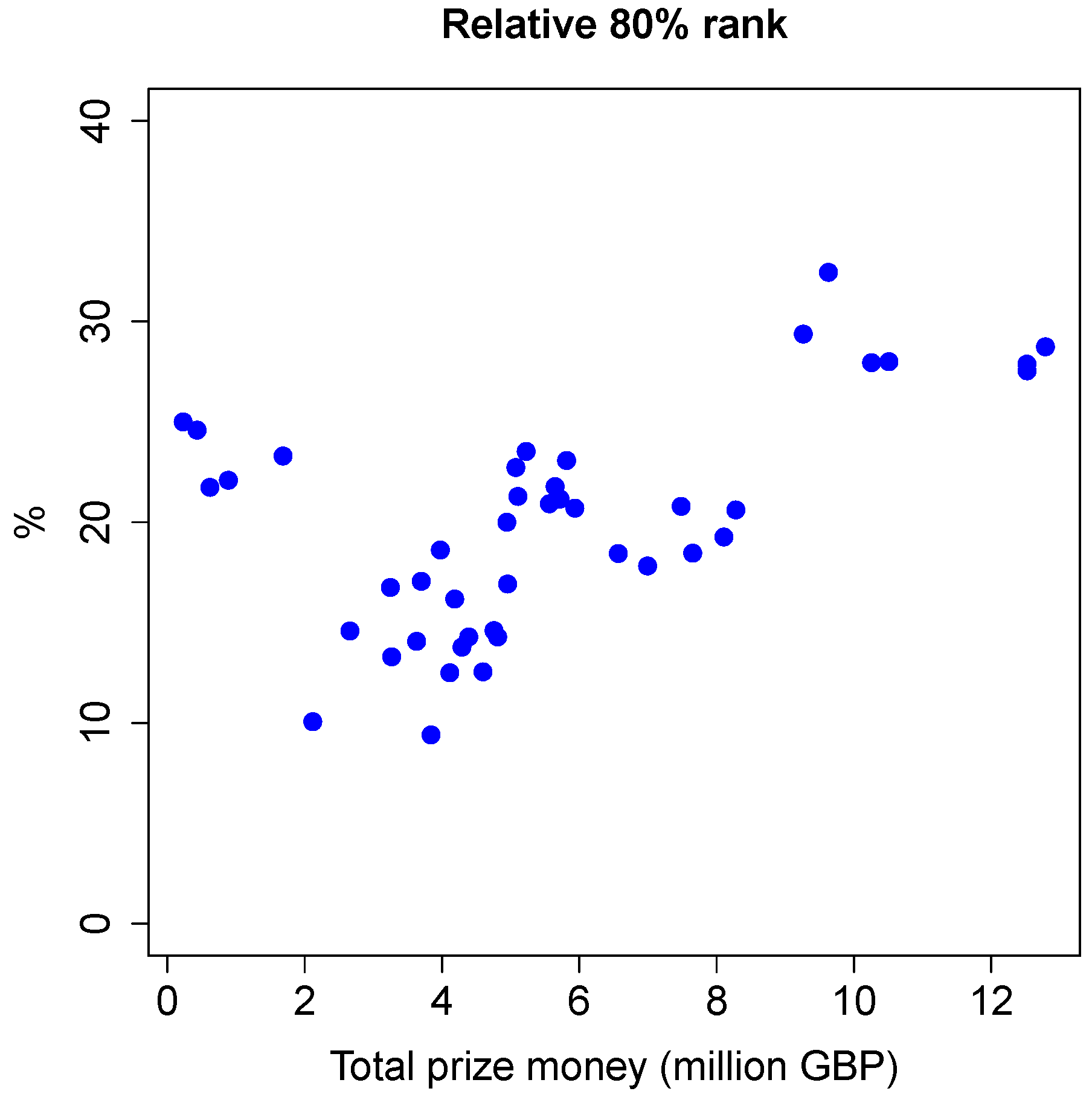
Figure 8 shows the
relative 80% prize money ranks. The result is very similar, except for the small cluster of points on the left (with less than 2 million GBP total prize money). These data points are from the first half of the 1980s, when the total number of players was still quite small. Otherwise, there is again a very clear increasing trend with increasing total prize money, which also seems to level off once the total amount of prize money becomes about ten million GBP or more.
Note that the relative 80% ranks vary between roughly 10% and 30%. However, the average over all seasons is 19.95%. Snooker rankings seem to follow the Pareto principle, or 80-20 rule, very closely indeed.
3.7. UK Players Share
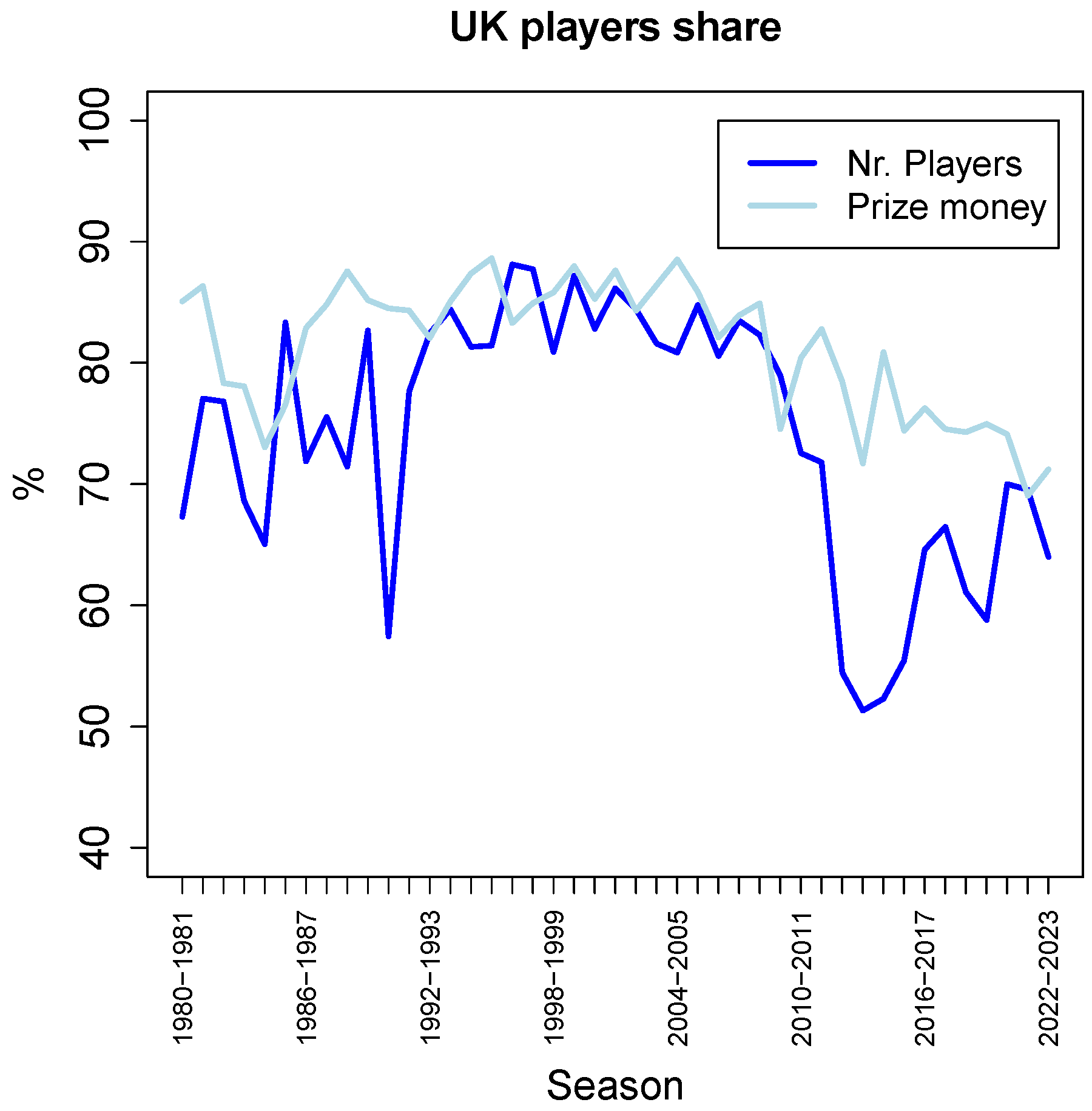
Finally,
Figure 9 shows the share of UK players in professional snooker. The dark blue line represents the percentage of UK players among all the players that earned any prize money in a given season. This percentage fluctuates between 50% and 90%, and is currently around 65%. The light blue line represents the percentage of the total amount of prize money that was earned by UK players. This percentage fluctuates between 70% and 90%, but with a slowly decreasing trend since the turn of the millennium.
As
Figure 9 seems to indicate, the share of prize money earned by UK players is generally larger than the percentage of UK players, as the light-blue line is mostly above the dark-blue line.
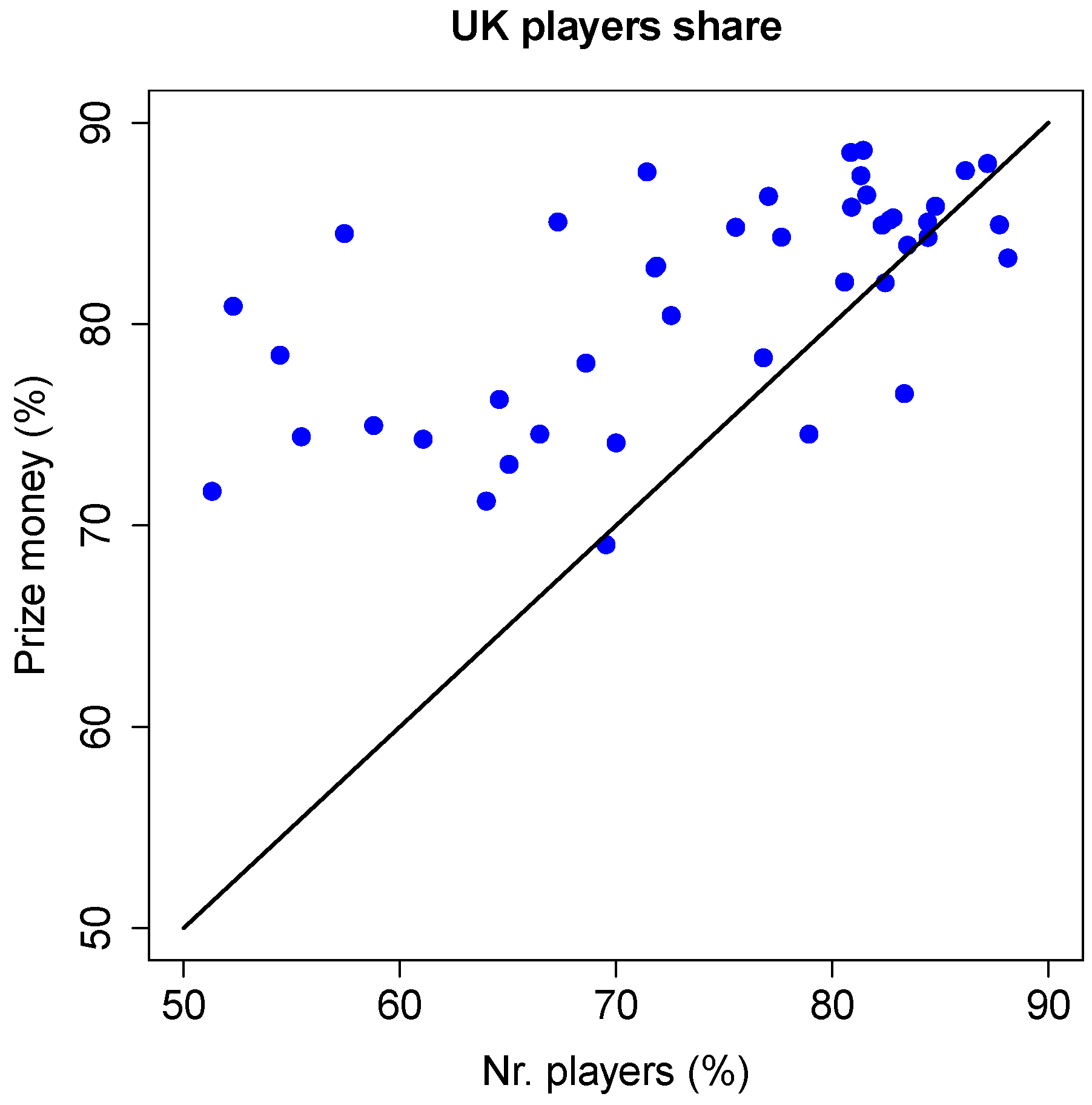
Figure 10 shows this more clearly, where the UK players prize money share (in percentage) is plotted against the corresponding percentage of UK players in each season. The diagonal line indicates where they would be equal.
The majority of points is clearly to the left of this diagonal line, where the share in prize money is indeed larger than the percentage of players. Only a few points are to the right of the diagonal line, and mostly by a relatively small distance.
The average share in prize money earned by UK players (over all seasons) is 81%, while the average percentage of UK players is 74%. A t-test on the hypothesis that these averages are equal results in a p-value of 0.0001 (i.e., a probability of 0.01%). This hypothesis can thus be rejected with full confidence, and the average UK share in prize money can be considered to be significantly larger than the average percentage of UK players. In other words, historically UK players have earned a significantly larger share of the available prize money than what could be reasonably expected given the actual percentage of UK players.
4. Conclusions
There is no discernible trend over time in the number of tournaments per season, but there is a fairly steady decline in the number of players since the rapid initial increase during the 1980s. With a clear and significant overall increase in total amount of prize money per season, this means that the average amount of prize money both per tournament and per player has increased. In fact, the average amount of prize money earned per player in one season has increased by about one order of magnitude, from around 5,000 GBP to around 50,000 GBP, over four decades.
However, given the highly skewed distribution of prize money among the players, a simple average is not very meaningful. A more informative measure is the 80% rank, which indicates how much a ranking is dominated by the top players. The relative 80% rank varies between roughly 10% and 30%, but with an average (over all seasons) of 19.95%. The Pareto principle, or 80-20 rule, thus seems to apply perfectly well to snooker rankings with (on average) 80% of the prize money being earned by the top 20% of players.
However, the 80% rank has actually increased with an increasing total amount of available prize money (at least up to a certain point), both for the absolute and for the relative 80% ranks. In other words, with a larger amount of available prize money, the rankings become
less dominated by the top players. More prize money is of course beneficial to all players, but relatively speaking even more so for the lower-ranked players, as they are able to earn an increasingly larger share of it. A similar conclusion was already drawn earlier [
6], but from a mathematically more complicated analysis. Here, a more straightforward and easier to understand analysis has been presented, and on a more complete data set.
Finally, the snooker tour is still highly dominated by UK players, both in terms of the number of players (50-90%) and their share in the prize money earned (70-90%), but with a declining trend in the latter. Moreover, their share in prize money is significantly larger than what could be expected given the percentage of UK players. Although it is not immediately obvious what an expected or “fair” percentage would be, it may be insightful to compare these statistics with for example badminton, another individual sport that was originally brought over from British India and then further developed into its modern form in the UK. Although snooker shares a similar history in that respect [
7], badminton seems to have become much more internationalized.
Hopefully these analyses and results will be helpful in any future discussions about prize money distributions in snooker or whether the tour is too UK-centric, by providing some relevant and quantitative statistics over the past four decades that are directly related to these delicate issues.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Hendon, D. The big snooker debate that will not go away: prize money distribution in a sport that rewards excellence. Eurosport. 2022. Available online: https://eurosport.com/snooker/the-great-snooker-debate-that-will-not-go-away-prize-money-distribution-in-a-sport-that-rewards-exce_sto8855369/story.shtml.
- Florax, R. CueTracker. https://cuetracker.net, 2023.
- Dunford, R.; Su, Q.; Tamang, E.; Wintour, A. The Pareto Principle. The Plymouth Student Scientist 2014, 7, 140–148. [Google Scholar]
- Kalpić, D.; Hlupić, N.; Lovrić, M. Student’s t-tests. In International Encyclopedi of Statistical Science; Lovrić, M., Ed.; Springer, 2011. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing. https://R-project.org, 2022.
- Hordijk, W. Snooker statistics and Zipf’s law. Stats 2022, 5, 985–992. [Google Scholar] [CrossRef]
- Everton, C. The History of Snooker and Billiards; Partridge Press, 1986. [Google Scholar]
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).