Geometrized Vacuum Physics. Part I. Algebra of Stignatures

Preprint

Article

Geometrized Vacuum Physics. Part I. Algebra of Stignatures

Altmetrics

Downloads

213

Views

100

Comments

Mikhail Batanov-Gaukhman^*

This version is not peer-reviewed

Submitted:

30 August 2023

Posted:

04 September 2023

Read the latest preprint version here

Alerts

Abstract

This article is the first part of a scientific project under the general title "Geometrized Vacuum Physics". This study is based on two main postulates: 1) independence of the propagation velocity of electromagnetic waves in vacuum from their frequency; 2) the constancy of the averaged zero vacuum balance, associated with the assertion that only mutually opposite formations are born from vacuum, so that on average they completely compensate for each other's manifestations. In this part of the "Geometrized Vacuum Physics" the foundations of the Algebra of Stignatures are laid, which is the mathematical and logical foundation of the entire project. In the next articles of this project it will be shown that the Algebra of Stignatures can be used for the development of "zero" (vacuum) technologies, algebraic genetics, vacuum cosmology, the vacuum standard model of "elementary particles", vacuum gravity and levitation, vacuum energy, ethics and aesthetics and many other branches of knowledge. At the end of this article, one of the many possible applications of the Algebra of Stignatures is given, in particular, the basics of the stignature-spectral analysis are outlined, with the help of which the possibilities of communication channels can be significantly expanded.

Keywords:

Subject: Physical Sciences - Theoretical Physics

1. Introduction

In modern physics, there are [1,2,3,4,5,6,7,8]: technical vacuum (discharged gas); physical vacuum (the lowest energy state of a set of scalar, vector, tensor and spinor quantum fields); Einstein vacuum (generally a curved 4-dimensional space-time continuum surrounding neutral or charged physical bodies); ideal vacuum (emptiness, i.e., 3-dimensional space, in which any curvature and particles are completely absent).

This first part of “Geometrized Vacuum Physics” focuses on the ideal vacuum in order to create a mathematical apparatus “Algebra of Stignatures”, suitable for the study of vacuum phenomena and the development of “zero” (vacuum) technologies. In subsequent articles of this project, a description of curved sections of vacuum and stable vacuum formations is expected.

First, we abstract from all kinds of vacuum processes, and consider the local region of a completely flat empty 3-dimensional space (i.e., ideal vacuum).

This work is based on three reliable (experimentally confirmed) facts:

1) all known electromagnetic waves, regardless of their oscillation frequency, propagate in vacuum with the same speed of light c = 299,792,458 m/s (fixed by the resolution of the 26-th General Conference on Weights and Measures, based on CODATA data). Despite the possible instability of the properties of emptiness, the postulate of the constancy of the speed of light in vacuum is accepted in this work as an initial axiom. At the same time, as will become clear below, the mathematical apparatus of the Algebra of Stignatures turned out to be independent of the propagation velocity of perturbations. Therefore, the Algebra of Stignatures is universal and applicable to the study of any 3-dimensional medium;

2) all averaged characteristics of an average flat area of vacuum (momentum, angular momentum, spin, etc.) are equal to zero;

3) if something is born from vacuum, then it must be in a mutually opposite form (particle - antiparticle, convexity - concavity, wave - antiwave, etc.). This property of vacuum is referred to in this work as “averaged zero vacuum balance” or “vacuum balance” for short.

The foundations of the Algebra of Stignatures developed in this work are proposed as a universal mathematical apparatus suitable for studying not only the properties of vacuum, but also any other liquid, solid and gaseous continuous media in which wave disturbances propagate at a constant speed. Also, the Algebra of Stignatures can be useful for philosophical rethinking of the knowledge of ancient civilizations and for application in many branches of scientific knowledge, for example, in: coding theory, algebraic genetics, vacuum energy, elementary particle physics, etc.

2. Materials and Method

2.1. Longitudinal stratification of ideal vacuum into λ_m,n-vacuums

Consider a 3-dimensional volume of an ideal vacuum, in which there are no particles and no curvature. In what follows, for brevity, the ideal vacuum will be referred to as “vacuum”.

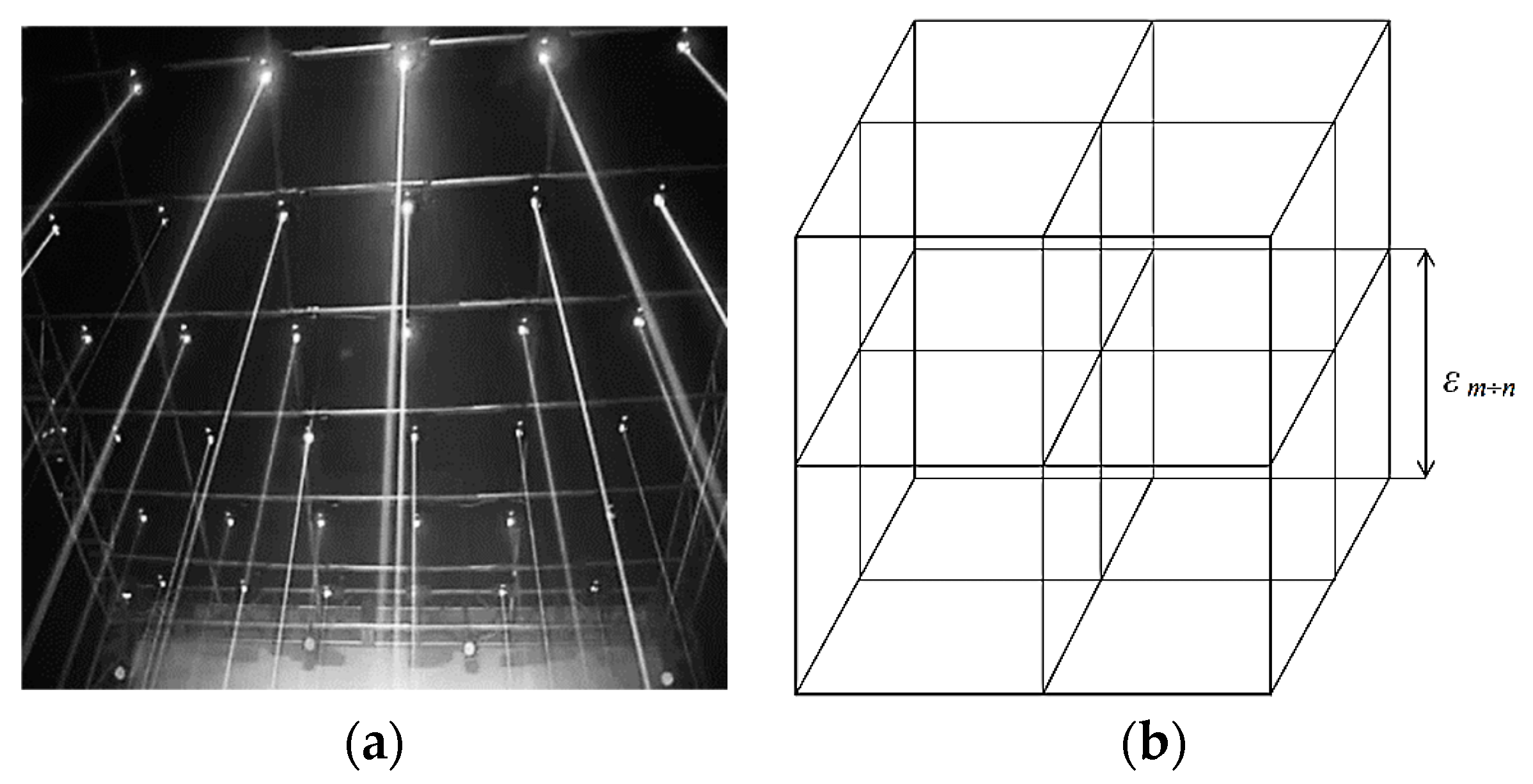
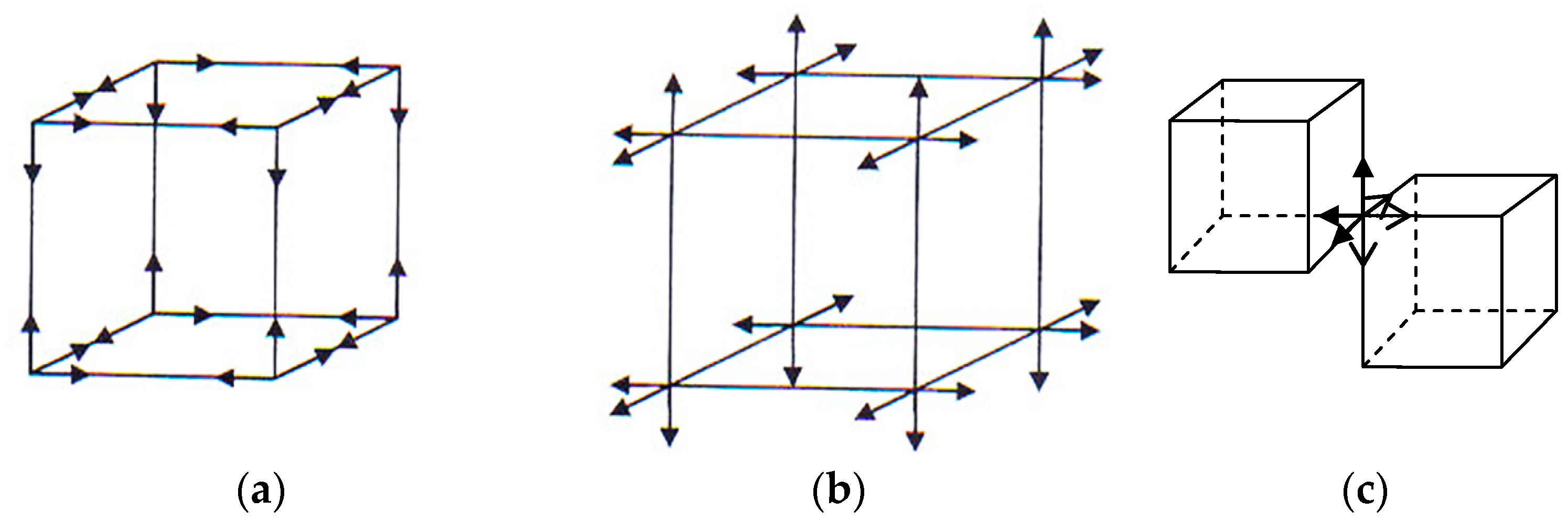
Let’s probe this volume of “vacuum” with laser beams from three mutually perpendicular directions, so that the beams form a 3-dimensional cubic lattice (Figure 1a,b).

Rays of light in a vacuum are not visible, but they can be visualized with a finely dispersed sol. Of course, a “vacuum” filled with a sol is not a perfect vacuum. Nevertheless, the rays propagate in the “vacuum” itself (i.e., between the particles of the sol), while the influence of the sol on the metric-dynamic properties of the macroscopic volume of the “vacuum” in the case under consideration can be neglected. In addition, if the sol is removed from this “vacuum” volume, then the rays will still remain in it, although they will not be visible.

Let, for example, to probe of “vacuum” are used laser beams of light (i.e., narrowly directed monochromatic electromagnetic oscillations) with a wavelength λ_-4,-5, taken from the range of lengths Δλ =10^–4 ÷10^–5 cm. Then we get a 3-dimensional lattice consisting of such mutually perpendicular laser beams, with the edge length of one cubic cell ε_-4,-5 ~ 100λ_-4,-5 (see Figure 1b). This cubic lattice will be called λ_-4,-5-vacuum (or 3D_-4,-5-landscape).

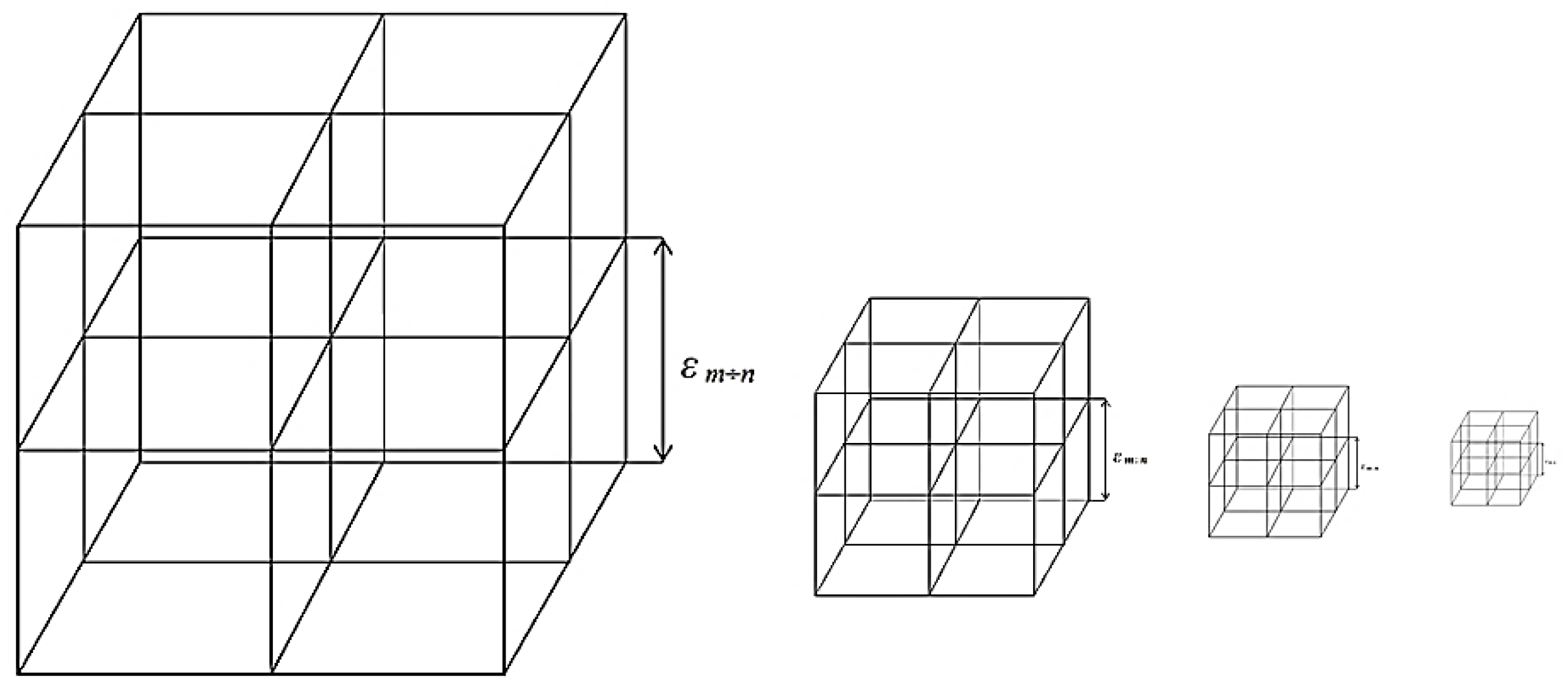
We divide the entire range of electromagnetic (light) wave lengths into a set of subranges Δλ =10^m ÷ 10ⁿ cm, where n = m +1 (m and n are integers). Then, in the same way as shown in Figure 1, we will probe the studied volume of the “vacuum” with monochromatic light rays with wavelengths λ_m,n from all subranges Δλ = 10^m ÷ 10ⁿ cm. As a result, we obtain an almost infinite number of nested λ_m,n-vacuums (i.e., 3Dm,n-landscapes) with the corresponding lengths of edges of cubic cells ε_m,n ~ 100λ_m,n (see Figure 2).

The value of the edge of the cubic cell of each λ_m,n-vacuum

ε_m,n ~ 10²λ_m,

(1)

follows from the condition of applicability of geometric optics λ_m,n → 0, i.e., when the thickness of the light beam is much smaller than the value of the corresponding cubic cell, while the beam thickness can be neglected.

The question remains open: – “Are there any restrictions on the frequency ω or the wavelength λ of the electromagnetic wave, both in the direction of their increase, and in the direction of decrease? If the critical values: ω_max = 2πс/λ_max and ω_min = 2πс/λ_min exist, these will be very important characteristics of the vacuum. Today, as far as the author knows, the frequency range of observed electromagnetic waves extends from 2 Hz to 10²⁰ Hz, while no restrictions on the expansion of this range have been experimentally found.

2.2. Geodesic lines of the curved section λ_m,n-vacuum

Long-term experimental data show that monochromatic light rays in the entire observed wavelength range Δλ propagate in “vacuum” at the same speed of light c and according to the same laws of electrodynamics. Therefore, if the region of vacuum under study is not curved, then all λ_m,n-vacuums (i.e., 3D_m,n-landscapes) will be represented as ideal cubic lattices (see Figs. 1 and 2), because the geodesic lines of all these non-curved λ_m,n-vacuums are direct rays of light. In this case, λ_m,n-vacuums will differ from each other only by the length of the edge of the cubic cell ε_m,n ~ 10²λ_m,n (see Figure 2).

However, if the region of vacuum under study turns out to be curved, then all λ_m,n-vacuums will differ somewhat from each other due to the fact that light rays with different wavelengths have different thicknesses. This circumstance is theoretically substantiated in the sections of geometric optics related to the resolution of optical devices [17,18] and is confirmed by experimental data (see Figure 3).

In this case, each λ_m,n-vacuum (i.e., 3D_m,n-landscape) will be unique (see Figure 4), since vacuum irregularities are averaged within the thickness of the probing light beam.

Therefore, one λ_m,n-vacuum is only one 3-dimensional “slice” of the curved vacuum region. For a more complete description of the curved section of the vacuum, it is necessary to have an infinite set of curved λ_m,n-vacuums nested in each other.

Thus, the local volume of vacuum is an infinitely complex system consisting of an infinite number of nested λ_m,n-vacuums. However, the situation is simplified by the fact that in the entire studied range of electromagnetic wave lengths, all λ_m,n-vacuums obey the same physical laws. Therefore, the knowledge gained in the study of one λ_k,r-vacuum is automatically extended to all other λ_m,n-vacuums.

Below, the mathematical apparatus of the Algebra of Stignatures is developed, designed to study the local volume of only one λ_m,n-vacuum. But this apparatus is suitable for studying not only all λ_m,n-vacuums, but also any other continuous media in which wave disturbances propagate at a constant speed.

2.3. Sixteen rotating 4-bases

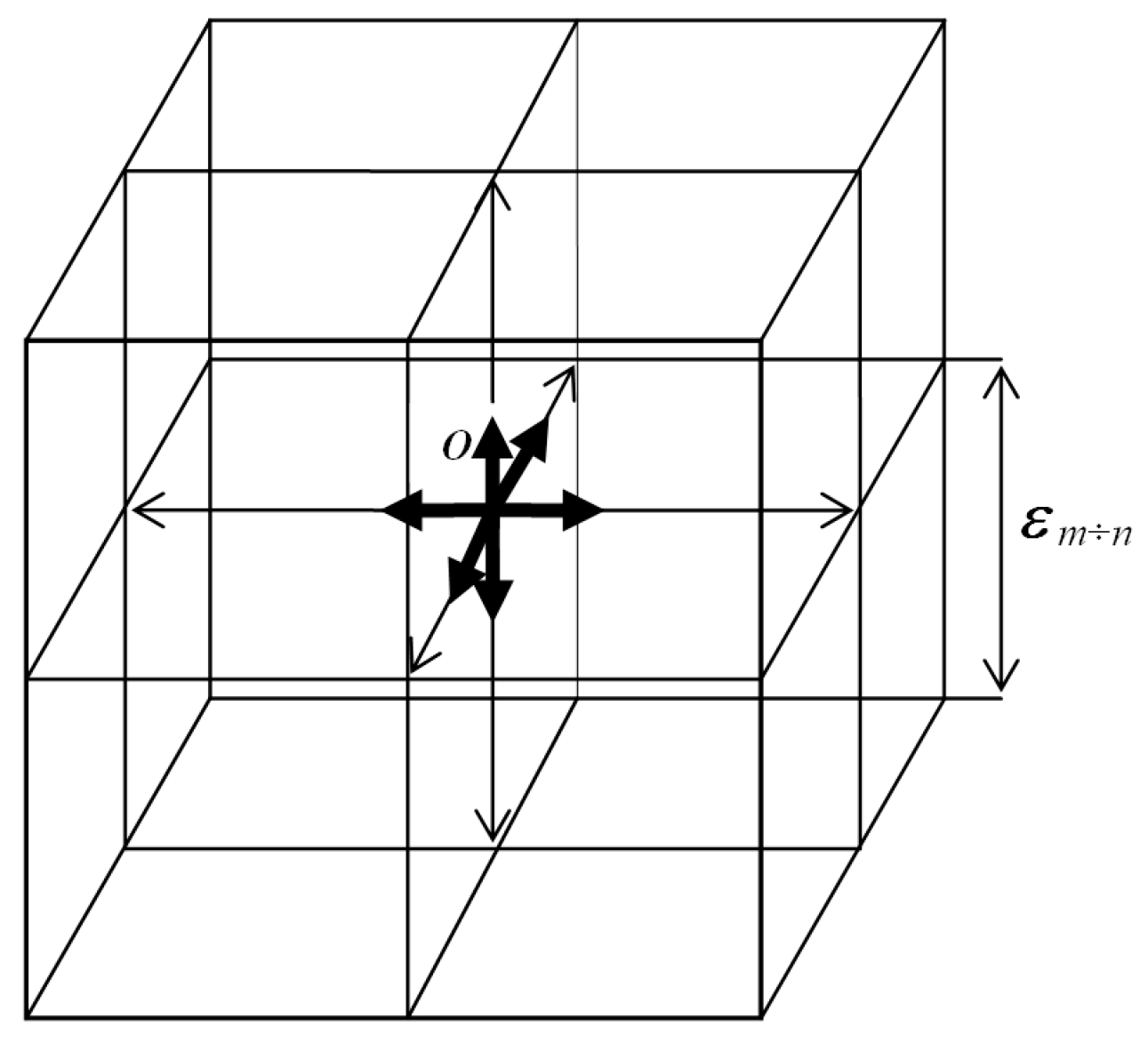
Let’s return to the consideration of the undistorted volume of one of the λ_m,n-vacuums (see Figure 1) and examine the “vacuum” region in the vicinity of the point O (see Figure 5).

We calculate how many orthogonal 3-bases originate at the central point O (see Figure 5). If we spread the 3-bases from the point O in different directions, then it turns out that there are 16 of them (Figure 6 a,b).

Eight 3-bases refer to the cubic cell itself (Figure 6a), and eight opposite 3-antibases refer to adjacent cubic cells (Figure 6b,c).

According to the “vacuum balance” condition, any movement in a vacuum must be accompanied by a similar anti-motion. Therefore, if one 3-basis (together with the cubic cell) is rotated clockwise, then this is only possible if the adjacent cubic cell (together with the 3-antibasis) is similarly rotated counterclockwise, since there is no fulcrum in vacuum.

In connection with the above, it is convenient to add to all eight 3-bases (Figure 6a) along the fourth time axis t, and to eight 3-antibases (Figure 6b) add along the fourth anti-axis (i.e., oppositely directed axis) of time – t.

The time axis t is determined by the angular frequency of rotation of the 3-basis (ie, the number of revolutions per unit time). The rotation of the 3-basis with a constant angular velocity is described by the expression dϕ /dt =ω (where ϕ and ω are the phase and angular frequency of rotation of the 3-basis). Integrating this expression, we get the time axis t =ϕ /ω.. The rotation of the 3-antibasis in the opposite direction similarly forms the anti-axis of time – t =ϕ /ω.

Thus, at the considered point О λ_m,n-vacuum (Figure 5) there are 8 + 8 = 16 orthogonal 4-bases (see Figure 6), which are shown in Figure 7.

2.4. Stignature of an affine 4-dimensional space

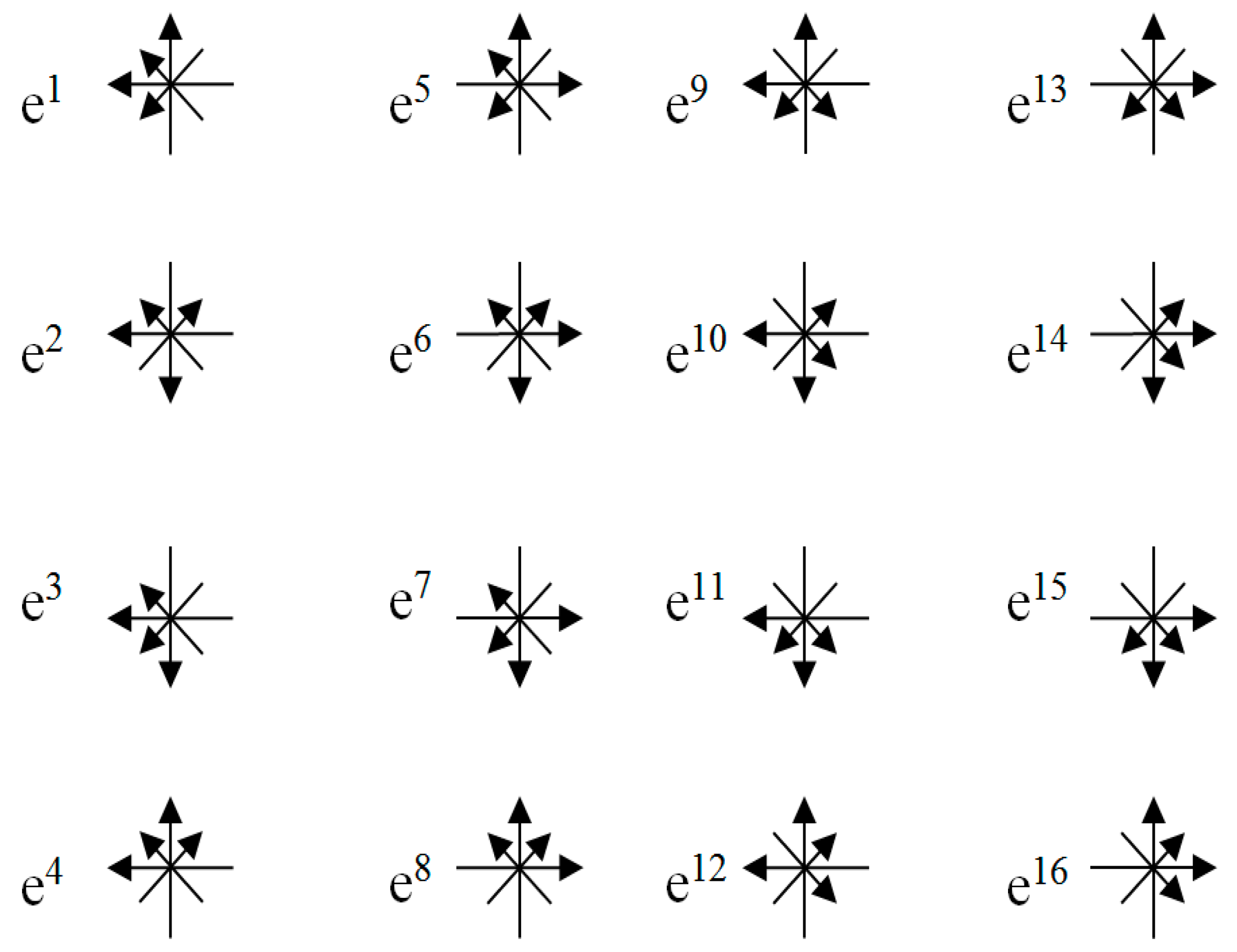
Each of the sixteen 4-bases shown in Figure 7 specifies the direction of the axes of a 4-dimensional affine (i.e., vectors) space. To introduce the characteristic “stignature” of an affine space, we first define the concept of “base”.

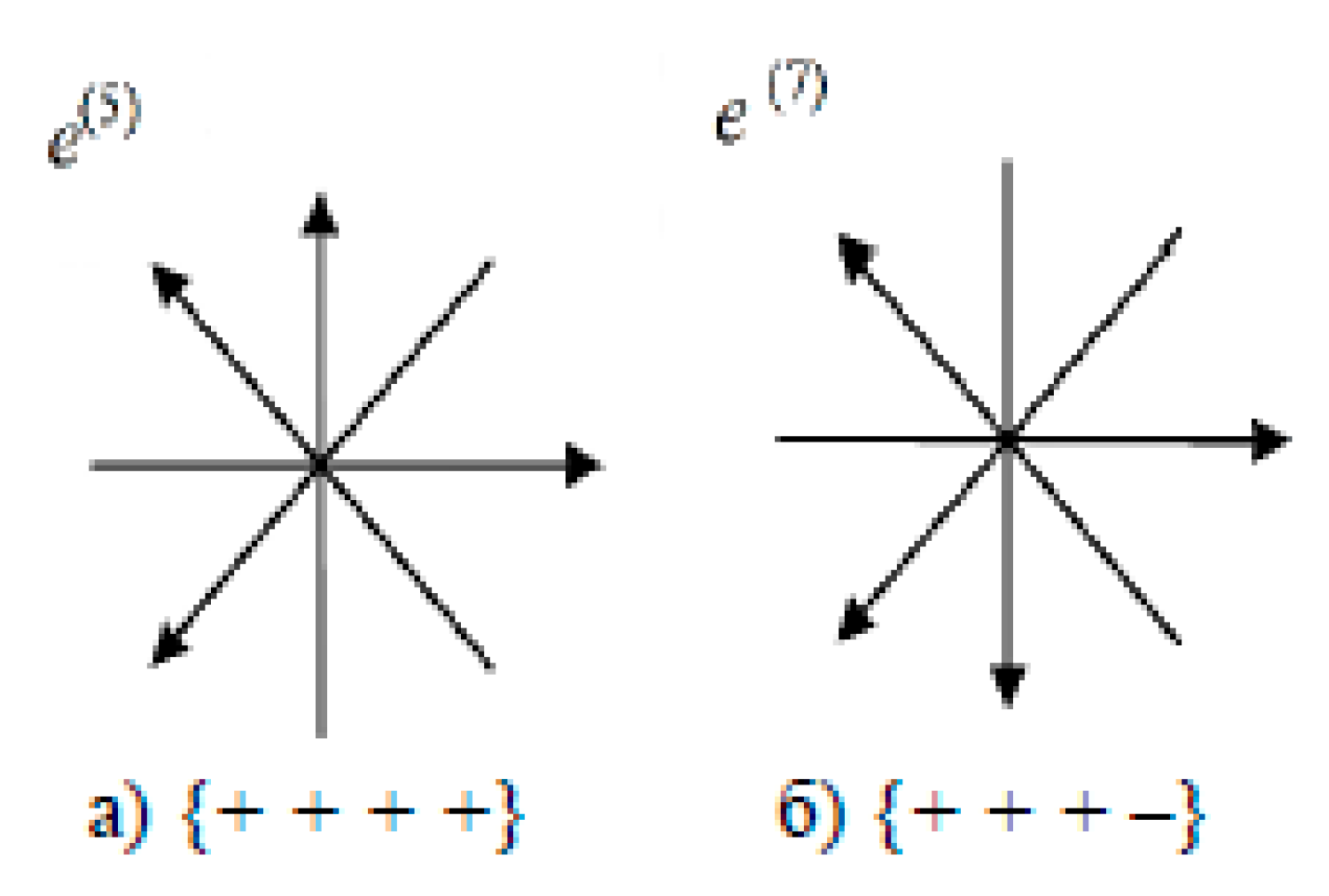
We choose from the sixteen 4-bases shown in Figure 7, one 4-basis, for example, e⁵ (e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) and let’s call it “base” (see Figure 8).

We conditionally accept that the directions of all unit vectors of the “base” are positive (see Figure 8)

e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) = (+1, +1,+ 1, +1) → {+ + + +}.

(2)

Here we introduce the abbreviated notation {+ + + +}, which we will call the “stignature” of the affine space given by the 4-basis e⁵ (that is, the “base”). That is, a stignature is a set of 4 signs that determine the direction of the axes of a 4-dimensional affine space in relation to the direction of the axes of the base affine space.

All other 4-bases shown in Figure 7 have the following signatures with respect to the directions of the “base” unit vectors (i.e., the 4-basis e⁽⁵⁾) (see Table 1).

Stignatures given in Table. 1 are combined into a 16-component matrix:

s t i g n (e_{i}^{(a)}) = (\begin{matrix} \{+ + + +\} & \{+ + + -\} & \{- + + -\} & \{+ + - +\} \\ \{- - - +\} & \{- + + +\} & \{- - + +\} & \{- + - +\} \\ \{+ - - +\} & \{+ + - -\} & \{+ - - -\} & \{+ - + +\} \\ \{- - + -\} & \{+ - + -\} & \{- + - -\} & \{- - - -\} \end{matrix}) .

(3)

Any other 4-basis from the sixteen 4-bases shown in Figure 7 can be chosen as the “base”. In this case, only the combinations of signs in the stignatures of affine spaces will change, but all properties of the matrix of signatures (3) will remain unchanged.

2.5. Stignature matrix properties

Stignature matrix (3) was obtained as a result of the development of vacuum physics. However, this matrix is a separate universal mathematical object that can be applied in various branches of scientific knowledge.

Let’s list some properties of the stignature matrix (3).

5.1. The sum of all 16 stignatures from matrix (3) is equal to the zero stignature

(4)

Ex. (4) can be represented in the following form

(5)

where the summation of the signs “+” and “–” is performed in each row and column in any direction according to the rules:

«–» + «–» = 2«–», «+» + «+» = 2«+», «+» + «–» = «–» + «+» = 0.

(6)

Operations with signs in (5) are performed in rows and columns (i.e., in ordered rows or by ranking), therefore this expression is called a ranking expression, and two columns consisting of stignatures are called “rankings”. The ranking expression (5) reveals the internal structure of the void and is called “zero splitting”.

5.2. The sum of all 64 signs included in the matrix (3) is equal to zero, that is, it satisfies the vacuum balance condition:5.3. There are four binary combinations of signs “+” and “–”, which we will call binary stignatures:

32«+» + 32«–» = 0.

(7)

H^{'} \leftrightarrow \{\begin{matrix} + \\ - \end{matrix}\}, V \leftrightarrow \{\begin{matrix} - \\ + \end{matrix}\}, H \leftrightarrow \{\begin{matrix} + \\ + \end{matrix}\}, I \leftrightarrow \{\begin{matrix} - \\ - \end{matrix}\}

(8)

or in transposed form

H^{' +} \leftrightarrow \{+ -\}, V^{+} \leftrightarrow \{- +\}, H^{+} \leftrightarrow \{+ +\}, I^{+} \leftrightarrow \{- -\} .

(9)

Combine (

\cup

) binary stignatures (8) or (9) according to the rules:

\{\begin{matrix} + \\ - \end{matrix}\} \cup \{\begin{matrix} - \\ + \end{matrix}\} = \{\begin{matrix} + & - \\ - & + \end{matrix}\}, \{\begin{matrix} + \\ + \end{matrix}\} \cup \{\begin{matrix} - \\ + \end{matrix}\} = \{\begin{matrix} + & - \\ + & + \end{matrix}\}, \{\begin{matrix} + \\ - \end{matrix}\} \cup \{\begin{matrix} - \\ - \end{matrix}\} = \{\begin{matrix} + & - \\ - & - \end{matrix}\}

and etc.,

\{+ +\} \cup \{+ +\} = \{+ + + +\}, \{+ -\} \cup \{+ +\} = \{+ - + +\}, \{- -\} \cup \{+ -\} = \{- - + -\}

(10)

and etc.

As a result, we get 16 signatures of the matrix (3):

(11)

5.4. The Kronecker union of the two-row matrix of binary signatures (9) forms the stignatures matrix (3):

(12)

where ⊕ is a symbol denoting the Kronecker union of binary stignatures according to the rules (10).

5.5. Stignature matrix (3) can be represented as a sum of diagonal and antisymmetric matrices5.6. Hadamard stignatures for noise-proof encryption of information

(13)

If we return the original units to the two-row stignatures (11), then we get 16 two-row matrices

(\begin{matrix} - 1 & - 1 \\ - 1 & - 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & - 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ - 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & 1 \\ - 1 & 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ - 1 & 1 \end{matrix})

(14)

(\begin{matrix} - 1 & - 1 \\ - 1 & 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} - 1 & - 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ - 1 & 1 \end{matrix}) (\begin{matrix} - 1 & 1 \\ - 1 & - 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ - 1 & - 1 \end{matrix}) .

(15)

of these, eight matrices are:

(\begin{matrix} - 1 & 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ - 1 & 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ 1 & 1 \end{matrix}) (\begin{matrix} 1 & 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} 1 & - 1 \\ - 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & - 1 \\ 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & 1 \\ - 1 & - 1 \end{matrix}) (\begin{matrix} - 1 & - 1 \\ - 1 & 1 \end{matrix})

(16)

are Hadamard matrices, because they satisfy the condition

Н (2) \otimes Н^{Т} (2) = 2 (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix})

(17)

When raising any of the matrices (16) to Kronecker powers, the Hadamard matrices H(n) are again obtained, satisfying the condition:

Н (n) \otimes Н^{Т} (n) = n I,

(18)

where I is an n×n diagonal identity matrix:

I = (\begin{matrix} 1 & 0 & . . . & 0 \\ 0 & 1 & . . . & 0 \\ . . . & . . . & . . . & 0 \\ 0 & 0 & 0 & 1 \end{matrix})

(19)

For example,

(20)

(21)

and so on according to the algorithm

Н(2)^⊗k = Н(2^k) = Н(2) ⊗ Н(2)^⊗k-1 = Н(2) ⊗ Н(2^k-1),

(22)

Hadamard matrices are used to construct error-correcting codes. In particular, Hadamard matrices are used to decipher the genetic code [11,12].

If in the matrices (20) and (21) again instead of 1 and –1 we use the signs {+} and {–}, then we obtain the rule for raising two-row stignatures to the Kronecker power, for example,

{\{\begin{matrix} + & + \\ + & - \end{matrix}\}}^{\otimes 2} = \{\begin{matrix} + & + \\ + & - \end{matrix}\} \otimes \{\begin{matrix} + & + \\ + & - \end{matrix}\} = \{\begin{matrix} + \{\begin{matrix} + & + \\ + & - \end{matrix}\} & + \{\begin{matrix} + & + \\ + & - \end{matrix}\} \\ + \{\begin{matrix} + & + \\ + & - \end{matrix}\} & - \{\begin{matrix} + & + \\ + & - \end{matrix}\} \end{matrix}\} = \{\begin{matrix} + & + & + & + \\ + & - & + & - \\ + & + & - & - \\ + & - & - & + \end{matrix}\}

(23)

{\{\begin{matrix} + & + \\ + & - \end{matrix}\}}^{\otimes 3} = \{\begin{matrix} + & + \\ + & - \end{matrix}\} \otimes \{\begin{matrix} + & + & + & + \\ + & - & + & - \\ + & + & - & - \\ + & - & - & + \end{matrix}\} = \{\begin{matrix} + & + & + & + & + & + & + & + \\ + & - & + & - & + & - & + & - \\ + & + & - & - & + & + & - & - \\ + & - & - & + & + & - & - & + \\ + & + & + & + & - & - & - & - \\ + & - & + & - & - & + & - & + \\ + & + & - & - & - & - & + & + \\ + & - & - & + & - & + & + & - \end{matrix}\}

(24)

double row stignatures,

\{\begin{matrix} - & + \\ + & + \end{matrix}\} \{\begin{matrix} + & + \\ - & + \end{matrix}\} \{\begin{matrix} + & - \\ + & + \end{matrix}\} \{\begin{matrix} + & + \\ + & - \end{matrix}\} \{\begin{matrix} + & - \\ - & - \end{matrix}\} \{\begin{matrix} - & - \\ + & - \end{matrix}\} \{\begin{matrix} - & + \\ - & - \end{matrix}\} \{\begin{matrix} - & - \\ - & + \end{matrix}\}

(25)

corresponding to matrices (15) will be called two-row Hadamard stignatures.

5.7. Noise-immune coding of genetic information

It was shown in [11,12] that Hadamard matrices (15) or two-row stignatures (25) can be used as the basis for studying noise-resistant genetic information. Deoxyribonucleic acid (DNA) molecules are built from four chemical elements (nucleotides):

(26)

These four nucleotides correspond to two bits of information or four binary stignatures (9)

(27)

Nucleotides (27) form: doublets, triplets and other more complex combinations of informational polymer, i.e., DNA molecules [11,12]:

(28)

(29)

These combinations of nucleotides correspond to the combinations of the “+” and “–” signs obtained from the two-row Hadamard stignatures (25), for example

{\{\begin{matrix} + & + \\ + & - \end{matrix}\}}^{\otimes 2} = \{\begin{matrix} + & + & + & + \\ + & - & + & - \\ + & + & - & - \\ + & - & - & + \end{matrix}\}, {\{\begin{matrix} + & + \\ + & - \end{matrix}\}}^{\otimes 3} = \{\begin{matrix} + & + & + & + & + & + & + & + \\ + & - & + & - & + & - & + & - \\ + & + & - & - & + & + & - & - \\ + & - & - & + & + & - & - & + \\ + & + & + & + & - & - & - & - \\ + & - & + & - & - & + & - & + \\ + & + & - & - & - & - & + & + \\ + & - & - & + & - & + & + & - \end{matrix}\}

(30)

Thus, the Algebra of Stignatures can be used to develop the theory of matrix coding of the space-time continuum.

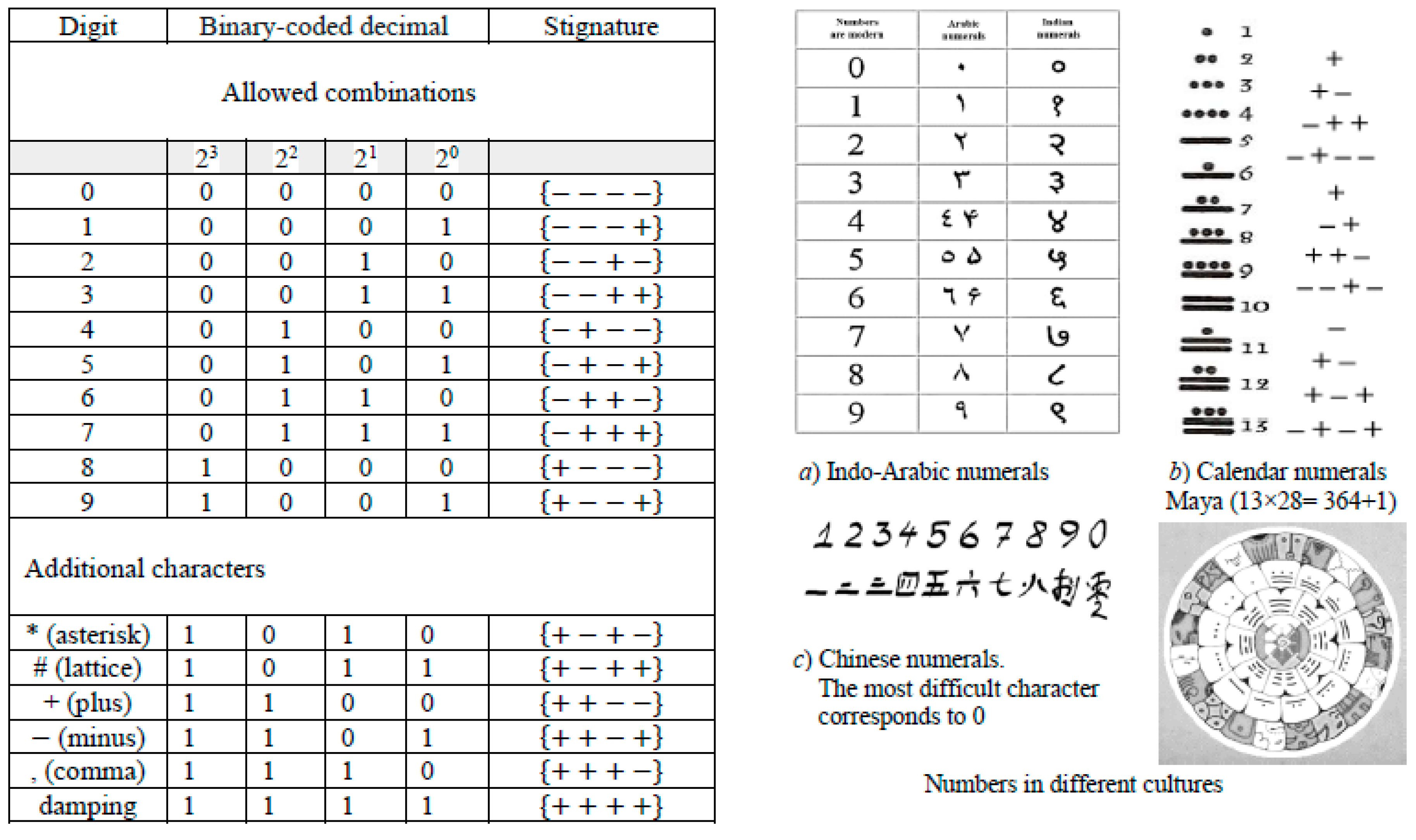
5.8. Binary-coded decimal and Arithmetic of Stignature

There is a complete correspondence between the binary-coded decimal (BCD) of digits and the 16 affine space stignatures from the matrix (3):

From Table 2 it follows that if 0 is replaced by “–”, and 1 is replaced by “+”, then digits from matrix (3) can be assigned numbers. In addition, by analogy with binary-decimal arithmetic, the arithmetic of stignatures can also be constructed, as shown in the example in Table 3.

Arithmetic of Stignature can be used to describe the nodal configurations of affine spaces.

5.9.“. Colored” quaternions

Sixteen stignatures (3) correspond to 16 types of “colored” quaternions:

(31)

The complete set of “colored” quaternions (31) can be applied in various branches of mathematics and physics. By direct calculation it is easy to verify that the sum of all 16 types of “colored” quaternions (31) is equal to zero

\sum_{k = 1}^{16} z_{k} = 0 .

(32)

Expression (32) shows that the superposition (addition) of all types of “colored” quaternions is balanced with respect to zero, i.e., satisfies the “vacuum balance” condition.

5.10. Classes of stignature

The signatures included in the matrix (3) can be divided into three classes:

Class 1: all signs in the stignature are the same - 2 stignatures:

{+ + + +} {– – – –}.

(33)

Class 2: two identical signs in a stignature - 6 stignatures:

{+ – – +} {+ + – –}{+ – + –}

(34)

{– + + –} {– – + +}{– + – +}.

(34)

Class 3: three identical characters in a stignature - 8 stignatures:

{– – – +} {– – + –}{– + – –}{+ – – –}

(35)

{+ + + –}{+ + – +}{+ – + +}{– + + +}.

(35)

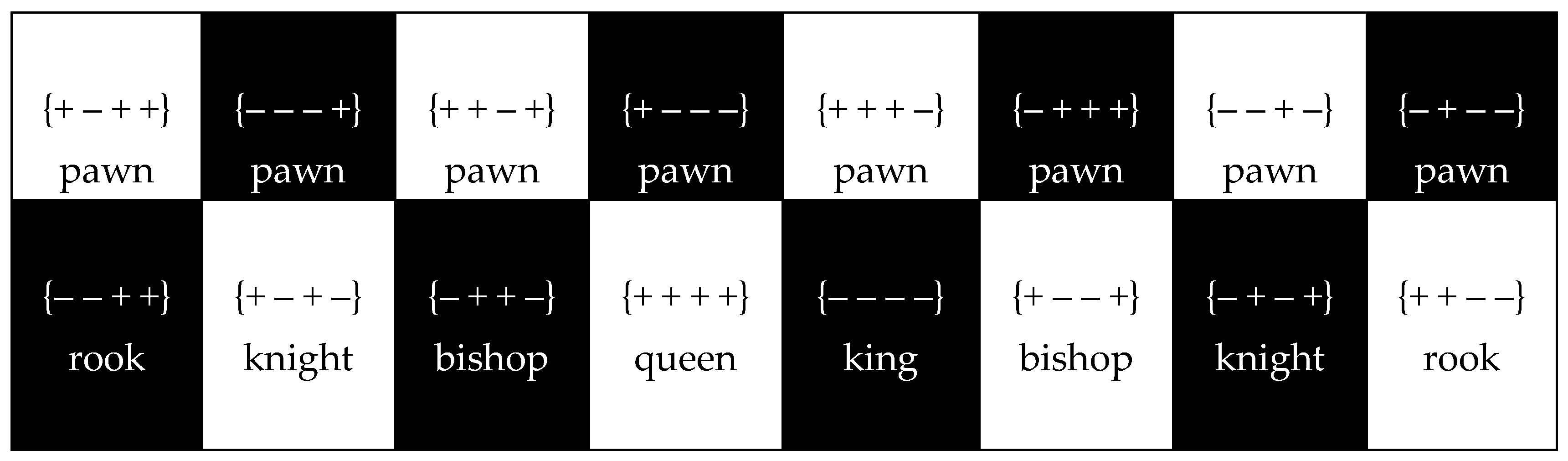
5.11. Chess analogy

The chessboard has 8 × 8 = 64 cells: 32 of them are black and 32 are white (see Figure 9). Also, in the matrix of signatures (3) there are 16 × 4 = 64 characters, of which 32 are plus “+” and 32 minus “–”:

(\begin{matrix} I I & H I & V I & H' I \\ I H & H H & V H & H' H \\ I V & H V & V V & H' V \\ I H' & H H' & V H' & H' H' \end{matrix}) \equiv (\begin{matrix} \{+ + + +\} & \{+ + + -\} & \{+ - + +\} & \{+ - + -\} \\ \{+ + - +\} & \{+ + - -\} & \{+ - - +\} & \{+ - - -\} \\ \{- + + +\} & \{- + + -\} & \{- - + +\} & \{- - + -\} \\ \{- + - +\} & \{- + - -\} & \{- - - +\} & \{- - - -\} \end{matrix}) .

At the beginning of the game, there are 32 chess pieces on the chessboard: 16 white and 16 black (see Figure 9). Also, in the matrix (3) there are 16 stignatures that coincide in properties with chess pieces in full accordance with their three classes (33) – (35) (see Figure 10):

Matrix (3) can describe both “light” (i.e., light 3D_m,n-landscapes), which corresponds to 16 white chess pieces, and “darkness” (emptiness), which corresponds to 16 black chess pieces.

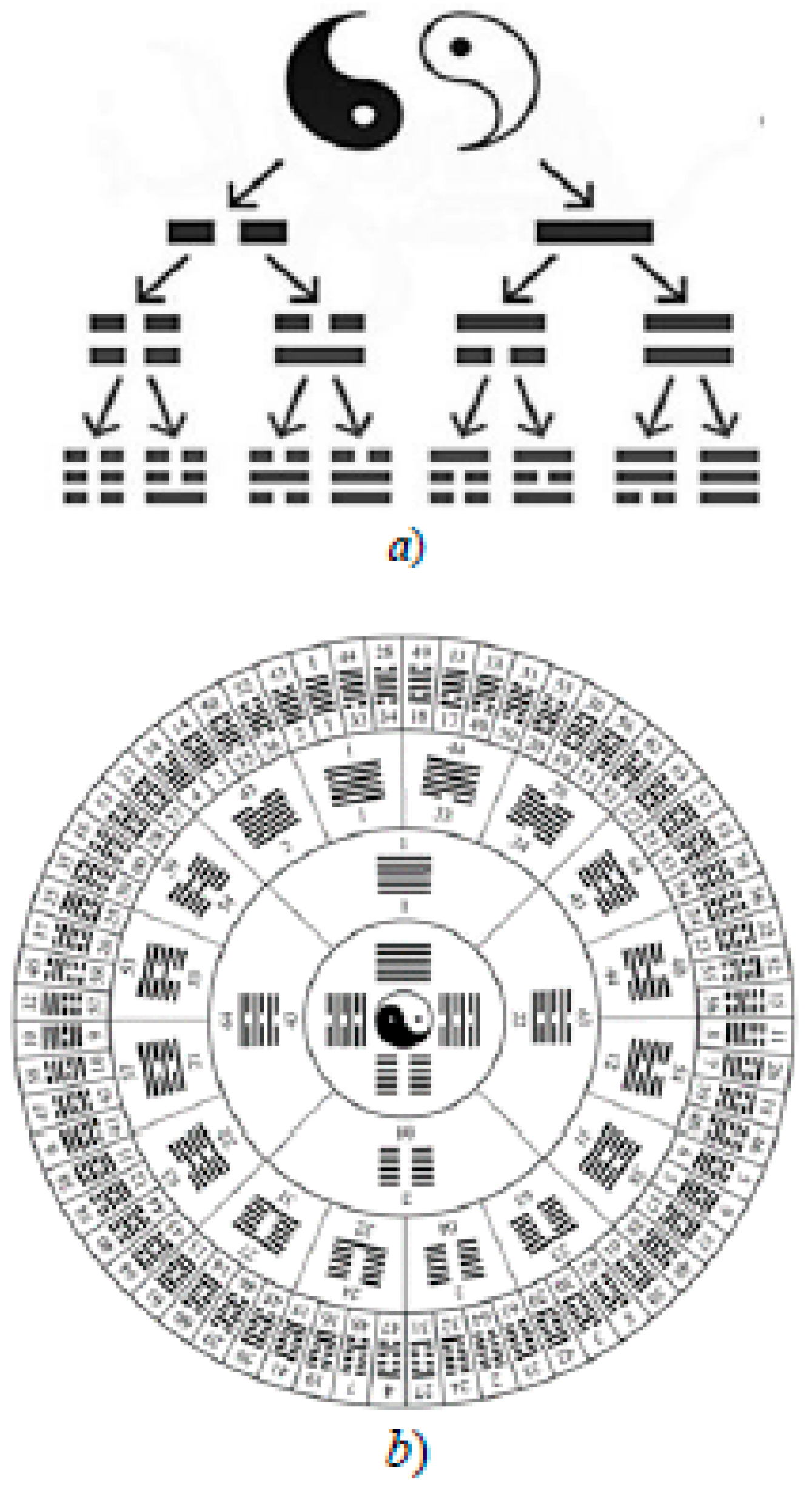
5.12. I Ching analogy

The I Ching (Chinese Book of Changes) is based on two Beginnings:

in the Algebra of Stignaturs there are also two initial signs:

The Book of Changes uses 8 trigrams (see Figure 11a). Similarly, there are eight 3-bases in the Algebra of Stignatures (see Figure 6a) with the following stignatures

(36)

and eight 3-antibases (Figure 6b) with opposite stignatures

(37)

In the Book of Changes, all possible combinations of two trigrams generate 64 hexagrams (Figure 11b), and in the Algebra of Stignatures, 64 combinations of each 3-basis with stignatures (36) with each 3-antibasis with opposite stignatures (37) are possible.

The three-logic of the Book of Changes is consistent with the four-logic of the Stignature Algebra if in the ranking expression (5) one column of signs is transferred to another side of equalities:

(38)

The Book of Changes also uses four combinations of two principles:

Similarly, in the Algebra of Signatures, four binary combinations of signs “+” and “–” (9) are possible:

{+ +}, {– –}, {+ –} {– +},

from which affine space signatures (11) are formed, etc.

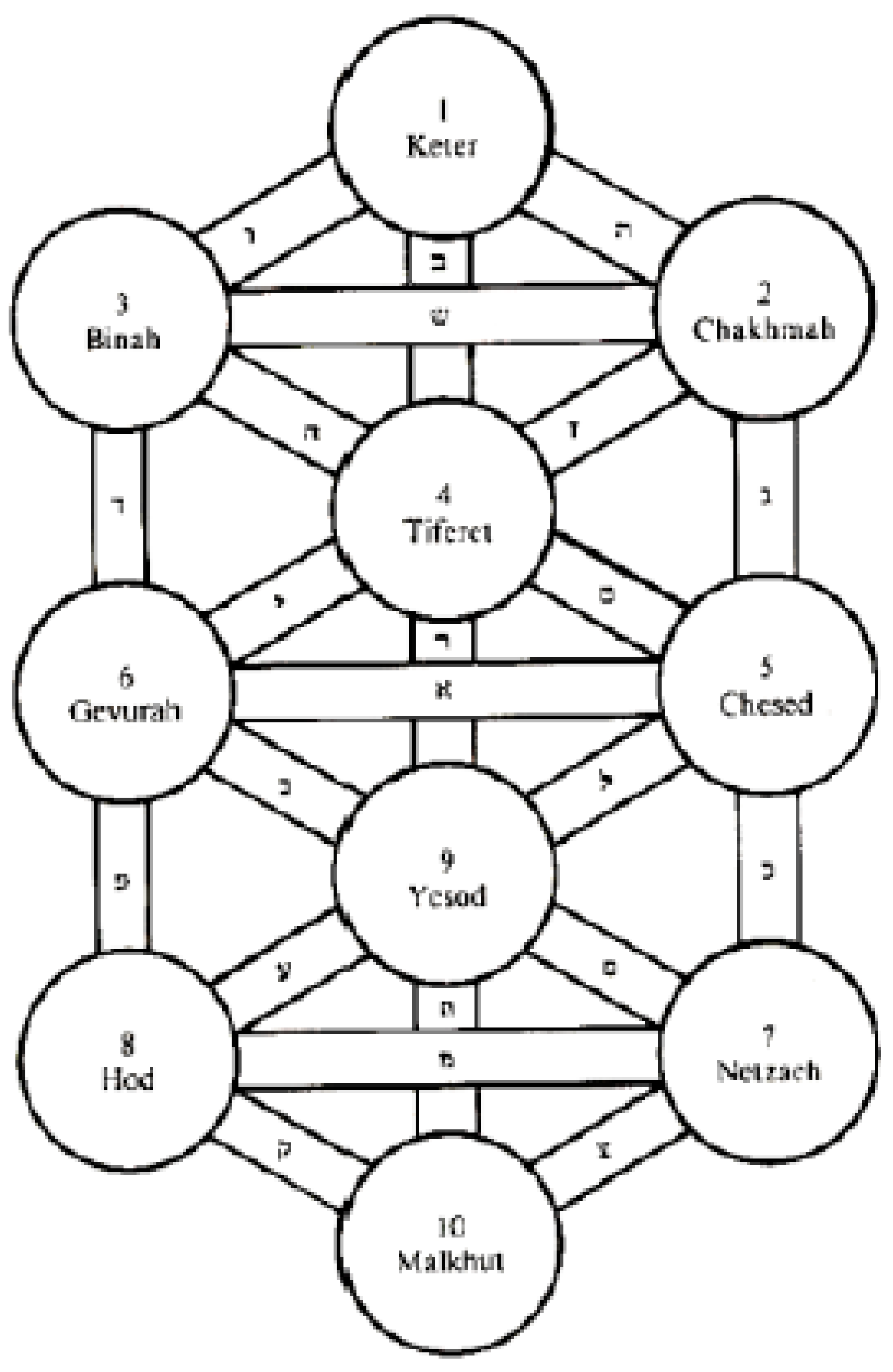
5.13. Hebrew analogy

Judaism is based on Algorithms for revealing the Great Name of the GOD ה-ו-ה-י [13]. Further, instead of Hebrew letters, the transliteration ה-ו-ה-י

\equiv

H′ V H I will be used.

One of the endless Revelations of the Name H′ V H I is called “Etz Chaim” (“Tree of Life” or “Tree of the Sefirot”):

{(\begin{matrix} I & H \\ H^{'} & V \end{matrix})}^{\otimes 2} = (\begin{matrix} I (\begin{matrix} I & H \\ H^{'} & V \end{matrix}) & H (\begin{matrix} I & H \\ H^{'} & V \end{matrix}) \\ H^{'} (\begin{matrix} I & H \\ H^{'} & V \end{matrix}) & V (\begin{matrix} I & H \\ H^{'} & V \end{matrix}) \end{matrix}) = (\begin{matrix} (\begin{matrix} I I & I H \\ I H^{'} & I V \end{matrix}) & (\begin{matrix} H I & H H \\ H H^{'} & H V \end{matrix}) \\ (\begin{matrix} H^{'} I & H^{'} H \\ H^{'} H^{'} & H^{'} V \end{matrix}) & (\begin{matrix} V I & V H \\ V H^{'} & V V \end{matrix}) \end{matrix}) .

(39)

The components of this matrix correspond to 10 Sephira (i.e., Qualities) of Spirituality:

Letter of the Name ה-ו-ה-י	Component of the Matrix of Qualities (39) (see Figure 12)	Sephirah
iWYXWYXtip of the Letter Yud	II	Keter
I	HH	Hochma
H	VV	Bina
V	IV, IH, IH′, VH, VH′, HH′WYXWYXVI, HI, H′I, HV, H′V, H′H	Tiphereth*
H′	H′H′	Malchut

where the Sefira Tipheret* consists of six dual Sefirot [13]:

Chesed (IV = –VI), Gevura (IH = –HI), Tiferet (IH′ = –H′I),

Netzach (VH = –HV), Hod (VH′ = –VH′), Yesod (HH′ = –H′H).

The Qualities Matrix (39) can be written as the sum of two matrices

(\begin{matrix} I I & 0 & 0 & 0 \\ 0 & H H & 0 & 0 \\ 0 & 0 & V V & 0 \\ 0' & 0 & 0 & H' H' \end{matrix}) + (\begin{matrix} 0 & H I & V I & H' I \\ I H & 0 & V H & H' H \\ I V & H V & 0 & H' V \\ I H' & H H' & V H' & 0 \end{matrix}) .

(40)

Similarly, the signature matrix (3) is the result of raising the two-row matrix to the second Kronecker power [13]

{(\begin{matrix} I & H \\ H^{'} & V \end{matrix})}^{\otimes 2} = {(\begin{matrix} \{+ +\} & \{+ -\} \\ \{- +\} & \{- -\} \end{matrix})}^{\otimes 2} = (\begin{matrix} \{+ + + +\} & \{+ + + -\} & \{+ - + +\} & \{+ - + -\} \\ \{+ + - +\} & \{+ + - -\} & \{+ - - +\} & \{+ - - -\} \\ \{- + + +\} & \{- + + -\} & \{- - + +\} & \{- - + -\} \\ \{- + - +\} & \{- + - -\} & \{- - - +\} & \{- - - -\} \end{matrix}) .

This matrix can also be represented as the sum of the diagonal and antisymmetric matrices (13)

(41)

Comparing the matrices (40) and (41), we find that the stignatures of the matrix (3) can reflect the characteristic properties of the corresponding Sefirot (Qualities) of the “Tree of Life” [13]

(42)

Thus, the following analogy can be traced between the ten Sephira (Quality) and the sixteen stignatures of the matrix (3):

(42a)

This analogy corresponds to the criteria of “Zero Philosophy”, emanating from “EIN SOF, Baruhu” (INFINITE NOTHING, Blessed be HE). In turn, from the “Zero Philosophy” follows the condition of “vacuum balance” and the structure of “split zero” (5), on which the geometrized vacuum physics and, in particular, the Algebra of Stignatures are based.

Let’s return to the representation of the Great Name of GOD ה-ו-ה-י in the form of binary stignatures (9)

(42b)

One of the infinite Algorithms for revealing the Name of the GOD ה-ו-ה-י

\equiv

H′ V H I is associated with 24 combinations of permutations of the letters H′ V H I [13]

(42c)

In the Lurianic Kabbalah, twelve of these combinations correspond to the 12 hours of the Day, and the remaining twelve combinations correspond to the 12 hours of the Night.

Combining four binary stignatures (42b) according to the rules (10) in the order corresponding to combinations of four letters of the Name H′VHI (42c) leads to 24 octaves (eights) of signs, or to 24 types of combination stignatures from matrix (3):

(42d)

5.14. Minkowski’s affine stignatures and musical harmony

We represent the ranking expression (5) (zero splitting) in the following simplified form

(43)

Let’s transfer the stignatures {– + + +} and {+ – – –} from the numerators of the ranks (43) to their denominators with inversion, i.e., with signs reversed. Such an operation does not violate the “vacuum balance” and leads to the ranking expression

(44)

In this case, in the denominator of the left rank in Ex. (44), the stignature of the affine 4-Minkowski space {+ – – –} was obtained, and in the denominator of the right rank in Ex. (44), the stignature of the affine 4-anti–Minkowski space { – + + +} was obtained.

Not only the ranking expression (44) leads to a balanced (with respect to zero) dyad of affine Minkowski stignatures

{+ – – –} + {– + + +} = 0.

The following ranking expressions that preserve the vacuum balance lead to the same result:

(45)

(46)

(47)

The Algebra of Stignature can be used as a musical score of spatial harmony. Just like in music, stignatures form balanced octaves (7+1= 8) of the form (44) and chords (3+1= 4) of the form (45) – (47). Moreover, in different situations, the Algebra of Stignatures uses a different number of signs “+” and “–” in proportions in relation to the total number: 1, 1/2, 1/8, 1/16, 1/32, 1/64, etc. This corresponds to the proportions of the duration of the notes: 1, 1/2, 1/8, 1/16, 1/32, 1/64, etc.

Ancient philosophers, beginning with the Pythagoreans, believed that Space was filled with harmonious musical rhythms and proportions. Music theory was later used by Johannes Kepler in «Harmonices Mundi» (Harmony of the World), which led to the discovery of the third law of celestial mechanics. It is possible that the combination of musical techniques with the Algebra of Stignatures algorithms will also lead to interesting results.

5.17. Pythagorean analogy (Algebra of Signatures)

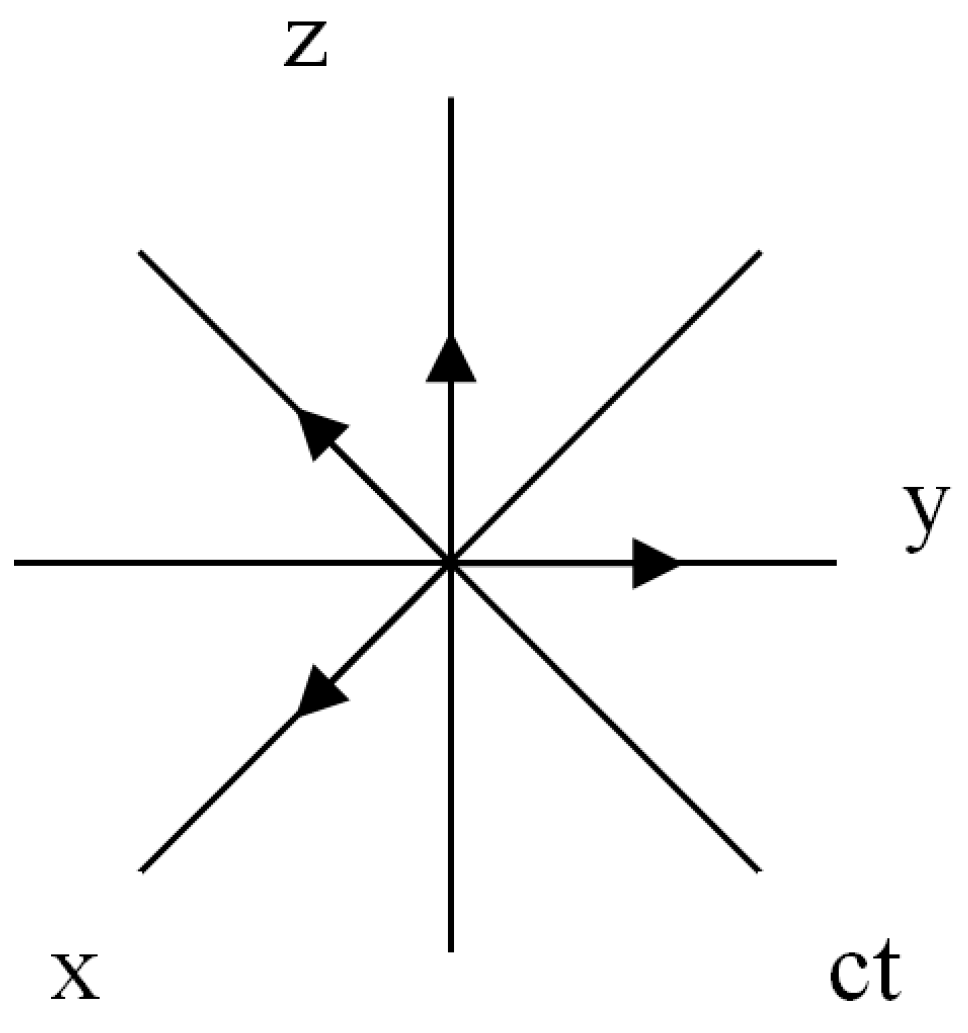
Let’s pass from affine spaces to metric spaces. For this, as an example, we use an affine space with a 4-basis e_i⁽⁷⁾(e₀⁽⁷⁾,e₁⁽⁷⁾,e₂⁽⁷⁾,e₃⁽⁷⁾) (see Figs. 7 and 13) with signature {+ + + –}. In this space, we define a 4-vector

ds⁽⁷⁾ = e_i⁽⁷⁾dxⁱ⁽⁷⁾ = e₀⁽⁷⁾dx⁰⁽⁷⁾ + e₁⁽⁷⁾dx¹⁽⁷⁾ + e₂⁽⁷⁾dx²⁽⁷⁾ + e₃⁽⁷⁾dx³⁽⁷⁾,

(48)

where dxⁱ⁽⁷⁾ is the i-th projection of the 4-vector ds⁽⁷⁾ onto the xⁱ⁽⁷⁾ axis, the direction of which is determined by the basis vector e_i⁽⁷⁾.

Similarly, we define the second 4-vector in the affine space with the 4-basis e_i⁽⁵⁾(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) (Figure 7 and Figure 13), with signature {+ + + +}

ds⁽⁵⁾ = e_i⁽⁵⁾dxⁱ⁽⁵⁾ = e₀⁽⁵⁾dx⁰⁽⁵⁾ + e₁⁽⁵⁾dx¹⁽⁵⁾ + e₂⁽⁵⁾dx²⁽⁵⁾ + e₃⁽⁵⁾dx³⁽⁵⁾.

(49)

We find the scalar product of 4-vectors (48) and (49)

(50)

For the case under consideration, the scalar products of basis vectors e_i⁽⁵⁾e_j⁽⁷⁾ are:

for i = j e₀⁽⁵⁾e ₀⁽⁷⁾ = 1, e₁⁽⁵⁾e₁⁽⁷⁾ = 1, e₂⁽⁵⁾e₂⁽⁷⁾ = 1, e₃⁽⁵⁾e₃⁽⁷⁾ = –1,

(51)

for i ≠ j, all e_i⁽⁵⁾e_j⁽⁷⁾ = 0.

(51)

In this case, expression (50) takes the form of a quadratic form

(52)

“Signature” (GRT term) is an ordered set of signs in front of the corresponding terms of the quadratic form.

To determine the signature of the metric space with the metric (52), instead of performing the scalar product of vectors (50), it is enough to multiply the signs of the 4-basis stignatures shown in Figure 18 by columns:

(53)

In the numerator of the rank (53), the signs in each column are multiplied according to the rules

{+} × {+} = {+}; {–} × {+} = {–};

(54)

the result of such multiplication is written in the denominator (under the line) of the same column. The execution of actions according to these rules will be called rank multiplication.

Just as it was done with the vectors ds⁽⁵⁾ and ds⁽⁷⁾ {see expressions (48) – (53)}, pairwise scalarly multiply vectors from all 16 affine spaces with 4 bases shown in Figure 7. As a result, we obtain 16 × 16 = 256 metric 4-spaces with 4-intervals of the form

ds^(аb)2 = e_i^(а)e_j^(b)dx^i(а)dx^j(b),

(55)

where a = 1, 2, 3, … , 16; b = 1, 2, 3, … , 16.

The signatures of these 16 × 16 = 256 metric 4-spaces can be defined, similarly to (53), by rank multiplications of the signs of the signatures corresponding to the affine spaces, for example:

(56)

Thus, point O (see Figure 5) is the place of intersection of all 256 metric 4-spaces with metrics (55) and stignatures (40). In this variety of intersecting metric spaces, there are many features and patterns that are studied by the Algebra of Signatures.

The fundamentals of the Algebra of Signature will be covered in the next article of this project. Here we only note that quadratic forms (i.e., metrics) of type (52), or

ds² = dx₀² + dx₁² + dx₂² + dx₃²

(57)

originate from the Pythagorean theorem с² = a² + b², the proof of which in about 520 BC, brought about the greatest revolution in the consciousness of mankind.

2.6. Spectra-stignature analysis

As an example, we use the Algebra of Stignatures to expand the possibilities of spectral analysis.

Let’s recall the well-known in quantum physics procedure for the transition from the coordinate representation to the momentum one. Let the probability distribution density of the location of an elementary particle be given as a function of space and time ρ(сt,x,y,z). This function is represented as a product of two amplitudes:

ρ(сt,x,y,z) = φ(сt,x,y,z) φ(сt,x,y,z).

(58)

Next, two Fourier transforms are performed

ψ (p_{c t}, p_{x}, p_{y}, p_{z}) = \int_{- \infty}^{\infty} ϕ (c t, x, y, z) \exp {i \frac{p}{η} (c t - x - y - z)} d Ω

(59)

stignature {+ – – –},

ψ * (p_{c t}, p_{x}, p_{y}, p_{z}) = \int_{- \infty}^{\infty} ϕ (c t, x, y, z) \exp {i \frac{p}{η} (- c t + x + y + z)} d Ω

(60)

stignature {– + + +},

where p = 2πη/λ is the generalized frequency; λ is the wavelength; η is the coefficient of proportionality (in quantum mechanics, η = ћ is the reduced Planck constant); dΩ = dctdxdydz is an elementary 4-dimensional volume.

The momentum (i.e., spectral) representation of the function ρ(сt,x,y,z) is obtained as a result of the product of two probability amplitudes (59) and (60)

G (p_{c t}, p_{x}, p_{y}, p_{z}) = ψ (p_{c t}, p_{x}, p_{y}, p_{z}) \cdot ψ * (p_{c t}, p_{x}, p_{y}, p_{z})

(61)

By analogy with the procedure (59) - (60), we formulate the basics of the spectral signature analysis. We represent the function ρ(сt,x,y,z) as a product of not two, but 8 “amplitudes”

ρ (с t, x, y, z) = φ_{1} (с t, x, y, z) φ_{2} (с t, x, y, z) φ_{3} (с t, x, y, z) \times \dots \times φ_{8} (с t, x, y, z) = \prod_{k = 1}^{8} ϕ_{k} (c t, x, y, z) .

(62)

Instead of the imaginary unit i , which was used in the integrals (59) and (60), we introduce into consideration eight objects ζ_r (where r = 1, 2, 3, … , 8) satisfying the anticommutative relations of the Clifford algebra:

ζ_m ζ_k + ζ_k ζ_m = 0 for m ≠ k , ζ_m ζ_m = 1,

(63)

or ζ_m ζ_k + ζ_k ζ_m = 2δ_km , where δ_km is the Kronecker symbol (δ_km= 0 for m ≠ k and δ_km = 1 for m = k).

(64)

These requirements are met, for example, by a set of 8×8 matrices of the type

(65)

Let’s perform eight “color” Fourier transforms:

(66)

where the objects ζ_m (60) perform the function of Clifford imaginary units.

We also find eight complex-conjugate Fourier images with opposite stignatures:

(67)

The integrals of the “colored” Fourier transform (61) and (62) include 16 linear forms with matrix signatures (3).

The spectral-stignature representation of the function ρ(сt,x,y,z) is obtained as a result of the product of eight corresponding pairs of “color” amplitudes (66) and their complex conjugate “color” amplitudes (67)

R (p_{c t}, p_{x}, p_{y}, p_{z}) = \prod_{k = 1}^{8} ψ_{k} (p_{c t}, p_{x}, p_{y}, p_{z}) ψ_{k} * (p_{c t}, p_{x}, p_{y}, p_{z})

(68)

The spectral-stignature Fourier analysis proposed here can be useful for the development of “zero” technologies, such as sealing vacuum communication channels, and many other branches of science and technology.

Carthusian crucifix

The orthogonal Cartesian coordinate system is mentally connected with the crucifixion of Jesus Christ. Modern science was created by the universities of medieval Europe, which looked at the world around them through a crosshair with a suffering Savior. Also, the signs of stignatures from matrix (3) characterize the directions of the axes of the multidimensional crucifixion, and are associated with the Stigmata (Greek στίγματος - signs, marks, ulcers, wounds) on the head, hands and feet of the crucified Messiah.

3. Conclusions

This work is the first of a series of articles under the general title “Geometrized vacuum physics from the standpoint of the Algebra of Signatures”, where, as a result, based on the study of vacuum properties, it is assumed:

- build a multilayer and multilevel cosmological model with the development of ideas about the nature of all known force interactions, including gravity;

- present metric-dynamic models of all elementary particles and quarks that are part of the Standard Model (with the exception of the Higgs boson);

- develop a theoretical foundation for the development of “zero” (i.e., vacuum) technologies, including vacuum ethics, aesthetics and energy.

This article proposes to explore a local area of ideal vacuum (or “vacuum”, i.e., void) by probing it with light rays with a monochromatic wavelength λ_m,n from three mutually perpendicular directions. As a result, a 3-dimensional light cubic lattice is formed in the “vacuum”, which is called the λ_m,n-vacuum (or 3D_m,n-landscape) with the edge length of the cubic cell ε_m,n ~ 100^⸳λ_m,n (see Figure 1 and 2). If we similarly probe the same volume of vacuum with monochromatic light rays with other wavelengths λ_m+k,n+k, then we get an infinite number of λ_m,n-vacuums nested into each other like nesting dolls (see Figure 2). Such an infinite hierarchical discrete sequence of 3D_m,n-landscapes is called a longitudinal bundle of a 3-dimensional volume of “vacuum” (emptiness).

The study of the geometric features of one ideal cubic cell of any of the λ_m,n-vacuums led to the development of the Algebra of Stignature. An analysis of the properties of the matrix of stignatures (3) showed that the Algebra of Stignatures is a unique mathematical and logical apparatus that has its mental roots in ancient philosophical traditions.

The foundations of the Algebra of Stignature presented in this article can be applied not only in vacuum physics (as will be shown in the following articles of this project), but also in many other branches of knowledge, for example, in: multidimensional geometry, topology, continuum mechanics, crystallography, spatial coding theory, algebraic genetics, relativity theory, etc. In this article, as an example, the use of the Algebra of Stignatures for the development of stignature-spectral analysis is presented.

Acknowledgments

I express my sincere gratitude to R. Gavriil Davydov, David Reid and R. Eliezer Rahman for their assistance. The discussion of the article was attended by Academician of the Russian Academy of Sciences Shipov G.I., Ph.D. Lukyanov V.A., Lebedev V.A., Prokhorov S.G. and Khramikhin V.P. Also, the author is grateful for the support of Salova M.N., Morozova T.S., Przhigodsky S.V., Maslov A.N., Bolotov A.Yu., Ph.D. Levi T.S., Musanov S.V., Batanova L.A., Ph.D. Myshelov E.P., Chivikov E.P.

References

Shipov, G. (1998). ”A Theory of Physical Vacuum”. Moscow ST-Center, Russia ISBN 5 7273-0011-8.
Chambers, A. . (2004). ”Modern Vacuum Physics”. Boca Raton: CRC Press, 2004. — ISBN 0-8493-2438-6.
Roberts, M.D. (2000). ”Vacuum Energy”. High Energy Physics” – Theory: hep–th/0012062. arXiv:hep-th/0012062. Bibcode:2000hep.th...12062R.
Barrow, J.D. (2002). ”The Book of Nothing: Vacuums, Voids, and the Latest Ideas About the Origins of the Universe”. Vintage Series. Vintage. pp. 71–72, 77. ISBN 978-0-375-72609-5. LCCN 00058894.
Di Teodoro, A. & Contreras, E. (2023). ”A vacuum solution of modified Einstein equations based on fractional calculus”. Eur. Phys. J C 83:434, arXiv:2305.15232 Related. arXiv:2305.15232.
Kiehn, R. M. (2006). ”A topological theory of the Physical Vacuum”. arXiv:gr-qc/0602118v2.
Kiehn, R. M. (2007). ”Part I. The Cosmological Vacuum from a Topological Perspective”. arXiv:0712.1180.
Okun, L. B. (2012). ”On the concepts of vacuum and mass and the search for higgs”. Modern Physics Letters A. Vol. 27. - P. 1230041. arXiv:1212.1031. [CrossRef]
Sedov, L.I. (1994) ”Continuum mechanics”. T.1. – M.: Nauka, 1994 [in Russian].
I. Kozlov, A. I. I. Kozlov, A. I. Logvin, and V. A. Sarychev (2005) ”Polarization of radio waves”. Moscow: Radio engineering, 2005. -703 pp. ISBN 5-93108-074-0 [in Russian].
Petoukhov, S.V. (2008). ”Matrix genetics, algebras of the genetic code, noise-immunity”. Moscow: RCD, 316 p. ISBN 978-5-93972-643-6 http://petoukhov.com/matrix-genetics-petoukhov-2008.pdf (in Russian).
Petoukhov, S.V. (2020). ”The rules of long DNA-sequences and tetra-groups of oligonucleotides”. arXiv:1709.04943v6.
Gaukhman, M.Kh. (2007). Algebra of signatures “NAMES” (orange Alsigna). - M.: LKI, 2007, p.228, ISBN 978-5-382-00077-0, (available at на www.alsigna.ru) [in Russian].
Gaukhman, M.Kh. (2007). ”Algebra of signatures “Emptiness” (yellow Alsigna). - M.: URSS, 2007. - 308 pages. ISBN 978-5-382-00580-5, (available at на www.alsigna.ru).
Gaukhman, M.Kh. (2008). ”Algebra of Signatures “Particles” (Green Alsigna). - M.: Librokom, 2008. - 422 pages. ISBN +978-5-397-00403-9, (available at www.alsigna.ru) [in Russian].
Gaukhman, M.Kh. (2017). ”Algebra of Signatures “Massless Physics” (violet Alsigna). Moscow: Filin, 2017. ISBN 978-5-9216-0104-8 (available at http://metraphysics.ru/).
Tyurin, Yu.I. , Chernov I.P., Kryuchkov Yu.Yu. (2009). “Optics”. Tomsk Polytechnic University Publishing House, p. 240, ISBN 5-98298-434-5 [in Russian].
Peatross, J. , Ware M. (2015). “Physics of Light and Optics”. Brigham Young University, p. 338, ISBN 978-1-312-92927-2.

Figure 1. a) Laser beams of light in vacuum, visualized with a fine sol; b) A 3-dimensional lattice in a “vacuum” consisting of mutually perpendicular monochromatic light rays with a wavelength λ_m,n, while the edge length of a given cubic cell is ε_m,n ~ 10²λ_m,n.

Figure 2. Discrete set of nested λ_m,n-vacuums of the same. 3-dimensional void volume, where λ_m,n > λ_m+1,n+1 >λ _m+2,n+2 >λ_m+3,n+3 ….

Figure 3. Experimental data on the thickness of the laser beam depending on the length. wave λ of the corresponding monochromatic radiation.

Figure 4. Illustration of a curved λ_m,n-vacuum embedded in curved λ_f,d-vacuum (where λ_f,d >λ_m,n).

Figure 5. Non-curved 3D light lattice of λ_m,n-vacuum, revealed from the “vacuum” (emptiness) by means of mutually perpendicular monochromatic rays of light with a wavelength λ_m,n. The cells of such a lattice are cubes with edge length ε _m÷n ~ 10²λ_m,n.

Figure 6. Sixteen 3-bases at the central point O of the studied volume of λ_m,n-vacuum a) 8 internal 3-bases; b) 8 outer 3-antibases; c) adjacent 3-bases.

Figure 7. Sixteen 4-bases starting at point O, obtained by adding to eight 3-bases (Figure 6a) of the fourth time axis and adding to eight 3-antibases (Figure 6b) the fourth anti-time axis.

Figure 8. An affine 4-dimensional space, the directions of the axes of which are given by the 4-basis e⁵(e₀⁽⁵⁾,e₁⁽⁵⁾,e₂⁽⁵⁾,e₃⁽⁵⁾) with the conventional signature {+ + + +}.

Figure 9. The chessboard.

Figure 10. Illustration of the full correspondence of the 16 stignatures of the matrix (3) to the 16 chess pieces.

Figure 11. Trigrams and hexagrams of the I Ching (Book of Changes).

Figure 12. Tree of ten Sefirot (Qualities).

Figure 13. Two 4-bases with different stignatures.

Table 1. Stignatures of affine spaces.

4-basis	Stignature	4-basis	Stignature
e¹ (e₀⁽¹⁾, e₁⁽¹⁾, e₂⁽¹⁾, e₃⁽¹⁾) = = (1, 1, –1, 1) → {+ + – +} e² (e₀⁽²⁾, e₁⁽²⁾, e₂⁽²⁾, e₃⁽²⁾) = = (1, –1, –1, –1) → {+ – – –} e³ (e₀⁽³⁾, e₁⁽³⁾, e₂⁽³⁾, e₃⁽³⁾) = = (1, 1, –1, –1) → {+ + – –} e⁴ (e₀⁽⁴⁾, e₁⁽⁴⁾, e₂⁽⁴⁾, e₃⁽⁴⁾) = = (1, –1, –1, 1) → {+ – – +} e_i⁽⁵⁾ (e₀⁽⁵⁾, e₁⁽⁵⁾, e₂⁽⁵⁾, e₃⁽⁵⁾) = = (1, 1, 1, 1) → {+ + + +} e⁶ (e₀⁽⁶⁾, e₁⁽⁶⁾, e₂⁽⁶⁾, e₃⁽⁶⁾) = = (1, –1, 1, –1) → {+ – + –} e⁷ (e₀⁽⁷⁾, e₁⁽⁷⁾, e₂⁽⁷⁾, e₃⁽⁷⁾) = = (1, 1, 1, –1) → {+ + + –} e⁸ (e₀⁽⁸⁾, e₁⁽⁸⁾, e₂⁽⁸⁾, e₃⁽⁸⁾) = = (1, –1, 1, 1) → {+ – + +}		e⁹ (e₀⁽⁹⁾, e₁⁽⁹⁾, e₂⁽⁹⁾, e₃⁽⁹⁾) = = (–1, 1, –1, 1) → {– + – +} e¹⁰ (e₀⁽¹⁰⁾, e₁⁽¹⁰⁾, e₂⁽¹⁰⁾, e₃⁽¹⁰⁾) = = (–1, 1, –1, –1) → {– – – –} e¹¹ (e₀⁽¹¹⁾, e₁⁽¹¹⁾, e₂⁽¹¹⁾, e₃⁽¹¹⁾) = = (–1, 1, –1, –1) → {– + – –} e¹² (e₀⁽¹²⁾, e₁⁽¹²⁾, e₂⁽¹²⁾, e₃⁽¹²⁾) = = (–1, –1, –1, 1) → {– – – +} e¹³ (e₀⁽¹³⁾, e₁⁽¹³⁾, e₂⁽¹³⁾, e₃⁽¹³⁾) = = (–1, 1, 1, 1) → {– + + +} e¹⁴ (e₀⁽¹⁴⁾, e₁⁽¹⁴⁾, e₂⁽¹⁴⁾, e₃⁽¹⁴⁾) = = (–1, –1, 1, –1) → {– – + –} e_i⁽¹⁵⁾ (e₀⁽¹⁵⁾, e₁⁽¹⁵⁾, e₂⁽¹⁵⁾, e₃⁽¹⁵⁾) = = (–1, 1, 1 –1) → {– + + –} e¹⁶ (e₀⁽¹⁶⁾, e₁⁽¹⁶⁾, e₂⁽¹⁶⁾, e₃⁽¹⁶⁾) = = (–1, –1, 1, 1) → {– – + +}

Table 2. Relationship between digits, BCD and stignatures.Table 3. An example of an arithmetic operation for adding stignatures.

Table 3. An example of an arithmetic operation for adding stignatures.

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

MDPI Initiatives

Important Links

Choose an area of interest and we will send you notifications of new preprints at your preferred frequency.

Disclaimer

Geometrized Vacuum Physics. Part I. Algebra of Stignatures

Abstract

1. Introduction

2. Materials and Method

2.1. Longitudinal stratification of ideal vacuum into λm,n-vacuums

2.2. Geodesic lines of the curved section λm,n-vacuum

2.3. Sixteen rotating 4-bases

2.4. Stignature of an affine 4-dimensional space

2.5. Stignature matrix properties

5.1. The sum of all 16 stignatures from matrix (3) is equal to the zero stignature

5.2. The sum of all 64 signs included in the matrix (3) is equal to zero, that is, it satisfies the vacuum balance condition:5.3. There are four binary combinations of signs “+” and “–”, which we will call binary stignatures:

5.4. The Kronecker union of the two-row matrix of binary signatures (9) forms the stignatures matrix (3):

5.5. Stignature matrix (3) can be represented as a sum of diagonal and antisymmetric matrices5.6. Hadamard stignatures for noise-proof encryption of information

5.7. Noise-immune coding of genetic information

5.8. Binary-coded decimal and Arithmetic of Stignature

5.10. Classes of stignature

5.11. Chess analogy

5.12. I Ching analogy

5.13. Hebrew analogy

5.14. Minkowski’s affine stignatures and musical harmony

5.17. Pythagorean analogy (Algebra of Signatures)

2.6. Spectra-stignature analysis

3. Conclusions

Acknowledgments

References

MDPI Initiatives

Important Links

Subscribe

2.1. Longitudinal stratification of ideal vacuum into λ_m,n-vacuums

2.2. Geodesic lines of the curved section λ_m,n-vacuum