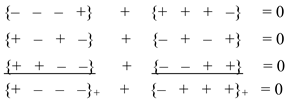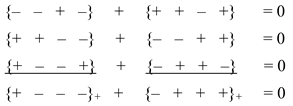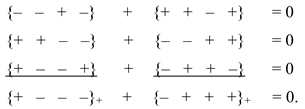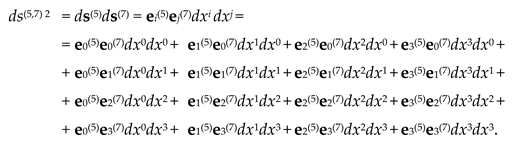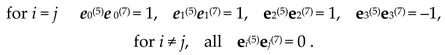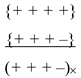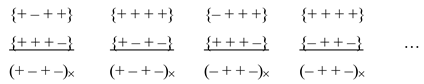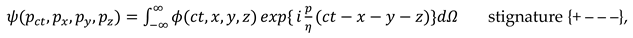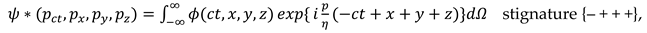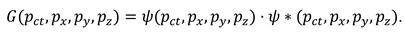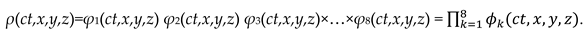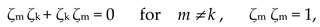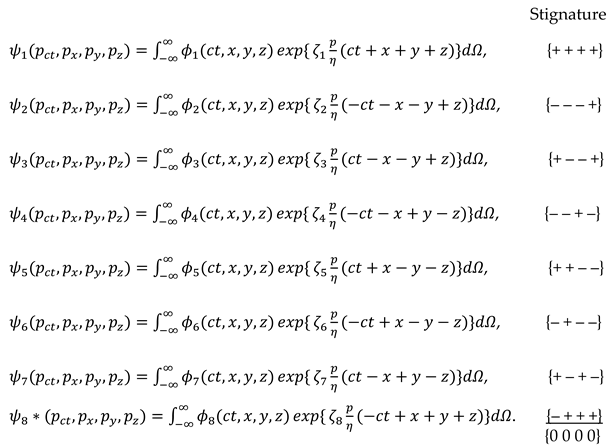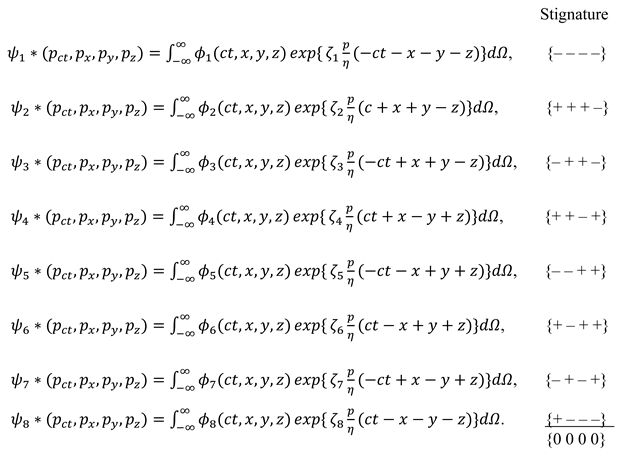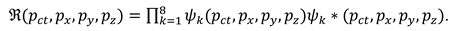2.1. Longitudinal stratification of ideal vacuum into λm,n-vacuums
Consider a 3-dimensional volume of an ideal vacuum, in which there are no particles and no curvature. In what follows, for brevity, the ideal vacuum will be referred to as “vacuum”.
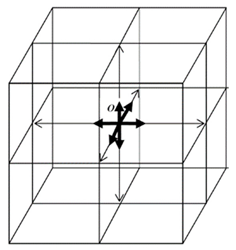
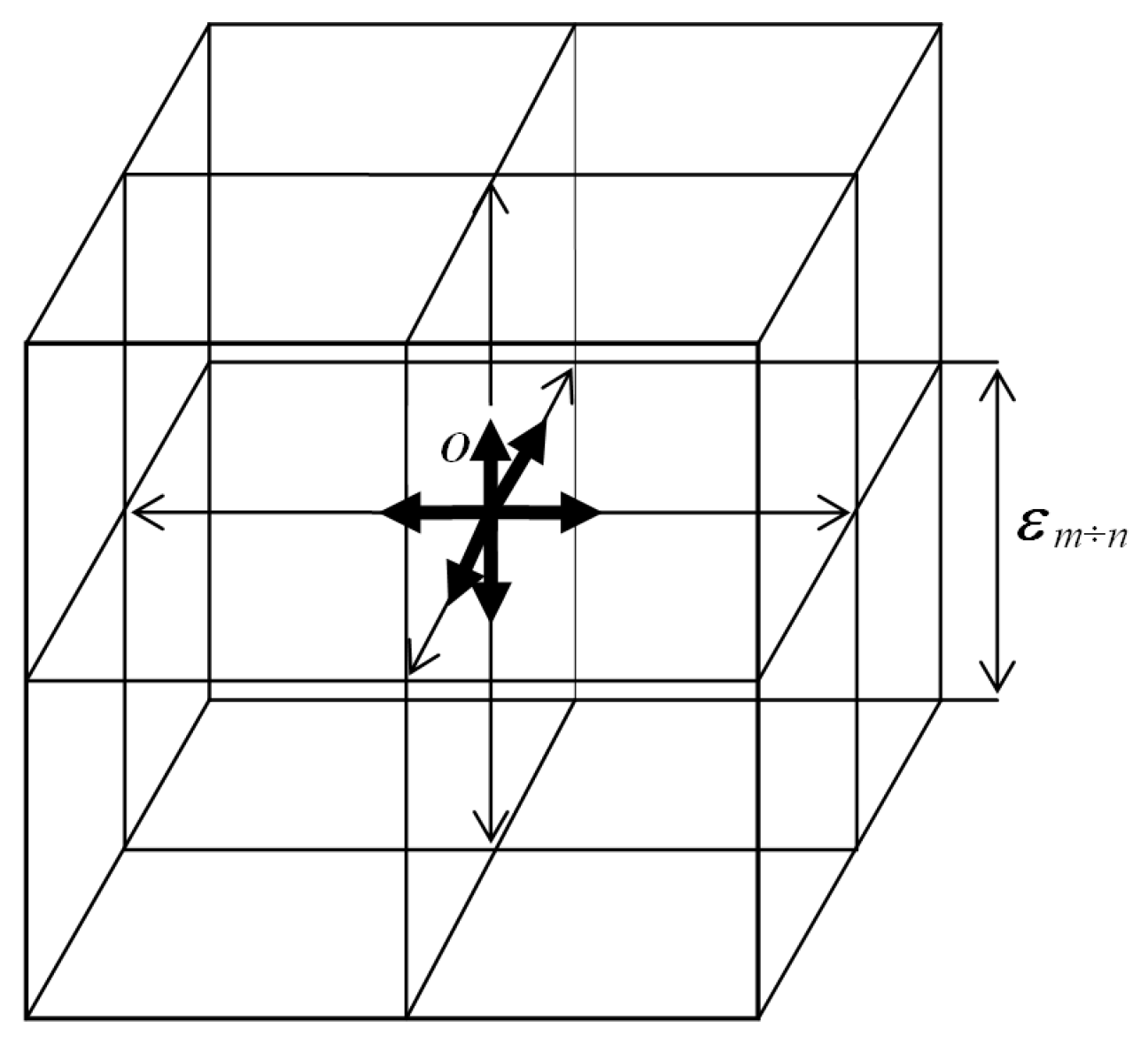
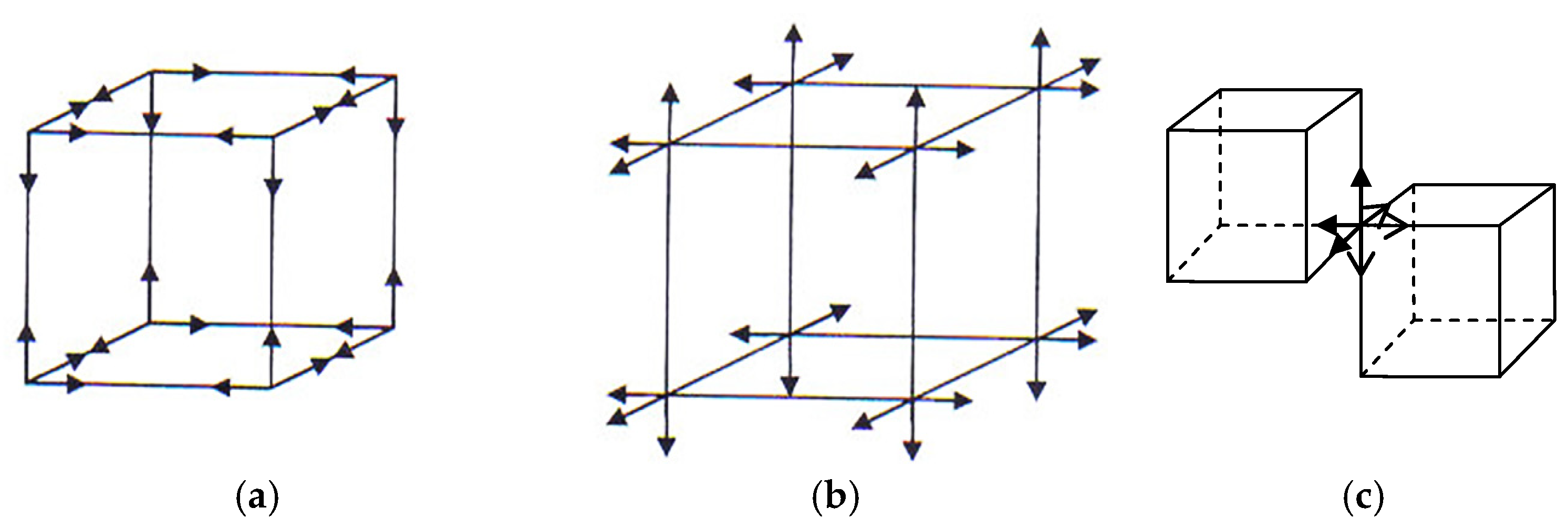
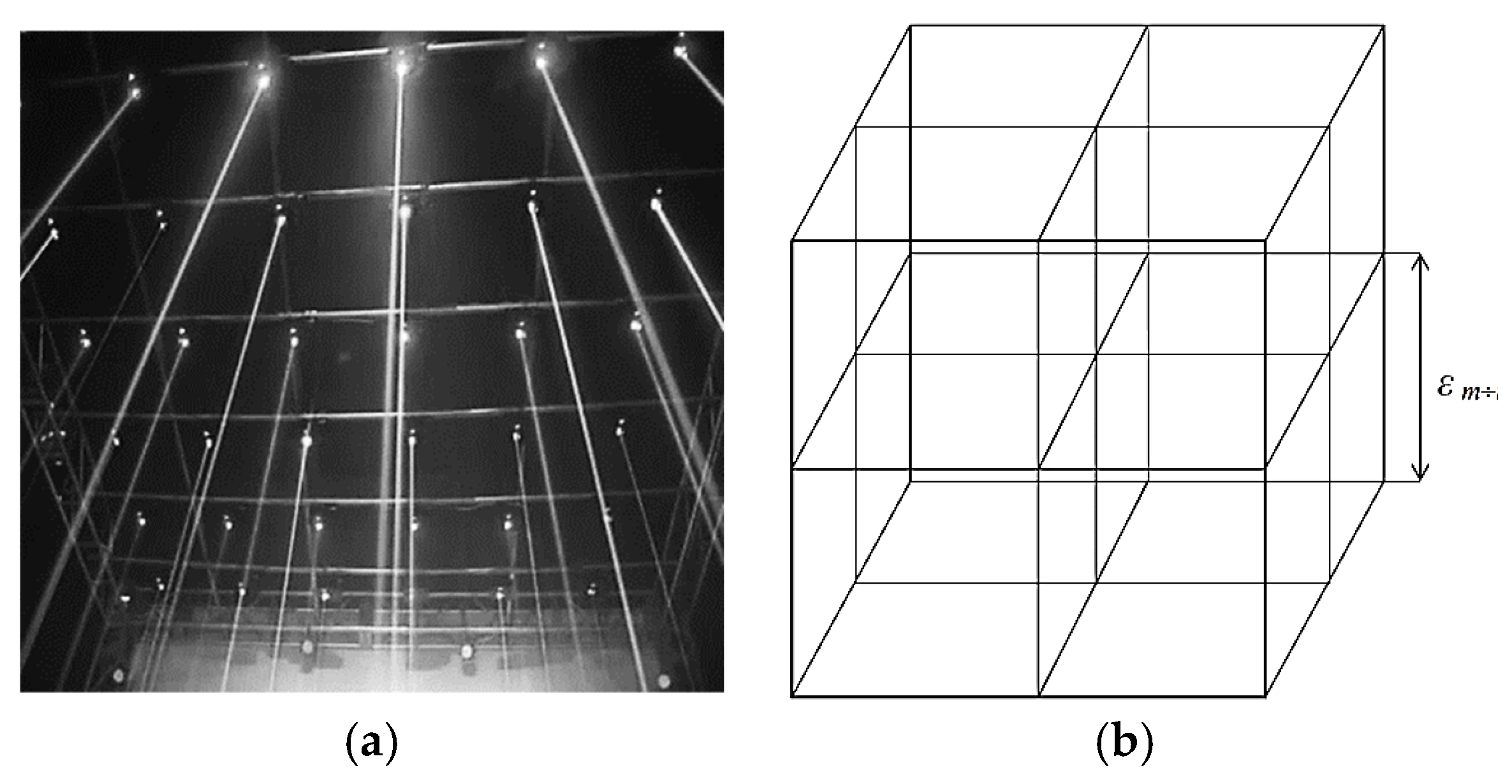
Let’s probe this volume of “vacuum” with laser beams from three mutually perpendicular directions, so that the beams form a 3-dimensional cubic lattice (
Figure 1a,b).
Rays of light in a vacuum are not visible, but they can be visualized with a finely dispersed sol. Of course, a “vacuum” filled with a sol is not a perfect vacuum. Nevertheless, the rays propagate in the “vacuum” itself (i.e., between the particles of the sol), while the influence of the sol on the metric-dynamic properties of the macroscopic volume of the “vacuum” in the case under consideration can be neglected. In addition, if the sol is removed from this “vacuum” volume, then the rays will still remain in it, although they will not be visible.
Figure 1.
a) Laser beams of light in vacuum, visualized with a fine sol; b) A 3-dimensional lattice in a “vacuum” consisting of mutually perpendicular monochromatic light rays with a wavelength λm,n, while the edge length of a given cubic cell is εm,n ~ 102λm,n.
Figure 1.
a) Laser beams of light in vacuum, visualized with a fine sol; b) A 3-dimensional lattice in a “vacuum” consisting of mutually perpendicular monochromatic light rays with a wavelength λm,n, while the edge length of a given cubic cell is εm,n ~ 102λm,n.
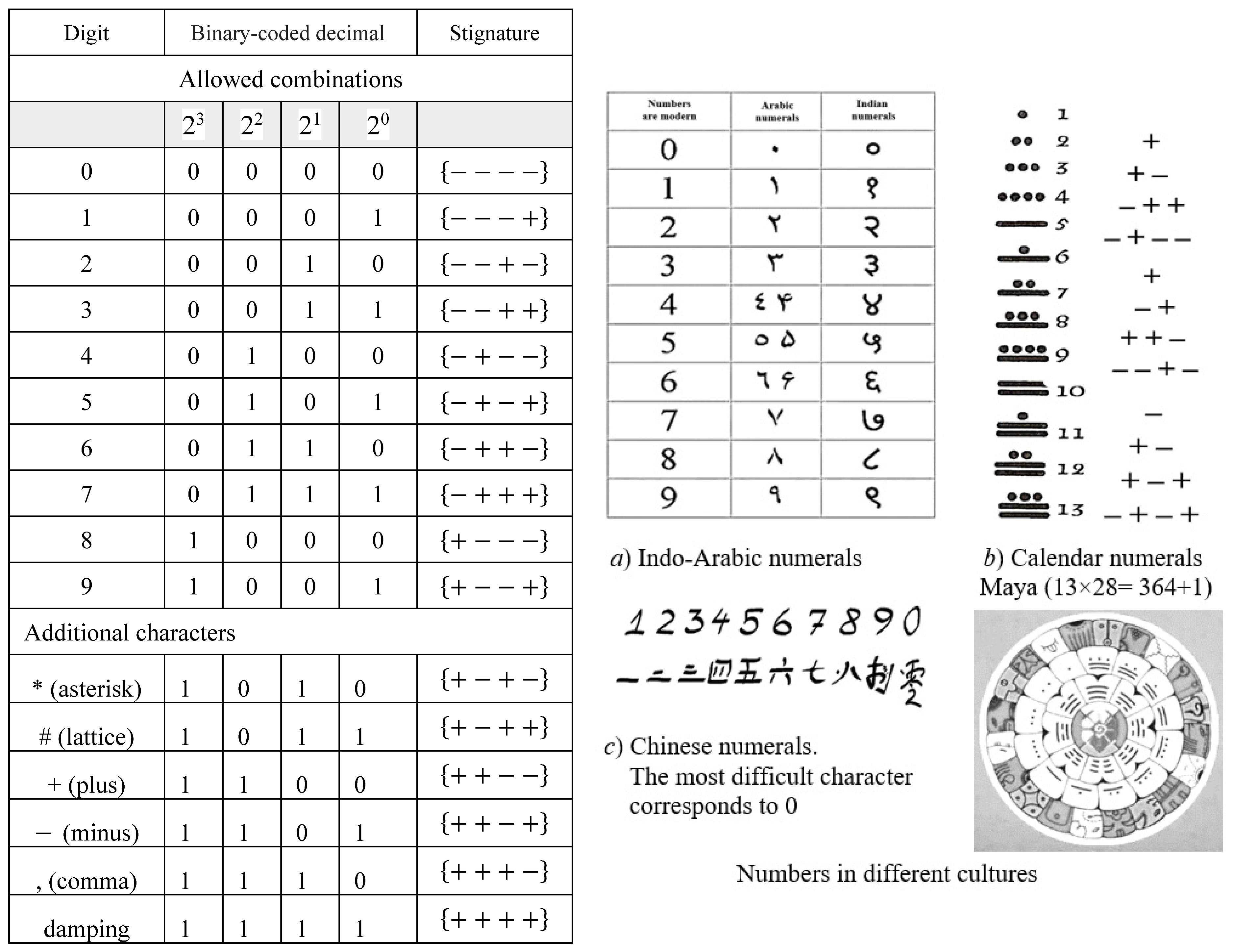
Let, for example, to probe of “vacuum” are used laser beams of light (i.e., narrowly directed monochromatic electromagnetic oscillations) with a wavelength
λ-4,-5, taken from the range of lengths Δ
λ =10
–4 ÷10
–5 cm. Then we get a 3-dimensional lattice consisting of such mutually perpendicular laser beams, with the edge length of one cubic cell
ε-4,-5 ~ 100
λ-4,-5 (see
Figure 1b). This cubic lattice will be called
λ-4,-5-vacuum (or 3D
-4,-5-landscape).
We divide the entire range of electromagnetic (light) wave lengths into a set of subranges Δ
λ = 10
m ÷ 10
n cm, where
n =
m +1 (m and n are integers). Then, in the same way as shown in
Figure 1, we will probe the studied volume of the “vacuum” with monochromatic light rays with wavelengths
λm,n from all subranges Δ
λ = 10
m ÷ 10
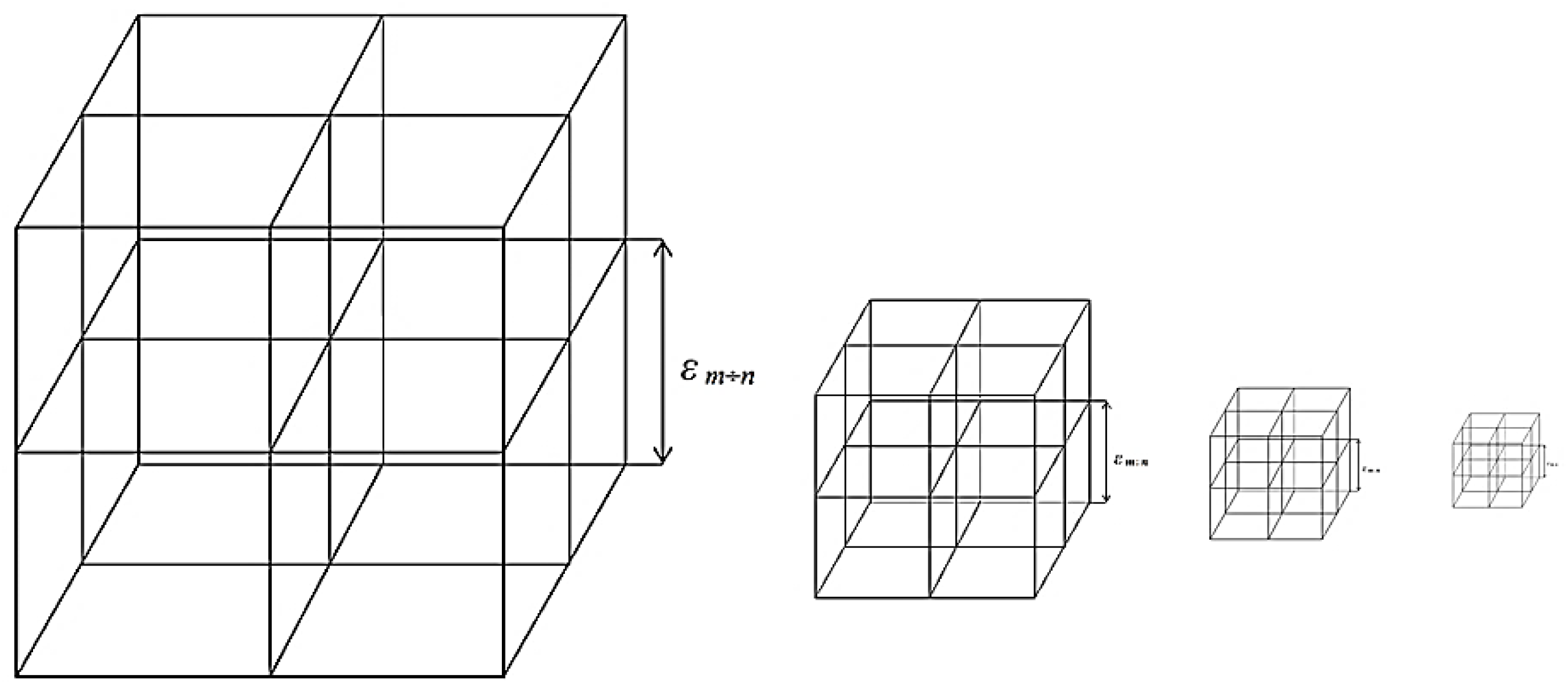
n cm. As a result, we obtain an almost infinite number of nested
λm,n-vacuums (i.e., 3Dm,n-landscapes) with the corresponding lengths of edges of cubic cells
εm,n ~ 100
λm,n (see
Figure 2).
The value of the edge of the cubic cell of each
λm,n-vacuum
follows from the condition of applicability of geometric optics λm,n → 0, i.e., when the thickness of the light beam is much smaller than the value of the corresponding cubic cell, while the beam thickness can be neglected.
The question remains open: – “Are there any restrictions on the frequency ω or the wavelength λ of the electromagnetic wave, both in the direction of their increase, and in the direction of decrease? If the critical values: ωmax = 2πс/λmax and ωmin = 2πс/λmin exist, these will be very important characteristics of the vacuum. Today, as far as the author knows, the frequency range of observed electromagnetic waves extends from 2 Hz to 1020 Hz, while no restrictions on the expansion of this range have been experimentally found.
2.5. Stignature matrix properties
Stignature matrix (3) was obtained as a result of the development of vacuum physics. However, this matrix is a separate universal mathematical object that can be applied in various branches of scientific knowledge.
Let’s list some properties of the stignature matrix (3).
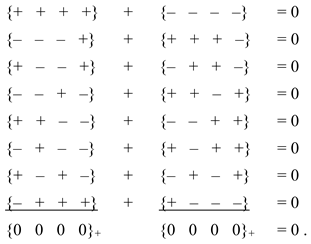
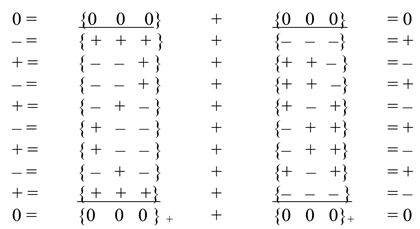
5.1. The sum of all 16 stignatures from matrix (3) is equal to the zero stignature
Ex. (4) can be represented in the following form
where the summation of the signs “+” and “–” is performed in each row and column in any direction according to the rules:
Operations with signs in (5) are performed in rows and columns (i.e., in ordered rows or by ranking), therefore this expression is called a ranking expression, and two columns consisting of stignatures are called “rankings”. The ranking expression (5) reveals the internal structure of the void and is called “zero splitting”.
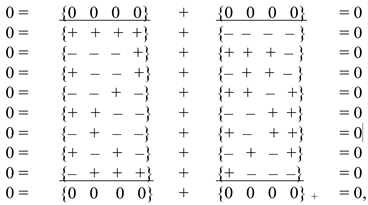
5.2. The sum of all 64 signs included in the matrix (3) is equal to zero, that is, it satisfies the vacuum balance condition:
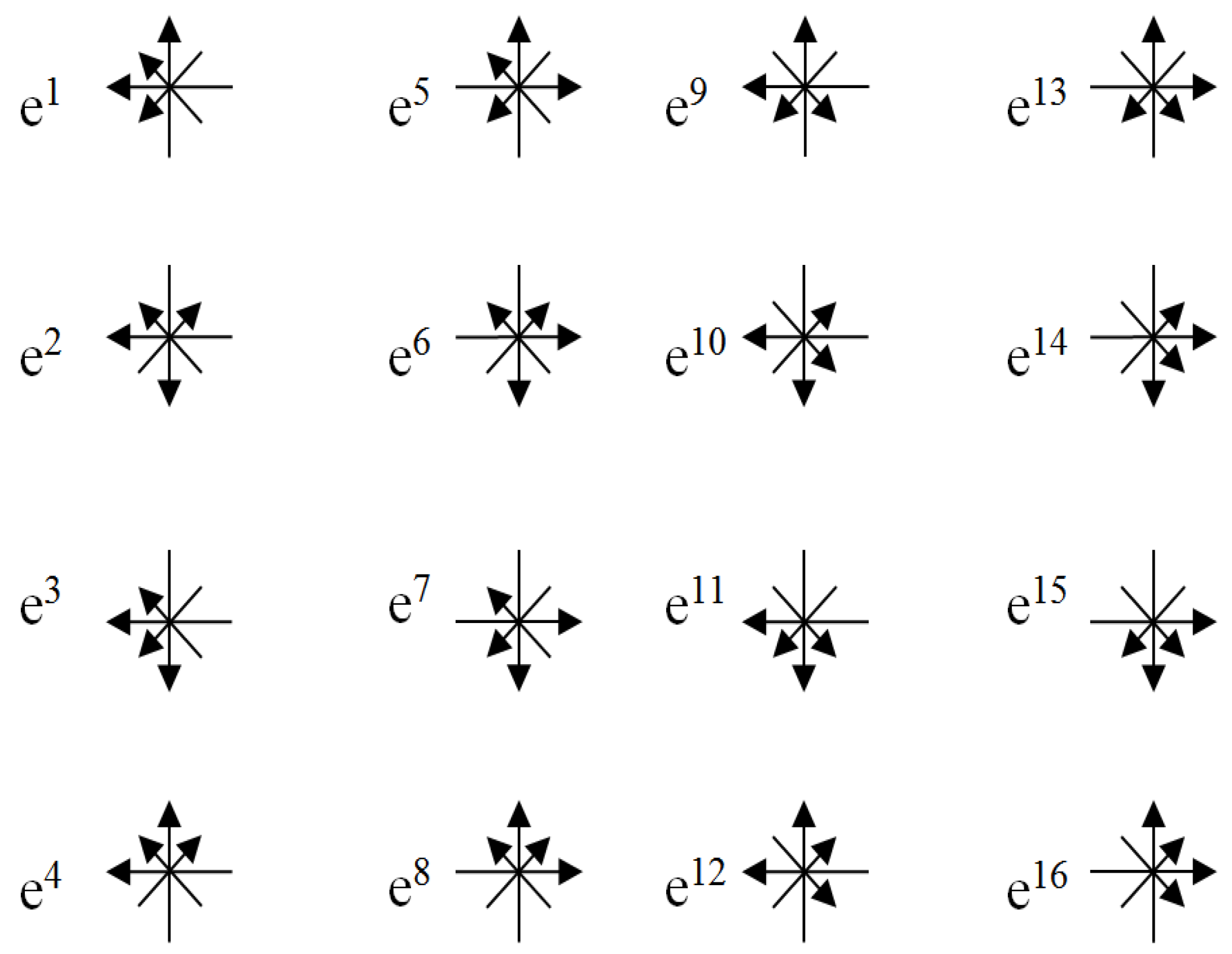
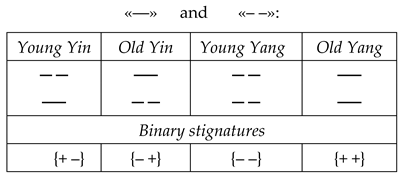
5.3. There are four binary combinations of signs “+” and “–”, which we will call binary stignatures:
or in transposed form
Combine (
) binary stignatures (8) or (9) according to the rules:
and etc., or
As a result, we get 16 signatures of the matrix (3):
5.4. The Kronecker union of the two-row matrix of binary signatures (9) forms the stignatures matrix (3):
where ⊕ is a symbol denoting the Kronecker union of binary stignatures according to the rules (10).
5.5. Stignature matrix (3) can be represented as a sum of diagonal and antisymmetric matrices
5.6. Hadamard stignatures for noise-proof encryption of information
If we return the original units to the two-row stignatures (11), then we get 16 two-row matrices
of these, eight matrices are:
are Hadamard matrices, because they satisfy the condition
When raising any of the matrices (16) to Kronecker powers, the Hadamard matrices H(
n) are again obtained, satisfying the condition:
where I is an
n×
n diagonal identity matrix:
For example,
and so on according to the algorithm
Hadamard matrices are used to construct error-correcting codes. In particular, Hadamard matrices are used to decipher the genetic code [
11,
12].
If in the matrices (20) and (21) again instead of 1 and –1 we use the signs {+} and {–}, then we obtain the rule for raising two-row stignatures to the Kronecker power, for example,
double row stignatures,
corresponding to matrices (15) will be called two-row Hadamard stignatures.
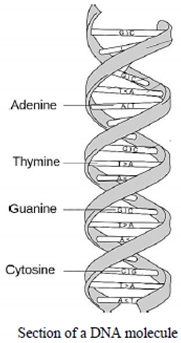
5.7. Noise-immune coding of genetic information
It was shown in [
11,
12] that Hadamard matrices (15) or two-row stignatures (25) can be used as the basis for studying noise-resistant genetic information. Deoxyribonucleic acid (DNA) molecules are built from four chemical elements (nucleotides):
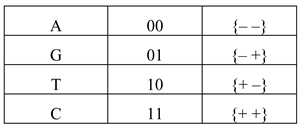
These four nucleotides correspond to two bits of information or four binary stignatures (9)
Nucleotides (27) form: doublets, triplets and other more complex combinations of informational polymer, i.e., DNA molecules [
11,
12]:
These combinations of nucleotides correspond to the combinations of the “+” and “–” signs obtained from the two-row Hadamard stignatures (25), for example
Thus, the Algebra of Stignatures can be used to develop the theory of matrix coding of the space-time continuum.
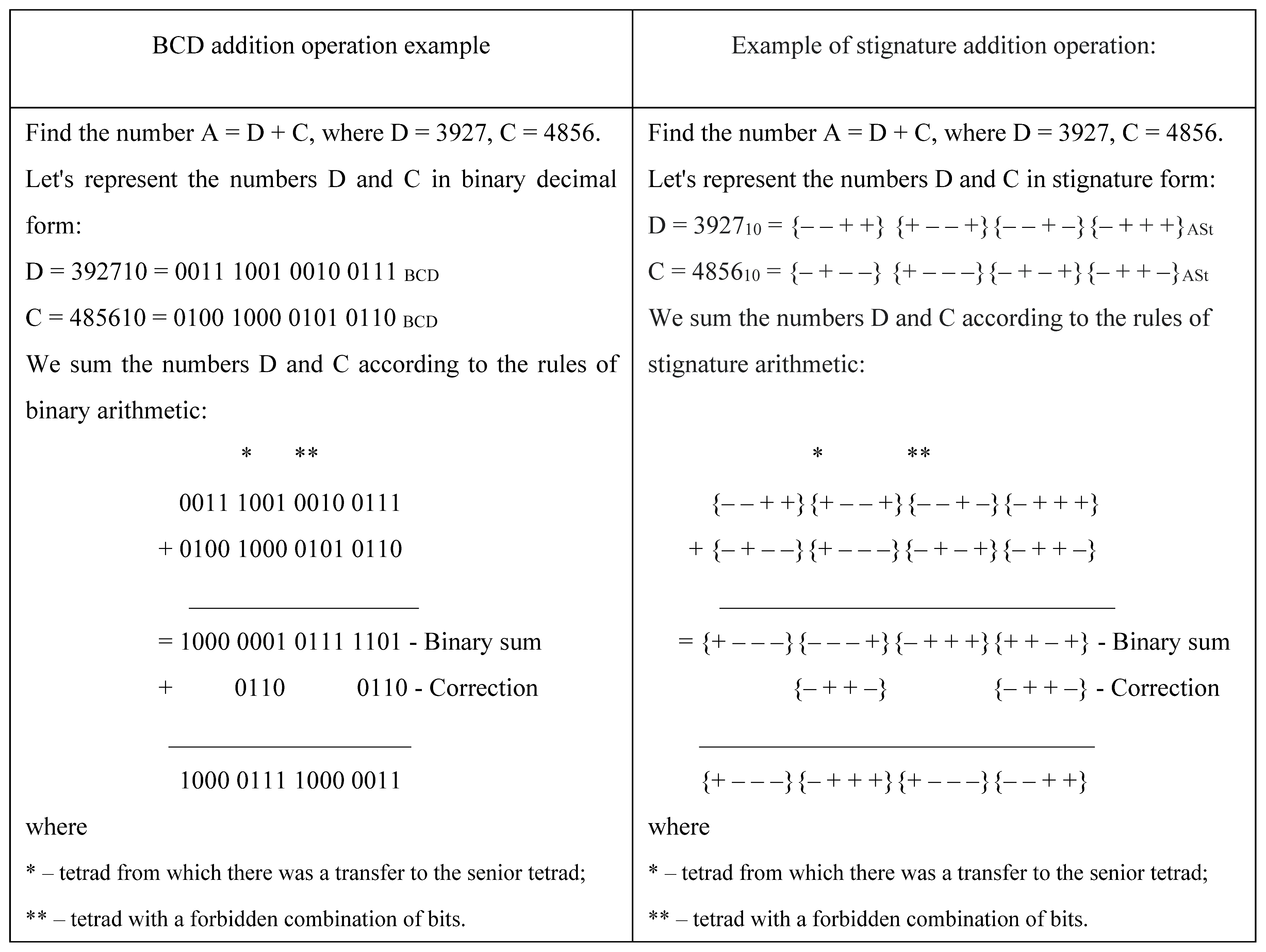
5.8. Binary-coded decimal and Arithmetic of Stignature
There is a complete correspondence between the binary-coded decimal (BCD) of digits and the 16 affine space stignatures from the matrix (3):
Table 2.
Relationship between digits, BCD and stignatures.
Table 2.
Relationship between digits, BCD and stignatures.
From
Table 2 it follows that if 0 is replaced by “–”, and 1 is replaced by “+”, then digits from matrix (3) can be assigned numbers. In addition, by analogy with binary-decimal arithmetic, the arithmetic of stignatures can also be constructed, as shown in the example in
Table 3.
Arithmetic of Stignature can be used to describe the nodal configurations of affine spaces.
5.9. “Colored” quaternions
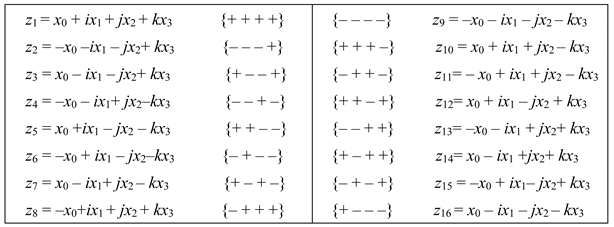
Sixteen stignatures (3) correspond to 16 types of “colored” quaternions:
The complete set of “colored” quaternions (31) can be applied in various branches of mathematics and physics. By direct calculation it is easy to verify that the sum of all 16 types of “colored” quaternions (31) is equal to zero
Expression (32) shows that the superposition (addition) of all types of “colored” quaternions is balanced with respect to zero, i.e., satisfies the “vacuum balance” condition.
5.10. Classes of stignature
The signatures included in the matrix (3) can be divided into three classes:
Class 1: all signs in the stignature are the same - 2 stignatures:
Class 2: two identical signs in a stignature - 6 stignatures:
Class 3: three identical characters in a stignature - 8 stignatures:
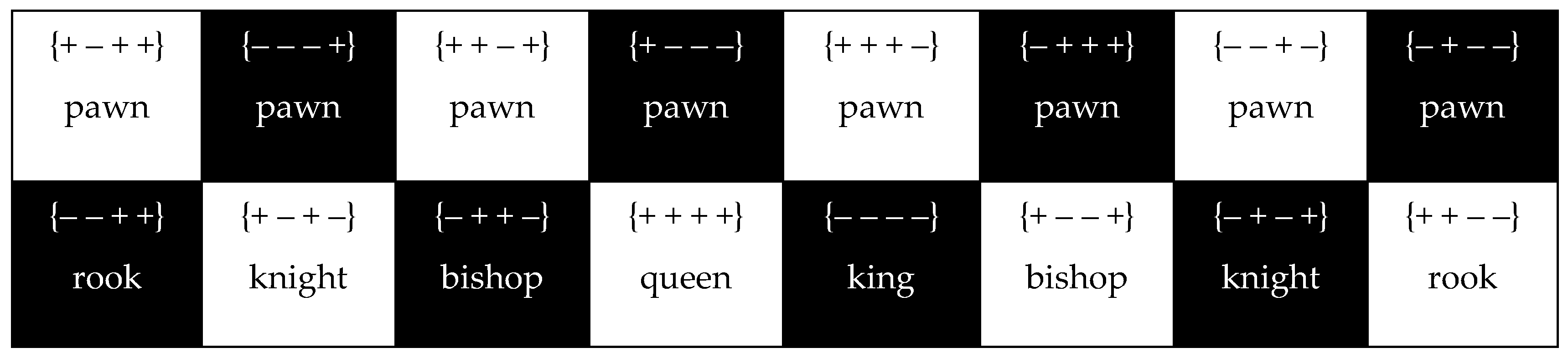
5.11. Chess analogy
The chessboard has 8 × 8 = 64 cells: 32 of them are black and 32 are white (see
Figure 9). Also, in the matrix of signatures (3) there are 16 × 4 = 64 characters, of which 32 are plus “+” and 32 minus “–”:
At the beginning of the game, there are 32 chess pieces on the chessboard: 16 white and 16 black (see
Figure 9). Also, in the matrix (3) there are 16 stignatures that coincide in properties with chess pieces in full accordance with their three classes (33) – (35) (see
Figure 10):
Matrix (3) can describe both “light” (i.e., light 3Dm,n-landscapes), which corresponds to 16 white chess pieces, and “darkness” (emptiness), which corresponds to 16 black chess pieces.
5.12. I Ching analogy
The I Ching (Chinese Book of Changes) is based on two Beginnings:
in the Algebra of Stignaturs there are also two initial signs:
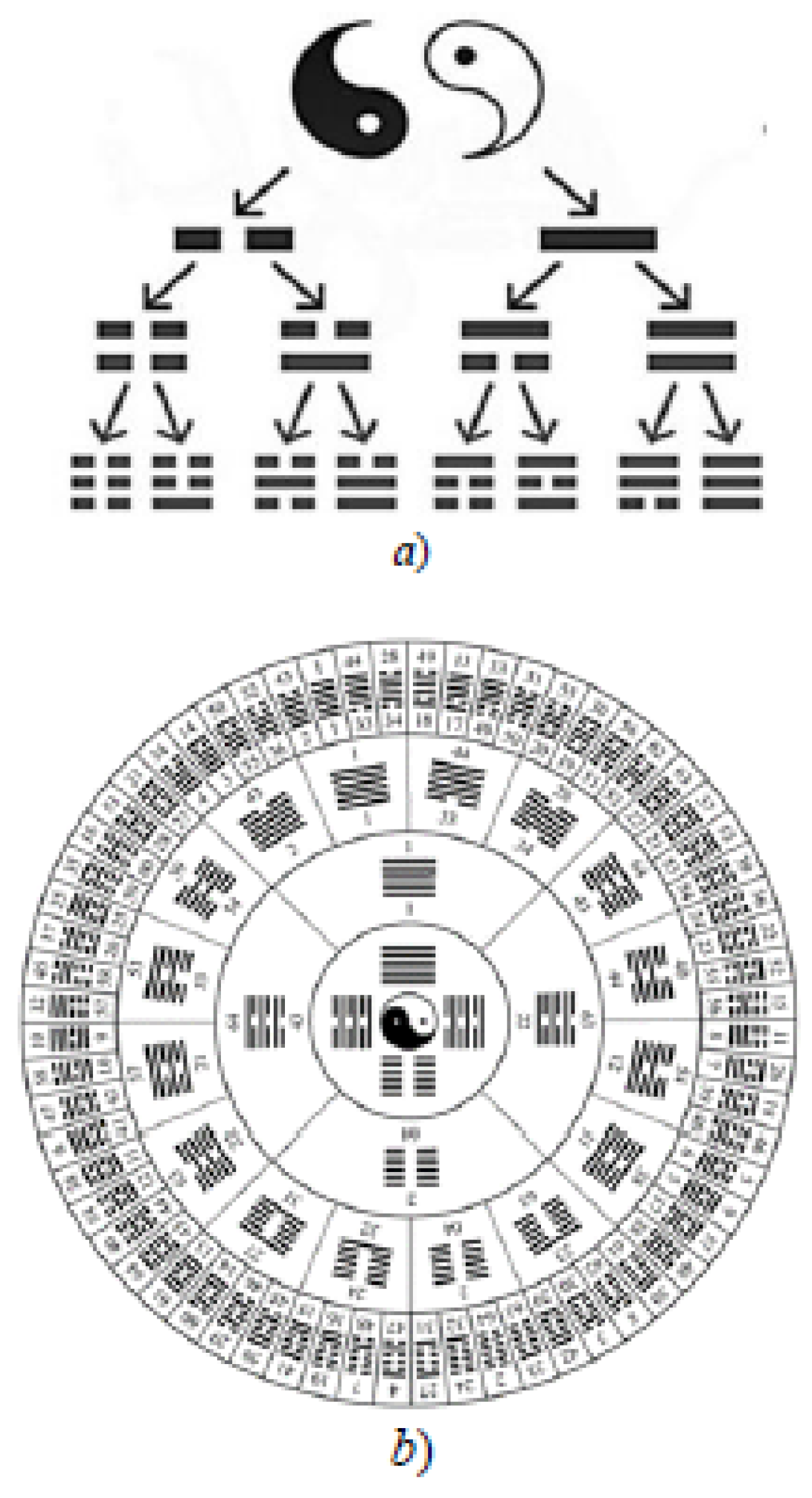
The Book of Changes uses 8 trigrams (see
Figure 11a). Similarly, there are eight 3-bases in the Algebra of Stignatures (see
Figure 6a) with the following stignatures
and eight 3-antibases (
Figure 6b) with opposite stignatures
In the Book of Changes, all possible combinations of two trigrams generate 64 hexagrams (
Figure 11b), and in the Algebra of Stignatures, 64 combinations of each 3-basis with stignatures (36) with each 3-antibasis with opposite stignatures (37) are possible.
Figure 11.
Trigrams and hexagrams of the I Ching (Book of Changes).
Figure 11.
Trigrams and hexagrams of the I Ching (Book of Changes).
The three-logic of the Book of Changes is consistent with the four-logic of the Stignature Algebra if in the ranking expression (5) one column of signs is transferred to another side of equalities:
The Book of Changes also uses four combinations of two principles:
Similarly, in the Algebra of Signatures, four binary combinations of signs “+” and “–” (9) are possible:
from which affine space signatures (11) are formed, etc.
5.13. Hebrew analogy
Judaism is based on Algorithms for revealing the Great Name of the GOD
[
13]. Further, instead of Hebrew letters, the transliteration
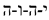
H′ V H I will be used.
One of the endless Revelations of the Name H′ V H I is called “Etz Chaim” (“Tree of Life” or “Tree of the Sefirot”):
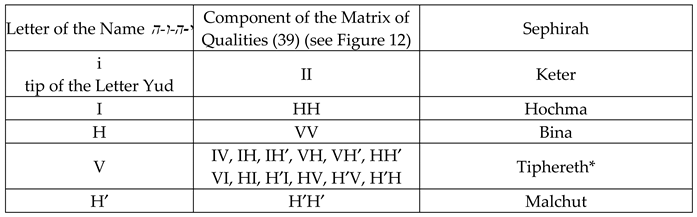
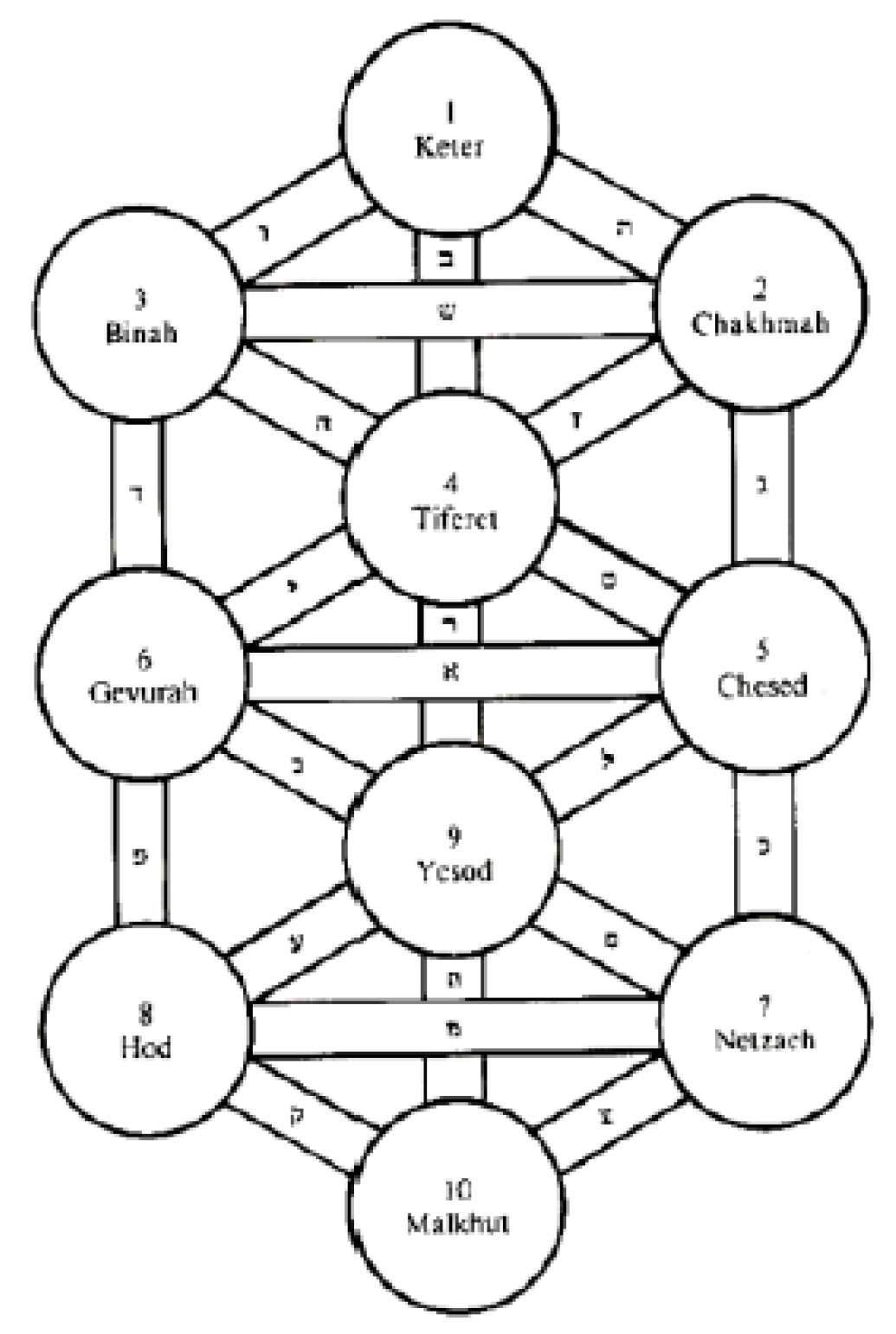
The components of this matrix correspond to 10 Sephira (i.e., Qualities) of Spirituality:
Figure 12.
Tree of ten Sefirot (Qualities).
Figure 12.
Tree of ten Sefirot (Qualities).
where the Sefira Tipheret* consists of six dual Sefirot [
13]:
The Qualities Matrix (39) can be written as the sum of two matrices
Similarly, the signature matrix (3) is the result of raising the two-row matrix to the second Kronecker power [
13]
This matrix can also be represented as the sum of the diagonal and antisymmetric matrices (13)
Comparing the matrices (40) and (41), we find that the stignatures of the matrix (3) can reflect the characteristic properties of the corresponding Sefirot (Qualities) of the “Tree of Life” [
13]
Thus, the following analogy can be traced between the ten Sephira (Quality) and the sixteen stignatures of the matrix (3):
This analogy corresponds to the criteria of “Zero Philosophy”, emanating from “EIN SOF, Baruhu” (INFINITE NOTHING, Blessed be HE). In turn, from the “Zero Philosophy” follows the condition of “vacuum balance” and the structure of “split zero” (5), on which the geometrized vacuum physics and, in particular, the Algebra of Stignatures are based.
Let’s return to the representation of the Great Name of GOD
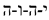
in the form of binary stignatures (9)
One of the infinite Algorithms for revealing the Name of the GOD
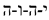
H′ V H I is associated with 24 combinations of permutations of the letters H′ V H I [
13]
In the Lurianic Kabbalah, twelve of these combinations correspond to the 12 hours of the Day, and the remaining twelve combinations correspond to the 12 hours of the Night.
Combining four binary stignatures (42b) according to the rules (10) in the order corresponding to combinations of four letters of the Name H′VHI (42c) leads to 24 octaves (eights) of signs, or to 24 types of combination stignatures from matrix (3):
5.14. Minkowski’s affine stignatures and musical harmony
We represent the ranking expression (5) (zero splitting) in the following simplified form
Let’s transfer the stignatures {– + + +} and {+ – – –} from the numerators of the ranks (43) to their denominators with inversion, i.e., with signs reversed. Such an operation does not violate the “vacuum balance” and leads to the ranking expression
In this case, in the denominator of the left rank in Ex. (44), the stignature of the affine Minkowski 4-space {+ – – –} was obtained, and in the denominator of the right rank in Ex. (44), the stignature of the affine 4-anti–Minkowski space { – + + +} was obtained.
Not only the ranking expression (44) leads to a balanced (with respect to zero) dyad of affine Minkowski stignatures
The following ranking expressions that preserve the vacuum balance lead to the same result:
The Algebra of Stignature can be used as a musical score of spatial harmony. Just like in music, stignatures form balanced octaves (7+1= 8) of the form (44) and chords (3+1= 4) of the form (45) – (47). Moreover, in different situations, the Algebra of Stignatures uses a different number of signs “+” and “–” in proportions in relation to the total number: 1, 1/2, 1/8, 1/16, 1/32, 1/64, etc. This corresponds to the proportions of the duration of the notes: 1, 1/2, 1/8, 1/16, 1/32, 1/64, etc.
Ancient philosophers, beginning with the Pythagoreans, believed that Space was filled with harmonious musical rhythms and proportions. Music theory was later used by Johannes Kepler in «Harmonices Mundi» (Harmony of the World), which led to the discovery of the third law of celestial mechanics. It is possible that the combination of musical techniques with the Algebra of Stignatures algorithms will also lead to interesting results.
5.17. Pythagorean analogy (Algebra of Signatures)
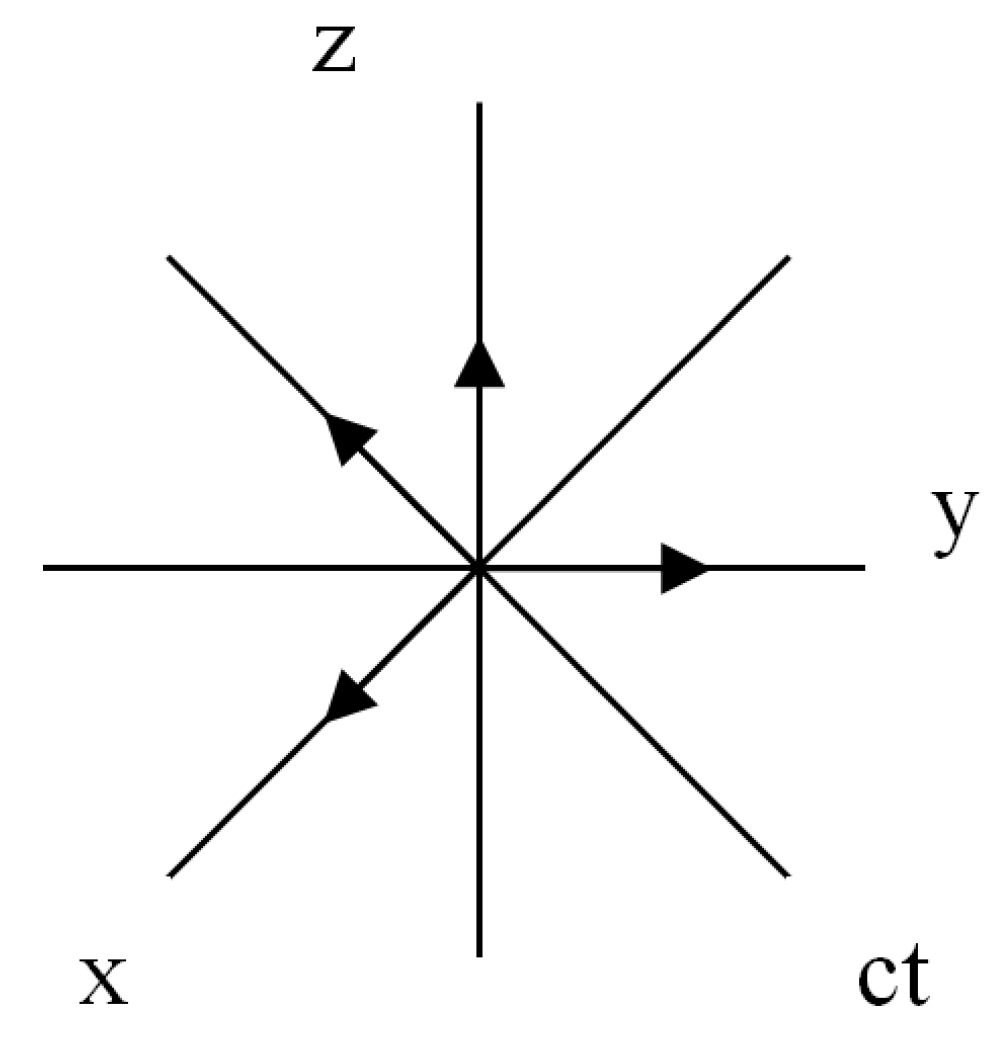
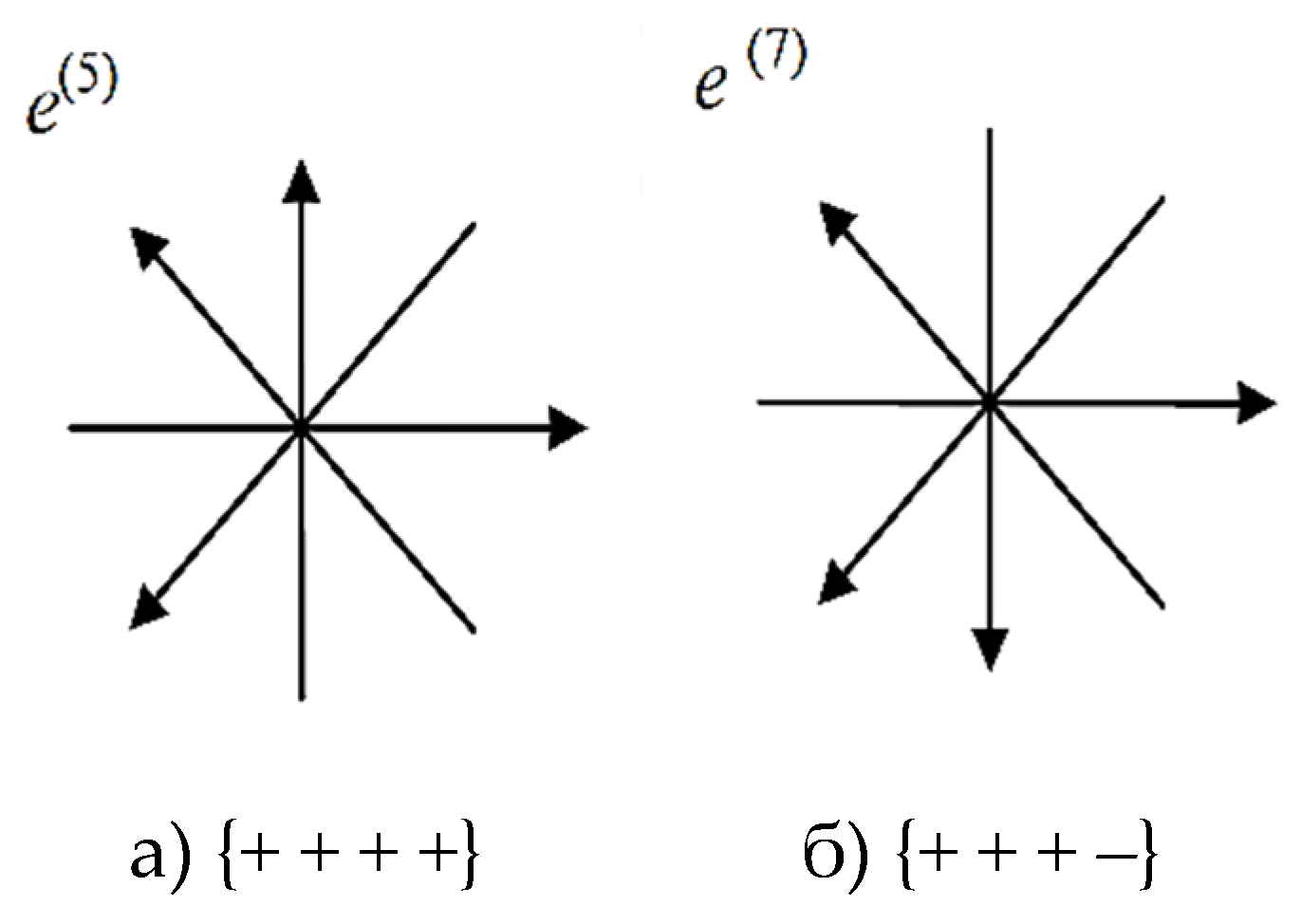
Let’s pass from affine spaces to metric spaces. For this, as an example, we use an affine space with a 4-basis
ei(7)(
e0(7),
e1(7),
e2(7),
e3(7)) (see Figs. 7 and 13) with signature {+ + + –}. In this space, we define a 4-vector
where d
xi(7) is the
i-th projection of the 4-vector d
s(7) onto the
xi(7) axis, the direction of which is determined by the basis vector
ei(7).
Similarly, we define the second 4-vector in the affine space with the 4-basis
ei(5)(
e0(5),
e1(5),
e2(5),
e3(5)) (
Figure 7 and
Figure 13), with signature {+ + + +}
We find the scalar product of 4-vectors (48) and (49)
For the case under consideration, the scalar products of basis vectors
ei(5)ej(7) are:
In this case, expression (50) takes the form of a quadratic form
“Signature” (GRT term) is an ordered set of signs in front of the corresponding terms of the quadratic form.
To determine the signature of the metric space with the metric (52), instead of performing the scalar product of vectors (50), it is enough to multiply the signs of the 4-basis stignatures shown in
Figure 13 by columns:
In the numerator of the rank (53), the signs in each column are multiplied according to the rules
the result of such multiplication is written in the denominator (under the line) of the same column. The execution of actions according to these rules will be called rank multiplication.
Just as it was done with the vectors
ds(5) and
ds(7) {see expressions (48) – (53)}, pairwise scalarly multiply vectors from all 16 affine spaces with 4 bases shown in
Figure 7. As a result, we obtain 16 × 16 = 256 metric 4-spaces with 4-intervals of the form
where
a = 1, 2, 3, … , 16;
b = 1, 2, 3, … , 16.
The signatures of these 16 × 16 = 256 metric 4-spaces can be defined, similarly to (53), by rank multiplications of the signs of the signatures corresponding to the affine spaces, for example:
Thus, point
O (see
Figure 5) is the place of intersection of all 256 metric 4-spaces with metrics (55) and stignatures (3). In this variety of intersecting metric spaces, there are many features and patterns that are studied by the Algebra of Signatures.
The fundamentals of the Algebra of Signature will be covered in the next article of this project. Here we only note that quadratic forms (i.e., metrics) of type (52), or
originate from the Pythagorean theorem
с2 =
a2 +
b2, the proof of which in about 520 BC, brought about the greatest revolution in the consciousness of mankind.
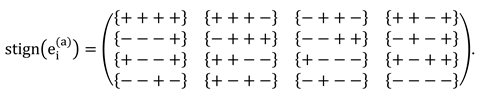
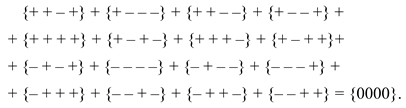
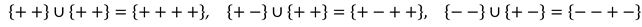 and etc.
and etc.
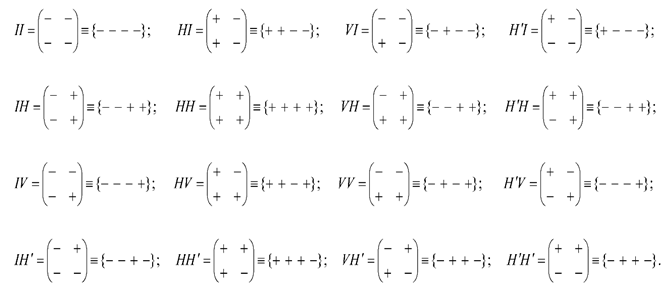
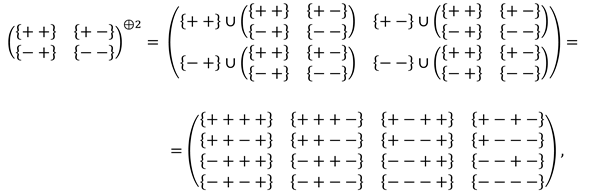
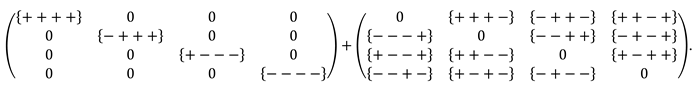
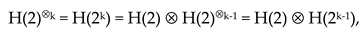

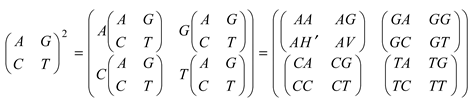
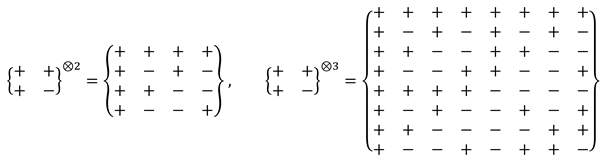
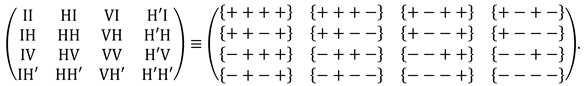
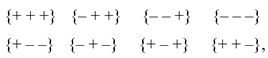
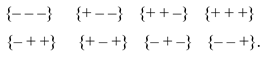
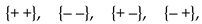
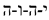 [13]. Further, instead of Hebrew letters, the transliteration
[13]. Further, instead of Hebrew letters, the transliteration 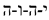 H′ V H I will be used.
H′ V H I will be used.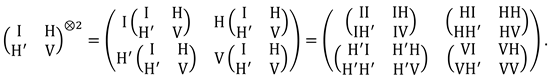

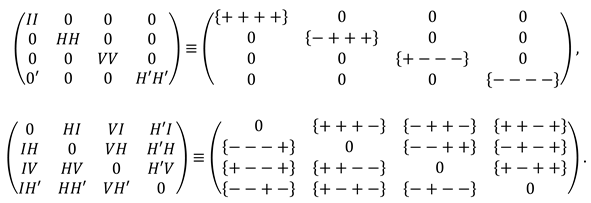

 in the form of binary stignatures (9)
in the form of binary stignatures (9)
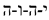 H′ V H I is associated with 24 combinations of permutations of the letters H′ V H I [13]
H′ V H I is associated with 24 combinations of permutations of the letters H′ V H I [13]