Submitted:
31 May 2023
Posted:
01 June 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Theoretical Approach
2.1. Using Dynamic Features to Detect Damage
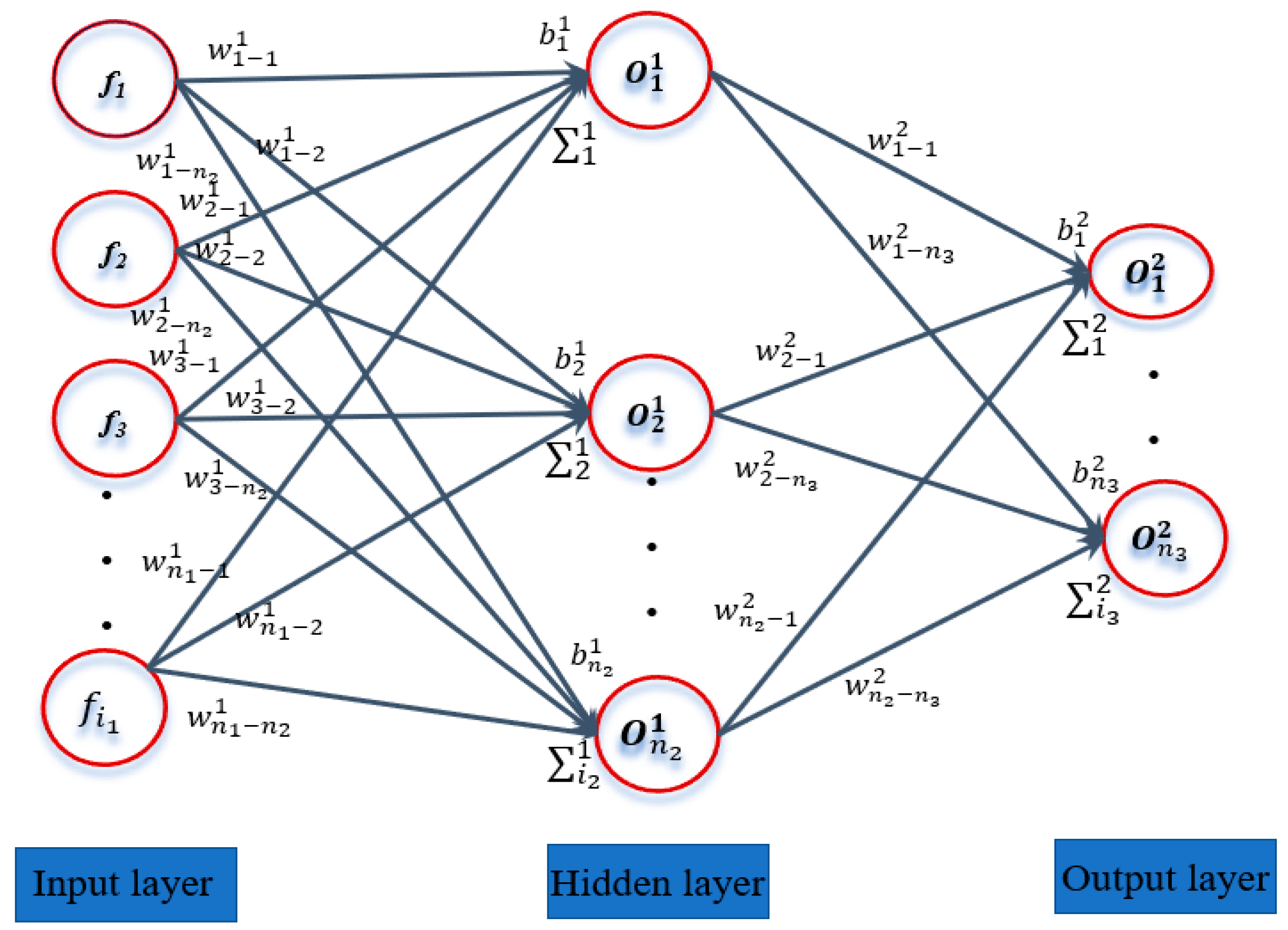
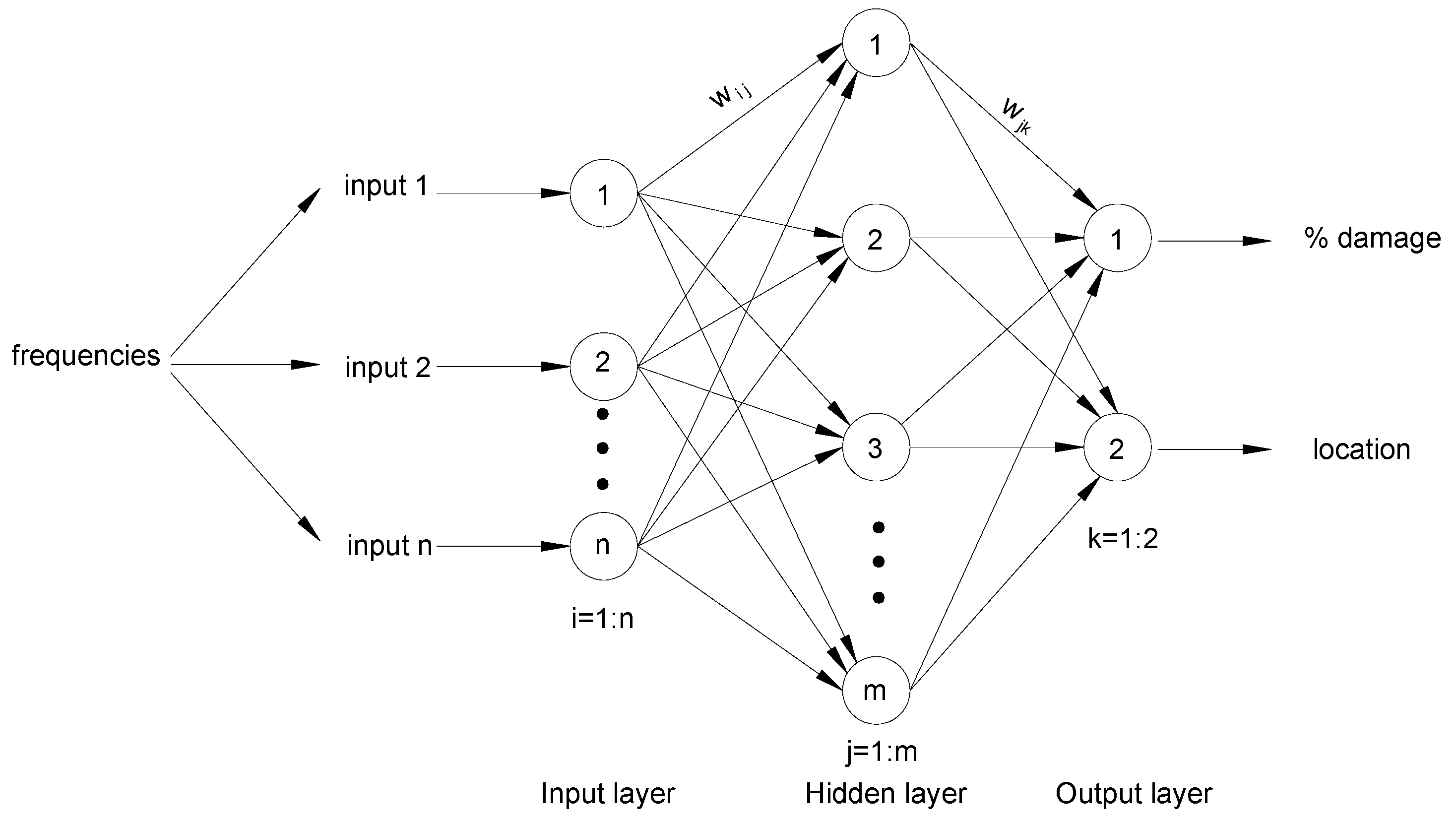
2.2. Artificial Neural Network
3. Case Study
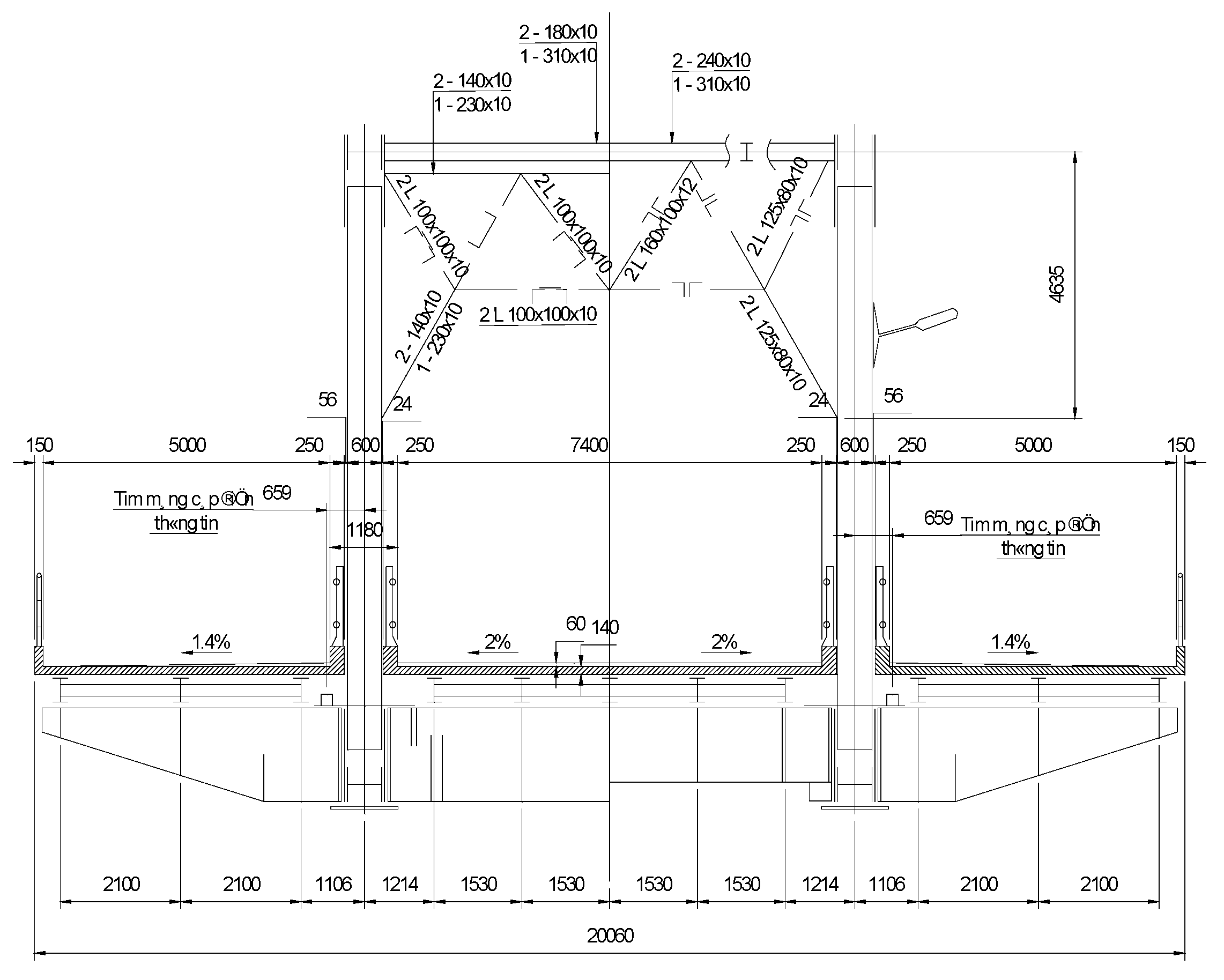
3.1. Chuongduong Bridge Introduction
3.2. On-Site Measurement Campaign before Damage
- a.
- Description of experiment
- b.
- Data processing and feature extraction
3.3. FEM Creation and Updating
- Initial FE model
| No | Truss members | Area (mm2) | Moment of inertia Iy (mm4) | Moment of inertia Iz (mm4) |
|---|---|---|---|---|
| 1 | Bridge gate frame | 4.27104 | 2.9109 | 1.15109 |
| 2 | Top lateral bracing | 4.75104 | 3.31109 | 1.75109 |
| 3 | Bottom lateral bracing | 4.75104 | 3.31109 | 1.75109 |
| 4 | Struts | 1.83104 | 1.03109 | 5.29107 |
| 5 | Diagonal chords | 4.17104 | 2.82109 | 1.04109 |
| 6 | Vertical chords | 1.83104 | 1.03109 | 5.29107 |
| 7 | Top chords | 1.83104 | 1.03109 | 5.29107 |
| 8 | Bottom chords | 1.83104 | 1.03109 | 5.29107 |
- b Update model parameters through particle swarm optimization (PSO) algorithm
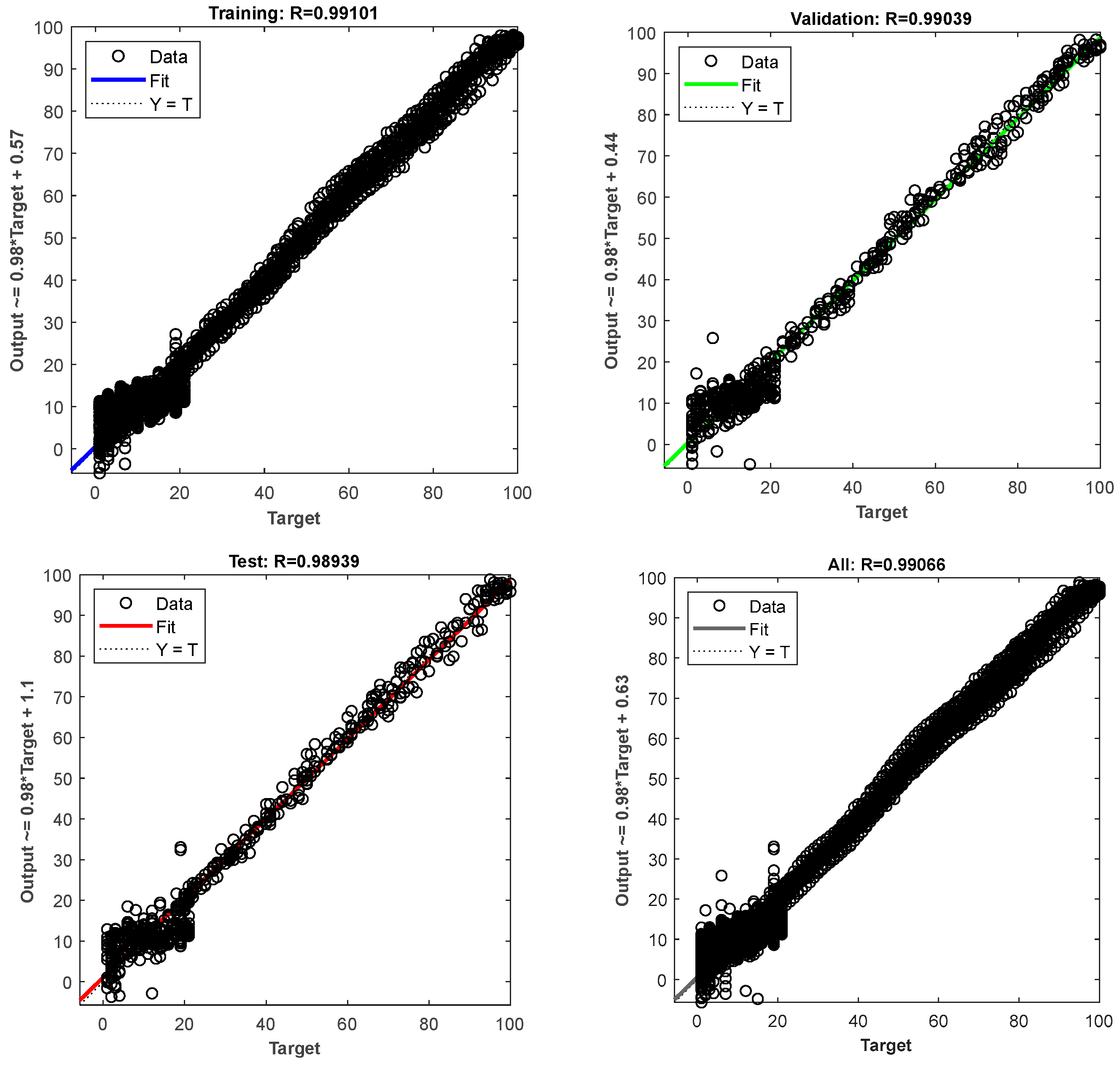
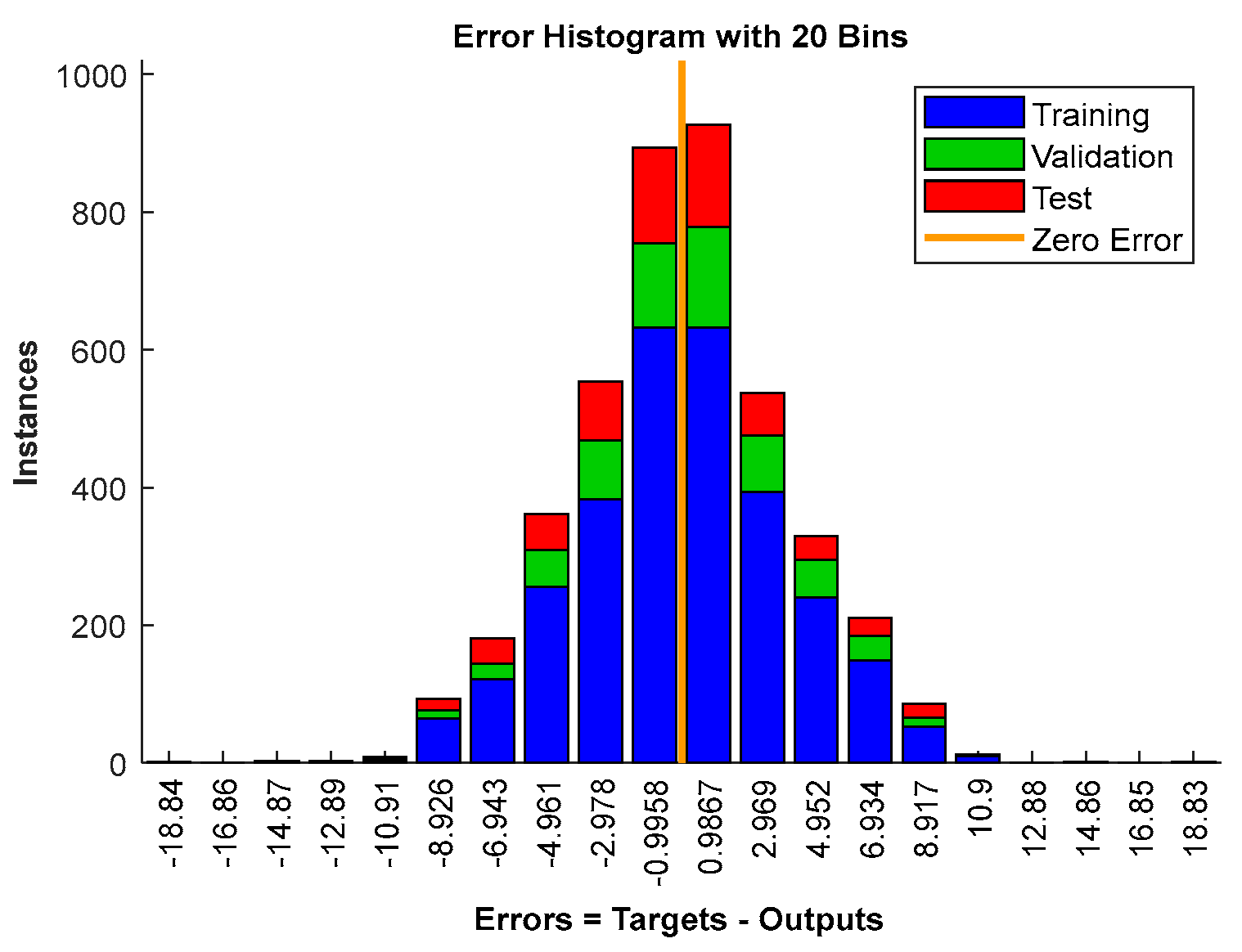
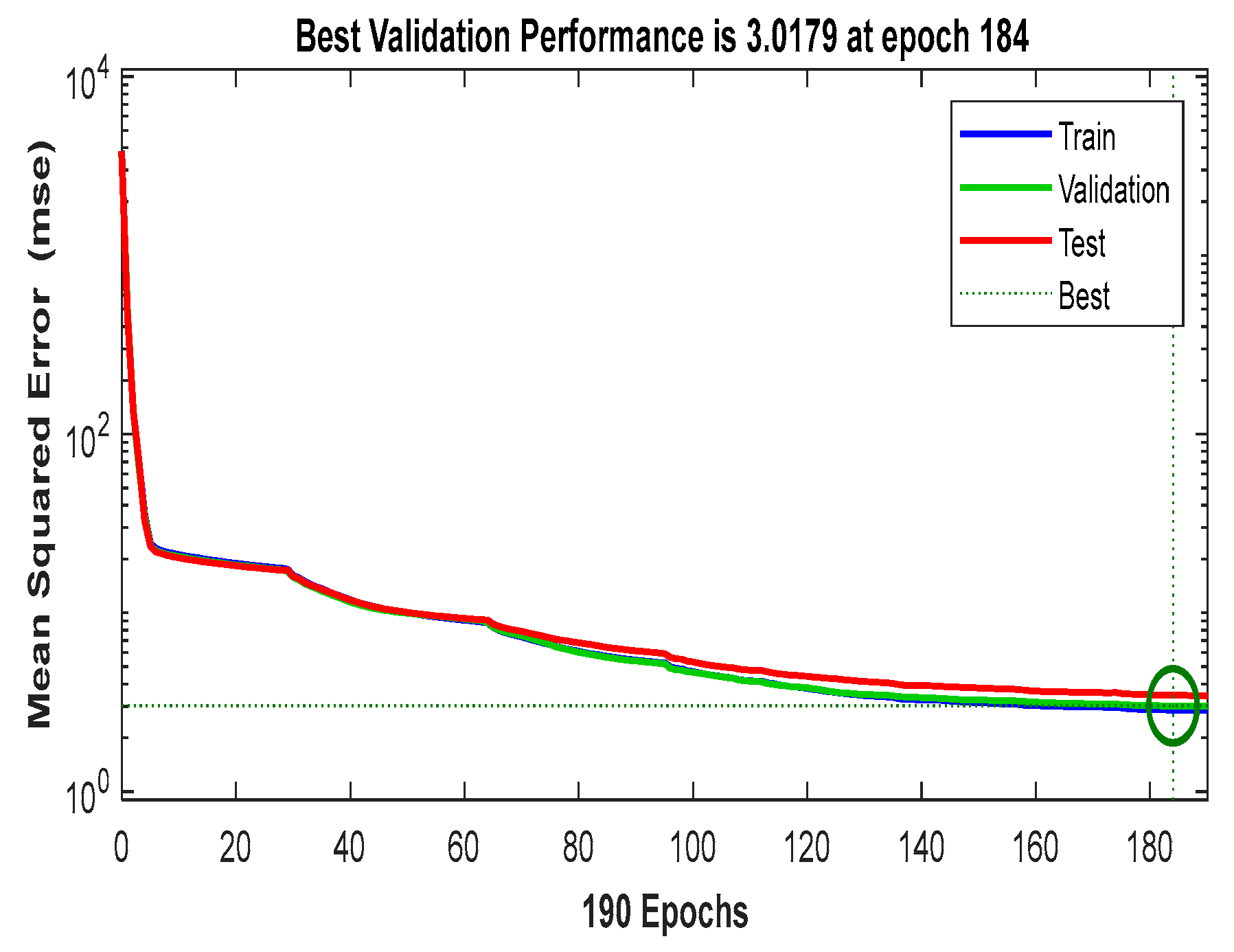
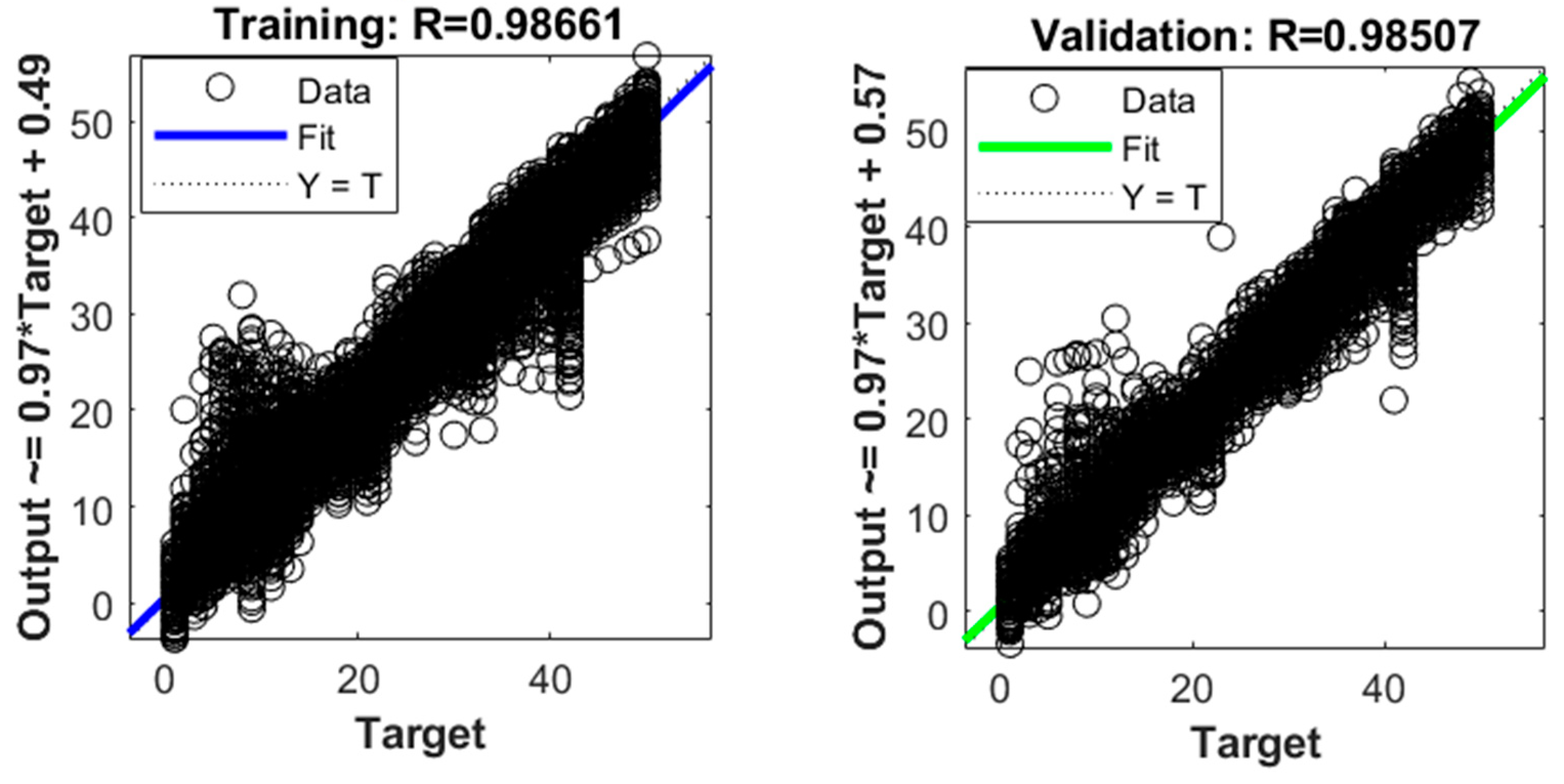
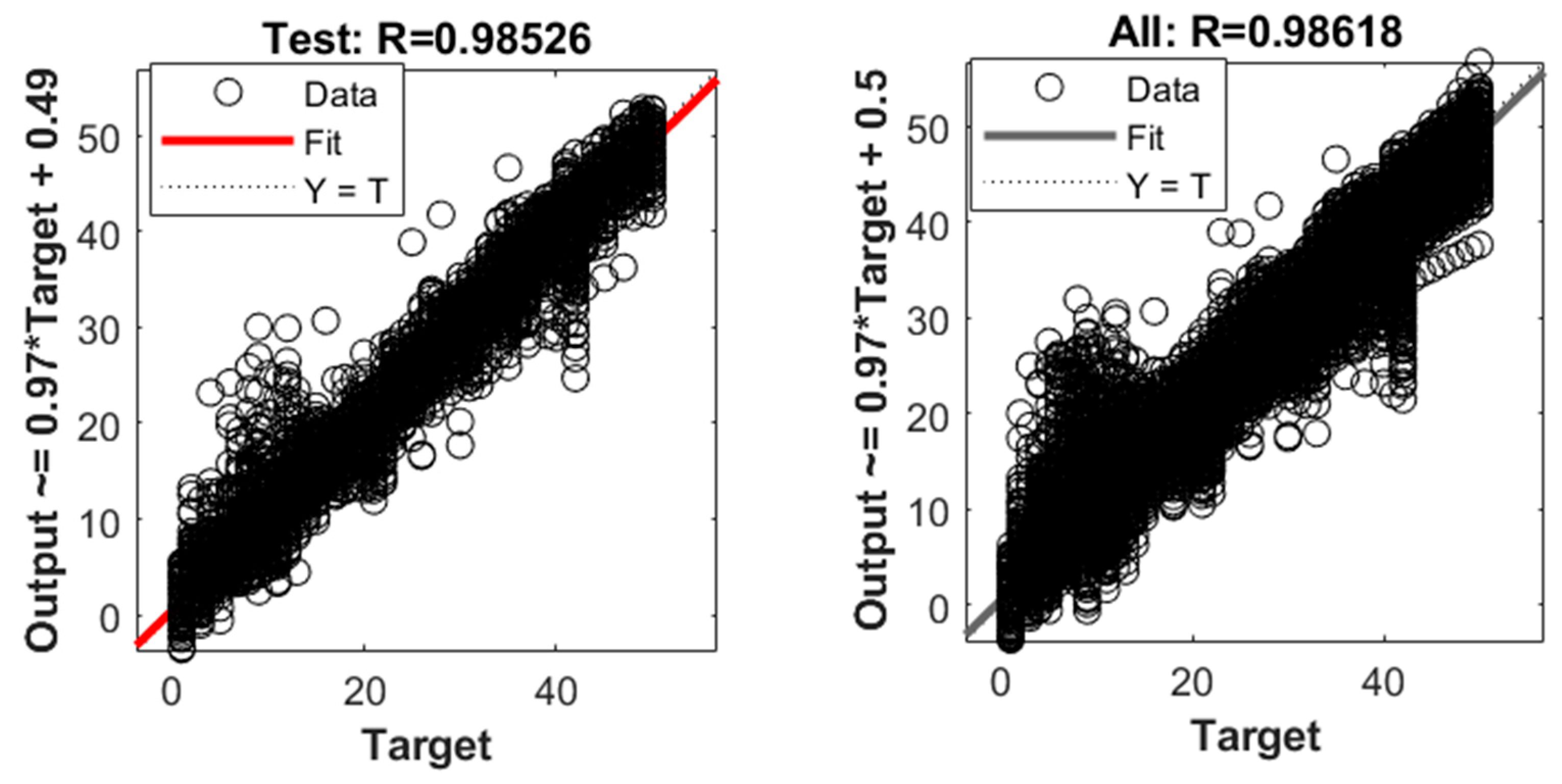
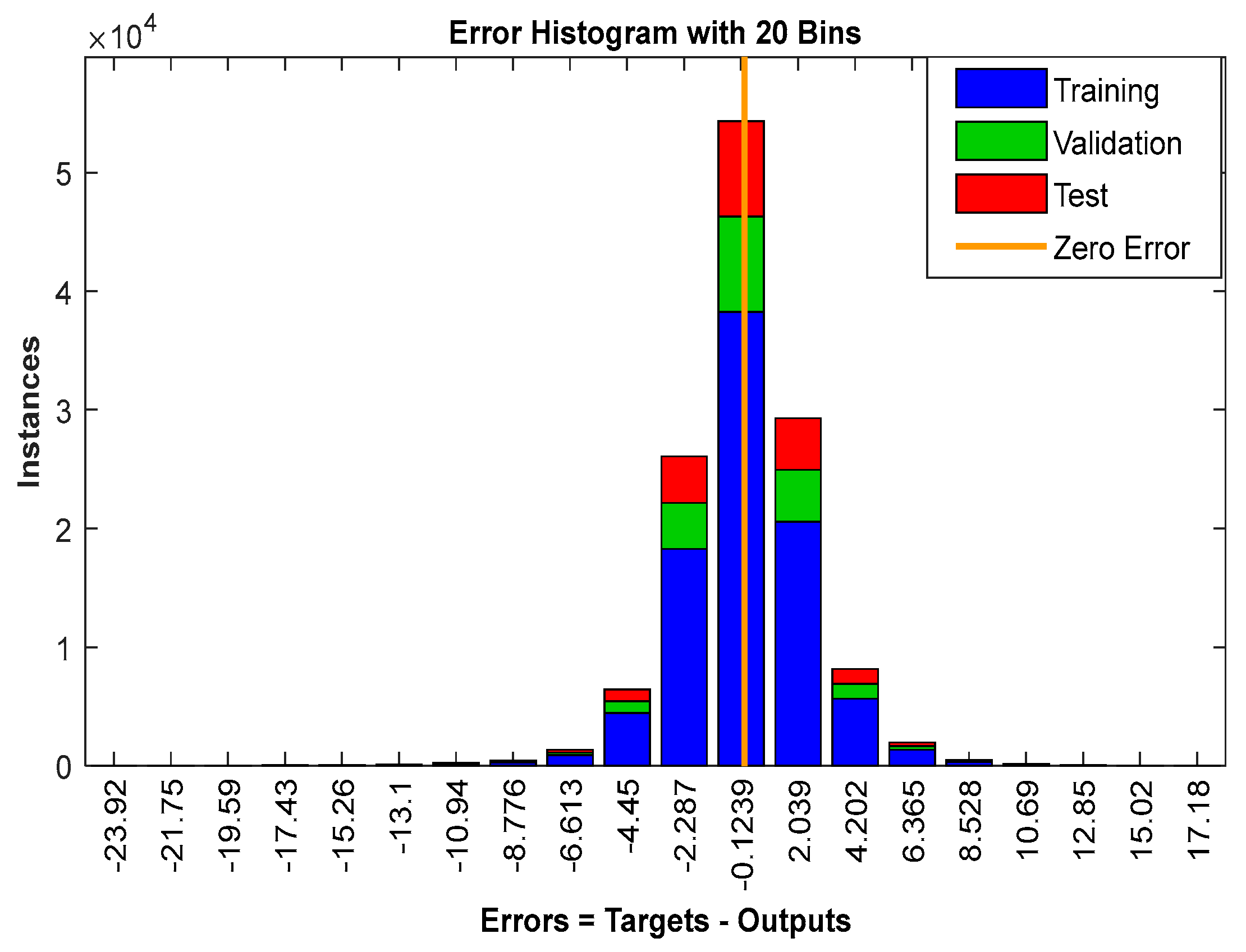
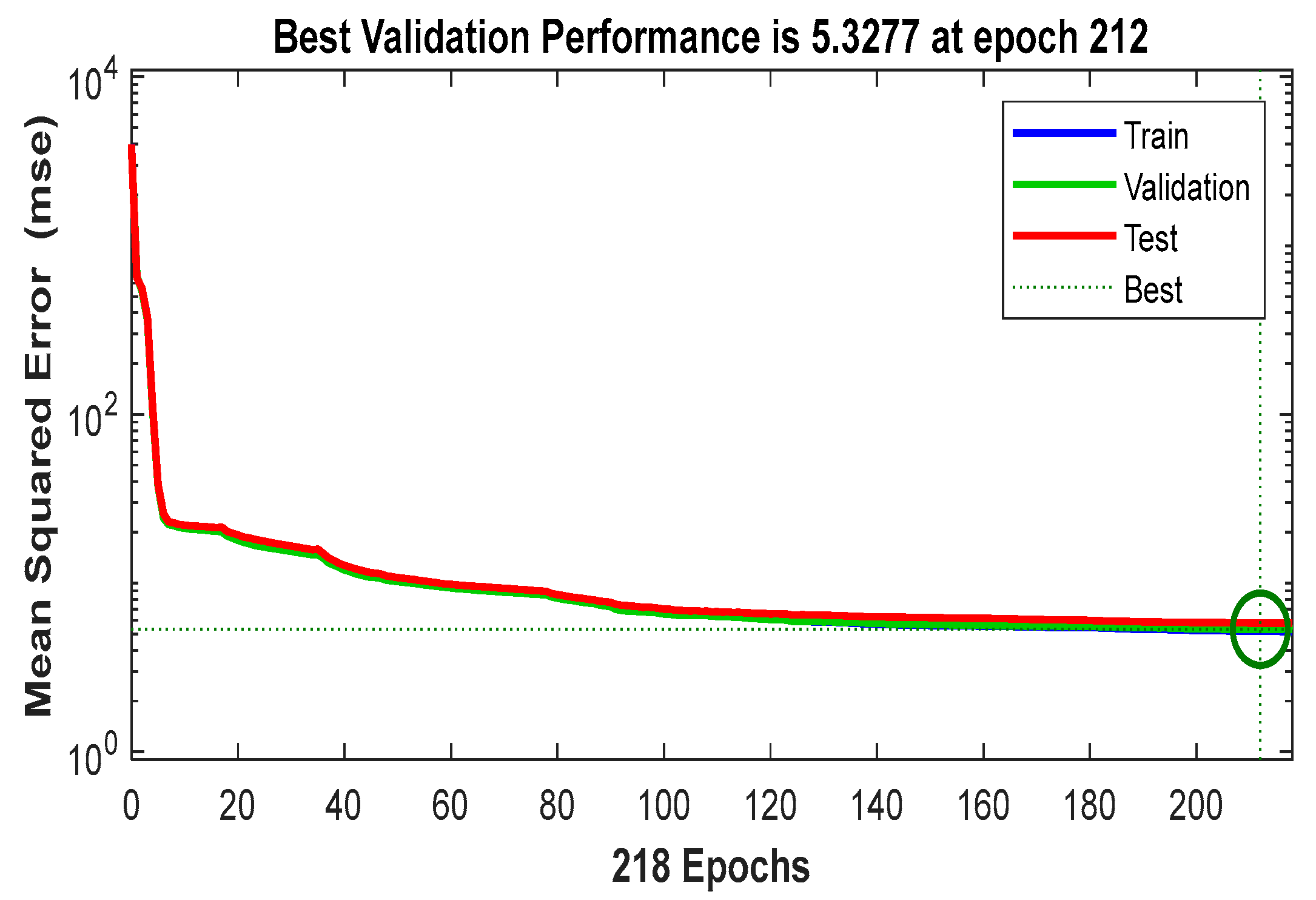
3.4. Generate Data and Train the ANN Model
3.5. The Service of the Trained ANN Model in Actual
4. Conclusions
- Before applying the ANN algorithm, an accurate (or relatively accurate) data source is required. This can be performed by creating a finite element model for extracting input data. However, if it is applied to actual works, it is necessary to have measures to update the model. In this study, particle swarm optimization (PSO) is used. Therefore, FEM can turn closer to the real behavior of the structures.
- Creating and organizing data from a finite element model is very important if want to get good results when training ANNs. With a large number of samples, training the network takes time, but the effect after training can make up for this.
- With the use of a trained ANN, failures can be detected and quantified. The proposed application results in a well-establishment with the actual test from an under-operating bridge.
- Compared with other methods, this approach has various advantages: saving human resources, being able to identify damage in hard-to-detect locations, and reducing the number of measuring points in the case of vibration tests.
- In the case study of this research, with a single failure, the ANN was able to identify and quantify the damage relatively accurately. For damage occurring on 2 elements, since there is no actual data, the network usage after training is done on the model. The results are quite satisfactory. The case where the data of 2 simultaneous damages seems to be more accurately predicted by the network. This can be explained because actual experimental data will more or less have noise, and at the same time affected by many factors. Meanwhile, the data used to confirm the case of 2 damages at the same time is taken directly from the model
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Encardio Rite Group [Updated] A Guide on Geodetic Survey and Monitoring - Encardio Rite. Available online: https://www.encardio.com/blog/a-guide-on-geodetic-survey-and-monitoring (accessed on 30 May 2023).
- Beshr, A.A.E.-W. Structural Deformation Monitoring and Analysis of Highway Bridge Using Accurate Geodetic Techniques. Engineering 2015, 07, 488–498. [Google Scholar] [CrossRef]
- Eteje, S.O. Detailed Geodetic Technique Procedures for Structural Deformation Monitoring and Analysis. International Journal of Scientific and Technological Research 2020. [Google Scholar] [CrossRef]
- Liu, S.; Liu, X.; Yang, F. Control Surveying and Structural Health Monitoring Applied in Large Bridge. Adv Mat Res 2013, 639–640, 243–246. [Google Scholar] [CrossRef]
- Lienhart, W. Geotechnical Monitoring Using Total Stations and Laser Scanners: Critical Aspects and Solutions. J Civ Struct Health Monit 2017, 7, 315–324. [Google Scholar] [CrossRef]
- Segalini, A.; Carri, A.; Savi, R. Role of Geotechnical Monitoring: State of the Art and New Perspectives. In Proceedings of the GEO-EXPO; Drustvo za geotehniku u Bosni i Hercegovini, October 10 2017; pp. 19–26. [Google Scholar]
- Viola, E.; Bocchini, P. Non-Destructive Parametric System Identification and Damage Detection in Truss Structures by Static Tests. Structure and Infrastructure Engineering 2013, 9, 384–402. [Google Scholar] [CrossRef]
- Ugalde, U.; Anduaga, J.; Martinez, F.; Iturrospe, A. A SHM Method for Detecting Damage with Incomplete Observations Based on VARX Modelling and Granger Causality. 2016.
- Martínez, D.; Obrien, E.J.; Sevillano, E. Damage Detection by Drive-by Monitoring Using the Vertical Displacements of a Bridge. Insights and Innovations in Structural Engineering, Mechanics and Computation - Proceedings of the 6th International Conference on Structural Engineering, Mechanics and Computation, SEMC 2016, 2016; 1915–1918. [Google Scholar] [CrossRef]
- Hjelmstad, K.D.; Shin, S. Damage Detection and Assessment of Structures from Static Response. J Eng Mech 1997, 123, 568–576. [Google Scholar] [CrossRef]
- Bakhtiari-Nejad, F.; Rahai, A.; Esfandiari, A. A Structural Damage Detection Method Using Static Noisy Data. Eng Struct 2005, 27, 1784–1793. [Google Scholar] [CrossRef]
- Doebling, S.W.; Farrar, C.R.; Prime, M.B. A Summary Review of Vibration-Based Damage Identification Methods. The Shock and Vibration Digest 1998, 30, 91–105. [Google Scholar] [CrossRef]
- Salawu, O.S. Detection of Structural Damage through Changes in Frequency: A Review. Eng Struct 1997, 19, 718–723. [Google Scholar] [CrossRef]
- Khatir, S.; Khatir, T.; Boutchicha, D.; Le Thanh, C.; Tran-Ngoc, H.; Bui, T.Q.; Capozucca, R.; Abdel-Wahab, M. An Efficient Hybrid TLBO-PSO-ANN for Fast Damage Identification in Steel Beam Structures Using IGA. Smart Struct Syst 2020, 25, 605–617. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W. Damage Detection and Evaluation II. Modal Analysis and Testing 1999, 345–378. [Google Scholar] [CrossRef]
- Carden, E.P.; Fanning, P. Vibration Based Condition Monitoring: A Review. 2004, 3, 355–377. [Google Scholar] [CrossRef]
- Catbas, F.N.; Brown, D.L.; Aktan, A.E. Use of Modal Flexibility for Damage Detection and Condition Assessment: Case Studies and Demonstrations on Large Structures. Journal of Structural Engineering 2006, 132, 1699–1712. [Google Scholar] [CrossRef]
- Alvandi, A.; Cremona, C. Assessment of Vibration-Based Damage Identification Techniques. J Sound Vib 2006, 292, 179–202. [Google Scholar] [CrossRef]
- Nhung, N.T.C.; Minh, T.Q.; Matos, J.C.; Sousa, H.S. Research and Application of Indirect Monitoring Methods for Transport Infrastructures to Monitor and Evaluate Structural Health. 2021.
- Mazurek, D.F.; Mazurek; F. , D. Modal Sensitivity to Damage in Multigirder Bridges. SPIE 1997, 3089, 1892. [Google Scholar]
- Doebling, S.; Farrar, C. Statistical Damage Identification Techniques Applied to the I-40 Bridge over the Rio Grande River. 1998.
- Alvandi, A. Contribution à l’utilisation Pratique de l’évaluation Dynamique Pour La Détection d’endommagements Dans Les Ponts. 2003.
- Doebling, S.W.S.; Farrar, C.R.C.; Prime, M.B.M.; Shevitz, D.W.D. Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in Their Vibration Characteristics: A Literature Review. Los Alamos National Laboratory 1996. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Lee, L.S.W. Vibration-Based Damage Detection Techniques for Structural Health Monitoring of Civil Infrastructure Systems. Structural Health Monitoring of Civil Infrastructure Systems 2009, 177–212. [Google Scholar] [CrossRef]
- Farrar, C.R.; Doebling, S.W.; Nix, D.A. Vibrationbased Structural Damage Identification. Philosophical Transactions of the Royal Society of London. Series A: Mathematical, Physical and Engineering Sciences 2001, 359, 131–149. [Google Scholar] [CrossRef]
- Khiem, N.T.; Lien, T. V. A Simplified Method for Natural Frequency Analysis of a Multiple Cracked Beam. J Sound Vib 2001, 245, 737–751. [Google Scholar] [CrossRef]
- Nguyen, T.; Chan, T.H.T.; Thambiratnam, D.P. Field Validation of Controlled Monte Carlo Data Generation for Statistical Damage Identification Employing Mahalanobis Squared Distance. 2014, 13, 473–488. [Google Scholar] [CrossRef]
- Zhang, Z.; Shankar, K.; Morozov, E. V.; Tahtali, M. Vibration-Based Delamination Detection in Composite Beams through Frequency Changes. 2014, 22, 496–512. [Google Scholar] [CrossRef]
- Jeong, M.-J.; Choi, J.-H.; Koh, B.-H. Isomap-Based Damage Classification of Cantilevered Beam Using Modal Frequency Changes. 2014.
- Gillich, G.R.; Ntakpe, J.L.; Abdel Wahab, M.; Praisach, Z.I.; Mimis, M.C. Damage Detection in Multi-Span Beams Based on the Analysis of Frequency Changes. J Phys Conf Ser 2017, 842, 012033. [Google Scholar] [CrossRef]
- Wang, L.; Lie, S.T.; Zhang, Y. Damage Detection Using Frequency Shift Path. Mech Syst Signal Process 2016, 66–67, 298–313. [Google Scholar] [CrossRef]
- Sha, G.; Radzieński, M.; Cao, M.; Ostachowicz, W. A Novel Method for Single and Multiple Damage Detection in Beams Using Relative Natural Frequency Changes. Mech Syst Signal Process 2019, 132, 335–352. [Google Scholar] [CrossRef]
- Khan, M.W.; Din, N.A.; Ul Haq, R. Damage Detection in a Fixed-Fixed Beam Using Natural Frequency Changes. Vibroengineering PROCEDIA 2020, 30, 38–43. [Google Scholar] [CrossRef]
- He, K.; Zhu, W.D. Structural Damage Detection Using Changes in Natural Frequencies: Theory and Applications. J Phys Conf Ser 2011, 305. [Google Scholar] [CrossRef]
- Mohan, V.; Parivallal, S.; Kesavan, K.; Arunsundaram, B.; Ahmed, A.K.F.; Ravisankar, K. Studies on Damage Detection Using Frequency Change Correlation Approach for Health Assessment. Procedia Eng 2014, 86, 503–510. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G. The Application of Machine Learning to Structural Health Monitoring. Philos Trans A Math Phys Eng Sci 2007, 365, 515–537. [Google Scholar] [CrossRef]
- Hakim, S.J.S.; Abdul Razak, H. Adaptive Neuro Fuzzy Inference System (ANFIS) and Artificial Neural Networks (ANNs) for Structural Damage Identification. Structural Engineering and Mechanics 2013, 45, 779–802. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Bui, T.T.; De Roeck, G.; Abdel Wahab, M. Damage Detection in Ca-Non Bridge Using Transmissibility and Artificial Neural Networks. Structural Engineering and Mechanics 2019, 71, 175–183. [Google Scholar] [CrossRef]
- Kaveh, A.; Maniat, M.; Kaveh, A.; Maniat, M. Damage Detection Based on MCSS and PSO Using Modal Data. Smart Struct Syst 2015, 15, 1253. [Google Scholar] [CrossRef]
- Mares, C.; Surace, C. An Application of Genetic Algorithms to Identify Damage in Elastic Structures. J Sound Vib 1996, 195, 195–215. [Google Scholar] [CrossRef]
- Seyedpoor, S.M. A Two Stage Method for Structural Damage Detection Using a Modal Strain Energy Based Index and Particle Swarm Optimization. Int J Non Linear Mech 2012, 47, 1–8. [Google Scholar] [CrossRef]
- Yu, L.; Xu, P. Structural Health Monitoring Based on Continuous ACO Method. Microelectronics Reliability 2011, 51, 270–278. [Google Scholar] [CrossRef]
- Guo, H.Y.; Li, Z.L. A Two-Stage Method to Identify Structural Damage Sites and Extents by Using Evidence Theory and Micro-Search Genetic Algorithm. Mech Syst Signal Process 2009, 23, 769–782. [Google Scholar] [CrossRef]
- Hao, H.; Xia, Y. Vibration-Based Damage Detection of Structures by Genetic Algorithm. Journal of Computing in Civil Engineering 2002, 16, 222–229. [Google Scholar] [CrossRef]
- Na, C.; Kim, S.P.; Kwak, H.G. Structural Damage Evaluation Using Genetic Algorithm. J Sound Vib 2011, 330, 2772–2783. [Google Scholar] [CrossRef]
- Edwin, R.; Mattias, S.; Guido, D.R. Macec - The Matlab Toolbox for Experimental and Operational Modal Analysis; 2021; Vol. MACEC 3.4.
- Pastor, M.; Binda, M.; Harčarik, T. Modal Assurance Criterion. Procedia Eng 2012, 48, 543–548. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. Proceedings of ICNN’95 - International Conference on Neural Networks 1995, 4, 1942–1948. [Google Scholar] [CrossRef]
- Zeugmann, T.; Poupart, P.; Kennedy, J.; Jin, X.; Han, J.; Saitta, L.; Sebag, M.; Peters, J.; Bagnell, J.A.; Daelemans, W.; et al. Particle Swarm Optimization. Encyclopedia of Machine Learning 2011, 760–766. [Google Scholar] [CrossRef]


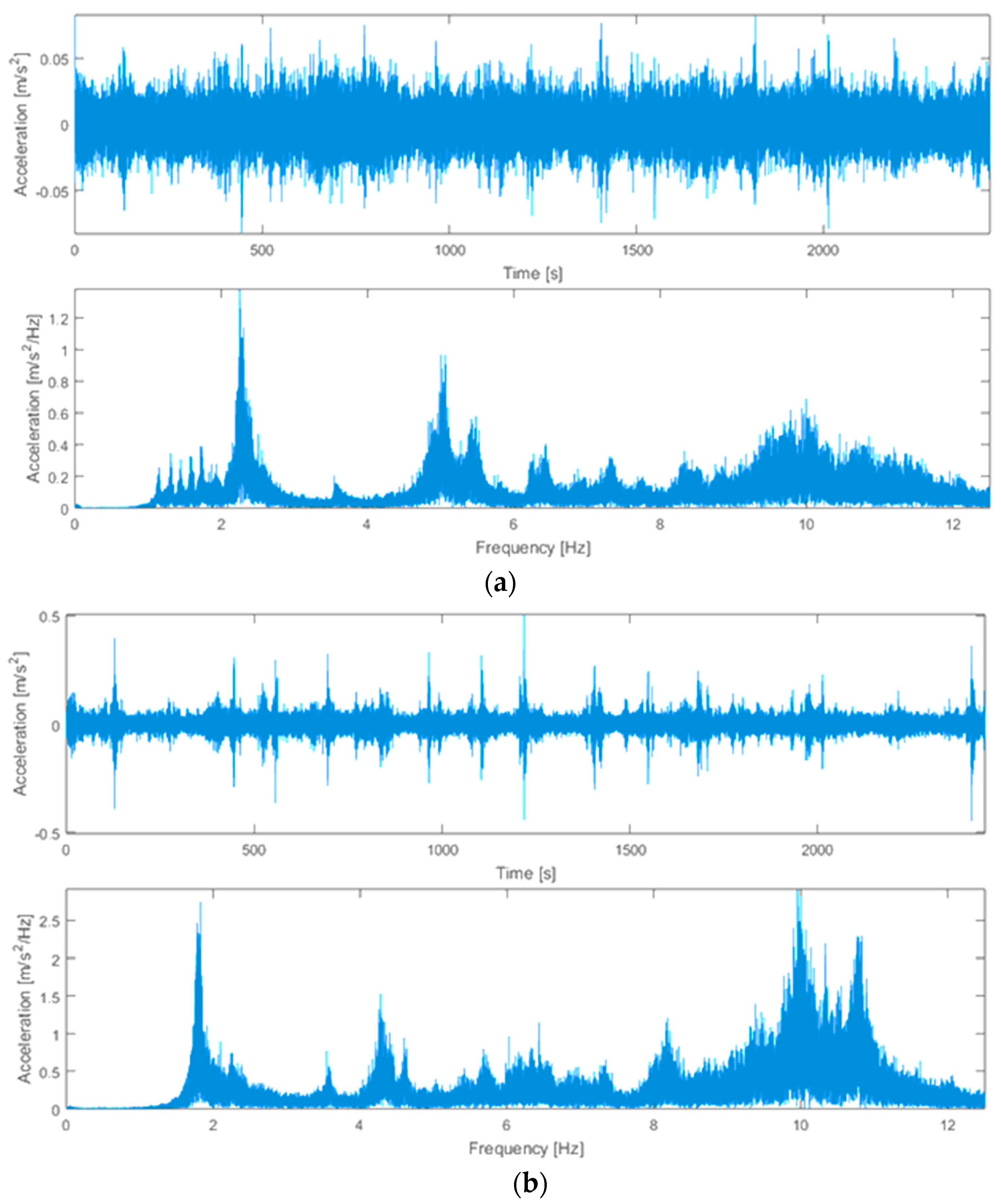
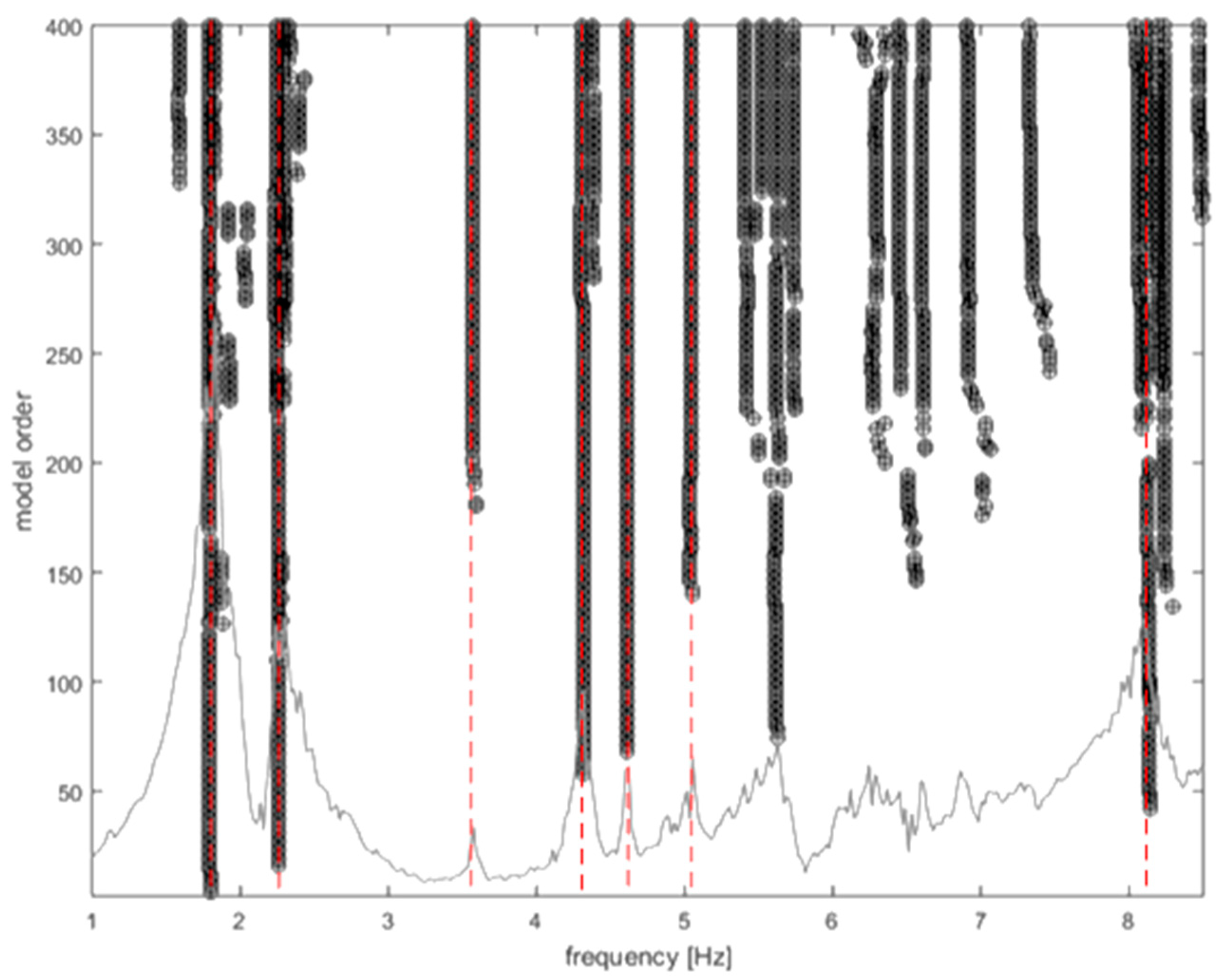

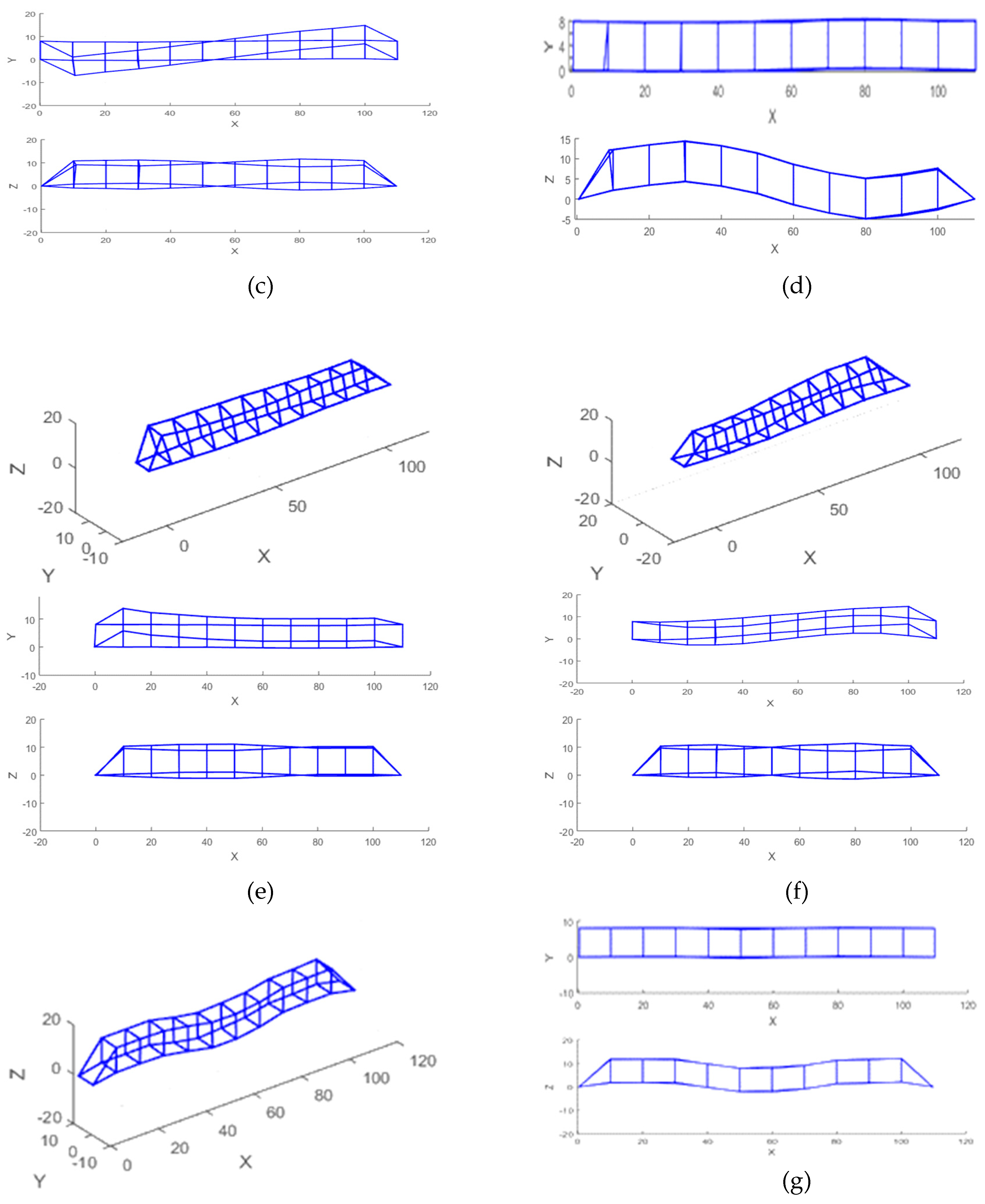
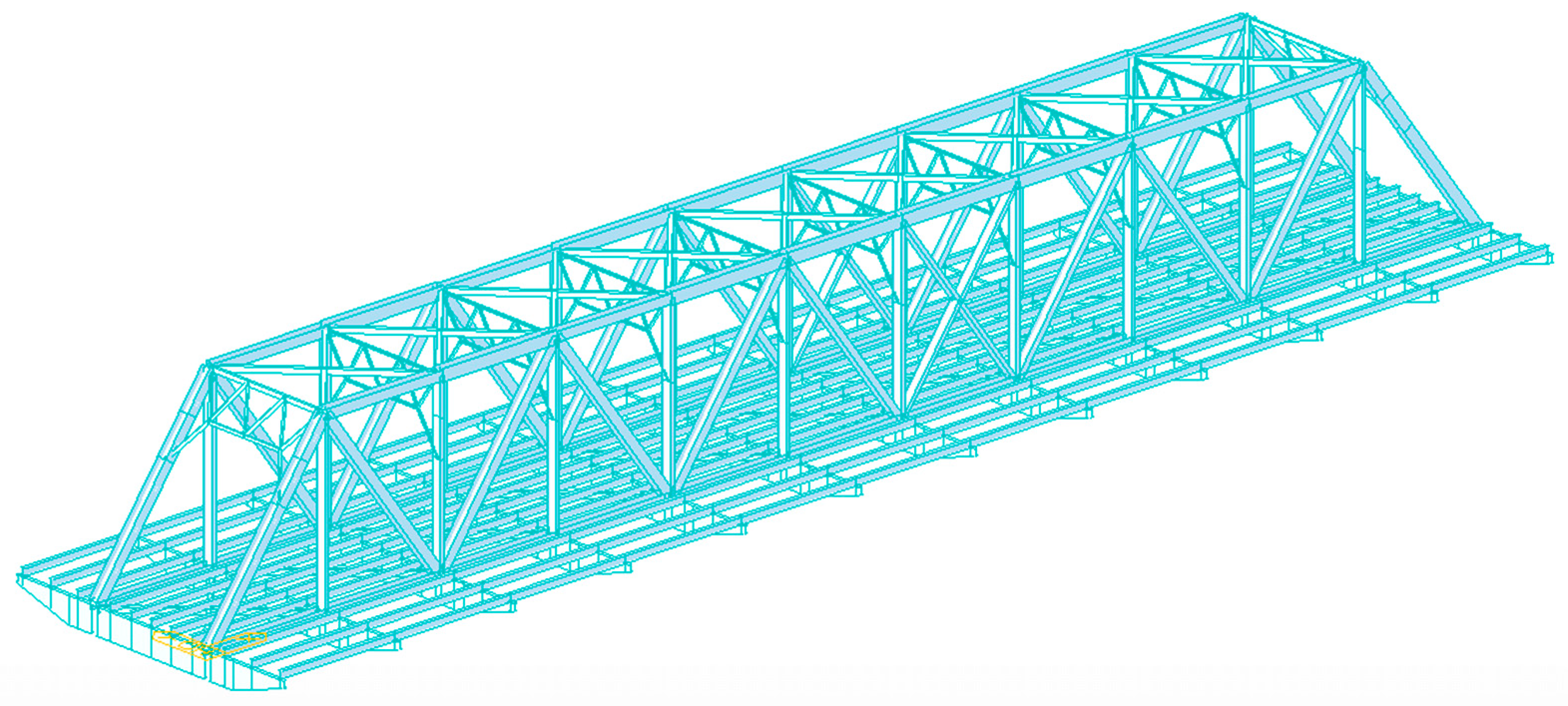

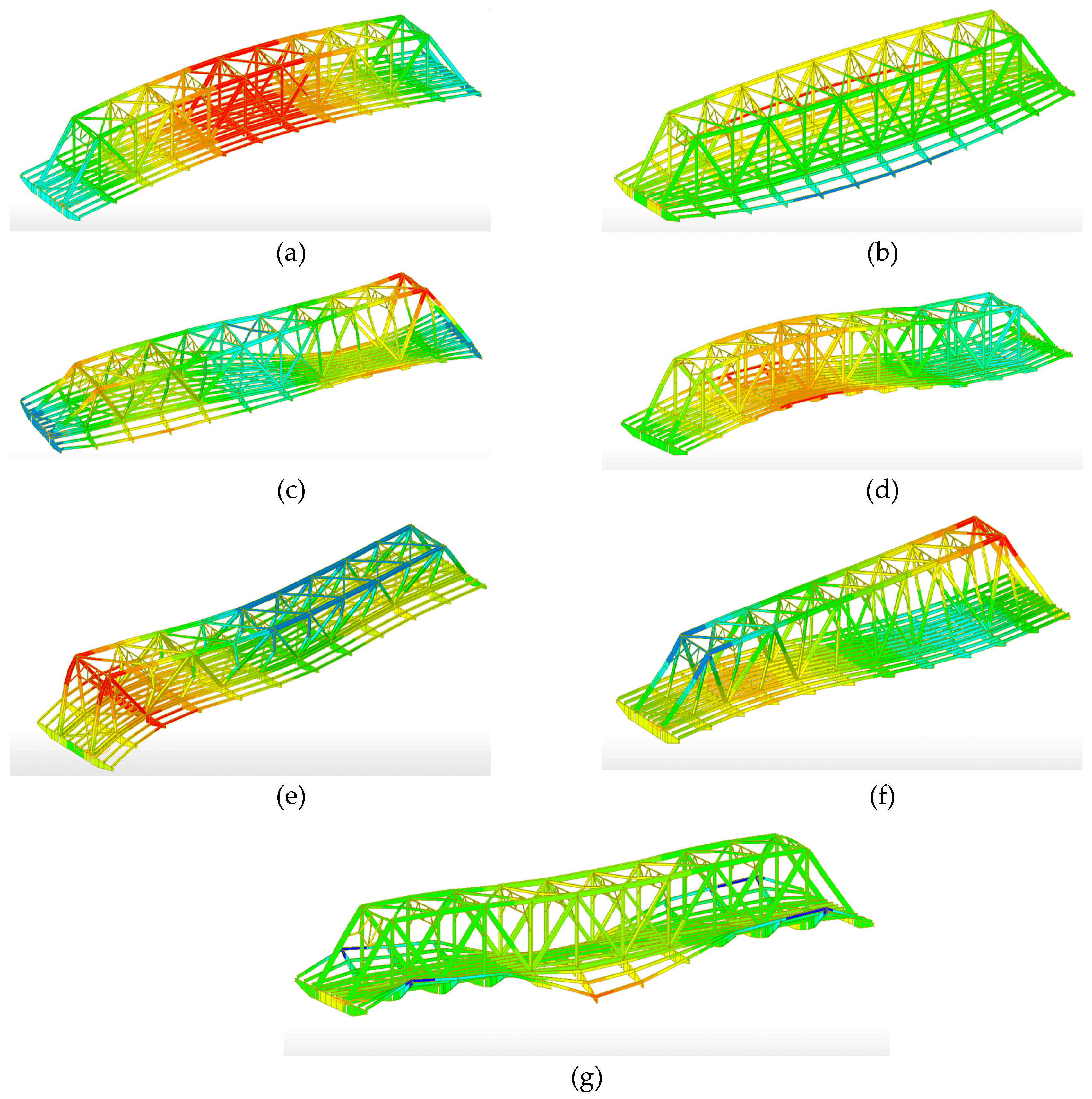

| No | Frequencies [Hz] | Damping ratios [%] | Modal phase collinearity | Mode type |
|---|---|---|---|---|
| 1 | 1.79 | 1.50 | 0.999 | First vertical bending |
| 2 | 2.25 | 1.06 | 0.998 | First lateral + torsion |
| 3 | 3.57 | 0.77 | 0.999 | Second torsion |
| 4 | 4.30 | 1.21 | 0.999 | Second vertical bending |
| 5 | 4.60 | 0.40 | 0.996 | lateral movement |
| 6 | 5.03 | 1.50 | 0.998 | Second lateral bending |
| 7 | 8.09 | 1.06 | 0.997 | Third vertical bending |
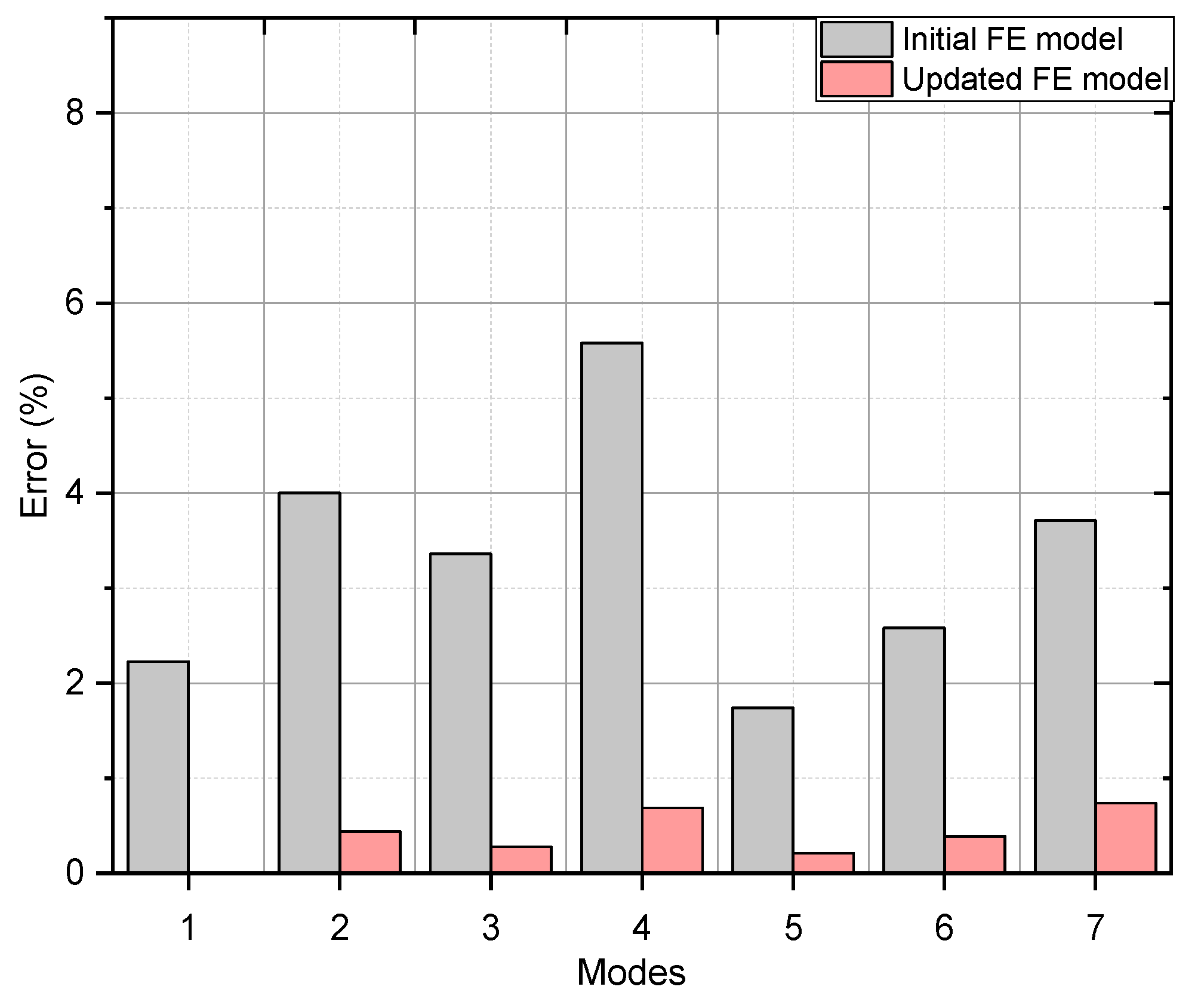
| Mode | f-simulation (Hz) |
f-measurement (Hz) | Error*(%) | MAC | Type |
|---|---|---|---|---|---|
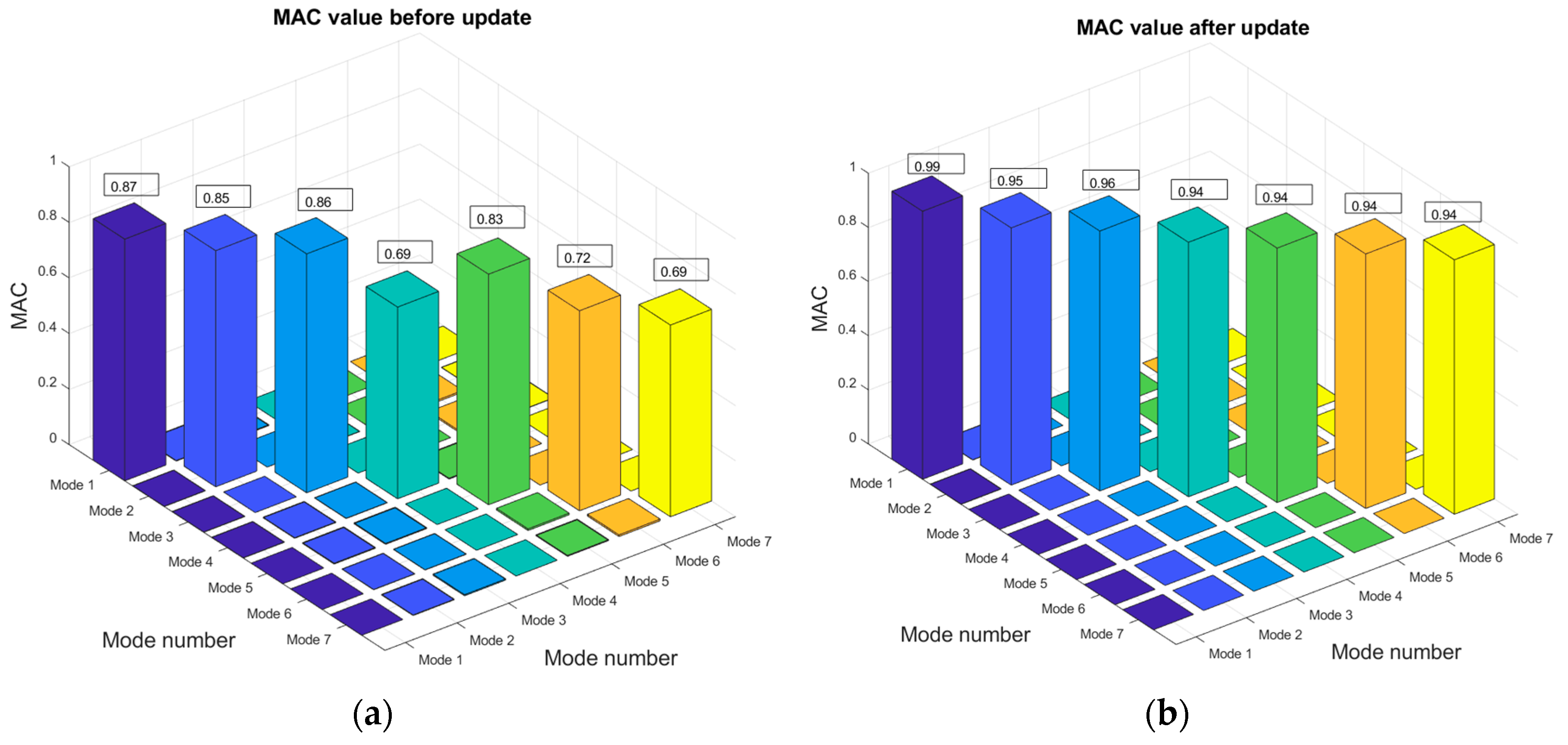
| 1 | 1.83 | 1.79 | 2.23 | 0.87 | 1st vertical bending |
| 2 | 2.34 | 2.25 | 4 | 0.85 | 1st lateral + torsion |
| 3 | 3.45 | 3.57 | 3.36 | 0.86 | 2nd torsion |
| 4 | 4.06 | 4.30 | 5.58 | 0.69 | 2nd vertical bending |
| 5 | 4.52 | 4.60 | 1.74 | 0.83 | lateral movement |
| 6 | 5.16 | 5.03 | 2.58 | 0.72 | 2nd lateral bending |
| 7 | 8.39 | 8.09 | 3.71 | 0.69 | 3rd vertical bending |
| No | Uncertain parameters | Initial value | Upper bound | Lower bound |
|---|---|---|---|---|
| 1 | Young’s modulus - Steel Es (GPa) |
200 |
210 |
190 |
| 2 | Weight density - Steel ρs (kg/m3) |
7850 |
8000 |
7800 |
| 3 | Masses of non-structural - mb (kg/m) |
3000 |
3000 |
5000 |
| No | Uncertain parameters | Initial value | Updated value |
|---|---|---|---|
| 1 | Young’s modulus - Steel Es (GPa) |
200 |
205.54 |
| 2 | Weight density - Steel ρs (kg/m3) |
7850 |
7956.5 |
| 3 | Masses of non-structural - mb (kg/m) |
3000 |
3600 |
| Mode | f-simulation(Hz) | f-measurement (Hz) | Error*(%) | MAC | Type |
|---|---|---|---|---|---|
| 1 | 1.79 | 1.79 | 0.00↓ | 0.99↑ | 1st vertical bending |
| 2 | 2.24 | 2.25 | 0.44↓ | 0.95↑ | 1st lateral + torsion |
| 3 | 3.58 | 3.57 | 0.28↓ | 0.96↑ | 2nd torsion |
| 4 | 4.33 | 4.30 | 0.69↓ | 0.94↑ | 2nd vertical bending |
| 5 | 4.61 | 4.60 | 0.21↓ | 0.94↑ | lateral movement |
| 6 | 5.05 | 5.03 | 0.39↓ | 0.94↑ | 2nd lateral bending |
| 7 | 8.15 | 8.09 | 0.74↓ | 0.94↑ | 3rd vertical bending |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).





