A Research on Manipulator Path Tracking based on Deep Reinforcement Learning

1. Introduction

A manipulator is a highly integrated mechanical system combined with electromechanical control. It is a typical multi-input multi-output nonlinear system, and its dynamics are time-varying and strongly coupled. As a complex system, it has many uncertainties, so its control is very complicated. In recent decades, researchers have carried out a lot of research on the control methods of manipulator. The existing control methods of robots include the computational torque control, robust adaptive control[1], adaptive neural network control [2], output feedback control [3,4,5,6], dead zone nonlinear compensation control [7], virtual decomposition control [8], and so on.

Path tracking [9] is an important topic in manipulator control. After successfully planning an optimal path using the path planning algorithm, how to make the end of the manipulator follow this optimal path is a problem that needs to be solved. Cai ZX [10] and Patolia H [11] decompose the speed and acceleration of each joint of the manipulator respectively. They adjust the desired speed or desired acceleration of each joint through position or speed feedback, and use the error as the control input. In the actual control of the manipulator, the end effector often clamps different objects, so it is difficult to accurately obtain the dynamic parameters of each link of the manipulator. At the same time, the existence of external interference and dynamic modelling errors make the manipulator track and control the belt. come difficult. Ma BL [12] proposed an adaptive control method, which dynamically adjusts the controller by identifying the system parameters online. In order to improve the stability of tracking, Spong MW [13] added a robust term to the control input to compensate for the deviation between the estimated model and the real model of the manipulator and limit the uncertain factors to a certain range. Purwar S [14] used the Lyapunov stability criterion to optimize the parameters of the neural network controller to improve the robustness and stability of the tracking in order to compensate for the error caused by the external disturbance and the linearization of the dynamic model.

The above methods all involve the process of precise dynamic modelling and inverse kinematics solutions. However, since the increase of the degree of freedom of the manipulator, the difficulty of dynamic modelling and the calculation amount of inverse kinematics solution will increase, and the inverse solution will not be unique. They all limit the applicability of methods [15,16,17,18]. In recent years, with a series of successful applications of reinforcement learning in decision control problems, it does not require system dynamics modelling, but only through trial and error learning by interacting with the environment, which provides new ideas for path tracking problems. The reinforcement learning [19] method can model the manipulator path tracking problem as a Markov decision process (MDP), and interact with samples to optimize the control policy. Guo X [20] used the depth value function method (DQN) to complete the path tracking of the UR5 manipulator. However, it discretizes the action space, and it is difficult to finely control the manipulator. Liu YC [21] realized the tracking control of the manipulator in the continuous action space, but its learning process is unstable, and the small changes of hyperparameters have a great impact on the performance of the algorithm. In the path tracking problem, since the output of the system follows a time-independent geometric path, most articles use the inverse kinematics method for path tracking. However, the manipulators capable of performing complex tasks usually have a high degree of freedom. As the degrees of freedom increase, the solutions of inverse kinematics will not be unique and more difficult, also the computational load will be larger.

In this paper, a reinforcement learning method for multi-DOF manipulator path tracking is proposed, which converts the tracking accuracy requirements and energy constraints into cumulative rewards obtained by the control strategy to ensure the stability and control accuracy of the tracking trajectory. The entropy of policy is used as an auxiliary gain of the agent and introduced into the training process of the control strategy, thereby increasing the robustness of the path tracking. We first explore the feasibility of deep reinforcement learning methods to solve the path following problem on a planar dual-link manipulator. Then, we verified it on the 6-DOF manipulator and analysed the effects of different training parameters and different dynamic characteristics on the path tracking effect of the manipulator. The results show that our method has good path tracking performance.

2. Problem Statement

We model the path tracking problem of manipulator as a Markov Decision Process (MDP), which represented by $<S, A, R, T, \gamma >$, where $s_t\in S$ represents the observations of the agent. The policy $\mathsf{\Pi }:S\to A$ maps the current environmental state $s_t$ to the control input $a_t\in A$ of each joint of the manipulator, $T\left(s_{t+1}|s_t, a_t\right)$ represents the dynamic characteristics of the robotic arm, that is, the probability that the system transitions from state $s_t$ to $s_{t+1}$ under the control of $a_t$. The expected path $P^{*}\in {\mathbb{R}}^{N\times 3}$ of the manipulator can be generated by traditional path planning methods, where N is the number of points on the path. The instantaneous reward obtained by the agent at time $t$ is represented by $r_t\in R$ ,which is related to the tracking accuracy of the robot arm on the desired path and the energy consumed. The policy continuously interacts with the manipulator system to obtain the sampling trajectory $\tau =\left\{s_0,a_0,\cdots ,s_t,a_t, \cdots ,s_T,a_T\right\}$. The goal of reinforcement learning is to optimize the policy so as to maximize the expected cumulative reward obtained by the agent:

$$\underset{}{{\mathrm{maximize}}_{\pi \in \Pi }}{{\rm E}}_{\tau ~p\left(\tau \right)}\left[{\displaystyle \sum _{t=0}^T{\gamma }^{t}r\left(s_t,a_t\right)}\right]$$

(1)

$$p\left(\tau \right)=p\left(s_0\right){\displaystyle \prod _{t=0}^T\pi \left(a_t|s_t\right)T\left(s_{t+1}|s_t,a_t\right)}$$

(2)

The framework of the robot arm path tracking model based on deep reinforcement learning is shown in Figure 1. The framework consists of four parts: desired path, control strategy, feedback controller, and manipulator body. The policy calculates the expected position/velocity of each joint at the next moment according to the desired path and the current state of the manipulator as the reference signal of the feedback controller. The feedback controller combines the current position and speed information of each joint to output the required joint torque to change the position of the end-point of the manipulator.

3. Method

3.1. Deep Q Network

The Deep Q-Network (DQN) algorithm [22] is a classic algorithm based on the value function method in deep reinforcement learning, which was originally derived from the Q-Learning algorithm in classical reinforcement learning. Q-Learning is an algorithm based on the Q value, which is defined as the expected future cumulative reward value of action a (action a must be finite and discrete) taken according to policy $\pi$ in state $S$:

$$Q_{\pi }\left(s,a\right)={{\rm E}}_{\pi }\left[{\displaystyle \sum _{t=0}{\gamma }^{t}r\left(s_t,a_t\right)}|s_0=s,a_0=a\right]$$

(3)

The optimal value $Q^{*}$ is defined as the maximized Q value, and the strategy that can get the optimal value is defined as the optimal strategy ${\pi }^{*}$. DQN uses a deep neural network $Q_{\pi }\left(s,a;\theta \right)$ with parameters $\theta$ to replace the Q value $Q_{\pi }\left(s,a\right)$, which can make the input The algorithm is still valid in the case of high-dimensional and continuous state $S$. In addition, the experience playback pool Replay Buffer and a target Q network with parameters ${\theta }^{\text{'}}$ are also added to DQN. The Replay buffer improves the utilization efficiency of samples, and the use of the target Q network solves the loss in the neural network function problem. The target Q network is defined as follows:

$$y=r+\gamma \underset{a^{\prime }}{\max }Q\left(s^{\prime },a^{\prime };{\theta }^{\prime }\right)$$

(4)

Therefore, this problem can be transformed into a supervised learning problem to solve, that is $\underset{\theta }{\mathit{min}}\sum \left(y-Q\left(s,a;\theta \right)\right)$, where $\theta$ every $\mathsf{\tau }$ steps copy their own parameters to ${\theta }^{\text{'}}$.

3.2. Soft Actor Critic

Although the DQN algorithm, which is a milestone in deep reinforcement learning, solves the problem of high-dimensional and continuous input states that cannot be solved by classical reinforcement learning, it still cannot solve the situation where the output actions are high-dimensional and continuous (such as multi-degree-of-freedom manipulator). Although the other deep reinforcement learning algorithms (such as DDPG [23], TD3 [24], and other algorithms) can handle the case where the output action is high dimensional and continuous, they usually have a high sample complexity and weak sample convergence, which lead to some additional hyperparameter tuning.

The Soft Actor-Critic (SAC) algorithm [25] is a reinforcement learning algorithm that introduces the maximum entropy theory. In the framework of the algorithm, the strategy not only needs to maximize the expected cumulative reward value, but also needs to maximize the expected entropy:

$${\pi }^{*}=\max {\displaystyle \sum _{t=0}^T{E}_{(s_t,a_t)~p_{\pi }}[r(s_t,a_t)+\alpha H(\pi (\cdot |s_t))]}$$

(5)

where $\mathsf{\alpha }$ is the weight of the entropy term, which can determine the relative importance of the entropy term relative to the reward term, thereby controlling the randomness of the optimal strategy.

In order to maximize this goal, a method of alternating policy evaluation and policy improvement is used in the maximum entropy framework - Soft Policy Iteration. In an environment where the state space is discrete, the method can obtain the soft Q-value from the randomly initialized function $Q:S\times A\to R$ and repeatedly apply the modified Bellman backup operator $T^{\pi }$ :

$$T^{\pi }Q(s_t,a_t)=r(s_t,a_t)+\gamma E_{s_{t+1\sim p}}[V(s_{t+1})]$$

(6)

where

$$V(s_t)=E_{a_t~\pi }[Q(s_t,a_t)-\log \pi (a_t|s_t)]$$

(7)

is the soft state value function used to calculate the policy value in policy evaluation. While in the continuous state, a neural network with parameters is first used to replace the soft Q-function $Q_{\theta }\left(s_t, a_t\right)$, and then it is trained to minimize the Bellman residual:

$$J_Q(\theta )=E_{(s_t,a_t)~D}\left[\frac{1}{2}{\left(Q_{\theta }(s_t,a_t)-\left(r(s_t,a_t)+\gamma E_{s_{t+1}~p}[V_{\overline{\theta }}(s_{t+1})]\right)\right)}^2\right]$$

(8)

which can also be optimized with stochastic gradients:

$${\stackrel{\wedge }{{\displaystyle \nabla }}}_{\theta }{J}_Q(\theta )={{\displaystyle \nabla }}_{\theta }{{\displaystyle Q}}_{\theta }(s_t,a_t)({{\displaystyle Q}}_{\theta }(s_t,a_t)-r(s_t,a_t)-\gamma {{\displaystyle V}}_{\overline{\theta }}(s_{t+1}))$$

(9)

where $V_{\overline{\theta }}\left(s_{t+1}\right)$ is estimated by the target network of Q and the Monte Carlo estimation of the soft state value function sampled from the experience pool.

Policy improvement is updating the policy in the direction of maximizing its available reward, therefore, the policy needs to be updated to the exponential form of the new soft Q-function and restricted to some parameterized distribution (such as Gaussian distribution) and then project it back into the acceptable policy space using an information projection defined in terms of the Kullback-Leibler (KL) divergence.

$${\pi }_{new}=\arg \underset{{\pi }^{\prime }\in \Pi }{\min }{D}_{KL}\left({\pi }^{\prime }(\cdot |s_t)\parallel \frac{\exp (Q^{{\pi }_{old}}(s_t,\cdot ))}{Z^{{\pi }_{old}}(s_t)}\right)$$

(10)

where $Z^{{\pi }_{old}}\left(s_t\right)$ can be ignored because it has no effect on the gradient. And parameterize the policy ${\pi }_{\varphi }\left(a_t|s_t\right)$ with a neural network that can output mean and variance to define a Gaussian distribution, and then learn the parameters of the policy by minimizing the expected KL divergence:

$$J_{\pi }\left(\varphi \right)=E_{s_t~D}\left[E_{a_t~{\pi }_{\varphi }}\left[\log {\pi }_{\varphi }(a_t|s_t)-Q_{\theta }(s_t,a_t)\right]\right]$$

(11)

However, since the Gaussian distribution $a~N\left(m,s\right)$ is difficult to find its gradient, it is converted into an easy-to-find gradient form $a=m+s\epsilon$, $\epsilon ~N\left(0, 1\right)$, i.e. $a_t=f_{\varphi }\left({\epsilon }_t,s_t\right)$, the policy network can then be optimized by applying the policy gradient to the expected future reward:

$$J_{\pi }\left(\varphi \right)=E_{s_t~D,{\epsilon }_t~N}\left[\log {\pi }_{\varphi }(f_{\varphi }({\epsilon }_t;s_t)|s_t)-Q_{\theta }(s_t,f_{\varphi }({\epsilon }_t;s_t))\right]$$

(12)

We can also approximate the gradient of Equation (12) with:

(13)

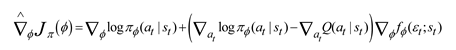
4. Experiments and Results

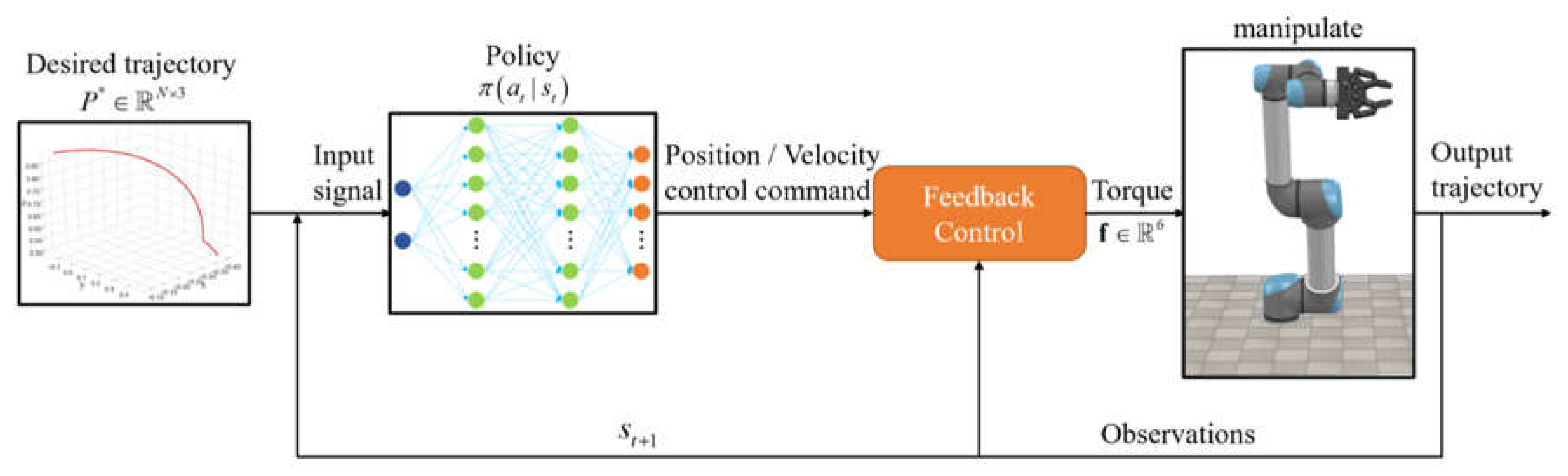
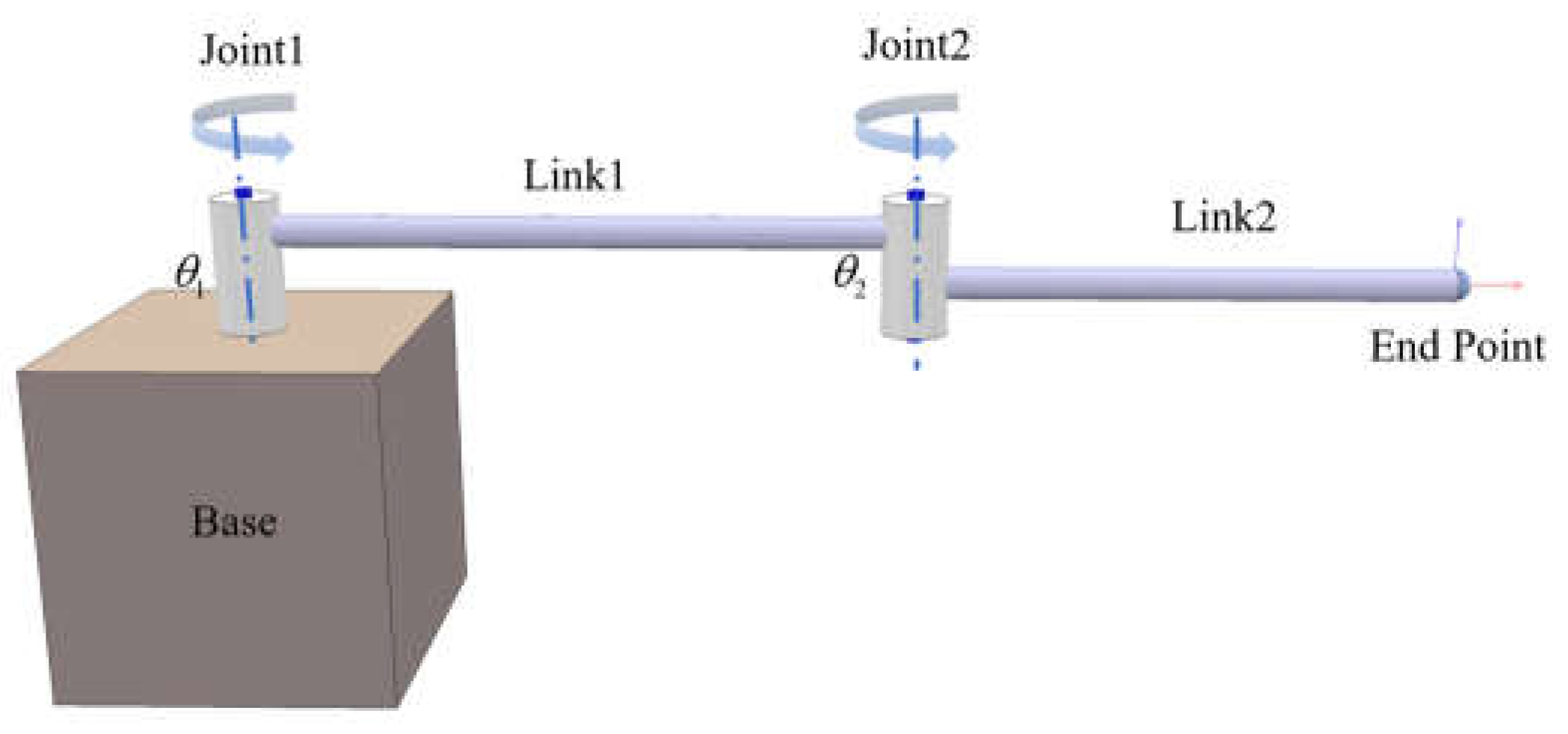
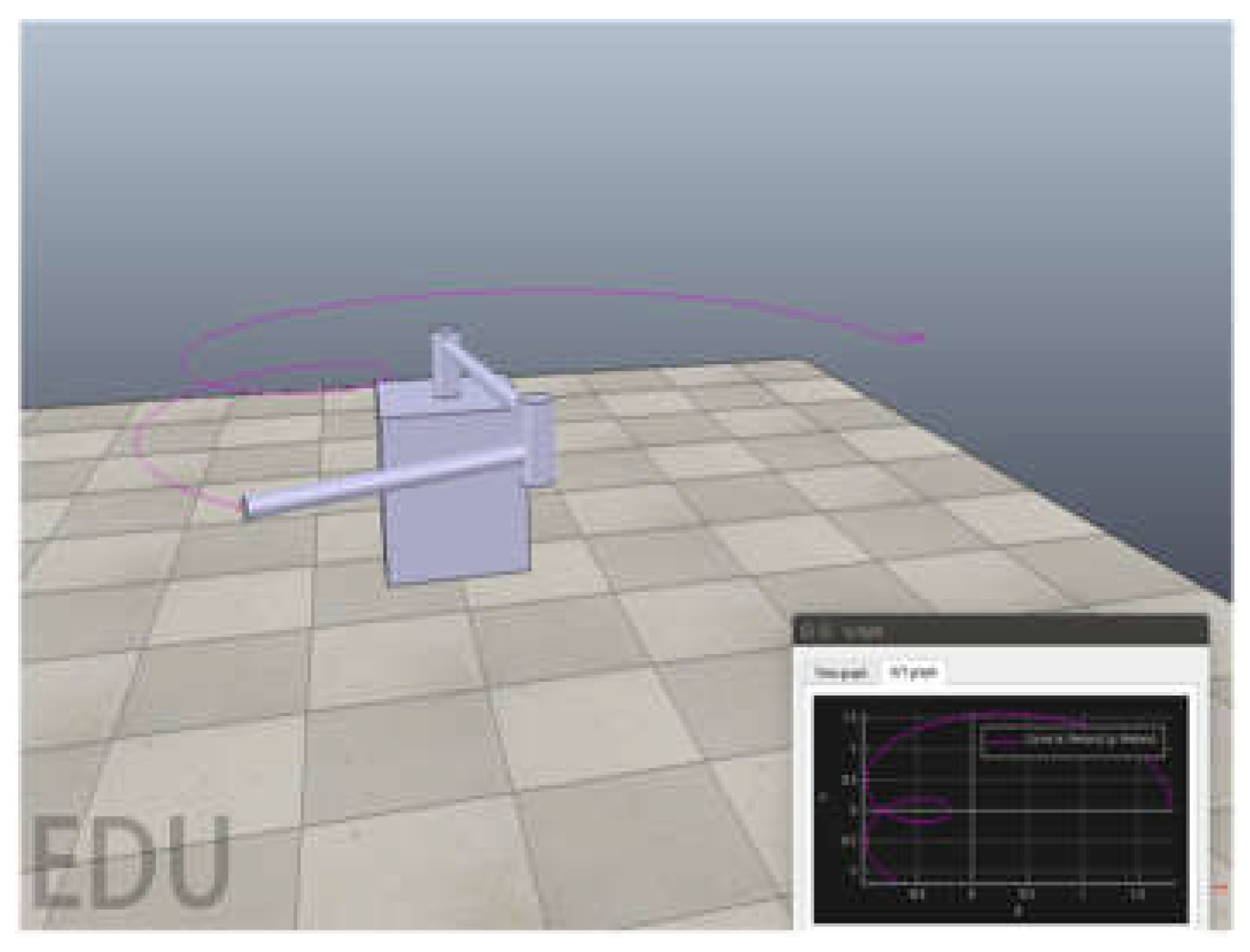
4.1. Planar two-link manipulator

The plane two-link manipulator simulation system is shown in Figure 2, and the simulation platform adopts V-REP PRO EDU 3.6.0. The settings of the two-link manipulator in the simulation environment are as follows. The length of the rods are $l_1=1.0m, l_2=0.8m$, and the mass of the rods are $m_1=0.1kg, m_2=0.08kg$. Each joint adopts the incremental control method, that is, the joint rotates a fixed angle $\left|\Delta \theta \right|$ in the direction given by the control signal ${\mathrm{a}}_{\mathrm{t}}$ at any time $t$; where $a_t≔\left[{\Delta \theta }_t^1,{\Delta \theta }_t^2\right]\in {\mathbb{R}}^2$,$\left|∆{\theta }_t^i\right|={0.05}^{°}, i=1, 2$. The state of the entire simulation system $s_t≔\left[{\theta }_t^1, {\theta }_t^2 , {\dot{\theta }}_t^1 , {\dot{\theta }}_t^2 ,x_t ,y_t ,x_t^{*} ,y_t^{*}\right]\in {\mathbb{R}}^8$, where ${\theta }_t^i,{\dot{\theta }}_t^i$ are the angle and angular velocity of each joint at $i$th time. $\left(x_t,{ y}_t\right)$ is the position of the endpoint of the manipulator at time $t$, and the desired target point position $\left(x_t^{*},{ y}_t^{*}\right)$ is set as follows:

$$\begin{array}{cc}\{\begin{array}{c}{x}_t^{*}=l_2\cos \left({\omega }_{1}t+{\omega }_{2}t\right)+l_1\cos \left({\omega }_{1}t\right)\\ y_t^{*}=l_2\sin \left({\omega }_{1}t+{\omega }_{2}t\right)+l_1\sin \left({\omega }_{1}t\right)\end{array},& {\omega }_1={\omega }_2=1 \mathrm{rad}/\mathrm{s}\end{array}$$

(14)

This experiment is mainly used to verify the feasibility of the reinforcement learning algorithm in the field of robotic arm path tracking. Because the experimental environment is simple and the output action dimension of the two-link robotic arm is low, it can be approximated as a discrete quantity, so the algorithm adopts the classic DQN algorithm. The strategy network structure in the DQN algorithm is: the input state is 8-dimensional, the output action is 2-dimensional, the hidden layer has two layers and the number of nodes in each layer is 50. The hyperparameters are set as: replaybuffer = 1e6, learning-rate = 3e-4, discount-factor = 0.99, batch-size = 64, the update between the Q network and the target Q network adopts the soft update method, and its soft parameter tau=0.001. In addition, the setting of the reward is: $r_t=\mathit{exp}\left(-\left|p_t^{*}-p_t\right|\right)$, where $p_t^{*}, p_t$ are the target path points at time t respectively and the position of the end point of the robot arm. The tracking curve results of this experiment are shown in Figure 3:

The red line is the desired target path, and the blue line is the actual running end path. From the tracking results in Figure 3, it can be seen that the method based on deep reinforcement learning perfectly achieves the tracking of the target path. Figure 4 shows the experimental results in the simulation environment:

The experimental results show that it is completely feasible to use the deep reinforcement learning algorithm to achieve path tracking on a simple two-link manipulator.

4.2. UR5 manipulator

After exploring the application of reinforcement learning in path tracking, and successfully applied to the two-link manipulator to achieve the tracking target. We will further explore the application of the multi-degree-of-freedom manipulator-UR5 to realize path tracking under continuous control. The UR5 simulation system is shown in Figure 5, and the simulation platform still uses V-REP PRO EDU 3.6.0. The system is used to realize the path tracking by using the deep reinforcement learning algorithm after the path is generated by the traditional path generation algorithm when there are obstacles. The system actions $a≔\left[a_1, a_2, a_3,{ a}_4,{ a}_5,{ a}_6,\right]\in {\mathbb{R}}^6$, and states set as $s≔\left[{\theta }_1, {\theta }_2, {\theta }_3, {\theta }_4, {\theta }_5, {\theta }_6, {\dot{\theta }}_1, {\dot{\theta }}_2, {\dot{\theta }}_3, {\dot{\theta }}_4, {\dot{\theta }}_5, {\dot{\theta }}_6, ∆x, ∆y, ∆z\right]\in {\mathbb{R}}^{15}$, where ${\theta }_i, {\dot{\theta }}_i$ is the angle and angular velocity of the first joint, $∆x, ∆y, ∆z$ are the distance between the endpoints p and the corresponding desired target points $p^{*}$. The initial position of the endpoint: [-0.095, -0.160, 0.892], the initial position of the target point: [-0.386, 0.458, 0.495]. The desired path is generated by the traditional RRT [26] path generation algorithm with the stride set to 100.

In addition, this experiment set up 4 additional variables to explore the impact of these factors on tracking performance:

• The upper control method of the manipulator adopts two control methods, position control or velocity control. The position control is the control of the joint angle, and the input action is the increment of the joint angle. The range of the increment at each moment is set as [- 0.05, 0.05] rad. The velocity control is the control of joint angular velocity. The input action is the increment of joint angular velocity. The increment range of each moment is set to [-0.8, 0.8] rad/s in the experiment. In addition, the underlying control of the manipulator adopts the traditional PID torque control algorithm.
• Adding the noise to the observations: We set up two groups of control experiments, one of which adds random noise to the observations, the noise is adopted from the standard normal distribution N(0,1), the size is 0.005 *N(0,1).
• Setting the time interval distance n. The target path points given by the manipulator at every n time are the target path points at the N*n time, where N=1, 2, 3..., and study the effect of different interval points on the tracking results. In our experiments, we set the interval distance interval=0, 5, 10 respectively.
• Terminal reward. Setting up a control experiment that during the training process, when the distance between the endpoint of the robotic arm and the target point is within 0.05m (the termination condition is met), an additional +5 reward is given to study its impact on the tracking results.

The continuous control reinforcement learning algorithm SAC is used in this experiment. All network structures are as follows: each network contains two hidden layers, the number of nodes in each layer is 200, and the activation function of the hidden layer is set to Relu. The hyperparameters are set as: replaybuffer = 1e6, discount-factor = 0.99, batch-size = 128, the update between the Q network and the target Q network adopts the soft update method, the soft parameter tau=0.01, and the learning rate of Actor and Critic network are both set to learning-rate = 1e-3, the weight coefficient of policy entropy during the entire training process $\alpha$=1e-3. The reward settings for this experiment are:

$$\begin{array}{ccc}{r}_t=-\Vert p_{\tau \left(t,n\right)}^{*}-p_t\Vert & ,& \tau \left(t,n\right)=\{\begin{array}{cc}n\left(\mathrm{floor}\left(t/n\right)+1\right)& n>1\\ t& n=1\end{array}\end{array}$$

(15)

where n is the interval distance. In addition, an experiment is terminated when the robot arm runs for 100 steps or the distance between the end point of the robot arm and the target point is within 0.05m.

The experimental results are shown in the following figures. Figure 6(a),(b) are the path tracking results without observation noise and with observation noise in the position control mode, respectively. Figure 6(c),(d) are the speed control results, respectively. The path tracking results with and without observation noise in the mode. Different time intervals are set in each picture, and the upper three curves of each picture are the results of not giving the terminal reward, and the lower three curves are the results of giving the terminal reward.

In addition, this experiment also quantitatively analyzed the tracking results, and calculated the average error between the obtained path and the target path under different experimental conditions and the average distance between the endpoint of the manipulator and the target point at the last moment. The results are shown in Table 1 and Table 2 shows:

The training process curve is shown in Figure 7:

Through the path tracing results, it can be found that:

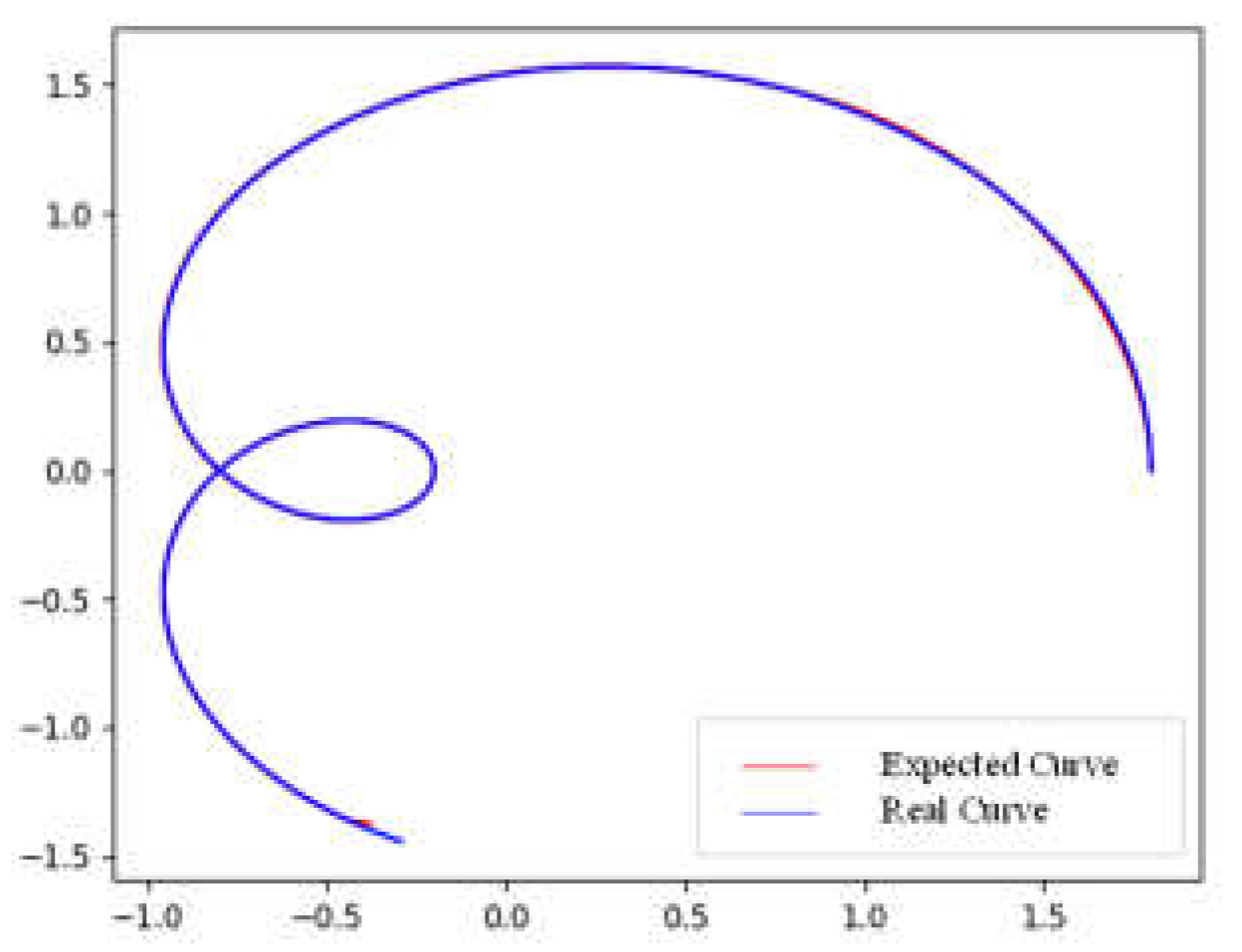
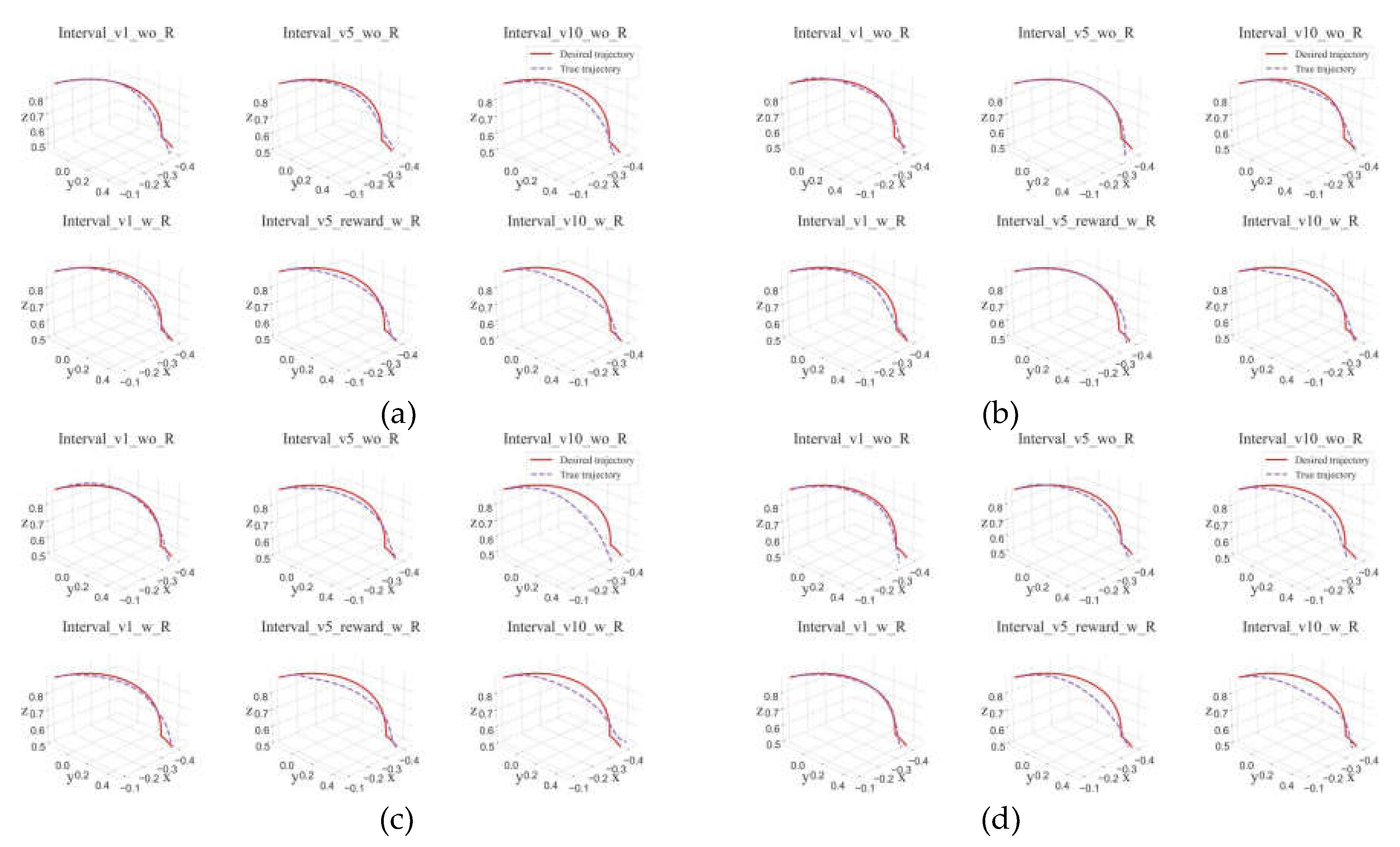
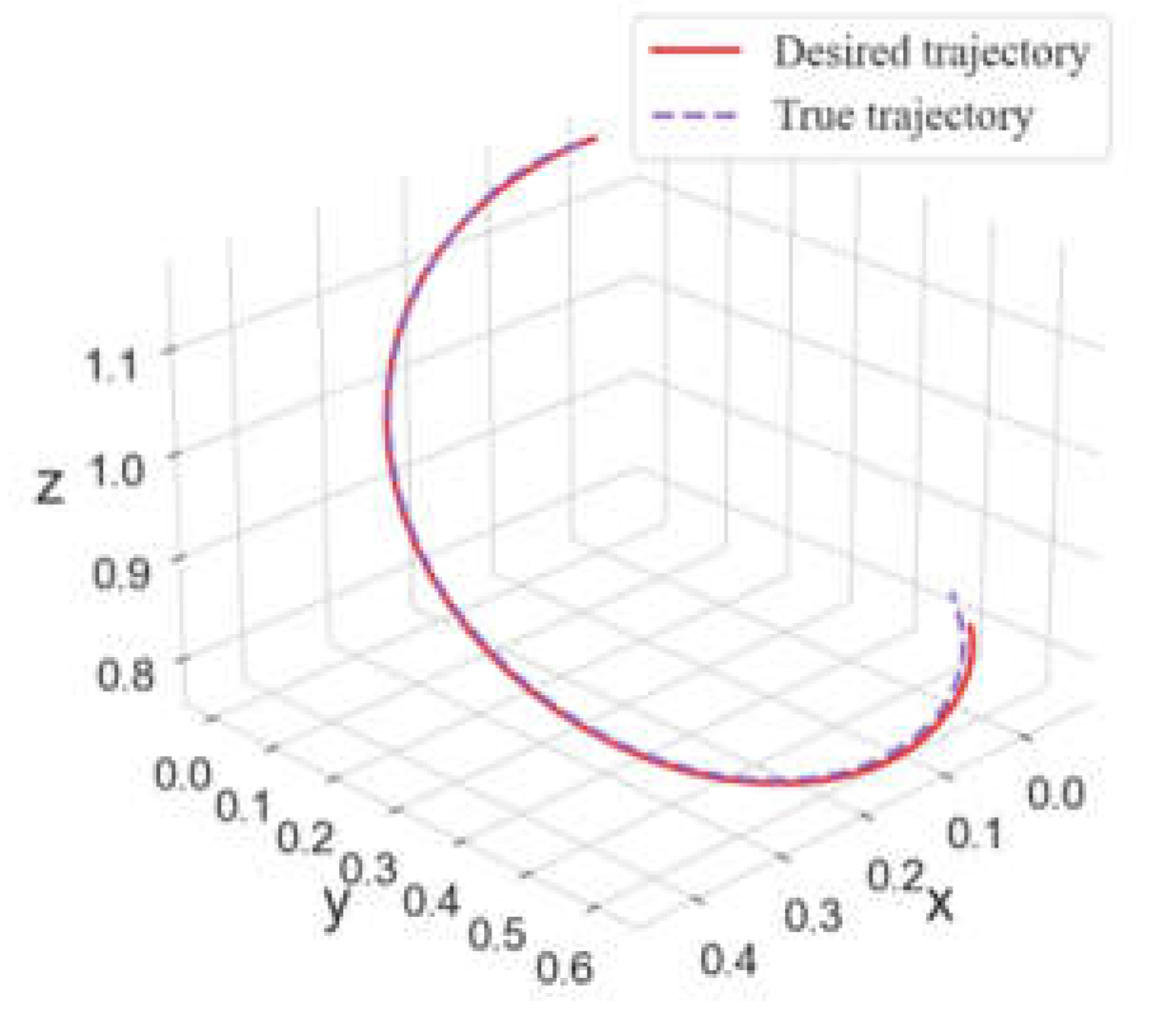
• In this experimental scenario, the target path generated by the RRT algorithm has obvious non-smoothness; while the tracking path generated by the reinforcement learning algorithm SAC based on the target path is also very smooth under the condition that the tracking accuracy is satisfied.
• By analyze the influence of the n value on the generated path, it can be found that when the n value is too large (n=10), its approaching effect on the target point is better, but its tracking effect on the target path is poor. But when n=1, the situation is opposite. Therefore, when selecting the value of n, it is necessary to balance the path tracking effect and the final position of the endpoint.
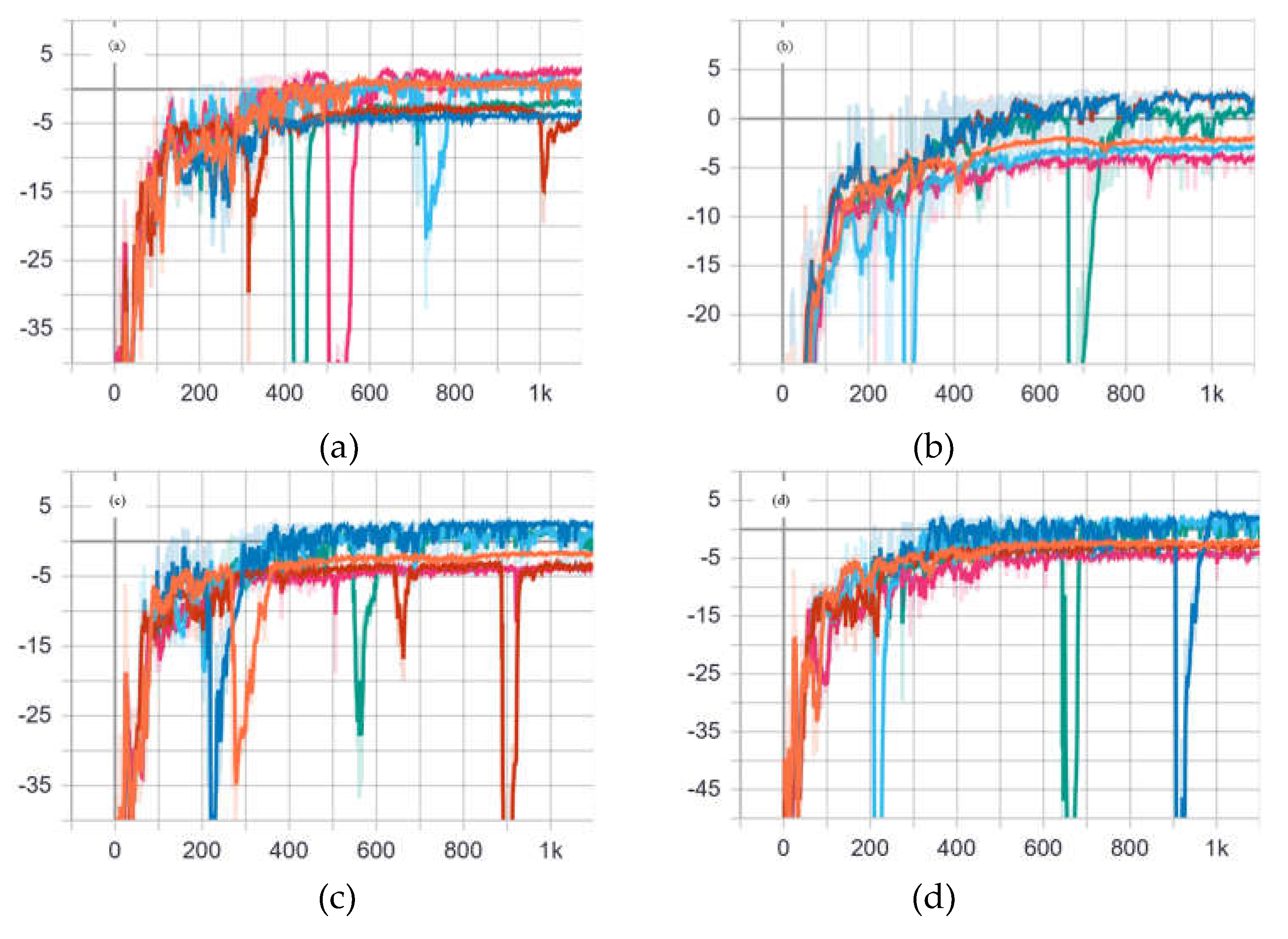
• Adding noise to the observations of the system during the simulation training process helps to improve the robustness of the control strategy and the anti-interference to noise, so that the strategy has better performance.
• During the simulation training process, when the endpoint of the manipulator reaches the allowable error range of the target point, adding a larger reward to the current strategy can make the approaching result of the robotic arm to the target point better, but it will lose some precision of path tracking;
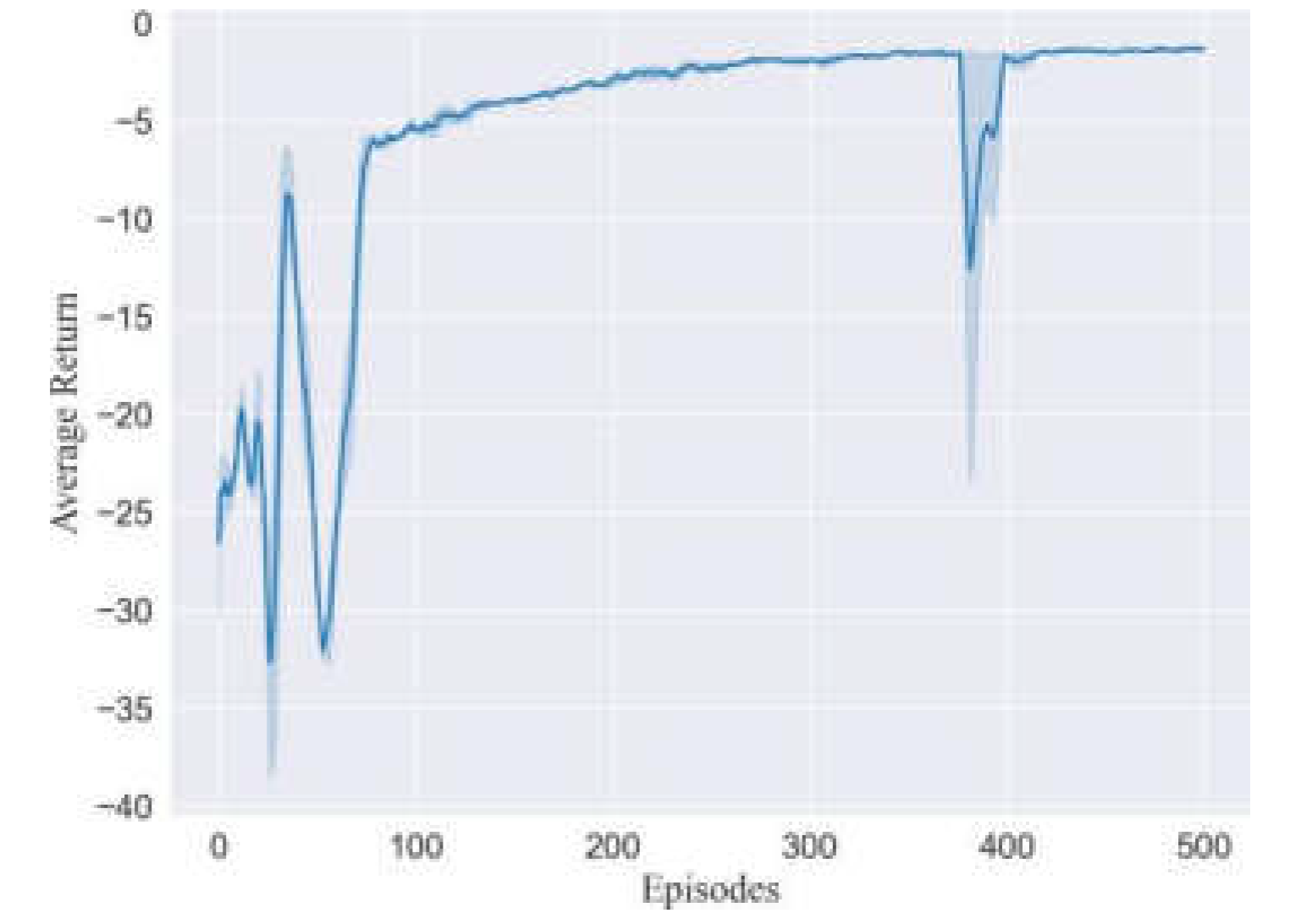
• Experiments show that the algorithm achieves good results in both position control and velocity control, and it can be seen from the curve of the training process that the curve can converge at an earlier time.

In addition, since the system dynamics model is not considered in the path tracking experiment based on deep reinforcement learning. In order to verify the advantage of the method based on deep reinforcement learning that does not need the dynamic model, we further explore the influence of the change of dynamic characteristics on the experimental results. So, we change the quality of the end effector, the trained model is tested, and the experimental results are shown in Table 3 and Table 4.

The experimental results show that in the model trained under the condition of fixed load quality, the path tracking based on deep reinforcement learning can still ensure sufficient stability when the load changes. That is, the change of dynamic characteristics will not affect the algorithm effect.

Furthermore, we also compare the results of the proposed algorithm and the traditional inverse kinematics method in terms of energy consumption and trajectory smoothness. The experimental results are shown in Table 5 and Table 6. Among them, the calculation method of the energy consumption of the manipulator during the entire path tracking process is:

$$E={\displaystyle {\int }_{t_0}^{t_M}P\left(t\right)}dt\cong {\displaystyle \sum _{k=0}^{M}P\left(k\right)}\cdot dt$$

(16)

$$P\left(k\right)={\displaystyle \sum _{i=1}^n{P}_i\left(k\right)}$$

(17)

$$P_i\left(k\right)={\tau }_i\left(k\right)\cdot \stackrel{.}{{\theta }_i}\left(k\right)$$

(18)

where $k$ is the $k$th path point in the entire path, $i$ is the $i$th joint of the manipulator, $\tau , \dot{\theta }$ is the joint torque and joint speed, M is the number of path points, $dt$ is the distance between the path-points.

The smoothness of the trajectory is measured by the angle between the tangent vectors of adjacent points of the curve, and the degree of smooth movement of the robotic arm is measured by analyzing the mean value of the turning angles in the entire trajectory.

The experimental results show that the algorithm proposed in this paper is superior to the traditional inverse kinematics method in terms of energy consumption and trajectory smoothness.

4.3. Redundant manipulator

The algorithm proposed in this paper is experimentally verified and analyzed on the UR5 manipulator. The experimental results show that the algorithm proposed in this paper can effectively solve the path tracking problem of the manipulator. In order to further verify the effectiveness and generalization of the algorithm in this paper, we also conduct the verification on a redundant manipulator. The 7-DOF redundant manipulator simulation system is shown in Figure 8. The simulation platform still uses V-REP PRO EDU 3.6.0, and the simulated manipulator uses the KUKA LBR ii wa 7 R800 redundant manipulator. The setting of actions is $a≔\left[a_1, a_2, a_3,{ a}_4,{ a}_5,{ a}_6,{ a}_7\right]\in {\mathbb{R}}^7$, and states set as $s≔\left[{\theta }_1, {\theta }_2, { \theta }_3, { \theta }_4, {\theta }_5, {\theta }_6, {\theta }_7, {\dot{\theta }}_1, {\dot{\theta }}_2, {\dot{\theta }}_3, {\dot{\theta }}_4, {\dot{\theta }}_5, {\dot{\theta }}_6, {\dot{\theta }}_7, ∆x, ∆y, ∆z\right]\in {\mathbb{R}}^{17}$,where ${\theta }_i, {\dot{\theta }}_i$ is the angle and angular velocity of the first joint and $∆x, ∆y, ∆z$ is the distance between the end-point $p$ of the manipulator and the corresponding desired target point $p^{\mathrm{*}}$. The initial position of the end-point is [0.0044, 0.0001, 1.1743], and the initial position of the target point is [0.0193, 0.4008, 0.6715]. The expected path is an arc trajectory generated by the path generation algorithm, and the step size is set to 50.

The setup of the redundant manipulator path tracking experiment is exactly the same as that of UR5. The experiment still uses the continuous control reinforcement learning algorithm SAC, and all network structures are also the same as the UR5 setup. That is, each network contains two hidden layers, the number of nodes in each layer is 200, and the activation function of the hidden layer is set to Relu. The hyperparameter settings are also: replaybuffer = 1e6, discount-factor = 0.99, batch-size = 128, the update between the Q network and the target Q network adopts the soft update method, the soft parameter tau=0.01, and the learning rate of Actor and Critic network are both set to learning-rate = 1e-3, the weight coefficient α=1e-3 of policy entropy during the whole training process.

The reward settings are also the same as before. The only difference is that the redundant manipulator path tracking experiment is an experiment to verify the generalization of the algorithm, so it does not involve the results when other hyperparameter conditions change. Therefore, the default separation distance in the reward setting is n=1.

Since this experiment is a verification experiment, this experiment only explores the path tracking results in the speed control mode. The path tracking results of the redundant manipulator are shown in Figure 9.

In addition, we consider the randomness of the sampling of the deep reinforcement learning algorithm. And in order to reflect the stability of our method, we also carried out multiple experiments under the setting of multiple random seeds. The training process curve of the experimental results is shown in Figure 10.

The experimental results show that our method still has a good tracking effect on the redundant manipulator, and the training results under different random seed settings show that our method can be guaranteed in terms of generalization and stability

5. Conclusion

In this paper, we introduce a method of using a deep reinforcement learning algorithm to realize the path tracking of the manipulator. The traditional path planning algorithm is used to generate the target path, and the deep reinforcement learning algorithm is used to generate the control signal to control the manipulator and realize the tracking of the target path. The experimental results show that the method has a good effect on the path tracking of the manipulator, which not only avoids the process of seeking the inverse kinematics solution, but also maintains good performance when the dynamic characteristics change. In addition, through further verification experiments on the path tracking of the redundant manipulator, the generalization and stability of our method are reflected. So, we think that our method has great significance for the research of the path tracking of the manipulator.