Generalized Legendre Wavelets, Definition, Properties and Their Applications for Solving Linear Differential Equations

Naglaa M. El-Shazly; Mohamed A. Ramadan; Taha Radwan

doi:10.20944/preprints202305.1001.v1

Submitted:

13 May 2023

Posted:

15 May 2023

You are already at the latest version

Abstract

In this work, we offer a novel and accurate method in order to find the solution of the linear differential equations over the intervals [0, 1) based on the generalization of Legendre wavelets. The mechanism is still upon workable implementation of the operational matrix of integration and its derivatives. This method reduces the problems into algebraic equations via the properties of generalized Legendre wavelet (GLW) together with the operational matrix of integration. The function approximation has been picked out in such a way so as to enumerate the connection coefficients in an facile manner. The proposed numerical technique, based on the GLW, has been examined on three linear problems as a consequence of this investigation. The outcomes have shown that this method, as opposed to some other existing numerical and analytical methods, is a very useful and advantageous for tackling such problems.

Keywords:

Generalized Legendre wavelet

;

operational matrix of integration

;

linear differential equations

;

product operation matrix

;

convergence analysis

;

accuracy

Subject:

Computer Science and Mathematics - Computational Mathematics

1. Introduction

Polynomial series and orthogonal functions play an essential rule for solving various problems of dynamic systems [1,2,3,4,5,6,7,8]. One of those problems is solving differential or integral equations. The major idea of employing orthogonal basis is that it decreases these problems in order to solve a system of linear algebraic equations, approximating some signals involved in these equations, by the use of both of the truncated orthogonal sequence and the matrix of integrations

P

to exclude the integral operations.

Consider the equation

\int_{0}^{t} χ (x) d x = P χ (x), ​

with the obtained operational matrix

P

by using the orthogonal functions’ basis

ψ_{0}, ψ_{1}, \dots, ψ_{n - 1}

and

χ = [ψ_{0}, ψ_{1}, \dots, ψ_{n - 1}]

.

Lately, Wavelets are very important in various studies such as science and engineering. Various authors have studied different forms of wavelets such as Fourier series, Walsh functions, Legendre polynomials, Bessel series and Chebyshev polynomials (see [9,10,11,12,13,14,15,16]). The Wavelet analysis is a probable mechanism to solve such difficulty in Physics, signal and image processing by deletion of numerous terms in gaining demand precision. Gu and Jiang [17] developed the Haar Wavelet operational matrix. Chen and Hsiao [18] solved some problems in image processing, communication and physics using the wavelet analysis. Shyam and Susheel [19] estimated a new theorem on preferable wavelet approximation of the functions from the generalized lipschitz class by the use of Haar scaling function.

By the use of Haar wavelets, Lepik [20] proposed the segmentation method to solve differential equations, numerically. Lepik [21] demonstrated that the Haar wavelet method is a strong tool for finding the solution of various forms of integral and partial differential equations, his method’s major feature is its simplicity and small calculation charge. Jhangeer et al. [22] studied the Bogoyavlenskii–Kadomtsev–Petviashvili (BKP) equation by means of Lie symmetry analysis. Tavassoli Kajani et al. [23] studied the Chebyshev wavelets matrix of integration, Sripathy et al. [24] presented the chebyshev wavelet method in order to solve some non-linear differential equations arising in engineering. Shyam and Rakesh [25] obtained five new estimates of any function

f

on

[0, 1)

having bounded derivative by the method of the extended Legendre wavelet. Owais et al. [26] developed the comprehensive theory of biorthogonal wavelets on the spectrum. Sharma and Lal [27] presented the operational matrix of integration by the use of the Legendre wavelet in order to solve different types of differential equations in both linear and non-linear forms. This manuscript is orderly as follows: in the second section, we present the definition of Legendre wavelet beside its properties. Also, we present the definition of the extended Legendre wavelet expansion together with the function approximation. In section 3, we offer a novel and accurate method for solving linear differential equations over the intervals [0, 1) based on the generalization of Legendre wavelets. The mechanism is still upon workable implementation of the operational matrix of integration and its derivatives. This method reduces the problems into algebraic equations. Our proposed numerical technique will be examined on three linear problems in the fourth section. We summarize our work in the fifth section.

2. Definitions and Preliminaries

2.1. Legendre wavelet and its properties

Considering a single function “mother wavelet”

ψ (t)

, from which wavelets represent a family of functions by dilating and transforming this single function. This family of continuous wavelets [17] has the following form:

ψ_{a, b} (t) = {| a |}^{- \frac{1}{2}} (\frac{t - b}{a}), a, b \in R, a \neq 0 .

(2.1)

The Legendre wavelets on the interval

[0, 1)

defined by

ψ_{n, m} (t) = {\begin{cases} \sqrt{m + \frac{1}{2}} 2^{\frac{k}{2}} L_{m} (2^{k} t - \hat{n}), \frac{\hat{n} - 1}{2^{k}} \leq t < \frac{\hat{n} + 1}{2^{k}}; \\ 0 o t h e r w i s e \end{cases}

(2.2)

for which

k

is positive integer,

n = 1, 2, \dots, 2^{k - 1}

and

\hat{n} = 2 n - 1

, the order of the Legendre Polynomial is denoted by

m = 0, 1, 2, \dots, M

and the normalized time is denoted by

t

. The Legendre Polynomials

L_{m}

which are obtained in the above definition is proposed as follows:

\begin{array}{l} L_{0} (t) = 1, \\ L_{1} (t) = t, \\ L_{m + 1} (t) = \frac{2 m + 1}{m + 1} t L_{m} (t) - \frac{m}{m + 1} L_{m - 1} (t), m = 1, 2, 3, \dots \end{array}

(2.3)

which are orthogonal over [-1,1] with weighting function

w (1) = 1

, for more details (see Balaji [28]).

2.2. Function approaches

A function

f (t)

which is defined on

[0, 1)

can be extended as Legendre Wavelet infinite series of the following type

f (t) = \sum_{n = 1}^{\infty} \sum_{m = 0}^{\infty} c_{n, m} ψ_{n, m} ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​ ​

(2.4)

where

c_{n, m} = 〈 f, ψ_{n, m} 〉

.

After being trimmed, Eq. (2.4) can be rewritten as follows.

f (t) \approx \sum_{n = 1}^{2^{k - 1}} \sum_{m = 0}^{M - 1} c_{n, m} ψ_{n, m} = C^{T} ψ (t) .

(2.5)

where

C = {[c_{1, 0} c_{1, 1} \dots c_{1, M - 1} \dots c_{2^{k - 1}, 0} c_{2^{k - 1}, 1} \dots c_{2^{k - 1}, M - 1}]}^{T}

and

ψ (t) = {[ψ_{1, 0} ψ_{1, 1} \dots ψ_{1, M - 1} \dots ψ_{2^{k - 1}, 0} ψ_{2^{k - 1}, 1} \dots ψ_{2^{k - 1}, M - 1}]}^{T}

.

2.3. Generalized Legendre Wavelet Expansion [25]

In this section we introduce a generalization for Legendre wavelets given in (2.2) .The proposed Generalized Legendre wavelets

(G L W)

on the interval

[0, 1)

are defined by

ψ^{(μ)}_{n, m} (t) = {\begin{cases} \sqrt{m + \frac{1}{2}} μ^{\frac{k}{2}} L_{m} (μ^{k} t - \hat{n}), \frac{\hat{n} - 1}{μ^{k}} \leq t < \frac{\hat{n} + 1}{μ^{k}}; \\ 0 o t h e r w i s e \end{cases}

(2.6)

for which

k

is positive integer,

n = 1, 2, \dots, μ^{k - 1}

and

\hat{n} = 2 n - 1

and the order of the Legendre Polynomial is denoted by

m = 0, 1, 2, \dots, M

and the normalized time is denoted by

t

.

Lemma 2.1 (Orthonormality of the generalized Legendre wavelets)

The generalized Legendre wavelets which are defined in Eq. (2.6) are orthonormal on

[\frac{\hat{n} - 1}{μ^{k}}, \frac{\hat{n} + 1}{μ^{k}}]

.

Proof:

First we show that

ψ^{(μ)}_{n, m} (t)

are orthogonal on

[\frac{\hat{n} - 1}{μ^{k}}, \frac{\hat{n} + 1}{μ^{k}}]

where

\hat{n} = 2 n - 1

.

From the definition of GLW given in Eq.(2.6), we have

\begin{array}{l} 〈 ψ^{(μ)}_{n, m} (t), ψ^{(μ)}_{n, m^{'}} (t) 〉 & = 〈 \sqrt{m + \frac{1}{2}} μ^{\frac{k}{2}} L_{m} (μ^{k} t - \hat{n}), \sqrt{m^{'} + \frac{1}{2}} μ^{\frac{k}{2}} L_{m^{'}} (μ^{k} t - \hat{n}) 〉 \\ = \sqrt{m + \frac{1}{2}} \sqrt{m^{'} + \frac{1}{2}} μ^{k} \int_{\frac{\hat{n} - 1}{μ^{k}}}^{\frac{\hat{n} + 1}{μ^{k}}} L_{m} (μ^{k} t - \hat{n}) L_{m^{'}} (μ^{k} t - \hat{n}) d t \end{array}

Set

μ^{k} t - \hat{n} = y

, then for

t = \frac{\hat{n} - 1}{μ^{k}}

, we have

y = - 1

, and for

t = \frac{\hat{n} + 1}{μ^{k}}

, we have

y = 1

and

d t = \frac{1}{μ^{k}} d y

.

Hence,

〈 ψ^{(μ)}_{n, m} (t), ψ^{(μ)}_{n, m^{'}} (t) 〉 = \sqrt{m + \frac{1}{2}} \sqrt{m^{'} + \frac{1}{2}} μ^{k} \int_{- 1}^{1} L_{m} (y) L_{m^{'}} (y) d y

Since the Legendre polynomials are orthogonal on

[- 1, 1]

, then we conclude that.

〈 ψ^{(μ)}_{n, m} (t), ψ^{(μ)}_{n, m^{'}} (t) 〉 = 0.

(2.7)

To show the generalized Legendre wavelets are orthonormal on

[\frac{\hat{n} - 1}{μ^{k}}, \frac{\hat{n} + 1}{μ^{k}}]

, we only need to show they are normalized, that is

{‖ ψ^{(μ)}_{n, m} (t) ‖}_{2}^{2} = 1

{‖ ψ^{(μ)}_{n, m} (t) ‖}_{2}^{2} = \int_{\frac{2 n - 2}{μ^{k}}}^{\frac{2 n}{μ^{k}}} (\frac{2 m + 1}{2}) μ^{k} L_{m}^{2} (μ^{k} t - 2 n + 1) d t

Set:

v = μ^{k} t - 2 n + 1

, then

d v = μ^{k} d t

Therefore we have

{‖ ψ^{(μ)}_{n, m} (t) ‖}_{2}^{2} = (\frac{2 m + 1}{2}) \int_{- 1}^{1} L_{m}^{2} (v) d v = (\frac{2 m + 1}{2}) (\frac{2}{2 m + 1}) = 1

(2.8)

From (2.7) and (2.8) it is clear that our generalized Legendre wavelets that are defined in Eq. (2.6) are orthonormal.

A function

f (t)

which is defined on

[0, 1)

can be expanded as generalized Legendre wavelet infinite series of the following type

f (t) = \sum_{n = 1}^{\infty} \sum_{m = 0}^{\infty} c_{n, m} ψ^{μ}_{n, m}

(2.9)

where

c_{n, m} = 〈 f, ψ^{μ}_{n, m} 〉

.

After being trimmed, Eq. (2.9) can be expressed as follows:

f (t) \approx \sum_{n = 1}^{μ^{k - 1}} \sum_{m = 0}^{M} c_{n, m} ψ^{μ}_{n, m} (t) = C^{T} ψ (t),

(2.10)

where

C = [c_{1, 0} c_{1, 1}, ..., c_{1, M}, c_{2, 0}, c_{2, 1}, ..., c_{2, M}, ..., c_{μ^{k - 1}, 0} c_{μ^{k - 1}, 1}, ..., c_{μ^{k - 1}, M}]^{T}

and

ψ (t) = {[ψ^{μ}_{1, 0} ψ^{μ}_{1, 1} \dots ψ^{μ}_{1, M} \dots ψ^{μ}_{2, 0} ψ^{μ}_{2, 1} \dots ψ^{μ}_{2, M} \dots ψ^{μ}_{μ^{k - 1}, 0} ψ^{μ}_{μ^{k - 1}, 1} \dots ψ^{μ}_{μ^{k - 1}, M}]}^{T} .

3.1. Generalized Legendre Wavelet Operational Matrix of Integration

Now, we will present our new generalized Legendre wavelet operational matrix of integration for

M = 3, K = 2, μ = 3

, then it used to solve the differential equations. The variation between exact solution and Legendre wavelet solution is negligible.

With the use of the definition of Legendre wavelet for

m = 0, 1, 2, 3

and

n = 1, 2, 3 .

we get that

ψ_{1, 0}^{^{μ}} (t) = {\begin{cases} \frac{3}{\sqrt{2}}, 0 \leq t < \frac{2}{9} \\ 0, o t h e r w i s e \end{cases}

(3.1)

ψ_{1, 1}^{^{μ}} (t) = {\begin{cases} 3 \sqrt{\frac{3}{2}} [9 t - 1], 0 \leq t < \frac{2}{9} \\ 0, o t h e r w i s e \end{cases}

(3.2)

ψ_{1, 2}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{5}{2}} [3 {(9 t - 1)}^{2} - 1], 0 \leq t < \frac{2}{9} \\ 0, o t h e r w i s e \end{cases}

(3.3)

ψ_{1, 3}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{7}{2}} [5 {(9 t - 1)}^{3} - 3 (9 t - 1)], 0 \leq t < \frac{2}{9} \\ 0, o t h e r w i s e \end{cases}

(3.4)

ψ_{2, 0}^{^{μ}} (t) = {\begin{cases} \sqrt{\frac{3}{2}}, \frac{2}{9} \leq t < \frac{4}{9} \\ 0, o t h e r w i s e \end{cases}

(3.5)

ψ_{2, 1}^{^{μ}} (t) = {\begin{cases} 3 \sqrt{\frac{3}{2}} [9 t - 3], \frac{2}{9} \leq t < \frac{4}{9} \\ 0, o t h e r w i s e \end{cases}

(3.6)

ψ_{2, 2}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{5}{2}} [3 {(9 t - 3)}^{2} - 1], \frac{2}{9} \leq t < \frac{4}{9} \\ 0, o t h e r w i s e \end{cases}

(3.7)

ψ_{2, 3}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{7}{2}} [5 {(9 t - 3)}^{3} - 3 (9 t - 3)], \frac{2}{9} \leq t < \frac{4}{9} \\ 0, o t h e r w i s e \end{cases}

(3.8)

ψ_{3, 0}^{^{μ}} (t) = {\begin{cases} \sqrt{\frac{3}{2}}, \frac{4}{9} \leq t < \frac{6}{9} \\ 0, o t h e r w i s e \end{cases}

(3.9)

ψ_{3, 1}^{^{μ}} (t) = {\begin{cases} 3 \sqrt{\frac{3}{2}} [9 t - 5], \frac{4}{9} \leq t < \frac{6}{9} \\ 0, o t h e r w i s e \end{cases}

(3.10)

ψ_{3, 2}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{5}{2}} [3 {(9 t - 5)}^{2} - 1], \frac{4}{9} \leq t < \frac{6}{9} \\ 0, o t h e r w i s e \end{cases}

(3.11)

ψ_{3, 3}^{^{μ}} (t) = {\begin{cases} \frac{3}{2} \sqrt{\frac{7}{2}} [5 {(9 t - 5)}^{3} - 3 (9 t - 5)] \frac{4}{9} \leq t < \frac{6}{9} \\ 0 o t h e r w i s e \end{cases}

(3.12)

Now by integrating Eq. (3.1), we have

\int_{0}^{t} ψ_{1, 0}^{^{μ}} (t) d t = {\begin{cases} \frac{3}{\sqrt{2}} t, 0 \leq t < \frac{2}{9} \\ \frac{\sqrt{2}}{3}, o t h e r w i s e \end{cases}

(3.13)

Now expanding Eq. (3.13) in the type of basis function, yields that

\int_{0}^{t} ψ_{1, 0}^{^{μ}} (t) d t = [\begin{matrix} \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & \frac{2}{9} & 0 & 0 & 0 & \frac{2}{9} & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

where

Ψ_{12} (t) = {[\begin{matrix} ψ_{1, 0}^{^{μ}} & ψ_{1, 1}^{^{μ}} & ψ_{1, 2}^{^{μ}} & ψ_{1, 3}^{^{μ}} & ψ_{2, 0}^{^{μ}} & ψ_{2, 1}^{^{μ}} & ψ_{2, 2}^{^{μ}} & ψ_{2, 3}^{^{μ}} & ψ_{3, 0}^{^{μ}} & ψ_{3, 1}^{^{μ}} & ψ_{3, 2}^{^{μ}} & ψ_{3, 3}^{^{μ}} \end{matrix}]}^{T} .

In the same procedure, making the same mechanism for the other functions of basis, implies that

\int_{0}^{t} ψ_{1, 1}^{^{μ}} (t) d t = [\begin{matrix} - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{1, 2}^{^{μ}} (t) d t = [\begin{matrix} 0 & - \frac{\sqrt{15}}{135} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{1, 3}^{^{μ}} (t) d t = [\begin{matrix} \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{2, 0}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & \frac{2}{9} & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{2, 1}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{2, 2}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{15}}{135} & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{2, 3}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & 0 & 0 & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{3, 0}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{3, 1}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{3, 2}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{15}}{135} & 0 & 0 \end{matrix}] Ψ_{12} (t)

\int_{0}^{t} ψ_{3, 3}^{^{μ}} (t) d t = [\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} \end{matrix}] Ψ_{12} (t)

Thus we propose the operational matrix of integration as follows:

P = [\begin{matrix} \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & \frac{2}{9} & 0 & 0 & 0 & \frac{2}{9} & 0 & 0 & 0 \\ - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & - \frac{\sqrt{15}}{135} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & \frac{2}{9} & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{15}}{135} & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{3}}{27} & 0 & \frac{\sqrt{15}}{135} & - \frac{\sqrt{3}}{27} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & - \frac{\sqrt{15}}{135} & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & \frac{1}{9} \end{matrix}] .

Thus,

\int_{0}^{t} Ψ_{12} (x) d x = P Ψ_{12} (t) .

(3.14)

3.2. Convergence criteria of the proposed (GLWM)

In this subsection, we discuss the theoretical analysis of the convergence of our approach to solve the general linear differential equation of order n defined below:

\begin{array}{l} y^{(n)} + P_{1} (t) y^{(n - 1)} + \dots + P_{n - 1} (t) y^{'} + P_{0} (t) y = h (t), \\ y (t_{0}) = y_{0}, y^{'} (t_{0}) = y_{1}, \dots, y^{(n - 1)} (t_{0}) = y_{n - 1} . \end{array}

(3.15)

Theorem 3.1

The series solution

y (t) = \sum_{n = 1}^{\infty} \sum_{m = 0}^{\infty} c_{n, m} ψ_{n, m}^{μ} (t)

defined in Eq.(2.9) using generalized Legendre wavelet method converges to

y (t) .

Proof:

Let

L^{2} (R)

be the Hilbert space.

Since we have shown that

ψ^{(μ)}_{n, m} (t) = \sqrt{m + \frac{1}{2}} μ^{\frac{k}{2}} L_{m} (μ^{k} t - \hat{n})

forms an orthonormal basis.

Let

y (t) = \sum_{i = 0}^{M} h_{n i} ψ_{n i}^{μ} (t)

be a solution of Eq. (3.15) where

h_{1 i} = 〈 y (t), ψ_{1 i}^{μ} (t) 〉

for

n = 1

in which

〈 ., . 〉

denotes the inner product.

Let we denote

ψ_{n i}^{μ} (t) = ψ_{}^{μ} (t)

and

α_{j} = 〈 y (t), ψ_{}^{μ} (t) 〉

y (t) = \sum_{i = 1}^{M} 〈 y (t), ψ_{1 i}^{μ} (t) 〉 ψ_{1 i}^{μ} (t)

Consider the sequences of partial sums

W_{n - 1} = \sum_{j = 1}^{n - 1} α_{j} ψ_{}^{μ} (t_{j}) and W_{m - 1} = \sum_{j = 1}^{m - 1} α_{j} ψ_{}^{μ} (t_{j})

Then,

〈 y (t), W_{n - 1} 〉 = 〈 y (t), \sum_{j = 1}^{n - 1} α_{j} ψ_{}^{μ} (t_{j}) 〉 = \sum_{j = 1}^{n - 1} {\bar{α}}_{j} 〈 y (t), ψ_{}^{μ} (t_{j}) 〉 = \sum_{j = 1}^{n - 1} {\bar{α}}_{j} α_{j} = {\sum_{j = 1}^{n - 1} | α_{j} |}^{2} .

Moreover,

\begin{array}{l} {‖ W_{n - 1} - W_{m - 1} ‖}^{2} = {‖ \sum_{j = m + 1}^{n - 1} α_{j} ψ_{}^{μ} (t_{j}) ‖}^{2} \\ = 〈 \sum_{i = m + 1}^{n - 1} α_{i} ψ_{}^{μ} (t_{i}), \sum_{j = m + 1}^{n - 1} α_{j} ψ_{}^{μ} (t_{j}) 〉 \\ = \sum_{i = m + 1}^{n - 1} \sum_{j = m + 1}^{n - 1} α_{i} {\bar{α}}_{i} 〈 ψ_{}^{μ} (t_{i}), ψ_{}^{μ} (t_{j}) 〉 \\ = {\sum_{i = m + 1}^{n - 1} | α_{i} |}^{2} \end{array}

As

n \to \infty

, by Bessel’s inequality, we get that

{\sum_{i = m + 1}^{n - 1} | α_{i} |}^{2}

is convergent, it yields that

{W_{n - 1}}

is a Cauchy sequence and it converges to

W

(say).

Now, we have

\begin{array}{l} 〈 W - y (t), ψ_{}^{μ} (t_{j}) 〉 & = 〈 W, ψ_{}^{μ} (t_{j}) 〉 - 〈 y (t), ψ_{}^{μ} (t_{j}) 〉 \\ = 〈 \lim_{n \to \infty} W_{n - 1}, ψ_{}^{μ} (t_{j}) 〉 - α_{j} \\ = \lim_{n \to \infty} 〈 W_{n - 1}, ψ_{}^{μ} (t_{j}) 〉 - α_{j} \\ = \lim_{n \to \infty} 〈 \sum_{j = 1}^{n - 1} α_{j} ψ_{}^{μ} (t_{j}), ψ_{}^{μ} (t_{j}) 〉 - α_{j} \\ = α_{j} - α_{j} = 0 \end{array}

Which is satisfied only in the case if

y (t) = W

. Thus,

y (t) = \sum_{j = 1}^{\infty} α_{j} ψ_{}^{μ} (t_{j})

.

4. Numerical test and discussion

To demonstrate the effectiveness of our proposed generalized Legendre wavelet method (GLWM), we implement GLWM to some ordinary differential equations of linear form with constant and variable coefficients. All the numerical test examples were carried out with MATLAB R2015a.

Example 1

We deem the differential equation

0.25 y^{'} + y = t, y (0) = 0 .

(4.1)

whose exact solution is given by

y (t) = \frac{1}{4} (e^{- 4 t} + 4 t - 1)

.

We apply Generalized Legendre wavelets (GLWM) for

M = 3

, k = 2

,

μ = 3

.

For this choice of

M, ​ k, μ

, the function approximation for

y (t)

will take the summation form:

y (t) \approx \sum_{n = 1}^{μ^{k - 1}} \sum_{m = 0}^{M} c_{n, m} ψ_{n, m}^{^{μ}} (t) = \sum_{n = 1}^{3} \sum_{m = 0}^{3} c_{n, m} ψ_{n, m}^{^{μ}} (t) = C^{T} Ψ,

where

C_{12 \times 1} = {[c_{1, 0} c_{1, 1} c_{1, 2} c_{1, 3} c_{2, 0} c_{2, 1} c_{2, 2} c_{2, 3} c_{3, 0} c_{3, 1} c_{3, 2} c_{3, 3}]}^{T}

and

Ψ_{12 \times 1} (t) = {[\begin{matrix} ψ_{1, 0}^{^{μ}} (t) & ψ_{1, 1}^{^{μ}} (t) & ψ_{1, 2}^{^{μ}} (t) & ψ_{1, 3}^{^{μ}} (t) & ψ_{2, 0}^{^{μ}} (t) & ψ_{2, 1}^{^{μ}} (t) & ψ_{2, 2}^{^{μ}} (t) & ψ_{2, 3}^{^{μ}} (t) & ψ_{3, 0}^{^{μ}} (t) & ψ_{3, 1}^{^{μ}} (t) & ψ_{3, 2}^{^{μ}} (t) & ψ_{3, 3}^{^{μ}} \end{matrix} (t)]}^{T} .

Now, we approximate the function

f (t) = t

in terms of the set of the basis functions

Ψ (t)

as:

f (t) = t ≅ e^{T} Ψ {(t)}_{12 \times 1} .

(4.2)

where in this case the coefficient vector

e

is given by

e = {[\begin{matrix} 0.0524 & 0 . 0302 & 0 & 0 & 0 . 1571 & 0 . 0302 & 0 & 0 & 0 . 2619 & 0 . 0302 & 0 & 0 \end{matrix}]}^{T}

and we present the operational matrix of integration

P_{12 \times 12}

as follows:

P_{12 \times 12} = (\begin{matrix} \begin{array}{l} 1 / 9 \\ 260 / 4053 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 260 / 4053 \\ 0 \\ 489 / 17045 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 489 / 17045 \\ 0 \\ 94 / 5005 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 94 / 5005 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 2 / 9 \\ 0 \\ 0 \\ 0 \\ 1 / 9 \\ 260 / 4053 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 260 / 4053 \\ 0 \\ 489 / 17045 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 489 / 17045 \\ 0 \\ 94 / 5005 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 94 / 5005 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{array} & \begin{array}{l} 2 / 9 \\ 0 \\ 0 \\ 0 \\ 2 / 9 \\ 0 \\ 0 \\ 0 \\ 1 / 9 \\ 260 / 4053 \\ 0 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 260 / 4053 \\ 0 \\ 489 / 17045 \\ 0 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 489 / 17045 \\ 0 \\ 94 / 5005 \end{array} & \begin{array}{l} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 94 / 5005 \\ 0 \end{array} \end{matrix})

Therefore, we obtain

\int_{x = 0}^{t} Ψ {(x)}_{12 \times 1} d x = P_{12 \times 12} Ψ_{12 \times 1} (t) .

(4.3)

Now we used this operational matrix in order to find the solution of the deferential Eq. (4.1).

By integrating equation (4.1) and using equations (4.2) and (4.3), we have

0.25 \int_{0}^{t} \frac{d y}{d x} d x + \int_{0}^{t} y (x) d x = \int_{0}^{t} e^{T} Ψ {(x)}_{12 \times 1} d x,

which can rewritten in the following form

0.25 C^{T} Ψ (t) + P C^{T} ​ Ψ (t) = e^{T} P Ψ {(t)}_{12 \times 1} .

Form which we obtain,

0.25 C^{T} + P C^{T} ​ = P^{T} e .

Taking the transpose of the last equation we get the following system of equations

(0.25 I + P^{T}) C^{} ​ = P^{T} e

and

I

is the

12 \times 12

identity matrix. Solving for the unknown vector

C

we get:

C = {[0 . 0526 0 . 0305 9 . 67 e - 5 1 . 64 e - 5 0 . 16 0 . 032 2 . 95 e - 4 1 . 72 e - 5 0 . 276 0 . 0351 5 . 08 e - 4 1 . 89 e - 5]}^{T}

Table 4.1 compares the approximate solutions gained using the proposed method and regular Legendre wavelet method [27] with the exact solutions. In comparison to the standard Legendre wavelets method, the proposed method clearly provides better accuracy.

Remark: We take both algebraic systems derived from applying our proposed technique (GLWM) and (LWM) are of the same size for the sake of fair comparison.

The accuracy comparison between our proposed method (GLWM) and the standard Legendre wavelets method (RLWM) [27] is evident as shown in Table 1 and Table 2. Also, the absolute errors for both methods are compared in Figure 1 as shown above. It is clear the suggested technique gives better accuracy compared to the regular Legendre wavelets.

Example 2

We deem the differential equation [3, 14]

0.25 y^{'} (t) + y (t) = u (t), y (0) = 0 .

(4.4)

where

u (t)

is the unit step function. The analytic solution of (4.4) is given by

y (t) = 1 - e^{- 4 t} .

This problem has been solved by Legendre wavelets with k = 3, M = 3 by Razzaghi and Yousefi [3], and by Chebyshev wavelets, with k = 2, M = 3 by Babolian and Fattahzadeh, see [14]. We apply Generalized Legendre wavelets (GLWM) for

M = 3

, k = 2

,

μ = 3

. We suppose that the unknown function

y (t) \approx \sum_{n = 1}^{μ^{k - 1}} \sum_{m = 0}^{M} c_{n, m} ψ_{n, m}^{μ} (t) = \sum_{n = 1}^{3} \sum_{m = 0}^{3} c_{n, m} ψ_{n, m}^{μ} (t) = C^{T} Ψ,

where

Ψ (t)

and

C

are as the preceding example. Integrating (4.4) from 0 to t and with the use of the operational matrix

P_{12 \times 12}

as computed in Example 1, we obtain

0.25 C^{T} Ψ (t) + P C^{T} ​ Ψ (t) = e^{T} P Ψ {(t)}_{12 \times 1} .

(4.5)

The above Eq. (4.5) holds for all the time t in the interval [0 , 1).

Thus, form which we obtain,

0.25 C^{T} + P C^{T} ​ = P^{T} e,

(4.6)

where

u (t)

is expressed as

u (t) = \frac{\sqrt{2}}{3} {[\begin{matrix} 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \end{matrix}]}^{T} Ψ {(t)}_{12 \times 1} = e^{T} Ψ {(t)}_{12 \times 1} .

Equation (4.6) can be expressed in the following form

Q C = D,

(4.7)

where

Q = 0.25 I + P^{T}, D = ​ P^{T} d .

Solving Eq. (4.7) for

C

, we obtain the approximate solution

y (t) = C^{T} Ψ .

In Table 3, a comparison is made between the approximate values using the present approach together with the exact solutions and the regular Legendre wavelets method.

It is evident that the proposed method (GLWM) gives better accuracy compared to regular Legendre wavelets method (RLWM). Note the numerical results for the case

M = 3

and

k = 2

are taken from [3], while the approximate solution and the absolute error for

M = 3

and

k = 3

, we wrote our own MATLAB program.

The absolute errors for our suggested approach (GLWM) and the conventional Legendre and Chebyshev wavelets methods are contrasted in the following table (Table (4)). The absolute errors displayed in the table below indicate how the suggested method (GLWM) outperforms the conventional Legendre and Chebyshev wavelets methods.

Remark:

Since these are only the points

t = 0.0, 0.1, 0.2

taken into consideration in [14], as can be seen in Table 1 on page 425, in [14], we take into account the absolute errors at these points.

The absolute errors list in the table above show the demonstrate the superiority of the proposed method (GLWM) against the regular Legendre and Chebyshev wavelets methods.

Example 3: Bessel differential equation of order zero

We deem the differential equation [14]

t y^{″} + y^{'} + t y = 0, y (0) = 1, y^{'} (0) = 0 .

(4.8)

A solution known as the Bessel function of the first kind of order zero denoted by

J_{0} (t)

is (O’Neil [29])

J_{0} (t) = \sum_{q = 0}^{\infty} \frac{{(- 1)}^{q}}{{(q!)}^{2}} {(\frac{t}{2})}^{2 q}

.We will first suppose that the unknown function

y^{″} (t)

is given by

y^{″} (t) = C^{T} Ψ (t) .

(4.9)

Using the boundary conditions in (4.8) and (4.9) yields that

y^{'} (t) = C^{T} P Ψ (t), ​ ​ y (t) = C^{T} P^{2} Ψ (t) + 1 .

Now, approximating

t, 1

where

t ≅ e^{T} Ψ (t), 1 ≅ d^{T} Ψ (t) .

Thus, our differential equation (4.8) is reduced to

e^{T} Ψ C^{T} Ψ + C^{T} P Ψ + e^{T} Ψ (C^{T} P^{2} Ψ + d^{T} Ψ) = 0,

which can be written as

Ψ^{T} (e^{T} Ψ) C^{} + Ψ^{T} P^{T} C + Ψ^{T} (e^{T} Ψ) P^{2^{T}} C + Ψ^{T} (e^{T} Ψ) d = 0.

(4.10)

In order to solve the example under investigation, we will use the following feature of the product of two generalized Legendre wavelet function vectors:

C^{T} Ψ (t) Ψ {(t)}^{T} \approx Ψ^{T} \tilde{C},

(4.11)

where

C = [c_{1, 0} c_{1, 1}, ..., c_{1, M}, c_{2, 0}, c_{2, 1}, ..., c_{2, M}, ..., c_{μ^{k - 1}, 0} c_{μ^{k - 1}, 1}, ..., c_{μ^{k - 1}, M}]^{T}

and in the same way we can gain

Ψ (t)

and

\tilde{C}

is a

μ^{k - 1} M \times μ^{j k - 1} M

matrix.

To represent the calculation process, we pick out

M = 3

, k = 2

,

μ = 3

.

In this case, we have

Now, we approximate the function

f (t) = t

in terms of the set of the basis functions

Ψ (t)

as:

f (t) = t ≅ e^{T} Ψ {(t)}_{12 \times 1},

(4.12)

where in this case the coefficient vector

e

is given by

e = {[\begin{matrix} \frac{\sqrt{2}}{27} & \frac{\sqrt{6}}{81} & 0 & 0 & \frac{\sqrt{2}}{9} & \frac{\sqrt{6}}{81} & 0 & 0 & \frac{5 \sqrt{2}}{27} & \frac{\sqrt{6}}{81} & 0 & 0 \end{matrix}]}^{T}

and

d = {[\begin{matrix} \frac{\sqrt{2}}{3} & 0 & 0 & 0 & \frac{\sqrt{2}}{3} & 0 & 0 & 0 & \frac{\sqrt{2}}{3} & 0 & 0 & 0 \end{matrix}]}^{T}

Moreover, we will use the following feature of the product of two generalized Legendre wavelet function vectors:

Ψ (t) Ψ^{T} (t) = (\begin{matrix} Ψ_{1} Ψ_{1}^{T} & 0 & 0 \\ 0 & Ψ_{2} Ψ_{2}^{T} & 0 \\ 0 & 0 & Ψ_{3} Ψ_{3}^{T} \end{matrix}),

(4.13)

where

Ψ_{i} Ψ_{i}^{T} = (\begin{matrix} ψ_{i, 0}^{μ} ψ_{i, 0}^{μ} & ψ_{i, 0}^{μ} ψ_{i, 1}^{μ} & ψ_{i, 0}^{μ} ψ_{i, 2}^{μ} & ψ_{i, 0}^{μ} ψ_{i, 3}^{μ} \\ ψ_{i, 1}^{μ} ψ_{i, 0}^{μ} & ψ_{i, 1}^{μ} ψ_{i, 1}^{μ} & ψ_{i, 1}^{μ} ψ_{i, 2}^{μ} & ψ_{i, 1}^{μ} ψ_{i, 3}^{μ} \\ ψ_{i, 2}^{μ} ψ_{i, 0}^{μ} & ψ_{i, 2}^{μ} ψ_{i, 1}^{μ} & ψ_{i, 2}^{μ} ψ_{i, 2}^{μ} & ψ_{i, 2}^{μ} ψ_{i, 3}^{μ} \\ ψ_{i, 3}^{μ} ψ_{i, 0}^{μ} & ψ_{i, 3}^{μ} ψ_{i, 1}^{μ} & ψ_{i, 3}^{μ} ψ_{i, 2}^{μ} & ψ_{i, 3}^{μ} ψ_{i, 3}^{μ} \end{matrix}), i = 1, 2, 3.

(4.14)

In (4.13) we used the fact that

ψ_{i, j}^{μ} ψ_{k, l}^{μ} = 0

for

i \neq k .

Also, we have

ψ_{i, 0}^{μ} ψ_{i, j}^{μ} = \frac{3}{\sqrt{2}} ψ_{i, j}^{μ}, i = 1, 2, 3, j = 0, 1, 2, 3,

ψ_{1, i}^{μ} ψ_{i, 1}^{μ} \approx \frac{3}{\sqrt{2}} ψ_{i, 0}^{μ} + \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ}, i = 1, 2, 3,

ψ_{i, 1}^{μ} ψ_{i, 1}^{μ} \approx \frac{6}{\sqrt{10}} ψ_{i, l - 1}^{μ}, i = 1, 2, 3, l = 2, 3,

ψ_{i, 2}^{μ} ​ ψ_{i, 3}^{μ} \approx \frac{27}{\sqrt{6} \sqrt{35}} ψ_{i, 1}^{μ}, i = 1, 2, 3.

Conserving only the elements of

Ψ (t)

yields that:

Ψ_{i} Ψ_{i}^{T} = (\begin{matrix} \frac{3}{\sqrt{2}} ψ_{i, 0}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 1}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 2}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 3}^{μ} \\ \frac{3}{\sqrt{2}} ψ_{i, 1}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 0}^{μ} + \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ} & \frac{6}{\sqrt{10}} ψ_{i, 1}^{μ} & \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ} \\ \frac{3}{\sqrt{2}} ψ_{i, 2}^{μ} & \frac{6}{\sqrt{10}} ψ_{i, 1}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 0}^{μ} + \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ} & \frac{27}{\sqrt{6 \sqrt{35}}} ψ_{i, 1}^{μ} \\ \frac{3}{\sqrt{2}} ψ_{i, 3}^{μ} & \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ} & \frac{27}{\sqrt{6 \sqrt{35}}} ψ_{i, 1}^{μ} & \frac{3}{\sqrt{2}} ψ_{i, 0}^{μ} + \frac{6}{\sqrt{10}} ψ_{i, 2}^{μ} \end{matrix}), ​ i = 1, 2, 3.

(4.15)

From (4.11) we get

Ψ^{T} (\tilde{E}) C^{} + Ψ^{T} P^{T} C + Ψ^{T} (\tilde{E}) P^{2^{T}} C + Ψ^{T} (\tilde{E}) d = 0,

(4.16)

or

\tilde{E} C^{} + P^{T} C + \tilde{E} P^{2^{T}} C + \tilde{E} d = 0,

(4.17)

where

\tilde{E}

can be computed in the same manner of (4.9) as follows:

\tilde{E} = (\begin{matrix} E_{1} & 0 & 0 \\ 0 & E_{2} & 0 \\ 0 & 0 & E_{3} \end{matrix})

E_{1} = (\begin{matrix} \frac{3}{\sqrt{2}} e_{1} & \frac{3}{\sqrt{2}} e_{2} & \frac{3}{\sqrt{2}} e_{3} & \frac{3}{\sqrt{2}} e_{4} \\ \frac{3}{\sqrt{2}} e_{2} & \frac{3}{\sqrt{2}} e_{1} + \frac{6}{\sqrt{10}} e_{3} & \frac{6}{\sqrt{10}} e_{2} & \frac{6}{\sqrt{10}} e_{3} \\ \frac{3}{\sqrt{2}} e_{3} & \frac{6}{\sqrt{10}} e_{2} & \frac{3}{\sqrt{2}} e_{1} + \frac{6}{\sqrt{10}} e_{3} & \frac{27}{\sqrt{6} \sqrt{35}} e_{2} \\ \frac{3}{\sqrt{2}} e_{3} & \frac{6}{\sqrt{10}} e_{3} & \frac{27}{\sqrt{6} \sqrt{35}} e_{2} & \frac{3}{\sqrt{2}} e_{1} + \frac{6}{\sqrt{10}} e_{4} \end{matrix})

= (\begin{matrix} \frac{1}{9} & \frac{\sqrt{3}}{27} & 0 & 0 \\ \frac{\sqrt{3}}{27} & \frac{1}{9} & \frac{\sqrt{60}}{135} & 0 \\ 0 & \frac{\sqrt{60}}{135} & \frac{1}{9} & \frac{\sqrt{35}}{105} \\ 0 & 0 & \frac{\sqrt{35}}{105} & \frac{1}{9} \end{matrix}) .

Similarly, we can compute

E_{2}

and

E_{3}

where we obtain:

E_{2} = (\begin{matrix} \frac{1}{3} & \frac{\sqrt{3}}{27} & 0 & 0 \\ \frac{\sqrt{3}}{27} & \frac{1}{3} & \frac{\sqrt{60}}{135} & 0 \\ 0 & \frac{\sqrt{60}}{135} & \frac{1}{3} & \frac{\sqrt{35}}{105} \\ 0 & 0 & \frac{\sqrt{35}}{105} & \frac{1}{3} \end{matrix}), E_{3} = (\begin{matrix} \frac{5}{9} & \frac{\sqrt{3}}{27} & 0 & 0 \\ \frac{\sqrt{3}}{27} & \frac{5}{9} & \frac{\sqrt{60}}{135} & 0 \\ 0 & \frac{\sqrt{60}}{135} & \frac{5}{9} & \frac{\sqrt{35}}{105} \\ 0 & 0 & \frac{\sqrt{35}}{105} & \frac{5}{9} \end{matrix}) .

Equation (4.17) is a set of algebraic equations which can be solved for Cwhich is given as:

C = - 0.2343 0.001259 0.0003123 - 5.349 e - 5 - 0.2256 0.003718 0.0003092 - 1.943 e - 5 - 0.2087 0.006028 0.0002839 - 1.285 e - 5]^{T}

The approximate solution utilizing the suggested approach (GLWM), the regular Legendre wavelets (RLWM) are compared in Table 3 to the solution function

J_{0} (t)

. Also, the absolute errors for both methods are compared in Table 3 and Figure 2 as shown below. It is clear the suggested method gives better accuracy compared to the regular Legendre wavelets.

5. Conclusion

In this paper, a novel and accurate mechanism so as to find the solution of linear differential equations over the intervals [0, 1) based on the generalization of Legendre wavelets is offered. Our technique reduced the problems into algebraic equations through the features of generalized Legendre wavelet (GLW) simultaneously with the operational matrix of integration. We chose the function approximation in such a manner so as to compute the connection coefficients in an easy manner. The proposed numerical technique, based on the GLW, has been examined on three linear problems as a consequence of this investigation.

6. Statements and Declarations

Competing Interests: The authors declare that they have no competing interests.
Authors' contributions: These authors contributed equally to this work.
Ethics approval: This article does not contain any studies with human participants or animals performed by any of the authors.
Availability of supporting data: The datasets used or analyzed during the current study available from the corresponding author on reasonable request.

References

Razzaghi, M.; Yousefi, S. Legendre wavelets direct method for variational problems. Math. Comput. Simul. 2000, 53, 185–192. [Google Scholar] [CrossRef]
Hwang, C.; Shih, Y.P. Laguerre series direct method for variational problems. J. Optim. Theory Appl. 1983, 39, 143–149. [Google Scholar] [CrossRef]
Razzaghi, M.; Yousefi, S. The Legendre wavelets operational matrix of integration. Int. J. Syst. Sci. 2001, 32, 495–502. [Google Scholar] [CrossRef]
Maleknejad, K.; Tavassoli Kajani, M.; Mahmoudi, Y. Numerical solution of linear Fredholm and Volterra integral equation of the second kind by using Legendre wavelets. Kybernetes 2003, 32, 1530–1539. [Google Scholar] [CrossRef]
Morlet, J.; Arens, G.; Fourgeau, E.; Glard, D. Wave propagation and sampling theory—Part I: Complex signal and scattering in multilayered media. Geophysics 1982, 47, 203–221. [Google Scholar] [CrossRef]
LDebnath, F.A. Shah, Wavelet transforms and their applications, Boston, Birkhäuser, (2002).
DeVore, R.A. Nonlinear approximation. Acta Numer. 1998, 7, 51–150. [Google Scholar] [CrossRef]
Meyer, Y. Wavelets: their past and their future. Prog. Wavelet Anal. Appl. 1993, 11, 9–18. [Google Scholar]
Chen, C.; Hsiao, C. A walsh series direct method for solving variational problems. J. Frankl. Inst. 1975, 300, 265–280. [Google Scholar] [CrossRef]
Cheng, C.F.; Tsay, Y.T.; Wu, T.T. Walsh operational matrices for fractional calculus and their application to distributed systems. J. Frankl. Inst. 1977, 303, 267–284. [Google Scholar] [CrossRef]
Hwang, C.; Shih, Y.-P. Solution of integral equations via Laguerre polynomials. Comput. Electr. Eng. 1982, 9, 123–129. [Google Scholar] [CrossRef]
Chang, R.Y.; Wang, M.L. Shifted Legendre direct method for variational problems. J. Optim. Theory Appl. 1983, 39, 299–307. [Google Scholar] [CrossRef]
Horng, I.-R.; Chou, J.-H. Shifted Chebyshev direct method for solving variational problems. Int. J. Syst. Sci. 1985, 16, 855–861. [Google Scholar] [CrossRef]
Babolian, E.; Fattahzadeh, F. Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration. Appl. Math. Comput. 2007, 188, 417–426. [Google Scholar] [CrossRef]
Razzaghi, M. Fourier series direct method for variational problems. Int. J. Control. 1988, 48, 887–895. [Google Scholar] [CrossRef]
Paraskevopoulos, P.; Sklavounos, P.; Georgiou, G. The operational matrix of integration for Bessel functions. J. Frankl. Inst. 1990, 327, 329–341. [Google Scholar] [CrossRef]
Guf, J.S.; Jiang, W.S. The Haar wavelets operational matrix of integration. Int. J. Syst. Sci. 1996, 27, 623–628. [Google Scholar] [CrossRef]
Chen, C.; Hsiao, C. Haar wavelet method for solving lumped and distributed-parameter systems. Iee Proc. - Control. Theory Appl. 1997, 144, 87–94. [Google Scholar] [CrossRef]
Lal, S.; Kumar, S. Best wavelet approximation of functions belonging to generalized Lipschitz class using Haar scaling function. Thai J. Math. 2017, 15, 409–419. [Google Scholar]
Lepik, Ü. Numerical solution of differential equations using Haar wavelets. Math. Comput. Simul. 2005, 68, 127–143. [Google Scholar] [CrossRef]
Lepik, Ü. 2007, March. Application of the Haar wavelet transform to solving integral and differential equations. In Proceedings of the Estonian Academy of Sciences, Physics, Mathematics (Vol. 56, No. 1).
Jhangeer, A.; Hussain, A.; Junaid-U-Rehman, M.; Khan, I.; Baleanu, D.; Nisar, K.S. Lie analysis, conservation laws and travelling wave structures of nonlinear Bogoyavlenskii–Kadomtsev–Petviashvili equation. Results Phys. 2020, 19, 103492. [Google Scholar] [CrossRef]
Kajani, M.T.; Vencheh, A.H.; Ghasemi, M. The Chebyshev wavelets operational matrix of integration and product operation matrix. Int. J. Comput. Math. 2009, 86, 1118–1125. [Google Scholar] [CrossRef]
Sripathy, B.; Vijayaraju, P.; Hariharan, G. Chebyshev wavelet based approximation method to some non-linear differential equations arising in engineering. Int. J. Math. Anal. 2015, 9, 993–1010. [Google Scholar] [CrossRef]
Lal, S. Generalized legendre wavelet method and its applications in approximation of functions of bounded derivatives. Palest. J. Math. 2019, 8, 373–389. [Google Scholar]
Ahmad, O.; Sheikh, N.A.; Nisar, K.S.; Shah, F.A. Biorthogonal wavelets on the spectrum. Math. Methods Appl. Sci. 2020, 44, 4479–4490. [Google Scholar] [CrossRef]
Sharma, V.K.; Lal, S. Solution of Differential Equations by Using Legendre Wavelet Operational Matrix of Integration. Int. J. Appl. Comput. Math. 2022, 8, 1–21. [Google Scholar] [CrossRef]
Balaji, S. Legendre wavelet operational matrix method for solution of fractional order Riccati differential equation. J. Egypt. Math. Soc. 2015, 23, 263–270. [Google Scholar] [CrossRef]
P. V. O’Neil, Advanced Engineering Mathematics, Belmont, California, Wadswort, (1987).

Figure 1. Absolute error comparison for Example 1 for M = 3; k = 2;

μ = 4

, against the Regular Legendre wavelets (RLWM) [27] solutions for M = 4; k = 3.

Figure 1. Absolute error comparison for Example 1 for M = 3; k = 2;

μ = 4

, against the Regular Legendre wavelets (RLWM) [27] solutions for M = 4; k = 3.

Figure 2. Absolute error comparison for Example 3 M = 3; k = 2; against the Regular Legendre wavelets (RLWM) [14] solutions for M=3 and k=3.

Table 1. Evaluation of differences between the approximate solution of Example 1 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against the exact and Legendre wavelets [27] solutions for M = 3; k = 3.

Table 1. Evaluation of differences between the approximate solution of Example 1 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against the exact and Legendre wavelets [27] solutions for M = 3; k = 3.

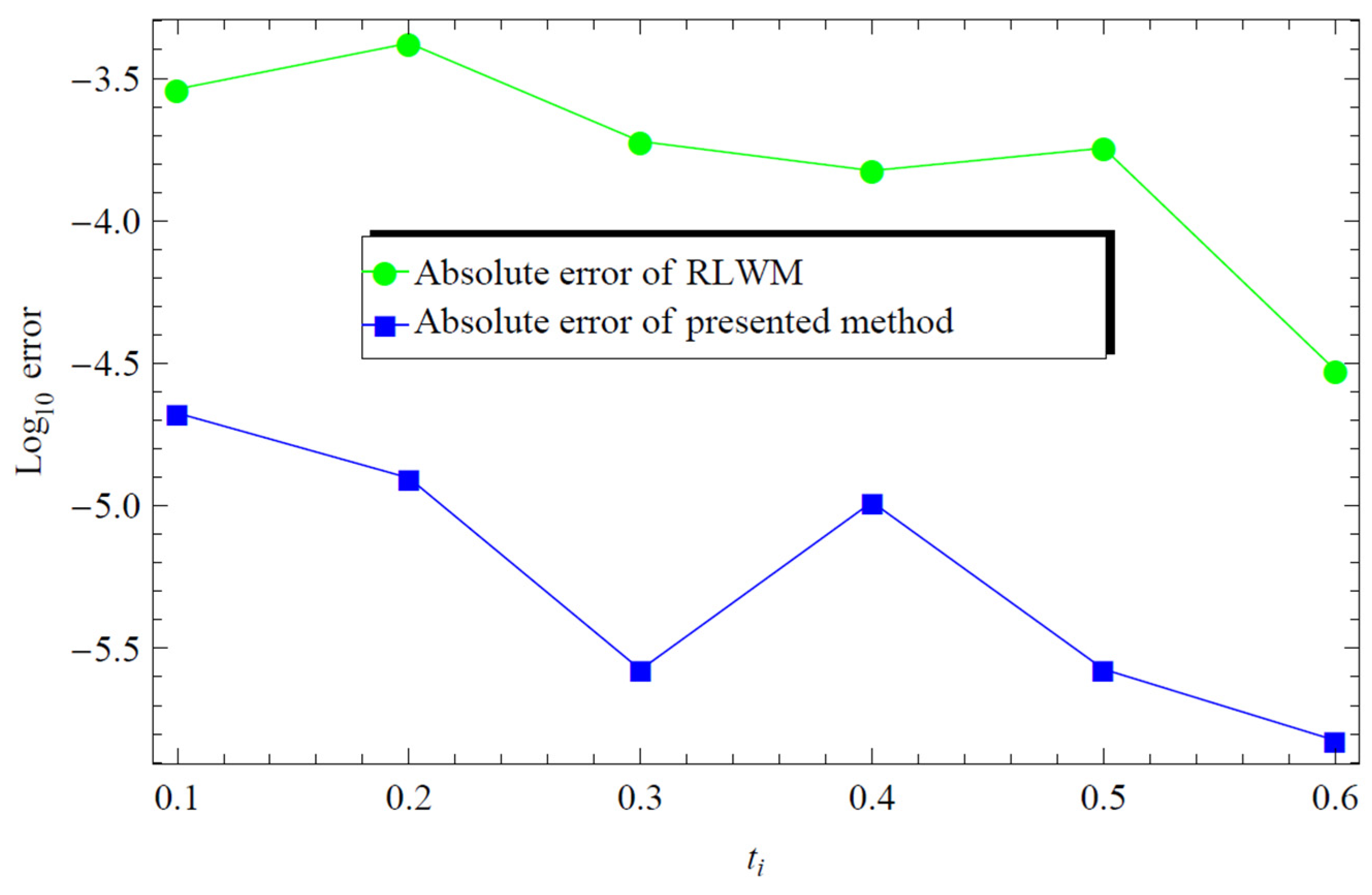
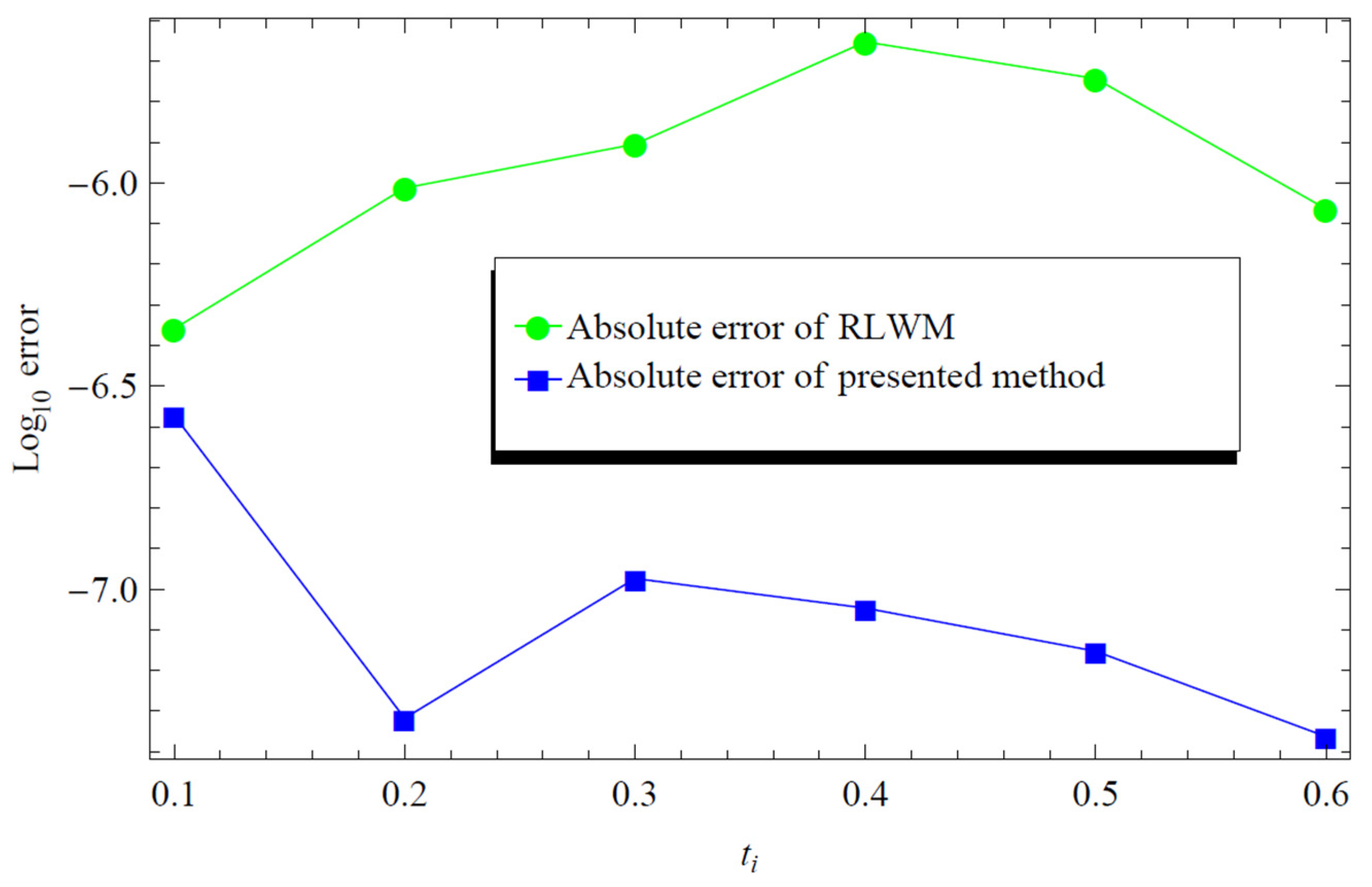
t	Exact Sol.	Generalized Legendre wavelets (proposed method) for $M = 3, k = 2, μ = 3$		Regular Legendre wavelets [27] for M=3 and k=3
t	Exact Sol.	Approximate Sol.	Absolute Error	Approximate Sol.	Absolute Error
0.1 0.2 0.3 0.4 0.5 0.6	0.01758 0.06233 0.12529 0.20047 0.28383 0.37268	0.017559 0.062345 0.1253 0.20048 0.28384 0.37268	2.1156e-05 1.253e-05 2.6631e-06 1.0317e-05 2.6723e-06 1.5045e-06	0.01787 0.06191 0.12548 0.20032 0.28365 0.37271	2.9000e-04 4.2000e-04 1.9000e-04 1.5000e-04 1.8000e-04 3.0000e-05

Table 2. Evaluation of differences between the approximate solution of Example 1 using generalized Legendre wavelets for M = 3; k = 2;

μ = 4

, against the exact and Legendre wavelets [27] solutions for M = 4; k = 3.

Table 2. Evaluation of differences between the approximate solution of Example 1 using generalized Legendre wavelets for M = 3; k = 2;

μ = 4

, against the exact and Legendre wavelets [27] solutions for M = 4; k = 3.

t	Exact Sol.	Generalized Legendre wavelets (proposed method) for $M = 3, k = 2, μ = 4$		Regular Legendre wavelets [27] for M=4 and k=3
t	Exact Sol.	Approximate Sol.	Absolute Error	Approximate Sol.	Absolute Error
0.1 0.2 0.3 0.4 0.5 0.6	0.01758 0.06233 0.12529 0.20047 0.28383 0.37268	0.017559 0.062345 0.1253 0.20048 0.28384 0.37268	2.1156e-05 1.253e-05 2.6631e-06 1.0317e-05 2.6723e-06 1.5045e-06	0.01787 0.06191 0.12548 0.20032 0.28365 0.37271	2.9000e-04 4.2000e-04 1.9000e-04 1.5000e-04 1.8000e-04 3.0000e-05

Table 3. Evaluation of differences between the approximate solution of Example 2 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against the exact and Legendre wavelets [3] solutions for

M = 3

; k = 2 and

k = 3

.

Table 3. Evaluation of differences between the approximate solution of Example 2 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against the exact and Legendre wavelets [3] solutions for

M = 3

; k = 2 and

k = 3

.

T	Exact Solution	(proposed method) for $M = 3, k = 2, μ = 3$		Regular Legendre wavelets for $M = 3$
T	Exact Solution	Appr. Sol	Absolute Error	Appr. Sol $k = 2$ [3]	Absolute Error	Appr. Sol $k = 3$	Absolute Error
0.0 0.1 0.2 0.3 0.4 0.5 0.6	0 0.3297 0.5507 0.6988 0.7981 0.8647 0.9093	0.0002416 0.3298 0.5506 0.6988 0.7981 0.8647 0.9093	0.0002416 8.462e-5 5.012e-5 1.065e-5 4.127e-5 1.069e-5 6.018e-6	0.0002 0.3284 0.5523 0.6980 0.7987 0.8653 0.9091	2.0e-4 0.00128 0.00163 8.06e-4 5.97e-4 6.35e-4 1.82e-4	0.0051813 0.3285 0.55233 0.69808 0.79872 0.86537 0.90912	5.1813e-03 1.1825e-03 1.6606e-03 7.3067e-04 6.1326e-04 7.0400e-04 1.5817e-04

Table 4. Evaluation of differences between the absolute errors of Example 2 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against Legendre wavelets [3] and Chebyshev wavelets method [14].

Table 4. Evaluation of differences between the absolute errors of Example 2 using generalized Legendre wavelets for M = 3; k = 2;

μ = 3

, against Legendre wavelets [3] and Chebyshev wavelets method [14].

T	(proposed method) for $M = 3, k = 2, μ = 3$	Legendre wavelets for $k = 2$		Chebyshev wavelets Method [14]
T	Absolute Error	Absolute Error $M = 3$	Absolute Error $M = 4$	Absolute Error $M = 3$	Absolute Error $M = 4$	Absolute Error $M = 5$
0.0 0.1 0.2	2.4160e-04 8.462e-5 5.012e-5	2.0e-4 1.2800e-03 1.6300e-03	5.1813e-03 1.1825e-03 1.6606e-03	1.2700e-02 1.4500e-02 3.8000e-03	2.1000e-03 1.3200e-03 1.7000e-03	0.2038e-3 0.0208e-3 0.1467e-3

Table 3. Evaluation of differences between the approximate values using our proposed approach (GLWM), ( RLWM) together with the solution of

J_{0} (t)

Table 3. Evaluation of differences between the approximate values using our proposed approach (GLWM), ( RLWM) together with the solution of

J_{0} (t)

T	$Exact solution < break / > J_{0} (t)$	$Generalized Legendre wavelets (proposed method) for M 3 =, μ = 3$		Regular Legendre wavelets for M=3 and k=3 [14]
T	$Exact solution < break / > J_{0} (t)$	Appr. Solution	Absolute Error	Appr. solution	Absolute Error
0.1 0.2 0.3 0.4 0.5 0.6	0.997502 0.990025 0.977626 0.960398 0.93847 0.912005	0.997501 0.990025 0.977626 0.960398 0.93847 0.912005	2.6760e-07 4.8122e-08 1.0624e-07 8.9834e-08 7.0354e-08 4.3358e-08	0.997502 0.990024 0.977625 0.960396 0.938468 0.912004	4.3793e-07 9.7224e-07 1.2465e-06 2.2267e-06 1.8072e-06 8.6350e-07

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.

Generalized Legendre Wavelets, Definition, Properties and Their Applications for Solving Linear Differential Equations

Abstract

Keywords:

Subject:

1. Introduction

2. Definitions and Preliminaries

2.1. Legendre wavelet and its properties

2.2. Function approaches

2.3. Generalized Legendre Wavelet Expansion [25]

3.1. Generalized Legendre Wavelet Operational Matrix of Integration

3.2. Convergence criteria of the proposed (GLWM)

4. Numerical test and discussion

5. Conclusion

6. Statements and Declarations

References

MDPI Initiatives

Important Links

Subscribe