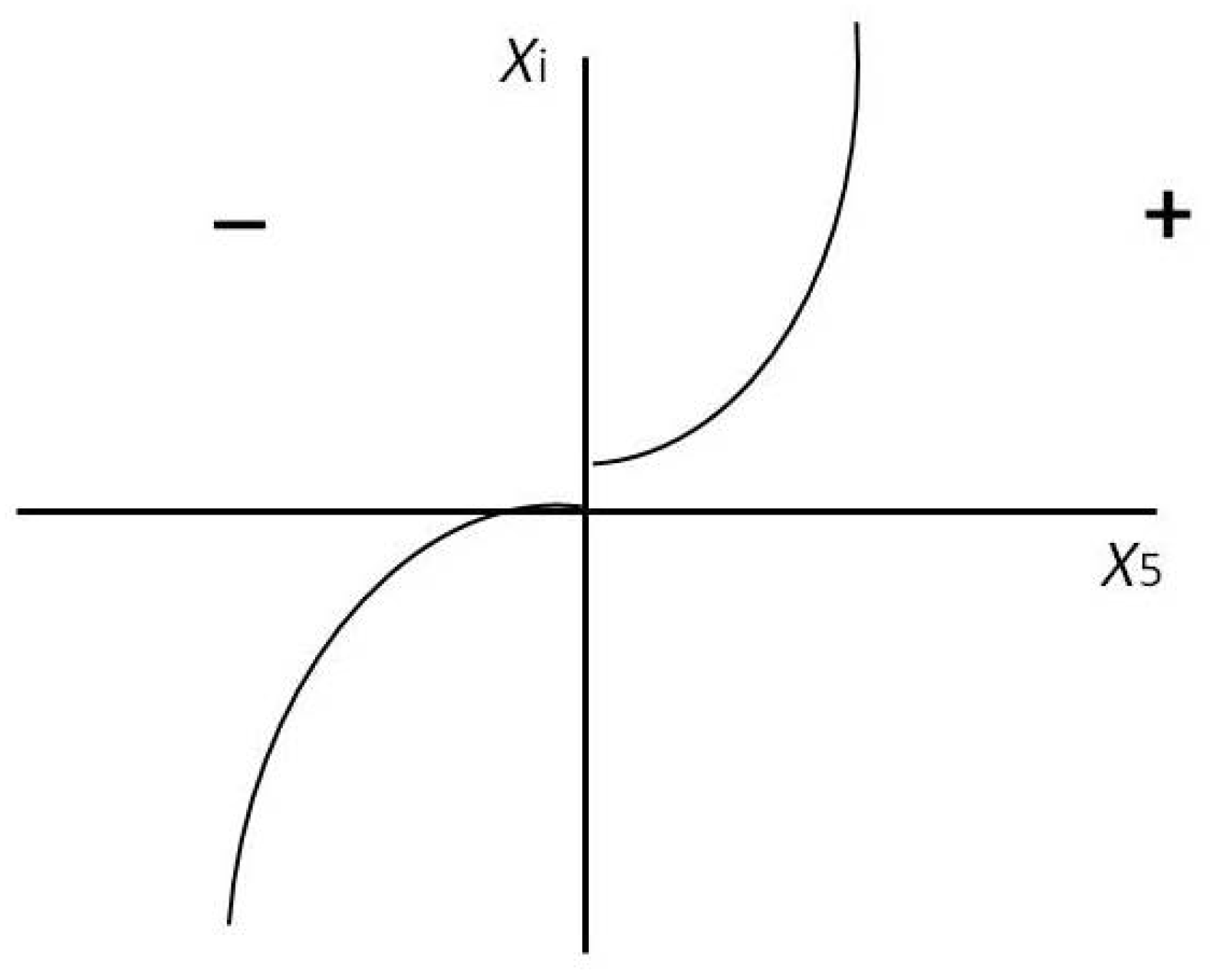Proposal for the Geometric Unification of All Known Forces in Nature

Wolfgang Osterhage

doi:10.20944/preprints202305.0726.v1

Submitted:

09 May 2023

Posted:

10 May 2023

You are already at the latest version

Abstract

As a first step a unification of the gravitational with the electromagnetic interaction within a classical framework is proposed. It is based on a V₅-geometry, with x₅ = q/m. The sole source term is mechanical stress energy, positioned along x₅. The trajectories of test-bodies are placed in V₄ (x₅ = const)-slices. The resulting field equation couples a geometric G-tensor to mechanical stress energy, its momentum with respect to V₅ and the change of this momentum with proper time τ. The following step proceeds to the quantization of space-time to enable the formalization of elementary particles und strong interaction. This is complimented by the inclusion of spin and the weak force, leading finally to a grand total equation, the stationary version of which corresponds to Schroedinger´s equation, the instationary version to the Einstein equation of General Relativity.

Keywords:

Unification

;

Geometry

;

Quantization

;

GUT

;

ToE

Subject:

Physical Sciences - Particle and Field Physics

Introduction

Four fundamental forces in nature have been identified: gravitation, electromagnetism, weak interaction and strong interaction. In electromagnetism electricity and magnetism had been unified in the 19^th century by James C. Maxwell. Weak interaction and electromagnetism were formally unified as electro-weak interaction by Abdus Salam and Steven Weinberg in the sixties of the 20^th century. Together with the quark model quantum chromodynamics had been developed into the standard model of particle physics. What was left aside in this model was gravitation. It plays a major role in another standard model, the cosmological one, based on the General Theory of Relativity. There have been many attempts to bridge the gap.

In the more recent past, tendencies success fully introduced group theory calculus into elementary particle physics, but the group theoretical tools seem to defy, for the time being, the integration of gravitational phenomena. Other attempts hope that String Theory may finally deliver the solution.

Geometric Unification of Classical Gravitational and Electromagnetic Interaction in Five Dimensions: a Modified Approach

Apart from the successful unification of the electric and the magnetic forces themselves, the-two fundamental interactions out of the remaining four attracting the most and most prolonged attention for unification attempts, are the gravitational and the electromagnetic ones. Pre-relativity phenomenology presented very little scope for such "attempts”, and only the description of gravitation by the Theory of General Relativity seemed to offer a promising basis: the geometric replacement of natural forces by manifold curvature. Thus, already rather soon after the introduction of General Relativity, first unification possibilities were explored. Einstein himself spent the main part of his later working life, searching for a real unification between gravitation and electromagnetism.

There is no need to go into detail with regard to the individual contributions to the unification at tempts between gravitation and electromagnetism (our main concern in this section). A variety of excellent reviews exists, being the result of or again a source for others [l,2]. One can distinguish basically two lines of approach: the affine connection method in four dimensions (space-time manifold) and the five dimensional manifold with its additional dimension being the ratio q/m (charge/mass).

The majority of present day theoreticians consider all past attempts as having been unsuccessful. This is certainly true for those yielding e.g., charged particle trajectories from the geodesic equations, which have no resemblance to reality (e.g., Einstein's affine connection theory). But other, more successful approaches are equally rejected on the grounds that either their unification emanates into already known physical structures and therefore renders itself meaningless (Weyl; his unified theory resulted in the established Maxwellian equations and therefore presented nothing excitingly new), or that the achieved unification was not a true one. Most of the five-dimensional theories are dismissed for the latter reason. It is argued, that a 5th dimension is physically unobservable. Another criterion is the non-total elimination of a characteristic electromag netic part of the stress energy tensor, which is practically true for any of the past attempts. However, the rejection arguments are nowadays open to debate again. Some authors [3] argue that a true unification has already been achieved by the incorporation of electromagnetic terms into the stress energy tensor in Einstein's field equation; on the other hand the (4 + n) -dimensionality concept sees a revival in gauge theoretical unification attempts of the "electroweak" with the strong force.

This section presents a new approach to the unifica tion of the gravitational with the electromagnetic interaction on a geometrical basis in 5 dimensions. Its results have been published previously [4], but are no longer available on a regular basis, since the journal (Zeitschrift für Naturforschung) has ceased to exist. Therefore the bulk of the article is repeated here.

Initially, only classical phenomena are considered. The criteria to be met for a "true" unification are defined. By taking these criteria and an elevated "principle of equivalence" as theoretical basis and a V₅-manifold with x₅ = q/m as tool, one is lead to a qualitative, heuristic outline of the whole unification concept. After its presentation the formulated results are laid down in a separate paragraph with an interpretation of the new resulting field equation.

Heuristic Concept

The criteria for a true unification between gravitation and electromagnetism are the following:

(a) Both interactions have to be described by the same field equation, relating all field effects to the same source terms. If the unification is placed on a geometric basis, one and the same geometric structure must serve as a medium for the description of all these field effects.

(b) On a geometric basis all forces have to be replaced by a coupling of a single type main source term to geometry. No special remaining terms relating to one or the other non-unified descriptions are permitted.

(c) All dimensions of an n-dimensional manifold, presenting the geometrical framework, must be in some way physically observable. There are two principal lines of approach conceivable: a phenomenological one, based on geometry, and a more axiomatic one. Both lead to the same consequences. Let us first consider the phenomenological one.

The concept of force itself seems to be at the root of the present day split into four different types of interaction. Therefore to abandon it and place the description of physical effects on directly observable quantities, i.e. dimensions and energy, is a pre-condition for unification. This is exactly, what General Relativity does: the gravitational force is replaced by the coupling of curvature of a space-time manifold to an energy source term. It is therefore likely that only geometrical attempts for unification will be successful. As a consequence, the electromagnetic "force" as well has to be replaced by a cou pling of a manifold curvature to an energy source term. Both the manifold, in which the action takes place, and the source have to be common to gravi tational and electromagnetic events. This excludes immediately the V₄-geometry of General Relativity as a unification basis and indicates for that at least a five-dimensional manifold. The common source has to be energy (related), bare of any specific terms with reference to one or the other interaction type.

The more axiomatic approach is outlined as follows: Let us postulate an "elevated principle of equivalence": "If an observer in a (special) inertial frame (i.e. a Faraday cage) is travelling in an 'accelerating' field, he can neither distinguish, whether he is moving in a gravitational or an electromagnetic or any other field, nor whether he is subjected to an apparent field (of any kind) due to acceleration of a reference frame."

This principle is a sufficient basis, to arrive with at the same conclusions, as the phenomenological approach did.

The following model in a V₅-manifold offers itself: We have three space-like, one time-like dimension and x₅ with (q/m) as affine parameter. Test-bodies and energy sources (masses, etc.) reside along x₅ according to their (q/m)-value in four-dimensional slices V₄ (x₅ = const). Each V₄ has its own space-time geometry. Let us for simplicity assume that a test-body or a source does never change position with respect to x₅ (in V₄(x₅

\equiv

0) only "neutral" test bodies move). For one and the same source term at a specific x₅ the strength of the curvatures of the various V₄'s is normally different. Thus the V₄'s may appear "blown-up" or "contracted" with reference to each other and probed by the trajectories of test-particles, due to the gross curvature of the whole V₅. Equally the gross curvature of the V₅ changes, and thus the relative blow-up or contraction of the V₄'s to each other, when the source is positioned at a different x₅. There is no real difference between a test-body and a source; their roles can be played by one and the same entity, and in mutual interactions of several test-bodies they are both at the same time. Thus we can postulate:

The curvature of the entire V₅ geometry is dependent on the stress energy of a source and the position of the source along x₅.

This is not quite all. As will be seen in the quanti tative results, curvature may also be coupled to the velocity of certain types of sources. Table 1 gives possible combinations test-body/source.

For the Illustration of the above, let us pick the most general example, where both test-body and source are "charged". The source A resides at x₅ = a. Thus the entire V₅ is curved initially with respect to the strength

|A|

and the position value a. If A would reside at x₅ = b

\neq

a the gross curvature of the V₅ would be different. A test-body C moves in a V₄(x₅ = c). In general c

\neq

a. The trajectory of C is dependent on the curvature of V₄ (c). A test-body D at x₅= d

\neq

c (

\neq

=a) would move in a different curved V₄ and thus project a different trajectory.

In traditional language the above means: the trajectory of a test-body with mass m_t1 and charge q_t1 under the influence of a source with mass m_s1 and charge q_s1 changes, when the source is replaced by one with

m_{s 2} \neq m_{s 1}

and

q_{s 2} \neq q_{s 1}

; or: the tra jectory of a test-body with m_t1 and q_t1 under the influence of a source with m_s1 and q_s1 is different from that of a test-body with

m_{t 2} \neq m_{t 1}

and

q_{t 2}

\neq q_{t 1}

under the influence of the same source.

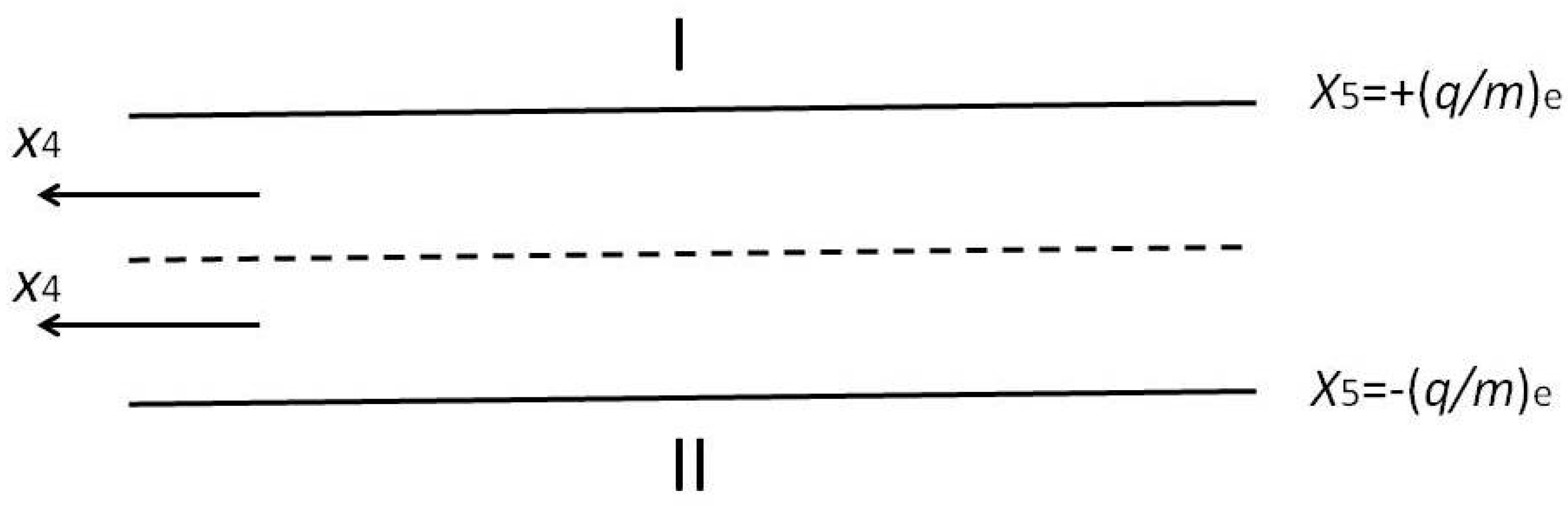
How does the general structure of a V₅ look like? Figure 1 illustrates that a five-dimensional universe is a flat sheet, or rather an assembly of an infinite number of V₄ sheets piled onto each other. It is not infinite in the x₅-direction, since the maximum observed and for the time being theoretically possible value for x₅ is (e/m_e), the ratio of the electron's charge over its mass. Therefore the regions I and II in Figure l are physically meaningless.

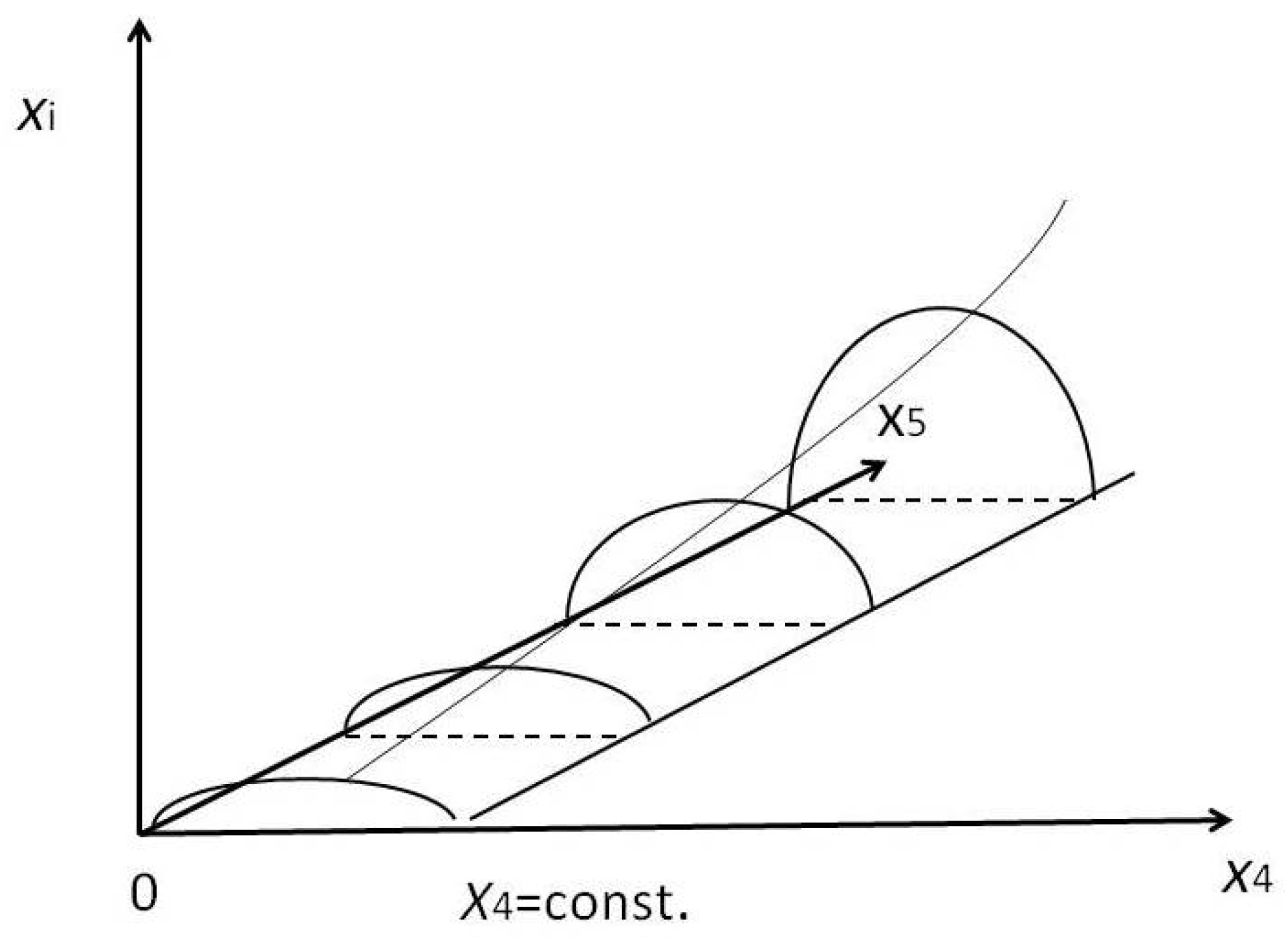
Figure 2 shows space-time curves (particle tra jectories e.g.) for constant time. The V₅, subjected to the influence of a source, somewhere situated along x₅, accommodates test-particles moving in various V₄ planes. The gross curvature of the V₅ determines the "blowing-up" of trajectories in the V₄'s along x₅. Thus, each geometry is coupled to one and the same source exactly as in General Relativity, only the coupling constants and the weight of the x₅-position change along x_5.

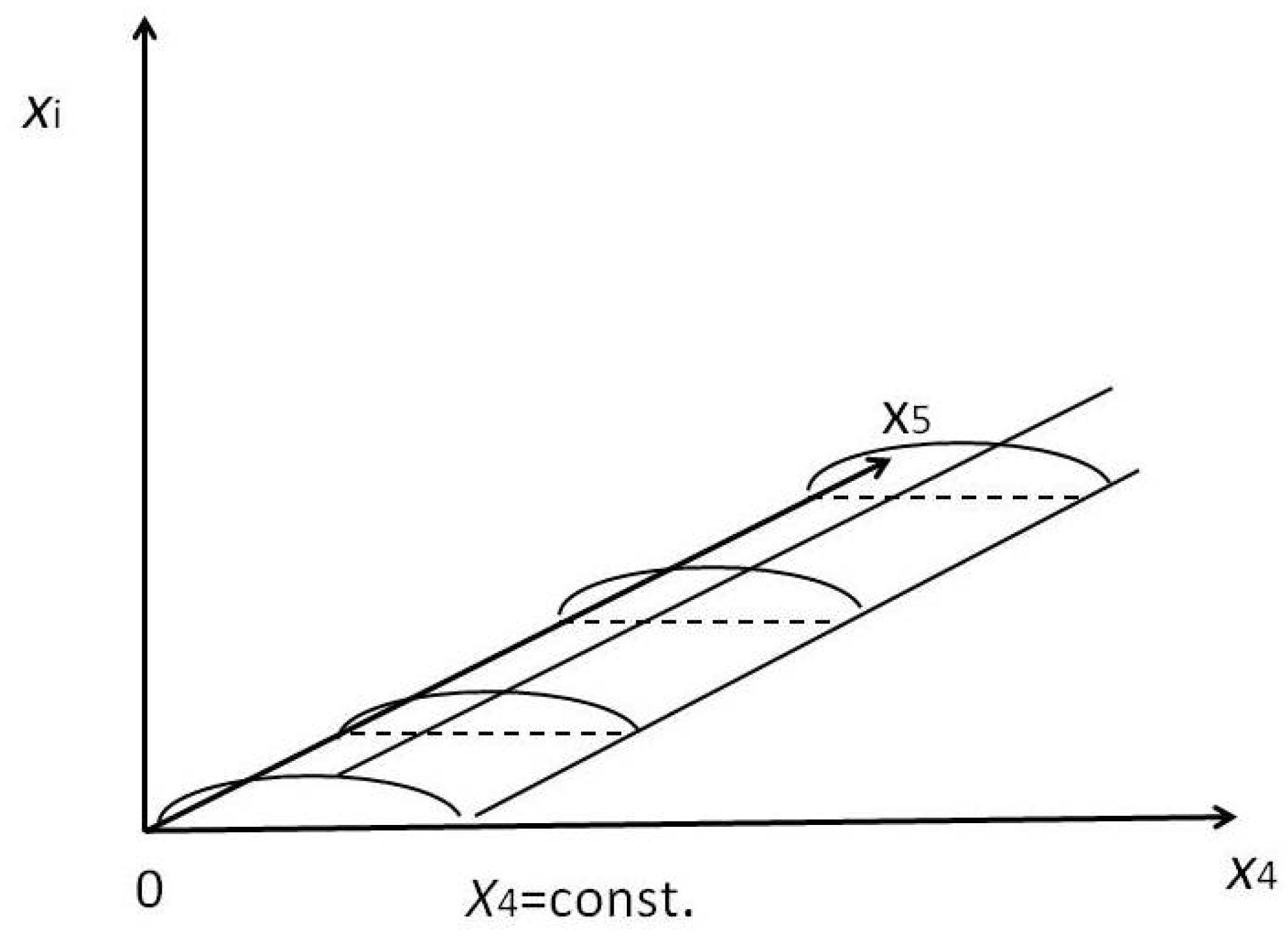
Figure 3 depicts the case q_s = 0. If a source is situated at x₅ = 0 the V₅ is flat and all V₄'s are curv ed in parallel (only "gravitation"). If a test-body is placed at x₅ = 0 it will always move on a geodesic, entirely determined by the strength of the source alone, independent of the position of the source and almost negligible with respect to the adjacent ones along x₅ as "rest-curvature".

As was already obvious from Fig. l, the V₅-univers is divided into two sectors, a positive and a negative (with respect to x₅ assignment). If a source curves the positive sector a certain way, this curvature will be repeated inversely in the negative sector (repulsion and attraction) (s. Figure 4).

What has been achieved so far? The model eliminates the concept of charge, by postulating that test-bodies and sources posses only mass or energy, positioned along a fifth dimension at various locations (charge eliminated by geometric concept). The electromagnetic force has been eliminated by coupling of the curvature of a five-dimensional manifold to "neutral" strength and position of such a source (always "neutral", only stress energy).

The unification criteria will be revisited after the quantitative presentation in the following.

Quantitative Results

The mathematically tedious construction of the new unified field equation shall not be outlined in detail here. Three main points have been observed:

(i) the quantitative presentation of the theory has to follow rigorously the heuristic expectations;

(ii) it has to result in Einstein's field equation for the case x₅ = 0;

(iii) the "electromagnetic" part of the stress energy tensor had to be reduced to its "mechanical" parts only, by extracting the charge and incorporating it into x₅ .

Thus the new unified field equation can be ex-pressed in the following way (without explicit indices):

G = (κ_{1} + κ_{2} x_{5} + u κ_{3} x_{5} \frac{\partial}{\partial τ}) T

(1)

T is the purely mechanical stress energy, u the 4-velocity of a test body,

\partial τ

an interval of proper time,

κ_{1} = 8 π

(2)

κ_{2} = 1 / (A_{1} ε_{r} ε_{0})

(3)

κ_{3} = \frac{μ_{r} μ_{0}}{4 π A_{2}} \int \frac{1}{r^{2}} s i n γ d S

(4)

with the various terms in κ₂ and κ₃ resulting from the old electromagnetic stress energy part.

G is the curvature tensor of the V₅ manifold. It can be constructed by the usual well known relations from General Relativity, i.e. the Riemannian tensor for V₅, the corresponding connection coefficients and the metric

∆ s = {(g_{μ ν} ∆ x^{μ} ∆ x^{ν})}^{1 / 2}

(5)

with

x=x_i and i = 1,2,3,4,5

x₄ time-like, x₅ "charge"-like (q/m),

15 metric coefficients g_μν ..

For the construction of G and the derivation of the geodesic equation one can either start from the global V₅ and end up at the various or particular V₄'s or from the V₄'s and build up the global V₅ geometry. Both approaches, which are complementary, may make use of a method, developed by Arnowitt, Deser and Misner [5], briefly ADM-method, which connects a V_n to a V_n-1. For the Riemann tensor this looks like (with explicit indices):

{}^{(n)}{R_{i j k}^{m}} = {}^{(n - 1)}{R_{i j k}^{m}} + {(n n)}^{- 1} (K_{i j} K_{k}^{m} - K_{i k} K_{j}^{m})

(6)

With

K_{i m} = n \begin{matrix} (n) \\ \nabla_{i} \end{matrix} e_{m}

(7)

K is called the extrinsic curvature operator, n a normal vector, dn would be the vectorial difference, generated by K, after transporting n parallel within a hyper-surface. Thus K relates the intrinsic curvature in a V_n-1 to the global extrinsic curvature of the V_n itself;

\begin{matrix} (n) \\ \nabla_{i} \end{matrix} e_{m} = {}^{(n)}{Г_{m i}^{μ}} e_{μ}

(8)

e_μ being a basis.

We can interpret the unified field equation as follows: The curvature of a V₅-manifold under the action of a unified gravitational/electromagnetic field depends on a mechanical stress energy tensor T, i.e. on its absolute value, its momentum with respect to x₅ and the change of this momentum with proper time.

This is a somewhat unexpected result and differs entirely in shape from the purely gravitational Ein stein equation. However, some assumptions and simplifications have been introduced along the lines of the development of the equation and these are briefly recalled here.

T was assumed to be fixed along x₅, therefore

\partial / \partial τ

has to be applied to T, rendering the source part dependent on a stress energy flux, corresponding when multiplied by x₅ to the classical magnetic forces arising from the movement of charges in traditional descriptions. If T is assumed to be changing along x₅, one would always have to con-sider

\partial (x_{5} T) / \partial τ

. This is e. g. important in ionization processes and mass conversion. In the first case the affine parameter in a geodesic equation is most likely x₄, resulting in a trajectory of a test-body as a geodesic in a V₄. In the second case x₅ could be affine parameter as well, resulting in the trajectory of a test-body changing its charge or mass during the interval under consideration.

The other assumption was that κ₂ and κ₅ were to be considered uniform in any of the directions. This may be true for most cases; in general, however, they should be presented as indexed tensors, their components differing according to possible anisotropies within a specific coordinate frame.

Elementary Particles and Strong Interaction

Further unification now has to proceed along the same lines as above: on a geometric basis. But it would have to include quantum theoretical elements. This means, the present field equation would have to be modified to include the quantization of geometry itself.

Heuristic Postulates

(a) The manifold in question, including space-time, has to be is quantized.

(b) Elementary particles with a rest mass m₀ > 0 are described as geometric entities, i.e. resonant structures of the quantized manifold, in which energy is trapped. These particles must be solutions of a quantum equation, relating trapped energy (rest mass) and topology.

(c) The quantum nature of the manifold becomes apparent only at short distances, i.e. in the “long” connection a correspondence principle becomes obvious, serving for the transition from microscopic quantum limits to macroscopic continuum physics.

Un-quantized systems exist only in generalization outside a certain limit. In reality nature is subjected to quantum rules. A geometric theory must reflect this. In the V₅-theory, geometry has to be quantized and thus provide the very basis for any static and dynamic behavior within the system as being characteristically of quantum nature. Quantum effects will be directly related to quantum geometry.

If the V₅ – manifold is quantized in geometrical terms (postulate (a)), the stress energy results from the agglomeration of any number and combination of quantized entities, e.g. nucleons or quarks. The quantum nature of the stress energy (“potential”) propagates itself into the surrounding “continuum” – up to sufficiently small distances! Thus the surrounding geometry shows a structure basically related to the entities “at the centre of it”.

An elementary particle can be defined as a certain amount of energy (rest mass), trapped in a highly curved resonant manifold configuration. Thus, if one takes into consideration a continuous manifold structure, when approaching smaller and smaller distances, i.e. reaching quantum conditions under inclusion of manifold quanta, “gravitational” (geometric-dynamical) interaction suddenly “jumps” into a quantum aspect of nature. Thus “gravitation” becomes the long range part of “strong interaction” for a heavy particle for example. For a “charged” particle the difference constitutes itself from the position of that particle along x₅.

Definitions

Let

\vec{r} = {(d s^{2})}^{\frac{1}{2}}

(9)

(a) being an event interval,

(b)

\vec{s}

the space-time (or manifold) number

(c) q the space-time (or manifold) quantum

(d)

\vec{R}

a space-time (or manifold) operator

In the quantum limit:

\vec{r} = s q

(10)

The following quantization rule is applied:

\vec{R} | \vec{s} > = q \vec{s} | \vec{s} > = | \vec{s} > q \vec{s}

(11)

\vec{R} | \vec{s} > = q \vec{s} | \vec{s} > = | \vec{s} > q \vec{s}

(11)

Quantum limit on the metric:

Δ s \geq q

(12)

\vec{r}

describes also an event:

\vec{r} | x_{1} \dots . x_{i} \dots . x_{n} >

(13)

Thus, an event dependent state of initially any kind can be expressed generally as:

| ψ (\vec{r}) >

(14)

This can be developed as:

| ψ_{\pm} (\vec{r}) > = | ψ_{s t a t} > e^{\pm i ω \vec{r}}

(15)

| ψ_{\pm} (\vec{r}) > = | ψ_{s t a t} > e^{\pm i ω \vec{r}}

(15)

with ω initially unknown.

The meaning of ψ:

{| < \vec{r} | ψ > |}^{2} d^{4} \vec{r}

(16)

which is the probability, that at the event

\vec{r}

within the “event space” (space-time manifold) the event is in the state |ψ>.

Clarification of

\vec{r}

:

\vec{r}

in geometric terms as metric corresponds to

\vec{r}

in quantum terms to a quantum event state, thus

s^{2} q^{2} = g_{i k} Δ x^{i} Δ x^{k}

(17)

To determine ω:

ω has to be related to the energy, trapped in events, or propagated along a world line; it therefore has to be found from the Einstein equation, which relates “event space” to (stress) energy.

Intermediate, semi-classical considerations, regarding the choice of a manifold metric

The choice – in principle – of the g_ik etc. is to be done arbitrary with a final restriction on at least one parameter, to suit the quantum condition (12). Thus only the choice of the final set is decisive: if. e.g., the time like part is chosen to be free, then one space like part is determined to fulfill the quantum condition et vice versa.

To carry through a full quantization, one has to define a quantum geometrical Hamiltonian, - an operator, which associates energy states with purely geometric entities: let us call it “Λ”.

Development of the Energy State Equation

Determining Λ and ω:

a) Λ

Λ carries the geometric information, which relates the manifold structure to energy states. It is therefore derived from G_μν (Einstein equation) under the observation of quantum rules:

G_μν → (quantized) Λ

(18)

b) ω

The remaining part of the Einstein equation, being capable of yielding information for ω, is the stress energy, thus fulfilling the requirements for ω, outlined above:

ω = 8πT_μν

(19)

To carry through a meaningful and consistent quantum relation between Λ and T in analogy to the Einstein equation, it is more useful to make

ψ

dependent on

{\vec{r}}^{2}

rather than on

\vec{r}

(without vector notation):

|ψ (r^{2}) > = e^{- i 8 π T_{μ ν} r^{2}}| ψ_{s t a t} (r^{2}) >

(20)

The transformation from r² to r² + Δr² is done via the transformation matrix U:

|ψ (r^{2}, r^{2} + Δ r^{2}) > = U| ψ (r^{2}) >

(21)

U can be expanded as:

U = 1 + K (r^{2}) Δ r^{2}

(22)

and with

K = -iΛ

(23)

(1 - i Λ Δ r^{2}) ψ (r^{2}) > = |ψ (r^{2}) > - i Λ Δ r^{2}| ψ (r^{2}) >

(24)

For mathematical convenience we make the transition:

Δr² → dr²

(25)

Thus

i \frac{d}{d r^{2}} |ψ (r^{2}) > = Λ| ψ (r^{2}) >

(26)

This is the instationary equation

Inserting the stationary terms leads to:

i \frac{d}{d^{2}} |ψ_{s t a t} (r^{2}) > = i (- i) 8 π T_{μ ν} (r^{2})| ψ_{s t a t} (r^{2}) > = 8 π T_{μ ν} (r^{2}) >

(27)

and finally to

Λ |ψ (r^{2}) > = 8 π T_{μ ν}| ψ (r^{2}) >

(28)

the stationary equation.

To arrive at energy states one has to rewrite (28):

and T_μν being

T_{I} = \frac{Δ E_{I}}{Δ V} \to \frac{d E_{I}}{d V}

(29)

leading to

Λ |ψ (r^{2}) > = 8 π \frac{d E_{I}}{d V}| ψ (r^{2}) >

(30)

and integrating

\int Λ | ψ (r^{2}) > d V = \int 8 π d E_{I} | ψ (r^{2}) >

(31)

leads to

\int Λ d V | ψ (r^{2}) > = 8 π E_{I} | ψ (r^{2}) >

(32)

the energy state equation

with

d V = d x_{i}^{l} l = 1,2, \dots ., i, \dots . n; l = 1,2, 3

(33)

Thus the volume V is the product of three factors; the factors can be three out of any combination of dimension elements of an n-dimensional manifold (e. g. dx₁dx₂dx₄ or dx₂dx₃dx₄ or dx₁dx₂dx₃ etc.).

Remarks to Equation (28):

a) (28) corresponds to Schroedinger´s equation, relating energy states to a field potential.

b) (28) corresponds formally to Einstein´s equation, relating geometry (quantized) to stress energy (quantized).

Inclusion of Spin

Spin plays an important role in the quantum mechanical application of the unified field equation; it shall be look at in this section. Basis is still Equation (1) (without indices)

G = (κ_{1} + κ_{2} x_{5} + u κ_{3} x_{5} \frac{\partial}{\partial τ}) T

(34)

According to F. Hehl et al. [6] the stress energy tensor can be split into

T \to T_{c} + T_{s}

(35)

with T_c mechanical stress energy

T_s spin angular momentum

T_{s} = Θ^{i j k} = [- 4 Θ_{. .}^{i k} Θ_{[e \dots k]}^{j l} - 2 Θ^{i k l} Θ_{. k l}^{j} + Θ^{k l i} Θ_{k l}^{. . j} + \frac{1}{2} g^{i j} (4 Θ_{m .}^{. k} Θ_{[e . . k]}^{m l}) + Θ^{m l k} Θ_{m k l}]

(36)

Thus

G_{5} = (κ_{1} + κ_{2} x_{5} + u κ_{3} x_{5} \frac{\partial}{\partial τ}) (T_{c} + T_{s}) = (κ_{1} + κ_{2} x_{5} + u κ_{3} x_{5} \frac{\partial}{\partial τ}) (T_{c} + Θ^{i j k})

(37)

if there is coupling between spin angular momentum and stress energy momentum, and the latter changes with time.

In case of weak coupling of

T_{s 1} = κ_{2} x_{5} Θ^{i j k}

(38)

and

T_{s 2} = u κ_{3} x_{5} \frac{\partial Θ^{i j k}}{\partial τ}

(39)

then

T_{s 1} = T_{s 2} = 0

(40)

and the spin equation reduces to:

G_{s}^{*} = (κ_{1} + κ_{2} x_{5} + u κ_{3} x_{5} \frac{\partial}{\partial τ}) T_{c} + κ_{1} T_{s} = G + κ_{1} T_{s}

(41)

with complete decoupling of spin from any charge effects.

Inclusion of Weak Force

According to the Fermi Model [7] the interaction density for charged and neutral weak processes is

L_{I}^{w e a k} (x) = \frac{4 G_{F}}{\sqrt{2}} = (j_{μ}^{(+)} (x) j^{(-) μ} (x) + j_{μ}^{(n)} (x) j^{(n) μ} (x))

(42)

\frac{4 G_{F}}{\sqrt{2}}

has to be found in the coupling constants κ_i, j_i in T. L_I^weak then transforms to

u = u_c + u_w

(43)

u_c correponds to u (originally purely electromagnetic).

u_{w 1} = \frac{4 G}{\sqrt{2}} ((u_{μ}^{(+)}) (x_{5}) u^{(-) μ} (x_{5}) + u_{μ}^{n} (x_{5}) u^{(n) μ} (x_{5})) = κ_{4} {(\dots .)}_{u_{w}}

(44)

leading finally to

G = (κ_{1} + κ_{2} x_{5} + (u_{c} + κ_{4} u_{w}) κ_{3} x_{5} \frac{\partial}{\partial τ}) T

(45)

Spin and Electro-Weak

The simplest case is a weak coupling between spin and charge:

G = (κ_{1} + κ_{2} x_{5} + (u_{c} + x_{4} u_{w}) κ_{3} x_{5} \frac{\partial}{\partial τ}) T_{c} + κ_{1} T_{s}

(46)

By taking the stationary equation (28), one arrives at:

T_{c} \to \frac{d E_{T_{c}}}{d x_{i}^{l}}

(47)

and

T_{s} \to \frac{d E_{T_{s}}}{d x_{i}^{l}}

(48)

Grand Total

The energy state equation reads:

\int Λ d_{x_{i}}^{l} | Ψ (r^{2}) > = ((κ_{1} + κ_{2} x_{5} + (u_{c} + κ_{4} u_{w}) κ_{3} x_{5} \frac{\partial}{\partial τ}) E_{T_{c}} + κ_{1} E_{T_{s}}) | Ψ (r^{2}) >

(49)

With all factors it transforms to:

\int Λ d_{x_{i}}^{l} |Ψ (r^{2}) > = ((8 π + \frac{1}{A_{1} ε_{r} ε_{0}} x_{5} + (u_{c} + \frac{4 G_{F}}{\sqrt{2}} u_{w}) \frac{μ_{r} μ_{0}}{4 π A_{2}} x_{5} \int \frac{1}{R^{2}} s i n γ d S \frac{\partial}{\partial τ}) E_{T_{B}} + 8 π E_{T_{S}})| Ψ (r^{2}) >

(50)

Conclusions

Summarizing, one can say that a formalism has been proposed to describe the nature of gravitational and electromagnetic fields in a unified way. The resulting field-equation reduces to the Einsteinian in the absence of an electromagnetic field, thus enlarging the context of General Relativity. The basis of the unification is a V₅-geometry coupled to a mechanical stress energy tensor, positioned along an x₅-dimension. The affine parameter of the 5th dimension is the ratio (q/m), charge/mass.

Let us go back to the criteria for true unification.

(a) Evidently the first condition is fulfilled: one field equation, a common source term, one and the same geometric structure.

(b) Only the mechanical stress energy remains as source; electromagnetic contributions have been accounted for by the type of coupling to geometry, the stress energy momentum along x₅ and the change with proper time of the latter.

(c) One could argue that x₅ is physically un-observable. If we forget its derivation from electromagnetism, however, and regard it as true geometric dimension, it is observable, when going backwards from the field equation: the position, along which a purely mechanical source is situated in this dimension, is observable by interpretation of the geodesics of test-bodies under the influence of such a source. Inversely, when we know the position of a source, we can predict the movement of test-bodies at a specific position along x₅. Thus the "depth" of x₅ can be probed, i.e. observed.

In succeeding steps the quantization of the event space has been achieved leading to stationary and instationary equations, which correspond to the Schroedinger und Einstein equations respectively. With the inclusion of spin and the weak force a grand total description of elementary particles and their interactions can be described by geometrical means only. The discrete geometry in event space is the sum of quantized energy states, depending on their location in a V₅ – manifold, their momentum relative to x₅, the change of these momentums with proper time, and spin energies.

References

Lichnerowicz, Theories Relativistes de la Gravitation et de l´Electromagnetisme, Masson et Cie (ed. 1955.
L. Witten (ed.), Gravitation: An Introduction to Current Research, J. Wiley & Sons Inc. 1962.
W. Misner et al., Gravitation, W. H. 1973.
W. Osterhage, Geometric Unification of Classical Gravitational and Electromagnetic Interaction in Five Dimensions, Z. Naturforsch. 1980.
R. Arnowitt et al., The Dynamics of General Relativity, in [2], p.
F. W. Hehl et al., General Relativity with Spin and Torsion, Rev. Mod. Phys., Vol. 48, No. 19 July; 3.
et al. 1983.

Figure 1. Global 5-Dimensional Universe.

Figure 2. Particle Trajectories for Constant Time in a Curved V₅-Manifold.

Figure 3. Particle Trajectories in a Flat V_5.

Figure 4. Positive and Negative Sectors of the V₅-Manifold under Curvature.

Table 1. Terminology.

Old		New
test-body	source	test-body	source
neutral	neutral	in V4(x5=0)	in V4(x5=0)
neutral	charged	in V4(x5=0)	in V4(x5 $\neq$ 0)
charged	charged	in V4(x5 $\neq$ 0)	in V4(x5 $\neq$ 0)
charged	neutral	in V4(x5 $\neq$ 0)	in V4(x5=0)

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).

Copyright: This open access article is published under a Creative Commons CC BY 4.0 license, which permit the free download, distribution, and reuse, provided that the author and preprint are cited in any reuse.