A Theoretical Explanation and Modification of the Lorentz Contraction Effect, and a Tentative Theoretical Explanation of the Planck Energy Formula

1. Introduction

The Lorentz contraction effect, first proposed by Hendrik Lorentz, is a phenomenon in which an object is shortened in the direction of its motion. Albert Einstein later explained this phenomenon through time transformation in the theory of special relativity [1]. However, we denied this explanation in our previous article [2,3]. Feynman attempted to explain the physical meaning of the Lorentz contraction effect in his "Feynman Lectures on Physics" [4], stating that the Lorentz contraction effect is a phenomenon caused by the compression of atoms during motion. However, we believe that this explanation is incorrect because any object will enter a state of uniform motion after acceleration, and the compression effect between atoms caused by acceleration will disappear after entering a state of uniform motion.

Of course, other physicists have attempted to explain the theoretical interpretation of the Lorentz contraction effect, such as M. Mansuripur (1984), who proposed a new theory based on the analysis of the principle of the invariance of the speed of light, namely, the "longitudinal component interaction theory." M. Mansuripur believes that the Lorentz contraction effect is caused by the application of the principle of the invariance of the speed of light in the framework of relativity, which is based on the longitudinal component interaction theory in relativity [6]. However, the main way of explanation in the article is still based on the foundation of special relativity.

We have proven in a paper on the spatial relativistic independence that under the premise of completely symmetrical relative motion, the Lorentz contraction is not established, and we pointed out that due to the constraints of energy conservation and momentum conservation, the relative motion between objects is not completely symmetrical in our universe [2]. This conclusion is different from the traditional Newtonian mechanics system and the viewpoint of special relativity. Based on this non-completely symmetrical relative motion between objects and the "Unified Theory of Force" [5], we can theoretically prove that Lorentz contraction effect exists between electrons and atoms due to the electric field, and this Lorentz contraction effect not only exists in the direction of motion of the object but also in all directions of the moving object.

At the same time, this contraction effect is not completely symmetrical, as it is thought in special relativity. For example, if a rocket accelerates away from the earth, there will be relative motion between the rocket and the earth. We can observe that the Lorentz contraction effect occurs on the rocket, but we cannot observe the Lorentz contraction effect occurring on the earth from the perspective of the rocket because we have proven in another article that this non-symmetry of relative motion between objects exists [2].

In this paper, we reinterpret the Lorentz contraction effect and provide a rigorous proof that the Lorentz contraction is a physical phenomenon based on the conservation of energy and momentum under non-completely symmetrical relative motion effects. We show that the Lorentz contraction effect not only occurs in the direction of motion but also simultaneously in any direction. This provides a new theoretical understanding of the Lorentz contraction effect, which has important implications for our understanding of the fundamental laws of physics.

In addition to the Lorentz contraction effect, we also explore the theoretical meaning of the Planck energy formula and its relationship with the Lorentz contraction effect. For the first time, we provide a theoretical explanation of the physical meaning of the Planck energy formula and associate the Planck energy formula with the Lorentz contraction effect. This can help us to have a deeper understanding of the true physical meaning behind the Planck energy formula.

Furthermore, based on our non-completely symmetrical relative motion theory and the "Unified Theory of Force," we make reasonable theoretical predictions about the basic structure of photons. We suggest that photons may have a similar basic structure to atoms and may be composed of two or more completely symmetric fundamental particles in motion under the influence of an electric field. This provides a new perspective on the nature of photons and their role in the fundamental laws of physics.

2. Theoretical Explanation and Revision of Lorentz Contraction Effect

In our previous article, we have proven that the relative motion between objects is not completely symmetrical in our universe due to the constraints of energy conservation and momentum conservation [2]. Based on this conclusion, we can theoretically prove that the Lorentz contraction effect exists between electrons and atoms due to the electric field.

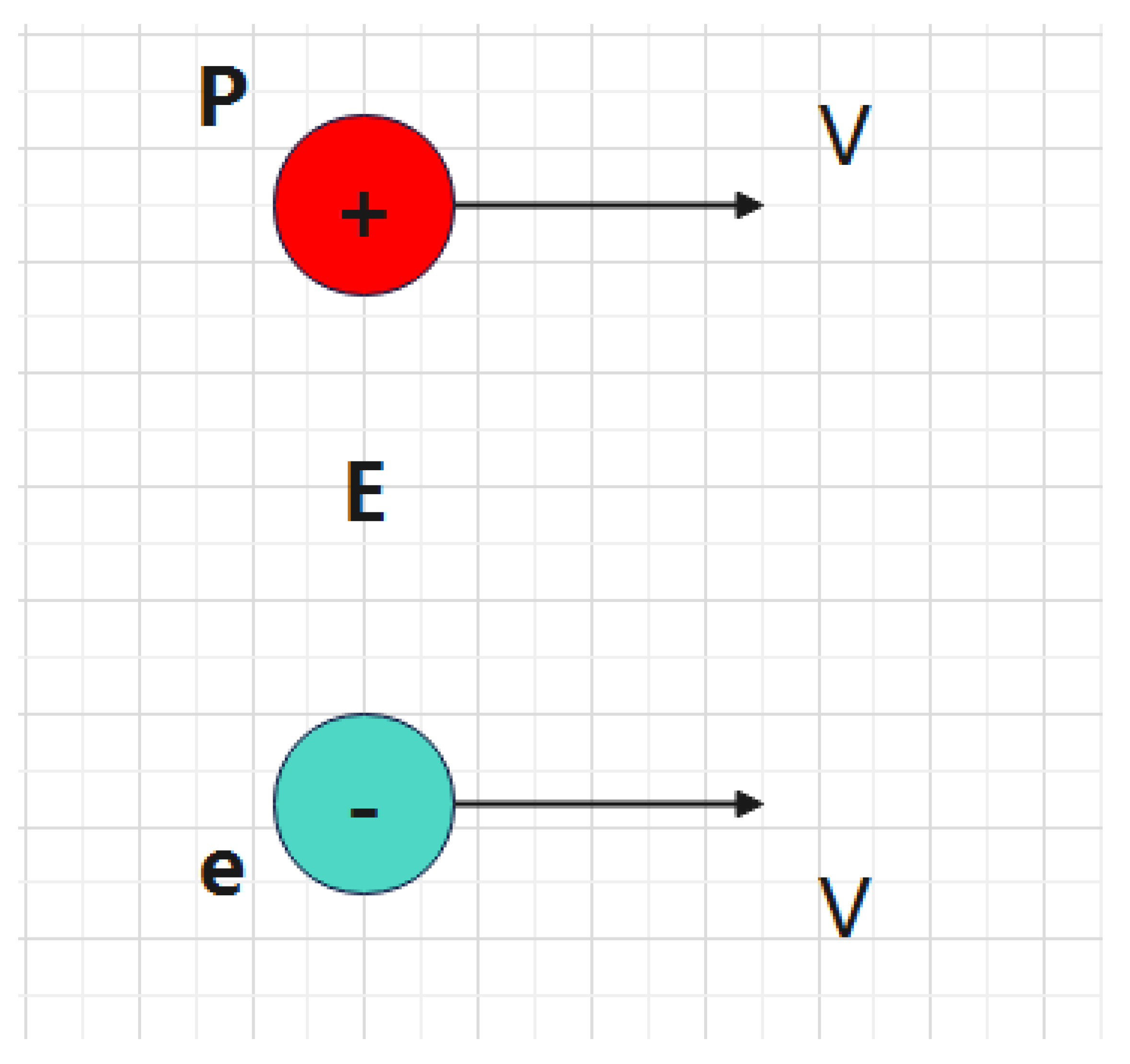
According to "Unified Theory of Force " [5], we know that the essence of the electric field is a spatial phenomenon caused by "energy loss${\mathit{E}}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}$". Meanwhile, through countless physics experiments, we have detected that the electric charge of electrons and protons does not change when they are accelerated. Therefore, we can provide a more reasonable theoretical explanation for the Lorentz contraction effect through the following thought experiment, as shown in Figure 1:

If we simultaneously accelerate an electron $e$ and a proton $P$, with a large initial distance between them, we can assume that their initial energy loss due to the missing energy is ${{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}$. According to the "Unified Theory of Force", both the electron $e$ and the proton $P$ will generate a companion energy field ${\mathit{E}}_{\mathit{f}\mathit{o}\mathit{l}\mathit{l}\mathit{o}\mathit{w}}$ during acceleration. After the electron and proton are accelerated to velocity $v$, we can allow them to combine into a hydrogen atom through mutual attraction.

If we allow the electron $e$ and the proton $P$ to combine into a hydrogen atom before acceleration, then their total energy (measured in mass) in the stationary state is:

$$m_H=m_e+m_p+∆m$$

where $∆m=\frac{{{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}{{\mathit{C}}^2}$, $m_H$ denotes the total mass of the hydrogen atom, $m_e$ denotes the mass of the electron, and $m_p$ denotes the mass of the proton. At this point, the equilibrium radius $r_0$ of the electron and proton is determined by the following electric potential energy formula:

$$E=k\frac{q_1{q}_2}{r}$$

Therefore, we obtain:

$$r_0=k\frac{q_1{q}_2}{{{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}=k\frac{e^2}{{{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}$$

(1)

However, when we accelerate the electron $e$ and the proton $P$, their dynamic masses become:

$$m_e^v=m_e\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}$$

$$m_p^v=m_p\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}$$

$${{\mathit{E}}^{\mathit{v}}}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}={{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}$$

If the electron $e$ and the proton $P$ then combine through mutual attraction to form a hydrogen atom, and considering that the electric charge of the electron and proton do not change, according to formula (1), the equilibrium radius $r_1$, in the absence of relativistic effects due to the motion arising from the mutual attraction between the electron and proton, will become:

$$r_1=k\frac{q_1{q}_2}{{{\mathit{E}}^{\mathit{v}}}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}=k\frac{e^2}{{{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}\bullet \sqrt{1-\frac{v^2}{c^2}}=r_0\bullet \sqrt{1-\frac{v^2}{c^2}}$$

(2)

We find that the equilibrium radius $r_1$ undergoes a contraction effect. Formula (2) is the familiar formula for the Lorentz contraction effect, but unlike the conclusion of the Lorentz contraction effect, this contraction effect occurs in all directions of the object, not just in the direction of the object's motion.

Moreover, this contraction effect is not completely symmetric, as believed in the theory of special relativity, but rather an asymmetric Lorentz contraction effect. For example, if a rocket accelerates away from the earth, relative motion occurs between the rocket and the earth. We can observe this Lorentz contraction effect on the rocket, but we cannot observe the earth undergoing this Lorentz contraction effect from the perspective of the rocket, as we have already proven the non-symmetry of relative motion between objects in another article [2].

In the above analysis, if we assume that the energy of the electric field is eventually converted into the kinetic energy of the electron, without considering relativistic effects, then in a hydrogen atom in the stationary state, the average velocity $\overline{v}$ of the electron $e$ is determined by the following formula:

$${{\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}={\frac{1}{2}m}_e\bullet {\overline{v}}^2$$

Therefore, we obtain:

$$\overline{v}=\sqrt{\frac{{{2\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}{m_e}}$$

When the electron $e$ and the proton $P$ are accelerated to velocity $v$ and then combine through mutual attraction to form a hydrogen atom, the average speed $\stackrel{̿}{v}$ at which the electron moves around the proton in circular motion, as observed from the perspective of the earth, is determined by the following formula:

$${{\mathit{E}}^{\mathit{v}}}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}=\frac{1}{2}{m}_e^v\bullet {\stackrel{̿}{v}}^2$$

Therefore, we obtain:

$$\stackrel{̿}{v}=\sqrt{\frac{{{2\mathit{E}}^{\mathit{v}}}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}}{m_e^v}}=\sqrt{\frac{{{2\mathit{E}}^0}_{\mathit{m}\mathit{i}\mathit{s}\mathit{s}\mathit{i}\mathit{n}\mathit{g}}\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}}{m_e\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}}}=\overline{v}}$$

From the above formula, we can see that although the radius of the hydrogen atom undergoes a Lorentz contraction effect after acceleration, the speed $\stackrel{̿}{v}$ at which the electron moves around the proton does not change. However, the motion period $T$ of the electron around the proton will change. Assuming that the motion period of the electron around the proton in the stationary state of the hydrogen atom is $T_0$, and the motion period of the electron around the proton after acceleration is $T_1$ (as observed from the perspective of the earth), and assuming that the electron moves around the proton in circular motion, we can easily obtain the following conclusion:

$$T_1=T_0\bullet \sqrt{1-\frac{v^2}{c^2}}$$

(3)

This is different from the conclusion of time delay in special relativity. In special relativity, relative motion is symmetric, while we point out here that relative motion speed is constrained by energy conservation and momentum conservation, and is actually asymmetric. At the same time, the conclusion in special relativity is the time delay effect, while we point out here that not only does the time delay effect not exist, but time acceleration effect will also occur (only when the moving object is observed, which is determined by the relative independence of space [2]).

Meanwhile, we observe that the form of the above formula (3) is consistent with the formula for dynamic mass, and we can rewrite it as:

$$m_e^v=m_e\bullet \sqrt{\frac{1}{1-\frac{v^2}{c^2}}=}{m}_e\bullet \frac{T_0}{T_1}$$

(4)

Assuming $m_e\bullet T_0=h_1$, $\frac{1}{T_1}={\omega }_1$, then the expression of the above formula (4) can be transformed into the following form:

$$m_e^v=h_1{\omega }_1$$

This is very similar in form to the Planck energy formula. If we assume that photons are also composed of two initially small mass objects that move relative to each other under the action of an electric field (or other fields with similar properties), we can easily explain the Planck energy formula for photons:

$$E=h\omega$$

Here, $E$ denotes the energy of the photon, $h$ denotes the Planck constant, and $\omega$ denotes the frequency of the photon. This is our theoretical explanation of the Planck energy formula, and I think this may be the first time in physics that a theory has been used to explain the physical meaning behind the Planck energy formula.

It should be noted that the important premise for the proof of the Lorentz contraction effect generated by asymmetric motion and the explanation of the Planck energy formula that we presented above is that the object has an electric field effect, similar to that of the electron and proton, where the electric charge does not change with motion. If it is a gravitational field, it will not have the effects mentioned above, because the mass of the object increases with the increase of the velocity, instead of being constant.

3. Conclusions

This paper is an applied paper based on the unified mechanics theory. In the case of asymmetric relative motion, we have, for the first time, theoretically explained the physical meaning of the Lorentz contraction effect through the constraints of energy conservation and momentum conservation, and strictly proven that this contraction effect occurs in all directions of the object, not just in the direction of motion as stated in special relativity, and that this contraction effect can be confirmed through physical experiments.

Conversely, we can infer that if the Lorentz contraction effect can be observed after the object is accelerated, it should have the characteristics of a basic atomic structure and electric field.

Furthermore, in this paper, we have, for the first time in physics, theoretically explained the Planck energy formula $E=h\omega$ and predicted that photons also have similar characteristic structures to atoms (of course, photons can be composed of two or more completely symmetrical basic particles moving relative to each other, rather than a structure consisting of a very massive proton and a very small electron).