Stator ITSC Fault Diagnosis of EMU Asynchronous Traction Motor Based on ApFFT Time-shift Phase Difference Spectrum Correction and SVM

1. Introduction

Three-phase AC asynchronous motors have become the main motors in industrial equipment due to their simple structure, high reliability, and low manufacturing costs [1,2,3]. The AC-DC-AC transmission mode is used in modern EMU traction systems, and three-phase AC squirrel-cage asynchronous motors are used as traction motors[4]. The working environment of the EMU traction motors is poor. Affected by mechanical stress, thermal stress, and electrical stress, EMU traction motors are prone to failure [5,6]. The fault types of three-phase AC asynchronous squirrel-cage motors in industrial applications mainly include stator insulation faults (37%), rotor broken bar faults (12%), bearing faults (41%), and other faults (10%) [7]. EMU traction motors are powered by inverters [8,9], which output PWM voltage. The high voltage stress generated by the PWM voltage makes the traction motor insulation system degrade faster [10,11]. The insulation system of an asynchronous traction motor is mainly composed of inter-turn insulation and the main insulation system [12]. Due to the space and insulation materials limitation, the inter-turn insulation is the weakest part. When an ITSC fault occurs, the inter-turn current will circulate between the short-circuit turns, quickly generating a large amount of heat [13]. It will reduce the motor's insulation condition and cause inter-phase or ground short-circuit faults[14]. The ITSC fault duration can vary from a few seconds to several hours. When the ITSC fault occurs early, timely maintenance can prevent the fault's further expansion and significantly reduce the maintenance cost. Since the ITSC fault of the asynchronous traction motor is more hidden than the main insulation system fault, it is more difficult to detect the incipient ITSC fault [15,16].

The ITSC fault diagnosis of three-phase asynchronous motors mainly includes model-based, signal process-based, and artificial intelligence-based diagnosis methods [17,18,19]. An accurate motor ITSC fault model is needed for model-based ITSC fault diagnosis. Model-based methods mainly include the parameter estimation method and residual estimation method. The parameter estimation method estimates the model parameters related to the ITSC fault [20,21,22]. Based on the three-phase asynchronous motor ITSC fault model under the dq axis, the particle filter algorithm is used to estimate multiple parameters to detect the stator ITSC fault and assess residual life[23]. This method only needs to measure the motor phase voltage and phase current, which is easy to achieve a real-time and non-intrusive diagnosis. A healthy motor model is necessary for the residual estimation method. The residual estimation method takes the detectable variables related to the ITSC fault as the state variables. It uses the difference between the state variables of the healthy motor estimated by the model and the measured variables as the residual to detect the ITSC fault [24,25]. The three-phase current is taken as the state variable, and the high-order sliding mode observer is used to observe the three-phase current of the healthy motor[26]. The residual of the observed and measured values is taken as the index for the ITSC fault.

The diagnosis method for the ITSC fault based on signal processing is mainly based on the electrical, magnetic, thermal, vibration, and acoustic signals. The stator ITSC fault is diagnosed by analyzing and processing the above signals in the time, frequency, or time-frequency domains [27,28,29]. The voltage or current signals can be used to realize non-intrusive diagnosis [30], saving costs without installing additional sensors. For the steady operation state, the FFT algorithm is generally used to calculate specific frequency components of the current or other signals to detect the ITSC fault [31]. With the continuous development of new signal processing methods, time-frequency analysis methods such as wavelet transform, WVD (Wigner-Ville distribution), and HHT (Hilbert-Huang transform) are also applied to the motors' fault diagnosis [32,33]. The discrete wavelet is used to decompose the stator current, and the maximum norm of the detail coefficient is used to detect the incipient ITSC fault [34].

Shallow machine learning and deep learning methods are also applied to motors' stator ITSC fault diagnosis[35,36,37,38]. The ITSC fault diagnosis method based on shallow machine learning is generally divided into three stages: data preparation, feature extraction, and model training. Particle swarm optimization and principal component analysis can be used for feature extraction. BP neural network and SVM models can be used as diagnosis models. BP neural network is trained based on the phase difference of the three-phase stator current[39]. The trained model can detect and locate stator the ITSC fault. If the deep learning network model, such as a convolution neural network, is adopted. Artificially extracting features is unnecessary, and the deep learning network will automatically extract them. The instantaneous value of the three-phase current is taken as the feature, the convolution neural network is taken as the diagnosis model, and the trained convolution neural network can accurately detect the ITSC fault of a three-phase asynchronous motor[40].

The research on the diagnosis method for ITSC fault of asynchronous motors stator has achieved many positive results, but diagnosis of EMU traction motors stator ITSC fault has unique requirements. Firstly, in previous studies, the degree of AC motor ITSC fault is generally evaluated based on the number of short-circuit turns when the inter-turn resistance is fixed. In the non-metallic short-circuit, the resistance between short-circuit turns is directly related to the damage degree of the fault to the motor. Secondly, most of the previous studies are in the condition of non-variable frequency speed regulation, and the steady speed of the motor is fixed. The traction motor will operate stably at different speeds according to operating conditions. Finally, the traction motor of EMU adopts vector control or direct torque control based on the current closed-loop. The fundamental frequency of voltage and current signals cannot be directly obtained, and a spectral correction method is needed to get a more accurate fundamental frequency.

The article is mainly divided into five parts. After the introduction, it mainly introduced the measurement method for the traction motor's ZSVC and the apFFT time-shift phase difference correction method. This method was used to calculate the traction motor's ZSVC fundamental frequency, the fundamental component amplitudes of the ZSVC and the three-phase current under a steady state. In the third part, an ITSC fault evaluating index related to the number of short-circuit turns and the inter-turn resistance was proposed. The index is based on the thermal power of the circulating current between short-circuit turns. At the same time, the SVM and the hyper-parameters optimization method were introduced in this part. In the following work, SVM was used to diagnose the ITSC fault. The fourth part is the experimental part. The EMU electric traction simulation experimental platform simulated the steady-state operation of the EMU. According to the fault degree index proposed in this article, the experimental samples were divided into normal, incipient, and serious fault samples, and the SVM ITSC fault diagnosis model was trained and tested. The last part summarizes all the research contents and puts forward the follow-up work.

2. Calculation of Signals Fundamental Component

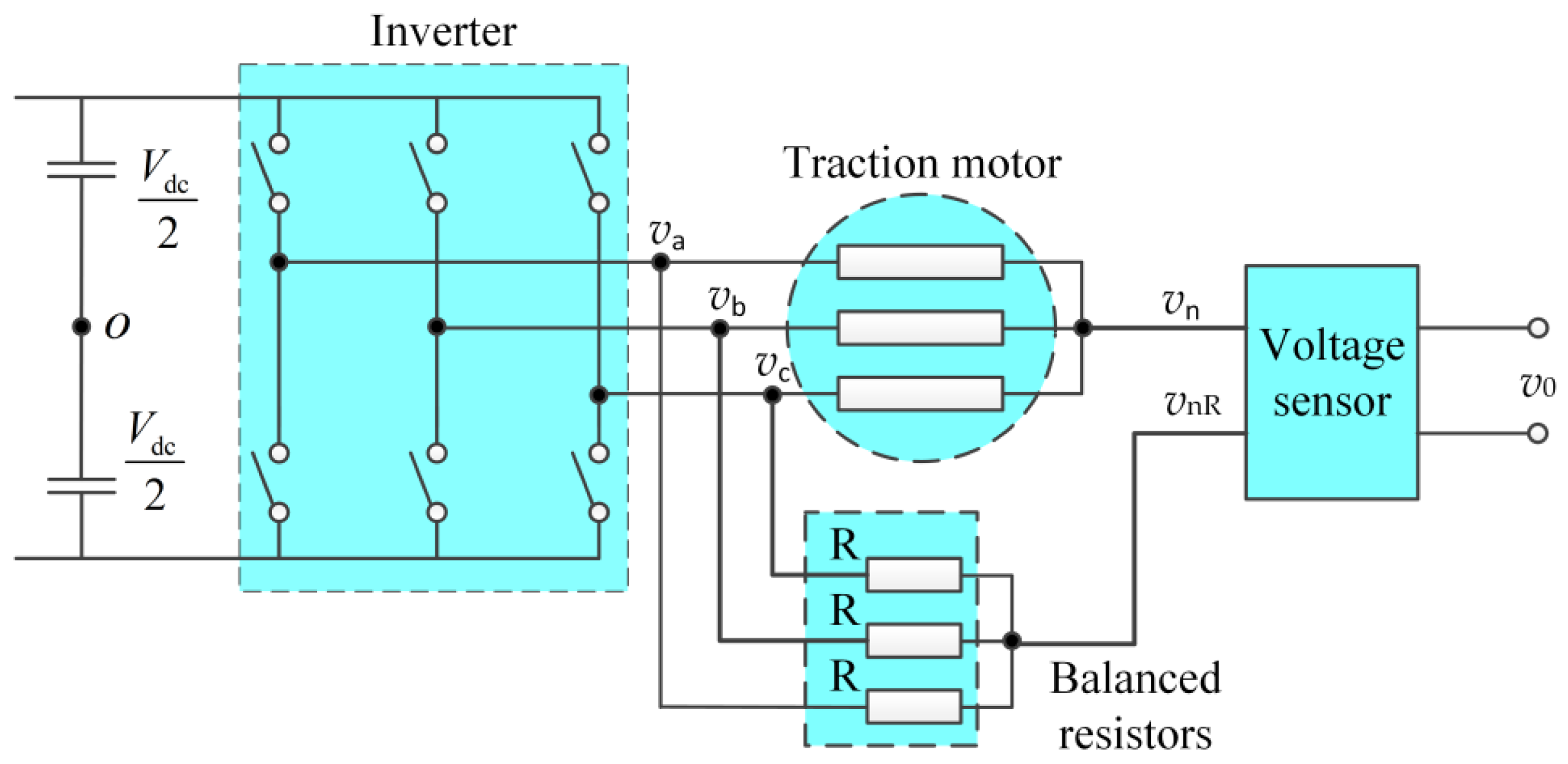
2.1. ZSVC Measurement method

The traction motors' current is measured for speed and torque control during the operation. Only the ZSVC needs to be measured additionally. The ZSVC of the three-phase asynchronous motor can effectively monitor the stator ITSC fault [41,42]. The measurement circuit is relatively simple, and installing sensors on the motor body is unnecessary. According to the ZSVC definition of a three-phase asynchronous motor [43,44], as shown in Formula(1), three voltage sensors are needed when measuring the three-phase voltage.

$$v_0=\frac{1}{3}\left(v_{an}+v_{bn}+v_{cn}\right).$$

(1)

Directly measuring three-phase voltage and calculating ZSVC according to Formula(1) can be applied to a sinusoidal power supply. The EMU traction motor is powered by an inverter. The inverter will generate ZSVC inherent in the PWM voltage pulse and related to the PWM modulation mode. Although its frequency is far from the fundamental frequency, if reasonable compensation and filtering are not carried out, frequency aliasing will occur, and the measurement will be affected. The ZSVC measurement of the traction motor in Figure 1 is adopted, and the three balanced resistors can eliminate the influence of the inverter [45].

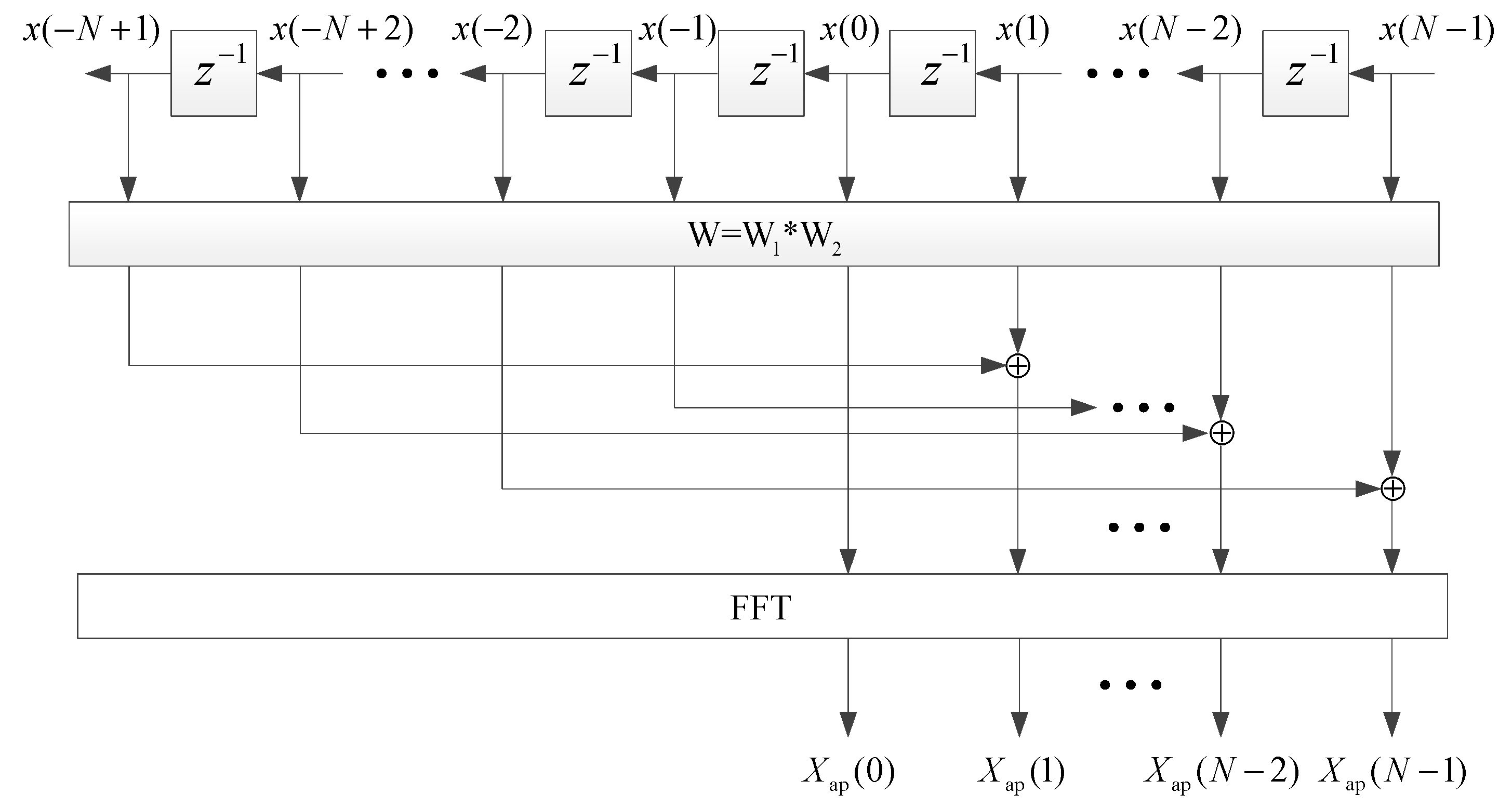
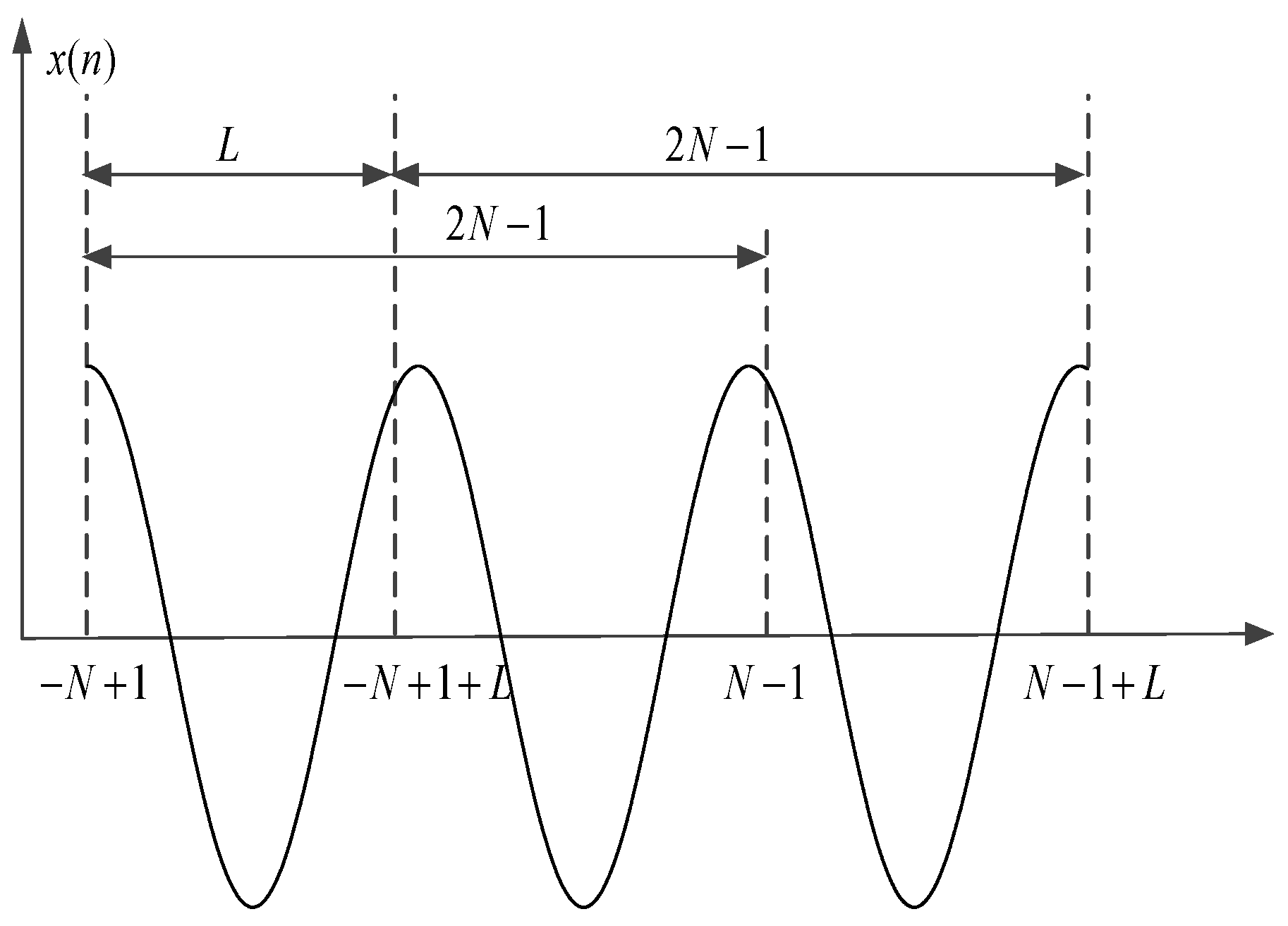
2.2. ApFFT time-shift phase difference correction

The apFFT time-shift phase difference correction mainly includes two parts, apFFT and time-shift phase difference correction. ApFFT algorithm can effectively suppress spectrum leakage caused by data truncation [46,47,48]. As shown in Figure 2, the required data points for the N-order spectrum analysis are x(-N+1), x(-N+2), …, x(-1), x(1), …,x(N-2), x(N-1) and total 2N-1 data points. W is a convolution window formed by convolution operation with the front window W₁ and the flipped rear window W₂. The front W₁ window and rear window W₂ are rectangular windows. It is called windowless apFFT spectral analysis. One of the front windows W₁ or rear W₂ is a rectangular window. It is called single-window apFFT spectral analysis. Neither the front window W₁ nor the rear window W₂ is rectangular. It is called double window apFFT spectrum analysis.

The N-order apFFT spectrum analysis mainly includes the preprocessing of 2N-1 point data and the FFT calculation. If the data is processed by windowless apFFT, it is equivalent to do the following operations on the data: first, divide 2N-1 data points into N segments with length N according to Formula (2); Then rotate the N segment data, taking the Nth data point, i.e., x (0), as the first data point of the data segment;

$$\begin{gathered} x_0={[x(0),x(1),x(2),\dots ,x(N-1)]}^T, \\ {x}_1={[x(-1),x(0),x(1),\dots ,x(N-2)]}^T, \\ {x}_2={[x(-2),x(-1),x(0),\dots ,x(N-3)]}^T, \\ \dots \dots \\ {x}_{N-1}={[x(-N+1),x(-N+2),\dots ,x(0)]}^T. \end{gathered}$$

(2)

Finally, add the shifted N segments of data by bit and normalize them to get x_ap in Formula (3), which is the N data points obtained after the windowless apFFT preprocessing.

$$x_{ap}=\frac{1}{N}{[Nx(0),(N-1)x(1)+x(-N+1),\dots ,x(N-1)+(N-1)x(-1)]}^T.$$

(3)

Perform N-point FFT on x_ap, that is, get the calculation result Xap (k) of windowless apFFT.

The second part of apFFT time-shift phase difference correction algorithm is time-shift phase difference correction[48,49]. The single-frequency complex exponential signal with frequency ω*, initial phase θ₀, and amplitude A is:

$$x(n)=A{e}^{j(w^{*}n+{\theta }_0)},$$

(4)

The data points are divided into two segments of the same length, as shown in Figure 3. The data interval of the first segment is [-N+1, N-1], assuming the spectral serial number is k*, the phase value of apFFT main spectral line is:

$${\phi }_X(k^{*})={\theta }_0,$$

(5)

The second data segment starts after the first data segment moving L data points. The data range is [-N+1+L, N-1+L]. The central data point of this data segment is x(-L), as shown in Figure 3. If apFFT is performed on the second segment of data, the phase of apFFT main spectral line is ${\phi }_{XL}(k^{*})$, which is the approximate estimation of the phase of data point x(-L), that is:

$${\phi }_{\mathrm{X} \mathrm{L}}(k^{*})={\theta }_0-{\omega }^{*}L,$$

(6)

The estimation of signal frequency can be obtained from Formula (5) and Formula (6):

$${\widehat{\omega }}^{*}=\left[{\phi }_X\left(k^{*}\right)-{\phi }_{XL}\left(k^{*}\right)\right]/L=\Delta \phi /L,$$

(7)

To eliminate the "phase ambiguity" phenomenon [50], the frequency estimation after phase compensation [51]:

$${\widehat{\omega }}^{*}=\left[{\phi }_X\left(k^{*}\right)-{\phi }_{XL}\left(k^{*}\right)\right]/L+2k^{*}\pi /N,$$

(8)

For the double-window apFFT, the signal amplitude estimation can be obtained:

$$\widehat{A}=\frac{\left|Y\left(k^{*}\right)\right|}{{\left|F_{\mathrm{g}}\left(k^{*}\Delta \omega -{\widehat{\omega }}^{*}\right)\right|}^2}.$$

(9)

In equation (9), Y(k^*) is the value of the double-window apFFT at the point k^*;$F_{\mathrm{g}}\left(k^{*}\Delta \omega -{\widehat{\omega }}^{*}\right)$ is obtained from binging$\left(k^{*}\Delta \omega -{\widehat{\omega }}^{*}\right)$into the Fourier transform of the window function. Generally, the window function is a cosine window, and its Fourier transform expression is determined.

3. Fault Diagnosis Method for Stator ITSC Fault of Traction Motor

3.1. Stator ITSC fault degree index

In previous studies, only the metallic short-circuit of windings is generally considered. The two windings are directly short-circuited without any resistance, and the motor's ITSC fault degree is evaluated by the number of short-circuit turns. In most cases, the metallic ITSC fault is caused by the expansion of the non-metallic ITSC fault. The non-metallic ITSC fault means some resistance between short-circuit turns. In this case, evaluating the ITSC fault only by the number of short-circuit turns is insufficient. The heat mainly causes damage to the traction motor caused by the ITSC fault. If the heat generated by the inductance is ignored, the thermal power of the inter-turn resistance is:

$$P_{\mathrm{f}}={\frac{U_{\mathrm{f}}}{R_{\mathrm{f}}}}^2=\frac{{(N_{\mathrm{f}}\ast \frac{U}{N_{\mathrm{s}}})}^2}{R_{\mathrm{f}}}=U^2\ast \frac{N_{\mathrm{f}}{}^2}{N_{\mathrm{s}}{}^2\ast R_{\mathrm{f}}},$$

(10)

P_f is the thermal power of the inter-turns resistance, U_f is the short-circuit turns voltage, R_f is the inter-turn resistance, U is the motor phase voltage, and N_s is the total number of turns of each phase winding. From Formula(10), it can be concluded that the heat generated by the short-circuit current after the ITSC fault is in direct proportion to$\frac{N_{\mathrm{f}}{}^2}{N_{\mathrm{s}}{}^2\ast R_{\mathrm{f}}}$.

Define the fault degree index of ITSC fault:

$${\lambda }_{\mathrm{f}}=\sqrt{\frac{N_{\mathrm{f}}{}^2}{N_{\mathrm{s}}{}^2\ast R_{\mathrm{f}}}}=\frac{N_{\mathrm{f}}}{N_{\mathrm{s}}}\ast \frac{1}{\sqrt{R_{\mathrm{f}}}}.$$

(11)

According to Formula(11), the ITSC fault degree index λ_f is related to the short-circuit turns number and the inter-turn resistance.

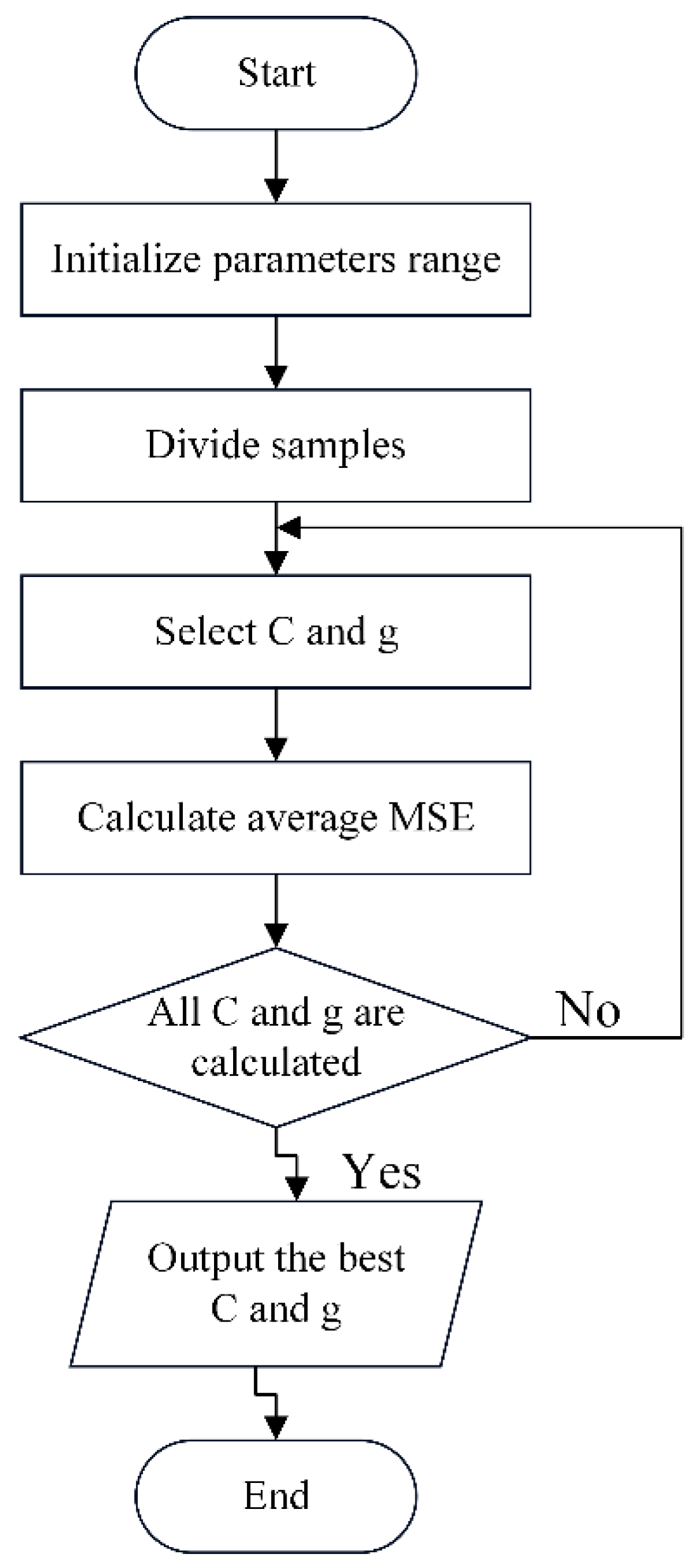
3.2. SVM model for fault diagnosis of ITSC fault and hyper-parameters optimization

The apFFT time shift phase difference spectrum correction algorithm is used to calculate the fundamental frequency of ZSVC, the fundamental component amplitudes of the traction motor's ZSVC and the three-phase current. The SVM-based fault diagnosis model of ITSC fault is established with the five parameters as input. The traction motor ITSC condition is divided into normal, incipient, and serious faults using the proposed index. Support Vector Machine (SVM) is a machine learning method based on statistical theory, mainly used to solve classification and regression problems [52,53,54,55]. Its core idea is to complete the model training based on the structural risk minimization principle. It has nonlinear solid approximation ability, good generalization performance, and good results in dealing with small samples and nonlinear problems. SVM uses nonlinear mapping $\varphi (x)$ to map the original data to the high-dimensional space to deal with nonlinear regression problems of multidimensional data.

The C-SVC model is a relatively standard two-class SVM model. The training set is:

$$T=\left\{\left(x_1,y_1\right),\cdots ,\left(x_l,y_l\right)\right\}\in {(X\times Y)}^l,$$

(12)

$x_i\in X=R^n,y_i\in Y=\{1,-1\}(i=1,2,\cdots ,l)$, x_i is the characteristic vector.

Select kernel function $K\left(x,x^{\prime }\right)$ and appropriate parameter C. The standard kernel functions $K\left(x,x^{\prime }\right)$mainly include linear, polynomial, and radial basis kernel functions. Lagrange dual problem of the original problem is:

$$\underset{\alpha }{\min }\frac{1}{2}{\displaystyle \sum _{i=1}^j{\displaystyle \sum _{j=1}^l{y}_i}}{y}_j{\alpha }_i{\alpha }_{j}K\left(x_i,x_j\right)-{\displaystyle \sum _{j=1}^l{\alpha }_j},$$

(13)

$$s.t.\hspace{1em}{\displaystyle \sum _{i=1}^l{y}_i}{\alpha }_i=0,\hspace{1em}0⩽{\alpha }_i⩽C,i=1,\cdots ,l,$$

Get the optimal solution:${\alpha }^{*}={\left({\alpha }_1^{*},\cdots ,{\alpha }_l^{*}\right)}^{\mathrm{T}}$

Select a positive component of $0<{\alpha }_j^{*}<C$ from ${\alpha }^{*}$, and calculate the threshold accordingly:

$$b^{*}=y_j-{\displaystyle \sum _{i=1}^l{y}_i}{\alpha }_i^{*}K\left(x_i-x_j\right)$$

(14)

The constructed decision function is:

$$f(x)=\mathrm{sgn}\left({\displaystyle \sum _{i=1}^l{\alpha }_i^{*}}{y}_{i}K\left(x,x_i\right)+b^{*}\right)$$

(15)

If the Gaussian radial basis function is used as the kernel function, g is the parameter of the Gaussian radial basis function:

$$K\left(x_i,x\right)=\exp \left(-\frac{{‖x_i-x_j‖}^2}{2\sigma }\right)=\exp \left(-g{‖x_i-x_j‖}^2\right)$$

(16)

In the SVM classification model, the selection of model penalty parameter C and Gaussian kernel function parameter g is directly related to the model performance. The K-CV is a standard cross-validation algorithm. The training data set is evenly divided into K sub-datasets in model training. Each sub-data set is used as the validation set in turn, and the rest K-1 sub-datasets are used as the training set to train K models. The average mean square error (MSE) of K models on the validation set is used as the performance index. The mean square error is:

$${\delta }_{\mathrm{MSE}}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{(y_i-{\overline{y}}_i)}^2}$$

(17)

In Formula(17), n is the number of samples, y_i is the predicted value, y_i is the target value.

Grid search is to select several discrete points on each dimension of the parameter space according to certain rules. The discrete points of different dimensions intersect in the parameter space to obtain the discrete solution. Calculate each discrete solution to obtain the optimal solution. Figure 4 is the flow chart of the hyper-parameter optimization using the K-CV and grid search method. Take the grid point as C=2^a, g=2^b, the step size is 1, and initialize the range of a and b. Divide the training samples equally. Each subset is used as a validation set, and the rest K-1 subsets are used as training sets to train K models and calculate the average MSE of the K models on the K validation sets. After calculating all the combinations of C and g at all grid intersections, C and g at the minimum average MSE are the optimal solutions.

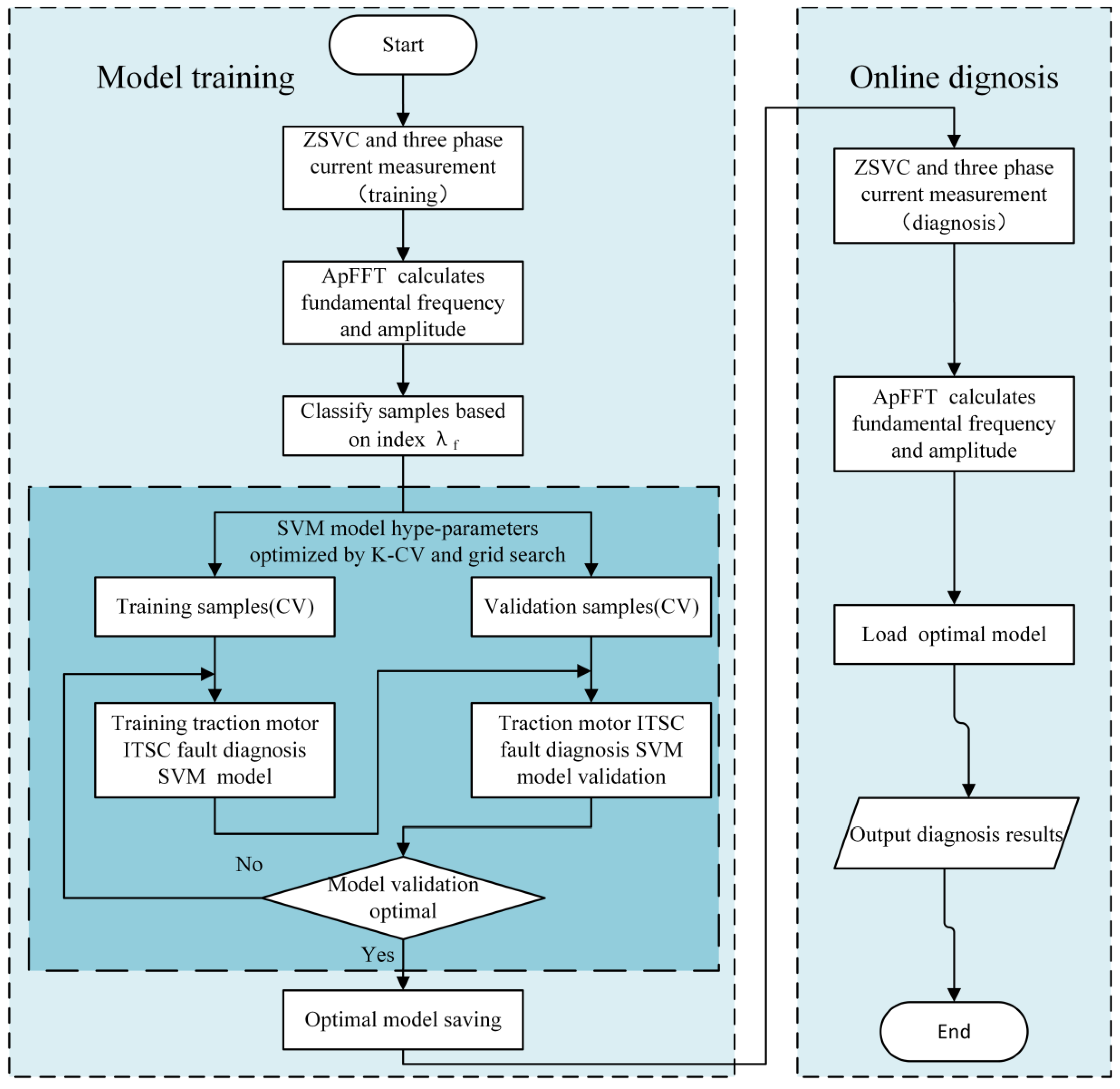
3.3. ITSC fault diagnosis procedure based on SVM model

As shown in Figure 5, the EMU traction motors ITSC fault diagnosis based on SVM includes two stages: model training and online diagnosis. In the model training stage, ZSVC and three-phase current are first measured with the circuit proposed in the article. Second, apFFT time-shift phase difference correction algorithm is used to calculate ZSVC fundamental frequency, the fundamental amplitudes of ZSVC and the three-phase current. Third, the ZSVC fundamental frequency, the amplitude of ZSVC, and the three-phase current are used as features. Based on the ITSC fault index λ_f, the samples are divided into three categories, normal, incipient, and serious fault. Fourth, the K-CV method divides all the samples into training and validation samples. The K-CV and grid search method is used to optimize the hyper-parameters. Last, the optimal ITSC fault diagnosis model is saved. In the online diagnosis stage, the ITSC fault features are acquired similarly to the training stage. The optimal ITSC fault diagnosis model is loaded, and input the fault features to the SVM model to predict the ITSC category.

4. EMU Electric Traction Simulation Experimental Platform

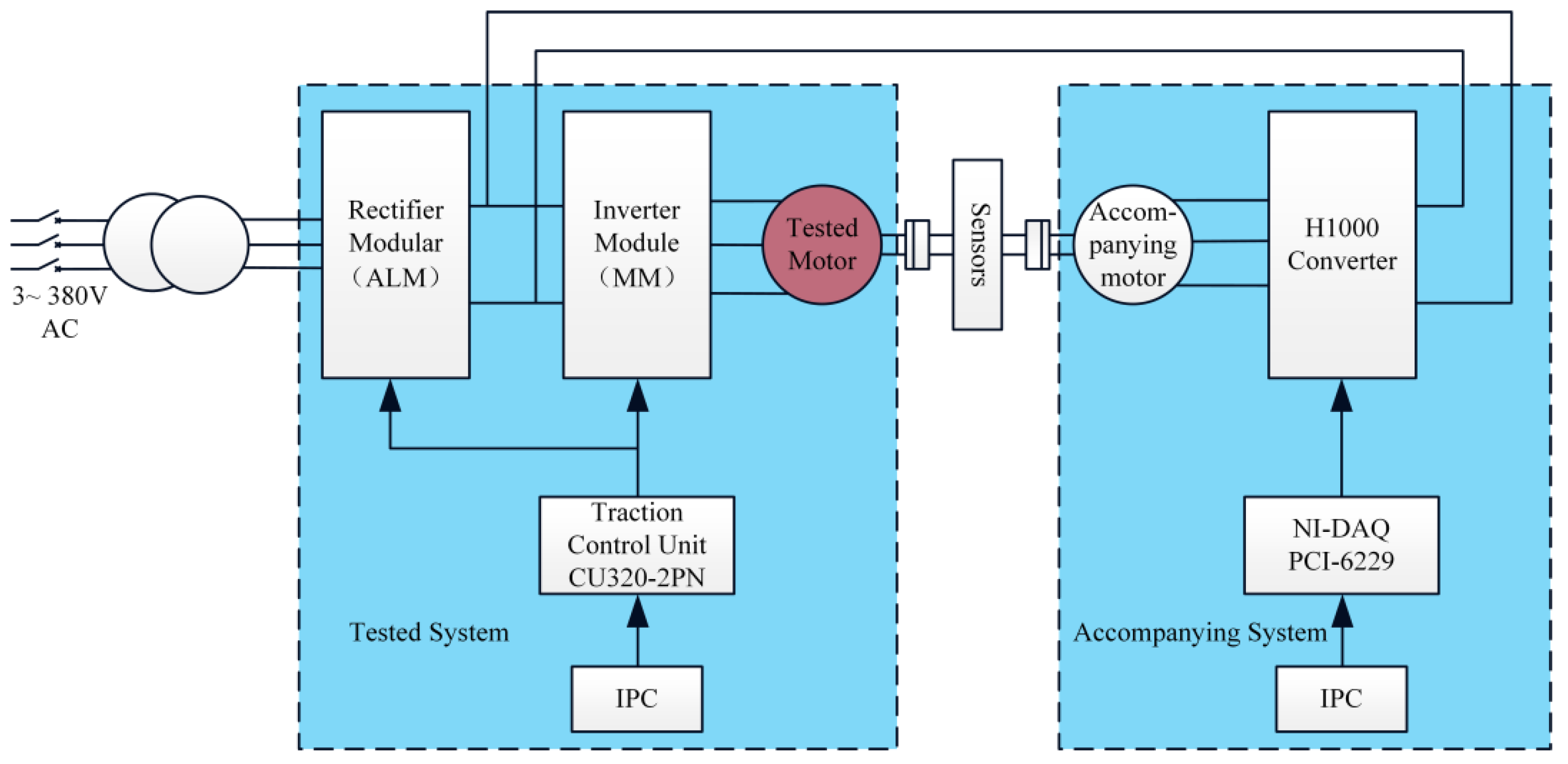
4.1. Overall design of the experimental platform

The experimental data are acquired from the mutual feed electric traction simulation experimental platform, shown in Figure 6. The platform mainly includes the tested system and the accompanying system. The tested system mainly includes S120 variable frequency speed control system and the tested motor. S120 controls the tested motor to operate according to the experimental conditions. S120 system mainly includes the CU320-2PN control unit, ALM rectifier, and MM inverter modules. The accompanying system mainly includes the accompanying motor and the H1000 converter. The PCI-6229 NI-DAQ gives the H1000 converter work instructions. The DC power supply of the tested system is obtained from the DC link of the accompanying system. When the tested motor works in the motor state, the accompanying motor works in the generator state. The accompanying system feeds electric energy back to the DC link to realize DC energy mutual feedback. The experimental platform has the advantages of energy saving, less pollution to the power grid, flexible experimental conditions design, etc.

Figure 7 shows the main parts of the experimental platform. The tested motor is a three-phase AC asynchronous squirrel-cage motor with three-phase winding taps pulled out, whose parameters are shown in Table 1. The accompanying motor is a normal motor with the same type and power.

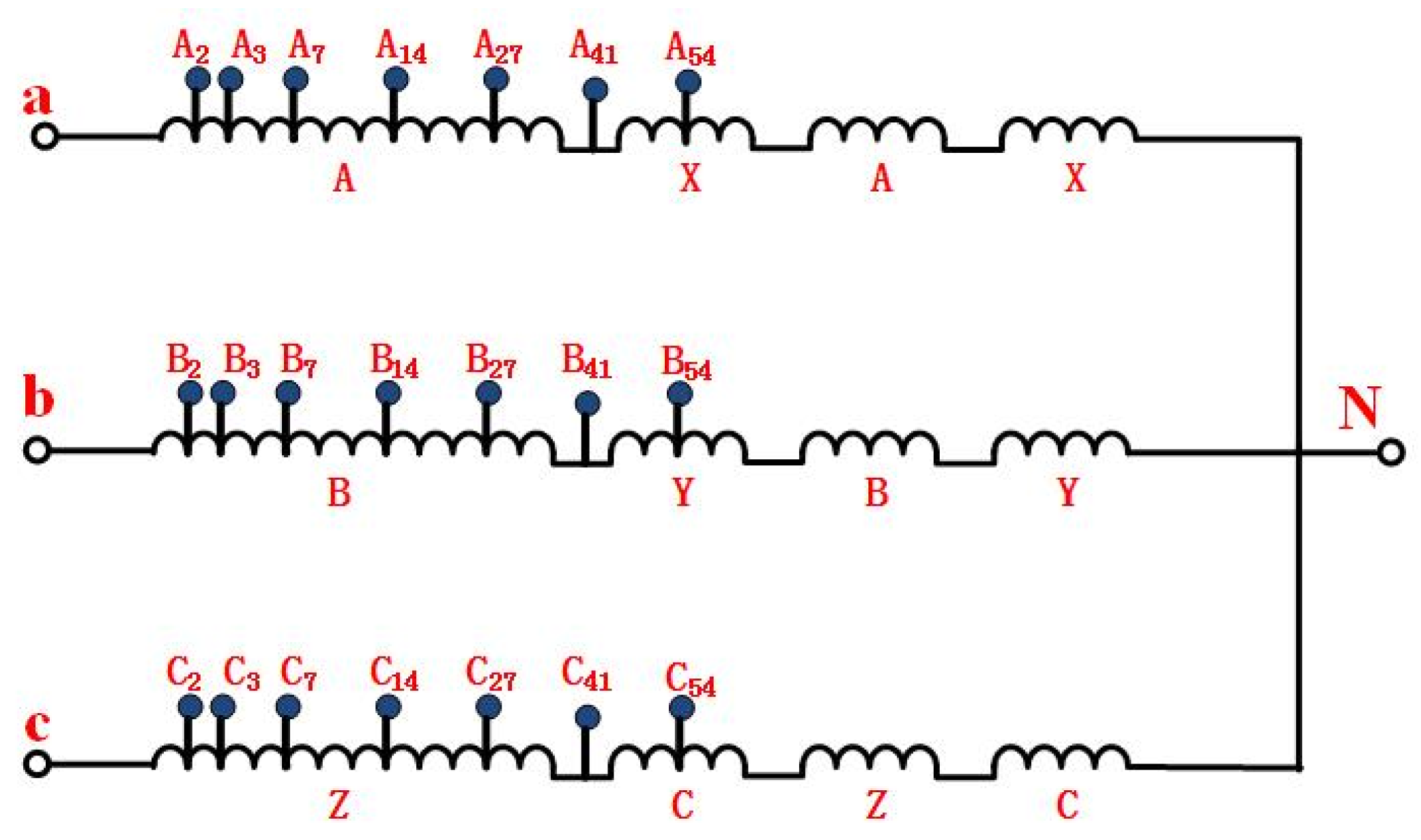
4.2. Setting ITSC faults on tested motor

Figure 8 shows that the winding taps are pulled out at different stator winding turns during manufacturing to simulate the ITSC fault. The taps can be connected externally to simulate the short-circuit fault between different turns. The power resistor simulates the inter-turn resistor between non-metallic short-circuit turns. The vacuum circuit breaker conveniently controls the short-circuit of different turns loop.

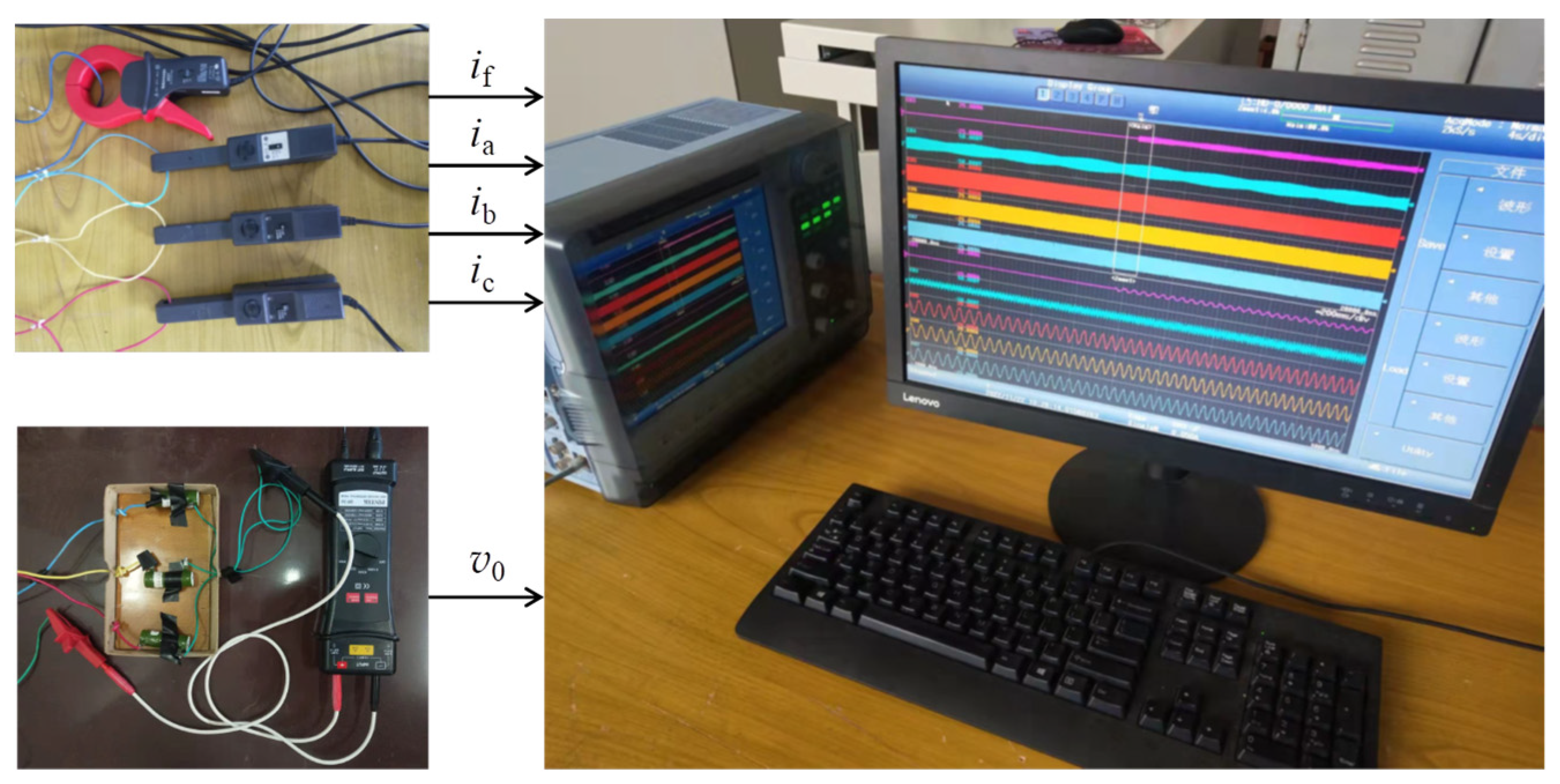
4.3. Signal measurement of the tested motor

The signal measurement is shown in Figure 9. The DL850E ScopeCorder is used for signal measurement. The LPF (low pass filter) is set to 400Hz, and the sampling frequency is 2000Hz. The A621 passive current probe is used to collect the inter-turn current. This current cannot be measured in the actual application. If the inter-turn current is too large, it will generate heat quickly to burn the motor. E3N active current probe is used to measure the three-phase current of the tested motor. The DP-50 voltage probe is used to measure the ZSVC using the measurement circuit as shown in Figure 2. The ZSVC measurement balanced resistors are three 15kΩ (1kW) power resistors.

5. Analysis of ITSC Fault Diagnosis Model Based on Experimental Samples

During the experiment, the S120 converter system controlled the tested motor to operate in the torque control mode, and the tested motor output a fixed electromagnetic torque. The H1000 converter controlled the accompanying motor according to the speed control mode, and the accompanying motor ran at a fixed speed. This experimental operation mode can simulate the steady operation conditions of EMU traction or electric braking at different speeds and torques.

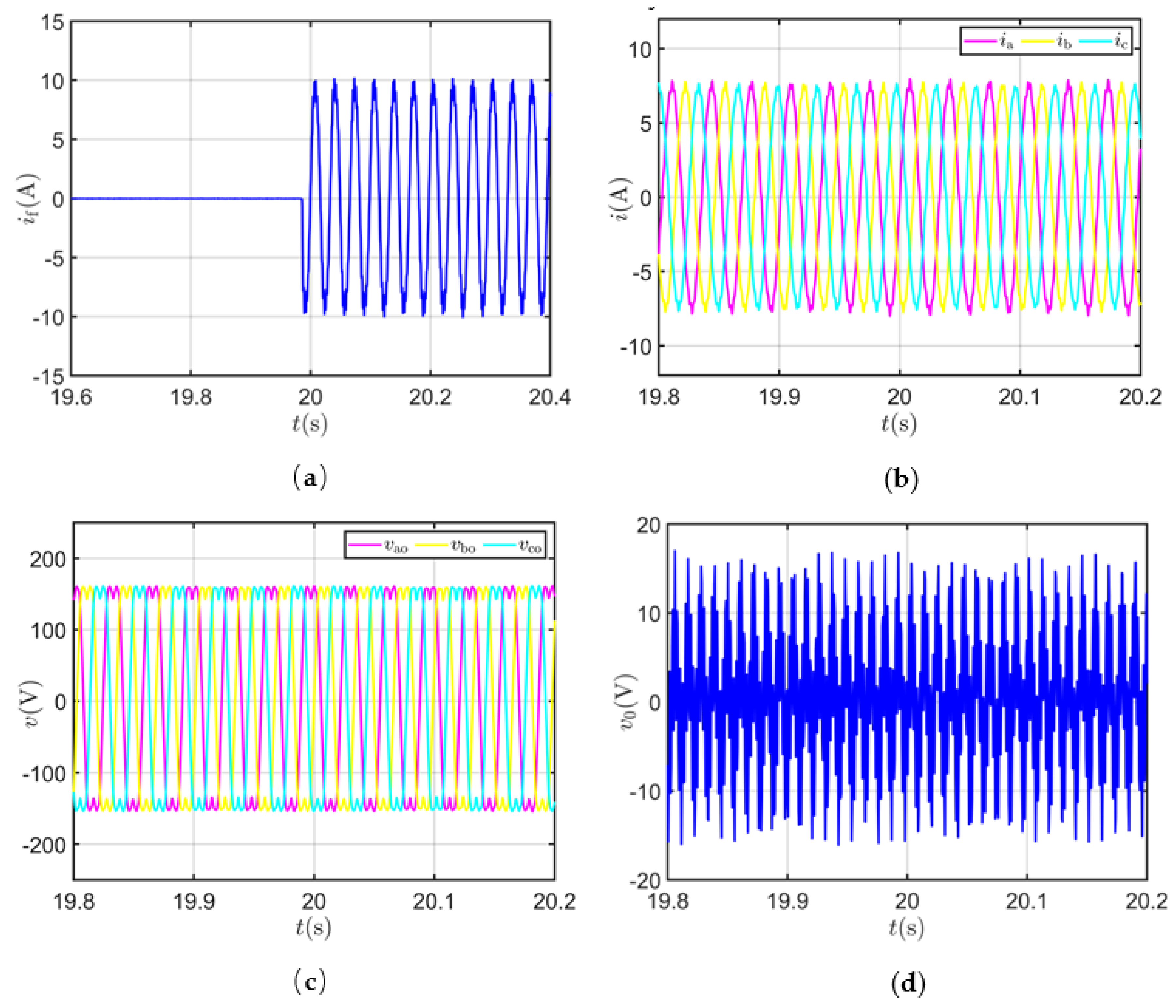
5.1. Analysis of motor signal with ITSC fault

The tested fault motor ran with 900rpm rotating speed, 10Nm electromagnetic torque, 12 short-circuit turns in the a-phase stator winding, and 1Ω inter-turn resistor. The insulation fault occurred at around 20s. It can be seen from Figure 10a that when the stator winding ITSC fault occurs, a sinusoidal inter-turn current with the same fundamental frequency as the power supply will be generated between the short-circuit turns. Figure 10b shows the three-phase current before and after the ITSC fault. Although the amplitude of the short-circuit current has reached about 10A, it has little impact on the three-phase current. Figure 10c shows the three-phase voltage output by the converter after the 400Hz LPF filter, and the output waveform conforms to the saddle waveform of SVPWM. Figure 10d shows the ZSVC before and after the ITSC fault, and the ZSVC will be studied and analyzed later.

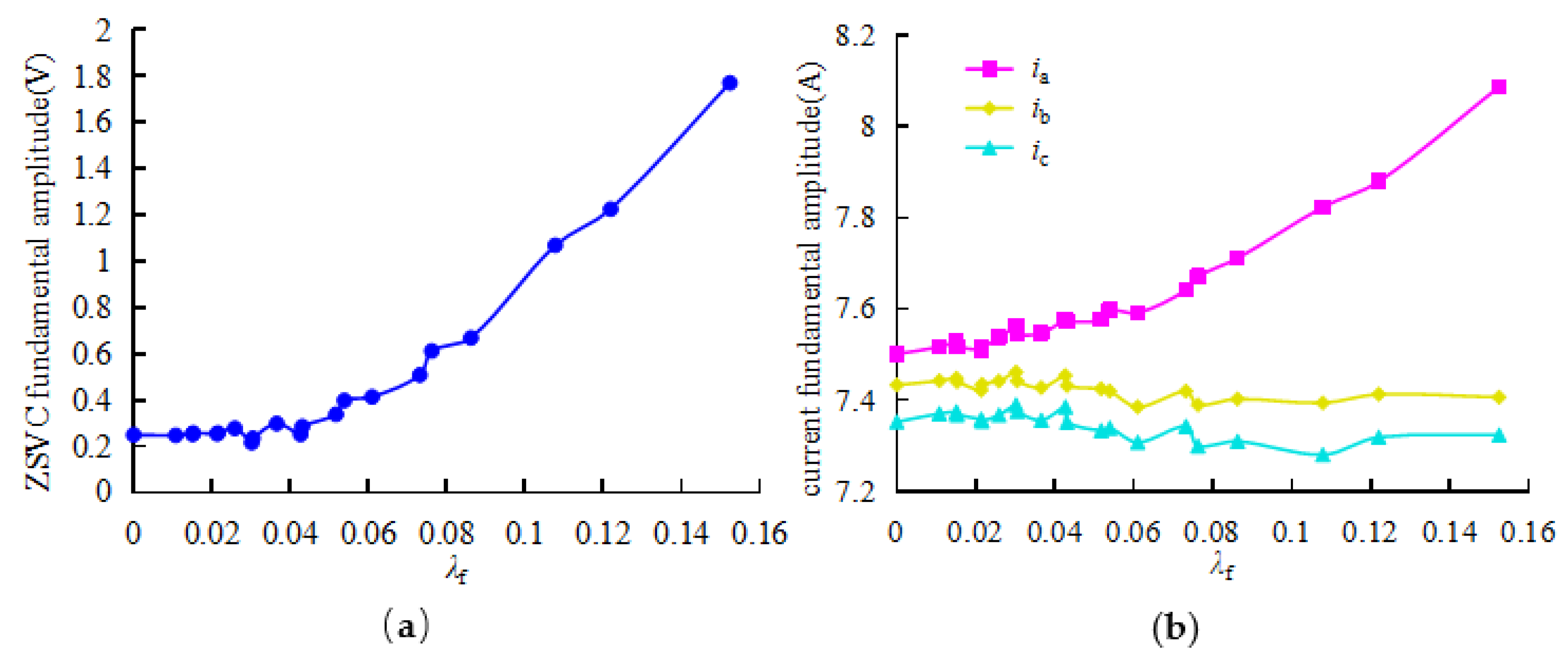
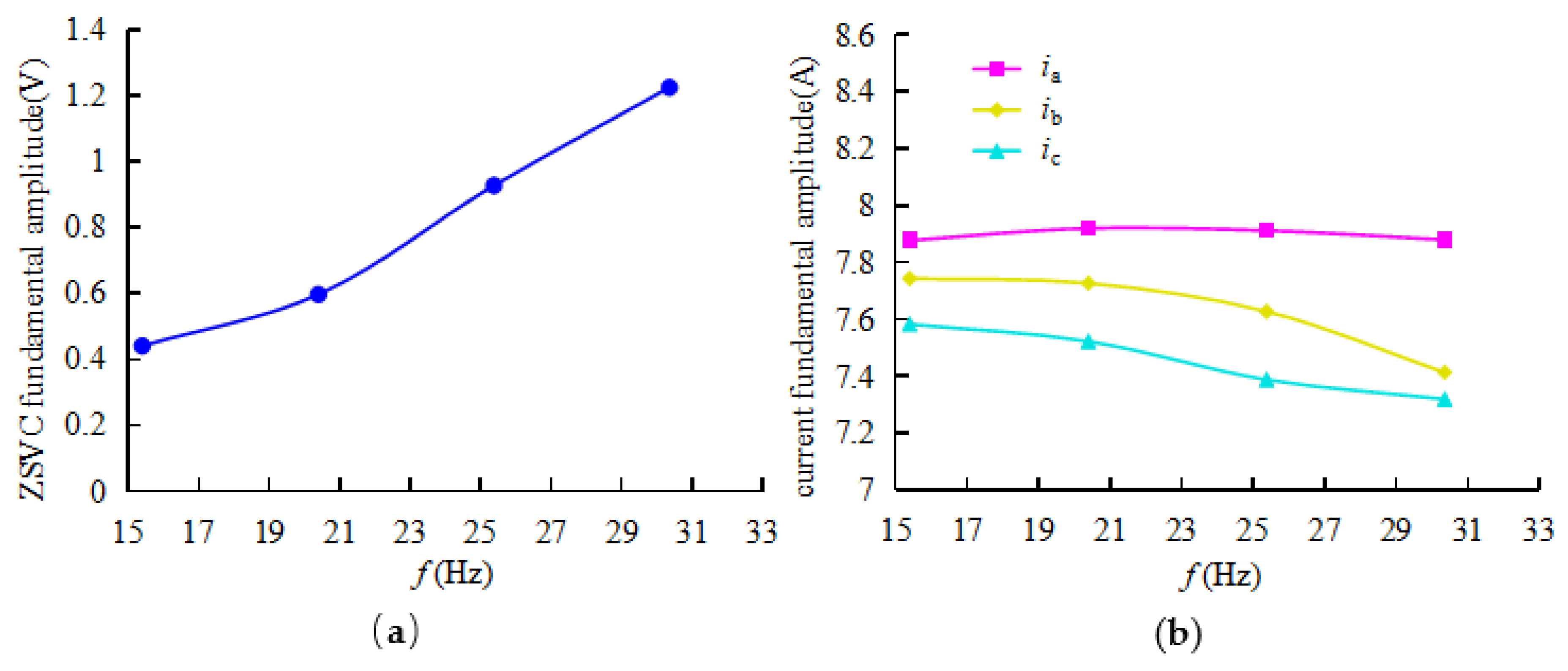
5.2. Analysis of ITSC fault features

The tested motor setting speed was 900rpm, and the setting electromagnetic torque was 10Nm. There was an ITSC fault in a-phase winding. The frequency of the ZSVC fundamental component, the fundamental amplitudes of ZSVC and the three-phase current were calculated using the apFFT time-shift spectrum correction algorithm with double Hanning windows. Based on Formula(11), 20 different indexes λ_f were calculated according to 5 different numbers of short-circuit turns and 4 different inter-turn resistance, as shown in Table 2.

Figure 11 shows the relation of ZSVC fundamental amplitude with fault degree index λ_f. It can be seen from Figure 11a that the ZSVC fundamental amplitude of the tested motor increases with the fault degree index λ_f. The fundamental amplitude of the ZSVC was about 0.2V under normal conditions, mainly caused by the asymmetry of the three-phase winding. It can be seen from Figure 11b that the fundamental amplitude of a-phase current increases with the ITSC fault degree. The b-phase and c-phase currents change little. Similarly, due to the unbalance of the three-phase winding, the three-phase current is unbalanced under normal conditions.

The electromagnetic torque was set to 10Nm， and the ITSC fault degree index λ_f was 0.07317. The influence of the fundamental frequency on the ZSVC and three-phase current was analyzed at 4 different speeds. It can be seen from Figure 12a that in the process speed regulation, the fundamental frequency changes with the experimental system setting speed. According to the control characteristics of variable frequency speed regulation, the three-phase voltage increases linearly with the increase in speed. The ZSVC also increases with the tested motor's fundamental frequency under the same λ_f. Figure 12a shows that the a-phase current does not change much, but the b-phase and c-phase currents decrease significantly with the increase of the fundamental frequency. The asymmetry of the three-phase current becomes more and more prominent.

According to the analysis above, the ZSVC fundamental component amplitude and the three-phase current asymmetry increases with the ITSC fault degree under fixed electromagnetic torque and speed. The three-phase current amplitude can reflect the electromagnetic torque value, and the speed is approximately linear with the fundamental frequency. Therefore, the ZSVC fundamental frequency, the fundamental amplitudes of ZSVC and the three-phase current are selected as the features to establish the ITSC fault diagnosis model.

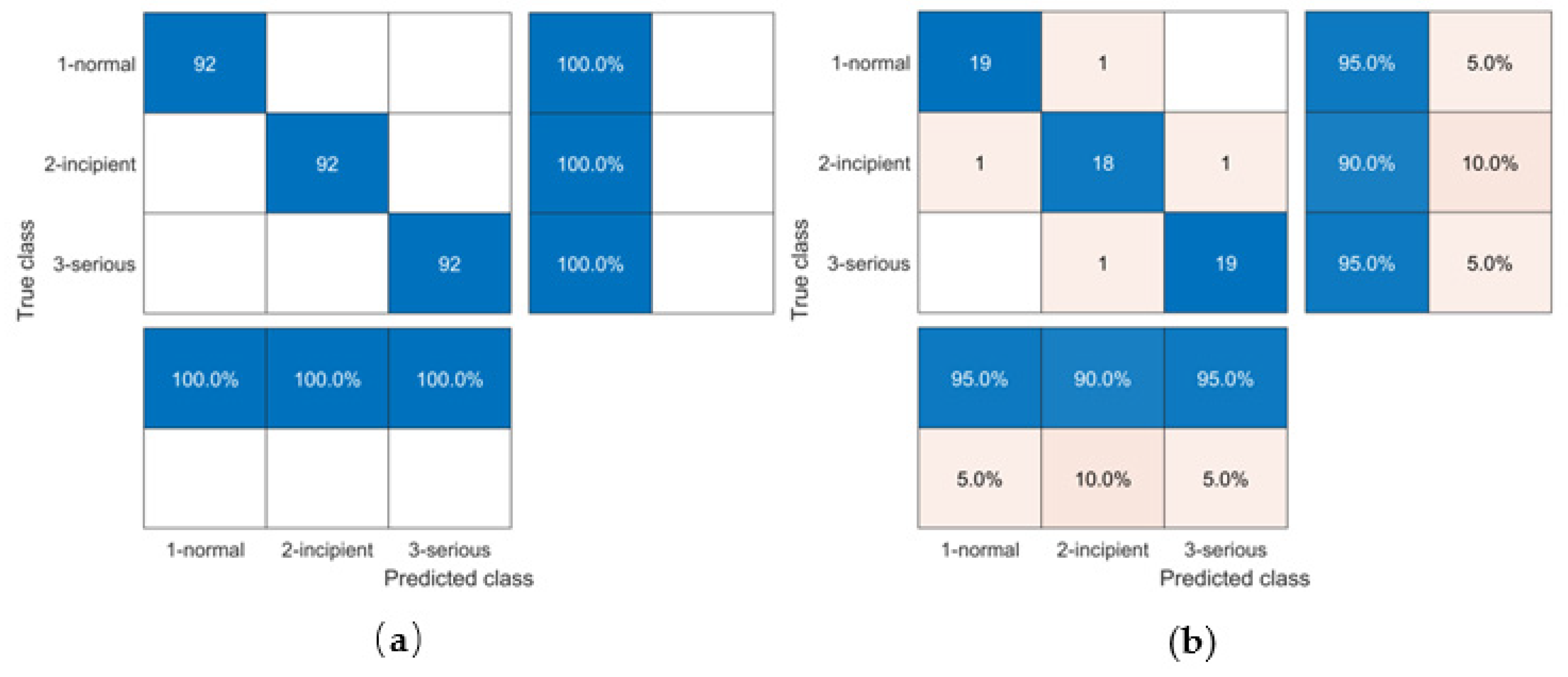
5.3. Analysis of SVM ITSC Fault Diagnosis Model Performance

The tested motor's data acquisition conditions are shown in Table 3. The tested motor with each fault degree index operated under 4 different speeds and electromagnetic torques. There were 20 different ITSC fault degree λ_f samples under each speed and electromagnetic torque, as shown in Table 2. So 320 fault samples were obtained. The samples with 0.03018≤λ_f＜0.06098 were defined as incipient ITSC fault samples. The samples with 0.06098≤λ_f were defined as serious ITSC fault samples. Thus the ITSC fault samples were divided into 112 incipient and 112 serious ITSC fault samples. Under each different speed and electromagnetic torque, 7 normal samples needed to be acquired. So 112 normal samples were obtained. Selected 92 samples from each category as training samples to establish an SVM-based ITSC fault diagnosis model. Selected 20 samples from each category as the test samples to test the fault diagnosis model. The grid search range was a=[-5,5],b= [-5,5].The parameter K was 3 in the K-CV method.

Figure 13 shows the prediction results of the SVM-based ITSC fault diagnosis model on the experimental samples. The model's prediction accuracy on the training data set is 100%, which can correctly detect and evaluate the fault degree of the ITSC fault. The prediction accuracy on the test data set is 93.33%. The confusion matrix in the test set shows that the misclassifications occur between the normal and the incipient samples, between the incipient and the serious fault samples. There is no misclassification between the normal and the serious fault samples.

6. Conclusions

The ITSC fault diagnosis of the asynchronous traction motor significantly ensures the EMU's safe operation and saves maintenance costs. The non-metallic ITSC fault degree assessing index λ_f was proposed based on the short-circuit thermal power. The index λ_f is related to the number of short-circuit turns and inter-turn resistance. ApFFT time-shift phase difference spectrum correction with double Hanning windows can accurately calculate the fundamental frequency of ZSVC, the fundamental amplitudes of ZSVC, and the three-phase current when the fundamental frequency of the vector control motor is unknown. The five parameters are used as fault features. SVM is used as the ITSC fault diagnosis model, and the SVM model hyper-parameters C and g are optimized by K-CV and the grid search method. The proposed method was verified by the EMU electric traction simulation experimental platform. According to the fault degree index λ_f proposed in this paper, the experimental samples were divided into three categories: normal, incipient fault, and serious fault. The prediction accuracy of the SVM model on the training data set was 100%, and the prediction accuracy on the test data set was 93.33%. There was no misclassification between normal samples and serious faults. The EMU traction motors work at different speeds and torque points during operation. The prediction results of different steady-state operating points can be integrated to improve the accuracy of the fault diagnosis model.