An Improved Salp Swarm Algorithm for Solving Node Coverage Optimization problem in WSN

1. Introduction

Wireless sensor network (WSN) is self-organizing network which is composed of a large number of low-power sensor nodes by wireless communication [1,2]. These sensor nodes have the ability of communication, calculation and perception which are easy to be deployed and have low cost and power consumption [3]. In recent years, WSN has been widely used in military, industrial, environmental detection, disaster relief, and other fields [4,5,6,7]. It provides great convenience for human life. By deploying it at scale within a region, information within a region can be collected and processed. The aim of the present study is to deploy a minimum number of sensor nodes to monitor a specific target area of interest. When wireless sensor network nodes need to be deployed to complex and harsh environments, random throwing deployment are often used to deploy wireless sensor network nodes. However, the random throwing deployment is easy to form coverage blind areas, resulting in low node utilization, waste of resources, and degradation of detection quality [8]. Therefore, it is necessary to optimize the coverage mode of wireless sensor network, so that the sensor nodes are evenly distributed and blind areas of the network coverage are reduced, in order to improve the coverage efficiency of wireless sensor network and reduce network construction costs.

In recent years, many new intelligent optimization algorithms have been proposed. Many scholars have improved them and applied them to the deployment optimization problems of WSN, and have obtained good results [9,10,11,12,13]. Literature [14] proposes an improved COOT Bird Algorithm to optimize the deployment of WSN nodes, which solves the problem that the original algorithm is easy to fall into local optimization and improves the coverage of the algorithm. Literature [15] used the ALO algorithm to address the problems of uneven node distribution and incomplete coverage in node deployment. Literature [16] proposed a new 3D improved virtual force coverage (3D-IVFC) algorithm for 3D coverage of nodes in WSN. It improves the coverage of WSN and shortens the deployment time of sensor nodes. There are still problems such as premature convergence, low local search ability, and inability to balance global search and local search ability. So, the node coverage can still be further improved.

Salp Swarm Algorithm (SSA) is a new type of swarm intelligence optimization algorithm proposed by Australian scholar Mirjalili in 2017 [17]. It has the advantages of less parameters and better balance between the local search and global search capabilities. This algorithm is widely used in path planning, image processing, photovoltaic systems and other fields. However, the original SSA algorithm also has the disadvantages of relying on the initial population, slow convergence speed, and easy to fall into local optimization. In this regard, scholars at home and abroad have proposed many improved SSA algorithm. Literature [18] introduces a novel hybrid algorithm inspired by the perturbation weight mechanism. The algorithm overcomes the the problems of poor real-time performance and low precision of the basic salp swarm algorithm. Literature [19] integrates random pair multiple leadership and simulated annealing mechanism in the SSA, so that the SSA can be applied to complex multimodal problems. The literature [20] adds an inertia weight to the leader update formula of the SSA. It improves the classification accuracy and feature reduction ability of the algorithm compared with other algorithms.

Because the original SSA algorithm has slow convergence speed and easily falls into local optimum. In order to better apply it to the deployment optimization problem of WSN, this paper proposes an adaptive salp swarm algorithm (ATSSA) based on the tent chaotic sequence and T-distribution mutation. The ATSSA is applied to node deployment optimization of WSN to improve the coverage rate of WSN sensor nodes.

2. WSN Node Coverage Model

This article assumes that the target area A monitored by the wireless sensor network is a rectangle with an area of $L\times W{\mathrm{m}}^2$. It is a two-dimensional area. The set of nodes can be denoted as $M=\{m_1,m_2,m_3,\mathrm{...},m_n\}$,, and the coordinates of each node $m_i$ can be denoted as $(x_i,y_i)$, where $i=1,2,3,\mathrm{...},n$.

For a two-dimensional wireless sensor network, its network model is as follows:

• Each sensor node has the same parameters, structure, and communication capabilities.
• Each sensor node has normal communication functions, sufficient energy and can move freely.
• Each sensor node can obtain data information and update the location information in time.
• The sensing radius of each sensor node is $R_s$ and the communication radius is $R_c$, both in units of meters, and $R_c\ge 2R_s$.

The sensing range of a sensor node is represented by a circular area with the node at its center and the radius $R_s$ equal to the sensing range. In this two-dimensional wireless sensor network (WSN) monitoring area, if there are n target monitoring points, the set of target monitoring points can be denoted as $N=\{n_1,n_2,n_3,\mathrm{...},n_z\}$, and the location coordinate of each target point $n_j$ is $(x_j,y_j)$, where $j=1,2,3,\mathrm{...},z$. If the distance between a target node $n_j$ and any sensor node is less than or equal to the sensing radius $R_s$, it means that $n_j$ is covered. The Euclidean distance between sensor node $m_i$ and target monitoring point $n_j$ is defined as:

$$d(m_i,n_j)=\sqrt{{(x_i-x_j)}^2+{(y_i-y_j)}^2}$$

(1)

The node-sensing model in this paper is a Boolean sensing model. When the sensing radius $R_s$ is greater than or equal to $d(m_i,t_j)$, the probability that the target is monitored is 1; otherwise, the probability that the target is monitored is 0. If the probability that the target point $n_j$ to be monitored is covered by the sensor node $m_i$ be p, then

$$P(m_i,n_j)=\{\begin{array}{c}1{\mathrm{R}}_s\ge d(m_i,n_j)\\ 0{\mathrm{R}}_s<d(m_i,n_j)\end{array}$$

(2)

In this 2D wireless sensor network (WSN) monitoring area, sensor nodes can collaborate with one another. Each monitoring point can be covered by multiple sensors simultaneously, so the probability that any monitoring target point $n_j$ is jointly sensed is:

$$P(M,n_j)=1-{\displaystyle \prod _{i=1}^k(1-P(m_i,n_j))}$$

(3)

The coverage rate can be defined as the ratio of the coverage area of all sensor nodes within the monitoring area to the total area of the monitoring area. Therefore, in the case of a 2D WSN monitoring area, the coverage rate can be calculated as follows:

$$Cov=\frac{{\displaystyle \sum _{j=1}^{z}P(M,n_j)}}{L\times W}$$

(4)

The node coverage optimization problem for WSN can be described by an integer linear programming model, the model is as follows:

$$MaxCov=\frac{{\displaystyle \sum _{j=1}^{z}P(M,n_j)}}{L\times W}$$

(5)

$$s.t.\{\begin{array}{cc}{\displaystyle \sum _{j=1}^{z}P(M,n_j)\ge 0}& 1\le j\le z\\ {\displaystyle \sum _{j=1}^{z}P(M,n_j)\le L\times W}& 1\le j\le z\\ d(m_i,n_j)\le R_s& 1\le \mathrm{i}\le k,1\le j\le z\end{array}$$

(6)

3. Salp Swarm Algorithm

The inspiration of the intelligent optimization algorithm of salps group comes from the aggregation behavior of salps group in the ocean, namely salps chain. Salp squirts feed on the phytoplankton in the water and move through the water by breathing in and spewing out seawater. The SSA algorithm mimics the foraging behavior of the organism. The population of SSA algorithm is divided into two groups. These two groups are leader and followers. The leaders take the position at the front of the chain, while the remainders of salps are known as followers. dim refers to the number of variables or dimensions in a given problem, and x represents the position of a salp. F denotes the food source, which is the target of the swarm in the search space.The leader updates his position according to the following equation：

$$x_j^i=\{\begin{array}{c}{F}_j+c_1((u{b}_j-l{b}_j)c_2+l{b}_j),c_3\ge 0.5\\ F_j-c_1((u{b}_j-l{b}_j)c_2+l{b}_j),c_3<0.5\end{array}$$

(7)

Where, $F_j$ is the food source in the jth dimension, $u{b}_j$ and $l{b}_j$ is the upper and lower bounds of the search space, $C_2$ and $C_3$ is a random number between [0,1], $C_2$ determines the length of the individual's next position movement, and $C_3$ determines whether the movement direction is positive or negative. $C_1$ is the main parameter that balances the ability to search and exploit in evolution, and its formula is as follows:

$$c_1=2\exp (-{(\frac{4T}{T_{\max }})}^2)$$

(8)

where T is the current iteration number, and $T_{\max }$ is the maximum number of iterations. The follower position is updated according to Newton's law of motion, which is formulated as follows.

$$x_j^i=\frac{1}{2}a{t}^2+v_0\Delta t+x_j^{i-1}$$

(9)

where, $x_j^{i-1}$ is the position of the $i-1$th salp individual in the j-dimensional space, $i\ge 2$, $\Delta t$ is time, v₀ is initial velocity, and acceleration is as follows:

$$a=(v_{final}-v_0)/\Delta t$$

(10)

Since $\Delta t$ is the difference between the two iteration times, unit time is desirable, and the initial velocity $v_0=0$, Equation (7) can be expressed as follows:

$$x_j^i=\frac{1}{2}(x_j^i+x_j^{i-1})$$

(11)

4. Improved Salp Swarm Algorithm

4.1. Population initialization and the chaotic tent map

Chaotic variables have the characteristics of randomness, ergodicity and regularity, which have been used by many scholars to optimize search problems [21]. Chaotic variables can not only effectively maintain the diversity of populations, but also help the algorithm to jump out of the local optimal and improve the global search ability. The initial population is evenly distributed in the search space, which is of great help to the algorithm optimization. When the SSA population is initialized, most of them are randomly generated. So, using chaotic sequence to initialize the SSA population can improve the convergence speed of SSA algorithm.

The basic idea of chaotic sequences is to generate sequences between [0,1] by mapping, and then transform them into the search space of individuals. Among various chaotic models, tent map can generate better uniform sequences. Therefore, this paper uses tent chaotic sequence to initialize the population of SSA algorithm, and its formula is as follows:

$$y_{j+1}^i=\{\begin{array}{c}\mu y_j^i,y_j^i<0.5\\ \mu (1-y_j^i),y_j^i\ge 0.5\end{array}$$

(12)

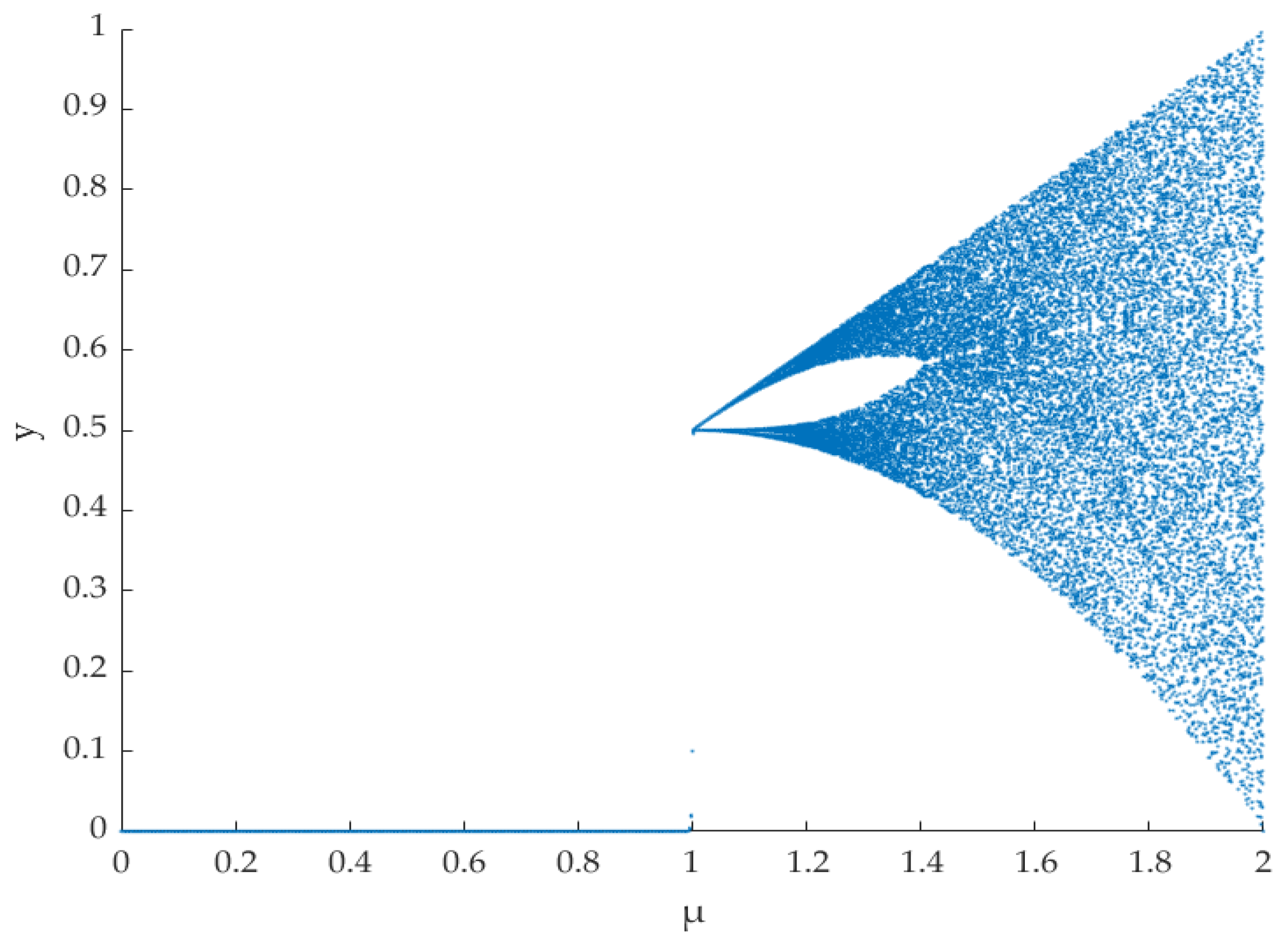
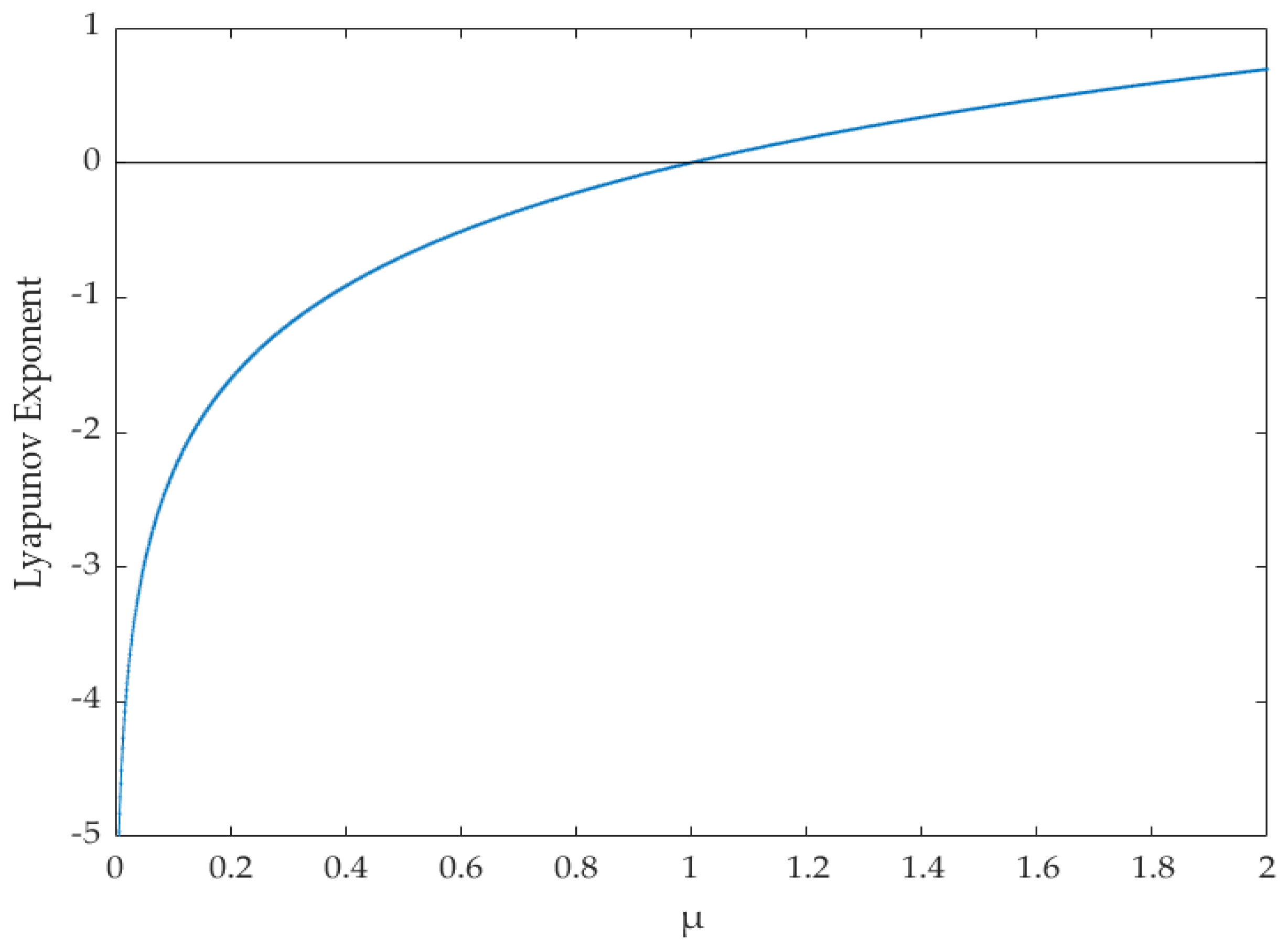
As shown in Figure 1 and Figure 2, $\mu \in （0.2]$ is a chaos parameter that controls tent chaotic sequence. According to the value of the parameter µ, the bifurcation diagram and Lyapunov exponential curve of the chaotic tent map are drawn. In Figure 1, it can be seen that when $\mu =2$ the chaotic tent map produces an approximately uniformly distributed chaotic sequence. In Figure 2, when $\mu >1$,the Lyapunov exponent curve is greater than 0. So, in this article, $\mu =2$. $i=1,\mathrm{2...},T_{tent}$ represents the number of iterations, $j=1,2,\mathrm{...},N_{tent}$ represents the population size.

In this paper, the chaotic sequence is set to N d-dimensional arrays, where d is the dimension of the salp swarm population. After iterating for i times, yi j is obtained. It is inversely mapped to the corresponding individual search space, and the variable $x_j^i$ is obtained, and the formula is as follows:

$$x_j^i=lb+(ub-lb)y_j^i$$

(13)

4.2. Positions updating

4.2.1. Positions updating of the leaders and adaptive t-distribution

The Gaussian Distribution (GD) and Cauchy Distribution (CD) are two boundary special cases of the T-distribution [22,23]. In terms of performance, the Gaussian distribution has strong local development ability, Cauchy distribution has strong global search ability, and the T-distribution has the advantages of both Gaussian distribution and Cauchy distribution [24]. The formula of probability density function of T-distribution with the adaptive parameter $\alpha$ is as follows:

$$p_t(x)=\frac{\Gamma (\frac{\alpha +1}{2})}{\sqrt{\alpha \pi }\Gamma (\frac{\alpha }{2})}{(1+\frac{x^2}{\alpha })}^{-\frac{\alpha +1}{2}},-\infty <x<+\infty$$

(14)

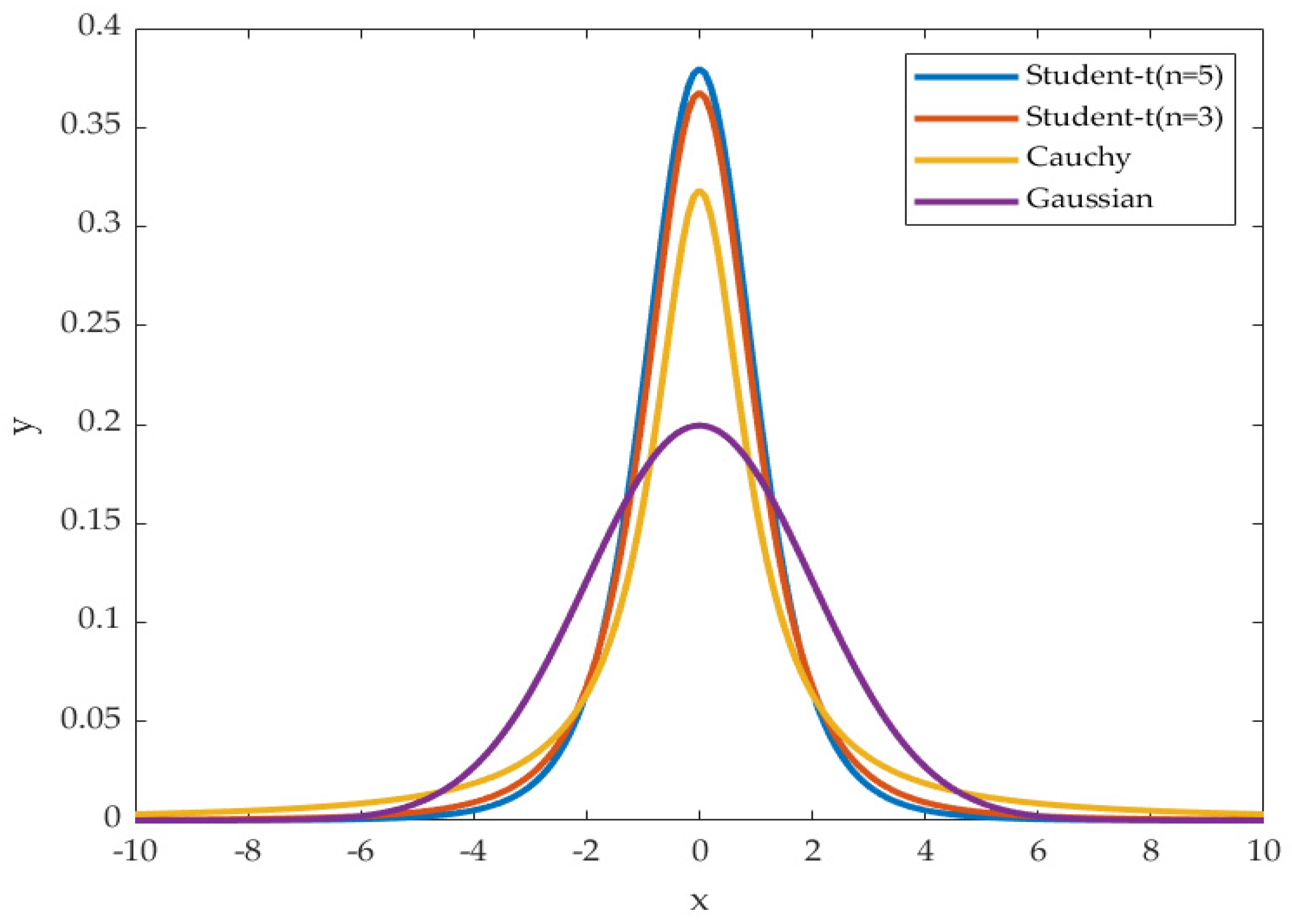
The T-distribution degree-of-freedom parameter $\alpha$ is set to the number of iterations. When T=1, the T-distribution is the standard Cauchy distribution. When the iteration starts, the T-distribution and the Cauchy distribution are more similar, and the global search ability is stronger. With the increase of T, the T-distribution gradually changes from Cauchy distribution to transforms into a Gaussian distribution, and the local search ability is stronger at this time, and the convergence speed of the algorithm is accelerated.

Figure 3 shows that the mutation probability at both ends of the t-distribution curve with a degree of freedom parameter of 5 is smaller than that of the curve with a degree of freedom parameter of 3. The mutation probability near the origin with the degree-of-freedom parameter 5 is greater than the mutation probability near the origin with the degree-of-freedom parameter 3. From the above analysis, it can be seen that with the increase of the degree-of-freedom parameters, the probability of large disturbances in the early stage of iteration is greater than that in the late stage of iteration, so it has better global exploration ability. Compared with the early iteration, the probability of small disturbance is greater in later stage. In this stage, the curve of T-distribution has better local exploration ability and accelerates the convergence speed of the algorithm.

The mutation strategy is a common improvement strategy used to jump out of the local optimal solution of the meta-heuristic algorithm. In this article, adaptive T-distribution mutation is used to enhance the ability of the SSA to jump out of local optimal solutions, and accelerate the convergence speed of SSA. The update formula of the leader of the SSA algorithm is improved with the T-distribution., and the parameter $C_2$ is replaced by ${(t(T)/\beta )}^2$, the new leader position update formula after replacement is as follows:

$$x_j^i=\{\begin{array}{c}{F}_j+c_1((u{b}_j-l{b}_j){(\frac{t（\mathrm{T}）}{\beta })}^2+l{b}_j)\hspace{0.33em}{c}_3\ge 0.5\\ F_j-c_1((u{b}_j-l{b}_j){(\frac{t（\mathrm{T}）}{\beta })}^2+l{b}_j)\hspace{0.33em}{c}_3<0.5\end{array}$$

(15)

where $\beta$ is the step control parameter, which controls the displacement length within 1, and this paper $\beta =3$.

4.2.2. Positions updating of the followers

The SSA performs local search by updating the follower location. In the SSA, the number of individual leader and follower are always split equally. In the early stage of algorithm iteration, the global search capability of the algorithm is increased by adjusting the update formula of followers. With the continuous iteration of the algorithm, the local search ability of the algorithm is gradually restored. Therefore, this paper adopts an adaptive strategy to update the follower's position, which improves the follower's global search ability in the early stage and ensures its local search ability in the later stage. The improved follower position update formula is as follows:

$$x_j^i=\frac{1}{2}(1+\omega )((1-\omega )(x_j^i+x_j^{i-1})+\omega P)$$

(16)

where $P$ is an one-dimensional vector whose length is the population dimension $\dim$. Vector $P$ update formula is as follows:

$$P_j=\{\begin{array}{c}{F}_j+c_1\ast ((u{b}_j-l{b}_j){(\frac{t(T)}{\beta })}^2+l{b}_j)\hspace{0.33em}{c}_3\ge 0.5\\ F_j-c_1\ast ((u{b}_j-l{b}_j){(\frac{t(T)}{\beta })}^2+l{b}_j)\hspace{0.33em}{c}_3<0.5\end{array}$$

(17)

$\omega$ is an adaptive parameter that controls whether the follower is affected by the vector P, and its update formula is as follows:

$$\omega =\{\begin{array}{c}1,\hspace{0.33em}\gamma (T_{\max }-T)/T_{\max }>\eta \\ 0,\hspace{0.33em}\gamma (T_{\max }-T)/T_{\max }<\eta \end{array}$$

(18)

where γ is a random number between [0,1], η is the control parameter, which controls whether the follower performs a global search or a local search, the value in this article is 0.3. When ω is 1, the followers’ positions are updated through the vector, and when ω is 0, the follower performs the local search with equation (11).

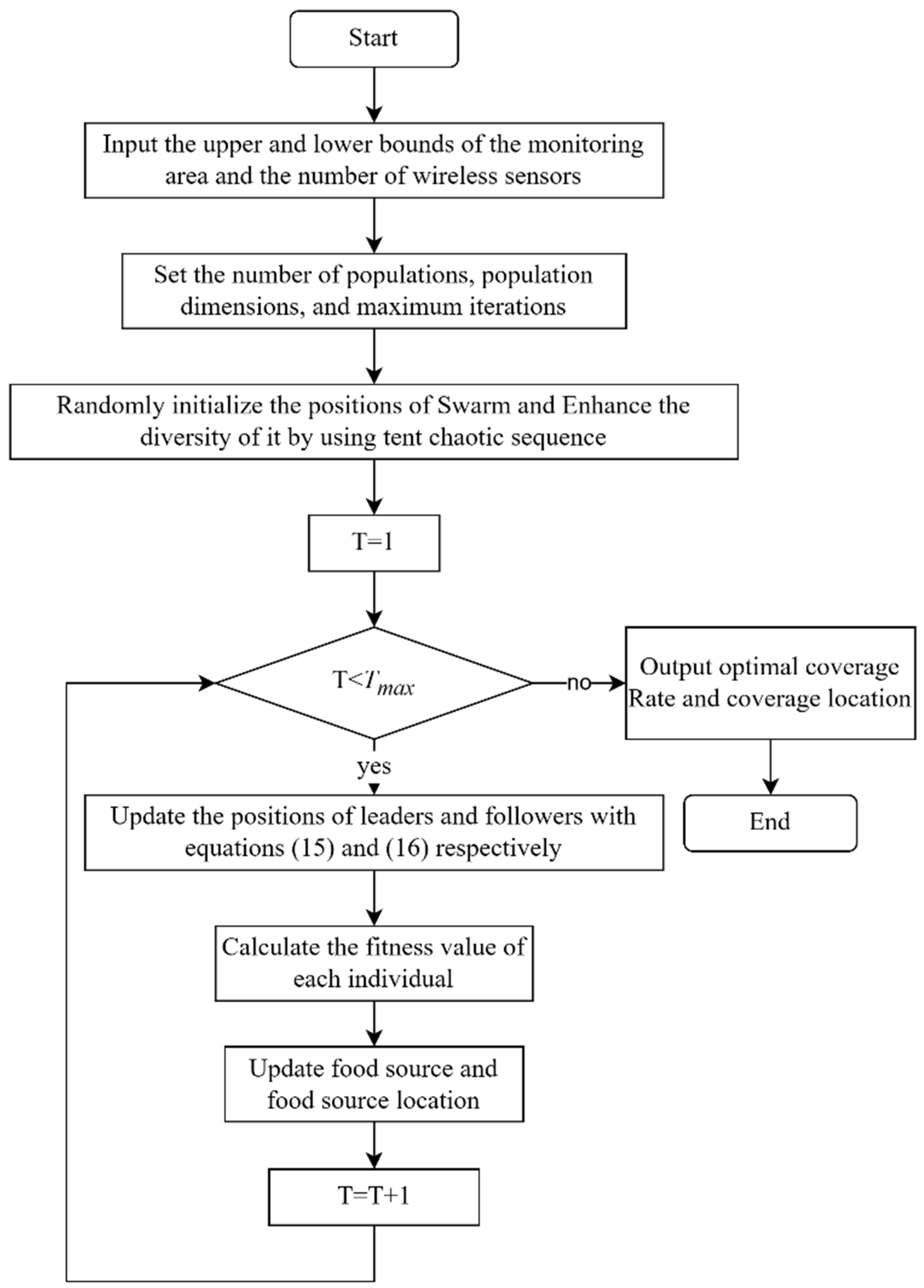
4.3. Implementation Steps of ATSSA

Step 1: Set the parameters of population size n, maximum number of iterations $T_{\max }$, upper bounds ub and lower bounds lb of the detection region, etc.

Step 2: Randomly initialize the positions of Salp Swarm and Enhance the diversity of the population by using the tent chaotic sequence in Equation (11).

Step 3: Take coverage Cov as the objective function, calculate the fitness value of each individual, and find the best individual as the initial food source.

Step 4: Update the position of leaders and followers according to Equation (15) and (16).

Step 5: Calculate the fitness value of each individual of the population, and update the food source and food source location.

Step 6: Determine whether the end condition is reached; if yes, proceed to the next step; otherwise, return to Step 4.

Step 7: The program ends and outputs the optimal fitness value and the best position.

5. Coverage Optimization Strategy

The coverage optimization strategy of WSN based on ATSSA abstracts the coverage optimization problem of WSN into a high-dimensional vector maximum optimization problem of ATSSA with $Cov$ as the objective function. The problem of wireless sensor location optimization in WSN coverage optimization is abstracted into the problem of food source search by the salp swarm. The final food source is the optimal coverage, and the food source is the location of wireless sensor. In the SSA, each individual of the salp swarm is a WSN coverage distribution. If the number of wireless sensors is n, the population dimension of the salp swarm is 2n, where the 2i and 2i-1 represent the ordinate and abscissa of the ith node respectively. The specific strategies are as follows:

Step 1: Input the upper and lower bounds of the monitoring area and the number of wireless sensors.

Step 2: Set the number of populations, population dimensions, and maximum iterations.

Step 3: Randomly initialize the positions of Swarm and Enhance the diversity of it by using the tent chaotic sequence.

Step 4: Update the position of leaders and followers with Equation (15) and (16).

Step 5: Calculate the fitness value of each individual of the population, and update the food source and food source location.

Step 6: Determine whether the end condition is reached; if yes, proceed to the next step; otherwise, return to Step 4.

Step 7: The program ends and outputs the optimal coverage Rate and coverage location.

Figure 4. Flowchart of the ATSSA coverage optimization algorithm.

Figure 4. Flowchart of the ATSSA coverage optimization algorithm.

6. Simulation Experiments and Analysis

In order to verify the effectiveness of the improved strategy of ATSSA algorithm and the performance of the algorithm, this paper sets up two experiments. Experiment 1 applies ATSSA algorithm, SSA algorithm [17], HHO algorithm [25] and WOA algorithm [26] to the coverage optimization of wireless sensor networks, the same parameters are set, and the four algorithms are respectively applied to the coverage optimization of wireless sensor networks to test the performance of ATSSA algorithm. Experiment 2 compares the minimum number of nodes required by each algorithm to achieve a specific coverage rate through experiments, so as to verify whether the coverage optimization of ATSSA algorithm can effectively save the deployment cost of wireless sensor networks.

The experiment is simulated on Windows 10 operating system and Matlab 2019b. The parameters used in the four algorithms are shown in the following table (Table 1):

6.1. Experiment 1

In this experiment, two different target field were set up. It’ s aim is to compare the performance of the ATSSA with the performance of other algorithms.

6.1.1. Target Field 1

The monitoring area is set as 50m×50m, the sensing radius is set as 5m, the communication radius is set as 10m, the number of wireless sensor nodes is set as 40, and the maximum number of iterations is set as 500.

Table 2. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$50\mathrm{m}\times 50\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of sensor nodes	$40$
Number of iterations	$500$

Table 2. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$50\mathrm{m}\times 50\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of sensor nodes	$40$
Number of iterations	$500$

In order to obtain universal results, ten experiments were conducted for each algorithm, and the average was taken as the result.

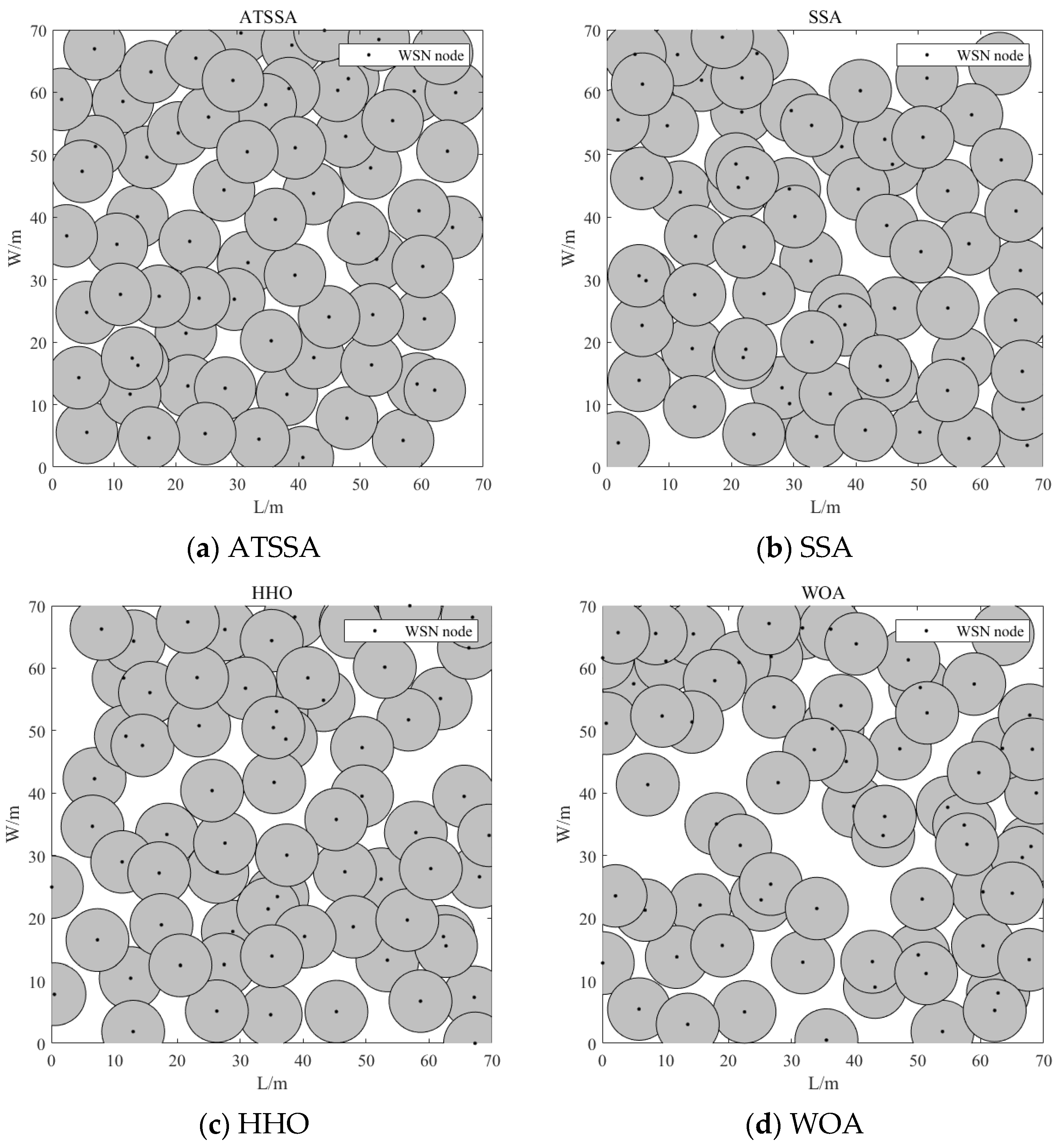
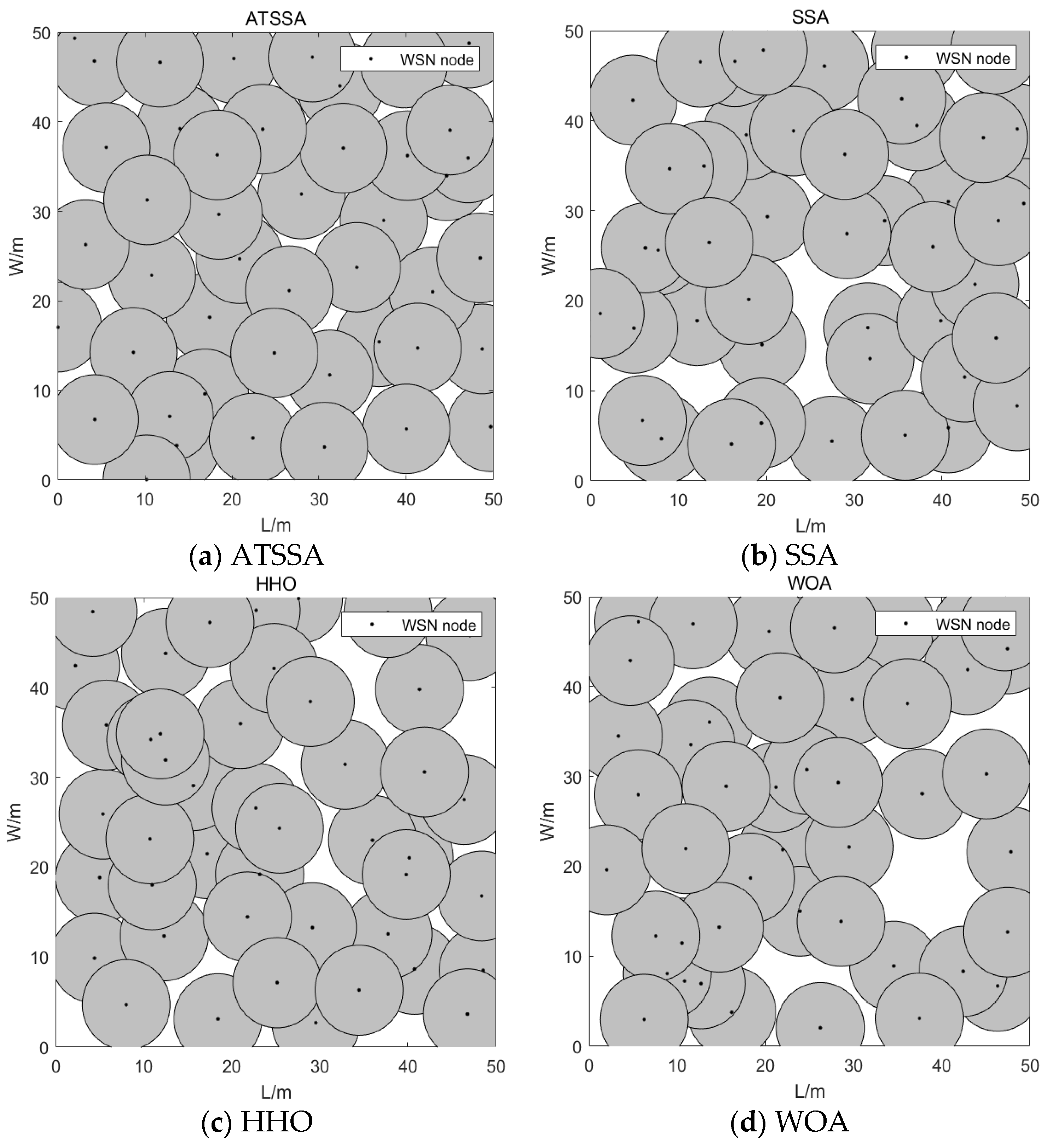
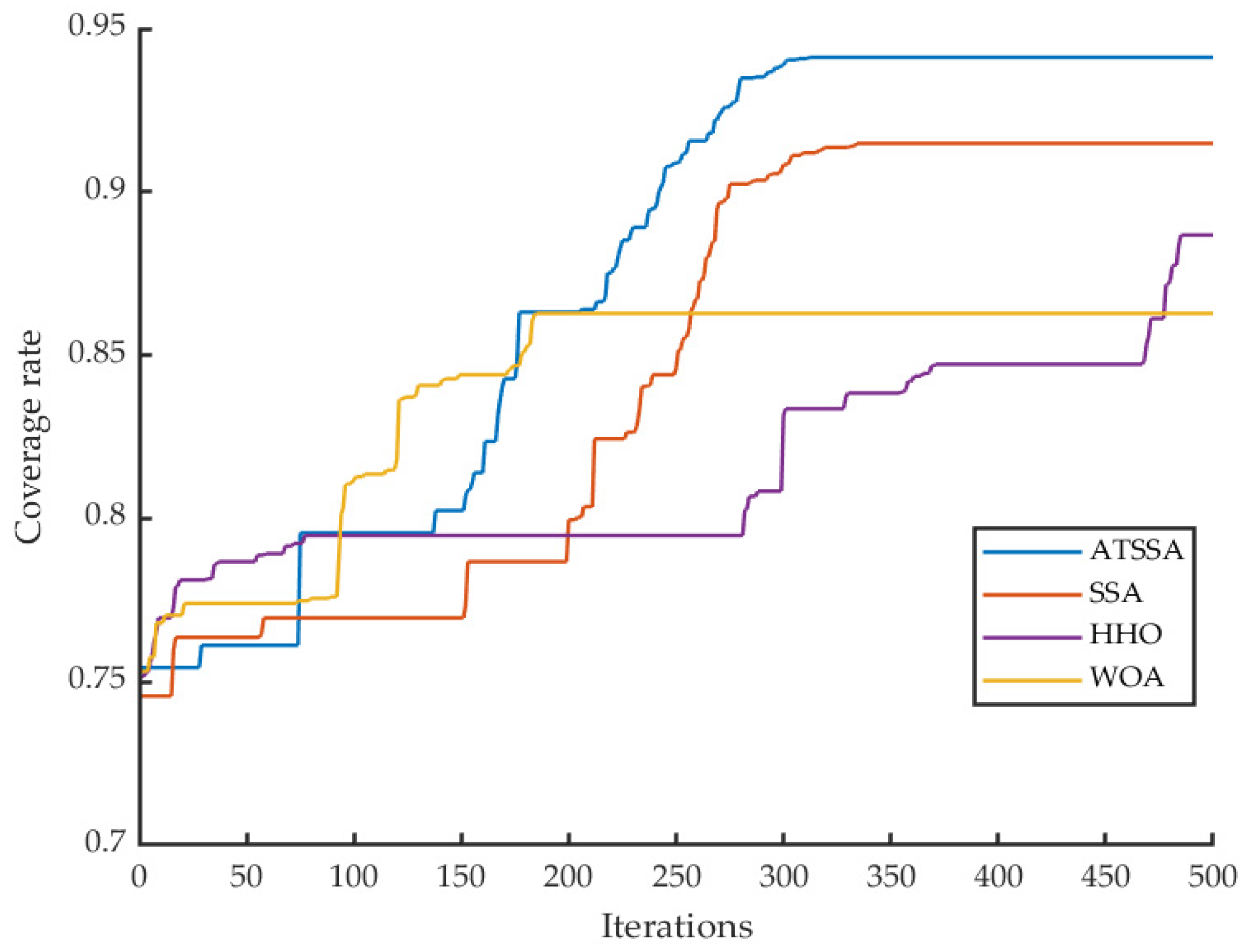
Figure 5 shows the deployment of wireless sensor network nodes obtained by using ATSSA algorithm(a), SSA algorithm (b), HHO algorithm (c) and WOA algorithm (d) respectively. As can be seen from the figure, compared with the other three algorithms, the deployment of sensor nodes after coverage optimization using ATSSA algorithm in this paper is more uniform. Figure 6 and Table 3 shows the optimization curve of coverage optimization using ATSSA algorithm, SSA algorithm, HHO algorithm and WOA algorithm respectively. It can be seen from the figure that WOA algorithm has fast convergence speed, but it is easy to converge prematurely, while HHO algorithm has strong global search ability, but it is difficult to converge. Compared with HHO algorithm and WOA algorithm, ATSSA algorithm and SSA algorithm have certain advantages in performance to improve the coverage efficiency of wireless sensor network. In the figure, when the algorithm starts, the coverage rate of ATSSA algorithm and SSA algorithm is similar. With the increase of iteration times, under the influence of the mutation mechanism of ATSSA algorithm, the convergence speed of ATSSA algorithm is obviously better than that of SSA algorithm. When the number of iterations reaches about 300, ATSSA algorithm and SSA algorithm tend to converge. The performance of ATSSA algorithm in coverage optimization of WSN is improved by about 3% compared with the original SSA algorithm.

6.1.2. Target Field 2

Set the monitoring area to 70m×70m, the sensing radius to 5m, the communication radius to 10m, the number of wireless sensor nodes to 40, and the maximum number of iterations to 1000.

Table 4. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$70\mathrm{m}\times 70\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of sensor nodes	$70$
Number of iterations	$1000$

Table 4. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$70\mathrm{m}\times 70\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of sensor nodes	$70$
Number of iterations	$1000$

Figure 7. Deployment of each algorithm node.

Figure 7. Deployment of each algorithm node.

In order to obtain universal results, ten experiments were conducted for each algorithm, and the average was taken as the result.

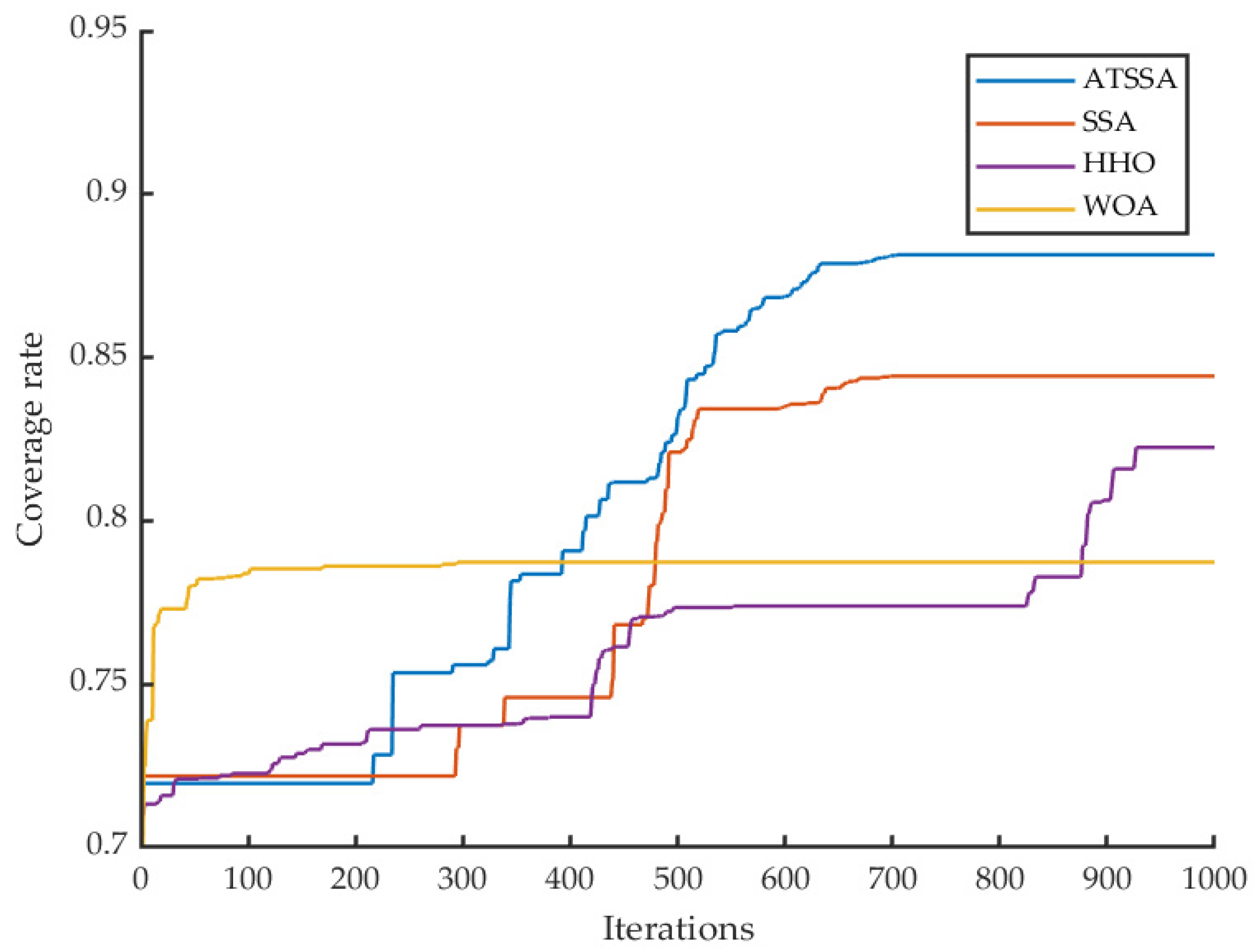
Compared with scenario 1, this scenario expands the area area, the number of sensor nodes is increased, and the maximum number of iterations of the algorithm is set to 1000. As shown in the Figure 8 and Table 5, in a larger area, the ATSSA algorithm still has significant advantages over other algorithms. In the ten experiments, the highest coverage of ATSSA algorithm was about 89% and the lowest coverage rate was about 86%, while the coverage rate of SSA was about 86% and the lowest coverage rate was about 82%, indicating that ATSSA algorithm not only performed better than SSA, but also its stability was better than SSA algorithm.

6.2. Experiment 2

Set the monitoring area to $50\mathrm{m}\times 50\mathrm{m}$, the sensing radius to 5m, the communication radius to 10m, and the maximum number of iterations to 500.

Table 6. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$50\mathrm{m}\times 50\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of iterations	$500$

Table 6. Experimental parameter settings for the node deployment area.

Parameters	Values
Area of deployment	$50\mathrm{m}\times 50\mathrm{m}$
Sensing radius	$5\mathrm{m}$
Communication radius	$10\mathrm{m}$
Number of iterations	$500$

In order to obtain universal results, ten experiments were conducted for each algorithm, and the average was taken as the result.

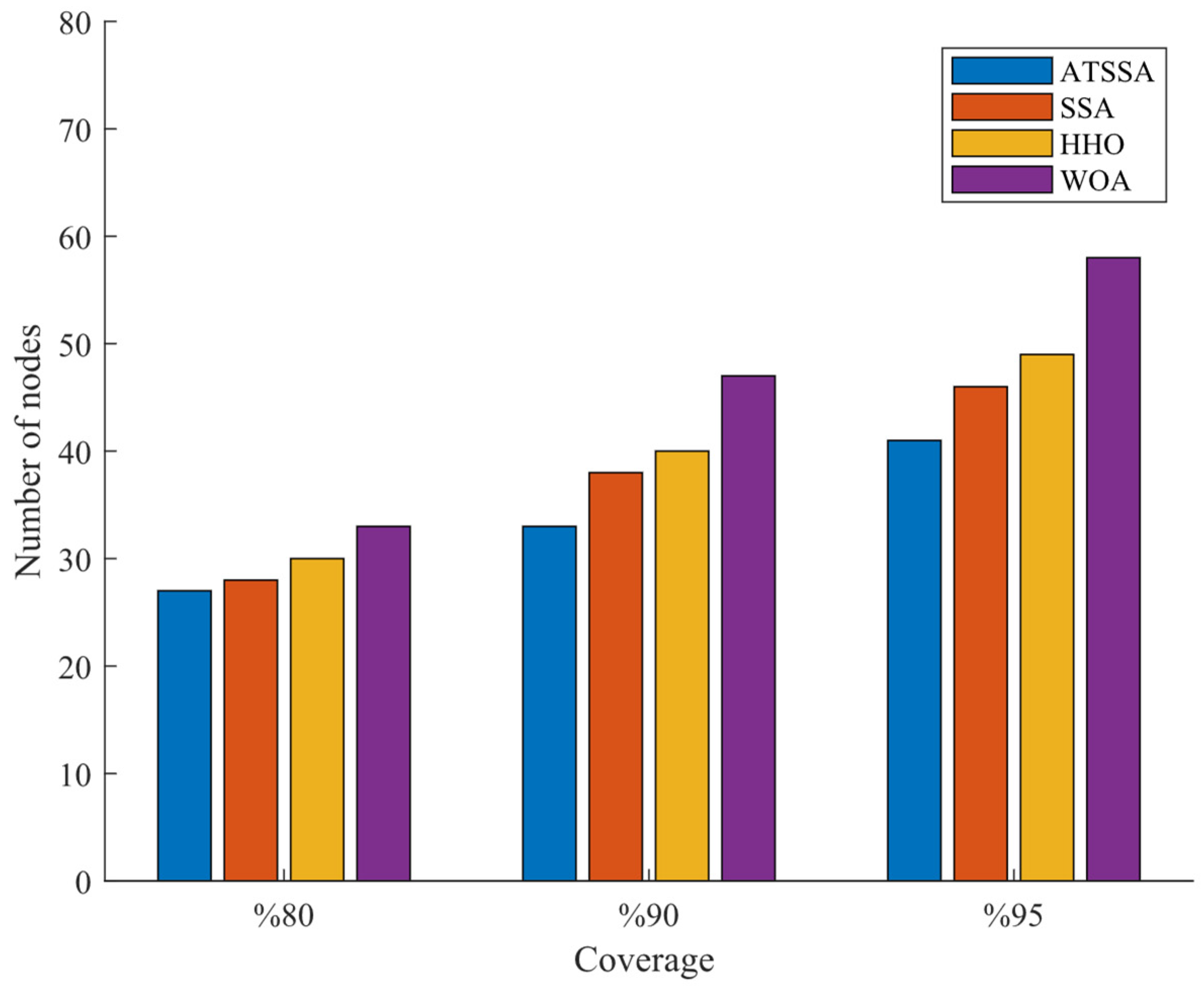
Figure 9 and Table 7 show the number of nodes required for different algorithms to optimize under specific coverage. When the coverage rate reaches 80%, the number of nodes required by ATSSA algorithm, SSA algorithm, HHO algorithm and WOA algorithm is 27, 28, 30 and 33 respectively. The difference between the algorithms is small, and ATSSA algorithm has small advantages. With the increase of coverage rate, ATSSA algorithm can save more nodes than other algorithms. When the coverage rate reaches 95%, ATSSA algorithm saves 6, 9 and 18 sensor nodes respectively compared with other algorithms. This study shows that the optimized deployment of wireless sensor network nodes by ATSSA algorithm can achieve better coverage and save more sensor nodes than other algorithms.