Submitted:
25 April 2023
Posted:
25 April 2023
You are already at the latest version
Abstract
Keywords:
1. Introduction
2. Review of research status
2.1. Reviews for technologies and applications
2.2. Problem
2.3. Comparative study of the reviewed WPPF models and methodologies
3. Opportunities and Challenges
3.1. Bee Colony Algorithm Combined with Data Regression Support Vector Machine
3.2. Wind Data Diversity
- (1)
- Wind speed prediction process
- (2)
- Establishment of power generation model
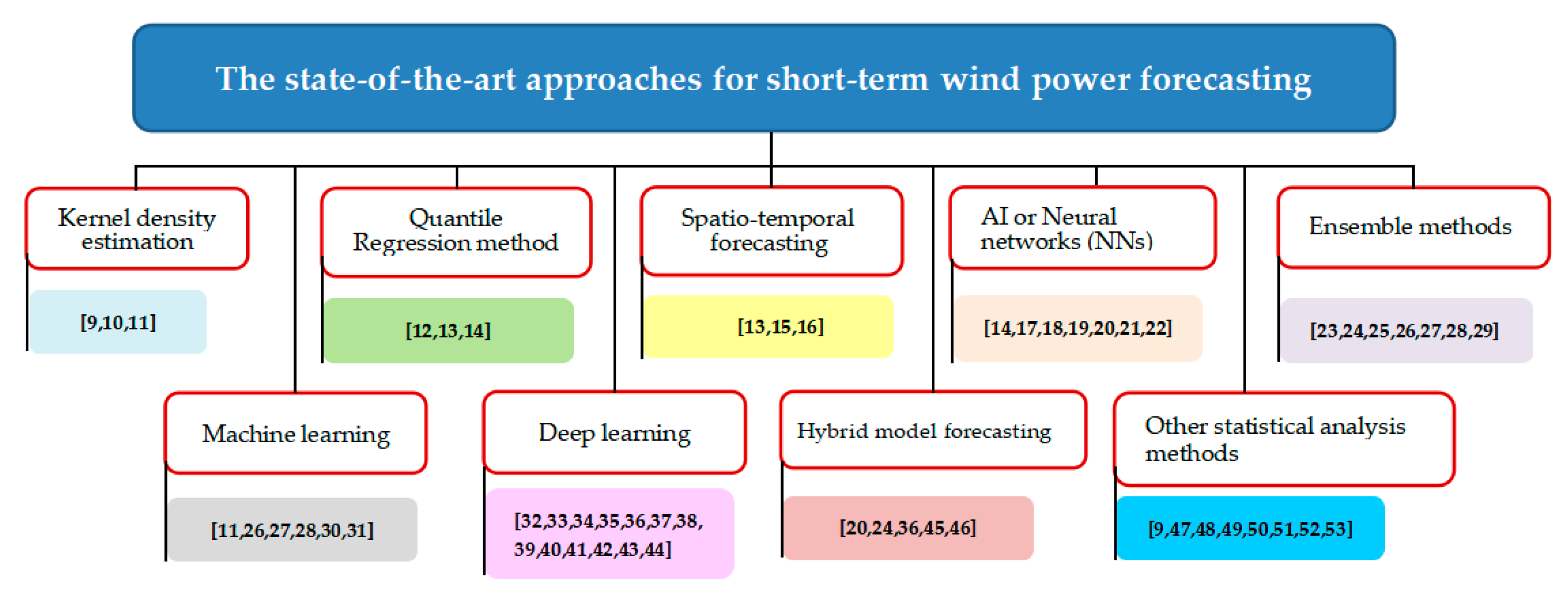
3.3. The state-of-the-art approaches for short-term wind power forecasting
Future studies and development
Conclusion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| BNN | Backpropagation Neural Network |
| QR | Quantile Regression |
| NWP | Numerical Weather Prediction |
| WPF | Wind Power Forecasting |
| WPPF | Wind Power Probabilistic Forecasting |
| WSF | Wind Speed Forecasting |
| WRF | Weather Research and Forecasting |
| WPG | Wind Power Generation |
| WFP | Wind Farm Parameterization |
| RWPF | Regional Wind Power Forecasting |
| QRNN | Quantile Regression Neural Network |
| CSTWPP | Convolutional Spatial-temporal Wind Power Predictor |
| STCN | Spatio-temporal Convolutional Network |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| IBA | Improved Backfill Algorithm |
| GPR | Gaussian Process Regression |
| MFF-SAM-GCN | Multi-Feature Fusion/Self-Attention Mechanism/Graph Convolutional Network |
| WMTSM | Weighted Multivariate Time Series Motifs |
| CLP | Conditional Linear Programming |
| ABQs | Adaptive Boundary Quantiles |
| WNN | Wavelet Neural Network |
| EMD | Empirical Mode Decomposition |
| EBSO | Enhanced Bee Swarm Optimization |
| LSTM | Long-Short Term Memory |
| CLSTM | Convolutional-Long Short Term Memory |
| DOCLER | Deep Optimized Convolutional LSTM-Based Ensemble Reinforcement Learning |
| SVM | Support Vector Machine |
| DR-SVM | Distributionally-Robust Support Vector Machines |
| SOM | Self-Organizing Map |
| k-NN | k-Nearest Neighbors |
| KNNR | K-Nearest Neighbour Based Routing Protocol |
| KDE | Kernel Density Estimation |
| ELM | Extreme Learning Machine |
| KELM | Kernel Based Extreme Learning Machine |
| Adaboost | Adaptive Boosting |
| PSO | Particle Swarm Optimization |
| LSSVM | Least Squares Support Vector Machine |
| GMMN | Generative Moment Matching Network |
| WindGMMN | Wind Power Using Generative Moment Matching Networks |
| MSIN | Multi-Step Informer Network |
| WPD | Wavelet Packet Decomposition |
| VMD | Variational Mode Decomposition |
| SSA | Salp Swarm Algorithms/Singular Spectrum Analysis |
| IGWO | Improved Grey Wolf Optimization |
| GRNN | Generalized Regression Neural Network |
| SVR | Support Vector Regression |
| HMMC | Higher-Order Multivariate Markov Chain |
| MSTAN | Multi-Source and Temporal Attention Network |
| ARMA | Auto-Regression Moving Average |
| ARIMA | Autoregressive Integrated Moving Average |
| MRE | Mean Relative Error |
| MAE | Mean Absolute Error |
| MBE | Mean Bias Error |
| RMSE | Root Mean Squared Error |
| MAPE | Mean Absolute Percent Error |
| nMBE | Normalized Mean Bias Error |
| nRMSE | Normalized Root Mean Squared Error |
| R2 | Coefficient of Determination |
| MG | Microgrid |
References
- WindEurope: Wind energy in Europe–2020 statistics and the outlook for 2021-2025. https://s1.eestatic.com/2021/02/24/actualidad/210224_windeurope_combined_2020_stats.pdf. Accessed 2 October 2021.
- Song, R.; Yang, L.; Chen, L.; Dong, Z. Capacity estimation method of lithium-ion batteries based on deep convolution neural network. Int. J. Bio-Inspired Comput. 2022, 1. [Google Scholar] [CrossRef]
- Wang, J.; Wang, X.; Ma, C.; Kou, L. A survey on the development status and application prospects of knowledge graph in smart grids. IET Gener. Transm. Distrib. 2020, 15, 383–407. [Google Scholar] [CrossRef]
- Kou, L.; Li, Y.; Zhang, F.; Gong, X.; Hu, Y.; Yuan, Q.; Ke, W. Review on Monitoring, Operation and Maintenance of Smart Offshore Wind Farms. Sensors 2022, 22, 2822. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Li, W.; Gulliver, T.A.; Li, S. Bayesian Deep Learning-Based Probabilistic Load Forecasting in Smart Grids. IEEE Trans. Ind. Informatics 2020, 16, 4703–4713. [Google Scholar] [CrossRef]
- Su, Z.; Wang, Y.; Luan, T.H.; Zhang, N.; Li, F.; Chen, T.; Cao, H. Secure and Efficient Federated Learning for Smart Grid With Edge-Cloud Collaboration. IEEE Trans. Ind. Informatics 2021, 18, 1333–1344. [Google Scholar] [CrossRef]
- Kou, L.; Liu, C.; Cai, G.; Wei, Zhang, Z.; Zhou, J.; Wang, X. Fault Diagnosis for Three-phase PWM Rectifier Based on Deep Feedforward Network with Transient Synthetic Features. ISA Trans, 2020, 101, 399-407. [CrossRef]
- Wang, J.; Gao, S.; Yu, L.; Zhang, D.; Xie, C.; Chen, K.; Kou, L. Data-driven Lightning-related Failure Risk Prediction of Overhead Contact Lines Based on Bayesian Network with Spatiotemporal Fragility Model. Reliab. Eng. Syst. Saf. 2023, 231, 109016. [Google Scholar] [CrossRef]
- Li, M.; Yang, M.; Yu, Y.; Lee, W.-J. A Wind Speed Correction Method Based on Modified Hidden Markov Model for Enhancing Wind Power Forecast. IEEE Transactions on Industry Applications 2022, 58, 656–666. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, W.; Liu, C.; Wang, B. Forecasted Scenarios of Regional Wind Farms Based on Regular Vine Copulas. J. Mod. Power Syst. Clean Energy 2020, 8, 77–85. [Google Scholar] [CrossRef]
- Mararakanye, N.; Dalton, A.; Bekker, B. Incorporating Spatial and Temporal Correlations to Improve Aggregation of Decentralized Day-Ahead Wind Power Forecasts. IEEE Access 2022, 10, 116182–116195. [Google Scholar] [CrossRef]
- Von Von Krannichfeldt, L.; Wang, Y.; Zufferey, T.; Hug, G. Online Ensemble Approach for Probabilistic Wind Power Forecasting. IEEE Trans. Sustain. Energy 2021, 13, 1221–1233. [Google Scholar] [CrossRef]
- Yu, Y.; Han, X.; Yang, M.; Yang, J. Probabilistic Prediction of Regional Wind Power Based on Spatiotemporal Quantile Regression. IEEE Trans. Ind. Appl. 2020, 56, 6117–6127. [Google Scholar] [CrossRef]
- Yu, Y.; Yang, M.; Han, X.; Zhang, Y.; Ye, P. A Regional Wind Power Probabilistic Forecast Method Based on Deep Quantile Regression. IEEE Trans. Ind. Appl. 2021, 57, 4420–4427. [Google Scholar] [CrossRef]
- Hu, T.; Wu, W.; Guo, Q.; Sun, H.; Shi, L.; Shen, X. Very Short-Term Spatial and Temporal Wind Power Forecasting: A Deep Learning Approach. CSEE Journal of Power and Energy Systems 2020, 6, 434–443. [Google Scholar]
- Dong, X.; Sun, Y.; Li, Y.; Wang, X.; Pu, T. Spatio-temporal Convolutional Network Based Power Forecasting of Multiple Wind Farms. J. Mod. Power Syst. Clean Energy 2022, 10, 388–398. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, Y.; Yan, J.; Han, S.; Li, L.; Long, Q. Improved Deep Mixture Density Network for Regional Wind Power Probabilistic Forecasting. IEEE Trans. Power Syst. 2020, 35, 2549–2560. [Google Scholar] [CrossRef]
- Medina, S.V.; Ajenjo, U.P. Performance Improvement of Artificial Neural Network Model in Short-term Forecasting of Wind Farm Power Output. J. Mod. Power Syst. Clean Energy 2020, 8, 484–490. [Google Scholar] [CrossRef]
- Akhtar, I.; Kirmani, S.; Ahmad, M.; Ahmad, S. Average Monthly Wind Power Forecasting Using Fuzzy Approach. IEEE Access 2021, 9, 30426–30440. [Google Scholar] [CrossRef]
- Akram, U.; Mithulananthan, N.; Raza, M.Q.; Shah, R.; Milano, F. RoCoF Restrictive Planning Framework and Wind Speed Forecast Informed Operation Strategy of Energy Storage System. IEEE Trans. Power Syst. 2020, 36, 224–234. [Google Scholar] [CrossRef]
- Sun, Y.; Li, Z.; Yu, X.; Li, B.; Yang, M. Research on Ultra-Short-Term Wind Power Prediction Considering Source Relevance. IEEE Access 2020, 8, 147703–147710. [Google Scholar] [CrossRef]
- Hao, J.; Zhu, C.; Guo, X. Wind Power Short-Term Forecasting Model Based on the Hierarchical Output Power and Poisson Re-Sampling Random Forest Algorithm. IEEE Access 2020, 9, 6478–6487. [Google Scholar] [CrossRef]
- Sun, S.; Fu, J.; Wei, L.; Li, A. Multi-Objective Optimal Dispatching for a Grid-Connected Micro-Grid Considering Wind Power Forecasting Probability. IEEE Access 2020, 8, 46981–46997. [Google Scholar] [CrossRef]
- Zou, Y.; Feng, W.; Zhang, J.; Li, J. Forecasting of Short-Term Load Using the MFF-SAM-GCN Model. Energies 2022, 15, 3140. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Wang, S.; Mahfoud, R.J.; Alhelou, H.H.; Hatziargyriou, N.; Siano, P. Performance Improvement of Very Short-term Prediction Intervals for Regional Wind Power Based on Composite Conditional Nonlinear Quantile Regression. J. Mod. Power Syst. Clean Energy 2022, 10, 60–70. [Google Scholar] [CrossRef]
- Lee, J.; Wang, W.; Harrou, F.; Sun, Y. Wind Power Prediction Using Ensemble Learning-Based Models. IEEE Access 2020, 8, 61517–61527. [Google Scholar] [CrossRef]
- Abbasipour, M.; Igder, M. A.; Liang, X. A Novel Hybrid Neural Network-Based Day-Ahead Wind Speed Forecasting Technique. IEEE Access 2021, 9, 151142–151154. [Google Scholar] [CrossRef]
- Tu, C.-S.; Hong, C.-M.; Huang, H.-S.; Chen, C.-H. Short Term Wind Power Prediction Based on Data Regression and Enhanced Support Vector Machine. Energies 2020, 13, 6319. [Google Scholar] [CrossRef]
- Lagos, A.; Caicedo, J.E.; Coria, G.; Quete, A.R.; Martínez, M.; Suvire, G.; Riquelme, J. State-of-the-Art Using Bibliometric Analysis of Wind-Speed and -Power Forecasting Methods Applied in Power Systems. Energies 2022, 15, 6545. [Google Scholar] [CrossRef]
- An, G.; Jiang, Z.; Cao, X.; Liang, Y.; Zhao, Y.; Li, Z.; Dong, W.; Sun, H. Short-Term Wind Power Prediction Based On Particle Swarm Optimization-Extreme Learning Machine Model Combined With Adaboost Algorithm. IEEE Access 2021, 9, 94040–94052. [Google Scholar] [CrossRef]
- Tan, L.; Han, J.; Zhang, H. Ultra-Short-Term Wind Power Prediction by Salp Swarm Algorithm-Based Optimizing Extreme Learning Machine. IEEE Access 2020, 8, 44470–44484. [Google Scholar] [CrossRef]
- alali, S.M.J. et al. New Hybrid Deep Neural Architectural Search-Based Ensemble Reinforcement Learning Strategy for Wind Power Forecasting. IEEE Trans. Ind. Appl. 2022, 58, 15-27.
- Jalali, S. M. J. et al. New Hybrid Deep Neural Architectural Search-Based Ensemble Reinforcement Learning Strategy for Wind Power Forecasting. IEEE Trans. Ind. Appl. 2022, 58, 15-27.
- Abedinia, O.; Bagheri, M.; Naderi, M.S.; Ghadimi, N. A New Combinatory Approach for Wind Power Forecasting. IEEE Syst. J. 2020, 14, 4614–4625. [Google Scholar] [CrossRef]
- Ye, L.; Dai, B.; Pei, M.; Lu, P.; Zhao, J.; Chen, M.; Wang, B. Combined Approach for Short-Term Wind Power Forecasting Based on Wave Division and Seq2Seq Model Using Deep Learning. IEEE Trans. Ind. Appl. 2022, 58, 2586–2596. [Google Scholar] [CrossRef]
- Zhang, H.; Yan, J.; Liu, Y.; Gao, Y.; Han, S.; Li, L. Multi-Source and Temporal Attention Network for Probabilistic Wind Power Prediction. IEEE Trans. Sustain. Energy 2021, 12, 2205–2218. [Google Scholar] [CrossRef]
- Piotrowski, P.; Baczyński, D.; Kopyt, M.; Gulczyński, T. Advanced Ensemble Methods Using Machine Learning and Deep Learning for One-Day-Ahead Forecasts of Electric Energy Production in Wind Farms. Energies 2022, 15, 1252. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, X.; Yang, J. Modified Particle Swarm Optimization with Attention-Based LSTM for Wind Power Prediction. Energies 2022, 15, 4334. [Google Scholar] [CrossRef]
- Blazakis, K.; Katsigiannis, Y.; Stavrakakis, G. One-Day-Ahead Solar Irradiation and Windspeed Forecasting with Advanced Deep Learning Techniques. Energies 2022, 15, 4361. [Google Scholar] [CrossRef]
- Miao, C.; Li, H.; Wang, X.; Li, H. Ultra-Short-Term Prediction of Wind Power Based on Sample Similarity Analysis. IEEE Access 2021, 9, 72730–72742. [Google Scholar] [CrossRef]
- Liao, W.; Yang, Z.; Chen, X.; Li, Y. WindGMMN: Scenario Forecasting for Wind Power Using Generative Moment Matching Networks. IEEE Trans. Artif. Intell. 2022, 3, 843–850. [Google Scholar] [CrossRef]
- Ko, M.-S.; Lee, K.; Kim, J.-K.; Hong, C.W.; Dong, Z.Y.; Hur, K. Deep Concatenated Residual Network With Bidirectional LSTM for One-Hour-Ahead Wind Power Forecasting. IEEE Trans. Sustain. Energy 2020, 12, 1321–1335. [Google Scholar] [CrossRef]
- Huang, X.; Jiang, A. Wind Power Generation Forecast Based on Multi-Step Informer Network. Energies 2022, 15, 6642. [Google Scholar] [CrossRef]
- Wu, X.; Jiang, S.; Lai, C.S.; Zhao, Z.; Lai, L.L. Short-Term Wind Power Prediction Based on Data Decomposition and Combined Deep Neural Network. Energies 2022, 15, 6734. [Google Scholar] [CrossRef]
- Aisyah, S.; Simaremare, A.A.; Adytia, D.; Aditya, I.A.; Alamsyah, A. Exploratory Weather Data Analysis for Electricity Load Forecasting Using SVM and GRNN, Case Study in Bali, Indonesia. Energies 2022, 15, 3566. [Google Scholar] [CrossRef]
- Han, Y.; Tong, X. Multi-Step Short-Term Wind Power Prediction Based on Three-level Decomposition and Improved Grey Wolf Optimization. IEEE Access 2020, 8, 67124–67136. [Google Scholar] [CrossRef]
- Sanjari, M. J.; Gooi, H. B.; Nair, N. -K. C. Power Generation Forecast of Hybrid PV–Wind System. IEEE Transactions on Sustainable Energy 2020, 11, 703-712.
- Bezerra, E.C.; Pinson, P.; Leao, R.P.S.; Braga, A.P.S. A Self-Adaptive Multikernel Machine Based on Recursive Least-Squares Applied to Very Short-Term Wind Power Forecasting. IEEE Access 2021, 9, 104761–104772. [Google Scholar] [CrossRef]
- Oh, E.; Wang, H. Reinforcement-Learning-Based Energy Storage System Operation Strategies to Manage Wind Power Forecast Uncertainty. IEEE Access 2020, 8, 20965–20976. [Google Scholar] [CrossRef]
- Zhao, Y.; Xue, Y.; Gao, S.; Wang, J.; Cao, Q.; Sun, T.; Liu, Y. Computation and Analysis of an Offshore Wind Power Forecast: Towards a Better Assessment of Offshore Wind Power Plant Aerodynamics. Energies 2022, 15, 4223. [Google Scholar] [CrossRef]
- Ma, J.; Yang, M.; Lin, Y.; Wang, C. Ultra-Short-Term Probabilistic Wind Turbine Power Forecast Based on Empirical Dynamic Modeling. IEEE Trans. Sustain. Energy 2019, 11, 906–915. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, S.; Zhang, H.; Yang, G. Wind Power Prediction Based on Multi-class Autoregressive Moving Average Model with Logistic Function. J. Mod. Power Syst. Clean Energy 2022, 10, 1184–1193. [Google Scholar] [CrossRef]
- Shavolkin, O.; Gerlici, J.; Shvedchykova, I.; Kravchenko, K. Solar–Wind System for the Remote Objects of Railway Transport Infrastructure. Energies 2022, 15, 6546. [Google Scholar] [CrossRef]
- Gu, X.; Wang, X. A Review on Wind Power Forecast Technologies. Power Syst. Technol. 2007, 31, 335–338. [Google Scholar]
- Wang, L.; Yang, G.; Gao, S. A Review on Modeling and Forecasting of Wind Power. Proc. Control Power Syst. 2009, 37, 118–121. [Google Scholar]
- Hanifi, S.; Liu, X.; Lin, Z.; Lotfian, S. A Critical Review of Wind Power Forecasting Methods—Past, Present and Future. Energies 2020, 13, 3764. [Google Scholar] [CrossRef]
- Dhiman, H. S.; Deb, D. A Review of Wind Speed and Wind Power Forecasting Techniques. Proc. North Amer. Power Symp. 2020, 1–11. [Google Scholar]
- Lu, P.; Ye, L.; Zhao, Y.; Dai, B.; Pei, M.; Tang, Y. Review of meta-heuristic algorithms for wind power prediction: Methodologies, applications and challenges. Appl. Energy 2021, 301. [Google Scholar] [CrossRef]
- Bazionis, I.K.; Karafotis, P.A.; Georgilakis, P.S. A review of short-term wind power probabilistic forecasting and a taxonomy focused on input data. IET Renew. Power Gener. 2021, 16, 77–91. [Google Scholar] [CrossRef]
- Lipu, M.S.H.; Miah, S.; Hannan, M.A.; Hussain, A.; Sarker, M.R.; Ayob, A.; Saad, M.H.M.; Mahmud, S. Artificial Intelligence Based Hybrid Forecasting Approaches for Wind Power Generation: Progress, Challenges and Prospects. IEEE Access 2021, 9, 102460–102489. [Google Scholar] [CrossRef]
- Landberg, L. Short-term prediction of the power production from wind farms. J. Wind Eng. Ind. Aerodyn. 1999, 80, 207–220. [Google Scholar] [CrossRef]
- Nielsen, T.S.; Tofting, John; Madsen, H. Experiences with Statistical Methods for Wind Power Prediction. 1999.
- Beyer, H.D.; Mellinghoff, H.; Monnich, K.; Waldl, H.P. Forecast of Regional Power Output of Wind Turbines. In Proceedings of the European Wind Energy Conference, Nice, France, 1–5 March 1999; p. 1073. [Google Scholar]
- Landberg, L. Short-term prediction of local wind conditions. J. Wind. Eng. Ind. Aerodyn. 2001, 89, 235–245. [Google Scholar] [CrossRef]
- Giebel, G.; Landberg, L.; Nielsen, T.S.; Madsen, H. The Zephyr-project. In The Next Generation Prediction System (Poster). In Proceedings of the CD-ROM European Wind Energy Association (EWEA) 2002, Paris, France, 2–5 April 2002. [Google Scholar]
- Landberg, L; Giebel, G.; Nielsen, H. A. et al. Short¬term Prediction¬An Overview. Wind Energy 2003, 6, 273–280.
- Xu, Q.; He, D.; Zhang, N.; Kang, C.; Xia, Q.; Bai, J.; Huang, J. A Short-Term Wind Power Forecasting Approach With Adjustment of Numerical Weather Prediction Input by Data Mining. IEEE Trans. Sustain. Energy 2015, 6, 1283–1291. [Google Scholar] [CrossRef]
- Bernhard, L.; Kurt, R.; Bernhard, E. et al. Wind Power Prediction in Germany-Recent Advances and Future Challenges. European Wind Energy Conference, Athens, 2006.
- Focken, U.; Lange, M.; Waldl, H.P. Previento–A Wind Power Prediction System with an Innovative Upscaling Algorithm. In Proceedings of the 2001 EuropeanWind Energy Association Conference, EWEC’01, Copenhagen, Danmark, 2 July 2001; pp. 826–829. [Google Scholar]
- Jorgensen, J.; Moehrlen, C.; Gallaghoir, B.O.; Mckeogh, E. HIRPOM: Description of An Operational Numerical Wind Power Prediction Model for Large Scale Integration of On-and Offshore Wind Power in Denmark. In Proceedings of the Poster on the Global Wind Power Conference and Exhibition, London, UK, 1 January–30 September 2002. [Google Scholar]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different timehorizons. In Proceedings of the North-American Power Symposium (NAPS) 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Costa, A.; Crespo, A.; Navarro, J.; Lizcano, G.; Madsen, H.; Feitosa, E. A review on the young history of the wind power short-term prediction. Renew. Sustain. Energy Rev. 2007, 12, 1725–1744. [Google Scholar] [CrossRef]
- Yang, X.Q. Research on Ultra-short-term Wind Power Combination Forecasting Model Based on Least Squares Support Vector Machine, Thesis, 2017, Hunan University.
- Gong, W.; Meyer, F.J.; Liu, S.; Hanssen, R.F. Temporal Filtering of InSAR Data Using Statistical Parameters From NWP Models. IEEE Trans. Geosci. Remote. Sens. 2015, 53, 4033–4044. [Google Scholar] [CrossRef]
- Carpinone, A.; Giorgio, M.; Langella, R.; Testa, A. Markov chain modeling for very-short-term wind power forecasting. Electr. Power Syst. Res. 2015, 122, 152–158. [Google Scholar] [CrossRef]
- Karadas, M.; Celik, H.M.; Serpen, U.; Toksoy, M. Multiple regression analysis of performance parameters of a binary cycle geothermal power plant. Geothermics 2015, 54, 68–75. [Google Scholar] [CrossRef]
- Babazadeh, H.; Gao, W.; Cheng, L.; Lin, J. An Hour Ahead Wind Speed Prediction by Kalman Filter. In Proceedings of the 2012 IEEE Power Electronics and Machines in Wind Applications, Denver, CO, USA, 16–18 July 2012. [Google Scholar]
- Zhang, J.; Wang, C. Application of ARMA Model in Ultra-Short Term Prediction of Wind Power. In Proceedings of the International Conference on Computer Sciences and Applications, San Francisco, CA, USA, 23–25 October 2013. [Google Scholar]
- Tagliaferri, F.; Viola, I.; Flay, R. Wind direction forecasting with artificial neural networks and support vector machines. Ocean Eng. 2015, 97, 65–73. [Google Scholar] [CrossRef]
- Wang, X.; Zheng, Y.; Li, L.; Zhou, L.; Yao, G.; Huang, T. Short-term Wind Power Prediction Based on Wavelet Decomposition and Extreme Learning Machine. In Proceedings of the Advances in Neural Networks 9th International Symposium on Neural Networks, Shenyang, China, 645-653., 11–14 July 2012. [Google Scholar]
- Zhang, Q.; Lai, K.K.; Niu, D.; Wang, Q.; Zhang, X. A Fuzzy Group Forecasting Model Based on Least Squares Support Vector Machine (LS-SVM) for Short-Term Wind Power. Energies 2012, 5, 3329–3346. [Google Scholar] [CrossRef]
- Tu, C.-S.; Tsai, W.-C.; Hong, C.-M.; Lin, W.-M. Short-Term Solar Power Forecasting via General Regression Neural Network with Grey Wolf Optimization. Energies 2022, 15, 6624. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, X. Recurrent neural network wind power prediction based on variational modal decomposition improvement. AIP Adv. 2023, 13, 025027. [Google Scholar] [CrossRef]
- Xiong, Jinlin; Peng, Tian; Tao, Zihan; Zhang, Chu; Song, Shihao; Nazir, Muhammad Shahzad A Dual-Scale Deep Learning Model Based on Elm-Bilstm and Improved Reptile Search Algorithm for Wind Power Prediction, Energy, 2023, 266, 126419. [CrossRef]
- Tarek, Z.; Shams, M.Y.; Elshewey, A.M.; El-Kenawy, E.-S.M.; Ibrahim, A.; Abdelhamid, A.A.; El-Dosuky, M.A. Wind Power Prediction Based on Machine Learning and Deep Learning Models. Comput. Mater. Contin. 2023, 74, 715–732. [Google Scholar] [CrossRef]
- Wang, Jianing; Zhu, Hongqiu; Zhang, Yingjie; Cheng, Fei; Zhou, Can A Novel Prediction Model for Wind Power Based on Improved Long Short-Term Memory Neural Network, Energy, 2023, v 265. [CrossRef]
- Yu, Min; Niu, Dongxiao; Gao, Tian; Wang, Keke; Sun, Lijie; Li, Mingyu; Xu, Xiaomin A Novel Framework for Ultra-Short-Term Interval Wind Power Prediction Based on RF-WOA-VMD and BiGRU Optimized By The Attention Mechanism, Energy, 2023, v 269. [CrossRef]
- Qin, Bin; Huang, Xun; Wang, Xin; Guo, Lingzhong Ultra-Short-Term Wind Power Prediction Based on Double Decomposition and LSSVM, Transactions of the Institute of Measurement and Control, 2023. [CrossRef]
- Wei, Hui; Wang, Wen-sheng; Kao, Xiao-xuan A Novel Approach to Ultra-Short-Term Wind Power Prediction Based on Feature Engineering and Informer, Energy Reports, 2023, 9, p 1236-1250. [CrossRef]
- Han, Yuchao; Tong, Xiangqian; Shi, Shuyan; Li, Feng; Deng, Yaping Ultra-short-term Wind Power Interval Prediction Based on Hybrid Temporal Inception Convolutional Network Model, Electric Power Systems Research, 2023, 217, 109159. [CrossRef]
- Sheng, Yiwei; Wang, Han; Yan, Jie; Liu, Yongqian; Han, Shuang Short-Term Wind Power Prediction Method Based on Deep Clustering-Improved Temporal Convolutional Network, 2023, Energy Reports, 9, p 2118-2129. [CrossRef]
- Hossain, A.; Gray, E.; Lu, J.; Islam, R.; Alam, S.; Chakrabortty, R.; Pota, H.R. Optimized Forecasting Model to Improve the Accuracy of Very Short-Term Wind Power Prediction. IEEE Trans. Ind. Informatics 2023, 19, 10145–10159. [Google Scholar] [CrossRef]
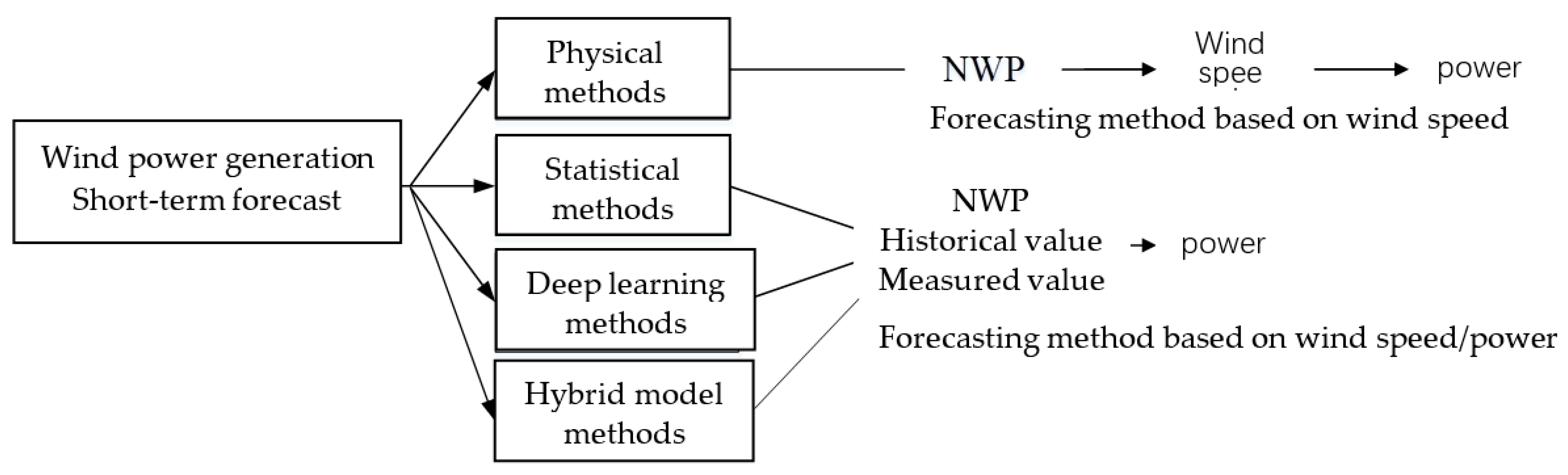
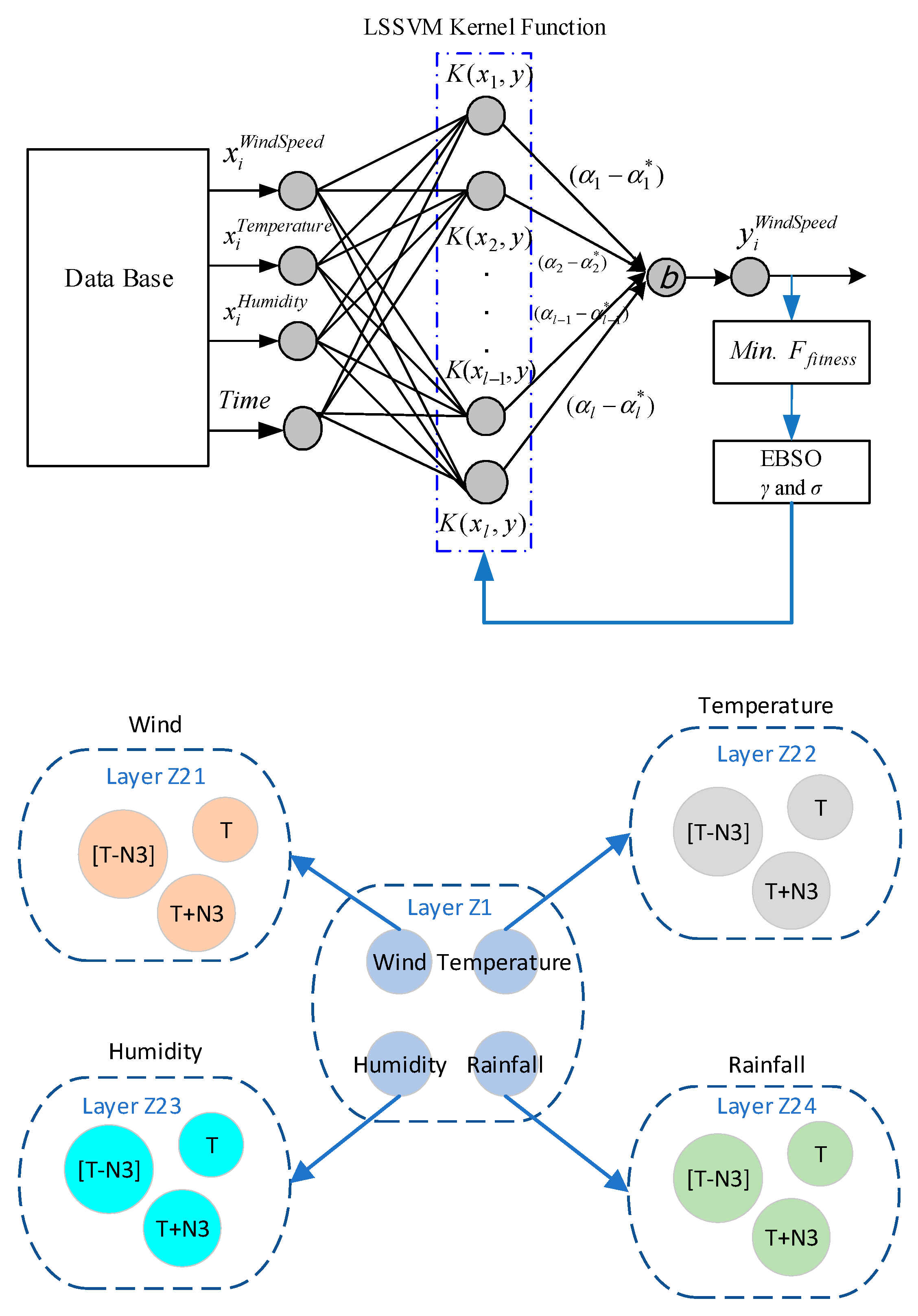
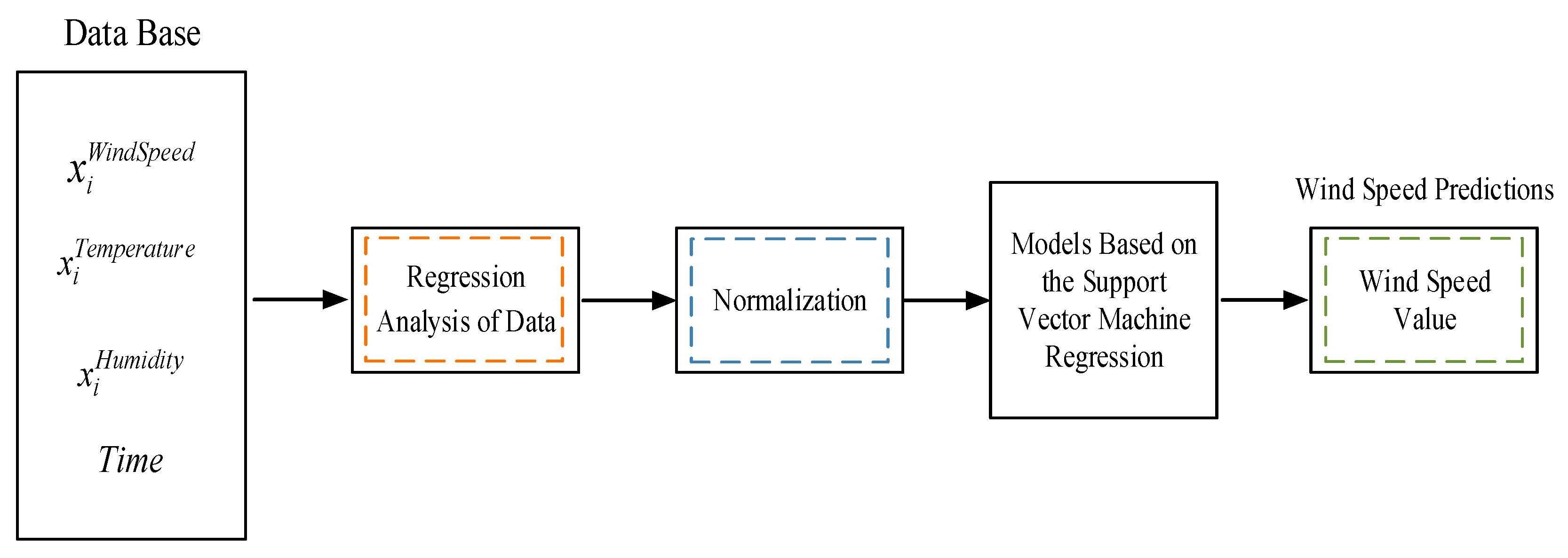
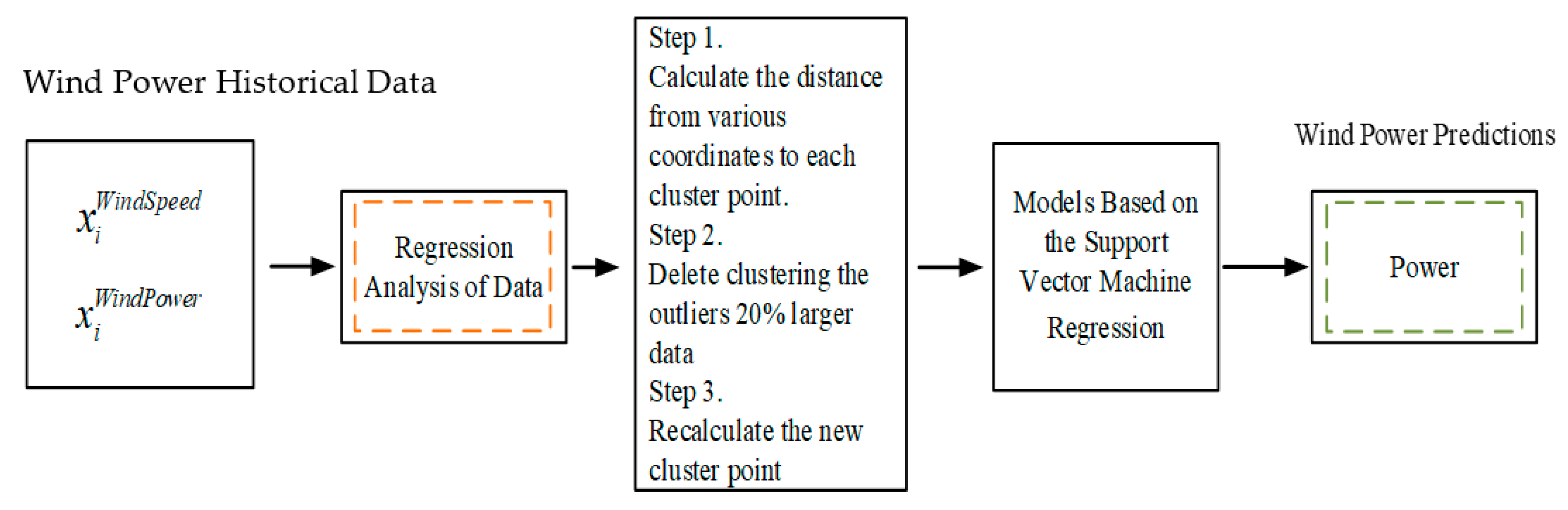
| Name of forecasting system | R&D institutions | Methods |
|---|---|---|
| Prediktor | Danish National Laboratory | Physical methods |
| SIPREÓLICO | University of Carlos III, Madrid, Spain | Physical methods |
| HIRPOM | University College Cork, Ireland | Physical methods |
| Previnto | University of Oldenburg, Germany | Physical methods |
| WPFS Ver 1.0 system | China Electric Power Research Institute | Physical methods/ Meta-heuristic |
| WPPT | Copenhagen University, Denmark | Statistical methods |
| AWPPS | MINES ParisTech | Statistical methods, Fuzzy ANN |
| RAL | Appleton Laboratory, Rutherford, UK | Statistical methods |
| GH Forecaster | Garrad Hassan, UK | Statistical methods |
| WPMS | Germany-ISET | Statistical methods, ANN |
| Zephry | Risø National Laboratory | Statistical /Physical methods |
| LocalPred-RegioPred | Spanish National Energy Center | Statistical /Physical methods |
| ANEMOS | 23 scientific research institutions in 7 EU countries | Statistical /Physical methods |
| eWind | True Wind USA, Inc. | Statistical /Physical methods |
| WEPROG | University College Cork, Ireland | Statistical /Physical methods |
| Time resolution | Reviewed works | Forecasting time scale |
|---|---|---|
| 1 min | [22,29] | Ultra short term |
| 5 min | [15,16,29,48,50] | Ultra short term |
| 10 min | [15,28,30,43,50] | Ultra short term |
| 15 min | [12,15,20,21,23,30,40,41,44,47,50] | Ultra short term |
| 30 min | [15,16,23,26,30,50,51,52] | Ultra short term |
| 1 hr | [14,16,18,23,24,27,30,33,35,36,37,38,39,42,45,49,53] | Short term |
| 2 hr | [16,25,30] | Short term |
| 3 hr | [16,30] | Short term |
| 4 hr | [25,30] | Short term |
| 24 hr | [9,11,17,29,41] | Short term |
| 48 hr | [31,33] | Short term |
| 72 hr-1 week | [13,29] | Medium term |
| 1 month-years | [19] | Long term |
| Ref | Method | Model Type | Parameters Used | Accuracy |
|---|---|---|---|---|
| [9] | -Other statistical analysis methods -Kernel density estimation |
Modified hidden Markov model | Wind speed, wind direction, wind power | RMSE=3.093 MAE=2.451 |
| [10] | -Kernel density estimation | Distance weighted kernel density estimation (KDE) and regular vine (R-vine) copula | Wind power output, wind speed | RMSE=0.1089 MAE=0.075 |
| [11] | -Kernel density estimation -Machine learning |
The k-NN and conditional KDE models | Historical wind power | MAE=3.18; RMSE=4.63; R2=0.94 |
| [12] | -Quantile regression method | A quantile passive–aggressive regression model for online convex optimization problems | Wind power | Pinball loss (PBL)=13.3 Average coverage error (ACE)=4.86%, Winkler score (WKS)=78.71 and Continuous ranked probability score (CRPS) =26.21 |
| [13] | -Spatiotemporal forecasting -Quantile regression method |
Spatiotemporal quantile regression (SQR) | Wind power data | RMSE=16.62%; MAE=11.23% |
| [14] | -Quantile regression method -AI or neural networks (NNs) |
A quantile regression neural network (QRNN) for regional wind power forecasting (RWPF) | Enhancing the abilities of nonlinear mapping and dealing with massive data | NMAE: DQR:9.086; QRNN:9.479 SBL:13.451; IFPA:13.967 NRMSE: DQR:10.917; QRNN:10.227 SBL:14.185; IFPA:14.538 |
| [15] | -Spatiotemporal forecasting | A convolution-based spatial–temporal wind power predictor (CSTWPP) | Historical wind power | MASE= 190.02 RMSE=7.49 |
| [16] | -Spatiotemporal forecasting | The spatiotemporal convolutional network (STCN) with a directed graph convolutional structure. | -Historical power data -STCN parameters selected by oneself |
MAEs =3.17% RMSEs =2.88%, |
| [17] | -AI or neural networks (NNs) | Improved deep mixture density network model | Wind speed, wind direction, wind vector, wind power | NRMSE=0.138 |
| [18] | -AI or neural networks (NNs) | New artificial neural network (ANN) models | Wind speed, wind direction, wind power output | Mean absolute relative error (MARE)=7.5%; Rj=5.4% (mean value of the Pearson correlation coefficient) |
| [19] | -AI or neural networks (NNs) | A fuzzy logic approach for prediction of wind power output | Wind speed, air density | RMSE=1.04%; MAD=0.91% MSE=1.05% |
| [20] | -AI or neural networks (NNs) -Hybrid model forecasting |
An ensemble neural forecast framework (ENFF) with three neural predictors for wind speed forecasting below. Elman neural network (ELM) Feedforward neural network (FNN) Radial basis function (RBF) neural network |
Wind speed, meteorological | Errors around 0.6 m/s |
| [21] | -AI or Neural networks (NNs) | Day-ahead numerical weather prediction (NWP) with neural network |
The persistence method with BP three rolling prediction effect | The model accuracy improved by 7.61% and the RMSE reduced by 8.76% |
| [22] | -AI or Neural networks (NNs) | -A classification model with the output wind power as the classification target -Use of Poisson re-sampling to replace the bootstrap method of the random forest to improve the training speed |
The random forest with Poisson re-sampling and set the parameters by oneself |
Mean square error (MSE) GBRT: 0.224; MLP: 0.117 Random forest with Bootstrap sampling: 0.111 Random forest with Poisson re-sampling: 0.096 |
| [23] | -Ensemble methods | The CEEMDAN-IBA-GPR model | Historical wind power data | Stand deviation =10.42 |
| [24] | -Ensemble methods -Hybrid model forecasting |
A multi-feature fusion self-attention mechanism graph convolutional network (MFF- SAM-GCN) forecasting model | Hyperparameter optimization of the predictive model by Bayesian optimization (BO) | RMSE of proposed (MFF-SAM- GCN) model is 0.0284, while the SMAPE is 9.453%, the MBE is 0.025, and R2 is 0.989. |
| [25] | -Ensemble methods | Weighted multivariate time series motifs (WMTSM) and conditional LP (CLP) combined with the adaptive boundary quantiles (ABQs) | Wind speed, wind power | Both MAE and RMSE of less than 10% |
| [26] | -Ensemble methods -Machine learning |
Ensemble learning models (GRF, RF, XGB) | Wind power, wind speed, gearbox bearing temperatures | R2 =98.9; RMSE=50.36 ; MAE=23.63 |
| [27] | -Ensemble methods -Machine learning |
The five algorithms include wavelet neural network (WNN) trained by improved clonal selection algorithm (ICSA), WNN trained by PSO, and extreme learning machine (ELM)-based neural network, etc. The best performing models are the WNN trained by ICSA and ELM-based NN models. | Selecting parameters by using particle swarm optimization | The average nRMSE for WNN trained by ISCA, ELM, RBF, MLP, WNN trained by PSO are 5.4059%, 6.925%, 10.294%, 12.407%, and 17.038%. The average nMAE for WNN trained by ISCA, ELM, RBF, MLP, and WNN trained by PSO, are 4.2893%, 5.4787%, 8.2527%, 9.5773%, and 13.4847%. |
| [28] | -Ensemble methods -Machine learning |
Enhanced bee swarm optimization (EBSO) to perform the parameter optimization for least squares support vector machine (LSSVM) | Picking parameters for LSSVM by enhanced bee swarm optimization (EBSO) | DR-SVM VMED(m/s): 6.895 MAE (m/s) : 0.723 RMSE(m/s): 0.932 MAPE(%): 11.87 CPU time(s): 148.15 |
| [29] | -Ensemble methods | An exhaustive review of the state of the art of wind speed and power forecasting models for wind turbines located in different segments of power systems | Data preprocessing (EMD and ICEEMDAN) and parameter optimization | No description |
| [30] | -Machine learning | The Adaboost-PSO-ELM method | Wind speed, wind direction, wind power | MAPE=0.0372; NBE=0.4621 RMBE=0.2950; R2=0.9857 |
| [31] | -Machine learning | Salp swarm algorithms–extreme learning machine (SSA-ELM) | Wind speed, wind direction, temperature, atmospheric pressure, and other data are sampled every 10 minutes | MAPE=1.2677 RMSE=0.2576 |
| [32] | -Deep learning | A deep optimized convolutional LSTM-based ensemble reinforcement learning strategy (DOCLER) | Wind power | RMSE=7.1322% MAE=4.6713% |
| [33] | -Deep learning | A variational mode decomposition (VMD) and convolutional long short-term memory network (Conv LSTM) model | Wind power | MRE(KW)=0.016 (should be %) MAE(KW)=792 (should be %) MSE(KW)=1568305.38 RMSE(KW)=1252.32 (should be %) |
| [34] | -Deep learning | A multi-source and temporal attention network (MSTAN) | Wind speed, pressure, temperature, humidity, and wind direction | NRMSE=0.154 NMAE=0.110 |
| [35] | -Deep learning | Two-dimensional convolution neural network trained by improved accidental floater PSO | Fine-tuning the weights of TDCNN by proposed AFPSO |
Average error of four seasons MAPE:3.76 NMAE:2.46 NRMSE:3.12 |
| [36] | -Deep learning -Hybrid model forecasting |
The WD-IGFCM-LSTMS model for the accuracy of short-term wind power forecasting (WPF) approach | The best parameters determined by IGWO algorithm | Case A: NMAE 10.32%; NRMSE 14.59% CR: 85.41%; QR: 91.53% Case B: NMAE 10.18%; NRMSE 13.52% CR: 86.48%; QR: 91.53% |
| [37] | -Deep learning | Deep neural network: LSTM method (best); MLP (second best) while using SVR, KNNR, and physical model with an expert correction |
More LSTM parameters and set these parameters by oneself | INT_OUT_EXT[GBT, RF, PHYS(v1&v2)→KNNR, MLP, LSTM] with additional expert SS:0.5925; nMAE[%]:11.3055 nRMSE:0.1618; nMBE:0.0146 |
| [38] | -Deep learning | -Optimizing the hyperparameters of the LSTM network by the modified PSO algorithm -A PSO_LSTM model |
Selecting parameters by PSO | MPSO_ATT_LSTM MAPE: 4.6%; MAE: 211.5 kW Device capacity > 20000kW |
| [39] | -Deep learning | Advanced deep learning techniques Encoder–Decoder LSTM |
Setting parameters by oneself | Annual and monthly errors |
| [40] | -Deep learning | The CNN-MLSTMs-T Model | Wind power | RMSE=0.1998; MAE=0.1523 |
| [41] | -Deep learning | Generative moment matching network (GMMN) | Historical wind power | PINAW=8.66MW; PICP=84% RMSE=127.10; MAE=0.6855MW |
| [42] | -Deep learning | Bidirectional long short-term memory (Bi-LSTM) | Manual adjustment layers | Error can be divided into training, test and validation errors |
| [43] | -Deep learning | Multi-step informer network (MSIN) | Manual selection of parameters | Multi-step informer network (MSIN) improves forecast accuracy by 29% compared with informer network for RMSE |
| [44] | -Deep learning | Long short-term memory neural network (LSTM) with the improved particle swarm optimization algorithm (IPSO) | Determining the LSTM and DENSE layers, the number of neurons | VMD-CNN-IPSO-LSTM MAE:2.92668; RMSE:3.59604 MAPE:0.20147; adj-R2:0.96639 |
| [45] | -Hybrid model forecasting |
Generalized regression neural network (GRNN) and support vector machine (SVM) |
Turning GRNN and SVM parameters by oneself | The GRNN model gives the CC value of 0.956, RMSE of 28.82, and the SVR model gives the CC value of 0.965 and RMSE value of 44.40. |
| [46] | -Hybrid model forecasting | The WPD-VMD-SSA-IGWO-KELM model | Wind speed |
NMAE=11.2% MAPE=4.2% |
| [47] | -Other statistical analysis methods | Higher-order multivariate Markov chain (HMMC) | Wind power; PV power, Heat index |
NRMSE=2.59 |
| [48] | -Other statistical analysis methods | Five minute-ahead wind power forecasts in terms of point forecast skill scores and calibration | To deduce the value of kernel methods for parameter adjustment | The error value is represented by a picture rather than a simple number. |
| [49] | -Other statistical analysis methods | RL-Based ESS operation strategy | No description | 1% point analysis gap to the optimal solution, which requires complete information, including future values |
| [50] | -Other statistical analysis methods | Regression and curve fitting by weather research and forecasting (WRF) and wind farm parameterization (WFP) | No description | No description |
| [51] | -Other statistical analysis methods | Empirical dynamic modeling (EDM)-based probabilistic forecast | Historical wind turbine power | CRPS (%)=5.12 |
| [52] | -Other statistical analysis methods | Multi-class autoregressive moving average (ARMA) | Historical wind power | RMSE=127.10 MAPE=1.25% |
| [53] | -Other statistical analysis methods | Renewable energy is directly distributed to power dispatch | Incorporating renewable energy into the power flow | With an increase in power by 1.6 times, there is a decrease in energy of RES by 15-19. |
| Work | Date of publication | Main contributions | Advantages | Disadvantages | Approaches |
|---|---|---|---|---|---|
| [9] | Jan./Feb. 2022 |
A wind power forecasting (WPF) system including WRF-based wind forecasting, modified HMM-based wind speed correction, and a kernel distribution estimation (KDE)-based WPF module | Enhancing the WPF accuracy from deterministic and probabilistic forecast | -Very time-consuming in huge computational burden -Complex configuration |
Classification and regression algorithms |
| [10] | January 2020 |
The model is more accurate and flexible than the Gaussian copula model | Abundant bi-variate copula functions are available to make the model more accurate | -Complex structure and hardware requirement | Classification and regression algorithms |
| [11] | November 2022 | Simple to improve the accuracy of aggregated point and wind power forecasts that can be derived from decentralized point forecasts | Providing system operators with a way of aggregating these forecasts while taking into account spatial and temporal correlations of wind power | -Being difficult in selecting good bandwidths in the presence of large datasets and high dimensionality | Classification and regression algorithms |
| [12] | April 2022 |
Online ensemble learning framework for wind power forecasting that utilizes solid individual forecasting models and new information | Higher accuracy and lower computation complexity | -Time-consuming computation process -Excessive parameter adjustment |
Classification and regression algorithms |
| [13] | Nov./Dec. 2020 |
An SQR model is proposed, which is a new nonparametric probabilistic prediction method | Providing an efficient framework for regional wind power probabilistic prediction with highly reliable performance | Complex nonlinear and high dimensional structure | Classification and regression algorithms |
| [14] | October 2021 |
On basis of the QRNN, the structure of the DNN is improved to adapt regional wind power forecasting as well as constructing the DQR | -The deep quantile regression is proposed to improve the performance of the QRNN -The local-connected method is applied to the input layer of the neural network for tackling the challenge of the massive data |
Each test takes 72 hours, so it is impossible to clearly determine its effects with no parameters and time | Classification and regression algorithms |
| [15] | June 2020 |
The deep architecture and nonlinearity of CSTWPP, spatial–temporal features inside the power of multiple wind farms can be effectively extracted. The accuracy of this short-term forecasting approach is significantly higher than existing models. | -The powerful ability of CSTWPP to extract spatial–temporal features from multiple wind farms -Superiority over other competing methods |
- Time-consuming computation process -Graphics processing units (GPU) is used to speed up the training process | Deep Learning algorithms |
| [16] | March 2022 |
-A deep learning architecture STCN based on a graph model for spatiotemporal wind power forecasting -A novel directed graph model and the corresponding GCN structure |
Fewer input time steps cause the STCN model to learn temporal features insufficiently, affecting the forecasting results | The STCN model exhibit certain interpret-ability, which is not available in traditional deep learning models |
Deep Learning algorithms |
| [17] | July 2020 |
The improved deep mixture density network (IDMDN) has better function approximation and density estimation ability than conventional shallow MDN | It is not necessary to obtain the deterministic prediction result firstly and acquire the probabilistic result by post-processing | -Slow convergence speed | Feed-forward neural network algorithms |
| [18] | May 2020 |
Improvement in the efficiency and stability of ANN models by varying the number of prior 1 h periods | Improvement of model performance, efficiency and stability for the performance of ANN- based WPF models | -Possible disadvantages of ANN Model in short term prediction of wind power generation | Feed-forward neural network algorithms |
| [19] | February 2021 |
Developing fuzzy model and model predictive control for prediction of wind power for the particularly selected location in India | The proposed models can be employed for the estimation of wind speed and wind power generation of any location in the world with having the complete information | -The time for calculating the wind power is 1 second. It is difficult to estimate the wind power during the summer period in which wind speed is very low. | Rule-based algorithms |
| [20] | January 2021 |
Development of a new ensemble neural forecast framework (ENFF) to accurately forecast the wind speed | -Enhancing the utilization of super-capacitor energy storage (SCES) as the N-1 contingency events -Being easily extended to N-1-1 contingency |
It is not economical to deploy energy storage only for VIS as these events are less frequent in power systems | Feed-forward neural network algorithms |
| [21] | August 2020 |
Located by the NWP information and time windows to improve the low forecasting accuracy of rolling WPP | The hybrid approach combined with neural network and persistence method | -The relevance of the day ahead is doubted due to the great change of wind -The setting of neural network parameters is a big issue |
Feed-forward neural network algorithms |
| [22] | January 2021 |
An improved random forest short-term prediction model based on the hierarchical output power | -Discretizing the power data to divide the large- scale training data and remove abnormal data -Fewer regression trees -Better performance |
The tree size has a great impact. -It is slow to run if there are more trees -It is not accurate if there are fewer trees |
Classification and regression algorithms |
| [23] | March 2020 |
The probabilistic wind power forecasting (WPF) results are utilized as one part in the micro-grid (MG) system for optimal dispatching | Automatically generate optimal compromise solutions for decision makers | Longer training duration | Classification and regression algorithms |
| [24] | April 2022 |
-A Bi-LSTM network and1D-CNN in parallel connection to form a multi-feature fusion (MFF) framework, which can extract spatiotemporal correlation features of the load data -The eigenvalue can be found to reduce the data |
-Enhancing the feature extraction capability of the 1D-CNN network by a self- attention mechanism | More LSTM parameter settings require to be adjusted |
Deep Learning algorithms |
| [25] | January 2022 |
-A hierarchical clustering method based on weighted multivariate time series motifs (WMTSM) is used to analyze the static, dynamic, and meteorological characteristics of regional wind power -Based on the clustering analysis, the correlation coefficients are formulated as the weights for the accuracy of samples to optimize the cost function of conditional LP (CLP) |
The result of clustering, the CLP for each cluster is quantified, which can improve the accuracy of sample utilization, and further enhance the performance of CNQR | -Highly affected by the accuracy of NWP and the static relationship between the wind power and speed | Feed-forward neural network algorithms |
| [26] | April 2020 |
Ensemble learning models provide a better prediction of wind power | Better performance of wind power prediction by the ensemble models considering lagged data | Spatiotemporal dependencies are not considered in ensemble learning models and machine learning models | Classification and regression algorithms |
| [27] | August 2020 |
-A novel hybrid neural network (NN)-based day-ahead (24 hour horizon) wind speed forecasting is proposed -Single- and multi-features and their effect on the accuracy of wind speed prediction are analyzed |
-Very effective for day-ahead wind speed prediction - Only need wind speed as a feature |
It is not clear how to select the eigenvalues of historical data | Feed-forward neural network algorithms |
| [28] | November 2020 |
The data regression (DR) algorithm gets meaningful training data to reduce the number of modeling data and improve the computing efficiency | Effectively reduce computing time by data regression algorithm | It is difficult to assess errors for wind speed forecasts due to large variations | Classification and regression algorithms |
| [29] | September 2022 | A comprehensive review of the state of the art of wind speed and power forecasting models is presented for wind turbines located in different segments of power systems | Due to the variable nature of wind speed and its relationship to meteorological variables, it is possible to study the accuracy of integrating physical forecasting methods into hybrid models | Individual forecasting algorithm has been replaced by hybrid algorithms combining mainly AI-based and statistical methods | Feed-forward neural network algorithms |
| [30] | July 2021 |
-This model has good generalization ability and robustness -Providing a more reliable basis for power grid dispatch |
Higher accuracy and better generalization ability by Adaboost-PSO-ELM wind power prediction model | The training samples are selected based on experience | Feed-forward neural network algorithms |
| [31] | March 2020 |
Improving the accuracy of ultra-short-term wind power prediction | Better performance based on SSA analog integrated circuit design | Longer training time | Feed-forward neural network algorithms |
| [32] | February 2022 |
A combined deep neural network model by integrating the advantages of the CNN and LSTM neural network | Excellent performance of the proposed algorithm in comparison to several state of-the-art WPF models | Low computational ability of the algorithm in selecting CLSTM hyperparameters | Deep Learning algorithms |
| [33] | July 2020 |
A short-term wind power forecasting model including VMD decomposition, ConvLSTM predictor and error series modeling | Removing the nonstationary features of the raw wind power series |
A large computational cost to obtain the optimal parameters | Deep Learning algorithms |
| [34] | October 2021 |
Multi-source NWP is used in WPPF, and its long-term temporal error pattern is discussed | -Higher deterministic prediction accuracy -Better probabilistic evaluation score |
-Time-consuming computation process -Complex configuration |
Deep Learning algorithms |
| [35] | September 2020 |
-The proposed forecasting engine composed two-dimensional convolution neural network (TDCNN) -Trained by improved optimization algorithm based on particle swarm optimization |
Fine-tuning the weights of TDCNN to increase the prediction accuracy of the forecast engine | Longer time for model training due to high requirement of data quality | Deep Learning algorithms |
| [36] | March/April 2022 | -The WD-IGFCM-LSTMS model -Six fluctuation features that reflect the shape characteristics are extracted to quantify the partitioned waves |
Improving the global searching ability of the GWO to select the initial clustering center of fuzzy C-means more effectively | -Longer time to calculate the parameters of fuzzy C-means, modeling and prediction of LSTM | Deep Learning algorithms |
| [37] | February 2022 |
Using meteorological forecasts from two NWP models (ECMWF and GFS) as input data yields better results than using a single NWP model | -Presenting real wind speed data and obtain higher accuracy of models with more numerical weather prediction (NWP) points | -We have tested it to find that too much input data will result in slow operation -Only one hour can be predicted | Deep Learning algorithms |
| [38] | June 2022 |
-Speeding up the convergence of the model dramatically to avoids falling into local optima. -Reducing the influence of man-made random selection of LSTM network hyperparameters on the prediction results | Lower influence of parameters | - LSTM has more parameters than SVM, GRMM, RBF, and other modeling methods, so it will become a big issue in computation process - The computation times will increase significantly when the amount of training data is large -The accuracy needs to be confirmed |
Deep Learning algorithms |
| [39] | June 2022 |
The encoder–decoder LSTM for medium-term wind speed based on a real-time measurement dataset, which were compared with two well- known conventional methods | Easy to determine the eigenvalue by using encoder–decoder | Improper correlation and weight ratio of coded data | Deep Learning algorithms |
| [40] | May 2021 |
The sample classification features mined by the CNN are submitted to the numerical prediction task as supplementary knowledge to help the training of the LSTM prediction models | -Effectively improve the accuracy of WPF based on sample similarity analysis | Exploring whether mode classification task can provide valuable knowledge for numerical prediction | Deep Learning algorithms |
| [41] | October 2022 |
-Based on historical observations, combined with deterministic point forecasts, WindGMMN is developed to generate a large number of realistic wind power scenarios with similar characteristics to real wind power -The proposed WindGMMN is unbound from statistical hypotheses -Producing a series of possible forecasting scenarios without a time horizon and number restrictions by simply adjusting parameters |
-Capturing the probability distribution characteristics of actual wind power scenarios -Reflecting the temporal correlations of wind power scenarios |
It is difficult to distinguish which prediction interval is better | Deep Learning algorithms |
| [42] | April 2021 |
Significant improvements in the peak value forecasting have been observed by using the fused network of short and long Bi-LSTM networks with DRNets | Bi-LSTM network can improve performance by eliminating propagated errors | -The test for bidirectional long short-term memory (Bi-LSTM) layers will be more troublesome -The LSTM prone to overfitting due to the increasing depth of DNN, which degrades the performance of the deep learning model |
Deep Learning algorithms |
| [43] | September 2022 | -Accurate mid- and long-term wind power forecasting can provide an important basis for power distribution and energy storage configuration after wind power grid-connected -A dynamic pressure model is introduced in MSIN to modify wind power generation forecast with having highly correlated physical characteristics |
-Multi-step informer network improves forecast accuracy by 29% compared with informer network -The multi-step process is beneficial to the anti-risk ability and security of the network |
In the case of ignoring meteorological factors such as surface temperature and relative humidity, the coupling factors between multiple wind turbines need to be considered in the research | Deep Learning algorithms |
| [44] | September 2022 | Considering the nonlinear and fluctuating characteristics of wind speed and wind power series, a hybrid short-term wind power forecasting model based on data decomposition (VMD) and joint deep neural network (CNN-LSTM) is proposed | The wind speed and wind power sequences in the input data are decomposed by variational mode decomposition to reduce the noise in the raw signal | Using IPSO to select the layers and neurons of LSTM would cause the issue of too long calculation time | Deep Learning algorithms |
| [45] | May 2022 |
-The GRNN model is better than the SVR model regarding the RMSE value -The inclusion of average electrical load data is possible when the forecasting system can obtain near real-time observation data of electricity load |
Which weather parameters affect the electricity load? Primary impact is temperature; secondary impact is wind speed. |
The temperature affects the power demand in terms of load forecasting | Feed-forward neural network algorithms |
| [46] | April 2020 |
Significantly increase the accuracy in short term wind power prediction | -Greatly extract the trend information of wind power -Better accuracy in short-term wind power prediction |
The structure of proposed nonlinear combination model | Feed-forward neural network algorithms |
| [47] | April 2020 |
A flexible framework for forecasting wind generated power in the case of disjointed batch of historical data to enhance the accuracy of wind power output modeling | Reaching better performance of the forecast algorithm | -Complex computation process -Increasing dimensions of the input vector |
Classification and regression algorithms |
| [48] | August 2021 |
Identifying changes in the time series, avoiding abrupt loss of information, and maintaining a controlled number of examples, since there is adaptive selection of the active kernel | Dealing with the increasing kernel matrix size associated with time and memory complexities, and the overfitting problem | -An accurate very-short term forecasts for one or multiple wind farms | Classification and regression algorithms |
| [49] | February 2020 |
-Improving learning performance by reducing the variance of the WPG forecast uncertainty -Extensive simulations based on practical WPG generation data and forecasting |
Managing the wind power generation (WPG) forecast uncertainty by a reinforcement leaning-based ESS operation strategy | -Requiring complete information, including future values, to achieve cross period prediction | Rule-based algorithms |
| [50] | June 2022 |
The weather research and forecasting (WRF) model is utilized with the wind farm parameterization (WFP) method for short-range wind power forecasting simulation | -The horizontal downsize method can prolong more than 10 km in the velocity field, especially for higher incoming wind velocity -Improving the accuracy of the power forecast for higher wind speed simulations | -Adding some complexity of the correlation works -There may be time and space difference between real-time data and geographical location. -Leading to uncertainty of data |
Classification and regression algorithms |
| [51] | April 2020 |
The proposed approach is effective on achieving probabilistic WTPF with high reliability as well as satisfactory sharpness | -Developed for the wind power forecasting by the EDM method -Applied to estimate the uncertain behavior of WTP |
-Obtaining the highest CRPS values -The poorest performance. |
Classification and regression algorithms |
| [52] | September 2022 | Lower training complexity in the proposed model to ensure prediction accuracy compared with traditional models | -Tackling seasonality and randomness of wind power with moderate model complexity -Effectively guarantees the convergence speed and efficiency of the training process |
If the input data are nonstationary so that the proposed data preprocessing fails, the proposed model may not be able to obtain accurate prediction results | Classification and regression algorithms |
| [53] | September 2022 | The load schedule, electricity consumption, use of installed power, boundary conditions of generation, and ensuring energy balance were taken into account | For the average monthly values of renewable energy sources generation with an increase in power by 1.6 times, there was a decrease in electricity consumption by 1.57–4 times. | The selection of the WG installation location for load object is difficult to comprehensively take into account, since the system load will vary from day to day | Rule-based algorithms |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).





