Fuzzy Adaptive Parameter in the Dai-Liao Optimization Method Based on Neutrosophy

1. Introduction and Background Results

Numerous iterative methods have been developed to solve the large-scale unconstrained optimization problem

$$\mathrm{minimize}f\left(\mathbf{x}\right),\mathbf{x}\in {\mathbb{R}}^n,$$

(1)

in which $f:{\mathbb{R}}^n\to \mathbb{R}$ is a continuously differentiable function and bounded below. Continuing well established notation, ${\mathbf{g}}_k=\mathbf{g}\left({\mathbf{x}}_k\right)=\nabla f\left({\mathbf{x}}_k\right)$ stands for the gradient vector of f at the actual iterative point ${\mathbf{x}}_k$, and further ${\mathbf{y}}_{k-1}={\mathbf{g}}_k-{\mathbf{g}}_{k-1}$ and ${\mathbf{s}}_{k-1}={\mathbf{x}}_k-x_{k-1}$. Utilizing the extended conjugacy condition

$${\mathbf{d}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}=-t{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1},t>0,$$

(2)

Dai and Liao in [1] suggested the conjugate gradient (CG) iterations

$$x_{k+1}={\mathbf{x}}_k+{\alpha }_k{\mathbf{d}}_k,$$

(3)

where the ${\mathbf{x}}_k$ is the last calculated iteration, ${\mathbf{x}}_{k+1}$ is a new iterative point, ${\alpha }_k$ is a positive step size parameter defined as the output of an inexact line search, and ${\mathbf{d}}_k$ is a descent direction. The search directions $\{{\mathbf{d}}_k,k\ge 0\}$ are created by the recurrent regulation

$${\mathbf{d}}_k=\left\{\begin{array}{cc}-{\mathbf{g}}_0,\hfill & k=0,\hfill \\ -{\mathbf{g}}_k+{\beta }_k^{\mathrm{DL}}{\mathbf{d}}_{k-1},\hfill & k\ge 1,\hfill \end{array}\right.$$

(4)

where ${\beta }_k^{\mathrm{DL}}$ is the CG coefficient which describes the type of CG method by the general rule

$${\beta }_k^{\mathrm{DL}}=\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}-t\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}},$$

(5)

wherein $t>0$ is an appropriate scalar. The Dai–Liao (DL) method guarantees global convergence for uniformly convex objective functions. These results have attracted a lot of attention, leading to the creation of several methods based on various patterns for defining ${\beta }_k$. Most of these methods were developed by modifying the conjugate gradient parameter ${\beta }_k^{\mathrm{DL}}$ [2,3,4,5,6,7,8,9]. For more details, see the survey on the DL family of nonlinear CG methods in [10]. One of rules for defining ${\beta }_k$ is denoted as ${\beta }_k^{\mathrm{MHSDL}}$ and defined in [7] by

$${\beta }_k^{\mathrm{MHSDL}}=\frac{{\mathbf{g}}_k^{\mathrm{T}}\widehat{{\mathbf{y}}_{k-1}}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}-t\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}},$$

(6)

such that $\widehat{{\mathbf{y}}_{k-1}}={\mathbf{g}}_k-\frac{\parallel {\mathbf{g}}_k\parallel }{\parallel {\mathbf{g}}_{k-1}\parallel }{\mathbf{g}}_{k-1}$ and $t>0$ is as in (5).

Due to the large influence of the size t on numerical results generated by the DL class of CG methods [11], one of the most common issues is the determination of an appropriate value t. We can distinguish two research directions based on the previous results in determining proper values t in the DL established CG iterations. The first direction of research consists of a group of DL methods that aim to find a suitable constant value for t[1,2,6,7,8] during iterations, while the second direction consists of a group of DL methods that propose a suitable control in recalculating t in each iteration. In this research, we prioritize the second research stream: find values t that changes appropriately accros iterations. The quantity t determined in kth iterative step will be denoted by $t_k^{\left(i\right)}$, where i is a variant of the algorithm for defining t.

Some of the most important adaptive choices for the DL parameter $t_k$ will be presented in the rest of this section. Hager and Zhang in [12,13] suggested the CG-DESCENT method, which is classified into the group of the DL CG methods (5) defined by $t\equiv t_k^{\left(1\right)}$ and

$$t_k^{\left(1\right)}=2\frac{\parallel {\mathbf{y}}_{k-1}{\parallel }^2}{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}.$$

(7)

Dai and Kou suggested DK method in [14] where the CG coefficient ${\beta }_k^{\mathrm{DK}}$ is of the form

$${\beta }_k^{\mathrm{DK}}=\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{d}}_{k-1}}-\left({\tau }_k+\frac{\parallel {\mathbf{y}}_{k-1}{\parallel }^2}{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}-\frac{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}{\parallel {\mathbf{s}}_{k-1}{\parallel }^2}\right)\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}.$$

(8)

In the equality (8), the parameter ${\tau }_k$ is defined utilizing the self-scaling memoryless BFGS method. It is also obvious from (8) that the DK method is involved into the DL CG class of methods where $t\equiv t_k^{\left(2\right)}$ is defined by

$$t_k^{\left(2\right)}={\tau }_k+\frac{\parallel {\mathbf{y}}_{k-1}{\parallel }^2}{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}-\frac{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}{\parallel {\mathbf{s}}_{k-1}{\parallel }^2}.$$

(9)

Babaie-Kafaki and Ghanbari in [15] proposed the subsequent two rules for calculating t in (5):

$$t_k^{\left(3\right)}=\frac{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\parallel {\mathbf{s}}_{k-1}{\parallel }^2}+\frac{\parallel {\mathbf{y}}_{k-1}\parallel }{\parallel {\mathbf{s}}_{k-1}\parallel }$$

(10)

and

$$t_k^{\left(4\right)}=\frac{\parallel {\mathbf{y}}_{k-1}\parallel }{\parallel {\mathbf{s}}_{k-1}\parallel }.$$

(11)

Andrei in [16] originated a new DL class, denoted DLE, where $t\equiv t_k^{\left(5\right)}$ is defined by

$$t_k^{\left(5\right)}=\frac{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\parallel {\mathbf{s}}_{k-1}{\parallel }^2}.$$

(12)

A special place in the DL iterations is occupied by the DL method with

$$t_k^{\left(6\right)}=\upsilon \frac{\parallel {\mathbf{y}}_{k-1}{\parallel }^2}{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}},$$

(13)

where $\upsilon >\frac{1}{4}$ is a constant, has been defined according to the sufficient descent condition

$${\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_k\le -c{\parallel {\mathbf{g}}_k\parallel }^2,\forall k\ge 0,$$

(14)

such that $c>0$ is a constant independent of the cost function convexity and the line search rules (for more details see [17]).

Lotfi and Hosseini in [18] suggested the subsequent rule

$$t_k^{\left(7\right)}=max\left\{t_k^{\left(7^{*}\right)},t_k^{\left(6\right)}\right\},$$

(15)

where

$$t_k^{\left(7^{*}\right)}=\frac{\left(1-{\hslash }_k\parallel g_{{k-1\parallel }^r}\right){\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{g}}_k+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{y}}_{k-1}^{\mathrm{T}}{\mathbf{s}}_{k-1}}{\hslash }_k\parallel {\mathbf{g}}_{k-1}{\parallel }^r{\parallel {\mathbf{s}}_{k-1}\parallel }^2}{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\hslash }_k\parallel {\mathbf{g}}_{k-1}{\parallel }^r{\parallel {\mathbf{s}}_{k-1}\parallel }^2},$$

(16)

$${\hslash }_k=C+max\left\{-\frac{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\parallel {\mathbf{s}}_{k-1}{\parallel }^2},0\right\}{\parallel {\mathbf{g}}_{k-1}\parallel }^{-r},$$

(17)

and $C,r$ are positive constants.

Ivanov et al. in [19] proposed a variant of the Dai-Liao CG method (6), known as the Effective Dai-Liao (EDL) CG method, where $t\equiv t_k^{\left(8\right)}$ is determined as

$$t_k^{\left(8\right)}=\frac{{∥{\mathbf{g}}_k∥}^2}{max\left\{1,{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{g}}_k\right\}+\left(max\left\{0,\frac{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{g}}_k}{\parallel {\mathbf{g}}_k{\parallel }^2}\right\}+1\right){∥{\mathbf{g}}_k∥}^2}.$$

(18)

The experiments performed in [19] verify that the EDL iterations outperform many existing CG variants.

The basics of neutrosophy. Neutrosophic logic was applied in [20] in regulating proper step sizes for a class of accelerated gradient-descent optimization methods. The approach in [20] assumes an additional fuzzy parameter which stabilizes the behavior of an important class of gradient-descent family. Motivated by that approach, in this research we apply neutrosophy in order to enhance performances of DL methods. Based on the review and analysis of the class of DL methods, we propose a new method for determining $t_k$. The proposed method defines $t_k$ as the output produced by an appropriate neutrosophic logic controller (NLC). Our idea is to replace the classical parameter $t_k$ by an adaptive neutrosophic logic parameter ${\nu }_k$, determined as the output of the NLC. Since $0\le t_k\le 1$ our decision is to define $t_k$ as the value of ${\nu }_k$, without additional parameters.

A fuzzy set theory utilizes a membership function (MF) ${\mathrm{T}}_{\mathsf{\Psi }}\left(\lambda \right)\in [0,1],\lambda \in \mathsf{\Lambda }$ in the universe $\mathsf{\Lambda }$ that defines the degree of membership of $\lambda$ in $\mathsf{\Psi }\subset \mathsf{\Lambda }$ [21]. The intuitionistic fuzzy set (IFS) $\mathsf{\Psi }$ is established using both degrees of membership and non-membership function $T_{\mathsf{\Psi }}\left(\lambda \right),F_{\mathsf{\Psi }}\left(\lambda \right)\in [0,1],\lambda \in \mathsf{\Lambda }$ [22], which are mutually corelated by ${\mathrm{T}}_{\mathsf{\Psi }}\left(\lambda \right),{\mathrm{F}}_{\mathsf{\Psi }}\left(\lambda \right):\mathsf{\Lambda }\to [0,1]$ and $0\le {\mathrm{T}}_{\mathsf{\Psi }}\left(\lambda \right)+{\mathrm{F}}_{\mathsf{\Psi }}\left(\lambda \right)\le 1$. The IFS theory was originally generalized in [23,24] by the the neutrosophic theory. The background of the neutrosophic logic is the utilization of the indeterminacy $\mathrm{I}\left(\lambda \right)$. In that direction, entries of a neutrosophic set are determined by three independent MFs [23,24]: the truth-MF $\mathrm{T}\left(\lambda \right)$, the indeterminacy-MF $\mathrm{I}\left(\lambda \right)$, and the falsity-MF $\mathrm{F}\left(\lambda \right)$. Due to the indeterminacy-MF, the neutrosophic logic is based on the symmetry involved in the ordered triple of MFs $(\mathrm{T},\mathrm{I},\mathrm{F})$ and the inequality $0\le \mathrm{T}+\mathrm{I}+\mathrm{F}\le 3$ if all three MFs are independent. Clearly, $\mathrm{T}$ is the symmetric pole to its opposite pole $\mathrm{F}$ with respect to $\mathrm{I}$, which represents an axis of the symmetry between $\mathrm{T}$ and $\mathrm{F}$ [25]. The same observation is valid for refined neutrosophic set that assumes the refined indeterminacies ${\mathrm{I}}_1$ and ${\mathrm{I}}_2$ between $\mathrm{T}$ and $\mathrm{F}$ [26]. The MFs of a neutrosophic set $\mathsf{\Psi }$ satisfy ${\mathrm{T}}_{\mathsf{\Psi }}\left(\lambda \right),{\mathrm{I}}_{\mathsf{\Psi }}\left(\lambda \right),{\mathrm{F}}_{\mathsf{\Psi }}\left(\lambda \right):\mathsf{\Lambda }\to [0,1]$, which which based on their independence implies $0\le {\mathrm{T}}_{\mathsf{\Psi }}\left(\lambda \right)+{\mathrm{I}}_{\mathsf{\Psi }}\left(\lambda \right)+{\mathrm{F}}_{\mathsf{\Psi }}\left(\lambda \right)\le 3$, and enables a symmetry between them. In [27], the authors originated a neutrosophic-based multiple criteria decision-making procedure based on previously introduced symmetry measure.

The benefits of the NL approach over the FL and IFL are discussed in [20].

Motivation and highlights of main results. Our task in this paper is to improve the behavior of DL class for solving unconstrained nonlinear optimization problems with the support of an appropriate neutrosophic logic system. The principal results obtained in this paper are presented as follows.

(1)

We examine the application of NL in determining the parameter t in the Dai-Liao CG method (5).

(2)

A theoretical analysis is accomplished to confirm the global convergence of the proposed method.

(3)

A numerical comparison is given between the proposed FDL algorithm and other known DL algorithms.

The sections of the paper are arranged as follows. Introduction, motivation and a brief review of obtained results are presented in Section 1. A neutrosophic-based control for defining appropriate changeable values $t_k$ is proposed in Section 2. Moreover, we present details of the FDL method. The global convergence behavior of the FDL method is examined in Section 3. Numerical comparison of the FDL method with main standard DL methods is presented in Section 4, and a comparison with some known variations of the DL class of methods, is also given. Final conclusions are presented in the concluding section.

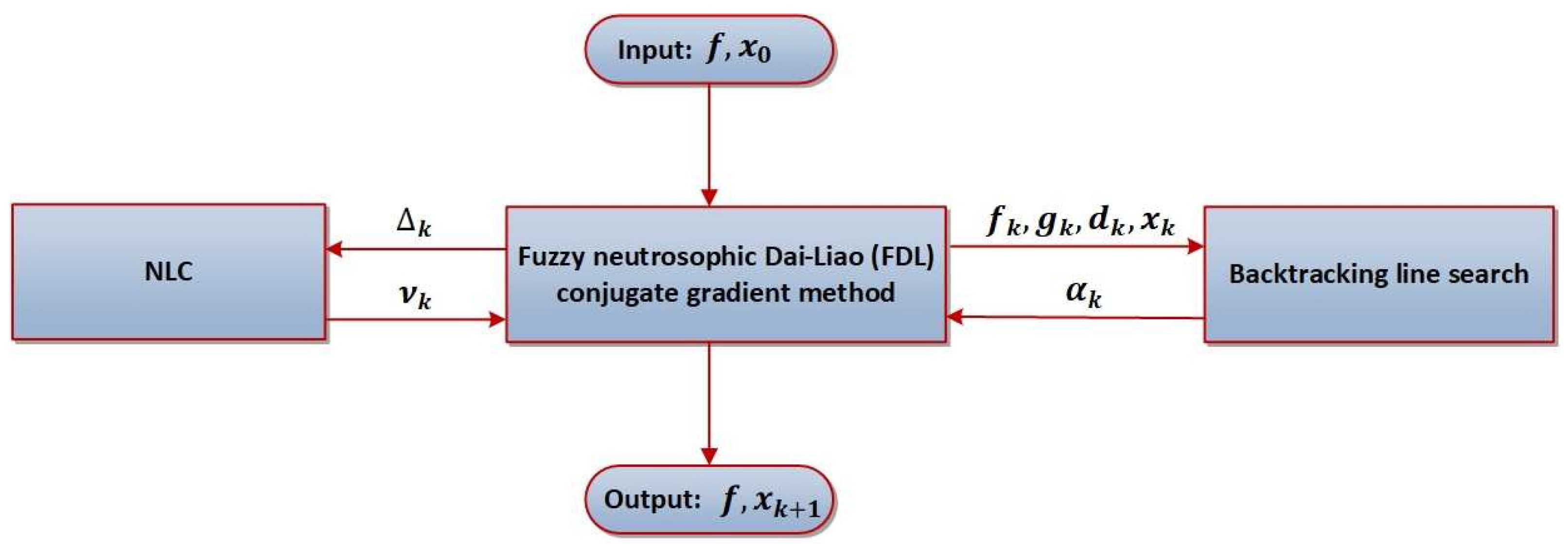
2. Fuzzy Neutrosophic Dai-Liao Conjugate Gradient Method

The fuzzy neutrosophic Dai-Liao CG method is defined as a modification of the Dai-Liao CG method (3), where the search directions $\left\{{\mathbf{d}}_k\right\}$ are calculated by the recurrence rule

$${\mathbf{d}}_k=\left\{\begin{array}{cc}-{\mathbf{g}}_0,\hfill & k=0,\hfill \\ -{\mathbf{g}}_k+{\beta }_k^{\mathrm{FDL}}{\mathbf{d}}_{k-1},\hfill & k\ge 1,\hfill \end{array}\right.$$

(19)

where the CG coefficient ${\beta }_k^{\mathrm{FDL}}$ is defined by

$${\beta }_k^{\mathrm{FDL}}=\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}-{\nu }_k\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}},$$

(20)

such that ${\nu }_k:={\nu }_k$ is a proper fuzzy neutrosophic parameter. Our intention is to define ${\nu }_k$ as a function of ${\mathsf{\Delta }}_k:=f\left({\mathbf{x}}_k\right)-f\left({\mathbf{x}}_{k+1}\right)$ i.e., ${\nu }_k:={\nu }_k\left({\mathsf{\Delta }}_k\right)$. More precisely, ${\nu }_k\left({\mathsf{\Delta }}_k\right)$ is defined subject to the following constraint

$$0\le {\nu }_k\left({\mathsf{\Delta }}_k\right)\le 1.$$

(21)

It is know that ${\nu }_k\left({\mathsf{\Delta }}_k\right)=0$ reduces (2) into

$${\mathbf{d}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}=0.$$

(22)

Hence, the equation (22) can be considered as a reflection of the conjugacy condition, which in conjuction with (4) determines the HS parameter [28]

$${\beta }_k^{\mathrm{HS}}=\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}.$$

(23)

Alternatively, for ${\nu }_k\left({\mathsf{\Delta }}_k\right)=1$, the equation (2) is considered as a conjugacy condition that implicitly satisfies the quasi-Newton characteristics. For more details on these cases, see [1,10].

The idea for defining a new parameter $tk$ in the Dai-Liao CG method (5) comes from the neutrosophic logic. According to this decision, our intention is to define $t_k={\nu }_k\left({\mathsf{\Delta }}_k\right)$ inside the interval $[0,1]$ according to neutrosophic principles.

The generic layout of the fuzzy neutrosophic Dai-Liao CG method is given in the diagram in Figure 1.

The input of the NLC presented in Figure 1 is ${\mathsf{\Delta }}_k:=f\left({\mathbf{x}}_k\right)-f\left({\mathbf{x}}_{k+1}\right)$ and the output is the desired step size ${\nu }_k$. This means that our basic idea is to define ${\nu }_k$ based on two consecutive values of the objective function f. On the other hand, the backtracking line search is reponsible for appropriate step lengths ${\alpha }_k$ in (3) and then the descent direction ${\mathbf{d}}_k$ by (19). Using ${\nu }_k$ it is possible to compute ${\beta }_k^{\mathrm{FDL}}$ in (20). Finally, (3) generates new iterative point $x_{k+1}$.

To develop the FDL method, it is necessary to plan three global steps: neutrosophistication, neutrosophic inference engine, and de-neutrosophistication (score function).

(1)

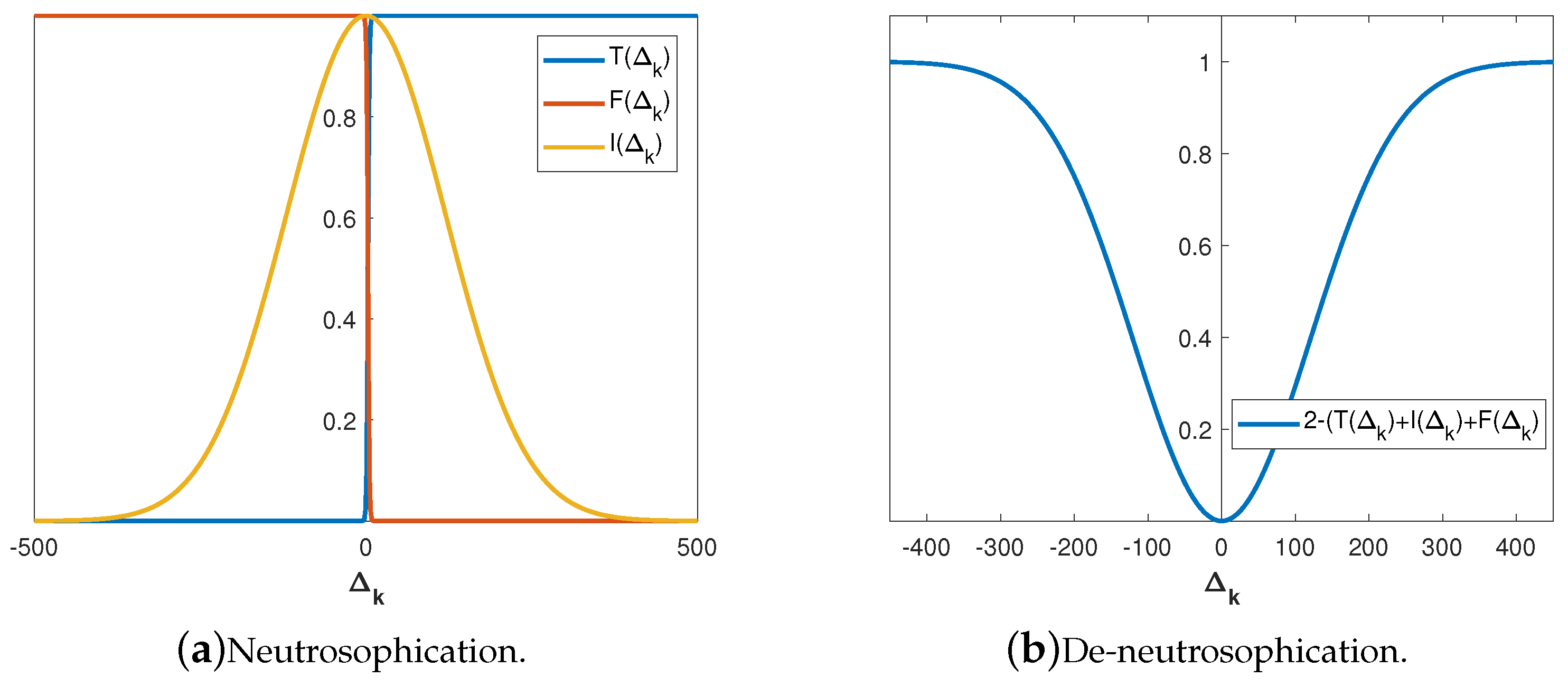
Neutrosophication maps the input ${\mathsf{\Delta }}_k:=f\left({\mathbf{x}}_k\right)-f\left({\mathbf{x}}_{k+1}\right)$ into neutrosophic ordered triplets $(\mathrm{T}\left({\mathsf{\Delta }}_k\right),\mathrm{I}\left({\mathsf{\Delta }}_k\right),\mathrm{F}\left({\mathsf{\Delta }}_k\right))$. The MFs are defined with the aim to improve the CG iterative rule exploiting numerical experience. The sigmoid function with the slope defined by ${\varsigma }_1$ at the crossover point $\mathsf{\Delta }={\varsigma }_2$ is a proper choice for $\mathrm{T}$:

$$\mathrm{T}\left(\mathsf{\Delta }\right)=1/\left(1+{\mathrm{e}}^{-{\varsigma }_1(\mathsf{\Delta }-{\varsigma }_2)}\right).$$

(24)

A proper choice for $\mathrm{F}$ is the following sigmoid function:

$$\mathrm{F}\left(\mathsf{\Delta }\right)=1/(1+{\mathrm{e}}^{{\varsigma }_1(\mathsf{\Delta }-{\varsigma }_2)}).$$

(25)

The Gaussian function with the standard deviation ${\varsigma }_1$ and the mean ${\varsigma }_2$ defines the indeterminacy $\mathrm{I}$:

$$\mathrm{I}\left(\mathsf{\Delta }\right)={\mathrm{e}}^{-\frac{{(\mathsf{\Delta }-{\varsigma }_2)}^2}{2{\varsigma }_1^2}}.$$

(26)

Then the neutrosophication of $\mathsf{\Delta }\in \mathbb{R}$ is defined as the transition $\mathsf{\Delta }\to \langle \mathrm{T}\left(\mathsf{\Delta }\right),\mathrm{I}\left(\mathsf{\Delta }\right),\mathrm{F}\left(\mathsf{\Delta }\right)\rangle$, where the MFs are determined in (24)–(26).

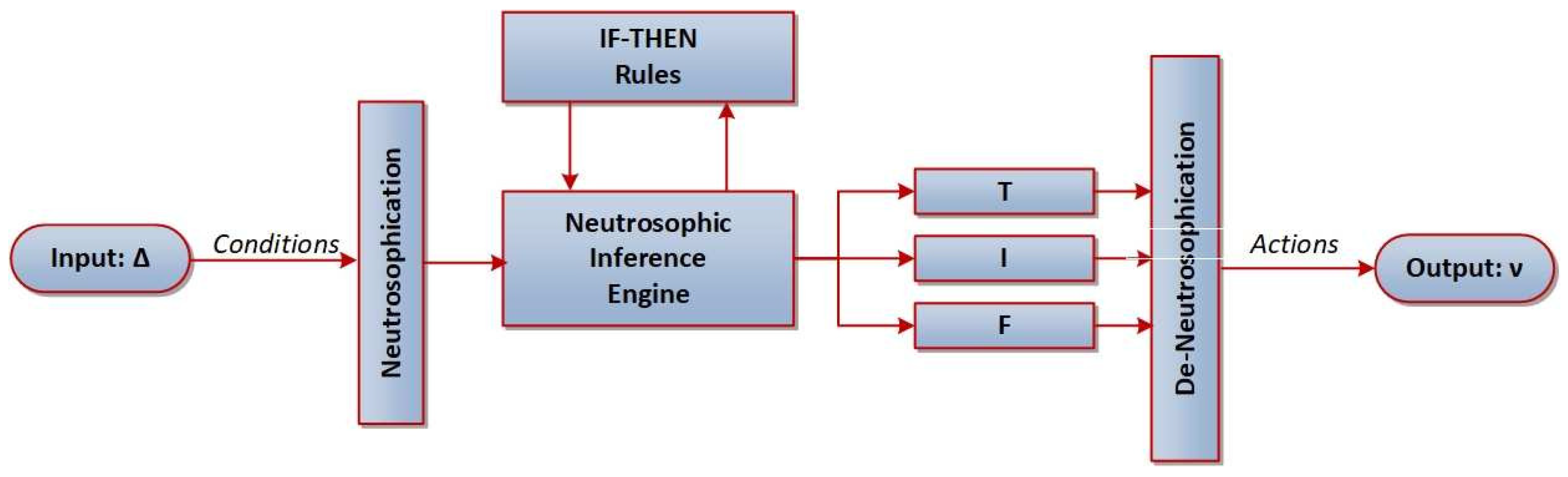
(2)

Neutrosophic inference between an input fuzzy set $\mathfrak{I}$ and an output fuzzy set is based on the subsequent “IF–THEN” regulations:

$$\begin{gathered} {\Re }_1:\mathrm{If}\mathfrak{I}=S_P⟹\mathfrak{O}=\{\mathrm{T},\mathrm{I},\mathrm{F}\} \\ {\Re }_2:\mathrm{If}\mathfrak{I}=S_N⟹\mathfrak{O}=\{\mathrm{T},\mathrm{I},\mathrm{F}\}. \end{gathered}$$

Fuzzy sets $S_P$ and $S_N$ point, respectively, to positive or negative errors. Applying the unification $\Re ={\Re }_1\cup {\Re }_2$, we define ${\mathfrak{O}}_i=\mathfrak{I}\circ {\Re }_i$, $i=1,2$, where ∘ denotes the fuzzy transformation. In addition, for a fuzzy vector $\zeta =\{\mathrm{T}\left({\mathsf{\Delta }}_k\right),\mathrm{I}\left({\mathsf{\Delta }}_k\right),\mathrm{F}\left({\mathsf{\Delta }}_k\right)\}$, it follows ${\kappa }_{\mathfrak{I}\circ \Re }\left(\zeta \right)={\kappa }_{\mathfrak{I}\circ {\Re }_1}\bigvee {\kappa }_{\mathfrak{I}\circ {\Re }_2}=sup({\kappa }_{\mathfrak{I}}\bigwedge {\kappa }_{{\mathfrak{O}}_i})$, $i=1,2$, where ⋀ and ⋁ denote the $(min,max,max)$ and $(max,min,min)$ operator, respectively. In this research, the centroid defuzzification method is utilized to generate a vector of crisp outputs ${\zeta }^{*}\in {\mathbb{R}}^3$:

$${\zeta }^{*}=\frac{{\int }_{\mathfrak{O}}\zeta {\kappa }_{\mathfrak{I}\circ \Re }\left(\zeta \right)\mathrm{d}\zeta }{{\int }_{\mathfrak{O}}{\kappa }_{\mathfrak{I}\circ \Re }\left(\zeta \right)\mathrm{d}\zeta }.$$

(3)

De-neutrosophication is based on the transformation $\langle \mathrm{T}\left({\mathsf{\Delta }}_k\right),\mathrm{I}\left({\mathsf{\Delta }}_k\right),\mathrm{F}\left({\mathsf{\Delta }}_k\right)\rangle \to {\nu }_k\in \mathbb{R}$ resulting in a crisp value ${\nu }_k$ and suggested as:

$${\nu }_k=2-\left(\mathrm{T}\left({\mathsf{\Delta }}_k\right)+\mathrm{I}\left({\mathsf{\Delta }}_k\right)+\mathrm{F}\left({\mathsf{\Delta }}_k\right)\right).$$

(27)

The diagram of Figure 2 presents the NLC based on the neutrosophic rules.

The settings in the NLC employed in numerical testing are arranged in Table 1.

Our imperative requirement is $0\le {\nu }_k\left({\mathsf{\Delta }}_k\right)\le 1$, requested in (21). This statement is verified in Lemma 1.

Lemma 1. 

The inequality (21) holds for the given choice of the score function (27) and the parameters given in the Table 1.

Proof. 

In order to prove (21), we need to replace the MFs (24), (25), and (26) in (27). After applying the parameters from Table 1, we get

$$\mathrm{T}\left({\mathsf{\Delta }}_k\right)=1/\left(1+{\mathrm{e}}^{-(\mathsf{\Delta }-3)}\right),\mathrm{F}\left({\mathsf{\Delta }}_k\right)=1/\left(1+{\mathrm{e}}^{\mathsf{\Delta }-3}\right),\mathrm{I}\left({\mathsf{\Delta }}_k\right)={\mathrm{e}}^{-\frac{{\mathsf{\Delta }}_k^2}{2*{120}^2}}$$

Elementary calculation gives

$${\nu }_k\left({\mathsf{\Delta }}_k\right)=2-\left(\mathrm{T}\left({\mathsf{\Delta }}_k\right)+\mathrm{I}\left({\mathsf{\Delta }}_k\right)+\mathrm{F}\left({\mathsf{\Delta }}_k\right)\right)=1-{\mathrm{e}}^{-\frac{{\mathsf{\Delta }}_k^2}{28800}}.$$

(28)

A careful analysis of the function (28) inside the interval ${\mathsf{\Delta }}_k\in (-\infty ,+\infty )$ discovers $min{\nu }_k\left({\mathsf{\Delta }}_k\right)=0$ and $max{\nu }_k\left({\mathsf{\Delta }}_k\right)=1$, which proves the inequality (21).    □

Graphs of $\mathrm{T}\left({\mathsf{\Delta }}_k\right),\mathrm{I}\left({\mathsf{\Delta }}_k\right),\mathrm{F}\left({\mathsf{\Delta }}_k\right)$ are displayed in Figure 3a. The fulfilment of the requirements (21) in the NLC output ${\nu }_k$ generated throughout the described de-neutrosophication is illustrated in Figure Figure 3b.

Remark 1. 

The objective function decreases with the flow of iterations and tends to the minimal value, which means ${lim}_{k\to \infty }{\mathsf{\Delta }}_k=0$, i.e., ${lim}_{k\to \infty }{\nu }_k\left({\mathsf{\Delta }}_k\right)=0$. Such behavior leads to ${\nu }_k\to 0$ as the minimum of f approaches, so the impact of the proposed neutrosophic strategy decreases and disappears, which agrees with our goal.

Remark 2. 

Obviously, larger values of ${\mathsf{\Delta }}_k$ lead to increasing values ${\nu }_k\left({\mathsf{\Delta }}_k\right)$ approaching to 1, which will be denoted as ${\nu }_k\left({\mathsf{\Delta }}_k\right)\nearrow 1$. In addition, based on the limit ${\mathsf{\Delta }}_k\to 0$, we anticipate smaller values ${\nu }_k\left({\mathsf{\Delta }}_k\right)$ approaching 0, i.e., ${\nu }_k\left({\mathsf{\Delta }}_k\right)\searrow 0$ in final iterations. As a result, ${\nu }_k\left({\mathsf{\Delta }}_k\right)$ is suitable as an adjustable regulator for the quantity t in the Dai–Liao CG method.

The backtracking line search from [29] begins from $\alpha =1$ and generates further step sizes which ensure decrease of the goal function in each iteration. Algorithm 1, restated from [30], is used to define the primary step size ${\alpha }_k$.

Algorithm 1 The backtracking line search.

Algorithm 2 of the FDL method is described as follows:

Algorithm 2 Fuzzy neutrosophic Dai-Liao (FDL) conjugate gradient method.

3. Convergence Examination

The subsequent assumptions are necessary during the theoretical examination of the FDL algorithm.

Assumption 1. 

$\left(1\right)$ The level set $\mho =\{\mathbf{x}\in {\mathbb{R}}^n|f\left(\mathbf{x}\right)\le f\left({\mathbf{x}}_0\right)\}$ of the iterative process (3) is bounded.

$\left(2\right)$ The objective f is continuously differentiable in a neighborhood $\mathcal{P}$ of ℧ with the Lipschitz continuous gradient $\mathbf{g}$. Such assumption initiates the existence of a constant $L>0$ such that

$$\parallel \mathbf{g}\left(\mathbf{u}\right)-\mathbf{g}\left(\mathbf{v}\right)\parallel \le L\parallel \mathbf{u}-\mathbf{v}\parallel ,\forall \mathbf{u},\mathbf{v}\in \mathcal{P}.$$

(29)

The Assumption 1 provides the existence of quantities $\mathsf{{\rm Y}}$ and $\gamma$ such that

$$\parallel \mathbf{u}-\mathbf{v}\parallel \le \mathsf{{\rm Y}},\forall \mathbf{u},\mathbf{v}\in \mathcal{P}$$

(30)

and

$$\parallel \mathbf{g}\left(\mathbf{u}\right)\parallel \le \gamma ,\forall \mathbf{u}\in \mathcal{P}.$$

(31)

If Assumption 1 holds, in view of the uniform convexity of f, there exists $\theta >0$ satisfying

$${(\mathbf{g}\left(\mathbf{u}\right)-\mathbf{g}\left(\mathbf{v}\right))}^{\mathrm{T}}(\mathbf{u}-\mathbf{v})\ge \theta {\parallel \mathbf{u}-\mathbf{v}\parallel }^2,\forall \mathbf{u},\mathbf{v}\in \mho ,$$

(32)

or equivalently,

$$f\left(\mathbf{u}\right)\ge f\left(\mathbf{v}\right)+g{\left(\mathbf{v}\right)}^{\mathrm{T}}(\mathbf{u}-\mathbf{v})+\frac{\theta }{2}{\parallel \mathbf{u}-\mathbf{v}\parallel }^2,\forall \mathbf{u},\mathbf{v}\in \mho .$$

(33)

It follows from (32) and (33) that

$${\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\ge \theta {\parallel {\mathbf{s}}_{k-1}\parallel }^2$$

(34)

and

$$f\left({\mathbf{x}}_{k-1}\right)-f\left({\mathbf{x}}_k\right)\ge -\mathbf{g}{\left({\mathbf{x}}_k\right)}^{\mathrm{T}}{\mathbf{s}}_{k-1}+\frac{\theta }{2}{\parallel {\mathbf{s}}_{k-1}\parallel }^2.$$

(35)

By (29) and (34), one concludes

$$\theta \parallel {\mathbf{s}}_{k-1}{\parallel }^2\le {\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\le L{\parallel {\mathbf{s}}_{k-1}\parallel }^2,$$

(36)

and further $\theta \le L$.

The inequality (36) implies

$${\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}={\alpha }_{k-1}{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}>0.$$

(37)

Taking into account ${\alpha }_{k-1}>0$ and the last inequality, we conclude

$${\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}>0.$$

(38)

Lemma 2. 

[31,32] Let the constraints in Assumption 1 hold and the points $\left\{{\mathbf{x}}_k\right\}$ be produced by the iterations (3)-(4). Then the following inequality is satisfied:

$$\sum _{k=0}^{\infty }{\displaystyle \frac{\parallel {\mathbf{g}}_k{\parallel }^4}{\parallel {\mathbf{d}}_k{\parallel }^2}}<+\infty .$$

(39)

Lemma 3. 

Observe the suggested Fuzzy neutrosophic Dai-Liao CG method defined by (3), (19), (20). If the search procedure guarantees (38), for all $k\ge 0$, then

$${\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_k\le -c{\parallel {\mathbf{g}}_k\parallel }^2$$

(40)

for some $c\ge 0$.

Proof. 

In the initial stage it follows ${\mathbf{g}}_0^{\mathrm{T}}{\mathbf{d}}_0=-{\parallel {\mathbf{g}}_0\parallel }^2$. Since $c=1$, obviously (40) is satisfied in the initial stage $k=0$. Assume (40) for some $k\ge 1$. Applying the inner product of both the left and right hand side in (4) with ${\mathbf{g}}_k^{\mathrm{T}}$, it is concluded

$$\begin{array}{cc}\hfill {\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_k& =-\parallel {\mathbf{g}}_k{\parallel }^2+{\beta }_k^{\mathrm{FDL}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =-\parallel {\mathbf{g}}_k{\parallel }^2+\left(\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}-{\nu }_k\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\right){\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =-\parallel {\mathbf{g}}_k{\parallel }^2+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}-{\nu }_k\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =-\parallel {\mathbf{g}}_k{\parallel }^2+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}-{\nu }_k\frac{{\alpha }_{k-1}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =-{\parallel {\mathbf{g}}_k\parallel }^2+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}-{\nu }_k\frac{{\alpha }_{k-1}{\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right)}^2}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}.\hfill \end{array}$$

(41)

Using (21) in conjunction with (38) and ${\alpha }_{k-1}>0$, we conclude

$${\nu }_k\frac{{\alpha }_{k-1}{\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right)}^2}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\ge 0.$$

(42)

Now from (41) and (42) it follows

$$\begin{array}{cc}\hfill {\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_k& \le -{\parallel {\mathbf{g}}_k\parallel }^2+\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =\frac{-\parallel {\mathbf{g}}_k{\parallel }^2{\left({\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\right)}^2+\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}\right)\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right)\left({\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\right)}{{\left({\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\right)}^2}.\hfill \end{array}$$

(43)

Applying the inequality $P^{\mathrm{T}}Q\le \frac{1}{2}{(\parallel P\parallel }^2+{\parallel Q\parallel }^2)$ to the equality (43) with $P=\frac{1}{\sqrt{2}}\left({\mathbf{d}}_{k-1}^T{\mathbf{y}}_{k-1}\right){\mathbf{g}}_k$ and $Q=\sqrt{2}\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right){\mathbf{y}}_{k-1}$, it is obtained

(44)

The requirement (40) is satisfied for $c=\left(\frac{3}{4}-\frac{L^2}{{\theta }^2}\right)$ in (44) and an arbitrary $k\ge 0$. □

Theorem 1 confirms the global convergence of the FDL flow.

Theorem 1. 

Let the constraints in Assumption 1 be valid and f be uniformly convex. Then the series $\left\{{\mathbf{x}}_k\right\}$ generated on the basis of (3), (19) and (20) fulfils the limit relation

$$\underset{k\to \infty }{lim\; inf}\parallel {\mathbf{g}}_k\parallel =0.$$

(45)

Proof. 

Suppose the opposite. Since (45) is not valid, we conclude the existence of $c_1>0$ satisfying

$$\parallel {\mathbf{g}}_k\parallel \ge c_1,\mathrm{for}\mathrm{all}k.$$

(46)

Squaring both sides of (19) one derives

$$\parallel {\mathbf{d}}_k{\parallel }^2=\parallel {\mathbf{g}}_k{\parallel }^2-2{\beta }_k^{\mathrm{FDL}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}+{\left({\beta }_k^{\mathrm{FDL}}\right)}^2{\parallel {\mathbf{d}}_{k-1}\parallel }^2.$$

(47)

Taking into account (20), we obtain

$$\begin{array}{cc}\hfill -2{\beta }_k^{\mathrm{FDL}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}& =-2\left(\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}-{\nu }_k\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{s}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\right){\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\hfill \\ \hfill & =-2\left(\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}-{\nu }_k\frac{{\alpha }_{k-1}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right)\hfill \\ \hfill & =-2\left(\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}-{\nu }_k\frac{{\alpha }_{k-1}{\left({\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}\right)}^2}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\right).\hfill \end{array}$$

(48)

Now from (42), it follows

$$\begin{array}{cc}\hfill -2{\beta }_k^{\mathrm{EDL}}{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}& \le 2\left|\frac{{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{y}}_{k-1}}{{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\right||{\mathbf{g}}_k^{\mathrm{T}}{\mathbf{d}}_{k-1}|\le 2\frac{\parallel {\mathbf{g}}_k\parallel \parallel {\mathbf{y}}_{k-1}\parallel }{\left|{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}\right|}\parallel {\mathbf{g}}_k\parallel \parallel {\mathbf{d}}_{k-1}\parallel \hfill \\ \hfill & =2\frac{{\alpha }_{k-1}\parallel {\mathbf{g}}_k{\parallel }^2\parallel {\mathbf{y}}_{k-1}\parallel \parallel {\mathbf{d}}_{k-1}\parallel }{{\alpha }_{k-1}{\mathbf{d}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\hfill \\ \hfill & =2\frac{\parallel {\mathbf{g}}_k{\parallel }^2\parallel {\mathbf{y}}_{k-1}\parallel \parallel {\mathbf{s}}_{k-1}\parallel }{{\mathbf{s}}_{k-1}^{\mathrm{T}}{\mathbf{y}}_{k-1}}\hfill \\ \hfill & \le 2\frac{\parallel {\mathbf{g}}_k{\parallel }^{2}L\parallel {\mathbf{s}}_{k-1}\parallel \parallel {\mathbf{s}}_{k-1}\parallel }{\theta \parallel {\mathbf{s}}_{k-1}{\parallel }^2}\hfill \\ \hfill & =\frac{2L}{\theta }{\parallel {\mathbf{g}}_k\parallel }^2.\hfill \end{array}$$

(49)

Now, an application of (20) initiates

(50)

Further (21) and (50) lead to

$${\beta }_k^{\mathrm{FDL}}\le \frac{\left(L+1\right)\parallel {\mathbf{g}}_k\parallel }{\theta \parallel {\mathbf{d}}_{k-1}\parallel }.$$

(51)

Using (49) and (51) in (47), we get

$$\begin{array}{cc}\hfill \parallel {\mathbf{d}}_k{\parallel }^2& \le \parallel {\mathbf{g}}_k{\parallel }^2+\frac{2L}{\theta }\parallel {\mathbf{g}}_k{\parallel }^2+\frac{{(L+1)}^2{\parallel {\mathbf{g}}_k\parallel }^2}{{\theta }^2{\parallel {\mathbf{d}}_{k-1}\parallel }^2}\parallel {\mathbf{d}}_{k-1}{\parallel }^2\hfill \\ \hfill & =\parallel {\mathbf{g}}_k{\parallel }^2+\frac{2L}{\theta }\parallel {\mathbf{g}}_k{\parallel }^2+\frac{{(L+1)}^2{\parallel {\mathbf{g}}_k\parallel }^2}{{\theta }^2}\hfill \\ \hfill & =\left(1+\frac{2L}{\theta }+\frac{{(L+1)}^2}{{\theta }^2}\right)\parallel {\mathbf{g}}_k{\parallel }^2\hfill \\ \hfill & =\left(\frac{\theta +2L}{\theta }+\frac{{(L+1)}^2}{{\theta }^2}\right)\parallel {\mathbf{g}}_k{\parallel }^2\hfill \\ \hfill & =\frac{(\theta +2L)\theta +{(L+1)}^2}{{\theta }^2}{\parallel {\mathbf{g}}_k\parallel }^2.\hfill \end{array}$$

(52)

Dividing both sides of (52) by ${∥{\mathbf{g}}_k∥}^4$ and utilizing (46), it can be decided

$$\begin{gathered} \frac{\parallel {\mathbf{d}}_k{\parallel }^2}{\parallel {\mathbf{g}}_k{\parallel }^4}\le \frac{(\theta +2L)\theta +{(L+1)}^2}{{\theta }^2}·\frac{1}{c_1^2}, \\ \frac{\parallel {\mathbf{g}}_k{\parallel }^4}{\parallel {\mathbf{d}}_k{\parallel }^2}\ge \frac{{\theta }^2·c_1^2}{(\theta +2L)\theta +{(L+1)}^2}. \end{gathered}$$

(53)

The inequalities in (53) imply

$$\sum _{k=0}^{\infty }\frac{\parallel {\mathbf{g}}_k{\parallel }^4}{\parallel {\mathbf{d}}_k{\parallel }^2}\ge \sum _{k=0}^{\infty }\frac{{\theta }^2·c_1^2}{(\theta +2L)\theta +{(L+1)}^2}=\infty .$$

(54)

Therefore, $\parallel {\mathbf{g}}_k\parallel \ge c_1$ causes a contradiction with Lemma 2. □

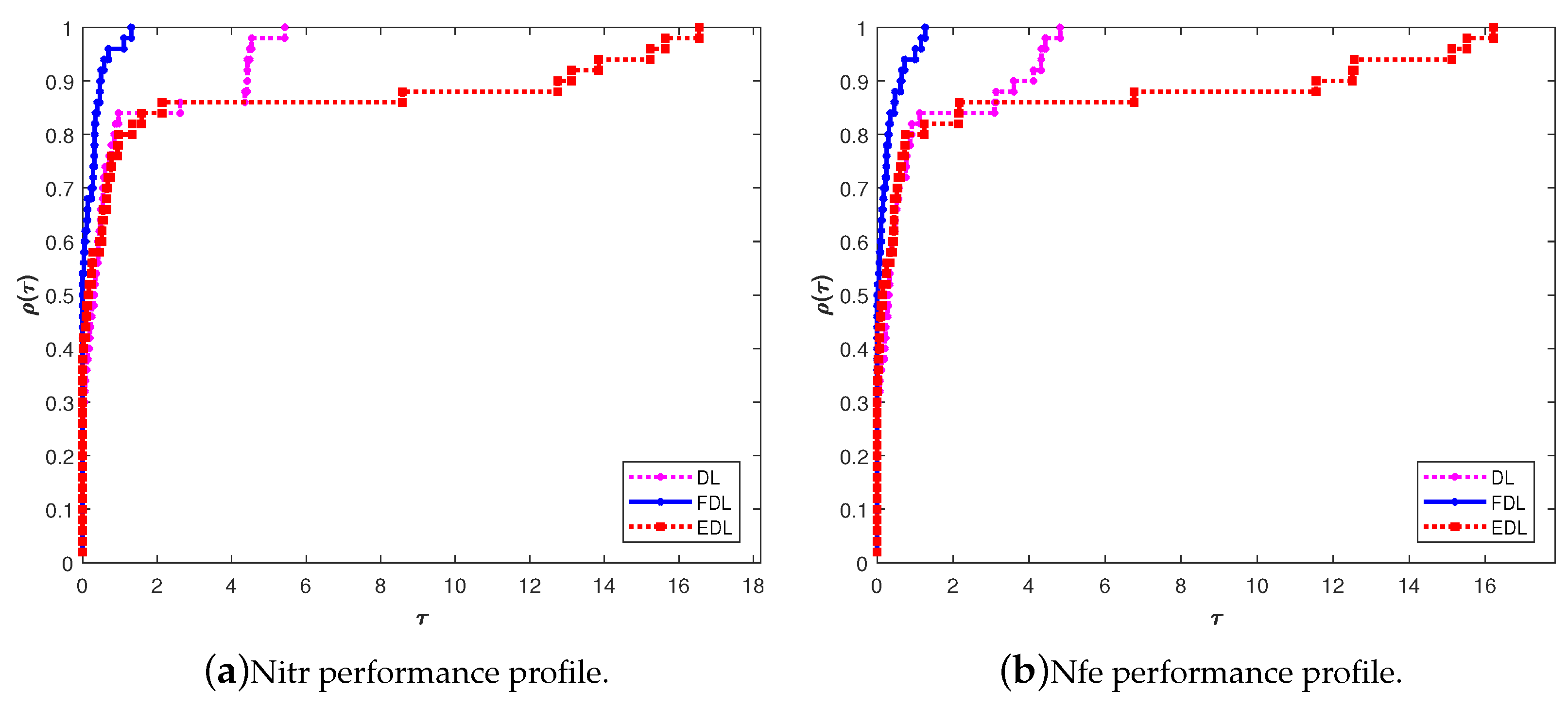
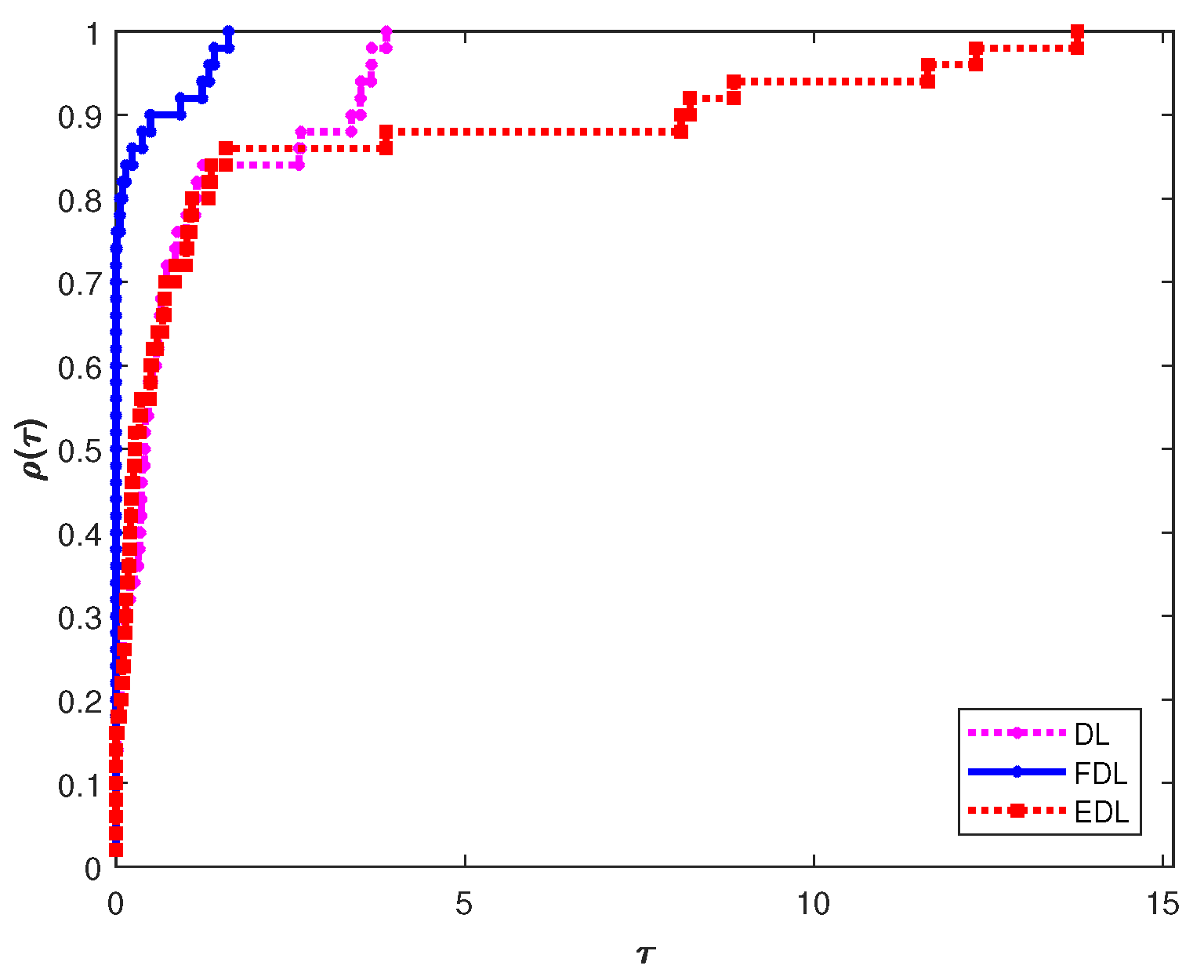
4. Numerical Results

In this section, numerical results obtained by the FDL method are analyzed and compared with the numerical results generated by the EDL [19] and DL [1] methods.

All the algorithms were written in Matlab R2017a and ran on a 64-bit Lenovo laptop (Intel Core i3 $2.0$ GHz, RAM 8 GB) with the Windows 10 operating system. The implementation of the FDL method is based on Algorithm 2, while EDL and DL implementation are based on algorithms given in [19] and [1], respectively.

The numerical testing is performed on 50 test functions collected in [33,34], with dimensions from the range $[100,20000]$. All three tested methods used start from the same initial point $x_0$ for each test function. Each case in testing is evaluated 10 times with gradually increased dimensions $n={10}^2$, $5\times {10}^2,{10}^3,3\times {10}^3,\times {10}^3,7\times {10}^3,8\times {10}^3$, ${10}^4$, $1.5\times {10}^4$ and $2\times {10}^4$.

The uniform terminating criteria for observed DL, EDL, and FDL algorithms are

$$\parallel {\mathbf{g}}_k\parallel \le ϵ\mathrm{and}\frac{|f\left({\mathbf{x}}_{k+1}\right)-f\left({\mathbf{x}}_k\right)|}{1+\left|f\right({\mathbf{x}}_k\left)\right|}\le \delta ,ϵ={10}^{-6},\delta ={10}^{-16}.$$

We are going to evaluate the efficiency of the FDL method and compare it with the EDL and DL methods under the backtracking search based on the parameters $\omega =0.0001$ and $\phi =0.8$.

Summary numerical results for DL, FDL, and EDL methods, performed on 50 test functions, are shown in Table 2, where `Test function’, `Nitr’, `Nfe’, and `Tcpu’ represent the name of the tested function, the total number of iterations, the total number of function evaluations, and the running time, respectively.

To visually compare the performance of tested methods, we used the performance profiles technique [35] on numerical results corresponding to Nitr, Nfe, and Tcpu criteria generated by DL, FDL, and EDL methods. An upper graph in a performance profile corresponds to the method that shows better performance. The vertical axis of each performance profile in figures undicates the percentage of test functions for which the considered method is the winner between compared methods, whereby the right-hand side corresponds to the percentage of successfully solved test functions.

Figure 4 and Figure 5 plot the performance profiles for the data in Table 2. Graphs in Figure 4 illustrate the performance profiles Nitr and Nfe for DL, FDL, and EDL iterations based on the data from Table 2. In Figure 4a, it is noticeable that DL, FDL, and EDL methods are able to solve all tested functions, wherein the FDL method produces the best results in $54.0$% (27 out of 50) of test functions compared with DL ($26.0$% (13 out of 50)) and EDL ($38.0$% (19 out of 50)). From Figure 4a, it is observed that the FDL graph reaches the top first, so FDL is the best relative to other examined methods with respect to the Nitr criterion.

Figure 4b indicates that the FDL graph is the most efficient and successfully solves all test cases. In addition, the obtained numerical results confirm that FDL performs well in most cases. Most specifically, FDL is the fastest because it solves about $48.0\%$ (24 out of 50) of tested functions with the least Nfe compared to the DL and EDL methods. Meanwhile, the DL and EDL are superior for solving $22.0\%$ (11 out of 50) and $30.0\%$ (15 out of 50) test functions, respectively. Hence, the numerical behavior of FDL is superior compared to the DL and EDL methods for the given test functions.

Figure 5 shows Tcpu performance profiles graphs of DL, FDL, and EDL methods. It is observable that DL, FDL, and EDL are able to solve all tested functions. Further examination leads to the conclusion that the FDL method is the best in $74.0$% (37 out of 50) of the test cases compared with DL ($12.0$% (6 out of 50)) and EDL ($16.0$% (8 out of 50)). Analysing the graphs in Figure 5, a clear conclusion is that the FDL graph comes to the top first, which confirms its dominance in terms of Tcpu.

By analyzing the results shown in Figure 4, Figure 5 and in Table 2, we conclude that the FDL method achieved better results. This observation leads us to the final conclusion that the proposed FDL method is effective for solving unconstrained optimization problems in terms of all three criteria (iterations, function evaluations, and processor time).

5. Conclusions

In current research, we propose a novel approach to determining the parameter t in the Dai-Liao CG iterations. New approach is based on finding suitable values for a non-negative parameter t in the DL method using neutrosophic logic. Utilizing $t={\nu }_k\left({\mathsf{\Delta }}_k\right)$ in (5), an original strategy in defining the Dai-Liao CG parameter ${\beta }_k^{\mathrm{FDL}}$ is proposed and a novel fuzzy neutrosophic Dai-Liao (FDL) CG method is presented.

Numerical experiments and comparisons with some well-known CG methods and the theoretical convergence analysis show effectiveness of the method. The numerical testing and initiated comparison are based on standard performance profiles, such as the total number of iterations (Nitr), the total number of function evaluations (Nfe), and the running time (Tcpu) performances for each function and each method. Analysis of the obtained numerical results revealed that the FDL method is the most efficient.

We are convinced that the obtained results will be a motivation for further research in defining improved DL methods strengthened by the neutrosophic logic.

Future scientific research in this direction can be continued in in several directions. Previous research has shown the effectiveness of the neutrosophic principle in scaled gradient descent methods and DL class of CG methods. The challenge is to apply such a principle to other non-linear optimization methods. On the other hand, there is a wide variety of different possibilities for defining the principles of neutrosophication and de-neutrosophication, which can be considered in future research. Finally, there is a great opportunity in improving the Neutrosophic inference engine used in this research.