Hestenes-Stiefel-Type Conjugate Direction Algorithm for Interval-Valued Multiobjective Optimization Problems

1. Introduction

Multiobjective optimization problems (MOPs, in short) involve the simultaneous optimization of two or more conflicting objective functions. Vilfredo Pareto [1] introduced the concept of Pareto optimality in the context of economic systems. A solution is called Pareto optimal or efficient, if none of the objective functions can be improved without deteriorating some of the other objective values (see, [2]). MOPs arise in scenarios where trade-offs are required, such as balancing cost and quality in business operations or improving efficiency while reducing environmental impact in engineering (see, [3,4]). As a consequence, various techniques and algorithms have been proposed to solve MOPs in different frameworks (see, [5,6,7]). For a more detailed discussion on MOPs, we refer to [2,8] and the references cited therein.

In many real world problems arising in engineering, science and related fields, we often encounter data that are imprecise or uncertain. This uncertainty can arise from various factors such as unknown future developments, measurement or manufacturing errors, or incomplete information in model development (see, [9,10]). In several optimization problems, the presence of imprecise data or uncertainty in the parameters or the objective functions is modeled as intervals. These optimization problems are termed interval-valued optimization problems (IVOPs, in short). IVOPs have significant applications in various fields, including management, economics and engineering (see, [11,12,13]). The foundational work on IVOPs is attributed to Ishibuchi and Tanaka [14], who investigated IVOPs by transforming them into corresponding deterministic MOPs. Wu [15] derived optimality conditions for a class of constrained IVOPs, employing the notion of Hukuhara differentiability and assuming the convexity hypothesis on the objective and constraint functions. Moreover, Wu [16] developed Karush-Kuhn-Tucker-type optimality conditions for IVOPs and derived strong duality theorems that connect the primal problems with their associated dual problems. Bhurjee and Panda [17] explored IVOPs by defining interval-valued functions in parametric forms. More recently, Roy et al. [18] proposed a gradient based descent line search technique employing the notion of generalized Hukuhara (gH, in short) differentiability to solve IVOPs.

In the theory of mathematical optimization, if the uncertainties involved in the objective functions of MOPs are represented as intervals, the resulting problems are referred to as interval-valued multiobjective optimization problems (IVMOPs, in short). IVMOPs frequently arise in diverse fields such as transportation, economics, and business administration [19,20]. As a result, several researchers have developed various methods to solve IVMOPs. For instance, Kumar and Bhurjee [21] studied IVMOPs by transforming them into their corresponding deterministic MOPs and establishing the relationships between the solutions of IVMOPs and MOPs. Upadhyay et al. [22] introduced Newton’s method for IVMOPs and established the quadratic convergence of the sequence generated by Newton’s method under suitable assumptions. Subsequently, Upadhyay et al. [23] developed quasi-Newton methods for IVMOPs and demonstrated their efficacy in solving both convex and non-convex IVMOPs. For a more comprehensive and updated survey on IVMOPs, see [24,25,26,27] and the references cited therein.

It is well-known that the conjugate direction method is a powerful optimization technique that can be widely employed for solving systems of linear equations and optimization problems (see, [28,29]). It has been observed that several real-life optimization problems emerging in different fields of modern research, such as electromagnetic scattering [30], inverse engineering [31], and geophysical inversion [32]. The conjugate direction method was first introduced by Hestenes and Stiefel [28], who developed the conjugate gradient method to solve a system of linear equations. Subsequently, Pérez and Prudente [29] introduced the HS-type conjugate direction algorithm for MOPs by employing an inexact line search. Wang et al. [33] introduced an HS-type conjugate direction algorithm for MOPs without employing line search techniques, and established the global convergence of the proposed method under suitable conditions. Recently, based on the memoryless Broyden-Fletcher-Goldfarb-Shanno update, Khoshsimaye-Bargard and Ashrafi [34] presented a convex hybridization of the Hestenes-Stiefel and Dai-Yuan conjugate parameters. From the above discussion, it is evident that HS-type conjugate direction methods have been developed to solve single-objective problems as well as MOPs. However, there is no research paper available in the literature that has explored the HS-type conjugate direction method for IVMOPs. The aim of this article is to fill the aforementioned research gaps by developing the HS-type conjugate direction method for a class of IVMOPs.

Motivated by the works of [28,29,33], in this paper, we investigate a class of IVMOPs and define the HS-direction for the objective function of IVMOPs. A descent direction property of the HS-direction is established at noncritical points. To determine an appropriate step size, we employ an Armijo-like line search. Moreover, an HS-type conjugate direction algorithm for IVMOPs is presented, and the convergence of this algorithm is established. Finally, the efficiency of the proposed method is demonstrated by solving various numerical problems employing MATLAB R2024a.

The primary contribution and novel aspect of this article are threefold. Firstly, the results presented in this paper generalize several significant results from existing literature. Specifically, we generalize the results established by Pérez and Prudente [29] on the HS-type method from MOPs to a more general class of optimization problems, namely, IVMOPs. Secondly, if the conjugate parameter is set to zero and if every component of the objective function of the IVMOP is a real-valued function rather than interval-valued function, then the proposed algorithm reduces to the steepest descent algorithm for MOPs, as introduced by Fliege and Svaiter [5]. Thirdly, it is imperative to note that the proposed HS-type algorithm is applicable to any IVMOP, where the objective function is continuously gH-differentiable. However, Newton’s and Quasi-Newton methods proposed by Upadhyay et al. [22,23] require the objective functions of the IVMOPs to be twice continuously gH-differentiable. In view of this fact, our proposed algorithm can be applied to a broader class of optimization problems compared to the algorithms introduced by Upadhyay et al. [22,23].

The rest of the paper is structured as follows. In Section 2, we discuss some mathematical preliminaries that will be employed in the sequel. Section 3 presents an HS-type conjugate direction algorithm for IVMOPs, along with a convergence analysis of the sequence generated by the algorithm. In Section 4, we demonstrate the efficiency of the proposed algorithm by solving several numerical examples via MATLAB R2024a. Finally, in Section 5, we provide our conclusions as well as future research directions.

2. Preliminaries

Throughout this article, the symbol $\mathbb{N}$denotes the set of all natural numbers. For $\mathit{n}\in \mathbb{N}$, the symbol ${\mathbb{R}}^{\mathit{n}}$ refers to the $\mathit{n}$-dimensional Euclidean space. The symbol ${\mathbb{R}}_{--}$ refers to the collection of all negative real numbers. The symbol ∅ is employed to denote an empty set. For any non-empty set $\mathfrak{X}$ and $m\in \mathbb{N}$, the notation ${\mathfrak{X}}^m$ represents the Cartesian product defined as

$${\mathfrak{X}}^{\mathit{m}}:=\underset{\left(\mathit{m}\mathrm{times}\right)}{\underbrace{\mathfrak{X}\times \dots \times \mathfrak{X}}}.$$

Let $\mathrm{y},\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$. Then the symbol $\langle \mathrm{y},\mathfrak{u}\rangle$ is defined as

$$\langle \mathrm{y},\mathfrak{u}\rangle :=\sum _{\mathit{k}=1}^{\mathit{n}}{\mathrm{y}}_{\mathit{k}}{\mathfrak{u}}_{\mathit{k}}.$$

For $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$, the symbol $\parallel \mathfrak{u}\parallel$ is defined as

$$\parallel \mathfrak{u}\parallel :=\sqrt{\langle \mathfrak{u},\mathfrak{u}\rangle }.$$

Let $\mathit{n},\mathit{m}\in \mathbb{N}$. Then, the notations ${\mathcal{I}}_{\mathit{n}}$ and ${\mathcal{I}}_{\mathit{m}}$ are used to represent the following sets:

$$\begin{array}{cc}\hfill {\mathcal{I}}_{\mathit{n}}& :=\{1,\dots ,\mathit{n}\},\hfill \\ \hfill {\mathcal{I}}_{\mathit{m}}& :=\{1,\dots ,\mathit{m}\}.\hfill \end{array}$$

Let $\mathrm{y},\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$. The following notations are employed throughout this article:

$$\begin{array}{cc}\hfill \mathrm{y}\leqq \mathfrak{u}& \iff {\mathrm{y}}_{\mathit{k}}\le {\mathfrak{u}}_{\mathit{k}},\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{n}},\hfill \\ \hfill \mathrm{y}<\mathfrak{u}& \iff {\mathrm{y}}_{\mathit{k}}<{\mathfrak{u}}_{\mathit{k}},\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{n}},\hfill \\ \hfill \mathrm{y}\le \mathfrak{u}& \iff \mathrm{y}\leqq \mathfrak{u}\mathrm{and}\mathrm{y}\ne \mathfrak{u}.\hfill \end{array}$$

For $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$ and $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$, we define

$${\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{k}}^{+}}}\left(\mathfrak{u}\right):=\underset{\beta \to 0^{+}}{lim}{\displaystyle \frac{\mathcal{G}({\mathfrak{u}}_{\mathit{1}},\dots ,{\mathfrak{u}}_{\mathit{k}}+\beta ,\dots ,{\mathfrak{u}}_{\mathit{n}})-\mathcal{G}({\mathfrak{u}}_{\mathit{1}},\dots ,{\mathfrak{u}}_{\mathit{k}},\dots ,{\mathfrak{u}}_{\mathit{n}})}{\beta }},$$

(1)

and

$${\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{k}}^{-}}}\left(\mathfrak{u}\right):=\underset{\beta \to 0^{-}}{lim}{\displaystyle \frac{\mathcal{G}({\mathfrak{u}}_{\mathit{1}},\dots ,{\mathfrak{u}}_{\mathit{k}}+\beta ,\dots ,{\mathfrak{u}}_{\mathit{n}})-\mathcal{G}({\mathfrak{u}}_{\mathit{1}},\dots ,{\mathfrak{u}}_{\mathit{k}},\dots ,{\mathfrak{u}}_{\mathit{n}})}{\beta }},$$

(2)

which denote the one-sided right and left $\mathit{k}$-th partial derivatives of $\mathcal{G}$ at the point $\mathfrak{u}$, respectively, assuming the limits defined in (1) and (2) are well-defined.

If for every $\mathit{k}\in {\mathcal{I}}_{\mathit{n}}$ and $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$, ${\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{k}}^{+}}}\left(\overline{\mathfrak{u}}\right)$ and ${\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{k}}^{-}}}\left(\overline{\mathfrak{u}}\right)$ exist, then we define:

$$\begin{array}{cc}\hfill {\nabla }_{-}\mathcal{G}\left(\overline{\mathfrak{u}}\right)& :=\left({\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{1}}^{-}}}\left(\overline{\mathfrak{u}}\right),\dots ,{\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{n}}^{-}}}\left(\overline{\mathfrak{u}}\right)\right),\hfill \\ \hfill {\nabla }_{+}\mathcal{G}\left(\overline{\mathfrak{u}}\right)& :=\left({\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{1}}^{+}}}\left(\overline{\mathfrak{u}}\right),\dots ,{\displaystyle \frac{\partial \mathcal{G}}{\partial {\mathfrak{u}}_{\mathit{n}}^{+}}}\left(\overline{\mathfrak{u}}\right)\right).\hfill \end{array}$$

The symbols $\mathfrak{C}\left(\mathbb{R}\right)$ and $\mathfrak{C}\left({\mathbb{R}}_{--}\right)$ are used to denote the following sets:

$$\begin{array}{cc}\hfill \mathfrak{C}\left(\mathbb{R}\right)& :=\left\{\left[\underline{\mathfrak{b}},\overline{\mathfrak{b}}\right]:\underline{\mathfrak{b}},\overline{\mathfrak{b}}\in \mathbb{R},\underline{\mathfrak{b}}\le \overline{\mathfrak{b}}\right\},\hfill \\ \hfill \mathfrak{C}\left({\mathbb{R}}_{--}\right)& :=\left\{\left[\underline{\mathfrak{b}},\overline{\mathfrak{b}}\right]:\underline{\mathfrak{b}},\overline{\mathfrak{b}}\in \mathbb{R},\underline{\mathfrak{b}}\le \overline{\mathfrak{b}},\overline{\mathfrak{b}}<0\right\}.\hfill \end{array}$$

Let $\mathfrak{p},\mathfrak{q}\in \mathbb{R}$. The symbol $\left[\mathfrak{p}\vee \mathfrak{q}\right]$ represents the following:

$$\left[\mathfrak{p}\vee \mathfrak{q}\right]:=\left[min\{\mathfrak{p},\mathfrak{q}\},max\{\mathfrak{p},\mathfrak{q}\}\right].$$

The interval $\mathfrak{X}:=[\underline{\mathfrak{b}},\overline{\mathfrak{b}}]\in \mathfrak{C}\left(\mathbb{R}\right)$ is referred to as a degenerate interval if and only if

$$\underline{\mathfrak{b}}=\overline{\mathfrak{b}}.$$

Let $\mathfrak{X}=[\underline{\mathfrak{p}},\overline{\mathfrak{p}}]$, $\mathfrak{Z}:=[\underline{\mathfrak{q}},\overline{\mathfrak{q}}]\in \mathfrak{C}\left(\mathbb{R}\right)$, and $\xi \in \mathbb{R}$. Corresponding to $\mathfrak{X},\mathfrak{Z},$ and $\xi$, we define the following algebraic operations (see, [22]):

$$\begin{array}{cc}\hfill & \mathfrak{X}\oplus \mathfrak{Z}:=[\underline{\mathfrak{p}}+\underline{\mathfrak{q}},\overline{\mathfrak{p}}+\overline{\mathfrak{q}}],\hfill \\ \hfill & \mathfrak{X}\ominus \mathfrak{Z}:=[\underline{\mathfrak{p}}-\overline{\mathfrak{q}},\overline{\mathfrak{p}}-\underline{\mathfrak{q}}],\hfill \\ \hfill & \xi \odot \mathfrak{X}=\left\{\begin{array}{cc}[\xi \underline{\mathfrak{p}},\xi \overline{\mathfrak{p}}],\hfill & \xi \ge 0,\hfill \\ \xi \overline{\mathfrak{p}},\xi \underline{\mathfrak{p}}],\hfill & \xi <0.\hfill \end{array}\right.\hfill \end{array}$$

The subsequent definition is from [35].

Definition 1.

Consider an arbitrary set $\mathcal{E}:=[\underline{\mathsf{e}},\overline{\mathsf{e}}]\in \mathfrak{C}\left(\mathbb{R}\right)$. Then, the symbol ${\parallel \mathcal{E}\parallel }_I$ represents the norm of $\mathcal{E}$ and is defined as follows:

$${\parallel \mathcal{E}\parallel }_I:=max\{\left|\underline{\mathsf{e}}\right|,\left|\overline{\mathsf{e}}\right|\}.$$

For $\mathfrak{X}:=[\underline{\mathfrak{p}},\overline{\mathfrak{p}}]$ and $\mathfrak{Z}:=[\underline{\mathfrak{q}},\overline{\mathfrak{q}}]\in \mathfrak{C}\left(\mathbb{R}\right)$, we adopt the following notations throughout the article:

$$\begin{array}{cc}\hfill & \mathfrak{X}{\leqq }_{LU}\mathfrak{Z}\iff \underline{\mathfrak{p}}\le \underline{\mathfrak{q}}\mathrm{and}\overline{\mathfrak{p}}\le \overline{\mathfrak{q}},\hfill \\ \hfill & \mathfrak{X}{<}_{LU}\mathfrak{Z}\iff \underline{\mathfrak{p}}<\underline{\mathfrak{q}}\mathrm{and}\overline{\mathfrak{p}}<\overline{\mathfrak{q}},\hfill \\ \hfill & \mathfrak{X}{\le }_{LU}\mathfrak{Z}\iff \mathfrak{X}{\leqq }_{LU}\mathfrak{Z}\mathrm{and}\mathfrak{X}\ne \mathfrak{Z}.\hfill \end{array}$$

Let $\mathcal{E}=({\mathcal{E}}_{\mathit{1}},\dots ,{\mathcal{E}}_{\mathit{m}})$, $\mathfrak{R}=({\mathfrak{R}}_{\mathit{1}},\dots ,{\mathfrak{R}}_{\mathit{m}})\in {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$. The ordered relations between $\mathcal{E}$ and $\mathfrak{R}$ are described as follows:

$$\begin{array}{cc}\hfill & \mathcal{E}{⪯}_{\mathit{m}}\mathfrak{R}\iff {\mathcal{E}}_{\mathit{k}}{\leqq }_{LU}{\mathfrak{R}}_{\mathit{k}},\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}},\hfill \\ \hfill & \mathcal{E}{\prec }_{\mathit{m}}\mathfrak{R}\iff {\mathcal{E}}_{\mathit{k}}{<}_{LU}{\mathfrak{R}}_{\mathit{k}},\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.\hfill \end{array}$$

The following definition is from [35].

Definition 2.

For arbitrary intervals $\mathfrak{X}:=[\underline{\mathfrak{p}},\overline{\mathfrak{p}}]$ and $\mathfrak{Z}:=[\underline{\mathfrak{q}},\overline{\mathfrak{q}}]\in \mathfrak{C}\left(\mathbb{R}\right)$, the symbol $\mathfrak{X}{\ominus }_{\mathrm{gH}}\mathfrak{Z}$ represents the gH-difference between $\mathfrak{X}$ and $\mathfrak{Z}$ and is defined as

$$\mathfrak{X}{\ominus }_{\mathrm{gH}}\mathfrak{Z}:=\left[\underline{\mathfrak{p}}-\underline{\mathfrak{q}}\vee \overline{\mathfrak{p}}-\overline{\mathfrak{q}}\right].$$

The notion of continuity for $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ is recalled in the subsequent definition (see, [35]).

Definition 3.

The function $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ is termed a continuous function at a point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ if for any $ϵ>0$, there exists some ${\delta }_{ϵ}>0$ such that for any $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$ satisfying $\parallel \mathfrak{u}-\overline{\mathfrak{u}}\parallel <{\delta }_{ϵ}$, the following inequality holds:

$$\parallel \mathcal{G}\left(\mathfrak{u}\right)-\mathcal{G}\left(\overline{\mathfrak{u}}\right){\parallel }_I<ϵ.$$

The subsequent definition is from Upadhyay et al. [23].

Definition 4.

The function $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ is said to be convex function if, for all ${\mathfrak{u}}_{\mathit{1}}$, ${\mathfrak{u}}_{\mathit{2}}\in {\mathbb{R}}^{\mathit{n}}$ and any $\beta \in [0,1]$, the following inequality holds:

$$\mathcal{G}((1-\beta ){\mathfrak{u}}_{\mathit{1}}+\beta {\mathfrak{u}}_{\mathit{2}}){\leqq }_{LU}(1-\beta )\odot \mathcal{G}\left({\mathfrak{u}}_{\mathit{1}}\right)\oplus \beta \odot \mathcal{G}\left({\mathfrak{u}}_{\mathit{2}}\right).$$

If there exists some $\gamma >0$ and a convex function $\Theta :{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$, such that the following condition holds:

$$\begin{array}{c}\hfill \mathcal{G}\left(\mathfrak{u}\right)=\Theta \left(\mathfrak{u}\right)\oplus {\displaystyle \frac{1}{2}}{\parallel \mathfrak{u}\parallel }^2\odot [\gamma ,\gamma ],\mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}},\end{array}$$

then $\mathcal{G}$ is said to be a strongly convex function on ${\mathbb{R}}^{\mathit{n}}$. Moreover, $\mathcal{G}$ is said to be locally convex (respectively, locally strongly convex) at a point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ if there exists a neighborhood $\mathcal{V}$ of $\overline{\mathfrak{u}}$ such that the restriction of $\mathcal{G}$ to $\mathcal{V}$ is convex (respectively, strongly convex).

The subsequent definition is from [36].

Definition 5.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ and $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$ with $\mathfrak{d}\ne 0$. The gH-directional derivative of $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ at $\overline{\mathfrak{u}}$ in the direction $\mathfrak{d}$ is defined as

$$D_{gH}\mathcal{G}(\overline{\mathfrak{u}},\mathfrak{d}):=\underset{\beta \to 0^{+}}{lim}{\displaystyle \frac{\mathcal{G}(\overline{\mathfrak{u}}+\beta \mathfrak{d}){\ominus }_{gH}\mathcal{G}\left(\overline{\mathfrak{u}}\right)}{\beta }},$$

provided that the above limit exists.

The subsequent definition from [36].

Definition 6.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ and $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ be defined as

$$\mathcal{G}\left(\mathfrak{u}\right):=[\underline{\mathcal{G}}\left(\mathfrak{u}\right),\overline{\mathcal{G}}\left(\mathfrak{u}\right)],\mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}.$$

Let the functions${\mathcal{G}}_1,{\mathcal{G}}_2:{\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$be defined as follows:

$$\begin{array}{ccc}\hfill {\mathcal{G}}_1\left(\mathfrak{u}\right)& :={\displaystyle \frac{\overline{\mathcal{G}}\left(\mathfrak{u}\right)+\underline{\mathcal{G}}\left(\mathfrak{u}\right)}{2}},\hfill & \hfill \mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}},\\ \hfill {\mathcal{G}}_2\left(\mathfrak{u}\right)& :={\displaystyle \frac{\overline{\mathcal{G}}\left(\mathfrak{u}\right)-\underline{\mathcal{G}}\left(\mathfrak{u}\right)}{2}},\hfill & \hfill \mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}.\end{array}$$

The mapping $\mathcal{G}$ is said to be gH-differentiable at $\overline{\mathfrak{u}}$ if, there exist vectors $w_1,w_2\in {\mathbb{R}}^{\mathit{n}}$ with $w_1:=\left({w_{\mathit{1}}}^{\left(1\right)},\dots ,{w_1}^{\left(\mathit{n}\right)}\right)$ and $w_2:=\left({w_2}^{\left(\mathit{1}\right)},\dots ,{w_2}^{\left(\mathit{n}\right)}\right)$, and error functions ${\mathcal{F}}_1,{\mathcal{F}}_2:{\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$, such that $\underset{z\to 0}{lim}{\mathcal{F}}_1\left(z\right)=\underset{z\to 0}{lim}{\mathcal{F}}_2\left(z\right)=0$, and for all $z\ne 0$ the following hold:

$${\mathcal{G}}_1\left(\overline{\mathfrak{u}}+z\right)-{\mathcal{G}}_1\left(\overline{\mathfrak{u}}\right)=\sum _{\mathit{k}=1}^n{w}_1^{\left(\mathit{k}\right)}{z}_{\mathit{k}}+\parallel z\parallel {\mathcal{F}}_1\left(z\right),$$

and

$$\left|{\mathcal{G}}_2\left(\overline{\mathfrak{u}}+z\right)-{\mathcal{G}}_2\left(\overline{\mathfrak{u}}\right)\right|=\left|\sum _{\mathit{k}=1}^n{w}_2^{\left(\mathit{k}\right)}{z}_{\mathit{k}}+\parallel z\parallel {\mathcal{F}}_2\left(z\right)\right|.$$

If $\mathcal{G}$ is gH-differentiable at every element $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$, then $\mathcal{G}$ is said to be gH-differentiable on ${\mathbb{R}}^{\mathit{n}}$.

The proof of the following theorem can be established using Theorem 5 and Propositions 9 and 11 from [36].

Theorem 1.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ and let $\mathcal{G}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ be defined as

$$\mathcal{G}\left(\mathfrak{u}\right):=[\underline{\mathcal{G}}\left(\mathfrak{u}\right),\overline{\mathcal{G}}\left(\mathfrak{u}\right)],\mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}.$$

If $\mathcal{G}$ is gH-differentiable at $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$, then for any $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$, one of the following conditions is fulfilled:

(i)

The gradients $\nabla \underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$ and $\nabla \overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$ exist, and

$$D_{\mathrm{gH}}\mathcal{G}\left(\overline{\mathfrak{u}};\mathfrak{d}\right)=\left[〈\nabla \underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\vee 〈\nabla \overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\right].$$

(ii)

If ${\nabla }_{-}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$, ${\nabla }_{-}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$, ${\nabla }_{+}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$, and ${\nabla }_{+}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)$ exist and satisfy:

$${\nabla }_{-}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)={\nabla }_{+}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),{\nabla }_{-}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right)={\nabla }_{+}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right).$$

Moreover,

$$D_{\mathrm{gH}}\mathcal{G}\left(\overline{\mathfrak{u}};\mathfrak{d}\right):=\left[〈{\nabla }_{-}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\vee 〈{\nabla }_{-}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\right],$$

or,

$$D_{\mathrm{gH}}\mathcal{G}\left(\overline{\mathfrak{u}};\mathfrak{d}\right):=\left[〈{\nabla }_{+}\underline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\vee 〈{\nabla }_{+}\overline{\mathcal{G}}\left(\overline{\mathfrak{u}}\right),\mathfrak{d}〉\right].$$

We define the interval-valued vector function $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$ as follows:

$$\mathcal{H}\left(\mathfrak{u}\right):=\left({\mathcal{H}}_{\mathit{1}}\left(\mathfrak{u}\right),\dots ,{\mathcal{H}}_{\mathit{m}}\left(\mathfrak{u}\right)\right),\mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}},$$

where ${\mathcal{H}}_{\mathit{k}}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)(\mathit{k}\in {\mathcal{I}}_{\mathit{m}})$ are interval-valued functions.

The subsequent two definitions are from [26].

Definition 7.

Let $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$ and $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$. Suppose that every component of $\mathcal{H}$ possesses gH-directional derivatives. Then, $\overline{\mathfrak{u}}$ is called a critical point of $\mathcal{H}$, provided that there does not exist any $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$, satisfying:

$$D_{gH}\mathcal{H}(\overline{\mathfrak{u}},\mathfrak{d})\cap {\left(\mathfrak{C}\left({\mathbb{R}}_{--}\right)\right)}^{\mathit{m}}\ne \varnothing ,$$

where $D_{gH}\mathcal{H}(\overline{\mathfrak{u}},\mathfrak{d}):=\left(D_{gH}{\mathcal{H}}_{\mathit{1}}(\overline{\mathfrak{u}},\mathfrak{d}),\dots ,D_{gH}{\mathcal{H}}_{\mathit{m}}(\overline{\mathfrak{u}},\mathfrak{d})\right)$.

Definition 8.

An element $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$ is referred to as descent direction of $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$ at a point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$, provided that some $\beta (\beta \in \mathbb{R},\beta >0)$ exists, satisfying:

$$\mathcal{H}(\overline{\mathfrak{u}}+t\mathfrak{d}){\prec }_{\mathit{m}}\mathcal{H}\left(\overline{\mathfrak{u}}\right),\mathrm{for}\mathrm{all}t\in (0,\beta ].$$

Definition 9.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$. Then, the function $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$ is said to be continuously gH-differentiable at $\overline{\mathfrak{u}}$ if every component of $\mathcal{H}$ is continuously gH-differentiable at $\overline{\mathfrak{u}}$.

Remark 1.

In view of Definitions 5 and 8, it follows that if $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\left(\mathfrak{C}\left(\mathbb{R}\right)\right)}^{\mathit{m}}$ is continuously gH-differentiable at $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ and if $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$ is a descent direction of $\mathcal{H}$ at $\overline{\mathfrak{u}}$, then

$$D_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},\mathfrak{d}\right){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

3. HS-Type Conjugate Direction Method for IVMOP

In this section, we present an HS-type conjugate direction method for IVMOPs. Moreover, we establish the convergence of the sequence generated by the above method.

Consider the following IVMOP:

$$\begin{array}{cc}\hfill \left(\mathrm{IVMOP}\right)& \mathrm{Minimize}\mathcal{H}\left(\mathfrak{u}\right):=({\mathcal{H}}_{\mathit{1}}\left(\mathfrak{u}\right),\dots ,{\mathcal{H}}_{\mathit{m}}\left(\mathfrak{u}\right)),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}},\hfill \end{array}$$

where the functions ${\mathcal{H}}_{\mathit{k}}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$$(\mathit{k}\in {\mathcal{I}}_{\mathit{m}})$ are defined as

$${\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u}\right):=\left[{\underline{\mathcal{H}}}_{\mathit{k}}\left(\mathfrak{u}\right),{\overline{\mathcal{H}}}_{\mathit{k}}\left(\mathfrak{u}\right)\right],\mathrm{for}\mathrm{all}\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}.$$

The functions ${\mathcal{H}}_{\mathit{k}}$$(\mathit{k}\in {\mathcal{I}}_{\mathit{m}})$ are assumed to be continuously gH-differentiable unless otherwise specified.

The notions of effective and weak effective solutions for IVMOP are recalled in the subsequent definition (see, [22]).

Definition 10.

A point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ is referred to as effective solution of the IVMOP if there is no other point $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$, such that

$$\mathcal{H}\left(\mathfrak{u}\right){⪯}_{\mathit{m}}\mathcal{H}\left(\overline{\mathfrak{u}}\right)\mathrm{and}\mathcal{H}\left(\mathfrak{u}\right)\ne \mathcal{H}\left(\overline{\mathfrak{u}}\right).$$

Similarly, a point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ is referred to as weak effective solution of the IVMOP provided that there is no other point $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$ for which:

$$\mathcal{H}\left(\mathfrak{u}\right){\prec }_{\mathit{m}}\mathcal{H}\left(\overline{\mathfrak{u}}\right).$$

In the rest of the article, we employ $\mathcal{P}$ to represent the set of all critical points of $\mathcal{H}$.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$.

In order to determine the descent direction for the objective function $\mathcal{H}$ of IVMOP, we consider the following scalar optimization problem with interval-valued constraints (see, Upadhyay et al. [26]):

$$\begin{array}{cc}\hfill {\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}& \mathrm{Minimize}\phi (\alpha ,\mathfrak{d}):=\alpha ,\hfill \\ \hfill & \mathrm{subject}\mathrm{to}{D}_{gH}{\mathcal{H}}_{\mathit{k}}(\overline{\mathfrak{u}},\mathfrak{d})+{\displaystyle \frac{1}{2}}\left[{\parallel \mathfrak{d}\parallel }^2,{\parallel \mathfrak{d}\parallel }^2\right]{\leqq }_{LU}[\alpha ,\alpha ],\hfill \\ \hfill & \mathit{k}\in {\mathcal{I}}_{\mathit{m}},\hfill \end{array}$$

where $\phi :\mathbb{R}\times {\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$ is a real-valued function. It can be shown that the problem ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$ has a unique solution.

Any feasible point of the problem ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$ is represented as $({\alpha }_{\overline{\mathfrak{u}}},{\mathfrak{d}}_{\overline{\mathfrak{u}}})$, where ${\alpha }_{\overline{\mathfrak{u}}}\in \mathbb{R}$ and ${\mathfrak{d}}_{\overline{\mathfrak{u}}}\in {\mathbb{R}}^{\mathit{n}}$. Let ${\mathcal{K}}_{\overline{\mathfrak{u}}}\subseteq {\mathbb{R}}^{n+1}$ denote the feasible set of ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$. We consider the functions $d:{\mathbb{R}}^{\mathit{n}}\to {\mathbb{R}}^{\mathit{n}}$ and $\alpha :{\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$, which are defined as follows:

$$\begin{array}{c}\hfill \left(\alpha \left(\overline{\mathfrak{u}}\right),d\left(\overline{\mathfrak{u}}\right)\right):=\underset{\left({\alpha }_{\overline{\mathfrak{u}}},{\mathfrak{d}}_{\overline{\mathfrak{u}}}\right)\in {\mathcal{K}}_{\overline{\mathfrak{u}}}}{argmin}\phi ({\alpha }_{\overline{\mathfrak{u}}},{\mathfrak{d}}_{\overline{\mathfrak{u}}}).\end{array}$$

From now onwards, for any $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$, the notation $\left(\alpha \right(\mathfrak{u}),d(\mathfrak{u}\left)\right)$ will be used to represent the optimal solution of the problem ${\left(\mathrm{P}\right)}_{\mathfrak{u}}$.

In the subsequent discussions, we utilize the following lemmas from Upadhyay et al. [26].

Lemma 1.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$. If $\overline{\mathfrak{u}}\notin \mathcal{P}$, then $d\left(\overline{\mathfrak{u}}\right)$ is a descent direction at $\overline{\mathfrak{u}}$ for $\mathcal{H}$.

Lemma 2.

For $\overline{\mathfrak{u}}\in {\mathbb{R}}^n$, the following properties hold:

(i)

If $\overline{\mathfrak{u}}\in \mathcal{P}$, then $d\left(\overline{\mathfrak{u}}\right)=0\in {\mathbb{R}}^{\mathit{n}}$ and $\alpha \left(\overline{\mathfrak{u}}\right)=0$.

(ii)

If $\overline{\mathfrak{u}}\notin \mathcal{P}$, then $\alpha \left(\overline{\mathfrak{u}}\right)<0$.

Remark 2.

From Lemma 1, it follows that if $\overline{\mathfrak{u}}\notin \mathcal{P}$, then the optimal solution of ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$ yields a descent direction. Furthermore, from Lemma 2, it can be inferred that the value of $\alpha \left(\overline{\mathfrak{u}}\right)$ can be utilized to determine whether $\overline{\mathfrak{u}}\in \mathcal{P}$ or not. Specifically, for any given point $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$, if $\alpha \left(\overline{\mathfrak{u}}\right)=0$, then $\overline{\mathfrak{u}}\in \mathcal{P}$. Otherwise, $\overline{\mathfrak{u}}\notin \mathcal{P}$, and in this case, $d\left(\overline{\mathfrak{u}}\right)$ serves as a descent direction at $\overline{\mathfrak{u}}$ for $\mathcal{H}$.

We recall the following result from Upadhyay et al. [26].

Lemma 3.

Let $\overline{\mathfrak{u}}\in \mathcal{P}$. If the functions ${\mathcal{H}}_{\mathit{k}}$ ($\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$) are locally convex (respectively, locally strongly convex) at $\overline{\mathfrak{u}}$, then $\overline{\mathfrak{u}}$ is a locally weak effective (respectively, locally effective) solution of IVMOP.

The proof of the following lemma follows on the lines of the proof of Lemma 3.

Lemma 4.

Let $\overline{\mathfrak{u}}\in \mathcal{P}$. If the functions ${\mathcal{H}}_{\mathit{k}}$ ($\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$) are strongly convex on ${\mathbb{R}}^{\mathit{n}}$, then $\overline{\mathfrak{u}}$ is an effective solution of IVMOP.

To introduce the Hestenes-Stiefel-type direction for IVMOP, we define a function $\tilde{\Phi }:{\mathbb{R}}^{\mathit{n}}\times {\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$ as follows

$$\tilde{\Phi }(\mathfrak{u},\mathfrak{d}):=\underset{\mathit{k}\in {\mathcal{I}}_{\mathit{m}}}{max}{\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u},\mathfrak{d}\right),\mathrm{for}\mathrm{all}(\mathfrak{u},\mathfrak{d})\in {\mathbb{R}}^{\mathit{n}}\times {\mathbb{R}}^{\mathit{n}},$$

(3)

where,

$$D_{gH}{\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u},\mathfrak{d}\right):=\left[{\underline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u},\mathfrak{d}\right),{\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u},\mathfrak{d}\right)\right],\mathrm{for}\mathrm{all}(\mathfrak{u},\mathfrak{d})\in {\mathbb{R}}^{\mathit{n}}\times {\mathbb{R}}^{\mathit{n}}.$$

In the following lemma, we establish the relationship between the critical point of $\mathcal{H}$ and the function $\tilde{\Phi }$.

Lemma 5.

Let $\tilde{\Phi }:{\mathbb{R}}^{\mathit{n}}\times {\mathbb{R}}^{\mathit{n}}\to \mathbb{R}$ be defined by (3), and $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$. Then, $\overline{\mathfrak{u}}$ is a critical point of $\mathcal{H}$ if and only if

$$\tilde{\Phi }(\overline{\mathfrak{u}},\mathfrak{d})\ge 0,\mathrm{for}\mathrm{all}\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}.$$

Proof. 

Let $\overline{\mathfrak{u}}$ be a critical point of $\mathcal{H}$. Then, by Definition 7, for every $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$there exists $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$ such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}(\overline{\mathfrak{u}},\mathfrak{d})\cap \mathfrak{C}\left({\mathbb{R}}_{--}\right)=\varnothing .$$

Consequently, it follows that ${\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}(\overline{\mathfrak{u}},\mathfrak{d})\ge 0$, which implies

$$\tilde{\Phi }(\overline{\mathfrak{u}},\mathfrak{d})\ge 0.$$

Conversely, suppose that

$$\tilde{\Phi }(\overline{\mathfrak{u}},\mathfrak{d})\ge 0,\mathrm{for}\mathrm{all}\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}.$$

Then, for any $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$there exists $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$ such that

$$\tilde{\Phi }(\overline{\mathfrak{u}},\mathfrak{d})={\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}(\overline{\mathfrak{u}},\mathfrak{d})\ge 0.$$

This further implies that for any $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$,

$$D_{gH}\mathcal{H}(\overline{\mathfrak{u}},\mathfrak{d})\cap {\left(\mathfrak{C}\left({\mathbb{R}}_{--}\right)\right)}^{\mathit{m}}=\varnothing .$$

Therefore, it follows that $\overline{\mathfrak{u}}$ is a critical point of $\mathcal{H}$. This completes the proof.    □

We establish the following lemma, which will be used in the sequel.

Lemma 6.

Let $\overline{\mathfrak{u}}\in {\mathbb{R}}^{\mathit{n}}$ and let $\left(\alpha \left(\overline{\mathfrak{u}}\right),d\left(\overline{\mathfrak{u}}\right)\right)$ be the optimal solution of the problem ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$. Then

$$\alpha \left(\overline{\mathfrak{u}}\right)=\tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right).$$

Proof. 

Since $\left(\alpha \left(\overline{\mathfrak{u}}\right),d\left(\overline{\mathfrak{u}}\right))\right)\in {\mathcal{K}}_{\overline{\mathfrak{u}}}$, therefore we have

$$D_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right){\leqq }_{LU}[\alpha \left(\overline{\mathfrak{u}}\right),\alpha \left(\overline{\mathfrak{u}}\right)],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(4)

From (4), we obtain

$${\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)\le \alpha \left(\overline{\mathfrak{u}}\right),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Consequently,

$$\tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)\le \alpha \left(\overline{\mathfrak{u}}\right).$$

(5)

Let us define ${\alpha }_{\overline{\mathfrak{u}}}:=\tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)$. Then, we have

$${\underline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)\le {\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)\le \tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right)={\alpha }_{\overline{\mathfrak{u}}},\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Therefore, we obtain

$$D_{gH}{\mathcal{H}}_{\mathit{k}}\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right){\leqq }_{LU}[{\alpha }_{\overline{\mathfrak{u}}},{\alpha }_{\overline{\mathfrak{u}}}],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

This implies that $\left({\alpha }_{\overline{\mathfrak{u}}},d\left(\overline{\mathfrak{u}}\right)\right)\in {\mathcal{K}}_{\overline{\mathfrak{u}}}$. Since $\left(\alpha \left(\overline{\mathfrak{u}}\right),d\left(\overline{\mathfrak{u}}\right))\right)$ is the optimal solution of the problem ${\left(\mathrm{P}\right)}_{\overline{\mathfrak{u}}}$, we obtain

$$\alpha \left(\overline{\mathfrak{u}}\right)\le {\alpha }_{\overline{\mathfrak{u}}}=\tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right).$$

(6)

Combining (5) and (6), we conclude

$$\alpha \left(\overline{\mathfrak{u}}\right)=\tilde{\Phi }\left(\overline{\mathfrak{u}},d\left(\overline{\mathfrak{u}}\right)\right).$$

This completes the proof.    □

Let $\mathit{s}\in \{0,1,2,\dots \}$ be fixed and let ${\left\{{\mathfrak{u}}^{\left(\mathit{r}\right)}\right\}}_{0\le \mathit{r}\le \mathit{s}}\subset {\mathbb{R}}^{\mathit{n}}$. We now introduce a Hestenes-Stiefel direction (HS-direction, in short) ${\mathsf{w}}_{\mathit{s}}^{\mathrm{HS}}$ at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$.

$${\mathsf{w}}_{\mathit{s}}^{\mathrm{HS}}:=\left\{\begin{array}{cc}d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right);\hfill & \mathrm{if}s=0,\hfill \\ d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}^{\mathrm{HS}}{\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}};\hfill & \mathrm{if}\mathit{s}\ge \mathit{1},\hfill \end{array}\right.$$

(7)

where ${\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}}$ represents the HS-direction at $(\mathit{s}-1)$-th step, and for $\mathit{s}\ge \mathit{1}$, ${\beta }_{\mathit{s}}^{\mathrm{HS}}$ is defined as

$${\beta }_{\mathit{s}}^{\mathrm{HS}}:={\displaystyle \frac{-\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right)+\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)}{\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}}\right)-\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}}\right)}}.$$

(8)

Remark 3.

If every component of the objective function $\mathcal{H}$ of the IVMOP is a real-valued function rather than interval-valued function, that is, $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\mathbb{R}}^{\mathit{m}}$, then Equation (7) reduces to the HS-direction defined for vector-valued functions, as considered by Pérez and Prudente [29]. As a result, the parameter ${\beta }_{\mathit{s}}^{\mathrm{HS}}$ introduced in (8) extends the HS-direction from MOPs to IVMOPs, which belong to a broader class of optimization problems. Moreover, when $m=1$, Equation (7) further reduces to the classical HS-direction for a real-valued function, defined by Hestenes and Stiefel [28].

It can be observed that ${\beta }_{\mathit{s}}^{\mathrm{HS}}$, defined in (8), become undefined when

$$\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}}\right)=\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}_{(\mathit{s}-\mathit{1})}^{\mathrm{HS}}\right),$$

and the direction ${\mathsf{w}}_{\mathit{s}}^{\mathrm{HS}}$ defined in Equation (7) may not provide a descent direction. Therefore, to address this issue, we adopt an approach similar to that proposed by Gilbert and Nocedal [37] and Pérez and Prudente [29]. Hence, we define ${\beta }_{\mathit{s}}$ and ${\mathsf{w}}^{\left(s\right)}$ as follows:

$${\beta }_{\mathit{s}}:=\left\{\begin{array}{cc}0,\hfill & \mathrm{if}\left({\beta }_{\mathit{s}}^{\mathrm{HS}}<0\mathrm{or}\mathrm{undefined}\right)\mathrm{or}s=0;\hfill \\ 0,\hfill & \mathrm{if}\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)>\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right),\hfill \\ {\displaystyle \frac{-\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right)+\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)}{\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)-\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)}},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(9)

and

$${\mathsf{w}}^{\left(s\right)}:=d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(s-1)}.$$

(10)

In the following lemma, we establish an inequality that relates the directional derivative of $\mathcal{H}$ at point ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ in the direction ${\mathsf{w}}^{(s-1)}$ to ${\beta }_{\mathit{s}}$.

Lemma 7.

Let ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ and ${\mathfrak{u}}^{(\mathit{s}-\mathit{1})}$ be noncritical points of $\mathcal{H}$. Suppose that ${\mathsf{w}}^{(s-1)}$ represents a descent direction of $\mathcal{H}$ at point ${\mathfrak{u}}^{(\mathit{s}-\mathit{1})}$. Then, we have

$${\beta }_{\mathit{s}}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)}){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(11)

Proof. 

In view of Definition 9, it follows that ${\beta }_{\mathit{s}}\ge 0$. Now, the following two possible cases may arise:

Case 1: If ${\beta }_{\mathit{s}}=0$, then

$${\beta }_{\mathit{s}}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)})=[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Therefore, the inequality in (11) is satisfied.

Case 2: Let ${\beta }_{\mathit{s}}>0$. Our aim is to prove that

$${\beta }_{\mathit{s}}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)}){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Since ${\beta }_{\mathit{s}}>0$, it suffices to show that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)}){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

On the contrary, assume that there exists $k\in {\mathcal{I}}_{\mathit{m}}$ such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)}){\nleqq }_{LU}[0,0].$$

(12)

This implies that

$$\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)>0.$$

(13)

Since ${\mathsf{w}}^{(s-1)}$ is a descent direction of $\mathcal{H}$ at point ${\mathfrak{u}}^{(\mathit{s}-\mathit{1})}$, we have

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

This implies that

$$\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)\le 0.$$

(14)

From (13) and (14), we obtain

$$\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)-\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},{\mathsf{w}}^{(\mathit{s}-\mathit{1})}\right)>0.$$

(15)

Now, if

$$\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)>\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right),$$

then from Definition 9, we obtain

$${\beta }_{\mathit{s}}=0,$$

which contradicts the assumption that ${\beta }_{\mathit{s}}>0$. On the other hand, if

$$\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)\le \tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right),$$

then

$$\tilde{\Phi }\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})},d\left({\mathfrak{u}}^{(\mathit{s}-\mathit{1})}\right)\right)-\tilde{\Phi }\left({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right)\le 0.$$

Using (15) and Definition 9, we obtain

$${\beta }_{\mathit{s}}\le 0,$$

which is a contradiction. This completes the proof.    □

Notably, for $\mathit{s}=0$, the direction ${\mathsf{w}}^{\left(s\right)}$, as defined in Equation (10), coincides with $d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)$. Thus, by Lemma 1, we conclude that ${\mathsf{w}}^{\left(s\right)}$ serves as a descent direction at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ for $\mathit{s}=0$. Therefore, in the following theorem, we establish that ${\mathsf{w}}^{\left(s\right)}$ serves as a descent direction at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ for $\mathit{s}\ge 1$, under appropriate assumptions.

Theorem 2.

Let ${\mathfrak{u}}^{\left(\mathit{r}\right)}$$\left(\mathit{r}\in \{0,1,\dots ,\mathit{s}\}\right)$ be noncritical points of $\mathcal{H}$. Suppose that ${\mathsf{w}}^{\left(\mathit{r}\right)}$, as defined in Equation (10), serves as descent direction of $\mathcal{H}$ at ${\mathfrak{u}}^{\left(\mathit{r}\right)}$ for all $\left(\mathit{r}\in \{0,1,\dots ,(\mathit{s}-\mathit{1}\left)\right\}\right)$. Then, ${\mathsf{w}}^{\left(\mathit{s}\right)}$ serves as a descent direction at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ for the function $\mathcal{H}$.

Proof. 

Since the functions ${\mathcal{H}}_{\mathit{k}}$ ($\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$) are continuously gH-differentiable, therefore to prove that ${\mathsf{w}}^{\left(\mathit{s}\right)}$ is a descent direction at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ it is sufficient to show that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)}){<}_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Let $\mathit{s}\ge 1$ be fixed. From Theorem 1, we have

$$\begin{array}{cc}\hfill D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)})=& D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}),\hfill \\ \hfill =& \left[{\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}\right)\right.\hfill \\ \hfill & \vee \left.{\nabla }_{+}{\overline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}\right)\right],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.\hfill \end{array}$$

(16)

Consider

$$\begin{array}{cc}\hfill {\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}\right)& ={\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^{T}d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T{\mathsf{w}}^{(\mathit{s}-1)}.\hfill \\ \hfill & \le \alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\overline{D}}_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{(s-1)}),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.\hfill \end{array}$$

(17)

Therefore, from (17), Lemmas 2 and 7, we obtain

$${\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}\right)<0,\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(18)

Similarly, we can prove that

$${\nabla }_{+}{\overline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)+{\beta }_{\mathit{s}}{\mathsf{w}}^{(\mathit{s}-1)}\right)<0,\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(19)

Therefore, from (16), (18) and (19), we conclude that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)}){<}_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(20)

This completes the proof.    □

Now, we introduce an Armijo-like line search method for the objective function $\mathcal{H}$ of IVMOP.

Consider $\mathfrak{u},\mathsf{w}\in {\mathbb{R}}^{\mathit{n}}$such that $\mathsf{w}$ is a descent direction at $\mathfrak{u}$ for the function $\mathcal{H}$. Let $\gamma \in (0,1)$. A step length t is acceptable if it satisfies the following condition:

$${\mathcal{H}}_{\mathit{k}}(\mathfrak{u}+t\mathsf{w}){\ominus }_{gH}{\mathcal{H}}_{\mathit{k}}\left(\mathfrak{u}\right){\leqq }_{LU}\left(\gamma t\right)\odot D_{gH}{\mathcal{H}}_{\mathit{k}}(\mathfrak{u},\mathsf{w}),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(21)

Remark 4.

If every component of the objective function $\mathcal{H}$ of the IVMOP is a real-valued function rather than an interval-valued function, that is, $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\mathbb{R}}^{\mathit{m}}$, then (21) reduces to the following Armijo-like line search, defined by Fliege and Svaiter [5]:

$$\mathcal{H}(\mathfrak{u}+t\mathsf{w})\le \mathcal{H}\left(u\right)+\gamma tJ\mathcal{H}\left(\mathfrak{u}\right)\mathsf{w},$$

where $J\mathcal{H}\left(\mathfrak{u}\right)$ represents the Jacobian of $\mathcal{H}$ at $\mathfrak{u}$.

In the next lemma, we prove the existence of such t which satisfies (21) for a given $\gamma \in (0,1)$.

Lemma 8.

If $\mathcal{H}$ is gH-differentiable and $D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}){<}_{LU}[0,0]$ for each $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, then for given $\gamma \in (0,1)$ there exists $\widehat{t}>0$, such that

$${\mathcal{H}}_k(\mathfrak{u}+t\mathsf{w}){\ominus }_{gH}{\mathcal{H}}_k\left(u\right){\leqq }_{LU}\left(\gamma t\right)\odot D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),\mathit{k}\in {\mathcal{I}}_{\mathit{m}},t\in (0,\widehat{t}).$$

Proof. 

Let $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$ be fixed. By the definition of the directional derivative of ${\mathcal{H}}_k$, there exists a function ${\tau }_k:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$ such that

$${\mathcal{H}}_k(\mathfrak{u}+t\mathsf{w}){\ominus }_{gH}{\mathcal{H}}_k\left(\mathfrak{u}\right)=t\odot D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})+t\odot {\tau }_k\left(t\right),$$

(22)

where ${\tau }_k\left(t\right)\to \left[0,0\right]$ as $t\to 0$.

From (22) and Definition 2, the possible two cases may arises:

Case 1:

$$\begin{array}{cc}\hfill & {\underline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\underline{\mathcal{H}}}_k\left(\mathfrak{u}\right)=t{\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})+t{\underline{ϵ}}_k\left(t\right),\hfill \\ \hfill & {\overline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\overline{\mathcal{H}}}_k\left(\mathfrak{u}\right)=t{\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})+t{\overline{ϵ}}_k\left(t\right).\hfill \end{array}$$

(23)

Since $D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}){<}_{LU}[0,0]$, therefore ${\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})<0$ and ${\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})<0$. Define

$$ϵ:=max\left\{-(1-\gamma ){\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),-(1-\gamma ){\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})\right\}>0.$$

(24)

Since ${\tau }_k\left(t\right)\to [0,0]$ as $t\to 0$, there exists ${\widehat{t}}_k>0$ such that

$$\parallel {\tau }_k{\left(t\right)\parallel }_I\le ϵ,\mathrm{for}\mathrm{all}t\in (0,{\widehat{t}}_k).$$

(25)

Substituting (24) and (25) in (23), we have

$$\begin{array}{cc}& {\underline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\underline{\mathcal{H}}}_k\left(\mathfrak{u}\right)\le t{\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})-t(1-\gamma ){\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),\mathrm{for}\mathrm{all}t\in (0,{\widehat{t}}_k)\hfill \\ & {\overline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\overline{\mathcal{H}}}_k\left(\mathfrak{u}\right)\le t{\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})-t(1-\gamma ){\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),\mathrm{for}\mathrm{all}t\in (0,{\widehat{t}}_k).\hfill \end{array}$$

This implies that

$${\mathcal{H}}_k(\mathfrak{u}+t\mathsf{w}){\ominus }_{gH}{\mathcal{H}}_k\left(u\right){\leqq }_{LU}\left(\gamma t\right)\odot D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),\mathrm{for}\mathrm{all}t\in (0,{\widehat{t}}_k).$$

(26)

Case 2:

$$\begin{array}{cc}\hfill & {\overline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\overline{\mathcal{H}}}_k\left(\mathfrak{u}\right)=t{\underline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})+t{\underline{ϵ}}_k\left(t\right),\hfill \\ \hfill & {\underline{\mathcal{H}}}_k(\mathfrak{u}+t\mathsf{w})-{\underline{\mathcal{H}}}_k\left(\mathfrak{u}\right)=t{\overline{D}}_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w})+t{\overline{ϵ}}_k\left(t\right).\hfill \end{array}$$

(27)

On the lines of the proof of Case 1, it can be shown that the inequality in (26) holds for all $t\in (0,{\widehat{t}}_k)$ for some ${\widehat{t}}_k>0$.

Since $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$ was arbitrary, we conclude that for each $k\in {\mathcal{I}}_{\mathit{m}}$, there exists ${\widehat{t}}_k>0$ such that (26) holds. Let us set $\widehat{t}:=min\{{\widehat{t}}_1,\dots ,{\widehat{t}}_m\}$, we have

$${\mathcal{H}}_k(\mathfrak{u}+t\mathsf{w}){\ominus }_{gH}{\mathcal{H}}_k\left(u\right){\leqq }_{LU}\left(\gamma t\right)\odot D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}},\mathrm{for}\mathrm{all}t\in (0,\widehat{t}).$$

This completes the proof.    □

Remark 5.

From Lemma 8, it follows that for $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$, if $D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}){<}_{LU}[0,0]$$(\mathit{k}\in {\mathcal{I}}_{\mathit{m}})$, then there exists some $\widehat{t}>0$ such that Equation (21) holds for all $t\in (0,\widehat{t})$. To compute the step length t numerically, we employ the following steps:

We start with $p=0$ and check whether Equation (21) holds for $t={\displaystyle \frac{1}{2^p}}$.

(a)

If the inequality in (21) is satisfied, we take $t={\displaystyle \frac{1}{2^p}}$ as the step length.

(b)

Otherwise, set $p:=p+1$ and update $t={\displaystyle \frac{1}{2^p}}$, repeating the process until the Equation (21) is satisfied.

In view of the fact that, as some $\widehat{t}>0$ exists such that Equation (21) holds for all $t\in (0,\widehat{t})$, and the sequence ${\left({\displaystyle \frac{1}{2^p}}\right)}_{p\in \mathbb{N}\cup \left\{0\right\}}$ converges to 0, the above process terminates after a finite number of iterations.

Thus, at any $\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}$ with $D_{gH}{\mathcal{H}}_k(\mathfrak{u},\mathsf{w}){<}_{LU}[0,0]$$(\mathit{k}\in {\mathcal{I}}_{\mathit{m}})$, we can choose η as the largest t from the set

$$\left\{{\displaystyle \frac{1}{2^p}}\mid p\in \mathbb{N}\cup \left\{0\right\}\right\},$$

such that Equation (21) is satisfied.

Now, we present the HS-type conjugate direction algorithm for IVMOP.

Remark 6.

It is worth noting that if ${\beta }_s$ in (10) is set to zero and if every component of the objective function $\mathcal{H}$ of the IVMOP is a real-valued function rather than interval-valued function, that is, $\mathcal{H}:{\mathbb{R}}^{\mathit{n}}\to {\mathbb{R}}^{\mathit{m}}$, then the Algorithm 1 reduces to the steepest descent algorithm for MOPs, as proposed by Fliege and Svaiter [5].

Algorithm 1 HS-Type Conjugate Direction Algorithm for IVMOP

1: Let $\gamma \in (0,1)$, initial point ${\mathfrak{u}}^{\left(\mathit{0}\right)}\in {\mathbb{R}}^{\mathit{n}}$, $ϵ>0$, and set $\mathit{s}=0$. 2: Solve the optimization problem ${\left(\mathrm{P}\right)}_{{\mathfrak{u}}^{\left(\mathit{s}\right)}}$ and obtain the values of $\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)$ and $d\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)$. 3: If $\left|\alpha \right({\mathfrak{u}}^{\left(\mathit{s}\right)}\left)\right|<ϵ$, then stop. Otherwise, proceed to the next step. 4: Calculate ${\mathsf{w}}^{\left(\mathit{s}\right)}$ using (10). 5: Select ${\eta }^{\left(\mathit{s}\right)}$ as the largest value of $t\in \left\{{\displaystyle \frac{1}{2^{\mathit{p}}}}:p\in \mathbb{N}\cup \left\{0\right\}\right\}$ that satisfies (21). Update the iterate as follows: $${\mathfrak{u}}^{(\mathit{s}+\mathit{1})}:={\mathfrak{u}}^{\left(\mathit{s}\right)}+{\eta }^{\left(\mathit{s}\right)}{\mathsf{w}}^{\left(\mathit{s}\right)}.$$ 6: Set $\mathit{s}:=\mathit{s}+1$, and go to Step 2.

It is worthwhile to note that if, at iteration $\mathit{s}$, Algorithm 1 does not reach Step 4, that is, if it terminates at Step 3, then in view of Lemma 2, it follows that ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ is an approximate critical point of $\mathcal{H}$. On the other hand, if Algorithm 1 converges in a finite number of iterations, then the last iterative point is an approximate critical point of $\mathcal{H}$. As a consequence of this fact, we establish the convergence of the infinite sequence generated by Algorithm 1. That is, $\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\ne 0$ for all $\mathit{s}\in \mathbb{N}$. Consequently, we have $\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)<0$ and ${\mathsf{w}}^{\left(\mathit{s}\right)}$ serves as a descent direction at ${\mathfrak{u}}^{\left(\mathit{s}\right)}$ for all $\mathit{s}\in \mathbb{N}$.

In the following theorem, we establish the convergence of the sequence generated by the Algorithm 1.

Theorem 3.

Let ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$ be an infinite sequence generated by Algorithm 1. Suppose that the set

$$\mathcal{T}:=\{\mathfrak{u}\in {\mathbb{R}}^{\mathit{n}}:\mathcal{H}\left(\mathfrak{u}\right){⪯}_{\mathit{m}}\mathcal{H}\left({\mathfrak{u}}^{\left(\mathit{0}\right)}\right)\},$$

is bounded. Under these assumptions, every accumulation point of the sequence ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$ is a critical point of the objective function of IVMOP.

Proof. 

From (21), for all $\mathit{s}\in \{0,1,2,\dots \}$, we have

$${\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{(\mathit{s}+\mathit{1})}\right){\ominus }_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right){\leqq }_{LU}\left(\gamma {\eta }^{\left(\mathit{s}\right)}\right)\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)}),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

Using Remark 1, for all $\mathit{s}\in \{0,1,2,\dots \}$, we obtain

$${\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{(\mathit{s}+\mathit{1})}\right){\ominus }_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right){\leqq }_{LU}\left(\gamma {\eta }^{\left(\mathit{s}\right)}\right)\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)}){\leqq }_{LU}[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(28)

This implies that

$${\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{(\mathit{s}+\mathit{1})}\right){\leqq }_{LU}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right),\mathrm{for}\mathrm{all}\mathit{s}\in \{0,1,2,\dots \}\mathrm{and}\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(29)

From (29), the sequence ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$ lies in $\mathcal{T}$ which is a bounded subset of ${\mathbb{R}}^{\mathit{n}}$. As a result, the sequence ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$ is also bounded. Hence, it possesses at least one accumulation point, say $\overline{\mathfrak{u}}$. We claim that $\overline{\mathfrak{u}}$ is a critical point of the objective function of IVMOP.

Indeed as ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$ is a bounded sequence in ${\mathbb{R}}^{\mathit{n}}$ and for all $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, ${\mathcal{H}}_{\mathit{k}}$ is gH-continuous on ${\mathbb{R}}^{\mathit{n}}$, therefore using (29), we conclude that, for all $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, the sequence ${\left({\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)\right)}_{\mathit{s}\in \mathbb{N}}$ is non-increasing and bounded. Consequently, from (28), it follows that

$$\underset{\mathit{s}\to \infty }{lim}{\eta }^{\left(\mathit{s}\right)}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left(\mathit{s}\right)},{\mathsf{w}}^{\left(\mathit{s}\right)})=[0,0],\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(30)

Since ${\eta }^{\left(\mathit{s}\right)}\in (0,1]$ for all $\mathit{s}\in \mathbb{N}$, therefore the value $\underset{\mathit{s}\to \infty }{lim\; sup}{\eta }^{\left(\mathit{s}\right)}$ exists. Therefore, the following two possible cases may arise:

Case 1: Let $\underset{\mathit{s}\to \infty }{lim\; sup}{\eta }^{\left(\mathit{s}\right)}>0$. Hence, employing (30) and taking into account the fact that $\overline{\mathfrak{u}}$ is an accumulated point of the sequence ${\left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)}_{\mathit{s}\in \mathbb{N}}$, there exist subsequence ${\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right)}_{\mathit{j}\in \mathbb{N}}$ and ${\left({\eta }^{{\mathit{s}}_{\mathit{j}}}\right)}_{\mathit{j}\in \mathbb{N}}$ of ${\left({\mathfrak{u}}^{\mathit{s}}\right)}_{\mathit{s}\in \mathbb{N}}$ and ${\left({\eta }^{\mathit{s}}\right)}_{\mathit{s}\in \mathbb{N}}$, respectively, such that

$$\underset{j\to \infty }{lim}{\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}=\overline{\mathfrak{u}},\underset{j\to \infty }{lim}{\eta }^{{\mathit{s}}_{\mathit{j}}}=\underset{\mathit{s}\to \infty }{lim\; sup}{\eta }^{\left(\mathit{s}\right)}>0,$$

and

$$\underset{j\to \infty }{lim}{D}_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)})=[0,0],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(31)

Our aim is to show that $\overline{\mathfrak{u}}$ is a critical point of $\mathcal{H}$. On the contrary, assume that $\overline{\mathfrak{u}}$ is a noncritical point of $\mathcal{H}$. This implies that there exists $\mathfrak{d}\in {\mathbb{R}}^{\mathit{n}}$ such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}(\overline{\mathfrak{u}},\mathfrak{d}){<}_{LU}[0,0],\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(32)

Since $\mathcal{H}$ is continuously gH-differentiable, therefore there exist $ϵ>0$ and $\delta >0$, such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}(\mathfrak{u},\mathfrak{d}){<}_{LU}[-ϵ,-ϵ],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}\mathrm{and}\mathrm{for}\mathrm{all}\mathfrak{u}\in B_{\delta }\left(\overline{\mathfrak{u}}\right),$$

(33)

where, $B_{\delta }\left(\overline{\mathfrak{u}}\right)$ represents an open ball of radius $\delta$ centered at $\overline{\mathfrak{u}}$.

Since ${\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\to \overline{\mathfrak{u}}$ as $j\to \infty$, therefore using (33), there exists $n_0\in \mathbb{N}$, such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}},\mathfrak{d}){<}_{LU}[-ϵ,-ϵ],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}\mathrm{and}\mathrm{for}\mathrm{all}j\ge n_0.$$

(34)

Now, for every $j\ge n_0$, by defining ${\alpha }_{{\mathit{s}}_{\mathit{j}}}:=\tilde{\Phi }\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}},\mathfrak{d}\right)$, we get

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}},\mathfrak{d}){\leqq }_{LU}[{\alpha }_{{\mathit{s}}_{\mathit{j}}},{\alpha }_{{\mathit{s}}_{\mathit{j}}}],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

This implies that, for every $j\ge n_0$,

$$\left({\alpha }_{{\mathit{s}}_{\mathit{j}}},\mathfrak{d}\right)\in {\mathcal{K}}_{{\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}}$$

(35)

Using (34) and (35), for all $j\ge n_0$, we obtain

$$\alpha \left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right)\le {\alpha }_{{\mathit{s}}_{\mathit{j}}}<-ϵ.$$

This implies that, for all $j\ge n_0$, we get

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}},d\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right)){<}_{LU}[-ϵ,-ϵ],\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(36)

Now, for all $j\ge n_0$ and $\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, we consider

$$\begin{array}{cc}\hfill D_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right)=& D_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},d\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right)+{\beta }_{{\mathit{s}}_{\mathit{j}}}{\mathsf{w}}^{({\mathit{s}}_{\mathit{j}}-1)}\right)\hfill \\ \hfill =& \left[{\nabla }_{+}{\underline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right))+{\beta }_{{\mathit{s}}_{\mathit{j}}}{\mathsf{w}}^{({\mathit{s}}_{\mathit{j}}-1)}\right)\right.\hfill \\ \hfill & \vee \left.{\nabla }_{+}{\overline{\mathcal{H}}}_{\mathit{k}}{\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right)}^T\left(d\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right))+{\beta }_{{\mathit{s}}_{\mathit{j}}}{\mathsf{w}}^{({\mathit{s}}_{\mathit{j}}-1)}\right)\right].\hfill \end{array}$$

Therefore, using (36), for all $j\ge n_0$ and $\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, we conclude that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}){<}_{LU}\left[-ϵ,-ϵ\right]+{\beta }_{{\mathit{s}}_{\mathit{j}}}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}\left(d\left({\mathfrak{u}}^{{\mathit{s}}_{\mathit{j}}}\right),{\mathsf{w}}^{({\mathit{s}}_{\mathit{j}}-1)}\right).$$

Now using Lemma 7, for all $j\ge n_0$ and $\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, we obtain

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}){<}_{LU}\left[-ϵ,-ϵ\right].$$

(37)

This leads to a contradiction with Equation (31).

Case 2: Let $\underset{\mathit{s}\to \infty }{lim\; sup}{\eta }^{\left(\mathit{s}\right)}=0$. Since ${\eta }^{\left(\mathit{s}\right)}\ge 0$, for all $\mathit{s}\in \mathbb{N}$, therefore we get

$$\underset{\mathit{s}\to \infty }{lim}{\eta }^{\left(\mathit{s}\right)}=0.$$

Now, for $p\in \mathbb{N}$, there exists ${\mathit{n}}_{\mathit{p}}\in \mathbb{N}$ such that

$${\eta }^{\left(\mathit{s}\right)}<{\displaystyle \frac{1}{2^{\mathit{p}}}},\mathit{s}\ge {\mathit{n}}_{\mathit{p}}.$$

Therefore, for $t={\displaystyle \frac{1}{2^{\mathit{p}}}}$, Equation (21) is not satisfied, that is for all $\mathit{s}\ge {\mathit{n}}_{\mathit{p}}$, we have

$${\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)}+{\displaystyle \frac{1}{2^{\mathit{p}}}}{\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right){\ominus }_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right){\nleqq }_{LU}{\displaystyle \frac{\gamma }{2^{\mathit{p}}}}\odot D_{gH}{\mathcal{H}}_{\mathit{k}}\left({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}\right),\mathrm{for}\mathrm{all}\mathit{k}\in {\mathcal{I}}_{\mathit{m}}.$$

(38)

Letting $\mathit{p}\to \infty$ (along a suitable subsequence, if necessary) in both sides of the inequality in (38), there exists $\mathit{k}\in {\mathcal{I}}_{\mathit{m}}$, such that

$$D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}){\nleqq }_{LU}\gamma \odot D_{gH}{\mathcal{H}}_{\mathit{k}}({\mathfrak{u}}^{\left({\mathit{s}}_{\mathit{j}}\right)},{\mathsf{w}}^{\left({\mathit{s}}_{\mathit{j}}\right)}),{\mathit{s}}_{\mathit{j}}\ge {\mathit{n}}_{\mathit{p}},$$

which leads to a contradiction. This completes the proof.    □

4. Numerical Experiments

In this section, we furnish several numerical examples to illustrate the effectiveness of Algorithm 1 and solve them by employing MATLAB R2024a.

In the following example, we provide an example of a strongly convex IVMOP to illustrate the significance of Algorithm 1.

Example 1.

Consider the following problem (P1) which belongs to the class of IVMOPs.

$$\begin{array}{cc}\hfill \left(\mathrm{P}1\right)& \mathrm{Minimize}\left({\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},{\mathfrak{u}}_{\mathit{3}}),{\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},{\mathfrak{u}}_{\mathit{3}})\right),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},{\mathfrak{u}}_{\mathit{3}})\in {\mathbb{R}}^3,\hfill \end{array}$$

where ${\mathcal{H}}_{\mathit{k}}:{\mathbb{R}}^3\to \mathfrak{C}\left(\mathbb{R}\right)$$(\mathit{k}=1,2)$ are defined as follows:

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},{\mathfrak{u}}_{\mathit{3}})& :=\left[{\left({\mathfrak{u}}_{\mathit{1}}-1\right)}^2+{\mathfrak{u}}_{\mathit{2}}^2+{({\mathfrak{u}}_{\mathit{3}}-1)}^2\vee {\mathfrak{u}}_{\mathit{1}}^2+{({\mathfrak{u}}_{\mathit{2}}-2)}^2+{({\mathfrak{u}}_{\mathit{3}}-3)}^2\right],\hfill \\ \hfill {\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},{\mathfrak{u}}_{\mathit{3}})& :=\left[e^{{\mathfrak{u}}_{\mathit{1}}}+e^{{\mathfrak{u}}_{\mathit{2}}}+e^{{\mathfrak{u}}_{\mathit{3}}}\vee {\mathfrak{u}}_{\mathit{1}}^2+{\mathfrak{u}}_{\mathit{2}}^2+{\mathfrak{u}}_{\mathit{3}}^2\right].\hfill \end{array}$$

Evidently, $(0,2,3)$ is a critical point of the objective function of (P1). Since the components of the objective function in (P1) are strongly convex, it follows from Lemma 4 that $(0,2,3)$ is an effective solution of (P1).

Now, we employ Algorithm 1 to solve (P1), with an initial point $(14,17,11)$. The stopping criterion is defined as $|\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)|<ϵ={10}^{-4}$. The numerical results for Algorithm 1 are shown in Table 1.

From Step 9 of Table 1, we conclude that the sequence converges to an approximate effective solution $(2.5519\times {10}^{-8},2,3)$ of (P1).

In Example 2, we consider a locally convex IVMOP to demonstrate the effectiveness of Algorithm 1.

Example 2.

Consider the following problem (P2) which belongs to the class of IVMOPs.

$$\begin{array}{cc}\hfill \left(\mathrm{P}2\right)& \mathrm{Minimize}\left({\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}}),{\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})\right),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})\in {\mathbb{R}}^{\mathit{2}},\hfill \end{array}$$

where ${\mathcal{H}}_{\mathit{k}}:{\mathbb{R}}^2\to \mathfrak{C}\left(\mathbb{R}\right)$$(\mathit{k}=1,2)$ are defined as follows:

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})& :=\left[{\displaystyle \frac{1}{2}}{\left({\mathfrak{u}}_{\mathit{1}}-1\right)}^2+{\left({\mathfrak{u}}_{\mathit{2}}-1\right)}^2-{\displaystyle \frac{1}{2}}{({\mathfrak{u}}_{\mathit{1}}-1)}^3\vee {\left({\mathfrak{u}}_{\mathit{1}}-{\mathfrak{u}}_{\mathit{2}}\right)}^2+e^{{\mathfrak{u}}_{\mathit{1}}+{\mathfrak{u}}_{\mathit{2}}}\right],\hfill \\ \hfill {\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})& :=\left[{\left({\mathfrak{u}}_{\mathit{1}}-1\right)}^2+{\left({\mathfrak{u}}_{\mathit{2}}-1\right)}^2\vee {\left({\mathfrak{u}}_{\mathit{1}}+1\right)}^2+{\left({\mathfrak{u}}_{\mathit{2}}+1\right)}^2\right].\hfill \end{array}$$

It is evident that $(1,1)$ is a critical point of the objective function of (P2). Since the components of the objective function in (P2) are locally convex at $(1,1)$, it follows from Lemma 3 that $(1,1)$ is a locally weak effective solution of (P2).

Now, we employ Algorithm 1 to solve (P2), with an initial starting point $(-4,12)$. The stopping criterion is defined as $|\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)|<ϵ={10}^{-4}$. The numerical results for Algorithm 1 are shown in Table 2.

From Step 3 of Table 1, we conclude that the sequence converges to locally weak effective solution $(1,1)$ of (P2).

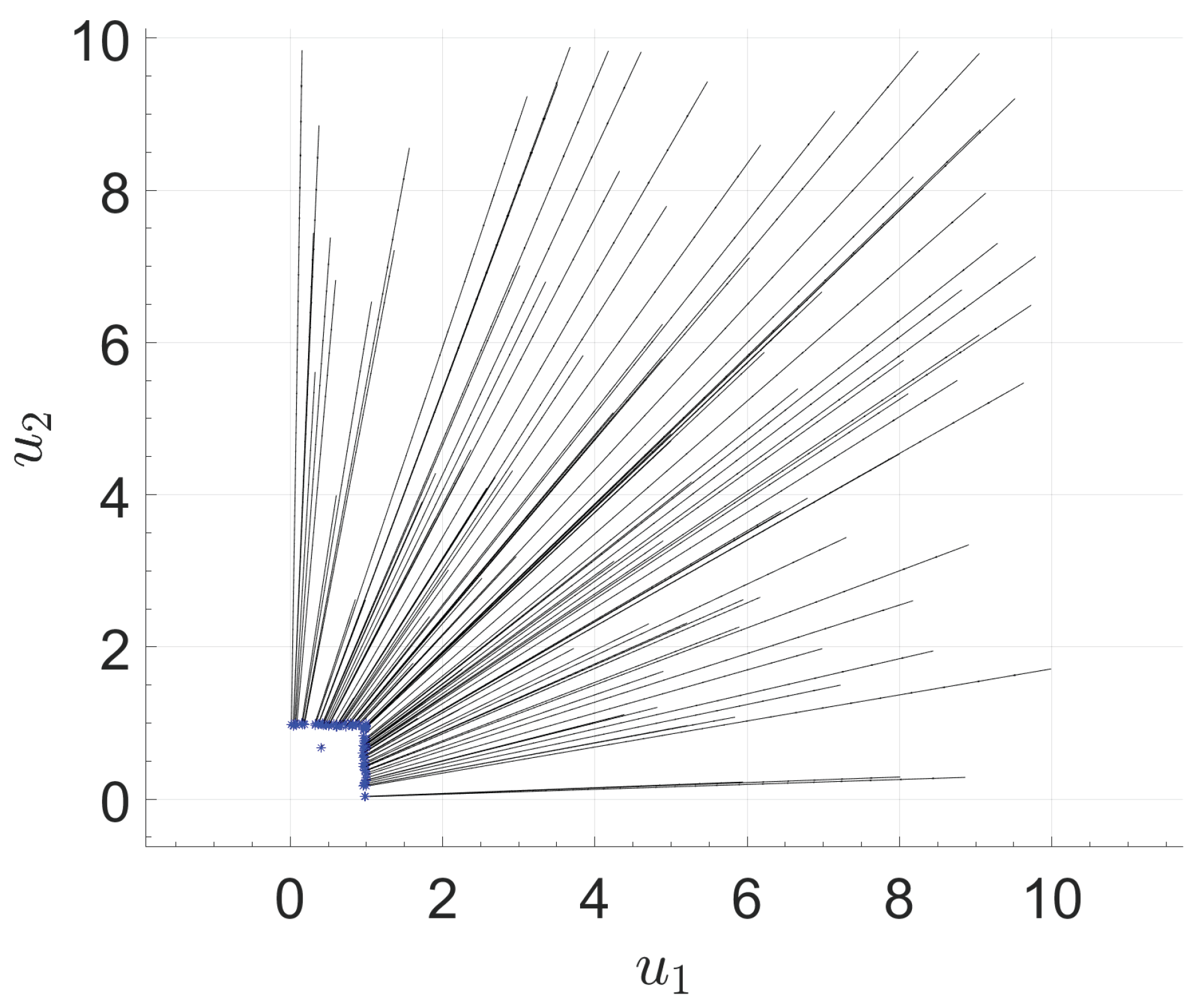
It is worth noting that the locally weak effective solution of an IVMOP is not an isolated point. However, applying Algorithm 1 with a given initial point can lead to one such locally weak effective solution. To generate an approximate locally weak effective solution set, we employ a multi-start approach. Specifically, we generate 100 uniformly distributed random initial points and subsequently execute Algorithm 1 starting from each of these points. In view of the above fact, in Example 2 we generate a set of approximate locally weak effective solutions by selecting 100 uniformly distributed random initial points in the domain $[0,10]\times [0,10]$ using the “rand” function of MATLAB R2024a. We use $|\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)|<ϵ={10}^{-4}$ or a maximum of 1000 iterations as the stopping criteria. The sequences generated from these points are illustrated in Figure 1.

In view of the works of Upadhyay et al. [22,23], it can be observed that Newton’s and Quasi-Newton methods are applicable to solve certain classes of IVMOPs in which the objective functions of IVMOPs are twice continuously gH-differentiable. In contrast, our proposed algorithm only requires the continuous gH-differentiability on the components of the objective function. In view of this, Algorithm 1 could be applied to solve a broader class of IVMOPs compared to the algorithms proposed by Upadhyay et al. [22,23]. To demonstrate this, we consider an IVMOP, where the first component of the objective function is not twice continuously gH-differentiable.

Example 3.

Consider the following problem (P3) which belongs to the class of IVMOPs.

$$\begin{array}{cc}\hfill \left(\mathrm{P}3\right)& \mathrm{Minimize}\left({\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}}),{\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})\right),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}})\in {\mathbb{R}}^2,\hfill \end{array}$$

where, ${\mathcal{H}}_{\mathit{1}}:{\mathbb{R}}^2\to \mathfrak{C}\left(\mathbb{R}\right)$ and ${\mathcal{H}}_{\mathit{2}}:{\mathbb{R}}^2\to \mathfrak{C}\left(\mathbb{R}\right)$ are defined as follows:

$${\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}}):=\left\{\begin{array}{cc}\left[{\displaystyle \frac{{({\mathfrak{u}}_{\mathit{1}}-3)}^2}{2}}+{\mathfrak{u}}_{\mathit{1}}\vee {\displaystyle \frac{{({\mathfrak{u}}_{\mathit{1}}-3)}^2}{2}}+{\mathfrak{u}}_{\mathit{1}}+{\mathfrak{u}}_{\mathit{2}}^2\right],\hfill & \mathrm{if}{\mathfrak{u}}_{\mathit{1}}\ge 3,\hfill \\ \left[{\displaystyle \frac{{\mathfrak{u}}_{\mathit{1}}^2}{4}}-{\displaystyle \frac{{\mathfrak{u}}_{\mathit{1}}}{2}}+{\displaystyle \frac{9}{4}}\vee {\displaystyle \frac{{\mathfrak{u}}_{\mathit{1}}^2}{4}}-{\displaystyle \frac{{\mathfrak{u}}_{\mathit{1}}}{2}}+{\displaystyle \frac{9}{4}}+{\mathfrak{u}}_{\mathit{2}}^2\right],\hfill & \mathrm{if}{\mathfrak{u}}_{\mathit{1}}<3,\hfill \end{array}\right.$$

and

$${\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}}):=\left[{({\mathfrak{u}}_{\mathit{1}}-3)}^2+{\mathfrak{u}}_{\mathit{2}}^2\vee {\mathfrak{u}}_{\mathit{1}}^2+{({\mathfrak{u}}_{\mathit{2}}-4)}^2\right].$$

It can be verified that ${\mathcal{H}}_{\mathit{1}}$ is gH-differentiable but not twice gH-differentiable. As a result, Newton’s and Quasi-Newton methods proposed by Upadhyay et al. [22,23] cannot be applied to solve (P3).

We solve (P3) by employing Algorithm 1 and MATLAB R2024a. We initialize the algorithm at the starting point $(9,4)$ and define the stopping criteria as $|\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)|<ϵ={10}^{-4}$. The numerical results for Algorithm 1 are shown in Table 3.

Therefore, in view of Step 17 in Table 3, the sequence generated by Algorithm 1 converges to an approximate critical point $(1.0022,3.5864)$ of the objective function of (P3).

In the following example, we apply Algorithm 1 employing MATLAB to solve a large-scale IVMOP for different values of $\mathit{n}$.

Example 4.

Consider the following problem (P4) which belongs to the class of IVMOPs.

$$\begin{array}{cc}\hfill \left(\mathrm{P}4\right)& \mathrm{Minimize}\left({\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},\dots ,{\mathfrak{u}}_{\mathit{n}}),{\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},\dots ,{\mathfrak{u}}_{\mathit{n}})\right),\hfill \\ \hfill & \mathrm{subject}\mathrm{to}({\mathfrak{u}}_{\mathit{1}},\dots ,{\mathfrak{u}}_{\mathit{n}})\in {\mathbb{R}}^{\mathit{n}},\hfill \end{array}$$

where ${\mathcal{H}}_{\mathit{k}}:{\mathbb{R}}^{\mathit{n}}\to \mathfrak{C}\left(\mathbb{R}\right)$$(\mathit{k}=1,2)$ is defined as follows:

$$\begin{array}{cc}\hfill {\mathcal{H}}_{\mathit{1}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},\dots ,{\mathfrak{u}}_{\mathit{n}})& :=\left[\sum _{\mathit{k}=1}^{\mathit{n}}{\left({\mathfrak{u}}_{\mathit{k}}-1\right)}^2\vee \sum _{\mathit{k}=1}^{\mathit{n}}{\left({\mathfrak{u}}_{\mathit{k}}+4\right)}^5\right],\hfill \\ \hfill {\mathcal{H}}_{\mathit{2}}({\mathfrak{u}}_{\mathit{1}},{\mathfrak{u}}_{\mathit{2}},\dots ,{\mathfrak{u}}_{\mathit{n}})& :=\left[\sum _{\mathit{k}=1}^{\mathit{n}}\left({\mathfrak{u}}_{\mathit{k}}^3+{\mathfrak{u}}_{\mathit{k}}^4\right)\vee \sum _{\mathit{k}=1}^{\mathit{n}}{\left({\mathfrak{u}}_{\mathit{k}}+1\right)}^2\right].\hfill \end{array}$$

We consider a random point, obtained using the built-in MATLAB R2024a functionrand(n,1), as the initial point of Algorithm 1. We define the stopping criteria as $|\alpha \left({\mathfrak{u}}^{\left(\mathit{s}\right)}\right)|<ϵ={10}^{-4}$ or reaching a maximum of 5000 iterations. Table 4 presents the number of iterations and the computational times required to solve (P4) using Algorithm 1 for various values of n, starting from randomly generated initial points.

The computations were carried out on an Ubuntu system with the following specifications:Memory:128.0 GiB,Processor:Intel^® Xeon^® Gold 5415+ (32 cores), andOS Type:64-bit.

5. Conclusions and Future Research Directions

In this article, we have investigated a class of unconstrained IVMOPs. We have defined the HS-direction for IVMOPs and established its descent property at noncritical points. To ensure efficient step size selection, we have employed an Armijo-like line search. Furthermore, we have proposed an HS-type conjugate direction algorithm for IVMOPs and derived the convergence of the sequence generated by the proposed algorithm. Finally, the efficiency of the proposed algorithm has been demonstrated through numerical experiments in convex, locally convex, and large-scale IVMOPs via MATLAB R2024a.

The results established in this article have generalized several significant results existing in the literature. Specifically, we have extended the work of Pérez and Prudente [29] on the HS-type conjugate direction method for MOPs to a more general class of optimization problems, namely, IVMOPs. Moreover, it is worth noting that, if the conjugate parameter is set to zero and if every component of the objective function of the IVMOP is a real-valued function rather than interval-valued function then the proposed algorithm reduces to the steepest descent algorithm for MOPs, as introduced by Fliege and Svaiter [5]. Furthermore, it is imperative to note that the proposed HS-type algorithm is applicable to any IVMOP where the objective function is continuously gH-differentiable. However, Newton’s method proposed by Upadhyay et al. [22] requires the objective function of the IVMOP to be twice continuously gH-differentiable. In view of this, our proposed algorithm can be applied to a broader class of optimization problems compared to the algorithms introduced by Upadhyay et al. [22].

It has been observed that all objective functions in the considered IVMOP are assumed to be continuously gH-differentiable. Consequently, the findings of this paper are not applicable when the objective function involved do not satisfy this requirement, which can be considered as a limitation of this paper. Moreover, the present work does not explore convergence analysis using alternative line search techniques, such as the Wolfe and Goldstein line searches.

The results presented in this article leave numerous avenues for future research works. An important direction for future research is the exploration of hybrid approaches that integrate a convex hybridization of different conjugate direction methods (see, [34]). Another key direction is investigating the conjugate direction method for IVMOP without employing any line search techniques (see, [38]).