Black Hole Construction from the Minkowski Manifold

I. Introduction

The Schwarzschild metric in Schwarzschild coordinates has a well-known coordinate singularity at the event horizon. This singularity is removed from the metric using coordinate transformations, with the most popular transformation being the Kruskal-Szekeres coordinates, which are regular at the horizon. However, the meaning of the the Kruskal-Szekeres coordinates in terms of spacelike and timelike basis vectors is not clear. For much of the spacetime, the Kruskal-Szekeres coordinates are mixtures of space and time such that the meaning of the slope of a worldline in these coordinates is not always clear. Nonetheless, these coordinates have been used to argue that the event horizon can be crossed by falling observers since there is no coordinate singularity in the Kruskal-Szekeres system. This has led to the acceptance of the existence of Black Holes into which objects can fall and can never escape back out to the external Universe.

In the reference text `Gravitation’ [1], the authors depict a falling worldline crossing the event horizon in Kruskal-Szekeres coordinates in Figure 32.1(b) of the text, though there is no accompanying calculation of the worldline in Kruskal-Szekeres coordinates. The only such calculation found in the literature is in [2], where the author claims to demonstrate that all worldlines are null at the horizon in Kruskal-Szekeres coordinates regardless of their state of motion. However, as the author notes in that work, the proof actually demonstrates that the Kruskal-Szekeres derivative of the falling worldline is undefined at $T=X>0$ in Kruskal-Szekeres coordinates. The author nonetheless concludes that in order for the extended spacetime to be consistent, the geodesic must in fact be null at the horizon.

The existence of Black Holes that can subsequently evaporate create an information paradox where information falling into a Black Hole is lost once the Black Hole evaporates due to Hawking radiation. Therefore, the possibility of objects falling into a Black Hole creates a physical paradox which has yet to be conclusively resolved.

If nothing was able to fall past the event horizon of the Schwarzschild metric, then there would be no information paradox to begin with. Therefore, this paper provides proof of the following hypotheses:

• The external Schwarzschild metric is describing a Minkowski manifold in which a hole has been made in the spacetime by stretching a point in space in the manifold into a 4-sphere, leaving a null space-time in the manifold inside the 4-sphere
• The internal Schwarzschild metric is describing a Minkowski manifold where the entire manifold has been compressed into a 4-sphere centered on a point in time. The 4-sphere is surrounded by null space-time
• The consequence of the first two hypotheses is that the internal and external Schwarzschild metrics are describing two separate, disconnected spherically symmetric spacetime manifolds
• The worldline of radially falling frames become null at the event horizon and the horizon itself becomes length contracted to a point in the falling frame as the frame approaches the horizon. The consequence of this is that the event horizon is the source of the Schwarzschild metric and the end point of gravitational collapse

Therefore, in this work, the analysis done in [2] is extended, providing an unambiguous proof that the falling worldline is null at the event horizon without having an undefined Kruskal-Szekeres derivative at the horizon.

II. Creating a Hole in the Minkowski Manifold

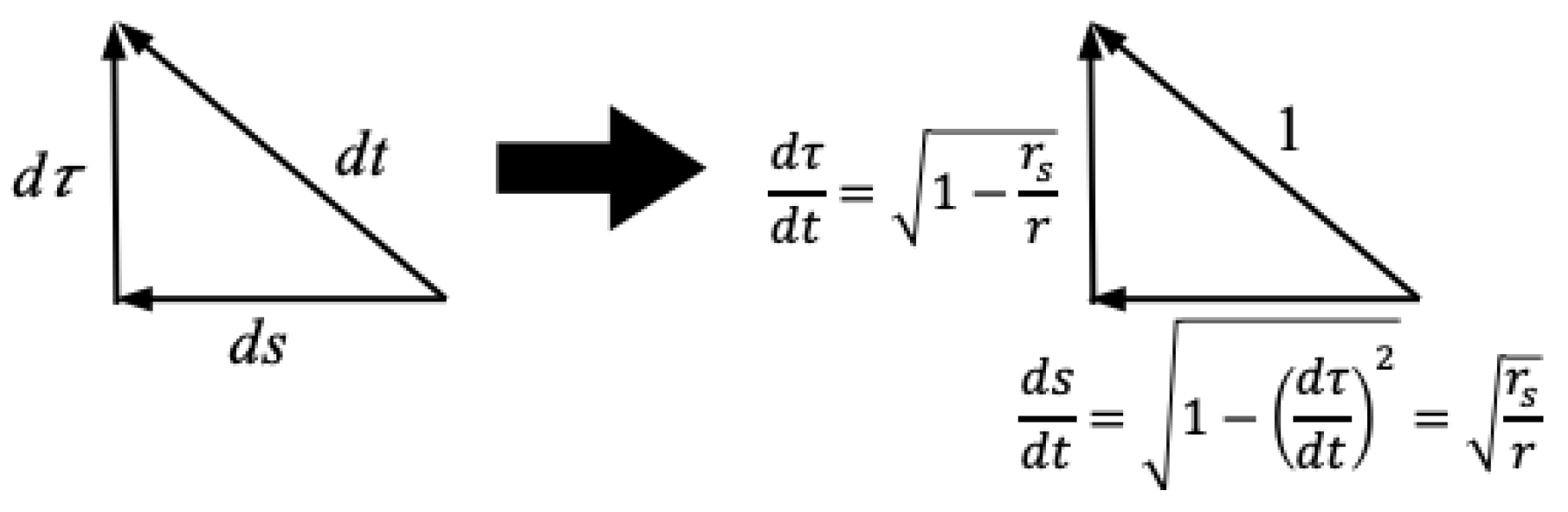
The Schwarzschild metric is the simplest non-trivial solution to Einstein’s field equations. It is the metric that describes every spherically symmetric vacuum spacetime. The the external form of the metric can be expressed as:

$$d{\tau }^2=\left(1-\frac{r_s}{r}\right)d{t}^2-\frac{1}{1-\frac{r_s}{r}}d{r}^2-r^{2}d{\mathsf{\Omega }}^2$$

(1)

Equation (1) is the external metric (where $r>r_s)$ with t being the timelike coordinate and r being the spacelike coordinate. The Schwarzschild radius of the metric is given by $r_s=2GM$ in units with $c=1$ and is commonly known as the Event Horizon. The external metric is the metric for an eternally spherically-symmetric vacuum centered in space.

But this metric comes from assuming a stress-energy tensor that is zero everywhere, meaning there is no mass anywhere in the manifold, even at the center. Therefore, this metric is describing a spherically symmetric Minkowski-like manifold. The question then becomes: how can the Minkowski manifold, which is massless everywhere, be deformed to give us the Schwarzschild metric?

Let us imagine Minkowski space-time which is flat everywhere in space and time. We choose a point in space (at all times) on the manifold and label it as the spatial origin $r=0$. Thus we use spherical coordinates to describe the metric with r as the spacelike coordinate. For future clarity, we will label the Minkowski time coordinate $\tau$, representing the proper time of observers at rest in their own frame.

Now we make a hole in the manifold by stretching the space-time at the point $r=0$ into a 4-sphere (because the hole is in space as well as in time at that location in space). In doing so, we have done two things:

• We have given the manifold an intrinsically spherical shape with an intrinsic center
• We have created a null space-time in the region inside the 4-sphere where space and time itself are absent (this would be the definition of creating a hole in the manifold)

So we assert that the Schwarzschild metric, which is the only spherically-symmetric solution to Einstein’s field equations describes 3 distinct, separate manifolds. When $\frac{r_s}{r}<1$, we get the manifold described above where there is a hole in the Minkowski manifold. The spacetime is not flat anywhere in this metric. We cannot actually set r to infinity in this metric, as this is mathematically dubious. The best we can do is say that the spacetime approaches the Minkowski space-time as $\frac{r_s}{r}$ approaches zero. The Minkowski metric is only achieved when $r_s=0$. Since $r_s=2GM$, we might think that this means that the Minkowski metric is just the Schwarzschild metric when there is no mass present on the manifold. But this is false. As mentioned previously, the Schwarzschild metric comes from solving the field equations with a zero stress-energy tensor (and assuming spherical symmetry). So the Schwarzschild metric with non-zero $r_s$ already assumes no mass or energy anywhere on the manifold. Therefore, by setting $r_s=0$, we are really saying is that there is no hole in the Minkowski manifold.

The internal metric, where $\frac{u}{r}>1$, is yet another distinct manifold. Note that we used u instead of $r_s$ because for the internal case, u is a timelike radius, not a spacelike radius, and the definition $r_s=2GM$ does not apply to this internal manifold. The internal manifold will be discussed further in Section III and a much deeper analysis of the internal metric is the topic of a future work.

Returning our attention to the external metric with non-zero $r_s$, we will now examine how the stretching of a point into a 4-sphere to create the hole in the manifold affects the Minkowski coordinates. Since the manifold is continuous, it is helpful to speak in terms of ’coordinate density’. If we give the Minkowski metric a coordinate density of 1 everywhere, a coordinate density greater than 1 indicates that the coordinates are spaced more closely together relative to the Minkowski metric.

Since we are stretching the center of the manifold from a point into a 4-sphere (as opposed to just ’cutting a hole out of the manifold’) with a finite radius, both the space and time coordinate densities will be affected such that their densities remain 1 infinitely far from the hole and increase as the hole is approached. In fact, since the hole was created from a single point, the coordinate densities will become infinite at the edge of the hole.

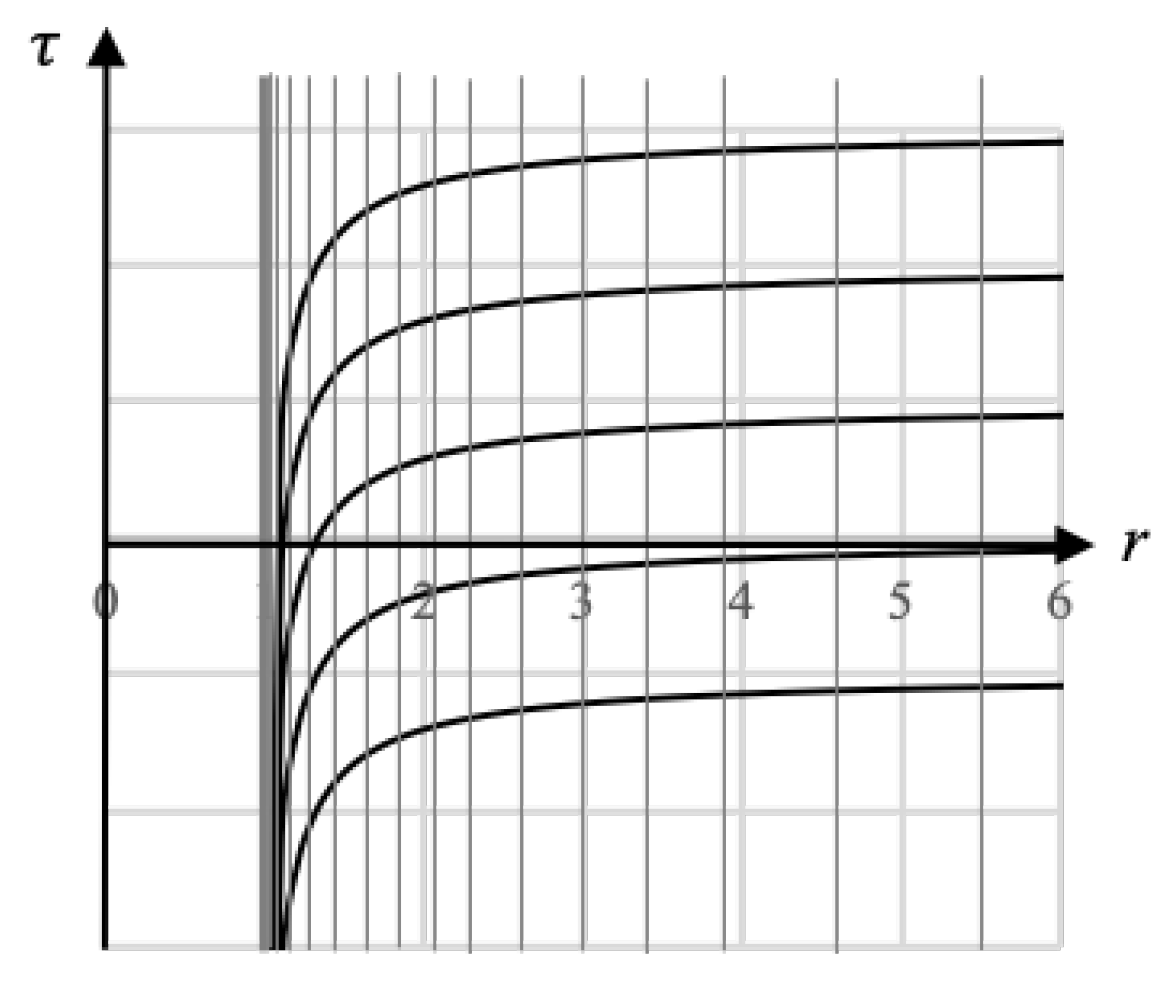
We can visualize the effect of the hole on the coordinates by looking at a space-time diagram in one spatial direction (the space-like axis represents a single ray emanating from the center of the manifold). Figure 1 shows the coordinates after the hole has been introduced into the manifold overlaid on top of the original Minkowski manifold. The curved lines represent the time coordinate t on the deformed manifold, and the non-uniformly spaced vertical lines represent the space coordinate (which we will call s to distinguish them from the r Minkowski coordinate) on the deformed manifold.

So we see that as we approach the edge of the hole (which we put at $r=1$ in Figure 1), both the spatial and temporal coordinate densities become infinite relative to the Minkowski background. Far from the hole, both the s and t coordinates become aligned with the r and $\tau$ coordinates because far from the hole, the spacetime remains Minkowskian.

We now assert that this scenario is what is being described by the Schwarzschild metric. In this case, the coordinate density ${\rho }_c$ is given by:

$${\rho }_c=\sqrt{\frac{1}{1-\frac{r_s}{r}}}$$

(2)

Where $r_s$, the Schwarzschild radius, is the radius of the hole (which is 1 in Figure 1). Therefore, the spacing of the s coordinates is given by:

$$\frac{ds}{dr}=\sqrt{\frac{1}{1-\frac{r_s}{r}}}={\rho }_c$$

(3)

And the spacing of the t coordinate lines at r is similarly given by:

$$\frac{dt}{d\tau }=\sqrt{\frac{1}{1-\frac{r_s}{r}}}={\rho }_c$$

(4)

Furthermore, reference [3] tells us that $\frac{dr}{dt}$ for an observer falling from rest at $r=r_0$ is given by:

$$\frac{dr}{dt}=-\left(1-\frac{r_s}{r}\right)\sqrt{\frac{\frac{r_s}{r}-\frac{r_s}{r_0}}{1-\frac{r_s}{r_0}}}$$

(5)

Combining Equations (5) and (3), we get the needed derivative:

$$\frac{ds}{dt}=\frac{dr}{dt}\frac{ds}{dr}=-\sqrt{1-\frac{r_s}{r}}\sqrt{\frac{\frac{r_s}{r}-\frac{r_s}{r_0}}{1-\frac{r_s}{r_0}}}$$

(6)

These are the velocity of an observer falling from rest at $r_0$ in r and s coordinates.

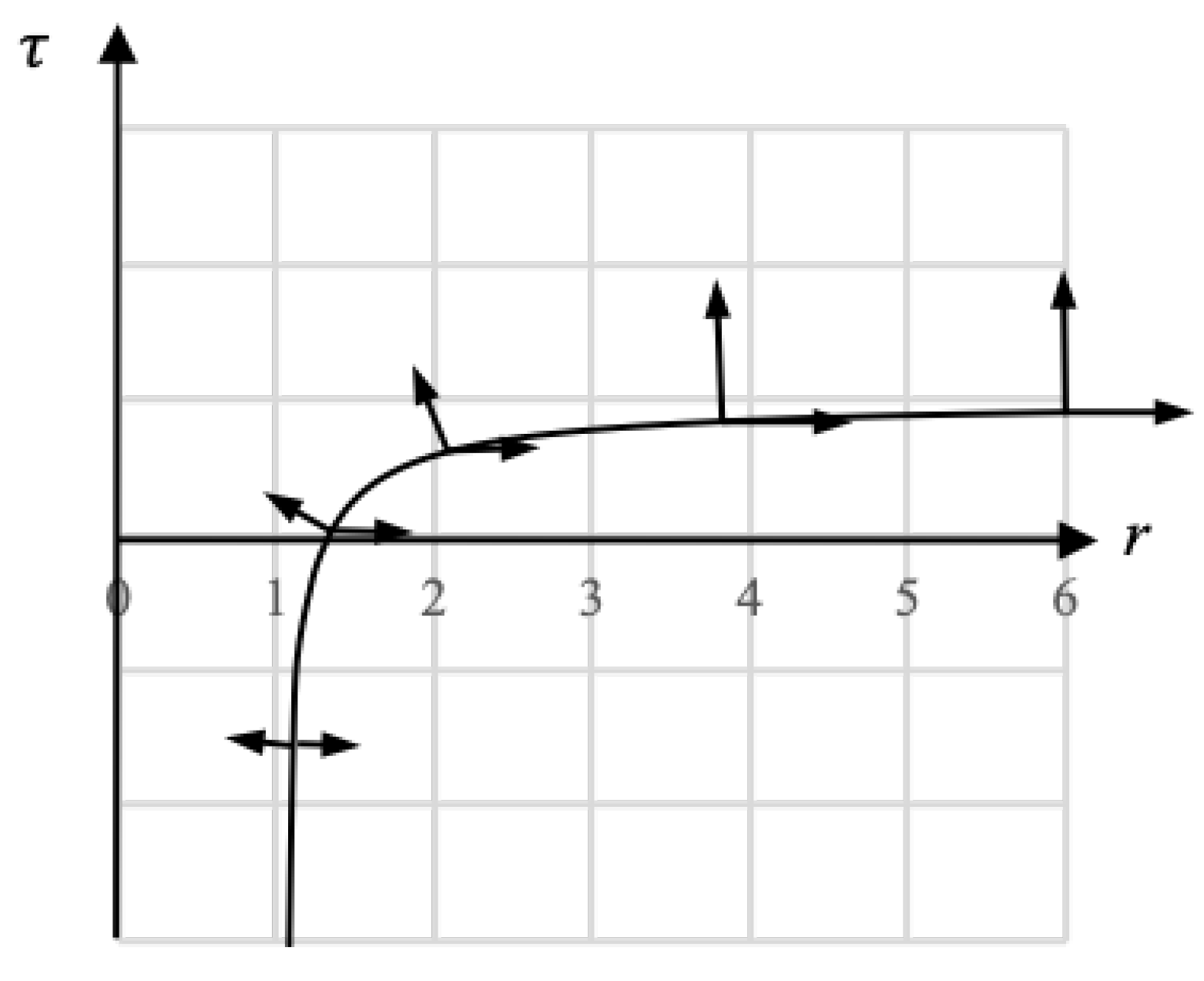
The spacing of the s coordinate is simple to understand because the coordinates are vertical and parallel. But the deformed time coordinate is more interesting due to the curvature of the coordinate lines. Let’s take one of these t coordinate lines and show the orientation of the s and t basis vectors at different distances from the edge of the hole. Figure 2 depicts this situation. The s basis vectors are horizontal and the t basis vectors are normal to the tangent of the t coordinate line. The decreasing lengths of the vectors reflect the increasing coordinate density of each basis as $r_s$ is approached.

In Figure 2, we see that $\frac{dt}{d\tau }$ goes to infinity at $r=r_s$ because we measure $dt$ in the direction of the t basis vector at r. As r approaches $r_s$, the t basis vector rotates relative to the $\tau$ basis, resulting in infinite density as the frame approaches $r_s$.

Figure 2 illustrates why an inertial observer is accelerated in the deformed manifold. In Minkowski spacetime, a frame moving relative to an observer at rest is Lorentz boosted relative to the rest frame with the magnitude of the boost increasing with increasing velocity. What we have here is the reverse. The geometry creates a non-zero boost of the inertial frame at r, and this boost gives the inertial frame a velocity toward $r_s$. The boost increases the closer we get to $r_s$, so the inertial observer accelerates toward $r_s$ as a result of this increase until the geodesic becomes null at $r_s$. Another way to look at this is that the inertial observer moves in the direction of the local $dt$ vector. So as the t axis tilts, there is a component of that vector in the spatial direction, resulting in a velocity toward the field source. The increasing tilt of the vector over space results in an acceleration toward the source.

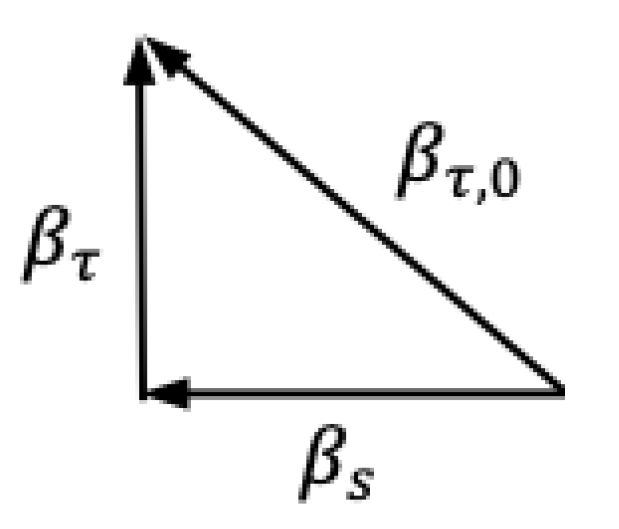
We also see why an observer wanting to remain at rest in the field must accelerate away from $r_s$ to do so. The rest observer must accelerate against the gradient of the Lorentz boosts at r in order to maintain her position. Figure 3 shows the tilted $dt$ vector in a boosted frame with its components in the $\tau$ and r directions from the Minkowski manifold. On the right side of the figure, we normalize the length of the $dt$ vector to 1 by dividing the vector and its components by $dt$:

The vertical component can also be expressed as $\frac{d\tau }{dt}=\frac{1-\frac{r_s}{r}}{\sqrt{1-\frac{r_s}{r}}}$, which is $\frac{d\tau }{dt}$ of an observer falling from rest at infinity divided by the local speed of light $\frac{ds}{dt}=\sqrt{1-\frac{r_s}{r}}$. The horizontal component is the velocity of the same observer divided by the local speed of light.

The acceleration the rest observer feels comes from the gradient of $\frac{d\tau }{dt}$ (the vertical component) at r:

$$\frac{d}{dr}\left(\frac{d\tau }{dt}\right)=\frac{r_s}{2r^2}\frac{1}{\sqrt{1-\frac{r_s}{r}}}=\frac{GM}{r^2}\frac{1}{\sqrt{1-\frac{r_s}{r}}}$$

(7)

Which is the expression for the proper acceleration of an observer at rest at r [4]. We see here that the acceleration a rest observer feels comes from opposing a gradient in the temporal velocity that an observer falling from infinity would experience at r. The falling observer flows along this gradient, accelerating toward the hole.

Furthermore, if we imagine a region of spacetime where the Lorentz boost was constant over r (this could also be a stationary point on the curved t coordinate), then an observer at rest at r would have her time dilated relative to the rest observer in Minkowski space-time as a result of the boost, but the observer would be inertial (i.e. the observer would not need to accelerate to stay at rest) since the gradient of the time dilation in that case would be zero. An observer in free fall in this scenario would accelerate up to the region where the gradient is zero and then continue falling at a constant speed relative to rest observers while in that region of the space-time.

Thus, we have shown that the geodesics of inertial observers become null at the edge of the hole and that there is no space-time inside the hole. Furthermore, the inertial geodesic remains at $r_s$ due to the fact that the length of the s and t basis vectors go to zero at $r_s$ per Figure 4. We can also see that the geodesic remains at the horizon by looking at Equation (6). We use Equation (6) instead of Equation (5) because the $ds$ and $dt$ densities are the same at any given r. This velocity to zero when $r=r_s$, proving that the geodesic remains at rest there.

Note that the magnitude of this velocity increases to a maximum at some $r>r_s$ (maximizing at $r=2r_s$ in the case of an observer falling from infinity) and then decreases to zero at $r_s$. We can see why this is the case in Figure 2 and Figure 3 where the magnitude of the velocity (not normalized by the local speed of light) comes from a combination of the tilt of the $dt$ vector as well as the length of the $dt$ vector. So before the maximum, the increase in the tilt of the vector has a greater contribution than the decrease in the length of the vector, so the velocity increases during the fall. After the maximum, the decrease in the length of the vector has a greater contribution than the increase in tilt, so the velocity decreases. We can see this interaction in Equation (5) where the $\left(1-\frac{r_s}{r}\right)$ comes from the scaling of the vector (which is the variable speed of light) and the square root expression comes from the tilt of the vector.

Creating the Schwarzschild manifold by making a hole in the Minkowski manifold makes the fact that geodesics come to rest at $r_s$ intuitive since there is by definition no space-time inside the hole of the manifold, so there is nowhere else in space for the geodesics to go, they must remain at rest there.

We can also derive Equation (6) from Figure 3. In this case, the observer starts falling from $r_0$. Figure 3 keeps the $dt$ vector at a constant length, it doesn’t include the contraction of the vector over r. This is reflected in the fact that $\frac{d\tau }{dt}$ and $\frac{ds}{dt}$ are divided by the speed of light in the figure. So the length of the vector is 1 in the figure because $\frac{d\tau }{dt}$ of an observer at rest at infinity, which is where the observer began to fall from in that case, is 1. In this case, the observer is falling from $r_0$, so the magnitude of the vector is $\frac{d\tau }{dt}$ of an observer at rest at $r_0$ which is $\sqrt{1-\frac{r_s}{r_0}}$. So we need to divide the vertical component $\frac{d\tau }{dt}$ by $\sqrt{1-\frac{r_s}{r_0}}$ to normalize the hypotenuse like we did in the first case such that:

$$\frac{d\tau }{dt}=\sqrt{\frac{1-\frac{r_s}{r}}{1-\frac{r_s}{r_0}}}$$

(8)

Solving for $\frac{ds}{dt}$ in the triangle we get:

$$\frac{ds}{dt}=\sqrt{1-\frac{1-\frac{r_s}{r}}{1-\frac{r_s}{r_0}}}=\sqrt{\frac{\frac{r_s}{r}-\frac{r_s}{r_0}}{1-\frac{r_s}{r_0}}}$$

(9)

Recall that both of the components in the triangle are normalized by the speed of light. So if we multiply each of these by the speed of light ${\left(\frac{ds}{dt}\right)}_c=-\sqrt{1-\frac{r_s}{r}}$, we get the values for $\frac{d\tau }{dt}$ and $\frac{ds}{dt}$ that we get by solving the metric using Equations (3) and (6).

Finally we can generalize Figure 3 as follows:

Where ${\beta }_{\tau }$ and ${\beta }_s$ are the temporal and spatial velocities at r divided by the speed of light at r of observers falling from rest at $r_0$. ${\beta }_{\tau ,0}$ is the temporal velocity at $r_0$ divided by the speed of light at $r_0$ of an observer falling from infinity. ${\beta }_{\tau ,0}$ can also be considered as the temporal velocity ${\left(\frac{d\tau }{dt}\right)}_0$ of the observer at rest at $r_0$.

III. A Note on the Internal Schwarzschild Metric

The internal Schwarzschild metric (where $r<r_s)$ is the inverse of the deformed Minkowski manifold described above. The internal metric describes a separate manifold where the entire Minkowski manifold has been compressed down to a 4-sphere of finite r, where r is the timelike coordinate in this case. The sphere is surrounded by null space-time. This manifold is also intrinsically spherical with an intrinsic center. The fact that the manifold itself has an intrinsic center is why we get a curvature singularity there. A detailed examination of nature of the internal metric will be the topic of a followup work where it will also be shown that due to cosmological reasons, a real geodesic can never actually reach the horizon. But in the rest of this paper, we will examine the inertial geodesic in Kruskal-Szekeres coordinates to show that the key results found here, namely that the free-falling geodesic becomes null at the horizon and that the geodesic does not cross the horizon, can be deduced from the Kruskal-Szekeres coordinate chart as well.

IV. The Falling Frame of the External Metric in Kruskal-Szekeres Coordinates

The Kruskal-Szekeres coordinates are the maximally extended coordinates for the Schwarzschild metric. The coordinate definitions and metric in Kruskal-Szekeres coordinates are given below (derivation of the coordinate definitions and metric can be found in reference [5] where $v=T$ and $u=X$).

$$\begin{array}{c}\hfill T=\sqrt{\left(\frac{r}{r_s}-1\right)e^{\frac{r}{r_s}}}sinh\left(\frac{t}{2r_s}\right)\\ \hfill X=\sqrt{\left(\frac{r}{r_s}-1\right)e^{\frac{r}{r_s}}}cosh\left(\frac{t}{2r_s}\right)\end{array}$$

(10)

With the full metric in Kruskal-Szekeres coordinates given by:

$$d{\tau }^2=\frac{4r_s^3}{r}{e}^{-\frac{r}{r_s}}\left(d{T}^2-d{X}^2\right)-r^{2}d{\mathsf{\Omega }}^2$$

(11)

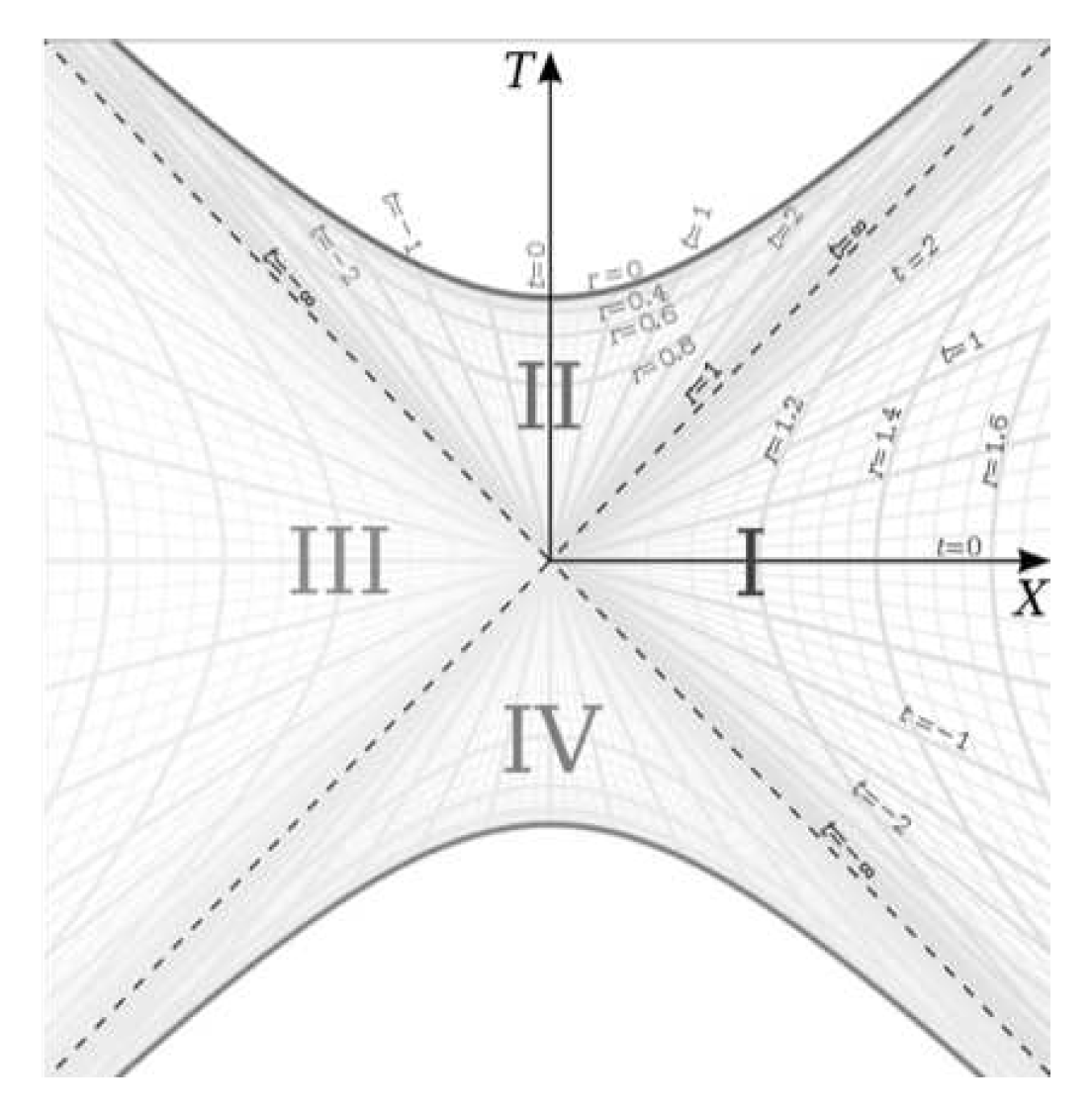
Finally, we plot the metric on the Kruskal-Szekeres coordinate chart [6] in Figure 5:

In this paper, we will be focusing on region I in this chart, which is the spherically symmetric spacetime around a spherically symmetric source in space.

We can see in Figure 5 that for a rest frame ($r=const$), that $\frac{dX}{dT}$ depends on the value of t we evaluate the derivative at since the derivative for the rest frame is the tangent to the hyperbola at t. Since the metric is time-symmetric, we know that the actual physics does not depend on the value of t and therefore, we need a deeper understanding of the meaning of the changing $\frac{dX}{dT}$ in the rest frame and how it relates to the falling frame at the same point.

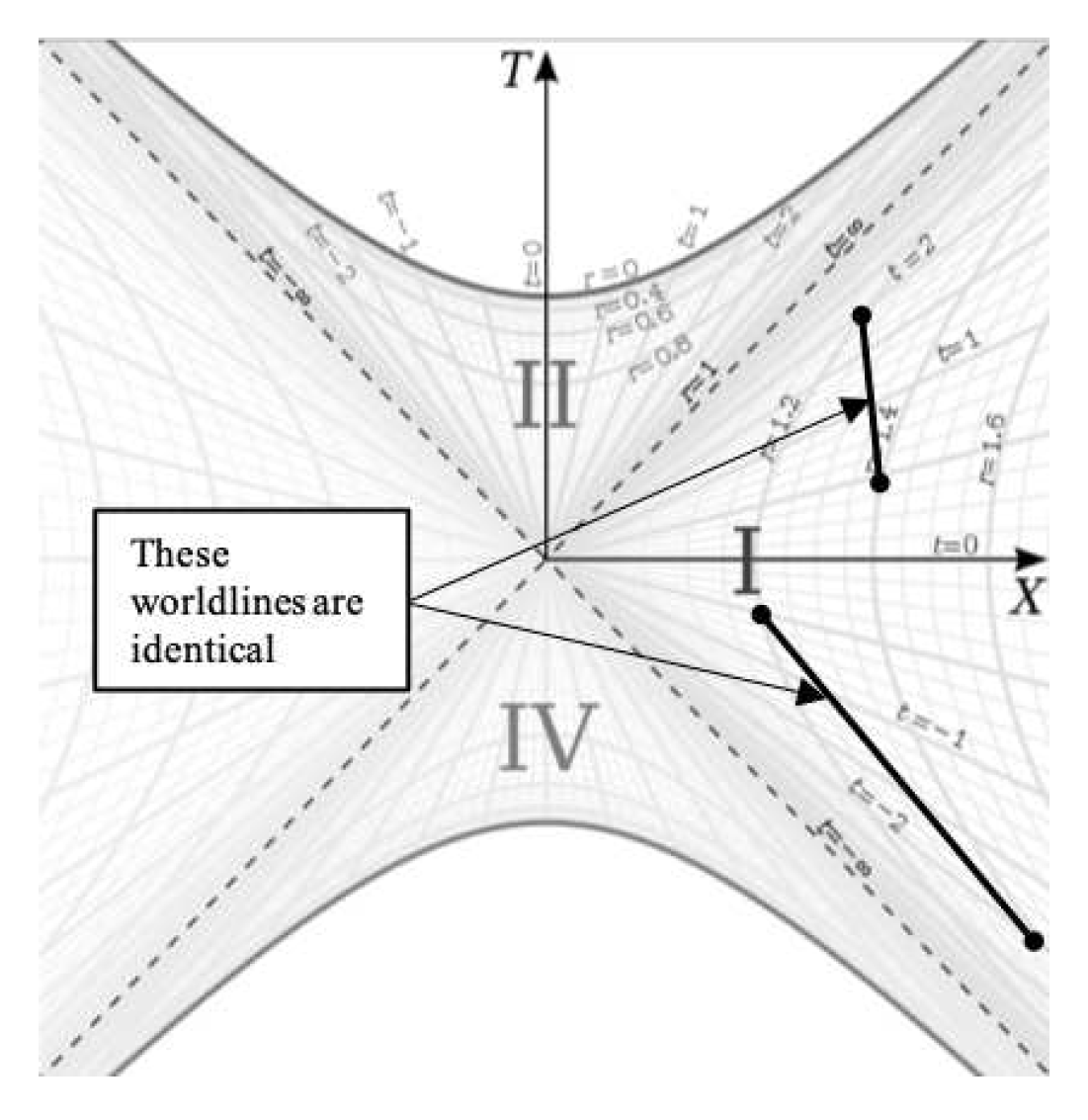
The time symmetry of the metric tells us that we can hyperbolically rotate the spacetime (rotate the t coordinates in the coordinate chart) without changing the physics. For example, Figure 6 shows two identical worldlines hyperbolically rotated relative to each other on the Kruskal-Szekeres coordinate chart.

These worldlines are the same because $\Delta r$ and $\Delta t$ are the same for both worldlines, such that their proper lengths are the same. So the time translation symmetry of the metric translates to hyperbolic rotational symmetry on the Kruskal-Szekeres coordinate chart.

We can use this fact to change how we visualize the worldline of an observer falling toward the horizon. Rather than drawing the line from $t=0$ at some r to $t=\infty$ at the horizon, we can continuously hyperbolically rotate the space as the observer falls such that the ’present’ state of the falling frame is always at $t=0$. An example of this is given in Figure 7.

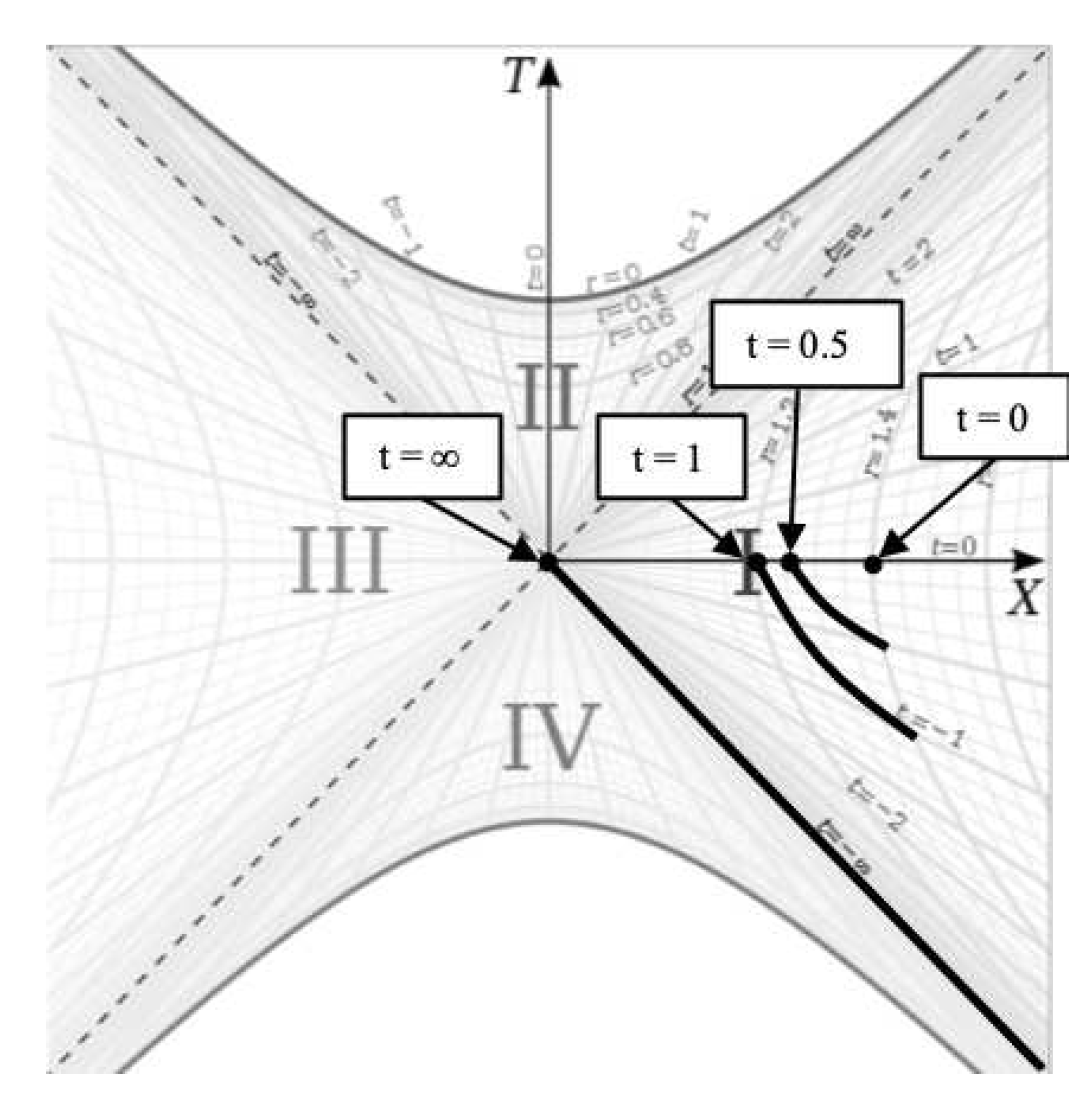
In Figure 7, the observer begins falling at $r=1.4r_s$. This is represented by the rightmost point on the X axis in the diagram. After $\Delta t=0.5$, the observer has fallen to a lower radius represented by the point to the left of the rightmost point. So rather than having the worldline grow up from $t=0$ as time passes, we hyperbolically rotated the worldline points down as time passes to keep the present point of the worldline on the X axis. This is a valid way of visualizing the worldline as a result of the time symmetry of the metric.

When using this construction, we see that the falling worldline reaches the $T=X=0$ point on the diagram. And if the worldline does indeed become null at the horizon, this means the worldline remains on the $T=-X$ line since that is the null geodesic representing the horizon.

It is notable that since the $T=\pm X$ lines are null geodesics at the same point in space ($r_s$), this means that all falling frames reach the horizon simultaneously regardless of where or when they begin falling relative to each other. This fact is more evident when drawing the worldlines the traditional way where they reach the horizon at $T=X>0$. If two frames start falling from different radii at $t=0$, they will intersect the the horizon at $t=\infty$ at different points along the $T=X$ line in the coordinate chart. But the proper distance between those points is zero and they are both at the same point in space, therefore the two points are in fact coincident.

There appears to be a conflict between the construction in Figure 7 and the traditional construction which has the worldline reach the horizon at $t=\infty$ along the $T=X$ line where T and X are greater than zero. This conflict is significant because the construction presented here shows a worldline that becomes null at the horizon whereas the traditional construction has a non-null worldline at the horizon. It is impossible for both to be true and therefore the discrepancy must be resolved. To resolve this conflict, we need a more detailed examination of the falling frame’s worldline in Kruskal-Szekeres coordinates.

Let us first take the differentials of T and X in Equation (10):

$$\begin{array}{cc}\hfill dX& =\frac{\partial X}{\partial r}dr+\frac{\partial X}{\partial t}dt\hfill \\ \hfill dT& =\frac{\partial T}{\partial r}dr+\frac{\partial T}{\partial t}dt\hfill \end{array}$$

(12)

Calculating the partial derivatives, rearranging and defining $R\equiv \frac{r{e}^{\frac{r}{r_s}}}{2r_s^2\sqrt{(\frac{r}{r_s}-1)e^{\frac{r}{r_s}}}}$ we get:

$$\begin{array}{cc}\hfill \frac{dX}{dt}& =R\left[\frac{dr}{dt}cosh\left(\frac{t}{2r_s}\right)+\left(1-\frac{r_s}{r}\right)sinh\left(\frac{t}{2r_s}\right)\right]\hfill \\ \hfill \frac{dT}{dt}& =R\left[\frac{dr}{dt}sinh\left(\frac{t}{2r_s}\right)+\left(1-\frac{r_s}{r}\right)cosh\left(\frac{t}{2r_s}\right)\right]\hfill \end{array}$$

(13)

Next, we need to calculate $\frac{dX}{dT}$ from Equation (13) by factoring out $\left(1-\frac{r_s}{r}\right)cosh\left(\frac{t}{2r_s}\right)$ from each equation and dividing:

$$\frac{dX}{dT}=\frac{dX}{dt}\frac{dt}{dT}=\frac{\frac{dr}{dt}{\left(1-\frac{r_s}{r}\right)}^{-1}+tanh\left(\frac{t}{2r_s}\right)}{\frac{dr}{dt}{\left(1-\frac{r_s}{r}\right)}^{-1}tanh\left(\frac{t}{2r_s}\right)+1}$$

(14)

This equation is the same equation derived in [2] but put in a slightly different form. Next, we make the following definitions:

$${\left(\frac{dX}{dT}\right)}_0\equiv tanh\left(\frac{t}{2r_s}\right)$$

(15)

This is the derivative of the rest frame at t since plugging $\frac{dr}{dt}=0$ into Equation (14), we get $\frac{dX}{dT}=tanh\left(\frac{t}{2r_s}\right)$. Since we know the Schwarzschild metric is independent of t, this derivative must be a non-physical artifact of the Kruskal-Szekeres coordinates at fixed r and is not related to any actual change in motion through space and time.

And we define the relative velocity of the frame in motion relative to the rest frame as:

$${\left(\frac{dX}{dT}\right)}_{rel}\equiv \frac{dr}{dt}{\left(1-\frac{r_s}{r}\right)}^{-1}$$

(16)

This is the relative velocity in Kruskal-Szekeres coordinates between the frame in motion and the rest frame at r. This derivative is 0 for the rest frame since $\frac{dr}{dt}=0$ in that frame. If we combine Equations (16) and (5) we get:

$${\left(\frac{dX}{dT}\right)}_{rel}=-\sqrt{\frac{\frac{r_s}{r}-\frac{r_s}{r_0}}{1-\frac{r_s}{r_0}}}$$

(17)

Which is well behaved and equal to -1 when $r=r_s$. Plugging these definitions into Equation (14), we get:

$$\frac{dX}{dT}=\frac{{\left(\frac{dX}{dT}\right)}_{rel}+{\left(\frac{dX}{dT}\right)}_0}{{\left(\frac{dX}{dT}\right)}_{rel}{\left(\frac{dX}{dT}\right)}_0+1}$$

(18)

We recognize that Equation (18) is the relativistic velocity addition formula giving us the total velocity as the relativistic sum of the rest frame velocity and the relative velocity between the moving frame and the rest frame. We can solve for ${\left(\frac{dX}{dT}\right)}_{rel}$ to get an expression for the relative velocity between a frame in motion and the rest frame in Kruskal-Szekeres coordinates:

$${\left(\frac{dX}{dT}\right)}_{rel}=-\frac{{\left(\frac{dX}{dT}\right)}_0-\frac{dX}{dT}}{1-{\left(\frac{dX}{dT}\right)}_0\frac{dX}{dT}}$$

(19)

Assuming that ${\left(\frac{dX}{dT}\right)}_0$ ranges from -1 to 1 and $1>\frac{dX}{dT}>-1$, we see that the relative velocity approaches 1 or -1 for all $\frac{dX}{dT}$ as the horizon is approached since the horizon is at $t=\pm \infty$, such that ${\left(\frac{dX}{dT}\right)}_0=1$ there. Equation (19) is also constant along a given hyperbola (i.e it is independent of t) since it represents the relative velocity between the moving and rest frames.

Equation (19) is essentially a hyperbolic rotation of a given worldline point along a hyperbola of constant r to $t=0$. The reason this gives us the relative velocity is that at $t=0$, the Schwarzschild basis vectors and Kruskal-Szekeres basis vectors are aligned there, meaning that the X and T in ${\left(\frac{dX}{dT}\right)}_{rel}$ are pure spacelike and timelike basis vectors and thus the derivative gives a true velocity relative to the rest frame. This is in contrast to the general $\frac{dX}{dT}$ which is a derivative without a clear spacetime meaning since the X and T coordinates are mixtures of space and time everywhere else.

It is also notable that Equation (18) is undefined when $t=\infty$ because since ${\left(\frac{dX}{dT}\right)}_{rel}=-1$ there and ${\left(\frac{dX}{dT}\right)}_0=1$ there, we get:

$${\left(\frac{dX}{dT}\right)}_{t=\infty }=\frac{-1+1}{-1+1}=\frac{0}{0}$$

(20)

This is also what was demonstrated in [2]. Therefore, under these conditions, $\frac{d\tau }{dT}$ and $\frac{d\tau }{dX}$ are undefined at the horizon when T and X are greater than 0. This suggests that there is a discontinuity in the worldline when reaching the horizon at $t=\infty$, even in Kruskal-Szekeres coordinates.

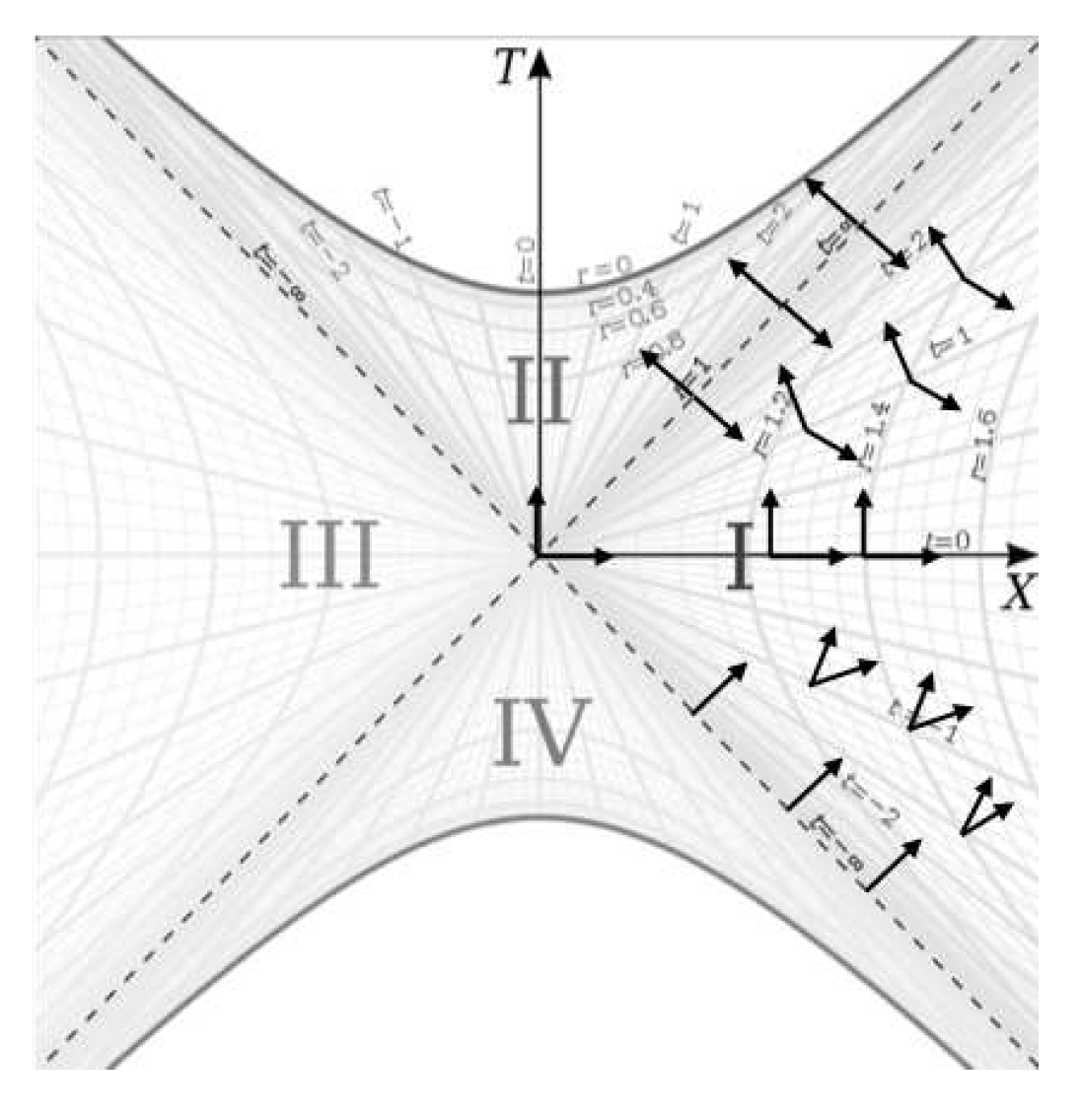
Figure 8 can help us see why Equation (14) becomes undefined at the horizon by depicting the space and time axes of the rest frames at different points on the Kruskal-Szekeres coordinate chart.

Along the X axis, the space and time bases are orthogonal and aligned with the Kruskal-Szekeres basis vectors. As t moves away from 0 in either direction, the rest frames in which the derivative is measured become increasingly Lorentz boosted. These boosts are an artifact of the Kruskal-Szekeres coordinates and not physical boosts. We know this because ${\partial }_t$ is a Killing vector. So if we move along a hyperbola of constant r, the space-time bases are boosted as t increases, but we know that the frame of the rest observer does not change over time due to the time symmetry of the manifold.

That the derivative is measured in increasingly boosted rest frames over time in Kruskal-Szekeres coordinates is not a problem anywhere except at $t=\pm \infty$. At those locations, the rest frame is infinitely Lorentz boosted such that the space-time bases are collinear because the rest frame is light-like at the horizon. In a light-like frame, the relative state of motion of other frames cannot be determined because in the light like frame, one cannot make measurements of space and time due to the collinearity of the bases.

Now let’s calculate the situation described in Figure 7 where we calculate the worldline falling along the X axis as the past worldline is hyperbolically rotated down. For this construction, we set $t=0$ in the equations since the derivative is always taken on the X axis. For this calculation, we put the metric in the following form (we will be examining radial infall so $d\mathsf{\Omega }=0$):

$$d{\tau }^2=\frac{4r_s^3}{r{e}^{\frac{r}{r_s}}}\left({\left(\frac{dT}{dX}\right)}^2-1\right)d{X}^2$$

(21)

Since we are keeping $t=0$, we can use the inverse of Equation (17) for $\frac{dT}{dX}$ in the equation. We can solve for r in terms of X by setting $t=0$ for the X equation in Equation (10) and solving for r:

$$r=r_s\left(W\left(\frac{X^2}{e}\right)+1\right)$$

(22)

Where W is the Product Log function. Substituting Equations (22) and (17) into Equation (21) allows us to integrate the worldline along the X axis:

$$d{\tau }^2=\frac{4r_s^2{e}^{-\left(W\left(\frac{X^2}{e}\right)+1\right)}}{W\left(\frac{X^2}{e}\right)+1}\left(\frac{1-\frac{r_s}{r_0}}{\frac{1}{W\left(\frac{X^2}{e}\right)+1}-\frac{r_s}{r_0}}-1\right)d{X}^2$$

(23)

Which goes to 0 as X goes to 0. But we can now show that this is exactly equivalent to falling in Schwarzschild coordinates by first using Equation (13) to solve for $dX$ when $t=0$:

$$\begin{array}{cc}\hfill dX& =\frac{r{e}^{\frac{r}{r_s}}}{2r_s^2\sqrt{(\frac{r}{r_s}-1)e^{\frac{r}{r_s}}}}dr\hfill \\ \hfill & =\sqrt{\frac{r{e}^{\frac{r}{r_s}}}{4r_s^3}}\frac{1}{\sqrt{1-\frac{r_s}{r}}}dr\hfill \end{array}$$

(24)

Substituting Equation (24) and the inverse of (16) into Equation (21) gives:

$$\begin{array}{cc}\hfill d{\tau }^2& =\left({\left(\left(1-\frac{r_s}{r}\right)\frac{dt}{dr}\right)}^2-1\right)\frac{1}{1-\frac{r_s}{r}}d{r}^2\hfill \\ \hfill & =\left(1-\frac{r_s}{r}\right)d{t}^2-\frac{1}{1-\frac{r_s}{r}}d{r}^2\hfill \end{array}$$

(25)

And we can see that Equation (25) is in fact the Schwarzschild metric in Schwarzschild coordinates.

Therefore it has been proven that the worldline construction shown in Figure 7 is equivalent to falling in Schwarzschild coordinates and it has been demonstrated that the worldline in that construction is light-like at the horizon. When we couple this finding with the fact that the Kruskal-Szekeres derivative is undefined at the horizon for any construction in which the worldline reaches the horizon at $T=X>0$, we can conclude that the event horizon is length contracted to a point in a falling frame approaching the horizon as a result of the fact that the worldline becomes null there.

Furthermore, we see from Equation (24) that $\frac{dr}{dX}$ is zero at $r=r_s$. Therefore, the falling frame remains at the horizon along the $T=\pm X$ lines in the Kruskal-Szekeres coordinate chart when it reaches the horizon.

V. The Falling Frame of the External Metric in Eddington-Finkelstein Coordinates

It has been shown using two different methods that the worldline of the falling observer becomes null at the horizon. If this is true in one system of coordinates, it must be true in all coordinate systems as a change of coordinates cannot change the physics of the manifold.

Nonetheless, let us examine another important coordinate system used to analyze the Schwarzschild metric, the Eddington-Finkelstein coordinates.

The metric in Eddington Finkelstein coordinates (with $d\mathsf{\Omega }=0$) for infalling particles is given by:

$$d{s}^2=-\left(1-\frac{r_s}{r}\right)d{v}^2+2dvdr$$

(26)

Where v is defined as:

$$v=t+r+r_{s}ln|\frac{r}{r_s}-1|$$

(27)

Infalling null geodesics are given by the condition $\frac{dv}{dr}=0$. If we take the derivative of Equation (27) and apply Equation (5) for the observer falling from rest at $r_0$ we obtain:

$$\begin{array}{cc}\hfill \frac{dv}{dr}& =\frac{dt}{dr}+\frac{1}{1-\frac{r_s}{r}}\hfill \\ \hfill & =-\frac{1}{1-\frac{r_s}{r}}\sqrt{\frac{1-\frac{r_s}{r_0}}{\frac{r_s}{r}-\frac{r_s}{r_0}}}+\frac{1}{1-\frac{r_s}{r}}\hfill \\ \hfill & =\frac{1}{1-\frac{r_s}{r}}\left(1-\sqrt{\frac{1-\frac{r_s}{r_0}}{\frac{r_s}{r}-\frac{r_s}{r_0}}}\right)\hfill \end{array}$$

(28)

Which, once again gives $\frac{0}{0}$ at the horizon, meaning the worldline’s derivative is undefined there as was the case with the Kruskal-Szekeres coordinates when we try crossing the horizon at $T=X>0$.

But we can take another approach and set $\frac{dv}{dr}=0$ and check where the worldline meets that condition. So we find where $\frac{dt}{dr}=-\frac{1}{1-\frac{r_s}{r}}$. For this condition, we require:

$$\sqrt{\frac{1-\frac{r_s}{r_0}}{\frac{r_s}{r}-\frac{r_s}{r_0}}}=1$$

(29)

Which is satisfied when $r=r_s$. Therefore, we find that the radial infalling worldline can also be shown to be null at the horizon in Eddington-Finkelstein coordinates

VI. Conclusion

Given the above analysis, it can be concluded that the external Schwarzschild metric can be accurately modeled by starting with the Minkowski manifold and stretching a point in that manifold into a 4-sphere. This stretching of a point into a sphere leaves a hole in the manifold of null space-time and makes the coordinate densities of both the space and time bases a function of position where the densities are infinite at the edge of the hole and decrease to 1 (the coordinate density of flat space-time) infinitely far from the hole. This model allows us to accurately model the dynamics of the Schwarzschild space-time using geometric techniques and allows the derivation of the proper acceleration of the rest observer using basic trigonometry. It was proven that the horizon (the edge of the hole) is indeed the endpoint of gravitational collapse and that all geodesics become null there.

A detailed analysis of the falling inertial geodesic was carried out in Kruskal-Szekeres and Eddington-Finkelstein coordinates as well. It was demonstrated that the same results mentioned above, namely the horizon being the end point of gravitational collapse where all geodesics become null, can be derived from those metrics as well.

Finally, the internal metric describes a separate spherically symmetric manifold which is the inverse of the external manifold. This manifold can be constructed by compressing the Minkowski manifold into a 4-sphere surrounded by null space-time and reversing roles of the space and time coordinates. Detailed analysis of the internal metric will be the topic of a followup work.