On the Thermodynamics of Matter

1. Introduction

Our first encounter with gravity came from the realization of Newton of gravity as an attractive force between every two objects in the universe, mathematically described by the universal law of gravitation. Despite being experienced by us in daily life, gravity remains the most mysterious force of all. Einstein realized gravity not as a fundamental force but as a very abstract phenomenon arising from the curvature of spacetime induced by matter and encoded in the famous Einstein’s field equation. General Relativity(GR) as we call the Einstein’s theory is a metric theory that beautifully explains every phenomenon observed at large scales to date. However, the theory is incompatible with another cornerstone and highly successful theory of Quantum Mechanics. Moreover being a metric theory, it admits certain unphysical solutions such as closed timelike curves and spacetime singularity. It also remains difficult to explain dark matter and dark energy within the framework of GR. The first link between thermodynamics and gravity came from the black hole physics where there is an apparent connection between horizon area and the entropy of the black hole. Hawking [1] first showed that the area of the horizon(A) of a black hole is a non-decreasing function of time.

$$\frac{dA}{dt}\ge 0$$

(1)

Bekenstein [2,3,4] took this further and asserted the equivalence of the horizon area with the thermodynamic parameter, entropy(S) as

$$S=\gamma A$$

(2)

where $\gamma$ is a constant. The claim got a robust description when Hawking [5] derived the temperature of the black hole, thus making the relation between the area and entropy clear. Later, in 1995, Jacobson [6] derived the Einstein’s equation from the proportionality of entropy and horizon area together with the relation $dQ=TdS$ connecting heat, entropy, and temperature. There are also closely related follow up articles [7,8,9,10,11]. Another work relating thermodynamics and gravity are due to Padmanabhan [12,13,14,15,16,17,18,19,20,21,22,23] and his collaborators [24,25,26,27,28]. These results suggest that gravity may be explained as an emergent phenomenon and has a thermodynamic or entropic origin. Recently, Verlinde [29] proposed Newtonian gravity as a physical entropic force, caused by changes in the information associated with the positions of material bodies, although, this description of Newtonian gravity as a physical entropic force has been technically questioned too [30,31,32,33]. Our goal here is different, we are making no connection with the background spacetime metric $g_{\mu \nu }$ and are thus not set to derive Einstein’s gravity as Jacobson and Padmanabhan did because we do not think that Einstein’s approach of describing gravity as background spacetime curvature is the only and ultimate reality. We are also not justifying or falsifying the claim of Verlinde of Newtonian gravity as a physical entropic force. Since we are not using the Einstein’s approach of gravity as spacetime curvature, we explicitly show then, how can we explain the gravitational redshift, the modified equation of motion for both massive and massless particles and the accelerated expansion of the universe. This way of describing gravity as a non-metric theory naturally does away with the inherent unphysical problems of a metric theory such as closed timelike curves and spacetime singularity. Keeping these things in mind, we begin our discussion by understanding this new connection between gravity and "information" in the system. In Section 3 we explain how the thermodynamic nature of our system changes the total energy and this leads to the extension of the spacetime to $5D$. In Section 4 we find the solution for a point mass in our theory. In Section 5 we review the Quantum Focusing Conjecture(QFC) [34] which conjectures that the quantum expansion $\Theta$, where $\Theta$ is given by

$$\Theta =\theta +\frac{4G\hslash }{\mathcal{A}}{S}_{out}^{\prime }$$

(3)

($\theta$ is the classical expansion and $\mathcal{A}$ is the width of null congruence along its generator), cannot increase along any congruence, which is valid for quantum states too

$$\frac{d\Theta }{d\lambda }\le 0$$

(4)

where $\lambda$ is an affine parameter. We briefly recall Casini’s work on relative entropy and Bekenstein bound in Section 6 and conclude the paper by showing using the QFC and the relation between Bekenstein bound and relative entropy how the second derivative of the radius of a null boundary(with respect to an affine parameter $\lambda$ along the generator) which respects the null energy condition(NEC) cannot decrease

$$\frac{d^{2}R}{d{\lambda }^2}\ge 0$$

(5)

This can be applied to a black hole’s event horizon and we get an additional constraint other than the Hawking area theorem.

2. Some Terminology

Figure 1. Oursystem consists of a source mass M and a "boundary" which is a data storing surface such as a holographic screen. T is the temperature of the bounding surface arising from the evenly distribution of the total energy E of the mass m as N bits of information as it approaches the holographic boundary.

Figure 1. Oursystem consists of a source mass M and a "boundary" which is a data storing surface such as a holographic screen. T is the temperature of the bounding surface arising from the evenly distribution of the total energy E of the mass m as N bits of information as it approaches the holographic boundary.

Let us first define some quantities relevant to our discussion and approach. Consider the system consisting of a source mass M and a boundary. The "boundary" here is a data storing surface such as a holographic screen. Motivated by the Bekenstein bound [35], let us define a quantity $C_D$ as the maximum degrees of freedom associated with the mass M at a distance R from the boundary as1

$$C_D=\frac{2\pi RM}{\hslash }$$

(6)

Another quantity $C_I$ is defined as the maximum degrees of freedom available. This is assumed to follow the holographic principle [36,37] which has strong pieces of evidence from the AdS/CFT correspondence [38] and black hole physics [3,5], such that the information about the volume of space is stored on the boundary. Thus we assume that the total degrees of freedom is given by

$$N=\frac{A}{l_p^2}$$

(7)

where A is the surface area of the boundary and $l_p$ is the Planck length. Therefore

$$C_I=N=\frac{A}{l_p^2}$$

(8)

The “disorder” D in the system which gives the ratio of the maximum degrees of freedom of the mass M to the maximum available degrees of freedom is therefore given by2

$$D=\frac{C_D}{C_I}$$

(9)

Now that we have defined some important quantities needed to present our approach, we turn towards a specific and important property of the boundary that is the temperature T. This can be found by invoking the use of the boundary as a holographic screen which can store data, thus as an object comes near this holographic screen, its total energy($p^0$) is stored on the boundary as evenly bits of information N. Since the distribution is even, we can use our good old equipartition rule of thermodynamics to find the temperature of the boundary as

$$p^0=\frac{1}{2}NT$$

(10)

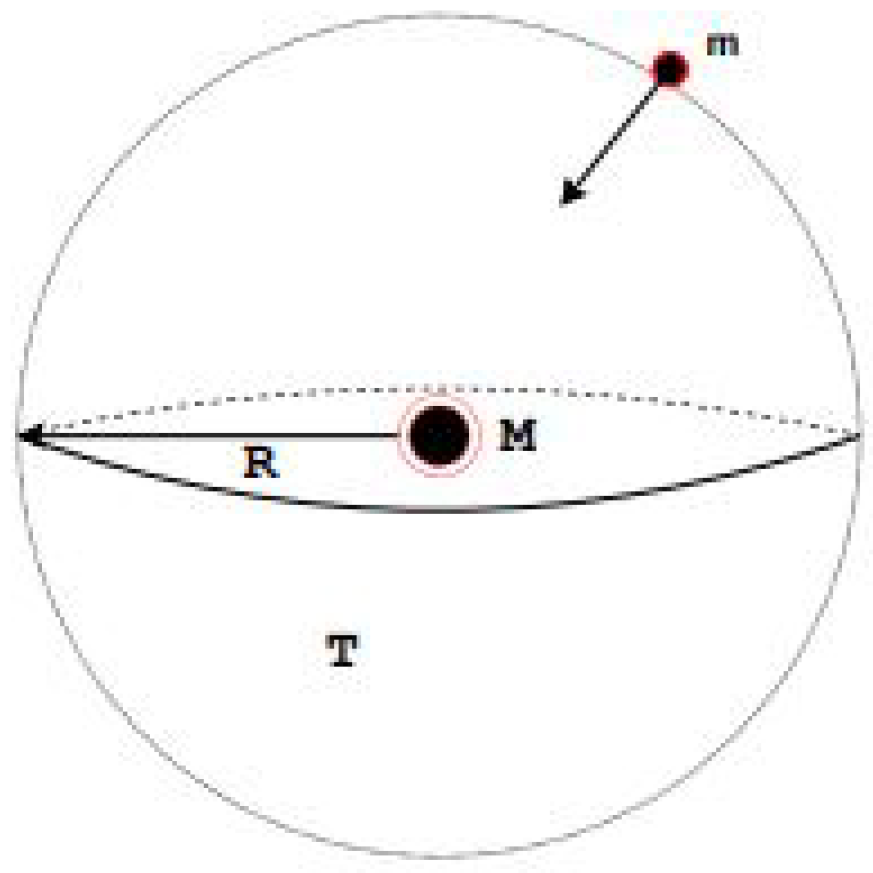
3. Effect on Total Energy

Due to the thermodynamic nature of our system, the total energy changes by the internal energy(U) and the fluctuation energy as we show now. The internal energy is given by

$$U=TS$$

(11)

where T is the temperature of the boundary and S is given by $C_D$. To find the degree of fluctuation in our system we expand the disorder D about its equilibrium position $x_0^{\mu }$

$$D=D_0+\frac{\partial D}{\partial x^{\mu }}{|}_{0}d{x}^{\mu }+\frac{1}{2}\frac{{\partial }^{2}D}{\partial x^{\mu }\partial x^{\nu }}{|}_{0}d{x}^{\mu }d{x}^{\nu }+.....$$

(12)

Note that here $\mu$ varies from 0 to 3 on $4D$ spacetime. Since $x_0^{\mu }$ is the equilibrium point for D, we have

$$\frac{\partial D}{\partial x^{\mu }}{|}_0=0$$

(13)

Thus, in second order we have:

$$\Delta D=D-D_0=\frac{1}{2}\frac{{\partial }^{2}D}{\partial x^{\mu }\partial x^{\nu }}{|}_{0}d{x}^{\mu }d{x}^{\nu }$$

(14)

The hessian $h_{\mu \nu }$ which captures the degree of “fluctuation” in our thermodynamic system is given as

$$h_{\mu \nu }={\partial }_{\mu }{\partial }_{\nu }D$$

(15)

Another important dimensionless quantity(which can be used to define the “length” of fluctuation) is defined as

$${\tilde{h}}_{\mu \nu }=\frac{A}{\pi }{h}_{\mu \nu }$$

(16)

where A is the surface area of the boundary. $d{l}^2$ is the length squared of fluctuation given by

$$d{l}^2=\frac{1}{2}{\tilde{h}}_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$$

(17)

We thus define the fluctuation energy as

$${\left(\frac{dl}{d\tau }\right)}^2=\frac{1}{2}{\tilde{h}}_{\mu \nu }\dot{d{x}^{\mu }}\dot{d{x}^{\nu }}$$

(18)

This thermodynamic expansion of the total energy comes at the expense of extending the $4D$ spacetime to $5D$ spacetime such that the non-zero metric elements are given by

$$g_{00}=1,g_{11}=g_{22}=g_{33}=g_{04}=g_{40}=-1$$

(19)

The fifth element of the “five-momentum” $p^{\mu }$ is defined as

$$p^4=U+\frac{dl}{d\tau }$$

(20)

4. Static Mass and Spherically Symmetric Solution

The total degrees of freedom on the boundary is

$$N=\frac{A}{l_p^2}=\frac{4\pi r^2}{l_p^2}$$

(21)

Thus

$$U=\frac{M{p}^0}{r}$$

(22)

for ${\tilde{h}}_{\mu \nu }$, only 11 component survives. Thus

$${\tilde{h}}_{11}=\frac{4M}{r}$$

(23)

Hence the fluctuation energy in our thermodynamic system is

$${\left(\frac{dl}{d\tau }\right)}^2=\frac{2M}{r}{\dot{r}}^2$$

(24)

Thus

$$\left(\frac{dl}{d\tau }\right)=\sqrt{\frac{2M}{r}}\dot{r}$$

(25)

So we get

$$d{x}^4=\frac{M}{r}dt+\sqrt{\frac{2M}{r}}dr$$

(26)

The spacetime interval is given as

$$d{s}^2=g_{\mu \nu }d{x}^{\mu }d{x}^{\nu }$$

(27)

where $g_{\mu \nu }$ is the fixed $5D$ background spacetime. Hence in the spherical coordinates we get the spacetime interval as

$$d{s}^2=d{t}^2-d{r}^2-r^2(d{\theta }^2+si{n}^2\theta {\varphi }^2)-\frac{2M}{r}d{t}^2-2\sqrt{\frac{2M}{r}}dtdr$$

(28)

Eq.(28) is the Gullstrand-Painleve metric and a coordinate transformation converts it to the well-known Schwarzschild metric given as

$$d{s}^2=\left(1-\frac{2M}{r}\right)d{t}^2-{\left(1-\frac{2M}{r}\right)}^{-1}d{r}^2-r^2(d{\theta }^2+si{n}^2\theta d{\varphi }^2)$$

(29)

5. Quantum Focusing Conjecture

Using the Quantum Focusing Conjecture(QFC) [34], we can show that the second derivative of the radius of a null boundary which respects the null energy condition(NEC) is non-negative. In this section we first review the formulation of QFC.

5.1. Generalised Entropy for Cauchy-splitting surfaces

Generalised entropy was originally defined in [40] in asymptotically flat space as the area A of all black hole horizons, plus the entropy of matter outside the black holes

$$S_{gen}=S_{out}+\frac{A}{4G\hslash }$$

(30)

Figure 2. A Cauchy surface C is divided into two parts by a surface E. $S_{out}$ is defined as entropy restricted to one side of splitting surface E.

Figure 2. A Cauchy surface C is divided into two parts by a surface E. $S_{out}$ is defined as entropy restricted to one side of splitting surface E.

A rigorous definition of $S_{out}$ can be given as the von Neumann entropy of the quantum state of the exterior of the horizon

$$S_{out}=-tr{\rho }_{out}ln{\rho }_{out}$$

(31)

The GSL was introduced to keep the second law of thermodynamics intact when matter entropy is lost in a black hole. Bekenstein conjectured that GSL [40] holds: the area increase of the black hole compensate for the lost matter entropy, so that the generalized entropy does not decrease. The notion of generalised entropy can be extended beyond the context of causal horizons [34]. Let E be a spacelike codimension-2 surface that splits a Cauchy surface C into two portions. By choosing any one of the two sides arbitrarily, we can define an entropy restricted to one side of C as $S_{out}$.

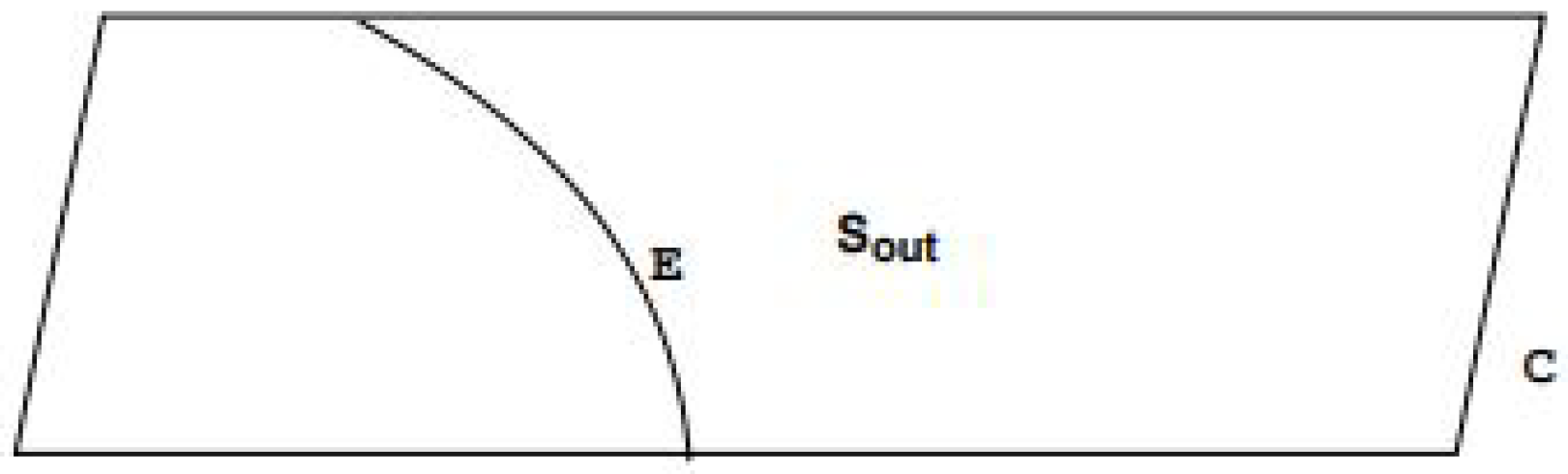
5.2. Quantum Focusing Conjecture

It conjectures [34] that the quantum expansion $\Theta$, where $\Theta$ is given by

$$\Theta =\theta +\frac{4G\hslash }{\mathcal{A}}{S}_{out}^{\prime }$$

(32)

($\theta$ is the classical expansion and $\mathcal{A}$ is the width of null congruence along its generator), cannot increase along any congruence, which is valid for quantum states too

$$\frac{d\Theta }{d\lambda }\le 0$$

(33)

where $\lambda$ is an affine parameter. The evolution of the expansion $\theta$ along congruence is determined by the Raychaudhuri equation:

$$\frac{d\theta }{d\lambda }=-\frac{{\theta }^2}{2}-{\sigma }_{ab}{\sigma }^{ab}-R_{ab}{k}^a{k}^b:$$

(34)

where $R_{ab}$ is the Ricci tensor, ${\sigma }_{ab}$ is the shear and $k^a$ is the (null) tangent vector to the congruence. This gives QFC as

$$0\ge {\Theta }^{\prime }={\theta }^{\prime }+\frac{4G\hslash }{\mathcal{A}}(S_{out}^{\prime \prime }-S_{out}^{\prime }\theta )=-\frac{1}{2}{\theta }^2-{\zeta }^2-8\pi G\langle T_{kk}\rangle +\frac{4G\hslash }{\mathcal{A}}(S_{out}^{\prime \prime }-S_{out}^{\prime }\theta )$$

(35)

$\zeta$ is shear. The special choice of congruence for $\theta =\zeta =0$, gives the Quantum Null Energy Condition (QNEC)

$$\langle T_{kk}\rangle \ge \frac{\hslash }{2\pi \mathcal{A}}{S}_{out}^{\prime \prime }$$

(36)

The entropy $S_{out}$ which refers to the entropy on a spacelike Cauchy surface can also be alternatively seen as the entropy of the state restricted to the part of null surface N [34]. The stress tensor $T_{ab}$ and entanglement entropy $S_{out}$ is related to relative entropy $S\left(\rho \right|\left|{\rho }_o\right)$ on a null surface by

$$\frac{2\pi \mathcal{A}}{\hslash }{T}_{kk}-S_{out}^{\prime \prime }=S^{\prime \prime }(\rho \left|\right|{\rho }_o)$$

(37)

where $T_{kk}=T_{ab}{k}^a{k}^b$, $k^a$ is a null vector, i.e, it satisfies $g_{\mu \nu }{k}^{\mu }{k}^{\nu }=0$. $\rho$ is an arbitrary state and ${\rho }_o$ is the vacuum state.

6. Relative Entropy and Bekenstein Bound

The Bekenstein bound is given as

$$S\le \lambda ER$$

(38)

where $\lambda$ is a constant, R is the size of the system, E is the total energy. Casini [41] showed that the above bound can be written in the form

$$S_V\le K_V$$

(39)

where $S_V$ is a localized entropy and $K_V$ is a localized energy. Using $K=-log{\rho }_V^0-log\left(tr{e}^{-K}\right)$ and $tr{\rho }_V=tr{\rho }_V^0=1$, this can be written as

$$tr\left({\rho }_{V}log{\rho }_V\right)-tr\left({\rho }_{V}log{\rho }_V^0\right)$$

(40)

This is simply the statement of the positivity of the relative entropy $S\left({\rho }_V\right|{\rho }_V^0)$ between the state ${\rho }_V$ and the vacuum state ${\rho }_V^0$ and thus the bound holds. Suppose the size of a system is L and radius of the boundary R, in the limit when the system is far enough from the boundary such as at the centre, $R⪆L$ then Eq.(39) reduces to Eq.(38). We will use this limit in the next section.

7. A constraint on the Expansion of Null Surfaces

Let a null surface N enclose a region of space which respects the null energy condition(NEC) given by

$$T_{kk}\ge 0$$

(41)

Then Eq.(37) holds for this surface. Assuming N to be spherical, let at an initial time its radius be R. On applying NEC, Eq. (37) becomes an inequality and we get,

$$S^{\prime \prime }\left(\rho \right||{\rho }_o)\ge -S_{out}^{\prime \prime }$$

(42)

The relationship between relative entropy and Bekenstein bound is given by

$$S\left(\rho \right||{\rho }_o)=K_v-S_v$$

(43)

where $K_v$ is localized energy and $S_v\equiv S_{out}-S_{out}^{\left(0\right)}$ is a localized entropy. Here $S_{out}^{\left(0\right)}$ is the vacuum entropy. Eq. (42) can be written explicitly in the form

$$\frac{d^{2}S\left(\rho \right||{\rho }_o)}{d{\lambda }^2}\ge -\frac{d^2{S}_{out}}{d{\lambda }^2}$$

(44)

where $\lambda$ is an affine parameter. Thus, we can write

$$\frac{d^2{K}_v}{d{\lambda }^2}-\frac{d^2{S}_{out}}{d{\lambda }^2}+\frac{d^2{S}_{out}^{\left(0\right)}}{d{\lambda }^2}\ge -\frac{d^2{S}_{out}}{d{\lambda }^2}$$

(45)

Since the vacuum entropy $S_{out}^{\left(0\right)}$ is independent of affine parameter $\lambda$ it gives

$$\frac{d^2{S}_{out}^{\left(0\right)}}{d{\lambda }^2}=0$$

(46)

Therefore, we get

$$\frac{d^2{K}_v}{d{\lambda }^2}\ge 0$$

(47)

Now as mentioned in the previous section, we use the limit $K_v\equiv \lambda ER$, where E is the total energy of the system(which is constant) and we finally get

$$\frac{d^{2}R}{d{\lambda }^2}\ge 0$$

(48)

We therefore conclude that the second derivative of the radius of a null boundary(with respect to an affine parameter $\lambda$ along the generator) which respects the NEC cannot decrease. Applying this to a black hole’s event horizon we get an additional constraint than the previously known Hawking area theorem.

8. Conclusion

This approach of describing gravity as information leads to a very important question that whether or not gravity is a fundamental force as popularly seen. We think the way gravity affects time strongly suggests that gravity can not be a force in the usual sense. Of course, we have to make an additional assumption that the degrees of freedom follows the holographic principle and scales as the area rather than the volume of space but this assumption is very robust in itself looking at black hole physics and gauge/gravity duality. The other important result we showed is that, if we assume a null surface which encloses matter that respects the NEC then the second derivative of its radius with respect to an affine parameter $\lambda$ along the generator is non-negative. This can be applied to a black hole’s event horizon.